Electric Vehicle Traction Battery Recycling Decision-Making Considering Blockchain Technology in the Context of Capacitance Level Differential Demand
Abstract
1. Introduction
- (1)
- What is the equilibrium decision for each member of the supply chain when there is a variation in the demand for capacitors in the electric vehicle market?
- (2)
- Given the costs associated with implementing blockchain technology and the benefits of enhanced recovery processes, under what conditions would a manufacturer opt for blockchain technology to achieve the optimal outcome? How do external factors such as recycling incentives, competitive intensity, and recycling cost optimization affect the recycling rate of decommissioned EV traction batteries and maximize benefits for supply chain members?
- (3)
- What is the recycling rate of decommissioned traction batteries across different recycling methods, and how does fluctuating demand for capacitance levels in the electric vehicle market influence this rate?
2. Electric Vehicle and Traction Battery Packs
3. Literature Review
3.1. Relevant Literature Research on Retired Traction Battery Recycling
3.2. Application of Blockchain Technology in Recycling-Related Fields
3.3. Research Gaps
- (1)
- In this paper, we develop a three-party evolutionary game model that examines the interactions among electric vehicle manufacturers, electric vehicle users utilizing ladder technology, and retailers. This model enhances the existing two-party game framework by integrating a traction battery recycling model with capacitance level preferences related to the demand for electric vehicle range in China.
- (2)
- Based on traction battery recycling, due to the lack of reliable regulation leading to unnecessary information exchange costs and security costs, etc., the introduction of blockchain technology to the cost optimization parameters of the traction battery recycling process enriches the existing theory of traction battery recycling and makes practical reference significance for the current stage of traction battery recycling.
- (3)
- The traction battery recycling supply chain is established by integrating key influencing factors, including recycling incentives and competition, while considering the dual consumer markets of the traction battery recycling sector and the secondary utilization market. Ultimately, this approach aims to optimize the recycling rate and maximize revenue.
4. Problem Statement
- (1)
- Similar to Savaskan et al. traction batteries produced by manufacturers from new and recycled materials do not differ in quality and are sold at the same price in the same market [37].
- (2)
- For an EV, the cost of the traction battery accounts for nearly 60 percent of the total cost. Therefore, we approximate the demand for traction batteries as the demand for EVs. BYD Enterprises, for instance, uses traction batteries developed in-house for their EVs. Market demand is a linear function of the retail price of the traction battery. Following the work of Liu et al. Yalabik and Fairchild, and Jiumei Chen, we will use the following demand function: [38].
- (3)
- According to current conditions, the construction of charging piles is sparse in most areas, leading many consumers to demand vehicles with longer ranges. Since the range of new energy vehicles is positively correlated with battery capacity, increasing the capacitance level of traction batteries not only boosts sales but also enhances their utility for echelon utilization. Retired traction batteries, primarily used for storage and downgraded applications, generate additional revenue for companies when they possess higher capacitance levels. In order to improve the battery capacitance level, the battery capacitance R&D cost of the battery manufacturer is related to the battery capacitance level as , where k is the R&D cost coefficient, and this kind of relational function has been widely used, such as by Bian et al. and Wang et al [39,40].
- (4)
- As consumers in both markets are highly variable, we assume that the demand for EVs is linear, there is no interaction between the demand for traction batteries in the EV market and the echelon utilization market, and the market demand for trapezoidal batteries is also a linear function.
- (5)
- In order for the function to be economically meaningful, , introducing the coefficients of the echelon utilization recycling incentive variable and the retailer recycling incentive coefficients , can obtain , , and .
- (6)
- According to Wu and Zhou we can set the relationship between the decommissioned battery recycling rate and the cost of recycling investment to be a quadratic function relationship recycling investment, such as and , and the recycling rate can be described as . If the retailer and the BCU enterprise are collected at the same time, then this can be described as an increasing function of the recycler’s recycling and a decreasing function of the other recycler’s recycling, as in the case of the functions and , . The recovery cost in this case is described as and [41].
- (7)
- To ensure that the function is meaningful, we require that 1-f2 > 0; this aligns with the prevailing competitive conditions in the market.
- (8)
- We assume that the traction battery market has witnessed multiple rounds of traction battery trading and traction battery recycling fixed traction battery market sales and recycling.
- (9)
- A description of symbols is provided in Table 1.
5. Mathematical Modeling
5.1. Retailer Recycling Model
5.2. Circular Supply Chain Model with Dual Recycling by BCU Enterprises and EV Retailers
5.3. EV Retailer Recycling Model Using Blockchain
5.4. Dual Recycling Supply Chain Model for Traction Battery Recycling by BCU Enterprises and EV Retailers Adopting Blockchain
5.5. Analysis of Equilibrium Results
5.6. Comparative Analysis of Recycling Programs
6. Data Simulation
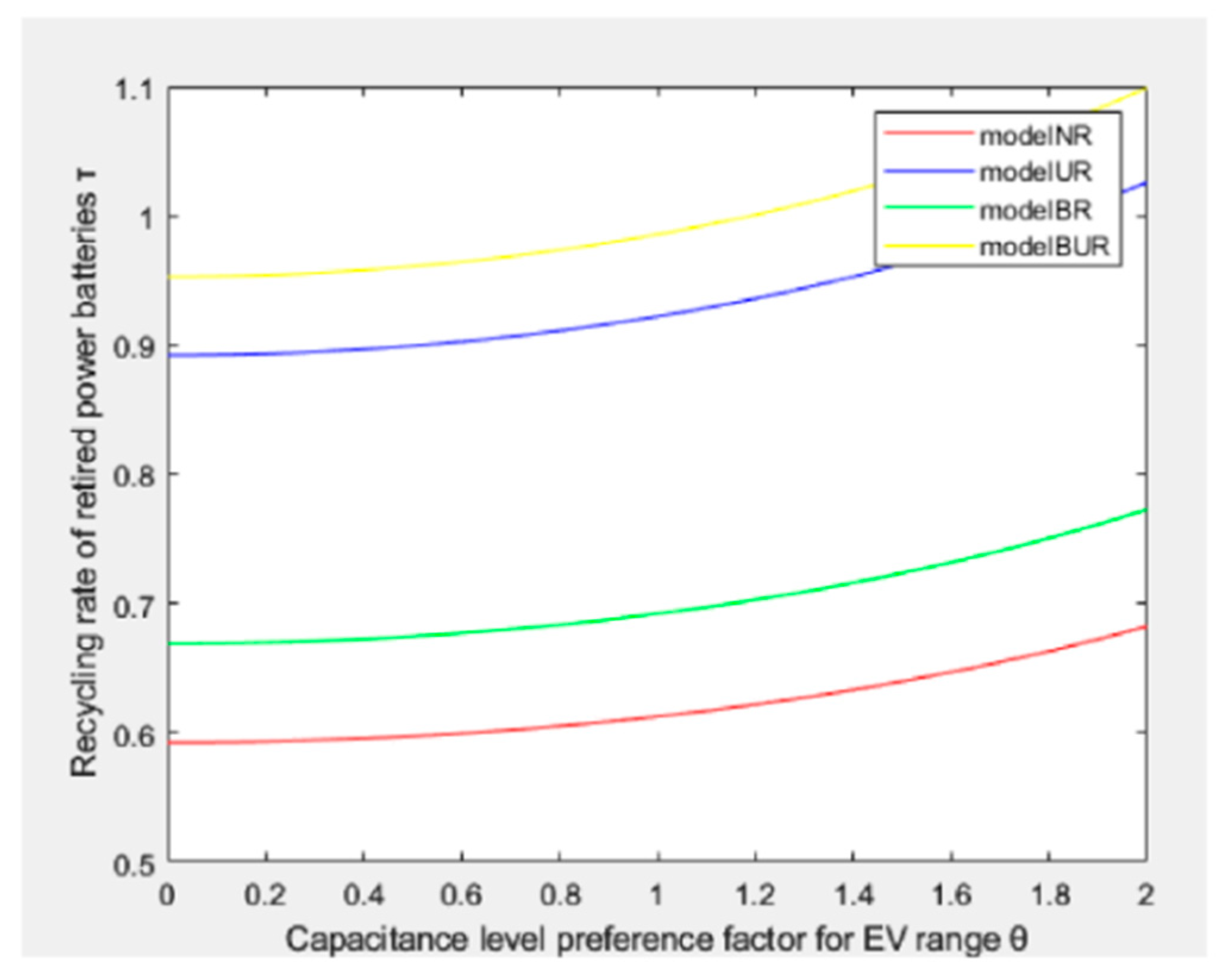
6.1. Analyze the Effect of Capacitance Level Preference Coefficient θ on Recovery Rates for EV Range
6.2. Analyze the Impact of the Recovery Cost Optimization Factor ȵ on Recovery Rates
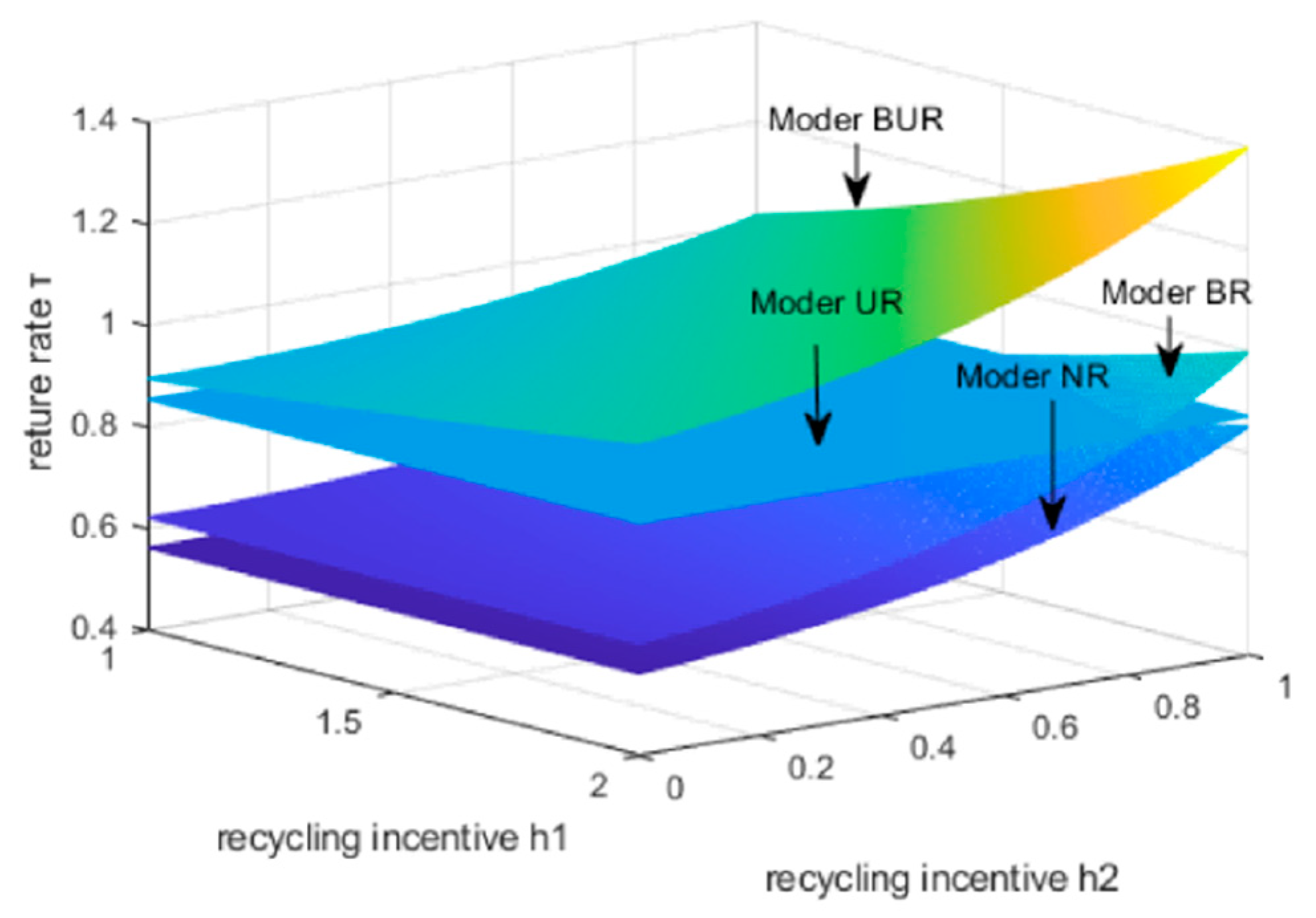
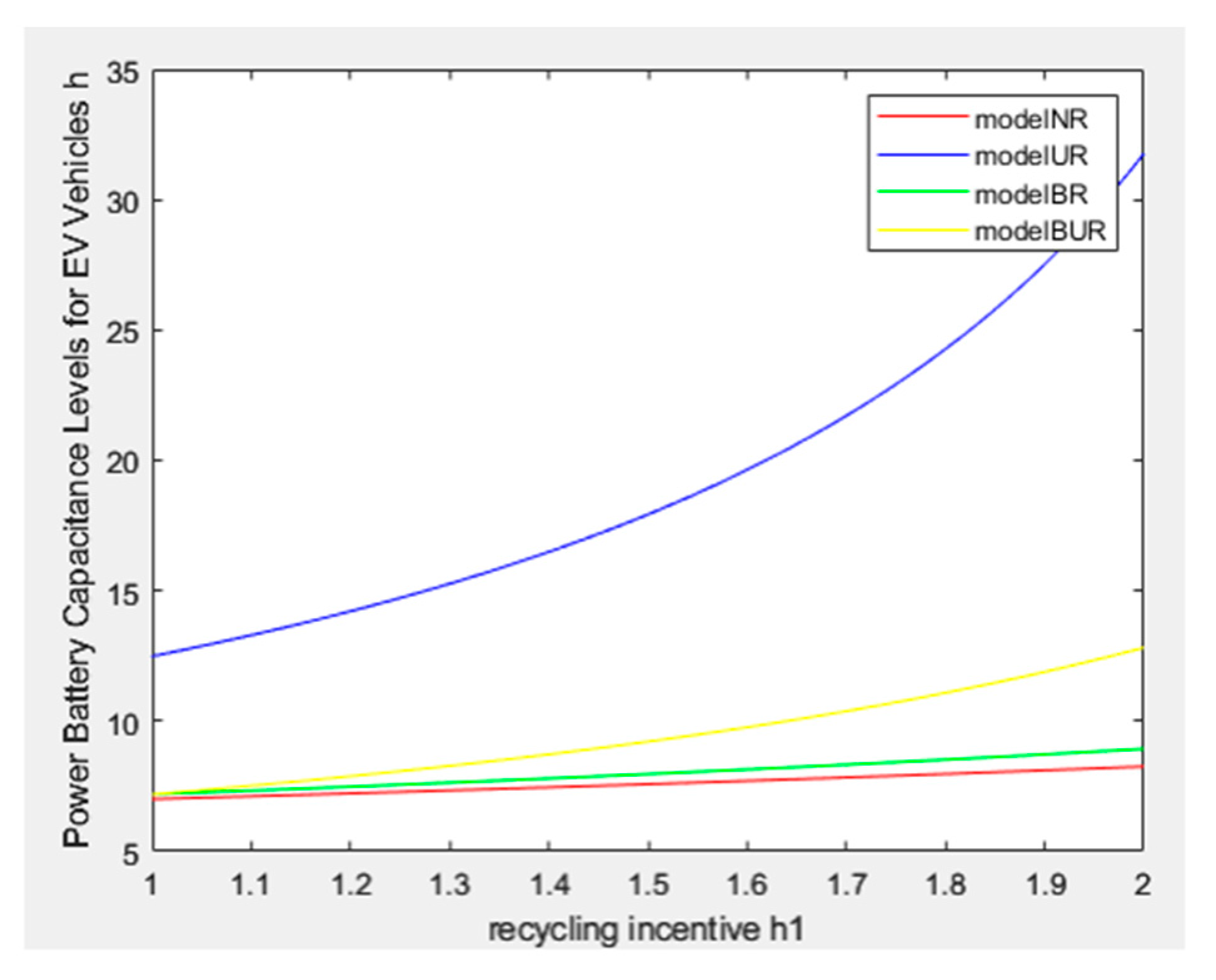
6.3. Analyze the Impact of the BCU Enterprise Incentive Factor h1 and the Retailer Recycling Incentive Factor h2 on Recycling Rates
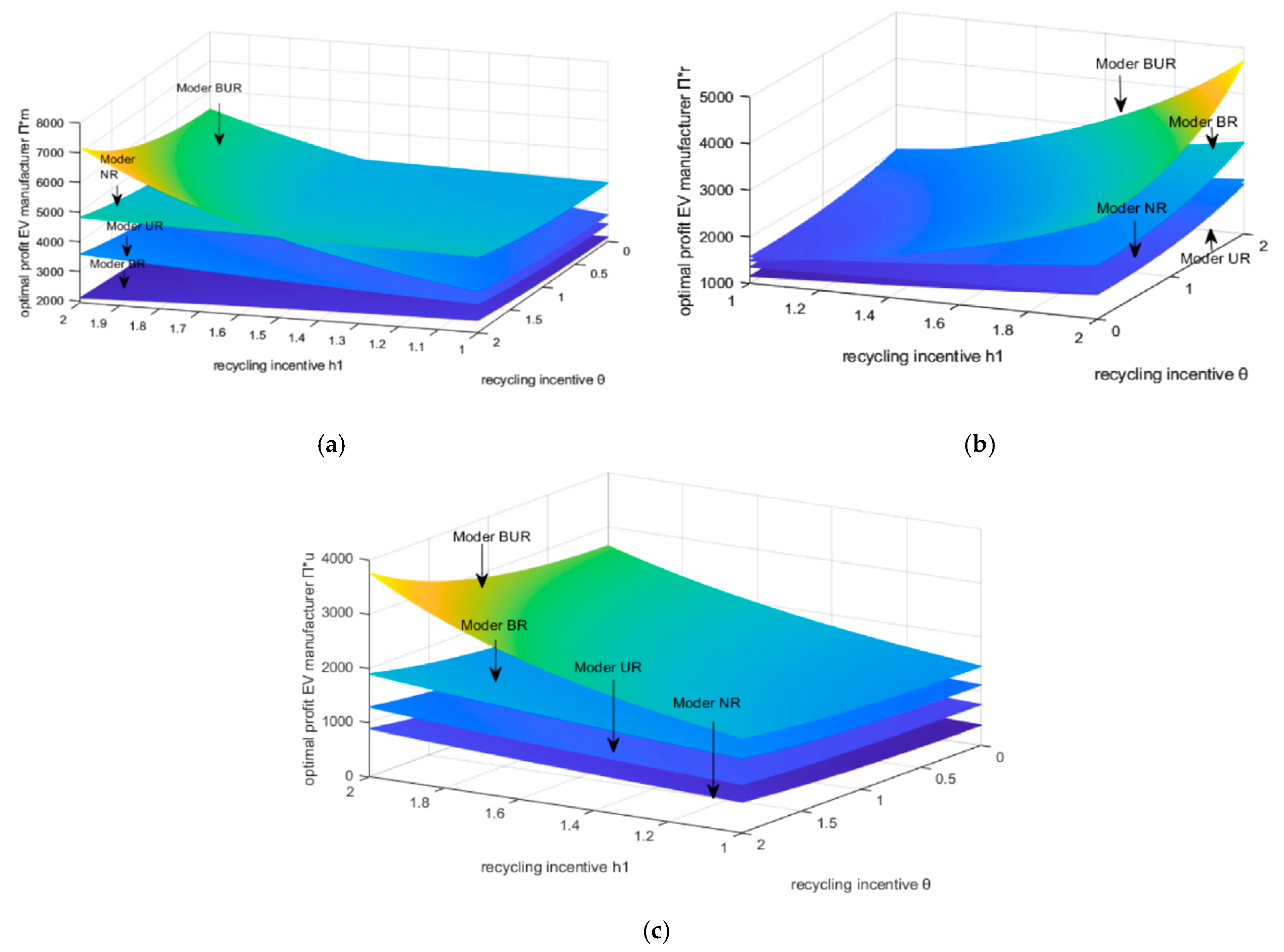
6.4. Analyze the Effects of the Capacitance Level Preference Coefficient θ and the BCU Enterprise Incentive Coefficient h1 on the Maximum Return
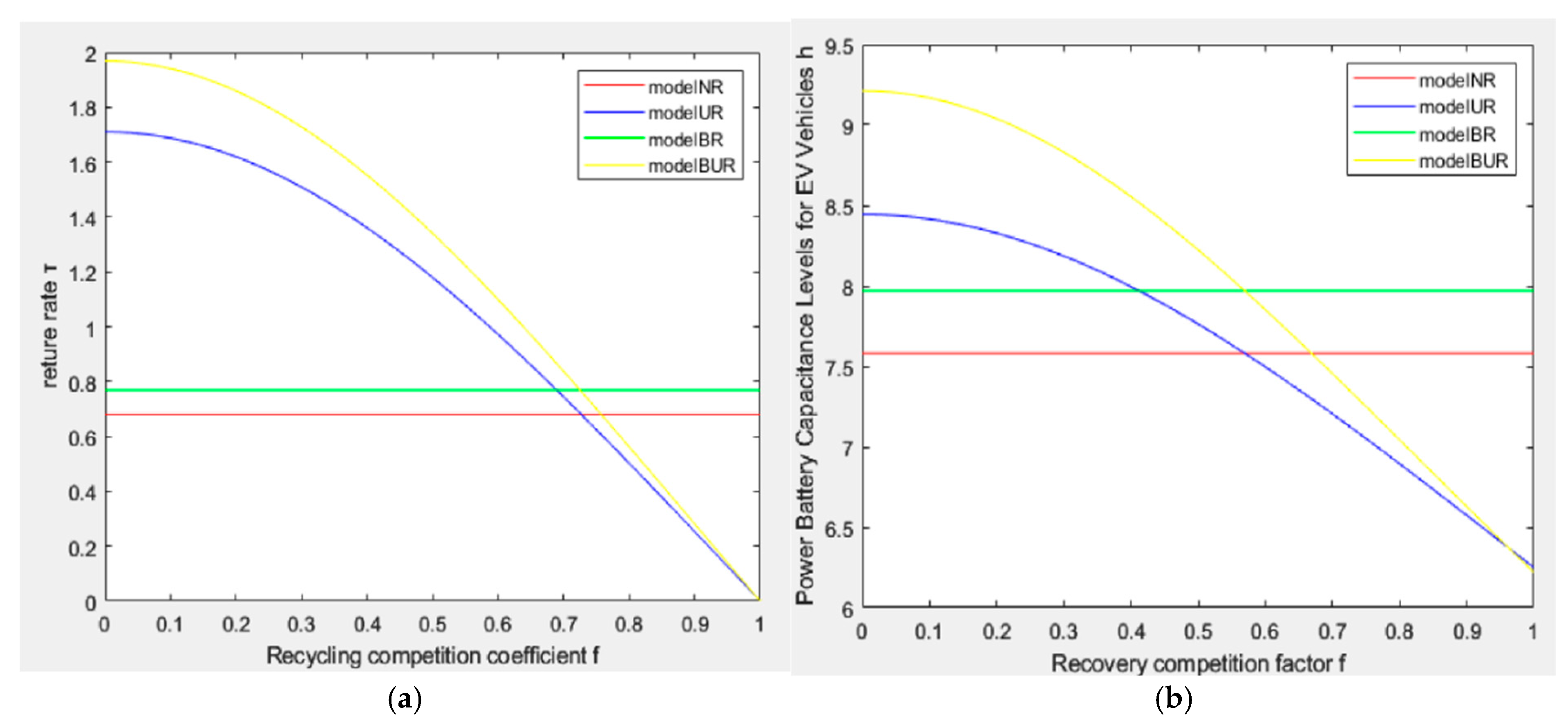
6.5. Analyze the Impact of Recovery Competition on Capacitance Levels and Recovery Rates
7. Summary
- (1)
- The capacitance level preference coefficient of electric vehicle (EV) range positively correlates with the recycling rate of decommissioned traction batteries. Increased demand for higher battery ranges in the EV market facilitates the recycling of these batteries. Higher-capacity batteries enable longer-range EVs, which typically incur higher costs for consumers. Consequently, consumers are incentivized to actively engage in the recycling of retired traction batteries to mitigate some of their EV purchase expenses. Manufacturers can modify the capacitance levels of batteries in response to market preferences and actively encourage consumer participation in the recycling of traction batteries.
- (2)
- In situations characterized by low competitive intensity, two-pass recycling is generally more advantageous than single-pass recycling. Consequently, manufacturers should typically consider implementing a two-channel recycling program.
- (3)
- The optimization of recycling costs through blockchain technology will be a significant factor for manufacturers considering its adoption in traction battery recycling. EV battery manufacturers are likely to embrace blockchain technology only when it substantially enhances recycling cost efficiency. Furthermore, in response to market demand for higher capacity levels to extend EV range, manufacturers may contemplate reducing recycling incentive costs for BCU enterprises. The resulting savings can be reinvested into research and development aimed at improving battery capacity levels, increasing the capacity of traction batteries, and implementing blockchain technology to enhance the recycling supply chain for traction batteries.
- (4)
- Recycling competition negatively impacts the recovery and capacitance levels of traction batteries. Excessive competition in recycling can significantly decrease both the recycling rates and capacitance levels of end-of-life traction batteries. Manufacturers should consider adopting blockchain technology to address these competitive challenges. Numerical analyses indicate that integrating blockchain technology into the recycling supply chain enhances its ability to withstand the pressures of intense recycling competition.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | Introduces |
| BCU | Enterprise comprehensive utilization |
| EOL | End-of-life |
| EV | Electric Vehicles |
| NR | EV retailer recycling model |
| UR | Circular supply chain model with dual recycling by BCU enterprises and EV retailers |
| BR | EV retailer recycling model using blockchain |
| BUR | Dual Recycling Supply Chain Model for traction battery recycling by BCU enterprises and EV retailers adopting blockchain |
Appendix A
References
- Tao, F.; Kishita, Y.; Scheller, C.; Blomeke, S.; Umeda, Y. Designing a sustainable circulation system of second-life traction batteries: A scenario-based simulation approach. Procedia CIRP 2022, 105, 733–738. [Google Scholar] [CrossRef]
- Zhong, X.H.; Chen, L.L.; Han, J.; Liu, W.; Jiao, F.; Qin, W. Current status and recycling of waste lithium-ion battery resources. J. Eng. Sci. 2021, 43, 161–169. [Google Scholar] [CrossRef]
- Dasaklis, T.K.; Voutsinas, T.G.; Tsoulfas, G.T.; Casino, F. A systematic literature review of blockchain-enabled supply chain traceability implementations. Sustainability 2022, 14, 2439. [Google Scholar] [CrossRef]
- VikramGoud, M.; Biswas, P.K.; Sain, C.; Babu, T.S.; Balachandran, P.K. Advancement of electric vehicle technologies, classification of charging methodologies, and optimization strategies for sustainable development A comprehensive review. Heliyon 2024, 10, e39299. [Google Scholar] [CrossRef]
- Amir, M.; Deshmukh, R.G.; Khalid, H.M.; Said, Z.; Raza, A.; Muyeen, S.M.; Nizami, A.S.; Elavarasan, R.M.; Saidur, R.; Sopian, K. Energy storage technologies: An integrated survey of developments, global economical/environmental effects, optimal scheduling model, and sustainable adaption policies. J. Energy Storage 2023, 72, 108694. [Google Scholar] [CrossRef]
- Kourkoumpas, D.-S.; Benekos, G.; Nikolopoulos, N.; Karellas, S.; Grammelis, P.; Kakaras, E. A review of key environmental and energy performance indicators for the case of renewable energy systems when integrated with storage solutions. Appl. Energy 2018, 231, 380–398. [Google Scholar] [CrossRef]
- Jing, L.; Gang, D.; Yin, J. Current situation and economic analysis of decommissioned battery recycling industry. CIESC J. 2020, 71, 494–500. [Google Scholar] [CrossRef]
- Zanoletti, A.; Carena, E.; Ferrara, C.; Bontempi, E. A Review of Lithium-Ion Battery Recycling: Technologies, Sustainability, and Open Issues. Batteries 2024, 10, 38. [Google Scholar] [CrossRef]
- Chen, J.M.; Zhang, W.; Gong, B.G. Optimal policy for the recycling of electric vehicle retired traction batteries. Technol. Forecast. Soc. Change 2022, 183, 121930. [Google Scholar] [CrossRef]
- Kuntz, P.; Lonardoni, L.; Genies, S. Evolution of Safety Behavior of High-Power and High-Energy Commercial Li-Ion Cells after Electric Vehicle Aging. Batteries 2023, 9, 427. [Google Scholar] [CrossRef]
- Meegoda, J.; Charbel, G.; Watts, D. Sustainable Management of Rechargeable Batteries Used in Electric Vehicles. Batteries 2024, 10, 167. [Google Scholar] [CrossRef]
- Díaz-Ramírez, M.C.; Ferreira, V.J.; García-Armingol, T.; López-Sabirón, A.M.; Ferreira, G. Battery Manufacturing Resource Assessment to Minimise Component Production Environmental Impacts. Sustainability 2020, 12, 6840. [Google Scholar] [CrossRef]
- Zhang, C.; Tian, Y.; Li, C. Decision-making of electric vehicle traction battery manufacturers for laddering utilisation under carbon cap-and-trade policy. Control Decis. Mak. J. Int. Soc. Electr. Veh. Manuf. 2022, 39. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Zhang, Q. Recycling mechanisms and policy suggestions for spent electric vehicles’ traction battery—A case of Beijing. J. Clean. Prod. 2018, 186, 388–406. [Google Scholar] [CrossRef]
- Amuta, O.; Kowal, J. State of Health Assessment of Spent Lithium–Ion Batteries Based on Voltage Integral during the Constant Current Charge. Batteries 2023, 9, 537. [Google Scholar] [CrossRef]
- Xie, J.; Li, J.; Yang, F. Multi-level contract decision optimisation for closed-loop supply chain of new energy vehicles. J. Manag. Eng. 2020, 34, 180–193. [Google Scholar] [CrossRef]
- Huang, M.; Song, M.; Lee, L.H.; Ching, W.K. Analysis for strategy of closed loop supply chain with dual recycling channel. Int. J. Prod. Econ. 2013, 144, 510–520. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Yang, W.X. Optimal design of electric vehicle battery recycling network—From the perspective of electric vehicle manufacturers.applied energy. Appl. Energy 2020, 275, 15328. [Google Scholar] [CrossRef]
- Shao, L.; Li, P.; Zhang, Z.; Luo, A. Blockchain technology-driven closed-loop traction battery supply chain information sharing mechanism and contract coordination. Sci. Technol. Manag. Res. 2024. [Google Scholar] [CrossRef]
- Júnior, C.A.; Sanseverino, E.R.; Gallo, P.; Koch, D.; Schweiger, H.G.; Zanin, H. Blockchain review for battery supply chain monitoring and battery trading. Renew. Sustain. Energy Rev. 2022, 157, 112078. [Google Scholar] [CrossRef]
- Habib, A.K.M.A.; Hasan, M.K.; Issa, G.F.; Singh, D.; Islam, S.; Ghazal, T.M. Lithium-Ion Battery Management System for Electric Vehicles: Constraints, Challenges, and Recommendations. Batteries 2023, 9, 152. [Google Scholar] [CrossRef]
- Kosuru, V.S.R.; Venkitaraman, A.K. A Smart Battery Management System for Electric Vehicles Using Deep Learning-Based Sensor Fault Detection. World Electr. Veh. J. 2023, 14, 101. [Google Scholar] [CrossRef]
- Zhao, S.X.; Wang, Y.C. Research on emergency distribution optimization ofmobile traction for electric vehicle in photovoltaic-energy storage-charging supply chain under the energy blockchain. Energy Rep. 2022, 8, 6815–6825. [Google Scholar] [CrossRef]
- You, J.X.; Ren, J. Investment evolution game of electric vehicle traction battery blockchain technology [J/OL]. J. Tongji Univ. 2023, 5105. [Google Scholar] [CrossRef]
- Yu, L.; Bai, Y.; Belharouak, I. Recycling of Lithium-Ion Batteries via Electrochemical Recovery: A Mini-Review. Batteries 2024, 10, 337. [Google Scholar] [CrossRef]
- Schlögl, G.; Grollitsch, S.; Ellersdorfer, C. Sustainable Battery Lifecycle: Non-Destructive Separation of Batteries and Potential Second Life Applications. Batteries 2024, 10, 280. [Google Scholar] [CrossRef]
- Paulauskas, N.; Kapustin, V. Battery Scheduling Optimization and Potential Revenue for Residential Storage Price Arbitrage. Batteries 2024, 10, 251. [Google Scholar] [CrossRef]
- Almutairi, Z.A.; Eltamaly, A.M. Synergistic Effects of Energy Storage Systems and Demand-Side Management in Optimizing Zero-Carbon Smart Grid Systems. Energies 2024, 17, 5637. [Google Scholar] [CrossRef]
- Silva, E.R.; Lohmer, J.; Rohla, M.; Angelis, J. Unleashing the circular economy in the electric vehicle battery supply chain: A case study on data sharing and blockchain potential. Resour. Conserv. Recycl. 2023, 193, 106969. [Google Scholar] [CrossRef]
- Centobelli, P.; Cerchione, R.; Del Vecchio, P.; Oropallo, E.; Secundo, G. Blockchain technology for bridging trust, traceability and transparency in circular supply chain. Inf. Manag. 2022, 59, 103508. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, X.; Jiang, Z.; Gong, Q.; Wang, Y. A blockchain-enabled framework for reverse supply chain management of traction batteries. J. Clean. Prod. 2023, 415, 137823. [Google Scholar] [CrossRef]
- Feng, H.; Wang, X.; Duan, Y.; Zhang, J.; Zhang, X. Applying blockchain technology to improve agri-food traceability: A review of development methods, benefits and challenges. J. Clean. Prod. 2020, 260, 121031. [Google Scholar] [CrossRef]
- Xing, P.; Yao, J. Power Battery Echelon Utilization and Recycling Strategy for NewEnergy Vehicles Based on Blockchain Technolog. Sustainability 2022, 14, 11835. [Google Scholar] [CrossRef]
- Zhang, M.; Li, X.; Ma, L. Research on traction battery secondary utilisation based on blockchain technology. Sci. Technol. Manag. Res. 2020, 40, 225–231. [Google Scholar] [CrossRef]
- Berger, K.; Rusch, M.; Schöggl, J.P.; Baumgartner, R.J. Sustainable and circular battery management—Conceptualization of an information model. In Proceedings of the 20th European Round Table on Sustainable Consumption and Production, Graz, Austria, 8–10 September 2021. [Google Scholar]
- Olivetti, E.A.; Ceder, G.; Gaustad, G.G.; Fu, X. Lithium-ion battery supply chain considerations: Analysis of potential bottlenecks in critical metals. Joule 2017, 1, 229–243. [Google Scholar] [CrossRef]
- Savaskan, R.C.; Bhattacharya, S.; Van Wassenhove, L.N. Closed-loop supplychain models with product remanufacturing. Manag. Sci. 2004, 50, 239252. [Google Scholar] [CrossRef]
- Yalabik, B.; Fairchild, R.J. Customer regulatory, and competitive pressure as drivers of environmental innovation. Int. J. Prod. Econ. 2011, 131, 519–527. [Google Scholar] [CrossRef]
- Bian, J.; Zhao, X. Tax or subsidy? An analysis of environmental policies in supply chains with retail competition. Eur. J. Oper. Res. 2020, 283, 901–914. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, D.; He, L. Contracting emission reduction for supply chains considering market low-carbon preference. J. Clean. Prod. 2016, 120, 72–84. [Google Scholar] [CrossRef]
- Wu, X.L.; Zhou, Y. The optimal reverse channel choice under supply chain competition. Eur. J. Oper. Res. 2017, 259, 63–66. [Google Scholar] [CrossRef]
- Wang, Z.R.; Wu, Q.H. Carbon emission reduction and product collection decisions in the closed-loop supply chain with cap-and-trade regulation. Int. J. Prod. Res. 2021, 59, 4359–4383. [Google Scholar] [CrossRef]
- Höhne, K.; Hirtz, E. With System Integration and Lightweight Design to Highest Energy Densities. Adv. Microsyst. Automot. Appl. 2013, 1, 205–214. [Google Scholar] [CrossRef]

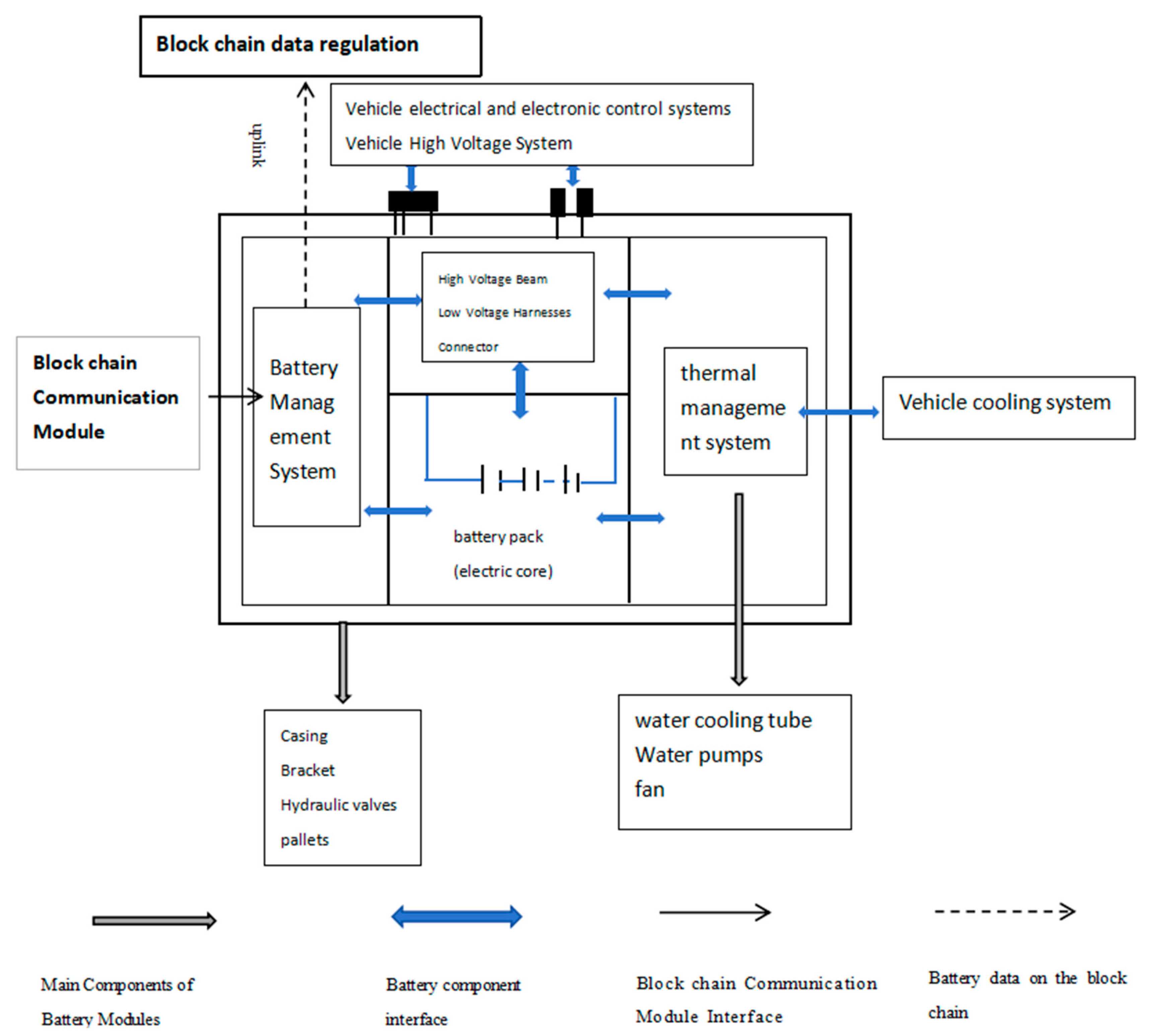

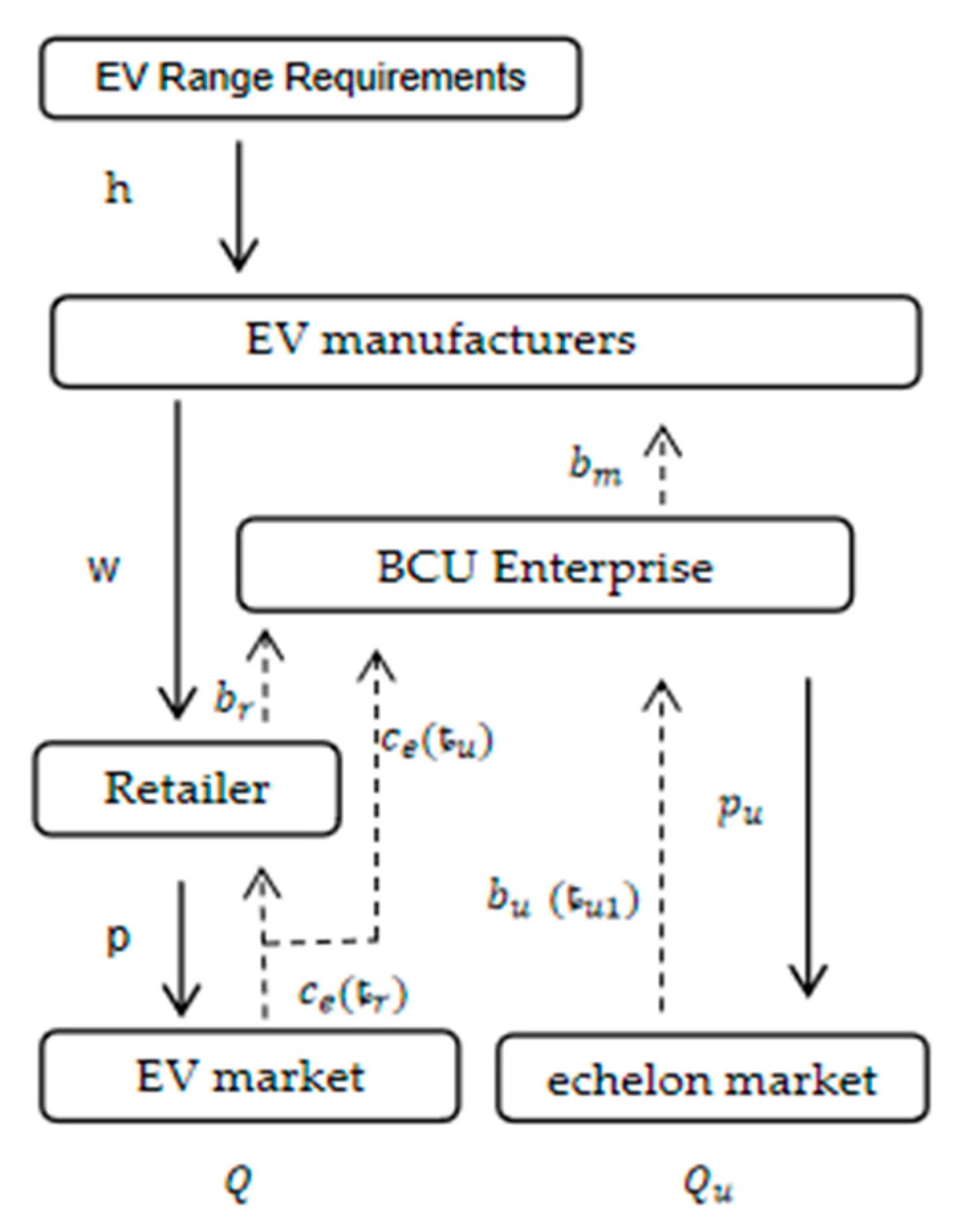
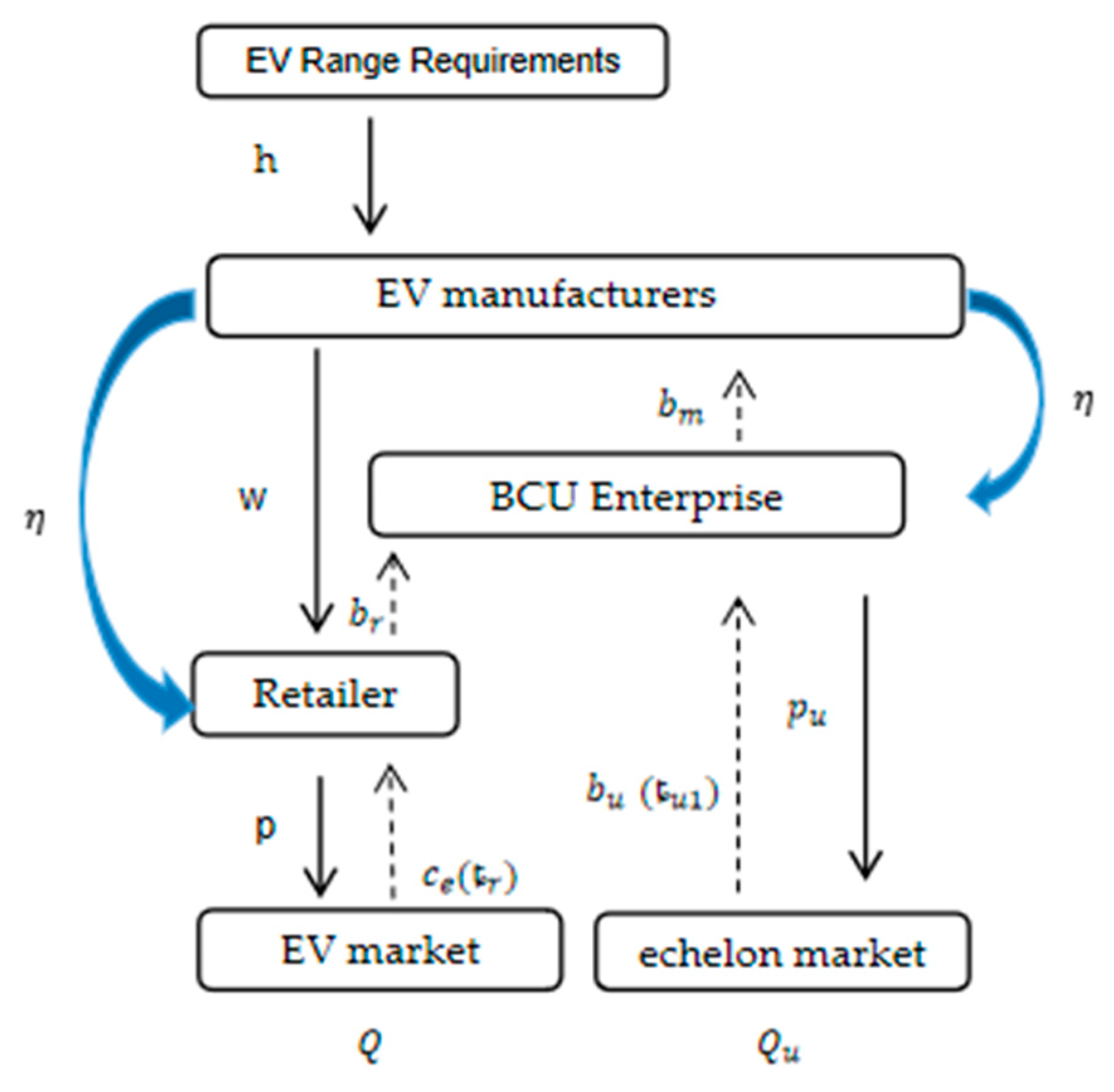

| Symbol | Symbol Definition |
|---|---|
| Decision variables | |
| Wholesale EV prices sold by EV manufacturers to EV retailers | |
| Sale price sold by EV retailers to the EV marketplace | |
| Traction battery capacitance levels for EV vehicles | |
| Recycling rates for traction cells recovered from the EV market by EV retailers | |
| Recycling rate of retired traction batteries (RPBs) recovered by BCU companies from the EV market | |
| Recycling rate of non-usable decommissioned traction batteries recovered by BUC enterprises from the market of laddered batteries | |
| Sale prices of BUC firms selling to the step-down market for step-down batteries | |
| Relevant parameters | |
| EV potential demand in the EV market | |
| Potential demand for reclassified batteries in the reclassified market | |
| Sale price elasticity coefficient of EV | |
| Capacitance level preference factor for EV range | |
| Coefficient of elasticity of sale price of gradient batteries | |
| Cost coefficients for the decommissioned traction battery recycling market and the gradient battery recycling market, respectively | |
| Recovery incentive coefficients for EV manufacturers to BUC firms and for BUC firms to EV sellers, respectively | |
| EV manufacturers’ transfer prices to BUC companies for retired traction cells | |
| Transfer prices for retired traction batteries from BUC companies to EV retailers | |
| Recycling prices for retired traction batteries | |
| Recycling prices for non-reusable echelon utilization batteries | |
| R&D costs for traction cell capacitors to improve EV range | |
| Unit cost of processing blockchain technology for traction batteries | |
| Manufacturing costs for traction battery manufacturing with new recycled materials | |
| Remanufacturing costs of traction batteries made from recycled materials | |
| Manufacturing costs of echelon utilization batteries | |
| Additional benefits of high-capacity decommissioned traction batteries for echelon utilization | |
| Optimization factor for recycling costs of decommissioned traction batteries | |
| Competition factor for recycling of decommissioned traction batteries | |
| formulas | |
| Number of EVs sold | |
| Number of echelon utilization batteries sold | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, L.; Wang, Y. Electric Vehicle Traction Battery Recycling Decision-Making Considering Blockchain Technology in the Context of Capacitance Level Differential Demand. World Electr. Veh. J. 2024, 15, 561. https://doi.org/10.3390/wevj15120561
Yang L, Wang Y. Electric Vehicle Traction Battery Recycling Decision-Making Considering Blockchain Technology in the Context of Capacitance Level Differential Demand. World Electric Vehicle Journal. 2024; 15(12):561. https://doi.org/10.3390/wevj15120561
Chicago/Turabian StyleYang, Lijun, and Yi Wang. 2024. "Electric Vehicle Traction Battery Recycling Decision-Making Considering Blockchain Technology in the Context of Capacitance Level Differential Demand" World Electric Vehicle Journal 15, no. 12: 561. https://doi.org/10.3390/wevj15120561
APA StyleYang, L., & Wang, Y. (2024). Electric Vehicle Traction Battery Recycling Decision-Making Considering Blockchain Technology in the Context of Capacitance Level Differential Demand. World Electric Vehicle Journal, 15(12), 561. https://doi.org/10.3390/wevj15120561





