Research on the SSIDM Modeling Mechanism for Equivalent Driver’s Behavior
Abstract
:1. Introduction
2. Behavior Switching Scenario Mining
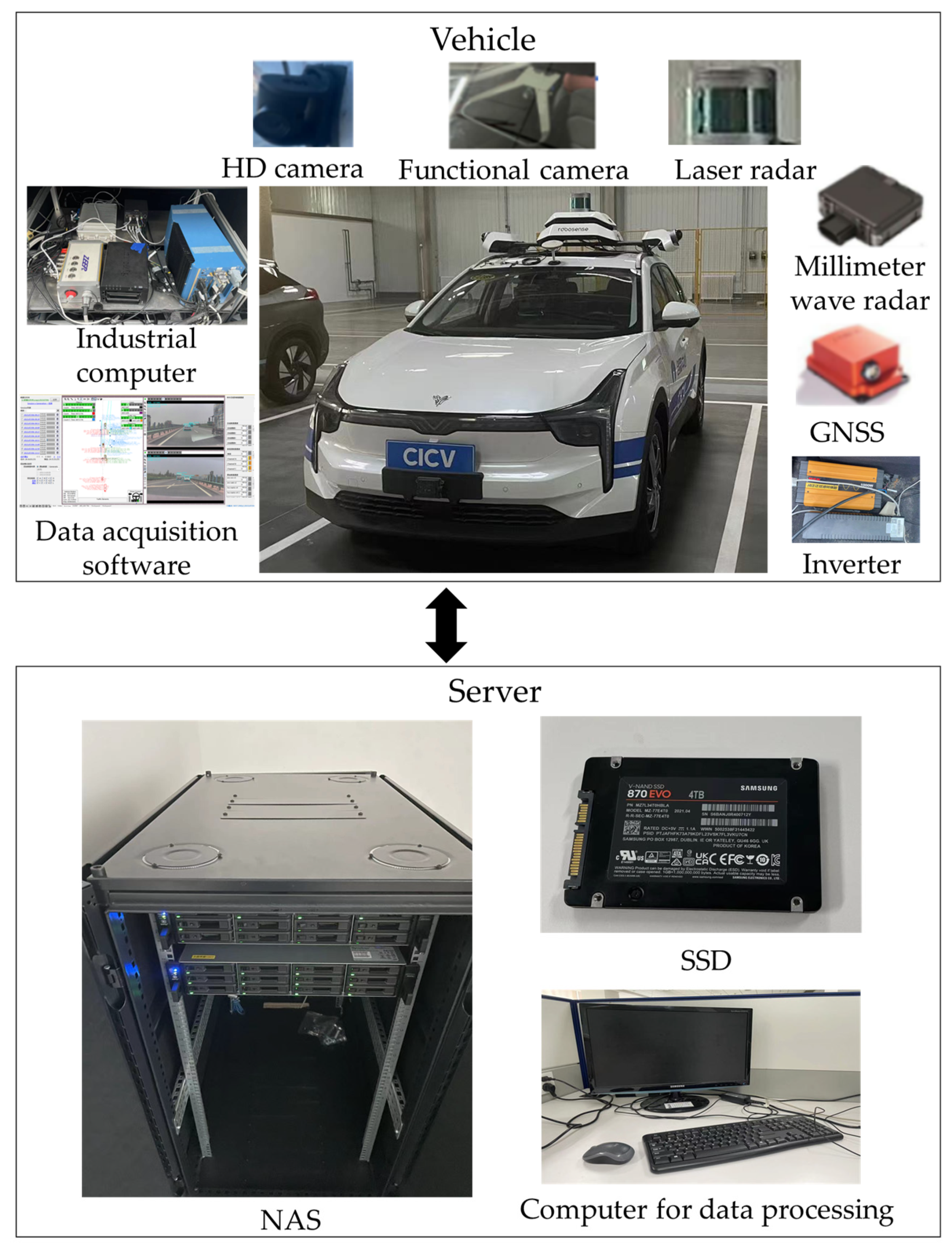
2.1. Natural Driving Data Collection
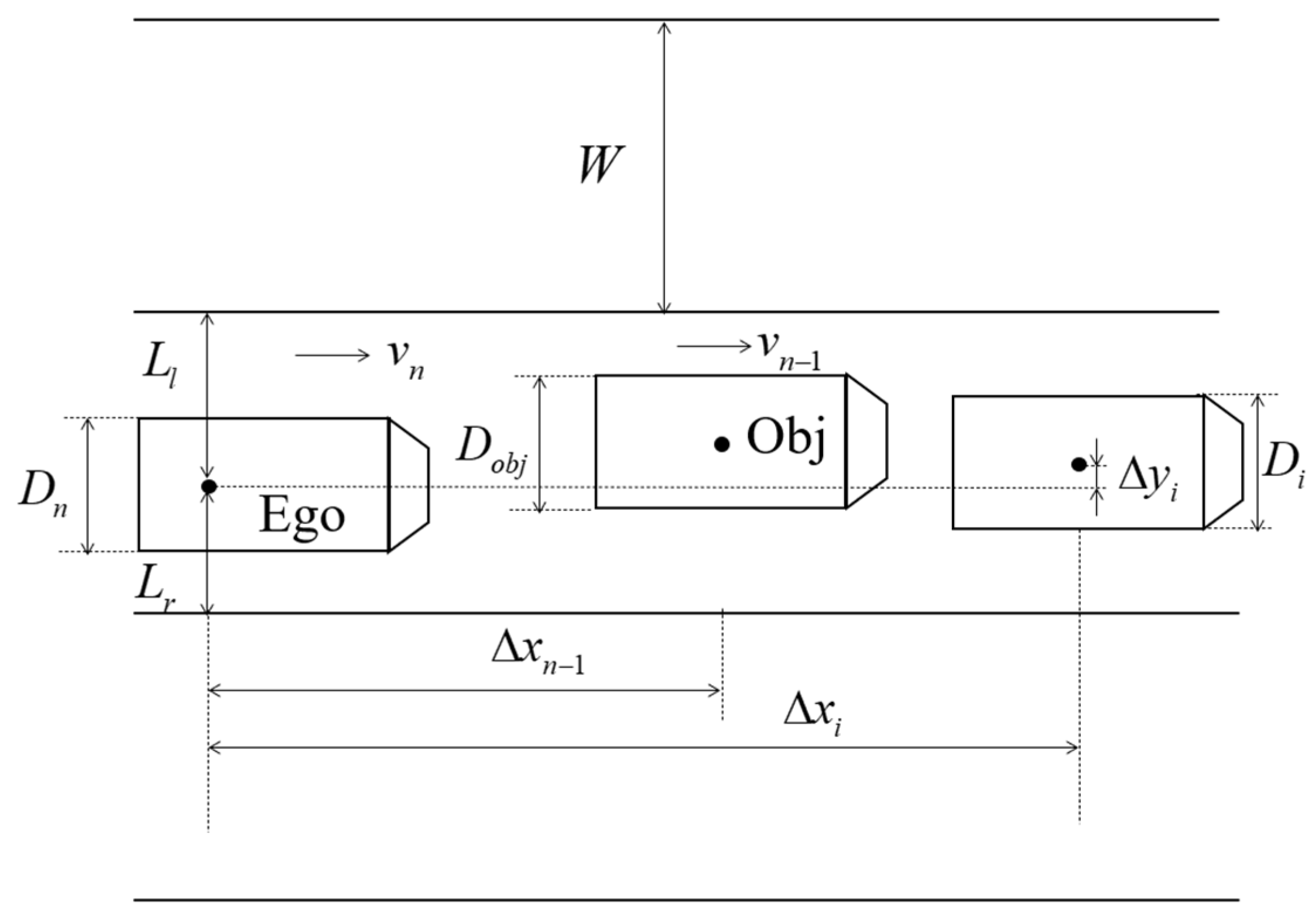
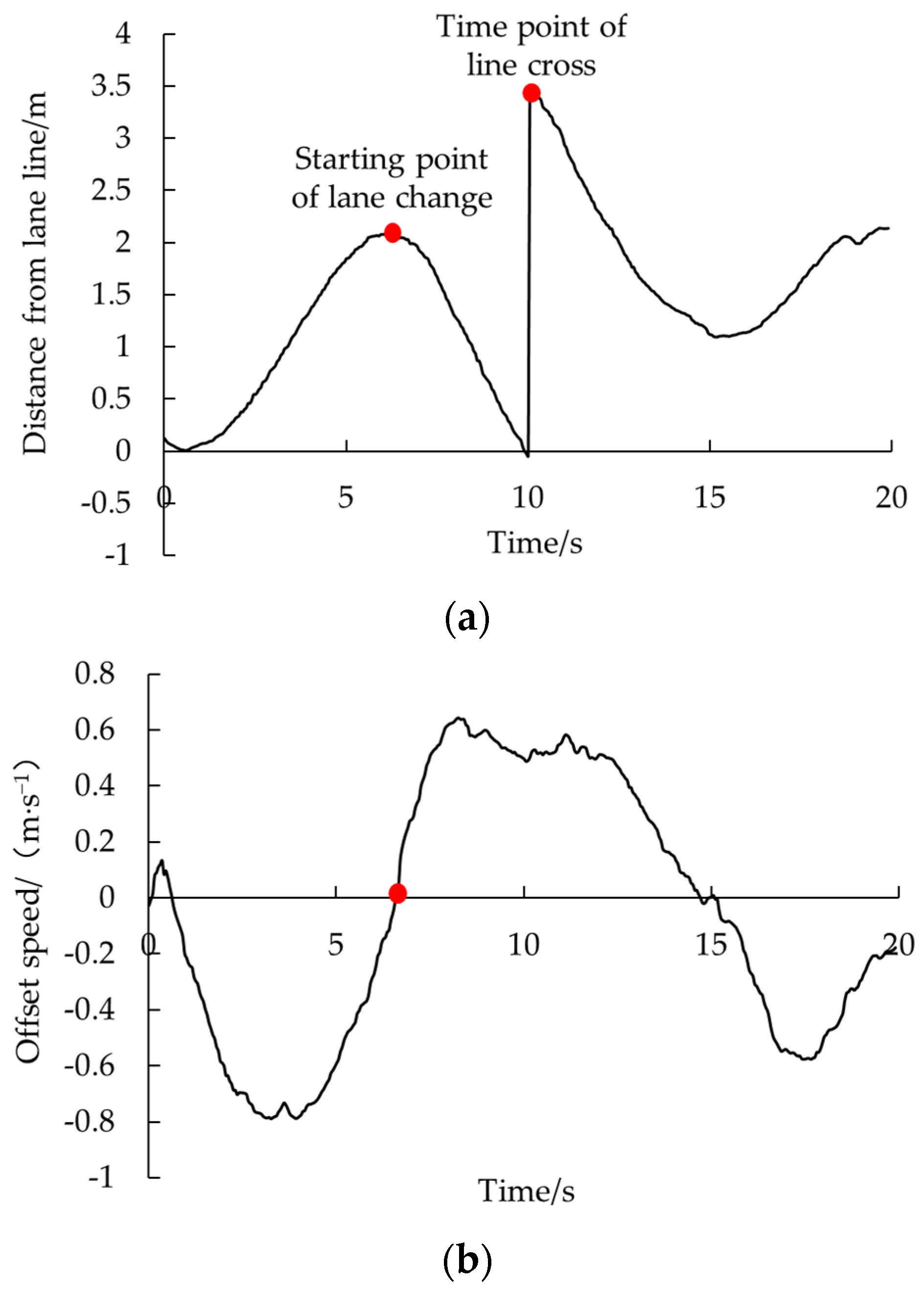
2.2. Behavior Scenario Mining
3. IDM Parameter Identification
3.1. IDM Modeling Mechanism
3.2. Model Parameter Identification
4. Construction of SSIDM
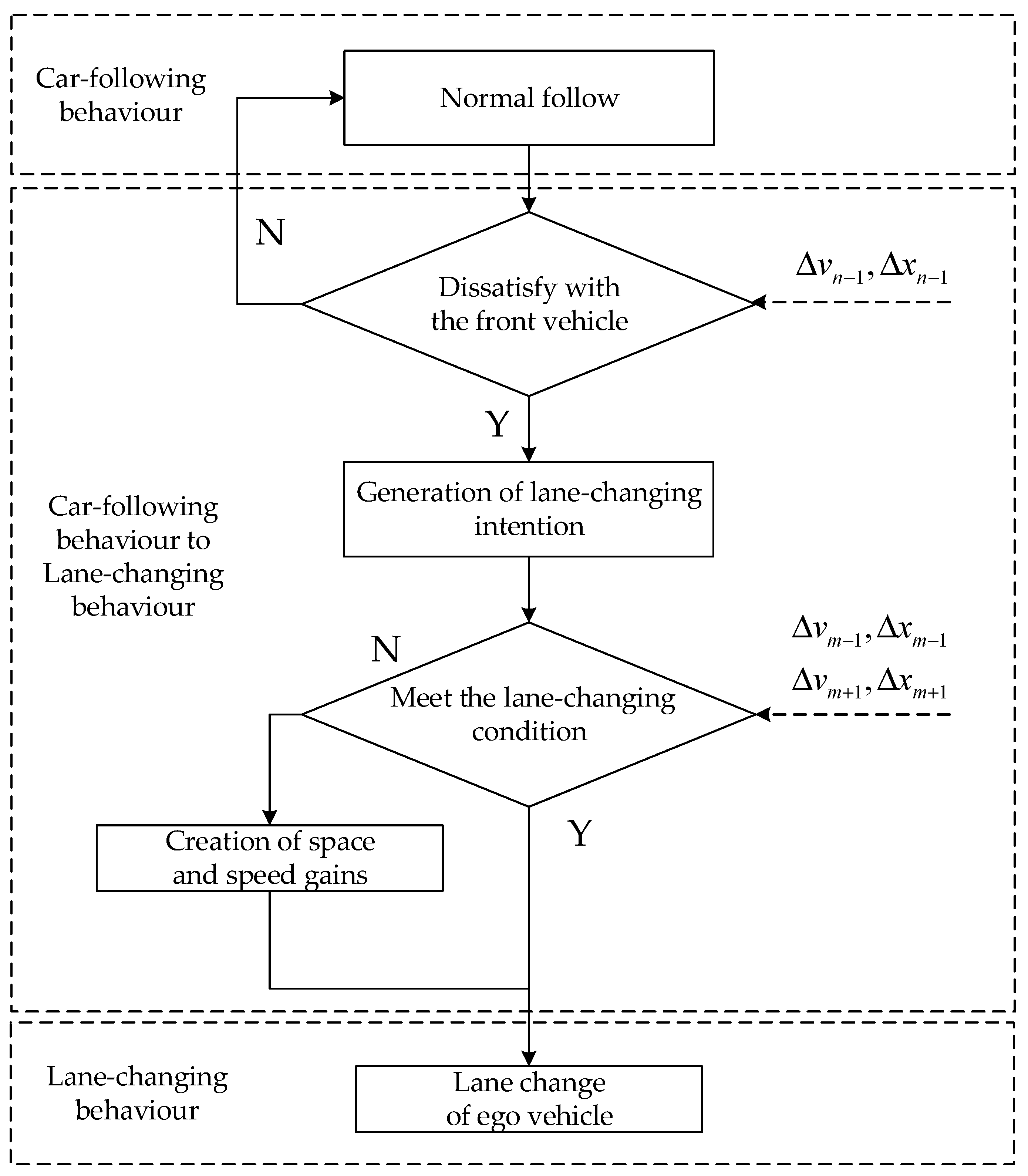
4.1. Modeling Mechanism of SSIDM
4.2. Solution of Switching Boundary Conditions
4.3. Model Unified Expression
- (1)
- When the target lane has no front and rear vehicle constraints.
- (2)
- When the target lane has front or rear vehicle constraints.
5. Model Validation
5.1. SSIDM Identification
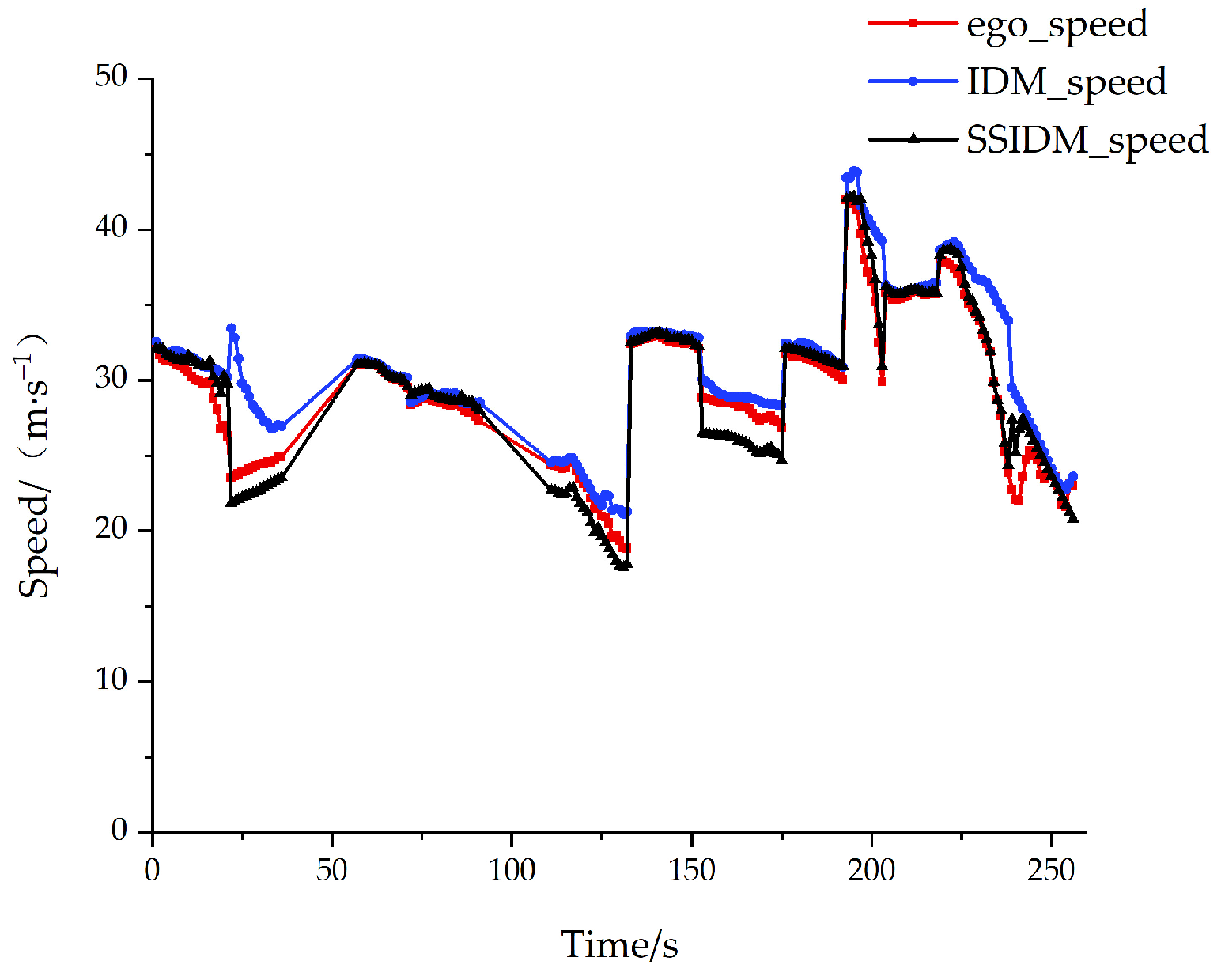
5.2. Comparison of Results
6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Miao, L.; Wang, F. Review on Research and Applications of V2X Key Technologies. Chin. J. Automot. Eng. 2020, 10, 1–12. [Google Scholar]
- Cao, X. Motion Control and Decision Planning for Car Following and Lane Changing of Autonomous Vehicle. Ph.D. Dissertation/thesis, Jilin University, Changchun, China, 2022. [Google Scholar]
- Zhu, M.; Wang, X.; Tarko, A.; Fang, S. Modeling Car-following Behavior on Urban Expressways in Shanghai: A Naturalistic Driving Study. Transp. Res. Part C Emerg. Technol. 2018, 93, 425–445. [Google Scholar] [CrossRef]
- Wang, X.; Sun, P.; Zhang, X.; Zhang, K. Calibrating Car-following Models on Freeway Based on Naturalistic Driving Data. China J. Highw. Transp. 2020, 33, 132–142. [Google Scholar]
- Treiber, M.; Hennecke, A.; Helbing, D. Congested Traffic States in Empirical Observations and Microscopic Simulations. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 62, 1805–1824. [Google Scholar] [CrossRef]
- Péter, T.; Háry, A.; Szauter, F.; Szabó, K.; Vadvári, T.; Lakatos, I. Mathematical Description of the Universal IDM-some Comments and Application. Acta. Polytech. Hung. 2023, 20, 99–115. [Google Scholar] [CrossRef]
- Qin, P.; Pei, S.; Yang, C.; Meng, Q.; Wan, Q. Influence of Road Geometrics on Car-following of the Intelligent Driver Model. J. Transp. Syst. Eng. Inf. Technol. 2017, 17, 77–84. [Google Scholar]
- Yi, Z.; Lu, W.; Xu, L.; Qu, X.; Ran, B. Intelligent Back-looking Distance Driver Model and Stability Analysis for Connected and Automated Vehicles. J. Cent. South Univ. (Sci. Technol.) 2020, 27, 3499–3512. [Google Scholar] [CrossRef]
- Sharath, M.; Velaga, N. Enhanced Intelligent Driver Model for Two-dimensional Motion Planning in Mixed Traffic. Transp. Res. Part C Emerg. Technol. 2020, 120, 102780. [Google Scholar] [CrossRef]
- Li, Y.; Lu, X.; Ren, C.; Zhao, H. Fusion Modeling Method of Car-Following Characteristics. IEEE Access 2019, 7, 162778–162785. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, C.; Qiu, X.; Wu, Y.; Li, S.; Wang, H. Car-following Behavior and Model of Chinese Drivers under Snow and Ice Conditions. J. Transp. Syst. Eng. Inf. Technol. 2020, 20, 145–155. [Google Scholar]
- Jin, P.; Yang, D.; Ran, B. Reducing the Error Accumulation in Car-Following Models Calibrated with Vehicle Trajectory Data. IEEE Trans. Intell. Transp. Syst. 2014, 15, 148–157. [Google Scholar] [CrossRef]
- Chang, X.; Li, H.; Rong, J.; Qin, L.; Yang, Y. Analysis on Fundamental Diagram Model for Mixed Traffic Flow with Connected Vehicle Platoons. J. Southeast Univ. Nat. Sci. Ed. 2020, 50, 782–788. [Google Scholar]
- Hu, X.; Zheng, M.; Zhao, J.; Long, B.; Dai, G. Stability Analysis of Mixed Traffic Flow Considering Personal Space under the Connected and Automated Environment. Appl. Sci. 2023, 13, 3231. [Google Scholar] [CrossRef]
- Péter, T.; Szauter, F.; Rózsás, Z.; Lakatos, I. Integrated Application of Network Traffic and Intelligent Driver Models in the Test Laboratory Analysis of Autonomous Vehicles and Electric Vehicles. Int. J. Heavy Veh. Syst. 2020, 27, 227–245. [Google Scholar] [CrossRef]
- Bouadi, M.; Jia, B.; Jiang, R.; Li, X.; Gao, Z. Stochastic Factors and String Stability of Traffic Flow: Analytical Investigation and Numerical Study Based on Car-following Models. Transp. Res. B-Methodol. 2022, 165, 1–33. [Google Scholar] [CrossRef]
- Wang, Z.; Zhou, X.; Wang, J. An Algebraic Evaluation Framework for a Class of Car-Following Models. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1–11. [Google Scholar] [CrossRef]
- Qu, D.; Wang, S.; Liu, H.; Meng, Y. A Car-following Model Based on Trajectory Data for Connected and Automated Vehicles to Predict Trajectory of Human-driven Vehicles. Sustainability 2022, 14, 7045. [Google Scholar] [CrossRef]
- Yuan, W.; Fu, R.; Guo, Y.; Peng, J.; Ma, Y. Drivers Lane Changing Intention Identification Based on Visual Characteristics. China J. Highw. Transp. 2013, 26, 132–138. [Google Scholar]
- Fu, R.; Zhang, H.; Liu, W.; Zhang, H. Review on Driver Intention Recognition. J. Chang’an Univ. Nat. Sci. Ed. 2022, 42, 33–60. [Google Scholar]
- Zhu, N.; Gao, Z.; Hu, H.; Lu, Y.; Zhao, W. Research on Personalized Lane Change Triggering Based on Traffic Risk Assessment. Automot. Eng. 2021, 43, 1314–1321. [Google Scholar]
- Chen, H.; Wang, J. A Decision-making Method for Lane Changes of Automated Vehicles on Freeways Based on Drivers Dissatisfaction. China J. Highw. Transp. 2019, 32, 1–9+45. [Google Scholar]
- Wang, J.; Gao, C.; Zhu, Z.; Yan, X. Multi-lane Changing Model with Coupling Driving Intention and Inclination. Promet 2017, 29, 185–192. [Google Scholar] [CrossRef]
- Ji, X.; Fei, C.; He, X.; Liu, Y.; Liu, Y. Intention Recognition and Trajectory Prediction for Vehicles Using LSTM Network. China J. Highw. Transp. 2019, 32, 34–42. [Google Scholar]
- Guo, Y.; Zhang, H.; Wang, C.; Sun, Q.; Li, W. Driver Lane Change Intention Recognition in the Connected Environment. Phys. A 2021, 575, 126057. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, Z.; Qu, Y.; Xie, D.; Sun, H. Vehicle Lane Change Intention Recognition Driven by Trajectory Data. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 63–71. [Google Scholar]
- Makridis, M.; Leclercq, L.; Ciuffo, B.; Fontaras, G.; Mattas, K. Formalizing the Heterogeneity of the Vehicle-driver System to Reproduce Traffic Oscillations. Transp. Res. C-Emerg. 2020, 120, 102803. [Google Scholar] [CrossRef]
- Adavikottu, A.; Velaga, N.; Mishra, S. Modelling the Effect of Aggressive Driver Behavior on Longitudinal Performance Measures During Car-following. Transp. Res. F-Traffic 2023, 92, 176–200. [Google Scholar] [CrossRef]
- Antin, J.; Wotring, B.; Perez, M.; Glaser, D. Investigating Lane Change Behaviors and Difficulties for Senior Drivers Using Naturalistic Driving Data. J. Saf. Res. 2020, 74, 81–87. [Google Scholar] [CrossRef]
- Li, X.; Oviedo-Trespalacios, O.; Afghari, A.; Kaye, S.; Yan, X. Yield or Not to Yield? An Inquiry into Drivers’ Behaviour When a Fully Automated Vehicle Indicates a Lane-changing Intention. Transp. Res. F-Traffic 2023, 95, 405–417. [Google Scholar] [CrossRef]



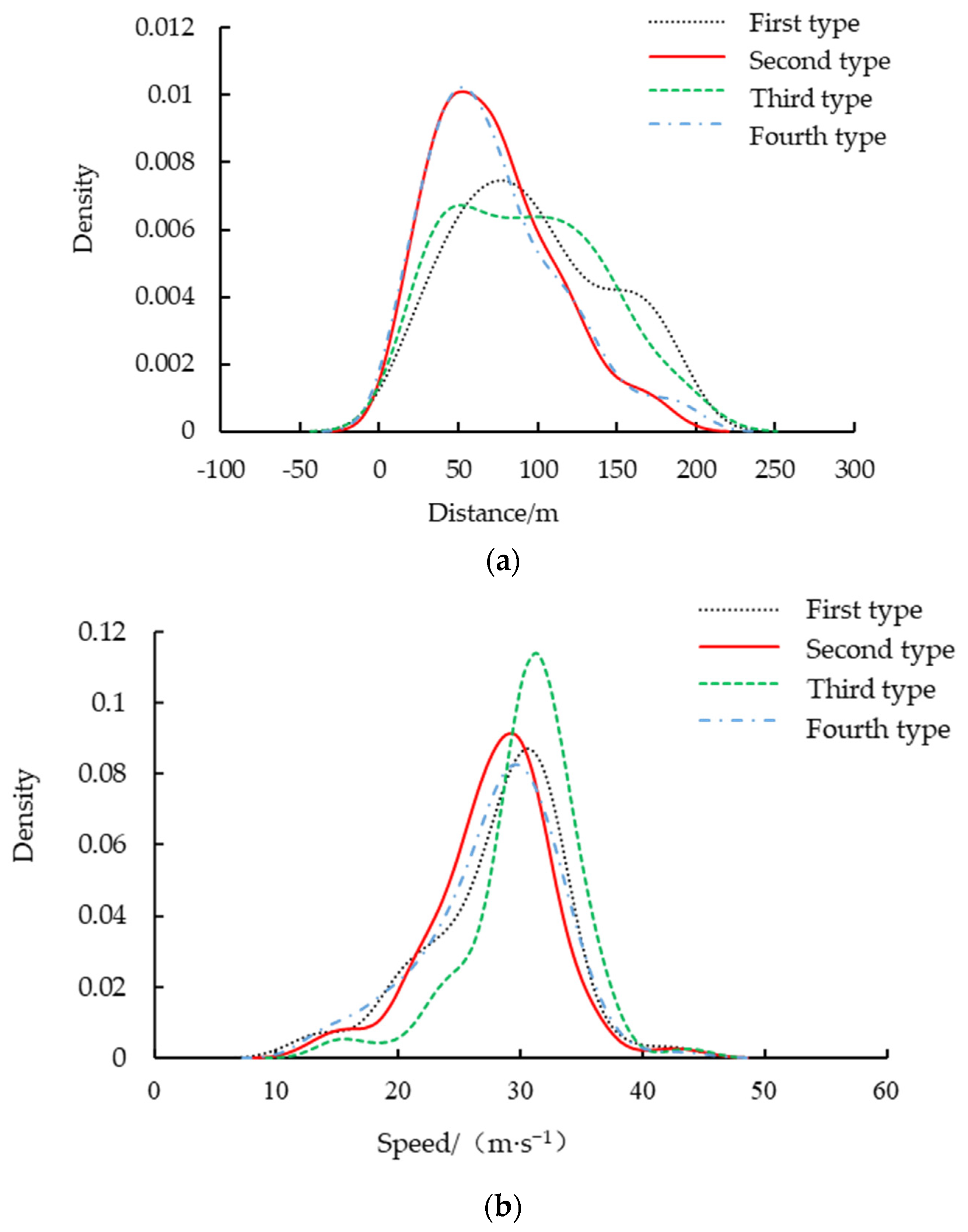
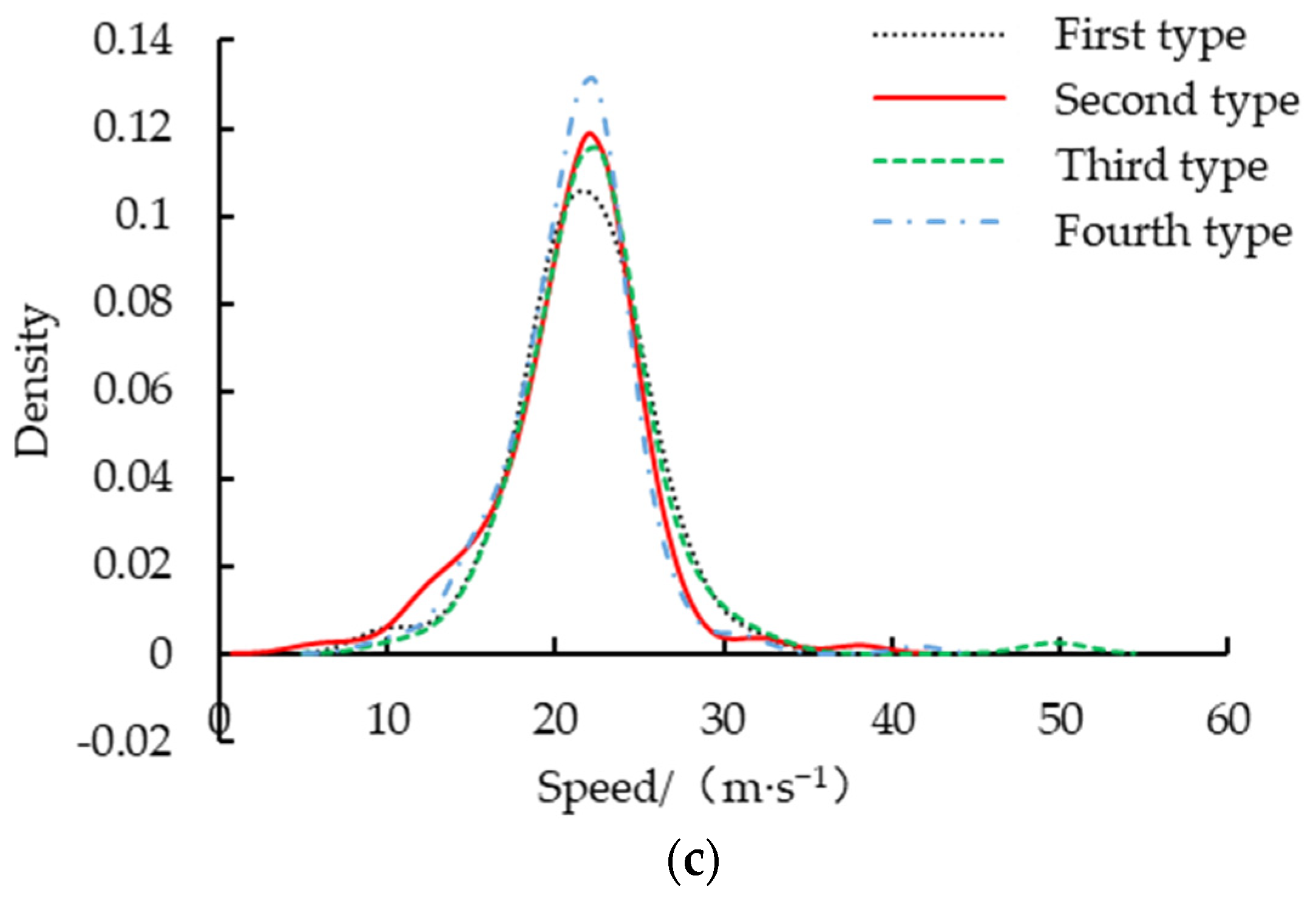

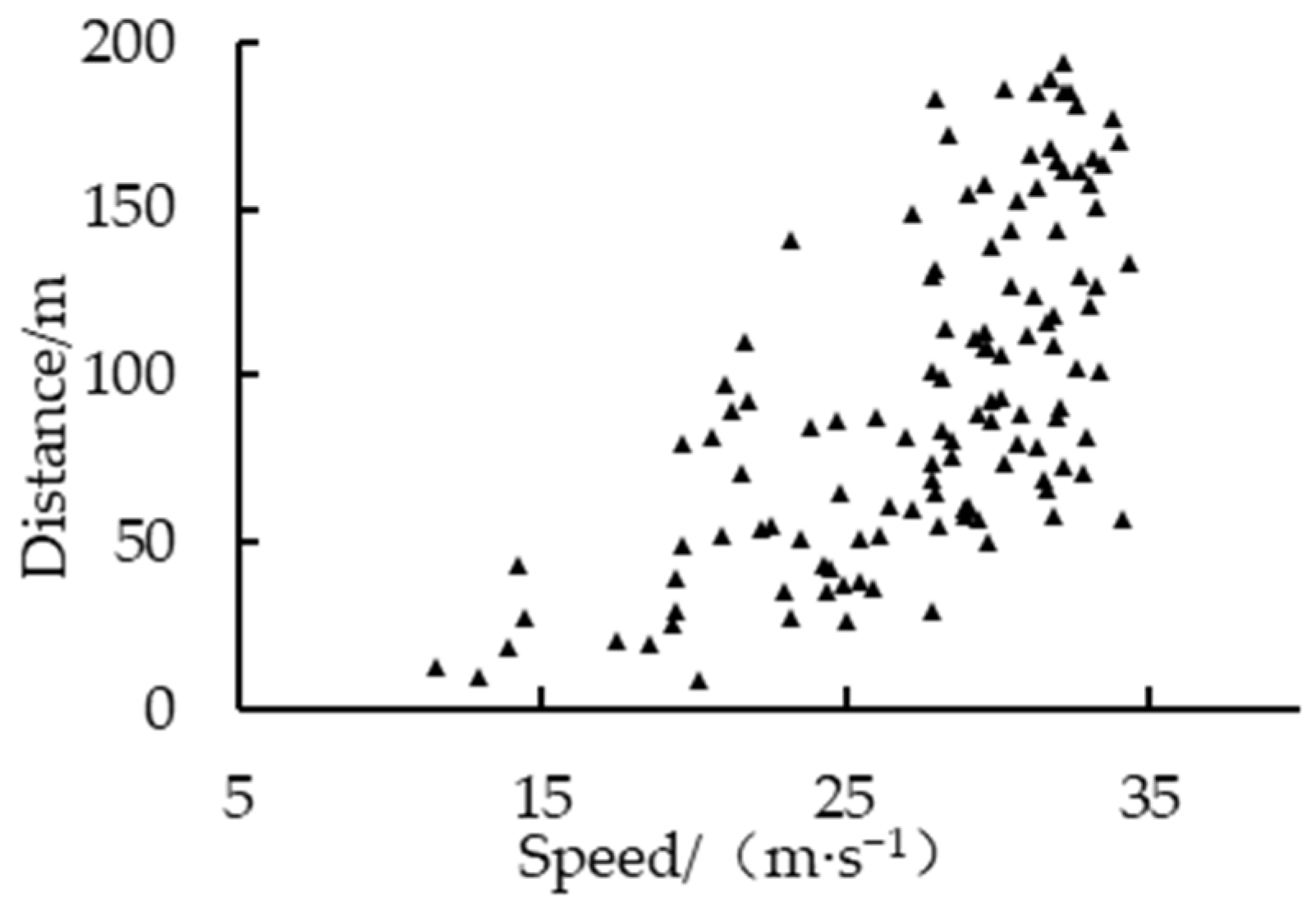
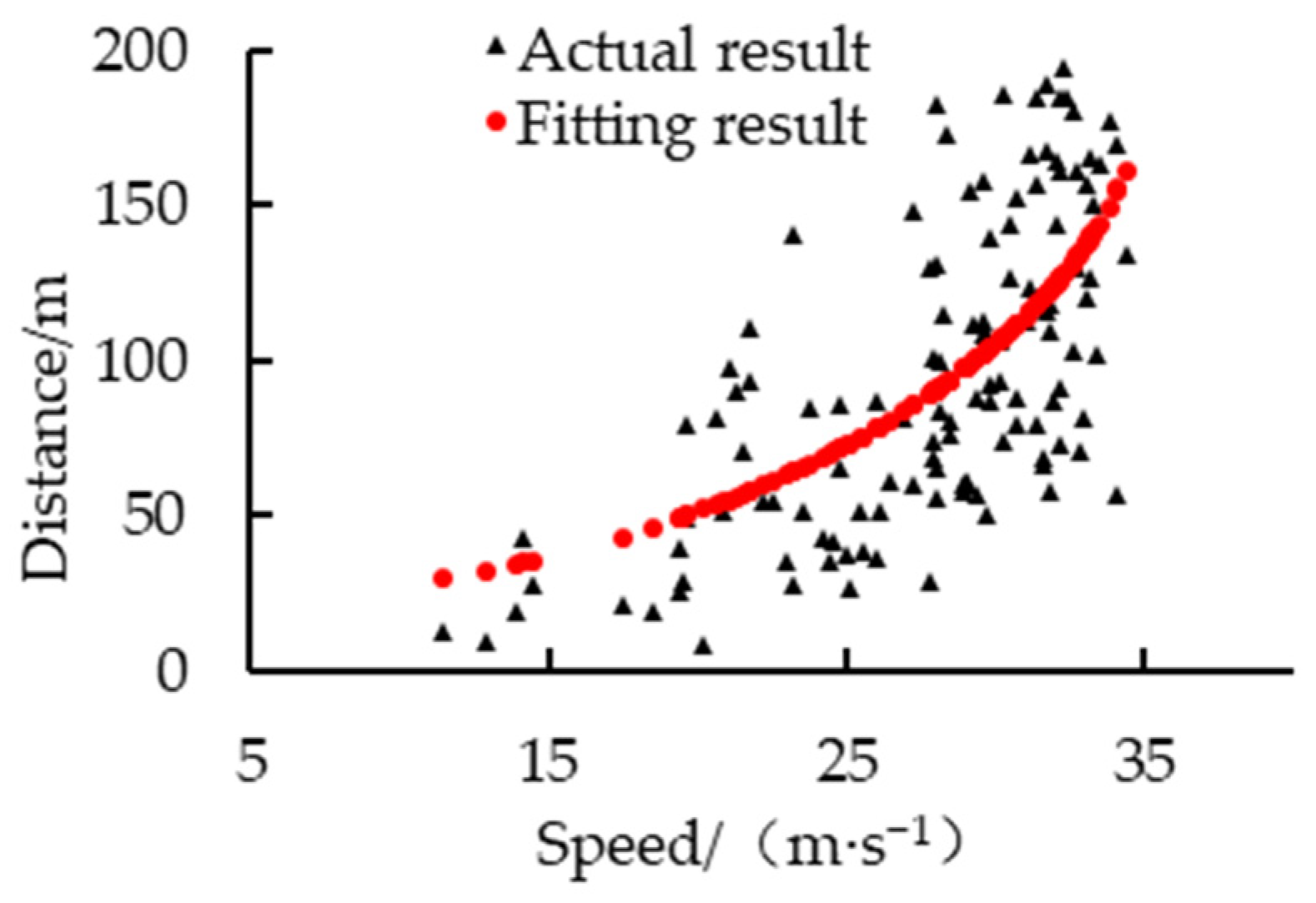


| Parameter | /(m·s−1) | /(m·s−2) | /(m·s−2) | /m | /s | |
|---|---|---|---|---|---|---|
| Value | 35.022 | 0.018 | 0.218 | 1.503 | 13.262 | 2.606 |
| Statistic | Mean Value | Standard Deviation | |
|---|---|---|---|
| First type | /(m·s−1) | 28.108 | 5.491 |
| /m | 95.569 | 48.412 | |
| /(m·s−1) | 21.602 | 3.915 | |
| Second type | /(m·s−1) | 27.788 | 4.879 |
| /m | 71.472 | 38.233 | |
| /(m·s−1) | 20.998 | 3.697 | |
| Third type | /(m·s−1) | 30.424 | 4.426 |
| /m | 91.829 | 47.457 | |
| /(m·s−1) | 21.209 | 3.581 | |
| Fourth type | /(m·s−1) | 27.811 | 5.393 |
| /m | 72.232 | 41.618 | |
| /(m·s−1) | 21.178 | 3.763 | |
| Fitting Function | Value | R2 | |
|---|---|---|---|
| k | 6.2 × 10−3 | 0.473 | |
| a | 2.723 | ||
| b | 26.281 | ||
| k | 6.841 | 0.401 | |
| a | 1.089 | ||
| b | 1.837 | ||
| a | 0.315 | 0.572 | |
| b | 34.879 | ||
| c | 180.245 | ||
| d | 197.179 | ||
| n | 2 | 0.431 | |
| a0 | 37.309 | ||
| a1 | −3.589 | ||
| a2 | 0.198 | ||
| Model | Mean Value | Standard Deviation | |
|---|---|---|---|
| SSIDM | 0.472 | 0.256 | |
| 0.186 | 0.149 | ||
| Model | Second Type | Third Type | Fourth Type | Mean Value |
|---|---|---|---|---|
| IDM | 3.113 | 10.647 | 2.582 | 5.169 |
| SSIDM | 2.962 | 3.383 | 1.238 | 2.172 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, R. Research on the SSIDM Modeling Mechanism for Equivalent Driver’s Behavior. World Electr. Veh. J. 2023, 14, 242. https://doi.org/10.3390/wevj14090242
Fang R. Research on the SSIDM Modeling Mechanism for Equivalent Driver’s Behavior. World Electric Vehicle Journal. 2023; 14(9):242. https://doi.org/10.3390/wevj14090242
Chicago/Turabian StyleFang, Rui. 2023. "Research on the SSIDM Modeling Mechanism for Equivalent Driver’s Behavior" World Electric Vehicle Journal 14, no. 9: 242. https://doi.org/10.3390/wevj14090242
APA StyleFang, R. (2023). Research on the SSIDM Modeling Mechanism for Equivalent Driver’s Behavior. World Electric Vehicle Journal, 14(9), 242. https://doi.org/10.3390/wevj14090242





