1. Introduction
A steering knuckle’s properties, such as strength, flexibility, and lightweight features, play a vital role in its design. The steering knuckle is intricately connected to the suspension, brake, and steering subassembly designs of a vehicle, allowing it to adapt to different weight and durability needs [
1]. The steering knuckle serves multiple essential functions, including mounting the wheel hub and bearing assembly, enabling the steering arm’s rotation around the wheel, and securing the brake calipers for the disk braking system. Moreover, it plays a crucial role in supporting the vehicle’s vertical weight. To ensure optimal performance, the steering knuckle must possess sufficient strength, stiffness, and durability. These attributes are essential to meet the dynamic and static assessment standards required in the competitive context of the student Formula One competition [
2]. Furthermore, achieving lightweight design in the steering knuckle structure is crucial to enhance a car’s energy efficiency and conservation. Researchers such as Chuan Ren et al. [
3] have utilized variable density TO to develop a lightweight racing frame. Additionally, Měsíček J et al. [
4] have employed bell crank topology in their work. These studies demonstrate the significance of employing innovative optimization techniques to achieve lightweight and efficient steering knuckle designs in the context of racing vehicles. The steering knuckle is categorized into two types: those with a spindle and those with a hub. The hub is the hollow section of the knuckle that replaces the spindle and houses the bearing supporting the wheel. In our drive suspension, the steering knuckle does not feature a spindle; instead, it incorporates a hub where the bearing and drive mechanism are fixed. The wheel’s bearing can be mounted using either a hole in the hub to bolt the bearing flange on or a snap ring to secure the bearing knuckle. This distinction in design is crucial in the context of the vehicle’s suspension system and influences the mounting of wheel bearings for optimal performance and stability [
5]. The hub is equipped with holes to bolt the bearing flange, facilitating the secure attachment of the bearing. The car’s suspension system plays a crucial role in ensuring ride comfort, steering stability, and optimal wheel motion characteristics, particularly when encountering changing road conditions or varying loads. In the context of TO, Pang and Toh Yen [
6] proposed an upgraded design for LW racing arms, while Bin ab Razak et al. [
7] explored the application of TO in the development of additional lightweight racing cars. These studies contribute to the advancement of lightweight design and optimization techniques for racing vehicles, ultimately improving their overall performance and efficiency. In racing equipment design, the main focus is on reducing the weight of the frame and knuckles. The suspension system’s properties depend on competitive conditions and design requirements, requiring the optimization of the variable density topology in the car’s design. This may involve adjusting the safety factor to save weight. Agarwal, S. et al. describe how fatigue analysis is used to assess the component’s durability under varying forces, simulating different loads to understand its performance. This analysis helps designers replace components before potential failure, preventing structural damage [
8]. Kothari, P. et al. highlighted that a static stress analysis alone is unable to capture the component’s performance. To understand its behavior under varying forces, fatigue studies are crucial. Making design adjustments based on these findings can increase the component’s lifespan and improve the overall design standard [
9].
2. Topology Optimization Method
TO is a technique used in the automotive and aerospace industries to reduce the weight of mechanical parts while maintaining their performance [
10]. This method involves conducting mechanical tests using finite element analysis (FEA) to optimize the geometry. TO is widely used in structurally lightweight design, determining which parts can be eliminated to reduce weight without compromising reliability and safety during load transfer in automotive assembly [
11]. Various techniques such as variable thickness, homogenization, variable density, and others can achieve the optimization of a product’s topology. The variable density technique, which uses discrete variables ranging from 0 to 1 to represent material density, is particularly prevalent in structural optimization. The goal is to optimize the distribution of material while considering constraints on the permitted amount of material [
12]. Overall, structural TO using the variable density approach is a discrete optimization problem involving cell expansion and contraction. It is crucial for creating efficient and effective designs for desired products. The following is a description of the matching mathematical model [
13]:
in which (
F) represents the load matrix;
C(
ρ) denotes the flexibility of a structure; the objective method calculates the structure’s stiffness; (
ρi) shows the design variable of an element and the relative density of the material;
U denotes the displacement matrix; (
T) denotes the boundary tractions on the traction part; (
K) is the overall stiffness matrix; and (
V) reflects the structural volume of the design variable state, where (
V0) represents the structure’s initial volume and (
f) defines the volume constraint parameter. The mathematical model of the racing suspension’s steering knuckle optimization design is then shown as follows:
In Equations (6)–(10), (dev) signifies the transition in the cell mesh density, (com1) denotes the types of distributed regions, (dis) signifies the static displacement, and (vol) is the volume fraction, which is equal to the difference between the current iteration step’s total volume and the ratio of the initial non-design area volume to the initial design area volume; limits for the upper limit of the mass fraction or the acquired material must not reach the material of the selected element.
2.1. Approach of Iterative Design
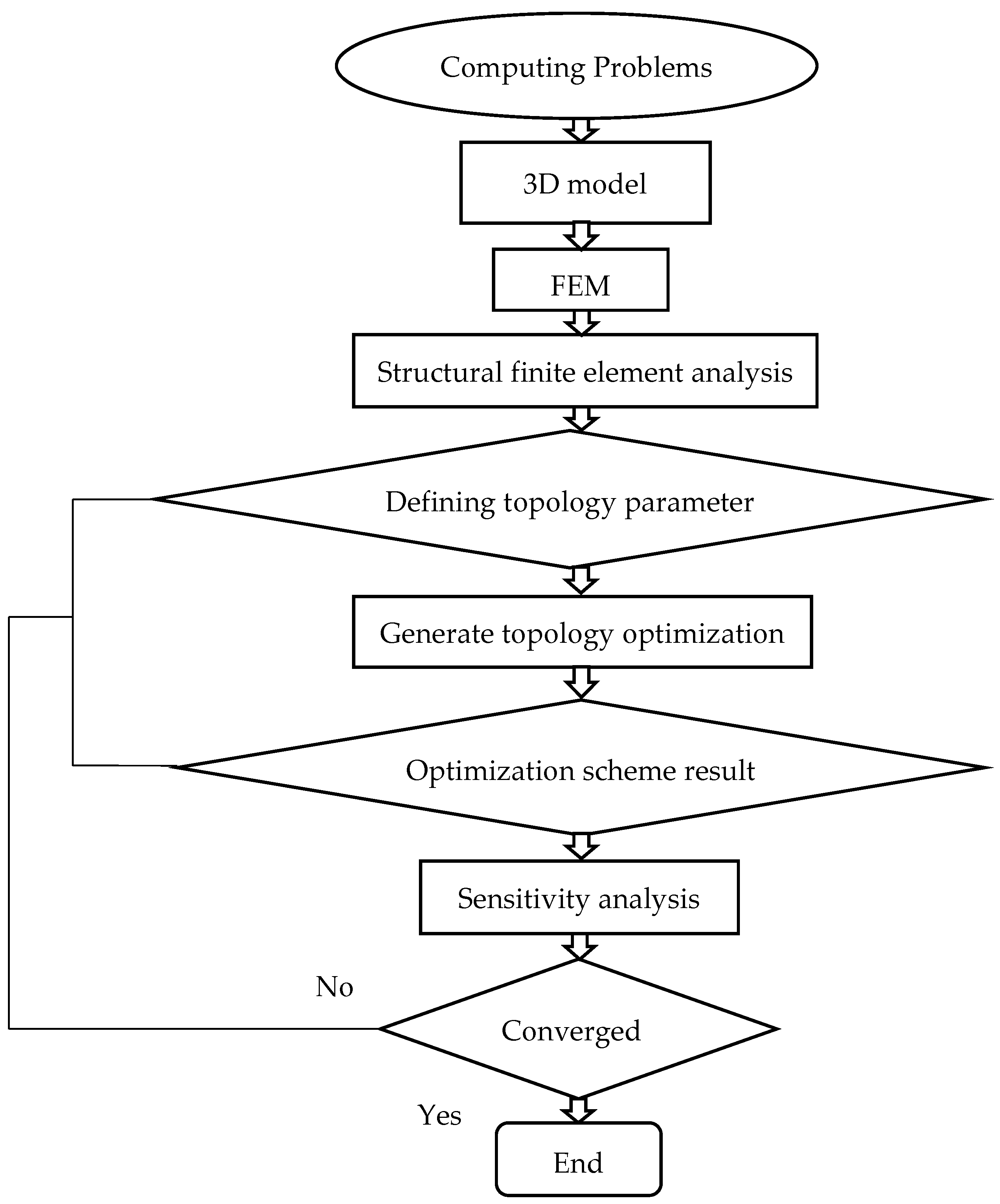
The knuckle design optimization in this study follows an iterative design methodology, which proves to be an effective alternative to generative design. The focus of this paper lies in mechanical component design optimization rather than generative design.
Figure 1 illustrates the detailed process. It begins with solving the knuckle design engineering problem, followed by creating a 3D geometry model of the knuckle and conducting FEA using ANSYS 22.2 Workbench. Topological computation is performed after structural optimization. The optimization parameters are selected and generated for the TO of three different materials. The resulting comparison helps identify the most optimal output of the TO method for the selected materials. Additionally, a fatigue analysis is conducted to assess the model’s fatigue life and a sensitivity analysis is combined with objective convergence.
Figure 1 provides an overview of the entire flowchart.
2.2. Material Selection and Its Properties
In this study, the mechanical properties of three materials, namely structural steel, steel 4130, and AISI 1020 steel, were evaluated. Structural steel served as the main material, while steel 4130 and AISI 1020 steel were the other two materials. The analysis was conducted for two mass retention levels: 40% and 48%.
Table 1 presents the mechanical properties of these materials. The AISI-1020 steel exhibited a yield strength of 350 MPa and a slightly lower tensile strength of 420 MPa. While not the strongest steel grade, it offers advantages in terms of ease of welding, processing, turning, and polishing. On the other hand, steel 4130 is easily weldable and commonly used in construction applications. Structural steel is preferred for LW construction due to its superior compression and stress qualities, despite having higher strength than other materials.
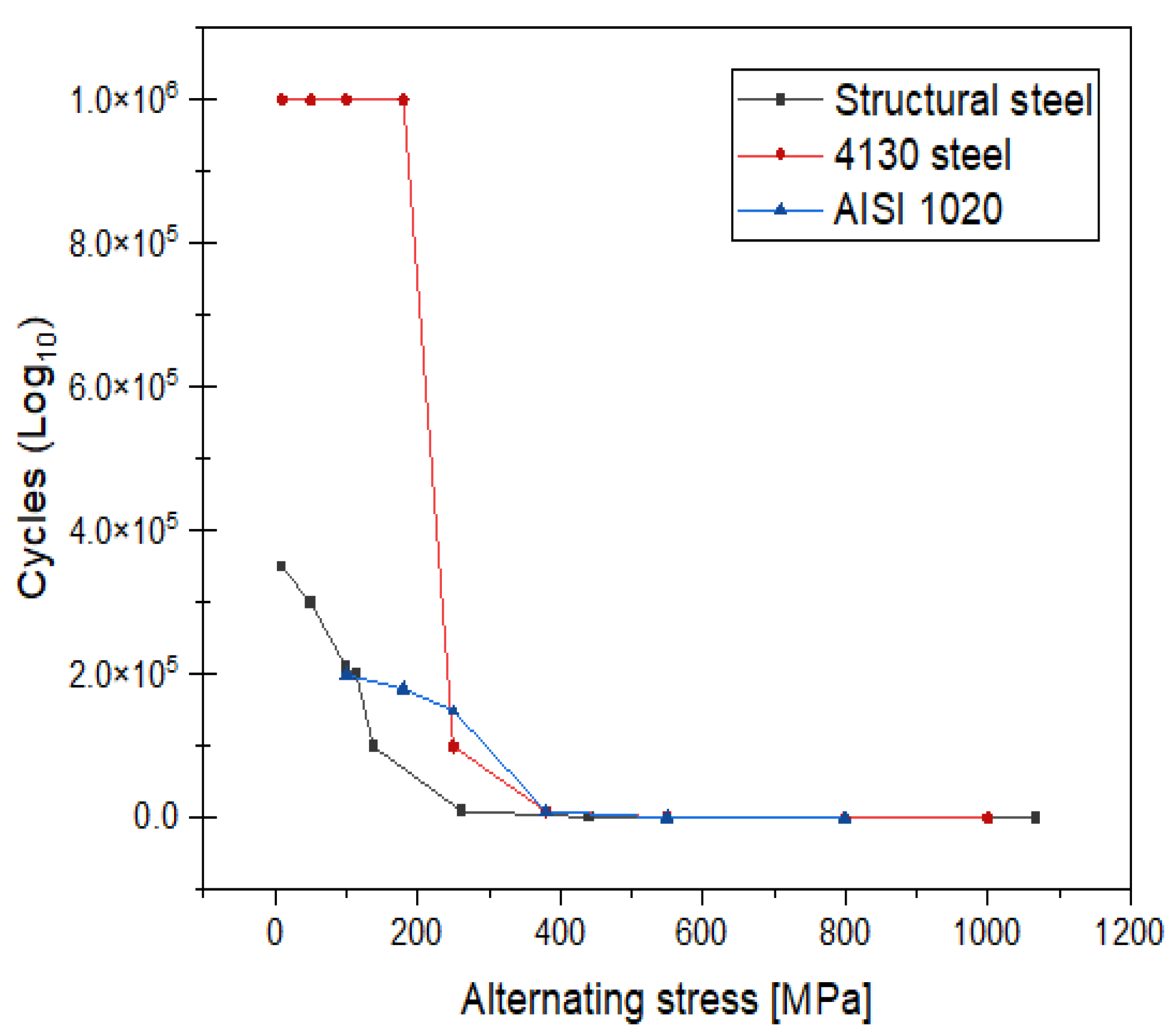
Figure 2 presents the SN curve for three materials, illustrating the relationship between alternating stress and the number of cycles. The curve depicts the part of the material that falls within the analyzed range, automatically calculating the cycles for that specific section. As stress in life decreases, the number of cycles increases. If a part experiences cycles below 1 × 10
5, it is considered low cycle fatigue (LCF), while cycles above 1 × 10
5 are termed high cycle fatigue (HCF). Parts that surpass 1 × 10
6 cycles will eventually reach an infinite number of cycles [
14]. This explains the concept of HCF and LCF based on the number of cycles experienced by a material under varying stress conditions. In the SN curve for structural steel, it is observed that as stress increases, the number of cycles also increases, while the number of cycles decreases as stress decreases.
Figure 2 illustrates the log-log plot of alternating stress versus the number of cycles for structural steel, 4130 steel, and AISI 1020. It shows the number of cycles used in the analysis. The results demonstrate that the number of cycles increases with higher stress and decreases with lower stress.
2.3. Constructive Analysis
The steering knuckle’s complex connections with multiple components require a contact area for finite element (FE) analysis. The FE model was integrated using ANSYS Workbench 22.2 software, along with an interface study to simulate external conditions. Mesh refinement was applied at critical locations to ensure proper mating surfaces. The research involves evaluating links and interconnections between different locations, with
Table 2 detailing the active presence and contact creation. Additionally, the analysis included studying load transfer to the surrounding region and interface nodes.
2.4. Mathematical Computation and Boundary Conditions
All the parameters presented for the steering knuckle’s loads and boundary conditions are calculated based on the dynamics of the vehicle and the knuckles of the car body [
15].
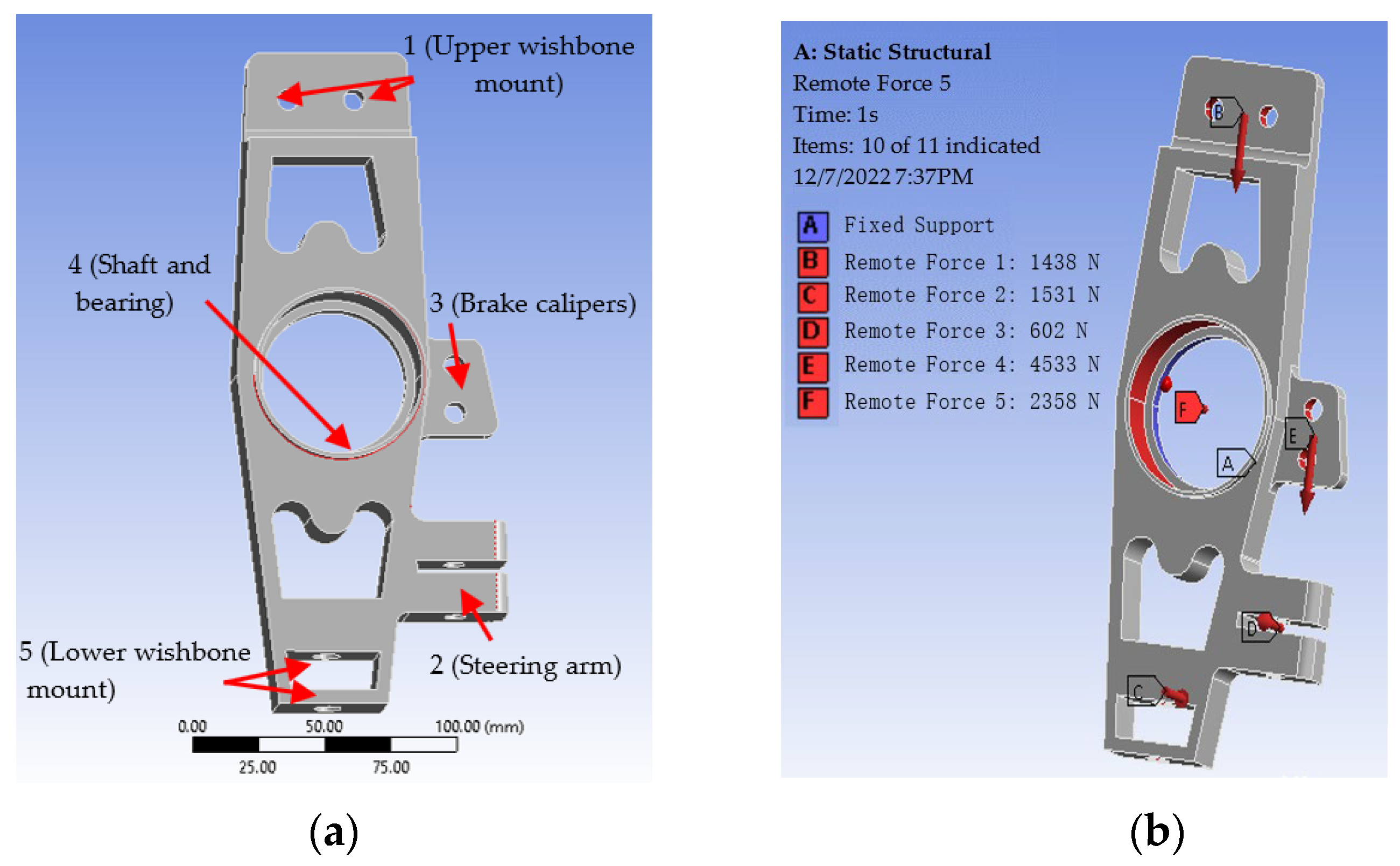
In this study, the steering knuckle is subjected to five distinct types of loads, which are simulated based on the formulas described in
Table 3. These loads include the static load, steering force, cornering force, and braking force. The static load represents the weight applied to the knuckle and is a combined force of 1438 N from gravity and mass. The steering force, with a magnitude of 2358 N, acts along the X-negative axis and is followed by the cornering force, which is active in the Y-negative direction and is equal to three times the G-force, resulting in a load of 2358 N on each knuckle. Additionally, the braking force is applied to the two mounting holes for the brakes, with a force of 4533 N in the negative Y direction. These carefully defined loads are crucial for accurately analyzing the behavior of the steering knuckle under various dynamic conditions in the racing car body.
3. Structural Analysis and Topology Optimization of the Steering Knuckle
In the context of the Formula SAE steering knuckle optimization analysis, the designated region exhibits an increased design thickness following surface smoothing. This augmented thickness allows for greater flexibility in optimizing both the geometry and load-bearing locations. As a result, the steering knuckle’s structural characteristics and performance can be effectively enhanced through the optimization process [
16]. Subsequently, the thickened geometry undergoes static analysis with different materials and two response constraints (40% and 48%). The TO analysis achieves an impressive 52–60% mass reduction compared to the original geometry. The design validation analysis validates the optimized geometry, comparing it with the original knuckle and evaluating fatigue and sensitivity. The design region is carefully defined, taking into account structural requirements, constraints, and design objectives. The key factors considered include strength, stiffness, fatigue life, and weight minimization. Geometric and material property constraints, such as allowable stress and strain, are also taken into consideration. The main design objectives are focused on achieving weight reduction, improved stiffness, and enhanced fatigue life while ensuring that the structural integrity of the steering knuckle is maintained. To determine volume fractions, a comprehensive approach was used, considering structural requirements, weight reduction goals, and manufacturing constraints. The systematic methodology prioritizes design constraints while aiming for weight reduction without compromising integrity, aligning with the specified objectives.
Furthermore, a density filter was incorporated into TO methodology to regulate the material distribution within the design domain. By applying a filter radius, we controlled the influence of neighboring elements during optimization, resulting in smoother and more practical designs that avoid complex and impractical geometries. The density filter had a significant impact on the final design, promoting convergence and preventing undesirable features like local stress concentrations and thin-walled structures. It improved manufacturability and practicality, ensuring a more gradual material distribution transition.
3.1. Mesh Sizing Determination of the Model
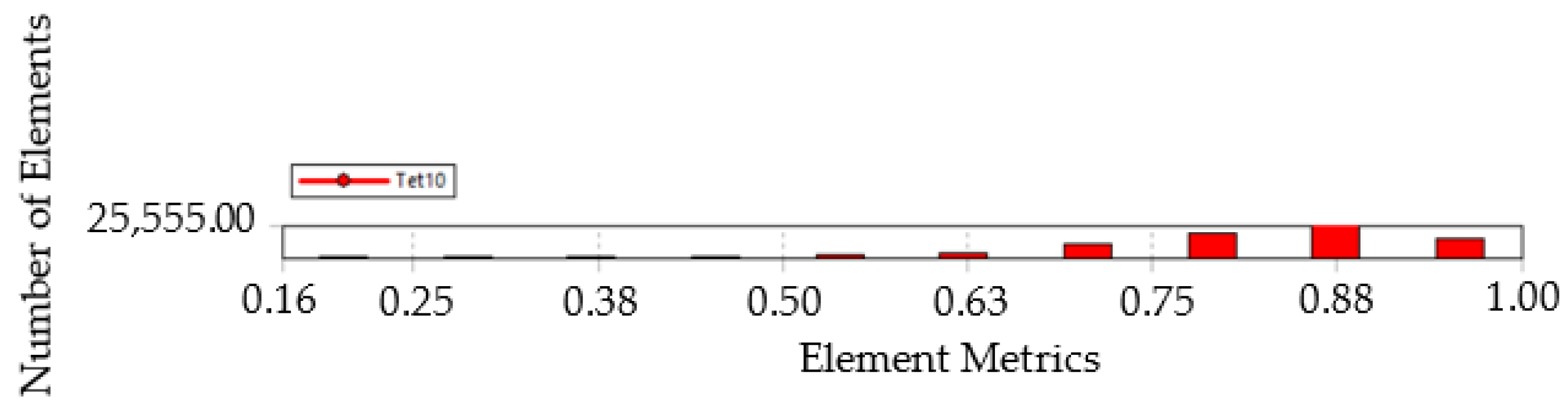
Initially, consecutive mesh sizes of 1.25 mm, 2.5 mm, and 3 mm were utilized to analyze the model and determine the appropriate mesh size. The geometry’s element type was quadratic in standard mechanical properties. Based on the mesh metric spectrum, a minimum value between 0 and 0.25 is considered excellent for a suitable mesh, while 0.80–0.94 is acceptable. Anything above 1.00 is deemed unacceptable [
17]. After the 1.25 mm and 2.5 mm mesh sizes were generated, it was observed that their mesh metric value was 1.25, which exceeded the acceptable threshold of 1 for model analysis. However, the 3 mm mesh size element provided the required mesh quality, as depicted in
Figure 3, with a mesh metric value above 0.16 but lower than 1.00. Subsequently, the model was subjected to a structural investigation, enabling the initiation of TO. To avoid excessive mesh refinement in the complex area of the optimized geometry, it was essential to maintain elements in a similar order as before, apply the patch-independent tetrahedron mesh technique control during the meshing process, and to disable mesh refinement.
3.2. Analysis Model Construction and Validation of Geometry
The representation of the steering knuckle geometry involves several steps, such as creating a model with internal and external carriers, determining the inner wall diameter, establishing upper and lower suspension mounting points, and creating construction points for the stabilizer rod.
Figure 4a illustrates the location points for the steering suspension, brake caliper, hub core, and steering rod mounting holes. Considering the competition rules and driving requirements, the steering rod experiences significant static and dynamic loads, necessitating a high safety factor for reliability. To ensure suitable material selection in this operating environment, the initial steering knuckle model undergoes topological optimization.
Figure 4b displays the geometry model after testing under constrained conditions and loads, clearly showing the hub’s inner and outer loading holes, hard point coordinates, and moving caliper mounting hole when subjected to braking and bending forces.
3.3. Strength Evaluation of the Analysis Model
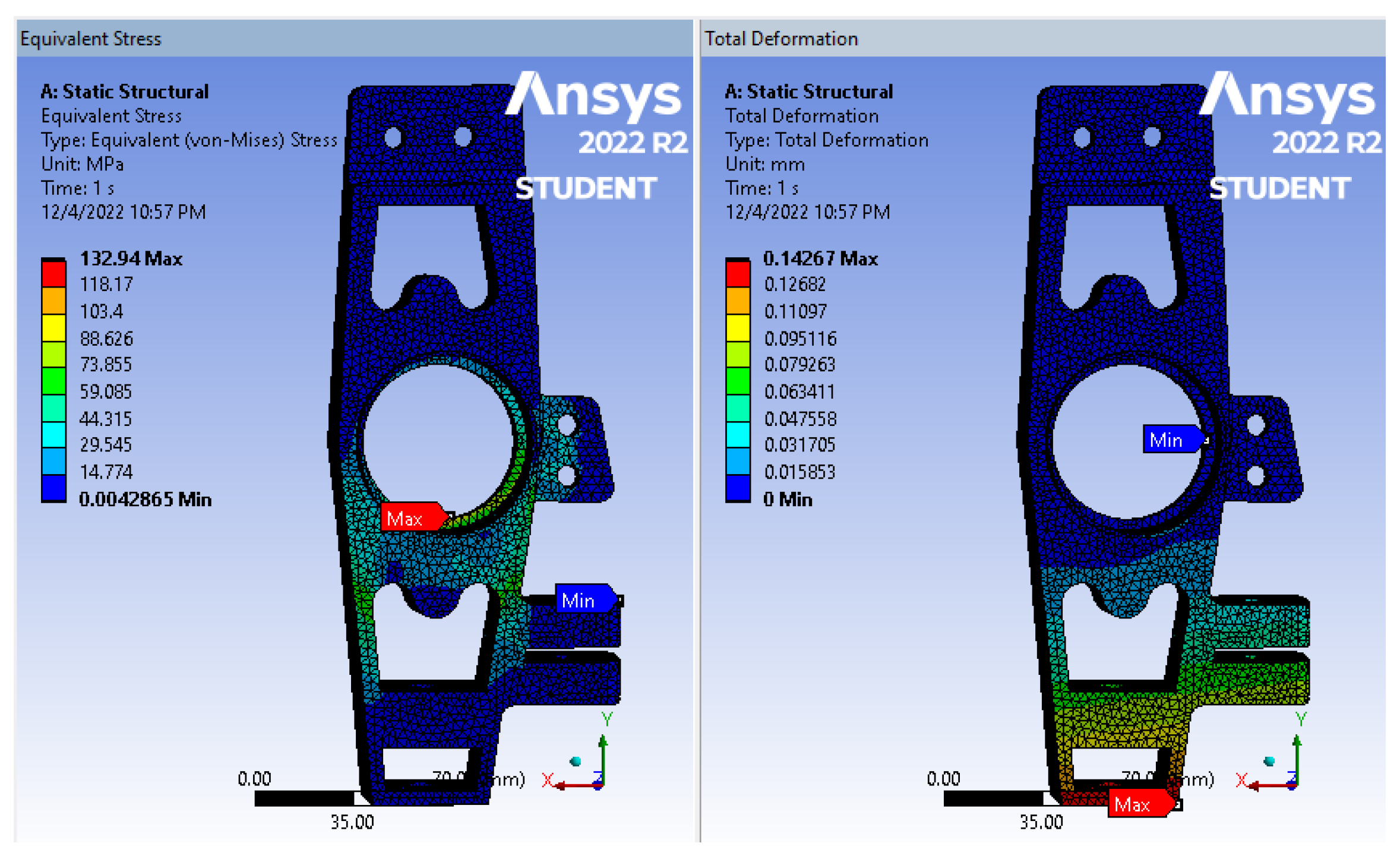
Figure 5 presents the stress and deformation contours of the steering knuckle under static loading, obtained using the finite element model in ANSYS 22.2 Workbench. The surface diagram reveals a maximum stress value of 132.94 MPa and a maximum deformation value of 0.14 mm. After the initial TO, static analysis of the model was performed using consistent constraints and loads from the first analysis. The results are presented in
Figure 6 and
Figure 7. For a second weight reduction, the constraints were adjusted for three different materials with two different mass limitations, all falling within the safe range, with the maximum stress value well below the yield limit. The TO aims to achieve mass reduction targets of 60% and 52% of the initial volume. Structural steel, with a yield strength of 250 MPa, was utilized as the material, allowing further weight reduction and optimization possibilities.
3.4. Topological Optimization of the Steering Knuckle
The original design mass of the steering knuckle is 1.74 kg, emphasizing LW topology. The topological range was determined based on the outcomes of the previous static analysis, as depicted in
Figure 6a. Following the TO evaluation, stress values were compared to the yield limit of each material. If the stress value exceeds the material’s yield limit, the model is unsuitable for further analysis. The optimization constraint was set at 62% of the mass for the selected region, where the blue area indicates the optimized region and the red area represents the non-optimized region.
Figure 6a displays the maximum and minimum stress values on the surface. The optimized structure of the steering knuckle was generated using specific TO parameters, shown in
Figure 6b. Three materials, namely steel 4130, AISI 1020, and structural steel, were considered for further TO constraints. In the first optimization, structural steel was selected as the main material, and subsequent analyses were conducted for the other two materials with mass reductions of 60% and 52%, respectively.
3.4.1. Finite Element Analysis for 52% Mass Reduction
After design validation and obtaining the TO surface, the geometry was processed into a 3D model. Prior to this, the geometry was smoothed and curved lines and faces were merged to ensure compatibility with further analysis and an accurate representation of topological findings. Once the surface smoothing was complete, the structure was ready for the final static analysis. The first TO was conducted and the geometric model underwent static analysis using compatible meshing principles, constraints, and loads.
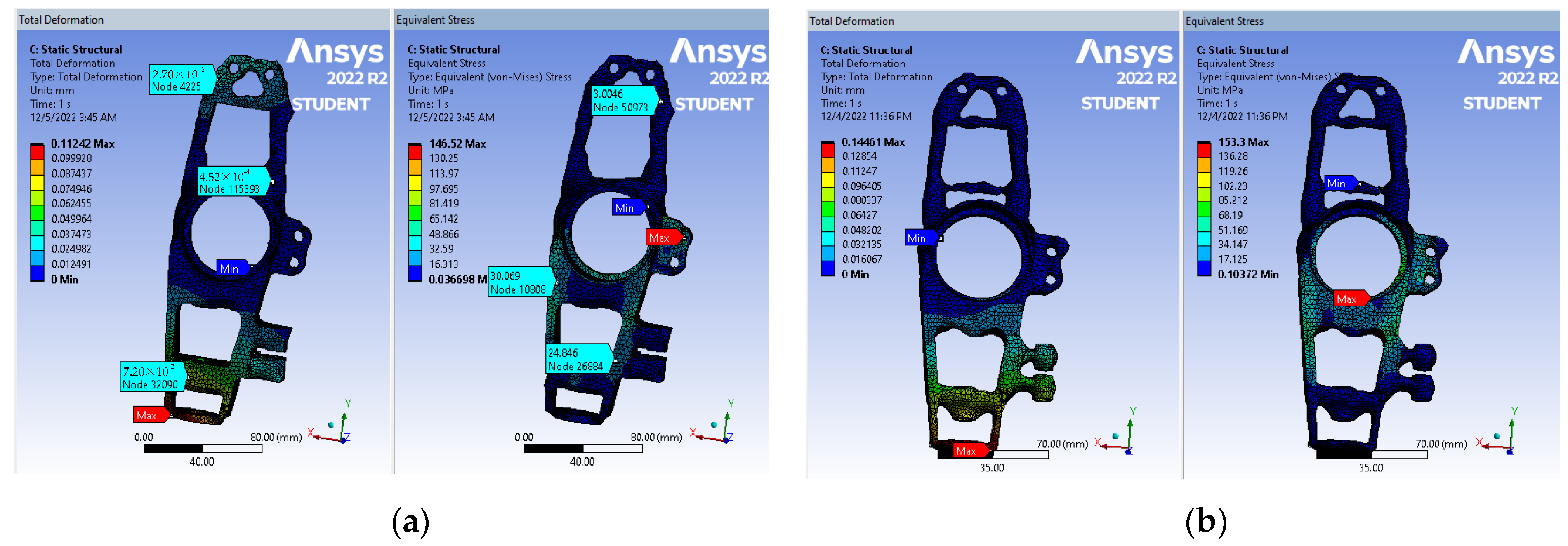
Figure 7a displays the results for the first optimized model using AISI 1020, showing a maximum deformation of 0.11 mm and maximum stress of 146.52 MPa on the right-side view, with a minimum stress value of 0.04 MPa. The model’s mass is reduced to 1.07 kg, which is 0.66 kg less than the original mass of 1.75 kg. The retained mass is 61.64%, and the stress value is well below the yield limit for this material model. Moving on to the second optimized model with structural steel, as shown in
Figure 7b, a similar procedure was followed. The static analysis of the geometric model was conducted after the first TO, with meshing principles, constraints, and loads being compatible with the analysis. The results show a maximum deformation of 0.14 mm, maximum stress of 153.3 MPa, and minimum stress of 0.11 MPa.
The mass of the structure’s model is reduced to 0.92 kg, which is 0.81 kg less than the original mass of 1.75 kg, resulting in a retained mass of 53.44%. For the next material, steel 4130, the optimization was conducted with structural steel, as depicted in
Figure 8. The results reveal a maximum deformation of 0.11 mm and a maximum stress of 105.93 MPa, with a minimum stress value of 0.13 MPa observed on the right-side view. The model’s mass is decreased to 1.05 kg, which is 0.68 kg less than the original mass of 1.74 kg, and the maximum stress values for both materials are within the yield limit. The retained mass is 60.72%. The mass reduction percentages for AISI 1020, structural steel, and steel 4130 are 38.36%, 46.56%, and 39.28%, respectively.
Table 4 provides a detailed comparison of the results.
3.4.2. Finite Element Analysis for 60% Mass Reduction
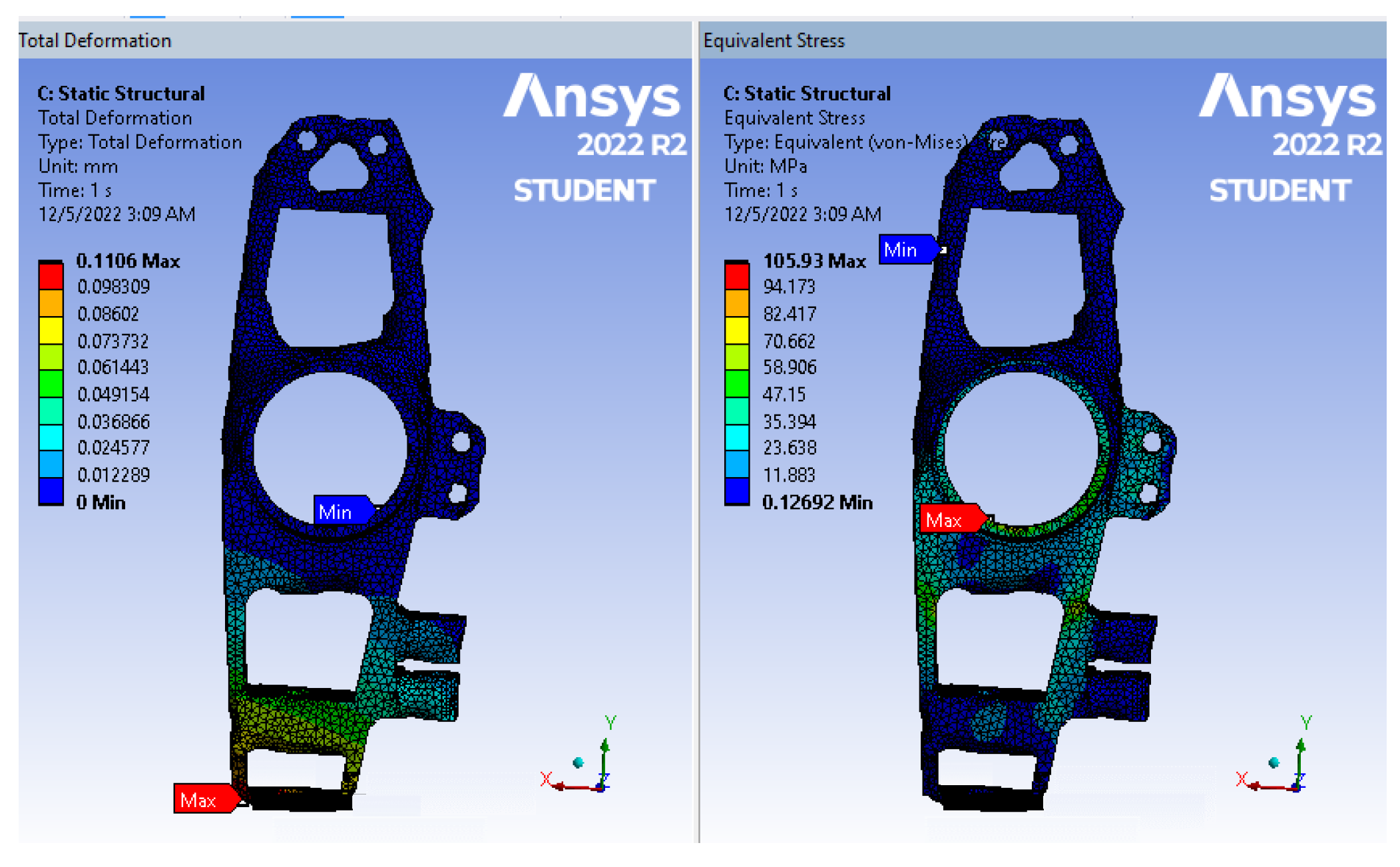
In this analysis, the first optimized result is presented for AISI 1020 steel in
Table 5, with a maximum deformation of 0.11 mm and a maximum equivalent stress of 84.38 MPa. The mass is reduced to 1.06 kg, 0.68 kg less than the original mass of 1.74 kg, resulting in a retained mass of 60.64%. For structural steel, the optimized result shows a maximum thickness of 0.14 mm and a maximum equivalent stress of 145.75 MPa, with a minimum equivalent stress of 0.276 MPa. The mass is reduced to 0.80 kg, with a retained mass of 46.51%. For steel 4130, the analyzed result indicates a maximum deformation of 0.10 mm, an equivalent stress of 83.52 MPa, and a minimum stress value of 0.55 MPa. The final mass for steel 4130 is 1.01 kg. The maximum stress values for all three materials are well below the yield limit, meeting the analysis requirements at the primary level. However, in terms of stiffness and weight reduction, steel 4130 outperforms the other two materials.
3.5. Fatigue Analysis
The fatigue analysis of the optimization geometry model was performed using ANSYS 22.2 Workbench with stress life as the analysis type. Load spectra were utilized to define fatigue load amplitudes and characterize diverse loading conditions experienced by components during real-world driving scenarios. This evaluation provided insights into fatigue life, durability, and performance of automotive components under varying conditions. The applied loads, representing forces during vehicle operation, included vertical, longitudinal, lateral, steering, and braking torque. Analysis and verification were conducted under turning brake conditions, emergency braking conditions, and emergency turning conditions after selecting the final material for the geometry. For the fatigue analysis, the Goodman analysis type with log-log SN curves was chosen. The “fatigue life” refers to the number of cycles the component can endure under constant-amplitude stress before failing from fatigue. If the loading is not constant, this estimation reflects the number of loading blocks until failure. The “fatigue damage” denotes the design life or available life, with values greater than 1 indicating failure before achieving the design life. The “Fatigue Safety Factor” represents the safety margin concerning fatigue failure at a certain design life, ranging up to 15. Values below one for the Fatigue Safety Factor imply failure before achieving the design life [
18].
In the racecar application the desired life of the steering knuckle is crucial, and it was estimated to be 5–10 months, exceeding 200 days, considering the demanding nature of the motorsport and extreme loading scenarios. Our fatigue analysis aims to ensure safety and reliability by designing for an infinite life under anticipated conditions while keeping stresses below the material’s fatigue limit. The “Fatigue Sensitivity” indicates how loading at a critical location on the model affects fatigue outcomes, and it can be determined by factors related to safety, harm, or life. Both the load variation limitations and the number of fill points are user adjustable to enhance fatigue analysis accuracy.
3.5.1. Fatigue Analysis for 52% and 60% Mass Reductions
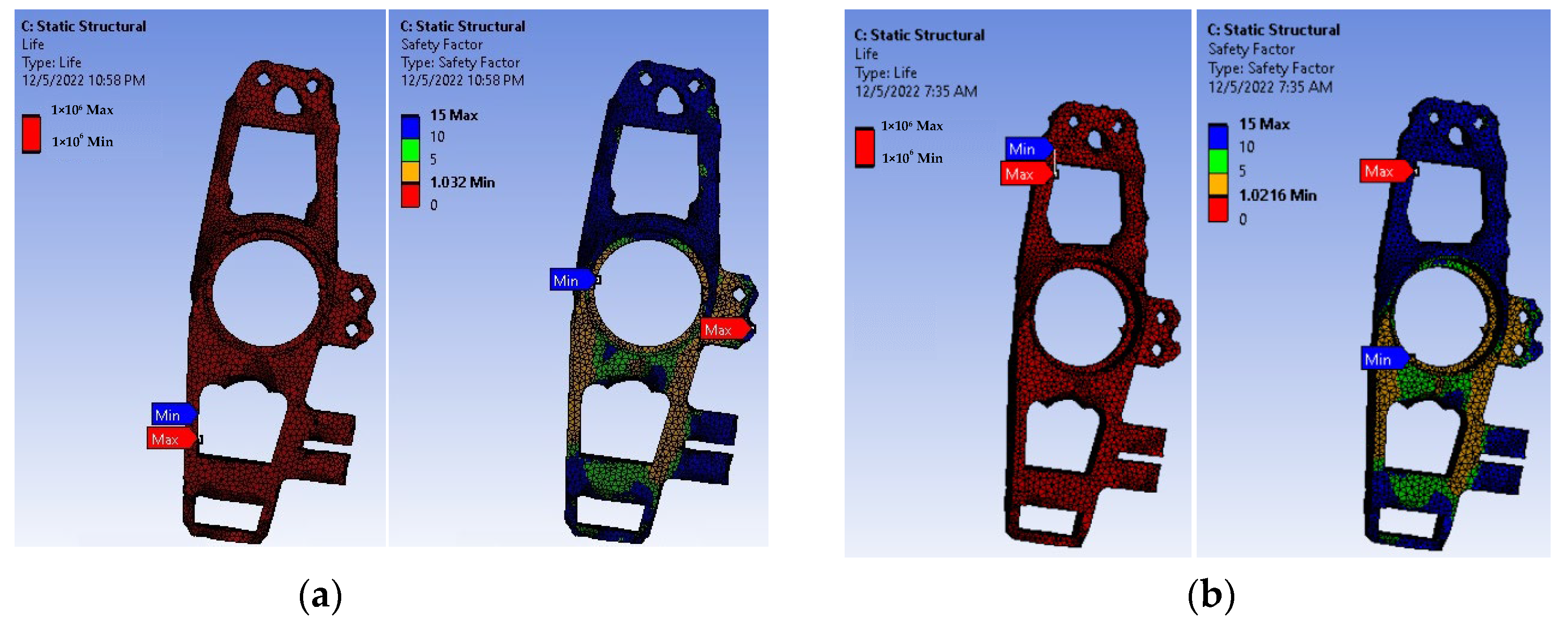
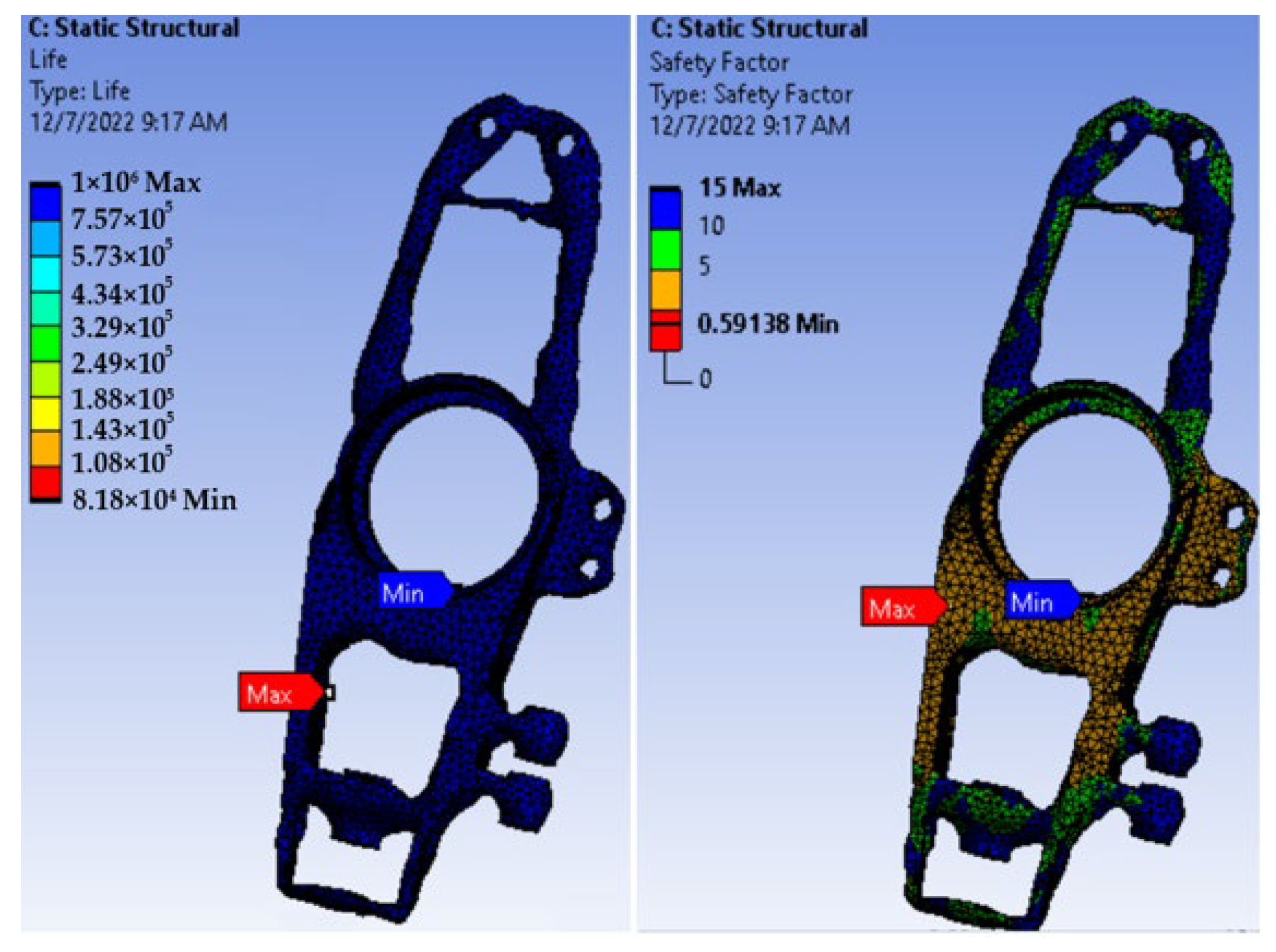
In the fatigue analysis, steel 4130 demonstrates excellent performance, with a safety factor above 4 and the capability to withstand up to 15 load cycles with a minimum of 1 cycle. The stresses remain below the endurance limit, and the safety factor surpasses the 2 × 10
5 fatigue life cycles, making it a highly suitable material choice. In contrast, structural steel exhibits a fatigue life of 67,999 cycles with a safety factor below 1, rendering it unsuitable for selection. AISI 1020 steel, on the other hand, showcases a minimum life cycle of 80,261 and a safety factor above 1 (2.12), making it a viable option for final selection based on fatigue considerations. In
Figure 9a and
Figure 10, the fatigue analysis for steel 4130 reveals a safety factor ranging from a minimum of 1.03 to a maximum of 15, with a fatigue life cycle of 1 × 10
5, indicating that this material model is suitable. However, in
Figure 9b, the fatigue life for AISI 1020 presents a minimum life cycle of 1 × 10
5 and a safety factor of 1.02, making it unsuitable for final selection. Turning to the results for structural steel, the minimum life cycle is 81,813, and the minimum safety factor is below 1, measuring 0.59. Thus, the structural steel model is unsuitable for final selection due to its inadequate fatigue performance.
3.5.2. Final Model and Material Selection
Table 6 presents the results of the final evaluation, which are based on data from the fatigue analysis. The selected final model geometry is steel 4130, which achieved a significant 60% mass reduction. Both structural steel and AISI 1020 steel demonstrate a fatigue life cycle exceeding the design life. However, only AISI meets the desired safety factor for the 60% mass reduction analysis. In contrast, steel 4130 achieves the desired fatigue life cycle at both 60% and 52% mass reduction levels. These fatigue analysis results play a crucial role in selecting the optimal material and ensuring the steering knuckle’s structural integrity and performance under various loading conditions.
4. Results and Discussion
4.1. Optimization of Result Analysis and Simulation Validation
The final geometry shape, made with steel 4130, maintains the same boundary conditions. The topology analysis results provided the final geometric shape for the structurally sound knuckle part, as depicted in
Figure 11a. The FEM model of the knuckle followed the same procedure as the initial analysis, illustrated in
Figure 11b. After the final TO, the model experienced static analysis, employing the same constraints and loads as the initial analysis conditions for steel 4130. The analysis aimed to evaluate the material’s final factor of safety, total deformation, and maximum stress value to ensure the model’s stiffness. The ultimate mass of the steering knuckle geometry structure was determined to be 0.93 kg.
4.2. Analysis Affirmation under Turning Brake Conditions
The results demonstrate that the final optimized geometric model maintains the same stiffness as the initial analysis model. The meshing principle, constraint boundary conditions, and loads at each joint remain unchanged from the initial static analysis conditions based on the turning brake condition. The material property input parameters for the 4130 steel are also consistent with the boundary state.
Figure 12 shows the computed stress contour and deformation contour, indicating a maximum stress value of 133.32 MPa and a maximum deformation value of 0.17. The safety factor is 1.03, and the stress value remains well below the yield limit. The fatigue analysis of this final model also retains the same safety factor above 1, meeting the required standards for safety performance.
4.3. Analysis Affirmation under Emergency Braking Conditions and Turning Conditions
In contrast to the analysis of the sharp turn condition, the geometric model was independently defined through meshing, material parameter settings, constraint boundary conditions, and load considerations specific to the emergency braking condition. The load applied to each connecting hole was meticulously calculated based on this scenario.
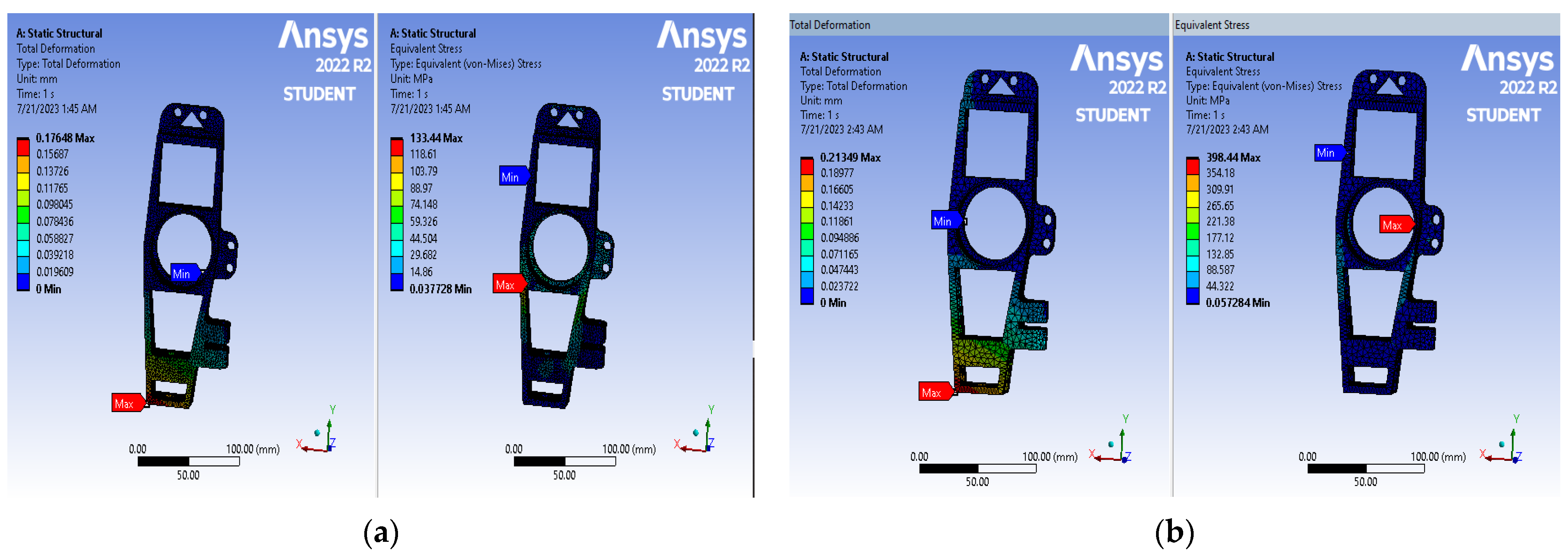
Figure 13a illustrates the analysis model of the knuckle, presenting the stress and deformation contours. The maximum stress value is recorded as 133.44 MPa, while the maximum deformation reaches 0.17. These results yield a safety factor of 1.06, satisfying the safety performance criteria.
Similarly, the geometric model was explicitly defined, encompassing meshing, material parameter settings, constraint boundary conditions, and load considerations specifically tailored to the emergency turning condition. The analysis model’s outcome is presented in
Figure 13b, illustrating stress and deformation contours resulting from rigorous analysis and computation. The maximum stress value is recorded at 398.44 MPa, while the maximum deformation reaches 0.21, resulting in a safety factor of 1.04, satisfying the safety performance requirements.
4.4. Discussion of the Fatigue Sensitivity Analysis of the Final Model
This research implies a work phase in the model’s development life cycle. By evaluating fatigue life prediction analytic capabilities early in the design process and applying computer-based digital processing techniques, which reflect material performance, the life cycle potential is greatly reduced [
19].
Figure 14a,b illustrate the combined objective convergence and full sensitivity analysis of the 4130 steel material in the model. According to the Fatigue Sensitivity graph, the model can tolerate a maximum of 1 × 10
6 cycles. However, when the load is increased by 1.25 times, the life span is shortened. Conversely, if the load is reduced to 0.75 times, the life span increases to 1 × 10
6 cycles. Furthermore, the life cycle remains the same when the load is increased from 0.5 to less than 1.25 times.
Figure 14a demonstrates that increasing the load by 1.25 times results in a decrease in life to less than 2.5 × 10
5 cycles. Conversely, reducing the load to 0.75 times leads to a life cycle of 7.5 × 10
5 cycles.
Additionally, when the load is reduced to 0.5, the model achieves a life cycle of 1 × 10
6 and still satisfies the requirements even when the load is increased to 1. The Fatigue Sensitivity output confirms a life cycle of 1 × 10
6.
Figure 14b presents the mass constraint graph after 18 iterations, along with the mass response criterion and the convergence value.
5. Conclusions
In this paper, a lightweight optimization of the FSAE steering knuckle was conducted using the TO method considering two different mass constraints (40% and 48%). Three materials, namely structural steel, 4130 steel, and AISI 1020 steel, were analyzed, providing Stress–Life (SN) curves for each material. Upon conducting a comprehensive material analysis, the results show that steel 4130 achieved a mass reduction of 42.70% under the same stress limit and 40% mass constraints. For structural steel and AISI 1020, the mass reductions were 53.49% and 39.36%, respectively, under the same conditions. Similarly, under the stress limit and 48% mass constraints, steel 4130, structural steel, and AISI 1020 achieved mass reductions of 39.28%, 46.56%, and 38.36%, respectively. Out of these materials, steel 4130 emerges as the optimal choice for the steering knuckle due to its superior performance in weight reduction, stress, deformation, and safety factors. The results of the TO process for the FSAE steering knuckle, focusing on weight reduction and increased stiffness, have been successfully achieved, particularly with steel 4130. Based on these findings, the following conclusions are drawn.
Firstly, a robust mathematical model for optimizing the steering knuckle’s topology was established after evaluating the structural TO approach. The geometry of the knuckle was designed to meet the suspension standards of the 2022 University Formula Competition.
Secondly, a comprehensive analysis was conducted, comparing three different materials (structural steel, steel 4130, and AISI 1020) with various response constraints for mass reduction. Among them, steel 4130 exhibited the most favorable output in terms of weight reduction, maximum stress, deformation, and safety factor under static conditions.
Thirdly, the final geometry model of the steering knuckle was further optimized, resulting in a lightweight (LW) steering knuckle with an impressive 42.70% mass reduction. Simulation tests under various boundary conditions confirmed that the LW knuckle design met all analysis criteria.
Fourthly, a fatigue analysis was performed on the three materials, with AISI 1020 and steel 4130 displaying superior endurance, reaching a minimum life cycle of 1 × 105 and 2 × 105 cycles, respectively. The safety factor for steel 4130 exceeded 1, meeting the final design requirements. A sensitivity analysis of the final model was also conducted and illustrated.
This research highlights the significance of material selection and the TO method in achieving a lightweight and high-performance steering knuckle for student formula racing vehicles. To further enrich the study and encourage future research, some intriguing open questions are proposed:
How can advanced optimization algorithms enhance lightweight steering knuckle design considering dynamic loads and multi-objectives?
What are the potential challenges and benefits of implementing lightweight steering knuckle design in a Formula SAE Electric Vehicle and adapting it to other vehicle configurations?
By addressing these open questions and exploring the suggested avenues for future research, the field of lightweight steering knuckle design can progress, benefiting both Formula SAE vehicles and broader automotive engineering endeavors.