Comparison and Analysis of Electromagnetic Characteristics of Basic Structure of Wireless Power Coil for Permanent Magnet Motors in Electric Vehicles
Abstract
1. Introduction
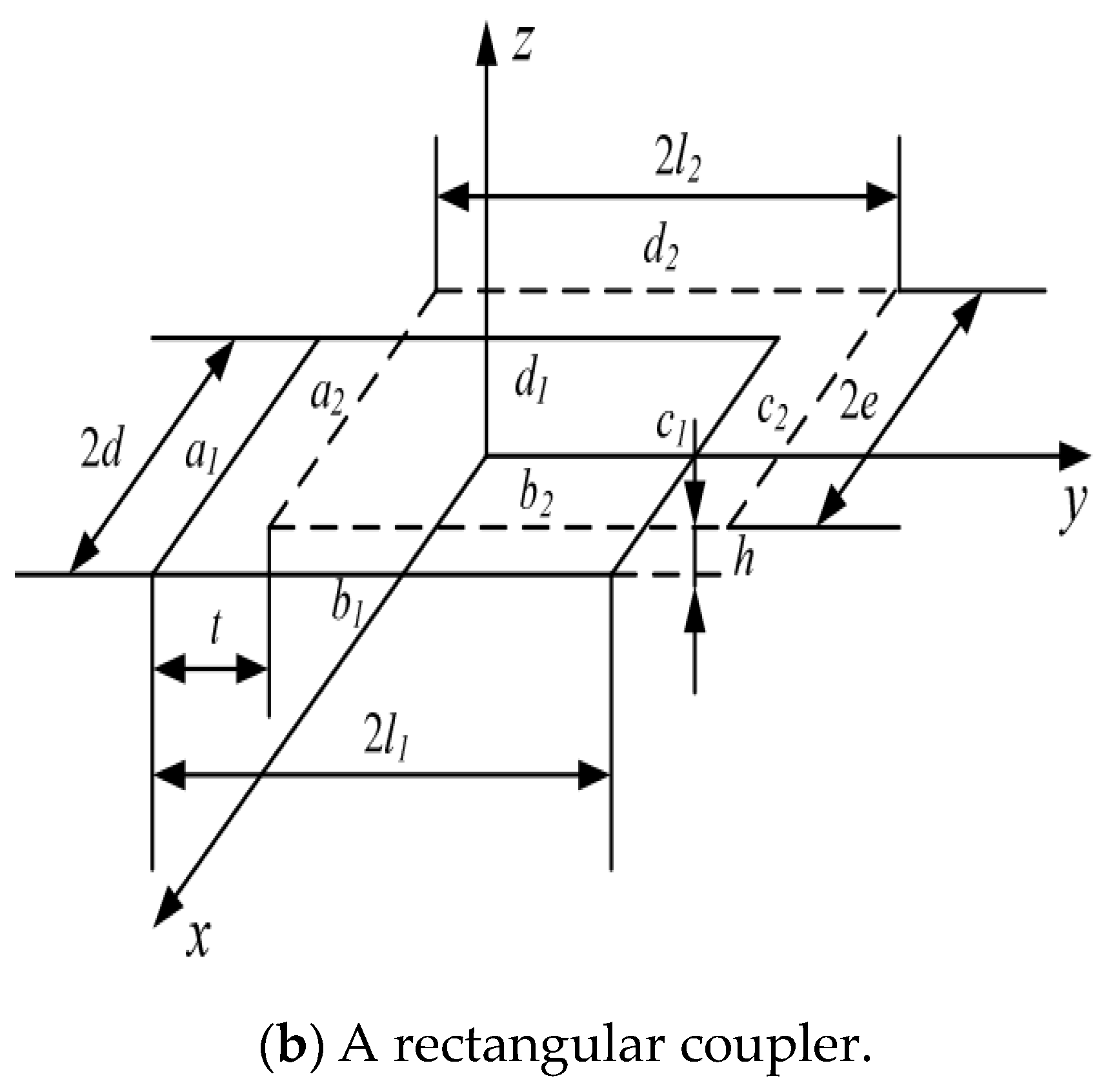
2. Modeling and Analysis
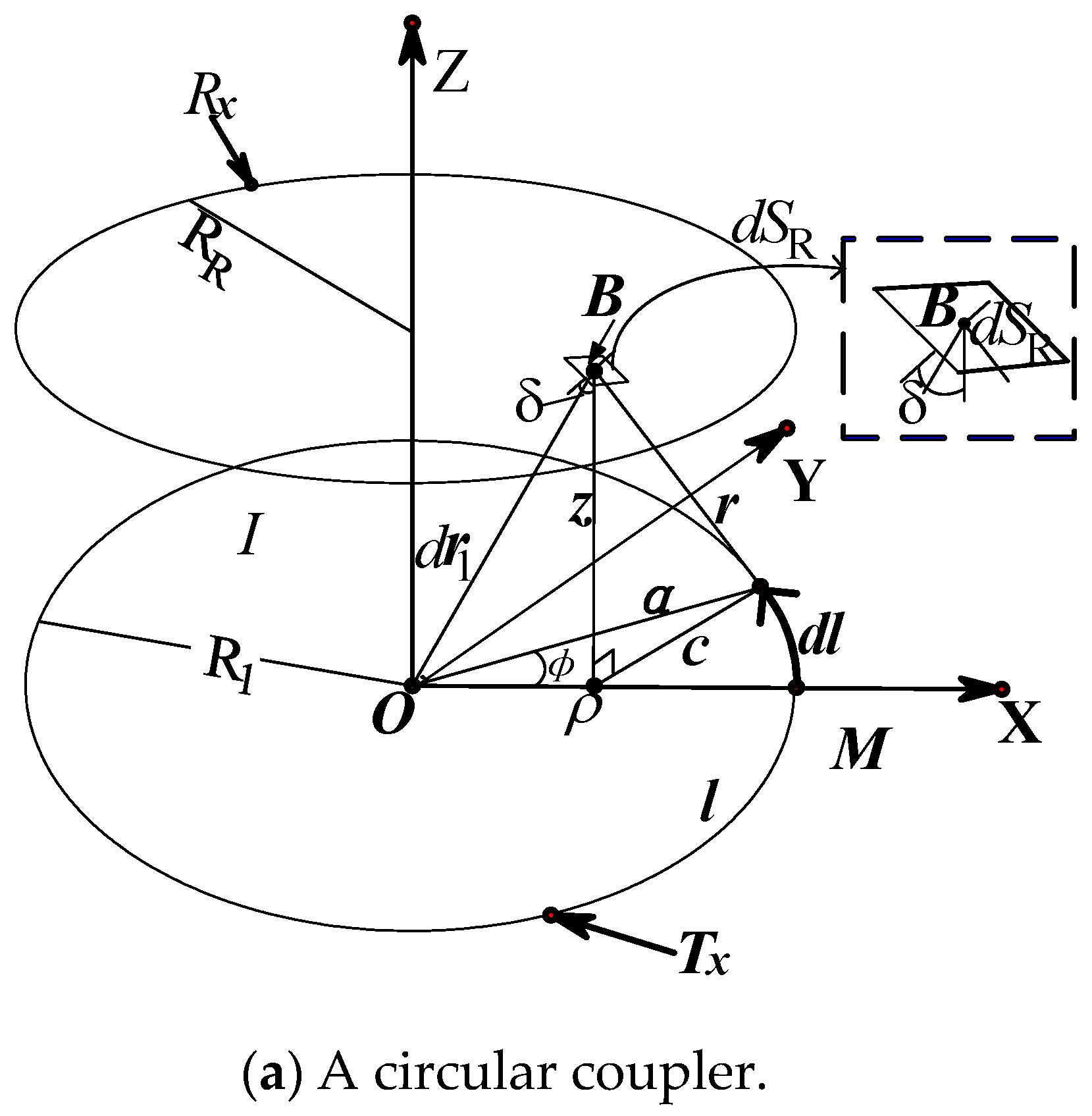
2.1. Derivation of Circular Coil Magnetic Flux Density
2.2. Derivation of Square Coil Magnetic Flux Density
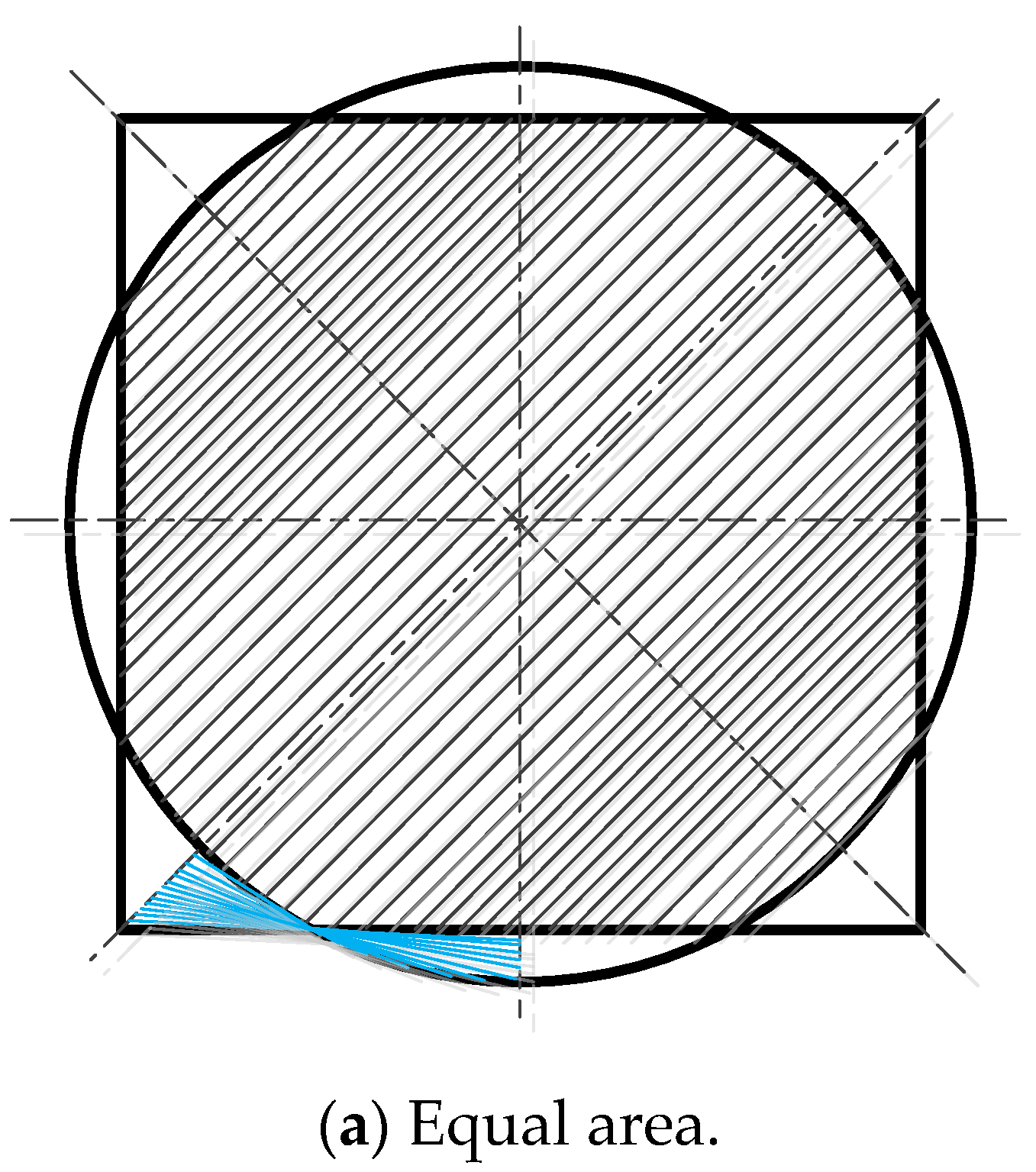
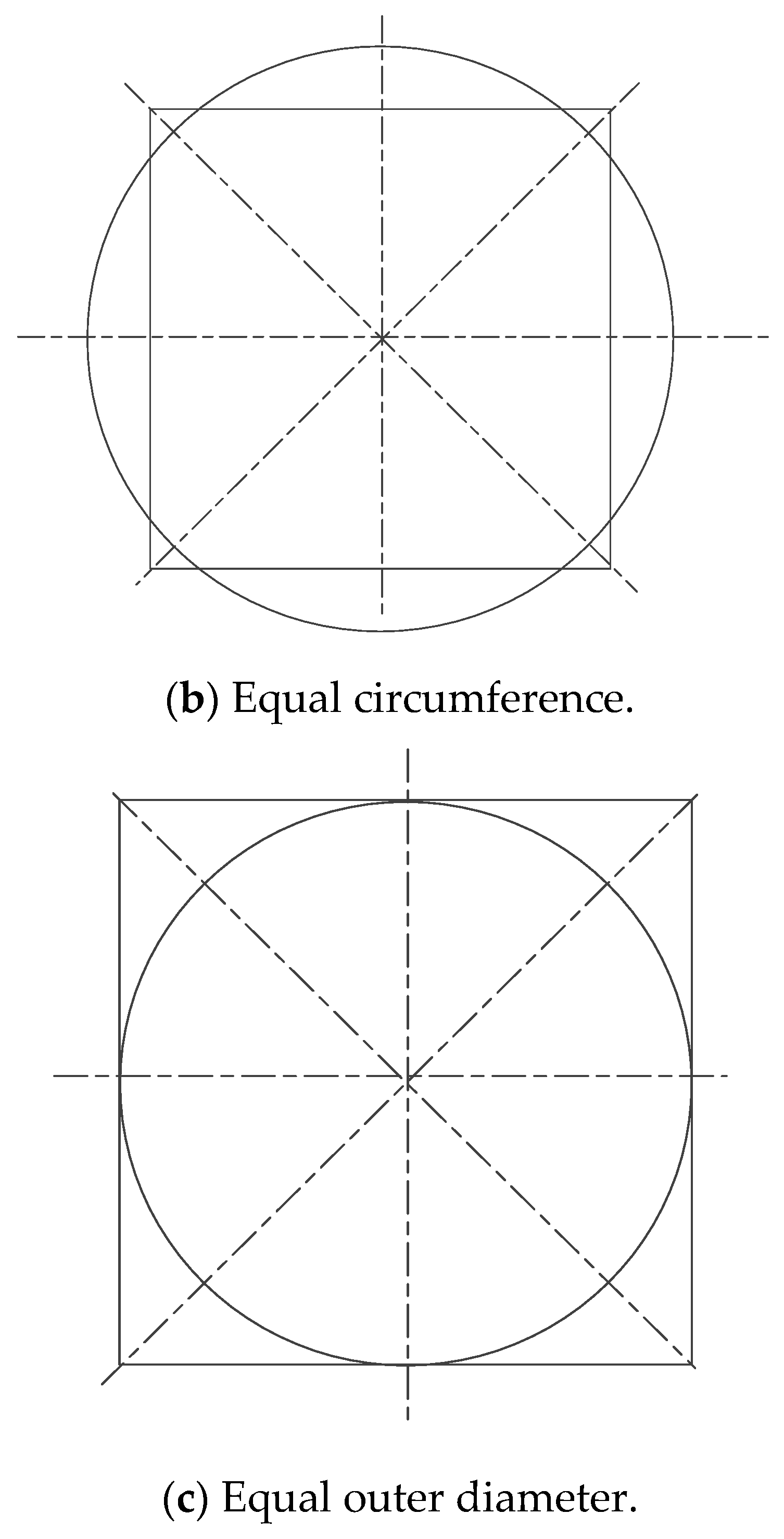
2.3. Qualitative Analysis of Electromagnetic Properties
3. Numerical Simulations
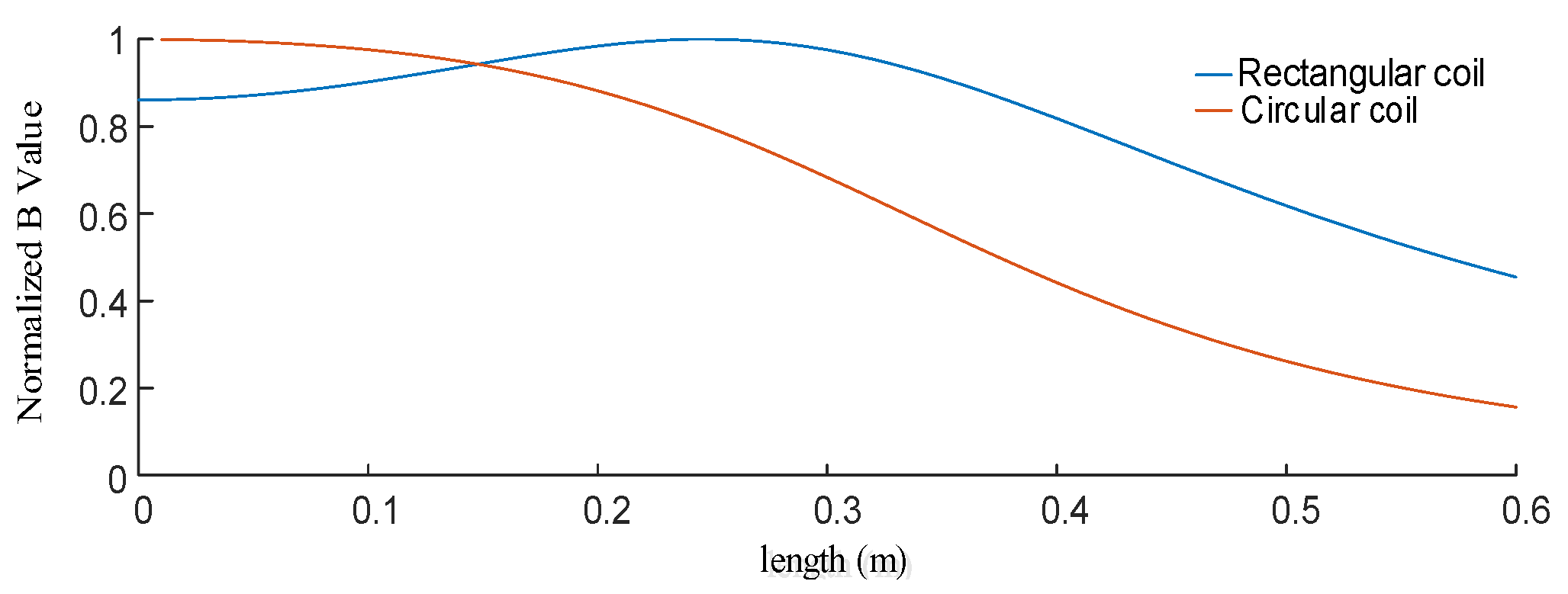
3.1. Normalized Coupling Coefficient Comparison
3.2. Coupling Mutual Inductance Comparison
4. Experimental Validation
5. Discussion of the Electromagnetic Characteristics of Two Basic Coil Shapes
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Z.; Liu, F.; Chen, K. New progress of wireless charging technology for electric vehicles. Trans. China Electrotech. Soc. 2016, 31, 30–40. (In Chinese) [Google Scholar]
- Assawaworrarit, S.; Yu, X.; Fan, S. Robust wireless power transfer using a nonlinear parity-time-symmetric circuit. Nature 2017, 546, 387. [Google Scholar] [CrossRef] [PubMed]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless power transfer via strongly coupled magnetic resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.F.; Huang, X.L.; Wang, W. Efficiency analysis of magnetic resonance wireless power transfer with three-dimensional transmitters. J. Appl. Phys. 2015, 117, 83. [Google Scholar] [CrossRef]
- Wake, K.; Laakso, I.; Hirata, A.; Chakarothai, J.; Onishi, T.; Watanabe, S.; De Santis, V.; Feliziani, M. Derivation of Coupling Factors for Different Wireless Power Transfer Systems: Inter- and Intralaboratory Comparison. IEEE Trans. Electromagn. Compat. 2017, 59, 677–685. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Y.; Liu, X.; Xu, D. S/CLC Compensation Topology Analysis and Circular Coil Design for Wireless Power Transfer. IEEE Trans. Transp. Electrif. 2017, 3, 496–507. [Google Scholar] [CrossRef]
- Budhia, M.; Boys, J.T.; Covic, G.A.; Huang, C.-Y. Development of a Single-Sided Flux Magnetic Coupler for Electric Vehicle IPT Charging Systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Budhia, M.; Covic, G.A.; Boys, J.T. Design and optimization of circular magnetic structures for lumped inductive power transfer systems. IEEE Trans. Power Electron. 2011, 26, 3096–3108. [Google Scholar] [CrossRef]
- Budhia, M.; Covic, G.; Boys, J. A new IPT magnetic coupler for electric vehicle charging systems. In Proceedings of the IECON 2010—36th Annual Conference on IEEE Industrial Electronics Society, Glendale, AZ, USA, 7–10 November 2010; pp. 2487–2492. [Google Scholar]
- Takanashi, H.; Sato, Y.; Kaneko, Y.; Abe, S.; Yasuda, T. A large air gap 3 kW wireless power transfer system for electric vehicles. In Proceedings of the Energy Conversion Congress and Exposition, Raleigh, NC, USA, 15–20 September 2012; pp. 269–274. [Google Scholar]
- Zaheer, A.; Kacprzak, D.; Covic, G.A. A bipolar receiver pad in a lumped IPT system for electric vehicle charging applications. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 283–290. [Google Scholar]
- Moon, S.; Kim, B.-C.; Cho, S.-Y.; Ahn, C.-H.; Moon, G.-W. Analysis and Design of a Wireless Power Transfer System with an Intermediate Coil for High Efficiency. IEEE Trans. Ind. Electron. 2014, 61, 5861–5870. [Google Scholar] [CrossRef]
- Kim, S.; Covic, G.A.; Boys, J.T. Tripolar Pad for Inductive Power Transfer Systems for EV Charging. IEEE Trans. Power Electron. 2017, 32, 5045–5057. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Yang, Q.; Liu, L.; Ma, J.; Zhang, X. A Novel Coil with High Misalignment Tolerance for Wireless Power Transfer. IEEE Trans. Magn. 2019, 55, 2800904. [Google Scholar] [CrossRef]
- Luo, Z.; Wei, X. Analysis of Square and Circular Planar Spiral Coils in Wireless Power Transfer System for Electric Vehicles. IEEE Trans. Ind. Electron. 2018, 65, 331–341. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, X.; Wang, W. Wireless power transfer with two-dimensional resonators. IEEE Trans. Magn. 2014, 50, 1–4. [Google Scholar] [CrossRef]
- Zhao, J. Research on Three-Dimensional Wireless Power Transmission System. Ph.D. Thesis, Southeast University, Nanjing, China, 2015. (In Chinese). [Google Scholar]


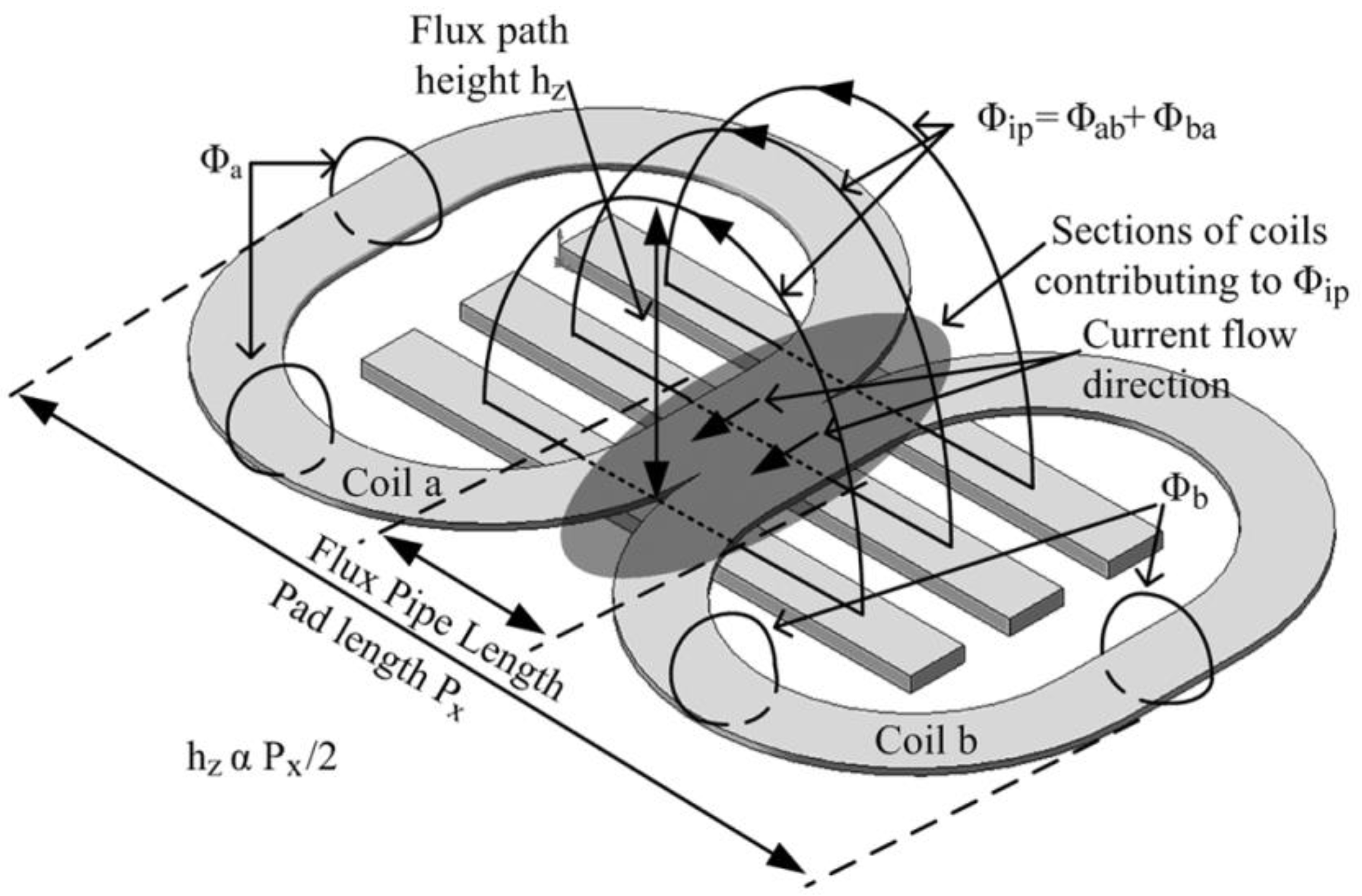
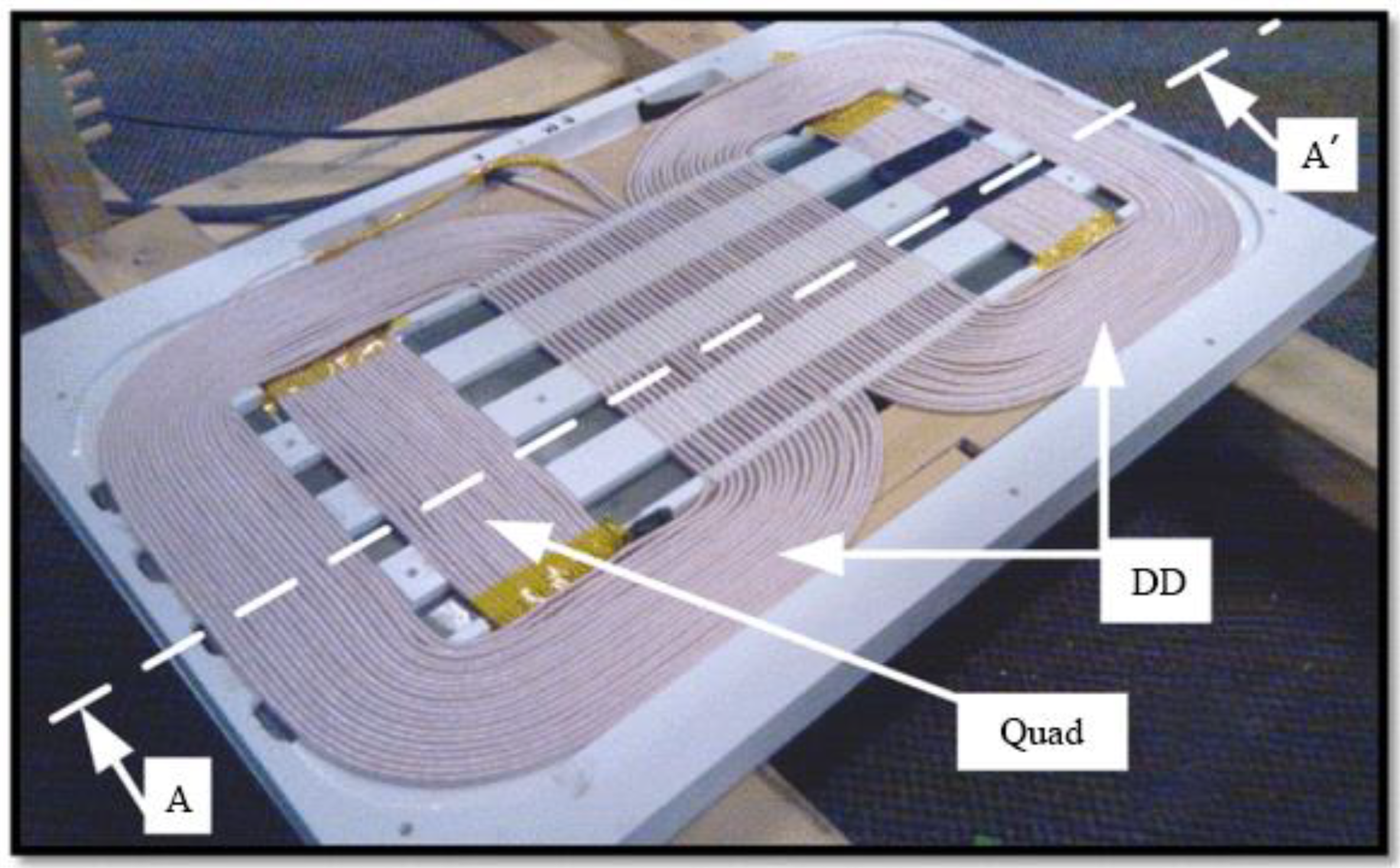
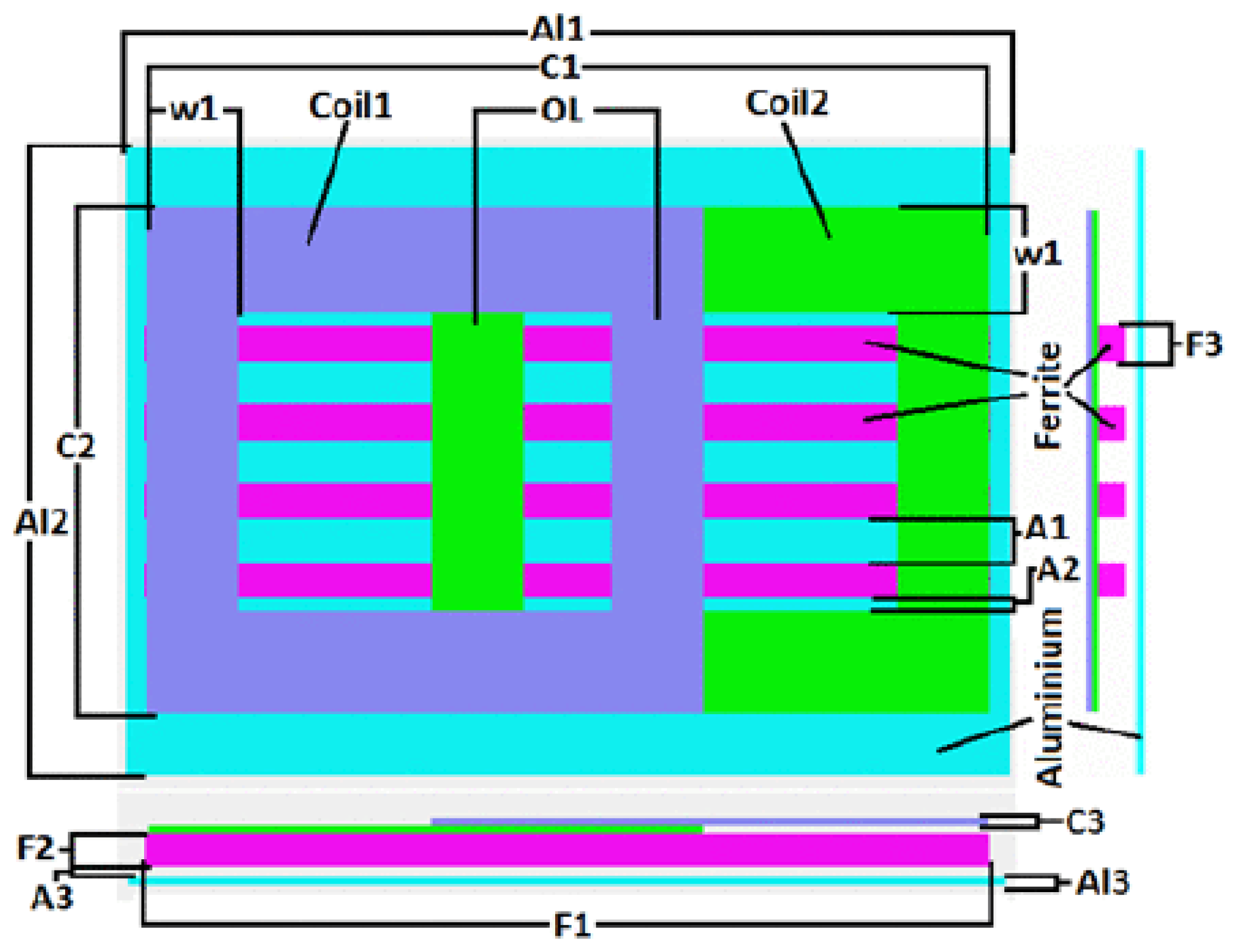








| Coil Type | Offset Resistance | Magnetic Leakage | Losses (nH) | Coefficient (%) |
|---|---|---|---|---|
| Flux pipe | better | larger | larger | 42 (offset) |
| H | better | larger | larger | 90 |
| DD | better | smaller | average | 95.66 |
| DDQ | better | smaller | smaller | 95 |
| BP | average | smaller | smaller | 92.85 |
| Coil Type | Pacing (m) | Area (m2) | Mutual Inductance (nH) | Coupling Coefficient (%) |
|---|---|---|---|---|
| circular | 0.3 | 0.09 | 30 | 2.52 |
| hybrid | 29 | 2.4 | ||
| rectangular | 28 | 2.23 | ||
| circular | 0.16 | 67.5 | 4.13 | |
| hybrid | 66.9 | 3.94 | ||
| rectangular | 65.5 | 3.75 | ||
| circular | 0.25 | 120 | 5.62 | |
| hybrid | 119.19 | 5.4 | ||
| rectangular | 117.5 | 5.15 |
| Coil Type | Pacing (m) | Area (m2) | Perimeter (m) | Outer Diameter (m) | Mutual Inductance (nH) | Coupling Coefficient (%) |
|---|---|---|---|---|---|---|
| circular | 0.3 | 0.09 | 1.06 | 0.34 | 30 | 2.52 |
| hybrid | 29 | 2.4 | ||||
| rectangular | 1.2 | 0.3 | 28 | 2.23 | ||
| circular | 0.11 | 1.2 | 0.38 | 42.22 | 3.12 | |
| hybrid | 34.95 | 2.69 | ||||
| rectangular | 0.09 | 0.3 | 28 | 2.23 | ||
| circular | 0.07 | 0.94 | 0.3 | 19.99 | 1.97 | |
| hybrid | 23.7 | 2.1 | ||||
| rectangular | 0.09 | 1.2 | 28 | 2.23 |
| Coil Type | Pacing | Mutual Inductance | Coupling Coefficient |
|---|---|---|---|
| (mm) | (uH) | (%) | |
| circular | 67.82 | 0.857 | 11.5 |
| hybrid | 0.844 | 11.21 | |
| rectangular | 0.735 | 9.66 | |
| circular | 79.17 | 0.609 | 8.17 |
| hybrid | 0.607 | 8.06 | |
| rectangular | 0.593 | 7.8 | |
| circular | 105.17 | 0.332 | 4.46 |
| hybrid | 0.329 | 4.37 | |
| rectangular | 0.326 | 4.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Zhao, L.; Zou, Y.; Chen, T. Comparison and Analysis of Electromagnetic Characteristics of Basic Structure of Wireless Power Coil for Permanent Magnet Motors in Electric Vehicles. World Electr. Veh. J. 2023, 14, 199. https://doi.org/10.3390/wevj14080199
Zhao J, Zhao L, Zou Y, Chen T. Comparison and Analysis of Electromagnetic Characteristics of Basic Structure of Wireless Power Coil for Permanent Magnet Motors in Electric Vehicles. World Electric Vehicle Journal. 2023; 14(8):199. https://doi.org/10.3390/wevj14080199
Chicago/Turabian StyleZhao, Junfeng, Lingyun Zhao, Yuwei Zou, and Tianjin Chen. 2023. "Comparison and Analysis of Electromagnetic Characteristics of Basic Structure of Wireless Power Coil for Permanent Magnet Motors in Electric Vehicles" World Electric Vehicle Journal 14, no. 8: 199. https://doi.org/10.3390/wevj14080199
APA StyleZhao, J., Zhao, L., Zou, Y., & Chen, T. (2023). Comparison and Analysis of Electromagnetic Characteristics of Basic Structure of Wireless Power Coil for Permanent Magnet Motors in Electric Vehicles. World Electric Vehicle Journal, 14(8), 199. https://doi.org/10.3390/wevj14080199






