1. Introduction
Electric vehicles are rapidly gaining importance in the automotive industry due to their potential to reduce greenhouse gas emissions and improve air quality. According to a report by the International Energy Agency (IEA) [
1], electric vehicle sales in 2020 reached a record high of 3.1 million, a 41% increase compared to the previous year (IEA, Paris, France, 2021). The report also predicts that by 2030, over 145 million electric vehicles will be on the road worldwide. Electric vehicles (EVs) have gained popularity due to their zero emissions when in motion, making them an environmentally friendly option for transportation. This characteristic is one of the reasons governments incentivize the purchase of electric vehicles by offering various subsidies and incentives to individuals and businesses. Electric vehicles consist of three essential components. Firstly, the battery system serves as the primary power source, storing and supplying electricity to propel the vehicle. Secondly, the electric motor converts electrical energy into mechanical motion, driving the wheels. Finally, the electric drive unit controls the power distribution and manages the overall performance of the vehicle’s propulsion system. Together, these components enable the efficient and eco-friendly operation of electric vehicles.
By allowing an EV to receive energy wirelessly during its motion, the range anxiety of EV drivers can be significantly reduced, particularly in cities with large travelling distances between the different locations [
2].
As electric vehicles become increasingly popular, it is essential to consider how they will be charged. Traditional charging methods require the vehicle to be plugged into a power source, which can be inconvenient for drivers who need to find a charging station and wait for their car to charge. This is where wireless charging via induction can provide a solution by using magnetic fields to transfer conveniently and efficiently. This technology could also increase the adoption of electric vehicles by reducing range anxiety and making charging more accessible. As electric vehicles continue to gain traction, it is clear that wireless charging via induction will play an essential role in the future of sustainable transportation.
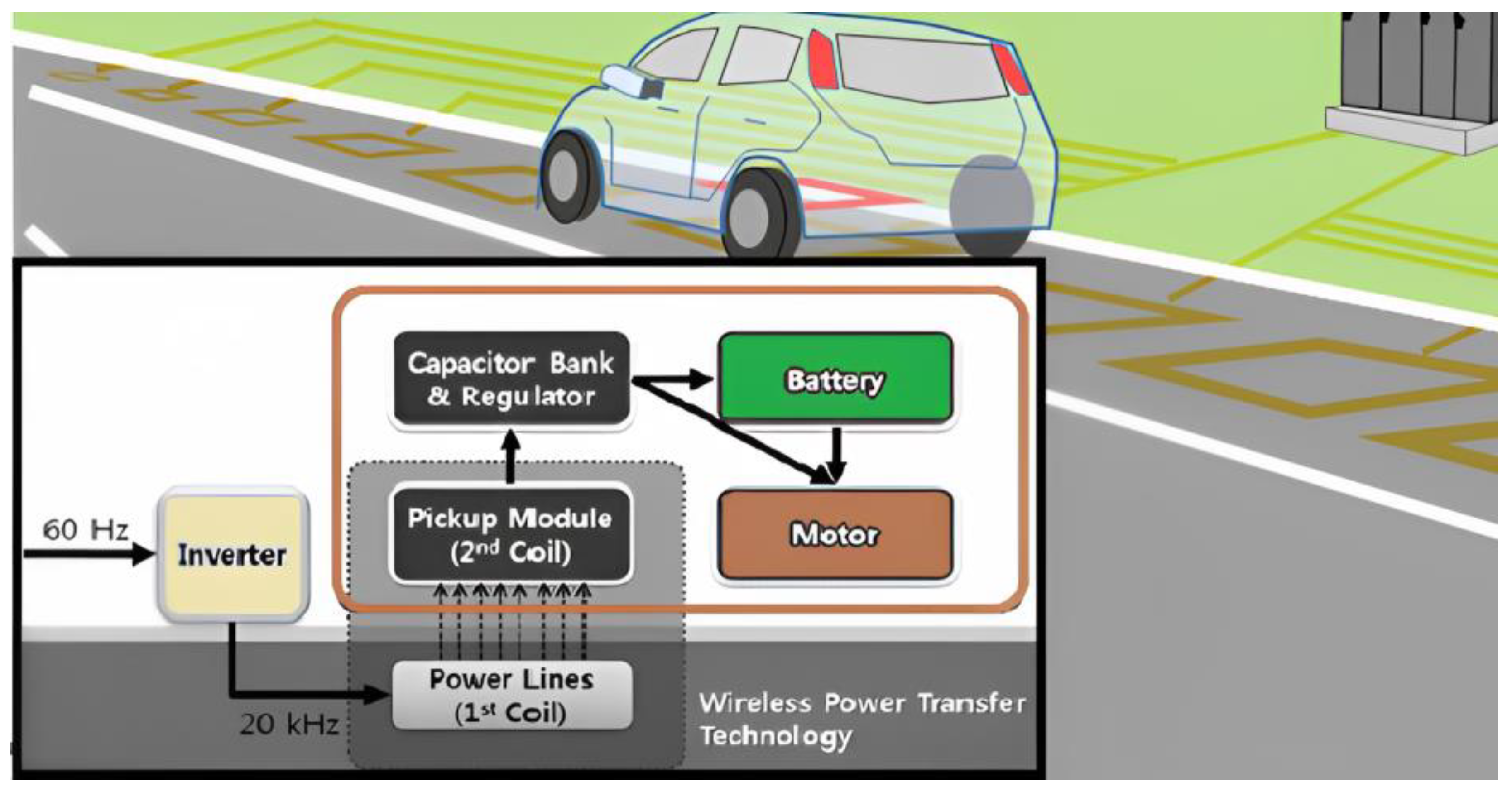
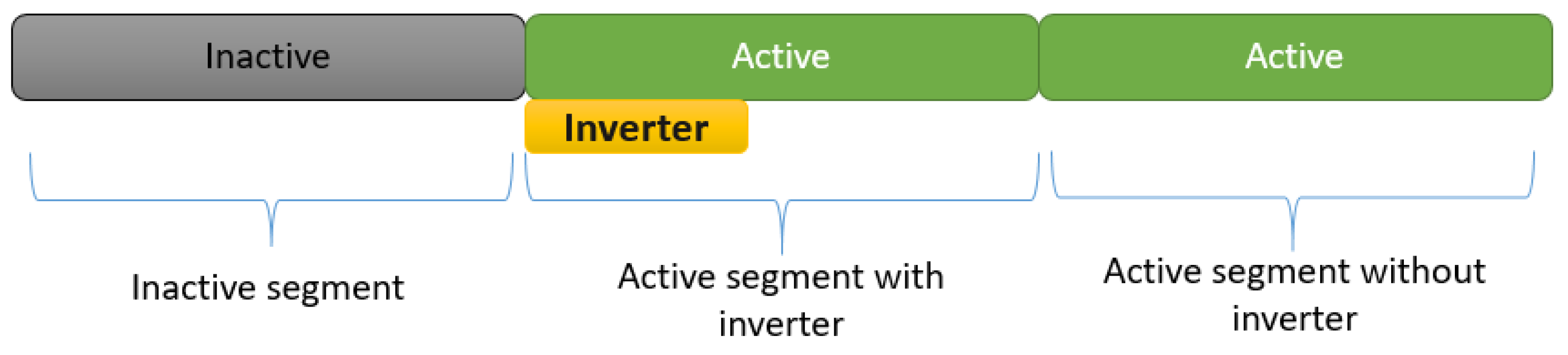
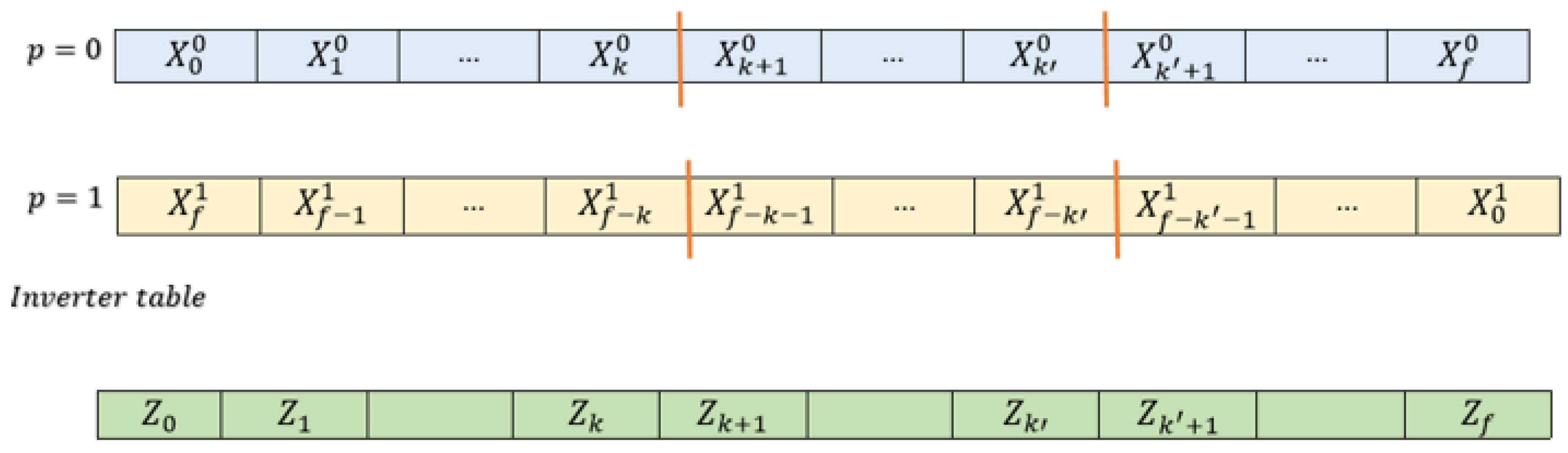
While wireless charging via induction is a promising technology for electric vehicles, it is essential to consider the cost implications. Installing wireless charging infrastructure for electric vehicles is currently more expensive compared to traditional charging methods. This cost disparity necessitates careful planning and significant investment for achieving widespread adoption. A wireless charging pad consists of an inverter and a series of segments designed for charging. The energy between two coils and wireless charging eliminates the need for cables and plugs.
A wireless charging system typically includes a power factor correction (PFC), inverter, primary topology, transmitting coil, receiving coil, secondary topology, rectifier, and load [
3]. The inverter converts AC power from the grid into the high-frequency AC power needed for the wireless charging process. The segments, made up of wire coils, generate a magnetic field when current is passed through them. This magnetic field induces a current in the receiving coil on the underside of the electric vehicle, which is then converted back into DC power to charge the battery. The charging pad regulates the amount of power transferred to the vehicle, ensuring the charging process is safe and efficient. By using this wireless charging method, electric vehicle owners can enjoy the convenience of charging without having to plug in their vehicle, making the process more efficient and user-friendly. A representative diagram is shown in
Figure 1.
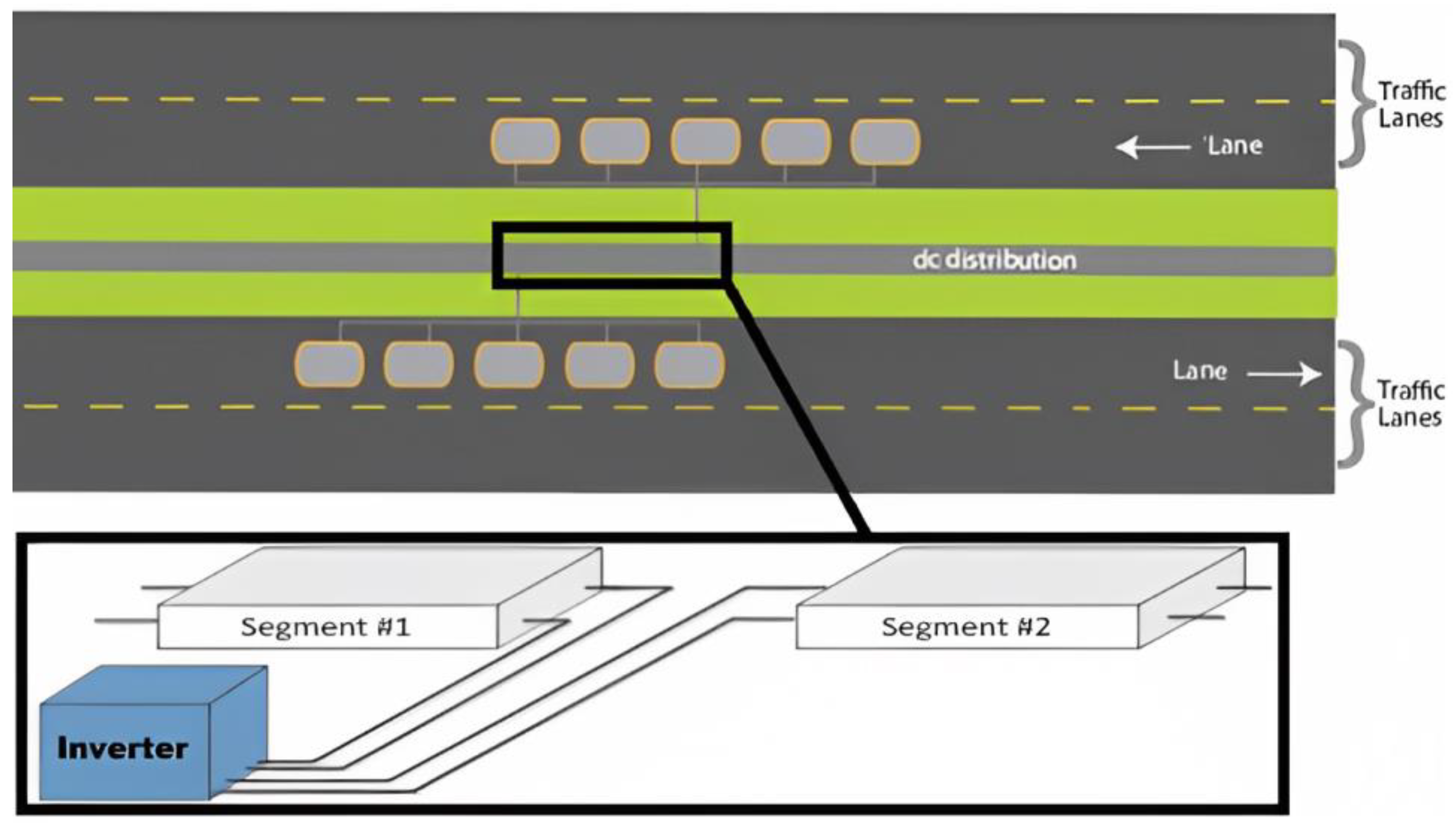
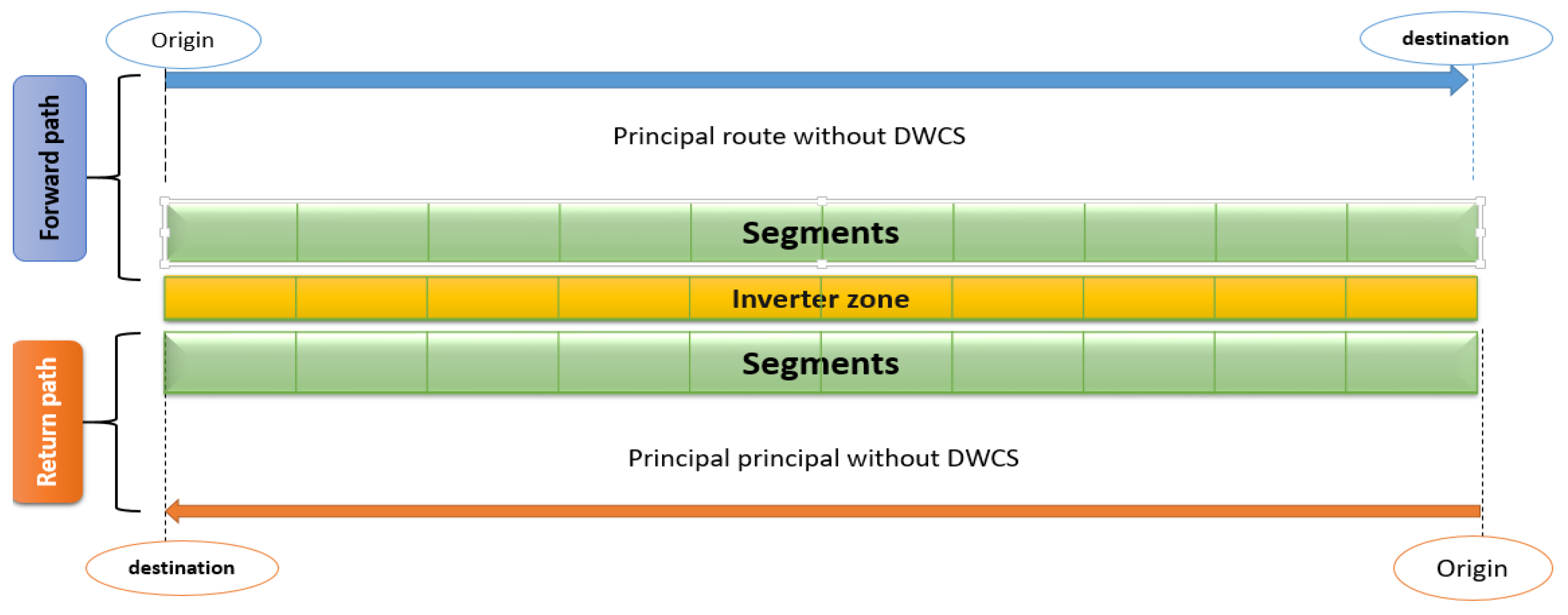
Wireless charging solves the problem of journeys with long distances like the highway. It is characterized by a long distance between the origin and the destination. The high speed of vehicles on this kind of road drains their battery very quickly, which requires very good planning to minimize the cost of the infrastructure installed on the highways. In particular, highways with unseparated lanes could benefit from wireless charging technology, as it allows for the simultaneous charging of electric vehicles in both lanes. This approach could also reduce the overall cost of the infrastructure, as the same inverter could be used for both lanes. This type of installation would require careful planning and coordination, as well as investment in the necessary infrastructure. However, the potential benefits of this approach could be significant, as it would provide a convenient and efficient charging option for electric vehicle drivers on highways. Furthermore, as the demand for electric vehicles continues to grow, installing wireless charging infrastructure on highways could accelerate the transition to a more sustainable transportation system.
Figure 2 shows the use of the same inverter for both highway lanes to minimize the infrastructure cost.
Among the main challenges of electric vehicles are charging methods and those related to the battery. In their article, Habib et al. [
4] provide an overview of various charging techniques for electric vehicles and examine their effects on power distribution systems. They also investigate coordinated and non-coordinated charging methods, delayed loading, and intelligent charge planning. The study concludes by examining the financial advantages of vehicle-to-grid (V2G) technology concerning charging approaches. Shuai et al. [
5] presented an overview of the contemporary economic model electric vehicles have created, considering the one-way and two-way energy flows enabled by EVs (wherein the vehicles can supply energy to the power grid). Their study scrutinized diverse EV charging infrastructures and techniques for unidirectional charging and bidirectional energy trading. They also investigated the feasibility of utilizing these vehicles as storage for renewable energy. Several researchers have also explored the various approaches proposed for charging electric vehicles. For instance, Tan et al. [
6] conducted a comprehensive analysis of the benefits and challenges of vehicle-to-grid (V2G) technology in both unidirectional and bidirectional charging modes. They also highlighted the obstacles associated with V2G implementation, such as battery degradation and high capital costs.
Additionally, they compiled a list of V2G optimization strategies that are classified based on the method used (e.g., Particle Swarm Optimization (PSO) and genetic algorithms (GAs)). Similarly, Hu et al. [
7] provided an overview and categorization of intelligent charging techniques for electric vehicle fleets, focusing on fleet operators. They discussed topics such as battery modelling, charging and communication standards, and driving patterns. Furthermore, they presented several control strategies for managing EV fleets, as well as mathematical algorithms for modelling them. In another study, Rahman et al. [
8] outlined various approaches utilized for addressing problems related to charging infrastructure for plug-in hybrid electric vehicles (PHEVs) and battery electric vehicles (BEVs).
Another significant aspect of electric vehicle (EV) charging pertains to battery management and battery health and longevity estimates, as these are crucial factors in enhancing battery lifespan. Li et al. [
9] provided an overview of recent developments in Big Data analytics that facilitate data-driven battery health assessment. They categorized the approaches based on their feasibility and cost-effectiveness and evaluated their advantages and limitations. Meanwhile, Liu et al. [
10] introduced a machine learning-based system that employs Gaussian process regression (GPR) to predict lithium-ion batteries’ ageing. In contrast, some studies have focused on advanced fault diagnosis techniques, since battery defects can lead to a decline in performance (Hu et al. [
11]).
Most of the travel on urban roads happens over short distances, which does not provide a significant challenge to the adoption of EVs. For most short-distance commutes, there is likely to be an opportunity to recharge at the destination without the need for dynamic charging. With most of the long-distance travel happening on highways, dynamic wireless charging infrastructure on highways can play a significant role in reducing range anxiety. High-power dynamic wireless charging systems will be necessary for roadway electrification to provide sufficient energy to EVs. In this context, we find the work of Wang et al. [
12], who presented a dynamic reversal approach for wireless charging lanes when automated and connected vehicles are present on a highway. This method seeks to enhance highway traffic flow and accommodate electric vehicles’ varying charging requirements in different directions. The authors created a mixed linear program to implement the proposed path reversal strategy and proved its effectiveness through numerical experiments. In their research, Bourzik et al. [
13,
14] suggested the installation of entry gates to Dynamic Wireless Charging (DWC) for EVs requiring a battery recharge and exit gates leading back to the main road for those who do not. Their study had two goals: first, to reduce the DWC usage cost for each vehicle type during the highway trip, and second, to identify the most cost-effective location for installing the gates on the road. The authors formulated the problem as a mathematical model and applied the non-dominated sorting genetic algorithm (NSGA-II) to obtain a solution.
Fuller [
15] introduced a flow-based model that aims to reduce the capital expenditure of implementing dynamic recharging infrastructure along California highways to accommodate the charging demands of EVs travelling between critical origins and destinations in the state. This model also considers the possibility of drivers reducing their EV’s speed while in the charging lanes to maximize energy replenishment. Xiaotong Sun et al. [
16] studied the most effective strategy for deploying static and dynamic charging infrastructure while taking into account the interdependence of transportation and power networks.
Ahmad et al. [
17] proposed a novel approach to reduce electric vehicle charging time by utilizing heterogeneous Battery Switching technology as an alternative charging option. They proposed a scheduling technique to minimize wait time and power loss at the designated Battery Switching Station. Zhang et al. [
18] introduced battery heterogeneity in the context of Battery Swapping (BS) services, where different types of electric vehicles (EVs) coexist, proposing a BS service framework based on battery heterogeneity.
Elbaz et al. [
19] presented a mathematical model that takes into account various factors affecting EV charging demand, including the number of EVs, alternative charging options, and the distance between charging stations. They also considered how different charging methods, such as dynamic and static charging, affect battery life.
In 2022, Elbaz et al. [
20] put forth a model to find the best spots to install wireless charging stations for EVs and determine the number of charging points at each location for the Round-Trip scenario. Meanwhile, Bourzik et al. [
21] investigated the issue of optimal locations for wireless charging infrastructure for heterogeneous battery EVs on highways with a single path. They used a road divided into equal-length segments to determine where to place the charging stations.
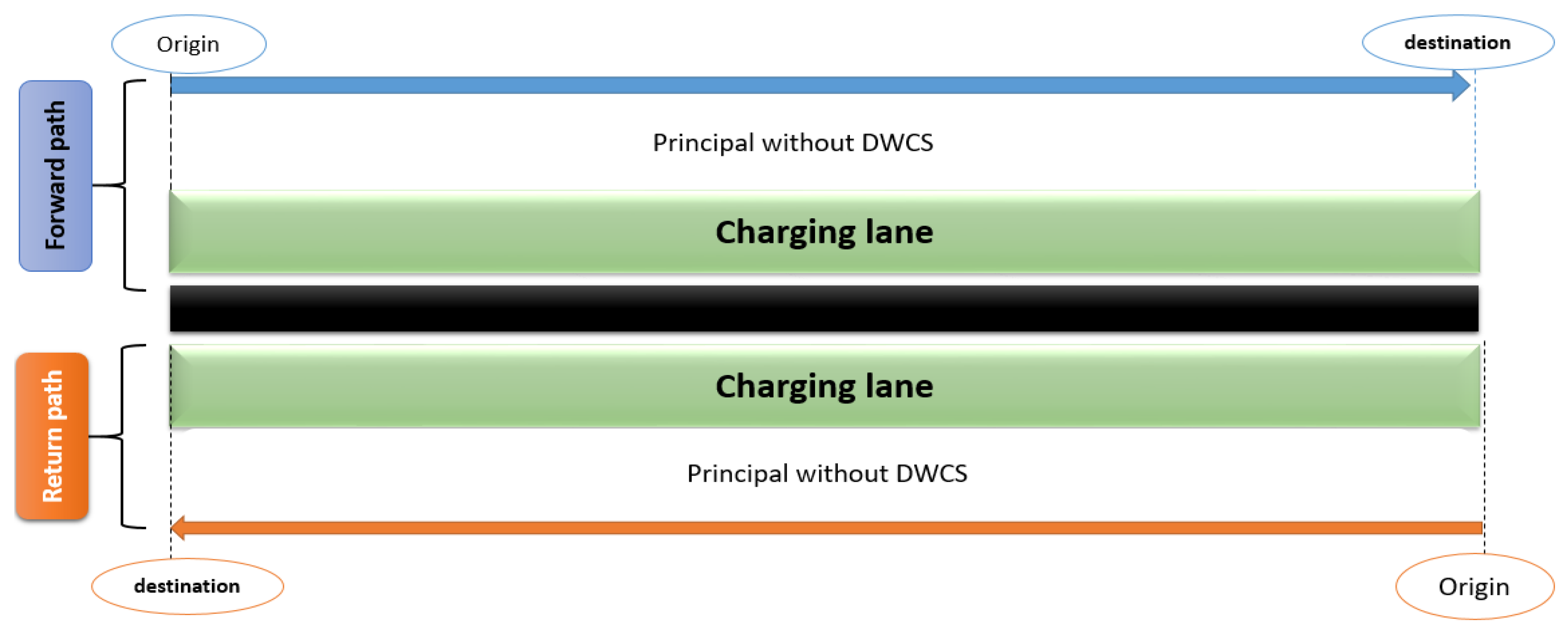
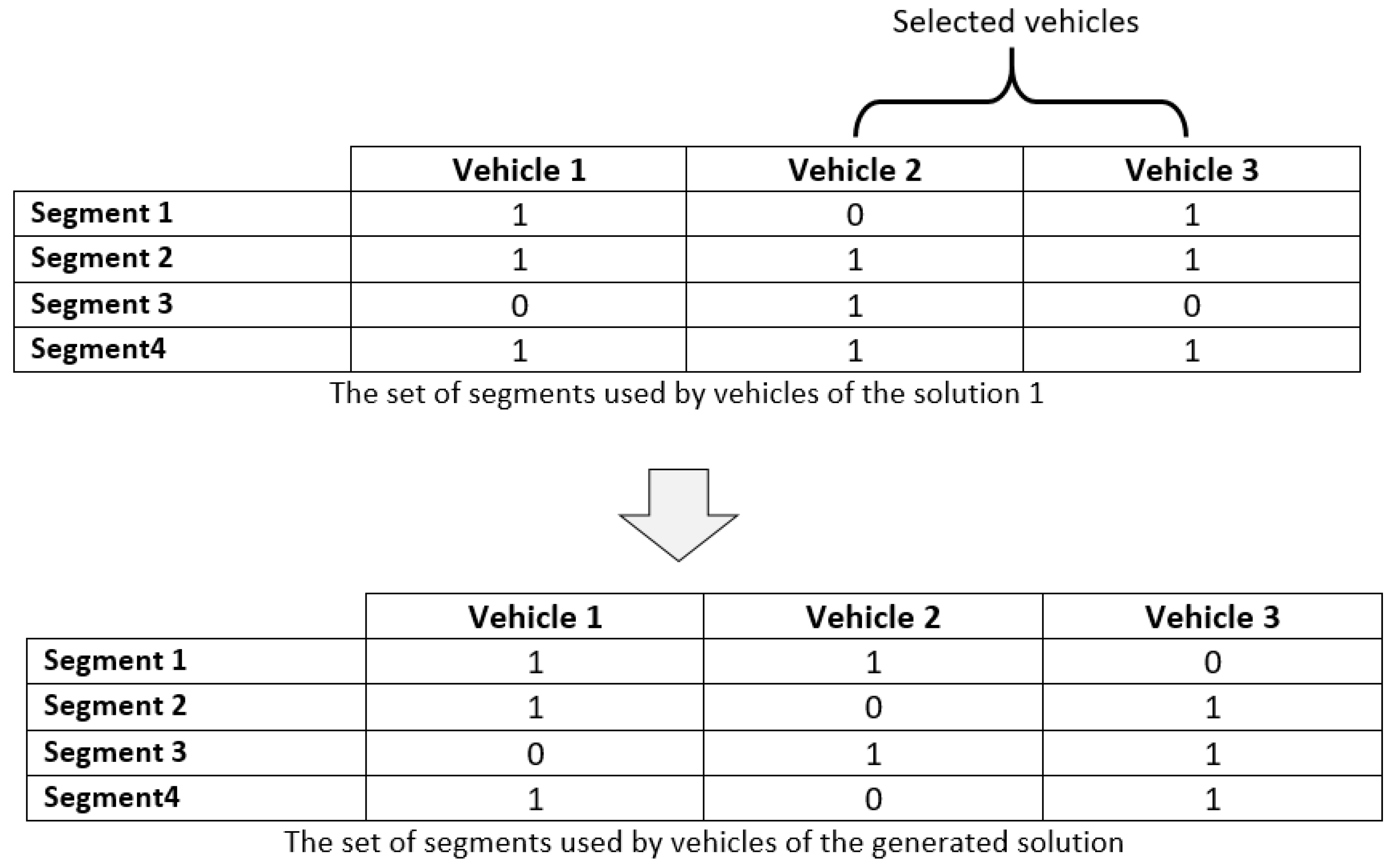
Most studies have concentrated on static or dynamic wireless charging infrastructure allocation, aiming to optimize its cost. However, this research focuses on a scenario where the electric vehicles are identical and treat the problem on the road with a single lane. Our contribution to this work is to propose a mathematical model for the study of the planning of electric vehicle infrastructure on highways by considering the two highway lanes simultaneously (for a round trip) with heterogeneous batteries. Then, one can solve the proposed mathematical model using a hybrid approach that combines genetic algorithms and local search techniques to balance diversification and intensification.
Initially, we explain the wireless charging technology. Subsequently, we propose an integer programming method to achieve an optimal infrastructure after describing the problem. The CPLEX optimizer is used to validate our model. Then, we apply an approximate method based on genetic algorithms and a local search on a real case study in the literature to compare with the case of studying each path separately. We analyze and discuss the results to highlight the effectiveness of our model, emphasizing the importance of studying the round trip and using the same inverters for both lanes to reduce infrastructure costs. Finally, we conclude by discussing the optimal placement of wireless charging infrastructures in transport networks. Electric vehicles have become the subject of much research today as they are considered the future of green logistics. This technology eliminates the need for various fuel types, and numerous studies have been conducted in this area.