Mixed Linear Model of a Safety Dispatch Model in an Active Distribution Network for Source–Grid–Load Interactions
Abstract
1. Introduction
2. Independent Grid Nodes Safety Control Model
2.1. System Safety Dispatch Control Target Model
2.2. Combination Optimization Model of Safety Control of Power Generation Nodes
2.3. Virtual Power Generation Safety Dispatching Model of Load Nodes
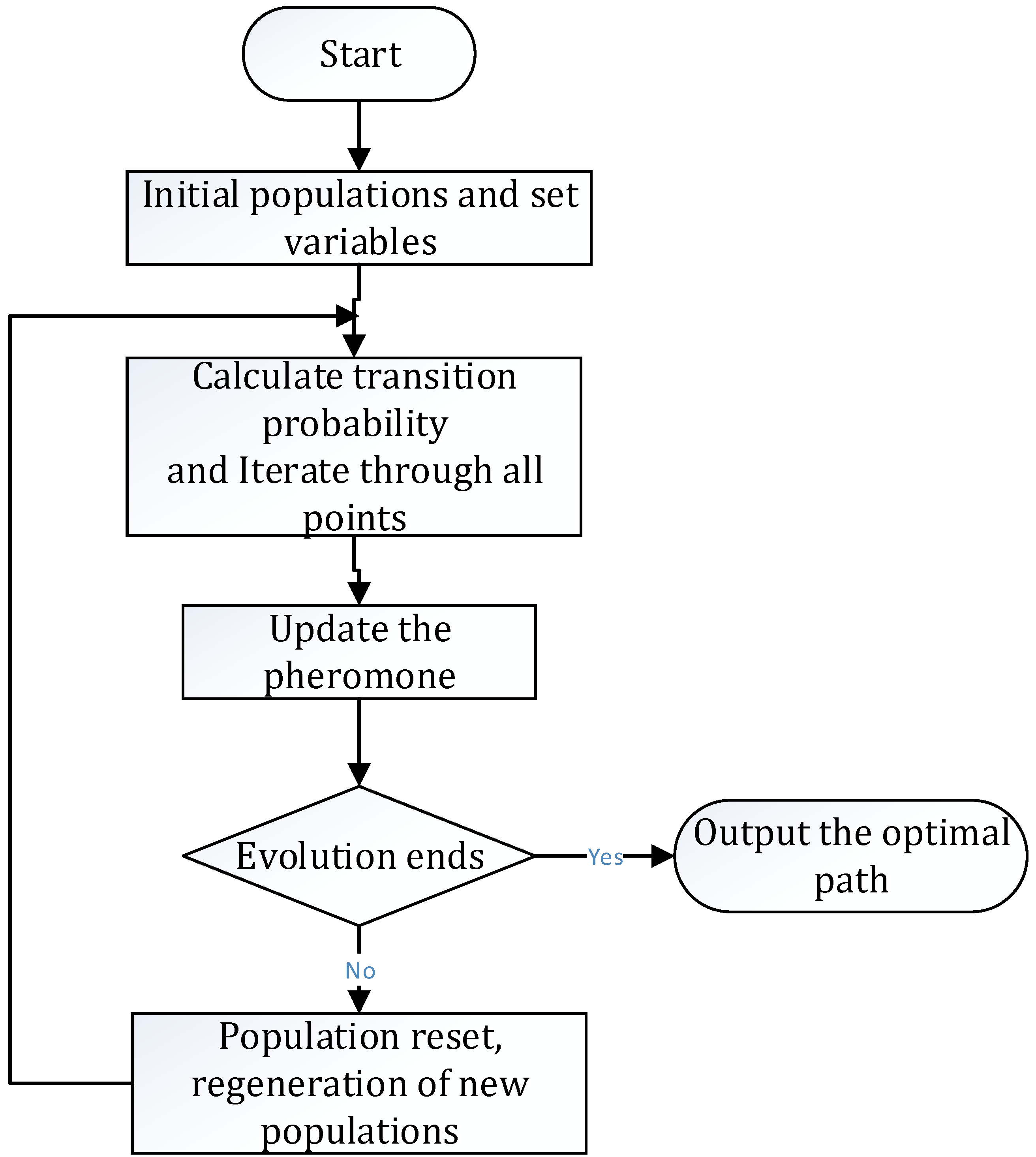
3. Optimization Model of Mixed Linear Multi-Node Combination
- (1)
- Set up multiple ants according to the specific optimization goals, and at the same time make three initial groups for the three sides of the source network load, and search separately;
- (2)
- Initialize an equal amount of pheromones on each path, as:
- (3)
- Take an ant, calculate the transition probability, select the next optimized calculation node according to the roulette method, and update the taboo table [16]. After each ant completes an optimized output, it releases pheromone on the path of the optimized combination. The amount of pheromone is proportional to the quality of the solution. Considering the correlation between nodes, a random local search strategy is adopted. It can optimize the operation of two adjacent nodes to the best one, and the amount of pheromone on the better node is also the largest. Later, the probability of ant selection increases;
- (4)
- Each ant takes the legal system node optimization path and retains the pheromone amount that the ant did not release between the nodes, and the ant dies;
- (5)
- Repeat steps 3–4 until all ants complete the optimization process;
- (6)
- Compute pheromone increments and pheromones for all optimization modes ;
- (7)
- Record this iteration path and update the current optimum combination to empty the taboo table;
- (8)
- Reach a predetermined number of iteration steps or stagnation (all ants choose the same path and the solution no longer changes) [17]; the algorithm ends with the current optimal solution as the optimal solution of the problem, otherwise the iteration continues.
- (1)
- Transfer probabilistic calculation formula:
- (2)
- Pheromone calculation formula:
- (3)
- Pheromone update method
4. Solving the Calculation Example
4.1. Basic Scenario
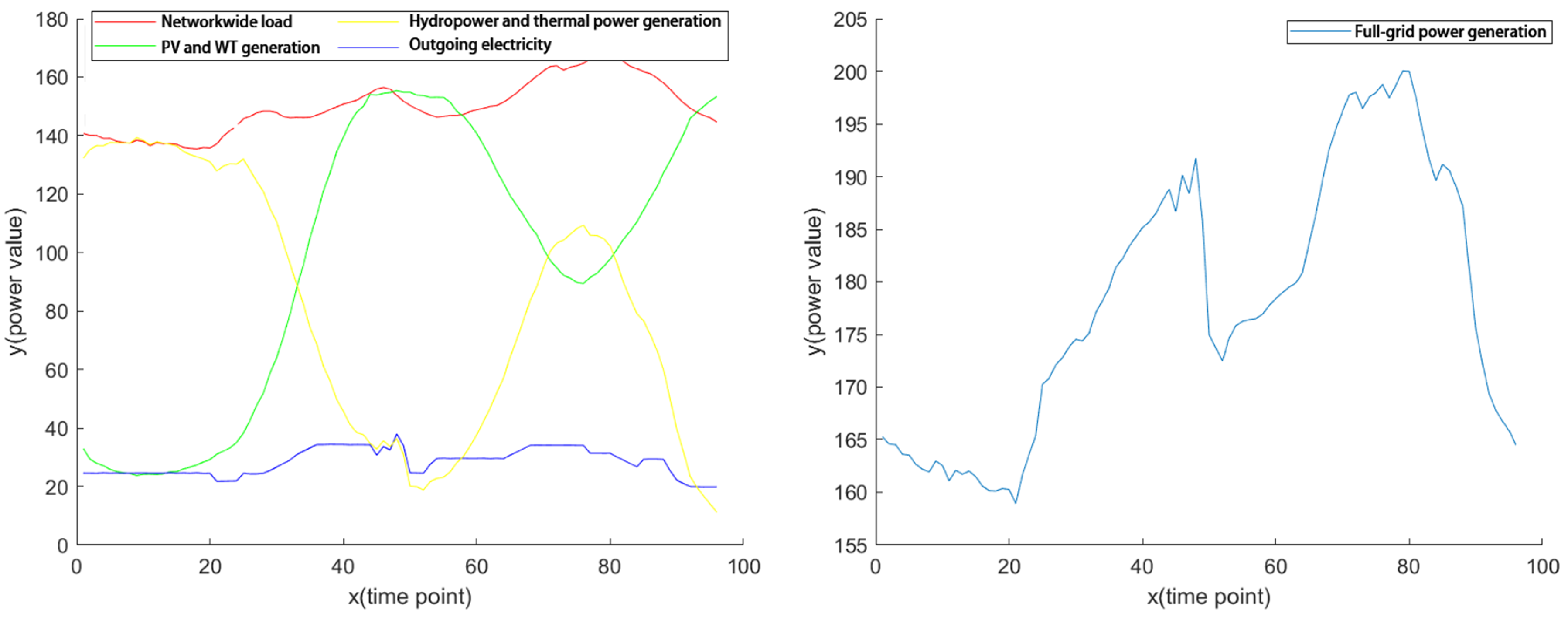
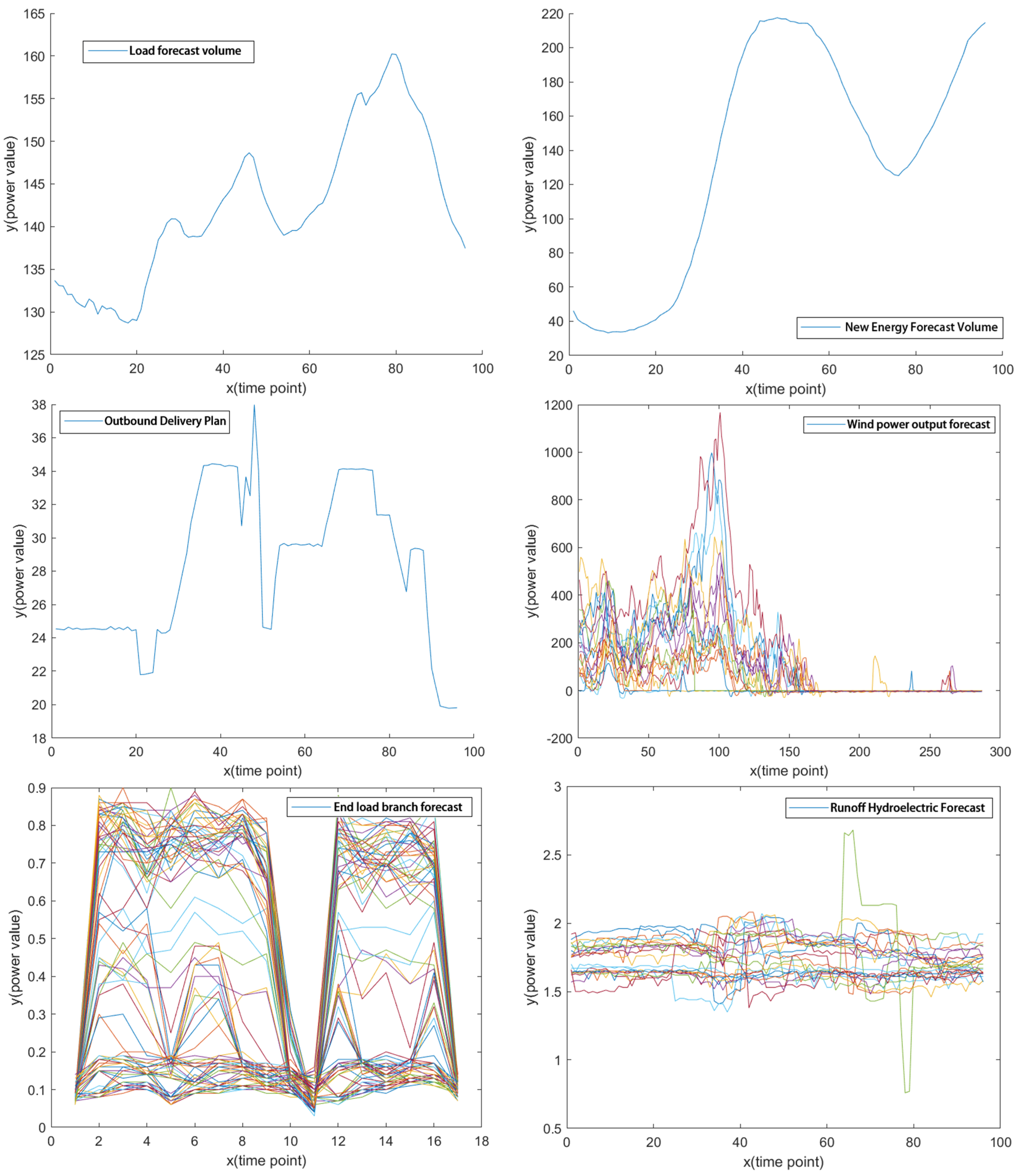
4.2. Distribution Network Operation Scenario
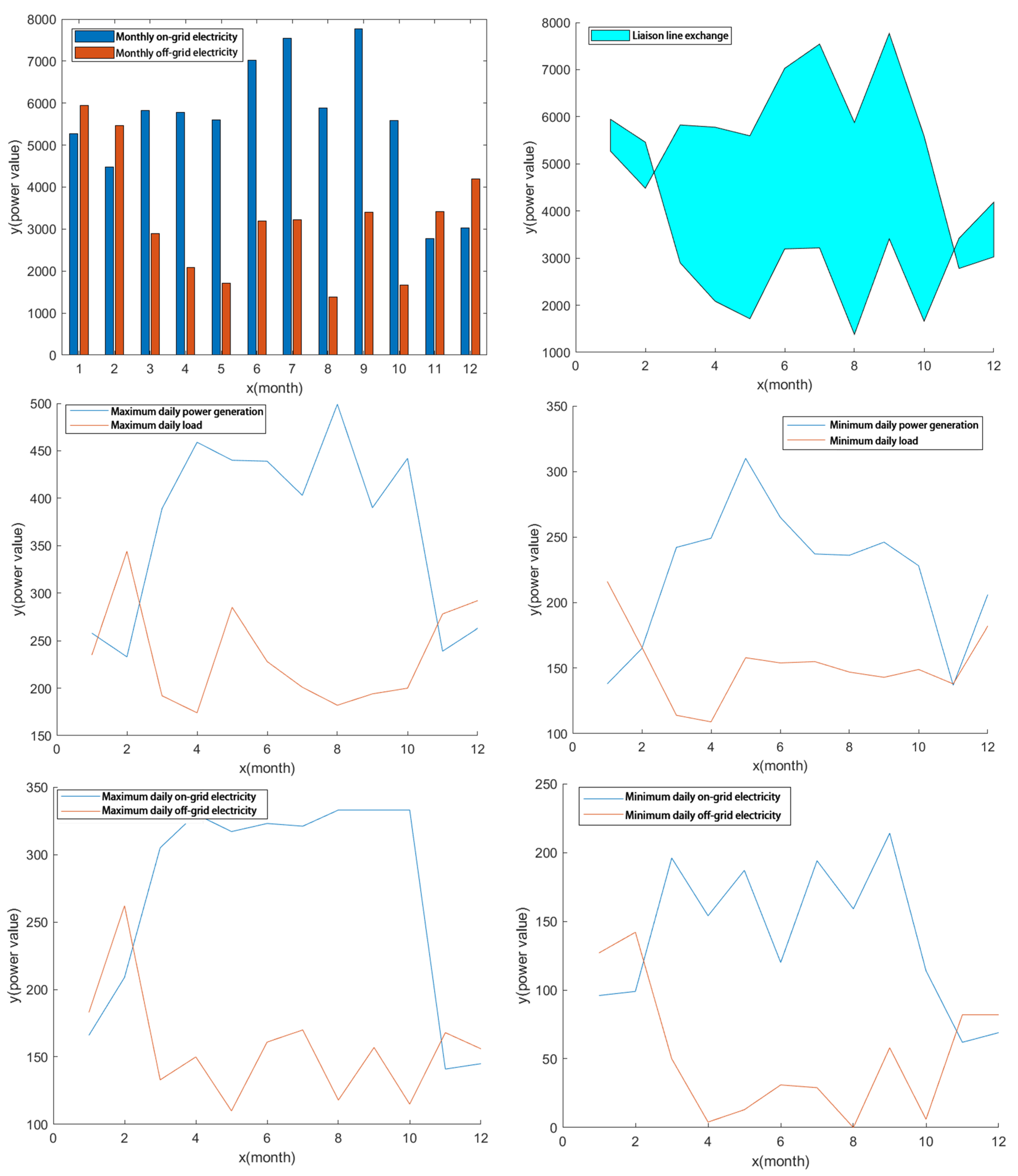
4.3. Model Calculation Results
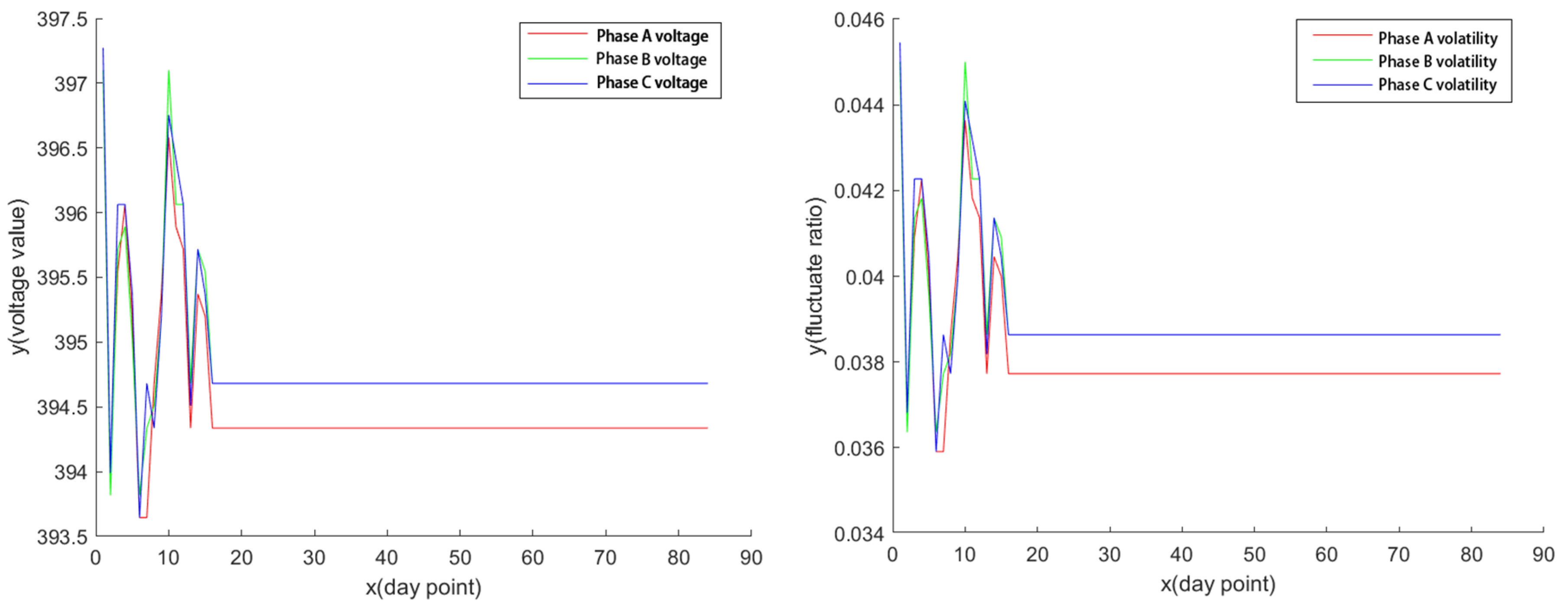
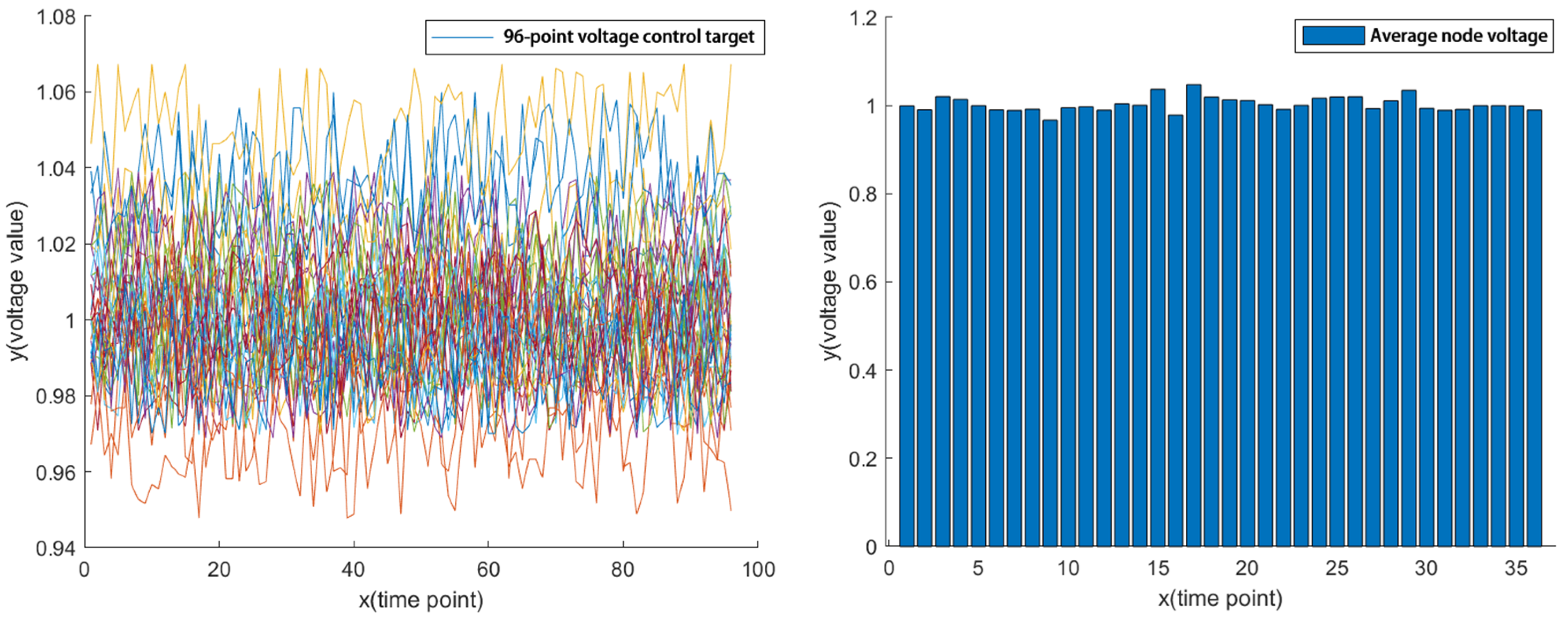
4.3.1. Grid Voltage Control Target Value
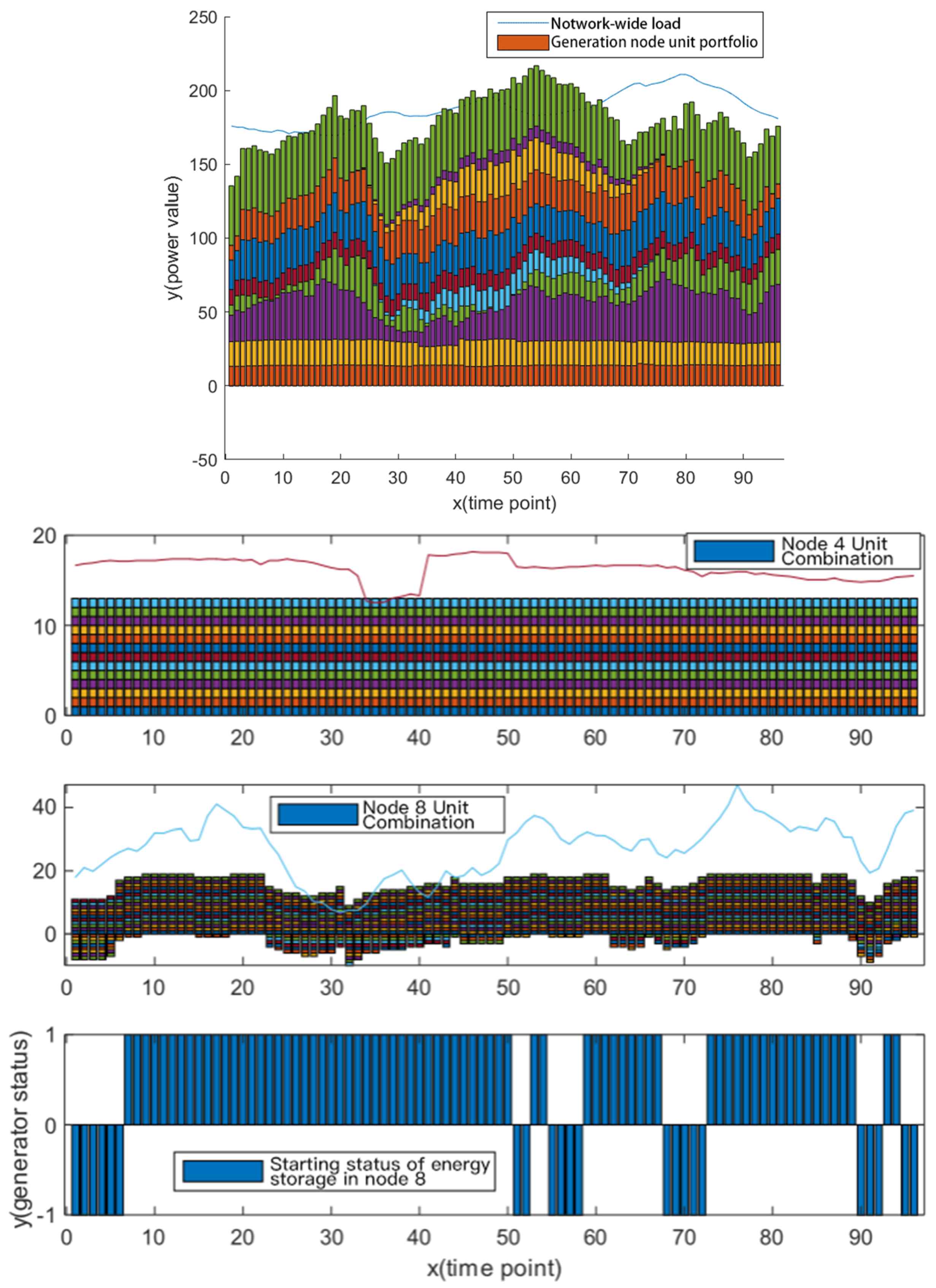
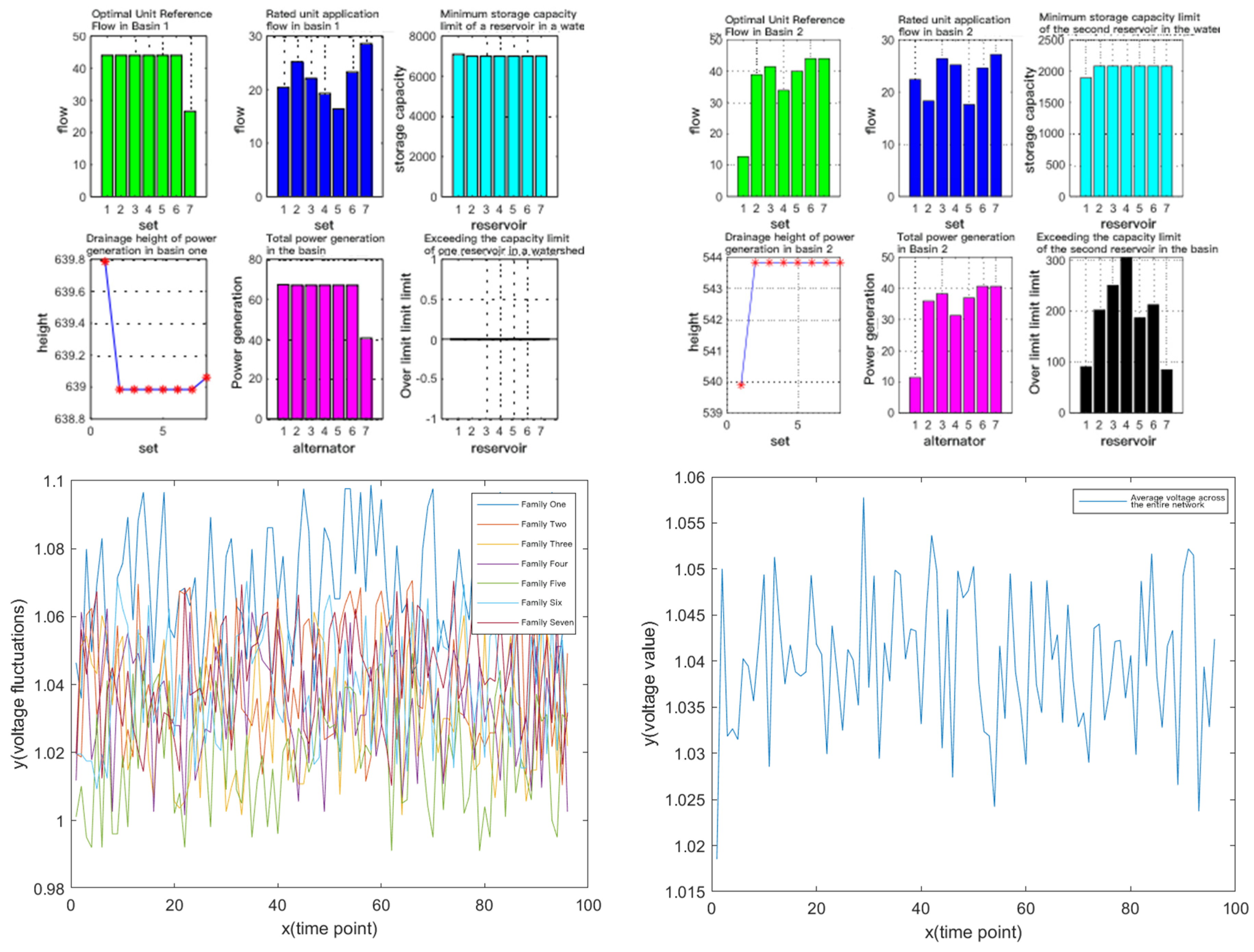
4.3.2. Optimization Result of Safety Control of Power Generation Nodes
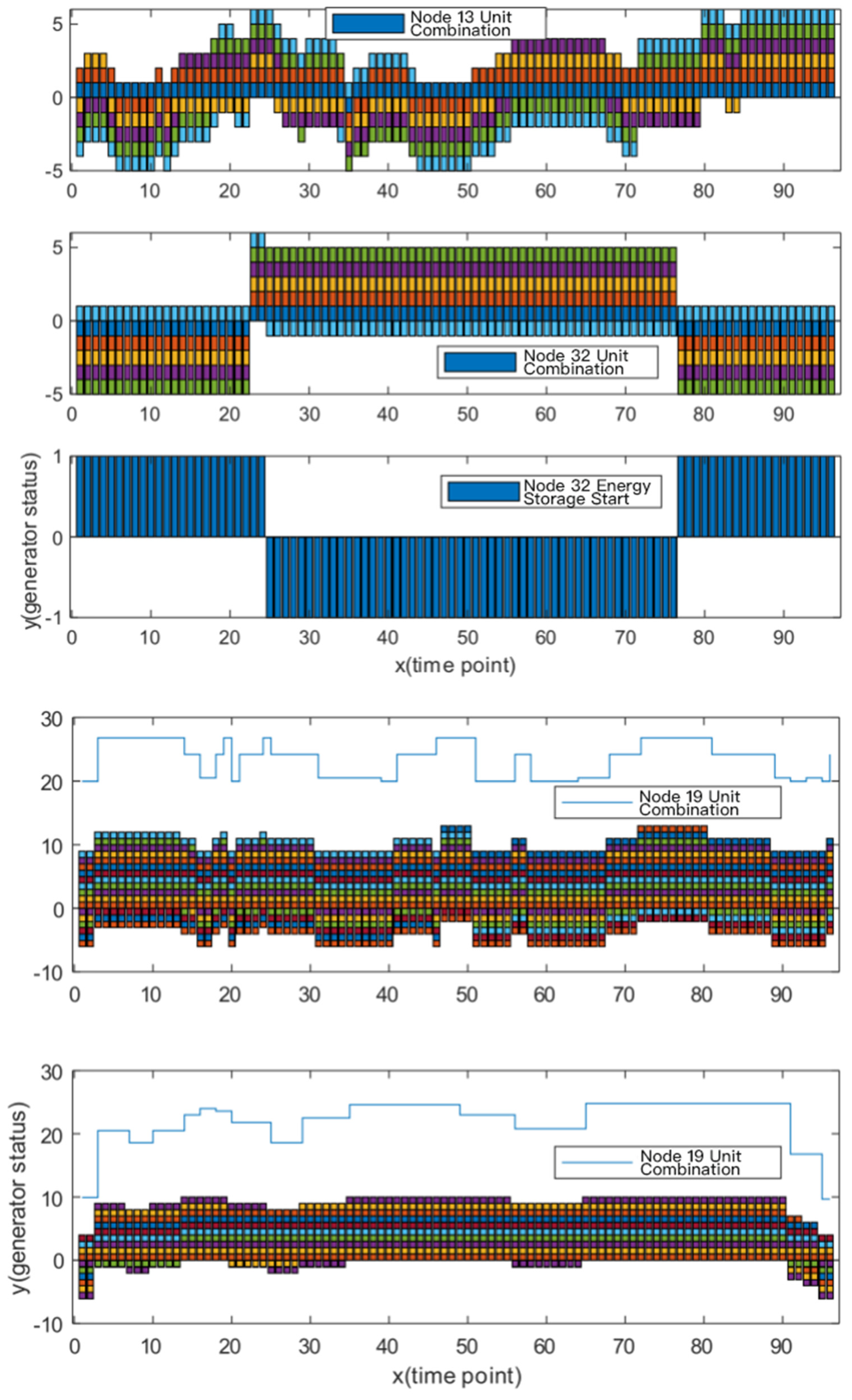
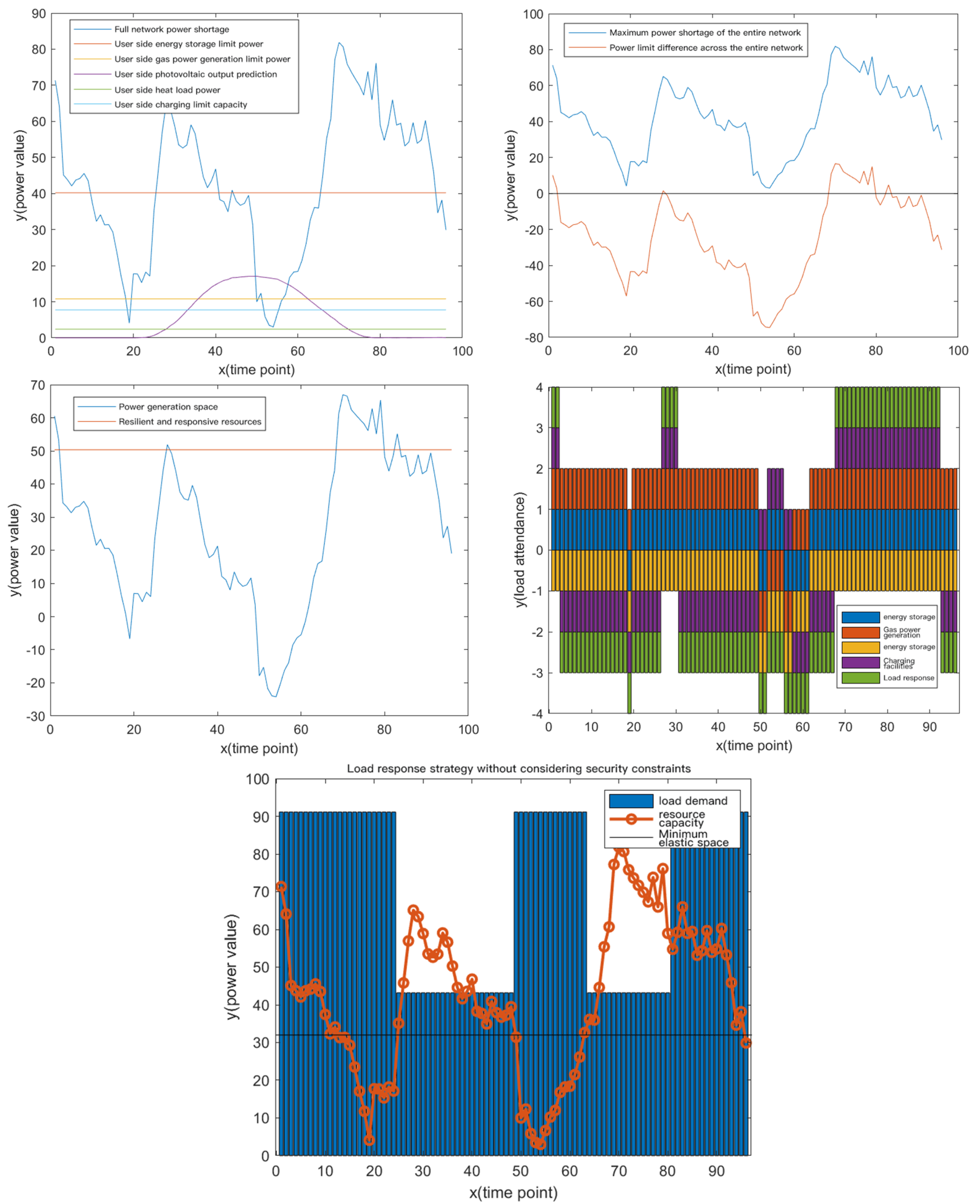
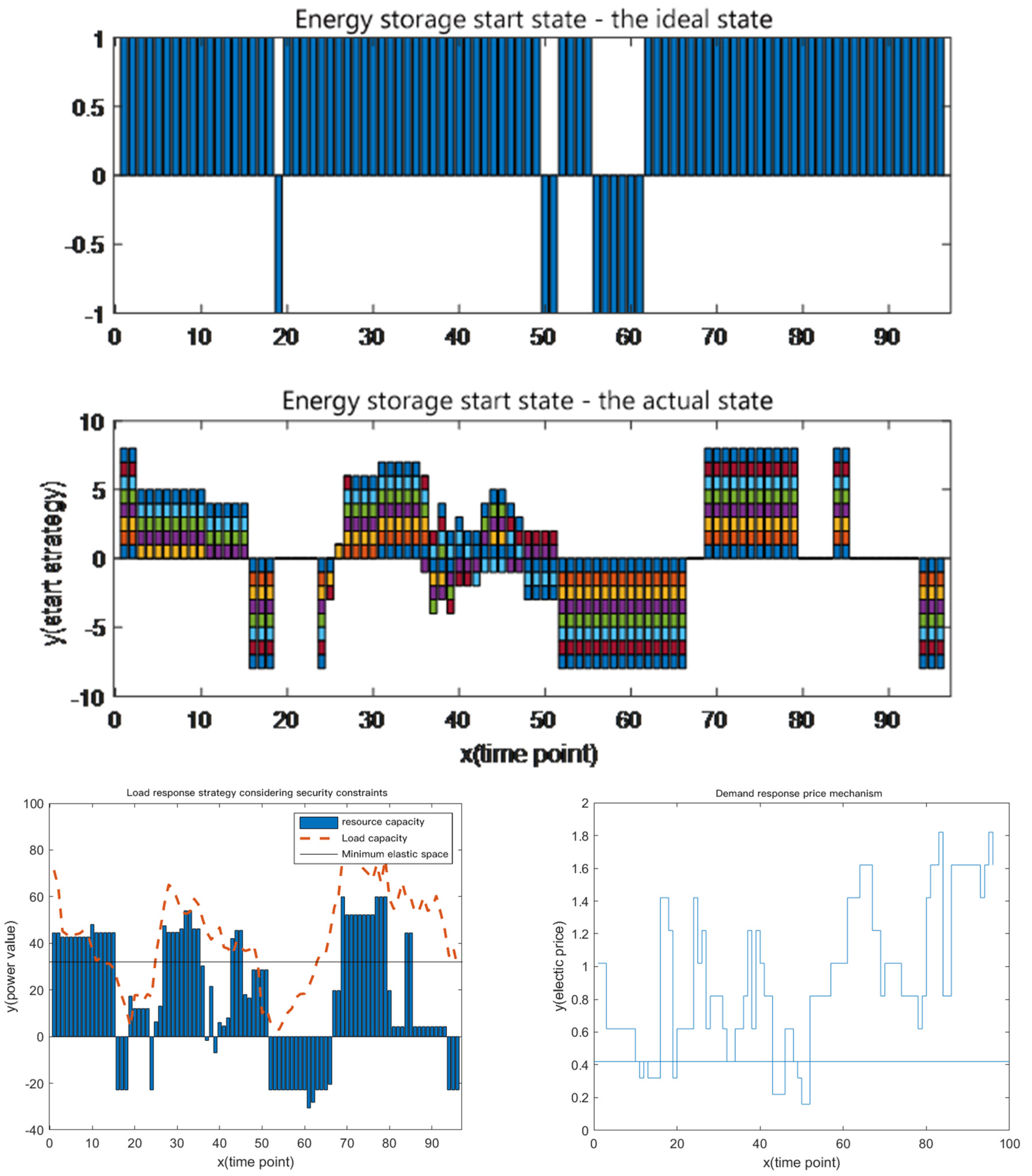
4.3.3. Optimization Result of Load Node Safety Control
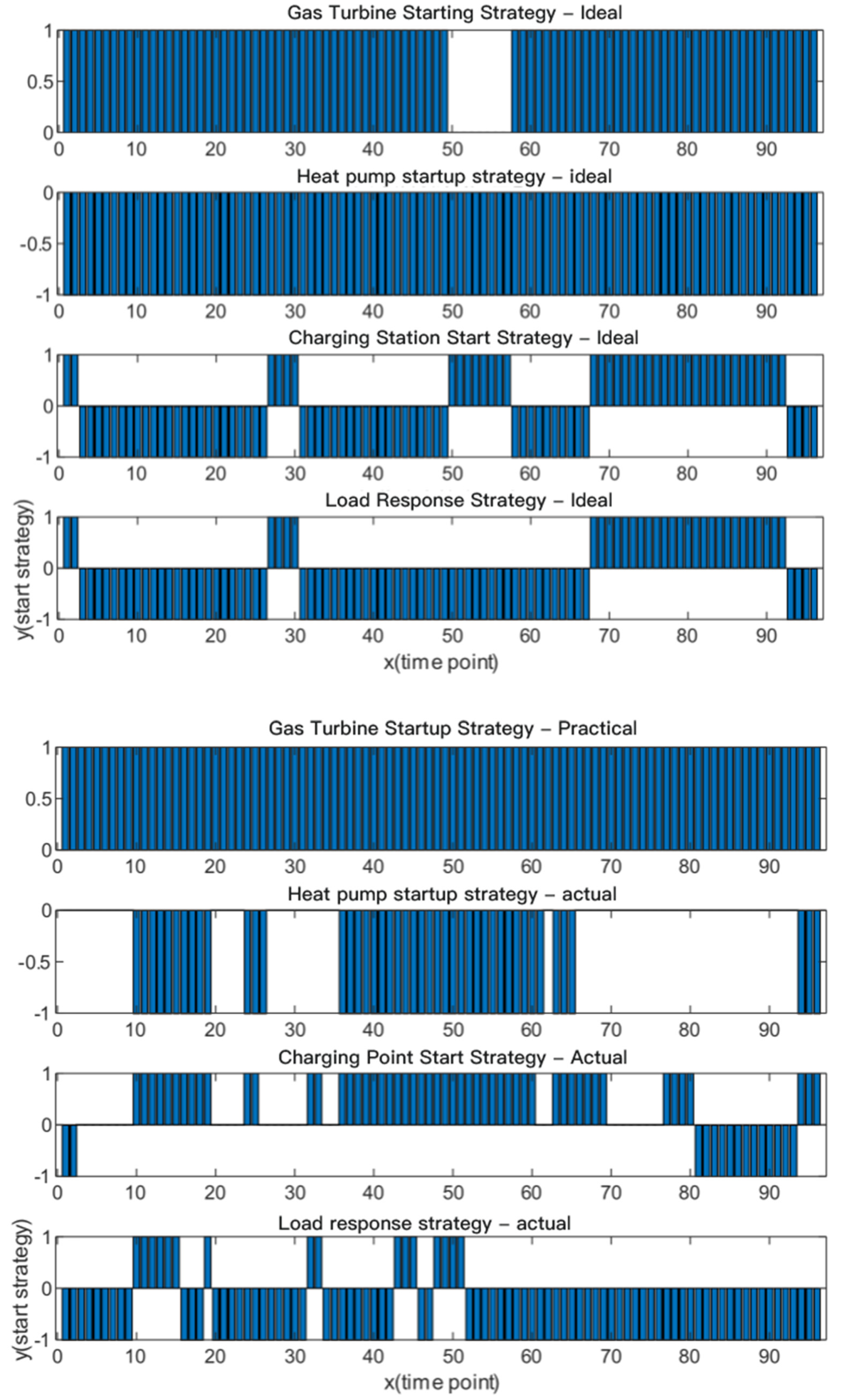
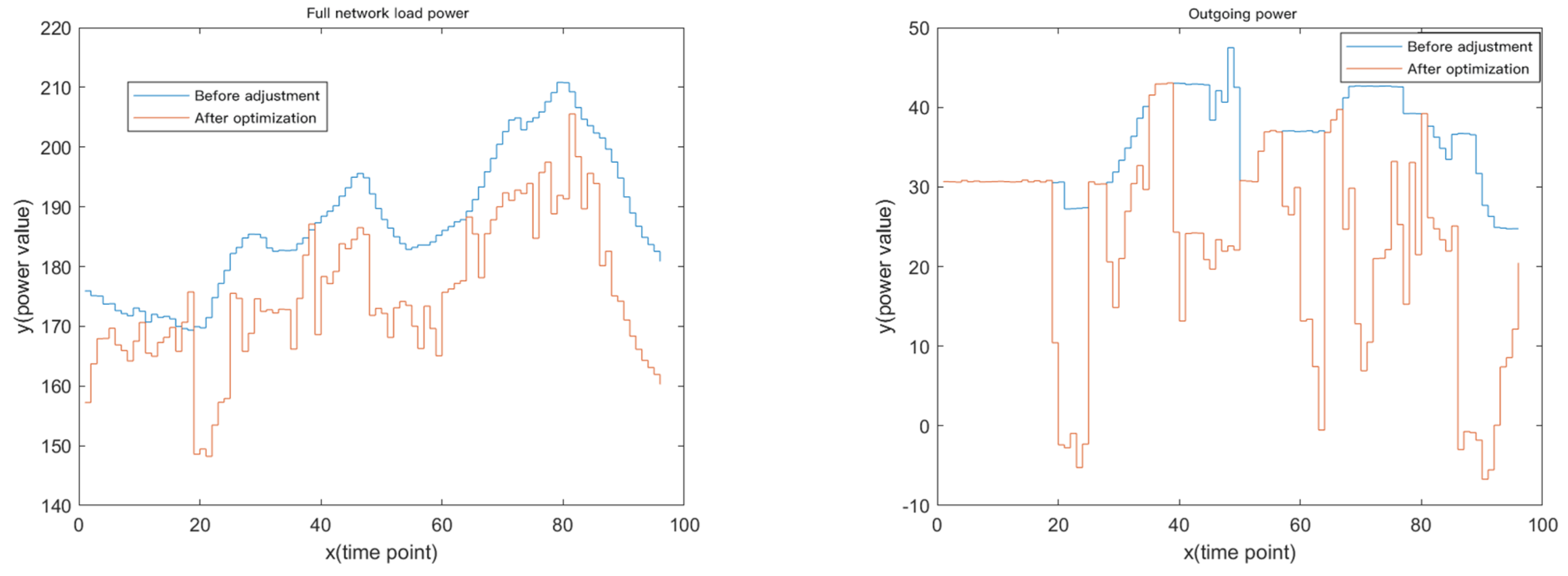
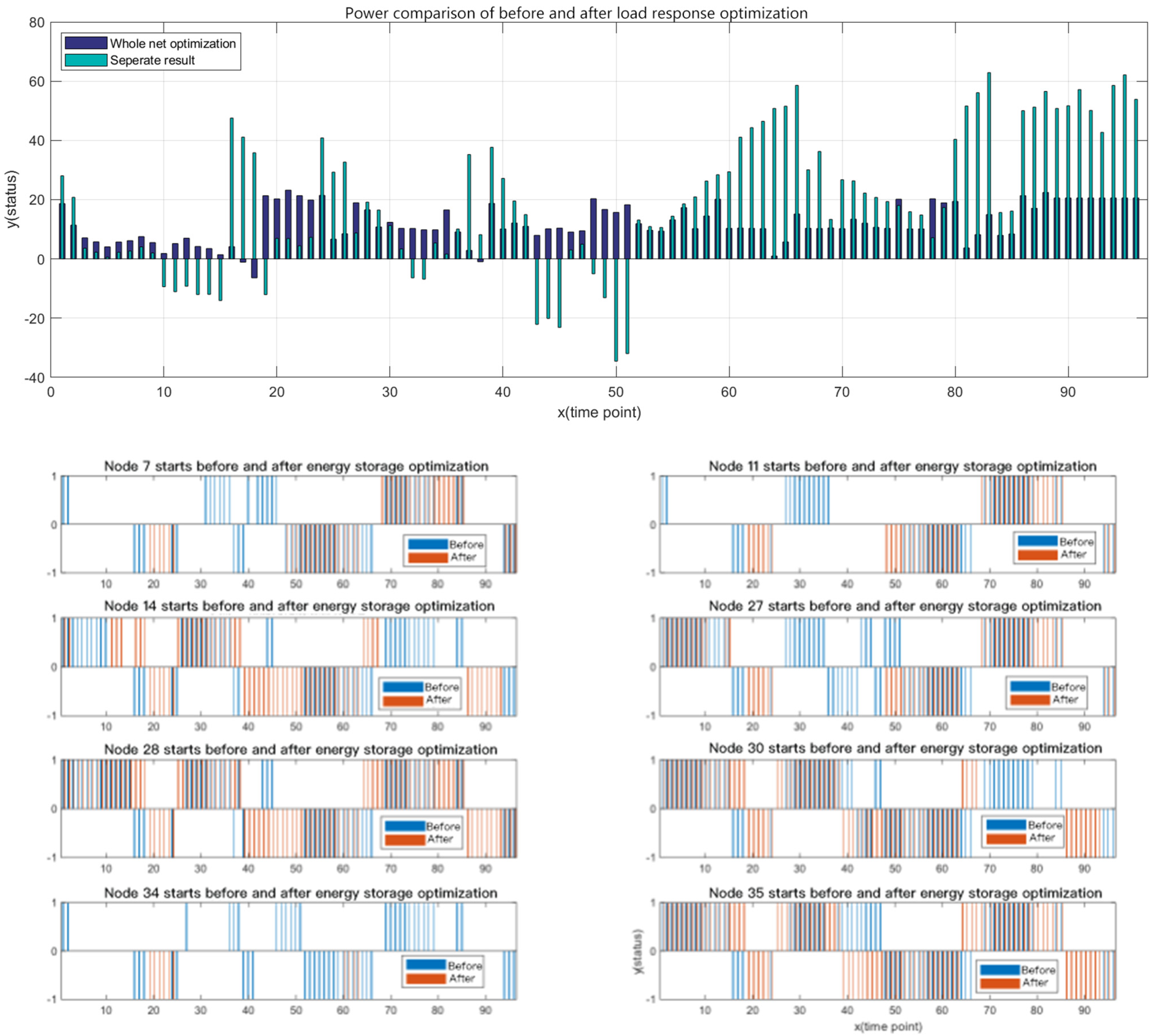
4.3.4. Combined Optimization
5. Conclusions
- (1)
- For power generation nodes, the mode of source-source interaction is adopted, the unit combination mode of the output node is considered, the safety control model of the power generation node is constructed, and the operating boundary conditions of the generator set are used as constraints to obtain the operating safety combination of the units in the network.
- (2)
- For the load node, this paper uses a flexible control model to calculate and analyze the safety scheduling strategy of the load; the model of node voltage deviation in one day is used as the ultimate objective function to solve the safety scheduling of the distribution network. After calculating the independent safety scheduling model, a joint optimization model is established according to a heuristic algorithm model to analyze the overall network security characteristics of the active distribution network, and a Lagrangian relaxation calculation is introduced to ensure that the optimization target is obtained in the active distribution network.
- (3)
- The model availability and accuracy of this section are verified through the actual grid calculation examples, and it is found via the actual comparison that the power quality in the network can be effectively optimized and adapted to the optimization analysis of the active distribution grid of various new energy scenarios.
- (4)
- The overall safety requirements of the source–network–load interaction, especially voltage stability, are the basis for ensuring that the source–network–load interaction can be implemented. Good distribution network planning and internal family division of the distribution network can maximize the internal reliability indicators of the distribution network. Therefore, in the design and planning of the new ADNs, a good family analysis is required. Some current grid plans can already meet this demand to a great extent.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiayi, H.; Chuanwen, J.; Rong, X. A review on distributed energy resources and MicroGrid. Renew. Sustain. Energy Rev. 2008, 12, 2472–2483. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q. State-of-the-art techniques for modelling of uncertainties in active distribution network planning: A review. Appl. Energy 2019, 239, 1509–1523. [Google Scholar] [CrossRef]
- ALKaabi, S.S.; Zeineldin, H.H.; Member, S.; Khadkikar, V. Planning active distributionnetworks considering multi-DG configurations. IEEE Trans. Power Syst. 2014, 29, 785–793. [Google Scholar] [CrossRef]
- Xing, H.; Cheng, H.; Zhang, Y.; Zeng, P. Active distribution network expansion planningintegrating dispersed energy storage systems. IET Gener. Transm Distrib. 2016, 10, 638–644. [Google Scholar] [CrossRef]
- Mashayekh, S.; Stadler, M.; Cardoso, G.; Heleno, M.; Madathil, S.C.; Nagarajan, H.; Bent, R.; Mueller-Stoffels, M.; Lu, X.; Wang, J. Security-constrained design of isolated multi-energy microgrids. IEEE Trans. Power Syst. 2018, 33, 2452–2462. [Google Scholar] [CrossRef]
- Koltsaklis, N.E.; Kopanos, G.M.; Georgiadis, M.C. Design and operational planning of energy networks based on combined heat and power units. Ind. Eng. Chem. Res. 2014, 53, 16905–16923. [Google Scholar] [CrossRef]
- Perković, L.; Mikulčić, H.; Pavlinek, L.; Wang, X.; Vujanović, M.; Tan, H.; Baleta, J.; Duić, N. Coupling of cleaner production with a day-ahead electricity market: A hypothetical case study. J. Clean. Prod. 2017, 143, 1011–1020. [Google Scholar] [CrossRef]
- Kumar, S.; Sushama, M. Sushama, Strategic demand response framework for energy management in distribution system based on network loss sensitivity. Energy Environ. 2020, 31, 1385–1402. [Google Scholar] [CrossRef]
- Tan, W.-S.; Hassan, M.Y.; Majid, M.S.; Abdul Rahman, H. Optimal distributed renewable generation planning: A review of diferent approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar] [CrossRef]
- Santos, S.F.; Fitiwi, D.Z.; Bizuayehu, A.W.; Shafie-khah, M.; Asensio, M.; Contreras, J.; Cabrita, C.M.; Catalão, J.P. Novel multi-stage stochastic DG investment planning with recourse. IEEE Trans. Sustain. Energy 2016, 8, 164–178. [Google Scholar] [CrossRef]
- Yang, Q.; Barria, J.A.; Green, T.C. Communication infrastructures for distributed control of power distribution networks. IEEE Trans. Ind. Inform. 2011, 7, 316–327. [Google Scholar] [CrossRef]
- Ehsan, A.; Yang, Q.; Cheng, M. A scenario-based robust investment planning model for multi-type distributed generation under uncertainties. IET Gener. Transm. Distrib. 2018, 12, 4426–4434. [Google Scholar] [CrossRef]
- Billinton, R.; Allan, R.N. Reliability Evaluation of Power Systems; Springer Science & Business Media: Boston, MA, USA, 2013. [Google Scholar]
- Heidari, A.; Agelidis, V.G.; Kia, M.; Pou, J.; Aghaei, J.; Shafie-Khah, M.; Catalão, J.P. Reliability optimization of automated distribution networks with probability customer interruption cost model in the presence of dg units’. IEEE Trans. Smart Grid. 2017, 8, 305–315. [Google Scholar]
- Niknam, T.; Kavousifard, A.; Aghaei, J. Scenario-based multiobjective distribution feeder reconfiguration considering wind power using adaptive modified particle swarm optimization. IET Renew. Power Gener. 2012, 6, 236–247. [Google Scholar] [CrossRef]
- Ghadi, M.J.; Ghavidel, S.; Rajabi, A.; Azizivahed, A.; Li, L.; Zhang, J. A review on economic and technical operation of active distribution systems. Renew. Sustain. Energy Rev. 2019, 104, 38–53. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Z.; Li, G.; Mu, Y.; Zhao, D.; Chen, C.; Shen, B. Optimal scheduling of isolated microgrid with an electric vehicle battery swapping station in multi-stakeholder scenarios: A bi-level programming approach via real-time pricing. Appl. Energy 2018, 232, 54–68. [Google Scholar] [CrossRef]
- Mahmood, S.A.; Zedan, M.J.M. Network Load Balancing in Teleconferencing Systems. In Proceedings of the 2022 8th International Engineering Conference on Sustainable Technology and Development (IEC), Erbil, Iraq, 23–24 February 2023; pp. 12–16. [Google Scholar]
- Kyriakou, D.G.; Kanellos, F.D. Optimal operation of microgrids comprising large building prosumers and plug-in electric vehicles integrated into active distribution networks. Energies 2022, 15, 6182. [Google Scholar] [CrossRef]
- Weishan, D.; Yongjuan, L. Research on grid-connected distributed power grids based on solar power generation systems. Power Technol. 2017, 1052–1054. [Google Scholar]
- Li, Y.; Wei, X.; Li, Y.; Dong, Z.; Shahidehpour, M. Detection of false data injection attacks in smart grid: A secure federated deep learning approach. IEEE Trans. Smart Grid 2022, 13, 4862–4872. [Google Scholar] [CrossRef]
- Siwu, L.; Sichang, X.; Fangmei, B.; Yulin, Y.; Xiaodi, M.; Chan, P. The analysis of business scenarios and implementation path of “5G+ Source-network-load-storage” multi-station integration. E3S Web Conf. 2021, 248, 02031. [Google Scholar]
- Li, Y.; Feng, B.; Wang, B.; Sun, S. Joint planning of distributed generations and energy storage in active distribution networks: A Bi-Level programming approach. Energy 2022, 245, 123226. [Google Scholar] [CrossRef]
- Fan, H.; Yu, Z.; Xia, S.; Li, X. Review on coordinated planning of source-network-load-storage for integrated energy systems. Front. Energy Res. 2021, 9, 641158. [Google Scholar] [CrossRef]
- Chen, X.U.E.; Jing, R.E.N.; Zhang, X.; Wang, P.; Zhou, X.; Liu, Y.; Kuang, H. An optimal dispatch method for high proportion new energy power grid based on source-network-load-storage interaction. In Proceedings of the 2021 4th International Conference on Electron Device and Mechanical Engineering (ICEDME), Guangzhou, China, 19–21 March 2021; pp. 119–122. [Google Scholar]
- Li, Y.; Zhang, M.; Chen, C. A deep-learning intelligent system incorporating data augmentation for short-term voltage stability assessment of power systems. Appl. Energy 2022, 308, 118347. [Google Scholar] [CrossRef]
- Xu, R.; Chen, C.; Chen, D.; Zhou, G.; Jin, Y.; Wu, X.; Lin, Z. Maximum openable capacity optimization method of active distribution network considering multiple users access. Energy Rep. 2022, 8, 43–50. [Google Scholar] [CrossRef]
- Piao, Z.; Peng, T.; Lu, S.; Zhang, Y.; Cheng, D.; Wang, J. Efficient collaborative utilization mode of “Source-network-load-storage” to improve energy-self-balance ability of microgrid. In Proceedings of the 2022 4th International Conference on Power and Energy Technology (ICPET), Beijing, China, 28–31 July 2022; pp. 498–503. [Google Scholar]
- Li, Y.; Yang, Z.; Li, G.; Zhao, D.; Tian, W. Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties. IEEE Trans. Ind. Electron. 2019, 66, 1565–1575. [Google Scholar] [CrossRef]
- Wang, J.; Huo, S.; Yan, R.; Cui, Z. Leveraging heat accumulation of district heating network to improve performances of integrated energy system under source-load uncertainties. Energy 2022, 252, 124002. [Google Scholar] [CrossRef]
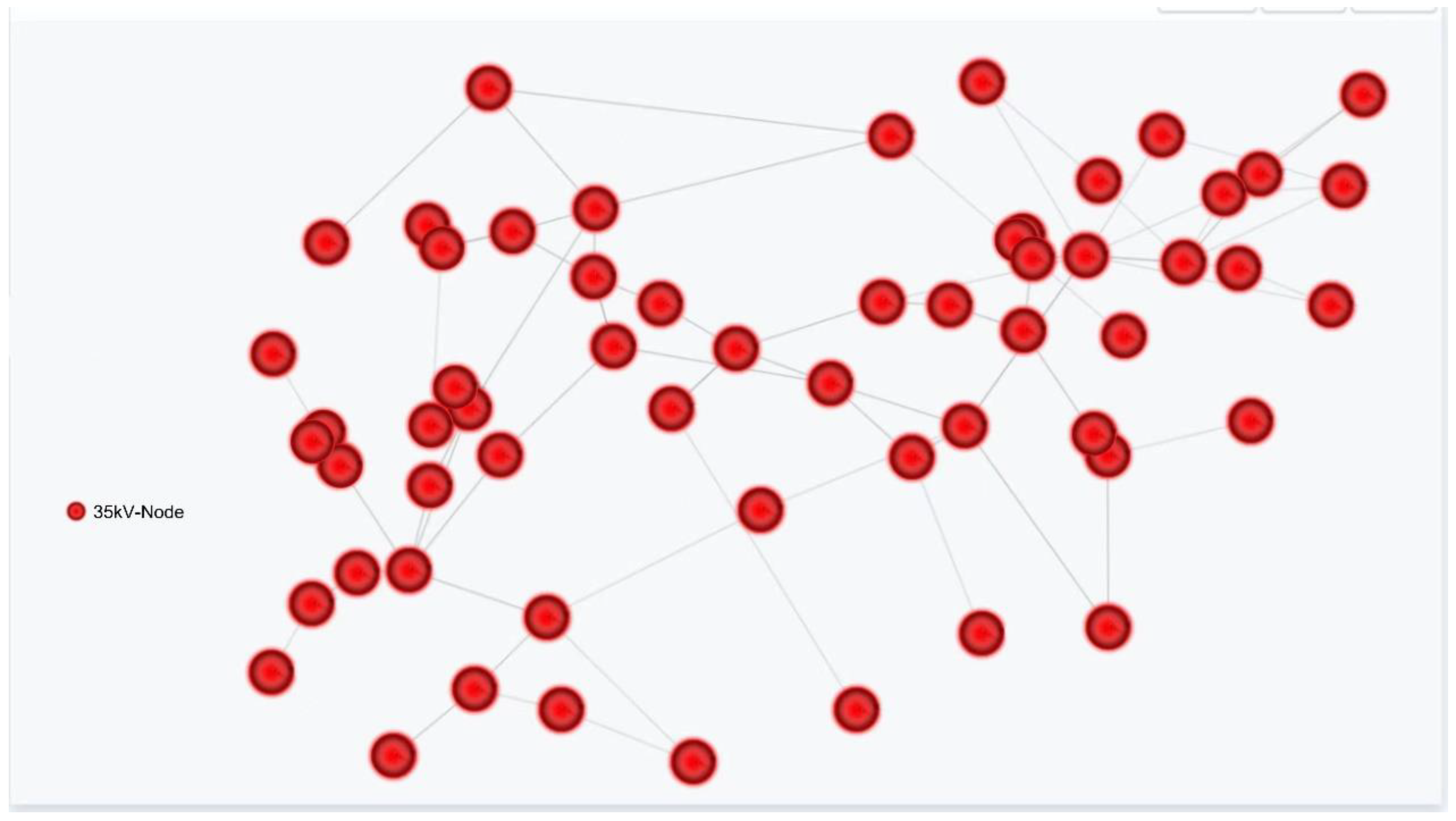





| Node Number | Node Type | Response Characteristics | Main Properties | Elastic Index |
|---|---|---|---|---|
| 1 | Load | Rigid | Commercial electricity consumption | 15.21% |
| 2 | Load | Rigid | Residential areas | 4.36% |
| 3 | Power generation | Elasticity | Cascading hydropower | 40.93% |
| 4 | Power generation | Rigid | Basin runoff is a small hydropower group | 12.67% |
| 5 | Load | Rigid | Chemical plant | 20.05% |
| 6 | Load | Rigid | Water works | 8.32% |
| 7 | Load | Elasticity | School, energy storage | 36.69% |
| 8 | Power generation | Elasticity | Wind power, energy storage | 28.96% |
| 9 | Load | Rigid | Mechanical plant | 9.13% |
| 10 | Load | Rigid | Food processing plant | 10.14% |
| 11 | Load | Elasticity | Commercial and self-built photovoltaic energy storage | 46.68% |
| 12 | Load | Rigid | Government office | 31.24% |
| 13 | Power generation | Rigid | Wind force | 16.21% |
| 14 | Load | Elasticity | Textile factory, belt energy storage | 16.46% |
| 15 | Load | Rigid | Paper mill | 8.83% |
| 16 | Power generation | Rigid | Photovoltaic power | 5.49% |
| 17 | Load | Elasticity | Cotton textile mill | 30.13% |
| 18 | Power generation | Rigid | Basin runoff is a small hydropower group | 10.25% |
| 19 | Power generation | Elasticity | Biomass power generation | 60.14% |
| 20 | Load | Rigid | Small textile mills | 14.32% |
| 21 | Load | Rigid | Automobile manufacturers | 10.93% |
| 22 | Load | Rigid | Energy storage battery manufacturer | 4.16% |
| 23 | Load | Rigid | Steel processing plant | 2.86% |
| 24 | Load | Rigid | Commercial office building | 20.57% |
| 25 | Load | Elasticity | Auto parts manufacturer, PV | 29.12% |
| 26 | Power generation | Elasticity | Gas-fired power generation | 63.17% |
| 27 | Power generation | Elasticity | Comprehensive energy demonstration park | 79.23% |
| Family Members | List of Load Nodes | List of Power Generation Nodes |
|---|---|---|
| 1 | 1, 2, 7, 9, 11, 17 | 4, 8 |
| 2 | 5, 15 | 19 |
| 3 | 6, 10, 12 | 13, 32 |
| 4 | 14, 21, 23, 33, 35 | 36 |
| 5 | 20, 22, 25 | 18, 26, 29 |
| 6 | 24, 30, 31 | 3 |
| 7 | 27, 28, 34 | 16 |
| Node Number | Node Type | Voltage Level | Main Parameters (Installed Capacity, in MW) |
|---|---|---|---|
| 3 | Cascading hydropower | 110 kV | 2 × 3.5 + 3 × 1.25 + 3 × 0.63 + 2 × 0.32 + 4 × 0.5 |
| 8 | Wind farm | 35 kV | 16 × 2 + 1 × 1.5 + 5, Storage: 16 |
| 19 | Biomass power generation | 35 kV | 8 × 1.5 + 4 × 3 + 3 × 5 |
| 26 | Gas-fired power generation | 10 kV | 4 × 4.5 + 6 × 1.5 |
| 32 | Photovoltaic power station | 10 kV | 1.2 × 5, Storage: 3.6 |
| 36 | Storage capacity and power station | 110 kV | 6 × 4.6 + 4 × 2.5 + 8 × 1.25 |
| 7 | Class II load | 10 kV | Storage: 1.5. Installation capacity: 3 |
| 11 | Class II load | 35 kV | Light: 1.2 × 3, Storage: 2, Installed capacity: 6.3 |
| 14 | Class I load | 110 kV | Storage: 3.5. Installation capacity: 4.6 |
| 25 | Class I load | 110 kV | Light: 1 × 4, installed capacity: 7.83 |
| 27 | Class II load | 35 kV | Light: 1 × 14, Storage: 12, Gas: 8 × 1.5, Heat: 0.4 × 6 Installed capacity: 34 |
| 28 | Class II load | 35 kV | Light 1.2 × 6, Storage: 10. Pile: 10 × 0.18 + 12 × 0.035 Installed capacity: 16 |
| 30 | Three types of load | 10 kV | Storage: 2. Installation capacity: 2.4 |
| 34 | Class II load | 35 kV | Storage: 6. Installation capacity: 6.3 |
| 35 | Class II load | 10 kV | Storage: 3.2, Pile: 6 × 0.36 + 14 × 0.24, installed capacity: 4.2 |
| Generation Node | Active Power (MW) | Capacity (MW) |
|---|---|---|
| 3 | 13.2019 | 15.28 |
| 4 | 16.6745 | 18.48 |
| 8 | 17.9025 | 38.5 |
| 13 | 6.8876 | 30 |
| 16 | −0.066 | 20 |
| 18 | 10.5206 | 12.48 |
| 19 | 19.968 | 39 |
| 26 | 9.936 | 27 |
| 29 | −0.1478 | 16 |
| 32 | 0.0443 | 6 |
| 36 | 40.3172 | 47.6 |
| Node Name | Voltage | Phase Angle | Node Name | Voltage | Phase Angle |
|---|---|---|---|---|---|
| BUS1 | 1 | 0 | BUS19 | 1.011764051 | −31.1464 |
| BUS10 | 0.989535501 | −19.7508 | BUS20 | 1.011727813 | −31.1951 |
| BUS11 | 1.019591909 | −23.7891 | BUS21 | 1.001133166 | −38.2493 |
| BUS2 | 1.011749759 | −31.1677 | BUS26 | 0.991429899 | −41.5284 |
| BUS22 | 1.001028601 | −38.277 | BUS27 | 1 | −27.8 |
| BUS23 | 0.988518931 | −30.1358 | BUS28 | 1.019514092 | −16.4535 |
| BUS24 | 0.988722183 | −30.0071 | BUS29 | 1.01950393 | −16.4518 |
| BUS25 | 0.991470488 | −41.5135 | BUS34 | 1.019493038 | −16.4671 |
| BUS3 | 0.967180274 | −41.2169 | BUS4 | 0.991399466 | −41.513 |
| BUS51 | 0.994779656 | −41.5325 | BUS5 | 1.009353618 | −22.8737 |
| BUS9 | 0.994544278 | −28.8754 | BUS50 | 1.033333767 | −31.8241 |
| BUS12 | 0.990260647 | −11.9921 | BUS52 | 0.994779656 | −41.5325 |
| BUS13 | 1.002626092 | −37.9659 | BUS6 | 0.989535501 | −19.7508 |
| BUS14 | 0.998759999 | −31.5197 | BUS30 | 0.988722183 | −30.0071 |
| BUS15 | 1.039171437 | −30.079 | BUS31 | 1 | −41.2368 |
| BUS16 | 0.977696715 | −20.1593 | BUS33 | 1 | −10.7673 |
| BUS17 | 1.046380497 | −5.50664 | BUS7 | 1 | −10.6603 |
| BUS18 | 1.019633416 | −23.8103 | BUS8 | 0.989868176 | −20.2014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, P.; Dong, J.; Zhu, Y. Mixed Linear Model of a Safety Dispatch Model in an Active Distribution Network for Source–Grid–Load Interactions. World Electr. Veh. J. 2023, 14, 159. https://doi.org/10.3390/wevj14060159
Jiang P, Dong J, Zhu Y. Mixed Linear Model of a Safety Dispatch Model in an Active Distribution Network for Source–Grid–Load Interactions. World Electric Vehicle Journal. 2023; 14(6):159. https://doi.org/10.3390/wevj14060159
Chicago/Turabian StyleJiang, Peng, Jun Dong, and Yuan Zhu. 2023. "Mixed Linear Model of a Safety Dispatch Model in an Active Distribution Network for Source–Grid–Load Interactions" World Electric Vehicle Journal 14, no. 6: 159. https://doi.org/10.3390/wevj14060159
APA StyleJiang, P., Dong, J., & Zhu, Y. (2023). Mixed Linear Model of a Safety Dispatch Model in an Active Distribution Network for Source–Grid–Load Interactions. World Electric Vehicle Journal, 14(6), 159. https://doi.org/10.3390/wevj14060159






