Research on Hierarchical Control Strategy of Automatic Emergency Braking System

Abstract

In order to improve the active safety of vehicles, the control strategy of the vehicle automatic emergency braking system is studied. The hierarchical control idea is used to model the control strategy. The upper controller is a collision time model for the decision-making of vehicle braking deceleration, and the collision time threshold is determined under the condition of considering comfort. According to the braking deceleration output by the upper controller, the lower controller controls the vehicle by adjusting the throttle opening and braking pipeline pressure through PID control. Based on the typical test conditions of C-NCAP, a joint simulation test of CarSim and Matlab/Simulink for hierarchical control strategy is carried out. In order to achieve further verification, several groups of test conditions are conducted, and finally its effectiveness is verified, which can ensure the safety of drivers.

1. Introduction

With the development of the social economy, vehicle ownership has increased significantly year by year, and problems such as traffic congestion and accidents have intensified rapidly [1]. Under the severe road traffic safety situation, autonomous emergency braking (AEB), as a key technology of vehicle active safety, can automatically control the vehicle in an emergency state to achieve effective collision avoidance or reduce collision intensity. It has become one of the popular topics grabbing scholars’ attention [2,3,4]. In the current technical range, the two variables of safety distance and safety time are usually used as the main considerations in the control strategy of an automatic emergency braking system to judge the safety state of the vehicle [5].

The safety distance model is based on the dynamics of the vehicle braking process. The early control strategy based on the safety distance model is generally two levels, the first level of early warning, and the second level of braking. When the relative distance between the self-vehicle and the target vehicle measured by the information acquisition module reaches the critical distance of early warning, the system prompts the driver to brake through a sound warning. If the driver has not taken braking measures, and the relative distance between the two vehicles reaches the critical braking distance, the system avoids collision by automatic braking. The Mazda [6,7], Honda [8], SeungwukMoon model proposed by Seoul University in South Korea and the Berkeley model [9] proposed by Berkeley University are the more classic safety distance models. The Mazda model considers many extreme conditions, and the braking strategy is more conservative, which means it is easy to cause interference to the driver. The Honda model achieves hierarchical control of early warning and active braking by comparing the relative motion parameters of the two vehicles. The SeungwukMoon model considers the road condition and combines the road adhesion coefficient estimation method to improve the safety distance model. The Berkeley model considers the problem that the reserved braking safety distance is too large or too small, and the Mazda model and Honda model are optimized.

In addition to the above classical safety distance models, many researchers have actively tried to study the AEB control strategy based on safety distance. Teng F. et al. [10] proposed an automobile anti-collision safety early warning algorithm based on an improved Berkeley model, preprocessed the reaction time and braking onset time and dynamically selected the calculation formula of safety early warning distance to meet the dynamic demand of safety early warning distance under different braking deceleration speeds. Gounis K. et al. [11] simulates a three-layer AEB control system based on safety distance. Collision risk is compared according to the relative distance from the vehicle in front and the relative distance threshold based on adaptive speed. The results are fed back to the rule-based monitoring module, which determines the required deceleration command and then provides the command to the low-level control module through a switching algorithm. In view of the collision avoidance problem of the vehicle fleet, Sidorenko G. et al. [12] pay attention to collision avoidance in the emergency braking scene and queue, and deduce the minimum safety workshop distance or lower bound to ensure no rear-end collision, and also design a two-layer emergency braking strategy of the vehicle fleet based on vehicle-to-vehicle (V2V) communication. Kim H. et al. [13] developed a pure distance-based AEB control algorithm that defined discrete minimum braking and stopping distance formulas based on a variety of different vehicle driving conditions in each case. Park J. et al. [14] proposed an emergency crash-avoidance system that includes not only braking but also steering control. Based on the relative motion with surrounding vehicles and lane information obtained through vision sensors, the minimum distance to avoid collision during braking and steering is calculated, respectively. In particular, in order to avoid lane change collision, the maximum lateral acceleration and angle of the trajectory are considered. In view of the low early-warning accuracy of vehicles during a lane change in different lanes, He X. et al. [15] proposed a safety distance model for the vehicle running side on curves, taking the angle between two vehicles and the speed as the main parameters to ensure that there was no collision risk after the lane change vehicle and self-driven vehicle were run for t time.

The safety time model uses time-to-collision (TTC), the remaining time when the self-vehicle and the front vehicle simultaneously maintain the current motion state until the collision occurs, as the indicator to judge the dangerous state of the driving, and compares it with the pre-set TTC threshold of early warning and emergency braking in the control strategy, so as to determine the AEB system to execute the early warning or braking function.

Among the studies on safety time models, the most representative one is the TTC model proposed by Tokyo A&M University. If the TTC value obtained through real-time calculation is less than the set value, the system automatically intervenes in the braking. Otherwise, the current driving state is safe by default. In addition, Seyedi M. et al. [16] selected four real-world rear-end collision scenarios with different collision characteristics, defined different forward collision warning (FCW)/AEB safety algorithms, and simulated important input parameters that affect collision results, such as speed, braking strength and driver reaction time. Bae J.J. et al. [17] designed a hierarchical braking control strategy based on collision time, and developed an autonomous braking algorithm that can satisfy both vehicle safety and riding comfort, which consists of a two-step braking strategy dependent on collision time. The first step is the partial braking strategy, which can provide both speed reduction and good ride comfort under normal braking conditions. The second step is the full braking strategy to avoid a forward collision during an emergency braking situation. In order to effectively improve vehicle safety on mountainous areas and other curved roads and reduce braking distance and time, Wu G. et al. [18] designed a DCT shifting strategy suitable for different drivers. In order to reflect the active safety protection of the automotive AEB system for vulnerable road users, many researchers have conducted more studies on the pedestrian AEB system. Park M.K. et al. [19] proposed a pedestrian target selection method based on a funnel plot for the pedestrian AEB system. By comparing the predicted position and current position of pedestrians, the speed before the accident can be inferred. The fusion information of vehicles and sensors can be used to calculate the alarm time and estimate the collision probability. Based on this, the effective collision avoidance between vehicles and pedestrians is realized under the condition that the vehicle speed is not higher than 40 km/h. Rosado A.L. et al. [20] proposed an AEB analysis model, which can predict the collision speed, stopping distance and time with high accuracy, and it can complete the decision-making process by analyzing the lateral movement behavior of pedestrians and searching for the deterministic calculation of pedestrians entering the collision area. Yang W. et al. [21] proposed a pedestrian collision avoidance control strategy based on fuzzy neural network control at the upper level and PID control at the lower level, introduced a genetic algorithm to optimize the fuzzy neural network model and verified the effectiveness of the strategy by using the pedestrian crossing test scene in C-NCAP.

At present, the control strategy of an automatic emergency braking system is generally based on the safety distance and safety time to judge the safety state of the vehicle. Each control strategy considers different emphases. Under the premise of not interfering with the driver’s normal driving, the longitudinal collision avoidance algorithm considering the pre-collision time has the best performance [22]. 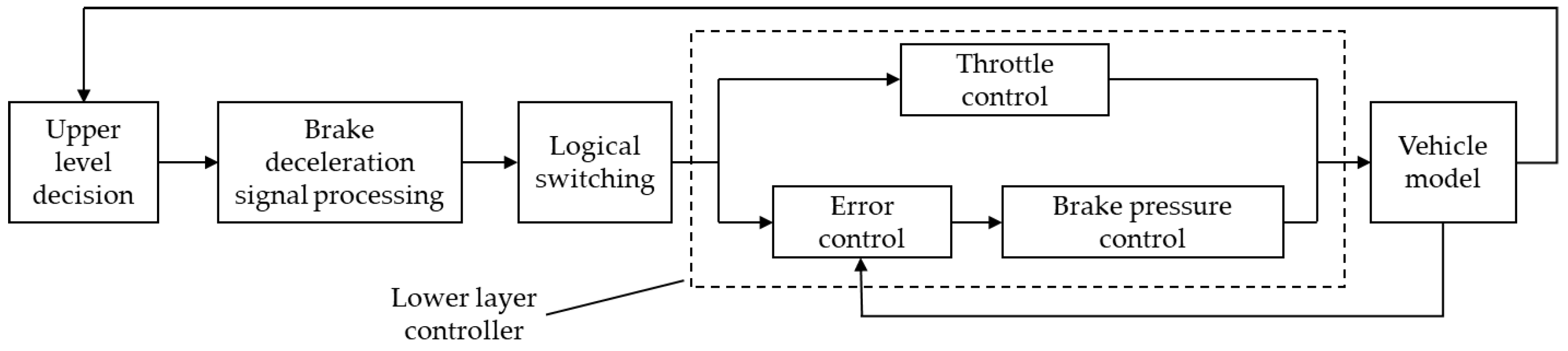However, the safety time model cannot clearly define the braking deceleration speed and the safety time threshold, and it lacks the consideration of occupant comfort, which cannot guarantee the reliability of the control strategy [23]. Therefore, in order to simplify the control system and improve the reliability and efficiency of the control strategy, aiming at the problem that the decision-making braking of the system needs to switch between different states in real time, the safety distance and time model can be combined to establish the hierarchical braking strategy on the premise of giving full consideration to occupant comfort and safety. The upper control model considers the pre-collision time to make decisions on braking deceleration, and the lower controller uses PID to control the vehicle braking pressure, so as to achieve control accuracy and efficiency.

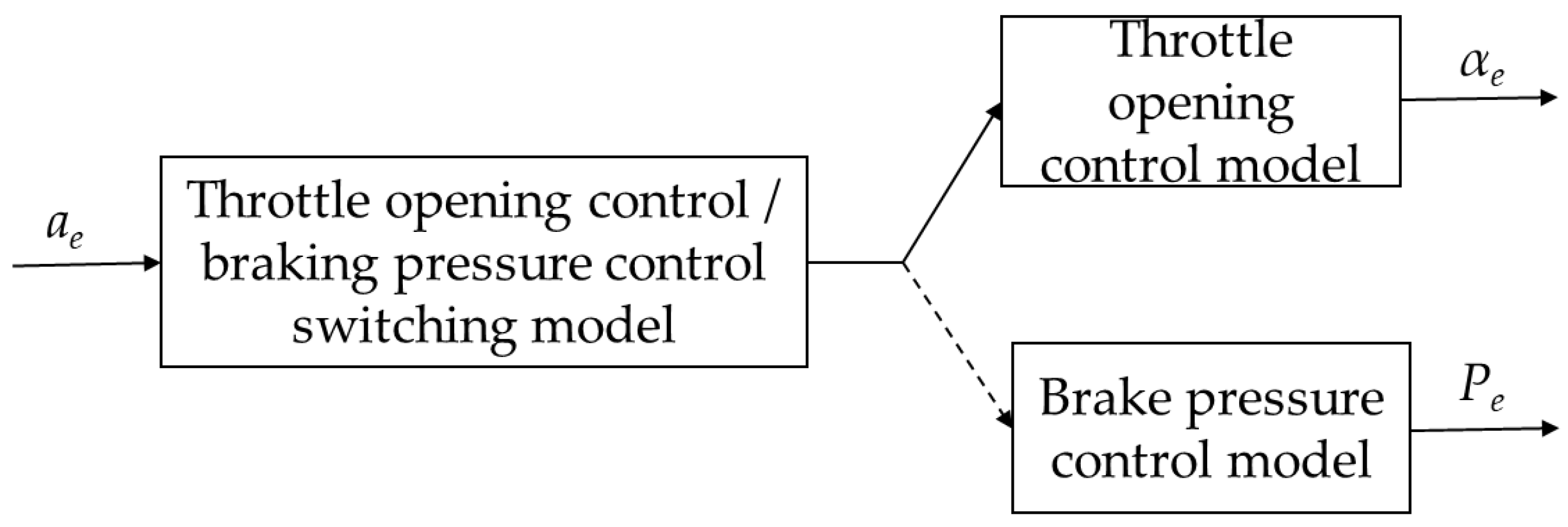
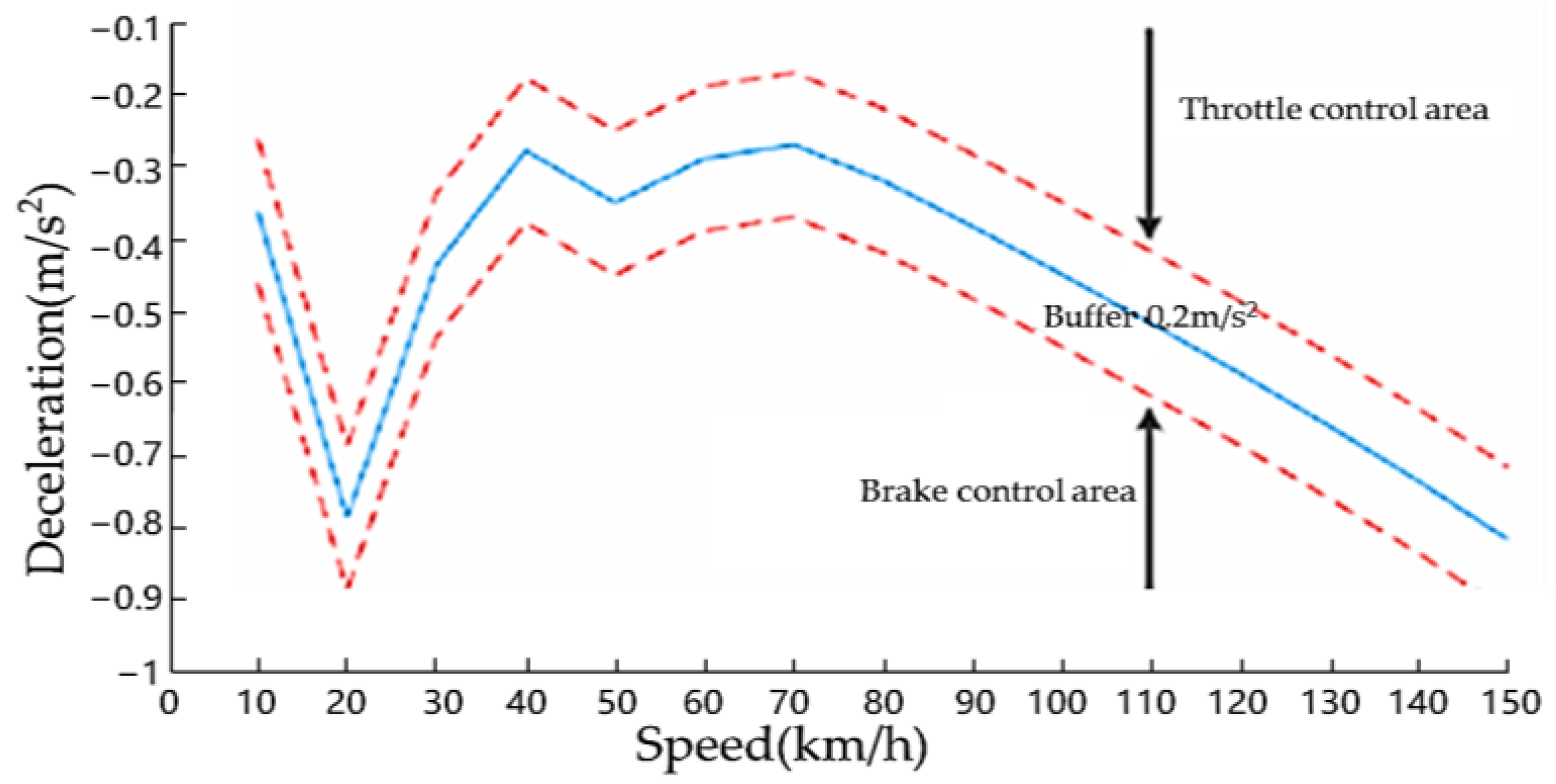
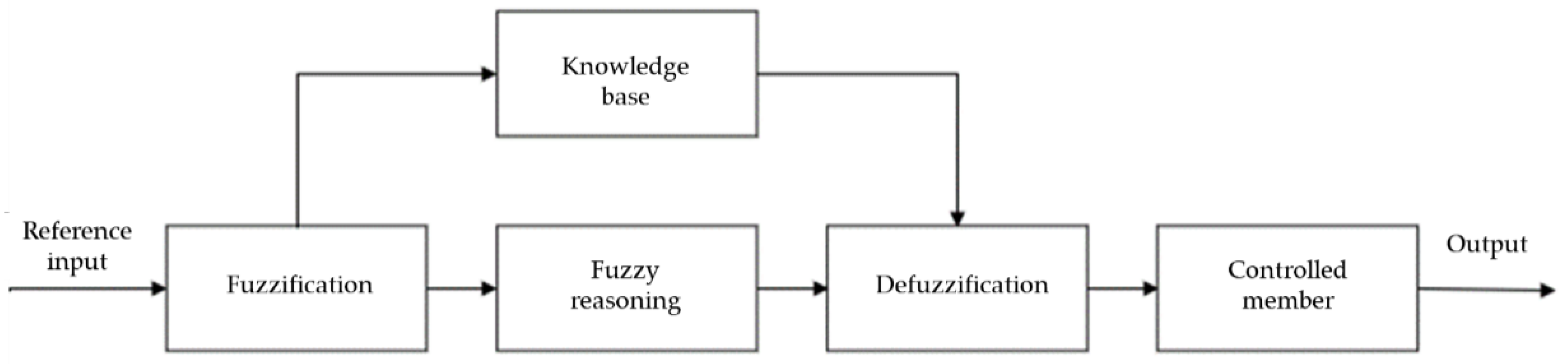
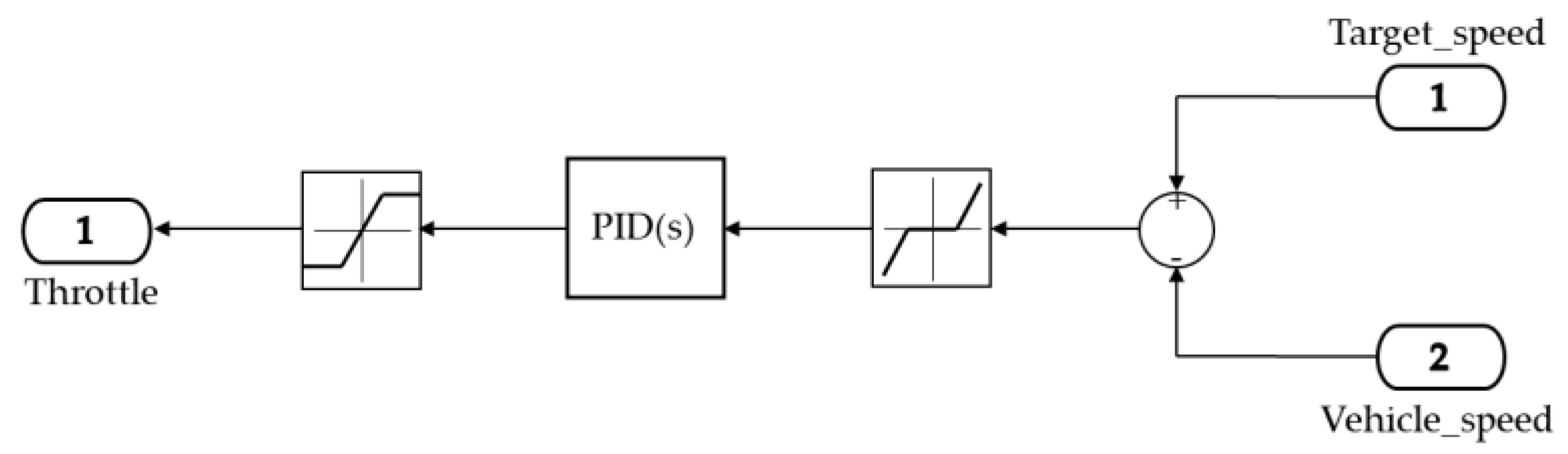
In this paper, a hierarchical control strategy based on safety time logic is studied. Firstly, the actual working condition requirements and the basic architecture of the AEB system are analyzed, and the control strategy and basic algorithm logic that meet the requirements are selected, that is, the hierarchical control strategy under the safety time logic. After that, according to the needs of the control strategy, the vehicle dynamics model and the inverse dynamics model of the matching vehicle upper system are established to obtain the necessary dynamic parameters of the algorithm. According to the known parameters, the AEB hierarchical control algorithm was built in Simulink. The upper layer adopts fuzzy control and the lower layer adopts PID control. The lower PID adjusts the speed by controlling the throttle opening and the brake pipeline pressure. Finally, in the CarSim and Simulink environment, the joint simulation proves that the control strategy can meet the actual needs under the E-NCAP standard and is feasible.

2. Vehicle Dynamics System Modeling

2.1. Software Overview

CarSim (2019) is the most widely used system-level vehicle dynamics simulation software in the automotive industry. It is a database used to convert parameters into graphics, a simulation modeler that specifically solves the mathematical structure of the vehicle, a module that converts data parameters and calculated motion into simulation animation and a professional drawer for drawing simulation curves. The simulation is real-time and accurate, and it is easy for users to get started [24,25].

As a simulation tool in the mathematical toolbox, Simulink (Matlab 2018b) has the characteristics of allowing users to observe the simulation process at all times. It provides a precise environment based on mathematical principles for block diagram design. It is a software integration package that can be used like a production line from establishing a dynamic system model to observing the simulation process to real-time simulation analysis. It is widely used in various systems [26].

In this paper, the vehicle dynamics model is constructed in CarSim (2019), and then the corresponding inverse dynamics model is built in Simulink according to the obtained vehicle dynamics model to provide parameter data basis for the subsequent research on control strategy.

2.2. Establishment of Vehicle Dynamics Model

In this paper, CarSim (2019)is used to establish the vehicle dynamics model. Because the vehicle parameters of the E-type vehicle are more in line with the experimental standards, such as its idle speed being 750 r/min, the gearbox being a 6-speed automatic transmission, the shift time being 0.5 s, the ABS of the brake not starting when the vehicle speed is less than 3 km/h and the wheel slip rate being about 0.2, and because many high-quality papers are based on the E-type car, CarSim (2019)is used for simulation analysis [27,28]. Therefore, this paper decides to choose the E-type vehicle as the vehicle model, and its related parameters are shown in

Table 1. Vehicle parameters.

Vehicle Parameters	Value	Vehicle Parameters	Value
Complete vehicle kerb mass/kg	1615	Main reducer reduction ratio	3.48
Air resistance coefficient	0.32	Tire rolling radius/m	0.36
Windward area/m2	2.73	Transmission efficiency of transmission system	0.9
Rolling resistance coefficient	0.02	Brake disc mass/kg	9.65

.

2.3. Establishment of Vehicle Inverse Dynamics Model

2.3.1. Switching Control Strategy of Inverse Dynamics Model

In this paper, the change in vehicle speed is controlled by controlling the throttle opening of the engine in the power system and the pressure of the brake pipe in the braking system. The structure of the vehicle inverse dynamics model is shown in Figure 1.

where $a_e$ is the expected acceleration of the vehicle, $P_e$ is the brake master cylinder pressure and ${\alpha }_e$ is the throttle opening.

In the actual driving process of the vehicle, the accelerator pedal and the brake pedal will not work at the same time, otherwise it will cause damage to the car. When the car needs to decelerate, if the required braking deceleration is small, the engine braking, air resistance and road resistance can be used to assist the braking; if the required braking deceleration is too large, the brake can be used for fast or emergency braking. Therefore, a switching logic model needs to be designed between the two to control its specific braking mode. At the same time, taking into account the vehicle in the real driving environment, frequent switching acceleration and deceleration and the algorithm control model will have a great adverse impact on the driver’s ride comfort. Therefore, the switching boundary between the two models cannot be set as a threshold point, but a buffer should be extended at the threshold point.

In CarSim (2019), the vehicle is first set to travel at a constant speed, and the throttle opening is set to 0 at a certain time. Due to the effects of air resistance and rolling resistance, the maximum deceleration of the vehicle at different initial speeds can be measured. The initial speed of the vehicle is set from 50 km/h to 150 km/h, the step size is 10 km/h and the simulation time is 10 s. Taking the initial speed of 60 km/h as an example, the corresponding deceleration curve shows that the maximum deceleration is −0.0293 g, and the speed is reduced from 60 km/h to 50.9 km/h within 10 s. Therefore, the width of the buffer selected in this paper is $△a=0.2{\mathrm{m}/\mathrm{s}}^2$, and the floating up and down is $0.1{\mathrm{m}/\mathrm{s}}^2$. From this, the maximum braking deceleration under various vehicle speed conditions is obtained when the throttle opening is 0, as shown in the blue line in Figure 2. Based on the blue line, a buffer of $\pm 0.1{\mathrm{m}/\mathrm{s}}^2$ is added to obtain the switching threshold of the throttle opening control model and the brake system control model.

According to the relationship between the expected acceleration and the actual acceleration, the following switching strategy for the throttle opening control model and the brake system control model is formulated: when $a-0.5\times △a\le a_e\le a+0.5\times △a$, the expected acceleration falls in the buffer area, that is, the preset deceleration can be achieved by adjusting the throttle opening, and the brake system does not need to intervene in this case. When $a_e>a+0.5\times △a$, the actual acceleration is lower than the expected acceleration, that is, it is necessary to increase the throttle opening to reach the preset acceleration, so as to meet the acceleration requirements of the vehicle. When $a_e<a-0.5\times △a$, the expected acceleration was not in the buffer area, that is, the expected deceleration requirements could not be met by controlling the throttle opening. At this time, the PID control would need to mobilize the brake system to intervene and control the brake pipeline pressure to achieve the higher deceleration requirements.

2.3.2. Throttle Opening Inverse Dynamics Control Model

In CarSim software (2019), let the simulated E-type vehicle move at a constant speed in a straight line at a speed of 0–120 km/h (step length of 10 km/h) to obtain the size of the throttle opening value at different speeds, and draw Figure 3. The relationship between throttle opening and vehicle speed cannot be approximately linear due to gear shifting. When the gear position is constant, the throttle opening increases monotonously with an increase in vehicle speed. The throttle opening—speed data under different gear positions are imported into Simulink, and the inverse dynamic control model of throttle opening is established.

2.3.3. Inverse Dynamic Model of Brake Pressure

The driving equation of a vehicle on a straight road can be simplified as follows:

$$F_t=F_f+F_w+F_j$$

(1)

where $F_t$ is the driving force of the vehicle; $F_f$ is the rolling resistance; $F_w$ is air resistance and $F_j$ is acceleration resistance.

By analyzing the vehicle driving equation (Equation (1)) and the expected deceleration, the force of the vehicle braking can be obtained as shown in Equation (2):

$$ma=-F_{xb}-Gf-\frac{C_{D}A{V}^2}{21.15}$$

(2)

where $F_{xb}$ is the ground braking force; $a$ is the acceleration of the vehicle; $F$ is the rolling resistance coefficient; $C_D$ is the air resistance coefficient; $A$ is the windward area and $V$ is the vehicle speed.

When the vehicle is braking, the ratio of the braking force $F_{xb}$ and braking pressure $P$ can be approximated to a certain value, as shown in Equation (3):

$$\frac{F_{xb}}{P}=K_b$$

(3)

According to Equation (2), the expected brake pressure is

$$P_e=\frac{\left|m{a}_e+Gf+\frac{C_{D}A{v}^2}{21.15}\right|}{K_b}$$

(4)

Combined with the actual structure of the E-type vehicle, Equation (3) can be transformed into the following:

$$\frac{T_{\mathrm{bf}}+T_{br}}{r}=K_b·P$$

(5)

where $T_{bf}$ is the front wheel braking torque; $T_{br}$ is the rear wheel braking torque; $r$ is the wheel radius and $P$ is the brake pressure.

3. Research on AEB System Control Strategy

3.1. AEB System Algorithm

When the vehicle is driving on the normal traffic road, the AEB system will obtain the vehicle braking state and braking deceleration value output by the upper decision module. Since it cannot be directly inputted into the vehicle model, it is necessary to perform braking deceleration signal processing. The acceleration value output by the upper controller is converted into a signal that can be directly inputted into the vehicle dynamics model. The AEB system discussed in this paper mainly relies on the control of throttle opening to carry out emergency auxiliary braking in non-critical situations. When the driver fails to respond to braking and the vehicle enters a critical condition, the AEB system converts to the braking system module through the logical switching function and uses the PID error control model to control the vehicle braking pressure. Its system structure is shown in Figure 4 below.

According to the requirements of the control strategy for the algorithm and the system architecture, the safety time logic algorithm based on the collision time is selected. The calculation formula is as follows:

$$\left\{\begin{array}{l}TTC=-\frac{x}{V_{rel}},(\mathrm{First}-\mathrm{order} TTC)\\ TTC=\frac{-V_{rel}-\sqrt{V_{rel}{}^2-2a_{rel}x}}{a_{rel}},(\mathrm{Second}-\mathrm{order} TTC)\end{array}\right.$$

(6)

where $x$ is the relative distance between the front and rear vehicles, $V_{rel}$ is the relative speed of the front and rear vehicles and $a_{rel}$ is the relative acceleration of the front and rear vehicles.

When the collision time threshold is different, the probability of avoiding accidents under different braking intensities is also different [23]. The specific parameters are shown in

Table 2. Collision avoidance probability under dual variables of braking strength and TTC threshold.

Brake Deceleration	Probability of Collision Avoidance at Different Times				Mean Value
	5%	25%	75%	95%
0.5 g	0.2 s	0.6 s	0.5 g	0.2 s	0.6 s
0.675 g	0.15 s	0.5 s	0.675 g	0.15 s	0.5 s
0.85 g	0.1 s	0.4 s	0.85 g	0.1 s	0.4 s

.

It can be seen from Table 2 that if the driver can brake at a deceleration of 0.5 g 1.8 s before the collision, the collision loss can be greatly reduced. According to the hierarchical braking control strategy, the TTC threshold is 2.6 s. When TTC is not within this range, the vehicle emergency braking system will intervene and take control.

The reaction time of different warning types of drivers in the event of an accident is also different. The specific parameters are shown in

Table 3. Driver reaction time in accidents (unit: s).

Early Warning Types	Average Value	Standard Deviation	µ	σ2	75%	85%	90%
Image warning	1.13	0.52	1.03	0.44	1.38	1.62	1.80
Sound warning	0.99	0.44	0.90	0.43	1.20	1.40	1.55
Image and sound	0.90	0.34	0.84	0.37	1.08	1.23	1.34

. After simplifying the data model, the driver’s reaction time can be approximated as a lognormal probability distribution with parameters $\mu$ and ${\sigma }^2$ [29].

It can be seen from the above table that the average reaction time of the driver is about 1.13 s after only receiving visual stimulation; when the emergency braking system of the vehicle stimulates the driver in terms of both hearing and vision, the average reaction time of the driver will be reduced to 0.9 s, because in real life the delay time of the actual brake will generally be 0.2 s. Therefore, 2.6 s is taken as the TTC threshold to determine the intervention time of automatic braking, and the TTC warning threshold using a warning light is calculated as 3.8 s; the TTC threshold of the warning light and the sound joint warning is 3.5 s.

The algorithm proposed in this paper will compare the size of the TTC obtained at each moment with the preset threshold. If $TTC>TT{C}_t$ (threshold), it indicates that there is a risk of collision at this time, and the system adopts the corresponding control strategy. This paper adopts the safe time logic algorithm, and carries out follow-up research on this basis.

3.2. Algorithm of Upper Fuzzy Control System

3.2.1. Upper TTC Control Logic

The AEB upper control algorithm in this paper uses the safe time logic algorithm to build the target vehicle scene in the CarSim model, and calculates the TTC value at the current time by using the radar output information such as the distance and the relative speed $V_{rel}$ between the self-vehicle and the target vehicle, and compares the calculated TTC value with the threshold value through the logical state machine to obtain the ideal deceleration $a_{\exp }$ in the current state.

3.2.2. Upper Fuzzy Control System

Fuzzy control is an algorithm that uses algorithms to simulate people to process and analyze data, also known as language control. Fuzzy control is often used to deal with control objects that cannot be described by accurate mathematical models, such as nonlinear, time-varying, incomplete model systems. The basic structure is shown in Figure 5.

The system obtains the input through the sensor, and compares the input value with the set value to obtain the error signal E. The error signal E is the input of the fuzzy control. The E is fuzzified and represented by fuzzy language to obtain a subset e of the fuzzy language set of the error E. The fuzzy decision is made according to the fuzzy relationship to obtain the fuzzy control amount u, and then the u is defuzzified into an accurate value and transmitted to the lower control system.

In this paper, the speed difference $\mathrm{\Delta }V$ and relative distance $\mathrm{\Delta }s$ between the self-vehicle and the target vehicle are taken as the input of fuzzy control. The self-vehicle is always behind the target vehicle, and when the AEB system starts to work, the self-vehicle speed must be greater than the target vehicle, so $\mathrm{\Delta }s\ge 0$ and $\mathrm{\Delta }V\le 0$. The universe of $\mathrm{\Delta }s$ is [0, 80] divided into 8 fuzzy sets: Z0, P1, P2, P3, P4, P5, P6 and P7; the universe of $\mathrm{\Delta }V$ is [−150, 0] divided into 11 fuzzy sets: Z0, N1, N2, N3, N4, N5, N6, N7, N8, N9 and N10. The desired deceleration $a_{\exp }$ is the output of the system, and the universe is [−10, 0] divided into eight fuzzy sets: Z0, N1, N2, N3, N4, N5, N6 and N7. Mamdani is adopted as the fuzzy relation rule, and the barycenter method is used to solve the fuzzy method.

On the premise of ensuring the driver’s safety, it is necessary to take into account the influence of the AEB system on ride comfort, so some fuzzy control rules are processed. The processing results are shown in

Table 4. Processing results.

$\mathbf{\Delta }\mathit{s}$	$\mathbf{\Delta }\mathit{V}$	a	$\mathbf{\Delta }\mathit{s}$	$\mathbf{\Delta }\mathit{V}$	a
Z0	Z0	N2	P4	N4	N1
Z0	N10	N7	P4	N6	N2
P1	N1	Z0	P5	N5	Z0
P1	N9	N7	P5	N5	N1
P2	N2	N1	P6	N6	N1
P2	N8	N6	P6	N4	Z0
P3	N3	N1	P7	N7	N1
P3	N7	N4	P7	N3	Z0

.

3.3. Lower PID Control

3.3.1. Throttle Opening PID Control

The PID control model of the throttle opening in the hierarchical control strategy proposed in this paper is shown in Figure 6. After subtracting the expected speed from the actual speed, a dead zone characteristic module is passed to avoid the actual operation process. Due to small speed changes, the electric throttle opening changes repeatedly. After the dead zone characteristic module processing, the PID control is no longer sensitive to small changes in the upper control signal. It can be received by the PID control module through the dead zone signal. The key to using the PID control module is to determine its three parameters Kp, Ki and Kd. The CarSim software (2019) is connected by Simulink, and different values are inputted. The actual speed of the output is observed in CarSim (2019). The three control parameters are determined using the trial and error method, Kp = 4.5, Ki = 1.5, Kd = 0 and the filter coefficient N = 100.

The output of the PID module needs to go through the saturation characteristic module, which will limit the size of the PID output value. When its output is within the preset range of the module, the control signal can be successfully transmitted to the electric throttle to adjust the opening. However, if the output value is too large or small, the saturation characteristic module will adjust it to the upper and lower limits accordingly. This module plays a limiting role, and the limiting range is 0~0.95.

This paper uses the logic state machine to further limit the throttle opening. When the expected acceleration calculated by the AEB algorithm is less than the maximum deceleration that can be provided when the throttle opening is 0, set the throttle opening to 0 to avoid the impact of the engine output on the braking effect. If the expected acceleration calculated by the AEB algorithm is greater than the maximum deceleration that can be provided when the throttle opening is 0 after 2 s, that is, the vehicle is in a safe state, keep the throttle open to avoid affecting the driver’s operation.

3.3.2. Brake System Pressure PID Control

The PID control model of the braking system in the hierarchical control strategy proposed in this paper is shown in Figure 7. In order to achieve the desired braking deceleration of the vehicle, this paper adds the brake master cylinder pressure control to the CarSim vehicle model in the Simulink model, which is similar to the throttle opening control. In order to achieve a better control effect, the PID controller is also selected here to adjust the brake master cylinder pressure.

The brake pressure is generated by the brake master cylinder under the current expected acceleration calculated by the vehicle driving equation in Figure 7. The module construction process is as follows:

After actual calculation, the rolling resistance and air resistance have little influence on the results, which can be ignored, and one only needs to add a correction factor $\delta$ for $m{a}_e$, $\delta =1.03$. Simplify it to

$$P_e=\frac{\left|\delta m{a}_e\right|}{K_b}$$

(7)

In CarSim, set the vehicle to move at a constant speed in a straight line and apply the known brake pressure P to it at a certain time, and the software will output the brake torque $T_{bf}$ and $T_{br}$ of the front and rear wheels.

4. Simulation Results and Analysis

In order to reduce rear-end traffic accidents caused by braking problems, automobile evaluation agencies such as Euro-NCAP, NHTSA, J-NCAP and C-NCAP have incorporated automatic emergency braking system into the rules of new vehicle evaluation, and they are constantly improving the corresponding test scenarios and requirements. Among numerous test and evaluation regulations, Euro-NCAP has the most comprehensive test for intelligent driving functions. It has developed three test scenarios for the AEB function: car-to-car rear stationary (CCRs), car-to-car rear moving (CCRm) and car-to-car rear braking (CCRb) [30]. In this paper, which relies on the joint simulation of CarSim and Simulink, the hierarchical control strategy algorithm under hierarchical early warning was simulated and tested, respectively, in these three typical test scenarios to verify the effectiveness of the control strategy.

4.1. CCRs Test

The test conditions are shown in

Table 5. CCRs test conditions.

Initial Self- Driving Speed/(km/h)	Self-Driving Movement State	Distance between Two Vehicles/m	Initial Speed of Target Vehicle/(km/h)	Target Vehicle Movement State
50	Uniform velocity	40	0	Static

(the target vehicle is always in front of the self-vehicle), and the simulation results are shown in Figure 8 and Figure 9.

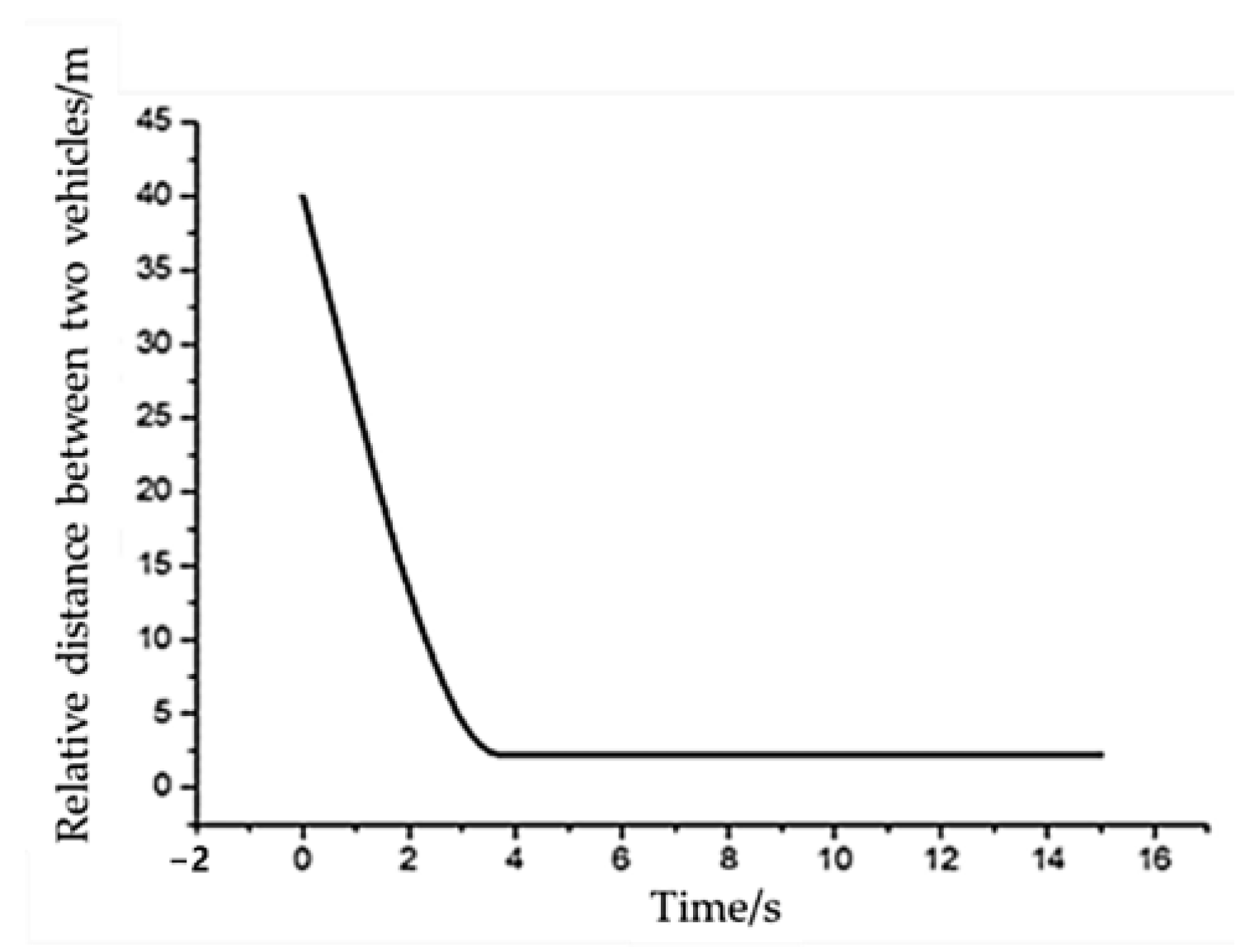
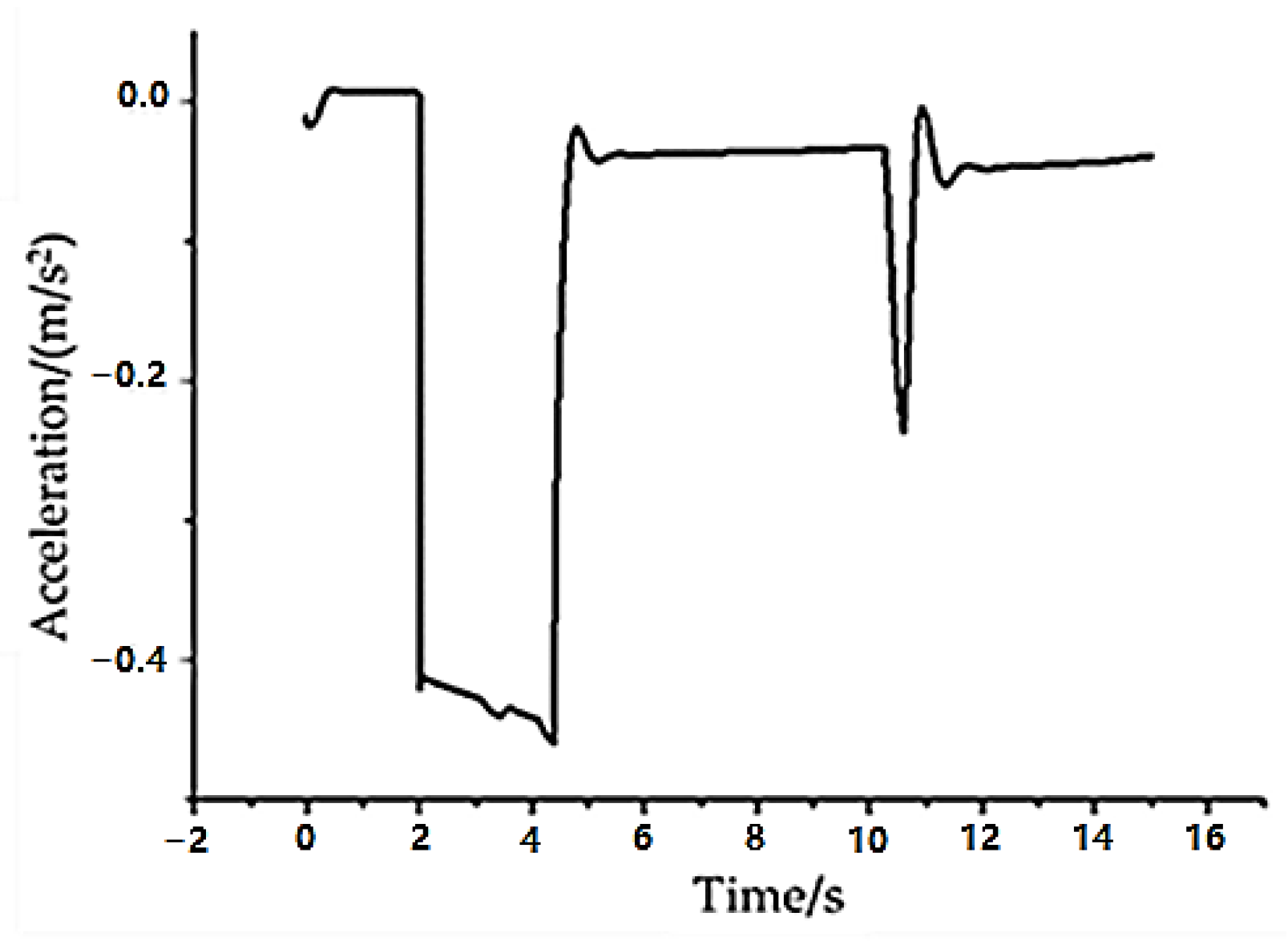
It can be seen from Figure 8 that the initial distance between the two vehicles is 40 m, and the self-vehicle is close to the front vehicle in a stationary state at a relative speed of 50 km/h at 40 m from the front vehicle. As the simulation progresses, the relative distance between the two vehicles gradually decreases. At 3.7 s, the distance between the two vehicles reaches the minimum value, and then the relative distance between the two vehicles remains unchanged at 2.22 m.

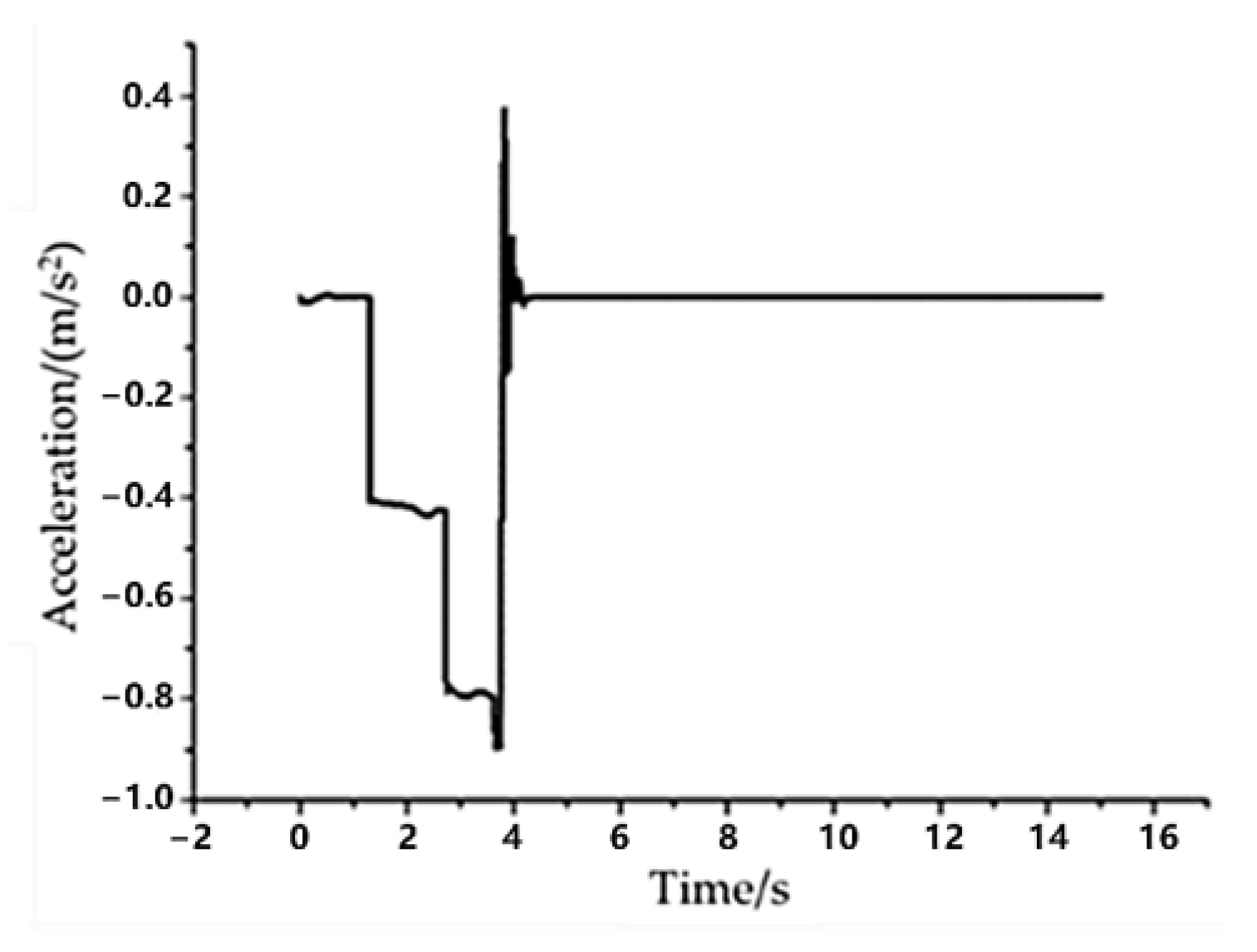
From Figure 9, it can be seen that under this simulation condition, the initial speed of the two vehicles is quite different. The AEB system detects the risk of collision when the simulation time is 1.3 s, and the calculated TTC value is less than the threshold of the first-level braking. Therefore, the deceleration of the self-vehicle begins to decrease from 0 until it brakes at a deceleration of −0.4 m/s². The deceleration is stable at about −0.4 m/s² in 1.3 s to 2.7 s. As the real-time distance between the two vehicles decreases, the collision risk level increases. In 2.7 s, the TTC value calculated by the AEB system is less than the secondary braking threshold. After receiving the secondary braking request, the braking system brakes, so that the vehicle acceleration rises to −0.8 m/s². Finally, the self-vehicle stops at a distance of 2.22 m from the target vehicle, avoiding the occurrence of collision.

In the simulation time of 2.7 s to 3.7 s, the actual deceleration following state of the self-vehicle is better. After 3.7 s of simulation time, the actual deceleration oscillation is due to the fluctuation in the self-vehicle deceleration detected by the sensor due to the braking of the self-vehicle. In general, the simulation results show that the designed control strategy can effectively avoid collision under the condition of a close-to-stationary target.

4.2. CCRm Test

The test conditions are shown in

Table 6. CCRm test conditions.

Initial Self- Driving Speed/(km/h)	Self-Driving Movement State	Distance between Two Vehicles/m	Initial Speed of Target Vehicle/(km/h)	Target Vehicle Movement State
50	Uniform velocity	40	30	Uniform velocity

(the target vehicle is always in front of the self-driving vehicle), and the simulation results are shown in Figure 10 and Figure 11.

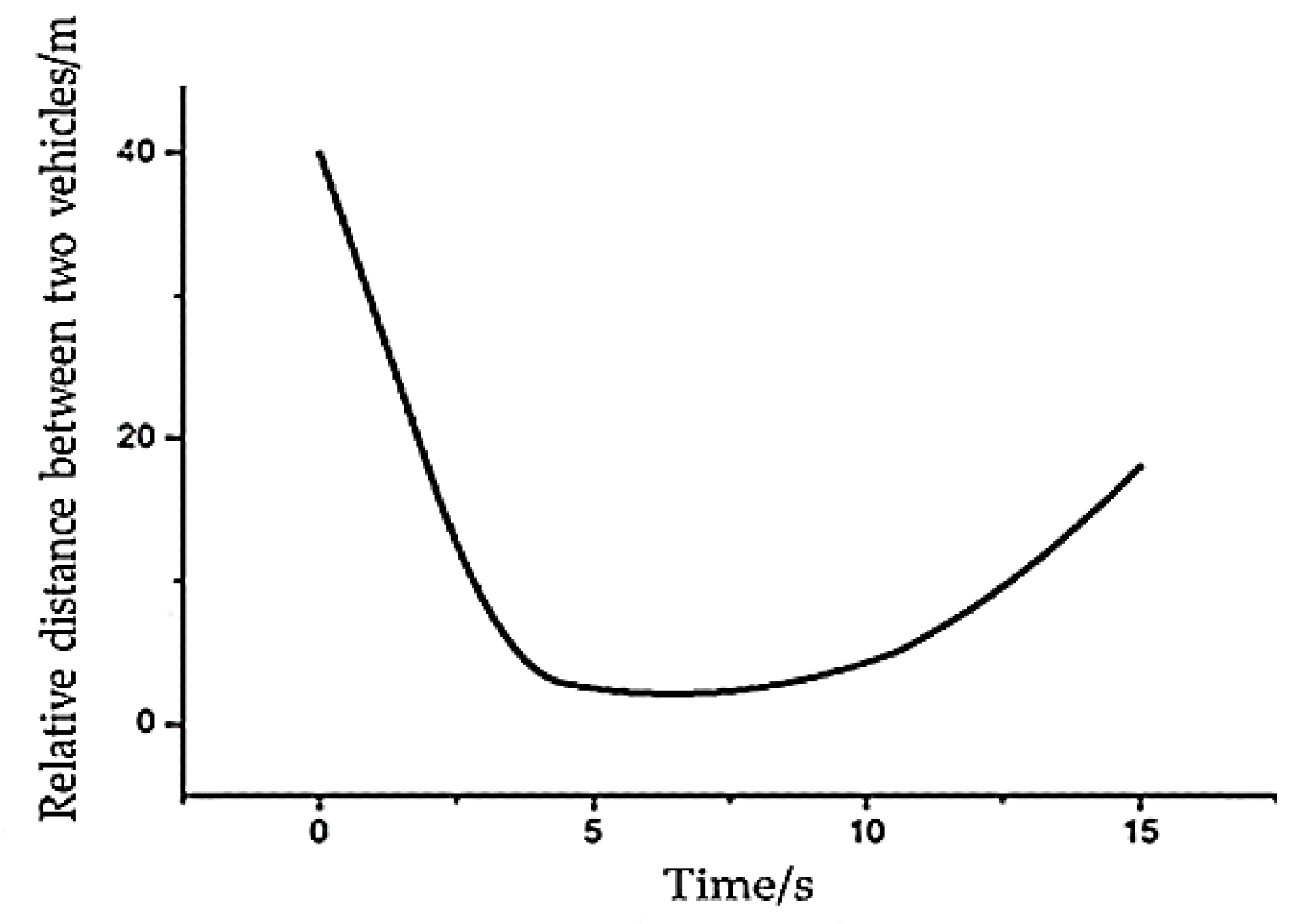
It can be seen from Figure 10 that the initial distance between the two vehicles is 40 m, and the self-vehicle is approaching the front vehicle at a relative speed of 30 km/h at 40 m from the front vehicle. As the simulation progresses, the relative distance between the two vehicles gradually decreases. At 4.4 s, the distance between the two vehicles reaches a minimum of 2.11 m, and then the relative distance between the two vehicles gradually increases.

From Figure 11, it can be seen that within the first 2 s of the simulation time, the distance between the self-driving and the target vehicle that is far away and the calculated TTC value do not reach the set thresholds. The self-vehicle maintains a uniform speed and the acceleration is stable at 0. In 2 s, the TTC value calculated by the AEB system reaches the first braking threshold, and the vehicle brakes at a deceleration of −0.4 m/s². In 4.4 s, the speed of the self-vehicle is equal to that of the target vehicle. The TTC value calculated by the vehicle is greater than the threshold set by the system. The AEB system issues an instruction to stop braking and restore the normal driving state of the self-vehicle. Under this condition, the nearest distance between the vehicles is 2.11 m.

In the simulation time of 2 s to 4.4 s, the actual deceleration of the self-driving basically reached −0.4 m/s², but due to the ground adhesion limit it will produce shock, resulting in unstable deceleration, even more than −0.4 m/s². After 4.4 s of simulation time, the actual deceleration oscillation was due to the fluctuation in self-vehicle deceleration detected by the sensor due to the braking of the self-vehicle. In general, the simulation results show that the designed control strategy can effectively avoid collision under the condition of being close to the uniform braking target vehicle.

4.3. CCRb Test

The test conditions are shown in

Table 7. CCRb test conditions.

Initial Self-Driving Speed/(km/h)	Self-Driving Movement State	Distance between Two Vehicles/m	Initial Speed of Target Vehicle/(km/h)	Target Vehicle Movement State
50	Uniform velocity	12	50	Slows down at $-4{\mathrm{m}/\mathrm{s}}^2$ after a constant speed of 4 s

(the target vehicle is always in front of the self-driving vehicle), and the simulation results are shown in Figure 12 and Figure 13.

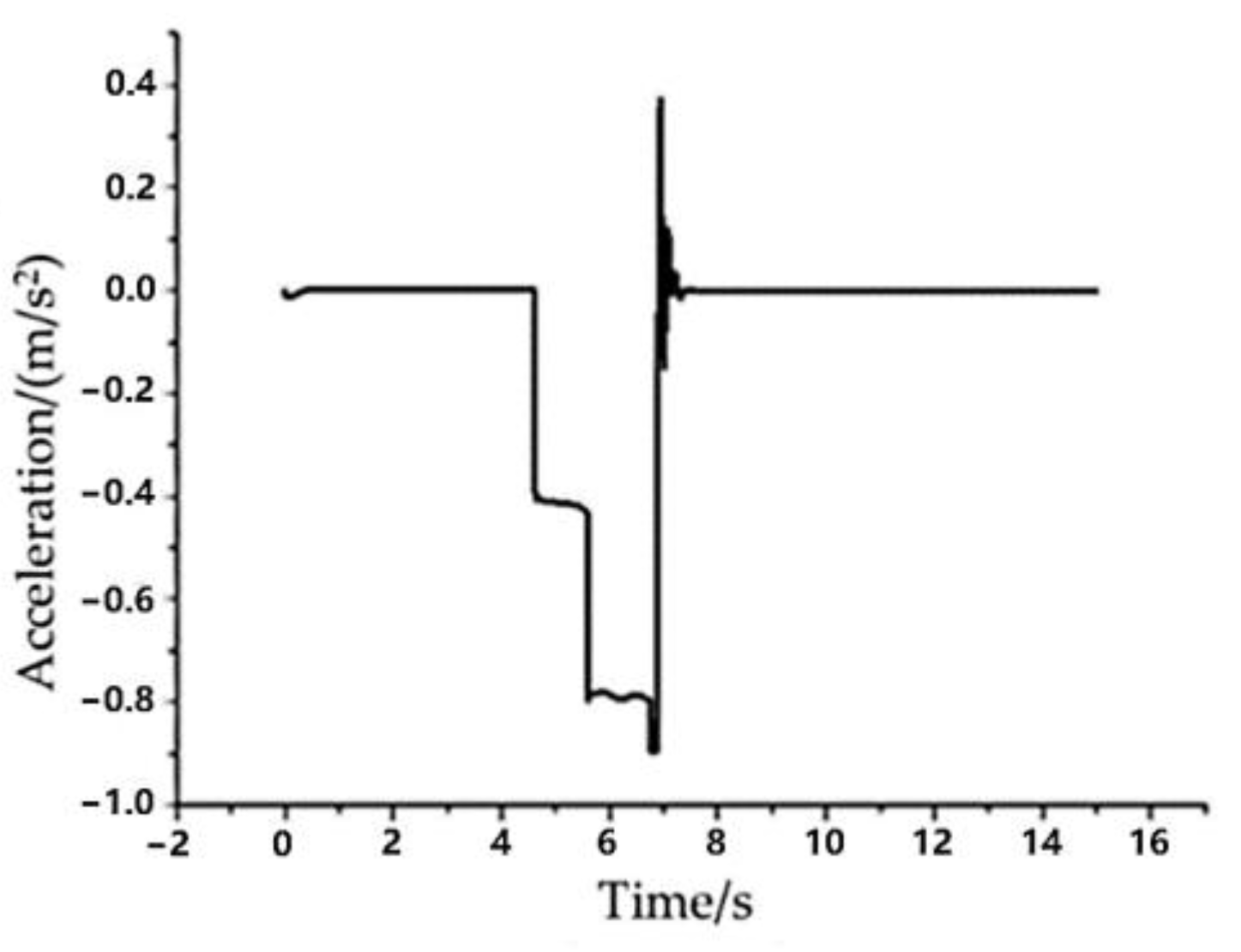
From Figure 12, it can be seen that the initial distance between the two vehicles is 12 m, and the self-vehicle is close to the front vehicle at a relative speed of 50 km/h at a distance of 12 m from the front vehicle. Because the front vehicle travels at a constant speed of 50 km/h for 4 s and then decelerates at −4 m/s², as the simulation progresses, the relative distance between the two vehicles gradually decreases. The distance between the two vehicles reaches the minimum value at 6.8 s, and then the relative distance between the two vehicles remains unchanged at 1.56 m.

It can be seen from Figure 13 that in the first 4 s of the simulation time, the AEB system is not involved because the relative speed between the front vehicle and the self-vehicle is 0. When the simulation time is close to 4.6 s, the TTC value reaches the primary braking threshold. The deceleration of the self-vehicle decreases from 0 to brake at a deceleration close to −0.4 m/s². At 5.6 s, the TTC value reaches the secondary braking threshold. At this time, the vehicle performs full braking, and the braking deceleration is close to −0.8 m/s² until the vehicle stops moving. At this time, the distance between the self-vehicle and the target vehicle is 1.56 m, which proves that under this condition, this algorithm can ensure that the vehicle does not collide. In this condition, the braking time of the vehicle with primary braking deceleration is shorter. This is because the distance between the self-vehicle and the target vehicle is relatively close, and the front vehicle brakes at a deceleration of −4 m/s², resulting in the calculated TTC value rapidly falling to the secondary braking TTC threshold. The AEB system quickly sends out the secondary braking deceleration signal, and the vehicle performs emergency braking.

In the simulation time of 5.6 s to 6.9 s, the actual deceleration following state of the self-vehicle is better. After 3.7 s of simulation time, the actual deceleration oscillation is due to the fluctuation in vehicle deceleration detected by the sensor due to the braking of the self-vehicle. In general, the simulation results show that the designed control strategy can effectively avoid collision when the front vehicle brakes urgently under the condition of close-range stable following.

In addition to the above working conditions, this paper also carried out simulation tests under multiple working conditions, and the simulation results are shown in

Table 8. Simulation test results.

Self-Driving Speed (km/h)	Target Vehicle Speed (km/h)	Initial Distance (m)	Target Vehicle Deceleration (m/s2)	Minimum Distance (m)
10	0	12	0	3.41
50	0	40	0	2.22
30	20	12	0	2.95
50	50	50	−2	1.23
50	50	12	−6	1.56
50	50	12	−2	1.05
50	50	40	−6	1.07

.

When the self-vehicle is close to the static vehicle at 12 m ahead at a relative speed of 10 km/h, the shortest distance between the two vehicles is 3.41 m. When the self-vehicle is close to the stationary vehicle at 40 m ahead at a relative speed of 50 km/h, the shortest distance between the two vehicles is 2.22 m. When the self-vehicle is close to the target vehicle at 12 m ahead at a relative speed of 30 km/h, the target vehicle runs at a constant speed of 20 km/h, and the shortest distance between the two vehicles is 2.95 m. When the self-vehicle is close to the target vehicle at 50 m ahead at a relative speed of 50 km/h, the target vehicle slows down at a speed of −2 m/s² from 50 km/h, and the shortest distance between the two vehicles is 1.23 m. When the self-vehicle is close to the target vehicle at 12 m ahead at a relative speed of 50 km/h, the target vehicle slows down at a speed of −6 m/s² from 50 km/h, and the shortest distance between the two vehicles is 1.56 m. When the self-vehicle is close to the target vehicle at 12 m ahead at a relative speed of 50 km/h, the target vehicle slows down at a speed of −2 m/s² from 50 km/h, and the shortest distance between the two vehicles is 1.05 m. When the self-vehicle is close to the target vehicle at 40 m ahead at a relative speed of 50 km/h, the target vehicle slows down at a speed of −6 m/s² from 50 km/h, and the shortest distance between the two vehicles is 1.07 m.

It can be seen from the overall simulation results that the vehicle will begin emergency braking when it enters the dangerous state, so that the vehicle will slow down and maintain a safe state, and the minimum relative distance is also reasonable. The automatic emergency braking system based on the safe time logic algorithm built in this paper has a good braking effect in an emergency and can avoid vehicle collision.

5. Conclusions

In this paper, an algorithm based on safety time logic is proposed. The TTC threshold of warning at all levels is calculated. The hierarchical control algorithm based on layered warning is verified by CarSim and Simulink joint simulation. Under typical and various working conditions of CCRs, CCRm and CCRb, the system meets the actual working conditions and operational feasibility, and improves the reliability and accuracy of the control strategy. The automatic emergency braking system based on collision time designed in this paper can meet the requirements of driving safety, and has a certain reference value for the development and design of the AEB system.

For low-speed driving conditions, although the algorithm proposed in this paper can ensure that the vehicle does not collide, because the algorithm only considers the safety event logic and does not consider the actual distance between the vehicles, the AEB system adopts emergency braking. The distance between the vehicle and the target vehicle is relatively large, which will cause some interference to the driver’s normal driving. Therefore, a safe distance model should be introduced into the control algorithm to avoid premature intervention of the system under low-speed driving conditions. In this paper, the simulation test was used to verify the effectiveness of the control strategy of the automatic emergency braking system, but the simulation results can only show the effectiveness of the control strategy to a certain extent. In later work, a hardware-in-the-loop test or real vehicle test can be used for verification.