Research on Trajectory Tracking Control of Driverless Electric Formula Racing Car Based on Game Theory
Abstract
1. Introduction
2. Game Theory Based on Trajectory Tracking Control Strategy
3. Design of the Controller
3.1. The Whole Vehicle Parameters of Driverless Electric Formula Racing Car
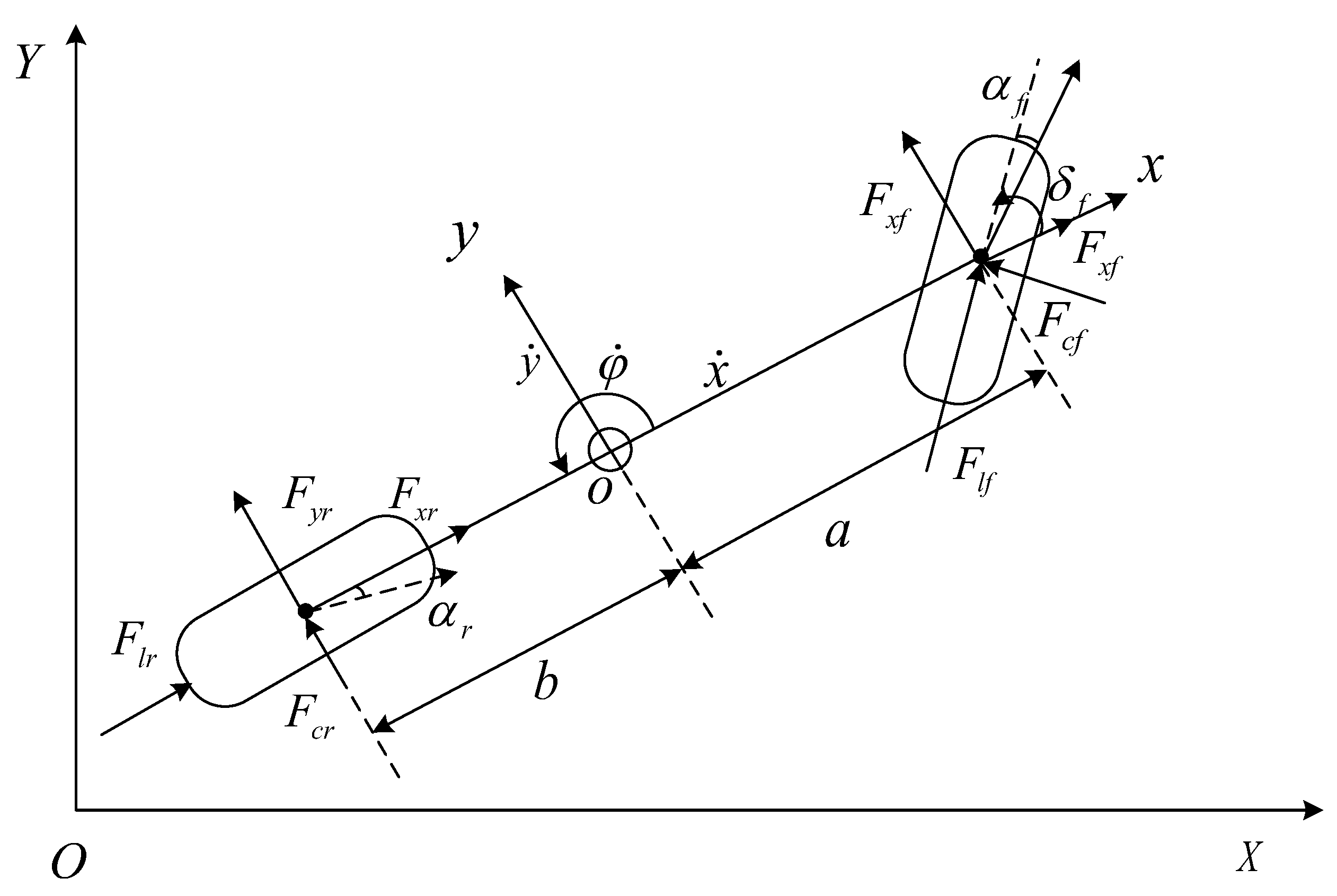
3.2. Vehicle Dynamics Modeling
3.3. Tire Force Analysis
3.4. Design of Model Predictive Controller
3.5. The Design Requirements of the Objective Function
- 1.
- The tracking process maintains a small tracking error, and the error can converge to zero quickly and steadily, and remain balanced.
- 2.
- The front wheel angle control input in the tracking process is as small as possible, and the change should be smooth.
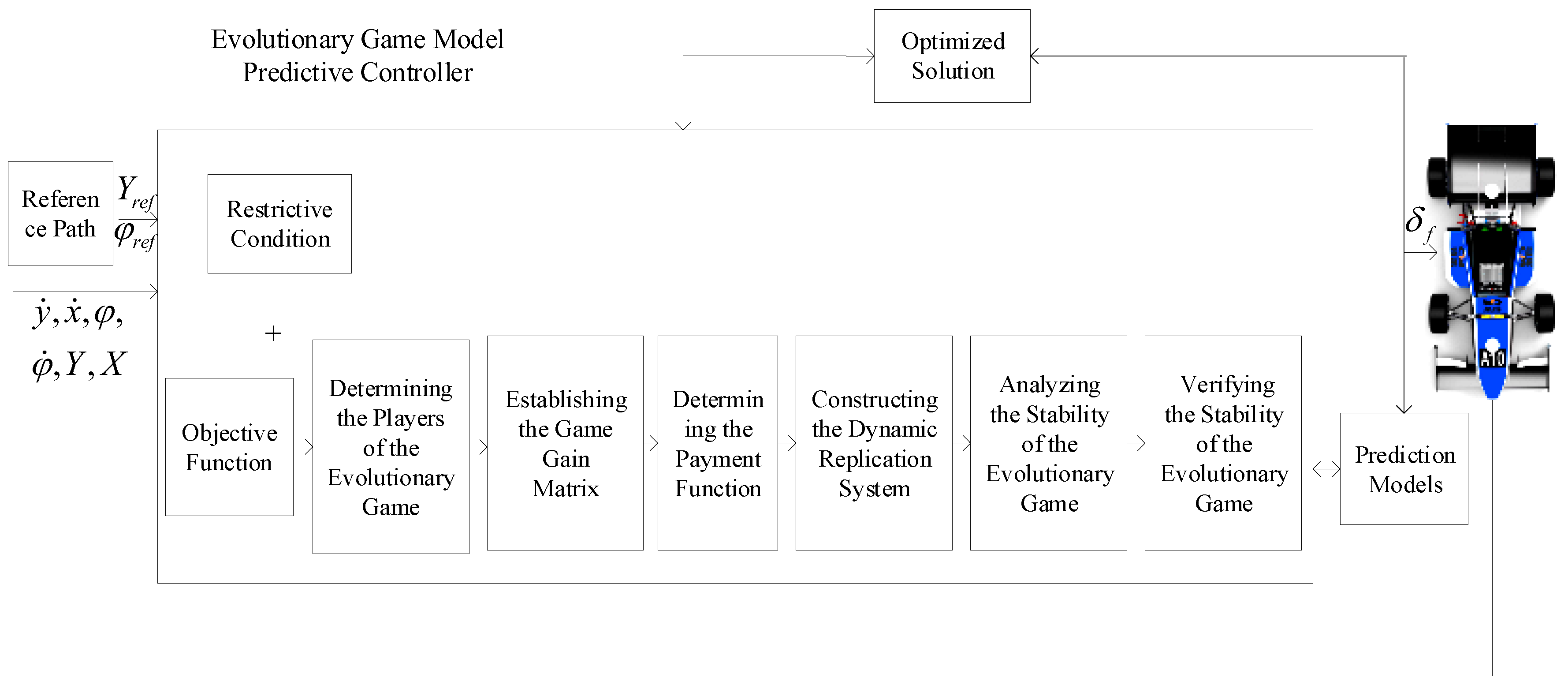
3.6. Evolutionary Game Model Predictive Controller Design
3.6.1. Determining the Players of the Evolutionary Game
3.6.2. Establishing the Game Gain Matrix
3.6.3. Determining the Payment Function
3.6.4. Constructing the Dynamic Replication System
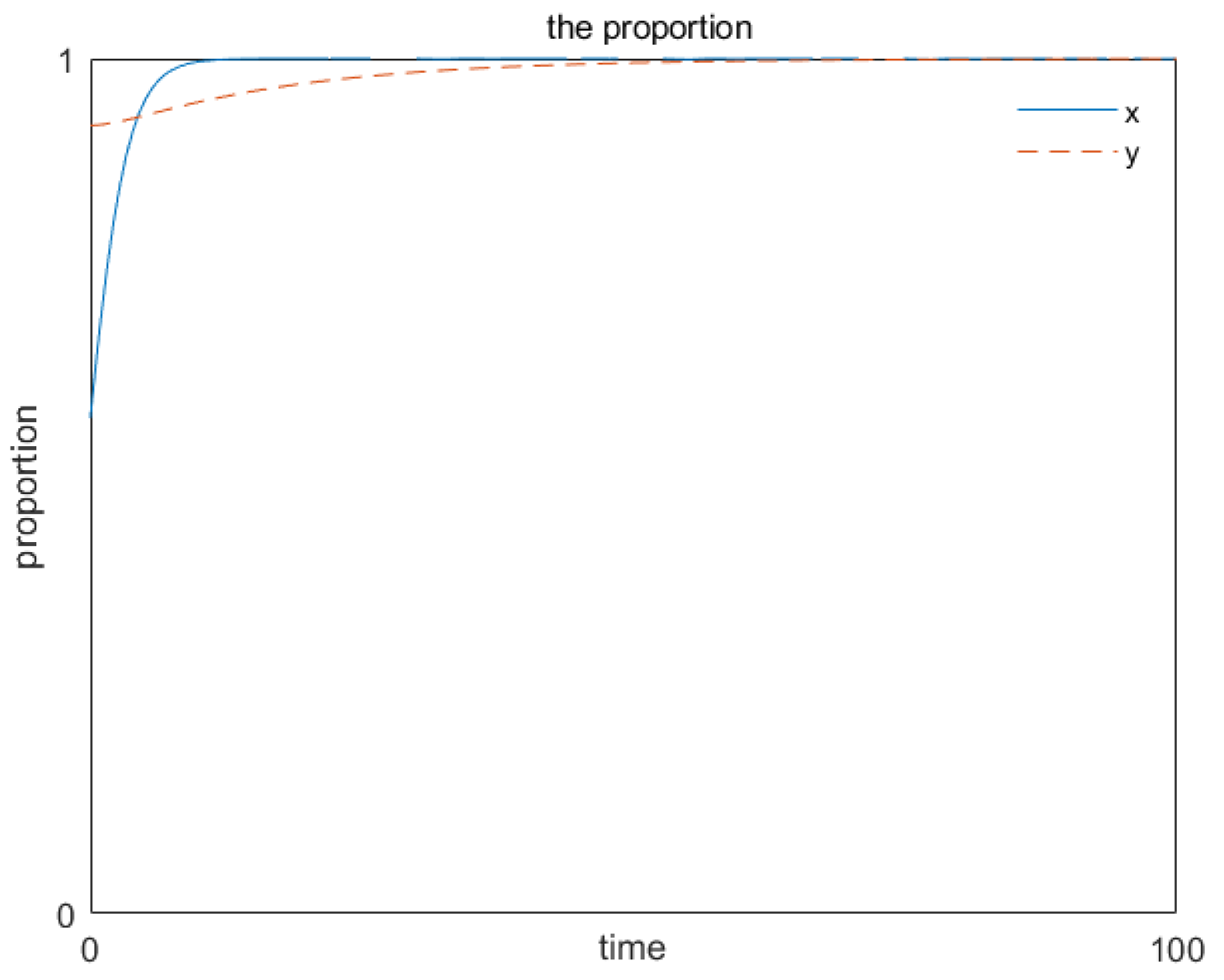
3.6.5. Analyzing the Stability of the Evolutionary Game
3.6.6. Verifying the Stability of the Evolutionary Game
4. Verifying the Stability of the Evolutionary Game
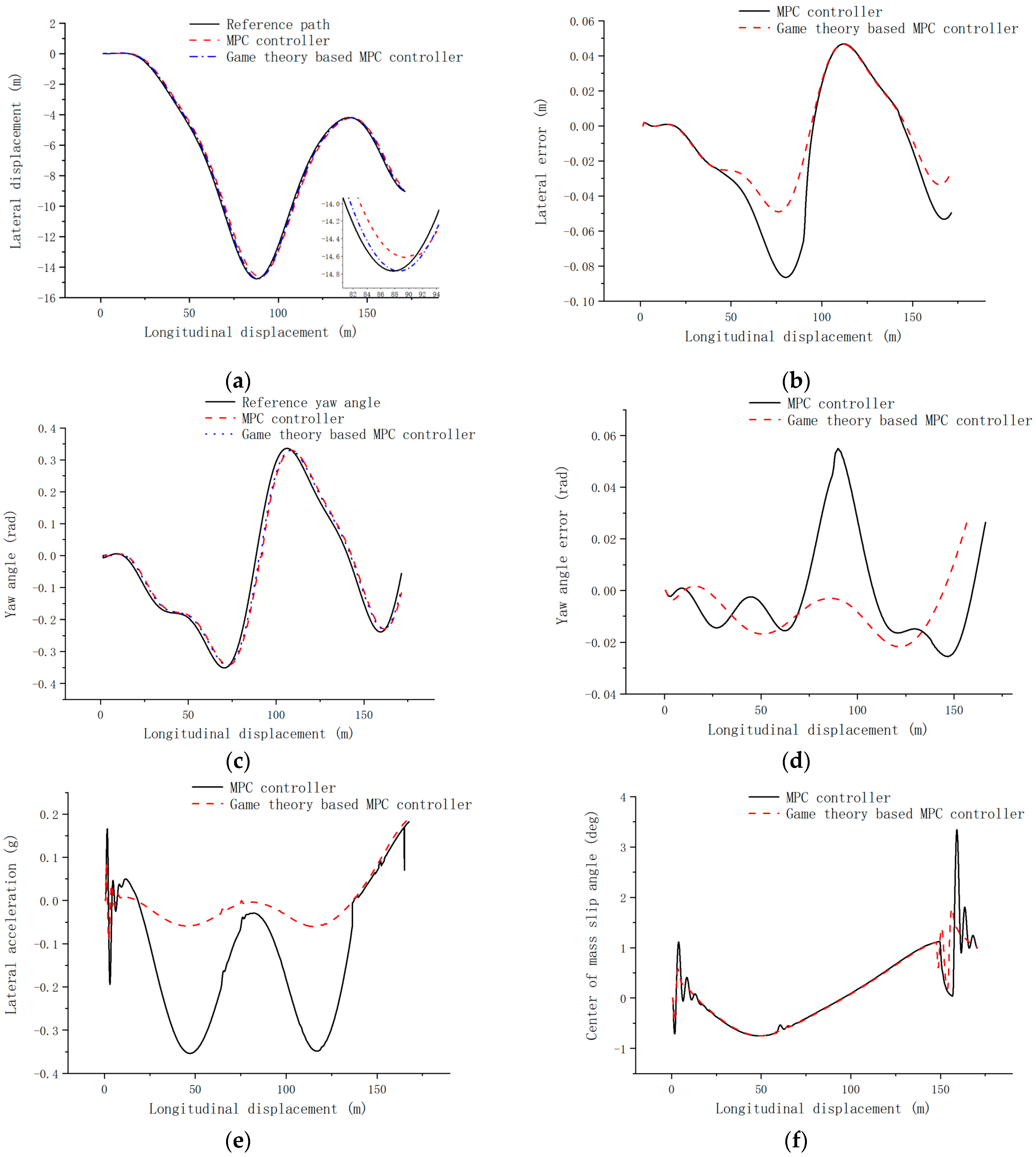
4.1. Low-Speed Road Simulation Verification
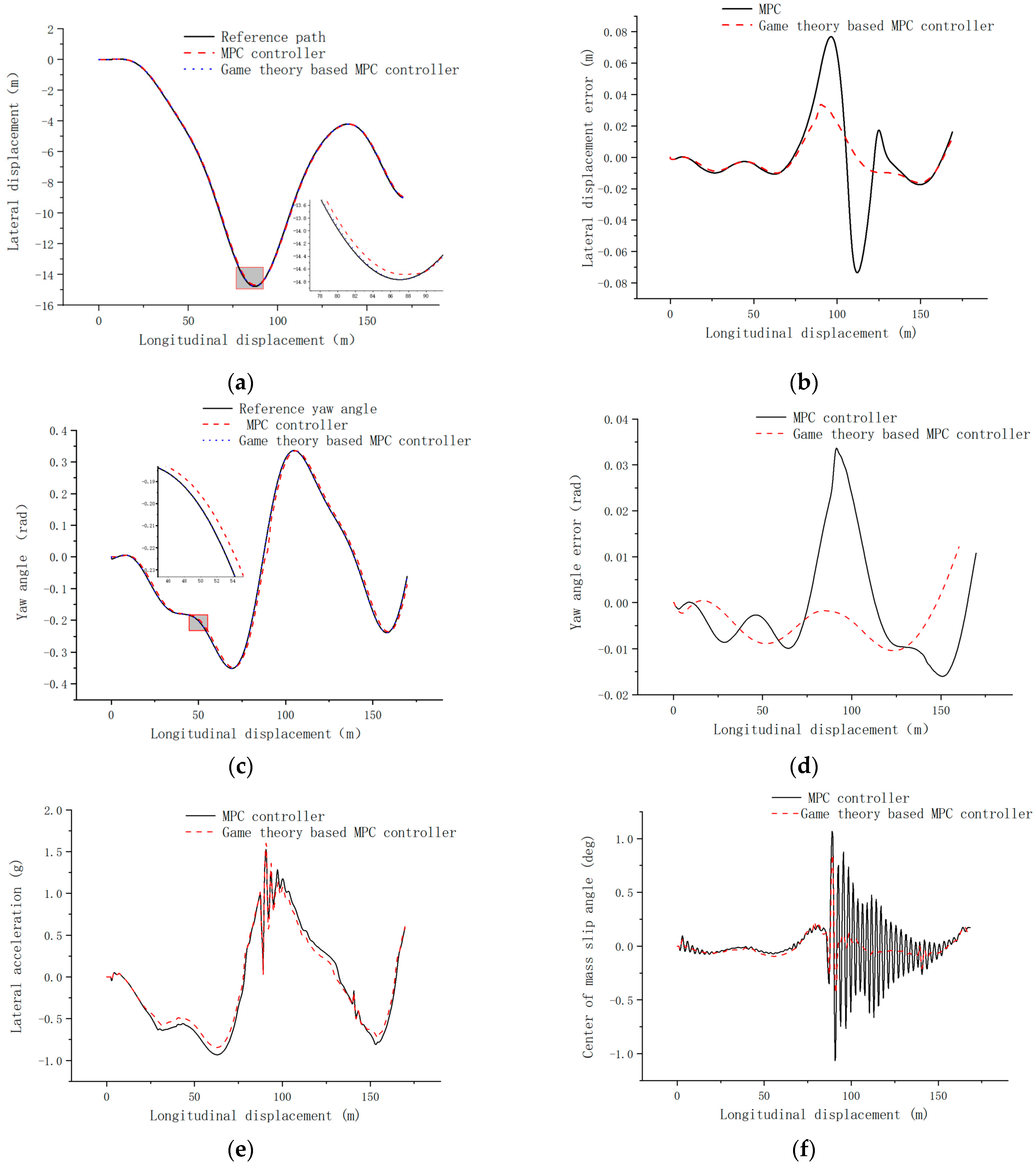
4.2. Medium-Speed Pavement Simulation Verification
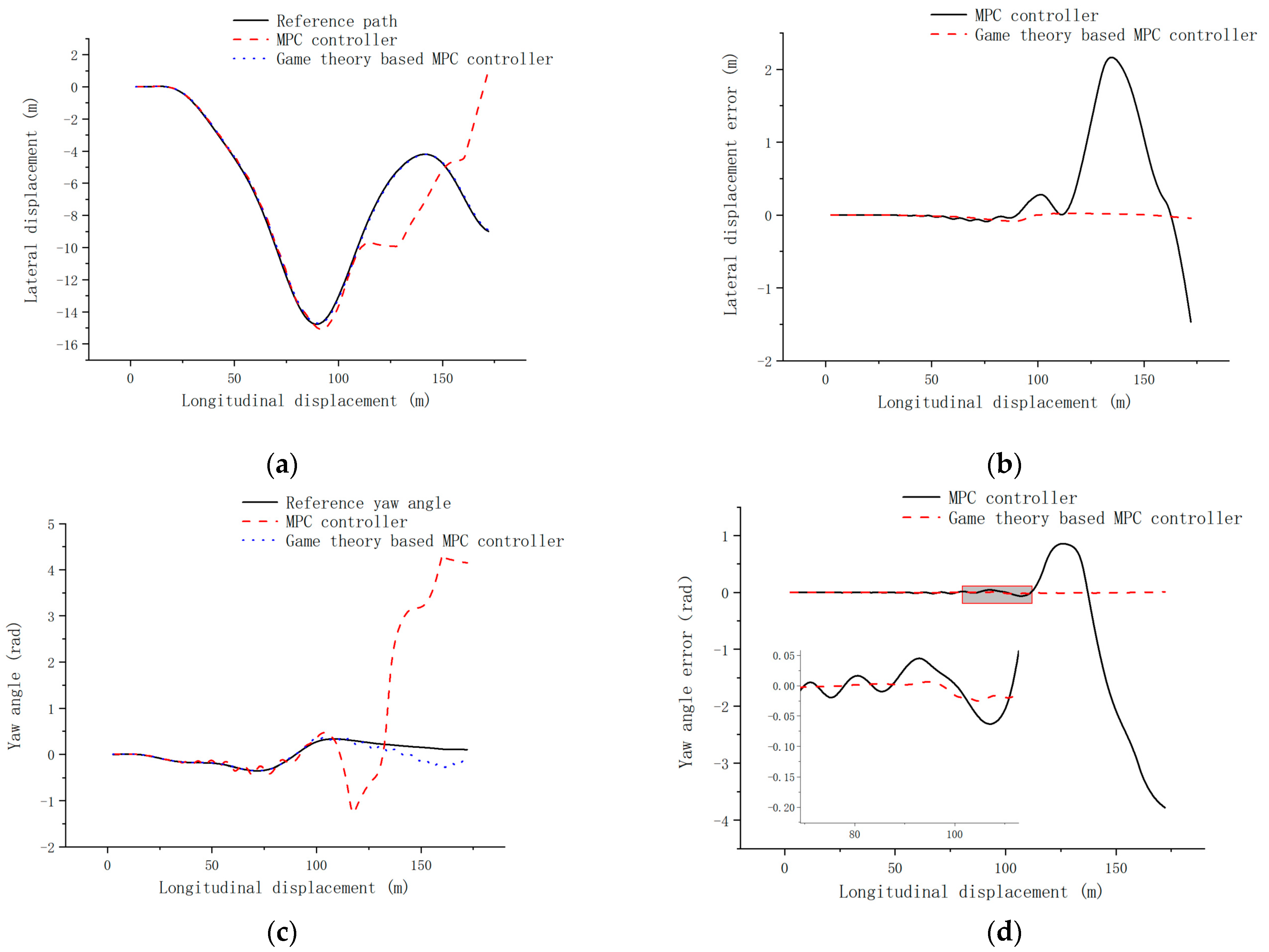
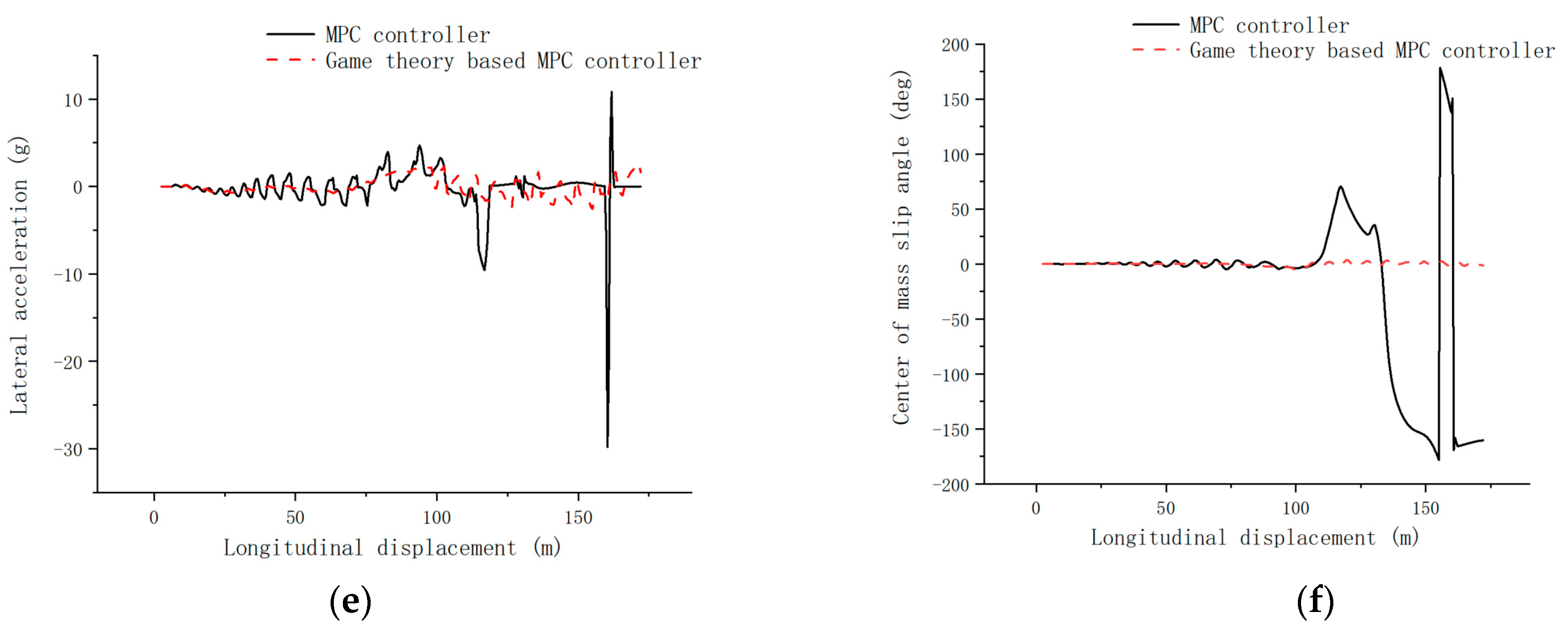
4.3. High-Speed Pavement Simulation Validation
5. Conclusions
- Our proposed trajectory tracking control strategy based on game theory effectively coordinates the weight coefficients of trajectory tracking accuracy and driving stability, solves the dual-objective optimization problem, and improves the trajectory tracking accuracy and driving stability.
- Combining the model predictive control with game theory, the model predictive controller based on the evolutionary game of both players is designed, the lateral error is controlled within 0.1 m, and the transverse swing angle error is controlled within 0.5 rad under the high-speed tracing condition, which has a smaller change of control increment and better control effect compared with the single model predictive controller.
- The model prediction controller based on the evolutionary game of both sides has good trajectory tracking with strong robustness at high, medium, and low speeds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, Q.; Xie, Y.; Guo, S.; Bai, J.; Shu, Q. Sensing system of environmental perception technologies for driverless vehicle: A review of state of the art and challenges. Sens. Actuators Phys. 2021, 319, 112566. [Google Scholar] [CrossRef]
- Nagai, M.; Mouri, H.; Raksincharoensak, P. Vehicle lane-tracking control with steering torque input. Veh. Syst. Dyn. 2002, 37 (Suppl. 1), 267–278. [Google Scholar] [CrossRef]
- Fukushima, H.; Kim, T.H.; Sugie, T. Adaptive model predictive control for a class of constrained linear systems based on the comparison model. Automatica 2007, 43, 301–308. [Google Scholar] [CrossRef]
- Zhao, F.; Wu, W.; Wu, Y.; Chen, Q.; Sun, Y.; Gong, J. Model Predictive Control of Soft Constraints for Autonomous Vehicle Major Lane-Changing Behavior With Time Variable Model. IEEE Access 2021, 9, 89514–89525. [Google Scholar] [CrossRef]
- Taghavifar, H.; Rakheja, S. Path-tracking of autonomous vehicles using a novel adaptive robust exponential-like-sliding-mode fuzzy type-2 neural network controller. Mech. Syst. Signal Process. 2019, 130, 41–55. [Google Scholar] [CrossRef]
- Ji, X.; Wang, J.; Zhao, Y.; Liu, Y.; Zang, L.; Li, B. Path Planning and Tracking for Vehicle Parallel Parking Based on Preview BP Neural Network PID Controller; Transactions of Tianjin University: Tianjin, China, 2015; Volume 21, pp. 199–208. [Google Scholar]
- Kapania, N.R.; Gerdes, J.C. Design of a feedback feedforward steering controller for accurate path tracking and stability at the limits of handling. Veh. Syst. Dyn. 2015, 53, 1687–1704. [Google Scholar] [CrossRef]
- Rosolia, U.; Bruyne, S.D.; Alleyne, A.G. Autonomous Vehicle Control: A Nonconvex Approach for Obstacle Avoidance. IEEE Trans. Control Syst. Technol. 2016, 25, 469–484. [Google Scholar] [CrossRef]
- Mata, S.; Zubizarreta, A.; Pinto, C. Robust tube-based model predictive control for lateral path tracking. IEEE Trans. Intell. Veh. 2019, 4, 569–577. [Google Scholar] [CrossRef]
- Ribeiro, A.M.; Fioravanti, A.R.; Moutinho, A.; de Paiva, E.C. Nonlinear state-feedback design for vehicle lateral control using sum-of-squares programming. Veh. Syst. Dyn. 2020, 60, 743–769. [Google Scholar] [CrossRef]
- Ji, X.; He, X.; Lv, C.; Liu, Y.; Wu, J. Adaptive-neural-network-based robust lateral motion control for autonomous vehicle at driving limits. Control Eng. Pract. 2018, 76, 41–53. [Google Scholar] [CrossRef]
- Bai, Y.; Li, G.; Jin, H.; Li, N. Research on Lateral and Longitudinal Coordinated Control of Distributed Driven Driverless Formula Racing Car under High-Speed Tracking Conditions. J. Adv. Transp. 2022, 2022, 7344044. [Google Scholar] [CrossRef]
- Su, J.; Wu, J.; Cheng, P.; Chen, J. Autonomous Vehicle Control through the Dynamics and Controller Learning. IEEE Trans. Veh. Technol. 2018, 67, 5650–5657. [Google Scholar] [CrossRef]
- Hu, Z.; Yu, Z.; Yang, Z.; Hu, Z.; Bian, Y. Rendering bounded error in adaptive robust path tracking control for autonomous vehicles. IET Control Theory Appl. 2022, 16, 1259–1270. [Google Scholar] [CrossRef]
- Sun, Z.; Zou, J.; He, D.; Zhu, W. Path-tracking control for autonomous vehicles using double-hidden-layer output feedback neural network fast nonsingular terminal sliding mode. Neural Comput. Appl. 2022, 34, 5135–5150. [Google Scholar] [CrossRef]
- Peicheng, S.; Li, L.; Ni, X.; Yang, A. Intelligent Vehicle Path Tracking Control Based on Improved MPC and Hybrid PID. IEEE Access 2022, 10, 94133–94144. [Google Scholar] [CrossRef]
- Liang, Z.C.; Zhang, H.; Zhao, J.; Wang, Y.F. Trajectory Tracking Control of Unmanned Vehicles Based on Adaptive MPC. J. Northeast. Univ. Nat. Sci. 2020, 41, 835–840. [Google Scholar]
- Xu, Y.; Tang, W.; Chen, B.; Qiu, L.; Yang, R. A model predictive control with preview-follower theory algorithm for trajectory tracking control in autonomous vehicles. Symmetry 2021, 13, 381. [Google Scholar] [CrossRef]
- Bai, G.; Meng, Y.; Gu, Q. Path tracking control of vehicles based on variable prediction horizon and velocity. China Mech. Eng. 2020, 31, 1277–1284. [Google Scholar]
- Zhang, K.; Sun, Q.; Shi, Y. Trajectory tracking control of autonomous ground vehicles using adaptive learning MPC. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5554–5564. [Google Scholar] [CrossRef]
- Li, G.; Zhang, S.; Liu, L.; Zhang, X.; Yin, Y. Trajectory tracking control in real-time of dual-motor-driven driverless racing car based on optimal control theory and fuzzy logic method. Complexity 2021, 2021, 5549776. [Google Scholar] [CrossRef]
- Ao, D.; Huang, W.; Wong, P.K.; Li, J. Robust backstepping super-twisting sliding mode control for autonomous vehicle path following. IEEE Access 2021, 9, 123165–123177. [Google Scholar] [CrossRef]
- Geng, G.; Lu, S.; Duan, C.; Jiang, H.; Xiang, H. Design of autonomous vehicle trajectory tracking controller based on Neural Network Predictive Control. In Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering; Sage: Thousand Oaks, CA, USA, 2023. [Google Scholar]
- Jiao, H.-Y.; Li, Y.; Yang, L.-Y. An Improved Guide-Weight Method Without the Sensitivity Analysis. IEEE Access 2019, 7, 109208–109215. [Google Scholar] [CrossRef]
- Shen, Y.; Hua, J.; Fan, W.; Liu, Y.; Yang, X.; Chen, L. Optimal design and dynamic performance analysis of a fractional-order electrical network-based vehicle mechatronic ISD suspension. Mech. Syst. Signal Process. 2023, 184, 109718. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, S.; Hu, X. A fault diagnosis method for lithium-ion battery packs using improved RBF neural network. Front. Energy Res. 2021, 9, 702139. [Google Scholar] [CrossRef]
- Zhou, X.; Zhu, X.; Wu, W.; Xiang, Z.; Liu, Y.; Quan, L. Multi-objective Optimization Design of Variable-Saliency-Ratio PM Motor Considering Driving Cycles. IEEE Trans. Ind. Electron. 2021, 68, 6516–6526. [Google Scholar] [CrossRef]
- Pacejka, H. Tire and Vehicle Dynamics; Elsevier: Oxford, UK, 2005. [Google Scholar]
- Gong, J.; Jiang, Y.; Xu, W. Model Predictive Control for Self-Driving Vehicles; Beijing Institute of Technology Press: Beijing, China, 2014. [Google Scholar]
- Zhang, J. Research on Models and Algorithms for Distributed Optimization Based on the Non-Cooperative Games; Zhejiang University: Hangzhou, China, 2014. [Google Scholar]
- Pae, D.S.; Kim, G.H.; Kang, T.K.; Lim, M.T. Path planning based on obstacle-dependent gaussian model predictive control for autonomous driving. Appl. Sci. 2021, 11, 3703. [Google Scholar] [CrossRef]
- Thomas, L.C. Games, Theory and Applications; Courier Corporation: North Chelmsford, MA, USA, 2012. [Google Scholar]
- Sun, Q.W.; Lu, L.; Yan, G.L.; Che, H.A. Asymptotic stability of evolutionary equilibrium under imperfect knowledge. Syst. Eng. Theory Pract. 2003, 7, 11–16. [Google Scholar]
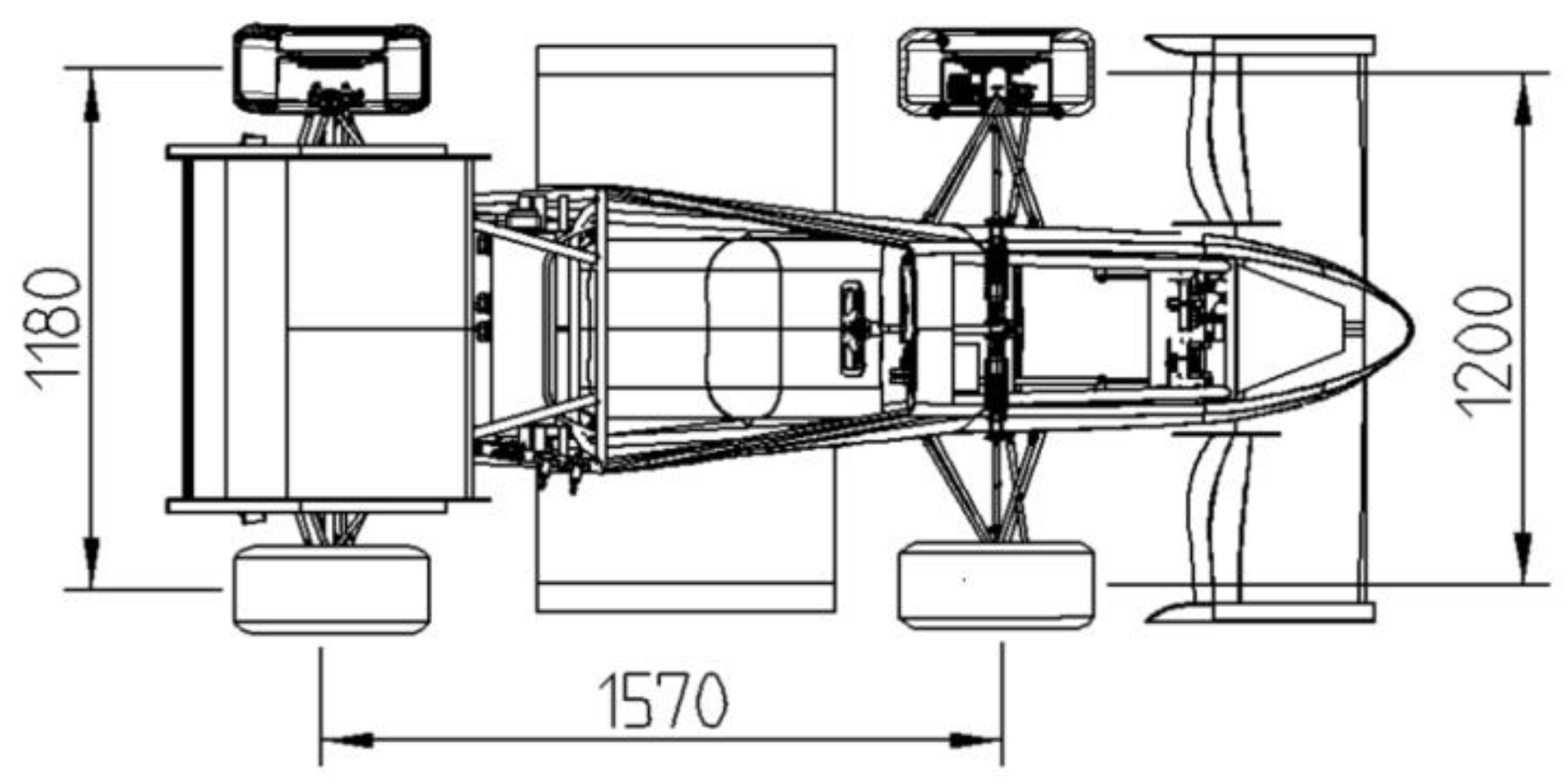
| Symbol | Parameters | Value | Units |
|---|---|---|---|
| m | Vehicle mass | 260 | kg |
| a | Distance from the center of mass to the front axis | 706.5 | mm |
| b | Distance from the center of mass to the rear axis | 863.5 | mm |
| L | Wheelbase of vehicle | 1570 | mm |
| radius of wheel | 228.6 | mm | |
| Height of the center of mass | 270 | mm | |
| Gauge of the front axle | 1200 | mm | |
| Gauge of the rear axle | 1180 | mm |
| Player | Q | R |
|---|---|---|
| Strategy space | = (High accuracy, Low accuracy) | = (Low stability, High stability) |
| Tracing Process and the Loss of Control Energy R | |||
|---|---|---|---|
| R1 Low stability (1 − x) | R2 High stability (x) | ||
| Cumulative path deviation value Q | Q1 Low accuracy (y) | (A,E) | (B,F) |
| Q2 High accuracy (1 − y) | (C,G) | (D,H) | |
| Equilibrium Point | ||
|---|---|---|
| 0 |
| Number | Equilibrium Point | Conditions | Stability | ||
|---|---|---|---|---|---|
| 1 | + | - | ESS | ||
| 2 | - | Uncertain | Unstable | ||
| 3 | - | Uncertain | Unstable | ||
| 4 | + | - | ESS | ||
| 5 | Saddle point under any condition | Uncertain | 0 | Saddle point |
| MPC Controller | MPC Controller Based on Game Theory | |
|---|---|---|
| Predicted time domain | 17 | 17 |
| Control time domain | 9 | 9 |
| Sampling period (s) | 0.01 | 0.01 |
| Weight matrix coefficients |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, T.; Li, G.; Li, N.; Bai, H. Research on Trajectory Tracking Control of Driverless Electric Formula Racing Car Based on Game Theory. World Electr. Veh. J. 2023, 14, 84. https://doi.org/10.3390/wevj14040084
Tian T, Li G, Li N, Bai H. Research on Trajectory Tracking Control of Driverless Electric Formula Racing Car Based on Game Theory. World Electric Vehicle Journal. 2023; 14(4):84. https://doi.org/10.3390/wevj14040084
Chicago/Turabian StyleTian, Tian, Gang Li, Ning Li, and Hongfei Bai. 2023. "Research on Trajectory Tracking Control of Driverless Electric Formula Racing Car Based on Game Theory" World Electric Vehicle Journal 14, no. 4: 84. https://doi.org/10.3390/wevj14040084
APA StyleTian, T., Li, G., Li, N., & Bai, H. (2023). Research on Trajectory Tracking Control of Driverless Electric Formula Racing Car Based on Game Theory. World Electric Vehicle Journal, 14(4), 84. https://doi.org/10.3390/wevj14040084








