Abstract
As the performances of energy management strategy (EMS) are essential for a plug-in hybrid electric bus (PHEB) to operate in an efficient way. The proximal policy optimization (PPO) based multi-objective EMS considering the battery thermal characteristic is proposed for PHEB, aiming to improve vehicle energy saving performance while ensuring the battery State of Charge (SOC) and temperature within a rational range. Since these three objectives are contradictory to each other, the optimal tradeoff between multiple objectives is realized by intelligently adjusting the weights in the training process. Compared with original PPO-based EMSs without considering battery thermal dynamics, simulation results demonstrate the effectiveness of the proposed strategies in battery thermal management. Results indicate that the proposed strategies can obtain the minimum energy consumption, fastest computing speed, and lowest battery temperature in comparison with other RL-based EMSs. Regarding dynamic programming (DP) as the benchmark, the PPO-based EMSs can achieve similar fuel economy and outstanding computation efficiency. Furthermore, the adaptability and robustness of the proposed methods are confirmed in UDDS, WVUSUB and real driving cycle.
1. Introduction
As the main transportation for human travel, internal combustion engine (ICE) vehicles consume much non-renewable energy and produce mass pollutant gases [1,2,3]. Vehicle electrification is one of the effective ways to alleviate the above problems [4]. Due to the impact of battery technology, hybrid electric vehicles (HEVs) play a crucial role in promoting the development of vehicle electrification [5]. At the same time, plug-in hybrid electric buses (PHEBs) have been gradually applied in urban traffic operations due to their lower fuel consumption and longer driving mileage [6].
Since HEVs have a complex power system and extra freedom degrees, the energy management problems have attracted researchers’ extensive attention [7]. The existing energy management strategies (EMSs) are mainly divided into rule-based, optimization-based, and learning-based EMSs [8]. The rule-based EMSs are usually developed from engineering practice based on the engine and motor optimal operating interval, including deterministic rule-based [9] and fuzzy rule-based EMSs [10]. These strategies have strong real-time performance but poor robustness, which makes it challenging to achieve the optimal control effect.
The optimization-based EMSs, including global optimization-based and instantaneous optimization-based EMSs, aim to reduce vehicle fuel consumption by minimizing the cost function. Global optimization strategies mainly include dynamic programming (DP) [11,12], Pontryagin’s minimum principle (PMP) [13,14] and convex optimization (CV) based EMSs [15,16]. These strategies can obtain optimal control results and great adaptability in different driving cycles. Nevertheless, the driving cycle and road information are required in advance and the computation complexity is high. Owing to these shortcomings, they are difficult to be applied as a real-time energy management controller. Instantaneous optimization strategies include model predictive control (MPC) [17,18] and equivalent consumption minimum strategy (ECMS) [19,20]. Although MPC and ECMS have strong real-time performance, their control effect depends on the prediction accuracy of future driving conditions or the value of oil-electric conversion efficiency separately.
Unlike conventional control algorithms, Machine learning (ML) can realize real-time control and strong adaptability. Therefore, EMSs based on ML have become a new research hotspot in recent years, especially reinforcement learning (RL) algorithms [21]. Typical RL can not only solve the sequential actions’ decision optimization problem but also have a long-term perspective by considering future returns.
Q-learning (QL) is the first employed in the energy management field and has achieved good results [22]. However, its control state and action space are discretized. Thus, it can not be applied in practice and easily cause “the curse of dimensionality” [23]. Then, scholars put forward the Deep Q Network (DQN) algorithm, which improves based on QL and solves the problem of discrete variables by using a neural network to fit the Q table. Simultaneously, DQN uses the experience replay method to improve learning efficiency and introduces a target network to make the training process more stable. Ref. [24] applied DQN for a power-split hybrid electric bus in energy management and the simulation results proved that the training rate was better than QL. In Ref. [25], DQN was conducted to optimize the fuel consumption for HEVs. The effectiveness and online application ability of the strategy were investigated.
Although DQN realizes the transformation from the discrete control state to the continuous control state, its action space is still discrete. To further deal with the implementation of continuous action space, the Deep Deterministic Policy Gradient (DDPG) algorithm is introduced for the energy management of HEVs. In Ref. [26], DDPG was used to solve optimal energy distribution issues in discrete-continuous mixed action space considering terrain information of driving routes. In Ref. [27], considering the traffic information and the number of passengers, a model-free DDPG with the Actor–Critic framework was adopted. The results showed that the optimization performance of the proposed strategy was close to that of DP. In Ref. [28], the DDPG algorithm was combined with the optimal braking-specific fuel consumption curves and the power battery charge-discharge characteristics. The proposed method had better fuel economy and robustness than rule-interposing Deep Q-Learning (DQL). However, many hyper-parameters are used to explore the environment in the DDPG algorithm, resulting in slow convergence speed and unstable training.
Given these inherent problems, some more developed RL algorithms have been introduced in the energy management field. In Ref. [29], an optimal EMS based on the Soft Actor–Critic (SAC) algorithm was designed for electric vehicles with hybrid energy systems to minimize power consumption. Compared with DQN and rule-based methods, the proposed strategy had more advantages in control effect and convergence speed. Although the SAC algorithm has fast training speed and good exploration ability, it needs to scale the reward, which affects the Q value. Therefore, it depends heavily on the reward function and is not suitable for solving multi-objective optimization problems. In Ref. [30], a rule-based controller was embedded in the Twin Delayed Deep Deterministic Policy Gradient (TD3) loop to eliminate unreasonable torque distribution. The convergence speed and robustness of the improved algorithm were superior to that of the DRL-based EMS. Since the TD3 algorithm adds noise to the action output by an Actor network, it is easy to generate a large number of boundary actions in exploration. Therefore, parameter tuning ability must be equipped when adopting this algorithm [31].
Proximal Policy Optimization (PPO) algorithms, including PPO-Clip and PPO-Penalty, use the Actor–Critic framework to realize continuous control state input and continuous action space exploration, avoiding the influence of discrete error on optimization results. A new Actor network is also introduced to separate the agent that learns online from the agent that interacts with the environment. This structure greatly accelerates the training speed and enhances computational efficiency. The Minorize-Maximization algorithm is used to ensure that its performance can be improved with each update policy. Thus, PPO algorithms are insensitive to hyper-parameter changes. Besides, since the PPO algorithms can regularize the Q value, they are not highly dependent on the reward function. After comprehensive analysis and consideration, the PPO-Clip algorithm and PPO-Penalty algorithm are adopted in the energy management of HEV in this paper, which have the strengths of stable training, simple parameter adjustment, and strong robustness.
In addition to the optimization algorithms, the determination of the objective function is also crucial. The existing EMSs of HEVs mainly target to improve fuel economy and maintain battery charge-sustaining [32,33] and someone has focused on battery degradation, but without adequately considering the power battery thermal dynamics. The charging and discharging capacity, cycle life, and safety of the battery are dramatically affected by its temperature change. When the battery temperature exceeds the optimal operating range, the battery aging is intensified, the cycle life attenuation is accelerated, and there is a risk of battery spontaneous combustion.
Motivated by the above literature review and discussion, the PPO-Clip and PPO-Penalty-based EMSs considering battery thermal characteristics are proposed for PHEB. The main contributions are summarized below.
(1) With a comprehensive consideration for performances in terms of energy saving, battery temperature as well as stable tracking for reference State of Charge (SOC), the PPO-based intelligent algorithm is employed to conduct the research on multi-objective energy management for PHEB.
(2) The trade-off issue among multiple PHEB energy management objectives is highlighted and addressed by intelligently adjusting the weight coefficients in the training process.
(3) The battery temperature is online estimated according to its heat generation/ dissipation characteristics, which is further introduced into the PPO-based EMS framework to ensure the battery operation with a rational temperature.
(4) With respect to DP-based EMS and other RL-based EMSs, extensive comparative simulations are conducted to highlight the effectiveness, superiority, adaptability and robustness of the PPO-based EMSs.
The rest of the paper is organized as follows. Section 2 presents the powertrain model of the PHEB. Section 3 describes the essential content of the RL algorithm and PPO-based EMSs. Section 4 analyzes the relationship between different objectives and illustrates the simulation results. Section 5 concludes the paper and briefly explains future research. The meanings of some abbreviations are summarized in Abbreviations.
2. System Modeling of PHEB
Referring to the vehicle architecture developed by Zhongtong Group, a single-shaft parallel PHEB model is established, as shown in Figure 1. The engine and motor are attached to the same axle and rotate at the same speed. After coupling the torque, the gearbox and final gear drive the vehicle by reducing speed and increasing torque. When it is fully charged, the power battery provides electric energy to the motor. When the battery’s remaining power is insufficient, the mechanical energy is converted into electrical energy by the motor to charge the battery. Thus, there are four working modes of the PHEB: pure electric mode, the engine alone working mode, engine and motor hybrid working mode, and brake recovery mode. The physical parameters of powertrain components are listed in Table 1. The dynamic equation of the vehicle can be described as:
where is the driving force of the vehicle, M is the vehicle mass, g is the gravitational acceleration, f is the rolling resistance coefficient, is the road slope, is the air resistance coefficient, is the air density, A is the frontal area of the vehicle, v is the vehicle velocity, is the correction factor.
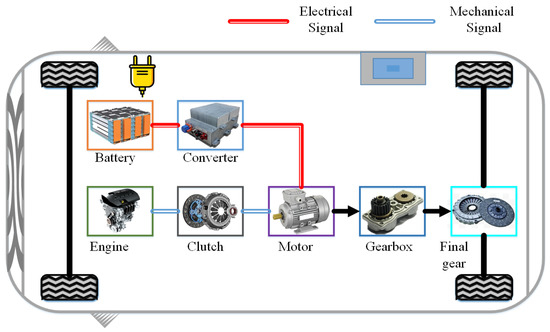
Figure 1.
The architecture of the PHEB powertrain.

Table 1.
Parameters of the PHEB.
2.1. Engine Model
The fuel consumption of the engine at a specific operating point is related to its speed and torque. By utilizing the varying continuity of the gearbox, the operating point of the engine can be adjusted to the optimal economic zone. The engine map is obtained from bench experiments, as shown in Figure 2. The fuel consumption of the engine per second can be calculated by:
where is the fuel consumption rate per unit time, is the engine torque (Nm), is the engine speed (rad/s).
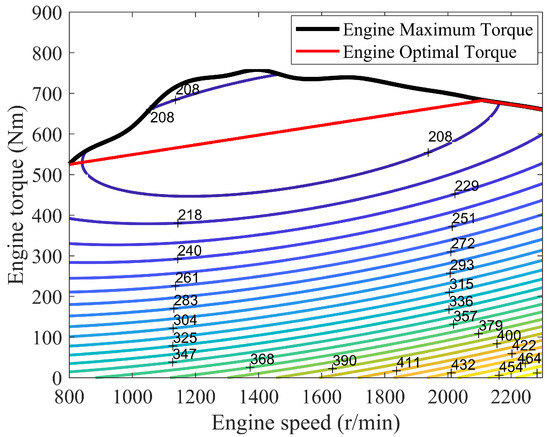
Figure 2.
Engine fuel consumption MAP.
2.2. Motor Model
The motor used in the PHEB model is a permanent magnet synchronous motor with electric mode, generating mode and idling mode. In electric mode, the battery outputs energy to the motor. In power mode, the motor converts mechanical energy into electrical energy and stores it in the battery. In idling mode, the motor and the battery do not exchange energy. The motor operating efficiency is shown in Figure 3. The output power of the motor can be computed as:
where is the motor operating efficiency, is the motor torque, is the motor speed.
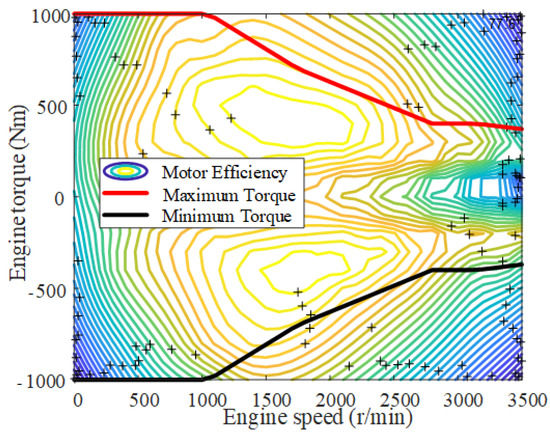
Figure 3.
Motor efficiency MAP.
2.3. Battery Electrical Model
The research focuses on lithium-ion batteries which are widely used in electric vehicles in this paper. It is found that the battery’s internal resistance is greatly affected by temperature, while the open-circuit voltage varies significantly with different SOC [34]. Consequently, considering battery temperature and SOC changes, a battery internal resistance model is established. For battery packs, the total voltage is as high as 560 V, and the nominal capacity is 90 Ah. The power balance of the battery system is described by:
where is the total battery power consumption, is the power flowing into or out of the battery, is the power loss due to internal resistance, is the charge and discharge current, is the internal resistance.
The dynamic characteristic of SOC is calculated from the expression:
where is the open-circuit voltage, is the nominal capacity. The experiment data including internal resistance and open-circuit voltage are shown in Figure 4.
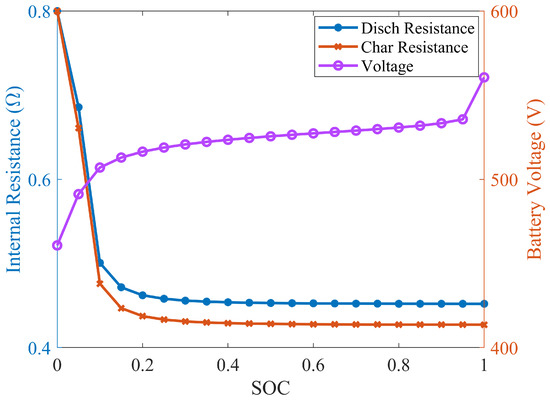
Figure 4.
The characteristic parameters of the single battery cell.
2.4. Battery Thermal Model
There are two main reasons for the battery temperature rise. The first one is the ohmic resistance heat and the other is the heat generated by a chemical reaction inside the battery. The ohmic resistance heat is irreversible and the chemical reaction heat is reversible. The battery heating rate is given by:
where is the terminal voltage, is the battery temperature.
The battery thermal model is established according to the energy conservation law. The heat balance process can be expressed as:
where is the battery mass, is the average specific heat capacity, h is the heat exchange coefficient, is the heat exchange area, is the environment temperature, is the battery heating rate.
After equivalent changes, the battery temperature estimation can be obtained by:
where is the initial battery temperature, is the battery temperature at the previous moment.
3. EMSs Based on PPO-Clip and PPO-Penalty
3.1. RL Algorithm
RL algorithm can solve sequential decision optimization problems, including two main components: agent and environment. The agent can complete specific tasks by learning policy when interacting with the environment. The state of the environment has Markov property and the future state of the system is only related to the current state and has nothing to do with the historical state. Therefore, RL is a Markov decision process (MDP), as a tuple (s, a, P, r). In the tuple, s is the state set, a is the action set, P is the state transition probability matrix and r is the reward function.
RL agent uses learning as a trial evaluation process. In the beginning, the agent randomly takes an action that impacts the environment. After that, the state of the environment will change and a reward will be generated and fed back to the agent. The agent selects the next action according to the reward and the current state. The interaction process is shown in Figure 5. The principle of action selection is to increase the probability of receiving a larger reward in the future. When the reward tends to a stable maximum value, the agent’s task is completed and the optimal results are obtained. In this paper, the agent is the energy and battery temperature management controller. The environment is the PHEB operating condition and powertrain system.
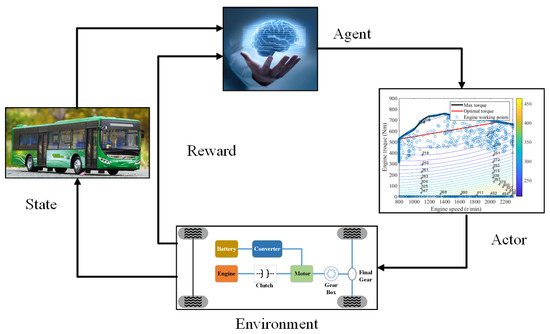
Figure 5.
Agent-Environment interaction.
3.2. PPO-Clip and PPO-Penalty Algorithms
The agent starts from a specific state until the end of the task, which is called a complete episode. In an episode with T moments, the agent constantly interacts with the environment, forming the following sequence :
Since the action taken by the agent may be different at the same state, the sequence is uncertain. When the policy function is , the probability of a sequence occurrence is:
The return for the sequence is the sum of the reward at each moment called . Therefore, the expected reward can be obtained as:
The policy gradient method is utilized to find the optimal policy. The gradient solution process is:
To reduce the variance of the policy gradient, the advantage function is used to replace the return function. The advantage function is calculated by:
where is the state-value function, is the reward function in times of k, is the action-value function, is the discount factor.
Besides, the idea of importance sampling is adopted and another new policy function is introduced. In this way, the data sampled by interacting with the environment can be reused and the training speed can be improved. The solution process can be expressed as:
where is the importance weight.
Since that the parameter distributions of the two policy functions and are close, and are considered equal. As a result, the update function of the network parameter can be written as:
The core idea of the PPO algorithms is to limit the policy update range by controlling the importance weight. OpenAI and DeepMind use the Clip function and KL penalty to realize, respectively, [35,36].
Method 1 (PPO-Clip): The importance weight is trimmed to a certain extent by introducing the Clip function. The update function becomes:
Method 2 (PPO-Penalty): KL divergence is used to calculate the similarity degree of the action probability distribution. The update function becomes:
The penalty for the difference between and distribution will be dynamically changed. If the KL divergence value is too large, the penalty will increase. On the contrary, the penalty will reduce if it is small to a certain value.
3.3. Design of Network and Algorithm
In this section, the PPO-Clip-based EMS and PPO-Penalty-based EMS will be illustrated in detail. First, define the critical elements of PPO algorithms: state s, action a, and reward function r.
State s: Considering that battery temperature changes have an impact on driving safety, in addition to battery SOC and vehicle dynamics, battery temperature is also taken as the input state in this paper.
where is the vehicle acceleration.
Action a: Thanks to the flexibility of the neural network, the output of continuous action is realized. To reduce the calculation burden, this paper only defines one action, namely the engine torque .
Then the motor torque is obtained by:
where is the demand torque, is the wheel radius, is the transmission ratio of gearbox, is the transmission ratio of final gear, and represents the driveline efficiency.
Reward function r: The PPO-Clip-based EMS and PPO-Penalty-based EMS not only target to minimize fuel consumption and keep SOC, but also slow down battery temperature rise. By restraining the battery temperature, the battery life will be prolonged and the operating cost will be reduced [34]. When the agent is in the learning stage, it keeps exploring and learning actions with more enormous rewards [37]. Therefore, the reward function can be described as:
where , and are the weight coefficients, which will affect the training speed and further affect whether the optimal energy distribution results can be achieved. Moreover, when solving multi-objective optimization problems, the weight coefficients need to be reasonably adjusted until the optimal tradeoff between multiple objectives is realized.
According to the variance of battery charge-discharge internal resistance characteristic, the SOC must locate in the optimal range to realize high efficiency [28]. In this article, the initial SOC and terminal SOC are set as 0.8 and 0.3.
Lithium-ion batteries typically operate at 0–40 C. Based on this, the reward function sets the maximum temperature limit as 313.15 K (40 C). When the current temperature is higher than the temperature upper limit, a negative reward will be punished.
PPO-Clip and PPO-Penalty algorithms are based on Actor–Critic architecture, including the Actor network and Critic network. The architecture is an online learning algorithm and parameter updates are very slow. To improve the training efficiency, another Actor network is introduced to separate the agent training online from the agent interacting with the environment. Thus, the PPO algorithms are composed of the Actor network parameterized by , another Actor network parameterized by and the Critic network. Figure 6 shows how PPO-Clip and PPO-Penalty algorithms are implemented in the energy management of PHEB. At first, the Actor network parameterized by interacts with the environment to obtain vehicle velocity, acceleration, battery temperature, and SOC. After the interaction is completed, the Actor network parameterized by makes decisions based on the current states and calculates the reward of the decision to obtain a series of trajectories . The trajectories are sent to the Actor network parameterized by and the Critic network for network parameter update and policy optimization. When the update of the Actor network parameterized by reaches a certain number of times, its parameters will be transferred to update the Actor network parameterized by . After several iterations, the optimal engine torque distributions are obtained when the expected reward converges to the maximum value [38]. The pseudo-codes of PPO-Clip and PPO-Penalty algorithms are listed as Algorithm 1.
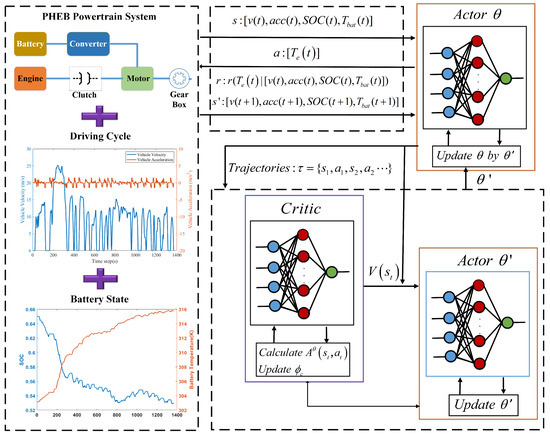
Figure 6.
PPO-based EMSs.
A fully connected neural network (Deep Neural Network) with one hidden layer is adopted for the Actor–Critic architecture in this paper. For the Actor network, the Relu function is used as the activation function, while the Sigmoid function is used as the output layer to constrain the output action between [0, 1]. The Critic network is similar to the Actor network, except the output layer is the Tanh function that maps state and action to estimated Q values [39]. The parameters of the neural network are described in Table 2.
| Algorithm 1 PPO-Clip and PPO-Penalty algorithms. |
|

Table 2.
The key parameters of PPO-based EMSs.
4. Simulation Results and Analysis
In this section, the performance of the PPO-Clip-based EMS and PPO-Penalty-based EMS will be evaluated in Urban Dynamometer Driving Schedule (UDDS), West Virginia Suburban Driving Schedule (WVUSUB) and real driving cycle collected in Jinan. The UDDS driving cycle is depicted in Figure 7, where the driving time, the average and maximum velocity are 1370 s, 8.7012 m/s, and 25.2 m/s, respectively.
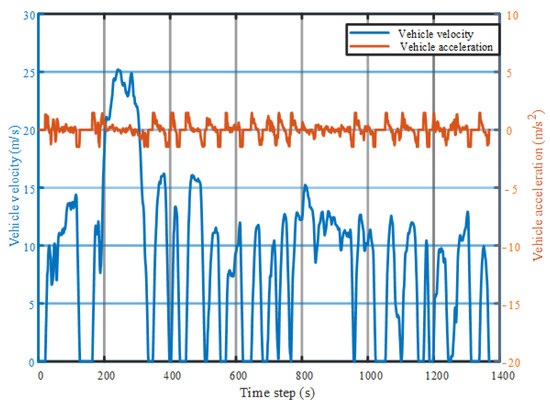
Figure 7.
The velocity and acceleration of the UDDS.
To realize a complete comparison, the electric consumption of PHEB will be converted into fuel consumption. The equivalent fuel consumption is calculated by:
where is the electric consumption, is the engine operating efficiency, is the heating value, is the diesel density. To simulate the complete battery SOC downward trend, the UDDS driving cycle is duplicated four times.
4.1. Tradeoff between Multiple Objectives
Since optimal solutions are diverse, multi-objective problems are difficult to solve. The optimal solution for one objective may be mutually exclusive from other objectives. To balance the multiple optimal results, the weight of each objective needs to be adjusted reasonably. For the energy management problem of PHEBs, it is hoped that the vehicle fuel consumption can be minimized and the power battery can be in the best operating state. To find the appropriate weight coefficient between the three objectives of minimizing fuel consumption, maintaining battery SOC and controlling battery thermal change, an intelligent optimization method is introduced. Firstly, the relationship between each objective is analyzed by adjusting the weight coefficient in proportion. Then, the optimal interval corresponding to different coefficients is determined according to the simulation results. Finally, the reward function is compared to determine the optimal weight coefficient.
The PPO-Clip-based EMS is taken as an example to adjust the weight coefficients of the three objectives in Equation (22). Firstly, fix , then set between and , and the value is mostly located between 1 and 10. The SOC trajectories with different are shown in Figure 8. When the is larger, the constraint on SOC is more strict so that the final SOC will be higher than 0.3. The simulation results with different are shown in Table 3. It reveals that fuel consumption increases gradually when SOC rises slowly. Simulation results confirm that the two objectives of improving fuel economy and maintaining SOC are mutually exclusive. By comparison, it can be concluded that the algorithm can achieve better results in fuel economy and SOC maintenance when the range is between and .
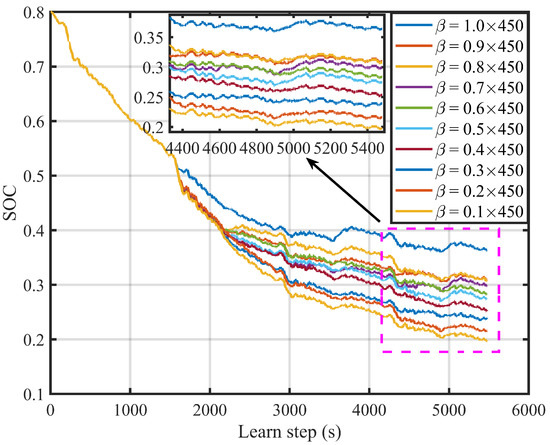
Figure 8.
SOC trajectories of different in 4 × UDDS.

Table 3.
Simulation results comparison between different .
After that, fix , , and let vary from 0.1 to 1. The value is mostly located between 1 and 10. The battery temperature rise curves are shown in Figure 9. It is evident that the larger the weight coefficient is, the lower the terminal battery temperature is. When , the SOC is the most stable, the temperature rise is the slowest, and the final battery temperature is the lowest. The simulation results between different are shown in Table 4. It can be discerned that when SOC decreases, the final battery temperature will increase. It testifies that the two objectives of maintaining SOC and lowering the battery temperature are mutually beneficial. When the ranges from 0.5 to 0.75, it leads to excellent control results on fuel consumption, battery charge sustaining, and battery temperature rise.
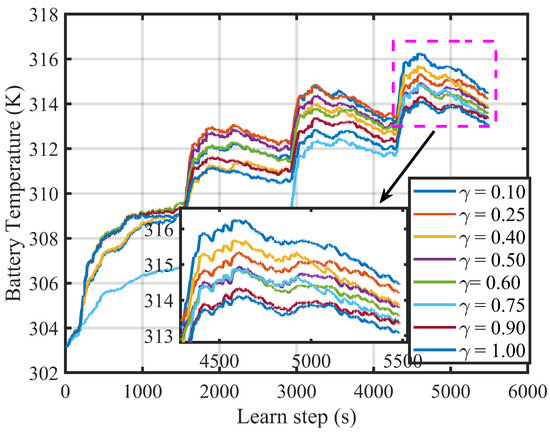
Figure 9.
Battery temperature rise curves of different in 4 × UDDS.

Table 4.
Simulation results comparison between different .
After that, set two random numbers and assign values to and randomly. The range of is (0.4, 0.7) and the range of is (0.5, 0.75). After the same training time, store the current values of and and the reward value of the last training result. After all the training, the reward value is compared, and the value of and corresponding to the minimum reward value is the optimal weight coefficient.
4.2. Effectiveness of EMSs Based on PPO-Clip and PPO-Penalty
In the RL algorithm, the agent tends to choose the action with an increased reward after a period of exploration and learning. The mean reward distributions are shown in Figure 10. In the beginning, both PPO-Penalty-based EMS and PPO-Clip-based EMS are in the stage of continuous exploration and their mean reward keeps rising. After that, the mean reward gradually tends to be stable. For PPO-Clip-based EMS, the previous exploration is sufficient. After stabilization, the mean reward is higher than that of PPO-Penalty-based EMS. From Episode 30 to Episode 50, PPO-Penalty-based EMS has a small section of invalid learning. In this case, the agent always outputs boundary values. After a period of self-adjustment, the mean reward gradually shows an upward trend and reaches a stable state.
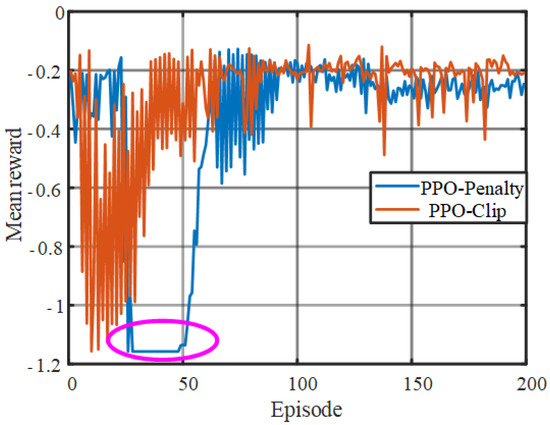
Figure 10.
The mean rewards of the PPO-based EMSs.
Compared with the original PPO-Clip-based EMS and original PPO-Penalty-based EMS without considering battery temperature, the effectiveness of the PPO-Clip-based EMS and PPO-Penalty-based EMS will be testified in battery temperature management. For original PPO-based EMSs, the state s is set as . The action a remains the same and the reward function is set as . After the training is completed, the battery temperature rise curves are shown in Figure 11 and simulation results are shown in Table 5. Compared to original PPO-based EMSs, when the final SOC and fuel consumption are close, the final battery temperatures of PPO-based EMSs drop by 1.509 K (1.509 C) and 1.038 K (1.038 C), respectively. It can be concluded that the proposed strategies have achieved excellent results in battery temperature management.
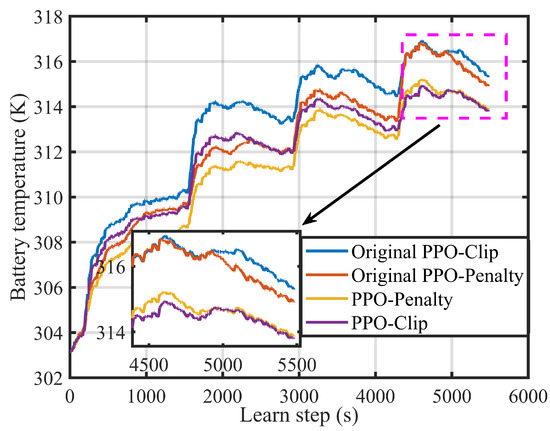
Figure 11.
Battery temperature rise curves with PPO algorithms in 4 × UDDS.

Table 5.
Terminal battery temperature comparison in 4 × UDDS.
4.3. Superiority of EMSs Based on PPO-Clip and PPO-Penalty
By comparing the results of fuel consumption, terminal battery state and training speed under different EMSs, the optimization performance of the EMSs is compared. In this section, DP serves as an off-line benchmark and the superiority of PPO-based EMSs is certificated by comparing with DQN-based EMS and DDPG-based EMS. The battery temperature rise curves of different strategies are shown in Figure 12. It can be found that the rising trends of the battery temperature are almost the same. The DP-based EMS has the best control effect on the battery temperature. Its final battery temperature is the lowest, which is 313.352 K (40.202 C). The SOC downward trends of different strategies are shown in Figure 13. The SOC can satisfy the restriction limit and finally be stabilized at around 0.3.
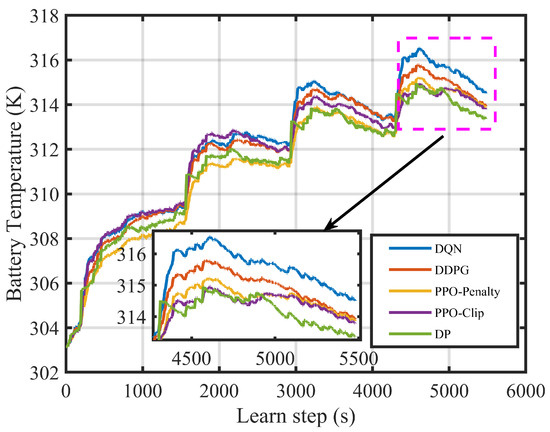
Figure 12.
Battery temperature rise curves of different approaches in 4 × UDDS.
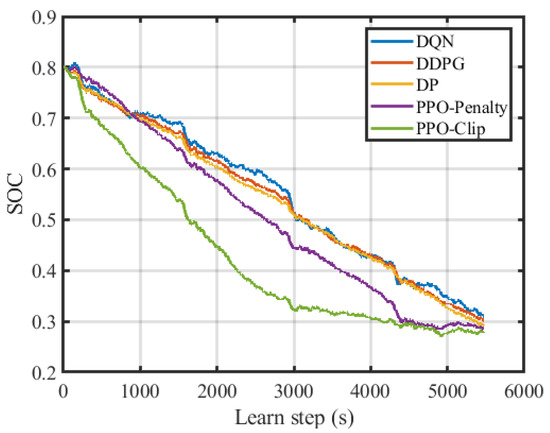
Figure 13.
Battery SOC trajectories in 4 × UDDS.
Figure 14 shows the engine working points of different strategies. In the DP-based EMS, the engine working points are denser and distributed between the maximum and optimal torque. The PPO-Penalty-based EMS and DDPG-based EMS have a large number of working points, most of which are located in the low fuel consumption area. For DQN-based EMS, the output engine torque is relatively single and centralized, which may be affected by the limited discrete action variable. Compared with the other algorithms, PPO-Clip-based EMS has fewer engine working points, which implies less fuel energy and more electric energy will be utilized.
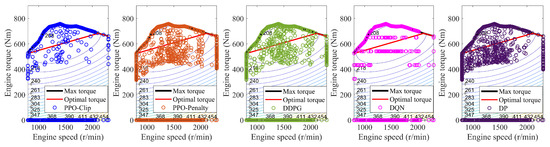
Figure 14.
Engine working points in 4 × UDDS.
There is no single solution for multi-objective optimization problems to optimize each objective simultaneously. In this case, the objective function is said to be conflicting, and there exists a (possibly infinite) number of Pareto optimal solutions. To solve the above problems, researchers usually set the weights of each goal according to the actual needs. Thus, the compromise of different goals can be achieved through quantification. In this paper, the weight of fuel consumption is set as the maximum to find a set of solutions as close as possible to the Pareto optimal domain. Despite that the PPO-based EMSs achieve a distinct advantage in fuel economy, the final SOC is lower than the other strategies. It is proved that in the multi-objective energy management problems of HEVs, the improvement of fuel economy is at the expense of SOC stability [40].
The fuel consumption and the computing time to run 200 episodes (DRL) are listed in Table 6. As shown in Table 6, the PPO-Penalty takes 1435 s for 200 training sessions, which is 200 repeated driving cycles. So running one driving cycle generally takes 1435/200 = 7.175 s. This is the time standard that can meet the requirements of real-time online control for the EMS of HEVs. In contrast, the 9504 s consumed by the DP algorithm is the time spent on running one driving cycle. It can be seen that although the DP algorithm has optimal control performance, it consumes a lot of computing time and cannot meet the real-time control requirements of vehicles. DP is limited by discrete variables and the optimization results are greatly affected by discrete precision. However, if the discrete precision is improved, the calculation time will increase. On the contrary, due to the flexibility of the neural network, PPO-Clip-based EMS and PPO-Penalty-based EMS can sufficiently explore continuous action space to obtain the optimal energy distribution results. Since PPO-based EMSs separate the agent that trains online from the agent that interacts with the environment, the computing time is greatly reduced. As a result, the trained PPO-based EMSs can be used as vehicle controllers, making real-time online applications possible.

Table 6.
The simulation results in 4 × UDDS.
4.4. Adaptability of EMSs Based on PPO-Clip and PPO-Penalty Algorithms
Although the effectiveness and superiority of PPO-Clip-based EMS and PPO-Penalty-based EMS are confirmed in UDDS, they would experience uncertainty in the different driving cycles. In this section, the West Virginia Suburban Driving Schedule (WVUSUB) is used to assess the adaptability of the PPO-based EMSs, as shown in Figure 15. The driving cycle is duplicated four times to train the PPO-based EMSs, where the driving time, average and maximum velocity are 1665 s, 7.1885 m/s, and 20.0242 m/s, respectively.
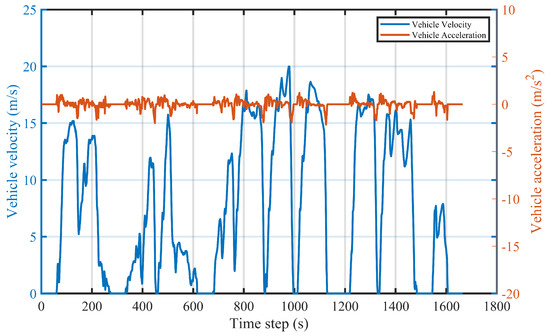
Figure 15.
The velocity and acceleration of the WVUSUB.
Figure 16 and Table 7 show battery temperature curves and the final battery temperature comparison results in 4 × WVUSUB. As can be seen from the graph, the battery temperature trends are roughly the same. When the temperature reaches the upper limit, the PPO-based EMSs can effectively reduce the battery temperature under the influence of the reward function.
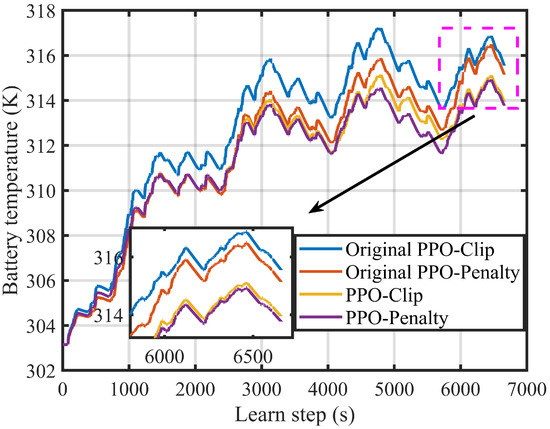
Figure 16.
Battery temperature rise curves in 4 × WVUSUB.

Table 7.
The simulation results of battery temperature in 4 × WVUSUB.
Similarly, by comparing the DQN-based EMS and DDPG-based EMS, the superiority of the PPO-based EMSs is corroborated again. The battery temperature rise curves are shown in Figure 17 and the curves are roughly the same. Compared with other DRL-based EMSs, PPO-based EMSs have the best battery temperature management effect. The results of fuel consumption are shown in Table 8. It is clear that PPO-Clip-based EMS and PPO-Penalty-based EMS reach 98.5% and 97.55% levels of the DP benchmark, respectively, which proves that the proposed strategies have fabulous adaptability.
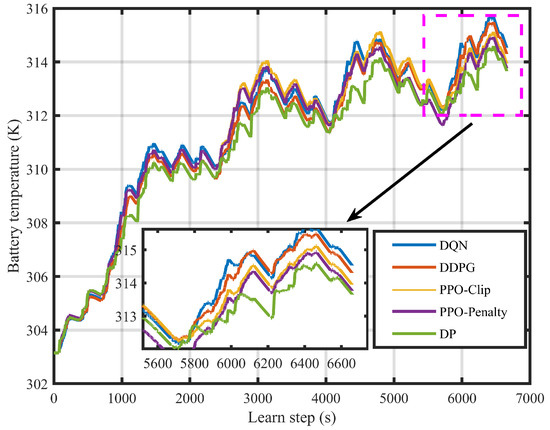
Figure 17.
Battery temperature rising curves of different EMSs in 4 × WVUSUB.

Table 8.
The simulation results of fuel consumption in 4 × WVUSUB.
4.5. Robustness of EMSs Based on PPO-Clip and PPO-Penalty
In practical applications, the vehicle velocity collected by sensors will inevitably be corrupted by noise. To verify the robustness of the PPO-based EMSs to unknown driving cycles, another driving cycle gathered in Jinan is used to train the EMSs, where the driving time, the average and maximum velocity are 6000 s, 7.7197 m/s, 21.6667 m/s, respectively. The corrupted driving cycle is shown in Figure 18 and the energy management results are listed in Table 9. The fuel consumption of PPO-based EMSs with noisy states is a little higher than the PPO-based EMSs with clean states but still lower than other RL-based EMSs. Besides, RL-based EMS can achieve superior fuel economy in comparison with ECMS and PPO algorithms-based EMSs can save about 8.6% fuel consumption. It can be concluded that PPO-Clip-based EMS and PPO-Penalty-based EMS have a significant advantage in energy management for hybrid electric vehicles and are robust to sensor noise.
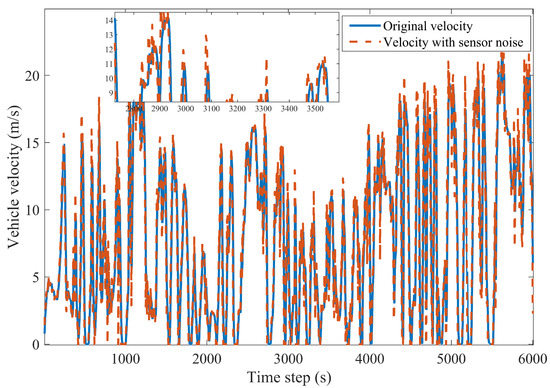
Figure 18.
The real driving cycle with sensor noise.

Table 9.
The simulation results in a real cycle.
5. Conclusions
To explore the suitable algorithm applied to the multi-objective energy management optimization problem of PHEB, the PPO-Clip-based EMS and PPO-Penalty-based EMS are investigated in this paper. In addition to maintaining SOC and improving fuel economy, the battery temperature is also taken into account as the optimization objective to keep the battery in optimal working condition. After assigning the proper weights among the three objectives, extensive comparisons are made for further verification. Compared with the original PPO-based EMSs, the proposed EMSs provide effective control of power battery temperature during driving, ensuring that the terminal battery temperature has a lower value. Besides, PPO-based EMSs can realize faster computing speed, lower fuel consumption, and slower battery temperature rise in comparison with DQN-based EMS and DDPG-based EMS. At the same time, the adaptability and robustness of the proposed EMSs are demonstrated under UDDS, WVUSUB and the real driving cycle. It can be concluded that PPO-Clip-based EMS and PPO-Penalty-based EMS express great talent in a comprehensive performance.
There are two aspects to improve the proposed EMSs in our future work. Firstly, a hardware-in-the-loop experiment and real vehicle validation will be conducted to improve the performance of the PPO-based EMSs. Secondly, real-time energy distribution will be realized online by connecting cloud data to promote practical applications.
Author Contributions
Conceptualization, C.Z. and W.C.; methodology, C.Z.; software, C.Z. and T.L.; validation, C.Z., W.C., and T.L.; formal analysis, C.Z.; investigation, C.Z.; resources, N.C.; data curation, C.Z. and W.C.; writing—original draft preparation, C.Z., N.C., and W.C.; writing—review and editing, C.Z., W.C. and N.C.; visualization, C.Z.; supervision, N.C.; project administration, N.C.; funding acquisition, N.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation for Automotive Industry Innovation Joint Fund under Grant U1864205 and Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (NO.2019JZZY020814).
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following nomenclature and abbreviations are used in this manuscript:
| vehicle driving force | total battery power consumption | ||
| M | vehicle mass | power flowing into or out of the battery | |
| g | gravitational acceleration | battery power loss | |
| f | rolling resistance coefficient | internal resistance | |
| road slope | charge and discharge current | ||
| air resistance coefficient | terminal voltage | ||
| air density | battery temperature | ||
| A | vehicle frontal area | battery mass | |
| v | vehicle velocity | average specific heat capacity | |
| correction factor | h | heat exchange coefficient | |
| fuel consumption rate | heat exchange area | ||
| engine torque | environment temperature | ||
| engine speed | battery heating rate | ||
| motor operating efficiency | initial battery temperature | ||
| motor torque | battery temperature at the previous moment | ||
| motor speed | diesel density | ||
| reward function in times of k | electric consumption | ||
| the action-value function | engine operating efficiency | ||
| heating value | discount factor |
References
- Ahmad, A.; Alam, M.S.; Chabaan, R. A Comprehensive Review of Wireless Charging Technologies for Electric Vehicles. IEEE Trans. Transp. Electrif. 2017, 4, 38–63. [Google Scholar] [CrossRef]
- Zhou, Y.; Ravey, A.; Péra, M.C. A survey on driving prediction techniques for predictive energy management of plug-in hybrid electric vehicles. J. Power Sources 2019, 412, 480–495. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, C.; Huang, Z.; Xu, L.; Liu, Z.; Liu, M. Real-time energy management strategy for fuel cell range extender vehicles based on nonlinear control. IEEE Trans. Transp. Electrif. 2019, 5, 1294–1305. [Google Scholar] [CrossRef]
- Flah, A.; Chokri, M. A Novel Energy Optimization Approach for Electrical Vehicles in a Smart City. Energies 2019, 12, 929. [Google Scholar]
- Xie, S.; Qi, S.; Lang, K. A data-driven power management strategy for plug-in hybrid electric vehicles including optimal battery depth of discharging. IEEE Trans. Ind. Inform. 2019, 16, 3387–3396. [Google Scholar] [CrossRef]
- Mohamed, N.; Aymen, F.; Ali, Z.M.; Zobaa, A.F.; Aleem, S.H.E.A. Efficient Power Management Strategy of Electric Vehicles Based Hybrid Renewable Energy. Sustainability 2021, 13, 7351. [Google Scholar] [CrossRef]
- Sabri, M.F.M.; Danapalasingam, K.A.; Rahmat, M.F. A review on hybrid electric vehicles architecture and energy management strategies. Renewable and Sustainable Energy Reviews. Renew. Sustain. Energy Rev. 2016, 53, 1433–1442. [Google Scholar] [CrossRef]
- Tran, D.D.; Vafaeipour, M.; El Baghdadi, M.; Barrero, R.; Van Mierlo, J.; Hegazy, O. Thorough state-of-the-art analysis of electric and hybrid vehicle powertrains: Topologies and integrated energy management strategies. Renew. Sustain. Energy Rev. 2020, 119, 109596. [Google Scholar] [CrossRef]
- Taherzadeh, E.; Dabbaghjamanesh, M.; Gitizadeh, M.; Rahideh, A. A new efficient fuel optimization in blended charge depletion/charge sustenance control strategy for plug-in hybrid electric vehicles. IEEE Trans. Intell. Veh. 2018, 3, 374–383. [Google Scholar] [CrossRef]
- Yin, H.; Zhou, W.; Li, M.; Ma, C.; Zhao, C. An adaptive fuzzy logic-based energy management strategy on battery/ultracapacitor hybrid electric vehicles. IEEE Trans. Transp. Electrif. 2016, 2, 300–311. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Li, W.; Shang, F.; Zhan, J. Hybrid-trip-model-based energy management of a PHEV with computation-optimized dynamic programming. IEEE Transactions on Vehicular Technology. IEEE Trans. Veh. Technol. 2017, 67, 338–353. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series–parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2008, 185, 1633–1643. [Google Scholar] [CrossRef]
- Schmid, R.; Buerger, J.; Bajcinca, N. Energy management strategy for plug-in-hybrid electric vehicles based on predictive PMP. IEEE Trans. Control Syst. Technol. 2021, 29, 2548–2560. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Xin, Z.; Brighton, J. Pontryagin’s minimum principle based model predictive control of energy management for a plug-in hybrid electric bus. Appl. Energy 2019, 236, 893–905. [Google Scholar] [CrossRef]
- Hu, X.; Murgovski, N.; Johannesson, L.M.; Egardt, B. Comparison of three electrochemical energy buffers applied to a hybrid bus powertrain with simultaneous optimal sizing and energy management. IEEE Trans. Intell. Trans. Syst. 2014, 15, 1193–1205. [Google Scholar] [CrossRef]
- Hadj-Said, S.; Colin, G.; Ketfi-Cherif, A.; Chamaillard, Y. Convex optimization for energy management of parallel hybrid electric vehicles. IFAC-PapersOnLine. IFAC-PapersOnLine 2016, 49, 271–276. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Sun, Y.; You, S. Model predictive control strategy for energy optimization of series-parallel hybrid electric vehicle. J. Clean. Prod. 2018, 199, 348–358. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Qi, S.; Tang, X.; Lang, K.; Xin, Z.; Brighton, J. Model predictive energy management for plug-in hybrid electric vehicles considering optimal battery depth of discharge. Energy 2019, 173, 667–678. [Google Scholar] [CrossRef]
- Zhu, L.; Tao, F.; Fu, Z.; Wang, N.; Ji, B.; Dong, Y. Optimization Based Adaptive Cruise Control and Energy Management Strategy for Connected and Automated FCHEV. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21620–21629. [Google Scholar] [CrossRef]
- Han, J.; Kum, D.; Park, Y. Synthesis of predictive equivalent consumption minimization strategy for hybrid electric vehicles based on closed-form solution of optimal equivalence factor. IEEE Trans. Veh. Technol. 2017, 66, 5604–5616. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; Van Den Driessche, G.; Hassabis, D. Mastering the game of Go with deep neural networks and tree search. J. Abbr. 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, J.; Shuai, B.; Williams, H.; He, Y.; Li, Z.; Yan, F. Multi-step reinforcement learning for model-free predictive energy management of an electrified off-highway vehicle. Appl. Energy 2019, 255, 113755. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Hu, Y.; Li, W.; Xu, K.; Zahid, T.; Qin, F.; Li, C. Energy management strategy for a hybrid electric vehicle based on deep reinforcement learning. Appl. Ences 2018, 8, 187. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Khajepour, A.; Wang, H.; Peng, J. Energy management for a power-split hybrid electric bus via deep reinforcement learning with terrain information. Appl. Energy 2019, 255, 113762. [Google Scholar] [CrossRef]
- Wu, Y.; Tan, H.; Peng, J.; Zhang, H.; He, H. Deep reinforcement learning of energy management with continuous control strategy and traffic information for a series-parallel plug-in hybrid electric bus. Appl. Energy 2019, 247, 454–466. [Google Scholar] [CrossRef]
- Lian, R.; Peng, J.; Wu, Y.; Tan, H.; Zhang, H. Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle. Energy 2020, 197, 117297. [Google Scholar] [CrossRef]
- Xu, D.; Cui, Y.; Ye, J.; Cha, S.W.; Li, A.; Zheng, C. A soft actor-critic-based energy management strategy for electric vehicles with hybrid energy storage systems. J. Power Sources 2022, 524, 231099. [Google Scholar] [CrossRef]
- Zhou, J.; Xue, S.; Xue, Y.; Liao, Y.; Liu, J.; Zhao, W. A novel energy management strategy of hybrid electric vehicle via an improved TD3 deep reinforcement learning. Energy 2021, 224, 120118. [Google Scholar] [CrossRef]
- Tang, X.; Chen, J.; Liu, T.; Qin, Y.; Cao, D. Distributed deep reinforcement learning-based energy and emission management strategy for hybrid electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 9922–9934. [Google Scholar] [CrossRef]
- Liu, T.; Wang, B.; Tan, W.; Lu, S.; Yang, Y. Data-driven transferred energy management strategy for hybrid electric vehicles via deep reinforcement learning. arXiv 2020, arXiv:2009.03289. [Google Scholar]
- Zhou, Q.; Du, C. A two-term energy management strategy of hybrid electric vehicles for power distribution and gear selection with intelligent state-of-charge reference. J. Energy Storage 2021, 42, 103054. [Google Scholar] [CrossRef]
- Tang, X.; Jia, T.; Hu, X.; Huang, Y.; Deng, Z.; Pu, H. Naturalistic data-driven predictive energy management for plug-in hybrid electric vehicles. IEEE Trans. Transp. Electrif. 2020, 7, 497–508. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Heess, N.; TB, D.; Sriram, S.; Lemmon, J.; Merel, J.; Wayne, G.; Silver, D. Emergence of locomotion behaviours in rich environments. arXiv 2017, arXiv:1707.02286. [Google Scholar]
- Du, G.; Zou, Y.; Zhang, X.; Liu, T.; Wu, J.; He, D. Deep reinforcement learning based energy management for a hybrid electric vehicle. Energy 2020, 201, 117591. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, W.; Cao, D.; Huang, Q.; Chen, Z.; Blaabjerg, F. Deep reinforcement learning–based approach for optimizing energy conversion in integrated electrical and heating system with renewable energy. Energy Convers. Manag. 2019, 202, 112199. [Google Scholar] [CrossRef]
- Wang, Y.; Tan, H.; Wu, Y.; Peng, J. Hybrid electric vehicle energy management with computer vision and deep reinforcement learning. IEEE Trans. Ind. Inform. 2020, 17, 3857–3868. [Google Scholar] [CrossRef]
- Wang, W.; Guo, X.; Yang, C.; Zhang, Y.; Zhao, Y.; Huang, D.; Xiang, C. A multi-objective optimization energy management strategy for power split HEV based on velocity prediction. Energy 2022, 238, 121714. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).