Adaptive Robust Path Tracking Control for Autonomous Vehicles Considering Multi-Dimensional System Uncertainty

Abstract

As the bottom layer of the autonomous vehicle, path tracking control is a crucial element that provides accurate control command to the X-by-wire chassis and guarantees the vehicle safety. To overcome the deterioration of control performance for autonomous vehicle path-tracking controllers caused by modeling errors and parameter perturbation, an adaptive robust control framework is proposed in this paper. Firstly, the 2-DOF vehicle dynamic model is established and the non-singular fast terminal sliding mode control algorithm is adopted to formulate the control law. The unmeasured model disturbance and parameter perturbation is regarded as the system uncertainty. To enhance the control accuracy, the radial basis forward neural network is introduced to estimate such uncertainty in real time. Then, the dynamic model of an active front steering system is established. The model reference control algorithm is applied for the steering torque control considering model uncertainty brought by the dissipation of manufacturing and mechanical wear. Finally, the Simulink–CarSim co-simulation platform is used and the proposed control framework is validated in two test scenarios. The simulation results demonstrate the proposed adaptive robust control algorithm has satisfactory control performance and good robustness against the system uncertainty.

1. Introduction

Promoted by growing demands on safety, efficiency, and low carbon emissions, the intelligent transportation system (ITS) has become one of the hottest fields of research in recent years. As the most important part, autonomous vehicles play a crucial role for the development of the ITS. Owing to the gradual reduction in sensor cost and the popularity of drive-by-wire chassis technology, advanced driver assistant systems are equipped by more and more vehicle manufacturers, such as autonomous emergency braking (AEB), lane-keeping assistance (LKA), and adaptive cruise control (ACC) [1,2,3]. With the continuous development of autonomous vehicles, it is estimated that one in ten cars will be fully autonomous-driving by the year 2030.

The key technology of autonomous vehicles includes environment perception, decision making, trajectory planning, and chassis control. As the bottom layer of the typical hierarchical architecture, vehicle chassis control is a vital part of autonomous vehicles, which implements accurate, stable, and safe tracking of desired trajectory by applying precise control instructions to actuators. As the fundamental function achieved by an autonomous vehicle, vehicle chassis control has been extensively researched, especially for vehicle trajectory tracking. Due to the complexity of the vehicle dynamic model with the multi degrees of freedom, non-linear, and multi-dimensional coupling characteristics, the simplicity of a vehicle dynamic model is widely adopted for model-based controller design, including linear quadratic regulators (LQRs) and model predictive control (MPC) to guarantee the real-time performance of the controller [4,5,6].

Salepour et al. proposed an integrated controller via LQR, which established a tracking optimization function and regulated the yaw moment [7]. Xu et al. considered the variation of road curvature and introduced the multiple point preview into the LQR controller that reduced the overshooting of the tracking error and smoothened the steering wheel angle [8]. Ji et al. adopted the linear tire model and formulated the MPC-based path-tracking controller with multiple constraints to guarantee the vehicle collision and stability safety [9]. Based on the prediction of the cut path of the obstacle vehicle, Chen et al. designed the model predictive tracking control with the dynamic prediction time domain, which avoided the collision effectively while tracking the desired path [10]. Guo et al. presented a dual-constraint vehicle collision avoidance control algorithm. The variable step MPC is utilized for path tracking. In addition, road boundaries and obstacles were integrated into the controller as constraints, which realized the vehicle obstacle avoidance with high tracking accuracy [11]. Funk et al. proposed a cooperative control mode in which two safety space models are defined in the process of vehicle collision avoidance to avoid collision and ensure vehicle stability. One is the vehicle stability limit, the other is the boundary of vehicle collision space. The variable predictive step MPC controller is used to take over the driver’s operation in case of danger [12,13].

However, the tracking performance of the model-based controller directly depends on the model accuracy. Most of the above control strategies adopted linear tire model based on the fixed lateral cornering stiffness. Although they have achieved considerable tracking effect in simulations and experimental tests, the deterioration of the tracking error under extreme conditions such as low friction coefficient and emergency lane-changing is inevitable. More seriously, the instability of the control system caused by model mismatch may lead to critical traffic accidents. To alleviate the negative impact of the varying cornering stiffness and acquire better system robustness, robust control is also widely considered in vehicle trajectory tracking control.

Hu et al. considered the variation in the vehicle speed and tire-cornering stiffness uncertainty during the trajectory tracking process, and established the time-varying parameter model and designed the H∞ output feedback robust controller. The gain-scheduling matrix is obtained by off-line optimization via genetic algorithm [14]. Guo et al. expanded the dimension of the vehicle dynamic model according to the upper and lower bounds of the uncertain parameters and designed the robust tracking controller to ensure the convergence of tracking errors even in the severe working conditions in which tire-cornering stiffness deviated far from its nominal value [15,16]. Chen et al. established the human–vehicle–road closed-loop model based on TS fuzzy theory for vehicle lane-keeping. The H_∞ robust steering torque compensation controller was designed to reduce the lateral offset [17]. Though H_∞ robust control guarantees the system robustness under a certain parameter perturbation range, the control performance is conservative. Adaptive control is considered as another suitable candidate. Akermi et al. proposed a path-tracking architecture with the combination of sliding mode control, fuzzy logic, and perturbations observer. The SMC gain is automatically adjusted by fuzzy organ [18]. Ao et al. developed the super twisting sliding model control algorithm based on Lyapunov theory and applied back-stepping technology. The system robustness is enhanced and the chattering phenomenon is attenuated [19]. Sun et al. proposed the adaptive non-singular fast terminal sliding mode (NFTSM) control for yaw stability control of a bus. Meanwhile, the robust least-squares allocation method is adopted for braking force distribution of each tire, which significantly improves the vehicle lateral stability under special driving conditions [20]. Most research focuses on the variation in the vehicle tire-cornering stiffness under different working conditions. Except for the vehicle state parameters, the system uncertainty of the vehicle chassis subsystem also has an important impact on the control performance.

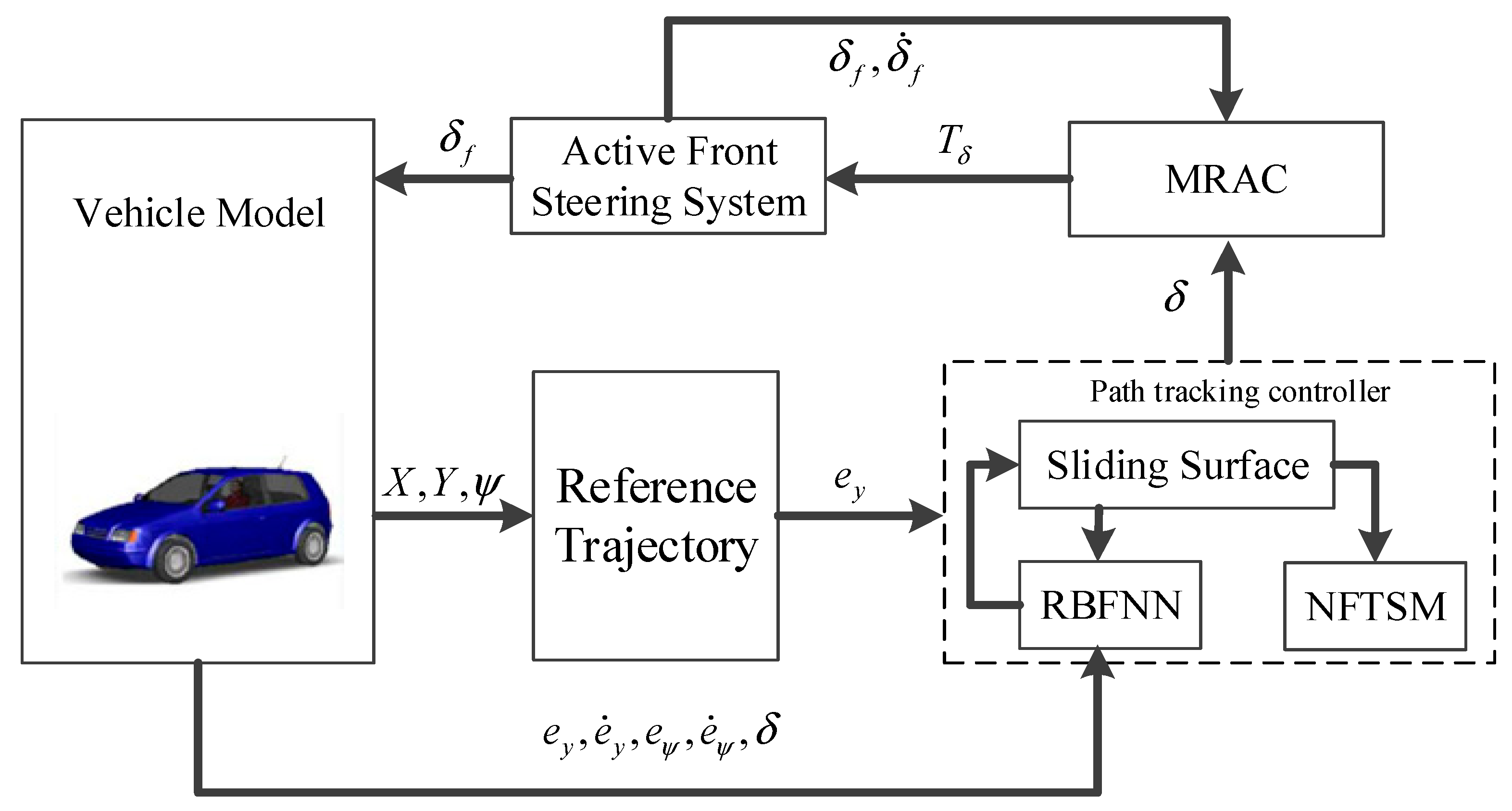
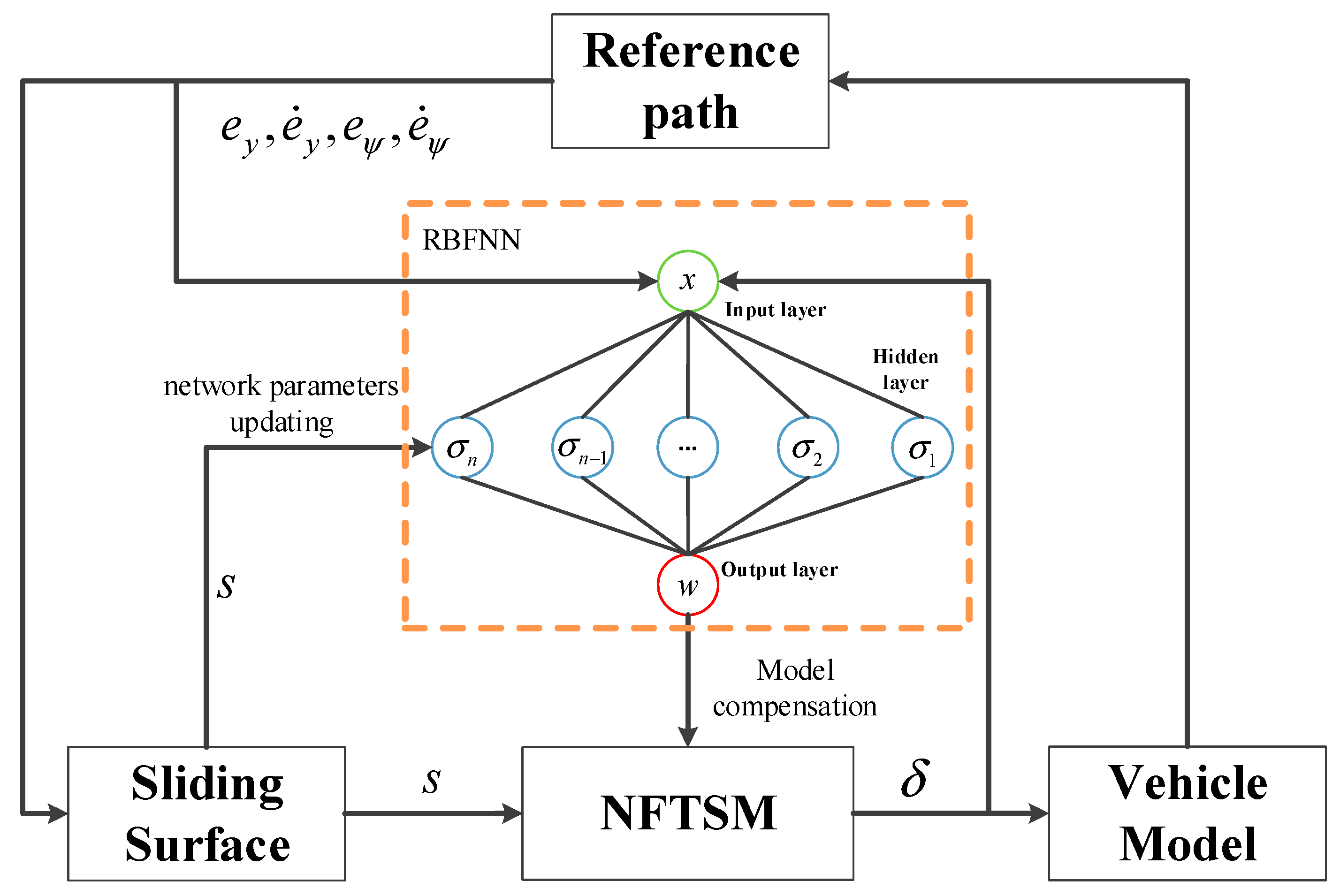
In this paper, a novel adaptive autonomous vehicle path-tracking controller is proposed. The control framework is shown in Figure 1. The main contributions are listed as follows:

(1)

The NFTSM controller is adopted for the vehicle lateral tracking control considering the vehicle dynamic model uncertainty and parameter disturbance, which has a faster convergence rate and transient response than a linear sliding model controller. In addition, the RBFNN is introduced to estimate and compensate the nonlinear uncertainty terms in real time, which enhances the control performance;

(2)

The steering system dynamics are established and the model reference adaptive control (MRAC) is utilized for the steering torque control to overcome the model uncertainty caused by the dissipation of production and system degradation

The rest of the paper is outlined as follows. In Section 2, the vehicle dynamic model is introduced for controller design. In Section 3, the path-tracking controller based on the NFTSM is established with the radial basis forward neural network (RBFNN) estimator. Then, the system stability and finite time convergence are analyzed. Section 4 provides the MRAC for steering torque control. The CarSim–Simulink co-simulation results are presented in Section 5 to verify the effectiveness and advantages of the proposed robust path-tracking control algorithm. Finally, the conclusions are drawn in Section 6.

2. Vehicle Dynamic Modeling

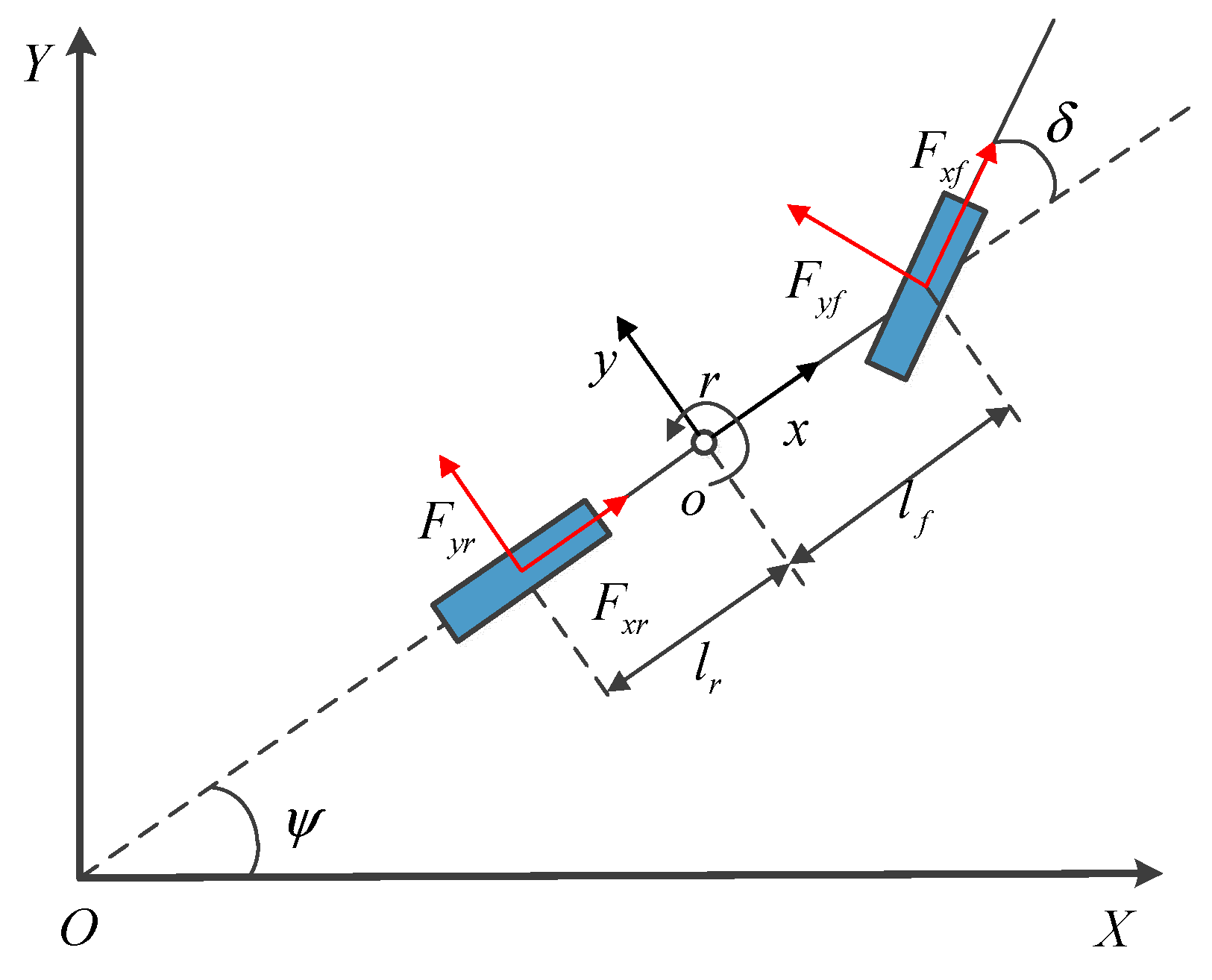
In this paper, the 2-DOF bicycle tracking model is utilized for controller design [21,22], which is shown in Figure 2.

To follow the reference trajectory, both lateral position error e_y and orientation error e_ψ should be eliminated. The relationship of e_y and e_ψ can be expressed as Equation (1) based on vehicle kinematic model:

$$\{\begin{array}{l}{\dot{e}}_y=u\sin e_{\psi }+v\cos e_{\psi }\\ {\dot{e}}_{\psi }=\dot{\psi }-{\dot{\psi }}_d\end{array},$$

(1)

where u, v, ψ represent the vehicle longitudinal speed, lateral speed, and heading angle, respectively. ψ_d is the desired heading angle. With the small angle assumption and simplified linear tire model, the vehicle dynamic model is described as:

$$\{\begin{array}{l}\dot{Y}=u\sin \psi +v\cos \psi \\ \dot{v}=\frac{1}{m}\left(F_{yf}+F_{yr}\right)-ur\\ \dot{\psi }=r\\ \dot{r}=\frac{1}{I_z}\left(l_f{F}_{yf}-l_r{F}_{yr}\right)\\ F_{yf}=C_f{\alpha }_f=C_f\left(\delta -\frac{v+l_{f}r}{u}\right)\\ F_{yr}=C_r{\alpha }_r=C_r\left(-\frac{v-l_{r}r}{u}\right)\end{array},$$

(2)

where $\dot{Y}$ is change rate of the vehicle lateral position in the global coordinate. l_f, l_r represent the distance from the center of gravity to the front and rear axle, respectively. r is the vehicle yaw rate. F_yf, F_yr denote the lateral force of the front and rear axle, respectively, which can be calculated by the cornering stiffness C_f, C_r and steering wheel angle δ.

Combining Equations (1) and (2), and defining the state vectors as $X={\left[e_y,{\dot{e}}_y,e_{\psi },{\dot{e}}_{\psi }\right]}^T$, the system input as U = δ and reference as $D={\dot{\psi }}_d$, the nominal state equation of tracking model can be written as:

$$\dot{X}=AX+BU+GD,$$

(3)

where

$$A=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& -\frac{C_f+C_r}{um}& \frac{C_f+C_r}{m}& -\frac{C_f{l}_f-C_r{l}_r}{um}\\ 0& 0& 0& 1\\ 0& -\frac{C_f{l}_f-C_r{l}_r}{I_{z}u}& \frac{C_f{l}_f-C_r{l}_r}{I_z}& -\frac{C_f{l}_f^2+C_r{l}_r^2}{I_z}\end{array}\right],B=\left[\begin{array}{c}0\\ \frac{C_f}{m}\\ 0\\ \frac{C_f{l}_f}{I_z}\end{array}\right],G=\left[\begin{array}{c}0\\ -\frac{C_f{l}_f-C_r{l}_r}{um}-u\\ 0\\ -\frac{C_f{l}_f^2+C_r{l}_r^2}{I_{z}u}\end{array}\right]$$

3. Path-Tracking Control Algorithm

In this section, the NFTSM is designed to eliminate the lateral position error that guarantees the vehicle accurately tracking the reference path. Meanwhile, the RBFNN is adopted to estimate the model uncertainty terms.

3.1. Control Law Design

Based on the nominal tracking error model presented in Equation (3), the second-time derivative of lateral position error could be written as:

$${\ddot{e}}_y=L+g\delta ,$$

(4)

where

$$L=-\left(\frac{C_f+C_r}{um}\right)\dot{Y}-\left(u+\frac{C_f{l}_f-C_r{l}_r}{um}\right)\dot{\psi }+u\left(\dot{\psi }-{\dot{\psi }}_d\right),$$

However, the simplicity model cannot accurately describe the dynamic characteristics of the vehicle in a complex environment. Moreover, the parametric perturbation and disturbances also deteriorate model accuracy. Hence, Equation (4) is rewritten as:

$${\ddot{e}}_y=L+g\delta +\varsigma ,$$

(5)

where ς is the system uncertainty that cannot be directly measured.

To eliminate lateral position error, the sliding surface is defined as:

$$s=e_y+p^{-1}{e}_y^{\alpha }+q^{-1}{\dot{e}}_y^{\beta },$$

(6)

which satisfies p > 0, q > 0, 1 < β < 2, β < α [20].

It can be seen that if |e_y| ≤ 1, Equation (6) can be approximated by ignoring the high order terms as:

$$s=e_y+q^{-1}{\dot{e}}_y^{\beta },$$

(7)

When system maintains on the sliding surface, Equation (7) is equivalent to:

$${\dot{e}}_y=-q^{\frac{1}{\beta }}{e}^{\frac{1}{\beta }},$$

(8)

which obviously reveals that the convergence rate is better than the linear sliding surface with the same parameters. If |e_y| ≤ 1, the ${\dot{e}}_y$ can be approximated by:

$${\dot{e}}_y=-{\left(q{p}^{-1}\right)}^{\frac{1}{\beta }}{e}_y^{\frac{\alpha }{\beta }},$$

(9)

Based on the sliding surface in Equation (6), the control law can be conceived as:

$$\delta ={\delta }_{eq}+{\delta }_{sw}-\varsigma ,$$

(10)

where δ_eq is equivalent control term, δ_sw is switching control term, and ς is system uncertainty. The equivalent control term is designed as:

$${\delta }_{eq}=-\frac{1}{g}\left(L+\left(1+p^{-1}\alpha e_y^{\alpha -1}\right)q{\beta }^{-1}{\dot{e}}_y^{2-\beta }\right),$$

(11)

To improve the approach speed and system robustness, the fast terminal-switching control term is proposed as:

$${\delta }_{sw}=-q{\beta }^{-1}\left({\lambda }_{1}s+{\lambda }_2{s}^{{\theta }_1}+{\lambda }_3{s}^{{\theta }_2}\right),$$

(12)

where λ₁, λ₂, λ₃ are positive constants.

3.2. RBFNN-Based System Uncertainty Estimator

Note that Equation (10) contains unmeasurable system uncertainty ς. Owing to the simple structure, fast learning, and fine approximation ability, RBFNN is much more widely used for complex dynamical system control than other neural networks such as multilayer perception, which not only has less network parameters for tuning, but can also avoid local minimum problems [23,24]. Here, the RBFNN is adopted to approximate the system uncertainty ς.

Define the ideal output and the actual output of RBFNN as f^* and f, which are expressed as:

$$f^{*}=w^{*}{}^T\sigma \left(x\right)+{\epsilon }^{*},$$

(13)

$$f=w^T\sigma \left(x\right)+\epsilon ,$$

(14)

where $w={\left[w_1,w_2,\dots ,w_n\right]}^T$, $\epsilon ={\left[{\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n\right]}^T$ represent the estimation of optimal network weight w^* and bias ε^*, respectively, n is number of nodes in the hidden layer of network, and $\sigma ={\left[{\sigma }_1,{\sigma }_2,\dots ,{\sigma }_n\right]}^T$ is Gaussian radial basis function, expressed as:

$${\sigma }_i\left(x\right)=\exp \left(-\frac{{\Vert x-c_i\Vert }^2}{2b_i^2}\right),i=1,2,\dots ,n,$$

(15)

where x is input vectors of the network. c_i and b_i are network parameters of the ith radial basis function. In this paper, the steering wheel angle δ and state vectors $e_y,{\dot{e}}_y,e_{\psi },{\dot{e}}_{\psi }$ are chosen as the network input.

Usually, the switching gain is set as larger to suppress the approximation error of the neural network. However, such a method is conservative, which leads to control chattering. Here, an adaptive compensation term is introduced, reducing network estimation error. The control law in Equation (10) can be redefined as:

$$\delta =-f-\frac{1}{g}\left(L+\left(1+p^{-1}\alpha e^{\alpha -1}\right)q{\beta }^{-1}{\dot{e}}^{2-\beta }\right)-p{\beta }^{-1}\left({\lambda }_{1}s+{\lambda }_2{s}^{{\theta }_1}+{\lambda }_3{s}^{{\theta }_2}\right)-\varsigma ,$$

(16)

To guarantee that the actual output of network f adaptively approximates the real one f^* and weight of the neural network is bounded, the update law of weight and error compensation term can be designed as:

$$\dot{w}={\mathsf{\Gamma }}_w\sigma s{q}^{-1}\beta \tau -{\mathsf{\Gamma }}_w{\eta }_w\psi s^{2}w,$$

(17)

$$\dot{\epsilon }={\mathsf{\Gamma }}_{\epsilon }s{q}^{-1}\beta \tau -{\mathsf{\Gamma }}_{\epsilon }{\eta }_{\epsilon }\psi s^2\epsilon ,$$

(18)

where Γ_w, η_w, Γ_ε, η_ε are positive constants and $\tau ={\dot{e}}^{\alpha -1}>0$.

Note that the network weight w and bias ε are updated iteratively online at each sampling time via Equations (17) and (18). The detailed structure of the RBFNN-based NFTSM control algorithm is shown in Figure 3.

3.3. System Performance Analysis

Next, the system stability and finite time control convergence are proven to illustrate the satisfactory system performance of the proposed control algorithm.

3.3.1. System Stability

Theorem 1.

For the path-tracking system expressed as Equation (3), the closed-loop system is global asymptotically stable and the weight and error compensation term of the network are bounded by choosing the control law as Equation (16) and adaptive update law as Equations (17) and (18).

Proof of Theorem 1.

Define the Lyapunov function as:

$$V_1=\frac{1}{2}\left(s^{T}s+\mathrm{tr}\left({\widehat{w}}^T{\mathsf{\Gamma }}_w^{-1}\widehat{w}\right)+{\widehat{\epsilon }}^T{\mathsf{\Gamma }}_w^{-1}\widehat{\epsilon }\right),$$

(19)

where $\widehat{w},\widehat{\epsilon }$ denote the error between estimation and actual value of network weight and approximation error, represented as $\widehat{w}=w^{*}-w$ and $\widehat{\epsilon }={\epsilon }^{*}-\epsilon$, respectively. Differentiating Equation (19), we obtain:

$${\dot{V}}_1=s^T\dot{s}-\mathrm{tr}\left({\widehat{w}}^T{\mathsf{\Gamma }}_w^{-1}\dot{w}\right)-{\widehat{\epsilon }}^T{\mathsf{\Gamma }}_w^{-1}\dot{\epsilon },$$

(20)

Substitute Equations (6) and (16)–(18) into (20):

$$\begin{array}{ll}\hfill {\dot{V}}_1& =s^T\left\{q^{-1}\beta {\dot{e}}^{\beta -1}\left[\widehat{f}-q{\beta }^{-1}\left({\lambda }_{1}s+{\lambda }_2{s}^{{\theta }_1}+{\lambda }_3{s}^{{\theta }_2}\right)-\epsilon \right]\right\}-\mathrm{tr}\left({\widehat{w}}^T{\mathsf{\Gamma }}_w^{-1}\dot{w}\right)-{\widehat{\epsilon }}^T{\mathsf{\Gamma }}_w^{-1}\dot{\epsilon }\hfill \\ & =s{q}^{-1}\beta \psi \widehat{\epsilon }-s\psi {\lambda }_{1}s-s\psi {\lambda }_2{s}^{{\theta }_1}-s\psi {\lambda }_3{s}^{{\theta }_2}-\mathrm{tr}\left({\widehat{w}}^T\sigma s{q}^{-1}\beta \psi \right)+\mathrm{tr}\left({\eta }_w\psi s^2{\widehat{w}}^{T}w\right)-{\widehat{\epsilon }}^T\epsilon q^{-1}\beta \psi +{\eta }_{\epsilon }\psi s^2{\widehat{\epsilon }}^T\epsilon \hfill \\ & =-\psi {\lambda }_1{s}^2-\psi {\lambda }_2{s}^{{\theta }_1+1}-\psi {\lambda }_3{s}^{{\theta }_2+1}+\mathrm{tr}\left({\eta }_w\psi s^2{\widehat{w}}^{T}w\right)+{\eta }_{\epsilon }\psi s^2{\widehat{\epsilon }}^T\epsilon \hfill \end{array}$$

(21)

where $\widehat{f}=f^{*}-f$. Since f is bounded, w^*, ε^* satisfies ‖w^*‖ ≤ w_max and |ε^*| ≤ ε_max. Based on the F-norm properties [25], we obtain:

$${\dot{V}}_1\le -\psi {\lambda }_1{s}^2-\psi {\lambda }_2{s}^{{\theta }_1+1}-\psi {\lambda }_3{s}^{{\theta }_2+1}-\eta \psi s^2{\left(\Vert \widehat{w}\Vert -\frac{w_{\max }}{2}\right)}^2+\eta \psi s^2\frac{w_{\max }}{4}-\eta \psi s^2{\left(\Vert \widehat{\epsilon }\Vert -\frac{{\epsilon }_{\max }}{2}\right)}^2+\eta \psi s^2\frac{{\epsilon }_{\max }}{4},$$

(22)

For Equation (22), if $\Vert \widehat{w}\Vert \ge w_{\max }$ and $\left|\widehat{\epsilon }\right|\ge {\epsilon }_{\max }$, it is obvious that $\dot{V}\le 0$. The closed system is asymptotically stable and $\Vert \widehat{w}\Vert ,\left|\widehat{\epsilon }\right|$ finally converge to $w_{\max }$ and ${\epsilon }_{\max }$, respectively.

If $\left|s\right|\ge 1$, Equation (22) can be further expressed as follows based on $s^{{\theta }_1+1}\ge s^2$:

$${\dot{V}}_1\le -\left({\lambda }_1+{\lambda }_2-\frac{\eta w_{\max }^2+\eta {\epsilon }_{\max }^2}{4}\right)\psi s^2,$$

(23)

Here, the ${\dot{V}}_1\le 0$ can be guaranteed only if the following inequality is satisfied:

$${\lambda }_1+{\lambda }_2\ge \left(\eta w_{\max }^2+\eta {\epsilon }_{\max }^2\right)/4,$$

(24)

Similarly, if $\left|s\right|<1$, ${\dot{V}}_1\le 0$ can be guaranteed under the condition that ${\lambda }_1+{\lambda }_3\ge \left(\eta w_{\max }^2+\eta {\epsilon }_{\max }^2\right)/4$.

In conclusion, by choosing the reasonable ${\lambda }_1,{\lambda }_2,{\lambda }_3$, Equation (22) demonstrates that the closed system retains asymptotic stability. When $\Vert s\Vert \to \infty$, $\Vert \widehat{w}\Vert \to \infty$, or $\Vert \widehat{\epsilon }\Vert \to \infty$, $V_1\to \infty$, the Lyapunov function is positive definite, which demonstrates that the closed-loop system is globally asymptotically stable.  □

3.3.2. Finite Time Convergence

Set another Lyapunov function as:

$$V_2=\frac{1}{2}{s}^{T}s,$$

(25)

Differentiating Equation (25), we obtain:

$$\begin{array}{ll}\hfill {\dot{V}}_2& =s^T\left\{q^{-1}\beta {\dot{e}}^{\beta -1}\left[\widehat{f}-q{\beta }^{-1}\left({\lambda }_{1}s+{\lambda }_2{s}^{{\theta }_1}+{\lambda }_3{s}^{{\theta }_2}\right)-\epsilon \right]\right\}\hfill \\ & =s{q}^{-1}\beta \psi {\widehat{w}}^T\sigma +s{q}^{-1}\beta \psi \widehat{\epsilon }-s\psi {\lambda }_{1}s-s\psi {\lambda }_2{s}^{{\theta }_1}-s\psi {\lambda }_3{s}^{{\theta }_2}\hfill \end{array}$$

(26)

Note that the range of the Gaussian function is [0,1], so $\Vert \sigma \Vert \le \sqrt{L}$, and ${\widehat{w}}^T\sigma$ is bounded due to $\Vert {\widehat{w}}^T\sigma \Vert \le \Vert {\widehat{w}}^T\Vert \Vert \sigma \Vert$. For the following inequalities:

$$\left|{\widehat{w}}^T\sigma \right|\le q{\beta }^{-1}{K}_{\sigma }\left|s\right|,$$

(27)

$$\left|\epsilon \right|\le q{\beta }^{-1}{K}_{\epsilon }\left|s\right|,$$

(28)

they are tenable if the following inequalities hold:

$$\Vert s\Vert \ge \frac{\Vert {\widehat{w}}^T\sigma \Vert }{q{\beta }^{-1}{K}_{\sigma }}={\mathsf{\Delta }}_1,$$

(29)

$$\Vert s\Vert \ge \frac{\epsilon }{q{\beta }^{-1}{K}_{\epsilon }}={\mathsf{\Delta }}_2,$$

(30)

where K_σ, K_ε are positive constants. Based on Equations (29) and (30), we can obtain the following inequality by setting $\Vert s\Vert ={\mathsf{\Delta }}_3\ge \max \left({\mathsf{\Delta }}_1,{\mathsf{\Delta }}_2\right)$ and substituting Equations (27) and (28) into (26):

$$\begin{array}{ll}\hfill \dot{V}& \le s\psi K_{\sigma }s+s\psi K_{\epsilon }s-s\psi {\lambda }_{1}s-s\psi {\lambda }_2{s}^{{\theta }_1}-s\psi {\lambda }_3{s}^{{\theta }_2}\hfill \\ & \le -\psi \left({\lambda }_1-K_{\sigma }-K_{\epsilon }\right)s^2-\psi {\lambda }_3{s}^{{\theta }_2+1}\hfill \end{array}$$

(31)

For simplicity, set ${\mathsf{\Theta }}_1={\lambda }_1-K_{\sigma }-K_{\epsilon }$, ${\mathsf{\Theta }}_2=\psi {\lambda }_3$. Once ${\lambda }_1\ge K_{\sigma }+K_{\epsilon }$ is guaranteed, the finite convergence time T_s satisfies:

$$T_s\le \frac{1}{2{\mathsf{\Theta }}_1\left(1-v\right)}\ln \frac{2{\mathsf{\Theta }}_1{V}_2{\left(0\right)}^{1-v}+2^v\left(1-v\right){\mathsf{\Theta }}_2}{2^v{\mathsf{\Theta }}_2},$$

(32)

where $v=\left({\theta }_2+1\right)/2$ and $V_2\left(0\right)$ is the initial value of the Lyapunov function. Equation (32) demonstrates that the sliding function s eventually converges in the field of Δ₃. Meanwhile, it can be perceived that the tracking performance is better with smaller Δ₃, which can be acquired by tuning parameters q and β.

4. MRAC for Active Steering System

This section provides a model reference adaptive control algorithm for steering torque generation that tracks the desired steering wheel angle calculated by the path-tracking controller. The feedback control law is designed via quadratic Lyapunov function to achieve the faster rate of convergence and better tracking performance.

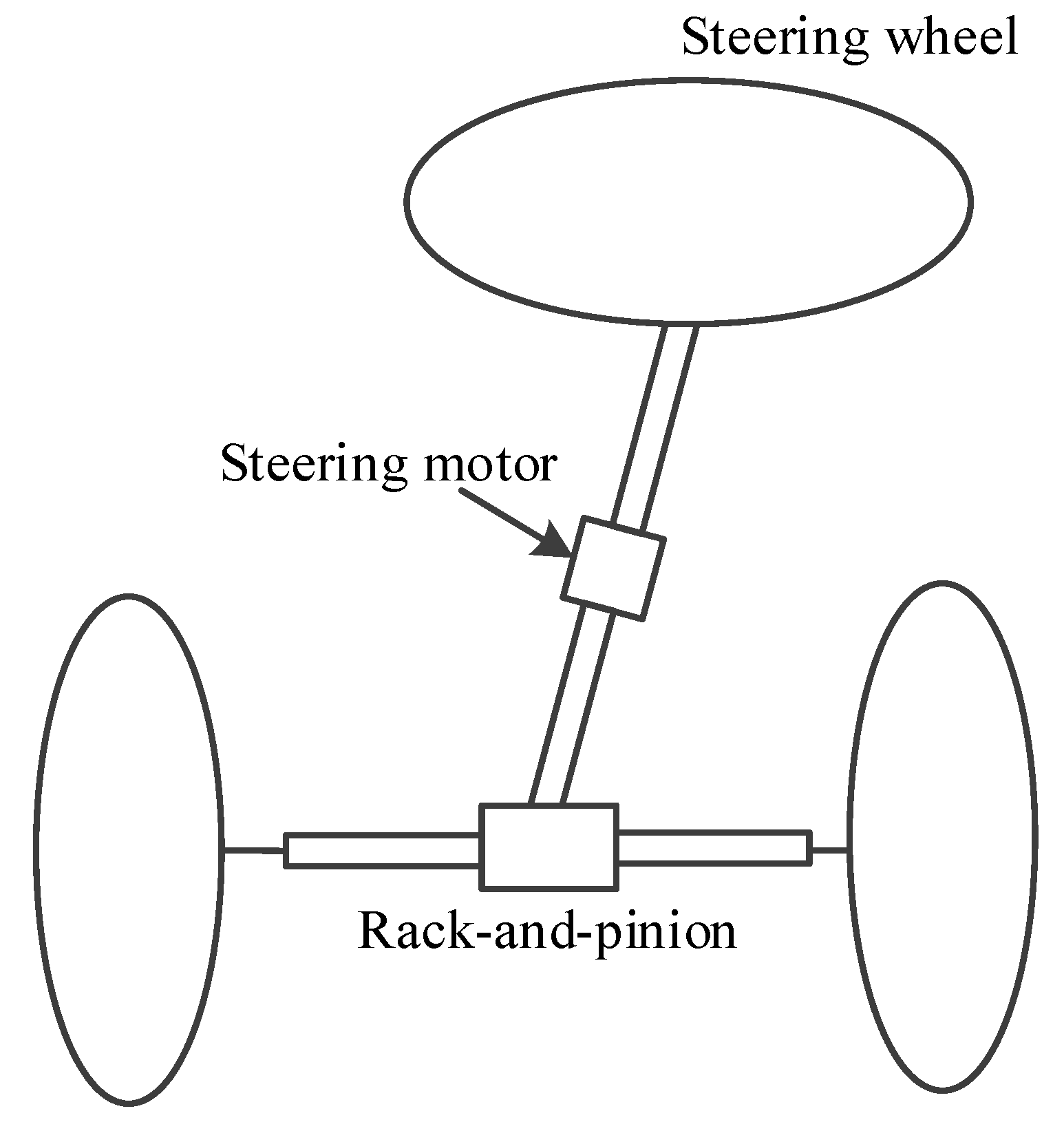
The structure of the active front wheel steering (AFS) system based on the steering-by-wire technology is shown in Figure 4. The dynamic model of AFS can be described as a second-order system:

$$J{\ddot{\delta }}_f+b{\dot{\delta }}_f+K{\delta }_f=T_{\delta },$$

(33)

where δ_f is the eventual front steering angle. J, b, K represent the nominal moment of inertia, damping coefficient, and angular stiffness of the steering system, respectively. T_δ is the output torque of the steering motor.

By specifying ${\omega }_n^2=K/J$ and $2\xi {\omega }_n=b/J$, the state–space Equation can be established with the measurable state vector $x_p={\left[{\delta }_f,{\dot{\delta }}_f\right]}^T$ and input $u_p=T_{\delta }$ as:

$${\dot{x}}_p=A_p{x}_p+B_p{u}_p,$$

(34)

where

$$A_p=\left[\begin{array}{cc}0& 1\\ -{\omega }_p^2& -2{\xi }_p{\omega }_p\end{array}\right],B_p=\left[\begin{array}{c}0\\ \frac{1}{J}\end{array}\right],$$

The object of MRAC is to design the input u_p that the closed–loop system is bounded to and the state vectors x_p that track the reference signals. Here the second-order low-pass filter is adopted to describe the reference model:

$${\dot{x}}_m=A_m{x}_m+B_m\delta ,$$

(35)

where

$$A_m=\left[\begin{array}{cc}0& 1\\ -{\omega }_r^2& -2{\xi }_r{\omega }_r\end{array}\right],B_m=\left[\begin{array}{c}0\\ 1\end{array}\right]$$

Here, $x_m={\left[{\delta }_r,{\dot{\delta }}_r\right]}^T$ is reference steering wheel angle and angular speed, and δ is the steering wheel command calculate by the path-tracking controller. ω_r and ξ_r are the cut-off frequency and damping coefficient of the filter.

It is obvious that if the following control law is applied,

$$u_p={\mathsf{\Omega }}_1^{*}{x}_p+{\mathsf{\Omega }}_2^{*}\delta ,$$

(36)

the closed-loop system can be expressed as:

$${\dot{x}}_p=\left(A_p+B_p{\mathsf{\Omega }}_1^{*}\right)x_p+B_p{\mathsf{\Omega }}_2^{*}\delta ,$$

(37)

If the ${\mathsf{\Omega }}_1^{*}$ and ${\mathsf{\Omega }}_2^{*}$ can be chosen as ${\mathsf{\Omega }}_1^{*}=B_p^{-1}\left(A_m-A_p\right)$, ${\mathsf{\Omega }}_2^{*}=B_p^{-1}{B}_m$, the closed-loop steering system is the same as the reference model, which implies that the state vector x_p asymptotically tracks x_m for any bounded reference signal δ [26].

$$\underset{t\to \infty }{\lim }{e}_{\delta }=\underset{t\to \infty }{\lim \left(x_p\left(t\right)-x_m\left(t\right)\right)}=0,$$

(38)

However, due to the gear abrasion, nonlinear characteristics of steering motor, and other factors, the dynamic model of AFS has parameter perturbation including J, b, K, which is difficult to accurately identify in real time. On the other hand, the different longitudinal tire forces between the left and right wheels, differential steering angle caused by scrub radius, and tire self-aligning moment also bring uncertainty to the steering system. The ${\mathsf{\Omega }}_1^{*}$ and ${\mathsf{\Omega }}_2^{*}$ cannot be obtained analytically in practice. Thus, the adaptive estimator has to be carried out for online estimation. Define the ${\widehat{\mathsf{\Omega }}}_1, {\widehat{\mathsf{\Omega }}}_2$ as the estimation values of ${\mathsf{\Omega }}_1^{*}, {\mathsf{\Omega }}_2^{*}$. The parameter error is represented as ${\tilde{\mathsf{\Omega }}}_1={\widehat{\mathsf{\Omega }}}_1-{\mathsf{\Omega }}_1^{*}, {\tilde{\mathsf{\Omega }}}_2={\widehat{\mathsf{\Omega }}}_2-{\mathsf{\Omega }}_2^{*}$. Combining Equations (35)–(38), the tracking error satisfies the followed Equation:

$${\dot{e}}_{\delta }=A_m{e}_{\delta }+B_P\left({\tilde{\mathsf{\Omega }}}_1{x}_p+{\tilde{\mathsf{\Omega }}}_2\delta \right),$$

(39)

Set the Lyapunov candidate as:

$$V_3=e_{\delta }^{T}P{e}_{\delta }+{\gamma }_x^{-1}{\tilde{\mathsf{\Omega }}}_1^T{\tilde{\mathsf{\Omega }}}_1+{\gamma }_{\delta }^{-1}{\tilde{\mathsf{\Omega }}}_2^T{\tilde{\mathsf{\Omega }}}_2,$$

(40)

where γ_x, γ_δ are the parameters learning rate, then the time derivative of Lyapunov function V₃ is:

$${\dot{V}}_3=e_{\delta }^{T}P\left(A_m{e}_{\delta }+B_P\left({\tilde{\mathsf{\Omega }}}_1{x}_p+{\tilde{\mathsf{\Omega }}}_2\delta \right)\right)+\left(e_{\delta }^T{A}_m^T+x_p^T{\tilde{\mathsf{\Omega }}}_1^T{B}_p^T+{\delta }^T{\tilde{\mathsf{\Omega }}}_2^T{B}_p^T\right)Pe+2{\gamma }_x^{-1}{\tilde{\mathsf{\Omega }}}_1^T{\dot{\tilde{\mathsf{\Omega }}}}_1+{\gamma }_{\delta }^{-1}{\tilde{\mathsf{\Omega }}}_2^T{\dot{\tilde{\mathsf{\Omega }}}}_2,$$

(41)

If the adaptive law is chosen as:

$${\dot{\tilde{\mathsf{\Omega }}}}_1={\dot{\mathsf{\Omega }}}_1=-{\gamma }_x{x}_p{e}_{\delta }^{T}P{B}_P,$$

(42)

$${\dot{\tilde{\mathsf{\Omega }}}}_2={\dot{\mathsf{\Omega }}}_2=-{\gamma }_{\delta }\delta e_{\delta }^{T}P{B}_P,$$

(43)

The Equation (41) can be written as:

$${\dot{V}}_3=e_{\delta }^T\left(P{A}_m+A_m^{T}P\right)e+2{\tilde{\mathsf{\Omega }}}_1^T\left(x_p{e}_{\delta }^{T}P{B}_p+{\gamma }_x^{-1}{\dot{\tilde{\mathsf{\Omega }}}}_1\right)+2{\tilde{\mathsf{\Omega }}}_2^T\left(\delta e_{\delta }^{T}P{B}_p+{\gamma }_{\delta }^{-1}{\dot{\tilde{\mathsf{\Omega }}}}_2\right)=-e_{\delta }^{T}P{e}_{\delta }\le 0,$$

(44)

Therefore, the adaptive control scheme is established in case that ${\tilde{\mathsf{\Omega }}}_1,{\tilde{\mathsf{\Omega }}}_2,e_{\delta }$ are bounded and $e_{\delta }\left(t\right)\to 0$ as $t\to \infty$.

5. Simulation Results and Discussion

Considering the certain risk for real vehicle experiments, especially for some extreme conditions at high speed and a variety of road friction coefficients, the MATLAB/CarSim co-simulation test was conducted in this work to verify the effectiveness and advantage of the proposed control architecture. The simulation scenarios and high fidelity vehicle dynamic model is established in CarSim and the controller is developed via Simulink.

In this section, two typical test scenarios including double-lane change maneuver and slalom-like maneuver are carried out to evaluate the control performance of the adaptive robust control. These two scenarios can obviously reflect the vehicle stability and system response in the process of high-speed obstacle avoidance and continuous steering, which are widely adopted for vehicle lateral stability evaluation.

5.1. Double-Lane Change (DLC) Maneuver

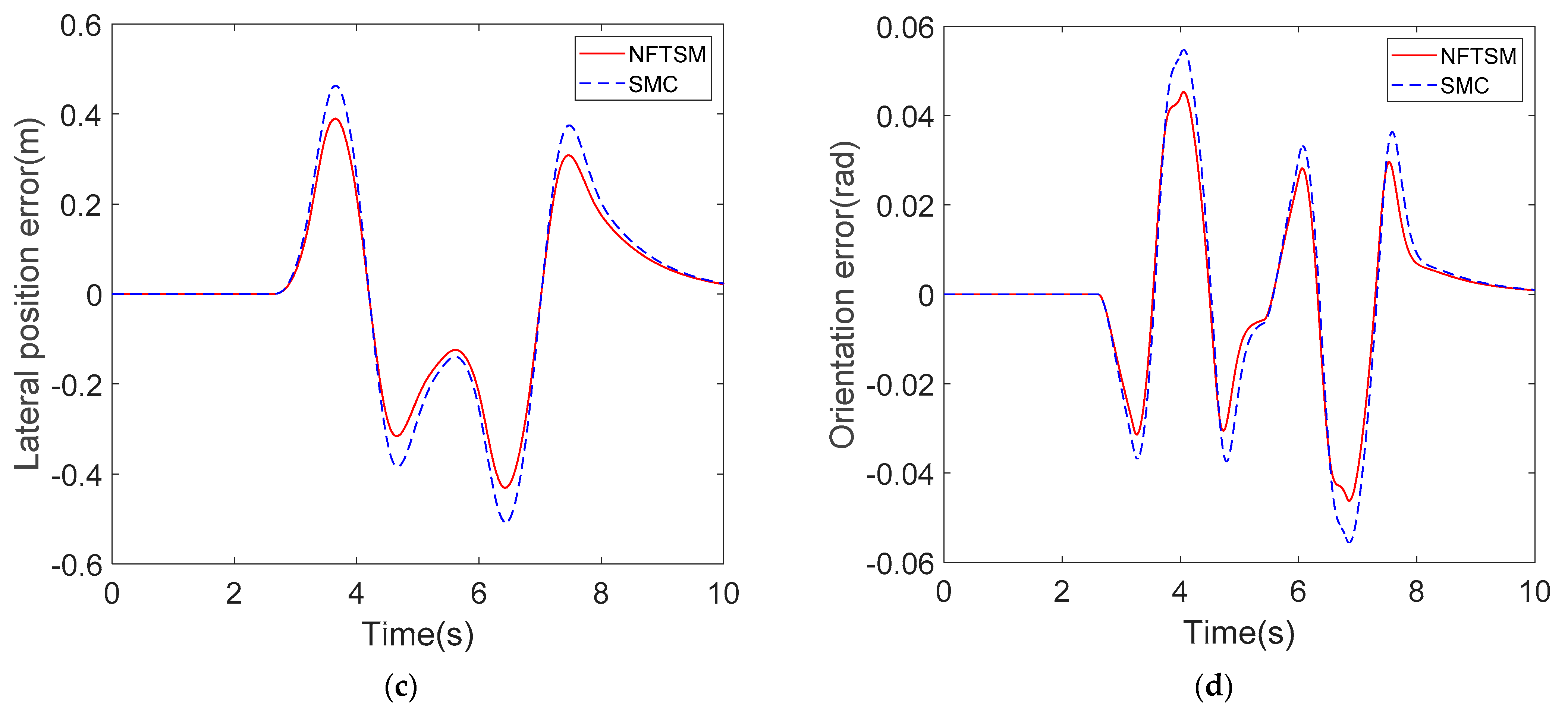
This test scenario simulates the vehicle emergency obstacle avoidance behavior at high speed. The vehicle longitudinal speed is kept at 90 km/h and the road friction coefficient is set as 0.5. The front and rear tire-cornering stiffness variation are regarded as the model uncertainty, which is set as only 60% of the nominal value. The tracking performance of two controllers is compared here. One is the proposed NFTSM controller and the other is the convention sliding mode control with linear sliding surface controller. The simulation results are shown in Figure 5.

Figure 5a–d illustrate the global vehicle trajectory, steering wheel angle, lateral position tracking error, and orientation error, respectively. From Figure 5a, it can be seen that both controllers accomplish the DLC maneuver. However, due to the high initial speed, poor road friction condition, and the perturbation of the tire-cornering stiffness, they fail to follow the reference path accurately. Due to the attenuation of the tire-cornering stiffness, the steering angle calculated based on the nominal dynamic model cannot generate the corresponding lateral force. Therefore, the conventional sliding mode controller has a relatively large deviation when the vehicle changes to the adjacent lane and switches back to the main lane because of the insufficient system input response. As shown in Figure 5b, the proposed adaptive controller generates larger steering angle during the lane-change process. The adaptive sliding mode controller identifies the parameters perturbation of the system through the RBFNN and gives the controller a certain amount of compensation. Thus, the path of the adaptive sliding mode control strategy is smoother in the tracking process and the offset of the reference path is smaller. Figure 5c,d reveal that the maximum lateral position error and orientation error of the conventional sliding mode control are 0.48 m and 0.053 rad, respectively, which are only 0.43 m and 0.046 rad, respectively, for the RBFNN-based NFTSM controller. The tracking error is reduced by about 10%. Therefore, it can be demonstrated that the adaptive control algorithm proposed in this paper has higher path tracking accuracy. It also has better robustness, especially when system uncertainty or parameter perturbation occur under complex working conditions.

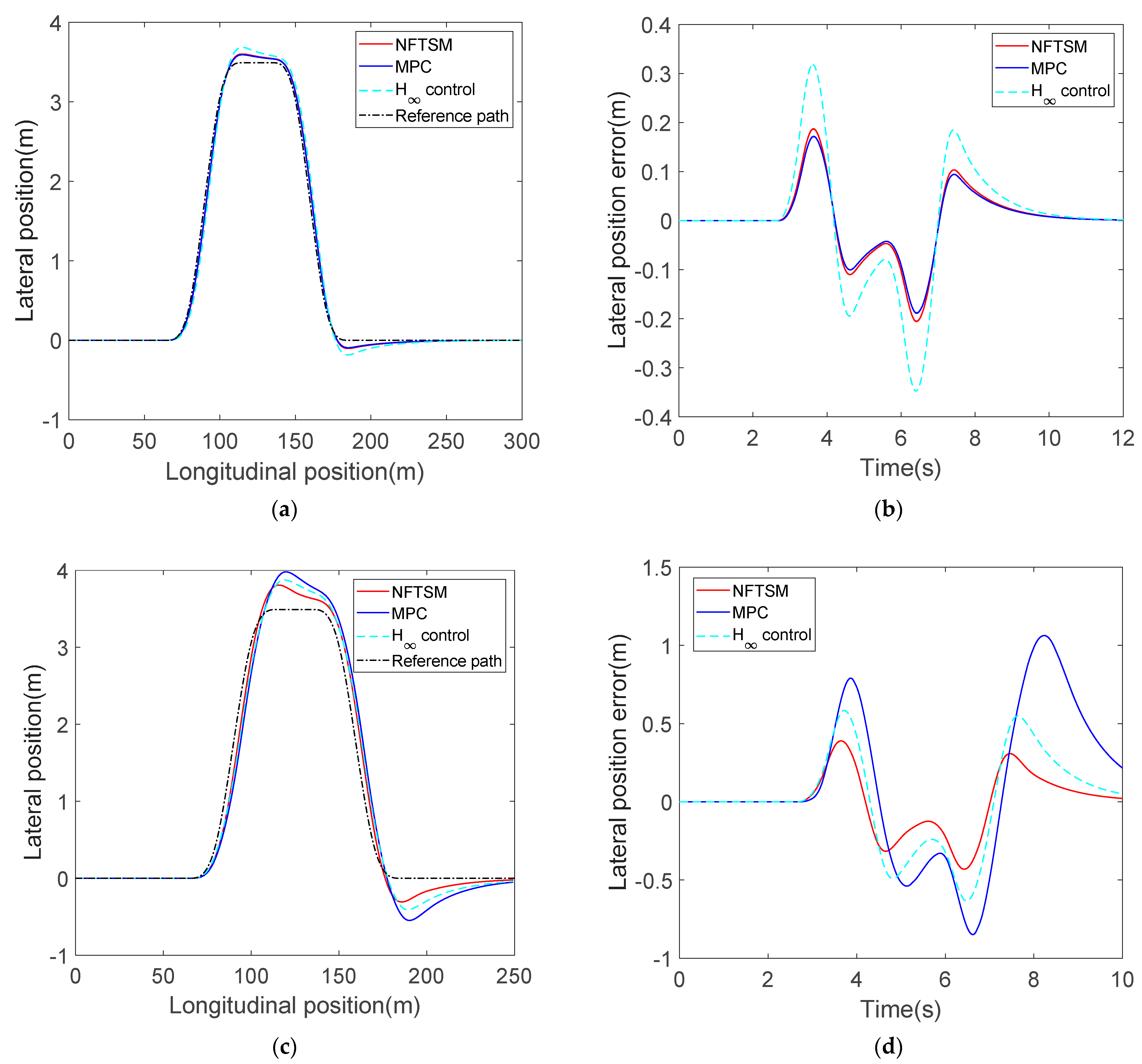
To further illustrate the advantage of the proposed controller, two other commonly used controllers are introduced for comparison as MPC and H_∞ robust control. Here, the tracking performance is compared under two conditions. One is when the control system is healthy (without any parameter perturbation or external disturbance) and the other one has tire-cornering stiffness variation, as stated above. The simulation results are shown in Figure 6.

The MPC is designed with a nominal vehicle dynamic model. Thus, it has the best tracking performance when the control system is totally healthy. The maximum lateral position error of MPC is only 0.17 m. On the contrary, the feedback gain matrix of the H_∞ controller is regulated by solving linear matrix inequalities considering the potential system uncertainty, which obtains a wide range of robustness by sacrificing certain control accuracy. The tracking error is largest when system is healthy, which reaches 0.31 m, although the tracking performance of the proposed NFTSM control is inferior to MPC. Its maximum lateral position error is 0.18 m, only about 7% worse than MPC. However, when parameter perturbation occurs, MPC no longer generates the optimal steering command. The tracking performance becomes the worst among these three controllers, and has the largest tracking error. In contrast, the H_∞ controller and NFTSM controller have better robustness against the tire-cornering stiffness variation. The proposed NFTSM controller, in particular, modifies the control law in real time by estimating system uncertainty online, which significantly reduces the tracking error compared with the fixed control gain of the H_∞ controller. Hence, compared with MPC and the H_∞ controller, the proposed control algorithm has better adaptability and a more balanced tracking performance in complex working conditions.

5.2. Slalom-like Maneuver

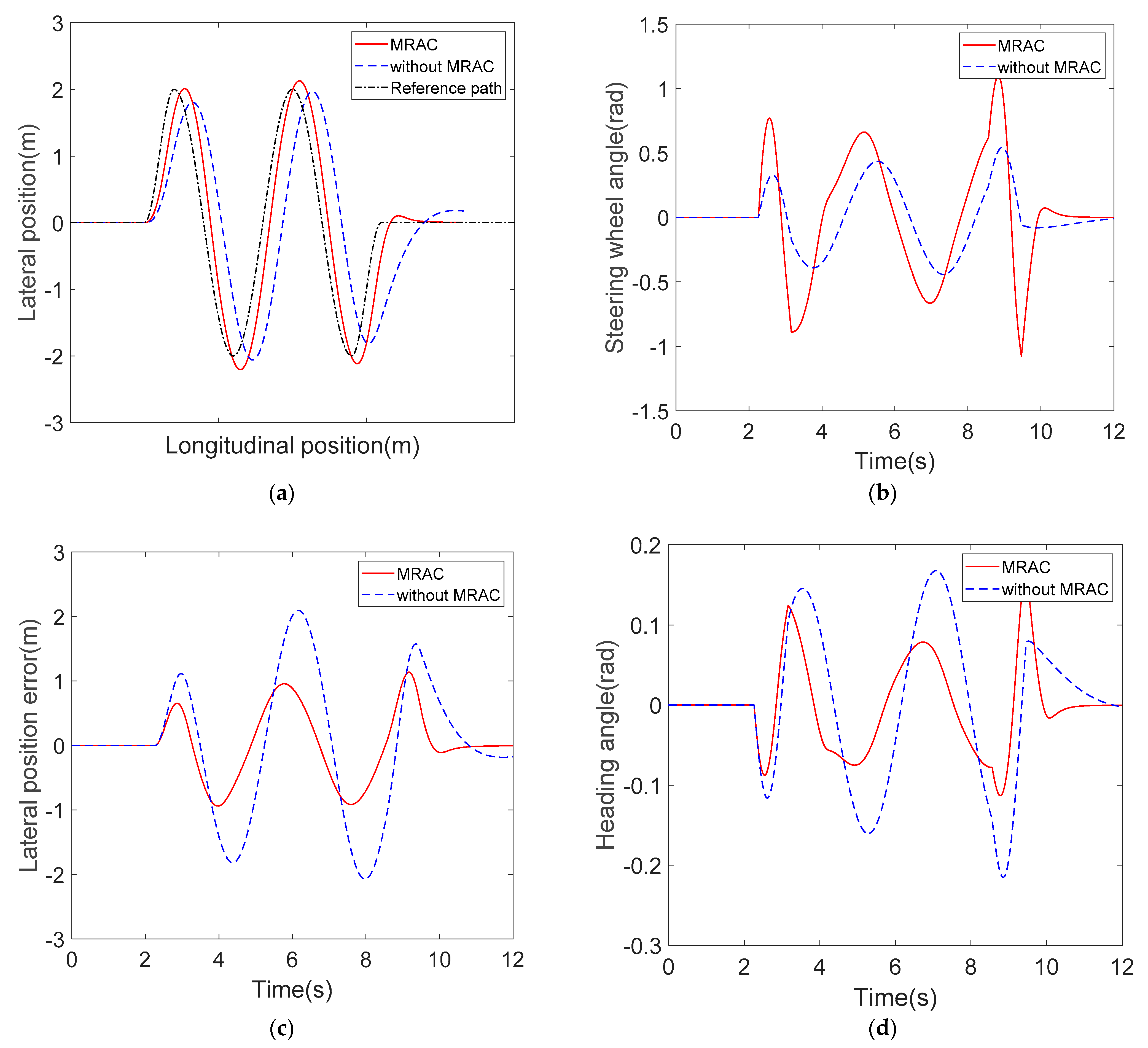
In this test scenario, the reference path is generated via continuous sinusoidal signal, which simulates the continuous obstacle avoidance maneuver. The initial vehicle speed is 80 km/h and the road friction coefficient is set as 0.85. This scenario mainly tests the system robustness and tracking accuracy under the condition that the AFS performance deteriorates. Thus, the damping coefficient and angular stiffness of the steering system are set as 50% higher than nominal value and the vehicle tire-cornering stiffness is still set as 60% of the nominal value. Similarly, to illustrate the advantage of the proposed control algorithm, another controller without MRAC is introduced here as the comparison. It has the same upper NFTSM controller but the steering torque is directly calculated by Equation (33) based on the nominal moment of inertia, damping coefficient, and angular stiffness of the steering system. The detailed simulation results are shown in Figure 7.

Figure 7a–d illustrate the global vehicle trajectory, steering wheel angle, lateral position tracking error, and orientation error, respectively. Due to the increase in the damping coefficient and angular stiffness of the steering system dynamics model, the system response speed decreases. The steering torque calculated by the controller without MRAC is based on the nominal model parameters, which is unable to generate enough steering wheel angle in time for the real steering system. It can be seen from Figure 7a,b that the response speed of steering wheel angle is slow, and there is a large time delay between the actual vehicle trajectory and the reference path. In addition, during the process of continuous steering for obstacle avoidance, the phenomenon of time delay is further amplified. On the contrary, the proposed controller in the paper adjusts the steering torque by comparing the response error between the actual steering system and reference model, which has a faster response speed and higher tracking accuracy. From Figure 7c,d, it is clear that the maximum lateral position error and orientation error of the control algorithm without MRAC are 2.1 m and 0.22 rad, respectively, which are only 1.2 m and 0.14 rad, respectively, for the proposed controller in this paper.

6. Conclusions

This paper proposed a cascade adaptive robust control architecture that overcomes the influence of multi-dimensional system uncertainty on control performance. The higher-level controller regarded the dynamic model error and parameter disturbance as the system uncertainty and adopted the NFTSM control algorithm with RBFNN estimator to generate the steering wheel angle command. The lower-level controller applied MRAC, considering the uncertainty of stiffness and damping coefficient in AFS to realize the accurate steering torque control. The system stability and finite time convergence are proven by choosing the appropriate Lyapunov function. Two simulation scenarios are carried out to validate the feasibility of the proposed control architecture. The simulation results reveal that the RBFNN-based NFTSM has satisfactory tracking performance under different road friction coefficients and has good robustness against varying tire-cornering stiffness. Meanwhile, it has better control accuracy and a faster convergence rate compared with the conventional sliding mode controller. On the other hand, the model reference adaptive steering torque controller could generate the accurate steering torque that follows the steering wheel angle command with the variation in the steering model parameters or under the circumstance that system performance deteriorates.