Analysis, Design and Realization of a Wireless Power Transfer Charger for Electric Vehicles: Theoretical Approach and Experimental Results
Abstract
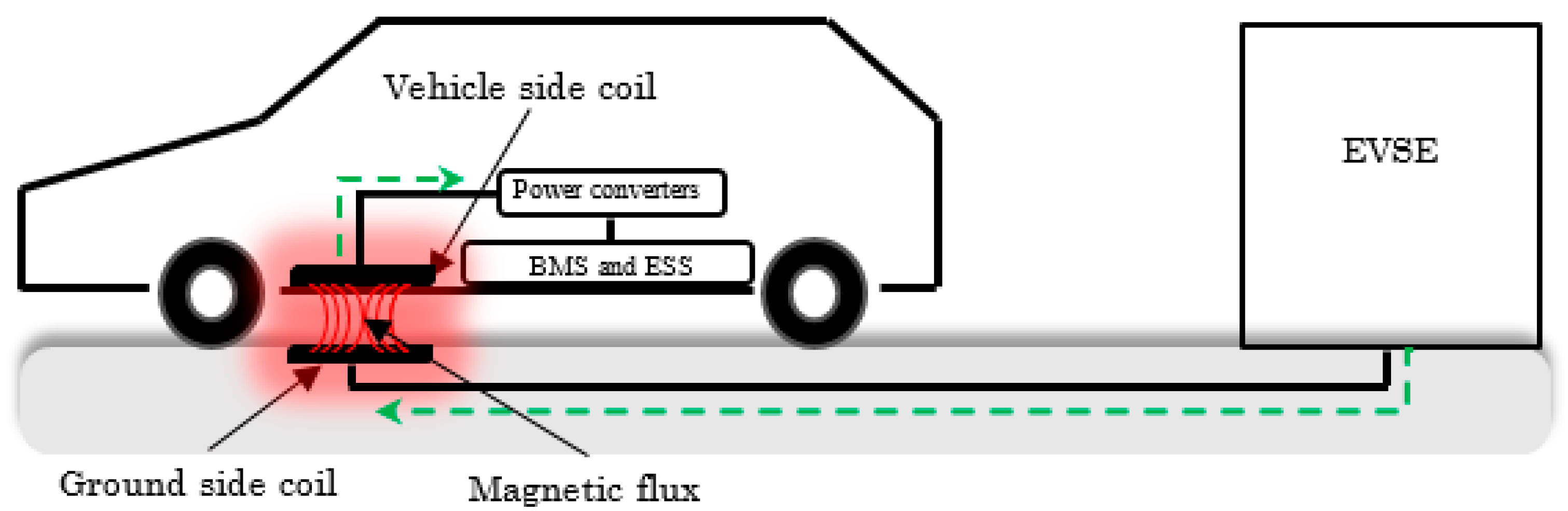
:1. Introduction
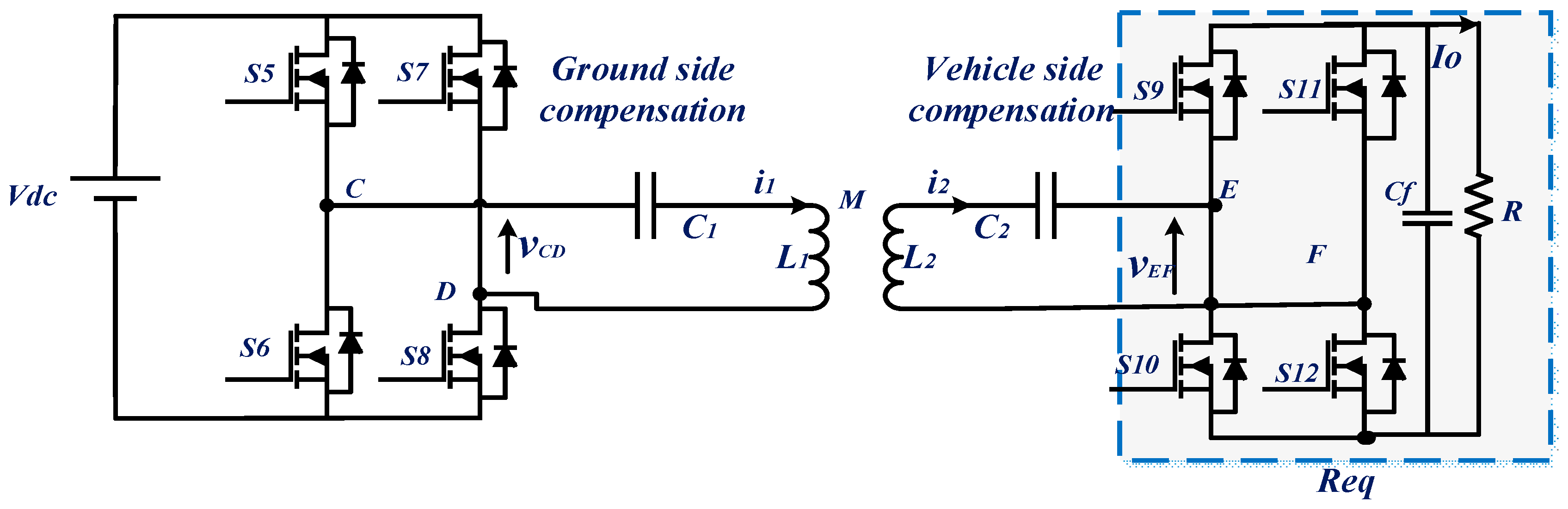
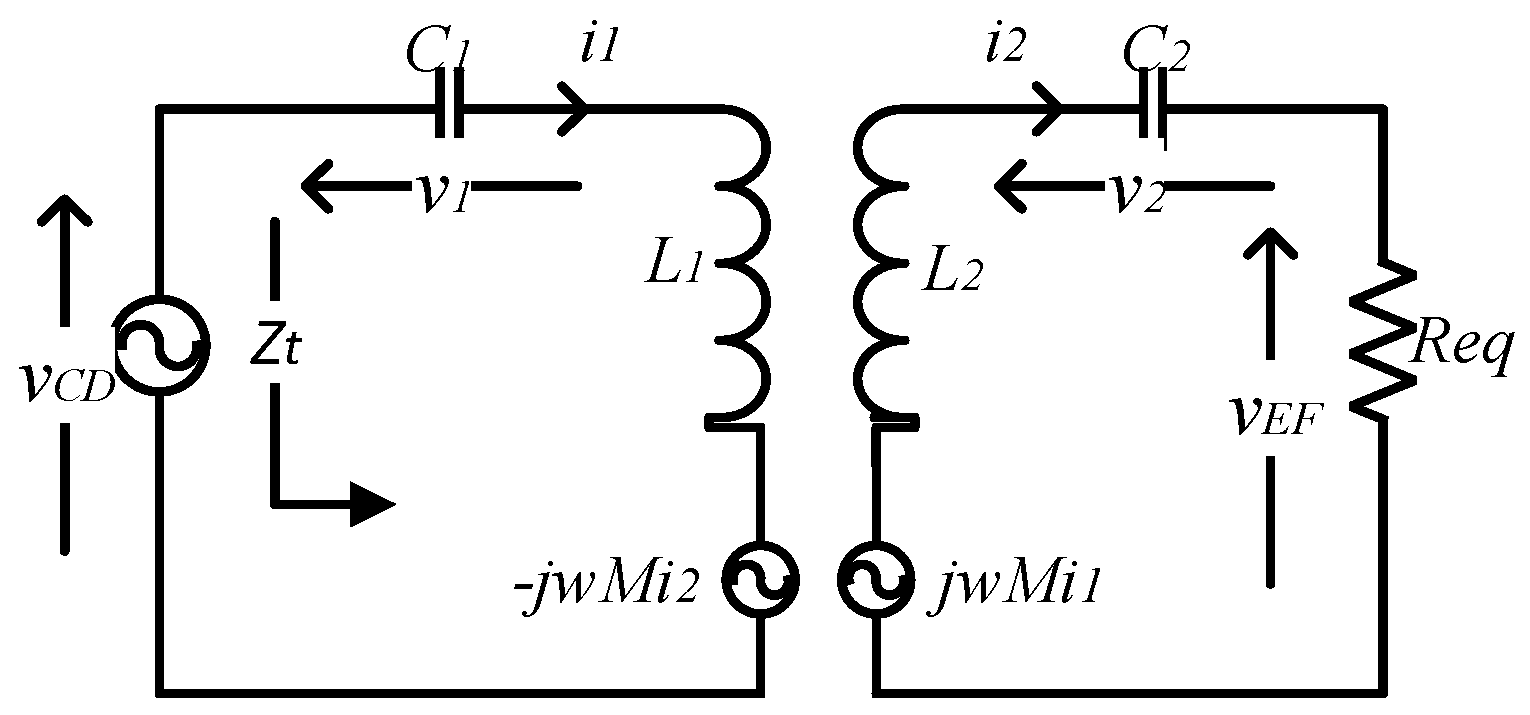
2. Analysis of Series–Series Compensated WPT Charger
2.1. Effect of the Compensation Network on the Efficiency of the WPT Charger
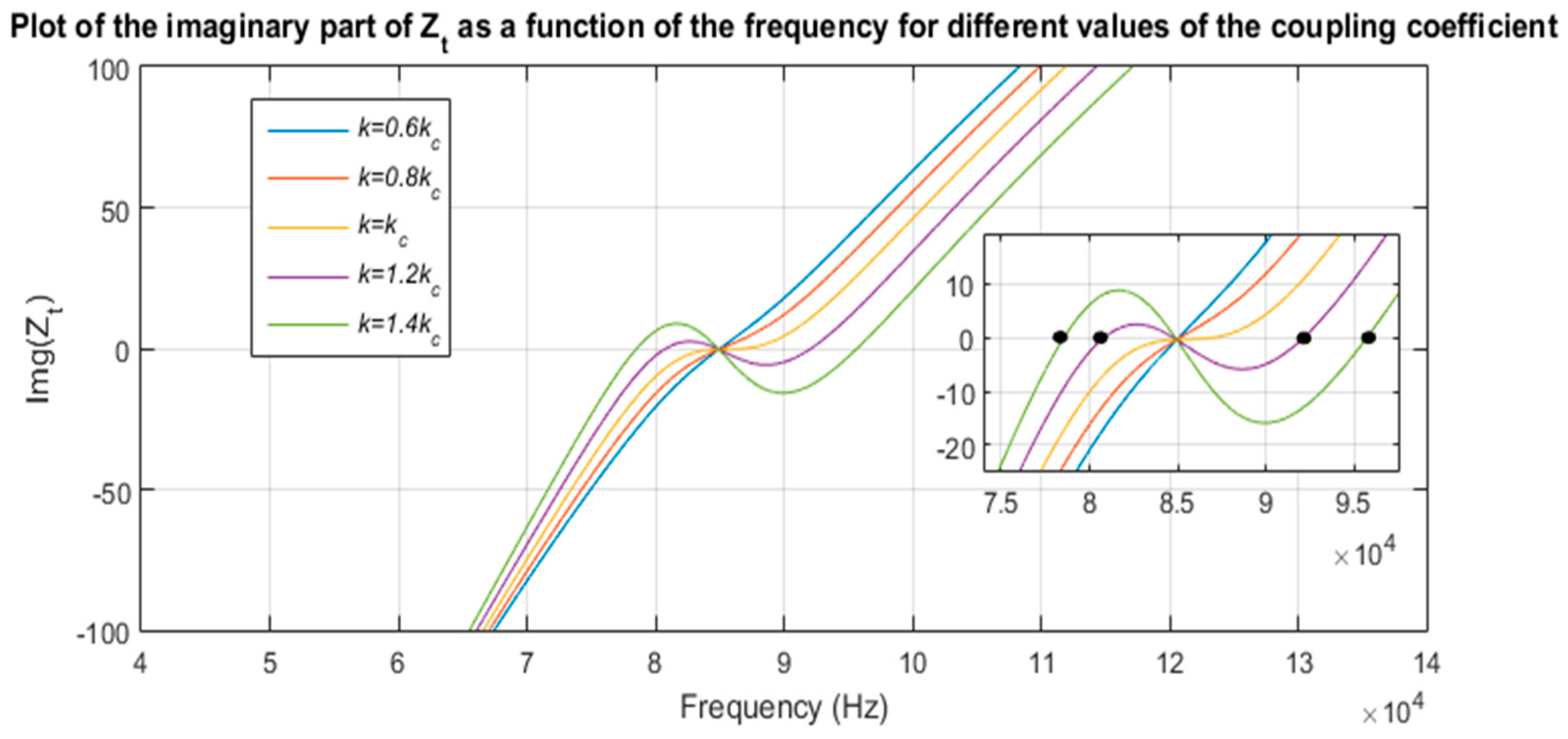
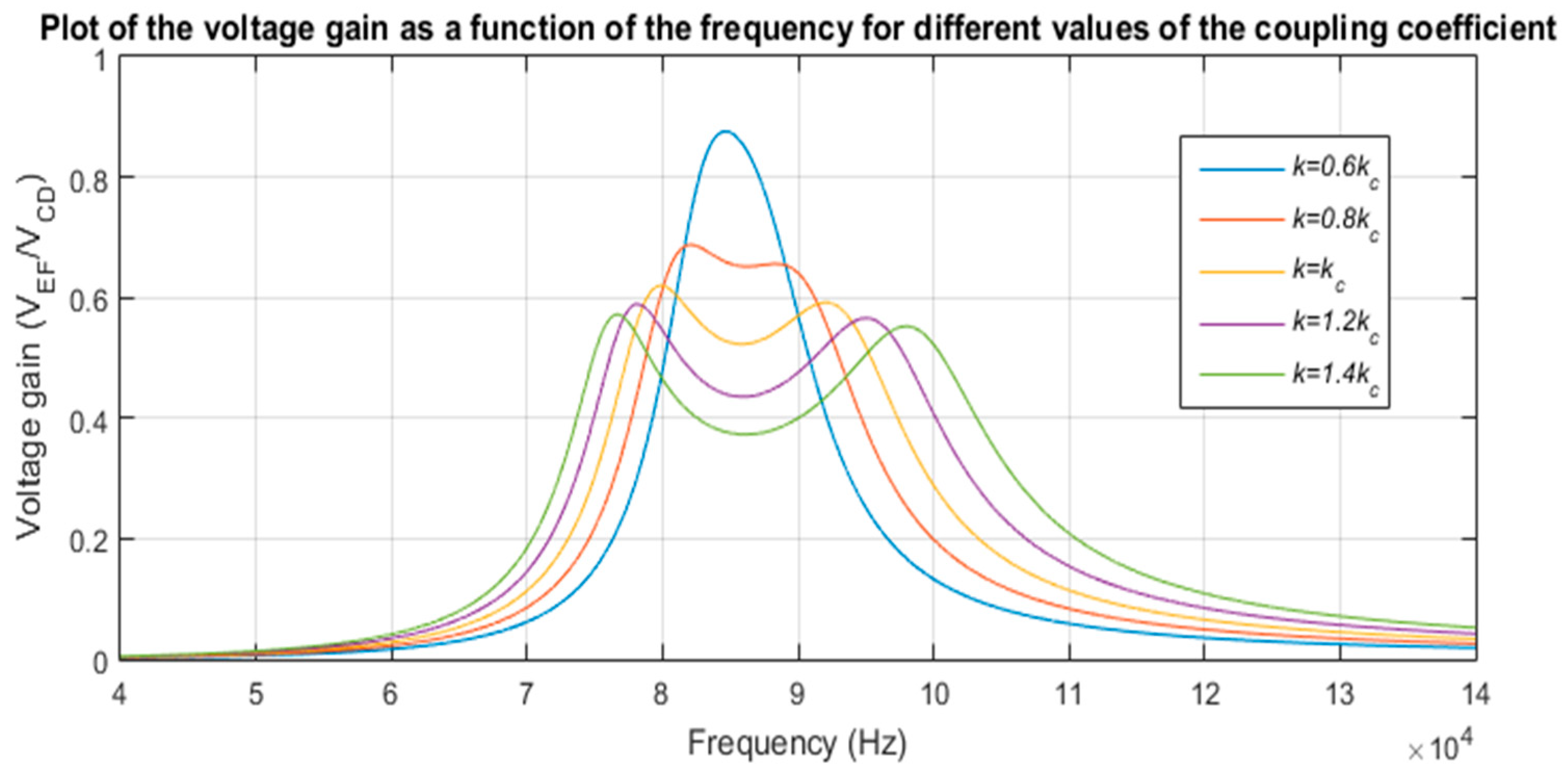
2.2. Effect of the Coupling Coefficient on the Power Transfer Efficiency
2.3. Bifurcation Phenomenon in a WPT Charger
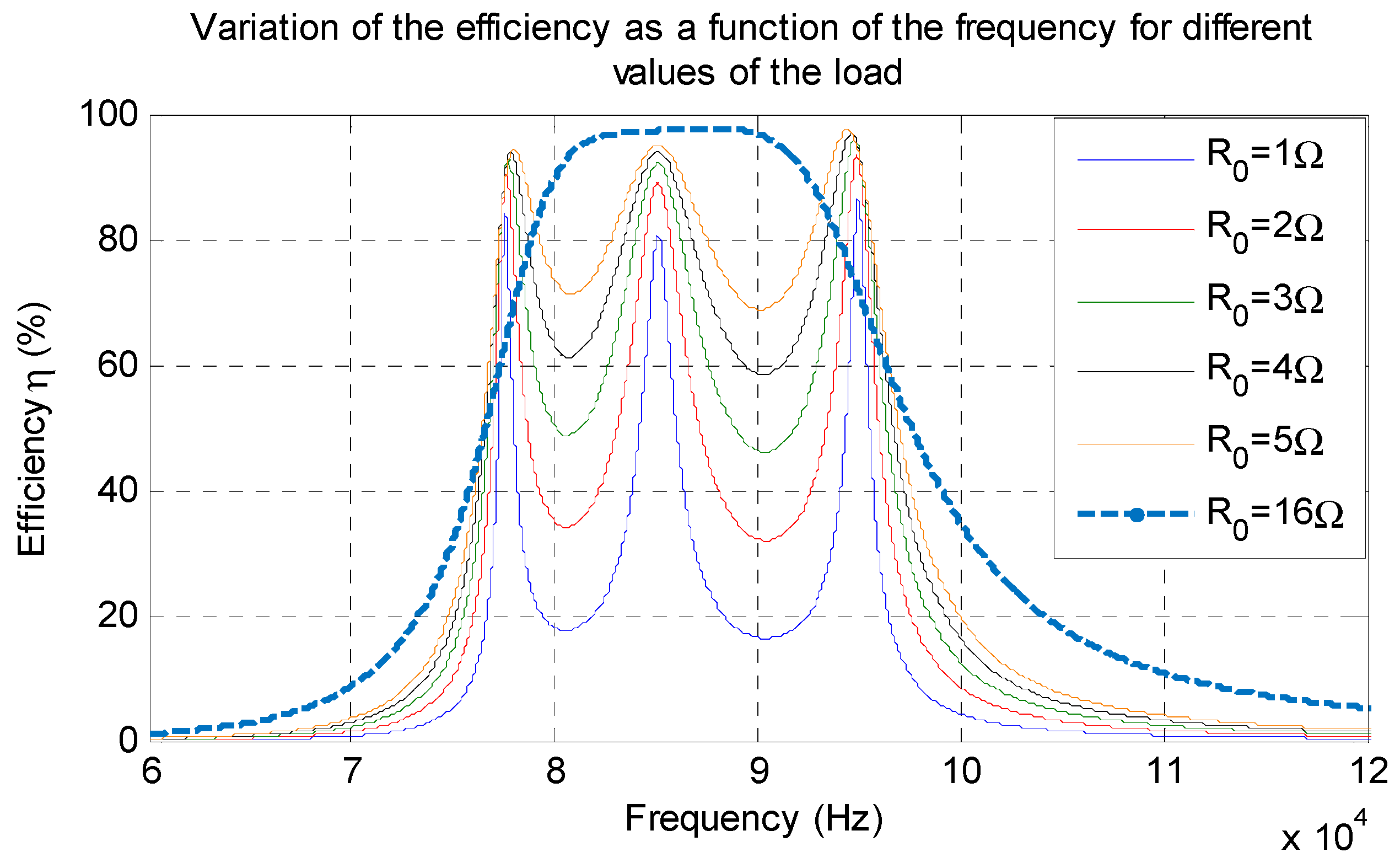
2.4. Effect of the Load Variations on the Power Transfer Efficiency
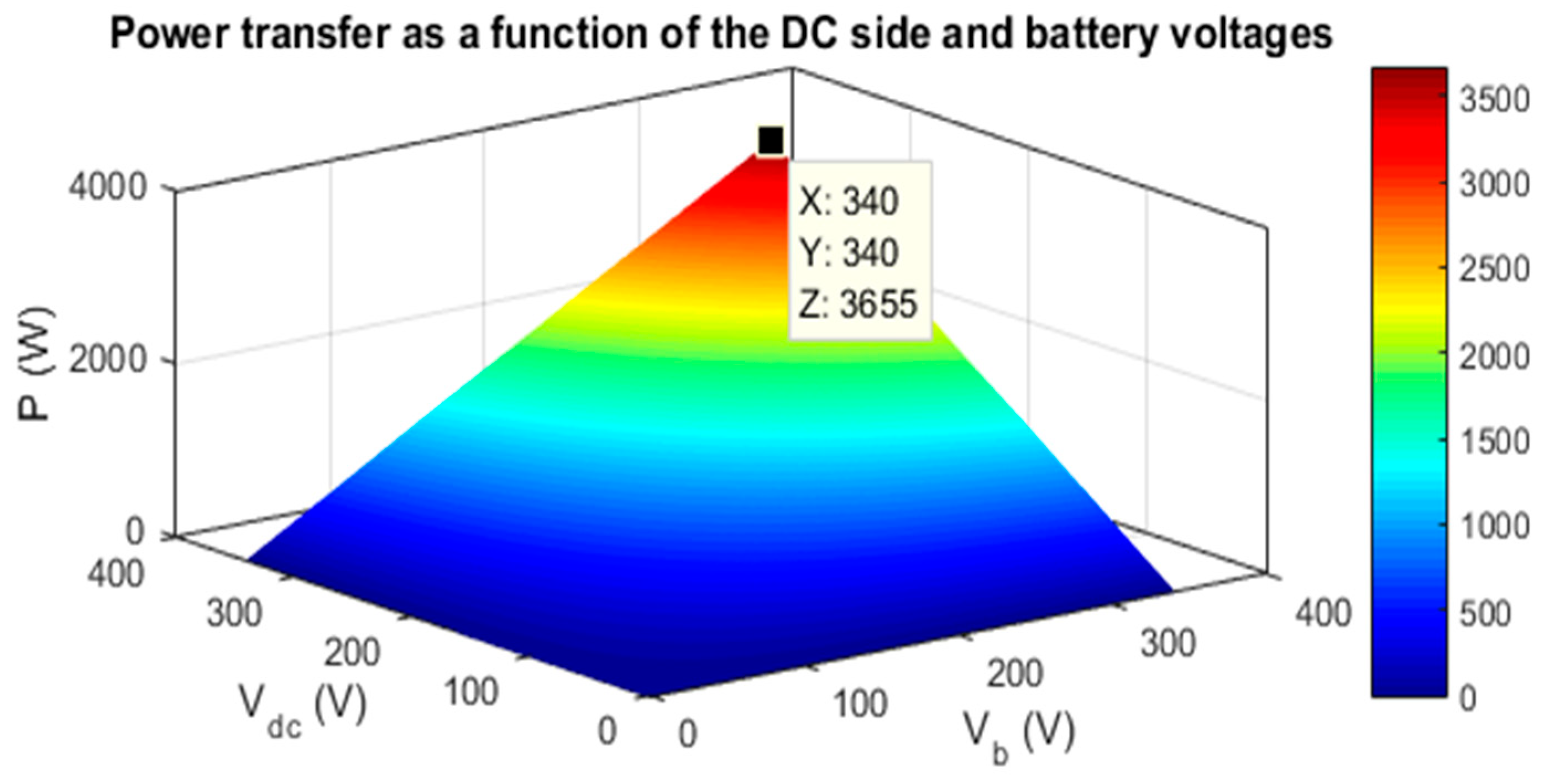
2.5. Effect of the DC Side and Battery Voltages on the Power Transfer
3. Design Steps of WPT Charger
3.1. Step 1: Choice of Ground- and Vehicle-Side Converter Technology
3.2. Step 2: Choice of Control and Communication Boards
3.3. Step 3: Design of Ground- and Vehicle-Side Coils
3.3.1. Conductor Wire Choice for Making Coils
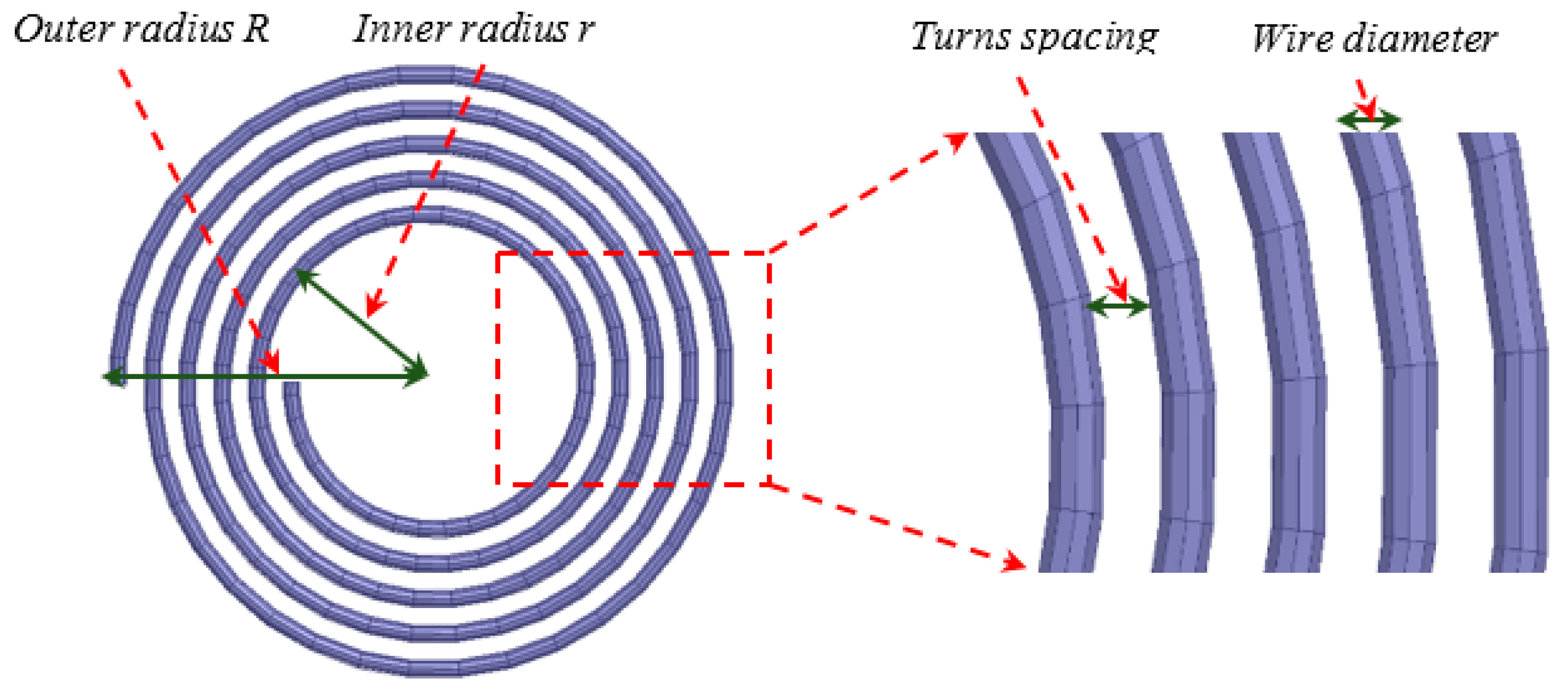
3.3.2. Coil Geometry Choice
3.3.3. Coil Inductance Calculation
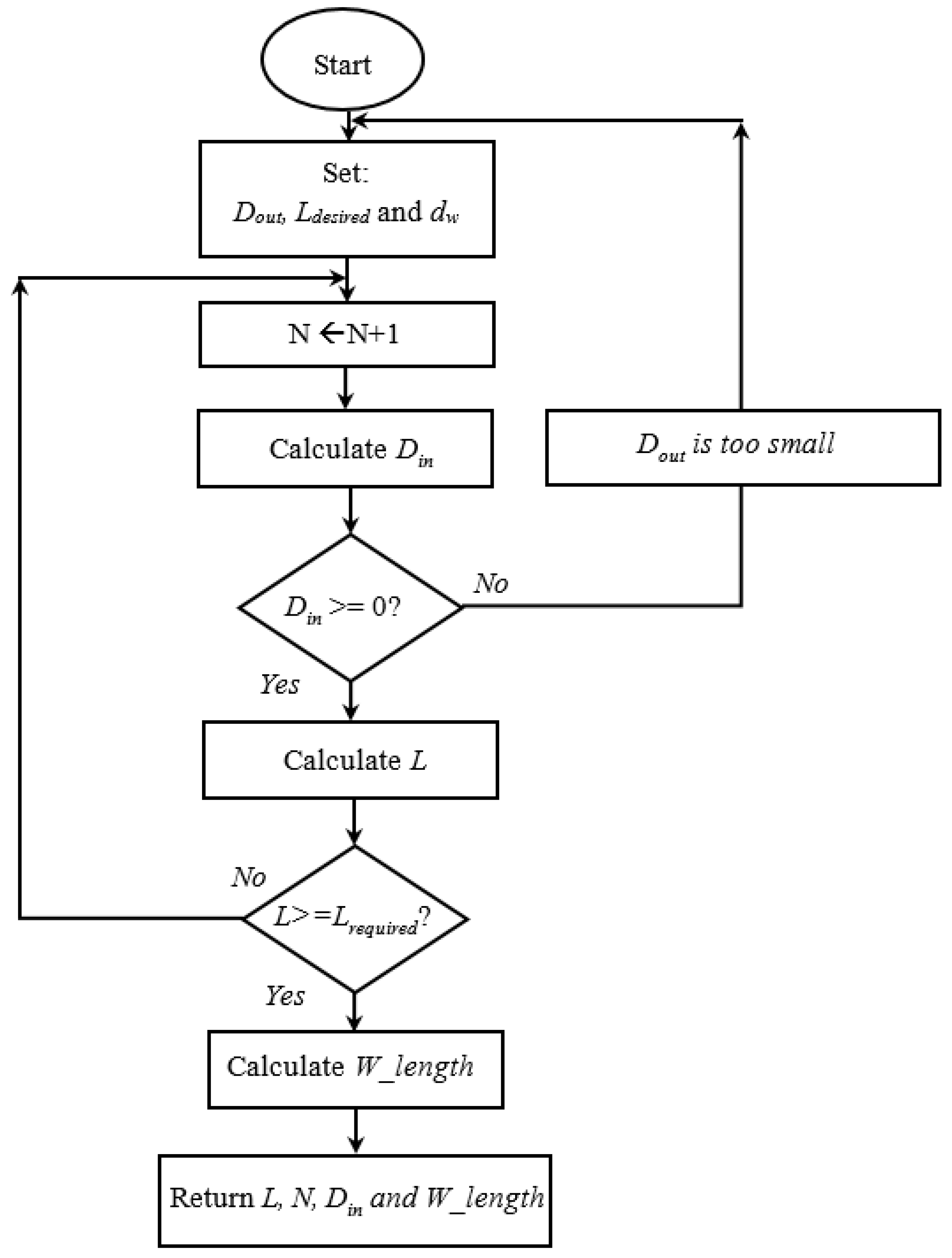
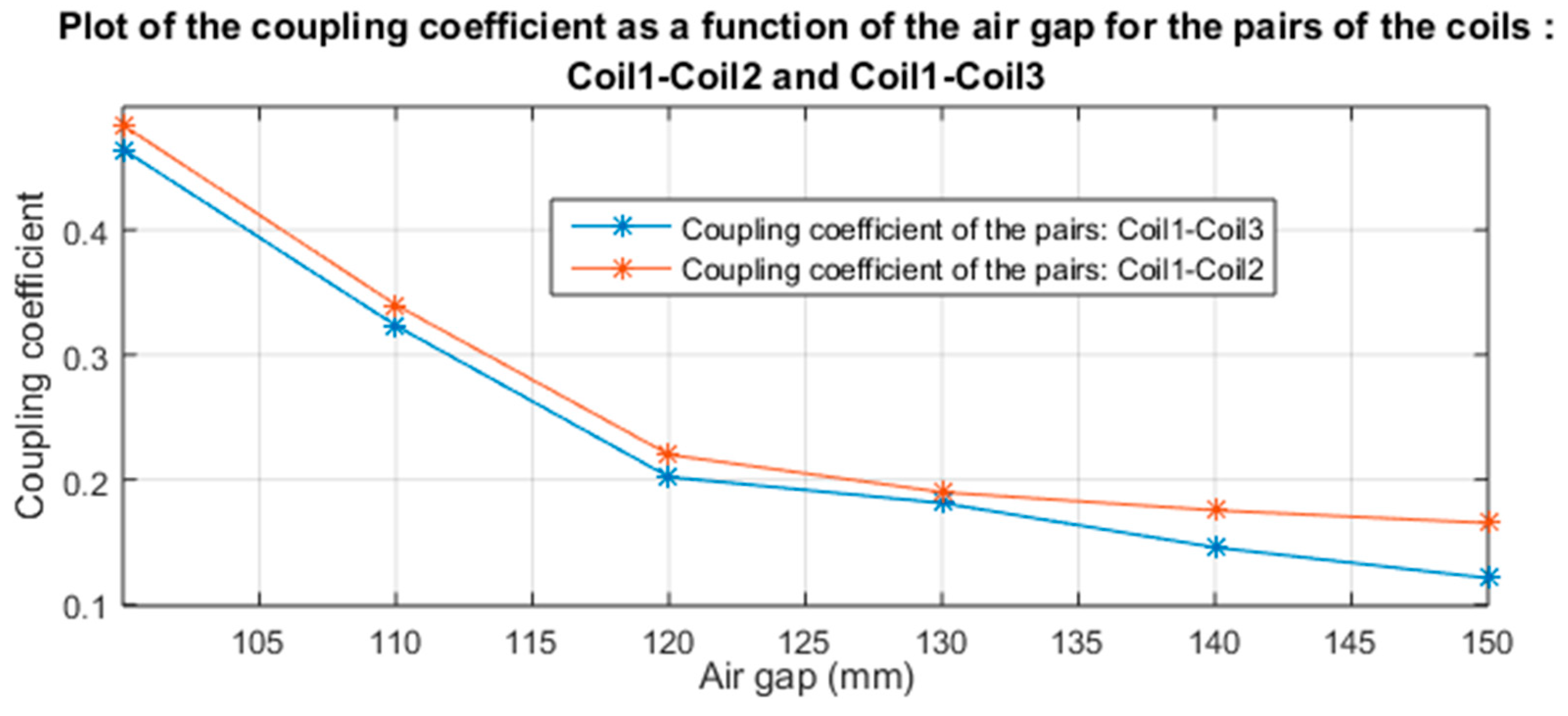
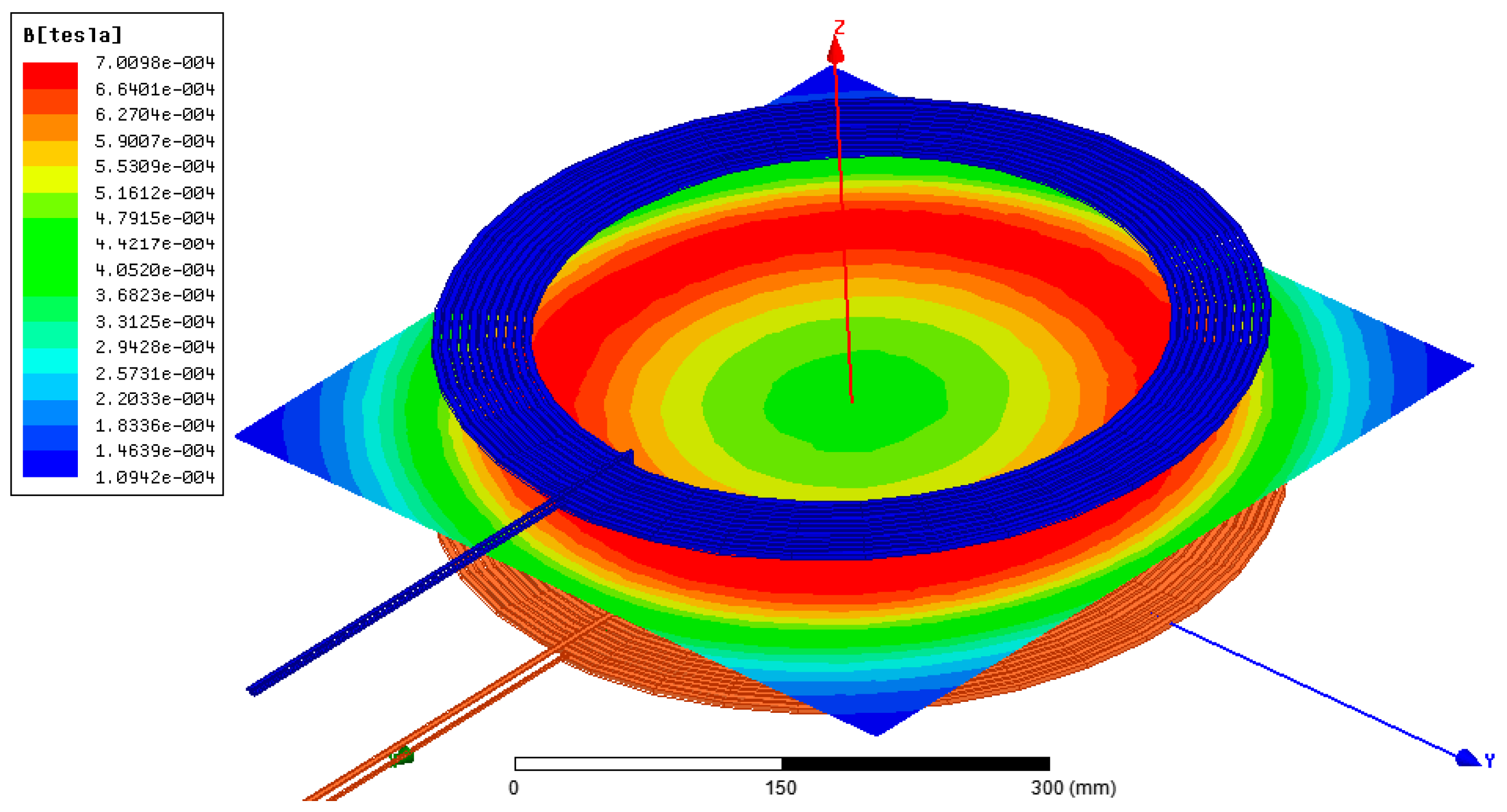
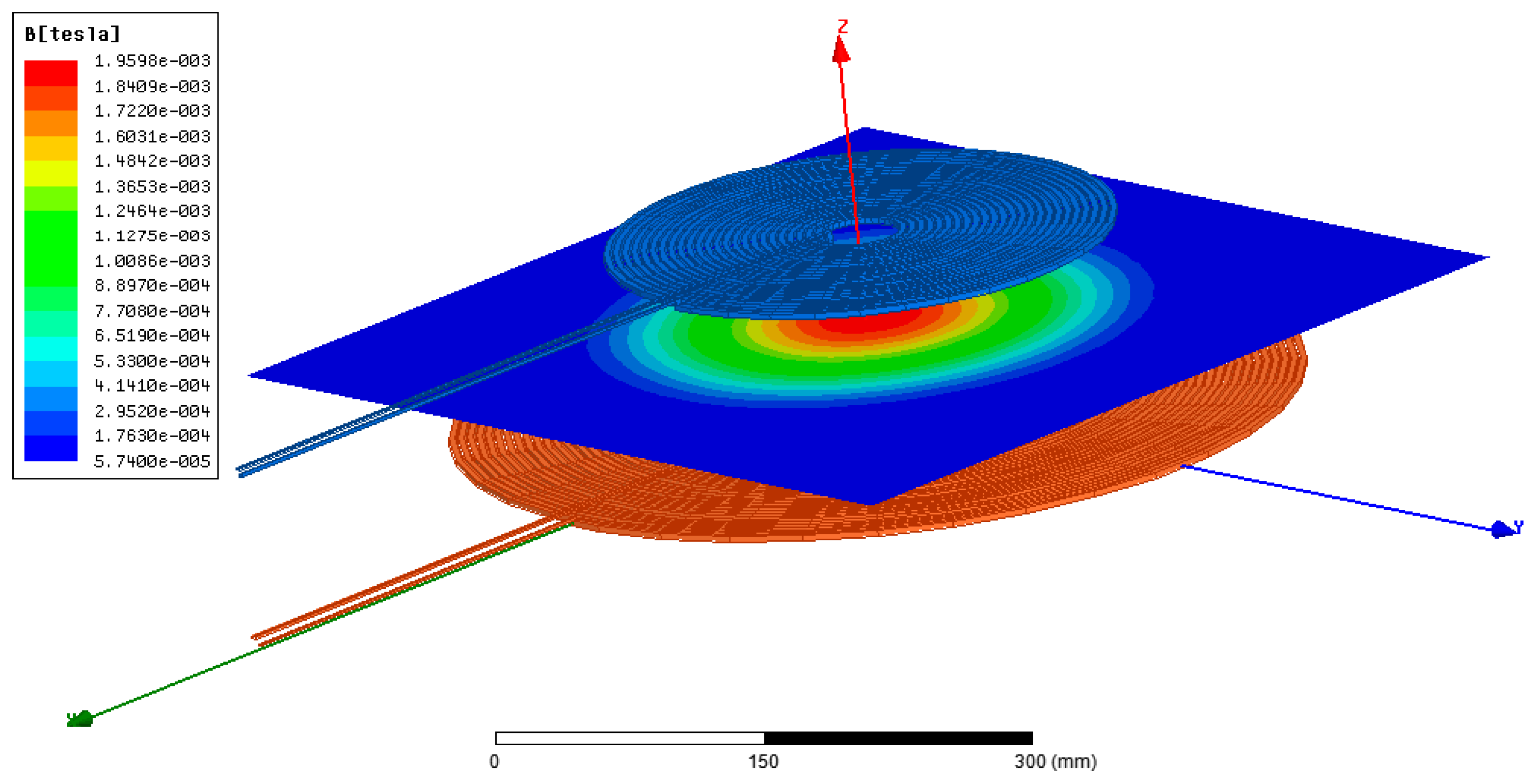
3.3.4. Choice of Parameters, Simulation and Realization of Coils
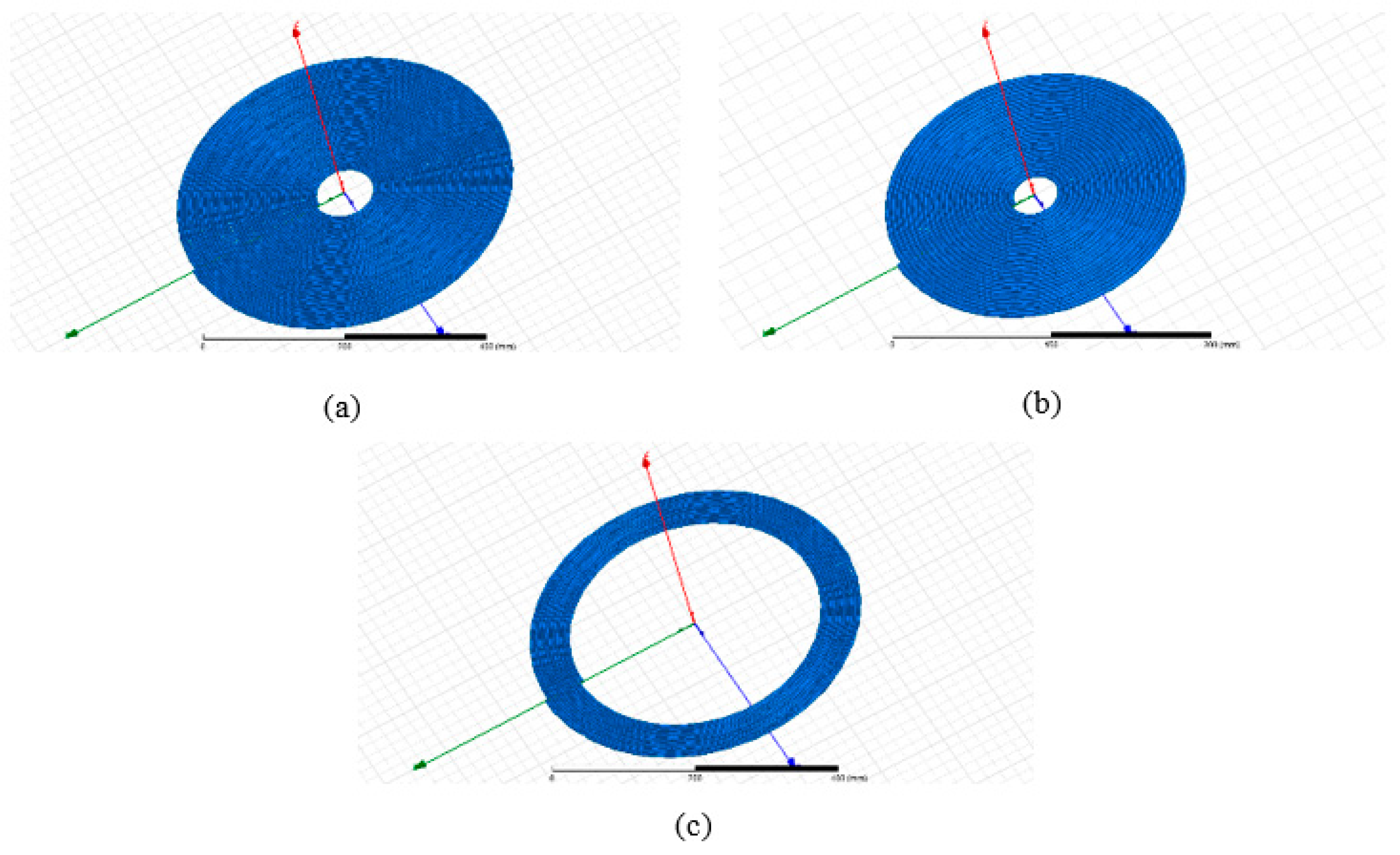
- Coil geometry 1 (hereinafter Coil1): this is the geometry of the ground-side coil. Its outer diameter is set to 48 cm. This choice is justified by the fact that the height of the created magnetic flux is approximately 1/4 of the outer diameter of the coil [23]. With this choice, for a nominal air gap of 12 cm, the coupling between the coils is ensured.
- Coil geometry 2 (hereinafter Coil2): this is the first geometry adopted for the coil on the vehicle side. Its outer diameter is set to 30 cm. The main reason for choosing a smaller diameter is to allow the vehicle-side coil to remain in the area covered by the ground-side coil even in the presence of misalignments.
- Coil geometry 3 (hereinafter Coil3): this is the second geometry adopted for the coil on the vehicle side. Its outer diameter is set to be the same as that of the ground-side coil (48 cm). This choice is justified assuming that the two coils must have the same external diameter so that all of the magnetic field created by the coil on the ground side will be captured by the one on the vehicle side.
3.4. Step 4: Design of Ground- and Vehicle-Side Compensation Boards
4. Experimental Results
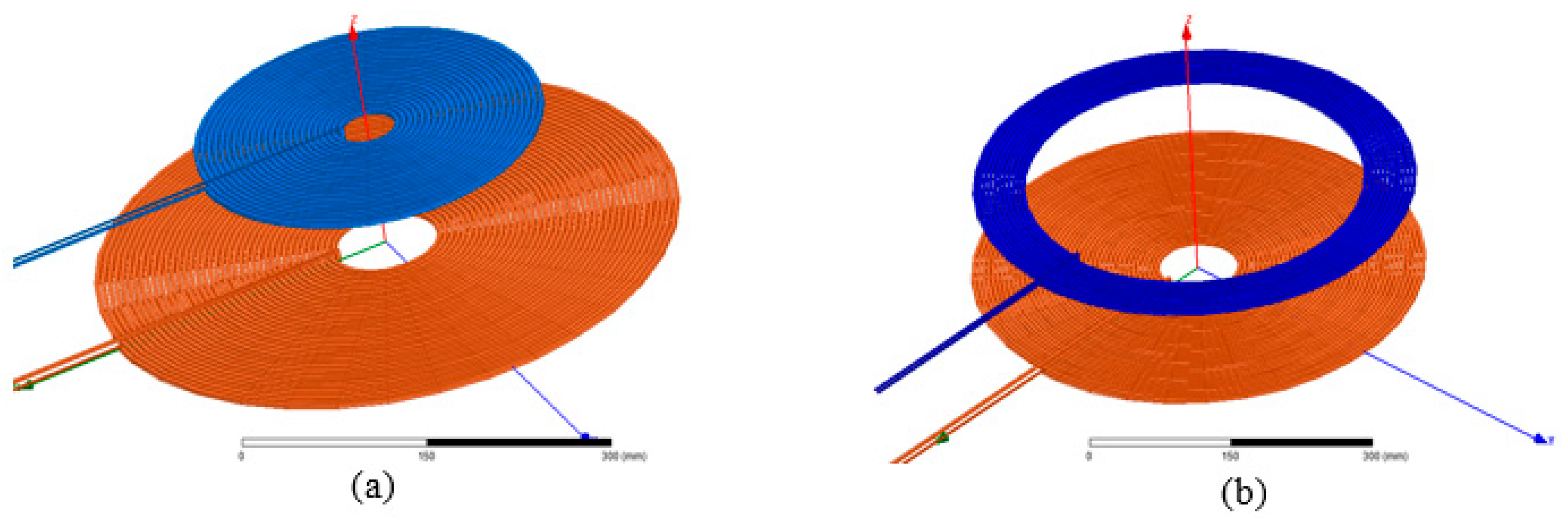
4.1. Test of the Realized Coils
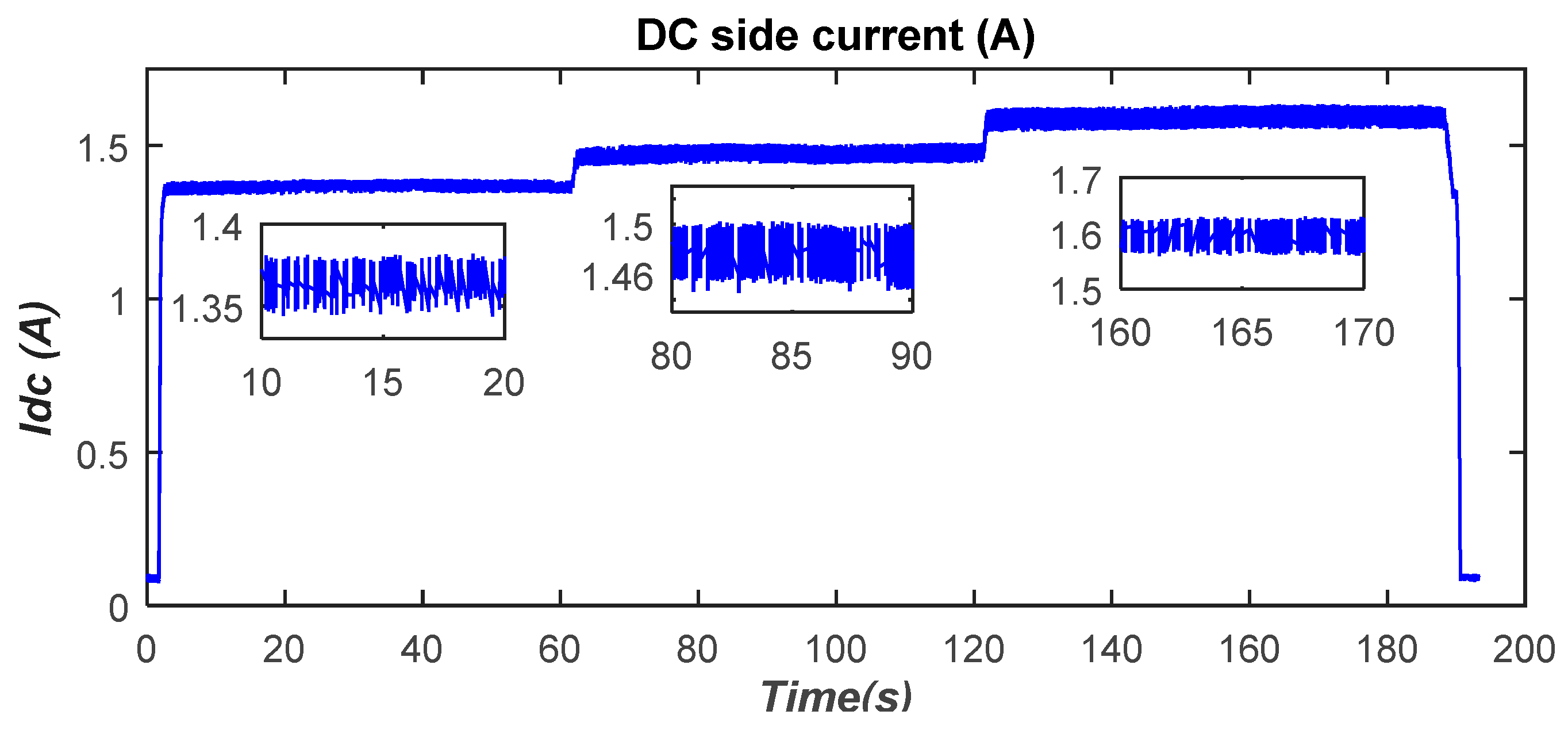
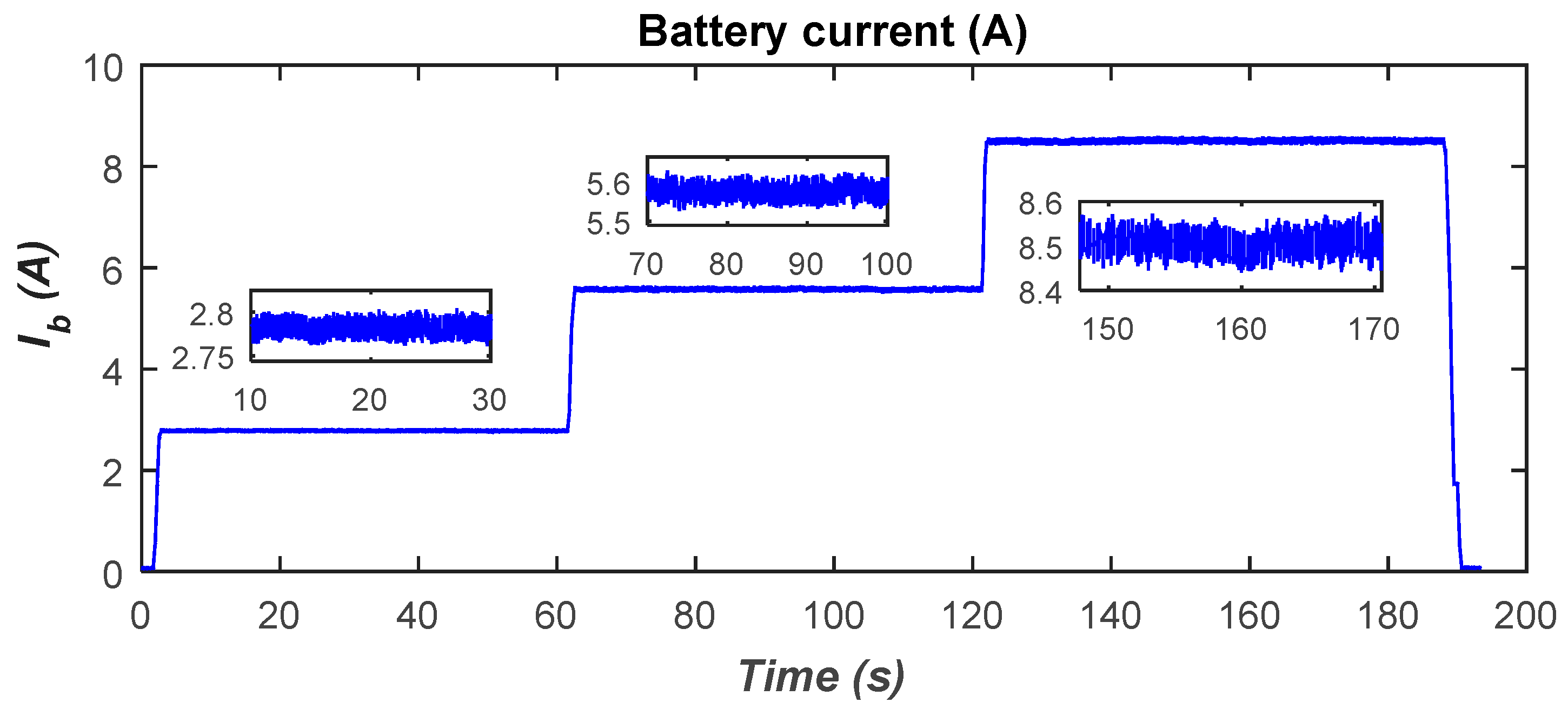
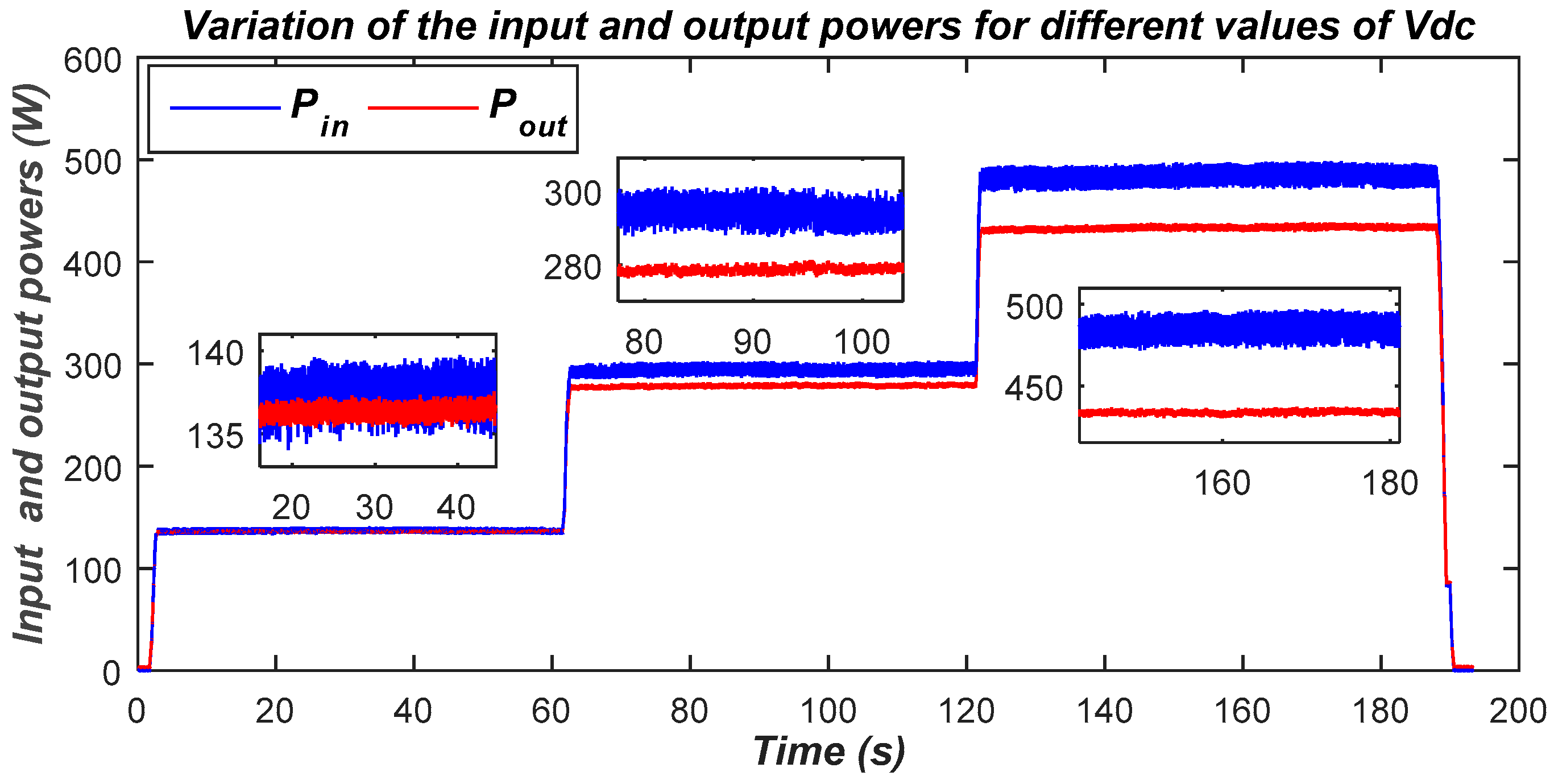
- Scenario 1: The coils are perfectly aligned and spaced from each other with a distance of ΔZ = 12 cm. In this case, a power of 300W is transferred from the ground side to the vehicle side; thus, the obtained power transfer efficiency is 95% for the pair of coils Coil1–Coil2, while that of Coil1–Coil3 is 89.5%.
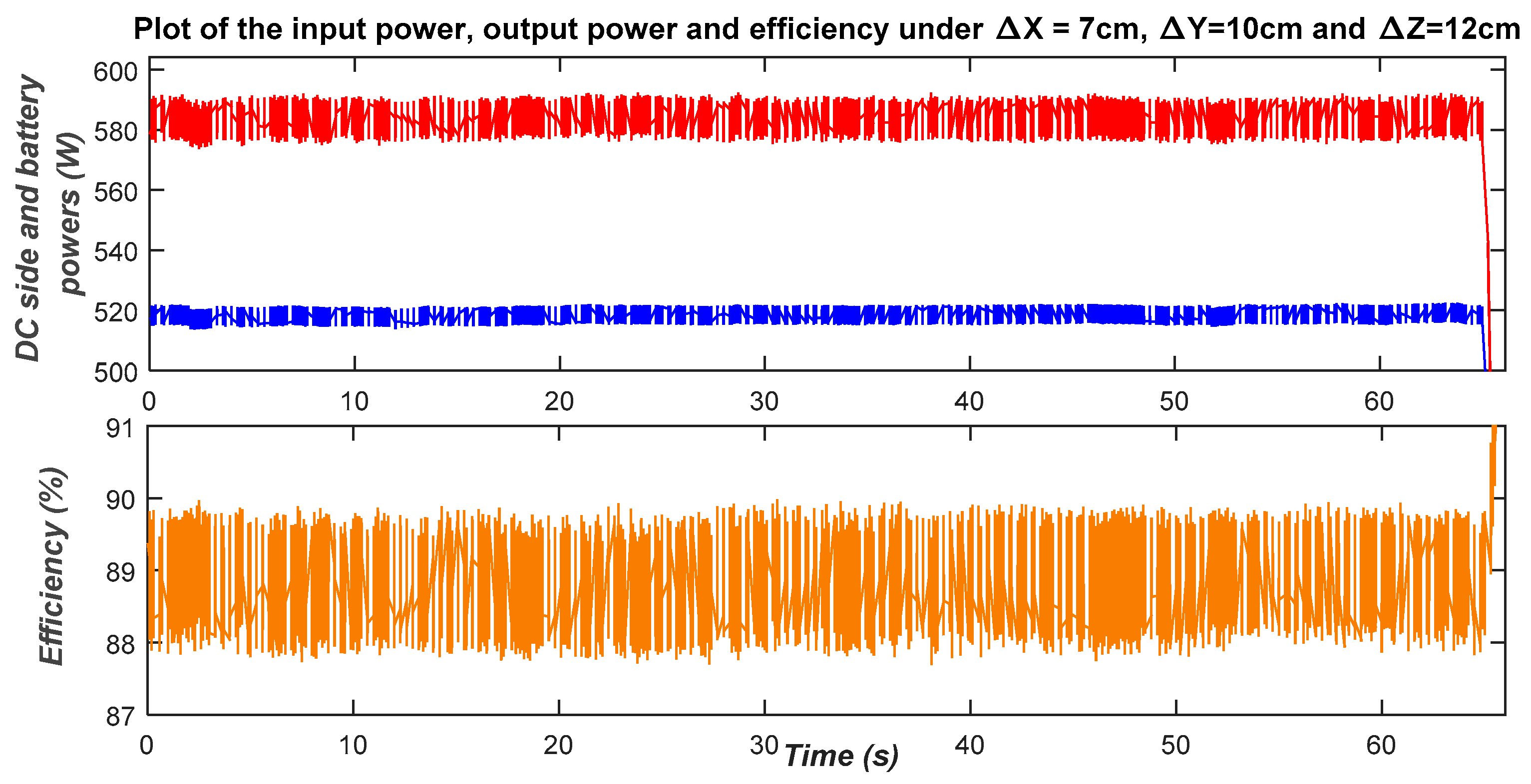
- Scenario 2: The coils are laterally misaligned in both directions (ΔX = 7 cm and ΔY = 10 cm) while the air gap between the coils is maintained at ΔZ = 12 cm. In this case, a power of 500 W is transferred from the ground side to the vehicle side; thus, the obtained power transfer efficiency is 89% for the pair of coils Coil1–Coil2, while that of Coil1–Coil3 is 78%.
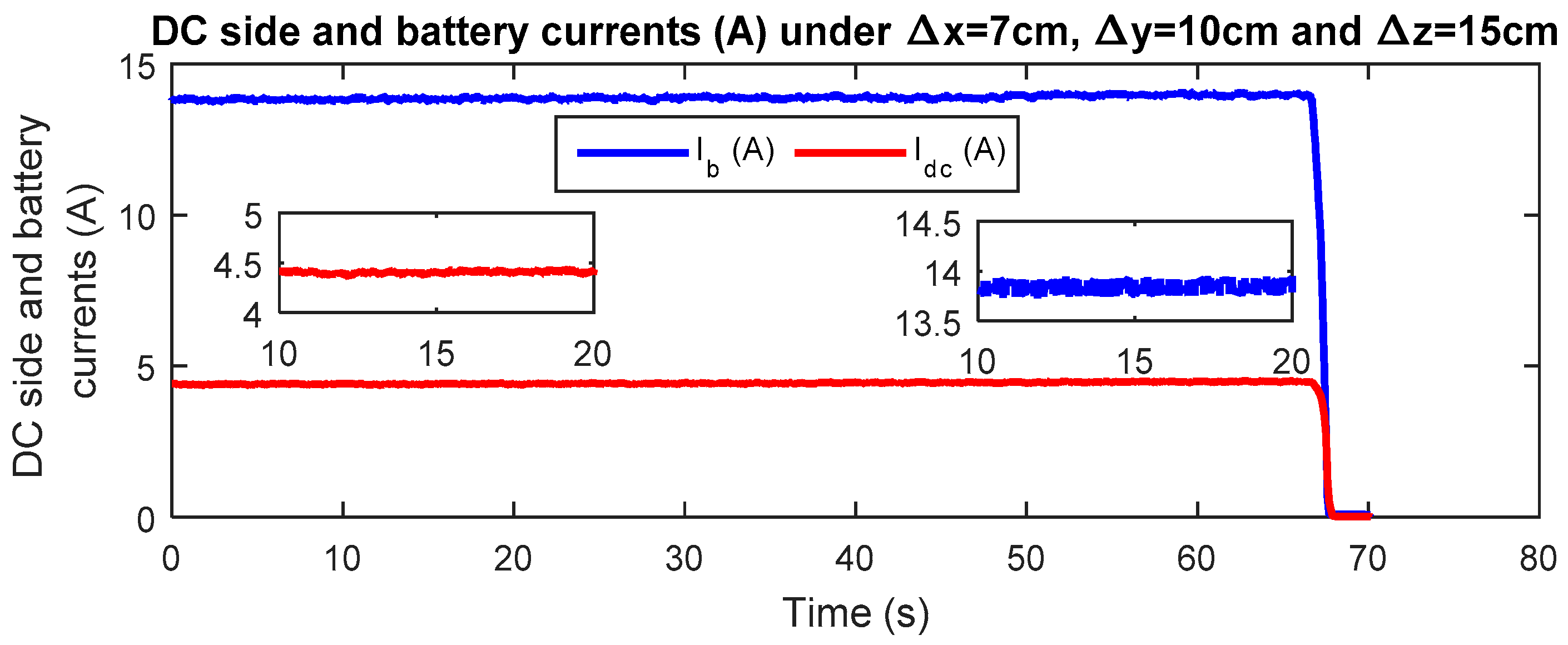
- Case 3: The air gap is maintained at its maximum (ΔZ = 15 cm) and the coils are misaligned in both directions (ΔX = 7 cm and ΔY = 10 cm). In this case, a power of 900 W is transferred from the ground side to the vehicle side; thus, the obtained power transfer efficiency is 83.5% for the pair of coils Coil1–Coil2, while that of Coil1–Coil3 is 72%.
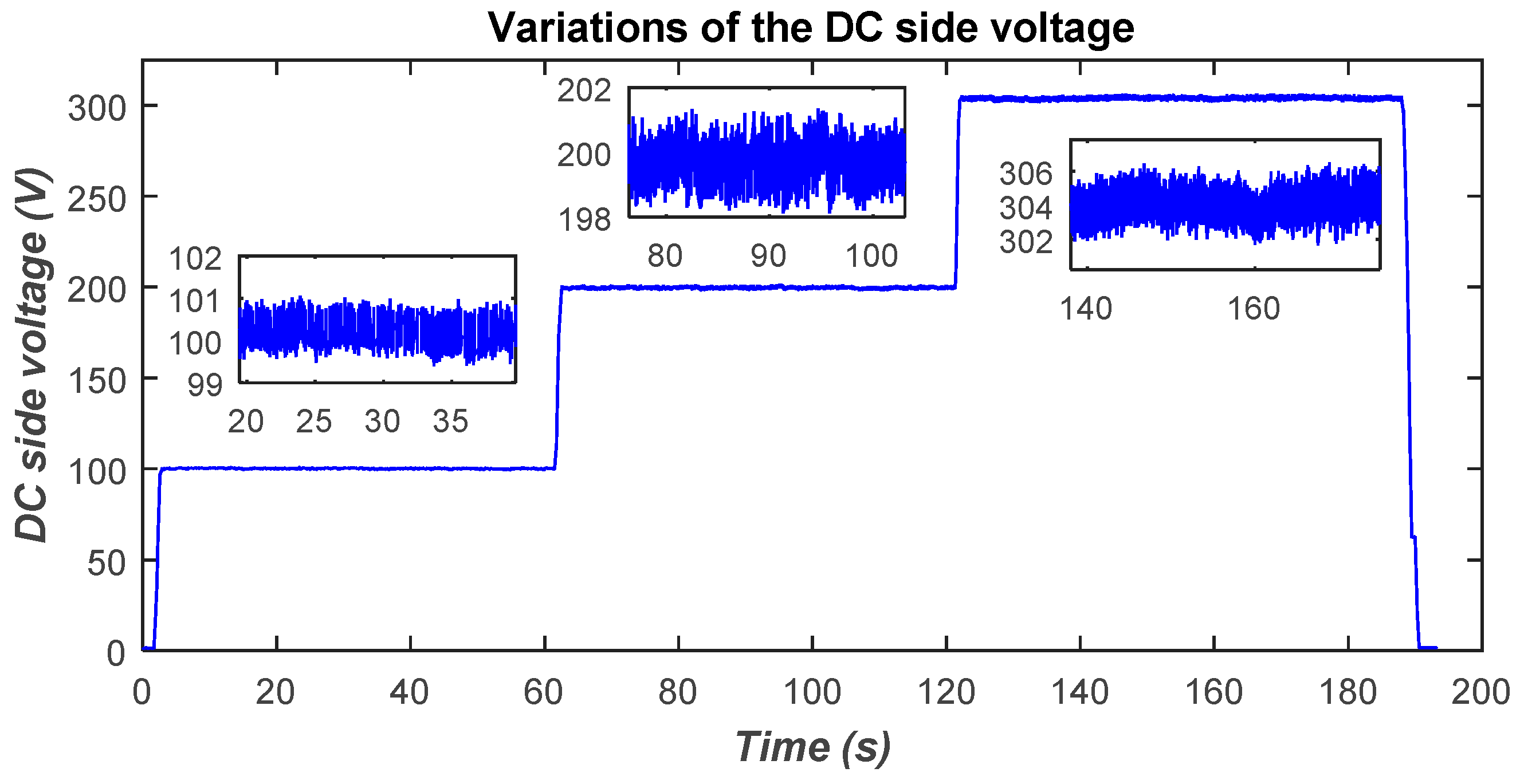
4.2. Effect of Variation of DC Side Voltage on Power Transfer
4.3. Effect Misalignments on Power Transfer
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Unterluggauer, T.; Rich, J.; Andersen, P.B.; Hashemi, S. Electric vehicle charging infrastructure planning for integrated transportation and power distribution networks: A review. eTransportation 2022, 12, 100163. [Google Scholar] [CrossRef]
- Lassioui, A.; El Fadil, H.; Belhaj, F.Z.; Rachid, A. Battery Charger for Electric Vehicles Based ICPT and CPT—A State of the Art. In Proceedings of the 2018 Renewable Energies, Power Systems Green Inclusive Economy (REPS-GIE), Casablanca, Morocco, 23–24 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Shareef, H.; Islam, M.; Mohamed, A. A review of the stage-of-the-art charging technologies, placement methodologies, and impacts of electric vehicles. Renew. Sustain. Energy Rev. 2016, 64, 403–420. [Google Scholar] [CrossRef]
- Gnann, T.; Funke, S.; Jakobsson, N.; Plötz, P.; Sprei, F.; Bennehag, A. Fast charging infrastructure for electric vehicles: Today’s situation and future needs. Transp. Res. Part Transp. Environ. 2018, 62, 314–329. [Google Scholar] [CrossRef]
- Biresselioglu, M.E.; Demirbag Kaplan, M.; Yilmaz, B.K. Electric mobility in Europe: A comprehensive review of motivators and barriers in decision making processes. Transp. Res. Part Policy Pract. 2018, 109, 1–13. [Google Scholar] [CrossRef]
- Bouanou, T.; El Fadil, H.; Lassioui, A.; Assaddiki, O.; Njili, S. Analysis of Coil Parameters and Comparison of Circular, Rectangular, and Hexagonal Coils Used in WPT System for Electric Vehicle Charging. World Electr. Veh. J. 2021, 12, 45. [Google Scholar] [CrossRef]
- Lukic, S.M.; Pantic, Z. Cutting the Cord: Static and Dynamic Inductive Wireless Charging of Electric Vehicles. Electrif. Mag. IEEE 2013, 1, 57–64. [Google Scholar] [CrossRef]
- Jayalath, S.; Khan, A. Design, Challenges, and Trends of Inductive Power Transfer Couplers for Electric Vehicles: A Review. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6196–6218. [Google Scholar] [CrossRef]
- Hwang, Y.J.; Kim, J.M. A Double Helix Flux Pipe-Based Inductive Link for Wireless Charging of Electric Vehicles. World Electr. Veh. J. 2020, 11, 33. [Google Scholar] [CrossRef] [Green Version]
- Zimmer, S.; Helwig, M.; Lucas, P.; Winkler, A.; Modler, N. Investigation of Thermal Effects in Different Lightweight Constructions for Vehicular Wireless Power Transfer Modules. World Electr. Veh. J. 2020, 11, 67. [Google Scholar] [CrossRef]
- Berger, A.; Agostinelli, M.; Vesti, S.; Oliver, J.A.; Cobos, J.A.; Huemer, M. A Wireless Charging System Applying Phase-Shift and Amplitude Control to Maximize Efficiency and Extractable Power. IEEE Trans. Power Electron. 2015, 30, 6338–6348. [Google Scholar] [CrossRef]
- Mahesh, A.; Chokkalingam, B.; Mihet-Popa, L. Inductive Wireless Power Transfer Charging for Electric Vehicles—A Review. IEEE Access 2021, 9, 137667–137713. [Google Scholar] [CrossRef]
- Lassioui, A.; Fadil, H.E.; Rachid, A.; El-Idrissi, Z.; Bouanou, T.; Belhaj, F.Z.; Giri, F. Modelling and sliding mode control of a wireless power transfer system for BEV charger. Int. J. Model. Identif. Control 2020, 34, 171–186. [Google Scholar] [CrossRef]
- Lassioui, A.; El Fadil, H.; Rachid, A.; Bouanou, T.; Giri, F. Adaptive Output Feedback Nonlinear Control of a Wireless Power Transfer Charger for Battery Electric Vehicle. J. Control Autom. Electr. Syst. 2021, 32, 492–506. [Google Scholar] [CrossRef]
- Aditya, K.; Williamson, S.S. Design Guidelines to Avoid Bifurcation in a Series–Series Compensated Inductive Power Transfer System. IEEE Trans. Ind. Electron. 2019, 66, 3973–3982. [Google Scholar] [CrossRef]
- Wang, C.-S.; Covic, G.A.; Stielau, O.H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems. IEEE Trans. Ind. Electron. 2004, 51, 148–157. [Google Scholar] [CrossRef]
- Gallium Nitride (GaN) versus Silicon Carbide (SiC). Available online: https://www.richardsonrfpd.com/docs/rfpd/Microsemi-A-Comparison-of-Gallium-Nitride-Versus-Silicon-Carbide.pdf (accessed on 28 August 2020).
- TMDSCNCD28335 Daughter Card|TI.com. Available online: https://www.ti.com/tool/TMDSCNCD28335 (accessed on 20 September 2021).
- Kim, H.; Song, C.; Kim, D.-H.; Jung, D.H.; Kim, I.-M.; Kim, Y.-I.; Kim, J.; Ahn, S.; Kim, J. Coil Design and Measurements of Automotive Magnetic Resonant Wireless Charging System for High-Efficiency and Low Magnetic Field Leakage. IEEE Trans. Microw. Theory Tech. 2016, 64, 383–400. [Google Scholar] [CrossRef]
- Luo, Z.; Wei, X. Mutual Inductance Analysis of Planar Coils with Misalignment for Wireless Power Transfer Systems in Electric Vehicle. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Bouanou, T.; Fadil, H.E.; Lassioui, A. Analysis and Design of Circular Coil Transformer in a Wireless Power Transfer System for Electric Vehicle Charging Application. In Proceedings of the 2020 International Conference on Electrical and Information Technologies (ICEIT), Rabat, Morocco, 7–7 March 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Buja, G.; Bertoluzzo, M.; Mude, K.N. Design and Experimentation of WPT Charger for Electric City Car. IEEE Trans. Ind. Electron. 2015, 62, 7436–7447. [Google Scholar] [CrossRef]
- Aditya, K. Design and Implementation of an Inductive Power Transfer System for Wireless Charging of Future Electric Transportation. Ph.D. Thesis, University of Ontario Institute of Technology, Oshawa, ON, Canada, 2016. Available online: http://ir.library.dc-uoit.ca/handle/10155/712 (accessed on 14 September 2014).












| Parameter | Value |
|---|---|
| Req | 12 Ω |
| L1 | 416 µH |
| L2 | 116 µH |
| r1 | 0.5 Ω |
| r2 | 0.1 Ω |
| Parameter | Value |
|---|---|
| Power (P) | 500 W |
| Maximum DC side voltage (Vdc) | 300 V |
| Nominal battery voltage (Vb) | 48 V |
| Power transfer frequency (fsw) | 85 kHz |
| Minimum efficiency (in presence of misalignments) | 80% |
| Required mutual inductance (M) | 44 µH |
| Air-gap distance | 100–150 mm |
| Coil1 | Coil2 | Coil3 |
|---|---|---|
|
|
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bentalhik, I.; Lassioui, A.; EL Fadil, H.; Bouanou, T.; Rachid, A.; EL Idrissi, Z.; Hamed, A.M. Analysis, Design and Realization of a Wireless Power Transfer Charger for Electric Vehicles: Theoretical Approach and Experimental Results. World Electr. Veh. J. 2022, 13, 121. https://doi.org/10.3390/wevj13070121
Bentalhik I, Lassioui A, EL Fadil H, Bouanou T, Rachid A, EL Idrissi Z, Hamed AM. Analysis, Design and Realization of a Wireless Power Transfer Charger for Electric Vehicles: Theoretical Approach and Experimental Results. World Electric Vehicle Journal. 2022; 13(7):121. https://doi.org/10.3390/wevj13070121
Chicago/Turabian StyleBentalhik, Issam, Abdellah Lassioui, Hassan EL Fadil, Tasnime Bouanou, Aziz Rachid, Zakariae EL Idrissi, and Ahmed Mohamed Hamed. 2022. "Analysis, Design and Realization of a Wireless Power Transfer Charger for Electric Vehicles: Theoretical Approach and Experimental Results" World Electric Vehicle Journal 13, no. 7: 121. https://doi.org/10.3390/wevj13070121
APA StyleBentalhik, I., Lassioui, A., EL Fadil, H., Bouanou, T., Rachid, A., EL Idrissi, Z., & Hamed, A. M. (2022). Analysis, Design and Realization of a Wireless Power Transfer Charger for Electric Vehicles: Theoretical Approach and Experimental Results. World Electric Vehicle Journal, 13(7), 121. https://doi.org/10.3390/wevj13070121










