Modeling and Simulation of Traction Power Supply System for High-Speed Maglev Train
Abstract
:1. Introduction
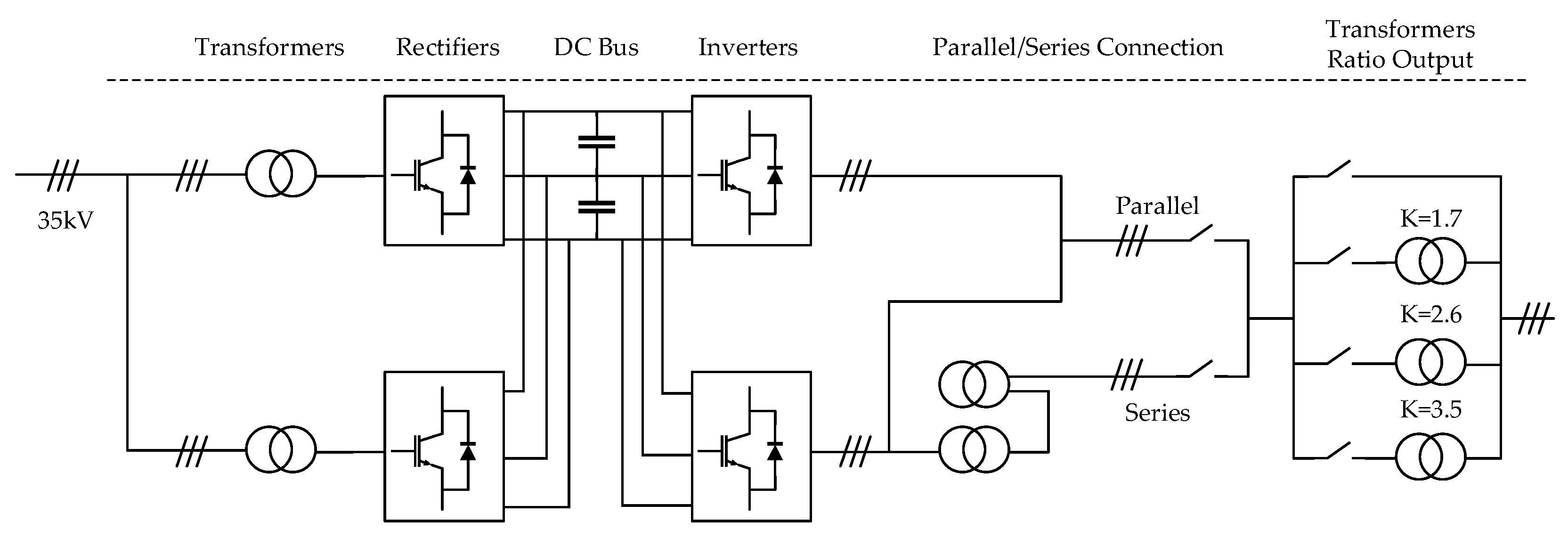
2. Traction Power Supply Simulation Model
2.1. Converter Model
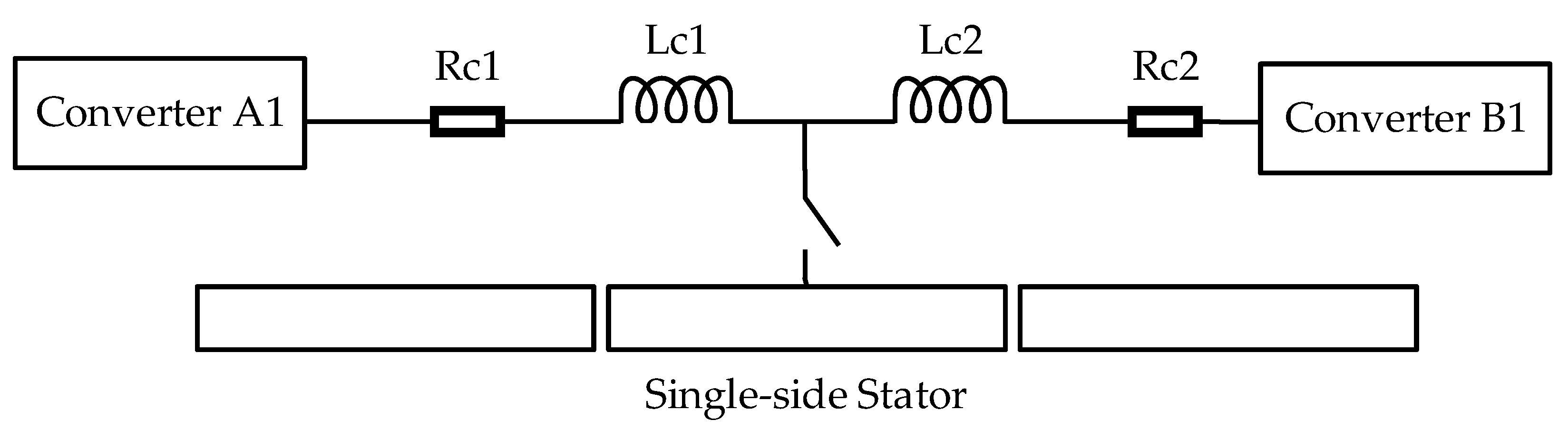
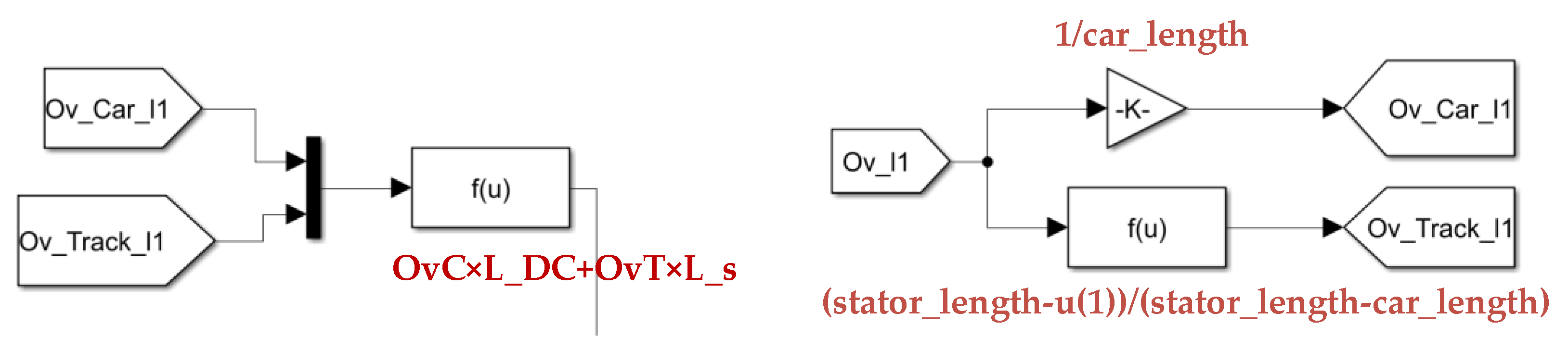
2.2. Variable-Length Cable Model
2.3. Long Stator Linear Synchronous Motor (LLSM) Model
2.3.1. Introduction of Motor Model
2.3.2. Motor Modeling Method
3. Traction Power Supply System Control Strategy
3.1. Single Motor Control Strategy
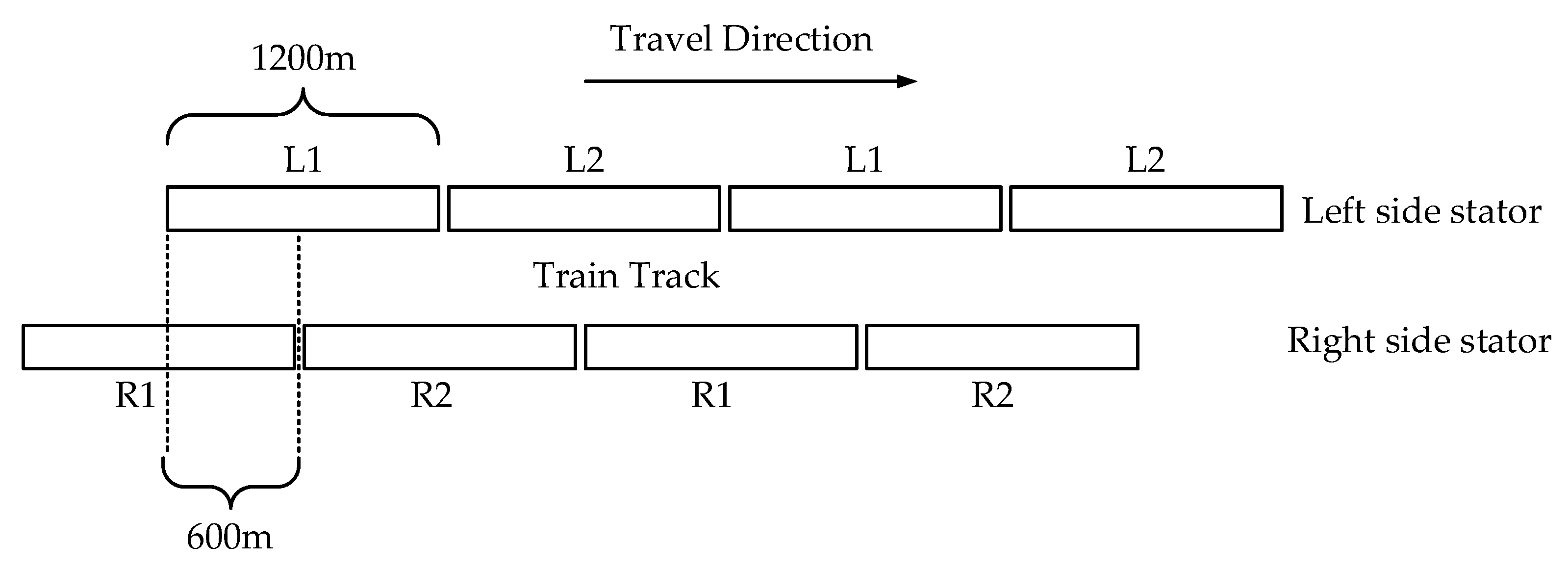
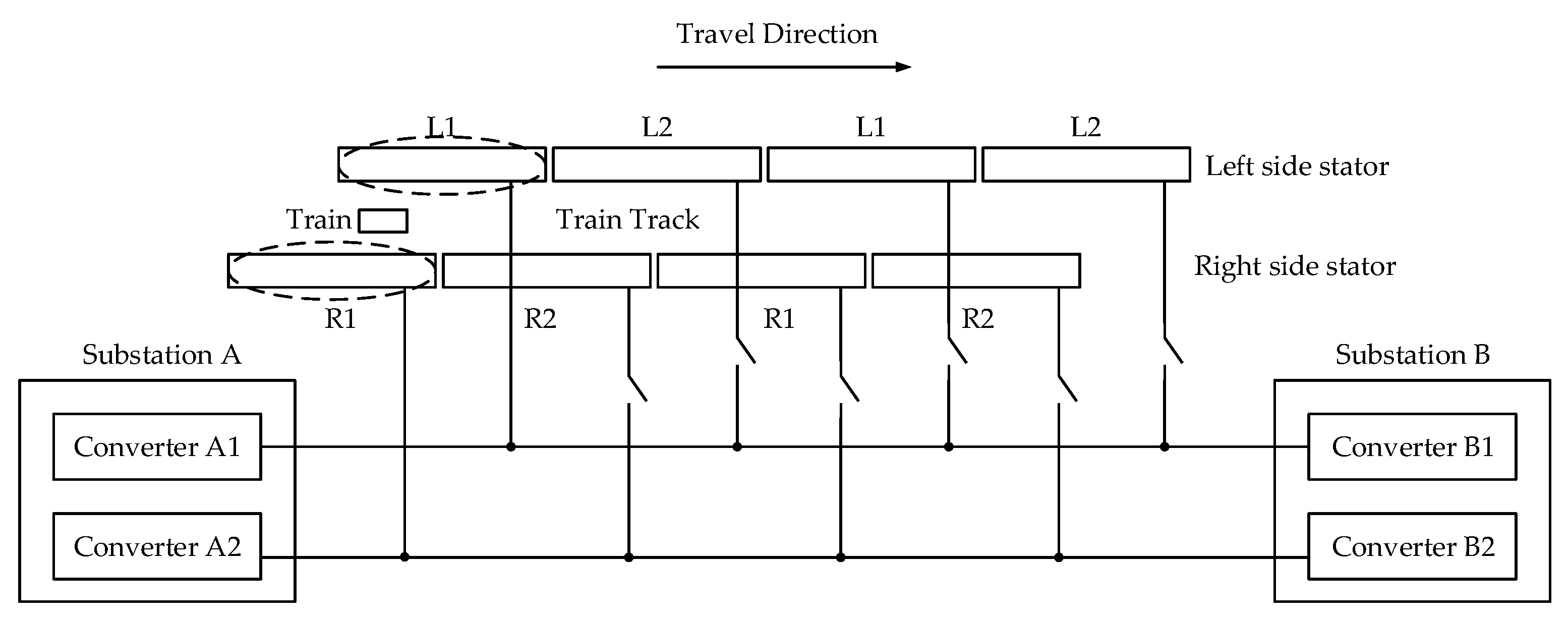
3.2. Stator Segmented Power Supply Method
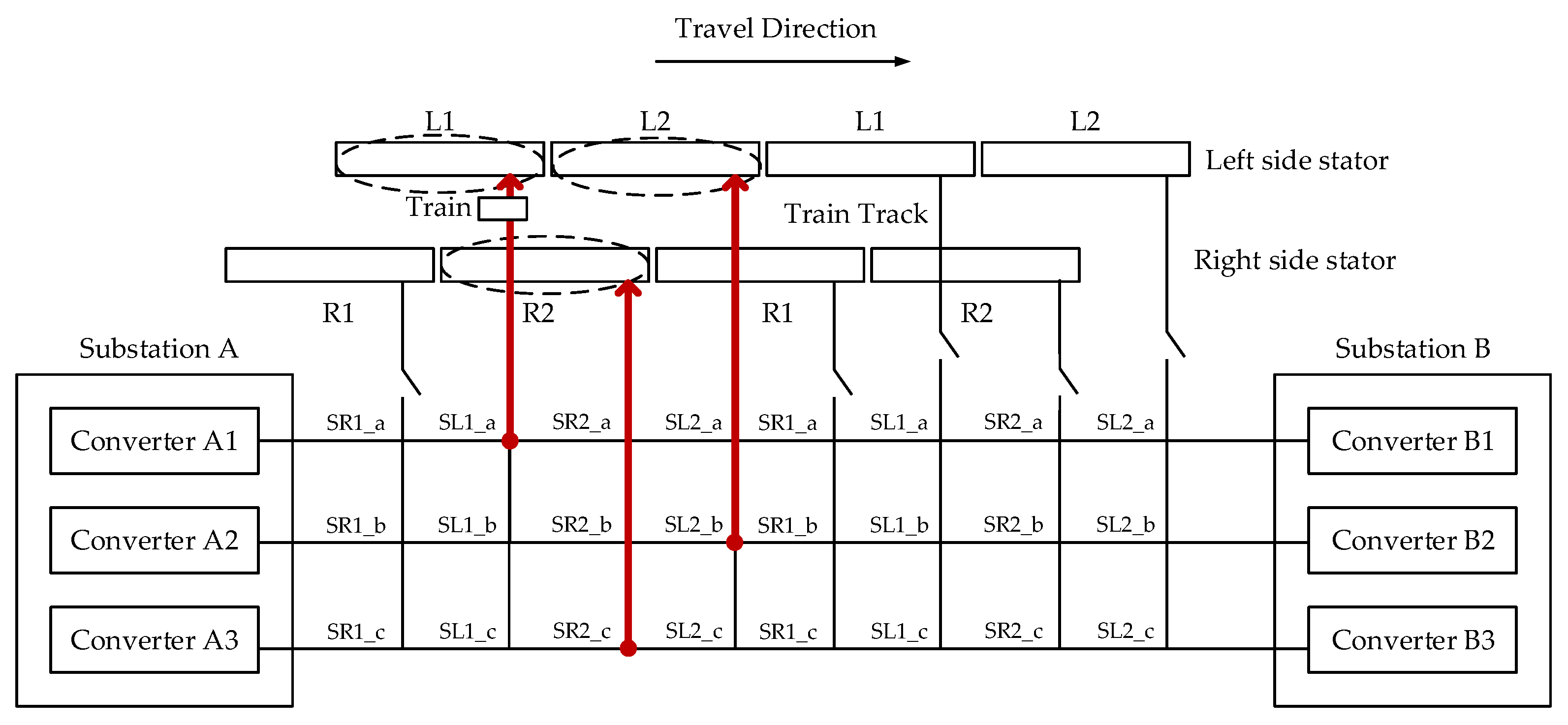
3.2.1. Two-Step Method
3.2.2. Three-Step Method
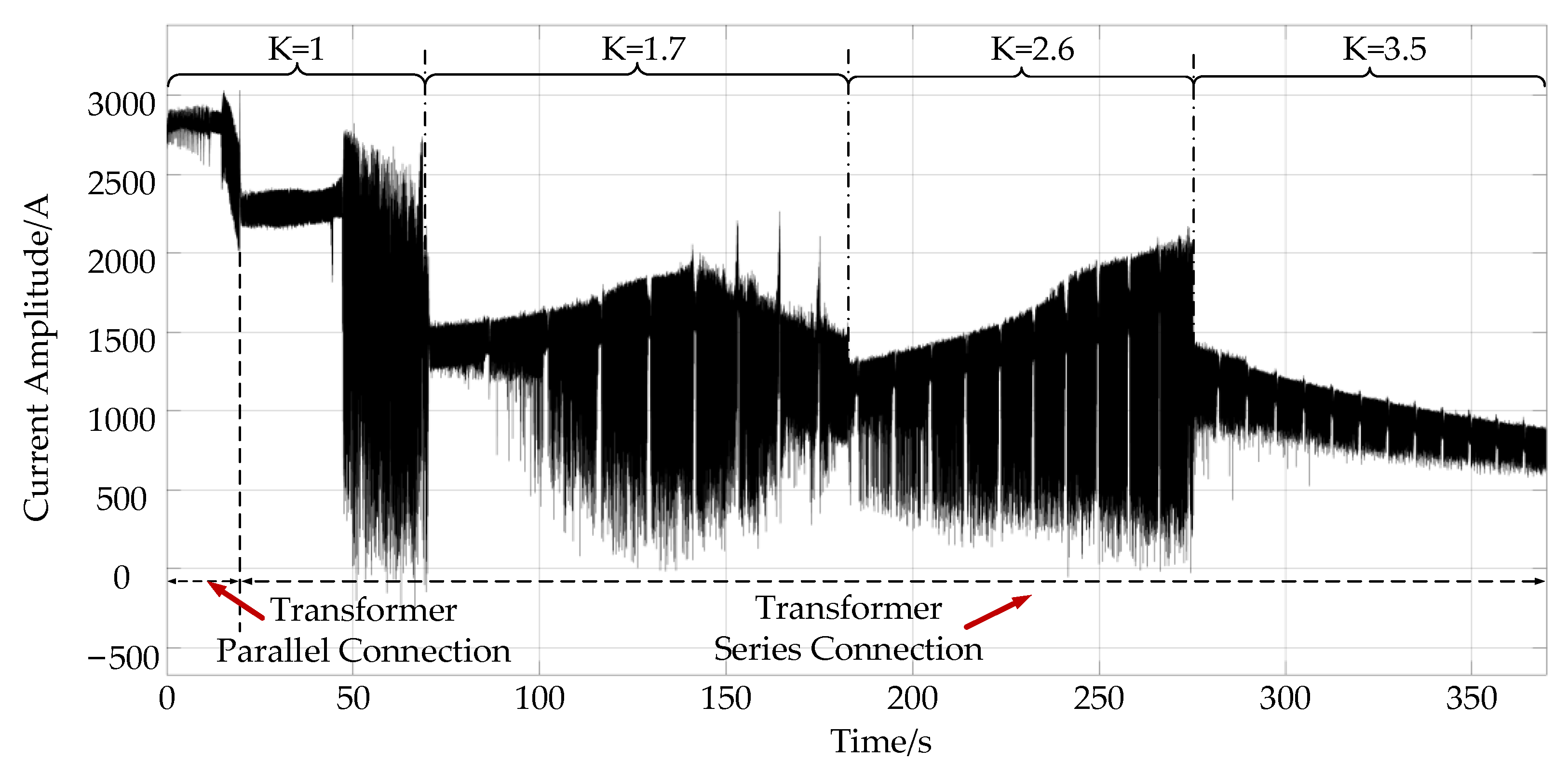
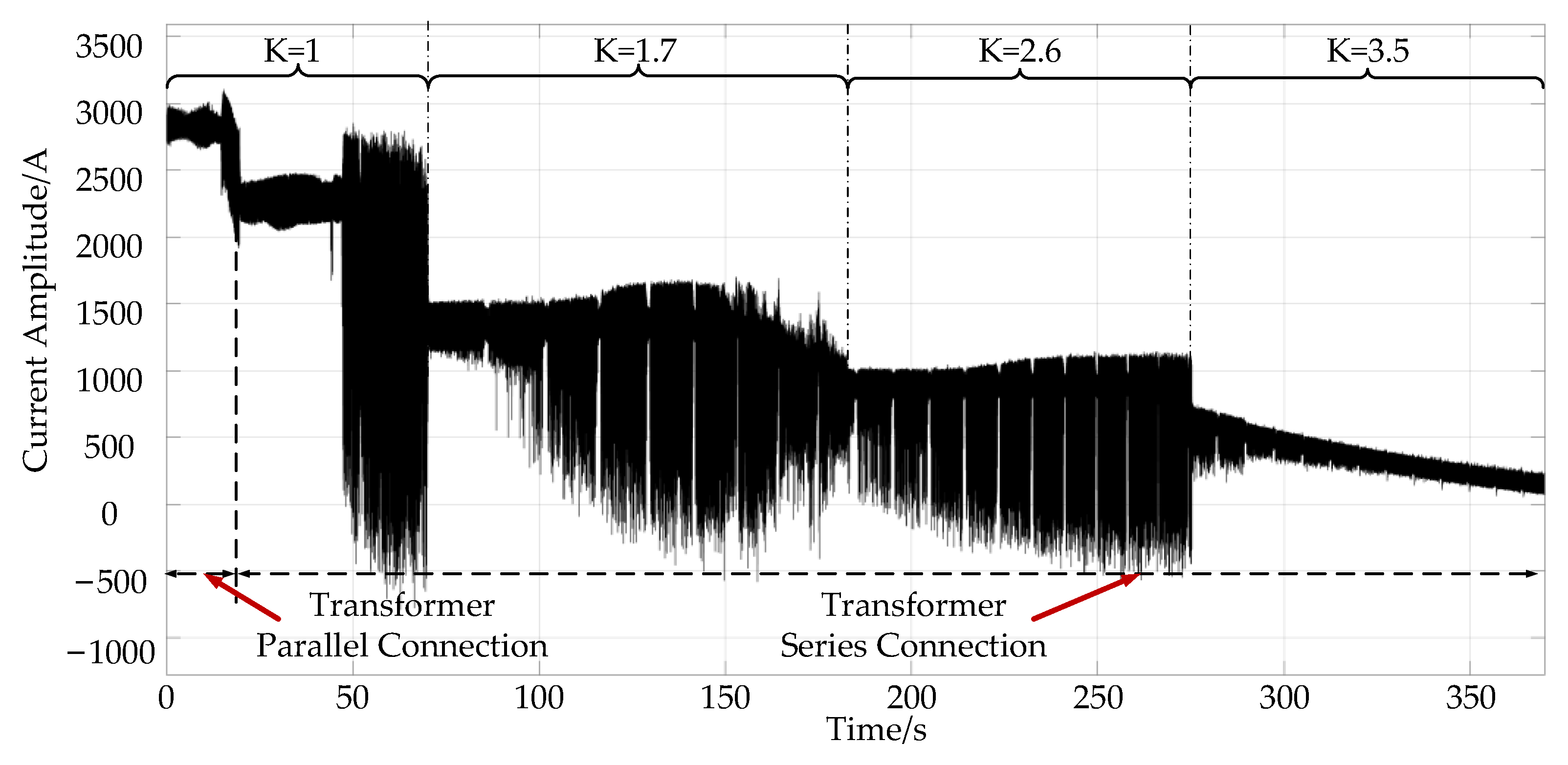
4. Models Simulation Results
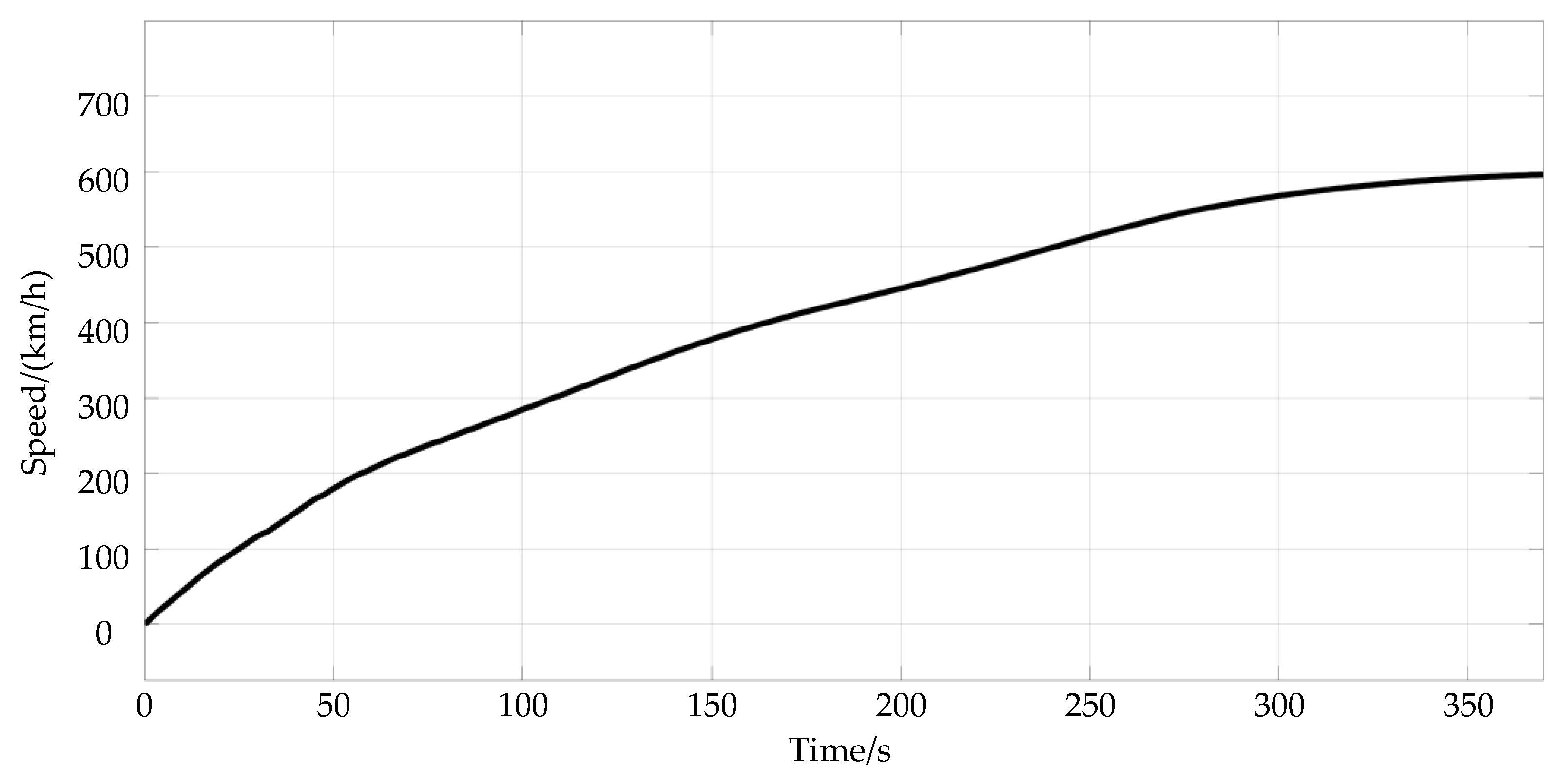
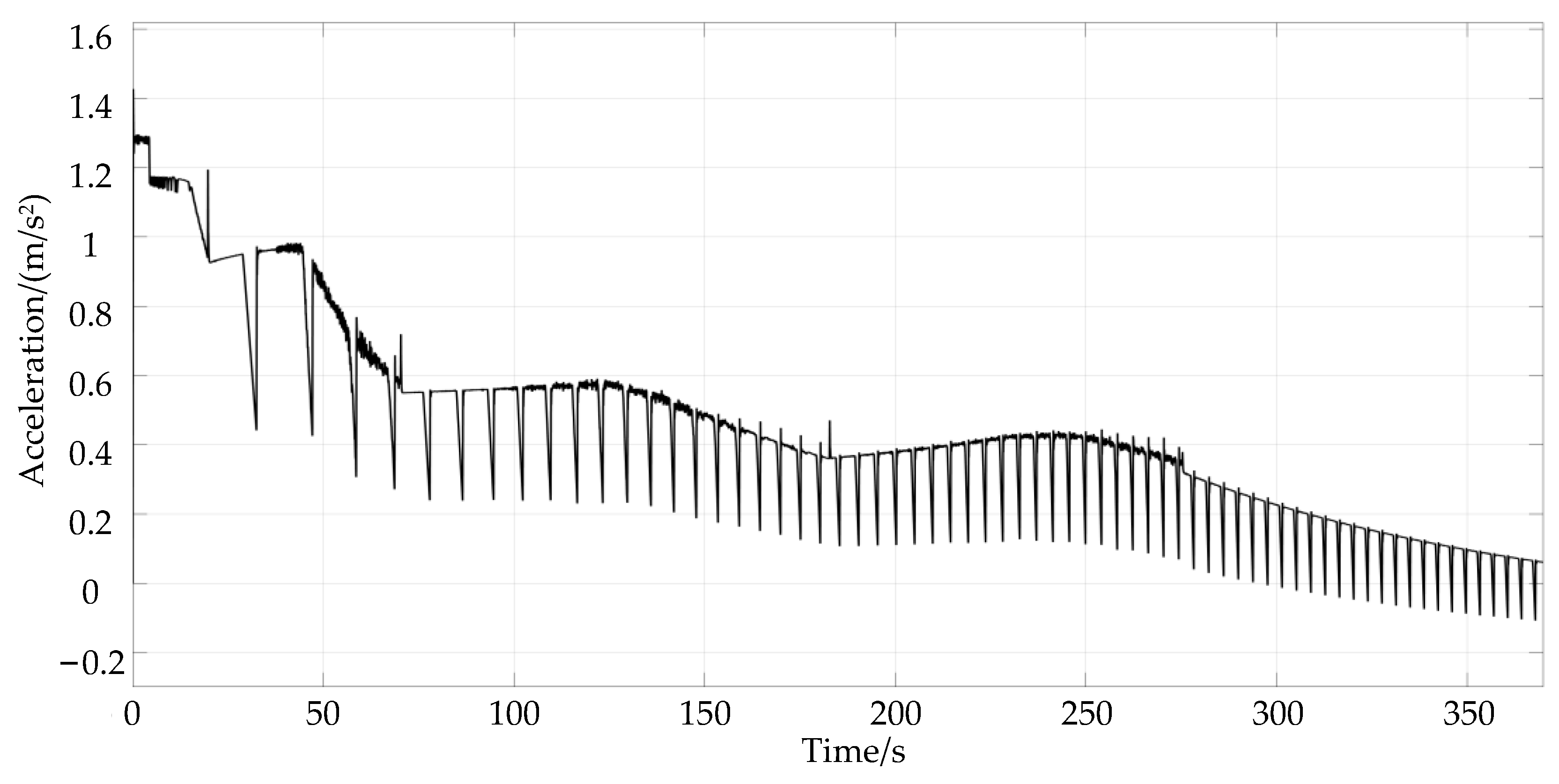
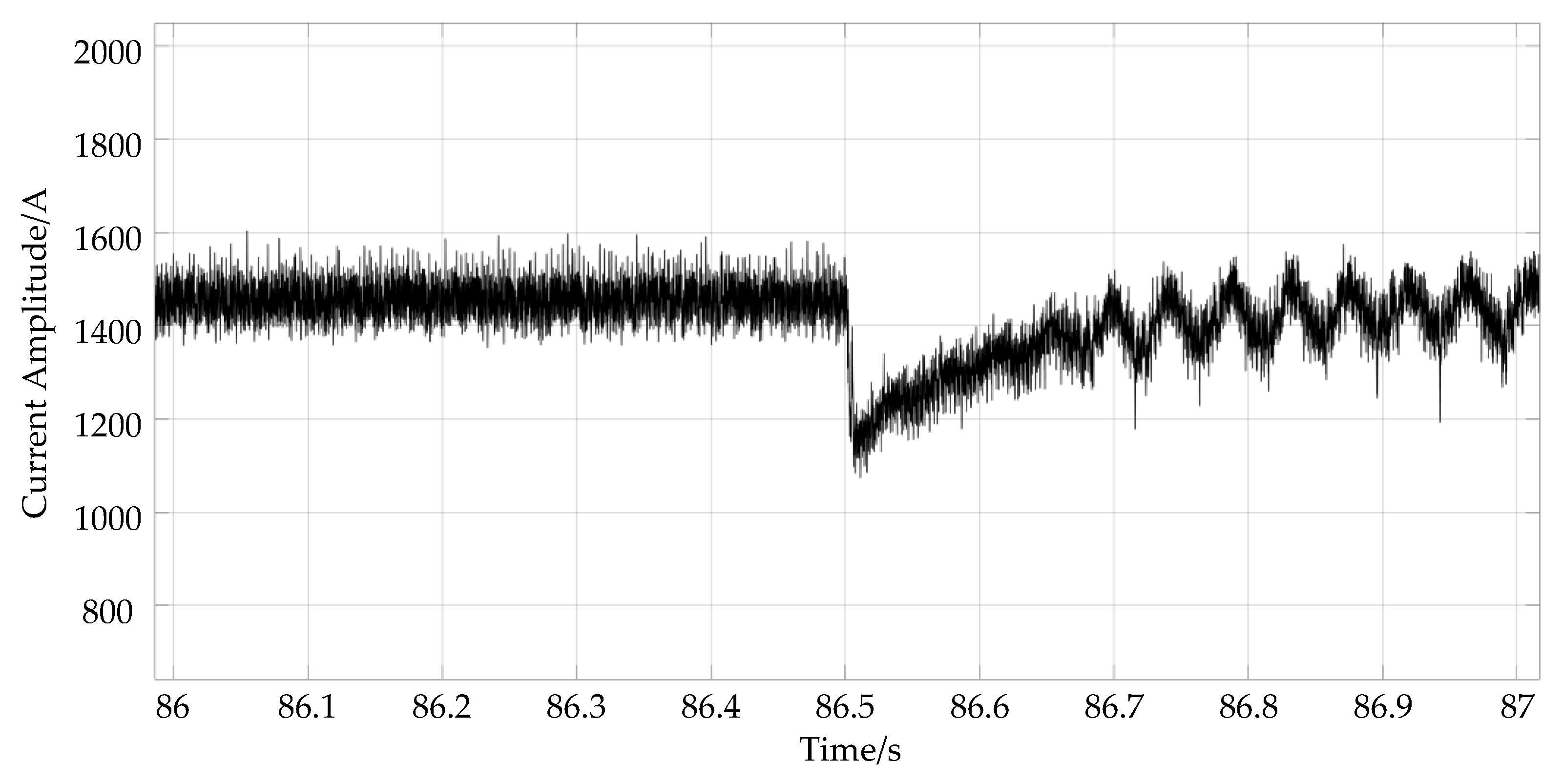
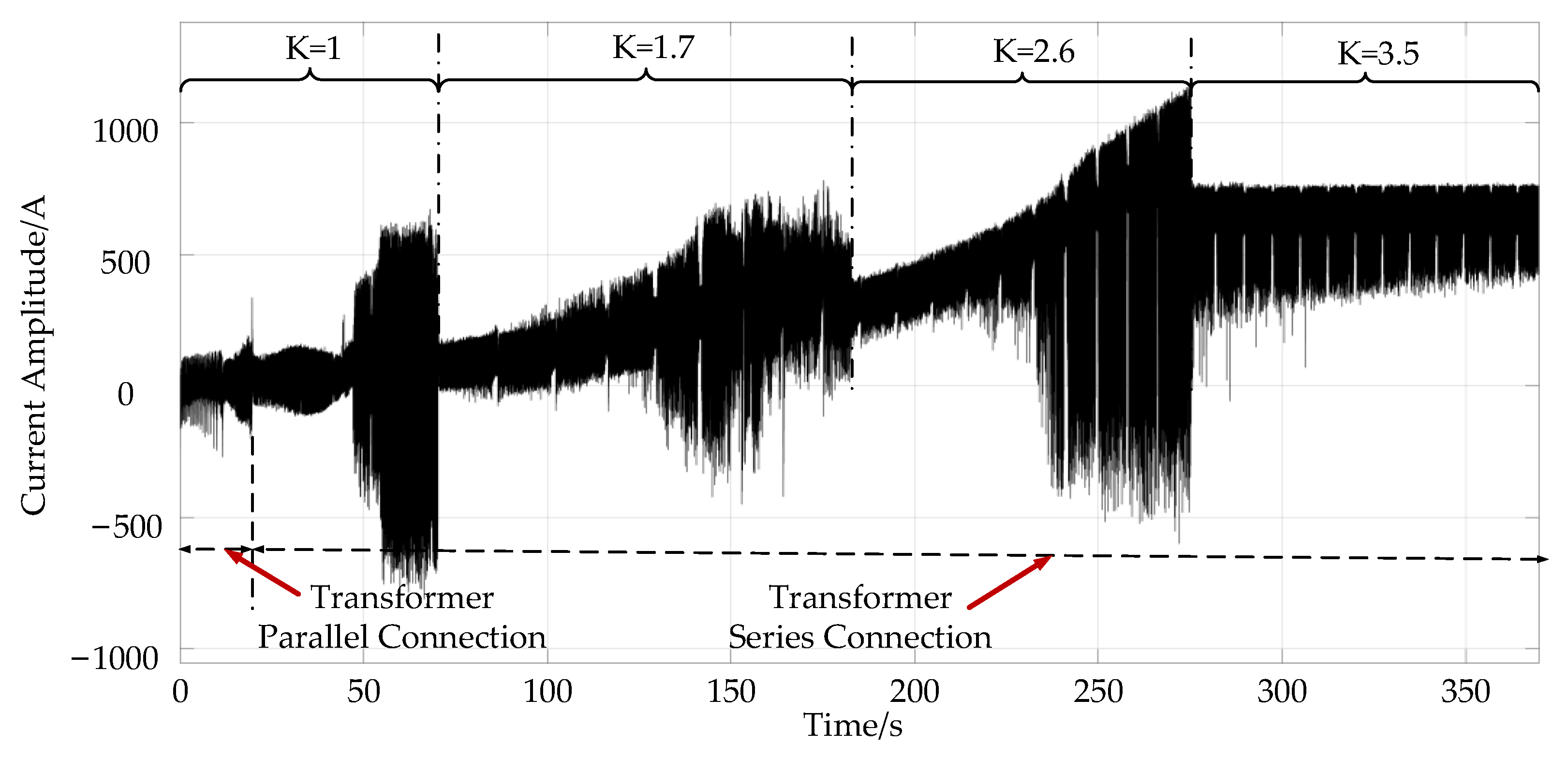
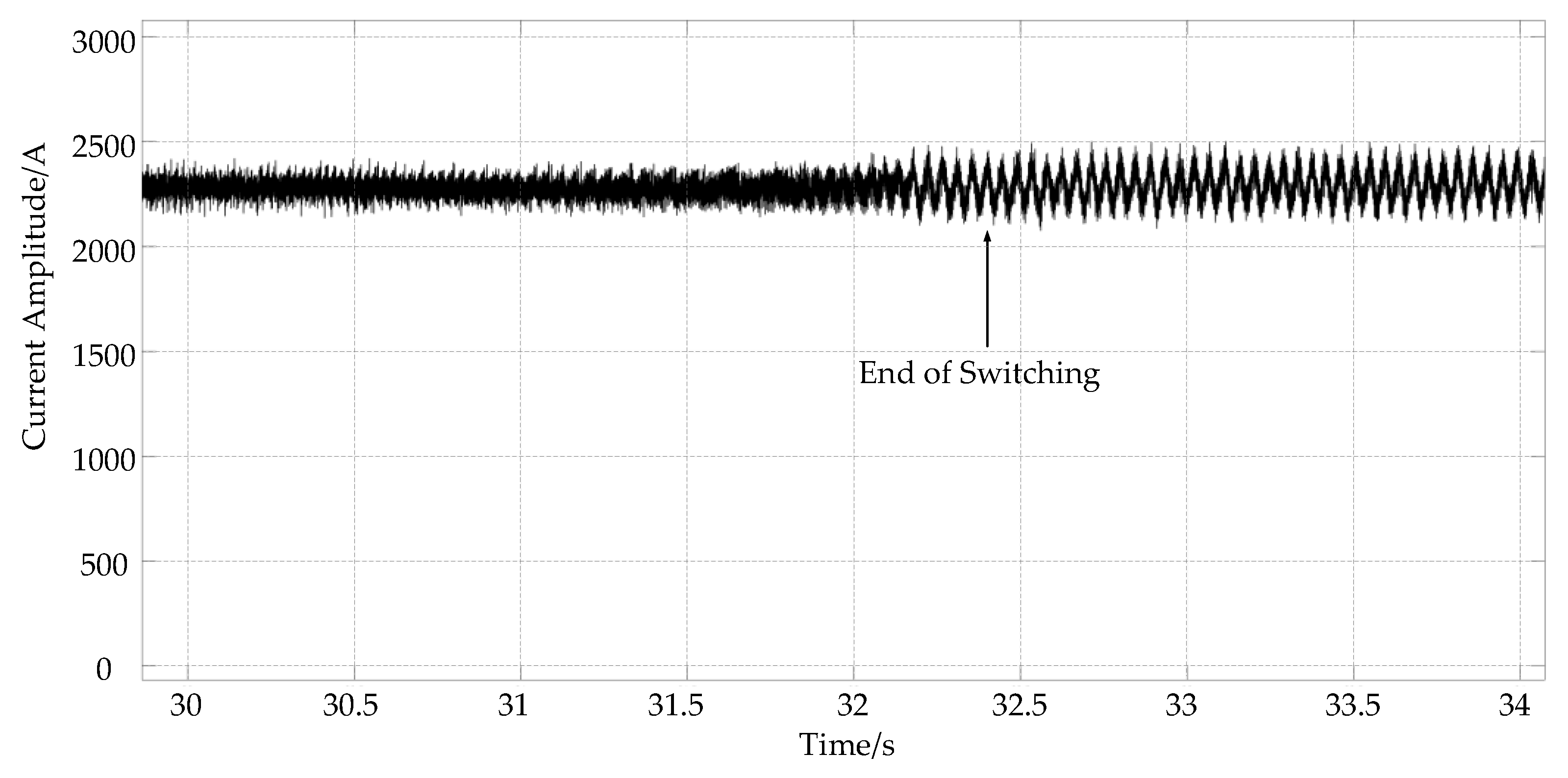
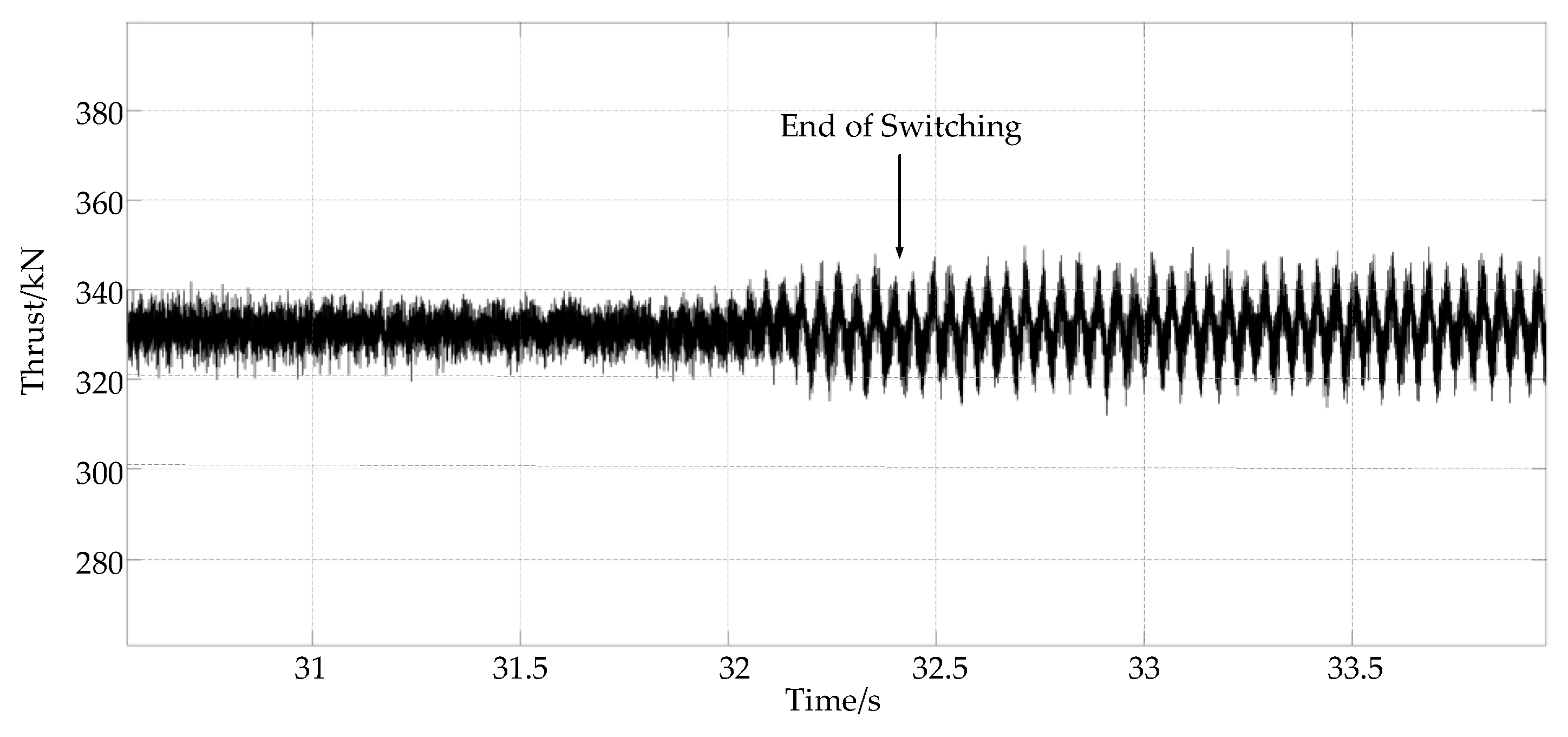
4.1. Simulation Results of the Two-Step Method
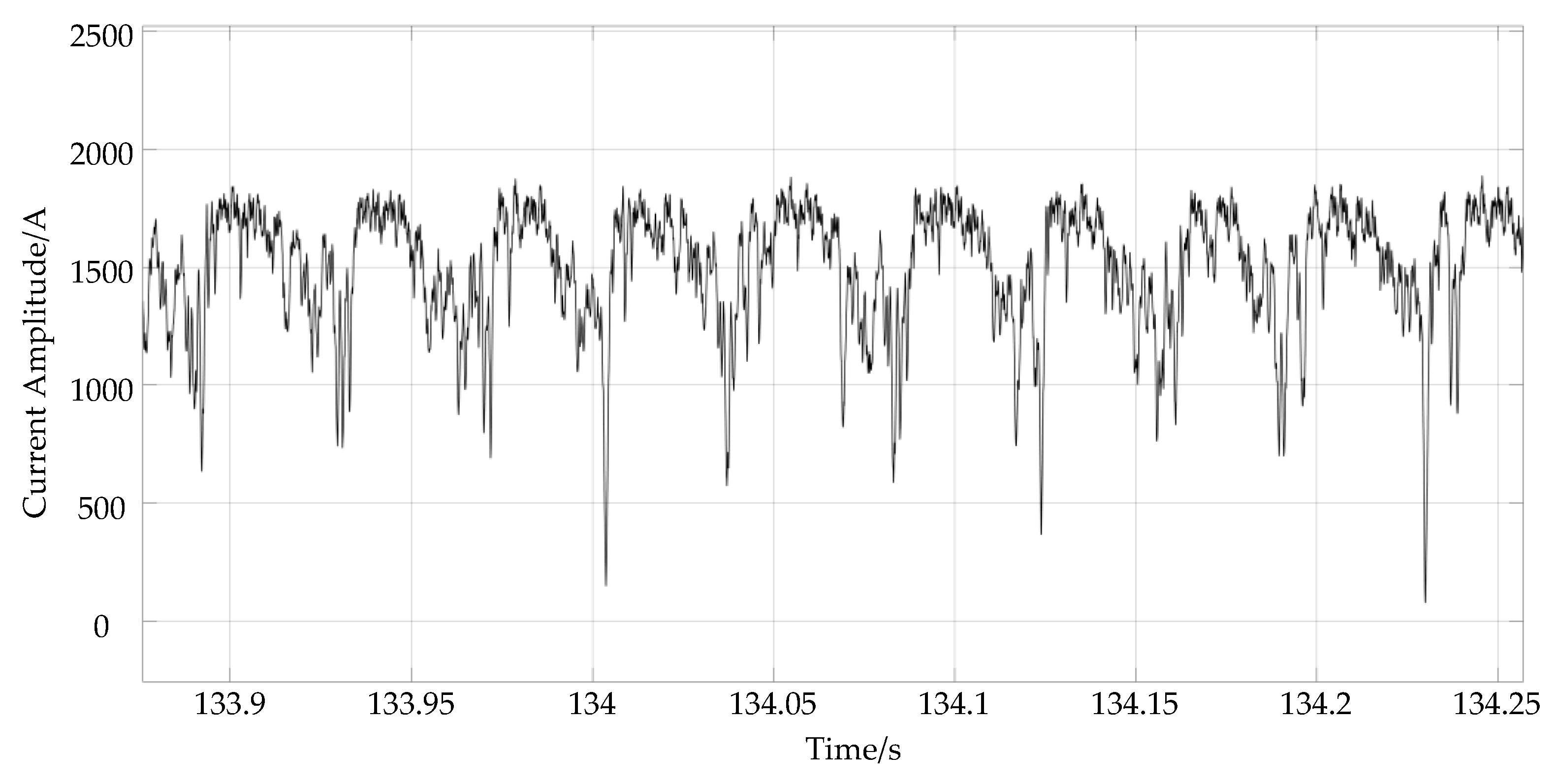
4.2. Simulation Results of the Three-Step Method
4.3. Simulation Results of LLSM with Faults
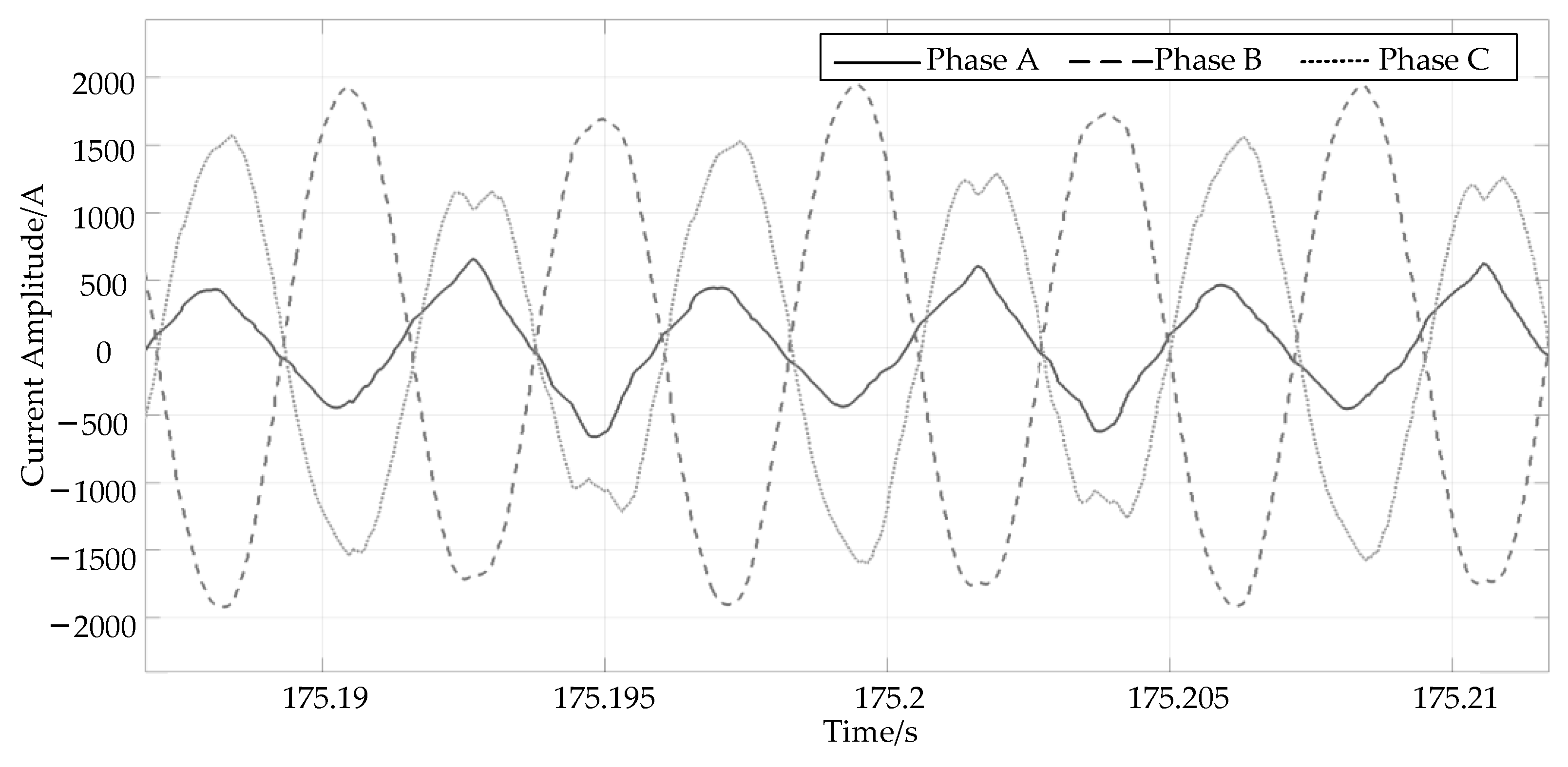
4.3.1. Single-Phase Disconnection Fault of LLSM
4.3.2. Phase-to-Phase Short-Circuit Fault of LLSM
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ou, T.; Hu, C.; Zhu, Y.; Zhang, M.; Zhu, L. Intelligent feedforward compensation motion control of maglev planar motor with precise reference modification prediction. IEEE Trans. Ind. Appl. 2020, 68, 7768–7777. [Google Scholar] [CrossRef]
- Jung, D.; DeSmidt, H. Vibration. A new hybrid observer based rotor imbalance vibration control via passive autobalancer and active bearing actuation. J. Sound Vib. 2018, 415, 1–24. [Google Scholar] [CrossRef]
- Kao, Y.-M.; Tsai, N.-C.; Chiu, H.-L. Five-dof innovative linear maglev slider to account for pitch, tilt and load uncertainty. Mech. Syst. Signal Process. 2017, 84, 673–698. [Google Scholar] [CrossRef]
- Luguang, Y. Progress of the maglev transportation in China. IEEE Trans. Appl. Supercon. 2006, 16, 1138–1141. [Google Scholar] [CrossRef]
- Lee, H.-W.; Kim, K.-C.; Lee, J. Review of maglev train technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar]
- Sun, Y.; Qiang, H.; Xu, J.; Lin, G. Internet of Things-based online condition monitor and improved adaptive fuzzy control for a medium-low-speed maglev train system. IEEE Trans. Ind. Inform. 2019, 16, 2629–2639. [Google Scholar] [CrossRef]
- Hao, L.; Huang, Z.; Dong, F.; Qiu, D.; Shen, B.; Jin, Z. Study on electrodynamic suspension system with high-temperature superconducting magnets for a high-speed maglev train. IEEE Trans. Appl. Supercon. 2018, 29, 1–5. [Google Scholar] [CrossRef]
- Gong, T.; Ma, G.; Cai, Y.; Qian, H.; Li, J.; Deng, Y.; Zhao, Z. Calculation and optimization of propulsion force of a real-scale REBCO magnet for EDS train. IEEE Trans. Appl. Supercon. 2019, 29, 1–6. [Google Scholar] [CrossRef]
- Ding, S.; Sun, J.; Han, W.; Deng, G.; Jiang, F. Modeling and analysis of a novel guidance magnet for high-speed Maglev train. IEEE Access 2019, 7, 133324–133334. [Google Scholar] [CrossRef]
- Zhai, M.; Hao, A.; Li, X.; Long, Z. Research on the active guidance control system in high speed maglev train. IEEE Access 2018, 7, 741–752. [Google Scholar] [CrossRef]
- Li, L.; Lu, Q. Investigation of linear generator for high speed maglev train by 2D finite element model. In Proceedings of the 2019 12th International Symposium on Linear Drives for Industry Applications (LDIA), Neuchâtel, Switzerland, 1–3 July 2019; pp. 1–6. [Google Scholar]
- Yang, Q.; Yu, P.; Li, J.; Chi, Z.; Wang, L. Modeling and Control of Maglev Train Considering Eddy Current Effect. In Proceedings of the 2020 39th Chinese Control Conference (CCC), Shenyang, China, 27–29 July 2020; pp. 5554–5558. [Google Scholar]
- Ren, Z.; Xiao, L.; Liu, H.; Wang, Q. Research on Control System of Electro-Magnetic Suspension Maglev Train. In Proceedings of the 2020 IEEE International Conference on Information Technology, Big Data and Artificial Intelligence (ICIBA), Atlanta, GA, USA, 10–13 December 2020; pp. 1085–1089. [Google Scholar]
- Sun, Y.; Xu, J.; Lin, G.; Ji, W.; Wang, L. RBF neural network-based supervisor control for maglev vehicles on an elastic track with network time delay. IEEE Trans. Ind. Inform. 2020, 18, 509–519. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, K.; Ouyang, Q. Intelligent traction control method based on model predictive fuzzy PID control and online optimization for permanent magnetic maglev trains. IEEE Access 2021, 9, 29032–29046. [Google Scholar] [CrossRef]
- Mersha, T.K.; Du, C. Co-Simulation and Modeling of PMSM Based on Ansys Software and Simulink for EVs. World Electr. Veh. J. 2021, 13, 4. [Google Scholar] [CrossRef]
- Zhang, Y.; Qing, G.; Zhang, Z.; Li, J.; Chen, H. Calculation and Simulation of Propulsion Power Supply System for High-speed Maglev Train. In Proceedings of the 2020 IEEE Vehicle Power and Propulsion Conference (VPPC), Gijón, Spain, 26–29 October 2020; pp. 1–5. [Google Scholar]
- Andriollo, M.; Martinelli, C.; Morini, A.; Tortella, A. Optimization of the on-board linear generator in EMS-MAGLEV trains. IEEE Trans. Magn. 1997, 33, 4224–4226. [Google Scholar] [CrossRef]
- Allotta, B.; Pugi, L.; Reatti, A.; Corti, F. Wireless power recharge for underwater robotics. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Do Chung, Y.; Lee, C.Y.; Lee, W.S.; Park, E.Y. Operating characteristics for different resonance frequency ranges of wireless power charging system in superconducting MAGLEV train. IEEE Trans. Appl. Supercon. 2019, 29, 1–5. [Google Scholar] [CrossRef]










| Parameters | Value |
|---|---|
| Stator Resistance () | 0.2796 |
| Self-Inductance (H) | 0.00048 |
| Mutual Inductance (H) | −0.00024 |
| Leakage Inductance (H) | 0.0022 |
| Mover Flux Linkage (Wb) | 3.9629 |
| Pitch Length (m) | 0.258 |
| Train Mass (kg) | 317,500 |
| Train Length (m) | 120 |
| Stator Segment Length (m) | 1200 |
| Number of Train Groups | 5 |
| Feeder Cable Resistance (/km) | 0.0368 |
| Feeder Cable Inductance (H/km) | 0.0000713 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Z.; Zheng, M.; Lu, Q. Modeling and Simulation of Traction Power Supply System for High-Speed Maglev Train. World Electr. Veh. J. 2022, 13, 82. https://doi.org/10.3390/wevj13050082
Zou Z, Zheng M, Lu Q. Modeling and Simulation of Traction Power Supply System for High-Speed Maglev Train. World Electric Vehicle Journal. 2022; 13(5):82. https://doi.org/10.3390/wevj13050082
Chicago/Turabian StyleZou, Ziyu, Mengfei Zheng, and Qinfen Lu. 2022. "Modeling and Simulation of Traction Power Supply System for High-Speed Maglev Train" World Electric Vehicle Journal 13, no. 5: 82. https://doi.org/10.3390/wevj13050082
APA StyleZou, Z., Zheng, M., & Lu, Q. (2022). Modeling and Simulation of Traction Power Supply System for High-Speed Maglev Train. World Electric Vehicle Journal, 13(5), 82. https://doi.org/10.3390/wevj13050082







