Adaptive Pre-Aim Control of Driverless Vehicle Path Tracking Based on a SSA-BP Neural Network
Abstract
:1. Introduction
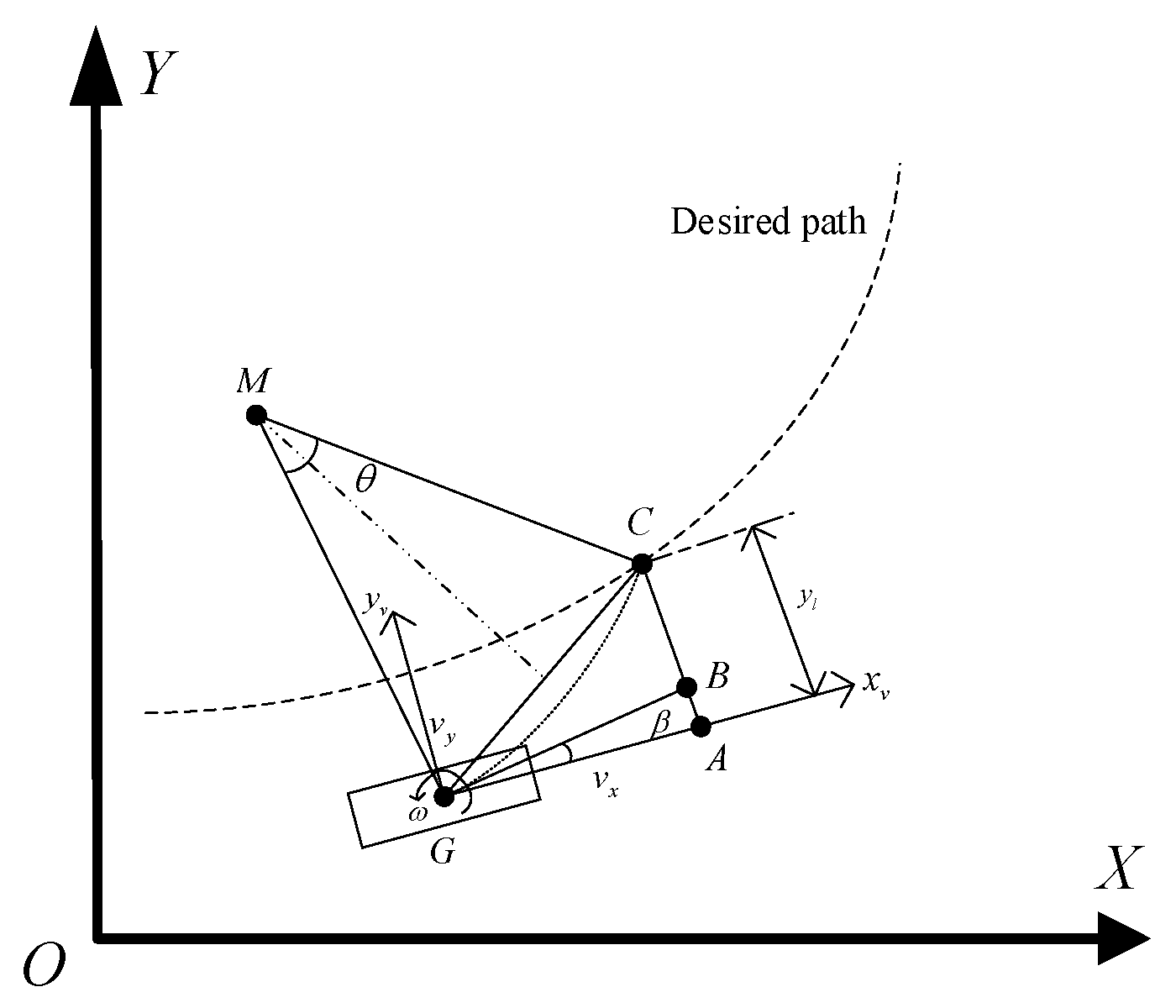
2. Vehicle Model
3. SSA-BP-Neural-Network-Based Adaptive Pre-Aim Control for Path Tracking
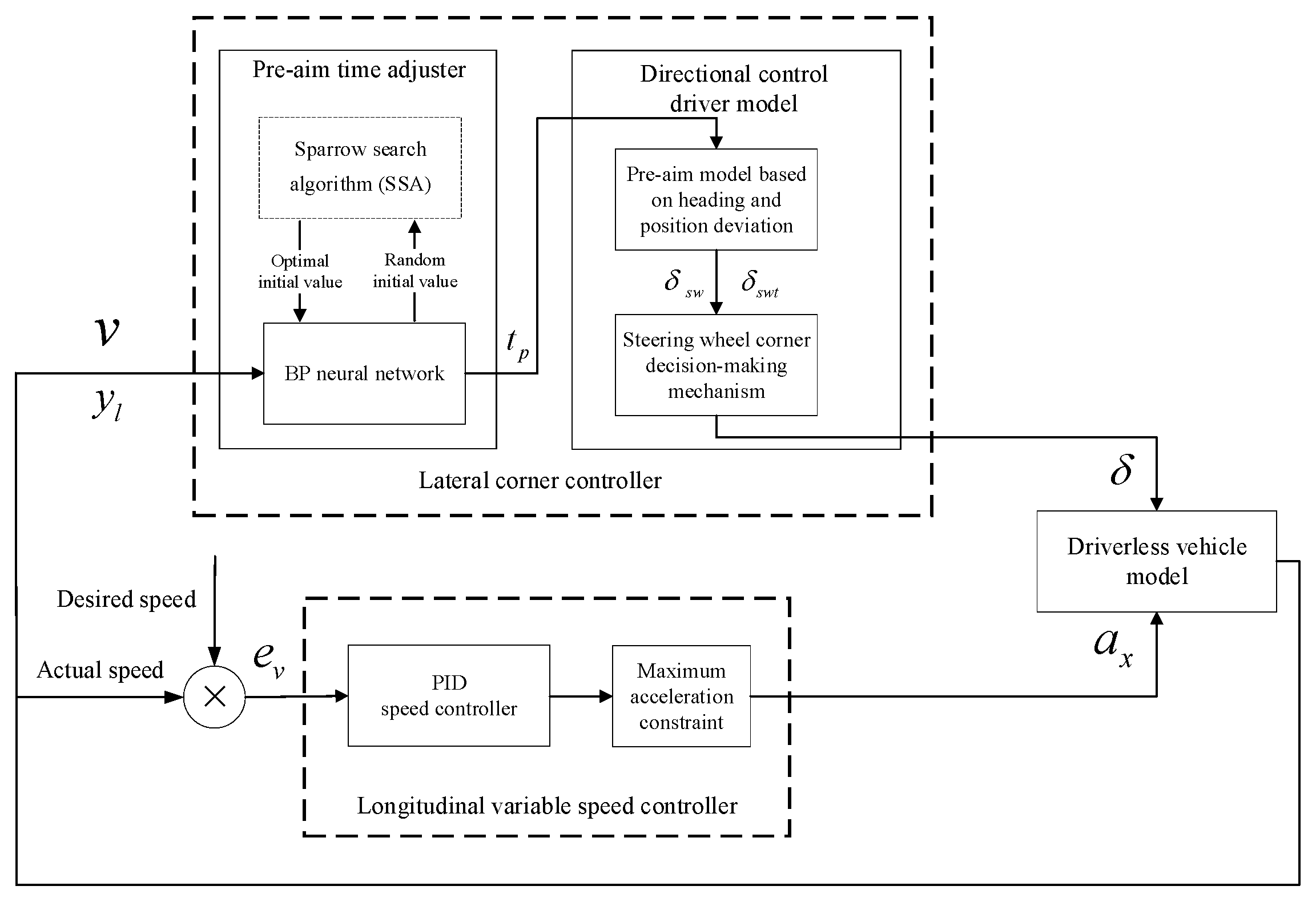
3.1. Overall Control Scheme
3.2. Directional Control Driver Model
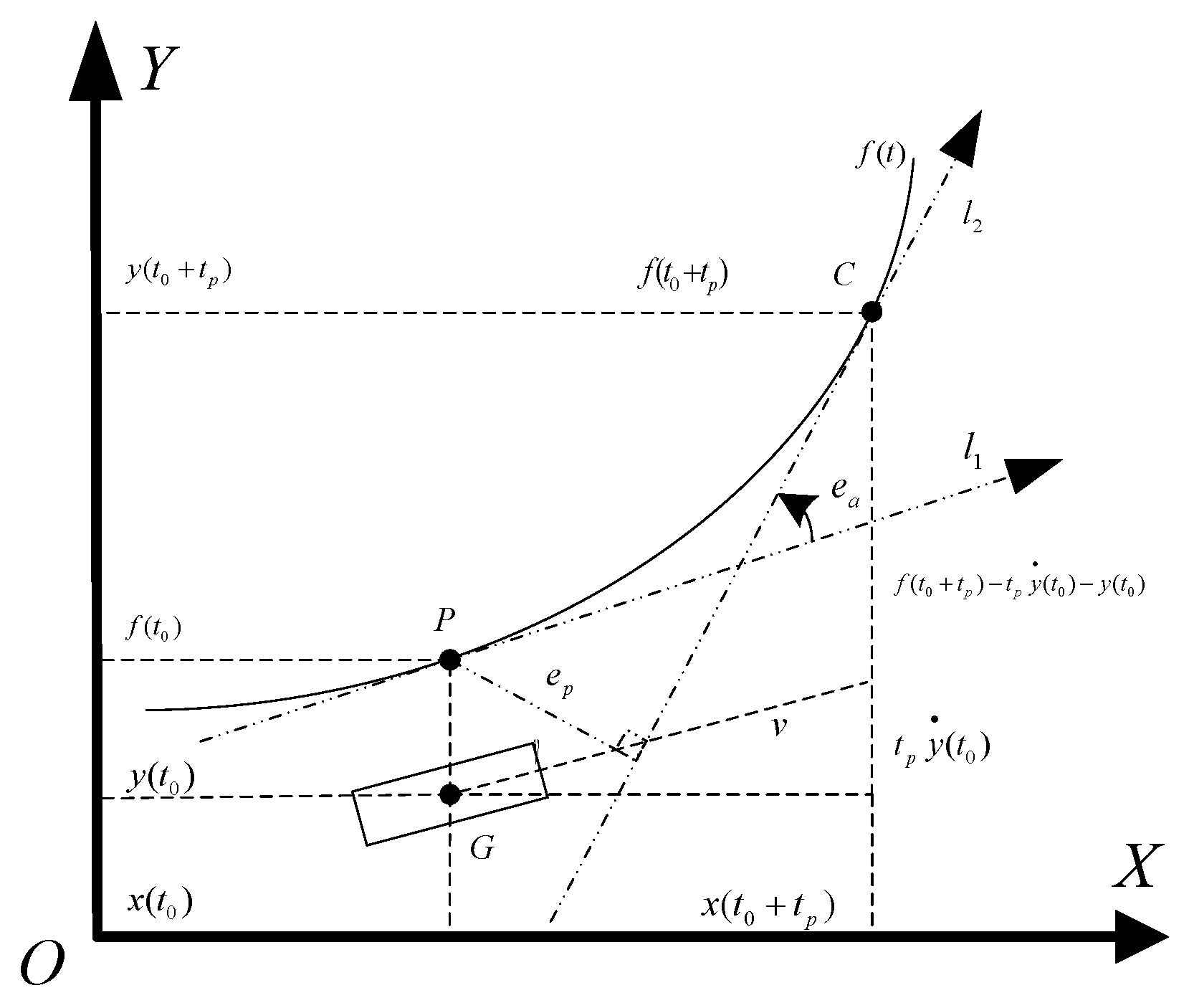
3.2.1. Pre-Aim Control Model
3.2.2. Steering Wheel Cornering Decision Mechanism
3.3. SSA-BP Neural Network Pre-Aim Time Adjuster
3.3.1. BP Neural Network
3.3.2. Sparrow Search Algorithm (SSA)
3.3.3. Pre-Aim Time Adjuster
- Firstly, the topology of the BP neural network and the input and output variables are determined, and the algorithm stopping condition is set as the maximum error value ;
- The weights and thresholds of the BP neural network are initialized, and the parameters related to the SSA algorithm, such as (, , , etc.), are defined;
- The fitness values of the sparrow population are calculated and ranked from smallest to largest to find the current optimal and worst values, where the initial fitness value is the training error of the random initial value of the BP neural network;
- Equations (20)–(22) are used to update the location of finders, joiners, and vigilantes, respectively;
- The optimal value of the sparrow position for this iteration is obtained, and the position is updated if the new position is better than the optimal value of the previous iteration; otherwise, no position update is performed;
- If the maximum number of iterations is reached, the search is stopped, and the global optimum and the best fitness value are output; otherwise, steps 3–5 are repeated;
- The parameters corresponding to the global optimum of the SSA algorithm are used as the initial weights and thresholds of the BP neural network, and the network is trained by inputting training and testing sample sets.
4. Simulation Experiments and Analysis
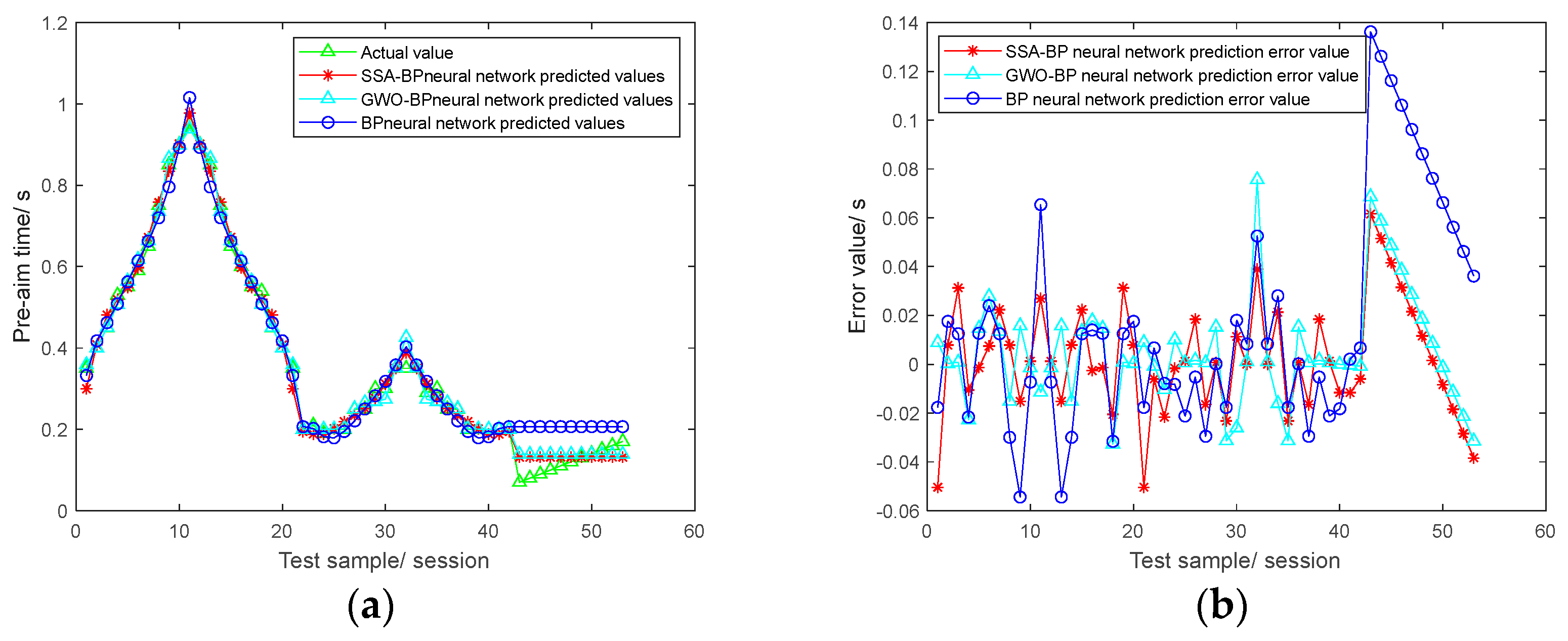
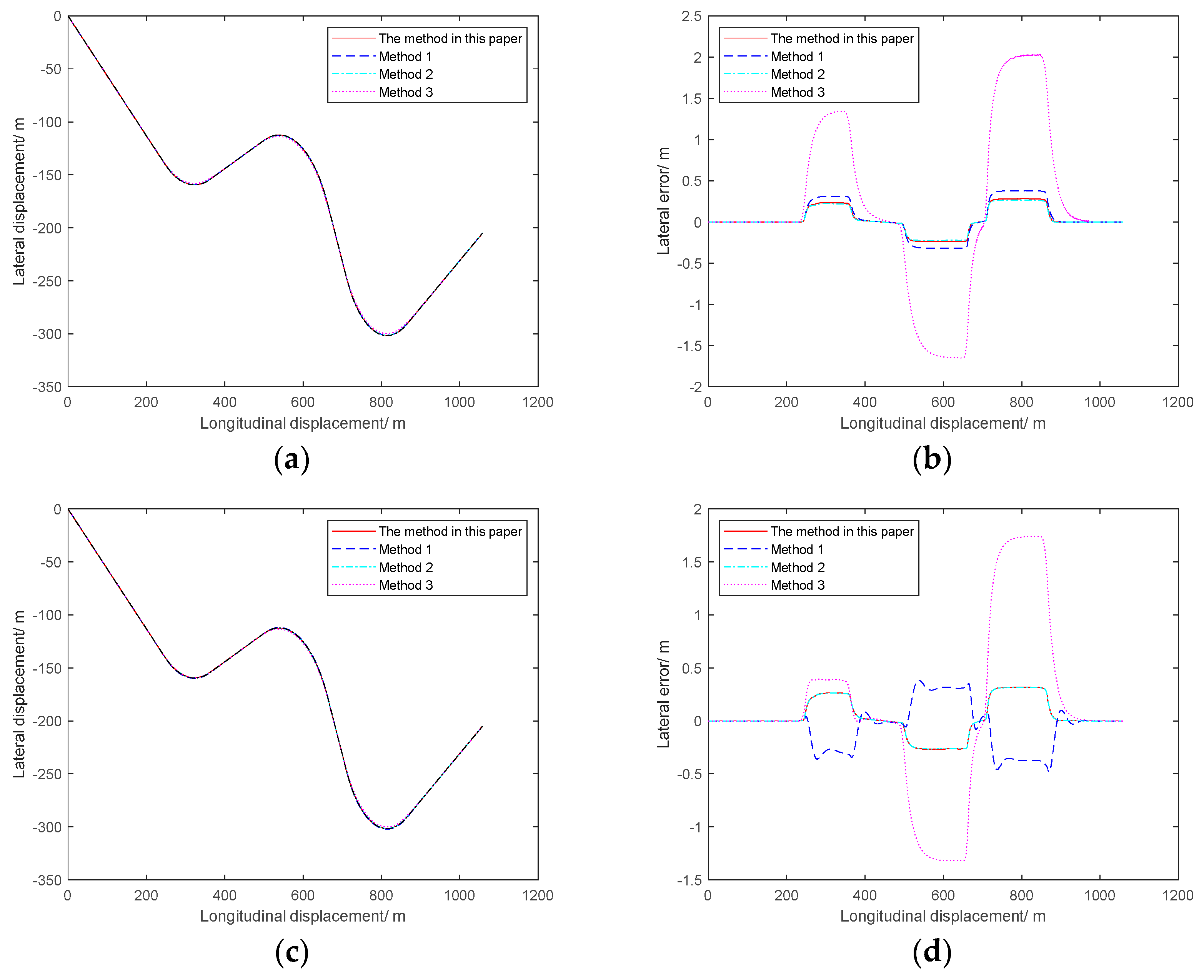
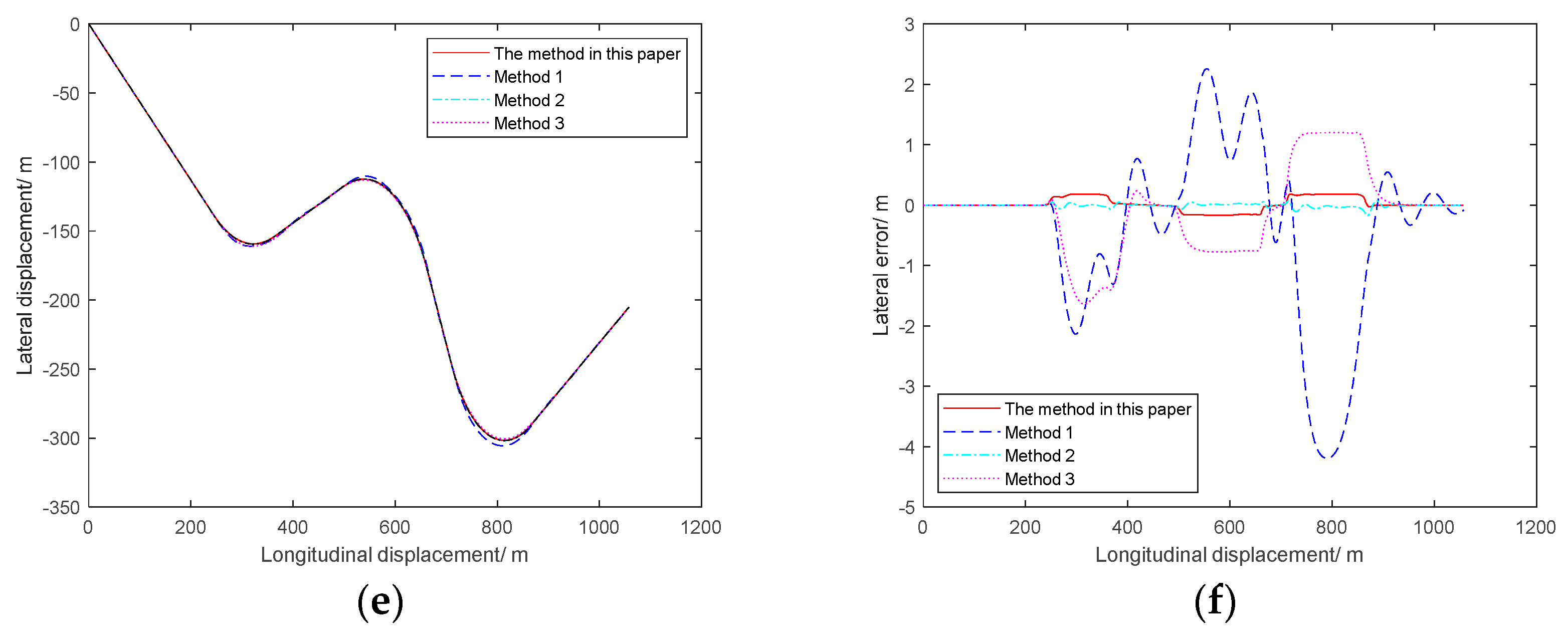
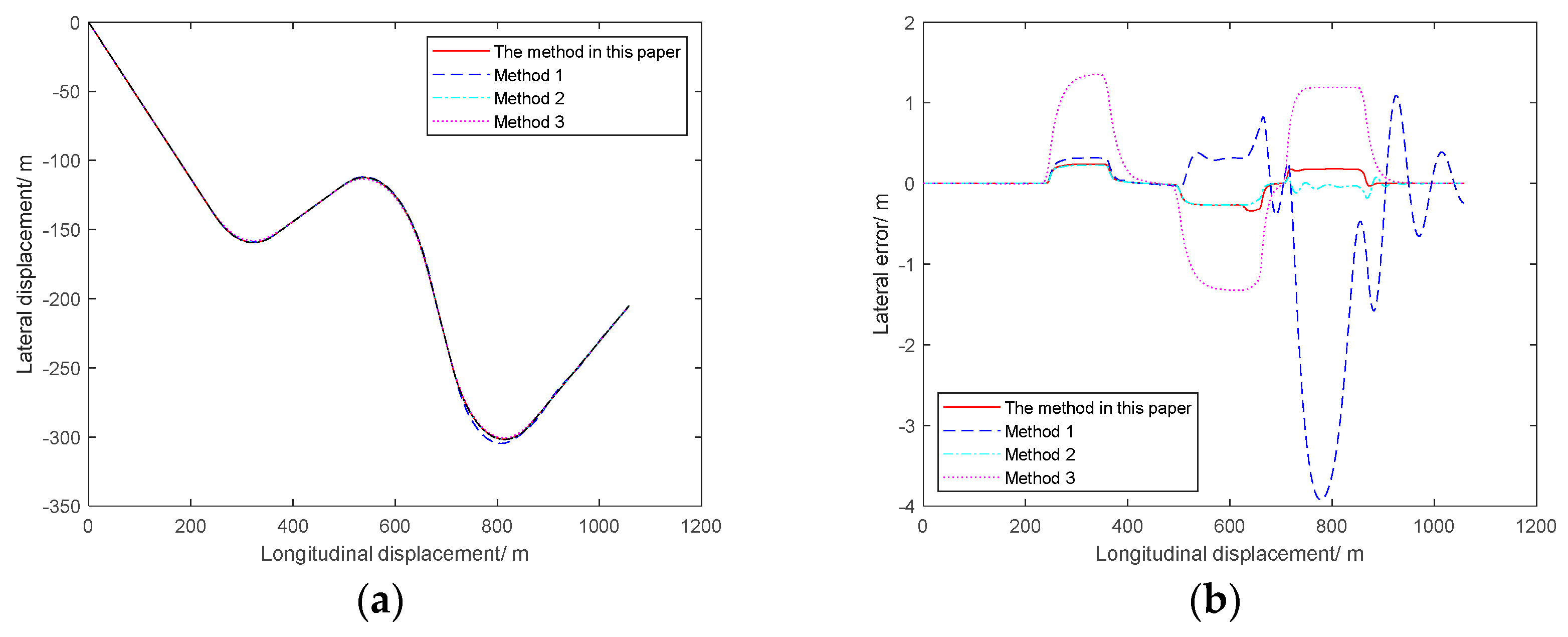
4.1. Variable-Speed Continuous Three-Curve Roads Tracking Experiment
4.2. Alt 3 Road Tracking Experiment
5. Conclusions
- Based on the vehicle model and the pre-aim control model, we built a “human–vehicle–road” closed-loop control system and proposed a new directional control driver model;
- The offline optimization of BP neural network primaries by the sparrow search algorithm (SSA) improves the prediction accuracy of the pre-aim time. Considering the law of pre-aim time selection under different driving conditions, the controller established by using the directional control driver model was used to conduct simulation experiments on the reference path (U-turn path). The SSA-BP neural network was trained with the obtained parameter samples to achieve the dynamic selection of pre-aim time;
- The longitudinal variable-speed controller was designed to reduce the coupling effect of longitudinal speed on path tracking, making the method in this paper more adaptable to a wide range of speed variation and able to achieve accurate path tracking under a variety of variable-speed working conditions;
- Through the tracking simulation experiments on two different roads, the results show that the maximum error value of the method in this paper is only 0.2673 m under the fixed-speed and variable-speed conditions, providing a new scheme for the research of path tracking pre-scanning control.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bellotti, F.; Kim, S.W.; Lian, F.L. Introduction to the Special Issue on Applications and Systems for Collaborative Driving. IEEE Trans. Intell. Transp. Syst. 2017, 18, 3457–3460. [Google Scholar] [CrossRef]
- Martinez, C.M.; Heucke, M.; Wang, F.Y.; Gao, B.; Cao, D. Driving Style Recognition for Intelligent Vehicle Control and Advanced Driver Assistance: A Survey. IEEE Trans. Intell. Transp. Syst. 2017, 19, 666–676. [Google Scholar] [CrossRef] [Green Version]
- Park, M.; Lee, S.; Han, W. Development of Steering Control System for Autonomous Vehicle Using Geometry-Based Path Tracking Algorithm. ETRI J. 2015, 37, 617–625. [Google Scholar] [CrossRef]
- He, H.; Shi, M.; Li, J.; Cao, J.; Han, M. Design and experiential test of a model predictive path following control with adaptive pre-aim for autonomous buses. Mech. Syst. Signal Processing 2021, 157, 107701. [Google Scholar] [CrossRef]
- Citlalli, G.S.; Yassine, R. Dynamic Speed Adaptation for Path Tracking Based on Curvature Information and Speed Limits. Sensors 2017, 17, 1383. [Google Scholar]
- Hong, S.; Hedrick, J.K. Roll prediction-based optimal control for safe path following. In Proceedings of the American Control Conference, IEEE, Chicago, IL, USA, 1–3 July 2015; pp. 3261–3266. [Google Scholar]
- Cao, J.; Lu, H.; Guo, K.; Zhang, J. A Driver Modeling Based on the pre-aim-Follower Theory and the Jerky Dynamics. Math. Probl. Eng. 2013, 2013, 1–10. [Google Scholar]
- Gang, C.; Su, S.H. Driver-behavior-based robust steering control of unmanned driving robotic vehicle with modeling uncertainties and external disturbance. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 1585–1596. [Google Scholar]
- Chen, T.; Li, X.; Sun, L.; Wei, L. Review and Prospect of Driver Model in Intelligent Vehicle Design. Automob. Technol. 2014, 6, 1–6. [Google Scholar]
- Guo, K. Modeling of Driver/Vehicle Directionl Control System. Veh. Syst. Dyn. 1993, 22, 141–184. [Google Scholar] [CrossRef]
- Chen, W.; Tan, D.; Wang, H.; Wang, J.; Xia, G. A kind of driver direction control model based on trajectory prediction. J. Mech. Eng. 2016, 52, 106–115. [Google Scholar] [CrossRef]
- Zhi-Gen, N.; Wan-Qiong, W.; Wei-Qiang, Z.; Zhen, H.; Chang-Fu, Z. Dynamic trajectory planning and tracking control of smart car lane changing based on trajectory pre-aim. J. Traffic Transp. Eng. 2020, 20, 147–160. [Google Scholar]
- Li, S.; Xu, Y.H.; Chen, J.; Zhu, P.X. Research on Vehicle Lateral Tracking Control Based on Arc Length pre-aim. Automot. Eng. 2019, 41, 668–675. [Google Scholar]
- Zhang, L.Z.; Guan, H.; Jia, X.; Lu, P.P.; Chen, Y.S. A Study on the Effect of Driver Model Parameters on the Performance of Driver-Vehicle-Road Closed-Loop System. Appl. Mech. Mater. 2014, 470, 604–608. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Luo, X.; Zhang, Z.; Gao, Y.; He, J.; Yue, B. Tracking control method of agricultural machinery navigation path based on pre-aim tracking model. Trans. Chin. Soc. Agric. Eng. 2019, 35, 11–19. [Google Scholar]
- Li, Y.H.; Liu, Y.; Feng, Q.L.; Nan, Y.F.; He, J.; Fan, J.C. Intelligent commercial vehicle path following control based on optimal pre-aim and model prediction. J. Automot. Saf. Energy 2020, 11, 462–469. [Google Scholar]
- Sun, M.X.; Man, X.M.; Wang, J.H.; Wang, J.H.; Guo, D.; Man, X.H. Overtaking path tracking control based on dynamics and pre-aim theory. J. Shandong Univ. Technol. (Nat. Sci. Ed.) 2021, 35, 33–38. [Google Scholar]
- Jiang, J.X.; Shi, P.L.; Zhou, L.H.; Zhang, L. Smart car path tracking control with variable pre-aim distance. J. Shandong Univ. Technol. (Nat. Sci. Ed.) 2021, 35, 70–74, 80. [Google Scholar]
- Diao, Q.Q.; Zhang, Y.N.; Zhu, L.Y. Horizontal and vertical fuzzy control of large curvature path for smart car with dual pre-aim points. China Mech. Eng. 2019, 30, 1445–1452. [Google Scholar]
- Chen, W.W.; Wang, J.E.; Wang, M.L.; Wang, J.B. Adaptive pre-aim Control of Lateral Movement of Intelligent Vehicles with Vision Navigation. China Mech. Eng. 2014, 25, 698–704. [Google Scholar]
- Zhao, Z.G.; Zhou, L.J.; Zhu, Q. Adaptive optimization of pre-aim distance for unmanned vehicle path tracking control. J. Mech. Eng. 2018, 54, 166–173. [Google Scholar] [CrossRef]
- Li, Y. Direction and Speed Integrated Control Driver Model and Its Application in ADAMS. Master’s Thesis, Jilin University, Changchun, China, 2008. [Google Scholar]
- Jin, X.Y.; Zhang, J.; Liu, Y.S.; Wang, Q.S. Research on adaptive optimal pre-aim model based on Stanley algorithm. Comput. Eng. 2018, 44, 42–46. [Google Scholar]
- Li, H.Z.; Li, L.; Song, J.; Yu, L.Y.; Wu, K.H.; Zhang, X.L. Optimal pre-aim driver model with adaptive pre-aim time. J. Mech. Eng. 2010, 46, 106–111. [Google Scholar]
- Xie, J.; Jiang, H.B.; Ma, S.D. Adaptive analysis of pre-aim time of smart car driver model. J. Jiangsu Univ. (Nat. Sci. Ed.) 2018, 39, 254–259. [Google Scholar]
- Ran, Y.Q.; Wu, W.; Di, X. Research on Pipe Network Leakage Location Model Based on Genetic Algorithm Optimized BP Neural Network. Water Resour. Power 2021, 39, 123–126, 122. [Google Scholar]
- Chai, Y.; Li, T.; Zhang, L. Production Forecast of Coalbed Methane Based on GA Optimized BP Neural Network. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), IEEE, Chengdu, China, 20–22 December 2019. [Google Scholar]
- Long, Y.; Deng, X.L.; Yang, X.X.; Hou, Z.X. Short-term rapid prediction of stratospheric wind field based on PSO-BP neural network. J. Beijing Univ. Aeronaut. Astronaut. 2021. [Google Scholar] [CrossRef]
- Pang, X.; Ma, H.; Su, P.; Tang, G.Y. TPPMA: New Adaptive BP Neural Network Based on PSO and PCA Algorithms. In Proceedings of the 2018 IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, QLD, Australia, 13–15 June 2018. [Google Scholar]
- Xie, L.X.; Wang, Z.H. Network security situation assessment method based on cuckoo search optimization BP neural network. J. Comput. Appl. 2017, 37, 1926–1930. [Google Scholar]
- Xuan, J.K. Research and application of a new type of swarm intelligence optimization technology. Donghua Univ. Xuan Jiankai 2020. Available online: https://cdmd.cnki.com.cn/Article/CDMD-10255-1020647458.htm (accessed on 20 February 2022).
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]



| Algorithm | Maximum Error | MAE | RMSE |
|---|---|---|---|
| BPNN | 0.1362 | 0.01583 | 0.047 |
| GWO-BPNN | 0.07554 | 0.004989 | 0.02331 |
| SSA-BPNN | 0.06156 | 0.002059 | 0.0229 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Luo, W.; Lan, H. Adaptive Pre-Aim Control of Driverless Vehicle Path Tracking Based on a SSA-BP Neural Network. World Electr. Veh. J. 2022, 13, 55. https://doi.org/10.3390/wevj13040055
Huang Y, Luo W, Lan H. Adaptive Pre-Aim Control of Driverless Vehicle Path Tracking Based on a SSA-BP Neural Network. World Electric Vehicle Journal. 2022; 13(4):55. https://doi.org/10.3390/wevj13040055
Chicago/Turabian StyleHuang, Yinggang, Wenguang Luo, and Hongli Lan. 2022. "Adaptive Pre-Aim Control of Driverless Vehicle Path Tracking Based on a SSA-BP Neural Network" World Electric Vehicle Journal 13, no. 4: 55. https://doi.org/10.3390/wevj13040055
APA StyleHuang, Y., Luo, W., & Lan, H. (2022). Adaptive Pre-Aim Control of Driverless Vehicle Path Tracking Based on a SSA-BP Neural Network. World Electric Vehicle Journal, 13(4), 55. https://doi.org/10.3390/wevj13040055






