The Optimal Deployment of the Entry and Exit Gates of Electric Vehicles Wireless Charging Transmitters on Highways
Abstract
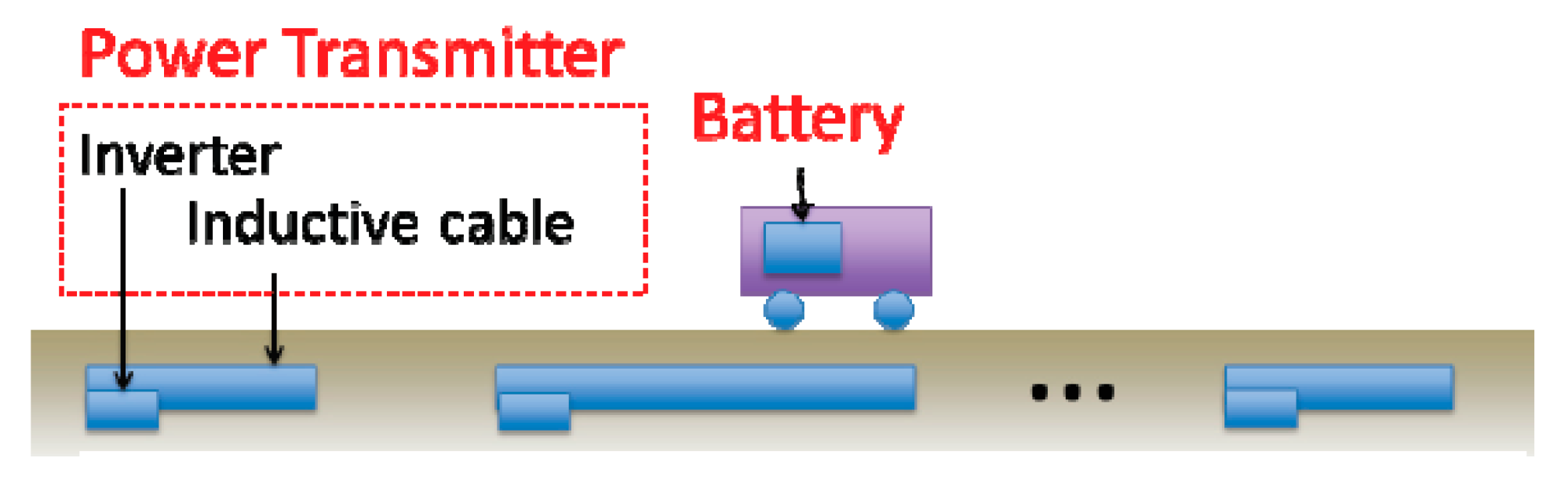
1. Introduction
- -
- Lead–acid batteries: lead–acid batteries offer limited capacity, despite their large size and weight, but they are economical and straightforward to produce or recycle. Used as a primary storage device for electric vehicles until the 1980s, it quickly gave way to other, more efficient technologies;
- -
- Nickel–cadmium batteries: Ni–Cd batteries, used in the production of electric vehicles in the 1990s, are now banned due to the toxicity of cadmium;
- -
- Nickel–metal hydride batteries: these portable rechargeable batteries were the most economical in the early 2000s: this is why they largely dominated the hybrid vehicle market until the advent of lithium-ion technology;
- -
- Lithium-ion batteries: developed in the early 1990s, lithium-ion batteries have gradually become the leading technology in the world of transport and consumer electronics. With a long lifetime, they offer a much higher energy density than all competing technologies and have no memory effect.
2. Literature Review
3. Problem and Modelling
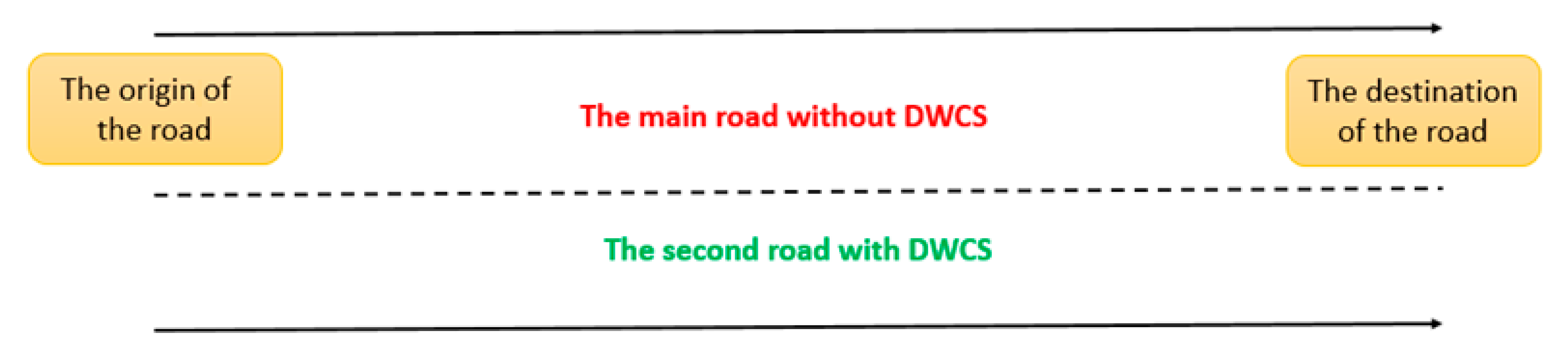
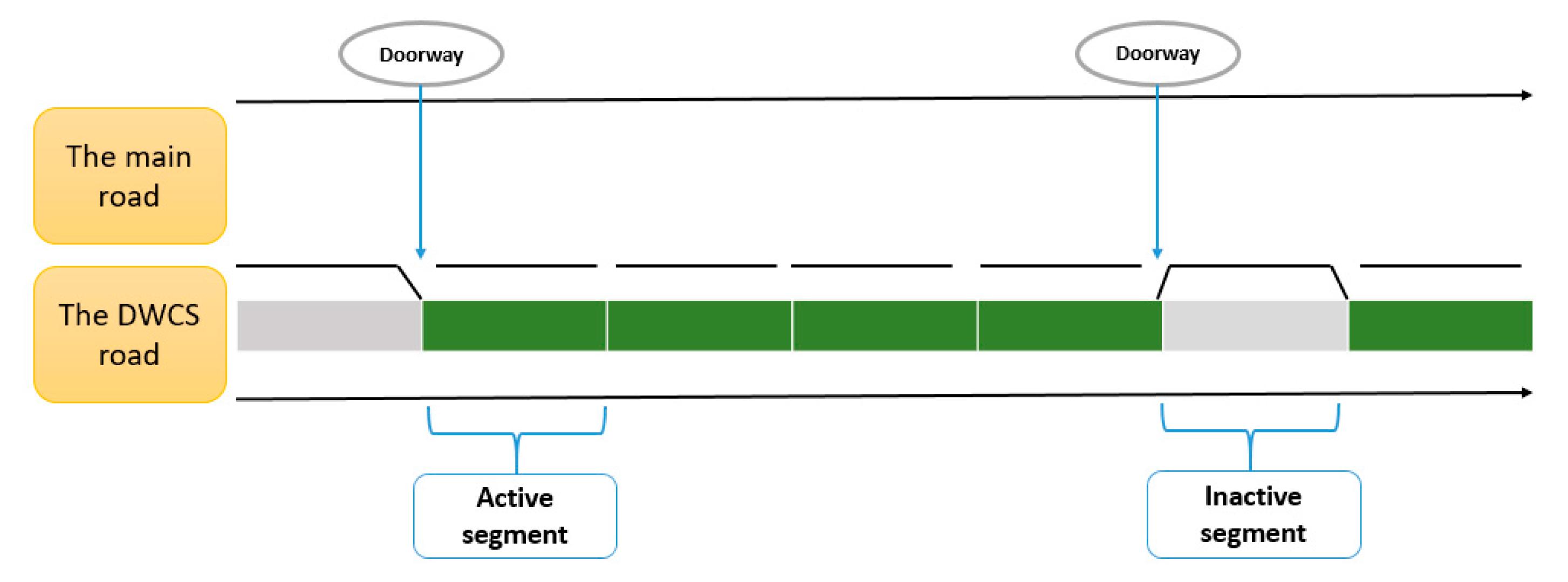
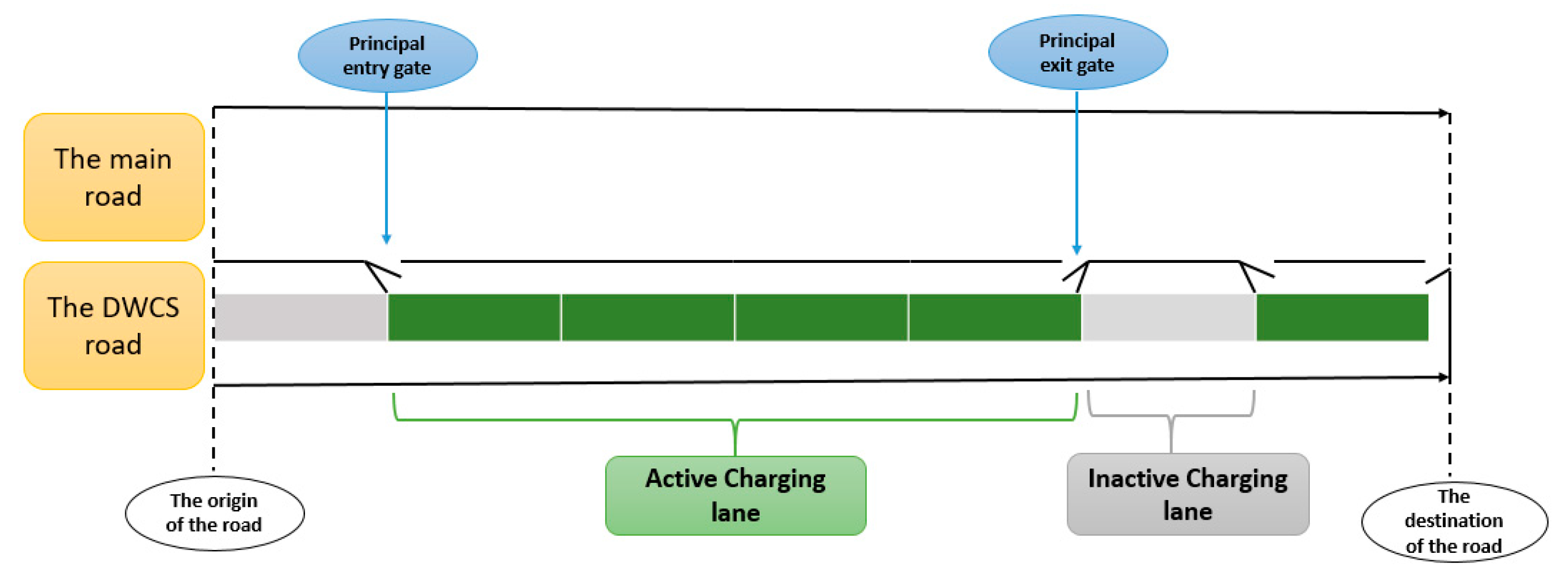
3.1. Problem Description and Objective
3.2. Problem Formulation, Data, and Decision Variables
3.3. Constraints
- If , the vehicle has not used lane between gates and ; this means that vehicle is on the main road, so if , the vehicle decides to use lane between gates and ; in this case, it enters the lane by the gate, found with the constraint ;
- If , vehicle uses lane between gates and , so if , the vehicle does not need to use lane between gates and and decides to leave the lane by the gate, found with the constraint ;
- If , vehicle α is on the main road between gates and and it stays on the main road between gates and , so vehicle does not use gate and involves . The same case if .
3.4. Objective Function
4. Problem Solving
4.1. Problem Validation
4.1.1. Transport Network Data
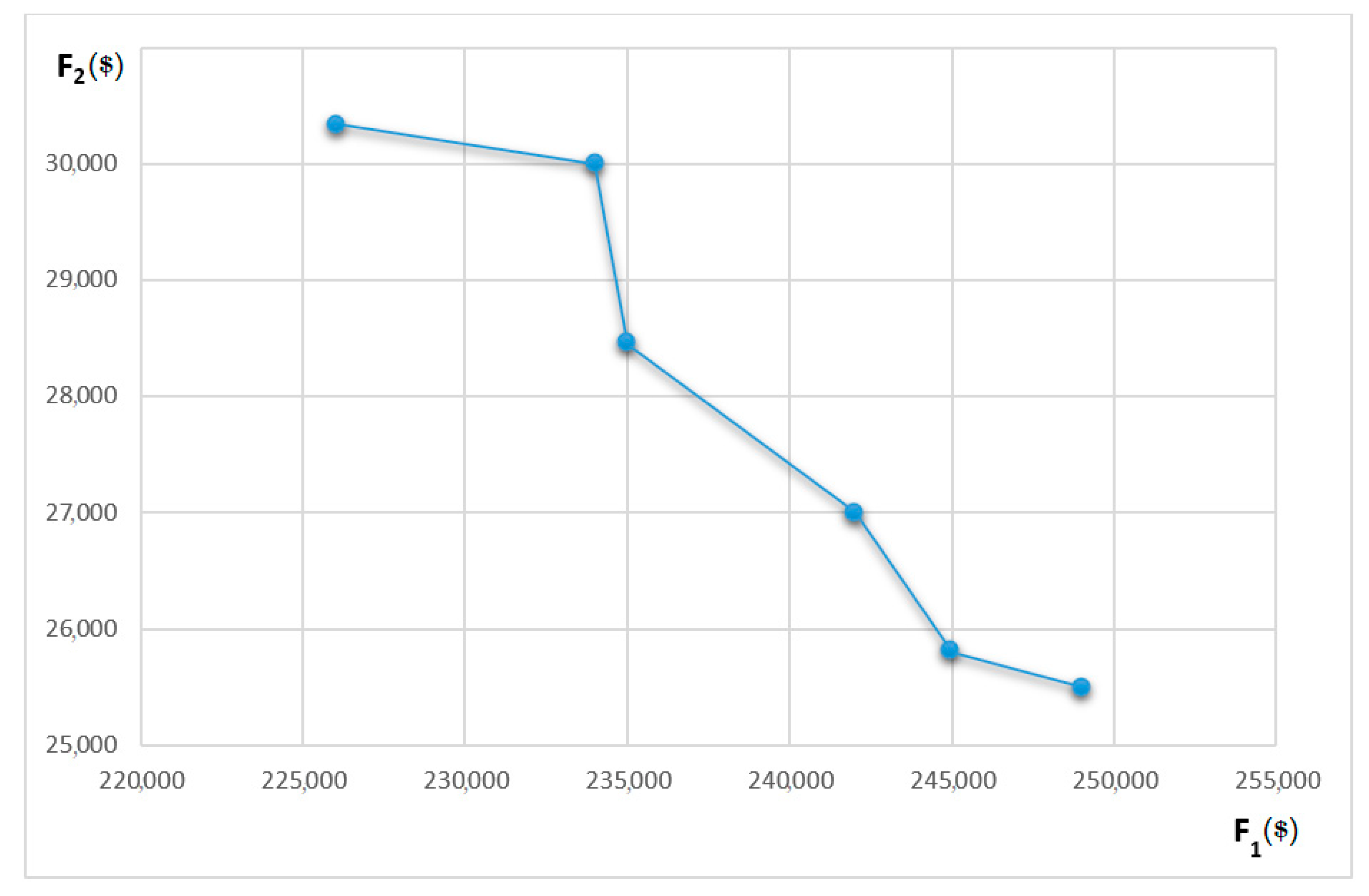
4.1.2. Results
4.2. Approach to Solving the Problem
4.2.1. NSGA-II
| Algorithm 1: NSGA-II |
|
1. 2. While 3. 4. 5. 6. 7. 8. 9. Apply crowding-distance-assignment 10. 11. 12. 13. 14. 15. 16. end while |
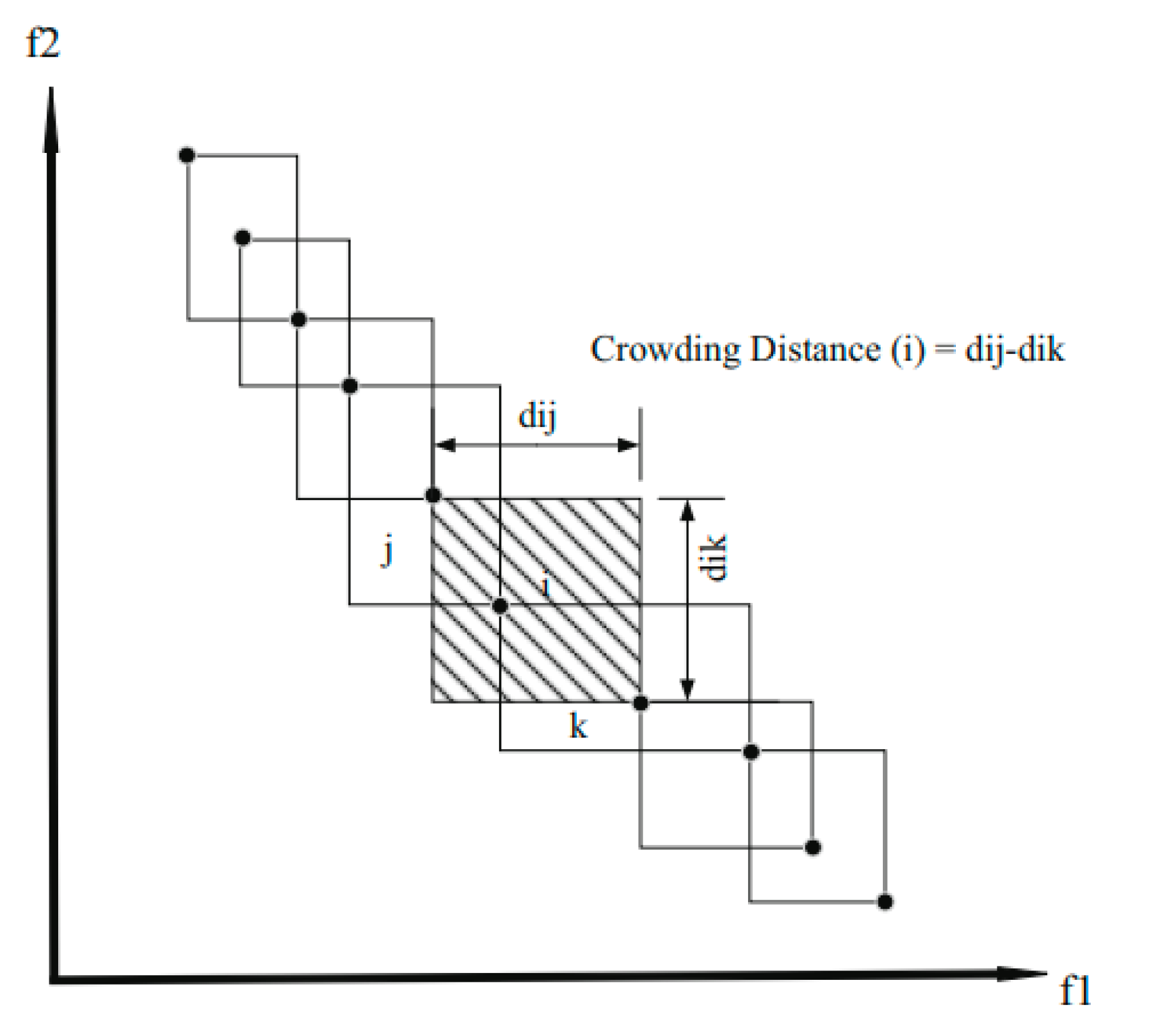
4.2.2. Crowding Distance (CD)
4.3. Application of the NSGA-II
4.3.1. Encoding Strategy
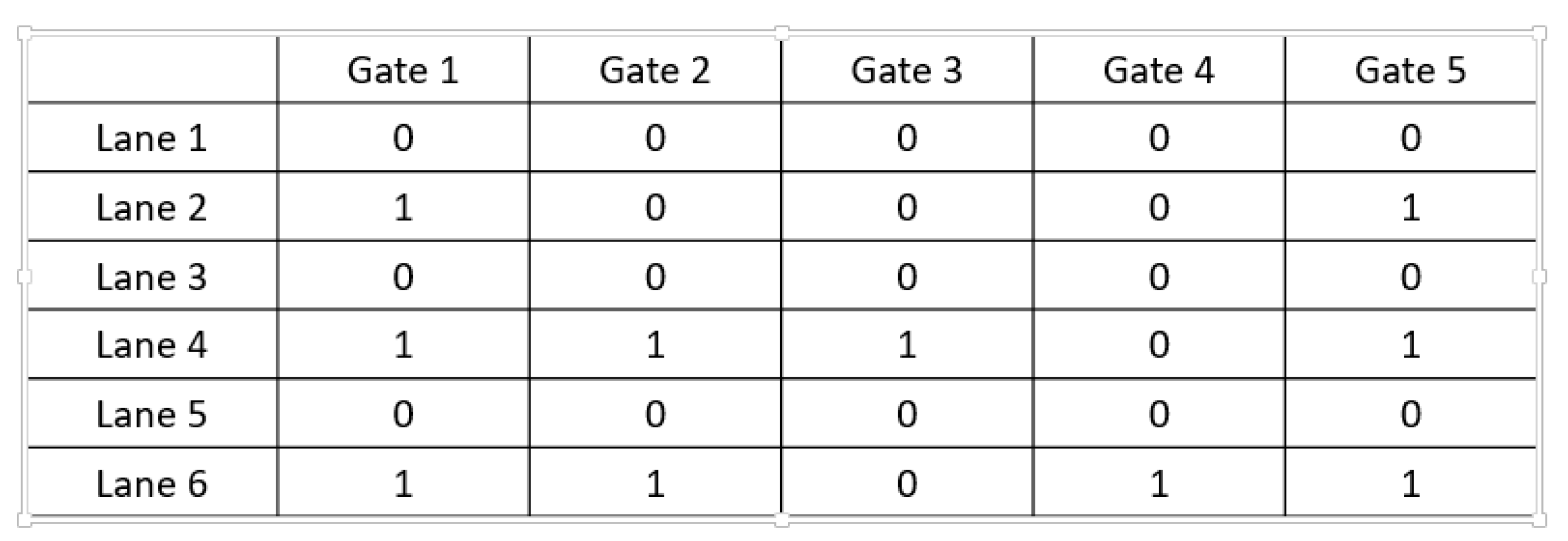
- Open gates in each charging lane of the road are coded in the form of a chromosome with a matrix, noted with:where is the number of charging lanes on the road and is the number of gates on charging lane . The number of columns of depends on, which differs from one charging lane to another; so, to generate , let be the number of columns of the matrix , with , so and .
- The used gates of each vehicle type is a table noted by B =, with:
4.3.2. Initial Population
- be the set of selected vehicles;
- be the set of vehicles indexed by ;
- be the set of open gates;
- be the set of the potential gates indexed by and ;
- be the set of the charging lane indexed by .
| Algorithm 2: Generation of an individual |
|
17. 18. for each vehicle 19. do: 20. 21. If the ensures the trip of the without remaining out of charge 22. 23. Else 24. for each charging lane 25. for each potential gate 26. and is active 27. Make the gate 28. end if 29. else if is inactive 30. 31. is closed 32. Make 33. end if 34. 35. end if 36. else Make closed 37. end for 38. end for 39. end while 40. end for |
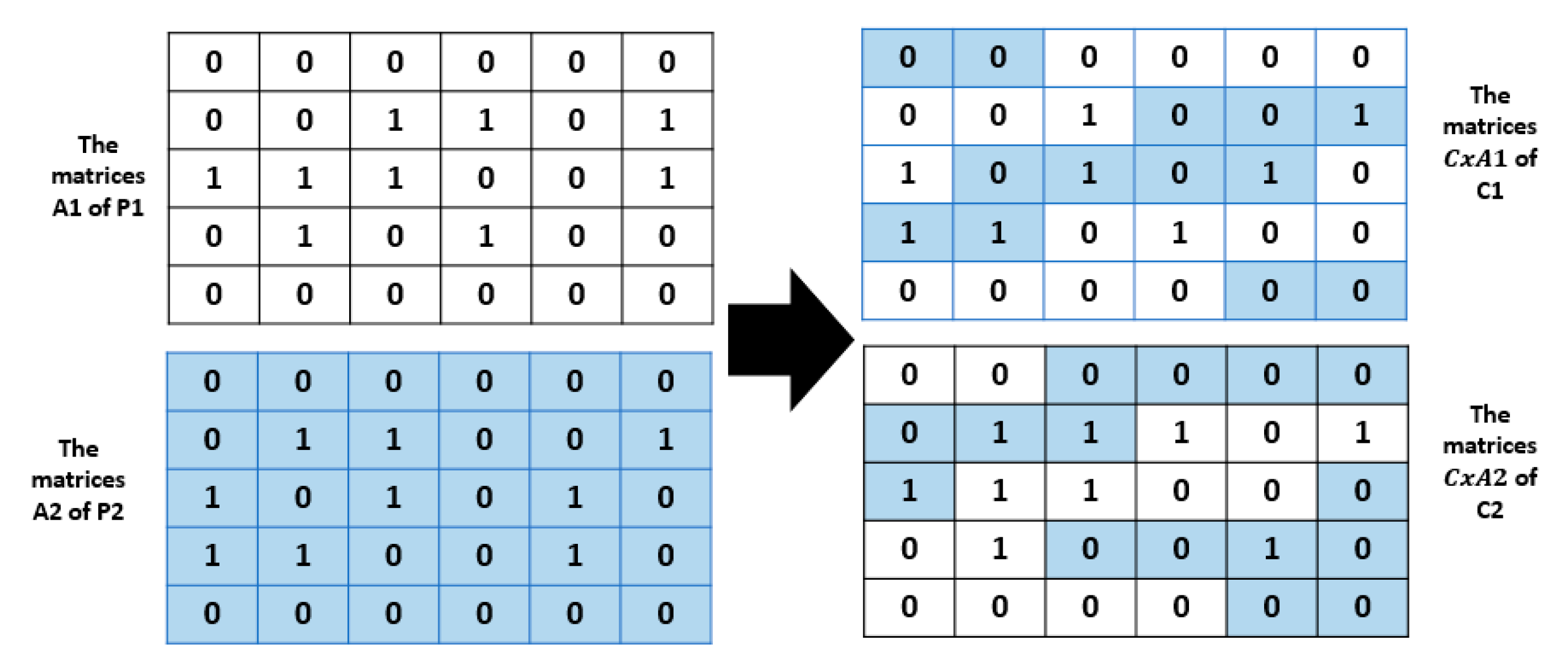
4.3.3. Crossover Procedure
- -
- For the first part of the crossover:
- -
- For the second part of the crossover:
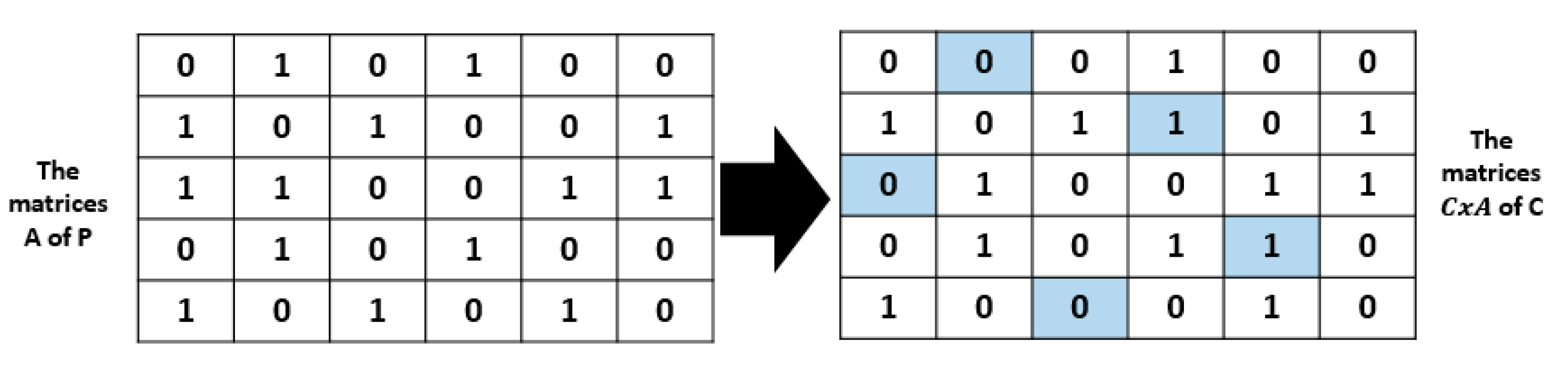
| Algorithm 3: Correction Algorithm |
|
1. for each vehicle 2. for each charging line 3. for each potential gate 4. If and is active 5. Make the gate open 6. end if 7. else 8. if is inactive 9. 10. is closed 11. Make 12. end if 13. 14. end if 15. end for 16. end for 17. end for |
4.3.4. Mutation Procedure
4.3.5. Case Study
4.3.6. Transport Network Data
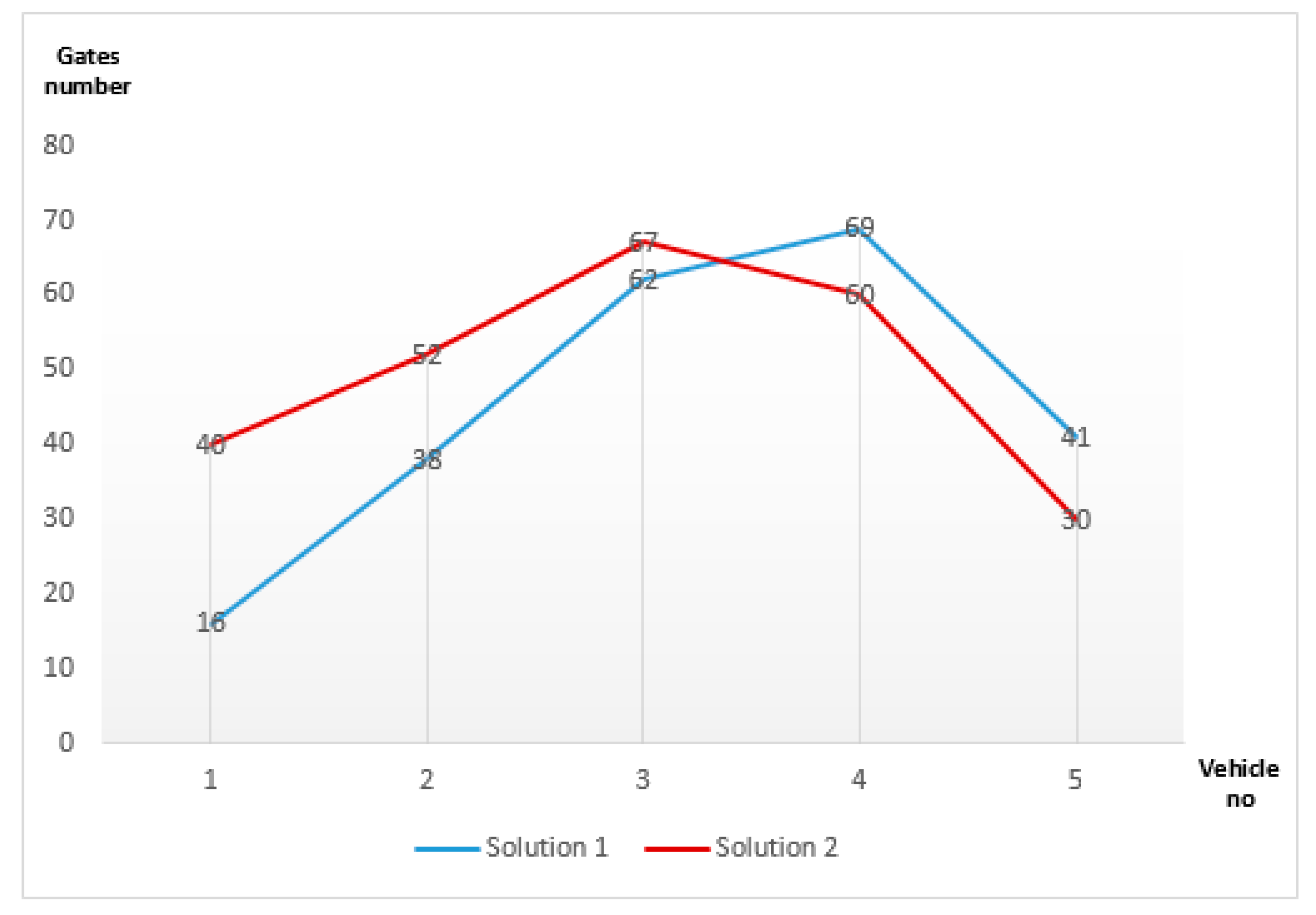
4.3.7. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Qiu, C.; Chau, K.T.; Ching, T.W.; Liu, C. Overview of wireless charging technologies for electric vehicles. J. Asian Electr. Veh. 2014, 12, 1679–1685. [Google Scholar] [CrossRef]
- Jeong, S.; Jang, Y.J.; Kum, D. Economic analysis of the dynamic charging electric vehicle. IEEE Trans. Power Electr. 2015, 30, 6368–6377. [Google Scholar] [CrossRef]
- Bourzik, M.; Hilali Alaoui, A.E.L. The Optimal location of the wireless charging infrastructure for electric vehicles with heterogeneous batteries in the highway. Int. J. Logist. Syst. Manag. 2022; in press. [Google Scholar]
- Rim, C.T.; Mi, C. Wireless Power Transfer for Electric Vehicles and Mobile Devices; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Alwesabi, Y.; Wang, Y.; Avalos, R.; Liu, Z. Electric bus scheduling under single depot dynamic wireless charging infrastructure planning. Energy 2020, 213, 118855. [Google Scholar] [CrossRef]
- Jang, Y.J.; Jeong, S.; Lee, M.S. Initial energy logistics cost analysis for stationary, quasi-dynamic, and dynamic wireless charging public transportation systems. Energies 2016, 9, 483. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Z. Robust planning of dynamic wireless charging infrastructure for battery-electric buses. Transp. Res. Part C Emerg. Technol. 2017, 83, 77–103. [Google Scholar] [CrossRef]
- Liu, Z.; Song, Z. Dynamic charging infrastructure deployment for plug-in hybrid electric trucks. Transp. Res. Part C Emerg. Technol. 2018, 95, 748–772. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Cao, J. Particle swarm optimization-based optimal power management of plug-in hybrid electric vehicles considering uncertain driving conditions. Energy 2016, 96, 197–208. [Google Scholar] [CrossRef]
- Chen, Z.; Yin, Y.; Song, Z. A cost-competitiveness analysis of charging infrastructure for electric bus operations. Transp. Res. Part C Emerg. Technol. 2018, 93, 351–366. [Google Scholar] [CrossRef]
- Fuller, M. Wireless charging in California: Range, recharge, and vehicle electrification. Transp. Res. Part C Emerg. Technol. 2016, 67, 343–356. [Google Scholar] [CrossRef]
- Mouhrim, N.; El Hilali Alaoui, A.; Boukachour, J. Pareto efficient allocation of in-motion wireless charging infrastructure for electric vehicles in a multipath network. Int. J. Sustain. Transp. 2019, 13, 419–432. [Google Scholar] [CrossRef]
- Elbaz, H.; Elhilali Alaoui, A. Optimal Installation of the Power Transmitters in the Dynamic Wireless Charging for Electric Vehicles in a Multipath Network with the Round-Trip Case. Int. J. Intell. Transp. Syst. Res. 2022, 20, 46–63. [Google Scholar] [CrossRef]
- Sun, X.; Chen, Z.; Yin, Y. Integrated planning of static and dynamic charging infrastructure for electric vehicles. Transp. Res. Part D Transp. Environ. 2020, 83, 102331. [Google Scholar] [CrossRef]
- Ko, Y.K.; Oh, Y.; Ryu, D.Y.; Ko, Y.D. Optimal Deployment of Wireless Charging Infrastructure for Electric Tram with Dual Operation Policy. Vehicles 2022, 4, 681–696. [Google Scholar] [CrossRef]
- Anand, R.; Aggarwal, D.; Kumar, V. A comparative analysis of optimization solvers. J. Stat. Manag. Syst. 2017, 20, 623–635. [Google Scholar] [CrossRef]
- Seshadri, A. A Fast Elitist Multiobjective Genetic Algorithm: NSGA-II; MATLAB Central. 2006, Volume 182. Available online: https://web.njit.edu/~{}horacio/Math451H/download/Seshadri_NSGA-II.pdf (accessed on 13 January 2022).
- Carlucci, S.; Cattarin, G.; Causone, F.; Pagliano, L. Multi-objective optimization of a nearly zero-energy building based on thermal and visual discomfort minimization using a non-dominated sorting genetic algorithm (NSGA-II). Energy Build. 2015, 104, 378–394. [Google Scholar] [CrossRef]
- Morell, J.Á.; Dahi, Z.A.; Chicano, F.; Luque, G.; Alba, E. Optimising Communication Overhead in Federated Learning Using NSGA-II. In International Conference on the Applications of Evolutionary Computation (Part of EvoStar); Springer: Cham, Switzerland, 2022; pp. 317–333. [Google Scholar]
- Da Silva, D.F.; Okada, L.F.; Assunção, W.K.; Colanzi, T.E. Intensifying the search-based optimization of product line architectures with crossover operators. Empir. Softw. Eng. 2022, 27, 166. [Google Scholar] [CrossRef]
- Chen, D.; Song, M. An improved knowledge-informed NSGA-II for multi-objective land allocation (MOLA). Geo-Spat. Inf. Sci. 2018, 21, 273–287. [Google Scholar]
- Chatelain, C.; Adam, S.; Lecourtier, Y.; Heutte, L.; Paquet, T. A multi-model selection framework for unknown and/or evolutive misclassification cost problems. Pattern Recognit. 2010, 43, 815–823. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X. An improved NSGA-II algorithm based on crowding distance elimination strategy. Int. J. Comput. Intell. Syst. 2019, 12, 513–518. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Hajmohammad, M.H. Multi-objective optimization of laminated composite shells for minimum mass/cost and maximum buckling pressure with failure criteria under external hydrostatic pressure. Struct. Multidiscip. Optim. 2017, 55, 1051–1062. [Google Scholar] [CrossRef]
- Chu, X.; Yu, X. Improved crowding distance for NSGA-II. arXiv 2018, arXiv:1811.12667. [Google Scholar]




| Vehicle 1 | Vehicle 2 | Vehicle 3 | Vehicle 4 | |
|---|---|---|---|---|
| 4.2 | 3 | 5 | 5.5 | |
| 25.2 | 19.6 | 19.5 | 34.7 | |
| 8 | 17.8 | 13.8 | 20 | |
| 2.7 | 3.8 | 5.7 | 4 | |
| Unit cost for using the DWCS road | 12.5 | 8.5 | 10 | 14 |
| Lane Number | Length | Lane Status | Potential Gates Number |
|---|---|---|---|
| 1 | 500 | Inactive | 0 |
| 2 | 750 | Active | 4 |
| 3 | 500 | Inactive | 0 |
| 4 | 500 | Active | 4 |
| 5 | 500 | Inactive | 0 |
| 6 | 1000 | Active | 4 |
| 7 | 750 | Inactive | 0 |
| 8 | 500 | Active | 4 |
| 9 | 500 | Inactive | 0 |
| 10 | 1000 | Active | 4 |
| 11 | 250 | Inactive | 0 |
| 12 | 250 | Active | 4 |
| 13 | 500 | Inactive | 0 |
| Minimizing the T.U.C | Minimizing the Open Gates | |
|---|---|---|
| Total cost of open gates on the road | 19,000 | 0 |
| T.U.C of vehicle 1 | 137.5 | 312.5 |
| T.U.C of vehicle 2 | 127.5 | 212.5 |
| T.U.C of vehicle 3 | 150 | 250 |
| T.U.C of vehicle 4 | 126 | 294 |
| Seg. No | Seg. Status | Lane No. | Lane Status | Seg. No | Seg. Status | Lane No. | Lane Status |
|---|---|---|---|---|---|---|---|
| 1-2 | Inactive | Inactive | 144 | Inactive | 57 | Inactive | |
| 3-4-5-6-7-8-9-10 | Active | 2 | Active | 145-146-147-148-149 | Active | 58 | Active |
| 11-12 | Inactive | 3 | Inactive | 150 | Inactive | 59 | Inactive |
| 13-14 | Active | 4 | Active | 151 | Active | 60 | Active |
| 15 | Inactive | 5 | Inactive | 152 | Inactive | 61 | Inactive |
| 16 | Active | 6 | Active | 153 | Active | 62 | Active |
| 17 | Inactive | 7 | Inactive | 154 | Inactive | 63 | Inactive |
| 18-19-20-21 | Active | 8 | Active | 155-156-157 | Active | 64 | Active |
| 22 | Inactive | 9 | Inactive | 158 | Inactive | 65 | Inactive |
| 23 | Active | 10 | Active | 159-160-161 | Active | 66 | Active |
| 24 | Inactive | 11 | Inactive | 162 | Inactive | 67 | Inactive |
| 25-26 | Active | 12 | Active | 163-164-165-166-167-168 | Active | 68 | Active |
| 27 | Inactive | 13 | Inactive | 169 | Inactive | 69 | Inactive |
| 28 | Active | 14 | Active | 170 | Active | 70 | Active |
| 29 | Inactive | 15 | Inactive | 171 | Inactive | 71 | Inactive |
| 30 | Active | 16 | Active | 172-173 | Active | 72 | Active |
| 31 | Inactive | 17 | Inactive | 174 | Inactive | 73 | Inactive |
| 32 | Active | 18 | Active | 175 | Active | 74 | Active |
| 33 | Inactive | 19 | Inactive | 176 | Inactive | 75 | Inactive |
| 34-35-36-37-38-39-40 | Active | 20 | Active | 177 | Active | 76 | Active |
| 41 | Inactive | 21 | Inactive | 178 | Inactive | 77 | Inactive |
| 42-43 | Active | 22 | Active | 179-180 | Active | 78 | Active |
| 44-45 | Inactive | 23 | Inactive | 181 | Inactive | 79 | Inactive |
| 46-47-48-49 | Active | 24 | Active | 182-183 | Active | 80 | Active |
| 50 | Inactive | 25 | Inactive | 184 | Inactive | 81 | Inactive |
| 60-70-71-72 | Active | 26 | Active | 185 | Active | 82 | Active |
| 73-74 | Inactive | 27 | Inactive | 186 | Inactive | 83 | Inactive |
| 75-76 | Active | 28 | Active | 187 | Active | 84 | Active |
| 77-78-79 | Inactive | 29 | Inactive | 188 | Inactive | 85 | Inactive |
| 80-81-82-83 | Active | 30 | Active | 189-190-191-192 | Active | 86 | Active |
| 84-85 | Inactive | 31 | Inactive | 193-194 | Inactive | 87 | Inactive |
| 86-87 | Active | 32 | Active | 195-196-197 | Active | 88 | Active |
| 88 | Inactive | 33 | Inactive | 189-190 | Inactive | 89 | Inactive |
| 89-90-91-92-93-94 | Active | 34 | Active | 191-192-193-194 | Active | 90 | Active |
| 95 | Inactive | 35 | Inactive | 195-196 | Inactive | 91 | Inactive |
| 96-97-98-99 | Active | 36 | Active | 197-198-199-200-201-202-203-204-205 | Active | 92 | Active |
| 100 | Inactive | 37 | Inactive | 206-207 | Inactive | 93 | Inactive |
| 101-102-103 | Active | 38 | Active | 208-209-210 | Active | 94 | Active |
| 104 | Inactive | 39 | Inactive | 211 | Inactive | 95 | Inactive |
| 105-106-107-108-109-110-111-112-113 | Active | 40 | Active | 212-213 | Active | 96 | Active |
| 114-115 | Inactive | 41 | Inactive | 214 | Inactive | 97 | Inactive |
| 116-117-118 | Active | 42 | Active | 215-216-217 | Active | 98 | Active |
| 119 | Inactive | 43 | Inactive | 218 | Inactive | 99 | Inactive |
| 120-121-122-123-124-125 | Active | 44 | Active | 219-220-221-222-223-224-225 | Active | 100 | Active |
| 126 | Inactive | 45 | Inactive | 226-227 | Inactive | 101 | Inactive |
| 127 | Active | 46 | Active | 228-229-230-231 | Active | 102 | Active |
| 128 | Inactive | 47 | Inactive | 232 | Inactive | 103 | Inactive |
| 129-130 | Active | 48 | Active | 233-234 | Active | 104 | Active |
| 131-132 | Inactive | 49 | Inactive | 235 | Inactive | 105 | Inactive |
| 133-134 | Active | 50 | Active | 236-237-238-139 | Active | 106 | Active |
| 135 | Inactive | 51 | Inactive | 240 | Inactive | 107 | Inactive |
| 136 | Active | 52 | Active | ||||
| 137 | Inactive | 53 | Inactive | ||||
| 138-139-140 | Active | 54 | Active | ||||
| 141 | Inactive | 55 | Inactive | ||||
| 142-143 | Active | 56 | Active |
| Battery Capacity | Energy Supply Rate | Energy Consumption Rate | Unit Cost for Using the DWCS Road | |
|---|---|---|---|---|
| Vehicle 1 | 7.6 | 1.1 | 29.5 | 13.5 |
| Vehicle 2 | 42.2 | 0.9 | 17.8 | 11 |
| Vehicle 3 | 11.6 | 1.3 | 30.6 | 17 |
| Vehicle 4 | 18.4 | 0.4 | 19.5 | 9 |
| Vehicle 5 | 16 | 1.2 | 25.8 | 15 |
| Lane No. | PG Number | Open Gates Number | Lane No. | PG Number | Number of Open Gates |
|---|---|---|---|---|---|
| 2 | 40 | 6 | 56 | 10 | 2 |
| 4 | 10 | 2 | 58 | 25 | 3 |
| 6 | 5 | 0 | 60 | 5 | 0 |
| 8 | 20 | 3 | 62 | 5 | 0 |
| 10 | 5 | 1 | 64 | 15 | 2 |
| 12 | 10 | 2 | 66 | 15 | 2 |
| 14 | 5 | 0 | 68 | 30 | 4 |
| 16 | 5 | 0 | 70 | 5 | 0 |
| 18 | 5 | 1 | 72 | 10 | 2 |
| 20 | 35 | 5 | 74 | 5 | 0 |
| 22 | 10 | 2 | 76 | 5 | 0 |
| 24 | 20 | 5 | 78 | 10 | 2 |
| 26 | 20 | 3 | 80 | 5 | 0 |
| 28 | 10 | 3 | 82 | 5 | 0 |
| 30 | 20 | 6 | 84 | 5 | 1 |
| 32 | 10 | 1 | 86 | 20 | 3 |
| 34 | 30 | 6 | 88 | 15 | 2 |
| 36 | 20 | 5 | 90 | 20 | 5 |
| 38 | 15 | 4 | 92 | 45 | 5 |
| 40 | 45 | 7 | 94 | 15 | 2 |
| 42 | 15 | 5 | 96 | 10 | 1 |
| 44 | 30 | 4 | 98 | 15 | 2 |
| 46 | 5 | 0 | 100 | 35 | 4 |
| 48 | 10 | 1 | 102 | 20 | 3 |
| 50 | 10 | 2 | 104 | 10 | 1 |
| 52 | 5 | 0 | 106 | 20 | 4 |
| 54 | 15 | 3 |
| Lane No. | PG Number | Number of Open Gates | Lane No. | PG Number | Number of Open Gates |
|---|---|---|---|---|---|
| 2 | 40 | 8 | 56 | 10 | 4 |
| 4 | 10 | 4 | 58 | 25 | 2 |
| 6 | 5 | 0 | 60 | 5 | 1 |
| 8 | 20 | 4 | 62 | 5 | 0 |
| 10 | 5 | 1 | 64 | 15 | 2 |
| 12 | 10 | 2 | 66 | 15 | 3 |
| 14 | 5 | 0 | 68 | 30 | 4 |
| 16 | 5 | 0 | 70 | 5 | 1 |
| 18 | 5 | 1 | 72 | 10 | 3 |
| 20 | 35 | 7 | 74 | 5 | 1 |
| 22 | 10 | 3 | 76 | 5 | 0 |
| 24 | 20 | 6 | 78 | 10 | 2 |
| 26 | 20 | 3 | 80 | 5 | 1 |
| 28 | 10 | 4 | 82 | 5 | 0 |
| 30 | 20 | 7 | 84 | 5 | 1 |
| 32 | 10 | 3 | 86 | 20 | 2 |
| 34 | 30 | 6 | 88 | 15 | 2 |
| 36 | 20 | 6 | 90 | 20 | 6 |
| 38 | 15 | 3 | 92 | 45 | 7 |
| 40 | 45 | 8 | 94 | 15 | 1 |
| 42 | 15 | 3 | 96 | 10 | 1 |
| 44 | 30 | 5 | 98 | 15 | 1 |
| 46 | 5 | 1 | 100 | 35 | 5 |
| 48 | 10 | 1 | 102 | 20 | 2 |
| 50 | 10 | 3 | 104 | 10 | 2 |
| 52 | 5 | 1 | 106 | 20 | 3 |
| 54 | 15 | 3 |
| T.U.C of Solution 1 | T.U.C of Solution 2 | |
|---|---|---|
| Vehicle 1 | 7020 | 6001 |
| Vehicle 2 | 4129 | 4059 |
| Vehicle 3 | 7803 | 6038 |
| Vehicle 4 | 3960 | 3010 |
| Vehicle 5 | 7425 | 6393 |
| T.U.C | Open Gate Cost | |
|---|---|---|
| Vehicle 1 | 12,920 | 215,000 |
| Vehicle 2 | 8514 | |
| Vehicle 3 | 15,096 | |
| Vehicle 4 | 6960 | |
| Vehicle 5 | 13,230 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourzik, M.; Elbaz, H.; Elhilali Alaoui, A. The Optimal Deployment of the Entry and Exit Gates of Electric Vehicles Wireless Charging Transmitters on Highways. World Electr. Veh. J. 2022, 13, 227. https://doi.org/10.3390/wevj13120227
Bourzik M, Elbaz H, Elhilali Alaoui A. The Optimal Deployment of the Entry and Exit Gates of Electric Vehicles Wireless Charging Transmitters on Highways. World Electric Vehicle Journal. 2022; 13(12):227. https://doi.org/10.3390/wevj13120227
Chicago/Turabian StyleBourzik, Mohammed, Hassane Elbaz, and Ahmed Elhilali Alaoui. 2022. "The Optimal Deployment of the Entry and Exit Gates of Electric Vehicles Wireless Charging Transmitters on Highways" World Electric Vehicle Journal 13, no. 12: 227. https://doi.org/10.3390/wevj13120227
APA StyleBourzik, M., Elbaz, H., & Elhilali Alaoui, A. (2022). The Optimal Deployment of the Entry and Exit Gates of Electric Vehicles Wireless Charging Transmitters on Highways. World Electric Vehicle Journal, 13(12), 227. https://doi.org/10.3390/wevj13120227






