MPC-Based Obstacle Avoidance Path Tracking Control for Distributed Drive Electric Vehicles
Abstract
1. Introduction
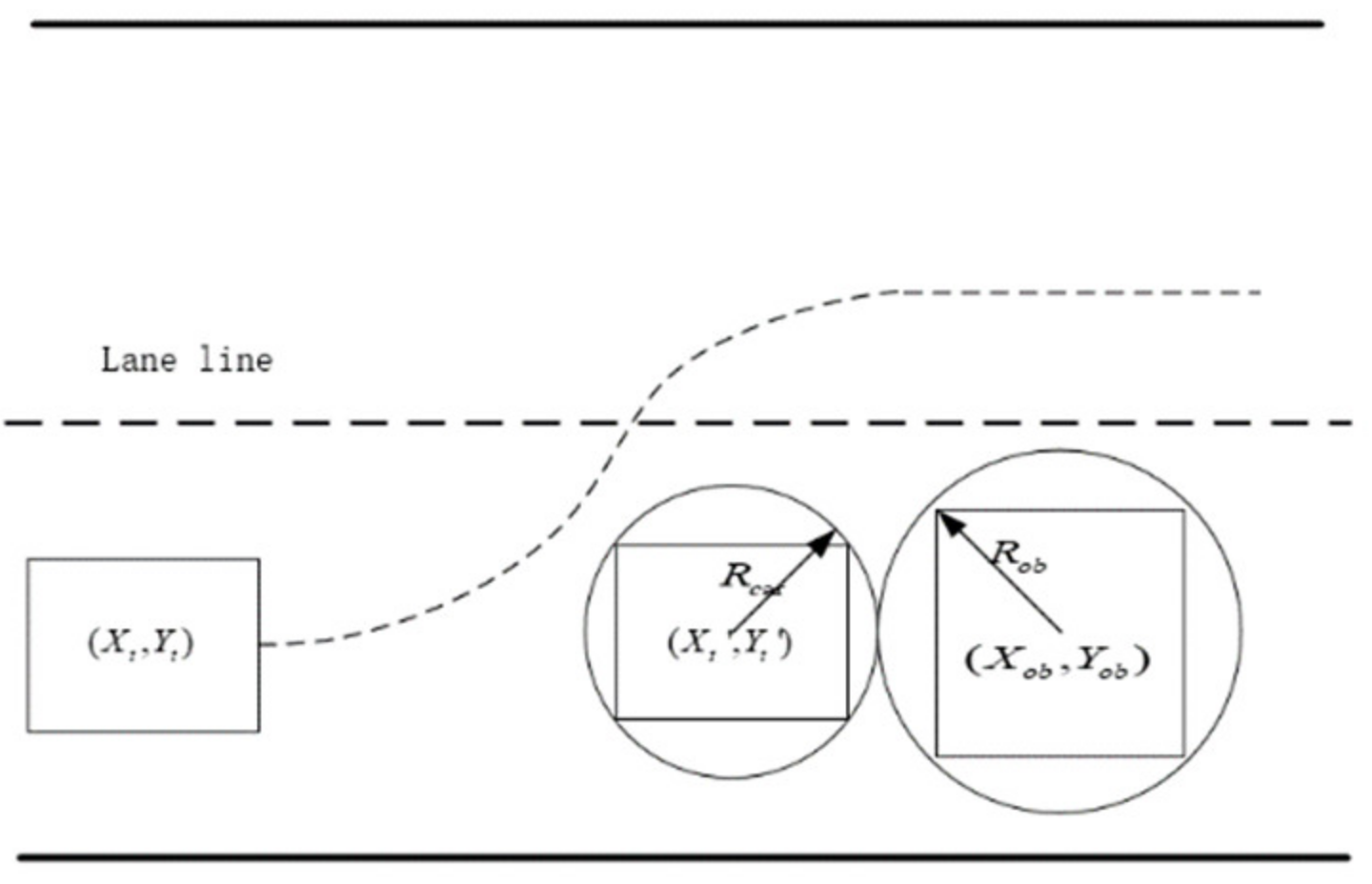
2. Path Planning
3. Path Tracking Control
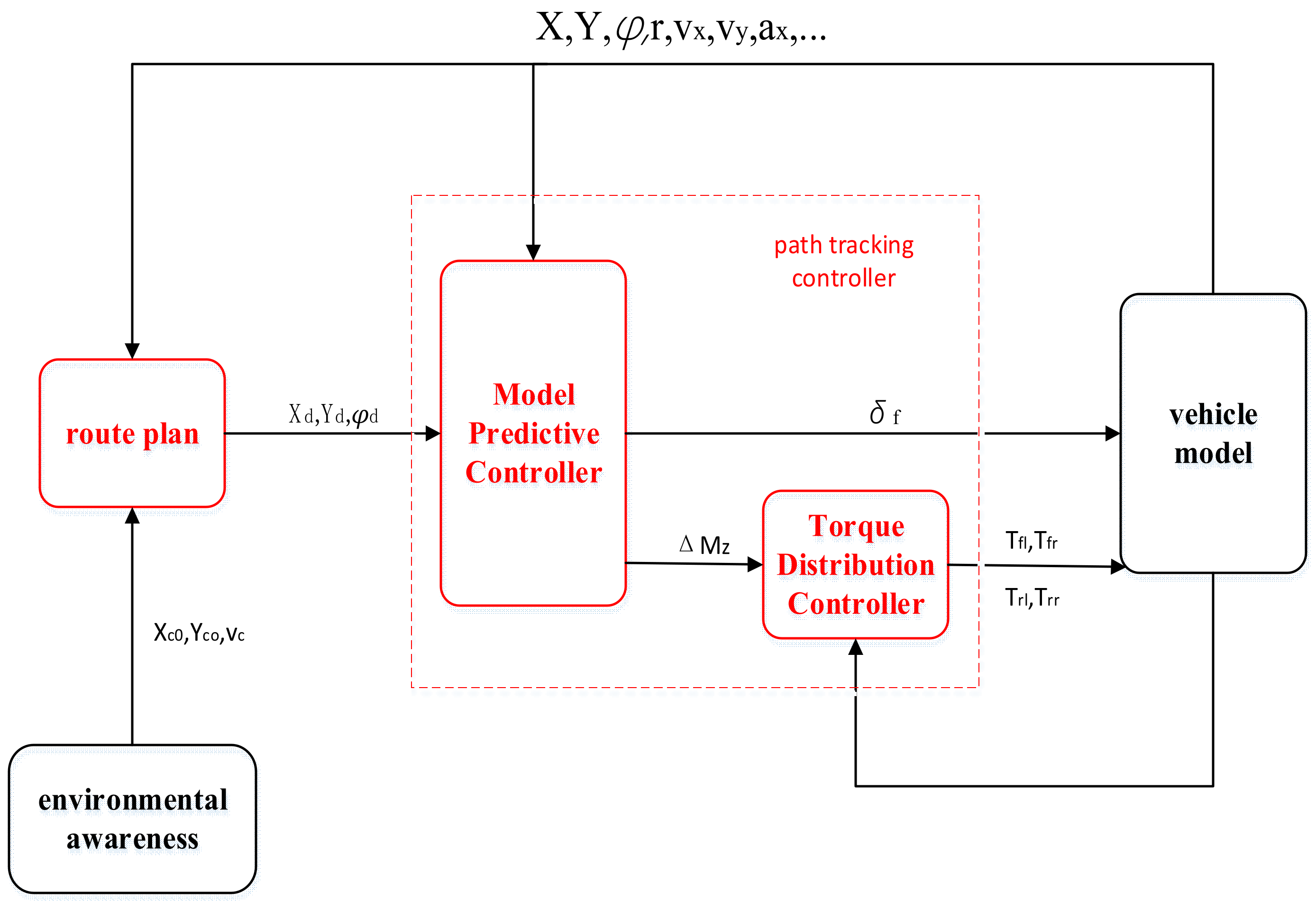
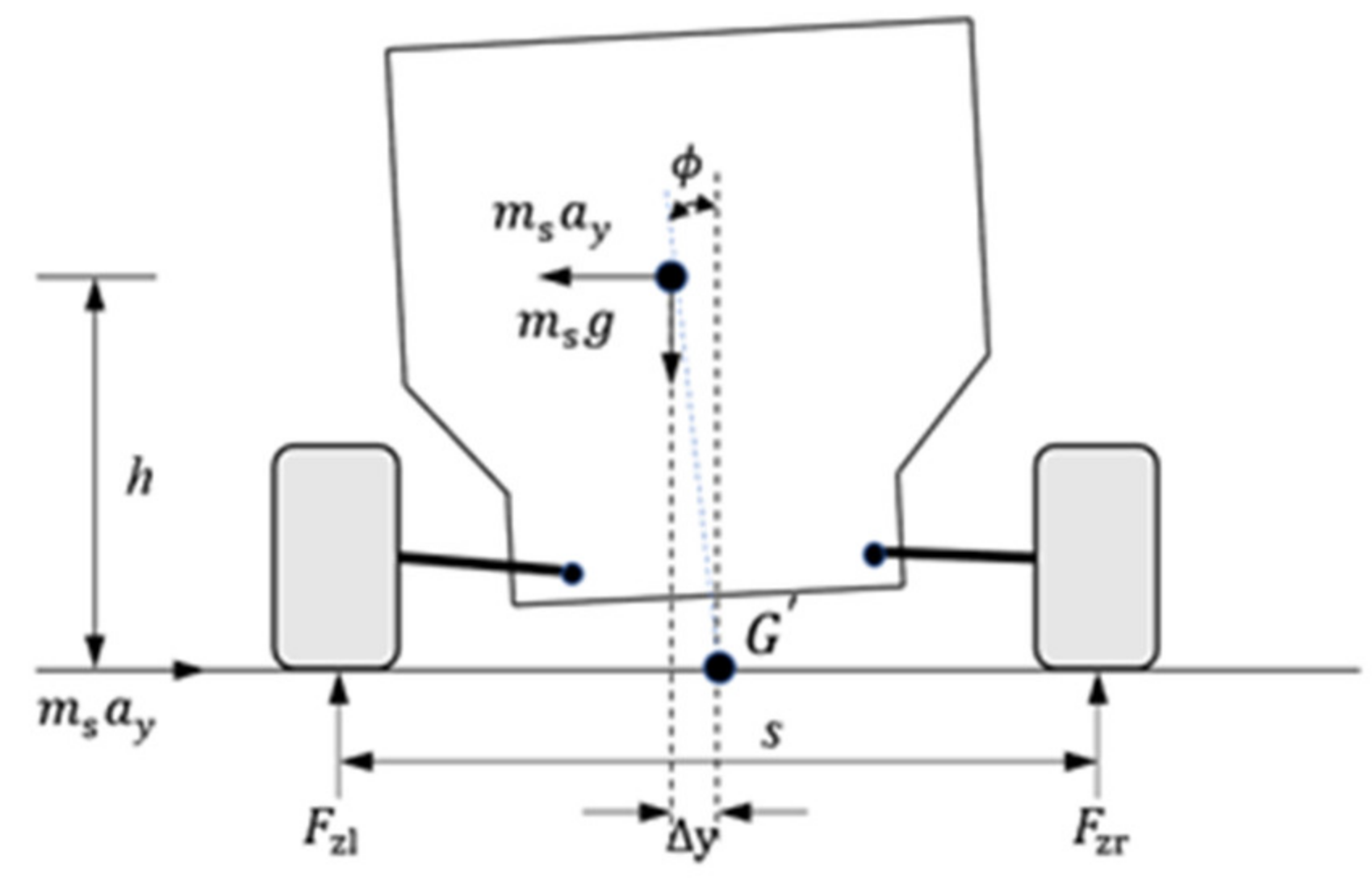
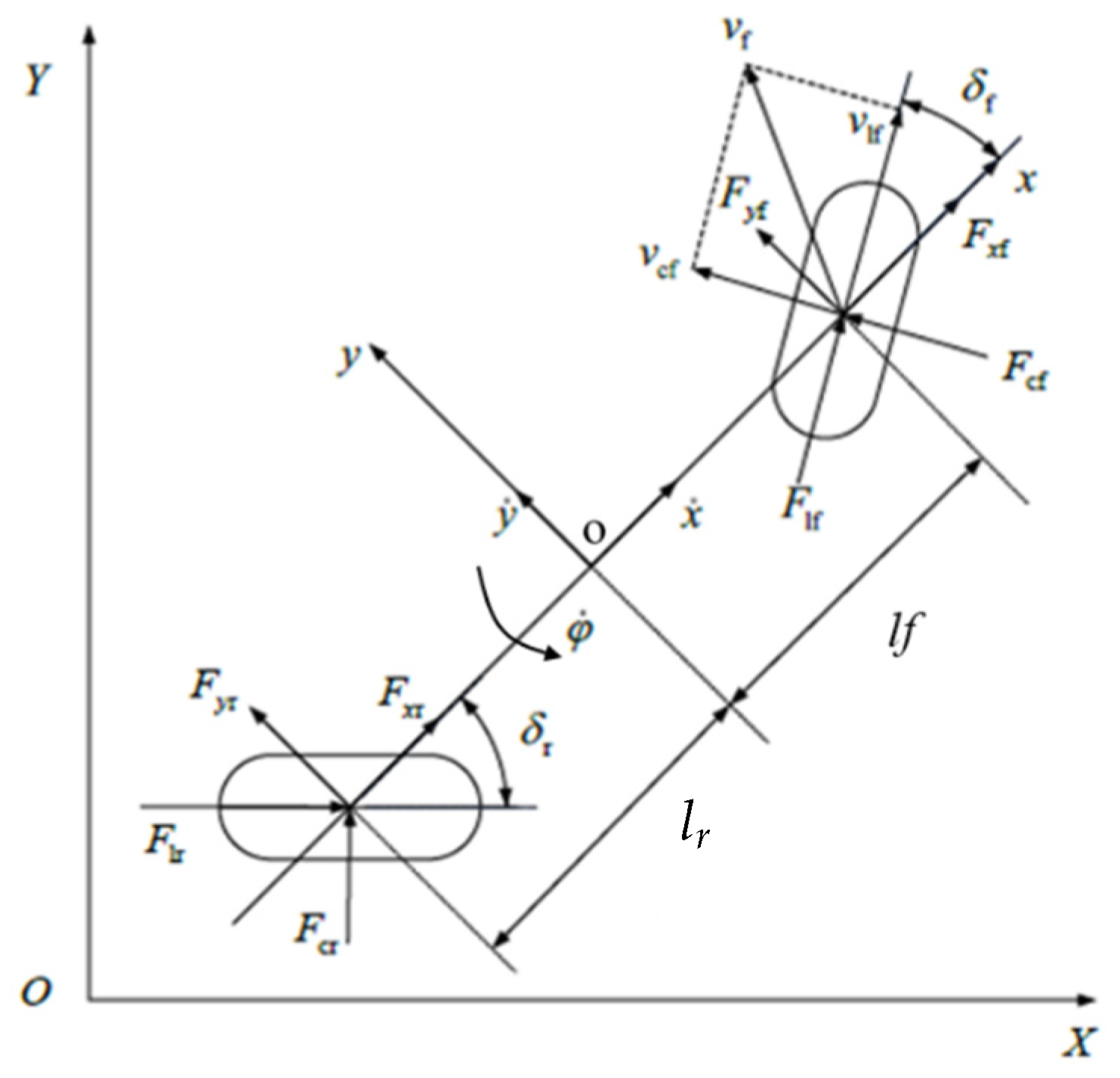
3.1. Establishment of Vehicle Dynamics Model
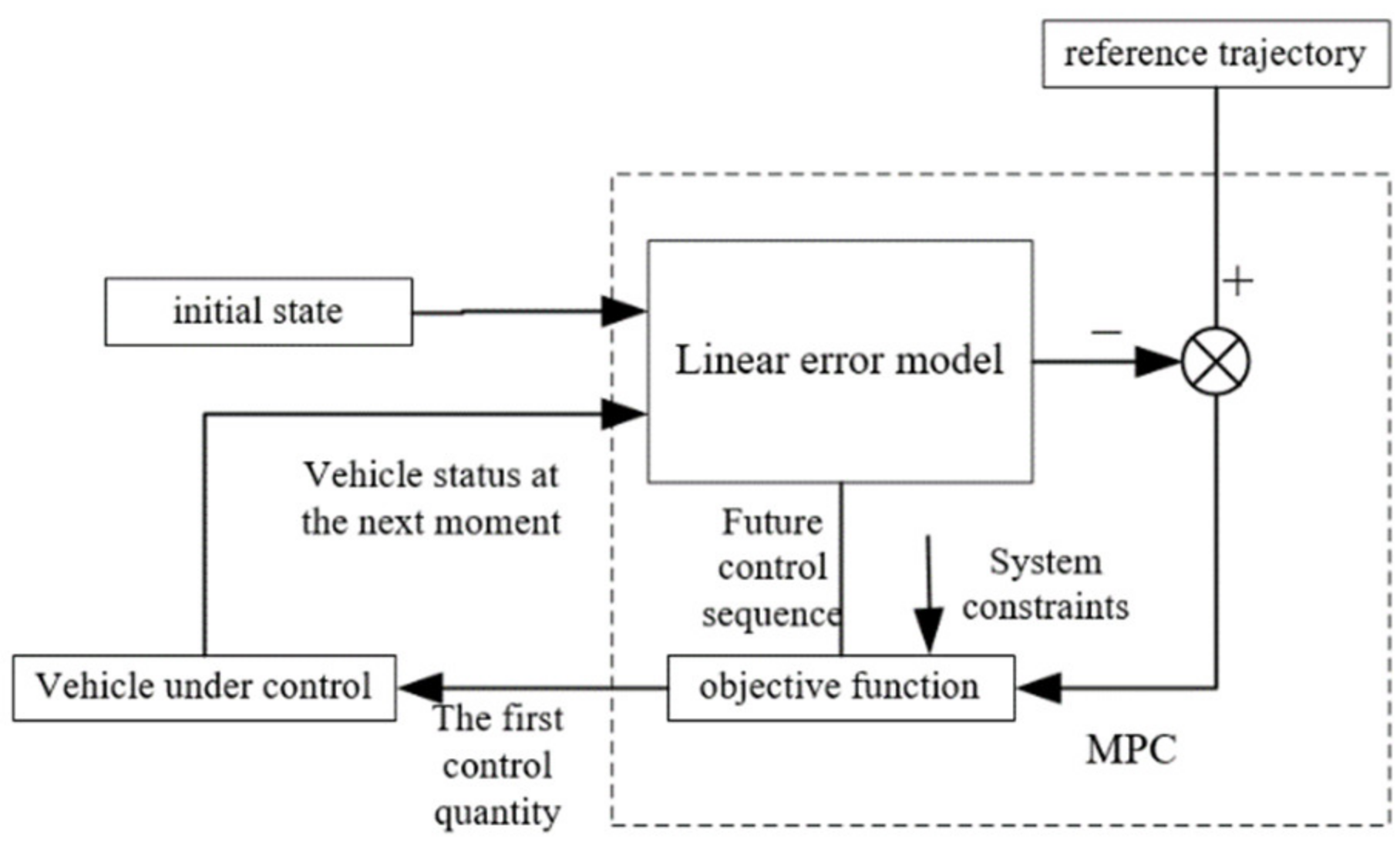
3.2. MPC Controller Design
3.3. Torque Distribution Controller Design
4. Simulation Analysis and Verification
4.1. Verification of Co-Simulation Platform
4.2. Simulation of Tracking Control Performance
5. Conclusions
- (1)
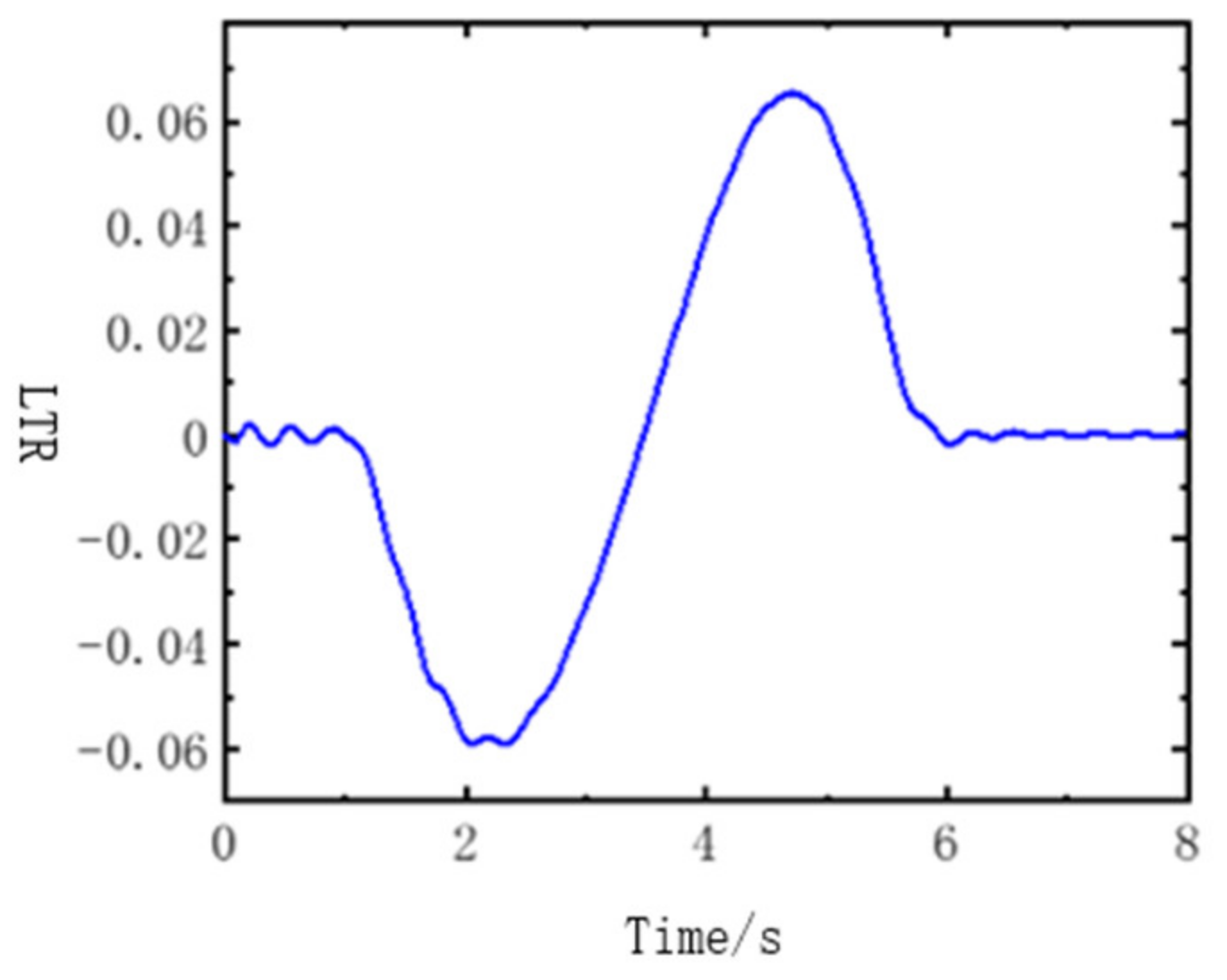
- Sixth-order polynomial for obstacle avoidance path planning is presented. Through the simulation results, it is verified that the planned path can be accurately tracked, and the LTR values are always within the safe range. The vehicle has no risk of rollover. The obstacle avoidance path and tracking controller in this paper can effectively meet the requirements of safe obstacle avoidance.
- (2)
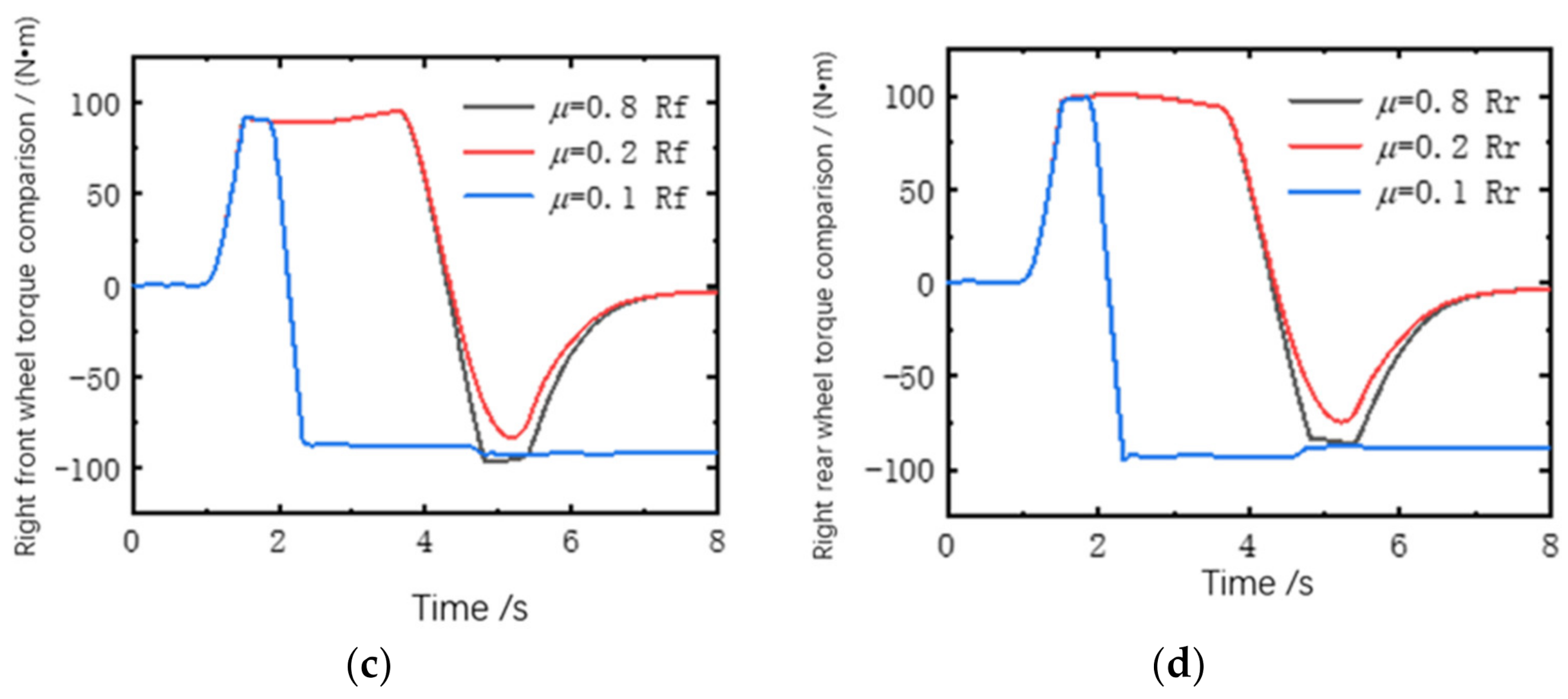
- In this paper, path planning, path tracking and torque distribution are combined to achieve safe obstacle avoidance through the tracking control of the obstacle avoidance path. The path-tracking controller not only realizes the intelligent obstacle avoidance process of unmanned vehicles but also combines it with distributed vehicles. The safety and stability are improved by the torque distribution strategy in the obstacle avoidance process compared with traditional vehicles. Simultaneously, simulations are carried out under different road adhesion coefficient conditions, and the simulation results show that the vehicle can still perform safe and stable automatic obstacle avoidance under the conditions of road adhesion coefficient μ = 0.2, indicating that the controller has good robustness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Global Status Report on Road Safety 2013: Supporting a Decade of Action; World Health Organization: Geneva, Switzerland, 2013.
- Toroyan, T. Global status report on road safety. Inj. Prev. 2009, 15, 286. [Google Scholar] [CrossRef] [PubMed]
- Chang, S.; Gordon, T. A flexible hierarchical model-based control methodology for vehicle active safety systems. Veh. Syst. Dyn. 2008, 46, 63–75. [Google Scholar] [CrossRef]
- Guo, J.; Hu, P.; Wang, R. Nonlinear coordinated steering and braking control of vision-based autonomous vehicles in emergency obstacle avoidance. IEEE Trans. Intell. Transp. Syst. 2016, 17, 3230–3240. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, W.; Zhang, L. Torque distribution control of electric vehicle driven by four wheel hub motor. J. Tongji Univ. Nat. Sci. Ed. 2008, 36, 5. [Google Scholar]
- Chen, T.; Chen, L.; Xu, X. Coordinated Control of Path Tracking and Stability of Distributed Driving Unmanned Vehicles. Automot. Eng. 2019, 41, 1109–1116. [Google Scholar]
- Zhang, B.; Li, Z.; Shen, G. Research on intelligent vehicle track tracking based on fuzzy neural network. Automot. Eng. 2019, 41, 7. [Google Scholar]
- Wang, Y.; Chen, Q.; Gao, L. A distributed driving vehicle path tracking method based on prediction-fuzzy joint control. Sci. Technol. Eng. 2020, 20, 15100–15108. [Google Scholar]
- Hu, J.; Zhong, X.; Chen, R. Intelligent Vehicle Path Tracking Control Based on Fuzzy LQR. Automot. Eng. 2022, 44, 17–25. [Google Scholar]
- Kou, F.; Zheng, W.; Zhang, X.; Yang, H.; He, J. Path following control of unmanned vehicle using state extended MPC and corner compensation. Mech. Sci. Technol. Aerosp. Eng. 2022, 4, 1–8. [Google Scholar]
- Wu, F.; Guo, S. Intelligent vehicle path tracking algorithm based on nonlinear model predictive control. Automot. Technol. 2020, 5, 1–7. [Google Scholar]
- Li, S.; Yang, Z.; Wang, X. Trajectory Tracking Control of Intelligent Vehicle Based on T-S Fuzzy Variable Weight MPC. J. Mech. Eng. 2022, 15, 1–14. [Google Scholar]
- Zhuang, Y.; Wu, Y.; Zhang, B. Coordinated Torque Control of Distributed Drive Electric Vehicle Based on Nonlinear MPC. J. Vib. Shock. 2021, 40, 9. [Google Scholar]
- Shino, M.; Nahai, M. Yaw-moment control of electric vehicle for improving handling and stability. JSAE Rev. 2001, 22, 473–480. [Google Scholar] [CrossRef]
- Zou, G.; Luo, Y.; Li, K. Optimal distribution method of all-wheel longitudinal force for four-wheel independent electric vehicle. J. Tsinghua Univ. Nat. Sci. Ed. 2009, 49, 719–722. [Google Scholar]
- One, E.; Hattori, Y.; Muragishi, Y. Vehicle dynamics integrated control for four-wheel-distributed steering and four-wheel-distributed traction/braking systems. Veh. Syst. Dyn. 2006, 44, 139–151. [Google Scholar] [CrossRef]
- Mokhiamar, O.; Abe, M. How the four wheels should share forces in an optimum cooperative chassis control. Control Eng. Pract. 2006, 14, 295–304. [Google Scholar] [CrossRef]
- Yu, Z.; Yang, P.; Xiong, L. Application of Control Distribution Theory in Vehicle Dynamics Control. Chin. J. Mech. Eng. 2014, 50, 99–107. [Google Scholar] [CrossRef]
- Mutoh, N. Driving and braking torque distribution methods for front-and rear-wheel-independent drive-type electric vehicles on roads wit low friction coefficient. IEEE Trans. Ind. Electron. 2012, 59, 3919–3933. [Google Scholar] [CrossRef]
- Yang, B.; Zhang, W.; Jiang, Z. Simulation analysis of obstacle avoidance path planning and tracking control for intelligent vehicles. China Test 2021, 47, 71–78. [Google Scholar]
- Ren, Y.; Zheng, L.; Zhang, W. Research on Active Collision Avoidance Control of Intelligent Vehicles Based on Model Predictive Control. Automot. Eng. 2019, 41, 405–410. [Google Scholar]
- Zhang, F.; Wei, M.; Huang, L. Research on vehicle emergency lane change control based on model predictive control. Mod. Manuf. Eng. 2017, 3, 57–64. [Google Scholar]
- Gong, J.; Jiang, W.; Xu, W. Model Predictive Control for Self-Driving Vehicles, 1st ed.; Beijing Institute of Technology Press: Beijing, China, 2014; pp. 22–25. [Google Scholar]




| Parameter Name | Value |
|---|---|
| Nc | 8 |
| Np | 25 |
| −0.02 | |
| 0.2 | |
| −0.25 g | |
| 0.25 g | |
| Q | [2000 0; 0 2000] |
| R | [3000 0; 0 1] |
| Parameters | Value |
|---|---|
| Vehicle sprung mass | 1743 |
| Vehicle mass m/kg | 1907 |
| Moment of inertia | 3246.9 |
| front wheelbase /m | 1.33 |
| rear wheelbase /m | 1.81 |
| The height of the center of mass above the ground h/m | 0.781 |
| Wheeltrack b/m | 2.029 |
| Lateral stiffness of front wheels | 116,050 |
| Lateral stiffness of rear wheels | 104,590 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Zhang, H.; Feng, Y. MPC-Based Obstacle Avoidance Path Tracking Control for Distributed Drive Electric Vehicles. World Electr. Veh. J. 2022, 13, 221. https://doi.org/10.3390/wevj13120221
Wu H, Zhang H, Feng Y. MPC-Based Obstacle Avoidance Path Tracking Control for Distributed Drive Electric Vehicles. World Electric Vehicle Journal. 2022; 13(12):221. https://doi.org/10.3390/wevj13120221
Chicago/Turabian StyleWu, Hongchao, Huanhuan Zhang, and Yixuan Feng. 2022. "MPC-Based Obstacle Avoidance Path Tracking Control for Distributed Drive Electric Vehicles" World Electric Vehicle Journal 13, no. 12: 221. https://doi.org/10.3390/wevj13120221
APA StyleWu, H., Zhang, H., & Feng, Y. (2022). MPC-Based Obstacle Avoidance Path Tracking Control for Distributed Drive Electric Vehicles. World Electric Vehicle Journal, 13(12), 221. https://doi.org/10.3390/wevj13120221





