State of Charge Estimation of Lithium-Ion Batteries Based on an Improved Sage-Husa Extended Kalman Filter Algorithm

Abstract

An improved Sage-Husa extended Kalman filter (SHEKF) algorithm is intended to improve the accuracy and stability of SOC prediction. In this paper, two different exponential weighting algorithms are used to adaptively select the forgetting factor for adaptive noise estimation. Moreover, the OCV-SOC curve is obtained using a 7-segment linear fitting method before the algorithms estimate the SOC. In addition, by combining this improved method with a third-order RC equivalent circuit model in the dynamic stress test (DST) case the convergence time is reduced by 0.15 s compared to the second-order RC equivalent circuit model. Following that, four different types of comparison experiments are carried out by comparing the improved algorithm to EKF and other SHEKF algorithms.The estimation accuracy under DST conditions of 0 °C, 25 °C and 45 °C is approximately 0.5%, 2.2% and 1.3% improvement compared to the EKF algorithm.

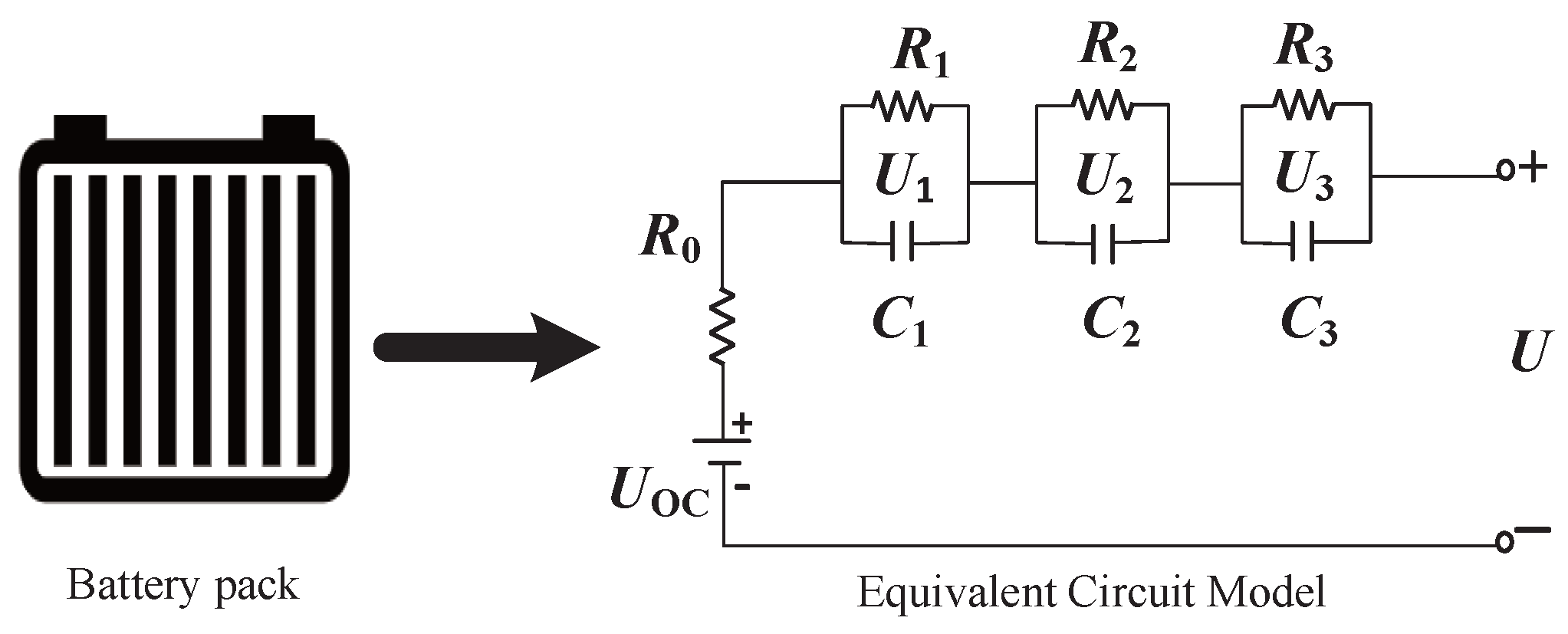
1. Introduction

New energy vehicles are gradually replacing conventional internal combustion engine-powered vehicles as a result of the growing energy crisis and environmental pollution [1]. One of the most promising new energy vehicles is electric vehicles (EVs), which have energy storage systems made up of several lithium-ion batterie packs. These days, popular research topics include the prediction of lithium-ion battery internal failures [2], the prediction of cycle life [3], the prediction of technology for the various stages of the battery life cycle, including production, use, secondary use, and material recycling [4], and the prediction of battery charge state. The goal of the research presented in this paper is to precisely predict the charge state of lithium-ion batteries. One of them, to ensure the stable operation of the battery management system (BMS), an accurate calculation of the SOC value is necessary. One of the most important things the BMS does is check the state of charge (SOC), which shows what percentage of the nameplate capacity is actually being used [5]. A precise estimate of SOC makes it possible to determine the amount of power that is still available in real time, obtain an exact picture of the state in which the battery is working, and select the charging strategy in a reliable manner. Additionally, the SOC can only be calculated using the pertinent factors because it cannot be directly measured [6]. Simultaneously, several variables, including the algorithm, the model, and the working environment, have an impact on the accuracy of estimation.

The open-circuit voltage (OCV) method [7], the ampere-hour (Ah) integration method, the Kalman filter (KF) and its improved algorithms [8], the fuzzy logic algorithm [9], and numerous additional potential SOC estimation methods. One of the most popular ways is the OCV method, but one of its main drawbacks is how long it takes to get the OCV of batteries. As a result, there is a disadvantage to this method when it comes to using OCV in practice. Additionally, although the Ah integral approach can directly determine SOC, it is challenging to apply alone since it requires the initial SOC value and high accuracy current measurement. The simplicity, clarity, and ease of understanding of these two approaches are advantages, but accuracy is a drawback that is hard to ensure.

Methods that are based on the model [10] constitute an additional subfield of strategy. Those methods rely heavily on the battery model [11]. Therefore, it is essential to create a reliable and accurate battery model [12]. Another, those methods can deal with unpredictability and disturbances by self-correcting within a closed-loop system, which improves the precision of estimating the SOC. The noise is unknown in reality, contrary to what the typical EKF or the unscented Kalman filter (UKF) expects. Numerous adaptive filtering algorithms that enable the estimate of noise have been thoroughly researched for battery SOC estimation to address this weakness. A filtering technique called adaptive filtering has the effect of suppressing filter divergence [13]. The Sage-Husa algorithm is a fine example of an algorithm for the measurement noise R and uncertain system noise Q. Although this algorithm is useful, it also has flaws such as excessive computing effort caused by ongoing noise growth and simple filter scattering.

Under the circumstances of abrupt current shifts, the Sage-Husa algorithm is prone to lose the positive characterization of the covariance matrix, which results in filtering scattering. As a consequence of this, Lv et al. [14] demonstrated that the Sage-Husa method is unable to independently estimate the measurement noise and the system noise, and they also examined the reasons for the algorithm’s filter scattering. Measurement noise R is thought to be known, whereas system noise Q is unknowable. Additionally, it is suggested that addition and subtraction operations be omitted from the corrected estimation of system noise Q in favor of just using the matrix’s multiplication and inverse operations. Moreover, the system noise needs to be guaranteed to be positive. Liu et al. performed a similar reduction of the system noise equation for the Sage-Husa [15] method. The distinction is that only an adaptive prediction of measurement noise is carried out in this research, which presupposes that system noise is known. Generally speaking, it is possible to minimize the complexity of the covariance matrix, but doing so would decrease the estimation accuracy. According to Li et al. [16], the system and measurement noise covariance matrices were both diagonalized. Although accuracy and stability have improved somewhat, the algorithm still has an average error of about 3.38 %. It demonstrates that there is room for the accuracy of this algorithm to be improved. To evaluate the gyroscope attitude angle, Jie et al. [17] used the singular value decomposition (SVD) Sage-Husa unscented Kalman filter (UKF), which deconstructs the derived filter covariance matrix P into its parts. The enhanced Sage-Husa UKF technique guarantees the accuracy standards and prevents mistakes from dispersing with time accumulation. Both the SVD and the square-root (SR) decomposition can increase the algorithm’s robustness and ensure that the covariance matrix is positive and definite. However, their algorithm complexity has significantly grown, which has resulted in a longer convergence time. In addition, Wang et al. [18] used a technique called covariance matching, as well as the adaptive filtering method developed by Sage-Husa. With this approach, computation is minimized while real-time performance is increased. Nevertheless, the accuracy of the algorithm can still be enhanced.

To tackle the above problems, the following enhancements are made in this paper. Section 2 describes the modified second-order RC model. Section 3 selects distinct forgetting factors for the two noises according to the condensed Sage-Husa algorithm. Both system and measurement noise are taken into account while performing adaptive estimate. To verify the correctness and stability of the improved algorithm, four types of methods are described in Section 4 of the paper. Finally, in Section 5, it is concluded that the instability problem of Sage-Husa algorithm is solved and the accuracy of the algorithm is increased.

2. Equivalent Circuit Model and Parameter Identification

2.1. Equivalent Circuit Model

From the literature [19,20], it can be seen that considering the influence of temperature on the battery, the electro-thermal model will become the focus of research. If temperature is not a consideration, the equivalent circuit model (ECM) is the best choice. Additionally, it stimulates the dynamic properties of the battery using a resistor-capacitor and voltage source, which has the important benefits of a straightforward principle and simple parameter identification. Because of its accuracy, complexity, and versatility, the second-order RC equivalent circuit model has become a widely used instrument in the field of academic research. However, the addition of the RC network to the third-order model serves to further highlight the effect of the cell’s polarization impedance on its performance. In references [21,22], the benefits and drawbacks of various equivalent models are enumerated. Figure 1 depicts the model of the equivalent circuit. The criteria for the onboard system are extremely strict and challenging to implement, while the higher-order RC network model is excessively complex. Here, the third-order model is adopted.

In Figure 1, the $U_{oc}$ is used to indicate the open-circuit voltage. U stands for the terminal voltage of battery. $R_0$ is a depiction of the battery’s ohmic resistance. The Ref. [23] provides a comprehensive explanation of the first two sessions of the RC. Additionally, $R_3$ and $C_3$ describe the concentration difference polarization resistance and capacitance, respectively. The absence of the RC network that would have represented the polarization resistor capacitance is the only distinction between the third-order model and the second-order model. Due to a lack of available space, only the third-order model’s depiction will be shown below. The third RC network is only eliminated in the second-order model. The RC model of the third-order produces the following mathematical relationship:

$$\left\{\begin{array}{c}{\dot{U}}_1=-\frac{1}{R_1{C}_1}{U}_1+\frac{I}{C_1}\hfill \\ {\dot{U}}_2=-\frac{1}{R_2{C}_2}{U}_2+\frac{I}{C_2}\hfill \\ {\dot{U}}_3=-\frac{1}{R_3{C}_3}{U}_3+\frac{I}{C_3}\hfill \end{array}\right.$$

(1)

where ${\dot{U}}_1$, ${\dot{U}}_2$ and ${\dot{U}}_3$ denote the derivative of $U_1$, $U_2$ and $U_3$ respectively.

The terminal voltage can be expressed as follows:

$$U=U_{oc}-I{R}_0-U_1-U_2-U_3$$

(2)

where the voltage reading at $R_1$ and $C_1$’s ends is the $U_1$. And the voltage reading at the endpoints of $R_2$ and $C_2$ is known as the $U_2$. Particularly, the voltage reading at $R_3$ and $C_3$’s ends is the $U_3$. Following are the components of the third-order model that must be determined. Where $\theta$ is the variable that stands in for the parameter that has to be identified.

$$\theta =\left[\begin{array}{cccccccc}{R}_0& R_1& R_2& R_3& C_1& C_2& C_3& U_{oc}\end{array}\right]$$

(3)

2.2. Parameter Identification

When performing parameter identification on the model, two types of methods are available: online parameter identification [24,25,26] and offline parameter identification. In this paper, the latter will be used for parameter identification of the model with three RC links.By extracting features from the pulse discharge experimental voltage fluctuation curve, the model parameters may be determined (as in Figure 2). The specific steps are listed below.

• Identification of $R_0$: $R_0$ is mainly composed of electrolyte resistance. Once the discharge current is performed or stopped, the terminal voltage of the battery model presented in Figure 1 decreases or increases. According to the discharge-static experiment, in the first moment of battery resting and the last moment of applying discharge current, the instantaneous drop of terminal voltage ($U_a$ drops rapidly to $U_b$, $U_c$ rises sharply to $U_d$) reflects the ohmic characteristics of the battery. Hence, the ohmic resistance $R_0$ is calculated by the Equation (4).

  $$R_0=\frac{(U_a-U_b)+(U_d-U_c)}{2I}$$

  (4)
• Parameter identification of RC parallel circuits: To begin, it is necessary to establish the values for the time constants ${\tau }_1$, ${\tau }_2$, and ${\tau }_3$. And then based on the determined time constants, the parameters of $R_1$, $R_2$, $R_3$, $C_1$, $C_2$ and $C_3$ are determined in detail. Furthermore, crucial for identification is the response of a first-order RC circuit classically consisting of a resistor R, a capacitor C, and a constant current I, which is given by Equation (5) below:

  $$U\left(\mathrm{t}\right)=U\left(t_0\right)+IR(1-e^{\frac{t_0-t}{\tau }})$$

  (5)
• The previous equation states that $\tau =RC$, and $t_0$ is the time that represents the beginning of the process. The following is the specific process to identify the parameters $R_1$, $R_2$, $R_3$, $C_1$, $C_2$, and $C_3$. Firstly, identify the time constants during the process $U_b$-$U_c$-$U_d$-$U_e$. Take note that there is no current flowing at all during the relaxation stage of the procedure. Then, the voltages $U_1$, $U_2$, and $U_3$ can then be computed using the following calculation based on Equation (5):

  $$\left\{\begin{array}{c}{U}_1\left(\mathrm{t}\right)=U_1\left(t_c\right)e^{\frac{t_c-t}{{\tau }_1}}\hfill \\ U_2\left(\mathrm{t}\right)=U_2\left(t_c\right)e^{\frac{t_c-t}{{\tau }_2}}\hfill \\ U_3\left(\mathrm{t}\right)=U_3\left(t_c\right)e^{\frac{t_c-t}{{\tau }_3}}\hfill \end{array}\right.$$

  (6)
  We can get Equation (7) from the output Equation (2).

  $$U\left(t\right)=U_{oc}\left(soc\right)-U_1\left(t_c\right)e^{\frac{t_c-t}{{\tau }_1}}-U_2\left(t_c\right)e^{\frac{t_c-t}{{\tau }_2}}-U_3\left(t_c\right)e^{\frac{t_c-t}{{\tau }_3}}$$

  (7)
  Additionally, rewrite Equation (7) as Equation (8).

  $$U\left(t\right)={\alpha }_1-{\alpha }_2{e}^{\frac{t_c-t}{{\beta }_1}}-{\alpha }_3{e}^{\frac{t_c-t}{{\beta }_2}}-{\alpha }_4{e}^{\frac{t_c-t}{{\beta }_3}}$$

  (8)

  where $t_c$ signifies the next period. And ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$, ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ are unknown coefficients, ${\alpha }_1=U_b(\infty )$ which is measured at the end of the polarization recovery process. The ideal coefficients ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$, ${\beta }_1$, ${\beta }_2$, and ${\beta }_3$ can be produced by using the MATLAB function “Custom Equation” in the Curve Fitting Toolbox. Therefore, the time constants ${\tau }_1$, ${\tau }_2$, ${\tau }_3$, and the voltages $U_1\left(t\right)$, $U_1\left(t\right)$, and $U_1\left(t\right)$ can be identified. The parameters $R_1$, $R_2$, $R_3$, $C_1$, $C_2$ and $C_3$ can then be determined using Equation (9).

  $$\left\{\begin{array}{c}{U}_1\left(t\right)=I{R}_1(1-e^{\frac{t_c-t}{{\tau }_1}})\hfill \\ U_2\left(t\right)=I{R}_2(1-e^{\frac{t_c-t}{{\tau }_2}})\hfill \\ U_3\left(t\right)=I{R}_3(1-e^{\frac{t_c-t}{{\tau }_3}})\end{array}\right.$$

  (9)
• Parameter identification of OCV-SOC curve: The steady voltage measured at both ends of the positive and negative electrodes when the battery is left in one location for an extended period of time is the open-circuit voltage (OCV). However, the functional connection between OCV and SOC is not linear. The analytical complexity of SOC estimation is increased by this nonlinearity. In most publications, polynomial fitting is used to obtain OCV-SOC curves. The precision of the SOC estimation is directly effected by the fitting order chosen because it determines the quality of the fitting effect. To enhance the precision of SOC estimation, consider the functional relationship between OCV and SOC as a piecewise linear relationship [27], and refine the fitting curve. The test points are divided into seven segments, each of which is a function of SOC in relation to OCV. The following linear Equation (10) can be used to represent each component.

  Table 1. The fitting parameter values corresponding to the piecewise linear graph of OCV-SOC.

  SOC	0.1–0.2	0.2–0.3	0.3–0.4	0.4–0.5	0.5–0.7	0.7–0.8	0.8–1
  $k_1$	3.387	3.453	3.525	3.477	3.216	3.22791	3.00967
  $k_2$	0.84	0.51	0.27	0.39	0.916	0.8847	1.17

  shows the values of $k1$ and $k_2$ that correspond to each curve. The 8th-order polynomial fitting curve was compared to the 7-segment linear fitting curve. As shown in Figure 3, the 7-segment linear fitting outperforms the 8th-order polynomial fitting at the start and finish of the discharge.

  $$U_{oc}=f\left(SOC\right)=k_1+k_{2}SOC$$

  (10)

3. Sage-Husa Extended Kalman Filter Algorithm

Kalman filter, extended Kalman filter and its improved unscented Kalman algorithms need to be used when their system noise and measurement noise are known and constant from beginning to end. Nevertheless, the SOC of the battery is impacted by a wide variety of unknown elements, including temperature or the conditions of the road, while actual driving of electric vehicles takes place. Consequently, noise is something that needs to be determined in an ongoing manner. Sage-Husa is one of the adaptive algorithms. It has a mediocre unbiased estimator of significant posterior noise. The algorithm’s core consists of dynamically estimating the statistical features of measurement noise and system noise in actual time utilizing data from measurement variables during the filtering process. Subsequently, the state parameter calculation for EKF makes use of the estimated noise parameters. The system’s estimated final state is calculated.

3.1. SHEKF Algorithm

Since Equations (1) and (2) in Section 2 should always be modified because the battery is a nonlinear system [28]. The rewritten equations of state and observation are presented in the following set of equations.

$$\left\{\begin{array}{c}{x}_k=A{x}_{k-1}+B{I}_{k-1}+w_k\hfill \\ y_k=H{x}_k+D{I}_{k-1}+v_k\hfill \end{array}\right.$$

(11)

where A stands for the state transfer matrix, B represents the state control matrix, H refers to the observation transfer matrix, and D describes the observation control matrix. The system noise matrix is denoted by $w_k$, and the measurement noise matrix is denoted by $v_k$.

$$\left\{\begin{array}{c}E\left[v_k\right]=r_k\hfill \\ E\left[w_k\right]=q_k\hfill \\ E\left[(v_k-r_k)(v_k^T-r_j)\right]=R_k{\delta }_{k,j}\hfill \\ E\left[(w_k-q_k)(w_k^T-q_j)\right]=Q_k{\delta }_{k,j}\hfill \\ E\left[(w_k-q_k)(v_k^T-r_j)\right]=0\hfill \end{array}\right.$$

(12)

where the measurement noise covariance matrix is denoted by $R_k$, and $Q_k$ embodies the system noise covariance matrix. $q_k$ represents the mean of $w_k$. $r_k$ indicates the mean of $v_k$.

The SHEKF algorithm adds to the basic equations of the discrete extended Kalman filter [29] the equations for real-time updating of $R_k$ and $Q_k$. Below are the formulas that have been added.

$$d_k=(1-b)/(1-b^{k+1})$$

(13)

$${\widehat{r}}_k=(1-d_k){\widehat{r}}_{k-1}+d_k(Z_k-H_k{\widehat{X}}_{k,k-1})$$

(14)

$${\widehat{q}}_k=(1-d_k){\widehat{q}}_{k-1}+d_k({\widehat{X}}_k-A_k{\widehat{X}}_{k-1})$$

(15)

$${\widehat{R}}_k=(1-d_k){\widehat{R}}_{k-1}+d_{k-1}[V_k{V_k}^T-H{P}_{k,k-1}{H}^T]$$

(16)

$${\widehat{Q}}_k=(1-d_k){\widehat{Q}}_{k-1}+d_{k-1}[K{V}_k{V_k}^T{K}^T+P_k-A{P}_{k-1}{A}^T]$$

(17)

where the forgetting factor is denoted by the letter b, and the weighting factor is characterized by the letter d. And the error covariance is represented by $P_k$. $V_k$ represents the difference between the terminal voltage measurement and the estimated value. After that, a short assessment of the Sage-Husa algorithm is provided below.

1. Write the recursive equation from Equation (16):

$$\begin{array}{c}{\widehat{Q}}_k=\frac{b^k(1-b)}{1-b^{k+1}}{\widehat{Q}}_0+\frac{b^{k-1}(1-b)}{1-b^{k+1}}\left[K_1{V}_1{V}_1^T{K}_1^T\right]+\hfill \\ \hfill \\ \frac{b^{k-2}(1-b)}{1-b^{k+1}}\left[K_2{V}_2{V}_2^T{K}_2^T\right]+.......+\frac{(1-b)}{1-b^{k+1}}\left[K_k{V}_k{V}_k^T{K}_k^T\right]\hfill \end{array}$$

(18)

From basic mathematics, it is known that d is gradually decreasing and approaching $1-b$ as k keeps increasing. Therefore, the predetermined initial value $Q_0$ is the quantity whose contribution to the estimated quantity Q decays fastest as k increases. In addition, the weight of the current time correction is the largest in the estimation of $Q_k$. Namely, the magnitude of the effect that the present instant has on the value of Q is a scaled version of the value of $1-b$.

2. With the assumption that the measurement noise’s predicted value is, the observation equation can be written as:

$$y_k=H{x}_k+D{I}_{k-1}+{\widehat{r}}_k+v_k$$

(19)

${\widehat{r}}_k$ is calculated as follows:

$${\widehat{r}}_k=y_k-H{x}_k-D{I}_{k-1}-v_k$$

(20)

A benchmarking with Equation (13) exposes that the final estimate is replaced by a one-step prediction during the estimation of the measurement noise expectation, and thus this is a suboptimal algorithm. Expectation estimation errors may gradually build up as a result of the prediction of the system noise and measurement noise expectation being suboptimal. Additionally, it causes a significant bias in the particular iteration. Even the evaluation of measurement noise or the variance in system noise may be impacted. Therefore, this component of the calculation ought to be disregarded. This is consistent with the study that was conducted and documented in the literature [30].

To sum up, for statistical computing of noise, the Sage-Husa extended Kalman filter algorithm is improved over the standard Kalman filter approach. However, the conventional Sage-Husa algorithm is prone to filtering divergence and instability under conditions of severe current variations. The covariance matrix loses its positivity as a result, which is the cause. The SHEKF algorithm enhancement concept was put up to address this issue.

3.2. Improvement of the SHEKF Algorithm

3.2.1. Simplifying Noise Covariance Matrix

Equation (16) reveals that in the first half term $(1-d_k){\widehat{R}}_{k-1}$, as long as the initial value of ${\widehat{R}}_k$ is positive definite, the multiplication result is also positive definite. This is because the range of the forgetting factor d is limited. To update the ${\widehat{R}}_k$ to be calculated, the second half term $d_{k-1}\left(V_k{V}_k^T\right)$ is used. When the filtering process is convergent, the error covariance $P_k$ will decrease, and if H is a specific value, $H{P}_{k,k-1}{H}^T$ will gradually decline and tend to zero. The noise covariance estimate barely makes a difference. The first half of Equation (17) has the same basic architecture as Equation (16). Additional, since A has a specific value as well, the two equations can be processed in the same way. In summary, the stability of the filtering is chosen in this paper at the expense of the measurement noise and system noise covariance matrix estimation’s objectivity. The adjusted noise equation is displayed by Equations (20) and (21).

$${\widehat{Q}}_k=(1-d_k){\widehat{Q}}_{k-1}+d_{k-1}\left(K_k{V}_k{V}_k^T{K}_k^T\right)$$

(21)

$${\widehat{R}}_k=(1-d_k){\widehat{R}}_{k-1}+d_{k-1}\left(V_k{V}_k^T\right)$$

(22)

3.2.2. Setting Two Improved Forgetting Factors

Because of the emphasis on the role of recent data in time-varying noise statistics, old data should be gradually forgotten, which can be accomplished by using an exponentially weighted decay method. In comparison to other adaptive extended Kalman filtering (AEKF) methods, the SHEKF algorithm includes a forgetting component. SHEKF can change the weights of the inputs at different times due to the forgetting factor, reducing their memory size. This prevents inaccurate and out-of-date data from influencing the filter and ensures that the most recent observations are fully utilized. The forgetting factor is usually represented by the symbol b, and its value varies depending on whether the system error becomes faster or slower, resulting in a different value. A value of $b=0$ indicates complete forgetting, whereas a value of $b=1$ indicates no forgetting at all. The lower the b, the greater the loss of knowledge.

In this paper, depending on how quickly or slowly the statistical characteristics of the system noise and measurement noise change, we select various exponential weighting methods. This is due to the fact that model error is the primary source of system noise. Solving this issue is necessary if the system is to be reliable. The fading memory exponential weighting method is employed due to the slow rate of change in the statistical characteristics of the system noise. The fading memory still retains all of the historical data from the past, but the weighting factor and impact on the total weighted sum decrease with age. To prevent being replaced by new data information, it is advised to forget the old data that contributes to system noise for a longer period of time. As a result, the system noise forgetting factor’s starting value can be decreased.

$$d_{1,k}=\frac{1-b_1}{1-b_1^k},0<b_1<1$$

(23)

Equation (23) is generated by substituting Equation (22) into Equation (20).

$${\widehat{Q}}_k=(1-d_{1,k-1}){\widehat{Q}}_{k-1}+d_{1,k-1}\left[K{V}_k{V}_k^T{K}^T\right]$$

(24)

And because measurement noise is primarily a product of its surroundings, its characteristics are poorly defined. If the value of the next moment is always very close to the value of the preceding moment, the filter instability caused by significant noise changes can be reduced. When the measurement noise changes quickly or abruptly, the filtered difference data that is too old has a small role in estimating the system error at the current time. When the sampling time is long, it is too old due to the relationship between the forgetting factor and the weighting coefficient. The weight assigned to the filtered difference data of s is very small, which not only has little effect on the estimation of the current moment, but also increases the calculation time due to the frequent and repeated weight factor assignment at each moment. To improve the estimation accuracy of time-variant measurement noise, on the one hand, and to reduce calculation time, only use data from a fixed period of time before the current moment to estimate the error, that is, apply the limited exponential weighting method to SOC estimation. The limited memory index weighting method must take into account the memory length limitation. The memory length in this paper is set to m, where m is a fixed natural number. That is, starting with the most recent data and moving back m generations, the newer data set is multiplied by a large forgetting factor, the older data set is multiplied by a relatively small forgetting factor, and the data before the m generation data is multiplied by a large forgetting factor in this m generation data. The data is completely erased, and a new matrix is created.

$$d_{2,\mathrm{m}}=\frac{1-b_1}{1-b_2^m},0<b_2<1$$

(25)

Equation (25) is obtained by substituting Equation (24) into Equation (21).

$${\widehat{R}}_m=b_2{\widehat{R}}_{m-1}+d_{2,m-1}\left[V_m{V}_m^T\right]$$

(26)

In order to obtain better results, this paper also makes certain differences in the initial values of the two forgetting factors. It is still based on the speed of change in the statistical characteristics of noise. According to the characteristics of the exponential function, the initial value of $b_1$ greater than the initial value of $b_2$.

As a result, Figure 4 depicts the summary flowchart of the modified SHEKF algorithm.

4. Experiments and Analysis

The battery research team at the Center for Advanced Life Cycle Engineering Research (CALCE) at the University of Maryland provided the test results for the batteries used in this work [31]. The literature [32] provides a detailed description of the battery test system utilized by CALCE to get these statistics. The battery model was INR18650 20R, and it had a 2000 mAh capacity rating. Additionally, the pulse current multiplier was 0.5C and the test ambient temperature was 25 °C. After receiving the data on the discharge of the battery, five different algorithms were compared.

Among these, SHEKF1 is an example of the revised version of the Sage-Husa algorithm that was presented in this paper. The fact that there is just one forgetting factor distinguishes SHEKF2 [33] from its predecessor, SHEKF1. In addition, the Sage-Husa algorithm is represented by SHEKF3 [34], which includes an adaptive estimation of the system noise Q in situations where the measurement noise R is already known. The Sage-Husa algorithm with adaptive estimation of R when Q is known is outlined in SHEKF4 [35]. The final algorithm is known as the EKF algorithm [36], therefore it does not include the adaptive estimation of noise. The end voltage value from the pulse discharge experiment serves as the voltage reference value. Additionally, the reference value for algorithm verification is the SOC value computed using the ampere-hour (Ah) integration method during a lengthy resting period. As evaluation metrics, the root means square error ($RMSE$) and the mean absolute error ($MAE$) are utilized to quantify the estimation mistakes produced by each of the five algorithms. The following definitions of $MAE$ and $RMSE$ are presented.

$$MAE=\frac{1}{N}\sum _{i=1}^N\left|X_{ij}-{\widehat{X}}_{ij}\right|$$

(27)

$$RMSE=\sqrt{\frac{1}{N}\sum _{i=1}^N{(X_{ij}-{\widehat{X}}_{ij})}^2}$$

(28)

4.1. Model Verification

The literature frequently makes use of the second-order RC model. However, the third-order model is not widely used since, despite increasing accuracy, the convergence time is proportionately longer. In this paper, the enhanced methods—a streamlined algorithm coupled with a third-order model are employed to resolve the issue.

The model validation approach of this paper is separated into two parts. In the preliminary stage, the model’s correctness is examined. By incorporating the specified model parameters into the end voltage solution formula, the simulated value of the end voltage is achieved. The size of the discrepancy between the measured and simulated values can be used to gauge the precision of model parameter identification. These two models are contrasted in this paper for the pulsed discharge and DST conditions, respectively.

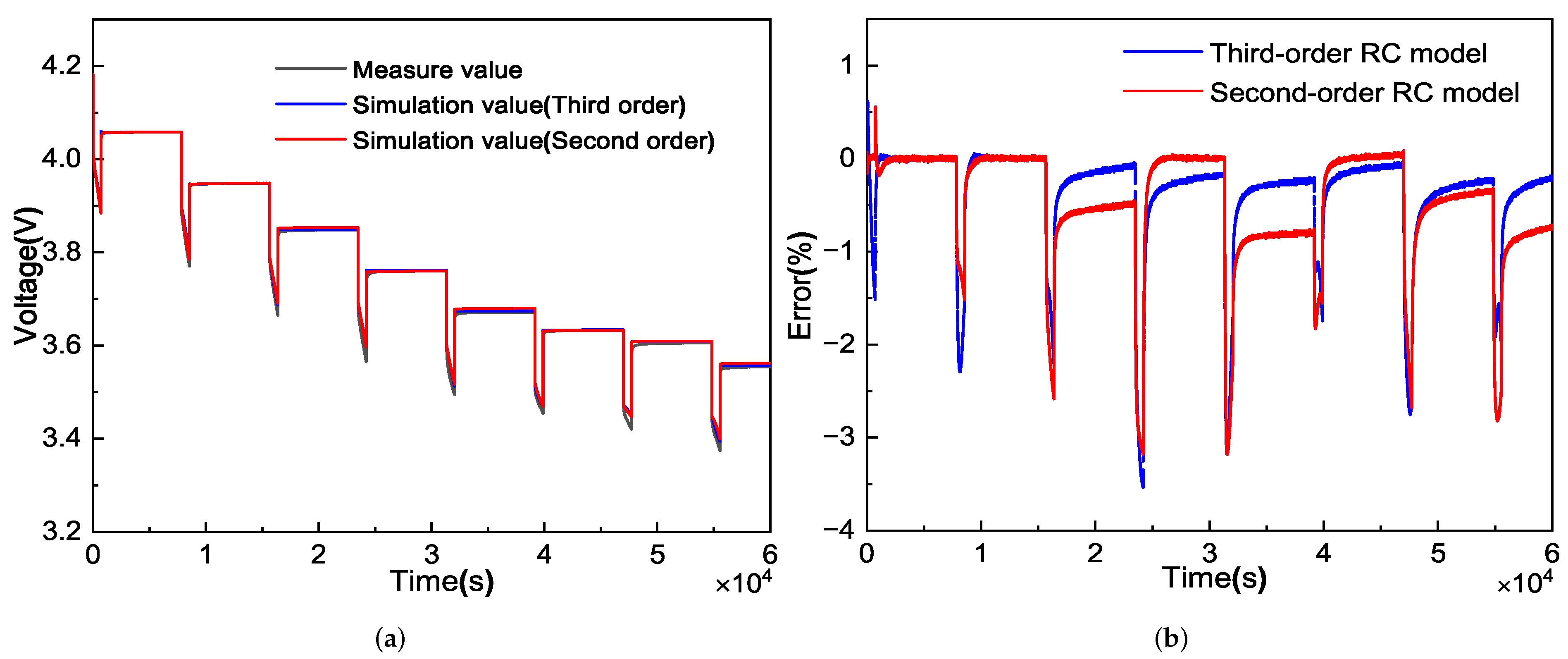
To start, the voltage measurement is obtained using pulse discharge experiments. Figure 5 displays the outcomes of the simulated values and the measured values of the cells for both models after substituting the parameter identification findings of the models. The highest inaccuracy of the third-order model and the second-order model can both be observed in the error plot to be less than 3.5%. It is shown that both models accurately represent the real battery situation.

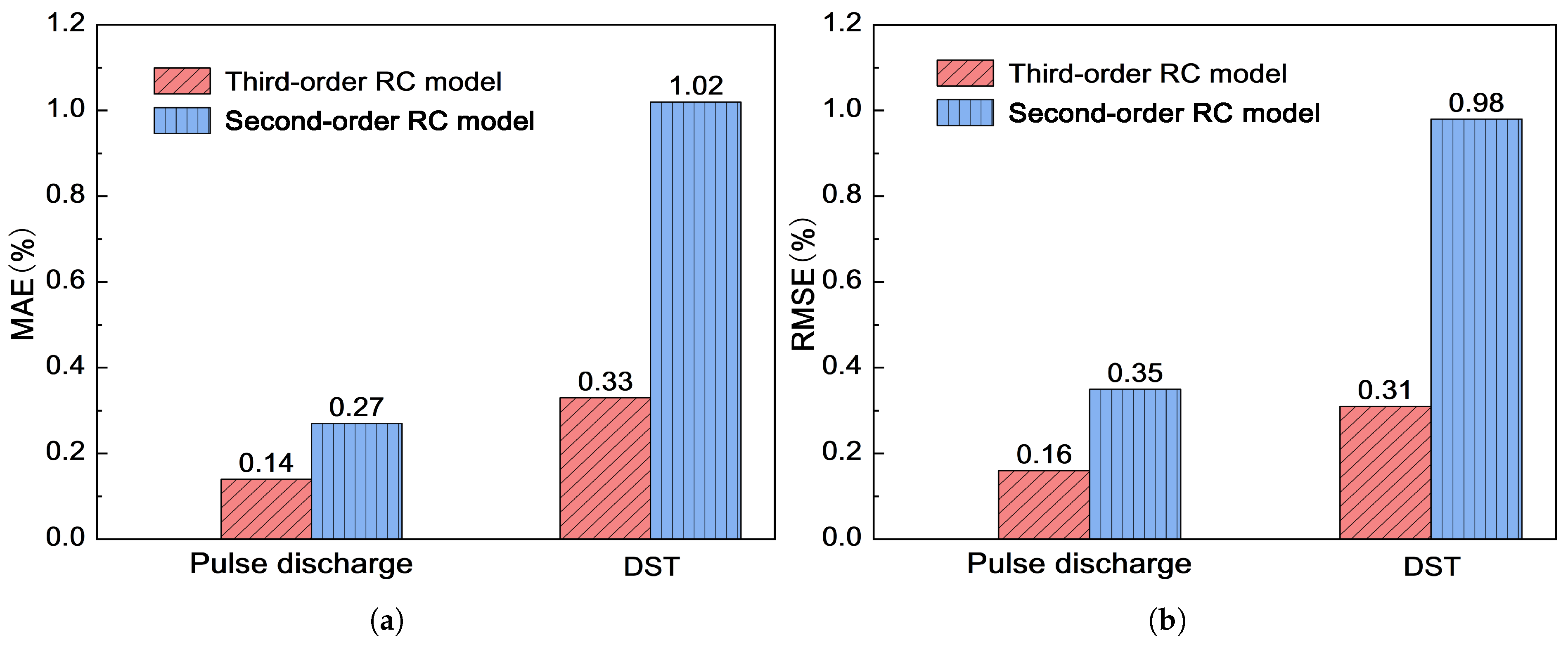
After that, an experiment using DST working conditions was used to get the voltage data. The simulated values and measured values of the battery are given in Figure 6 after the parameter identification findings of the two models were again swapped. The greatest error of the models is less than 3%, as can be seen from the error plot. Additionally, we can deduce from Figure 7 that the third-order model’s mean error is significantly lower than the second-order model’s. Furthermore, we can infer from Figure 7 that the third-order model’s mean error is roughly 0.33%. The second-order model’s mean inaccuracy is roughly 1%.

The convergence time of model is then verified as the second step. To guarantee the validity of the measurements, the experiment was conducted five times, and the findings were averaged. The results are displayed in

Table 2. Algorithm convergence schedule.

	Pulse Discharge		DST
Experiment Number	Third Order/s	Second Order/s	Third Order/s	Second Order/s
1	7.016	6.824	2.008	2.139
2	6.901	7.098	2.131	2.366
3	6.865	6.819	2.115	2.478
4	7.098	6.890	2.149	2.222
5	6.791	6.9474	2.308	2.278
Average value	7.149	7.101	2.142	2.296

below. According to Table 2, the third-order model’s convergence time is 0.0482 s longer than that of the second-order under the pulse discharge condition, whereas it is 0.154 s shorter under the DST condition. Without taking into account the impact of computational mistakes, it can be said that the simplification approach can be used to get over the higher-order model’s issue with a slow convergence rate.

In conclusion, the third-order model has a higher level of model accuracy than the second-order model. When the battery output current value fluctuates frequently, the third-order RC model performs better and is more stable. Figure 7 provides a clearer visual example of this. In other words, when the operating conditions are more complicated, the third-order model is preferable to the second-order model.

4.2. Evaluation of Correct Initial SOC Value

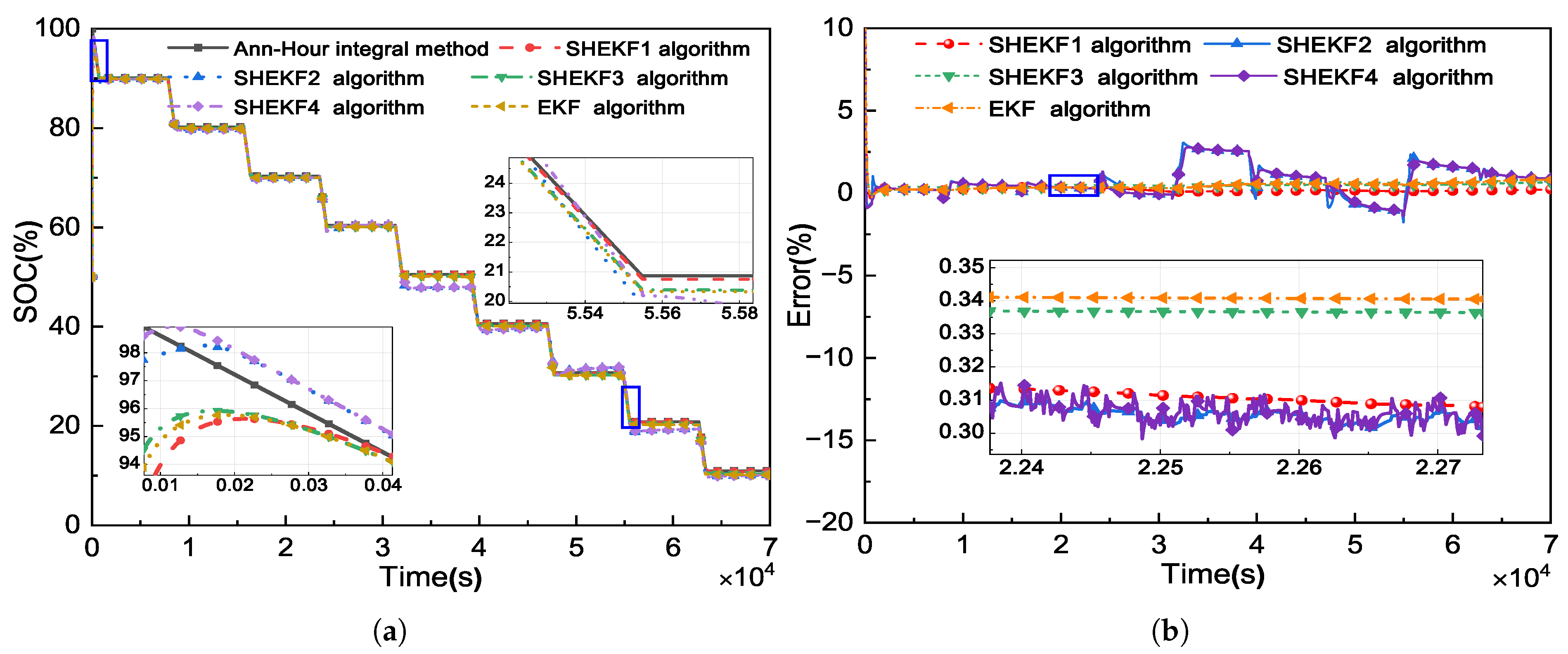
To verify the accuracy and consistency of the proposed algorithms that was presented in this paper, which is the primary objective of this section. The values corresponding to the true values are assigned to the initial values of SOC. Under the same initial circumstances, the five algorithms are contrasted. Figure 8 displays the outcomes of SOC estimate utilizing the different algorithms as well as any errors that may have occurred. Figure 8 demonstrates that the improved algorithm estimates SOC more accurately than the other algorithms. There is a greater estimation error in the first stage because SHEKF1 and SHEKF2 integrate adaptive estimation of the measurement noise. Adaptive estimate on the measurement noise R is exceedingly difficult because of its extreme instability. Because of this, many academics contend that adaptive estimation of Q and R cannot be done at the same time. Figure 8 shows that when the initial SOC value is accurate, the revised algorithm is noticeably more stable. And the algorithm proposed in this paper can converge to the true value when the sampling time is about 870 s.

When the SOC value at startup is accurate, the $MAE$ and $RMSE$ for each algorithm are listed in

Table 3. RMSE and MAE with correct initial SOC value.

Algorithm	SHEKF1	SHEKF2	SHEKF3	SHEKF4	EKF
$MAE$(%)	0.20	0.92	0.38	0.89	0.43
$RMSE$(%)	0.16	0.73	0.35	0.71	0.40

. According to the table, the revised SHEKF1 algorithm reduces the mean absolute error by 0.23% when compared to EKF. The SHEKF3 algorithm, which has been used extensively in publications, has a forecast error that is 0.05% less than that of EKF. The comparison of SHEKF1 and SHEKF3 shows that the improved algorithm proposed outperforms the commonly used adaptive algorithm for estimating EV battery state of charge SOC. SOC estimation accuracy is lower for the SHEKF2 algorithm, which estimates both measurement noise and system noise, and the SHEKF4 algorithm, which only estimates measurement noise. This also demonstrates that the method of simultaneously simplifying the noise covariance matrix and estimating only R will sacrifice some accuracy, which is not applicable in estimating the SOC of lithium batteries.

4.3. Evaluation of Incorrect Initial SOC Value

Incorrect initial values will directly impact the estimation precision of the algorithm. During the operation of an electric vehicle, the preliminary SOC worth is not constant. Consequently, the estimation algorithm must be robust to the initial SOC value. Given that the electric vehicle charge is between 50% and 20%, it is even more important to ensure that the battery charge is correct. As a result, this paper uses the incorrect initial SOC values of 0.5 and 0.2 to test the algorithm’s effectiveness. 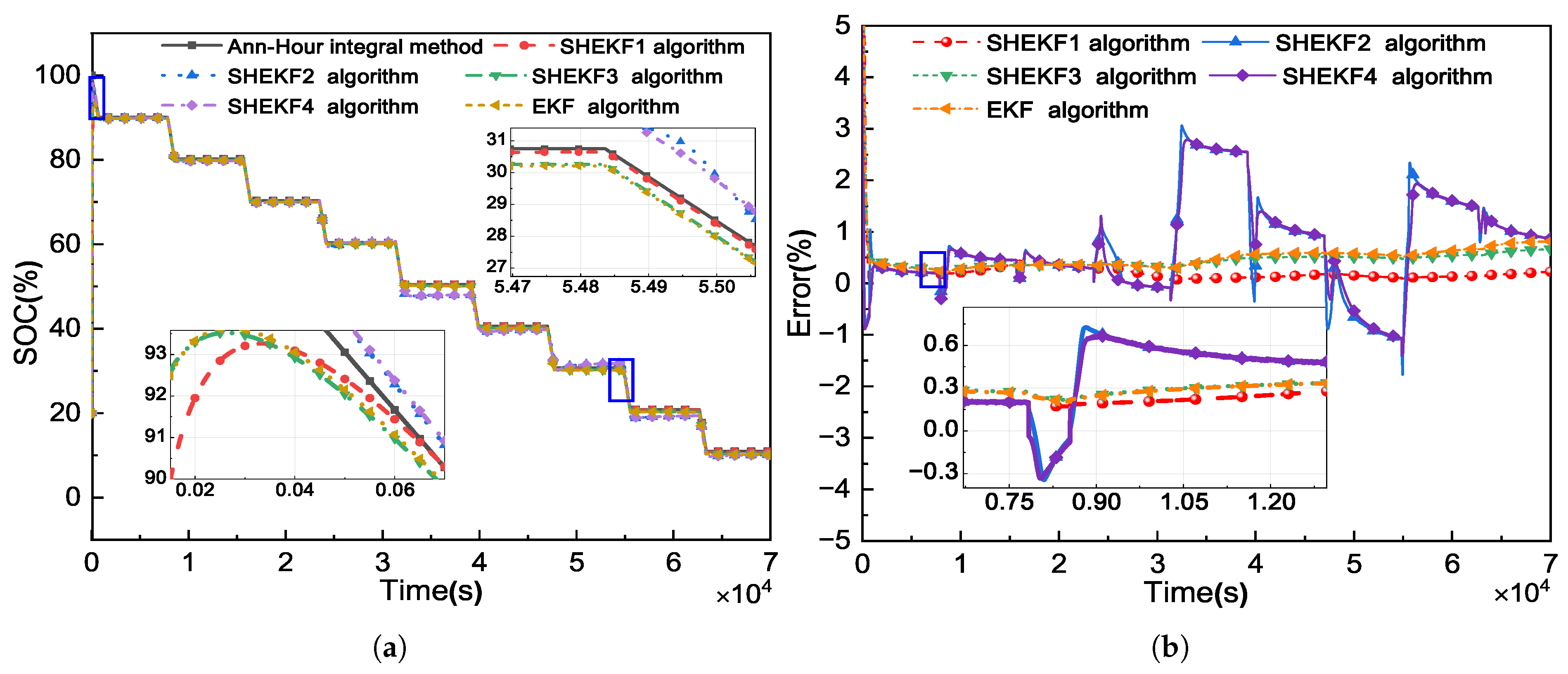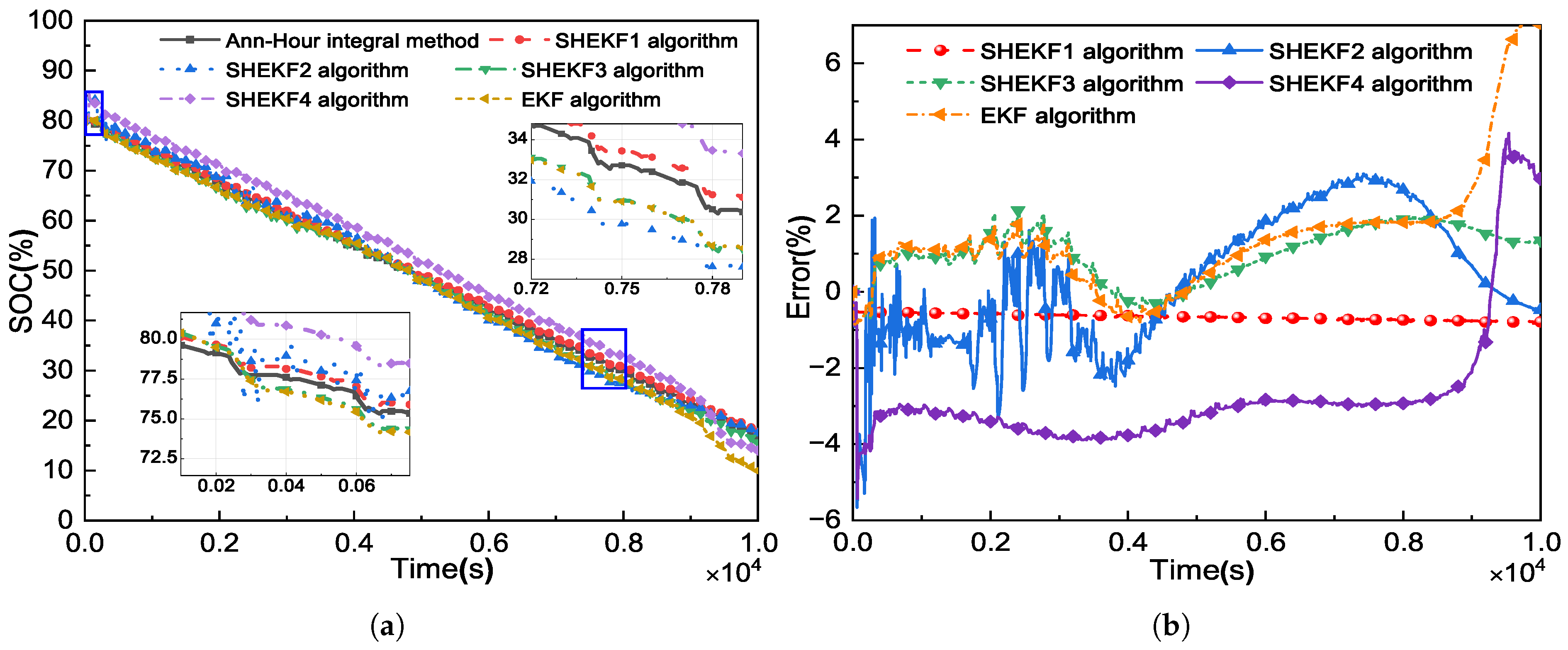Figure 9a,b show the simulation results when SOC is set to 0.5 as the starting value. Furthermore, the simulation results are shown in Figure 10a,b, and SOC is set to 0.2 at the start.

Figure 9a and Figure 10a illustrate that the presented algorithm that this paper proposes is more resistant to the initial setting of the SOC. The improved algorithm can converge to the true value after approximately 400 s of sampling. Even in low SOC time periods, the improved algorithm can improve estimation. Furthermore, as shown in Figure 9b and Figure 10b, the improved algorithm’s maximum error does not exceed 0.4%. The maximum error between the two algorithms SHEKF2 and SHEKF4 is greater than 3%.

To put it another way, the numerical results obtained by using each of the five different algorithms are depicted in Figure 11. Figure 11 clearly shows that regardless of the initial SOC value, the improved algorithm proposed in this paper outperforms other algorithms. It can be deduced that a larger difference between the initial and accurate SOC values has a greater impact on SOC estimation. Although the EKF algorithm, which is directly based on the SHEKF algorithm, removes adaptive noise estimation, the effect is superior to the SHEKF2 and SHEKF4 algorithms. In the case of different initial SOC values, the EKF algorithm’s estimation error varies by a maximum of 0.13%. This demonstrates that the inaccurate SOC initial value is equivalent to a portion of the noise, and the EKF algorithm cannot perform adaptive noise estimation. To improve the accurateness of the SOC, an algorithm that is not robust to the initial value of the SOC should permit the initial value to be set as close to the actual value as possible.

4.4. Impact of the Forgetting Factor on SOC Estimation

The inclusion of a forgetting factor distinguishes the Sage-Husa algorithm from other adaptive algorithms. This adaptive algorithm’s basic goal is to emphasize the importance of recent data while gradually forgetting the importance of earlier data. However, the forgetting factor must be chosen in accordance with the system’s actual working environment. Relying on the fast and slow change degrees of these two types of noise, this paper’s forgetting factor for system noise and measurement noise is determined. The reasons for this are discussed further in the Section 3. Some simulation experiments show that the algorithm’s accuracy and stability increase as the difference between the forgetting factor of the system noise and the initial value of the measured noise increases. Furthermore, in this paper, the optimal forgetting factor initial value difference was 0.045 (i.e., $b1=0.995$, $b2=0.95$).

Figure 12 shows that as the difference between the initial values of the two forgetting factors decreases, so do the algorithm’s maximum error and stability. The $RMSE$ and $MAE$ of the difference between the various forgetting factors of the modified algorithm are summarized in

Table 4. RMSE and MAE under different forgetting factors.

Algorithm	Difference = 0.047	Difference = 0.045	Difference = 0.04	Difference = 0.03
$MAE$(%)	0.20	0.20	0.52	0.70
$RMSE$(%)	0.18	0.16	0.31	0.51

. The data in Table 4’s first and second columns can be used to demonstrate that, when it exceeds 0.045, the algorithm is not significantly affected by the difference between the two forgetting factors’ initial values.

Furthermore, the simulation results show that when the difference between the initial values of the two forgetting factors is 0.03, the estimation error is 0.5% higher than when the difference is 0.045. It is advantageous to improve the algorithm’s accuracy by treating the forgetting factors of the two types of noise differently.

4.5. The Algorithm Performance under DST Working Condition

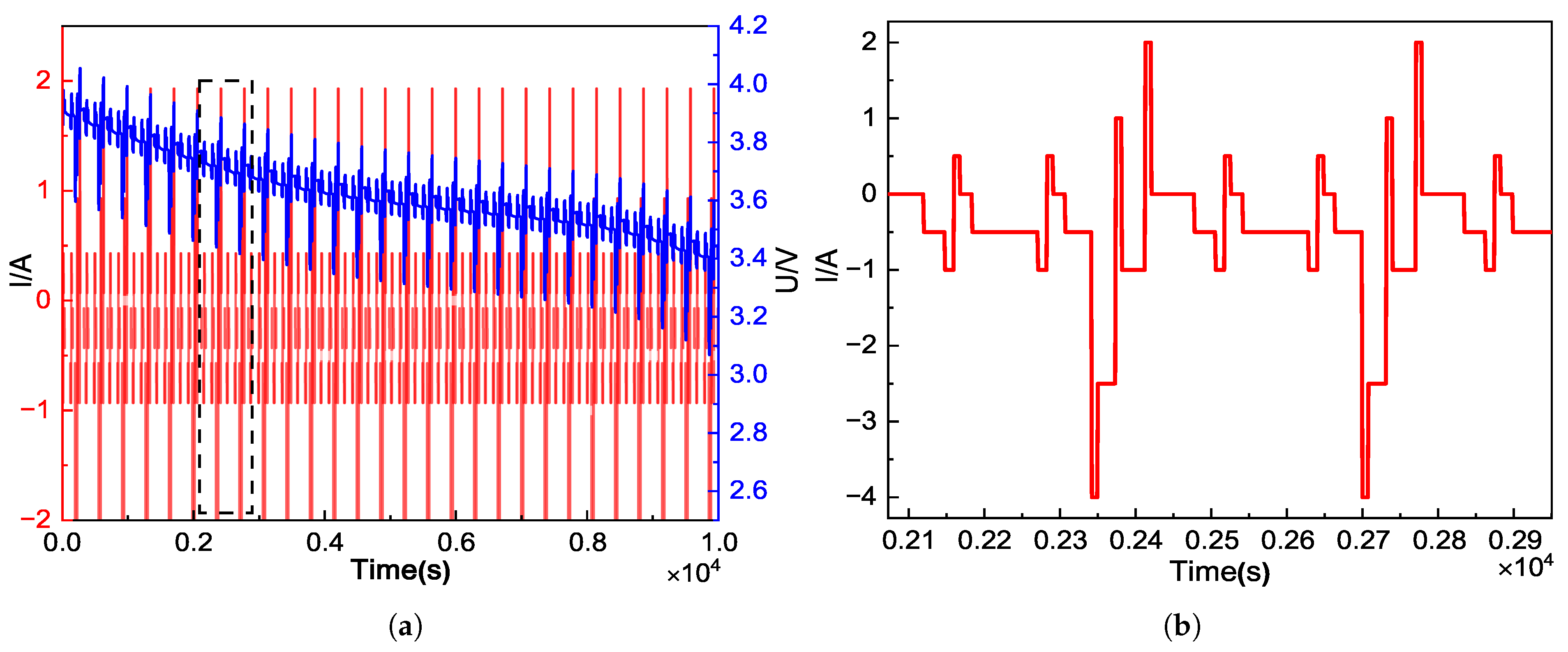
The capacity of Li-ion batteries can be impacted by temperature. As a result, one of the determining factors in estimating SOC is temperature. This section simulates the operation of a Li-ion battery power system using the US dynamic stress test (DST). To test the effectiveness of the enhanced algorithm, three different kinds of temperature data representing low temperature (0 °C), normal temperature (25 °C) and high temperature (45 °C) were also selected. The precise current and amplification curves for the DST operating conditions are shown in Figure 13. Each current is made up of many tiny cycles that operate over a very long dynamic period. As a result, the DST operating environment can represent the battery usage more accurately. In this discharge case, five algorithms are used to calculate the SOC, with an initial SOC value of 0.8 for each algorithm. The estimated SOC curve and the estimation error at 25 °C are shown in Figure 14. The SHEKF1 algorithm has the smallest $MAE$, which is about 2% smaller than the error of the EKF algorithm, according to a comparison of the data in each column of

Table 5. RMSE and MAE under 25 °C DST condition.

Algorithm	SHEKF1	SHEKF2	SHEKF3	SHEKF4	EKF
$MAE$(%)	0.27	0.97	0.90	1.02	2.42
$RMSE$(%)	0.27	0.86	0.78	0.91	0.88

in the first place.

Figure 15 and Figure 16 show the estimated SOC curves’ results and estimation errors at 0 °C and 45 °C, respectively. Figure 14b, Figure 15b and Figure 16b show a clear correlation between temperature change and an increase in the SOC estimation algorithm’s error. To make it easier to understand the benefits and drawbacks of each algorithm, the error data for the three temperatures are condensed in Table 5,

Table 6. RMSE and MAE under 0 °C DST condition.

Algorithm	SHEKF1	SHEKF2	SHEKF3	SHEKF4	EKF
$MAE$(%)	1.81	3.25	2.37	2.99	2.36
$RMSE$(%)	0.90	3.16	2.09	2.63	2.07

and

Table 7. RMSE and MAE under 45 °C DST condition.

Algorithm	SHEKF1	SHEKF2	SHEKF3	SHEKF4	EKF
$MAE$(%)	0.67	1.34	1.16	3.12	2.01
$RMSE$(%)	0.67	0.90	1.08	2.23	1.88

. Similar to the 25 °C pulse discharge condition, the $MAE$ of the SHEKF3 algorithm is almost 0.8% less than that of the SHEKF1 and SHEKF4 algorithms. Table 6’s comparison of the data in each column still demonstrates the SHEKF1 algorithm’s superiority. The SHEKF1 algorithm has a 1.4% smaller error than the SHEKF1 algorithm, which has the largest error.

The information in Table 5 and Table 6 is compared for analysis. The temperature drops from 25 °C to 0 °C, while the $RMSE$ and $MAE$ of the SHEKF1 algorithm both rise by about 1.5% and 0.6%, respectively. The $MAE$ of the SHEKF1 algorithm increased by about 0.4% when comparing the data in Table 6 and Table 7. The superiority of the improved algorithm, which is the SHEKF1 algorithm in the calculation example, is identified after comparing the five algorithms for SOC estimation at the aforementioned three temperatures.In addition, the SHEKF1 algorithm has roughly 1.3% less error than the EKF algorithm, as shown by a comparison of the data in each column of Table 7.

4.6. Discussion

Analyzing the aforementioned simulation experimental data can lead to the following conclusions:

i. SOC estimation algorithms based on models, such as the Sage-Husa and EKF algorithms, are highly model-dependent. If the model is not accurate enough, none of these algorithms can calculate SOC accurately enough. The accuracy of SOC estimation may be jeopardized if the model fails. As a result, it is critical to validate the developed models before performing SOC estimation. Furthermore, the superiority of the third-order model over the second-order model is not readily apparent under operating conditions with reasonably consistent current variation. However, when dealing with complex current variations, the third-order model outperforms the second-order model significantly. The reason for this is that sudden changes in current can exacerbate cell polarization. The former increases the number of RC links to more accurately describe the actual state of the battery polarization phenomenon. In terms of convergence time, this paper believes that combining the simplified algorithm with the third-order RC model can reduce the algorithm’s convergence time. The convergence time of the simplified and improved algorithm SHEKF1 combined with the third-order RC model is 0.15 s faster under DST conditions than the second-order RC model. This suggests that combining the higher-order model with the simplified algorithm can result in high accuracy without increasing the algorithm’s convergence time.

ii. The streamlined Sage-Husa algorithm continues to be utilized comparatively more frequently than the original Sage-Husa algorithm.Eliminating the factors that cause the noise covariance matrix to become non-negative definite can improve the filtering’s stability, albeit at the expense of some precision. Additionally, the technique of directly removing the subtractive part that could result in filter divergence is incredibly effective despite being very basic and crude. As a result, it is essential to reduce the complexity of the covariance matrix created by the two noises and do away with the estimation of the expectation created by the two noises.The experiments in this paper show that the simplified SHEKF algorithm is very effective.

iii. SHEKF1 and SHEKF2 comparison shows that the adjustment of the two forgetting factors can be more flexible. When compared to the Sage-Husa algorithm with one forgetting factor, the Sage-Husa algorithm with two forgetting factors significantly improves SOC estimation accuracy. Furthermore, the EKF algorithm is transformed into the EKF algorithm by removing the adaptive noise estimation based on the simplified SHEKF algorithm. This EKF algorithm outperforms the SHEKF2 and SHEKF4 algorithms in terms of stability. Many papers propose the SHEKF3 algorithm, which simplifies the SHEKF algorithm and adaptively estimates only the system noise and has an error of no more than 1.5% less than the EKF. The improved SHEKF1 algorithm has a maximum error of 2.2% less than the EKF and is resistant to the initial value of the SOC. To summarize, future improvements to the SHEKF algorithm should focus on different treatment of system noise and measurement noise in order to reduce computational degree and achieve higher precision.

iv. As demonstrated in Section 4 of this paper, the magnitude of the selected forgetting factor value correlates directly with the precision of SOC estimation. However, there is no accepted formula to measure whether the set forgetting factor is reasonable or not. Therefore, the best results were obtained by setting the forgetting factor to 0.95 for the Q and 0.995 for the R through several simulations. In addition, the SOC estimation is thought to be more accurate when there is a greater disparity between the two. In the actual SOC estimation, it is necessary to consider both stability and real-time performance. Since the causes of system noise and measurement noise are distinct, two optimization algorithms, asymptotic memory index weighting and limited memory index weighting, are selected to make adaptive adjustments to the noise. Numerous experimental data demonstrate that this processing yields superior SOC estimation results.

5. Conclusions

An estimate of SOC is obtained in this paper using a model-based methodology. The model part uses a third-order RC equivalent circuit instead of the second-order model that is typically used in literature. For the algorithm, two forgetting factors are used in a simplified Sage-Husa extended Kalman filter (SHEKF) algorithm.Using the limited memory index weighting method and the asymptotic memory index weighting method, the forgetting factors are chosen so that they adapt to the different levels of fast and slow changes in the measurement noise and the statistical properties of the system noise. The SOC estimation accuracy has increased by 0.2% when contrasted with the EKF algorithm. The enhanced algorithm for estimating SOC outperforms other SHEKF algorithms in terms of robustness and accuracy.The improved algorithm for estimating SOC outperforms other SHEKF algorithms in terms of accuracy and persistence. Furthermore, by combining the third-order model with this simplified method, the problem of the higher-order model’s long convergence time can be solved. The improved algorithm converges 0.154 s quicker than the second-order model for the DST condition.