Optimization of Control Strategy for Orderly Charging of Electric Vehicles in Mountainous Cities

Abstract

In light of the increasing number of electric vehicles (EV), disorderly charging in mountainous cities has implications for the stability and efficient utilization of the power grid. It is a roadblock to lowering carbon emissions. EV aggregators are a bridge between EV users and the grid, a platform to achieve energy and information interoperability, and a study of the orderly charging of EVs to reach carbon emission targets. As for the objective function, the EV aggregator considers the probability of EV charging access in mountainous cities, the SOC expectation of EV users, the transformer capacity constraint, the charging start time, and other constraints to maximize revenue. Considering the access probability of charging for users in mountainous cities, the optimized Lagrange relaxation method is used to solve the objective function. The disorderly charging, centralized optimized charging, and decentralized optimized charging modes are investigated using simulation calculations. Their load profiles, economic benefits, and computational efficiency are compared in three ways. Decentralized optimal charging using the Lagrange relaxation method is shown to be 50% more effective and to converge 279% faster than centralized optimal charging.

1. Introduction

EVs connected to the grid for orderly charging are a key measure to combat energy depletion and environmental pollution and achieve carbon emission reduction [1]. There will undoubtedly be effects on the grid as a result of a widespread EV connection to the active distribution system [2]. In order to lower the risk to grid operation, increase grid profitability, and enhance power quality, an orderly charging plan for electric vehicles is needed [3]. EV charging piles serve as an infrastructure for information and energy interoperability between EVs and the grid, and EV aggregators control the orderly charging of EVs to realize cost savings for low-carbon EV–grid interaction and improvement of electric energy utilization and to achieve the effective coordination of users and electric vehicle aggregators [4].

At present, domestic and foreign experts in the industry have conducted a lot of research about the orderly charging management of EVs. In the literature [5], a multi-objective particle swarm algorithm is utilized to help in solving the volatile energy dispatch problem for orderly charging of EVs. The aim is to reduce both the dispatch cost and the overall load variance. In the literature [6], an improved second-order cone algorithm is applied to address the EV grid dispatch control strategy. The Cplex mathematical solver is called upon to solve the objective function using the Yalmip modelling toolbox in Matlab. The algorithm is tested in an IEEE-33 node power system, which has a high level of reliability and makes the grid more stable. The literature [7] uses the NSGA-II algorithm to establish a tariff model to solve the spread of EVs over time and space for orderly charging. Reduced the valley-peak difference and ensured the benefits of EV aggregators according to EV travel rules. In the literature [8], in addition to a PSO algorithm, a combination of competitive learning, inverse learning, and local searching is used to solve the EV charging management strategy with the aim of reducing the grid running cost and the minimum charging cost for EV users. Still, the computational complexity of the algorithm is too large. The literature [9] establishes a two-layer optimization model combining a lesser model for EV charging load optimization and a top model for EV charging pricing. The model is verified using real-world power system operational data with the lowest EV customer charging cost as the goal. The simulation results show that the optimized model can better reduce the grid valley-peak difference and shrink the charging cost of users. However, the model’s flaw is that it does not take into account how the uncertain charging habits of EV users might affect things. The literature [10] establishes an optimization model considering the uncertainty of EV access and the volatility of volatile energy sources, uses price demand to adjust the charging load, and proposes a joint algorithm for solving multi-objective problems. The NSGA-II algorithm is used to solve a function to maximize the revenue of the electricity supplier. The case verifies the algorithm’s effectiveness, but the type of EV and charging method is not considered. The literature [11] proposes a multi-stage optimization strategy that considers aggregator demand management and electricity transportation. A mixed integer and linear programming model is used to converge the optimal value of the objective function, and tariff incentives are used to guide orderly charging. Default penalties are used as an incentive aid to improve contract charging. The program strategy verifies that the combination of incentives and penalties greatly reduces the waste of charging resources. The literature [12] collates and analyses a large amount of accurate data on EVs, considering the time dimension factor, grid-side load fluctuations, and the maximum charging capacity on the user side. The objective function is solved using a genetic algorithm solution toolbox. When compared to random charging, the empirical validation shows that ordered charging decreases the valley difference and load fluctuation by 22% and 22.7%, respectively.

Most of the aforementioned literature is on centralized charging of EVs, but there is less literature that integrates factors such as economic benefits of EV aggregators, solving for the convergence speed of ordered charging, and the impact of decentralized control strategies on the grid. In the context of large-scale EV access to the grid, the convergence speed of the EV charging information solution is not considered, which will lead to information congestion and further prevent the orderly charging of EVs, resulting in “peak on peak” and affecting the stable operation of the grid. Some papers do not consider the revenue of aggregators, but only the stability of the grid, which may lead to a lack of aggregators’ ability to dispatch cars and prevent the effective orderly charging control of EVs. Some studies only consider the aggregator’s revenue, but not the load profile of the grid, and the charging time of EVs is concentrated in the peak period of people’s electricity consumption, resulting in the overload of the power system.

In this paper, in order to mitigate the peak and valley fluctuations caused by disorderly EV charging, an optimization strategy of EV time-sharing charging and EV decentralized charging is proposed, taking into account the actual length of EV charging, EV response speed, electricity prices, and operators’ profits [13]. Comprehensive consideration of the orderly controlled charging of EVs makes it possible for users and aggregators to sign charging contracts, which not only ensures the income of aggregators, but also regulates the grid load through contract charging, realizing a win-win situation for aggregators, EV users, and the grid. Based on the orderly charging of EVs in mountainous cities, the influence of terrain on EV charging is further refined to enhance the applicability of EVs in various terrains, which is meaningful for the orderly charging of EVs under mountainous cities. Based on the charging access probability of EV users under mountainous cities, the Lagrange relaxation method is used to optimize the objective in order to enhance the solution speed of the solved objective function and the gain of EV aggregators and shorten the solution time.

2. EV Centralized Charging Scheduling Model

The scenario in this paper is set in the context of a charging contract between an electric vehicle user and an aggregator [14], and the aggregator provides the user with certain infrastructure, such as charging pile installation, communication services, and battery repair and replacement services. Based on these conditions, the charging demand of the EV user is met and the EV of the contracted user is controlled for orderly charging and utility-scale EV operation [15,16].

2.1. Analysis of Charging Behavior for a Single EV

2.1.1. Charging Characteristics under Daily Mileage Demand

EV travel time and charging time are determined by users’ daily travel patterns and are key to analyzing their charging behavior [17]. Typically, EV users pay for charging according to the service tariff [18], which guides them to charge during low peak periods of electricity consumption and minimizes grid-side load peaks. For EV users, charging costs can be reduced [19]. Before the implementation of time-sharing tariffs, EV users were randomly selecting charging locations and charging times based on their daily habits [20]. Based on the results of the 2017 U.S. Department of Transportation survey of private automobiles in the USA, it is known that EV users’ travel and return times roughly follow a normal distribution. EVs’ daily mileage also roughly follows a normal distribution [21].

Each EV user will have an approximate usage pattern, and the specific time of arrival at the charging post has uncertainty, but it itself conforms to certain spatio-temporal characteristics [22]. According to big data laws, there are fixed behavioral contingencies that will have a certain inevitability, and the same is true for user charging behavior [23]. Mathematical modeling of the probability of charging a user meets the laws of probability. Thus, the time of EV access to the grid is represented by the equation of the probabilistic model.

The travel behavior of EV users in mountainous cities is influenced by spatial and temporal characteristics, where the complex characteristics of space greatly affect the travel patterns of users [24]. Living and working distance is also a feature of mountain city travel, with different travel characteristics from those of the plains.

The travel probability model of EV users in mountainous cities, with many uncertainties [25], is a critical factor affecting travel patterns [26]. The probabilistic model of the “access probability” of EVs based on contractual response mechanisms can reduce the uncertainty of user charging. In constructing a probabilistic model, the probability of EV $P_{\mathrm{it}}$ access is expressed as:

$$P_{\mathrm{it}}=\underset{n\to \infty }{\lim }\frac{1}{n}{N}_t=\underset{n\to \infty }{\lim }\frac{1}{n}{\displaystyle \sum _{i=1}^n{\xi }_{\mathrm{it}}}$$

(1)

In the equation, $P_{\mathrm{it}}$ denotes the access probability of such vehicles at the moment. $N_t$ denotes the number of visits of these vehicles at the time of t. n on behalf of the number of samples. When ${\xi }_{\mathrm{it}}=0$ means the EV is not connected, and when ${\xi }_{\mathrm{it}}=1$ means the EV is not connected.

It is possible to answer the following equation using the definition of expectation. The above equation can be rewritten as follows.

$$P_{\mathrm{t}}=E({\xi }_{\mathrm{it}})$$

(2)

Therefore, at a certain time, the expected value of the possibility of the user accessing the power grid for charging is equivalent to the expected value of the actual charging situation. The above equation can be rewritten as follows.

$$E(S_{\mathrm{t}})={\displaystyle \sum _{\mathrm{i}}{P}_{\mathrm{it}}}E(S_{it})$$

(3)

In summary, utilizing the dependability studies’ method of Monte Carlo simulation [27,28,29], the time probability density function of the first EV access to the grid is obtained by transforming the EV visit time to enter an uncertainty of access to the grid study via sampling and combining the user travel probability characteristics under mountainous cities as shown below.

$$f_g\left(x_t\right)=\left\{\begin{array}{l}\frac{1}{{\sigma }_t\sqrt{2\pi }}\exp \left[-\frac{{\left(x_t+24-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right]\hspace{1em}0<x_t\le {\mu }_t-12\hfill \\ \frac{1}{{\sigma }_t\sqrt{2\pi }}\exp \left[-\frac{{\left(x_t-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right]\hspace{1em}\hspace{1em}{\mu }_t-12<x_t\le 24\hfill \end{array}\right.$$

(4)

In the above equation, $x_g$ is expressed as the moment when the EV gets connected into the power system. The expected value is ${\mu }_t=17.8$; the standard deviation is ${\sigma }_t=3.2$.

The probability density function for the moment when the EV charging is completed and leaves the grid is expressed as:

$$f_l\left(x_t\right)=\left\{\begin{array}{c}\frac{1}{{\sigma }_t\sqrt{2\pi }}\exp \left[-\frac{{\left(x_l-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right]\hspace{1em}\hspace{1em}\hspace{1em}0<x_l\le {\mu }_t+12\\ \frac{1}{{\sigma }_t\sqrt{2\pi }}\exp \left[-\frac{{\left(x_l-24-{\mu }_t\right)}^2}{2{\sigma }_t^2}\right]\hspace{1em}\hspace{1em}{\mu }_t+12<x_l\le 24\end{array}\right.$$

(5)

In the above equation, $x_l$ denotes the moment when the electric car returns; the expected value is ${\mu }_t=8.9$; and the standard deviation is ${\mu }_t=3.2$.

2.1.2. Initial Charge State Constraint

The initial nuclear state of the EV is an important factor in determining whether the user charges the car or not. Once the user decides to use the charging pile to charge their EV, the default situation is that the EV user agrees to submit to the reasonable regulation of the EV aggregator [30]. The initial charge state of the EV before this departure is then derived based on the setting of the EV user’s expectation for the EV and the electrical energy consumed by the EV user while driving 100 km [31].

$$S_{c,i}=S_{e,i}-\frac{R{H}_{100,i}}{100B_{c,i}}$$

(6)

In the above equation, $S_{e,i}$ represents the expected target for the charge state achieved by the ith EV. $S_{c,i}$ represents the initial charge state of the ith EV, and $B_{c,i}$ represents the capacity rating for the battery of the ith EV. $H$ represents the mileage of the EV in a day, and $H_{100,i}$ represents the electric energy consumed by the ith EV to drive 100 km under daily conditions.

Charging to achieve the user’s expectation of the battery charge state must satisfy a charging time greater than or exceeding the minimum charging time, and the constraint on the charging time of an EV is shown below [32].

$$\frac{S_{e,i}-S_{c,i}}{P_e}\le x_{l,i}-x_{g,i}$$

(7)

$P_e$ expresses the rated power of EV charging, $x_{l,i}$ indicates that the ith EV leaves the grid at this time. $x_{g,i}$ indicates that the ith EV is connected at this time.

2.1.3. Miles Traveled

The function of distance traveled by EVs are expressed using the following equation [33].

$$f_d(R)=\frac{1}{R{\sigma }_d\sqrt{2\pi }}\exp \left[-\frac{{\left(\ln R-{\mu }_d\right)}^2}{2{\sigma }_d^2}\right]$$

(8)

In the above equation, $R$ represents the mileage of the EV in a day. ${\mu }_d=3.31$, ${\sigma }_d=0.87$.

2.2. Electric Vehicle State Model

The state of the EV is represented by a set of data matrices (time connected to the grid, time away from the unit, daily driving range, initial battery charge, battery state expectation, whether to obey the dispatch, charging state, 100 km power consumption, charging power and efficiency, battery capacity) representing the parameters [34,35].

(1)

Detailed statistics of an EV’s status data, which is a prerequisite for an EV aggregator to conduct orderly charging. The time to start charging your EV and departure time from the power system is the EV trip end time and trip start time, and the values used in the scenario are obtained by combining the latest travel data from across the United States.

(2)

The daily driving range of EVs is a factor that affects the initial state of the battery.

(3)

The initial battery charge is charging information for EVs arriving at charging posts. The battery state expectation represents the highest level of user satisfaction, and the minimum charge state is the minimum charge requirement for the next trip the user plans.

(4)

Whether or not to obey the dispatch is determined by the EV’s choice and state of charge.

(5)

The charge state indicates whether the EV is charging or not and is expressed as:

$${\mathit{S}}_{\mathit{i}}^{\mathit{j}}=\left\{\begin{array}{l}1, \mathit{Being} \mathit{charged}\hfill \\ 0, \mathit{Not} \mathit{charged}\hfill \end{array}\right.$$

(9)

In the equation, $S_i^j$ denotes the charging state of the ith EV in period j, and there is only one state of the EV at this time.

2.3. Electric Vehicle Centralized Charging Scheduling Model

EVs are dispatched as objects of the aggregator dispatch model, provided that the aggregator provides users with infrastructure such as smart charging piles and communication platforms [36]. The user must also perform according to the signed contract and obey the aggregator’s orderly charging dispatch.

2.3.1. The Objective Function

The EV aggregator is a service provider to individual vehicle customers, charging customers for services at the charging service price and paying the electricity sales company for electricity at the time share tariff. The aggregator earns a profit by earning the difference between the two tariffs, with the objective of maximizing the aggregator’s net revenue and minimizing load fluctuations.

$$\max \sum _{i=1}^N\sum _{j=1}^{96}{P}_e{S}_{i,j}\mathsf{\Delta }t\left(p-p_j\right)$$

(10)

where $N$ is the number of vehicles that obey the aggregator’s scheduling every day. $\mathsf{\Delta }t$ denotes a 15 min period. The 24 h of a day are averaged into 96 time periods. $P_e$ means the rated charging power of EVs. $p$ is the charging service price charged by the aggregator to the customer. $p_j$ is the price of electricity purchased by the aggregator from the electricity sales company in the jth period of the day.

The above equation can be converted to find the minimum value, which is equivalent to the following equation.

$$\min \sum _{i=1}^N\sum _{j=1}^{96}{P}_e{S}_i^j\mathsf{\Delta }t\left(p_j-p\right)$$

(11)

2.3.2. User Requirements Constraints

The electric vehicle battery capacity should be higher than the user’s expectation, but less than its maximum rated capacity. Avoid causing battery damage.

$$S_{e,i}\le S_{c,i}{B}_c+\sum _{j=1}^J{P}_e{\eta }_r{S}_i^j\mathsf{\Delta }t\le B_c$$

(12)

$$0\le P_A\le P_{MAX}$$

(13)

where ${\eta }_r$ indicates the charging efficiency. The battery capacity of the EV leaving the grid should be greater than the user expects and less than the battery standard holding capacity. $P_A$ indicates the actual charging power. $P_{MAX}$ is the maximum charging power of the EV.

2.3.3. Control Time Constraints

The user sets the inbound time $T_t$ to be in the control period $J_t$, and the relationship between the two is as follows.

$$J_t=\left[T_t/\mathsf{\Delta }t\right]$$

(14)

where $[ ]$ denotes the rounding function that discards the decimal part, $T_t$ denotes the EV entry time, and $J_t$ is the EV charging period.

The charging period satisfies between $J_t+1$ and $J_d$, and the time when the user leaves the grid is within the control period. $S_i^j$ indicates that the charging state is:

$$S_i^j=\left[\begin{array}{ccccccccc}{j}_{1,1}& \cdots & j_{1,t}& j_{1,t+1}& \cdots & j_{1,d}& j_{1,d+1}& \cdots & j_{1,96}\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ j_{i,1}=0& \cdots & 0& 1& \cdots & 1& 0& \cdots & 0\\ ⋮& \ddots & ⋮& ⋮& \ddots & ⋮& ⋮& \ddots & ⋮\\ j_{N,1}& \cdots & j_{N,t}& j_{N,t+1}& \cdots & j_{N,d}& j_{N,d+1}& \cdots & j_{N,96}\end{array}\right]$$

(15)

2.3.4. Transformer Capacity Constraint

Electric vehicles connected to the grid must consider the transformer capacity of the area to avoid exceeding the transformer capacity range and causing grid fluctuations.

$$\sum _{i=1}^N{P}_e{S}_i^j+p_j^l<P_{MAX},j=1,\dots ,96$$

(16)

$p_j^l$ is the size of the base load in the control time period j.

2.3.5. Charging Constraint

Charging starts when the battery of an electric vehicle is below 40% of its rated capacity. Normally the EV is charged to 95% of its rated capacity and stops charging.

$$0.4\le S_{c,i}\le S_{e,i}\le 0.95$$

(17)

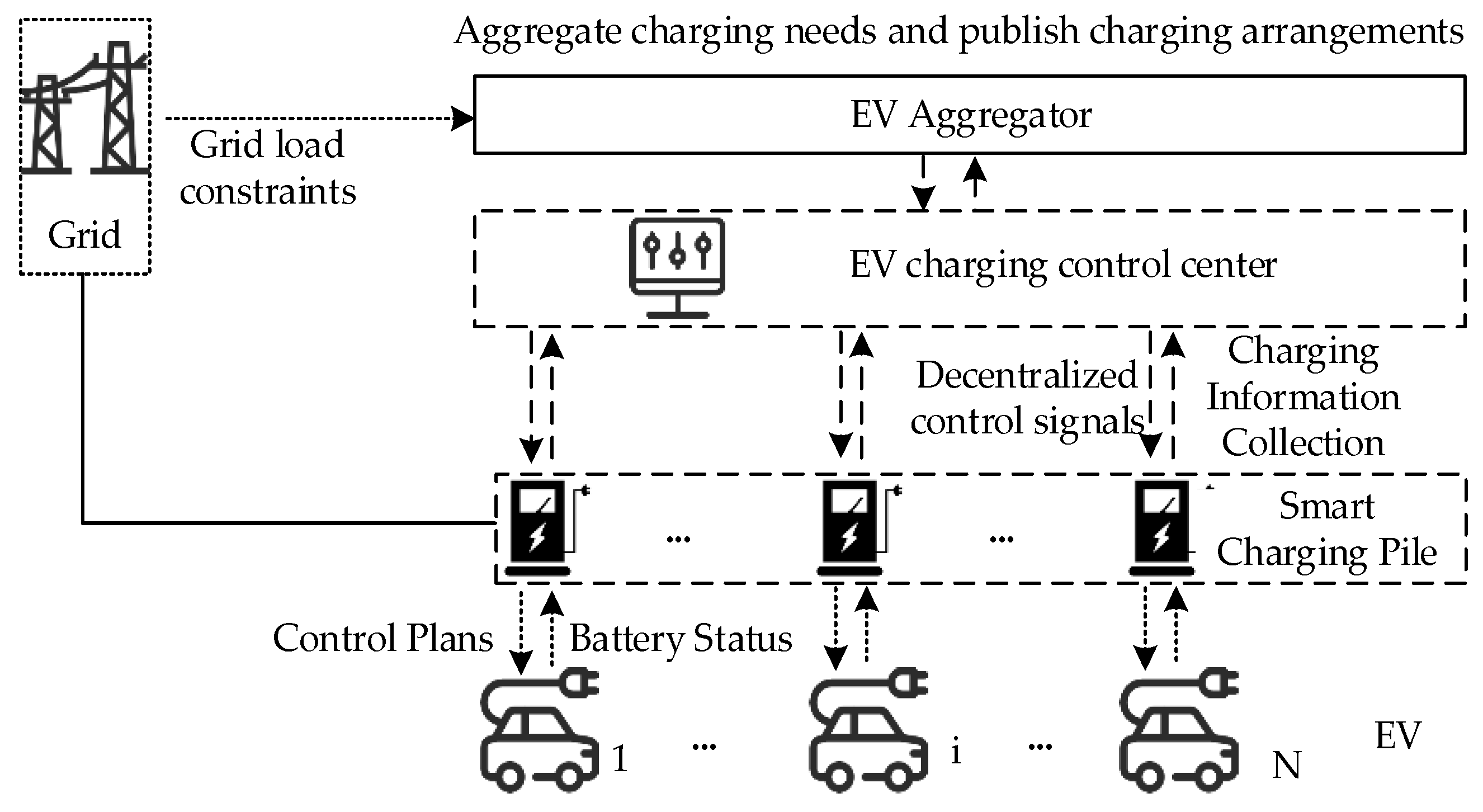
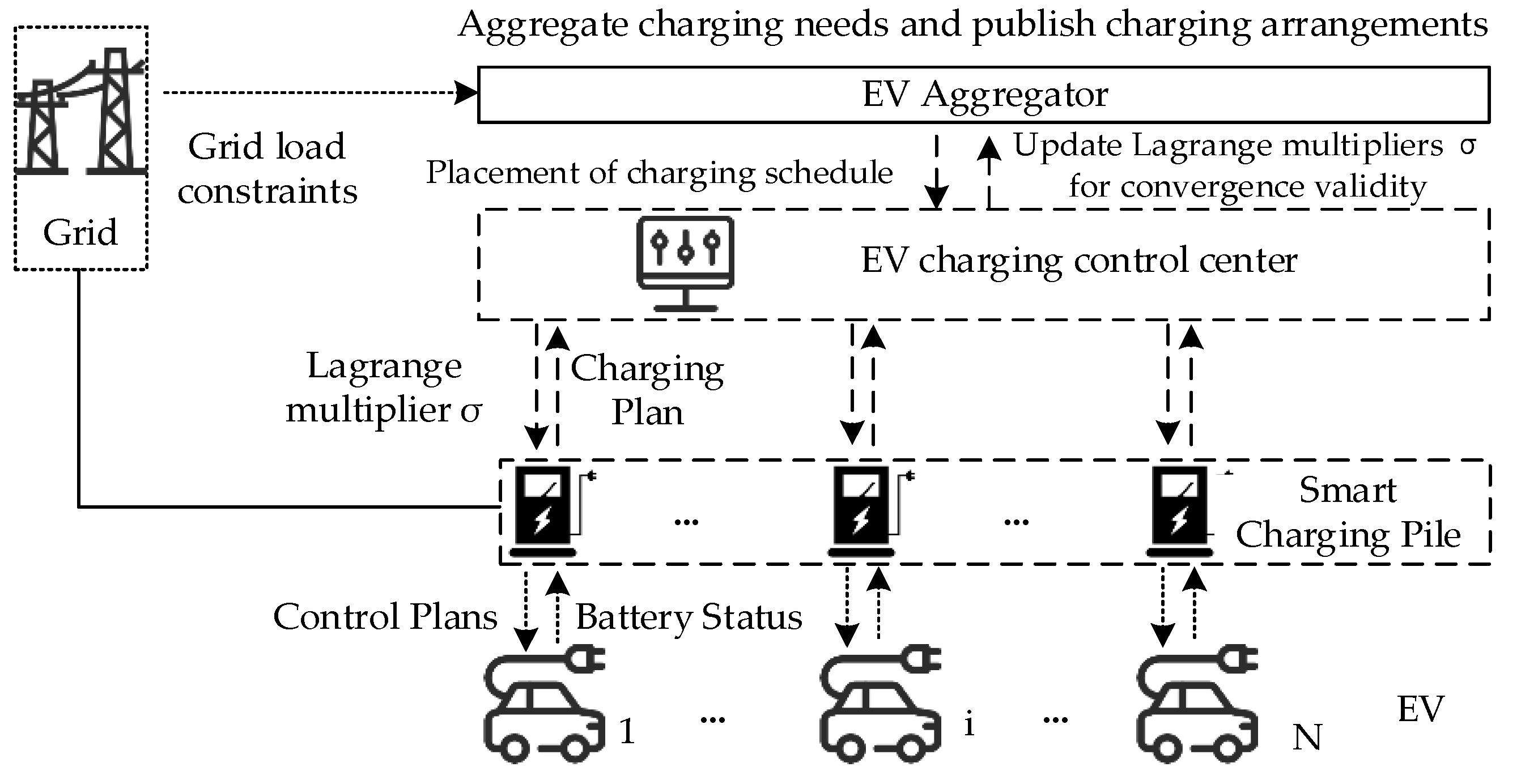
3. Dispersion Control Optimization Strategy under Lagrange Relaxation Method

3.1. Decentralized Charging Strategy

The decentralized optimization strategy controls the charging order through independent decentralized charging posts [37]. The charging information, including initial battery status, start charging time, end charging time, battery status at the end, etc., is read by the smart charging post and transmitted to the aggregator through the information collector. The planned tariff with the initial value of the Lagrange multiplier is transmitted to the control center to generate the new service charging tariff. The smart charger calculates again and finally determines the new charging schedule. The charging schedule for each time period is calculated according to this schedule control strategy. Optimized control model is shown in Figure 1.

3.2. Lagrange Relaxation Problem for the Original Problem

The Lagrange relaxation method is solved by absorbing the complex constraints into the objective function and keeping the objective function linear [38]. Then, only simple restrictions are available overall. According to the Lagrange relaxation principle [39], the transformer capacity constraint is removed, and the Lagrange multiplier is multiplied by the transformer capacity constraint, which is reflected as a penalty term in the original objective function. The following equation is obtained after simplifying the Lagrange relaxation problem for the original problem.

$$\begin{array}{cc}L\left(S_i^j,\sigma \right)& ={\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^{96}}{P}_e{S}_i^j\mathsf{\Delta }t\left(P_j-P\right)+{\displaystyle \sum _{j=1}^{96}}\sigma \left(P_e{\displaystyle \sum _{i=1}^N}{S}_i^j+P_j^l-P_{MAX}\right)=\\ & P_e{\displaystyle \sum _{i=1}^N}{\displaystyle \sum _{j=1}^{96}}\left[\mathsf{\Delta }t\left(P_j-P\right)+\sigma \right]S_i^j+{\displaystyle \sum _{j=1}^{96}}{\theta }_j\left(P_j^l-P_{MAX}\right)\end{array}$$

(18)

$\sigma$ is a Lagrange multiplier, it is also a $1\times 96$ dimensional vector, $\sigma =[{\sigma }_1,{\sigma }_2,{\sigma }_3\cdots {\sigma }_{96}]$, and requires $\sigma >0$.

According to the mutual independence of the travel characteristics of a single EV, the above Lagrange relaxation problem can be regarded as a collection of sub-problems. Then, the following process is completed by the individual EV smart charging unit, and the Lagrange relaxation problem for the ith sub-problem of a single EV is as follows.

Objective function:

$$\min L(S_i^j,\sigma )=P_e{\displaystyle \sum _{j=j_{i,t}}^{j_{i,d}}{S}_i^j[\Delta t(p_j-p)+\sigma ]}+\frac{1}{N}{\displaystyle \sum _{j=1}^{96}\sigma (P_j^l-P_{MAX})}$$

(19)

The power constraint for each vehicle in the ith sub-problem is shown below.

$$S_{c,i}{B}_{c,i}\le S_{c,i}{B}_{c,i}+{\displaystyle \sum _{j=j_{i,t}+1}^{j_{i,d}}\Delta t{P}_e{\eta }_r\le S_{e,i}}$$

(20)

3.3. Pairing Problems

The pairwise problem can be obtained from the Lagrange relaxation problem of the original problem, and the Lagrange multipliers $\sigma$ are viewed as control factors in the pairwise issues.

The Lagrangian dual function of the primary issue is as follows.

$$\xi (\sigma )=\min L(S_i^j,\sigma )$$

(21)

The dual problem of the primary question is as follows.

$$\max \psi (\sigma )$$

(22)

where $\sigma \ge 0$, the initial Lagrange value can be determined. Equations (9), (11), and (12) are used as constraint equations for each electric vehicle Lagrange sub-questions problem. Solving for all pairwise problems gets $S_i^j$.

3.4. The Upper and Lower Boundary of the Original Problem

Importing the above-derived $S_i^j$ into the original problem’s objective function yields the best answer to the original puzzle. The optimized value of the initial problem is the upper bound of the optimal value, denoted as $S$. Similarly, taking it to the dual question, the optimal solution is a lower bound on the optimized value, denoted as $X$.

3.5. Dual Gap Problem

Determine whether the difference between S and X can reach the accuracy value. If it does, the optimal value obtained by solving the lower bound of the dual problem is considered to be the best solution for the original question. If it is not satisfied, the update of the Lagrange multiplier $\sigma$ is continued.

3.6. Sub-Gradient Method

The solution uses the sub-gradient method for updating $\sigma$, setting $\omega$ as the number of iterations and the initial value of the Lagrange multiplier $\sigma$ when $\omega =1$ is given. The iterative formula is as follows.

$$\sigma (\omega +1)=\sigma (\omega )+\upsilon (\omega )\frac{\varphi (\omega )}{{‖\varphi (\omega )‖}^1}$$

(23)

In the equation, $\nu$ is the iteration step, $\varphi$ is the sub-gradient, ${‖\varphi (\omega )‖}^1$ is expressed as a one-parameter number of $\varphi (\omega )$, and $\varphi (\omega )$ can be written in the form of a column vector.

$$\varphi (\omega )={\left[{\varphi }_1(\omega ),{\varphi }_2(\omega )\cdots {\varphi }_{96}(\omega )\right]}^T$$

(24)

The dual problem sub-gradient function of the original problem is shown below.

$${\varphi }_j(\omega )=p_j^l+{\displaystyle \sum _{i=1}^N{P}_e}{S}_i^j-P_{MAX},j=1,2,\cdots 96$$

(25)

3.7. Step Length Problem

The calculation of the step length is shown below.

$$\nu (\omega )=\frac{1}{a+\omega b}$$

(26)

Among them, the appropriate values of a and b should be determined to increase the solving speed of the algorithm. The relationship between a and b needs to satisfy b < a, and the specific values are obtained in the process of the debugging simulation.

3.8. Determine if the Dual Gap Meets the Accuracy Requirements

The iterative process continues and is continuously updated until the convergence reaches the required accuracy $\epsilon$, and the following equation is satisfied.

$$\frac{S-X}{X}<\epsilon$$

(27)

The iteration stops if the accuracy requirement is met and the lower bound is roughly approximated as the best way to solve the objective function. The sub-problem’s objective function and constraints are both convex functions. According to convex optimization theory, the algorithm must converge and discover the optimal solution. In order for the method to converge properly, the parameters must be adjusted.

3.9. Decentralized Optimization Flow Chart

The policy control flow on the basis of the Lagrange relaxation method is located in Figure 2, and the optimal value is solved by updating the Lagrange multiplier using the sub-gradient method.

4. Example Analysis

4.1. Decentralized Optimization Mechanism on the Basis of Lagrangian Relaxation Method

The Lagrange relaxation method requires several convergent iterations to reach the optimal solution, and its decentralized optimization management mechanism is shown in Figure 3.

4.2. Simulation Scene Setting

In this simulation, only the load connected to the grid for residential home electric vehicles is considered. The simulation scenario is set under the transformer of a 10 KV distribution network. The capacity of the transformer is 7700 kVA, the efficiency is set to 0.95, and the power factor is 0.85. Maximum load capacity in transformer equipment is 6218 kw. In addition, the times of EV access and departure from the grid are obtained via Monte Carlo sampling. From a realistic point of view, the power purchase cost by aggregators is based on the local time-of-use tariff, and the service tariff includes a labor service fee pricing level of 1 yuan/kW·h, taking a charging station in Chongqing city as an example.

According to an estimate of the amount of EVs that need to be charged in mountainous cities and the way that they are currently developing there, the capacity of EVs is set as 32 kw·h, and the rated charging power is 7 kw. Normally, charging starts when the EV battery is below 40% of its rated capacity, and stops when the EV battery reaches 95% of its total capacity. Set the charging efficiency factor of electric vehicles to 0.95. The service tariff is not discussed, and the specific charging tariffs are shown in

Table 1. Time share tariffs.

Time Period	Grid Electricity Sales Prices (kW·h)	Service Charging Tariff (kW·h)
00:00–08:00	0.365	1
08:00–12:00	0.869	1
12:00–14:30	0.687	1
14:30–17:00	0.687	1
17:00–21:00	0.869	1
21:00–24:00	0.687	1

.

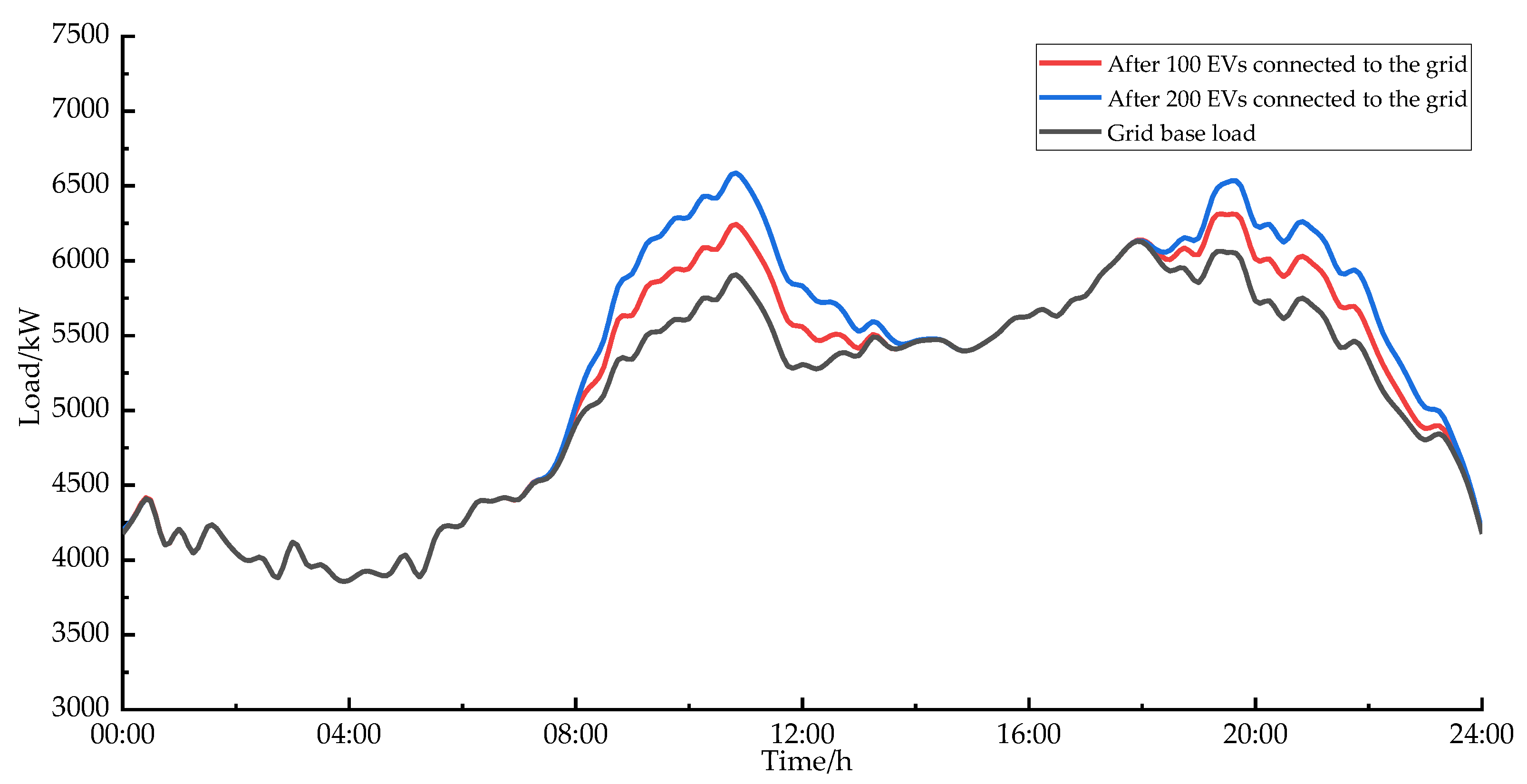
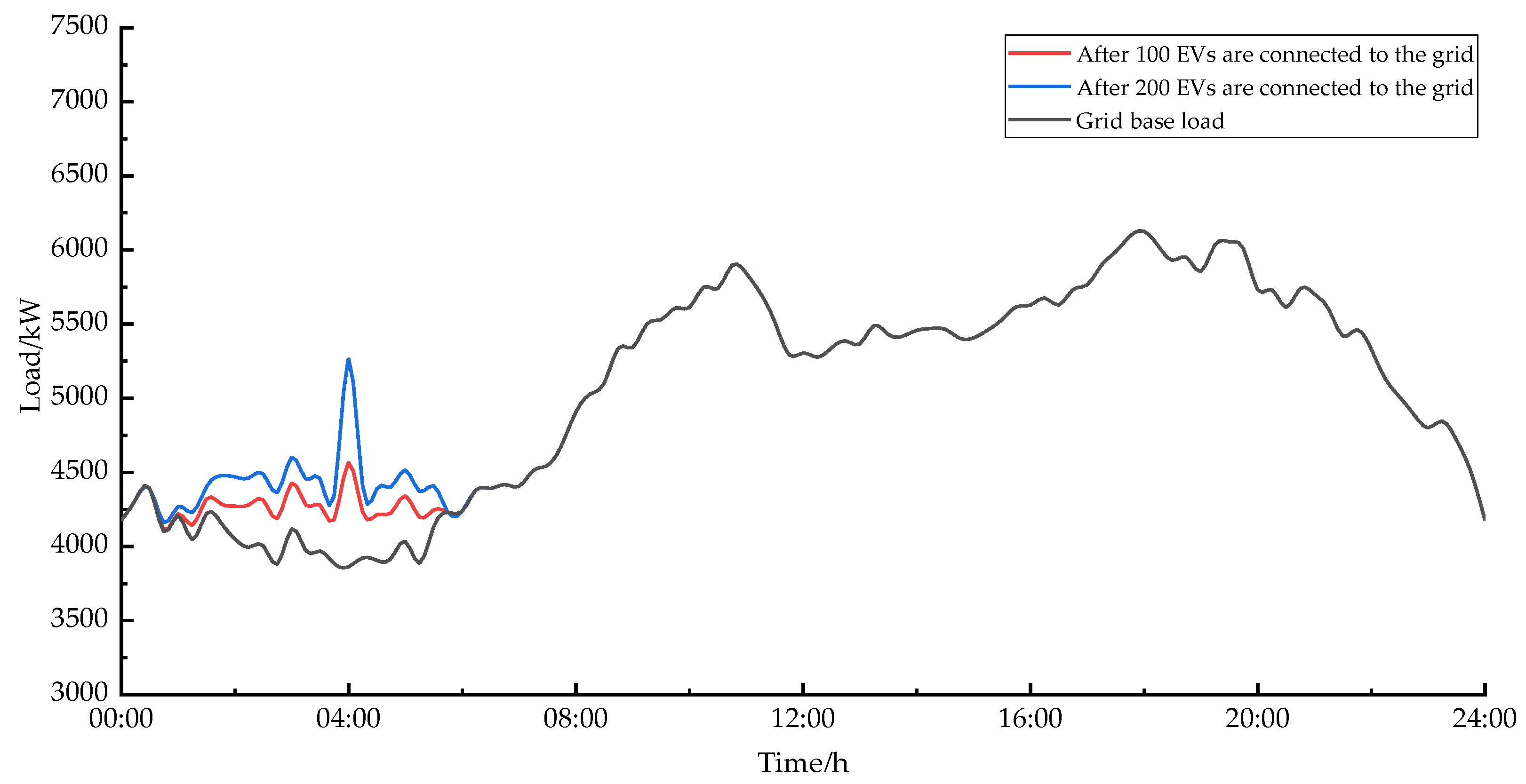
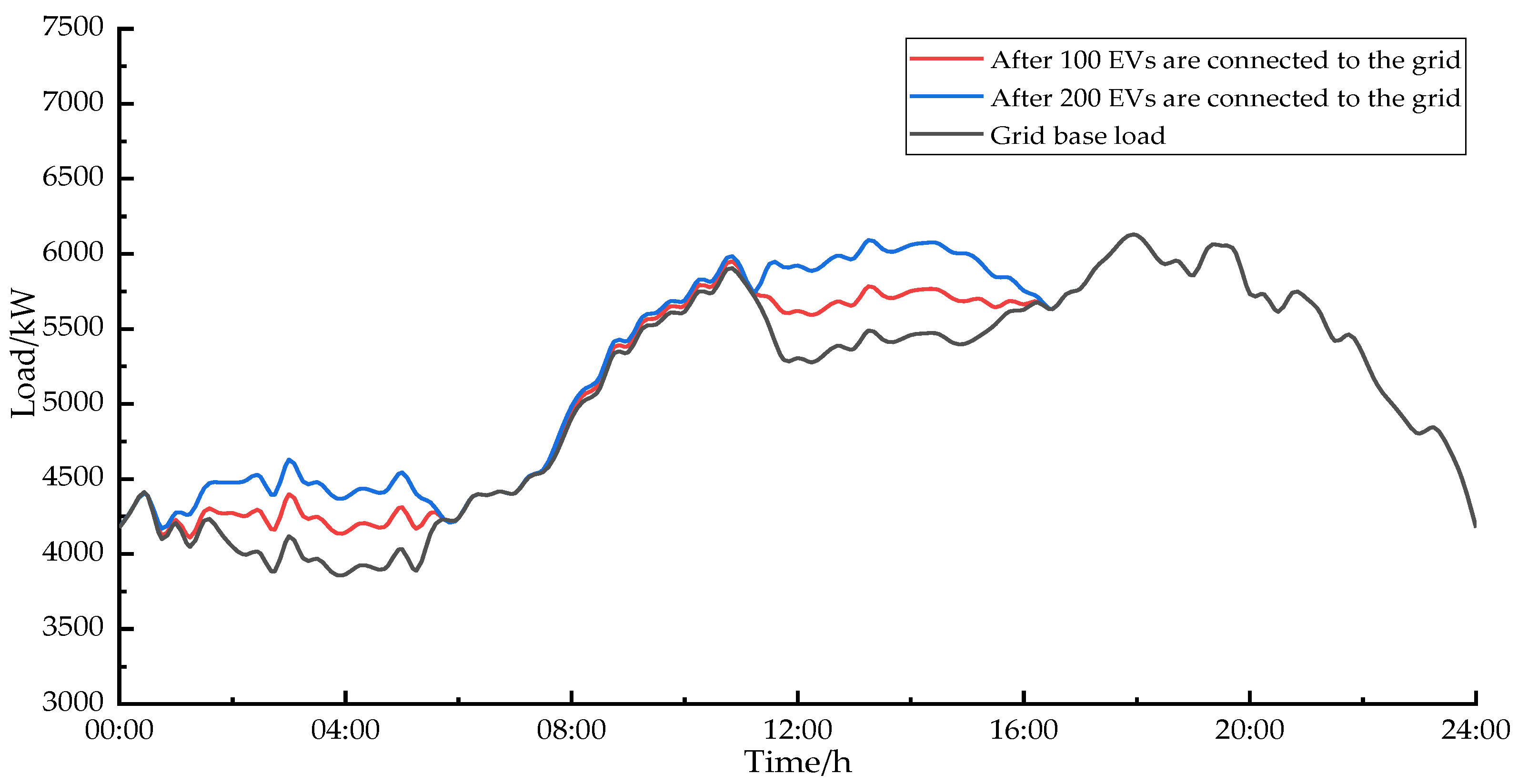
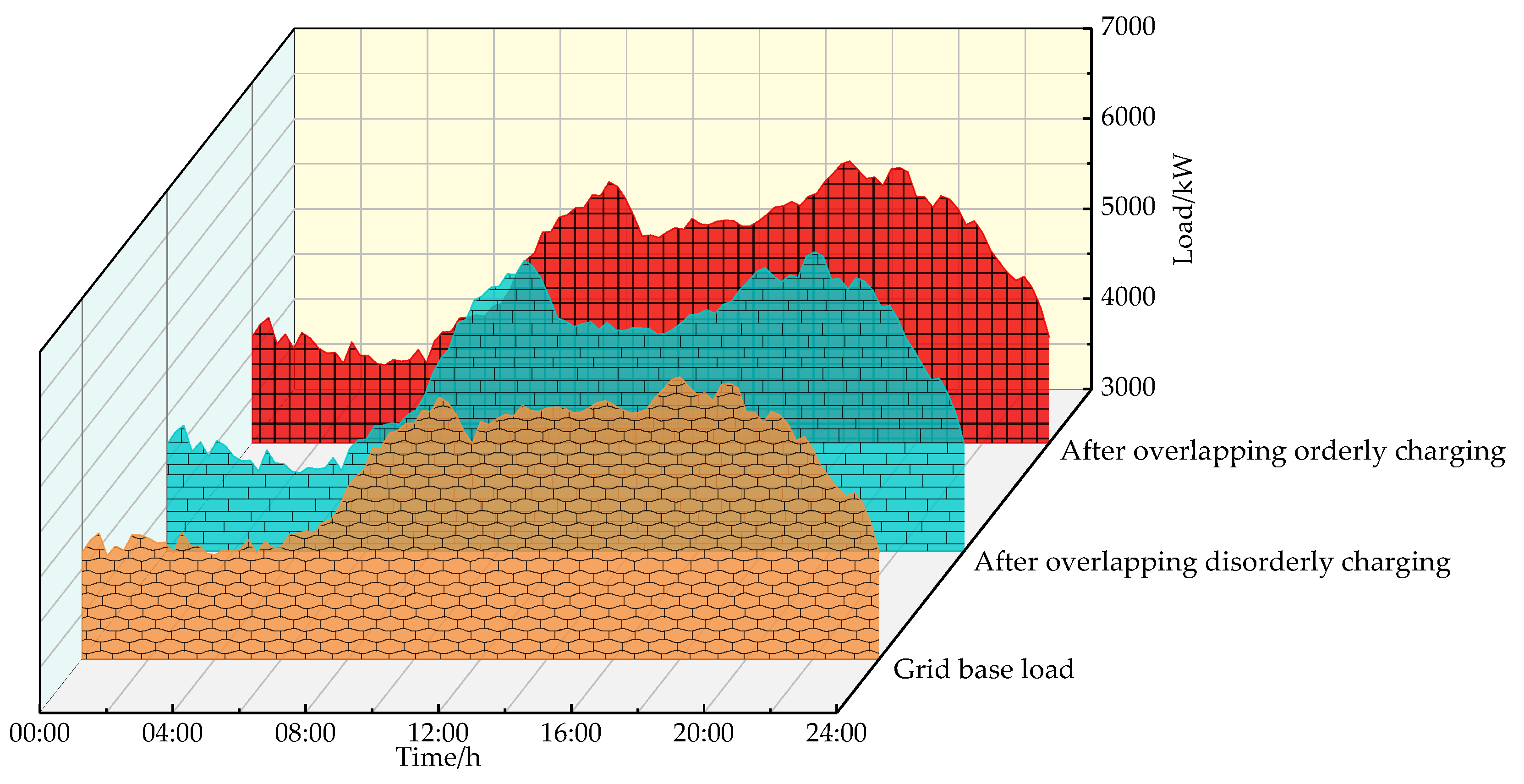
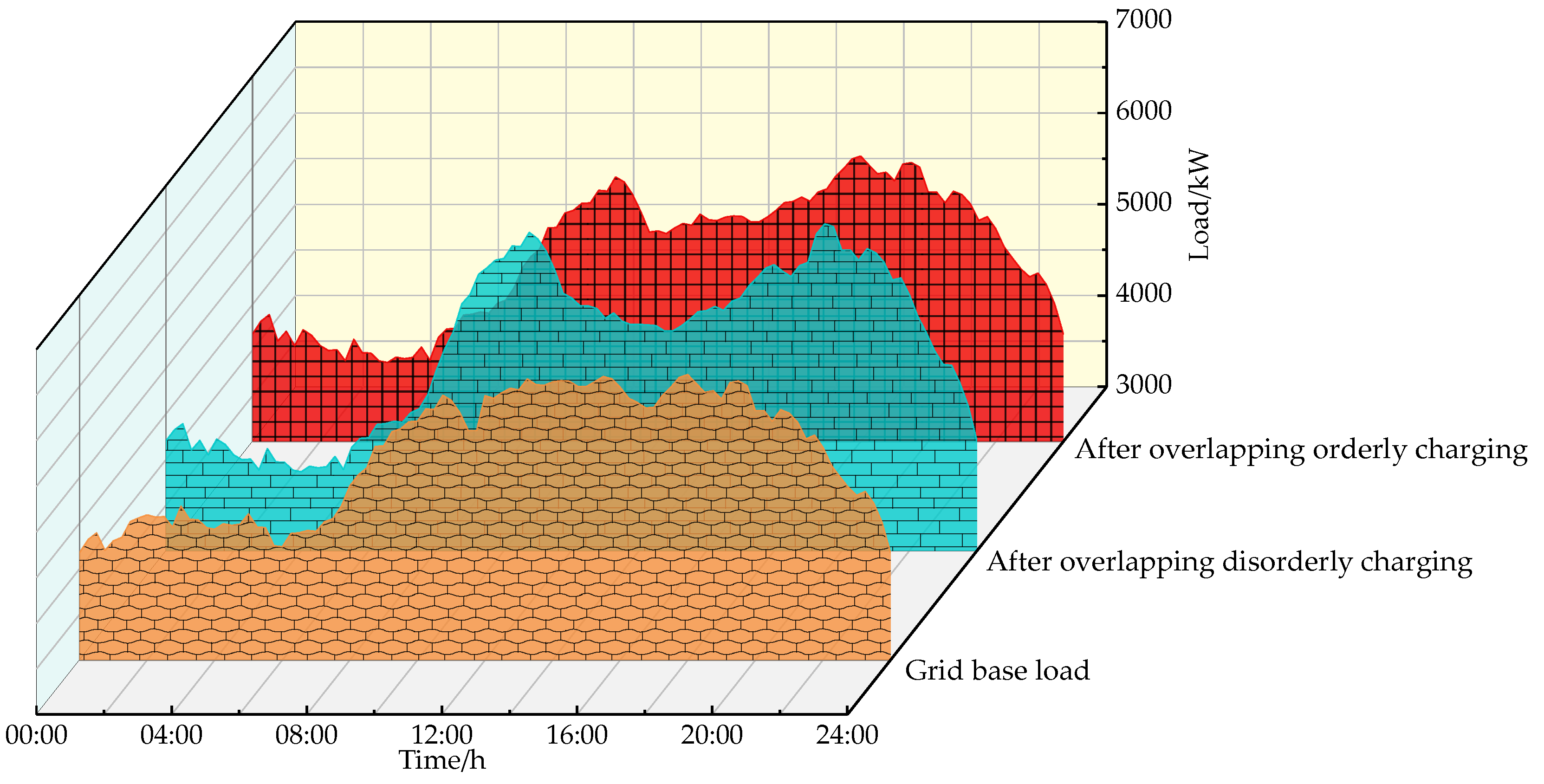
4.3. Experimental Results and Analysis

Charging of 100 and 200 EVs in one day was simulated via the Monte Carlo method, respectively. A Lagrangian relaxation-based technique was used to simulate load profiles for disordered charging, centralized optimal charging, and contract-controlled charging.

Disorderly charging. Assuming that all EVs access the power system and start charging and the battery reaches maximum charge and is suspended, the resulting load curve is shown in Figure 4, which shows disorderly charging will inevitably cause a peak in the load. In this scenario, the maximum carrying capacity of the transformer is 6218 kw, and the maximum power limit of the transformer will be exceeded when 100 and 200 EVs are charged in a disorderly manner.

Centralized optimized charging. From Figure 5, it can be seen that centralized optimized charging mostly concentrates on charging from 00:00 to 06:00, which can effectively realize the function of load filling. Furthermore, centralized optimized charging for 200 EVs will generate a new load peak, which is generated by the optimization of the maximum aggregator gain of centralized optimized charging as an objective function, however, its peak does not go over the transformer’s permitted load capacity limit, so it is allowed to centrally optimize operation.

The sub-gradient approach is planned to be used in the decentralized optimal charging depending on the Lagrange relaxation method to repeat the Lagrange multipliers and set the values of a and b. Set a = 2, b = 0.3, and set the number of iterations to 11 to obtain the load profile graph shown in Figure 6.

From the above figure, it can be concluded that the decentralized charging strategy maximizes the charging efficiency based on the considered transformer capacity constraint, and the aggregator schedules the EV charging during the low peak load period according to the user’s charging demand to avoid exceeding the rated transformer capacity limit.

Contrast analysis. It can be seen from Figure 7 and Figure 8 that orderly charging under decentralized control has a greater impact on peak shaving and valley filling as automobiles become more prevalent. The decentralized control, although a new peak will appear, does not exceed the transformer capacity limit. At the same time, the Lagrange relaxation method considers the constraints in the solution process, and the optimized decentralized charging strategy can help coordinate the grid load.

All the simulation data in this charging strategy simulation are obtained from a single sampling result. The charging gains and calculated efficiencies under various charging strategies are analyzed.

As shown in

Table 2. Comparison of returns under different optimization strategies.

Number of Vehicles	Benefits/Yuan
	Disorderly Charging	Centralized and Optimized Charging	Dispersion Optimization Charging Based on Lagrange Relaxation Method
100	405.2	865.6	1122.9
200	980.6	1630	2424.9

, EV users get the benefits under three charging methods according to the aggregator for unordered charging, centrally controlled ordered charging, and decentralized controlled ordered charging. According to Table 2, it can be seen that the benefits of centralized optimized charging for 100 vehicles are twice as high as those of disordered charging, and the benefits of decentralized optimized charging are 1.3 times as high as those of centralized optimized charging. In addition, 200 vehicles of centralized optimized charging are 1.7 times as high as those of disordered charging, and the benefits of decentralized optimized charging are 1.5 times as high as those of centralized optimized charging. For every one-fold increase in the number of electric vehicles under a Lagrange decentralized control strategy, the aggregator’s revenue increases by an additional 15%.

Ordered charging can promote the development of EVs and reduce the national electricity generation due to load shedding by regulating the charging of EVs in the valley hours. Each EV can save 3.89 kWh of electricity generated by the generator in a day. For 100 EVs, for example, according to the orderly charging strategy under the Lagrange relaxation method in this paper, it can save 14.2 million kWh of electricity in a year. Most of the electricity in China is from thermal power generation (i.e., 71). One hundred EVs can reduce thermal power generation by 101,000 kWh a year while reducing carbon emissions by 100.5 tons of carbon dioxide and saving 40 tons of standard coal, meeting the economic benefits of aggregators while also achieving environmental benefits.

The computational efficiencies of various charging optimization strategies are shown in

Table 3. Comparison of computational efficiency under different optimization strategies.

Number of Vehicles	Calculation Time/s
	Centralized and Optimized Charging	Dispersion Optimization Charging Based on Lagrange Relaxation Method
100	50.262	14.021
200	103.624	27.312

. The data are obtained from simulations in MATLAB R2020b on a computer configured with an Intel i5-9300H CPU 2.40 GHz dual-core processor running with 16 GB of memory and a 64-bit operating system The manufacturer of the equipment is acer, purchased in Hangzhou, China. The computation of centralized optimal charging is expanding together with the scope of EVs. The computational tasks based on the Lagrange relaxation method are parallel, and it can be seen that the decentralized optimal charging strategy can efficiently solve the ordered charging of large-scale EVs in much less time than the centralized charging optimization. It effectively avoids the dimensional difficulties associated with scaled vehicles and reduces the communication time and communication blockage. It avoids the problems of “difficult dimensionality” and “communication congestion” faced by centralized optimization after the number of EVs increases and is suitable for real-time scheduling because it is relatively unaffected by the scale of EV scheduling. In terms of charging revenue, the charging revenue obtained using the efficiency of the Lagrange relaxation-based decentralized optimization strategy is marginally better compared to central optimization. Both are much higher than the charging revenue under disordered charging, showing that the current method of ordered charging can significantly decrease carbon emissions and achieve economic and environmental benefits.

4.4. Contrast Analysis

In order to verify the effectiveness of the proposed Lagrange relaxation method for mountainous cities, The algorithm is compared with alternating direction multiplier method, multi-objective genetic algorithm and improved multi-objective genetic algorithm.. In order to verify the comparison results for different sizes of electric vehicles, 500 electric vehicles are uniformly used for the solution speed analysis, and it can be seen from

Table 4. Comparison analysis table.

Algorithm Type	Calculation Time/s
Lagrange relaxation method	38.26
Traditional multi-objective genetic algorithm	51.07
Modified multi-objective genetic algorithm	59.42
Alternating direction multiplier method	112.17

that the Lagrange relaxation method saves 55.3% and 34.4% more of the solution time than the traditional multi-objective genetic algorithm and the improved genetic algorithm and shortens the vehicle scheduling time by 193.2% compared to that under the alternating direction multiplier method. It can be seen that the Lagrange relaxation method has a faster solution speed than other algorithms by relaxing away the complex constraint functions under the condition of the guarantee of the aggregator’s gain, as the scale of EVs brought into the active distribution network becomes larger and larger.

5. Conclusions

This research focuses on large-scale EV optimum operation in mountainous cities using decentralized optimization strategies focused on the Lagrange relaxation method. The effect of the user’s terrain on the probability of travel is considered. The decentralized optimization strategies rely on the Lagrange relaxation method decomposing the original problem into N sub-problems for solving, and iterative Lagrange multipliers are performed via the sub-gradient method by discriminating whether the accuracy requirements are satisfied, and the computational efficiency is significantly improved.

(1)

The efficiency of this algorithm is better compared to the centralized charging model of this algorithm. The algorithm also has a higher solution speed compared with other algorithms, which is more practical for the growing scale of electric vehicles.

(2)

The access probability of EV charging for users in mountainous cities is considered, the influence weight of terrain is increased, and the gains of the solved EV pieces aggregators are more accurate, which is conducive to the orderly charging control strategy of aggregators.

(3)

The optimized EV load curve is smoother, which plays the role of “peak-shaving and valley-filling”, and the effect of peak-shaving and valley-filling is more obvious as the scale of EVs grows larger, which also ensures the service tariff revenue of aggregators.

There are also some shortcomings in this paper, which studies the decentralized optimization strategy of aggregators purely to maximize their charging revenue, without considering factors such as the real-time electricity price and battery capacity. In the simulation results, both centralized optimization and a distributed solution model for the Lagrange relaxation method causes load spikes during the low tariff hours. Subsequently, combining the peak regulation revenue, novel energy management, and grid interaction towards a low-carbon future of EV aggregators, the objective of reducing the peak-to-valley difference needs to be further studied.