1. Introduction
The production of ethanol in Perú dates back to 2009, and according to the USDA [
1], in 2020, the forecasted status of ethanol production/consumption and exports (in millions of litres) was 170 for production, 187 for consumption, and 162 for exports. In the country’s fuel market, ethanol is mixed with gasoline with a percentage of 7.8%, and its commercial name is
gasohol. As most of the ethanol produced in the country is exported, and the amount of gasoline imports has been on the rise in recent years, raising the percentage of ethanol in local fuel is something that can be considered.
On the other hand, in the metropolitan area of the city of Lima, 60% of the air pollution comes from the vehicle fleet, according to a report presented by the Ministerio de Ambiente [
2] of the country. A possible response to this might be increasing the percentage of ethanol in the local fuel blend, as the existing literature suggests that doing so decreases the amount of vehicle emissions. For example, a study presented by Tibaquira et al. [
3] regarding the changes in emissions and fuel consumption as the percentage of ethanol in gasoline–ethanol fuel blends increases showed that the user did not detect changes in the behaviour of the vehicle or changes in torque, power, or acceleration. This study was done on small vehicles and engines using four gasoline–ethanol blends (E0, E10, E12, and E15). Regarding the behaviour of vehicle emissions, the increment in combustion efficiency resulted in a small increase in the CO
2 emissions and a reduction in CO and HC. Finally, there was no change in the behaviour of the vehicle parts or a deterioration of them.
Another study presented by Saikrishnan et al. [
4] supports these findings and the hypothesis of a reduction in emissions due to better combustion, and it also notes that there is an increase in fuel consumption due to the fact that ethanol has less calorific power. The study was done on a three-cylinder four-stroke SI engine with four gasoline–ethanol fuel blends (E0, E5, E10, E15), and the results showed that the E10 blend outperformed the other blends tested.
As for studies performed on on-road vehicles, Yao et al. [
5] tested two different spark ignition engines using a blend of gasoline and ethanol with 15% ethanol (E15), where one of the engines operated with a carburettor and the other used an electrical injection system. The results, when compared with commercial gasoline, showed that the CO emissions were lower by 32% in the case of the engine with the carburettor (2.07 g/km) and by 10% for the other engine (2.38 g/km). For total hydrocarbon (THC) emissions, the tests resulted in a reduction by 10% for the engine with the electrical injection system, while, in the case of the carburettor engine, the results were not shown. Finally, in the case of NO
x emissions, a reduction of 36% was shown for the engine with the carburettor, whereas the other engine showed an increase of 3%. From these results, the authors concluded that the blend can be used for both injection systems without secondary problems.
The same findings were accounted for by Yuan et al. [
6], who performed tests on five different vehicles: one flexible-fuel vehicle (FFV) and four non-flexible-fuel vehicles (non-FFV). The vehicles were all light vehicles, and the purpose of the study was to determine whether the non-FFV vehicles could adapt to mid-level blends. This is important because according to the Worldwide Fuel Charter [
7], the maximum recommended percentage of ethanol is 10%, and in the case of Lima, most of the vehicles of the fleet correspond to non-FFV vehicles. As for the fuel blends used in the test, four different blends were used on three ethanol percentages: E0 corresponding to no ethanol in the blend, E10 with 10% ethanol in the blend, and E27 as a mid-level gasoline–ethanol fuel blend. For the E10 blend, both regular and premium gasoline were tested. The results obtained showed that the non-FFV vehicles were able to adapt to the blends tested. As for the vehicle emissions, there was a decrease in the case of CO
2, CO, and NO
x for the case of E27, whereas in the case of E10 and E10P (corresponding to premium gasoline) there was not a significant difference in vehicle emissions.
Regarding the performance under different conditions and with different gasoline bases for the gasoline–ethanol blend, Hernandez et al. [
8] carried out a study using regular gasoline (87 octane, R) and premium gasoline (92 octane, P). The percentages of ethanol used in this study were E5 and E15, which resulted in four blends, named E5R, E15R, E5P, and E15P. Three light vehicles were selected: a 2004 Nissan Tsuru (with engine 1.6 L, 132 hp, 6400 rpm), 2005 VW Derby (with engine 1.8 L, 132 hp, 5500 rpm), and 2008 Jeep Compass (with engine 2.4 L, 172 hp, 5400 rpm). Three kinds of tests were performed: cold-start (the engine had not been used in the last 12 h), hot-start (the vehicles were turned off for 10 min prior to the start of the test), and constant speed (the vehicles were driven in traffic-free streets in a 3 km circuit). The results obtained showed a reduction in fuel consumption for all gasoline–ethanol blends in relation to their pure gasoline counterparts. In the case of E5R, the reduction was 4.4%, while it was 9.9% for E15. For the premium fuel blends, the reduction was smaller: 2.9% for E5P and 5.5% for E15P. Furthermore, among the vehicles, the Jeep Compass showed the least reduction in fuel consumption. With regard to vehicle emissions, the E15P blend showed the fewest emissions (0.77 g/km of CO, 0.0032 g/km of HC, and 0.017 g/km of NO
x). The HC emissions were, in general, higher for blends using premium gasoline (0.032 g/km for E15P and 0.038 g/km for E5P), compared to the values for regular gasoline (0.024 g/km for E15R and 0.024 g/km for E5R). These results showed that changes in technology can help to reverse the effect of the smaller calorific power of ethanol in terms of performance.
As seen from the studies presented, there exists a need to quantify the effects of increasing the content of ethanol in gasoline–ethanol blends in Perú, due to both the existence of ethanol as a resource and the environmental impact of its use. This study presents an analysis of the fuel consumption and vehicle emissions, such as CO
2, CO, HC, and NO
x, in a light vehicle that uses a spark ignition engine. The gasoline–ethanol blends used were E7.8, which corresponds to the blend used commercially in the country, and E10, which is the maximum recommended percentage of ethanol, according to the Worldwide Fuel Charter [
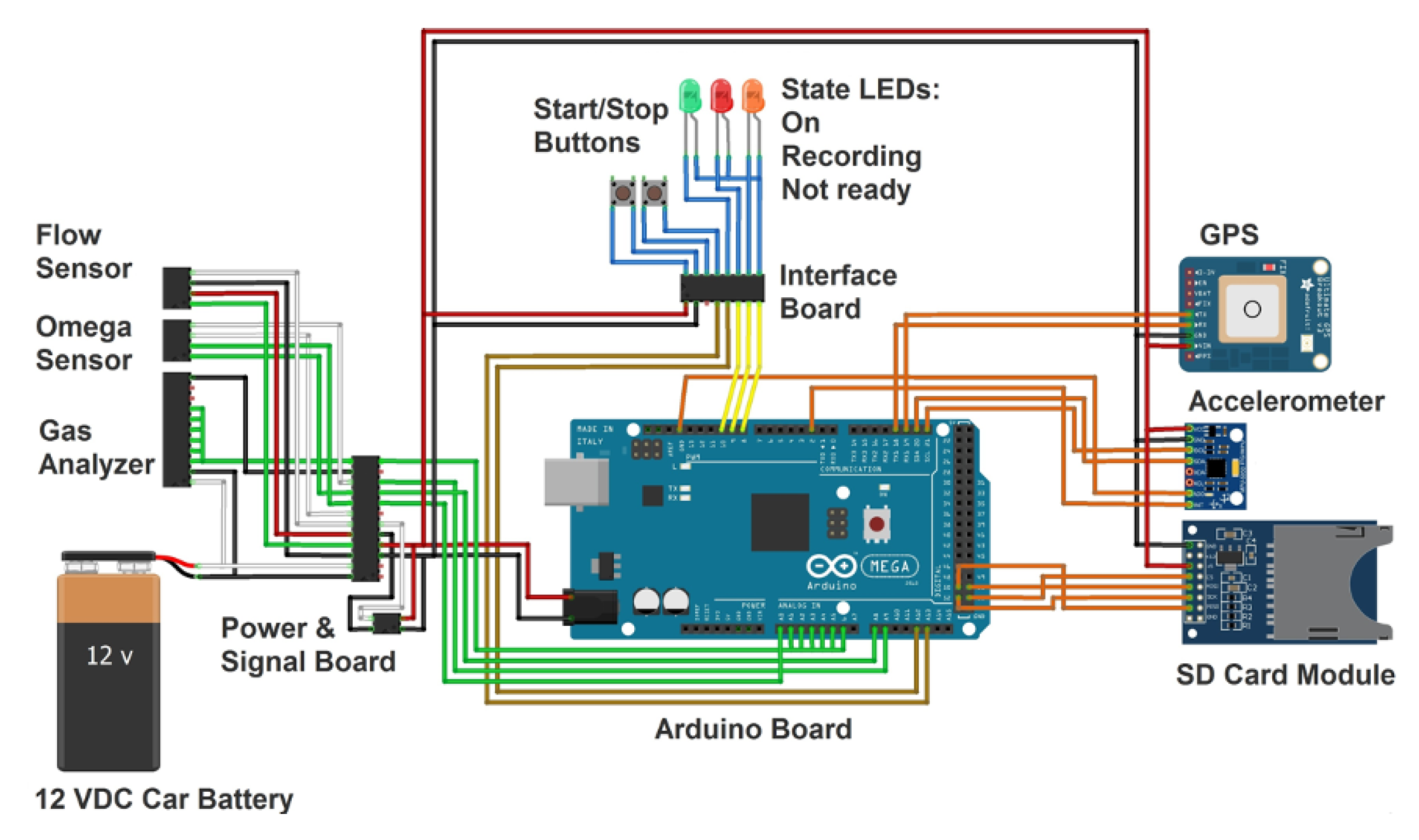
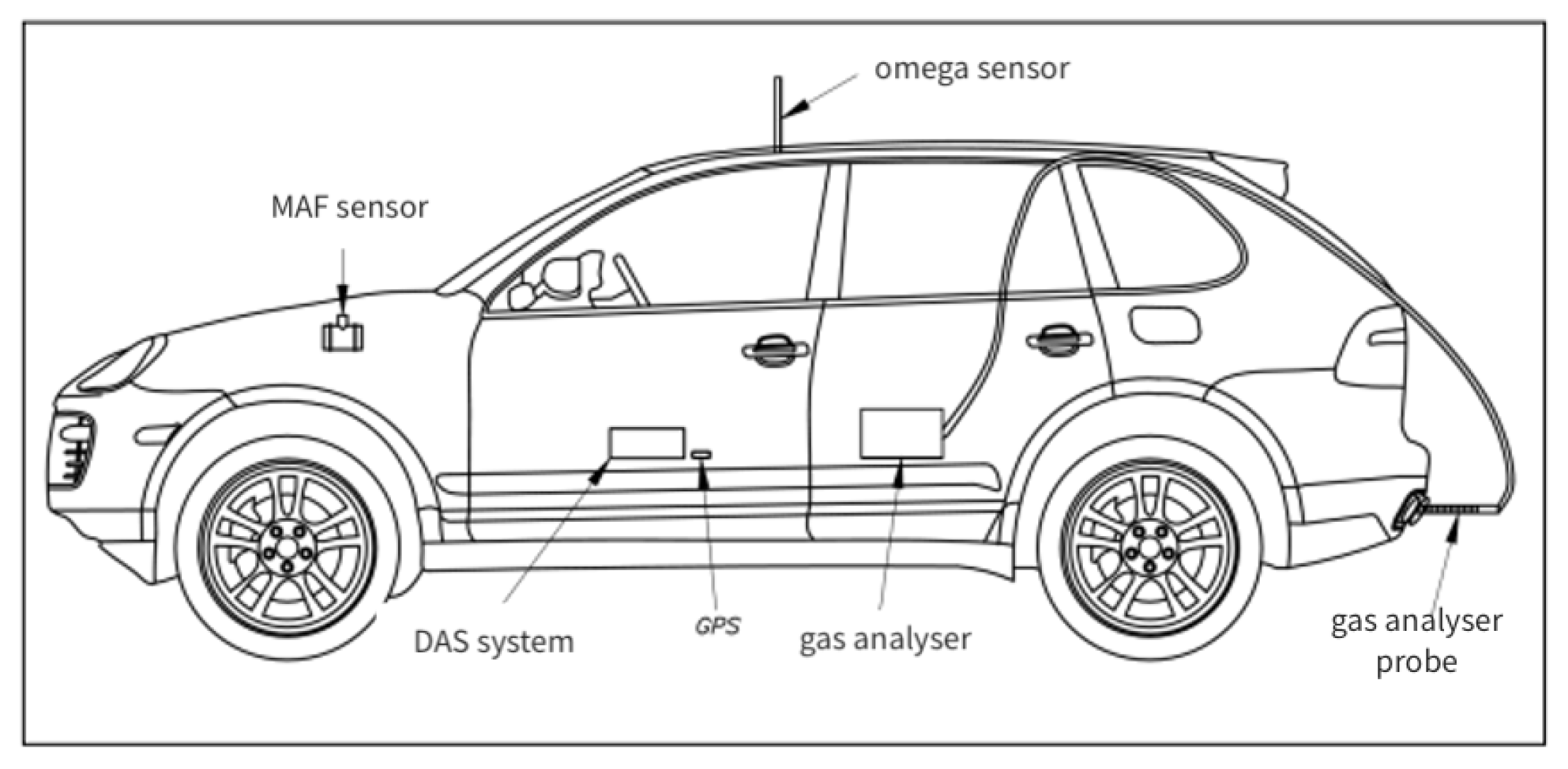
7]. The vehicle used was equipped in such a way that allowed for the collection of data for the identified variables in real-time during the tests. For the calculations, the fuel consumption was calculated based on air intake measurements and the air–fuel ratio, whereas the exhaust emissions concentrations were directly measured using a portable gas analyser. Finally, to conduct a first analysis of the behaviour of the vehicle emissions, we used a parameter denoted as vehicle-specific power (VSP), which allowed us to establish a relationship between the operational conditions of the vehicle and its emissions.
The use of VSP for the analysis of the emissions was first introduced by Jimenez-Palacios [
9] as a parameter which establishes a relationship between vehicle emissions, the kinematic characteristics of the vehicle (e.g., speed and acceleration), and the vehicle specifications themselves. The relationships between said kinematic parameters being influential factors in the level of emissions have been well-documented in the literature (see, e.g., [
10,
11]) for the case of gasoline and diesel powered vehicles, and the authors have concluded that the most influential factors are those associated with acceleration, power demand, speed, and gearshift. These factors are taken into account during the calculation of the VSP, although the VSP is not the only parameter associated with said characteristics, as evidenced by the studies performed by Zhai et al. [
12]. Still, the advantage of this parameter, over the others, is that while others might have a better correlation with emissions, they are not as accessible as VSP.
3. Results and Discussion
Once the data processing was finished, the results for both fuel blends (E7.8 and E10) were compared, based on the different aspects covered by the data available, whose main points were vehicle-specific power, fuel consumption, and vehicle emissions.
3.1. Vehicle-Specific Power
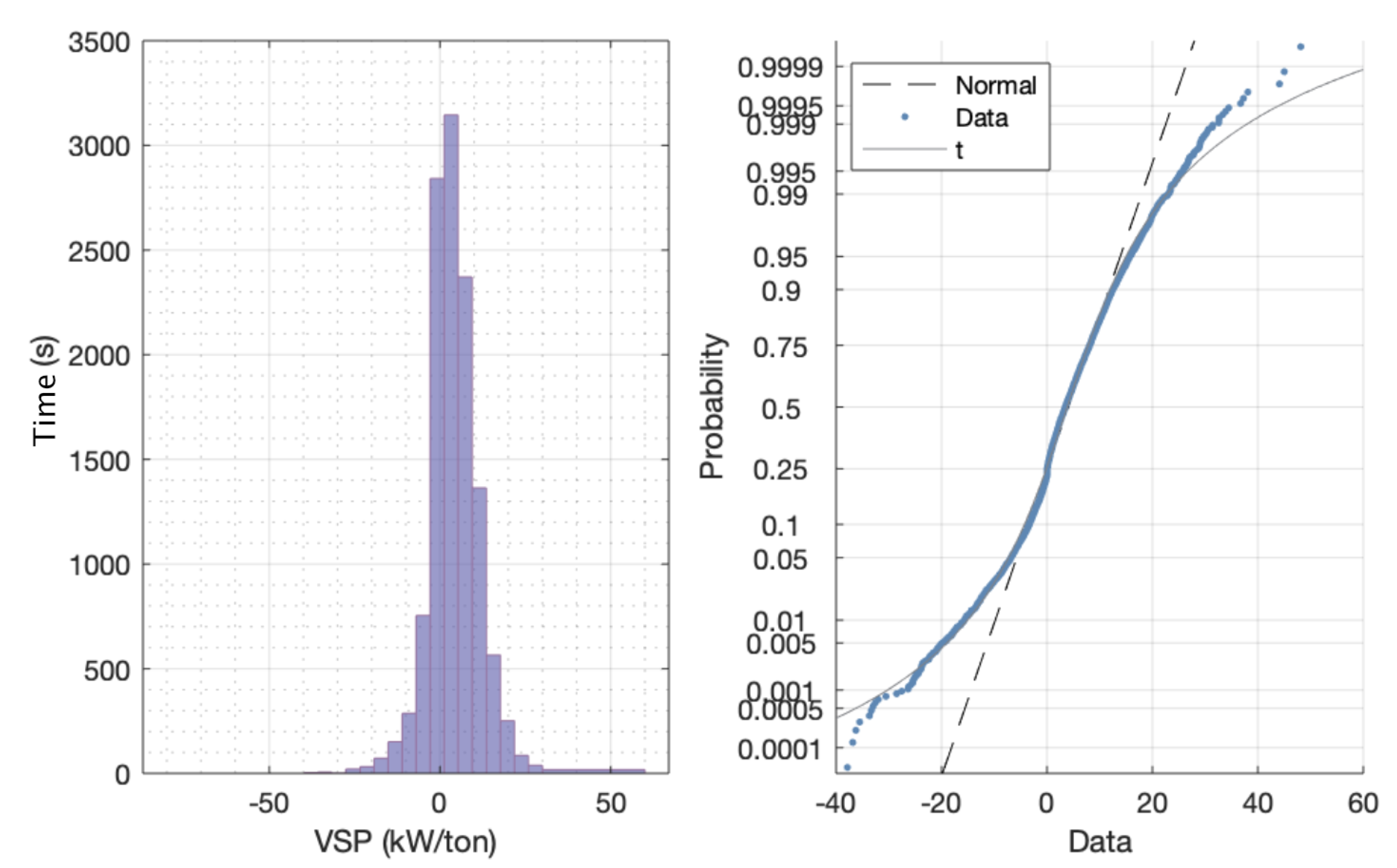
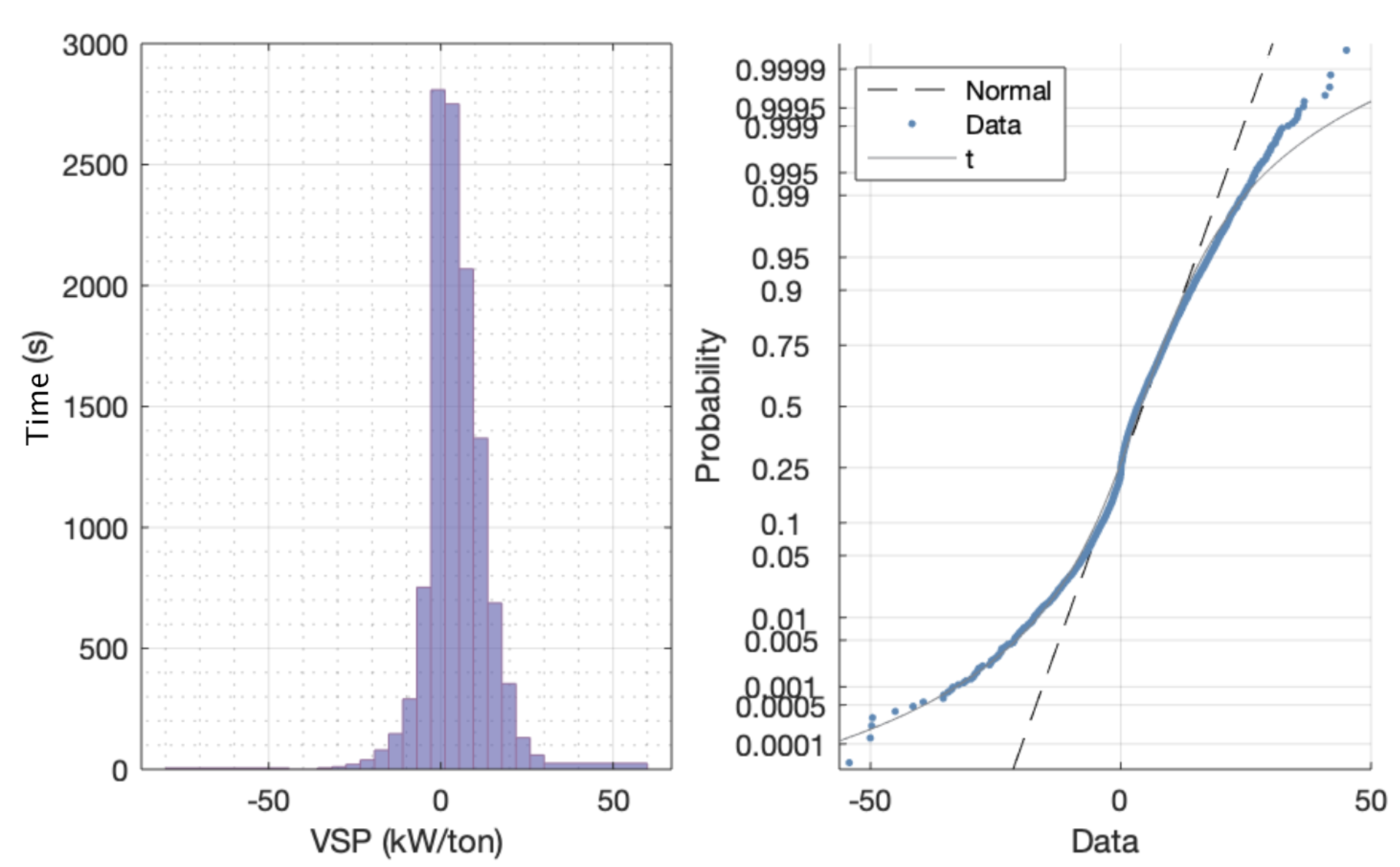
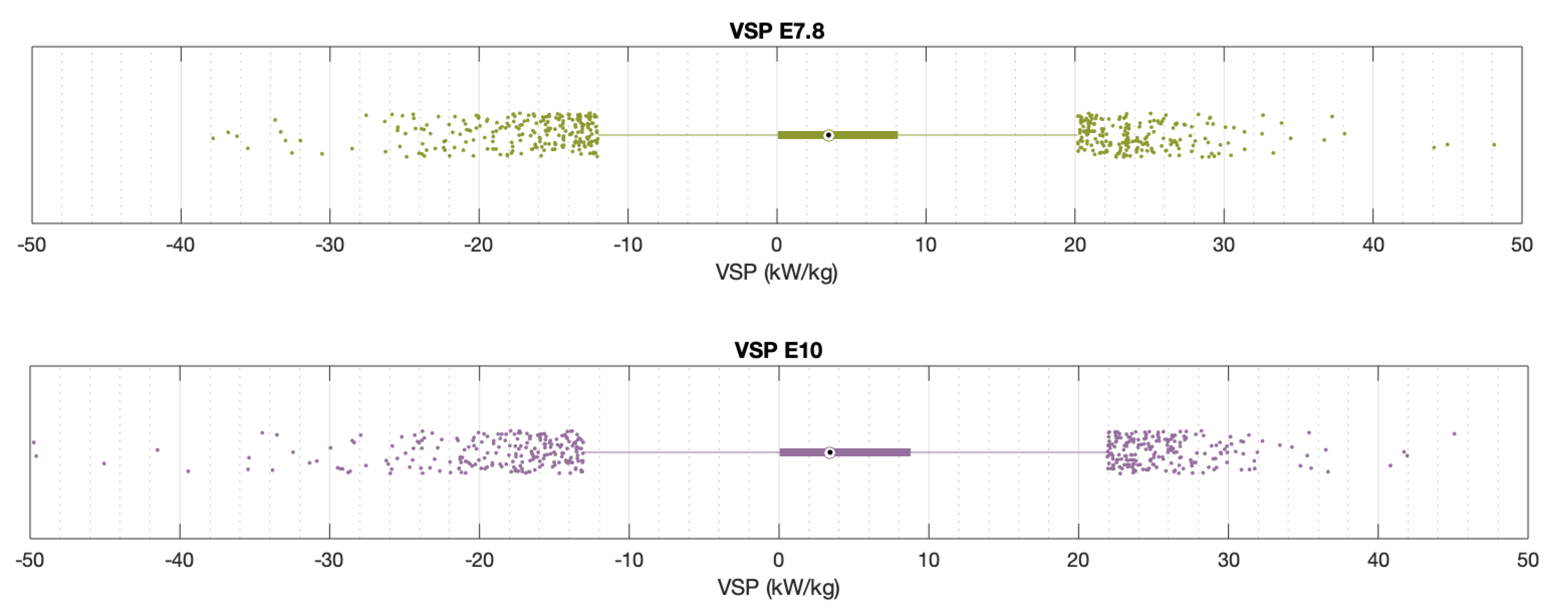
In the case of the vehicle-specific power, the first comparison was carried out based on the VSP values for each blend. The results showed that, despite the fact that the VSP does not take the fuel used into account during the calculation, there was a change in its distribution. This difference can be visualised by comparing the resulting box-plots (
Figure 9), as well as by looking at the statistical summary for each of the distributions (
Table 4 and
Table 5).
There were two key differences found between the distributions of the blends: dispersion and centre mean. First, in the case of the distributions’ dispersion, the difference was measured using the interquartile range (IQR), as well as the standard deviation (). In both cases, the E10 blend presented higher values, and the differences found were 0.12 for the variance and 0.65 for the IQR. The difference in the means () also showed a higher value for the E10 blend, with a difference of 0.46, which means that most of the distribution was located to the right of the distribution for the E7.8 blend.
These are important points to take into account when analysing the relationship between the emissions mass flow and the VSP, as these distributions define the range in which the emissions are significant, and in the case of the E10 blend, it was larger. Another point to be taken into account is the difference in distribution symmetry which, in this study, was measured using a parameter known as medcouple (MC). Again, the E10 blend had a higher value than that of E7.8, which means that the E10 distribution was less symmetric and, in this case, had a longer tail to the left.
Finally, regarding the true distribution that generated the empirical data collected, and based on the differences encountered while taking into account that the VSP itself does not take into account the fuel used, it is reasonable to evaluate whether the distributions which generated the samples taken were different. For that purpose, a Kolmogorov–Smirnoff test was conducted in order to determine whether the distance between the fuel blend distributions was large enough to be able to affirm that they were, in fact, different. Then, the results showed that the samples came from different distributions.
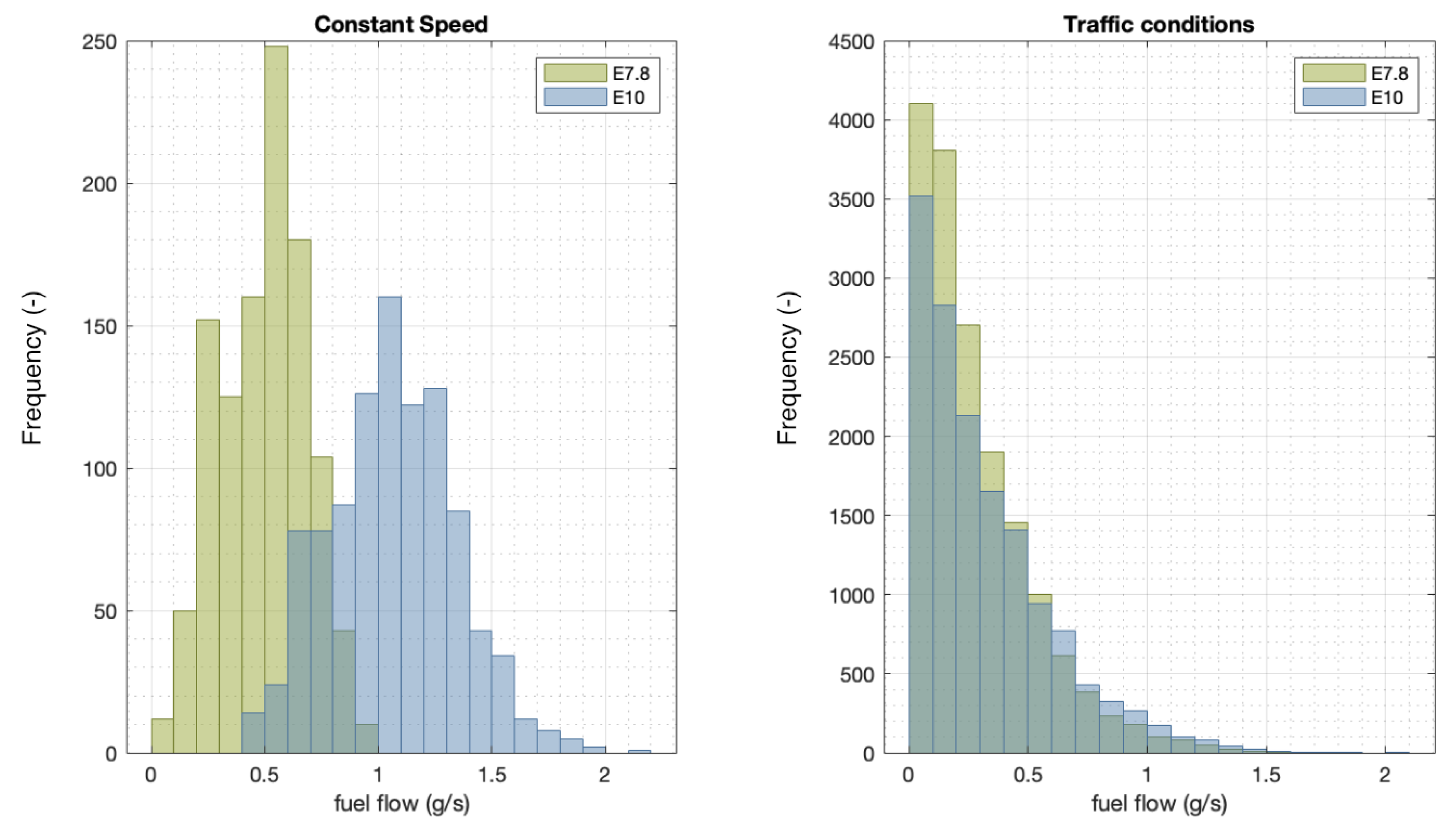
3.2. Fuel Consumption
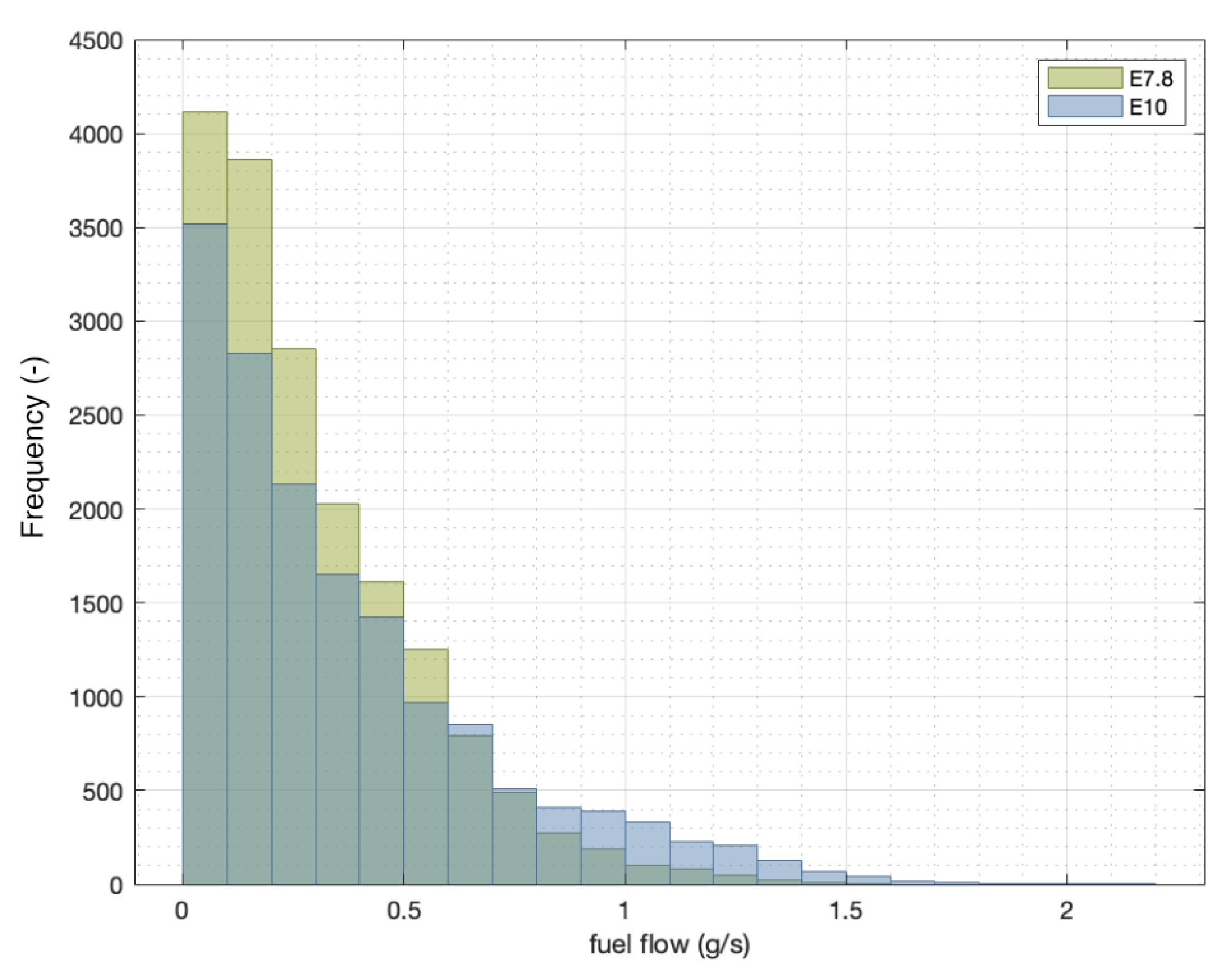
Regarding fuel consumption, the calculations were carried out for each of the tests, and the comparisons drawn between fuel blends can be seen in
Table 6 and in the histogram comparison (
Figure 10).
The results show that the main difference in fuel flow between blends lay in the sparsity of the distributions, where the E10 blend had a higher standard deviation value (0.09 difference), which also shows in the value of the mean (0.07 difference). Moreover, there was a strong difference in how fat the tail was for both distributions, which means that there was a higher probability of the E10 blend having a higher fuel flow which, in turn, means a higher fuel consumption.
A comparison was also made for the different driving regimes tested (
Figure 11), which helped to explain the shape of the tail mentioned earlier and provided insight into how the fuel behaved in the constant speed case.
In the constant speed case, the shape of the distribution was completely different from the tests in traffic conditions, with a bell-shaped distribution instead. The placement of the curves in relation to each other was more noticeable, with the E10 blend showing higher fuel flows in general, which could be measured by the difference in the mean values, having a value of 0.57.
With that in mind, the tail shape of the E10 plot in
Figure 10 can be explained, as the values corresponding to the tests at constant speed were located in that range (from approximately 0.5 to 1.5). In contrast, in the case of the E7.8 blend, the values at constant speed were lower and had a much less noticeable effect on the shape of the overall curve.
Finally, this means that, in terms of fuel flow, the E7.8 blend proved to be more stable as the speed changed, as the curve was closer to the mean of the tests in traffic conditions.
3.3. Vehicle Emissions
In the case of vehicle emissions, the analysis was conducted using bins for the VSP range. This means that the range of the VSP was split, which allowed us to visualise how the mass flow distribution changes as the value of the VSP increases. The bins were chosen based on the IVE [
17] method and allowed for the establishment of a baseline for the comparison between fuel blends.
Table 7 shows the bins corresponding to the main statistical values—Q
1, mean (
), and Q
3—for each of the fuel blends.
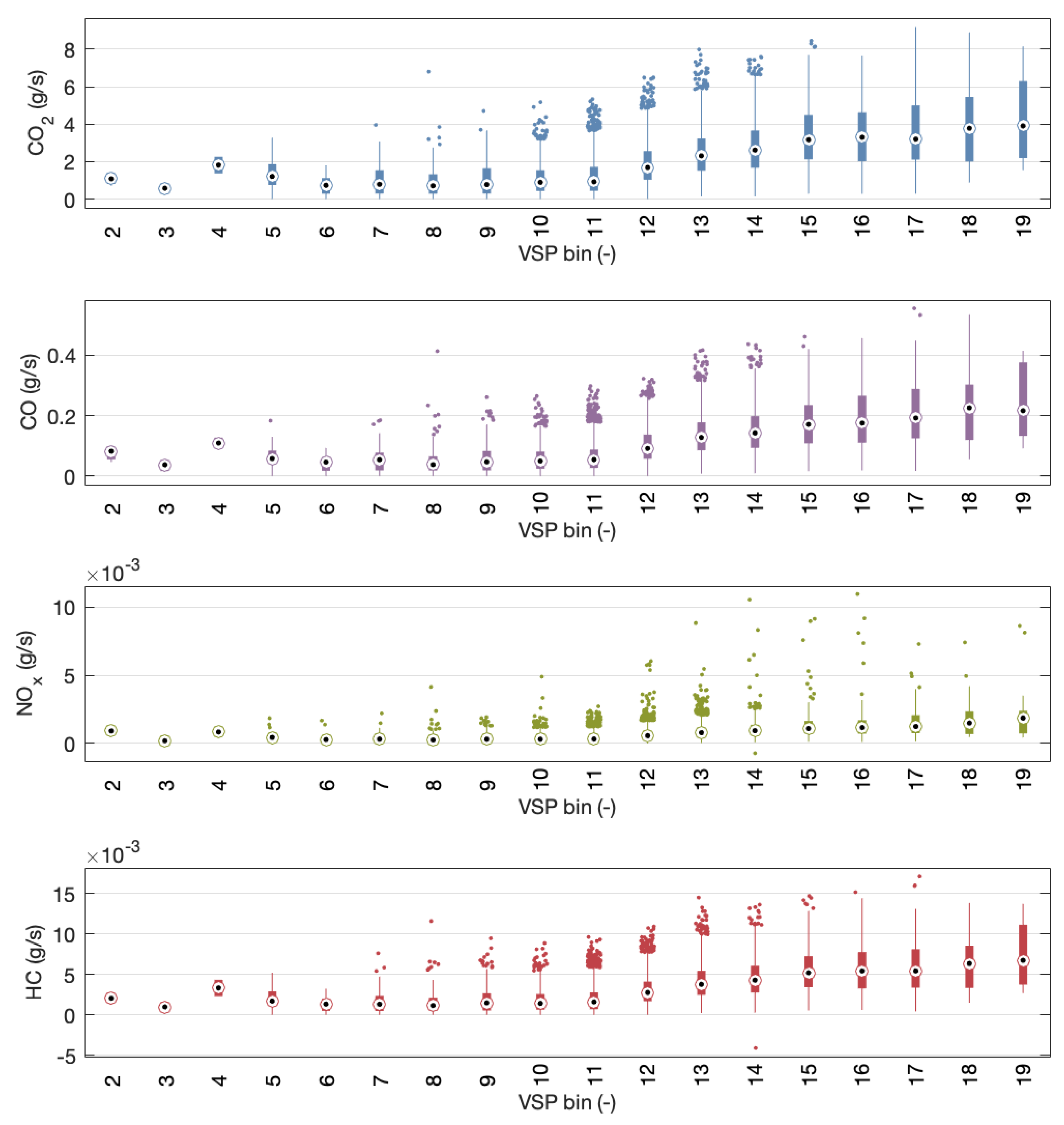
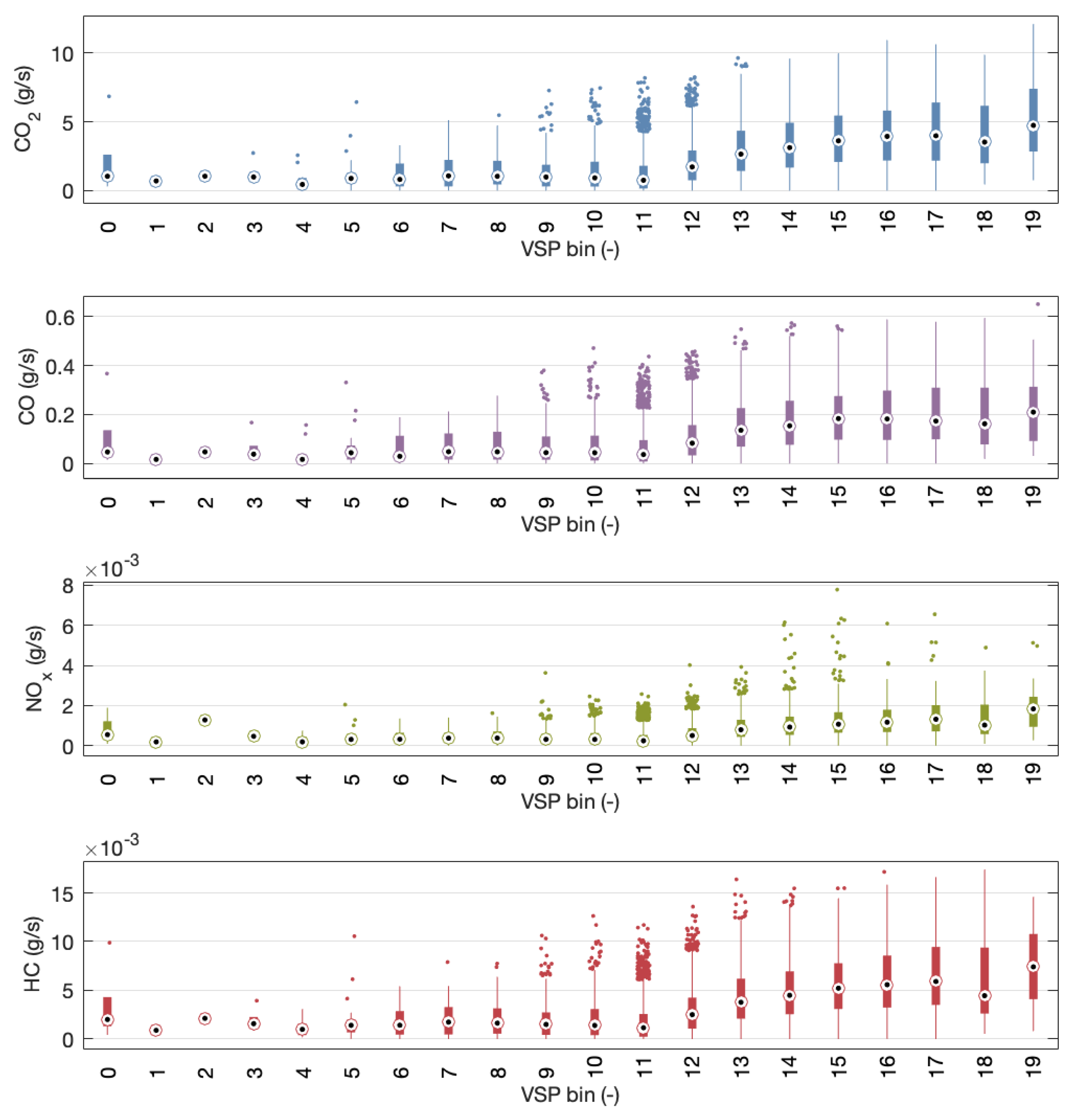
The analysis was carried out in two ways: first, box plots were used to see if any pattern emerged (see
Figure 12 and
Figure 13 for E7.8 and E10, respectively). Then, the individual histograms were plotted in order to take a closer look at the individual distributions.
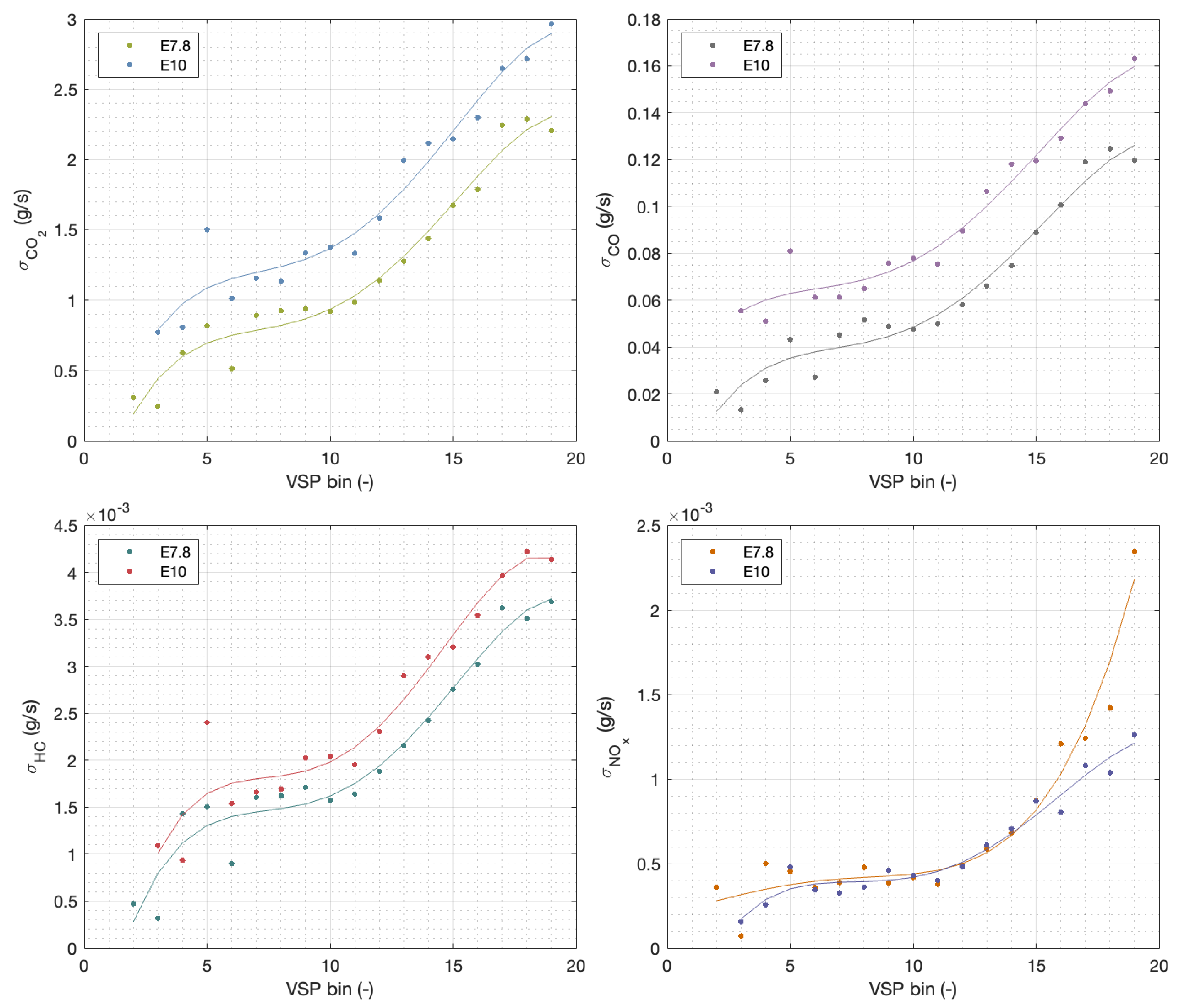
In the case of the box plots shown in
Figure 12 and
Figure 13, the means of each of the contaminant species showed a similar trend, where the mean values of the box plot for bins below bin 11 (i.e., VSP values between −2.9 and 1.2) were close to zero, and the mass flow value increased for bins with higher values, up to bin 15 (13.6 and 17.7). After bin 15, the values stabilised. These results are similar to those presented by [
9].
Still, these is another point to be made about the actual time the vehicle tested spent in those bins and, by extension, the number of points available to construct the individual box plots. From the values shown in
Table 6, the bins that were considered to be part of the distribution were those between N°s 8 and 16, with heavy emphasis in bins 11 to 13, where the number of points increased noticeably, and which were the bins containing 50% of the points.
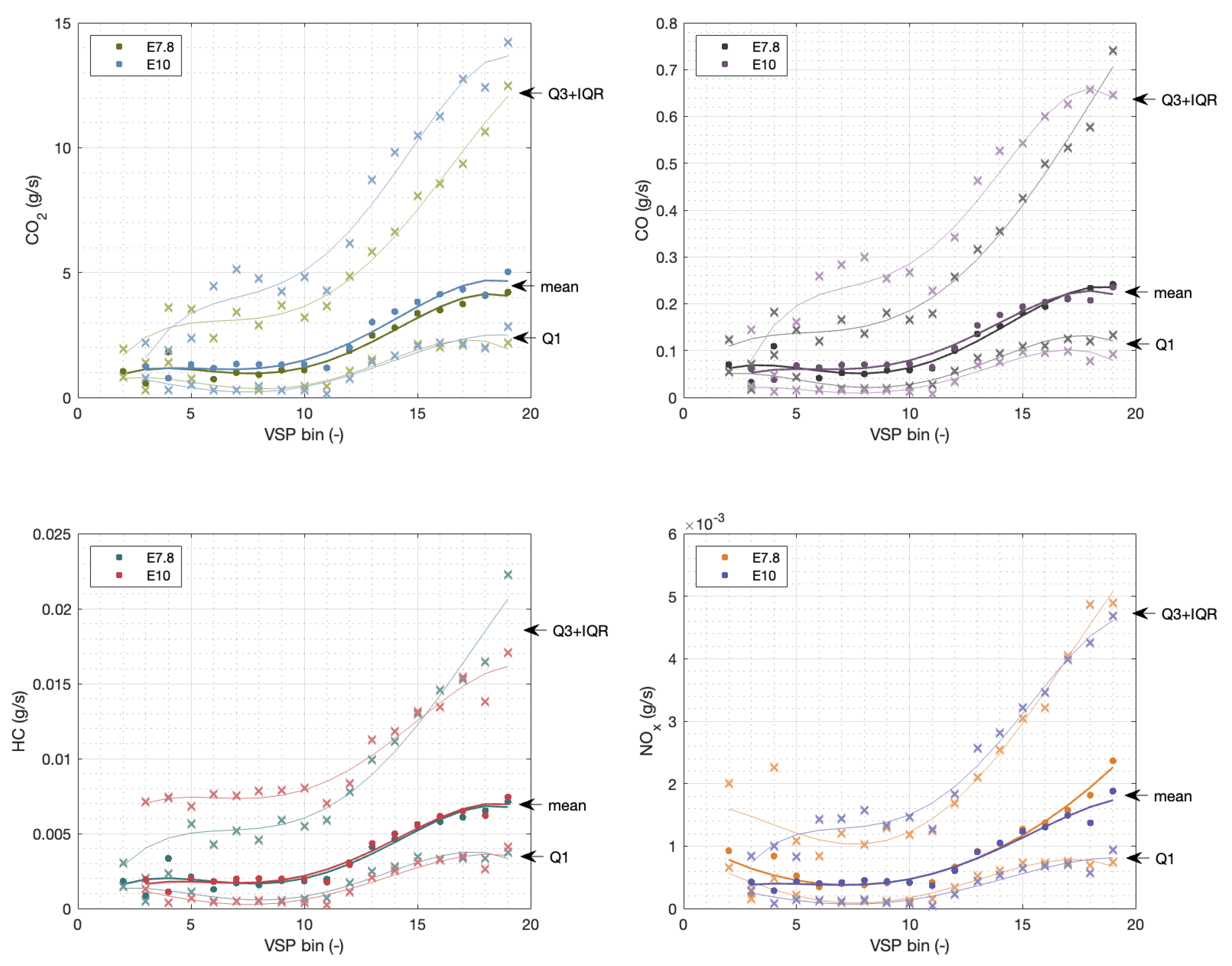
Finally, based on the box plots shown above, a comparison of the behaviour between E7.8 and E10 was made (
Figure 14). The values chosen for comparison were Q
1 (25th percentile), the mean, and Q
3 + 1.5 IQR, which corresponds to the maximum representative value of the distribution.
In the plots (
Figure 14), we found some common behaviours. All four plots showed no significant difference between the means and Q
1 values for both blends. On the other hand, in the CO
2, CO, and HC plots, the values of Q
3 + 1.5IQR for the E10 fuel blend were consistently higher throughout the VSP bins. This means that, although the mean value of the pollutant mass flow did not change when E10 was used, there was a higher probability of the E10 blend resulting in higher mass flow emissions. In the case of the NO
x, there was no significant change in either of the values plotted, which may be attributed to the fact that the measurements were taken in the vehicle exhaust pipe, after the catalytic converter.
These results indicate that the main difference between fuel blends was in the sparsity of the samples, which can be better viewed in the plot for the standard deviation per bin, as shown in
Figure 15.
4. Conclusions
From the results obtained it can be concluded that it is possible to establish a methodology for the experimental evaluation of fuel consumption as well as vehicle emissions in the city of Lima Metropolitana. From this, it can be further stated that vehicle-specific power is a parameter that has some correlation with emissions mass flow.
In regards to fuel consumption, the distributions obtained for the tests performed in traffic conditions showed similar values, whereas in the tests performed at a constant speed, for the E10 blend, the fuel flow increased by 28.55%; this can be attributed to the reduction in the fuel’s lower calorific value with the increase in ethanol.
As for the vehicle emissions and VSP, it was shown that there is a correlation between both, which confirms what was shown by previous studies. However, when comparing the main statistical values (Q1, mean, Q3 + 1.5IQR) for each of the species in the study (CO, CO2, HC, and NOx), there was no significant difference between the two fuel blends. Still, the main difference found was in the dispersion of the distribution, which can be seen more clearly in the standard deviation values for each of the emission species. The average values obtained were as follows: 0.5 for CO2, 0.03 for CO, 0.4 for HC, and a value close to zero in the case of NOx, which can be attributed to the fact that, at the point of measurement, the exhaust gas treatment has already occurred.
For continuing research, the authors suggest continuing the study of the effect of increasing the percentage of ethanol in gasoline–ethanol fuel blends on other vehicles to determine the existing relationship between the kinematic variables and the vehicle emissions. Another important point to take into account is the improvement of the model used to determine the mass flow of the emissions measured. This can be done by studying the kinetics of the blend, which might give a better understanding of the combustion process as well as the reactions that occur in the catalyst of the vehicle.