Research on Anti-Skid Control Strategy for Four-Wheel Independent Drive Electric Vehicle
Abstract
1. Introduction
2. Dynamic Model Establishment
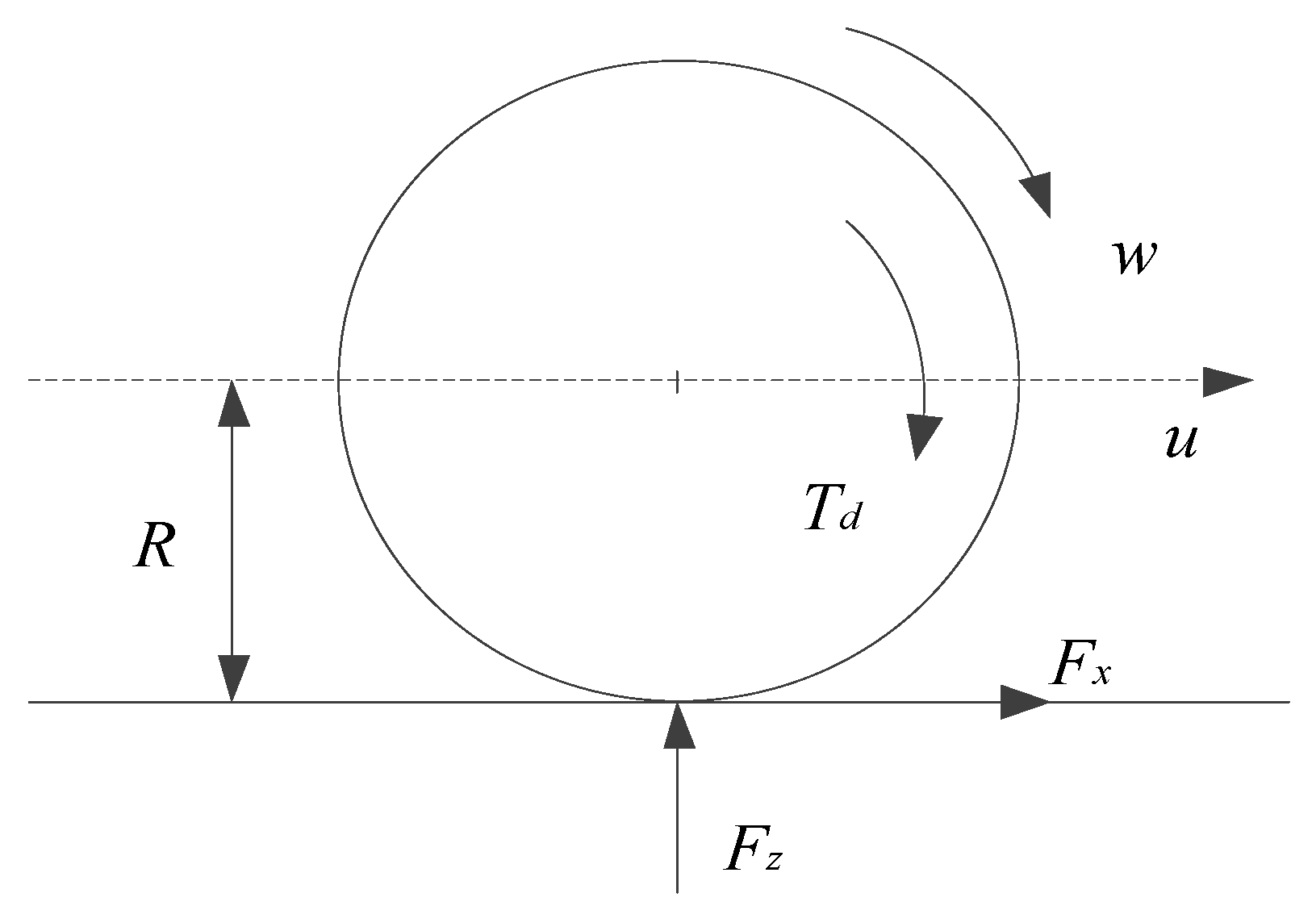
2.1. Vehicle Dynamics Model
2.2. Tire Model
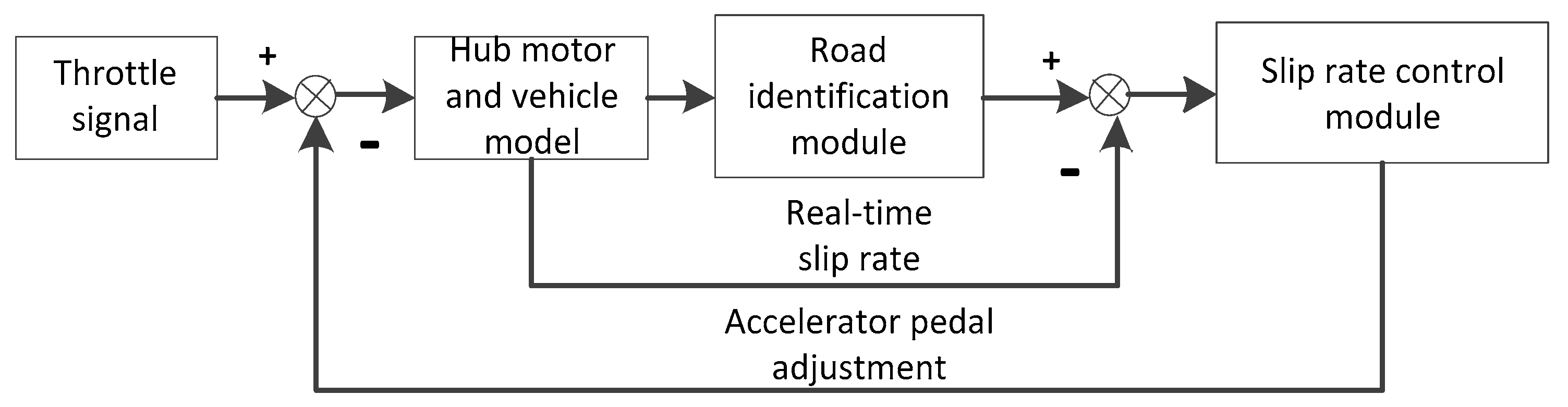
3. Design on Driving Anti-Skid Control Strategy
- (1)
- The current slip rate of the driving wheels and the road adhesion coefficient is calculated according to the vehicle dynamics model, tire model and motor model. The road slip rate and the wheel adhesion coefficient are used as the input of the road surface recognition controller, the current road surface condition is determined according to the road surface recognition controller, and the road surface parameters of the current road surface are calculated.
- (2)
- Then, the slip rate control module is input, and the optimal slip ratio suitable for the current road surface is determined through the control algorithm. By adjusting the pedal signal, the wheel speed and the vehicle speed can be adjusted in realtime to prevent the wheel from slipping.
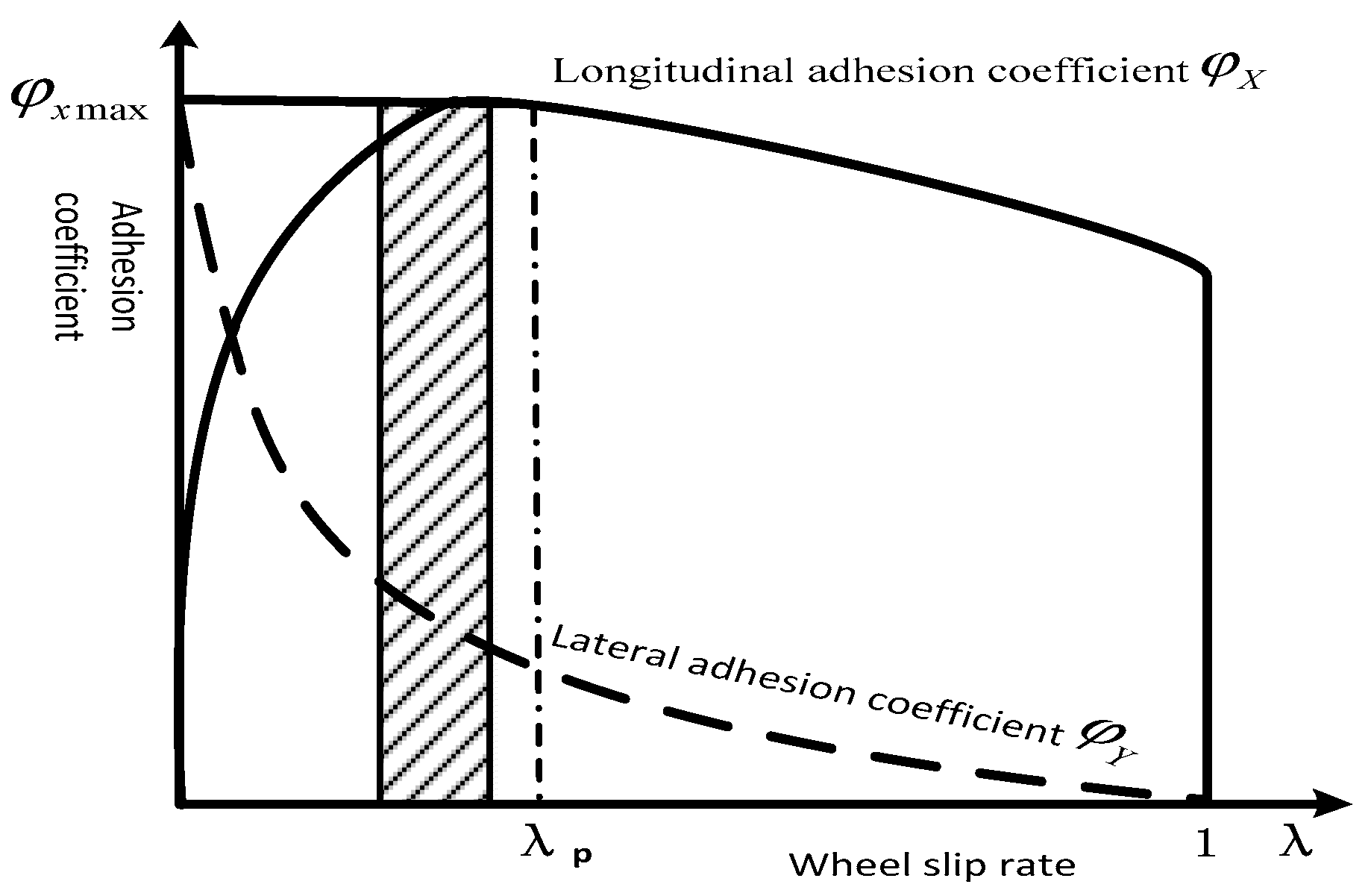
3.1. Wheel Slip Mechanism
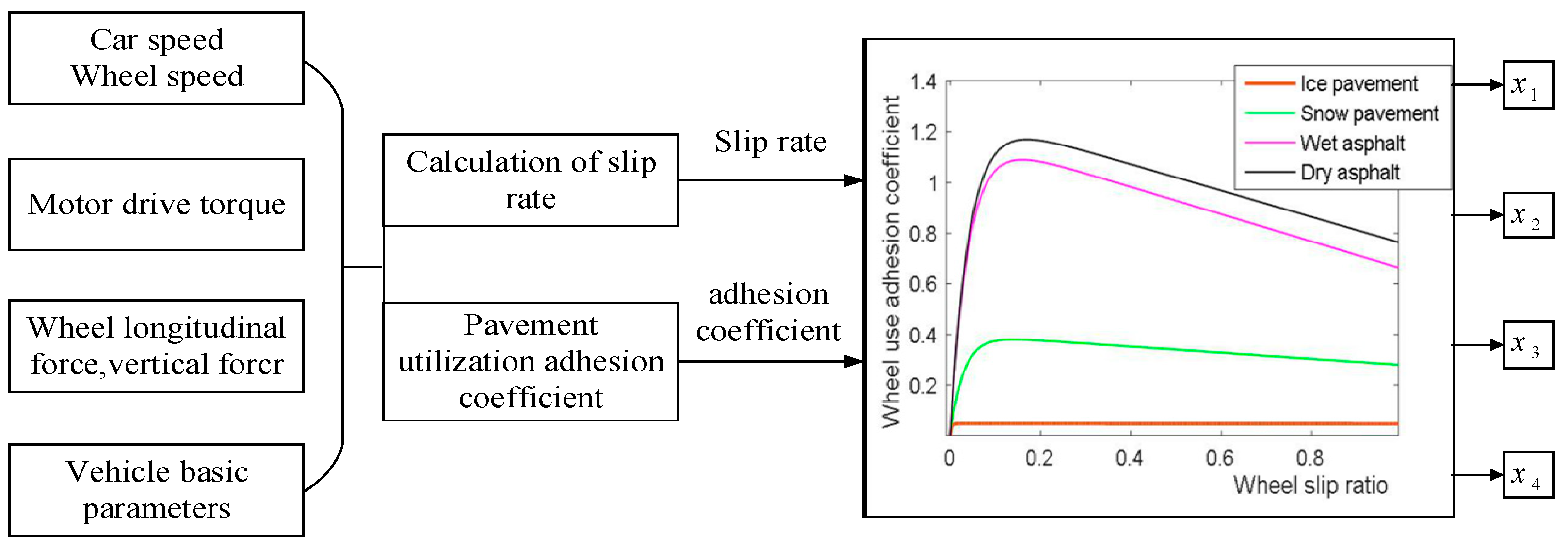
3.2. Road Identification Module
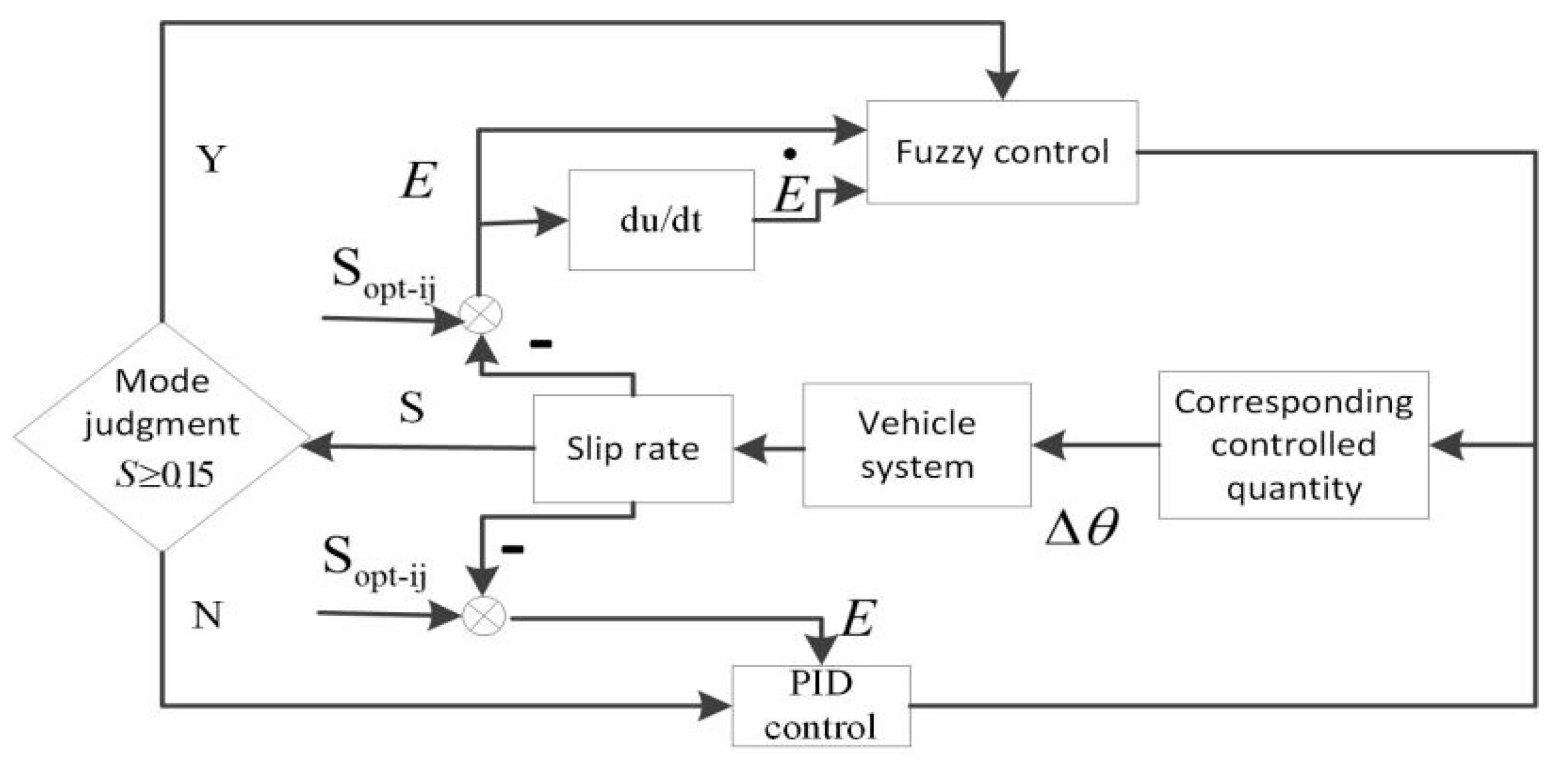
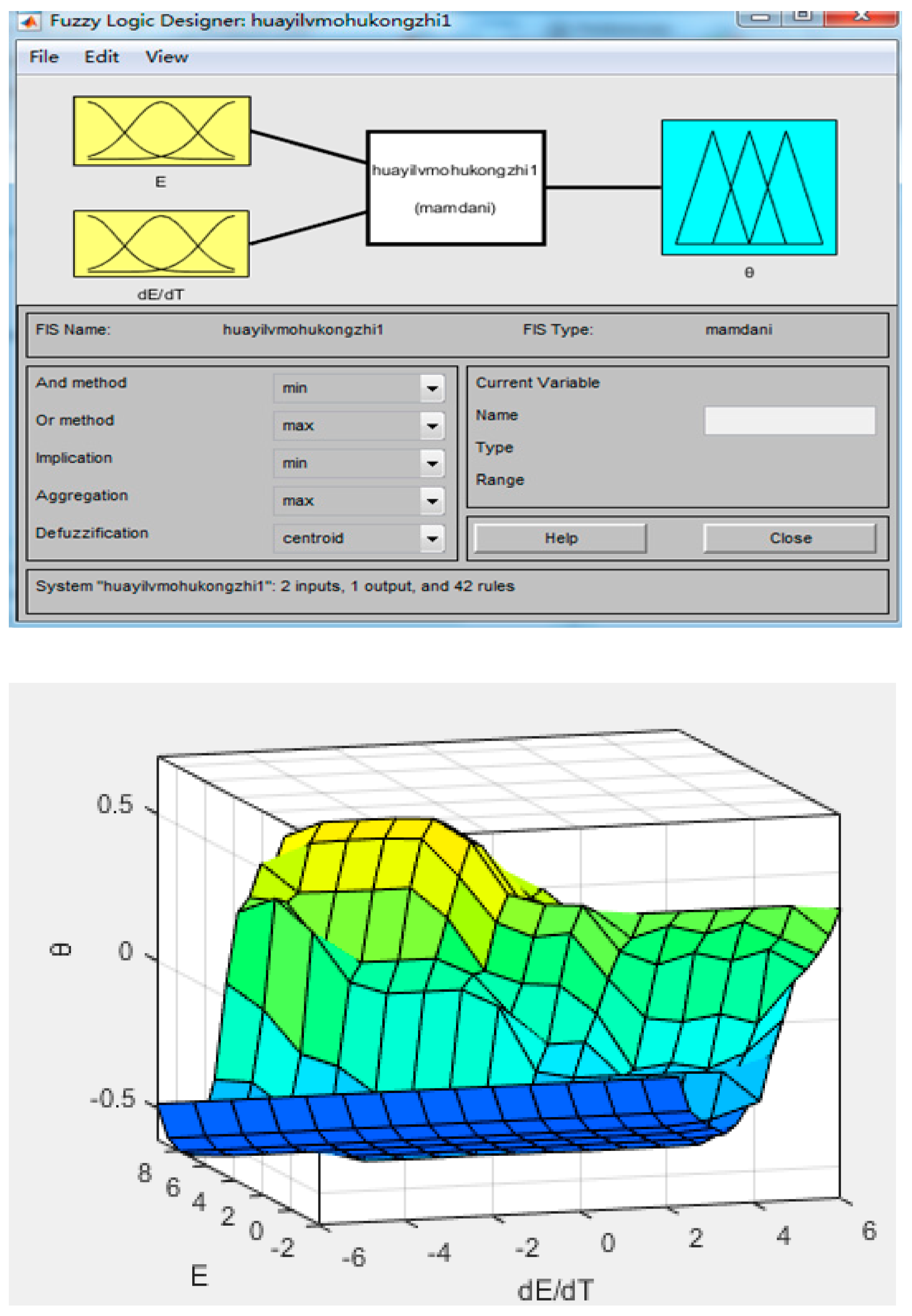
3.3. Slip Rate Control Module
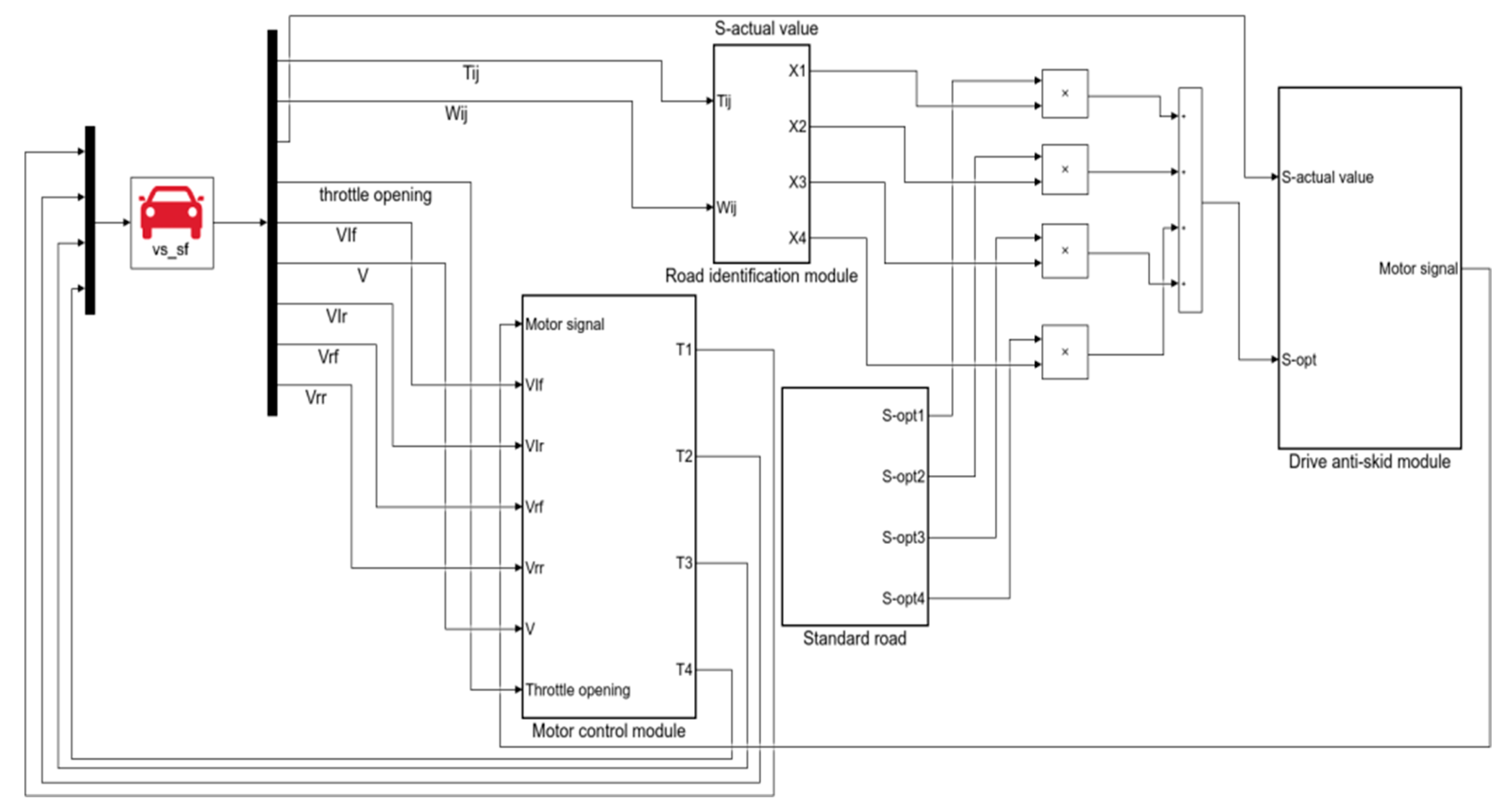
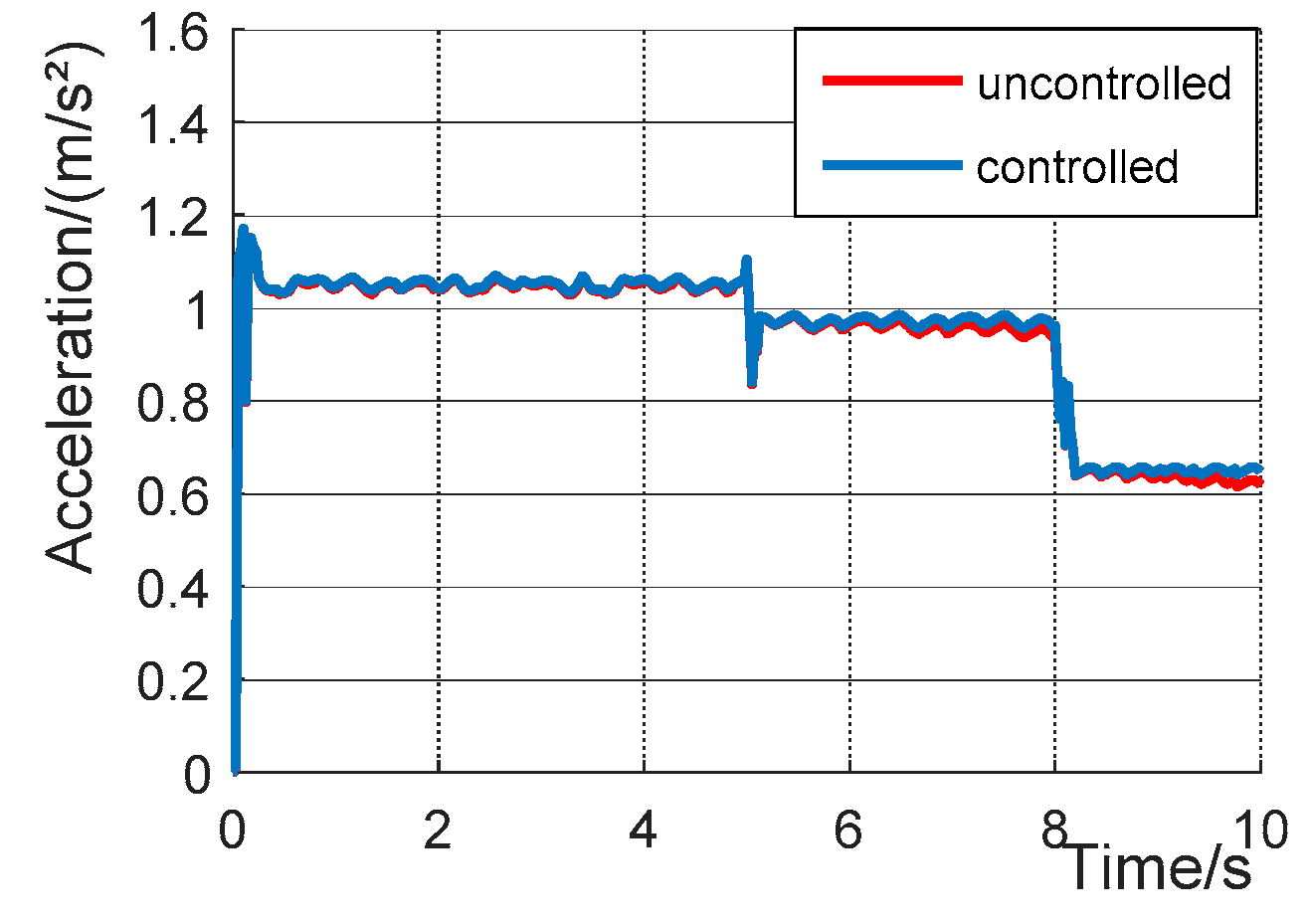
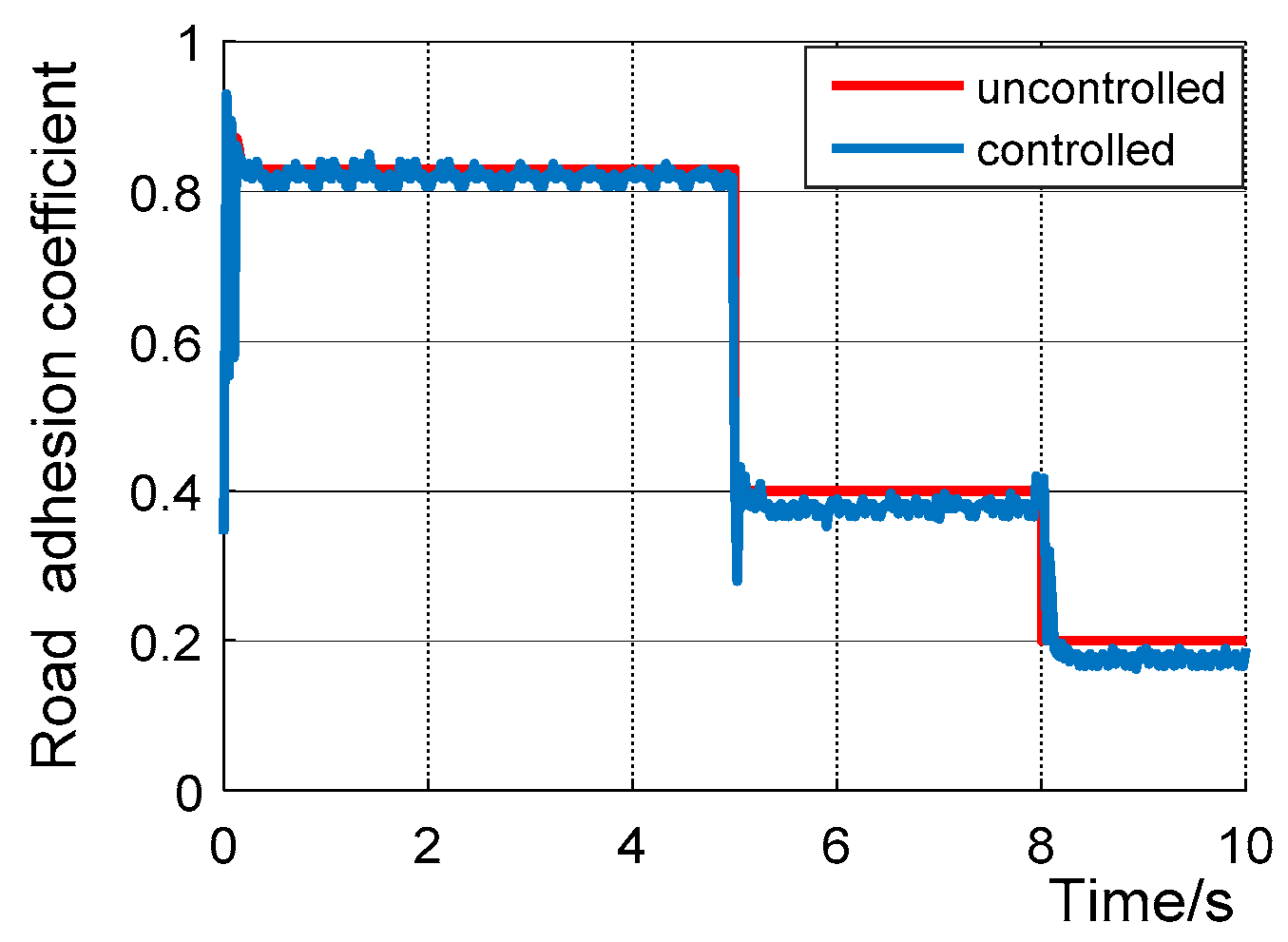
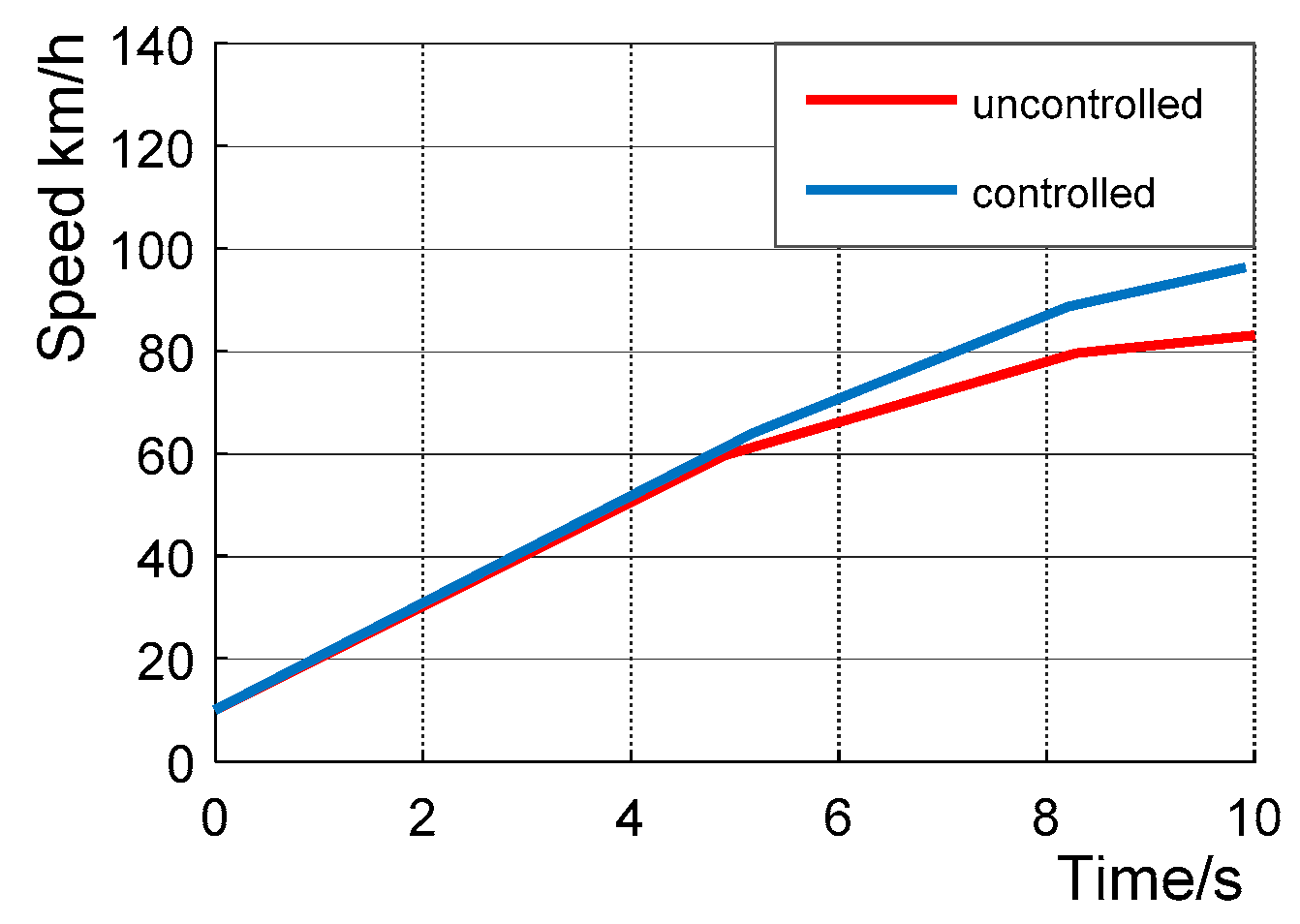
4. The Simulation Analysis
4.1. Road Recognition Module Verification
4.2. Slip Rate Control Module Verification
5. Conclusions
- (1)
- The pavement recognition module establishes the standard pavement curve μ-s curve, and calculates the maximum adhesion coefficient of the pavement and the optimal slip rate when the vehicle is sliding.
- (2)
- The slip rate control module adopts a fuzzy PID control algorithm. The change rate of the difference between the real-time slip rate of the wheel and the target slip rate E and E is input, the torque adjustment signal is output, and the pedal signal is calculated and output to the wheel hub motor to further prevent the vehicle from slipping.
- (3)
- Carsim/Simulink software modeling is completed, and simulation verification of driving anti-skid controller is carried out. The results show that the road surface identification module in the driving anti-skid control strategy can quickly identify the current road surface conditions, and the slip rate control module can reasonably control the output motor driving torque, reasonably and effectively reduce the slip degree of the vehicle, and avoid the slip of the vehicle. Simulation results verify the feasibility of the control strategy. In the process of driving anti-skid, the standard road surface selected is not comprehensive enough and needs to be further optimized, so as to improve the efficiency and accuracy of road surface identification.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yin, G.; Wang, R.; Wang, J. Robust control for four wheel independently-actuated electric ground vehicles by external yaw-moment generation. Int. J. Automot. Technol. 2015, 16, 839–847. [Google Scholar] [CrossRef]
- Alipour, H.; Sabahi, M.; Sharifian, M.B.B. Lateral stabilization of a four wheel independent drive electric vehicle on slippery roads. Mechatronics 2015, 30, 275–285. [Google Scholar] [CrossRef]
- Ma, C.; Xu, M.; Wang, H. Wang Dynamic emulation of road/tyre longitudinal interaction for developing electric vehicle control systems. Veh. Syst. Dyn. 2011, 49, 433–447. [Google Scholar] [CrossRef]
- Shuai, Z.; Zhang, H.; Wang, J.; Li, J.; Ouyang, M. Lateral motion control for four-wheel-independent-drive electric vehicles using optimal torque allocation and dynamic message priority scheduling. Control Eng. Pract. 2014, 24, 55–66. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Wang, J. Robust gain-scheduling energy-to-peak control of vehicle lateral dynamics stabilization. Veh. Syst. Dyn. 2014, 52, 309–341. [Google Scholar] [CrossRef]
- Liu, X.; Li, M.; Xu, M. A new anti-skid control method for electric vehicles using the motor torque and the wheel acceleration with experimental verification. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 231, 347–359. [Google Scholar] [CrossRef]
- Zheng, L. Analysis of the Lateral Stability for Four-wheel Independent Driving Electric Vehicles. In Proceedings of the 2014 International Conference on Applied Mechanics and Mechanical Automation (AMMA 2014), Macau, China, 20–21 May 2014; Science and Engineering Research Center: Macau, China, 2014; Volume 590, pp. 394–398. [Google Scholar]
- He, H.; Peng, J.; Xiong, R.; Fan, H. An Acceleration Slip Regulation Strategy for Four-Wheel Drive Electric Vehicles Based on Sliding Mode Control. Energies 2014, 7, 3748–3763. [Google Scholar] [CrossRef]
- Liang, Z. Design and Research of Electric Vehicle Wheel Rim Four-Wheel Drive System; Zhejiang University: Hangzhou, China, 2018. [Google Scholar]
- Zhang, T. Research on Driving Anti-Skid Control of Distributed Driven Electric Vehicles; Nanjing University of Science and Technology: Nanjing, China, 2017. [Google Scholar]
- Sakai, S.-I.; Sado, H.; Hori, Y. Anti-skid control with motor in electric vehicle. In Proceedings of the International Workshop on Advanced Motion Control, Nagoya, Japan, 30 March–1 April 2000; pp. 317–322. [Google Scholar]
- Economou, J.T.; Colyer, R.E. Fuzzy-hybrid modelling of an Ackerman steered electric vehicle. Int. J. Approx. Reason. 2006, 41, 343–368. [Google Scholar] [CrossRef][Green Version]
- Vasiljevic, G.; Griparic, K.; Bogdan, S. Experimental testing of a traction control system with on-line road condition estimation for electric vehicles. In Proceedings of the 21st Mediterranean Conference on Control and Automation, Platanias, Greece, 25–28 June 2013. [Google Scholar]
- Zhang, L.; Li, L.; Qi, B.; Song, J.; Xu, H. Torque adaptive drive anti-skid control for distributed drive electric vehicles. J. Mech. Eng. 2013, 49, 106–113. (In Chinese) [Google Scholar] [CrossRef]
- Li, J.; Su, Y.; Kui, H. Research on Driving Anti-skid Control Strategy of Four-wheel Drive Hybrid Electric Vehicle. Automot. Eng. 2017, 39, 296–303. (In Chinese) [Google Scholar]
- Huang, L.; Wang, W.; He, Z. Research on integrated control strategy of electric vehicle direct yaw moment and driving anti-skid. Automot. Technol. 2019, 6, 41–46. (In Chinese) [Google Scholar]
- Wang, Z.; Zhou, Y.; Lee, G. The Sliding Mode Control about ASR of Vehicle with Four Independently Driven In-Wheel Motors Based on the Exponent Approach Law. Energy Procedia 2016, 88, 827–832. [Google Scholar] [CrossRef][Green Version]
- Wang, H.-L.; Shi, Z.-K. Vehicle dynamics model and safety analysis on mountainous road. Control Theory Appl. 2015, 32, 837–843. [Google Scholar]
- Yu, Z.; Wang, G.; Xiong, L.; Leng, B. Analysis of anti-skid control effect of driving electric bus with distributed drive. Automot. Technol. 2016, 3, 18–25. (In Chinese) [Google Scholar]
- Liu, W.; He, H.; Peng, J. Driving Control Research for Longitudinal Dynamics of Electric Vehicles with Independently Driven Front and Rear Wheels. Math. Probl. Eng. 2013, 2013, 408965. [Google Scholar] [CrossRef]



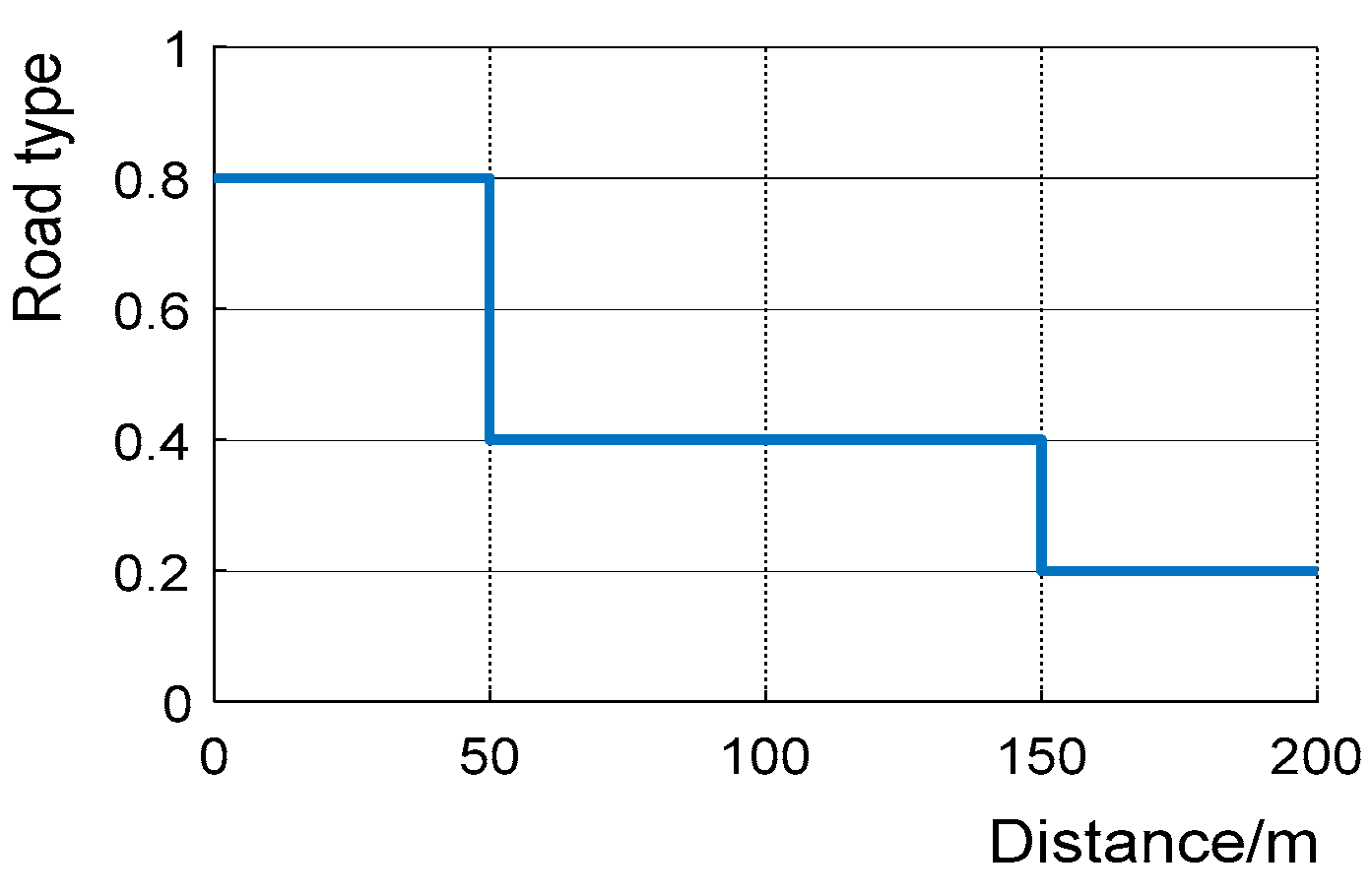
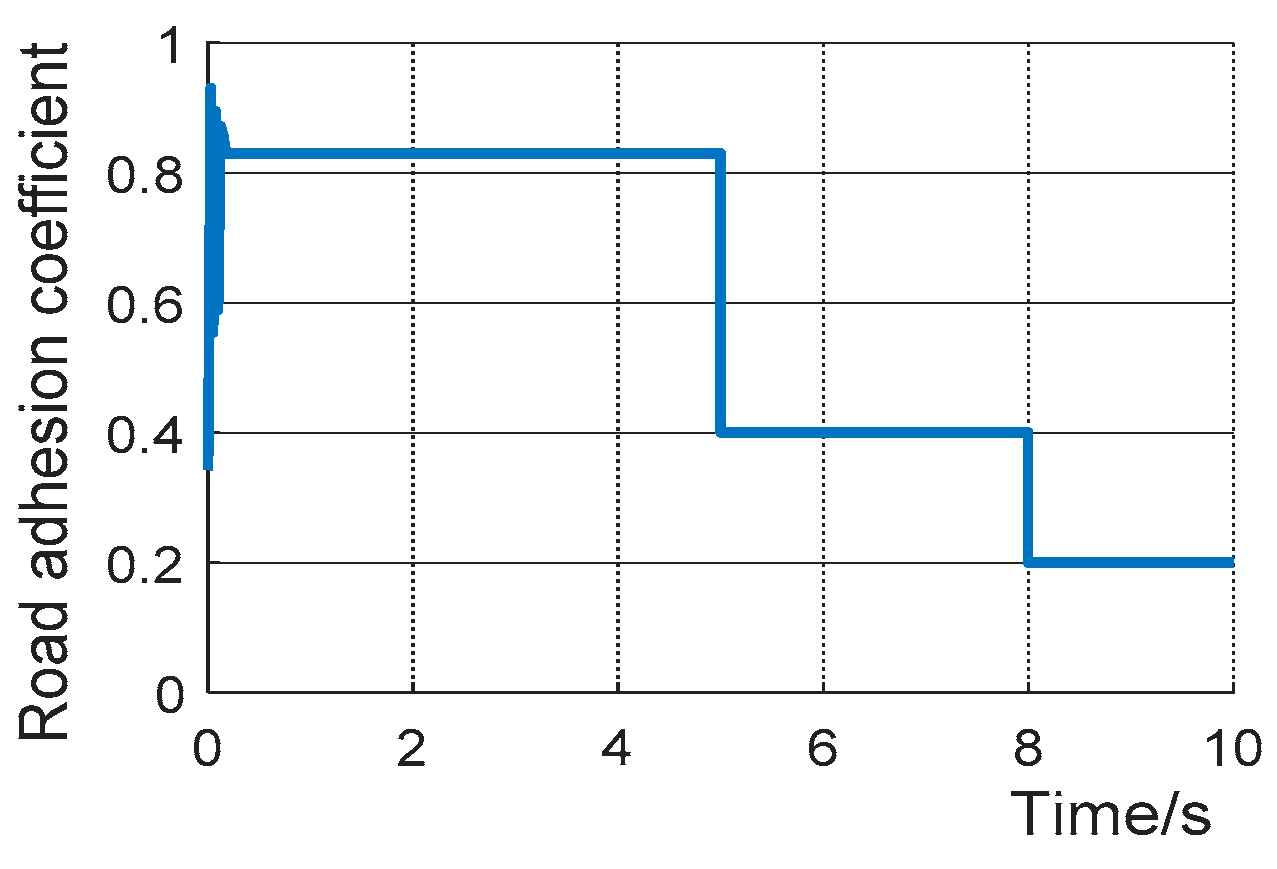
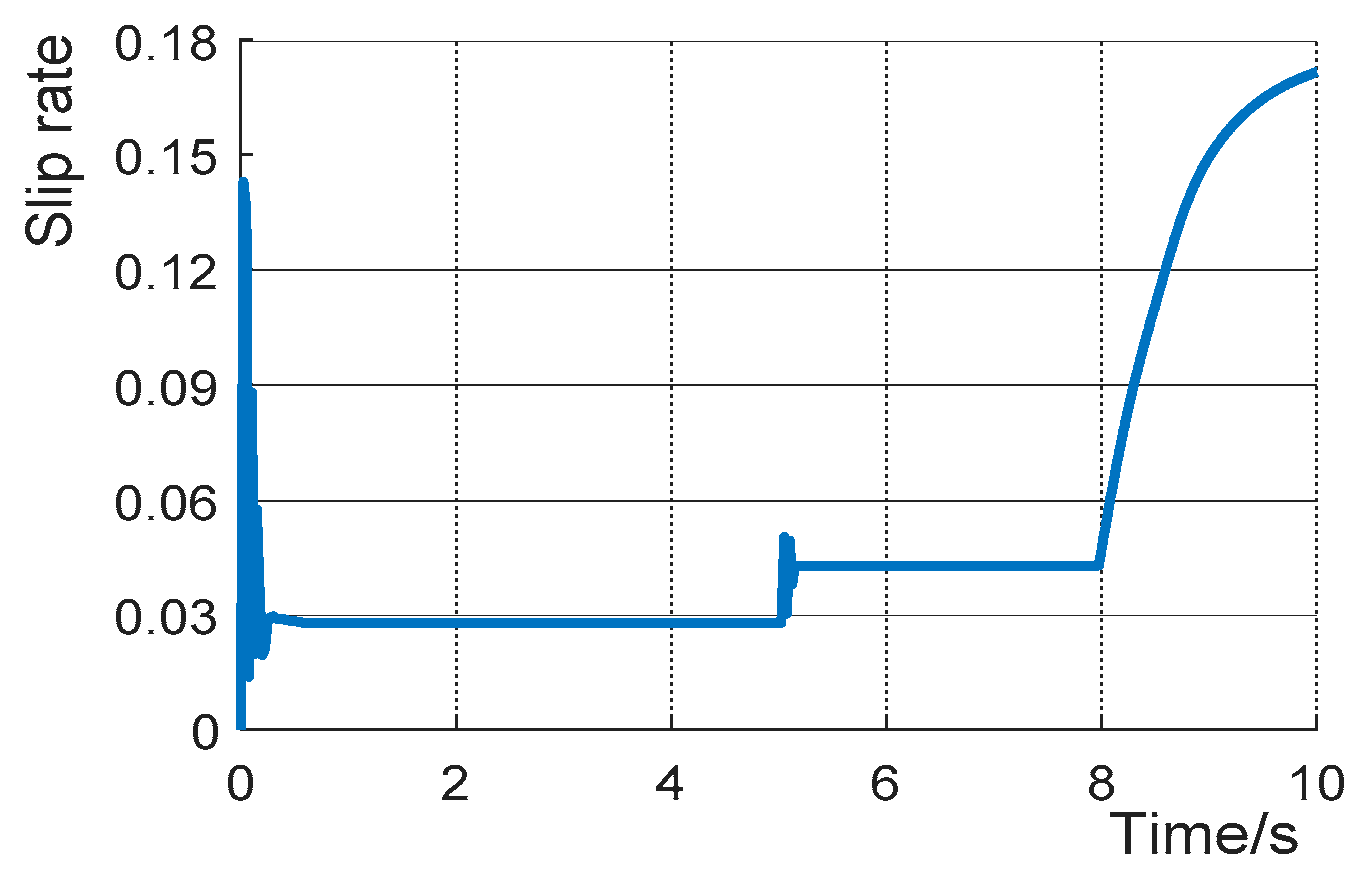

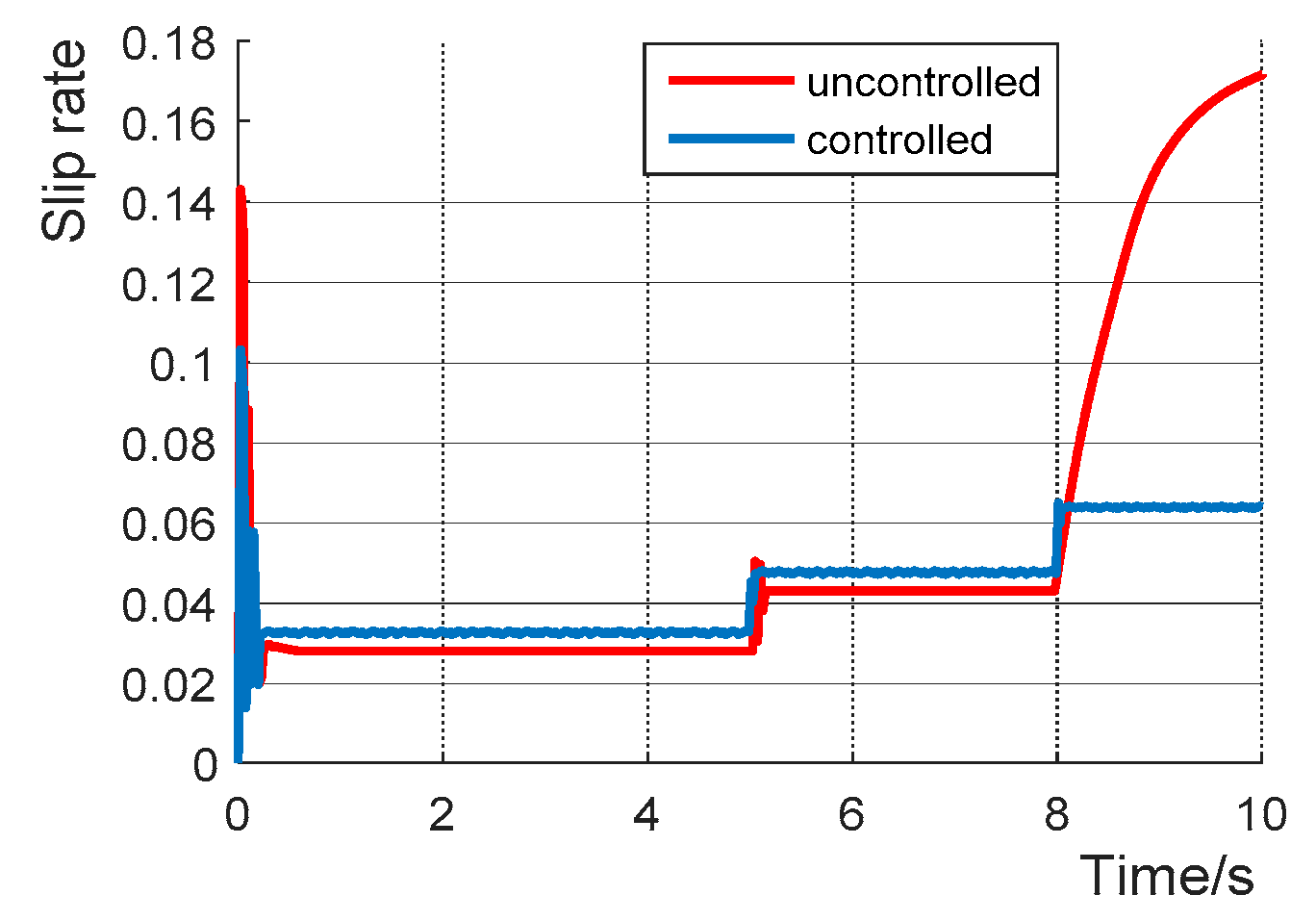
| Parameter Road Type | Dry Asphalt | Wet Asphalt | Snow Pavement | Ice Pavement |
|---|---|---|---|---|
| C1 | 1.2801 | 0.857 | 0.1946 | 0.05 |
| C2 | 23.99 | 33.822 | 94.129 | 306.39 |
| C3 | 0.52 | 0.3470 | 0.0646 | 0.001 |
| Sopt | 0.170 | 0.131 | 0.065 | 0.03 |
| μmax | 1.171 | 0.8 | 0.190 | 0.05 |
| Adhesion Coefficient Slip Rate | Dry Asphalt S | Wet Asphalt M | Snow Pavement B | Ice Pavement VB |
|---|---|---|---|---|
| Dry asphalt H | ES | D | TD | TD |
| Wet asphalt M | GS | ES | TD | TD |
| Snow pavement L | TD | TD | ES | D |
| Ice pavement VL | TD | TD | GS | ES |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Ma, J.; Chang, B.; Wang, J. Research on Anti-Skid Control Strategy for Four-Wheel Independent Drive Electric Vehicle. World Electr. Veh. J. 2021, 12, 150. https://doi.org/10.3390/wevj12030150
Zhang C, Ma J, Chang B, Wang J. Research on Anti-Skid Control Strategy for Four-Wheel Independent Drive Electric Vehicle. World Electric Vehicle Journal. 2021; 12(3):150. https://doi.org/10.3390/wevj12030150
Chicago/Turabian StyleZhang, Chuanwei, Jian Ma, Bo Chang, and Jianlong Wang. 2021. "Research on Anti-Skid Control Strategy for Four-Wheel Independent Drive Electric Vehicle" World Electric Vehicle Journal 12, no. 3: 150. https://doi.org/10.3390/wevj12030150
APA StyleZhang, C., Ma, J., Chang, B., & Wang, J. (2021). Research on Anti-Skid Control Strategy for Four-Wheel Independent Drive Electric Vehicle. World Electric Vehicle Journal, 12(3), 150. https://doi.org/10.3390/wevj12030150






