Insulation Monitoring of Dynamic Wireless Charging Network Based on BP Neural Network
Abstract
:1. Introduction
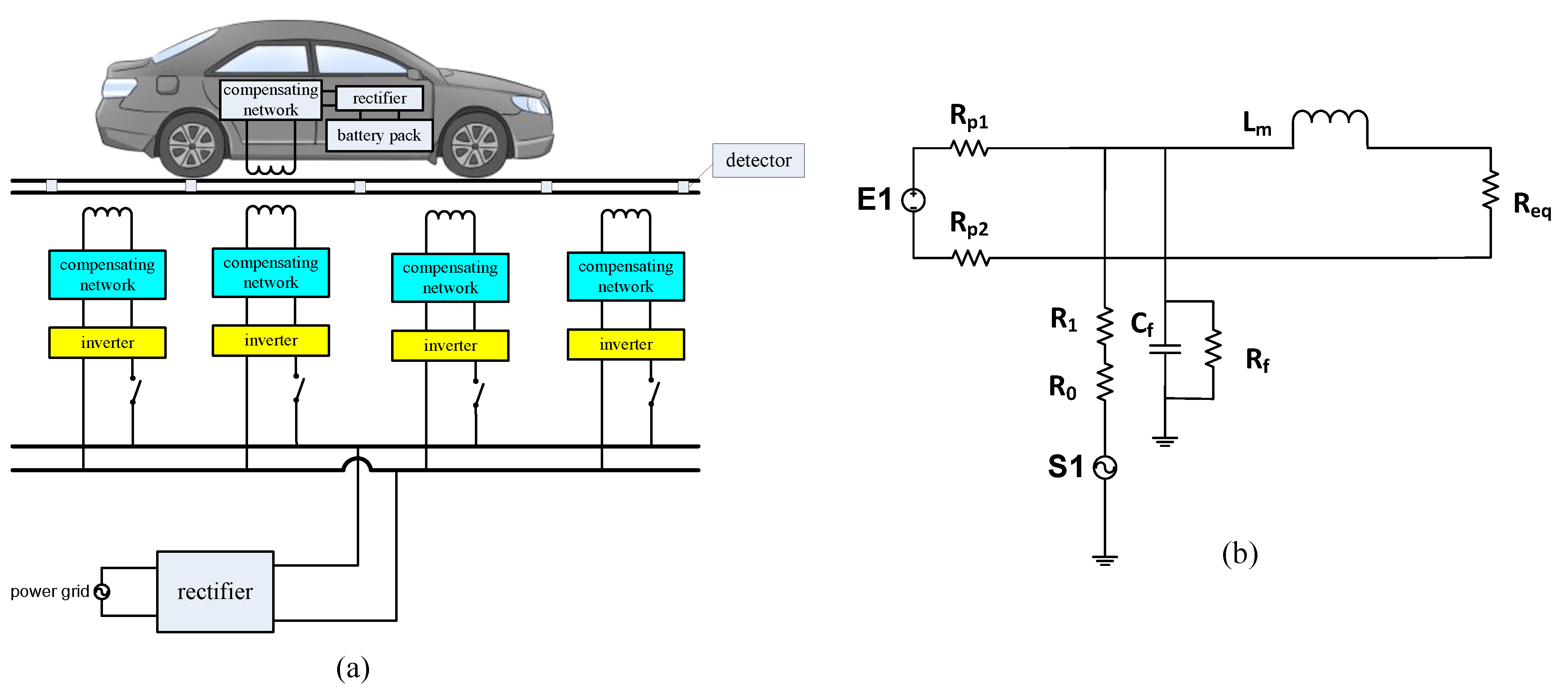
2. Calculation Model of Insulation Monitoring
3. Insulation Monitoring Based on BP Neural Network
3.1. Subsection
3.1.1. Improvement of BP Neural Network
3.1.2. Parameter Design of BP Neural Network
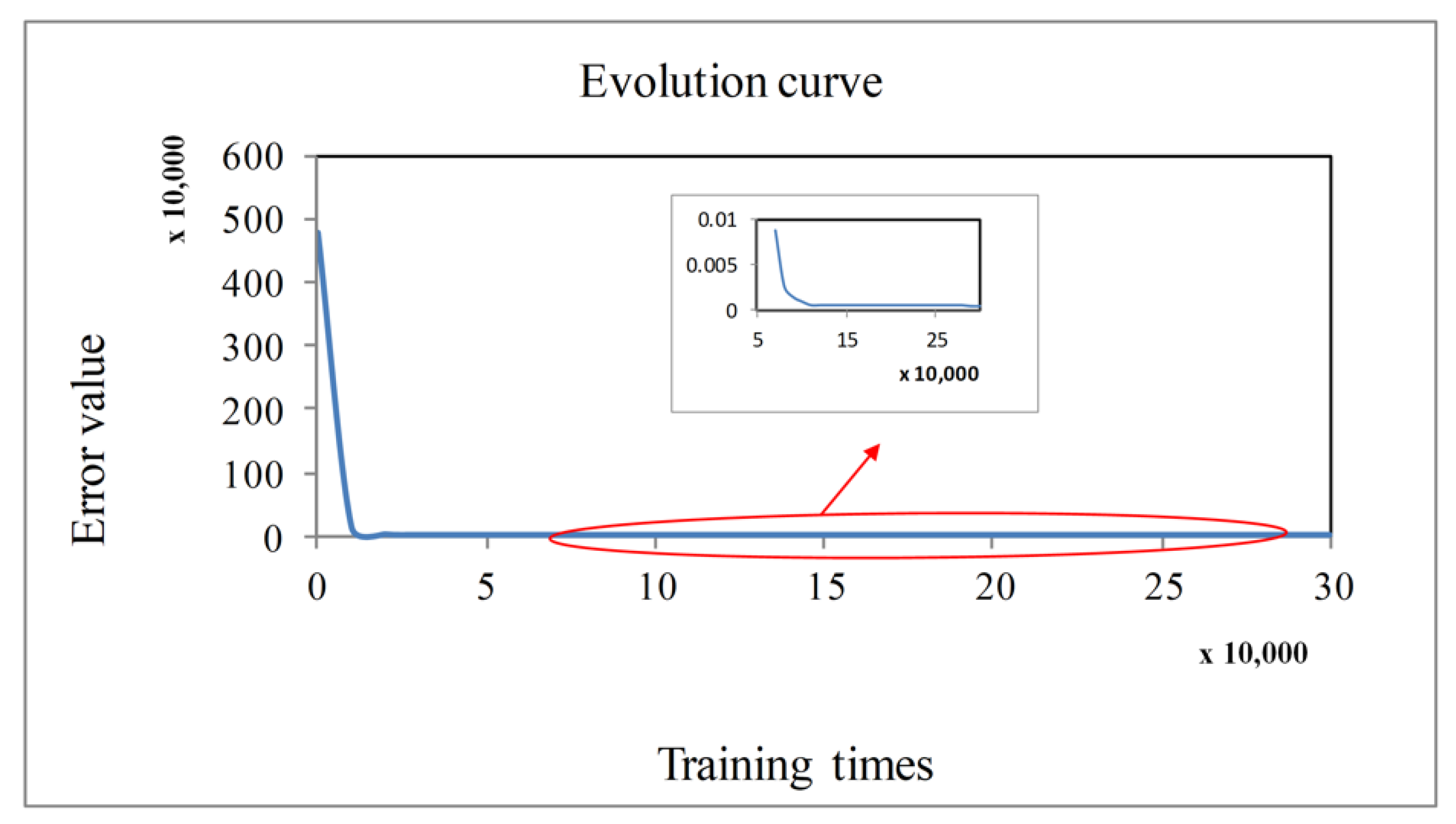
3.2. Neural Network Training Process
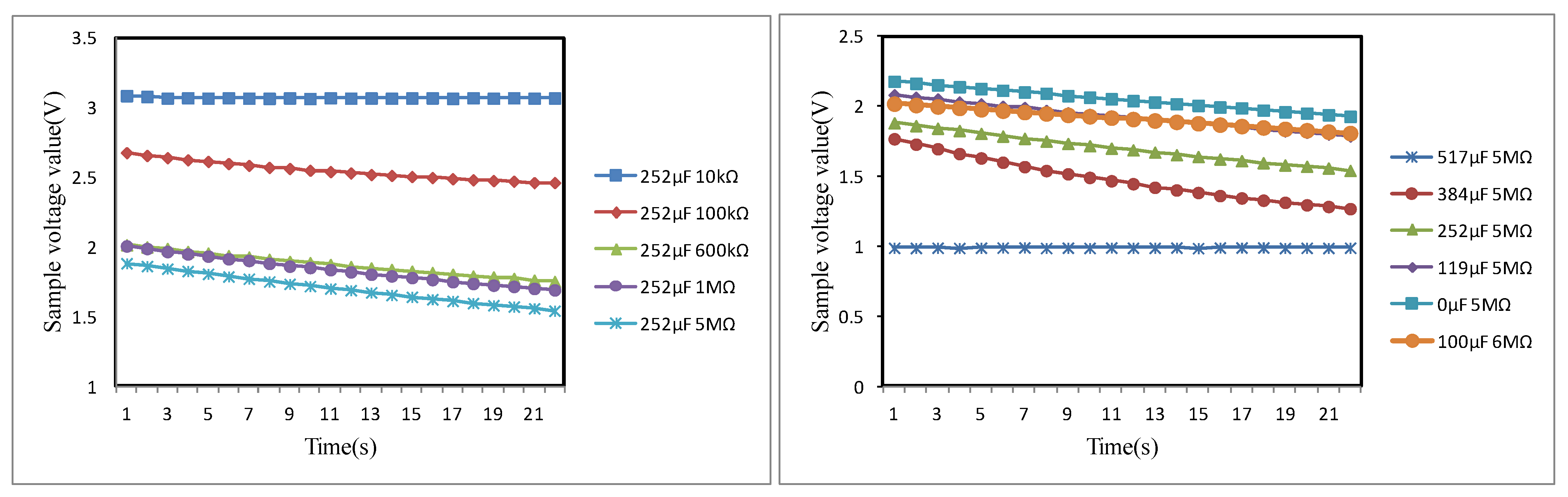
4. Simulation and Analysis
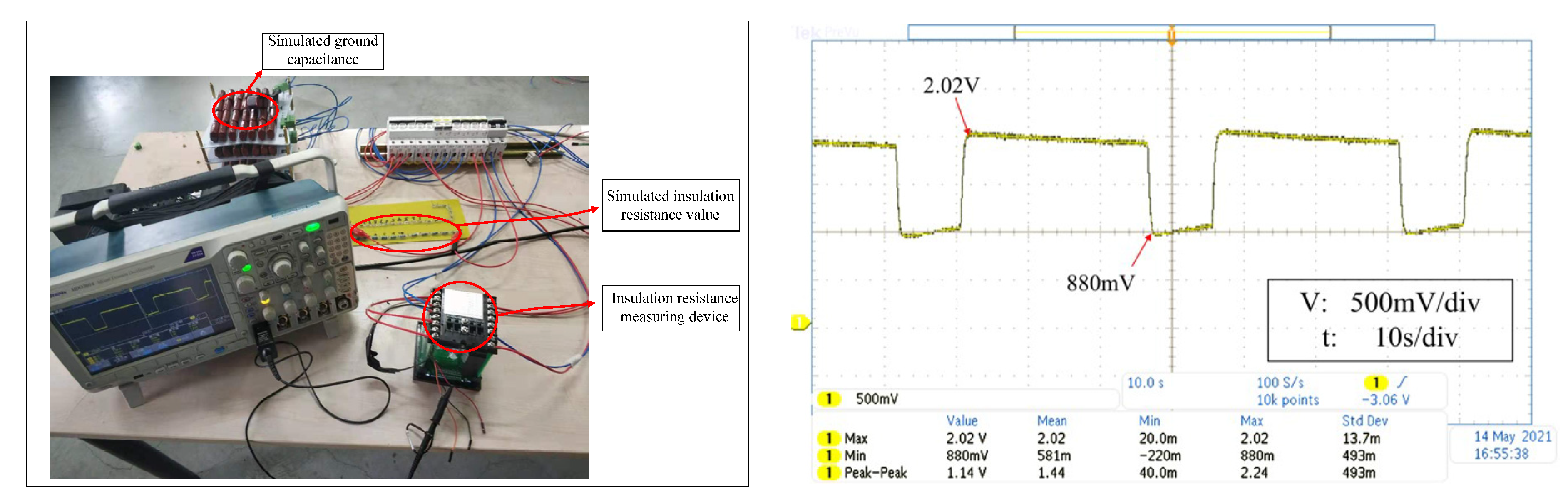
4.1. Build the Actual Experimental Circuit
4.2. Recognition Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Su, H.; Zhou, Z.; Liu, Z.; Zhang, L. Research review and prospect of intelligent dynamic wireless charging system for electric vehicles. Chin. J. Intell. Sci. Technol. 2020, 2, 1–9. [Google Scholar]
- Wang, W.; Yang, T.; Shao, X.; Qiang, L.V.; Song, P. Study on insulation monitoring of low voltage it system based on injection signal. Electrotech. Electric. 2012, 49–55. [Google Scholar]
- Li, C. Analysis on online supervision system of high voltage cable insulation condition of coal mine. Mech. Manag. Dev. 2016, 31, 70–86. [Google Scholar]
- Yu, S.; Zeng, T.; Li, Y.; Hu, Y.; Liu, L.; Wen, J.; Liu, H.; Wang, X. Design of insulation monitoring device based on improved single frequency method. China Meas. Test. 2020, 46, 78–82. [Google Scholar]
- Hu, Y.; Zeng, T.; Li, Y.; Yu, S.; Liu, L.; Wen, J.; Liu, H.; Wang, X. Design of insulation monitoring device based on improved dual frequency injection method. Instrum. Tech. Sens. 2020, 47–51. [Google Scholar]
- Wang, X. Application of low voltage insulation monitoring and fault location system based on AMP measurement method. Electr. Eng. 2020, 49–51. [Google Scholar] [CrossRef]
- Yu, H.; Jiao, S.; Yang, F. Design of insulation monitoring equipment for direct current network in ship. Chin. J. Ship Res. 2010, 5, 56–58. [Google Scholar]
- Li, L.; Zou, J.; Sun, H. Research and realization the DC system grounding fault detector. In Proceedings of the 6th International Symposium on Test and Measurement, Dalian, China, 1–4 June 2005; p. 7444. [Google Scholar]
- Wu, Z.; Wang, L. Research on intelligent on-line insulation monitoring device for electric vehicle. Low Volt. Appar. 2009, 20–22. [Google Scholar]
- Zhang, J.; Li, S.; Qi, K.; Wang, C.; Zhang, Q.; Huang, H. On line insulation impedance monitoring and fault location of ITN shore power system based on AC injection method. Mar. Electr. Electron. Eng. 2020, 40, 19–25. [Google Scholar]
- Makarenko, A. Multiple-valued and branching neural networks. Eng. World 2020, 2, 20–28. [Google Scholar]
- Al-Mawsawi, S.A.; Haider, A.; Alfaris, Q. Neural Network Model Predictive Control (NNMPC) Design for UPFC. WSEAS Trans. Comput. 2020, 19, 201–207. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Q. Short term power load forecasting of regional distribution network based on BP neural network. Softw. Dev. 2021, 49–52. [Google Scholar] [CrossRef]
- Wang, M.; Jing, Z.; Sun, B. Prediction of short-term market clearing price based on BP neural network. China Electr. Power Educ. 2011, 100–102. [Google Scholar] [CrossRef]

| Parameter Name | Parameter Value |
|---|---|
| Number of input nodes | 1 |
| Number of output nodes | 1 |
| Number of hidden layers | 4 |
| Number of hidden layer nodes | (50, 50, 50, 50) |
| Initial learning rate | 0.001 |
| Learning accuracy | 0.000001 |
| Training times | 3000000 |
| Analog Value of Capacitance to Ground | True Value of Insulation Resistance | Calculated Insulation Resistance Value | Error Value |
|---|---|---|---|
| 253 μF | 2.616 kΩ | 2.791 kΩ | +6.68% |
| 388 μF | 12.31 kΩ | 13.402 kΩ | +8.87% |
| 387 μF | 85.627 kΩ | 89.737 kΩ | +4.80% |
| 63 μF | 599.73 kΩ | 598.83 kΩ | −0.15% |
| 491 μF | 174.96 kΩ | 184.92 kΩ | +5.69% |
| 350 μF | 732.31 kΩ | 756.22 kΩ | +3.27% |
| 123 μF | 1.462 MΩ | 1.496 MΩ | +2.33% |
| 37 μF | 8.897 MΩ | 9.041 MΩ | +1.62% |
| 260 μF | 5.006 MΩ | 5.103 MΩ | +1.93% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, F.; Pei, W.; Li, Q.; Chu, Z.; Zhao, W.; Wu, S.; Zhang, X.; Han, C. Insulation Monitoring of Dynamic Wireless Charging Network Based on BP Neural Network. World Electr. Veh. J. 2021, 12, 129. https://doi.org/10.3390/wevj12030129
Wen F, Pei W, Li Q, Chu Z, Zhao W, Wu S, Zhang X, Han C. Insulation Monitoring of Dynamic Wireless Charging Network Based on BP Neural Network. World Electric Vehicle Journal. 2021; 12(3):129. https://doi.org/10.3390/wevj12030129
Chicago/Turabian StyleWen, Feng, Wenjie Pei, Qiang Li, Zhoujian Chu, Wenhan Zhao, Shuqi Wu, Xiang Zhang, and Chen Han. 2021. "Insulation Monitoring of Dynamic Wireless Charging Network Based on BP Neural Network" World Electric Vehicle Journal 12, no. 3: 129. https://doi.org/10.3390/wevj12030129
APA StyleWen, F., Pei, W., Li, Q., Chu, Z., Zhao, W., Wu, S., Zhang, X., & Han, C. (2021). Insulation Monitoring of Dynamic Wireless Charging Network Based on BP Neural Network. World Electric Vehicle Journal, 12(3), 129. https://doi.org/10.3390/wevj12030129







