Study on the Stability Control of Vehicle Tire Blowout Based on Run-Flat Tire
Abstract
:1. Introduction
2. Establishment of Run-Flat Tire Model
2.1. Run-Flat Tire Model before Blowout
2.2. Run-Flat Tire Model after Blowout
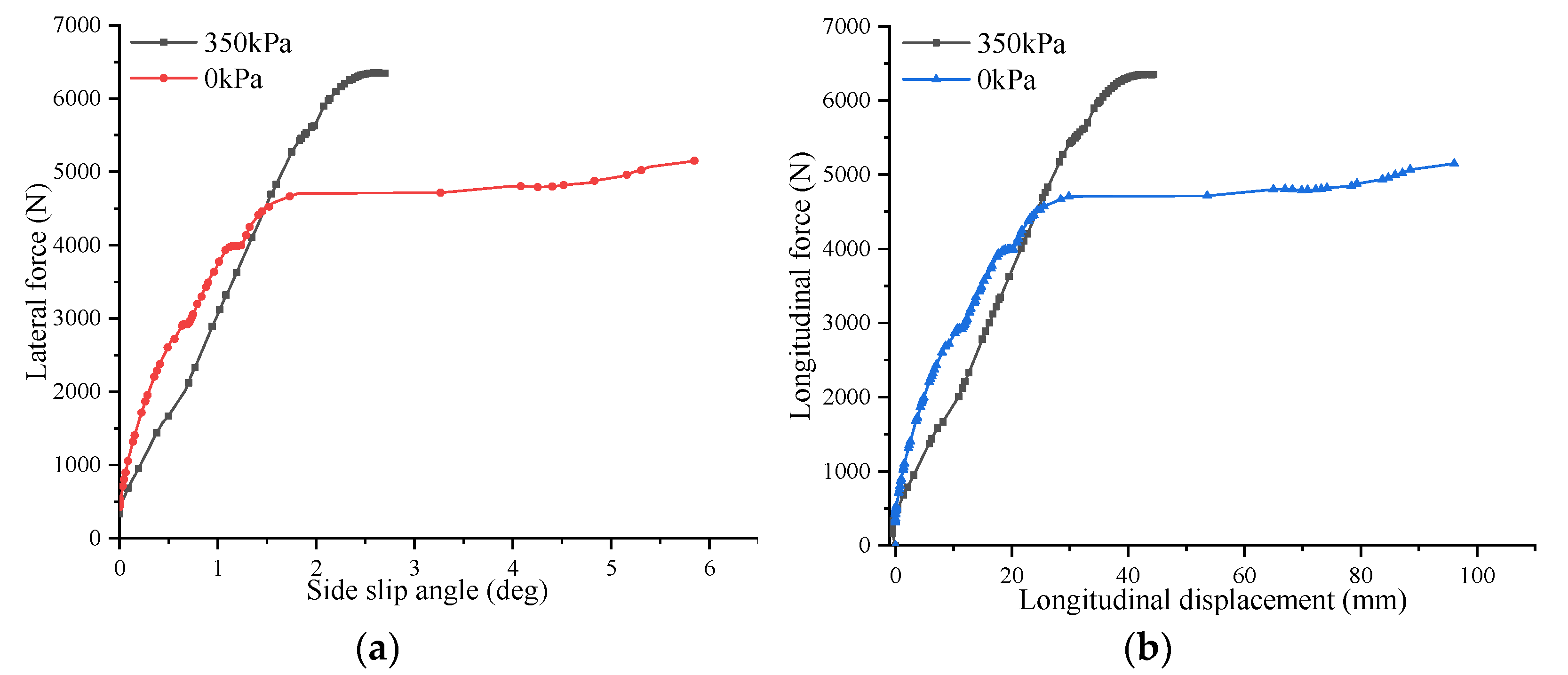
2.2.1. Cornering Stiffness and Longitudinal Stiffness after Tire Blowout
2.2.2. Change of Rolling Resistance Coefficient after Tire Blowout
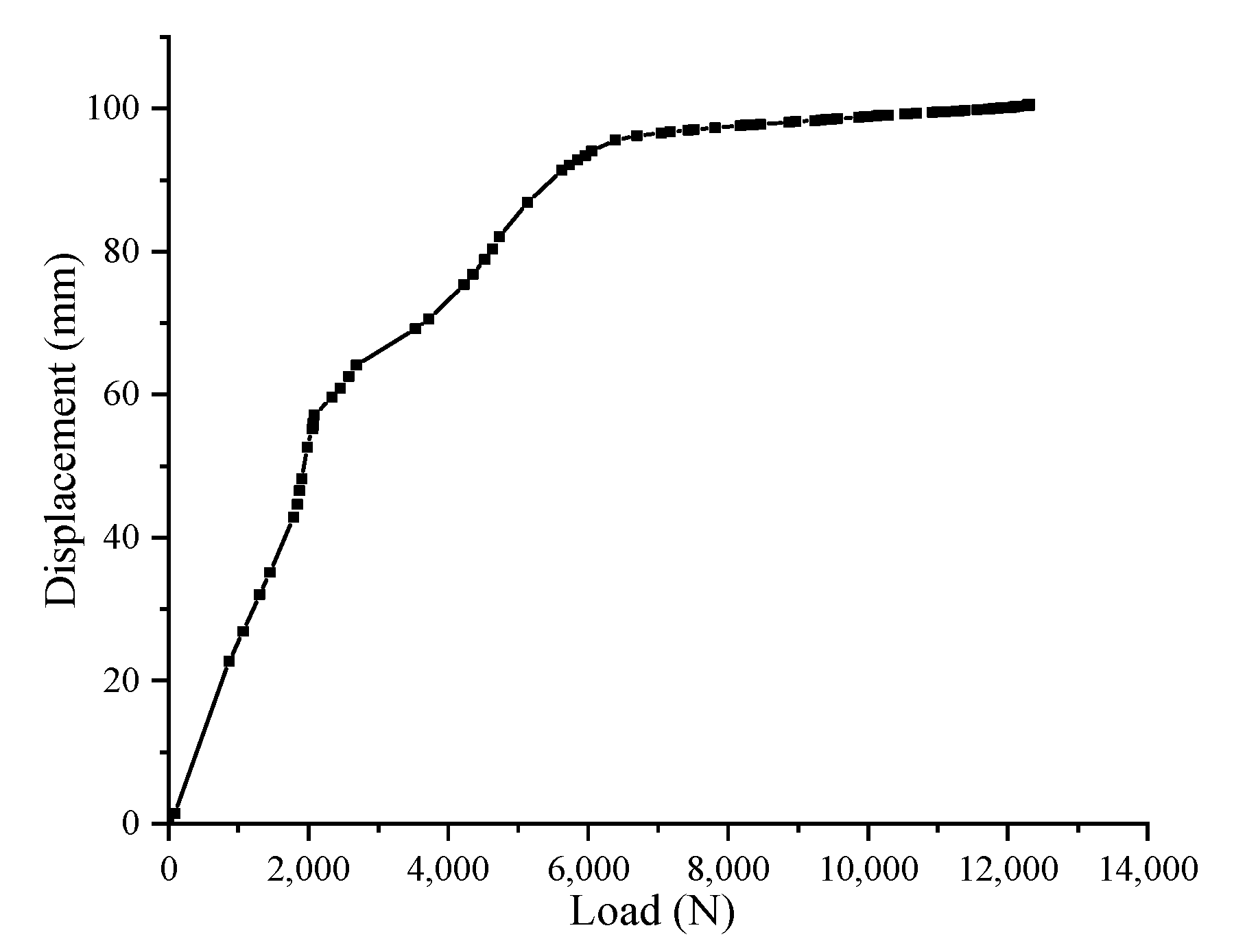
2.2.3. Change of Effective Rolling Radius after Tire Blowout
3. Two Degrees of Freedom Model and Control System
3.1. Two Degrees of Freedom Model
3.2. Differential Braking Control System
4. Simulation Results and Test Analysis
4.1. Tire Blowout Dynamic Response
- (1)
- Left front tire blowout
- (2)
- Left rear tire blowout
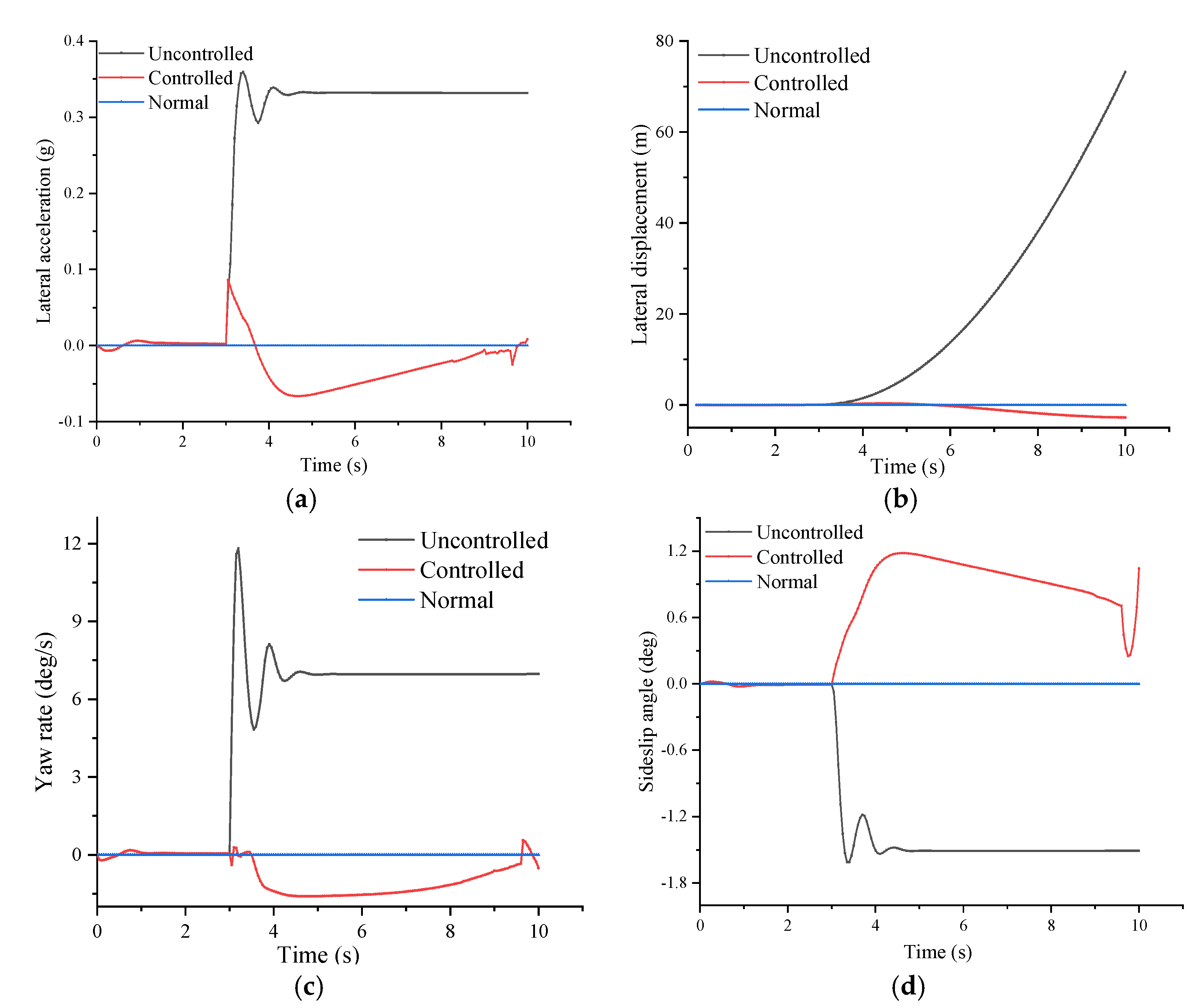
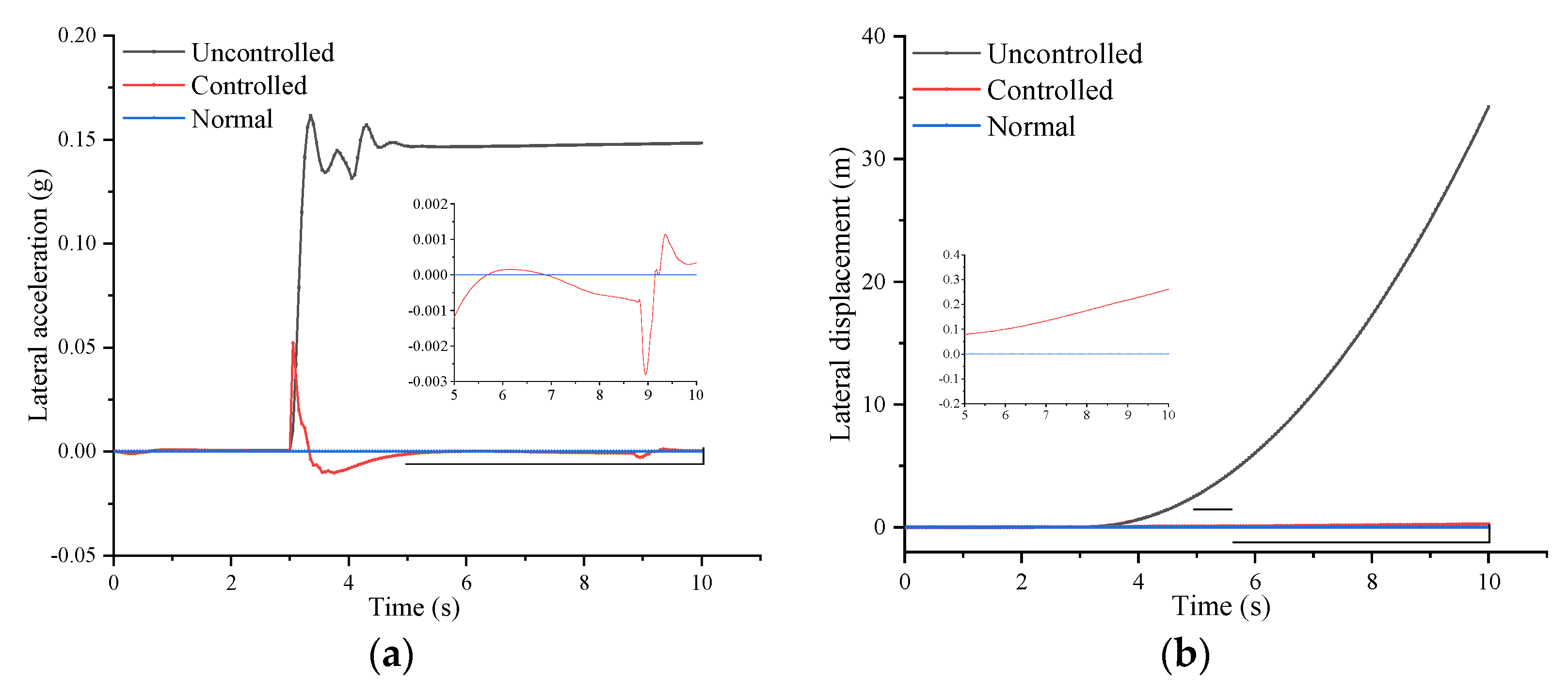
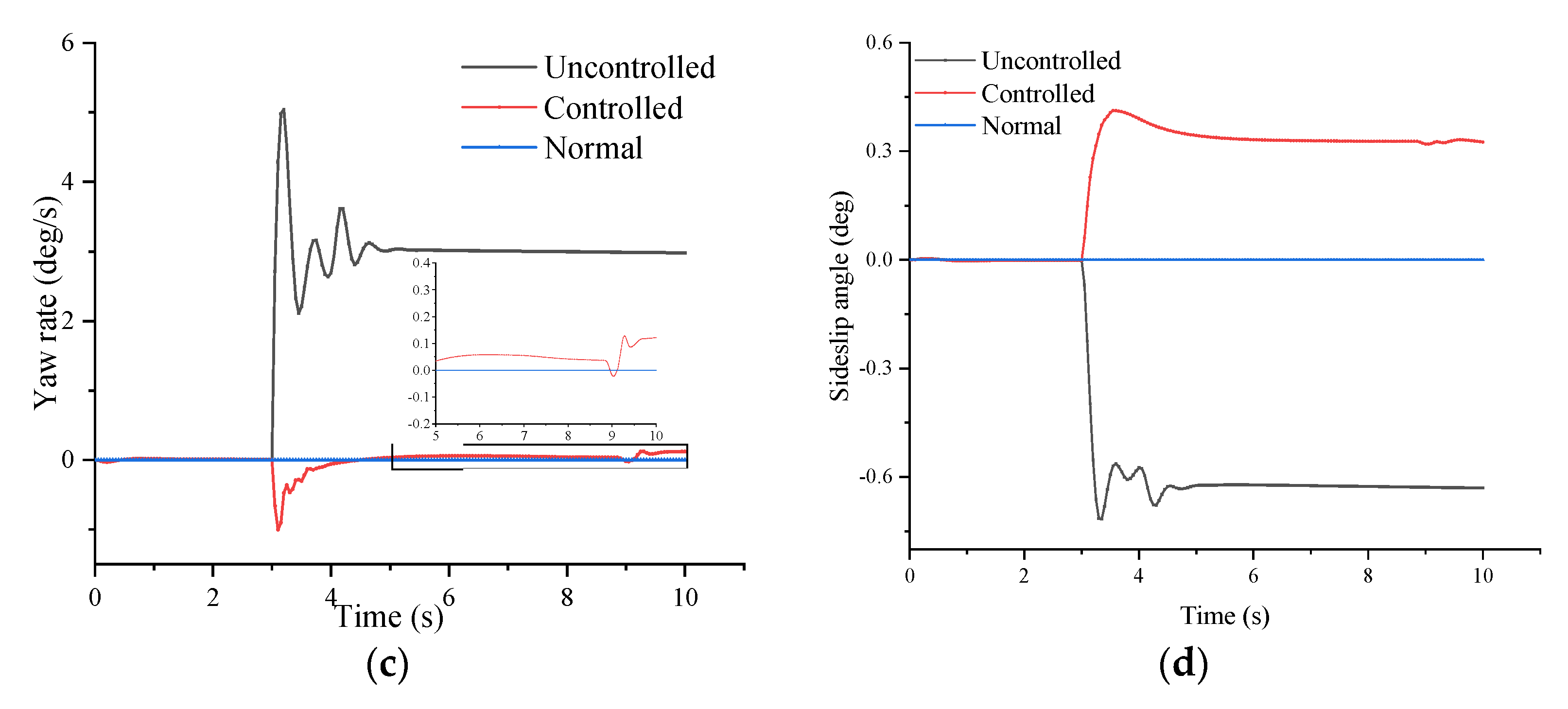
4.2. Stability Control Analysis
- (1)
- Left front tire control results
- (2)
- Left rear tire control results
5. Conclusions
- (1)
- The difference between the left front tire and left rear tire blowout condition of inserts supporting run-flat tire and normal tire was compared. The results show that the characteristic parameters of the two tires are similar. When the front tire blowout occurs, the yaw of the inserts supporting run-flat tire is larger, and when the rear tire blowout occurs, the yaw of the normal tire is larger.
- (2)
- The stability of the inserts supporting run-flat tire after tire blowout is controlled according to the difference between the ideal yaw rate and the sideslip angle and the actual value. The simulation results show that the differential braking control can better maintain the running track of the vehicle, significantly improve the stability of the vehicle, and whether the track adjustment effect of the rear tire of inserts supporting run-flat tire is better.
Author Contributions
Funding
Conflicts of Interest
References
- Huang, J.; Guo, K.; Song, X.; Liu, W. Vehicle stability control method after tire blow-out. China Mech. Eng. 2009, 20, 2006–2010. [Google Scholar]
- Liu, Y.; Yu, S.Y.; Gu, X.L. Trajectory control of vehicles with blowout tire on expressway based on fuzzy PID algorithm. J. Jilin Univ. Inf. Sci. Ed. 2015, 33, 380–388. [Google Scholar]
- Chen, Q.; Li, X.; Guo, L.; He, R. Research on estimated calculation model of additional yaw torque after vehicle tire blow-out. China Mech. Eng. 2014, 25, 422–425. [Google Scholar]
- Li, S.; Guo, K.; Chou, T. Stability control of vehicle with active front steering under extreme conditions. Automot. Eng. 2020, 42, 191–198. [Google Scholar]
- Liu, P.; Sun, L.; Yang, M.; Yuan, F. Research on ideal vehicle reference model for yaw stability control. J. Chongqing Univ. Technol. Nat. Sci. 2020, 34, 17–24. [Google Scholar]
- Chen, L.; Xie, Y.; Cai, Y.; Sun, X.; Teng, C.; Zhou, K. Stable tracking control of autonomous vehicles at extreme conditions. Automot. Eng. 2020, 42, 1016–1026. [Google Scholar]
- Guo, Y.; Lu, Y.; Fu, R.; Yang, F. Simulation and analysis of lateral stability of large coach. China J. Highw. Transp. 2018, 31, 156–164. [Google Scholar]
- Liu, W.; Zhang, X. Study on fuzzy sliding mode control algorithm of vehicle stability control after a tire blowout. Mech. Sci. Technol. Aerosp. Eng. 2019, 38, 1944–1953. [Google Scholar]
- Jing, H.; Liu, Z. Gain-scheduling robust control for a tire-blow-out road vehicle. J. Automob. Eng. 2019, 233, 344–362. [Google Scholar] [CrossRef]
- Bai-Nan, L.; Hong-Yan, G.; Hong, C. Trajectory tracking and stability control for vehicle after tire blow-out. Electr. Mach. Control 2013, 17, 97–104. [Google Scholar]
- Chen, D.; Wu, N.; Shi, N. Steering system and vertical load dynamic response of vehicle with tire burst. China J. Highw. Transp. 2014, 27, 112–119. [Google Scholar]
- Erlien, S.M.; Fujita, S.; Gerdes, J.C. Shared steering control using safe envelopes for obstacle avoidance and vehicle stability. IEEE Trans. Intell. Transp. Syst. 2016, 17, 441–451. [Google Scholar] [CrossRef]
- Wang, F.; Chen, H.; Guo, K.; Cao, D. A novel integrated approach for path following and directional stability control of road vehicles after a tire blow-out. Mech. Syst. Signal Process. 2017, 93, 431–444. [Google Scholar] [CrossRef]
- Yang, L.; Yue, M.; Tian, H.; Yao, B. Tire blow-out control for direct drive electric vehicles using reconfiguration of torque distribution and vertical load. Trans. Inst. Meas. Control 2020, 42, 1547–1558. [Google Scholar] [CrossRef]
- Choi, M.; Choi, S.B. MPC for vehicle lateral stability via differential braking and active front steering considering practical aspects. J. Automob. Eng. 2016, 230, 459–469. [Google Scholar] [CrossRef]
- Wang, F.; Chen, H.; Cao, D. Nonlinear Coordinated Motion Control of Road Vehicles After a Tire Blowout. IEEE Trans. Control Syst. Technol. 2016, 24, 956–970. [Google Scholar] [CrossRef]
- Wang, X.; Zang, L.; Wang, Z.; Zhao, Z.; Lin, F.; Teng, F. Analysis of mechanical characteristics of inserts supporting run-flat tire during pressure relief. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 235. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D. UniTire: Unified tire model. J. Mech. Eng. 2016, 52, 90–99. [Google Scholar] [CrossRef]
- Guo, K.H.; Huang, J.; Song, X.L. Analysis and control of vehicle movement with blown-out tire. Automot. Eng. 2007, 29, 1041–1045. [Google Scholar]
- Wang, Y.L. Study on Vehicle Dynamic Response to Tire Blow-out Based on CarSim and UniTire; Jilin University: Changchun, China, 2007. [Google Scholar]
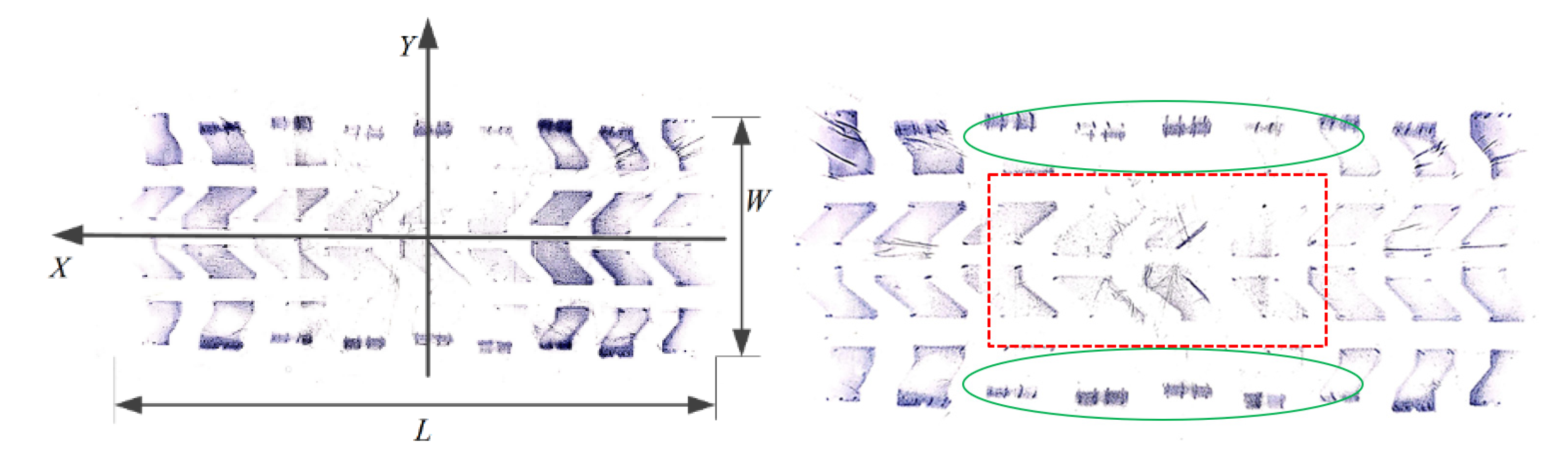


| F/N | W/mm | L/mm | S/mm2 | |
|---|---|---|---|---|
| Whole contact area | 12,250 | 235 | 580 | 136,300 |
| Insert contact area | 12,250 | 132 | 258 | 34,056 |
| ∆r | ∆β | ||||||
|---|---|---|---|---|---|---|---|
| NB | NM | NS | ZO | PS | PM | PB | |
| NB | PB | PB | PB | PB | PM | PS | ZO |
| NM | PB | PB | PM | PM | PM | PS | ZO |
| NS | PM | PM | PM | PM | PS | ZO | NS |
| NO | PM | PS | PS | ZO | NS | NS | NM |
| ZO | PM | PM | PS | ZO | NS | NS | NM |
| PS | PS | PS | ZO | NM | NM | NM | NM |
| PM | ZO | ZO | NM | NM | NB | NB | NB |
| PB | ZO | NS | NM | NB | NB | NB | NB |
| Parameter/Unit | Parameter Symbol | Parameter Value |
|---|---|---|
| Sprung mass/kg | Ms | 2290 |
| Height of center of mass/mm | h | 810 |
| Front axle distance/mm | a | 1180 |
| Rear axle distance/mm | b | 1170 |
| Wheel base/mm | l | 2950 |
| Effective rolling radius/mm | Re | 455 |
| Static load radius/mm | R0 | 467 |
| Rim diameter/mm | D | 419 |
| Width of tire section/mm | B | 317 |
| Radial stiffness/N⋅mm−1 | Kt | 405 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zang, L.; Wang, Z.; Lin, F.; Zhao, Z. Study on the Stability Control of Vehicle Tire Blowout Based on Run-Flat Tire. World Electr. Veh. J. 2021, 12, 128. https://doi.org/10.3390/wevj12030128
Wang X, Zang L, Wang Z, Lin F, Zhao Z. Study on the Stability Control of Vehicle Tire Blowout Based on Run-Flat Tire. World Electric Vehicle Journal. 2021; 12(3):128. https://doi.org/10.3390/wevj12030128
Chicago/Turabian StyleWang, Xingyu, Liguo Zang, Zhi Wang, Fen Lin, and Zhendong Zhao. 2021. "Study on the Stability Control of Vehicle Tire Blowout Based on Run-Flat Tire" World Electric Vehicle Journal 12, no. 3: 128. https://doi.org/10.3390/wevj12030128
APA StyleWang, X., Zang, L., Wang, Z., Lin, F., & Zhao, Z. (2021). Study on the Stability Control of Vehicle Tire Blowout Based on Run-Flat Tire. World Electric Vehicle Journal, 12(3), 128. https://doi.org/10.3390/wevj12030128







