Temperature Prediction of PMSMs Using Pseudo-Siamese Nested LSTM
Abstract
1. Introduction
2. Pseudo-Siamese Nested LSTM Network
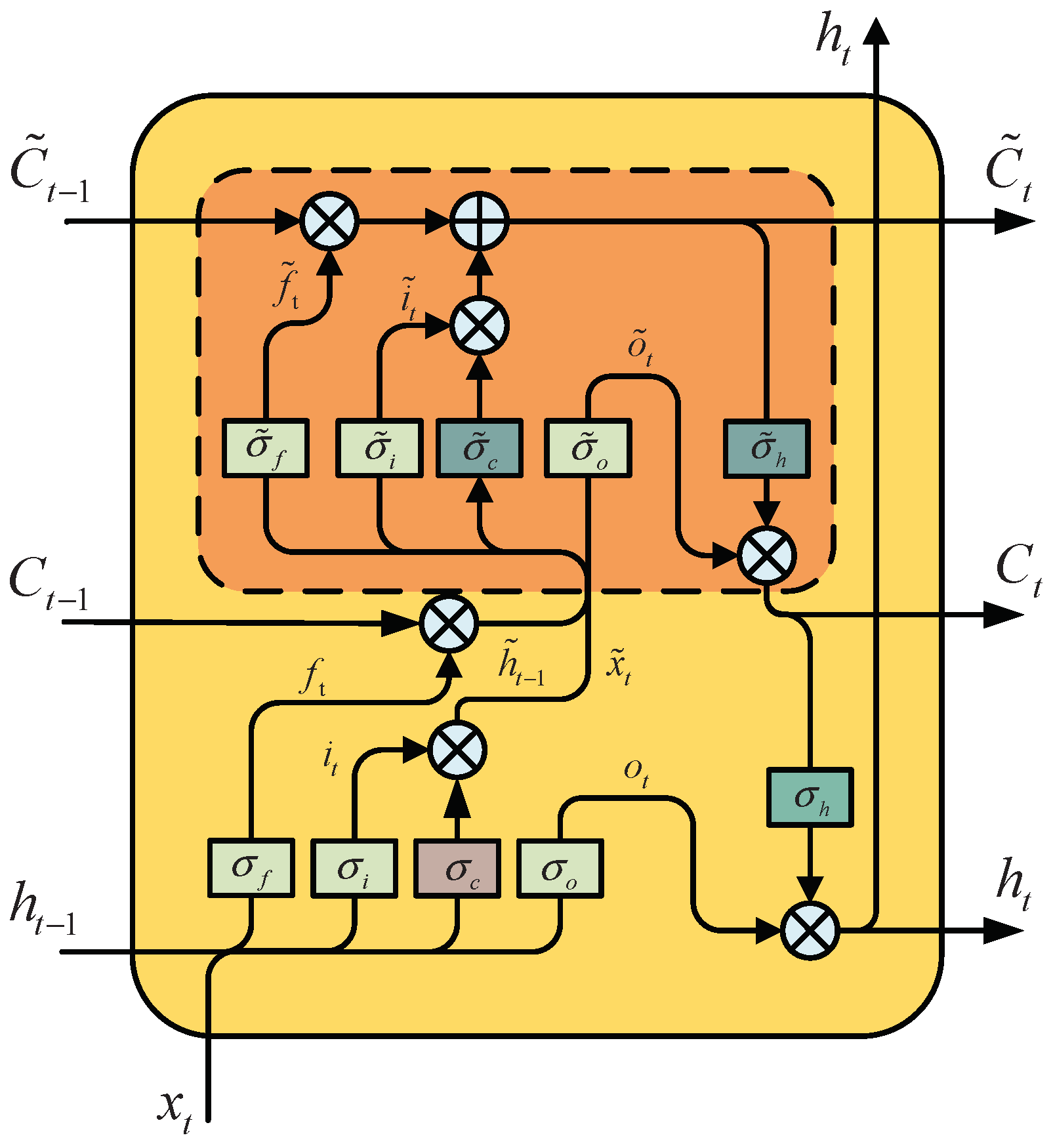
2.1. Nested LSTM Network
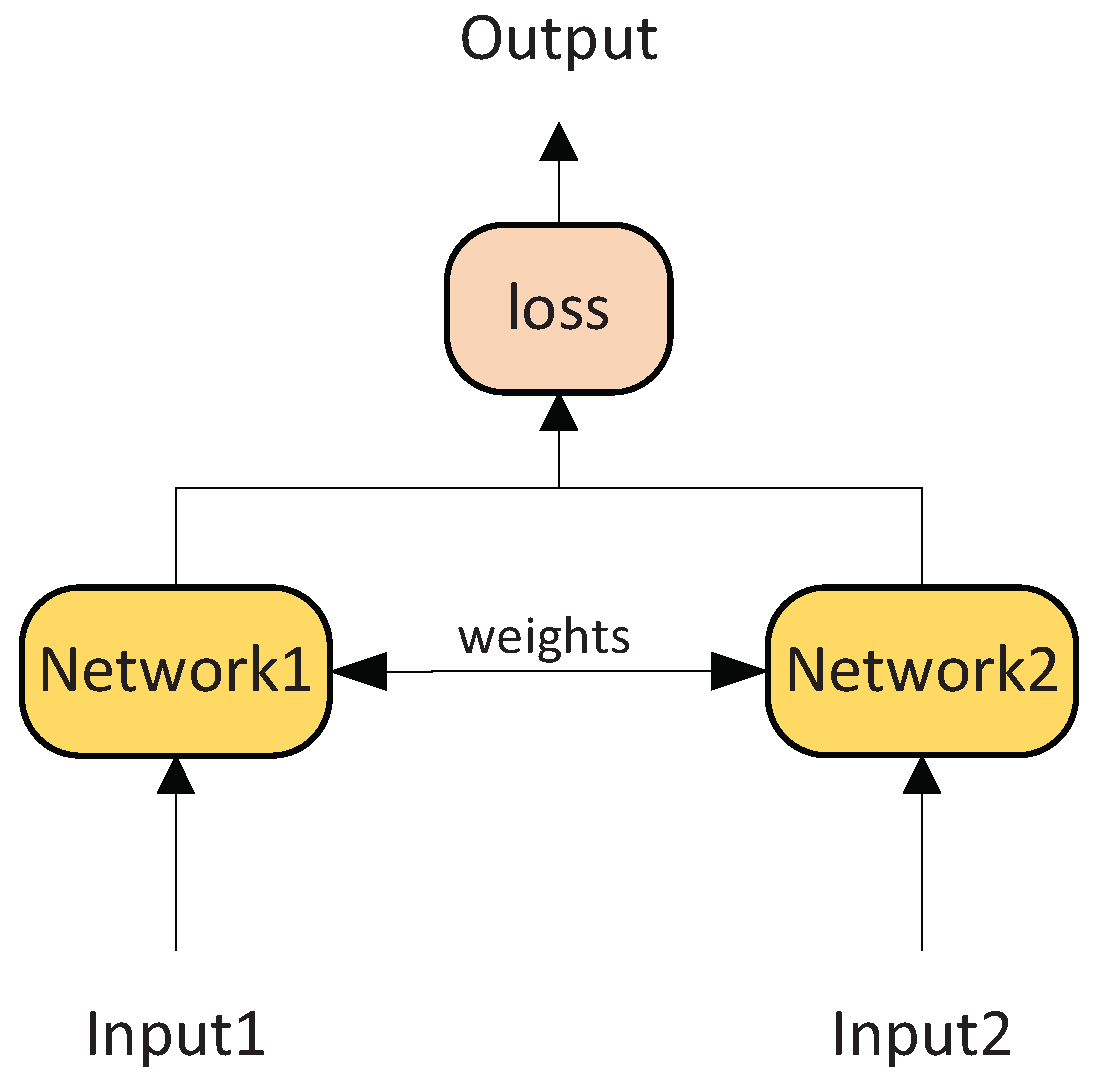
2.2. Model Architecture Proposed
3. Temperature Benchmark Data Set and Valuation Indicators
3.1. Temperature Benchmark Data Set
3.2. Evaluation Indicators
4. Learning Rate Optimization
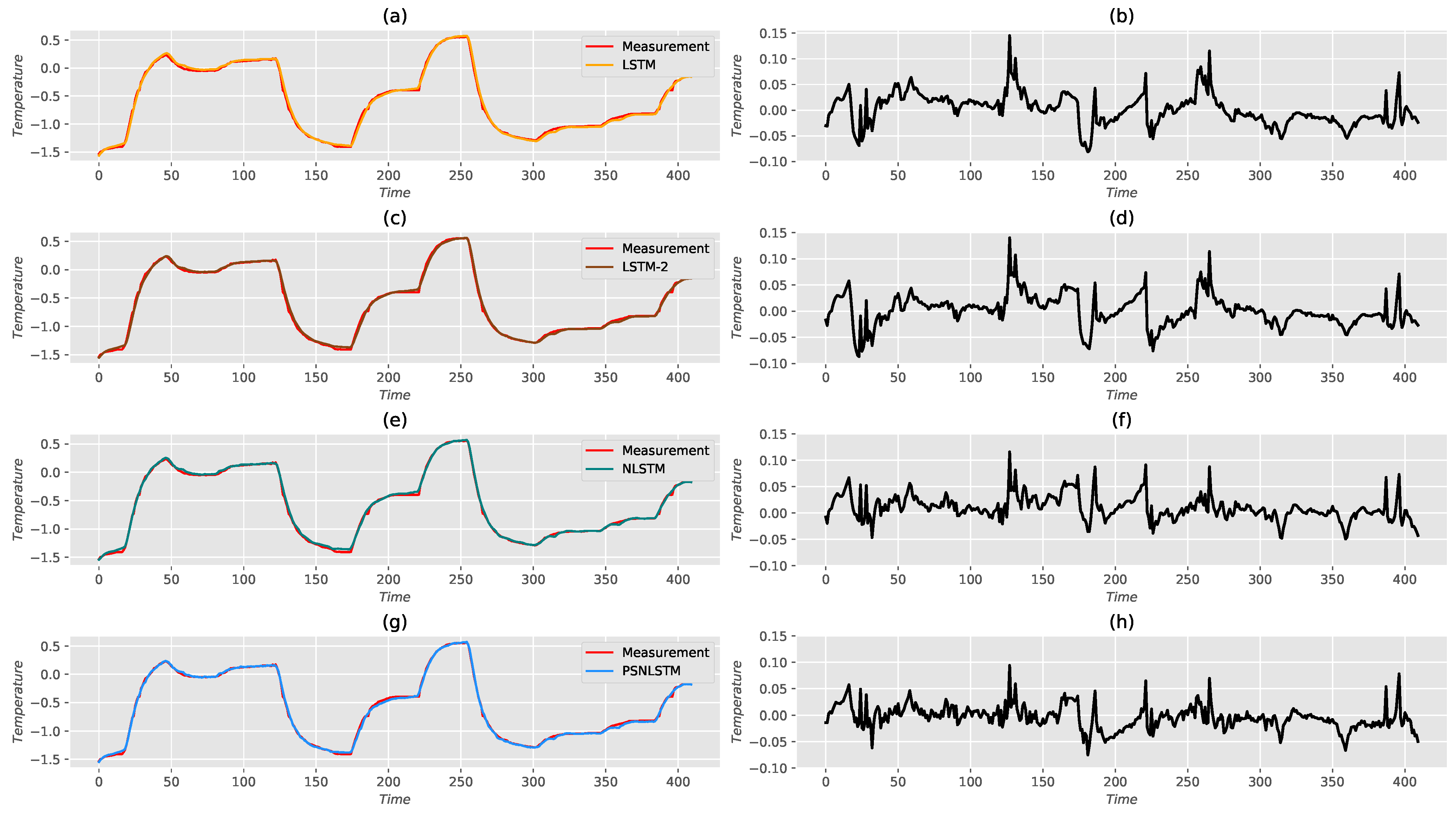
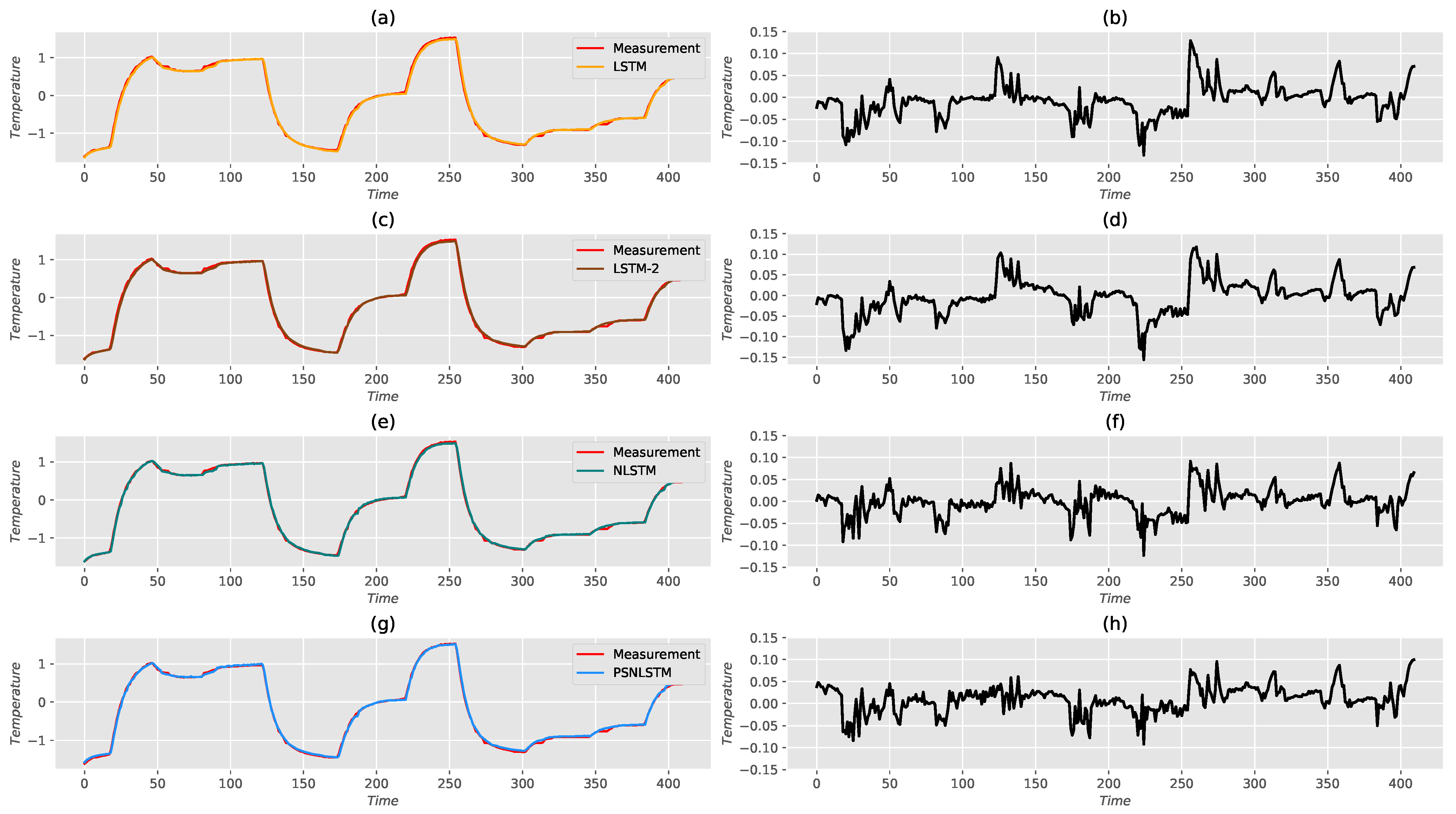
5. Performance Assessment
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fan, T.; Li, Q.; Wen, X. Development of a High Power Density Motor Made of Amorphous Alloy Cores. IEEE Trans. Ind. Electron. 2013, 61, 4510–4518. [Google Scholar] [CrossRef]
- Wu, P.S.; Hsieh, M.F.; Cai, W.L.; Liu, J.H.; Huang, Y.T.; Caceres, J.F.; Chang, S.W. Heat Transfer and Thermal Management of Interior Permanent Magnet Synchronous Electric Motor. Inventions 2019, 4, 69. [Google Scholar] [CrossRef]
- Guo, H.; Ding, Q.; Song, Y.; Tang, H.; Wang, L. Predicting Temperature of Permanent Magnet Synchronous Motor Based on Deep Neural Network. Energies 2020, 13, 4782. [Google Scholar] [CrossRef]
- Zhu, Y.; Xiao, M.; Lu, K.; Wu, Z.; Tao, B. A simplified thermal model and online temperature estimation method of permanent magnet synchronous motors. Appl. Sci. 2019, 9, 3158. [Google Scholar] [CrossRef]
- Habibinia, D.; Rostami, N.; Feyzi, M.R.; Soltanipour, H.; Pyrhönen, J. New finite element based method for thermal analysis of axial flux interior rotor permanent magnet synchronous machine. IET Electr. Power. Appl. 2019, 14, 464–470. [Google Scholar] [CrossRef]
- Feng, G.; Lai, C.; Iyer, K.L.V.; Kar, N.C. Improved high-frequency voltage injection based permanent magnet temperature estimation for PMSM condition monitoring for EV applications. IEEE Trans. Appl. Supercon. 2020, 30, 1–5. [Google Scholar] [CrossRef]
- Boglietti, A.; Cavagnino, A.; Staton, D.; Shanel, M.; Mueller, M.; Mejuto, C. Evolution and modern approaches for thermal analysis of electrical machines. IEEE Trans. Ind. Electron. 2009, 56, 871–882. [Google Scholar] [CrossRef]
- Kral, C.; Haumer, A.; Lee, S.B. A Practical Thermal Model for the Estimation of Permanent Magnet and Stator Winding Temperatures. IEEE Trans. Veh. Technol. 2017, 67, 216–225. [Google Scholar] [CrossRef]
- Qiao, G.; Wang, M.; Liu, F.; Liu, Y.; Zheng, P.; Sui, Y. Analysis of Magnetic Properties of AlNiCo and Magnetization State Estimation in Variable-Flux PMSMs. IEEE Trans. Magn. 2019, 55, 1–6. [Google Scholar] [CrossRef]
- Wallscheid, O.; Huber, T.; Peters, W.; Böcker, J. A critical review of techniques to determine the magnet temperature of permanent magnet synchronous motors under real-time conditions. EPE J. 2016, 26, 11–20. [Google Scholar] [CrossRef]
- Balamurali, A.; Kundu, A.; Clandfield, W.; Kar, N.C. Non–invasive parameter and loss determination in PMSM considering the effects of saturation, cross–saturation, time harmonics and temperature variations. IEEE Trans. Magn. 2020, 57, 8202206. [Google Scholar]
- Giangrande, P.; Madonna, V.; Nuzzo, S.; Spagnolo, C.; Gerada, C.; Galea, M. Reduced Order Lumped Parameter Thermal Network for Dual Three-Phase Permanent Magnet Machines. In Proceedings of the 2019 IEEE Workshop on Electrical Machines Design, Control and Diagnosis (WEMDCD), Athens, Greece, 22–23 April 2019; pp. 71–76. [Google Scholar]
- Rostami, N.; Feyzi, M.R.; Pyrhonen, J.; Parviainen, A.; Niemela, M. Lumped-parameter thermal model for axial flux permanent magnet machines. IEEE. Trans. Electr. Power. Appl. 2017, 49, 1178–1184. [Google Scholar] [CrossRef]
- Yu, X.; Shi, S.; Xu, L.; Liu, Y.; Miao, Q.; Sun, M. A Novel Method for Sea Surface Temperature Prediction Based on Deep Learning. Math. Probl. Eng. 2020, 2020, 1–9. [Google Scholar] [CrossRef]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzz. 1998, 6, 107–116. [Google Scholar] [CrossRef]
- Wallscheid, O.; Kirchgässner, W.; Böcker, J. Investigation of long short-term memory networks to temperature prediction for permanent magnet synchronous motors. In Proceedings of the 2017 International Joint Conference On Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017; pp. 1940–1947. [Google Scholar]
- Kirchgässner, W.; Wallscheid, O.; Böcker, J. Deep residual convolutional and recurrent neural networks for temperature estimation in permanent magnet synchronous motors. In Proceedings of the 2019 IEEE International Electric Machines and Drives Conference (IEMDC), San Diego, CA, USA, 11–15 May 2019; pp. 1439–1446. [Google Scholar]
- Moniz, J.R.A.; Krueger, D. Nested lstms. In Proceedings of the Ninth Asian Conference on Machine Learning (ACML2017), Seoul, Korea, 15–17 November 2017; pp. 15–17. [Google Scholar]
- Li, Y.; Yu, Z.; Chen, Y.; Yang, C.; Li, Y.; Allen, L.X.; Li, B. Automatic Seizure Detection using Fully Convolutional Nested LSTM. Int. J. Neural Syst. 2020, 30, 2050019. [Google Scholar] [CrossRef]
- Ma, X.; Zhong, H.; Li, Y.; Ma, J.; Cui, Z.; Wang, Y. Forecasting transportation network speed using deep capsule networks with nested lstm models. IEEE Trans. Intell. Transp. 2020, 99, 1–12. [Google Scholar] [CrossRef]
- Roy, S.K.; Harandi, M.; Nock, R.; Hartley, R. Siamese networks: The tale of two manifolds. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV2019), Seoul, Korea, 27 October–2 November 2019; pp. 3046–3055. [Google Scholar]
- Hughes, L.H.; Schmitt, M.; Mou, L.; Wang, Y.; Zhu, X.X. Identifying corresponding patches in SAR and optical images with a pseudo-siamese CNN. IEEE Geosci. Remote Sens. Lett. 2018, 15, 784–788. [Google Scholar] [CrossRef]
- Pontes, E.L.; Huet, S.; Linhares, A.C.; Torres-Moreno, J.M. Predicting the semantic textual similarity with siamese CNN and LSTM. arXiv 2018, arXiv:1810.10641. [Google Scholar]
- Wallscheid, O.; Böcker, J. Global identification of a low-order lumped-parameter thermal network for permanent magnet synchronous motors. IEEE Trans. Energy Convers. 2015, 31, 354–365. [Google Scholar] [CrossRef]
- Goyal, P.; Dollár, P.; Girshick, R.; Noordhuis, P.; Wesolowski, L.; Kyrola, A.; Tulloch, A.; Jia, Y.; He, K.J. Accurate, large minibatch sgd: Training imagenet in 1 h. arXiv 2017, arXiv:1706.02677. [Google Scholar]
- Loshchilov, I.; Hutter, F. Decoupled weight decay regularization. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Kingma, D.P.; Adam, B.J. A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Reddi, S.J.; Kale, S.; Kumar, S. On the convergence of adam and beyond. arXiv 2019, arXiv:1904.09237. [Google Scholar]
- Dozat, T. Incorporating nesterov momentum into adam. In Proceedings of the Workshop track at International Conference on Learning Representations (ICLR2016), San Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]




| Parameter Name | Symbol |
|---|---|
| Ambient temperature | |
| Coolant temperature | |
| Voltage d-component | |
| Voltage q-component | |
| Motor speed | |
| Actual torque | |
| Current d-component | |
| Current q-component | |
| Permanent Magnet temperature | |
| Stator yoke temperature | |
| Stator tooth temperature | |
| Stator winding temperature | |
| unique ID |
| Hyper-Parameter | LSTM | LSTM-2 | NLSTM | PSNLSTM |
|---|---|---|---|---|
| Hidden layer | 3 | 4 | 4 | 4 |
| Units | 64 | 64 | 64 | |
| Time steps | 7 | 7 | 7 | |
| Weight | normal | normal | normal | normal |
| Optimizer | Nadam | Nadam | Nadam | Nadam |
| Learning rate | 0.001 | 0.001 | 0.001 | 0.001 |
| Warm-up epochs | 10 | 10 | 10 | 10 |
| Epochs | 100 | 100 | 100 | 100 |
| Gaussian noise | ||||
| Drop out | 0.2 | 0.2 | 0.2 | 0.2 |
| Model | MSE (%) | MAE (%) | RMSE (%) | STDPE | |
|---|---|---|---|---|---|
| LSTM | 0.0927 | 2.3625 | 3.0448 | 99.7374 | 0.0304 |
| LSTM-2 | 0.0897 | 2.2004 | 2.9947 | 99.7460 | 0.3000 |
| NLSTM | 0.0627 | 1.7879 | 2.5044 | 99.8223 | 0.0230 |
| PSNLSTM | 0.0508 | 1.6860 | 2.2537 | 99.8561 | 0.0222 |
| Model | MSE (%) | MAE (%) | RMSE (%) | STDPE | |
|---|---|---|---|---|---|
| LSTM | 0.1321 | 2.4961 | 3.6339 | 99.8435 | 0.0661 |
| LSTM-2 | 0.1683 | 2.9113 | 4.1018 | 99.8006 | 0.0615 |
| NLSTM | 0.0934 | 2.1675 | 3.0567 | 99.8892 | 0.0510 |
| PSNLSTM | 0.0998 | 2.455845 | 3.1598 | 99.8816 | 0.0467 |
| Model | MSE (%) | MAE (%) | RMSE (%) | STDPE | |
|---|---|---|---|---|---|
| LSTM | 0.4380 | 4.0302 | 6.6183 | 99.6873 | 0.0357 |
| LSTM-2 | 0.3902 | 4.4855 | 6.2463 | 99.7215 | 0.0409 |
| NLSTM | 0.2609 | 3.3056 | 5.1074 | 99.8138 | 0.0306 |
| PSNLSTM | 0.2198 | 3.4557 | 4.6888 | 99.8430 | 0.0301 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Cen, Y.; Cen, G.; Yao, X.; Zhao, C.; Zhang, Y. Temperature Prediction of PMSMs Using Pseudo-Siamese Nested LSTM. World Electr. Veh. J. 2021, 12, 57. https://doi.org/10.3390/wevj12020057
Cai Y, Cen Y, Cen G, Yao X, Zhao C, Zhang Y. Temperature Prediction of PMSMs Using Pseudo-Siamese Nested LSTM. World Electric Vehicle Journal. 2021; 12(2):57. https://doi.org/10.3390/wevj12020057
Chicago/Turabian StyleCai, Yongping, Yuefeng Cen, Gang Cen, Xiaomin Yao, Cheng Zhao, and Yulai Zhang. 2021. "Temperature Prediction of PMSMs Using Pseudo-Siamese Nested LSTM" World Electric Vehicle Journal 12, no. 2: 57. https://doi.org/10.3390/wevj12020057
APA StyleCai, Y., Cen, Y., Cen, G., Yao, X., Zhao, C., & Zhang, Y. (2021). Temperature Prediction of PMSMs Using Pseudo-Siamese Nested LSTM. World Electric Vehicle Journal, 12(2), 57. https://doi.org/10.3390/wevj12020057






