Integrated Charger-Inverter for High-Performance Electric Motorcycles
Abstract
1. Introduction
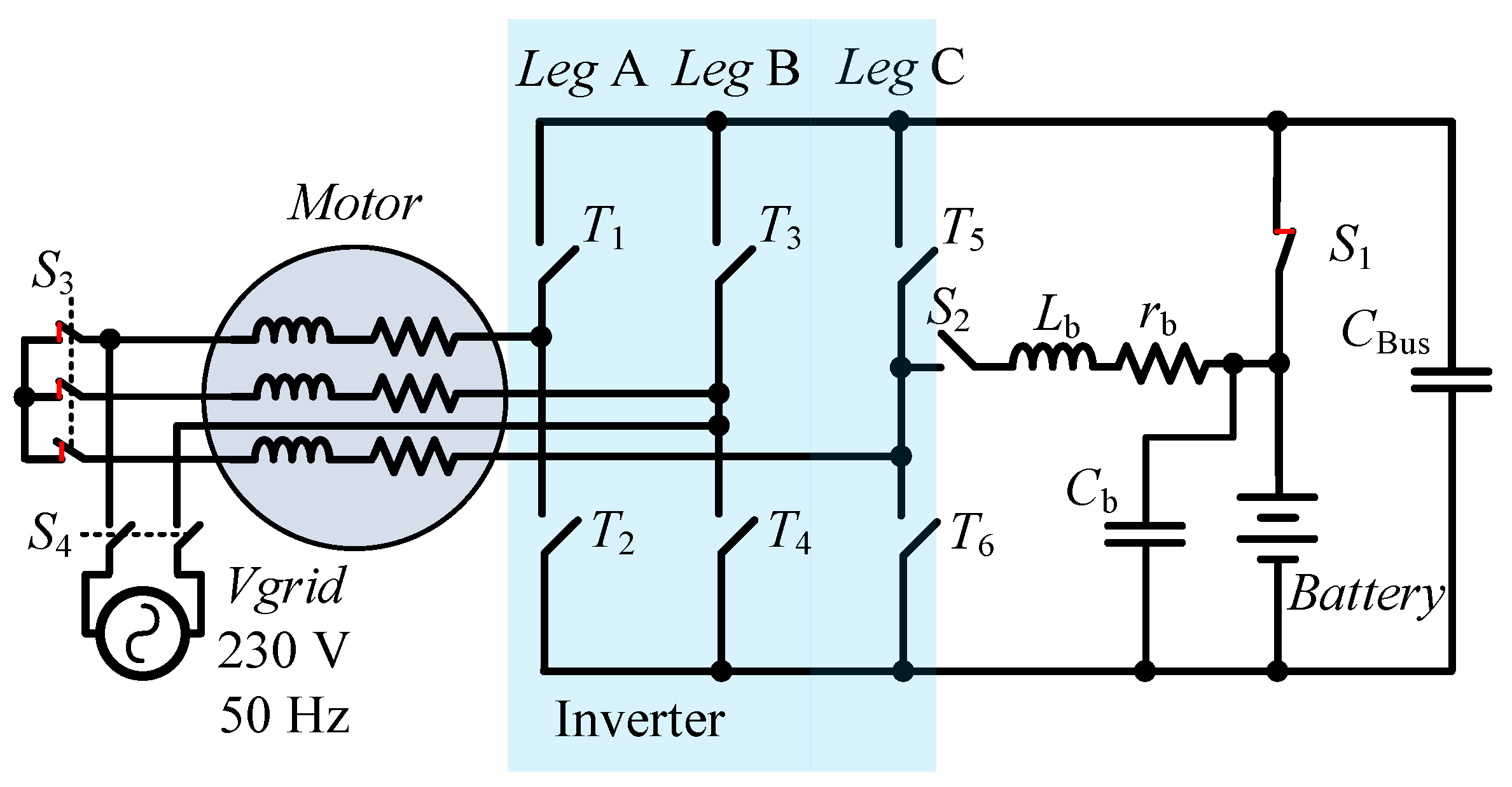
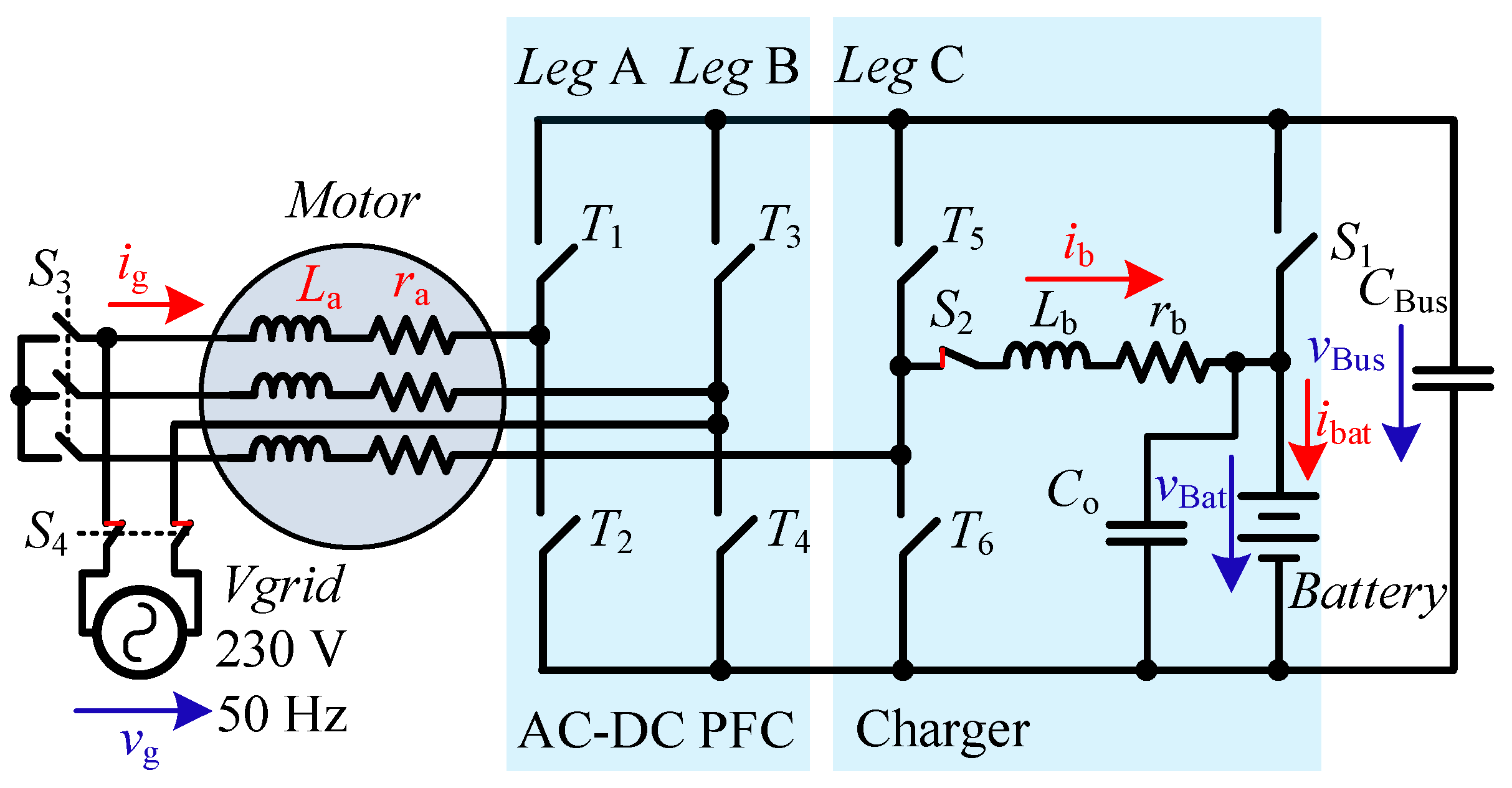
2. Integrated Charger-Inverter
2.1. Topology
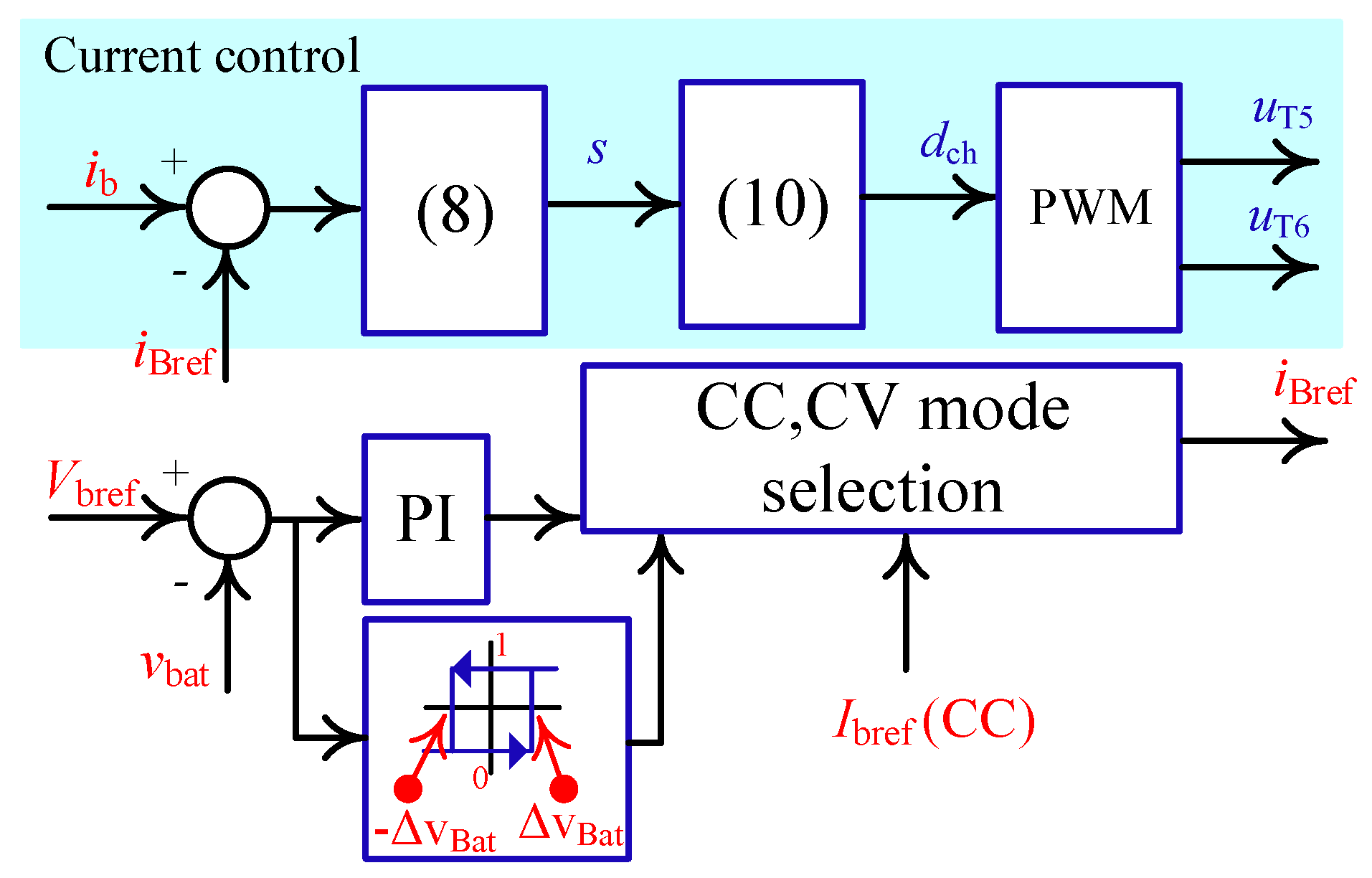
2.2. Control Algorithm
3. Component Sizing
3.1. Inductors
3.2. Capacitors
3.3. Specific Power Comparison
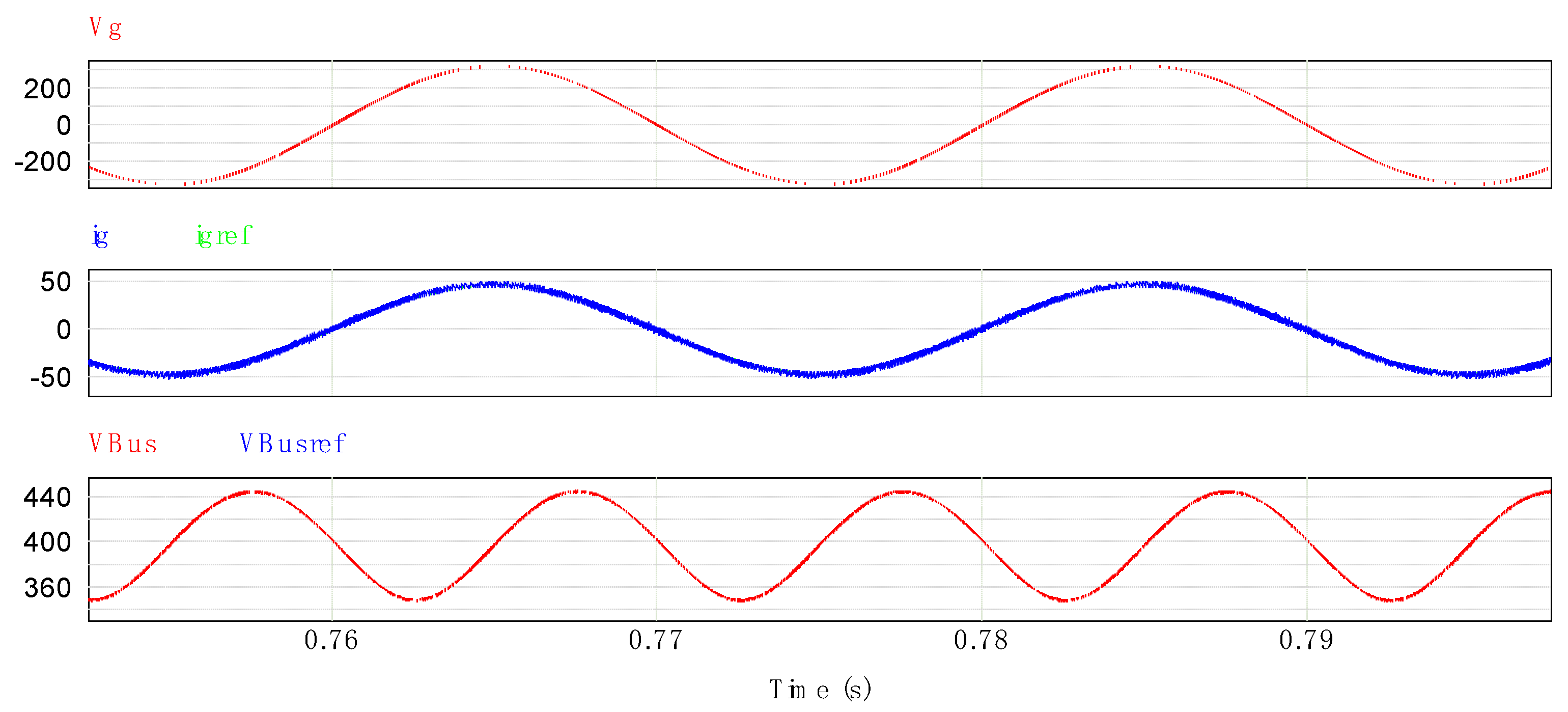
4. Simulation Results
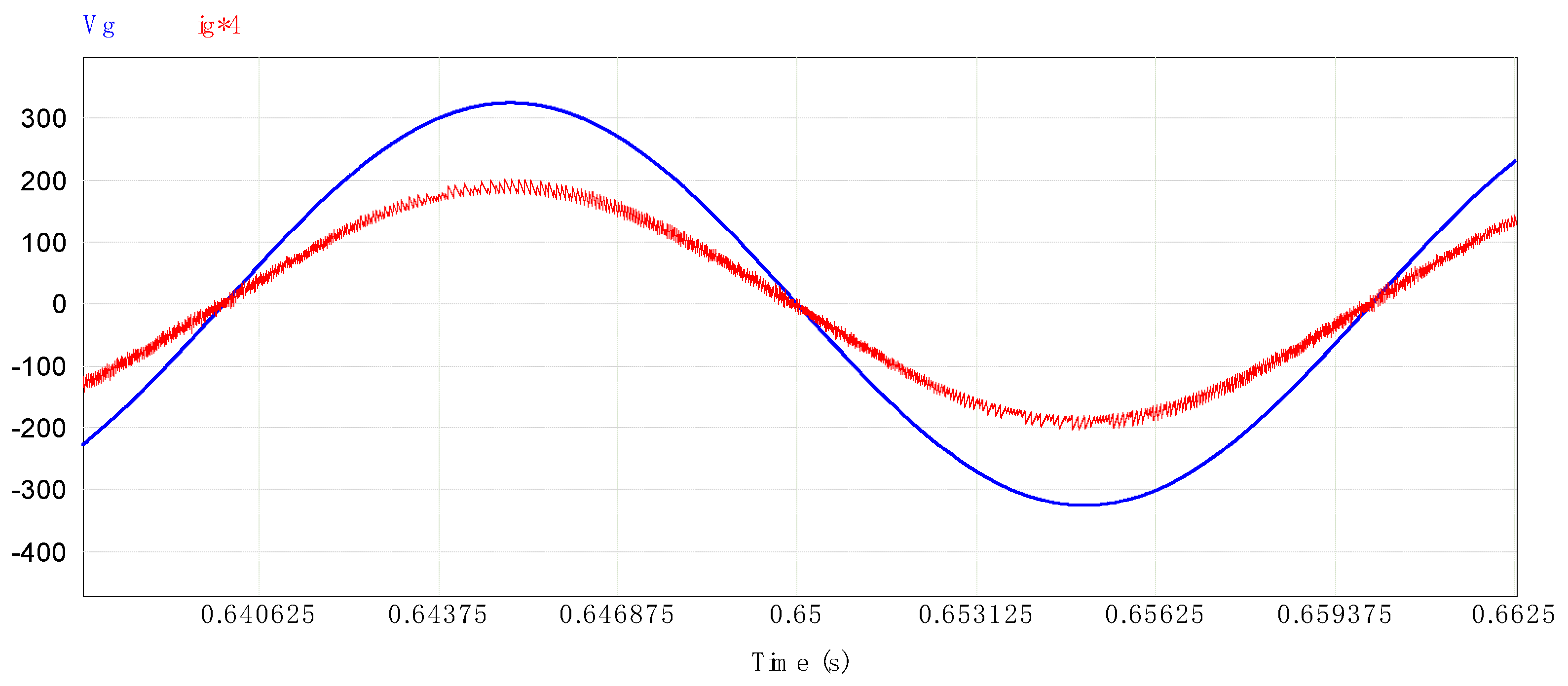
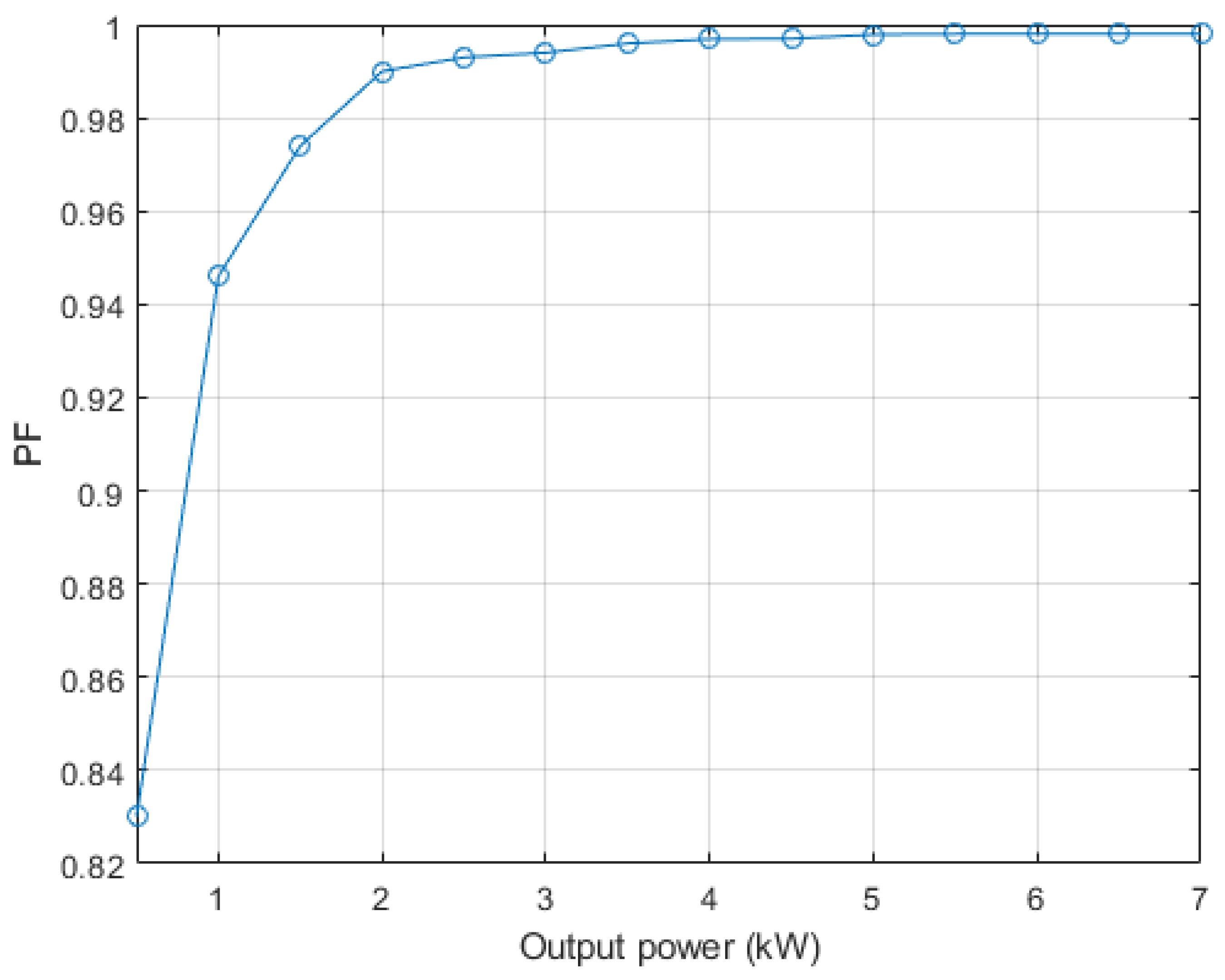
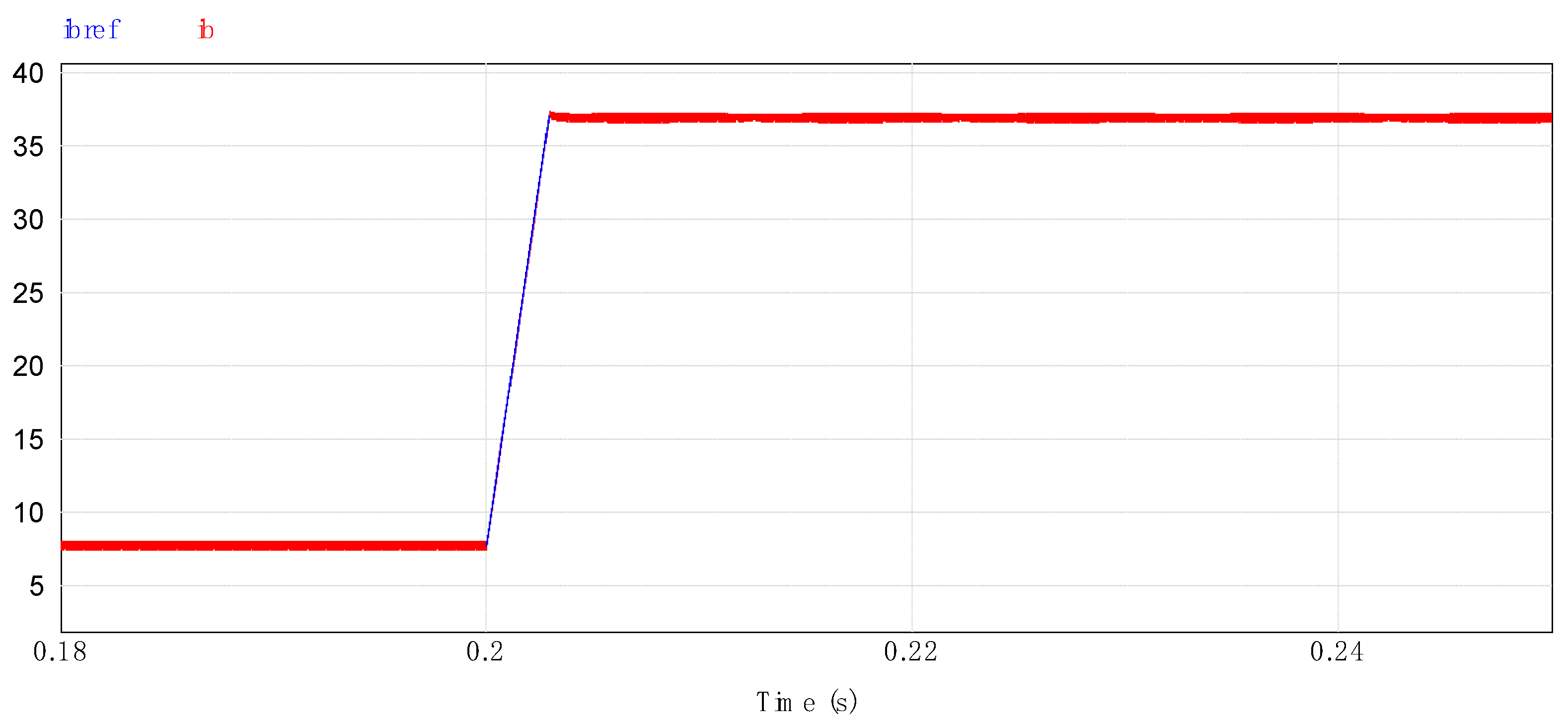
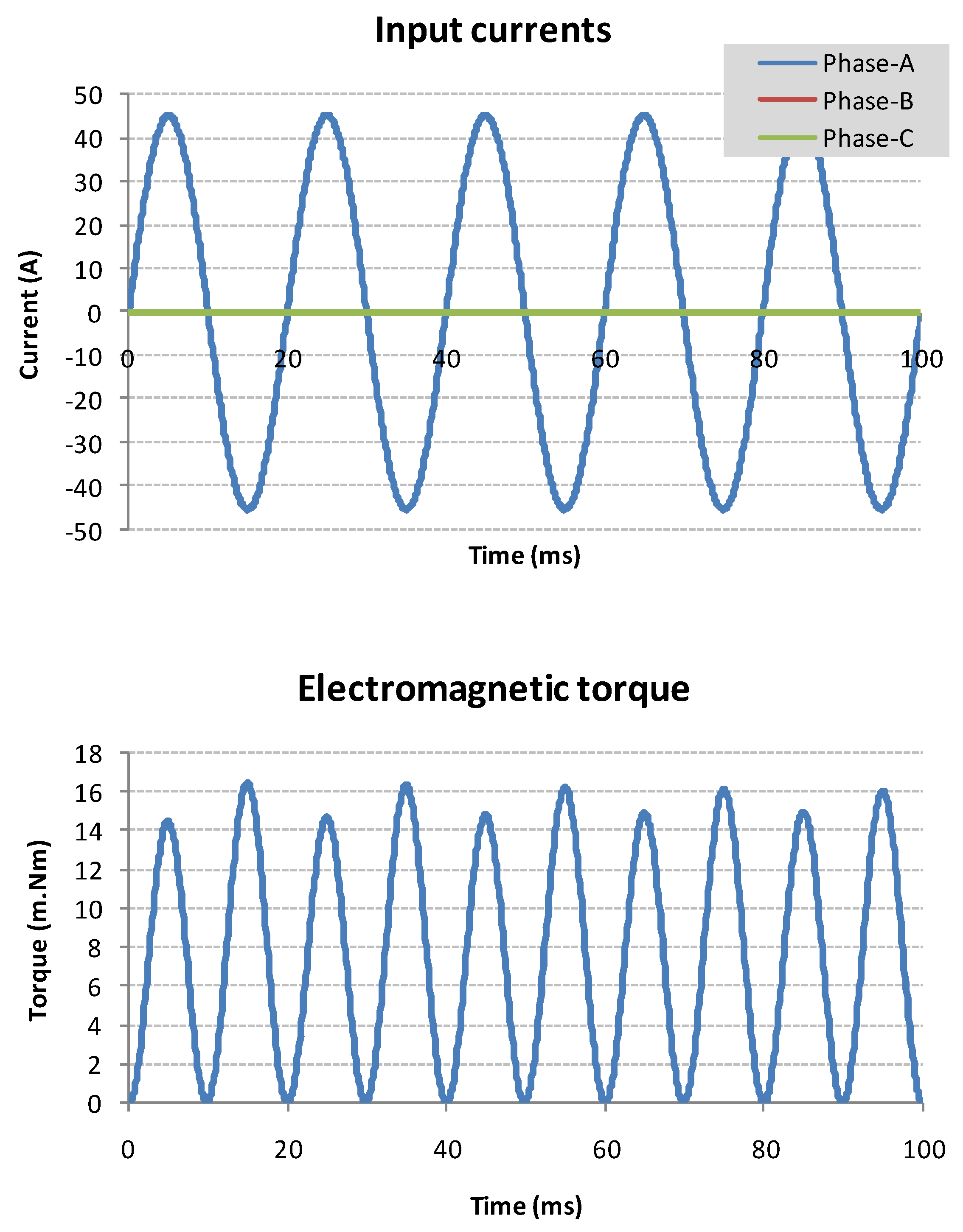
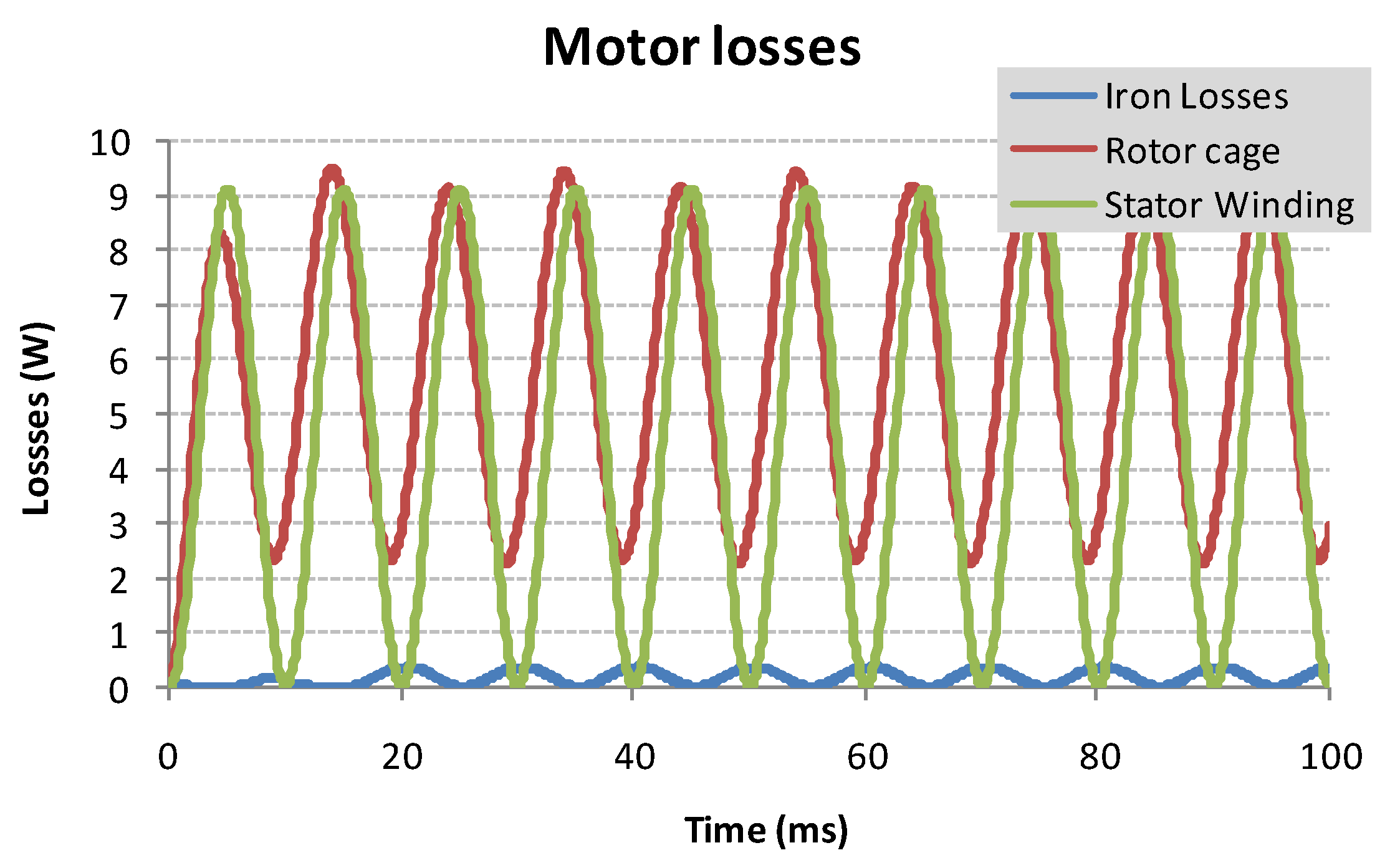
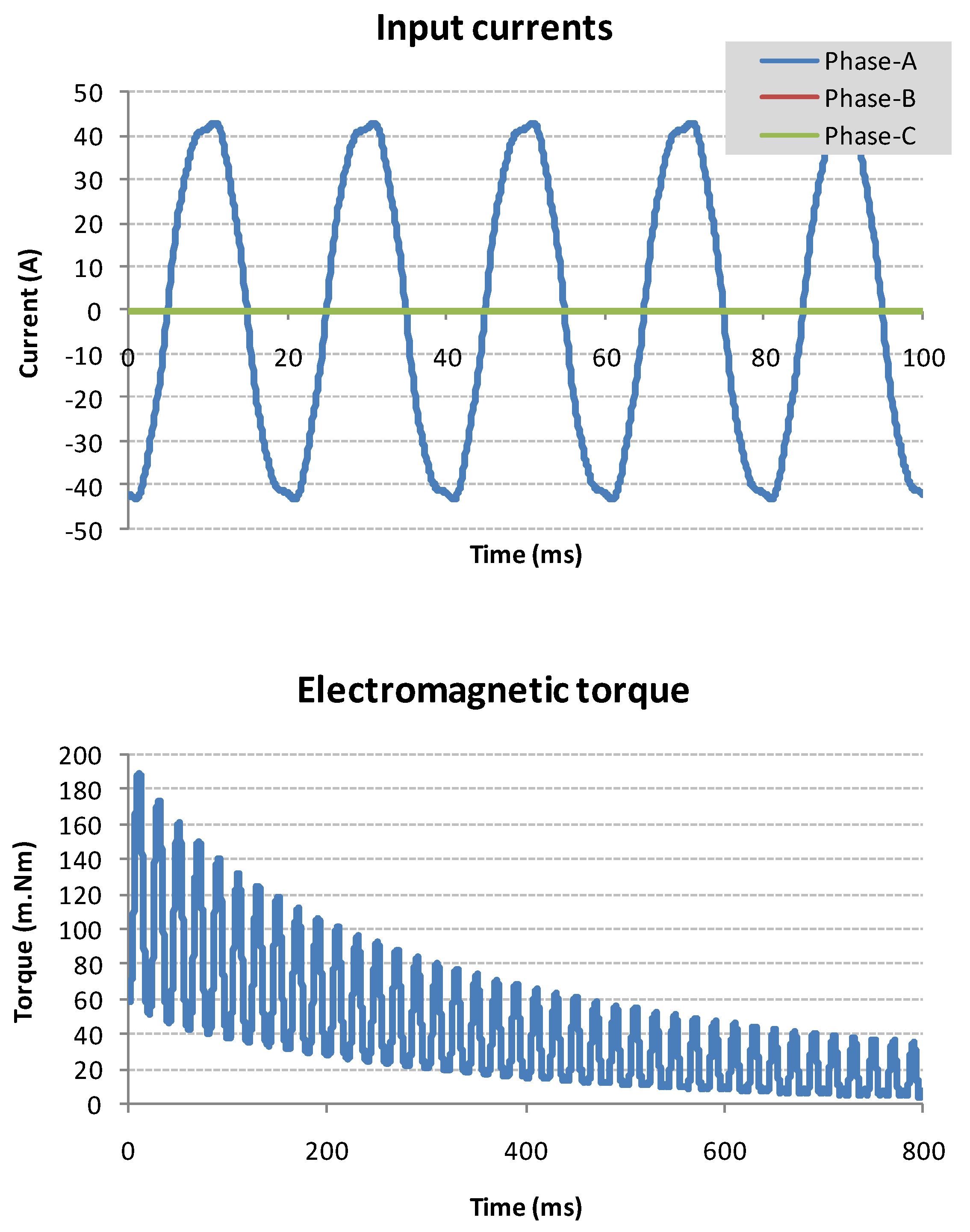
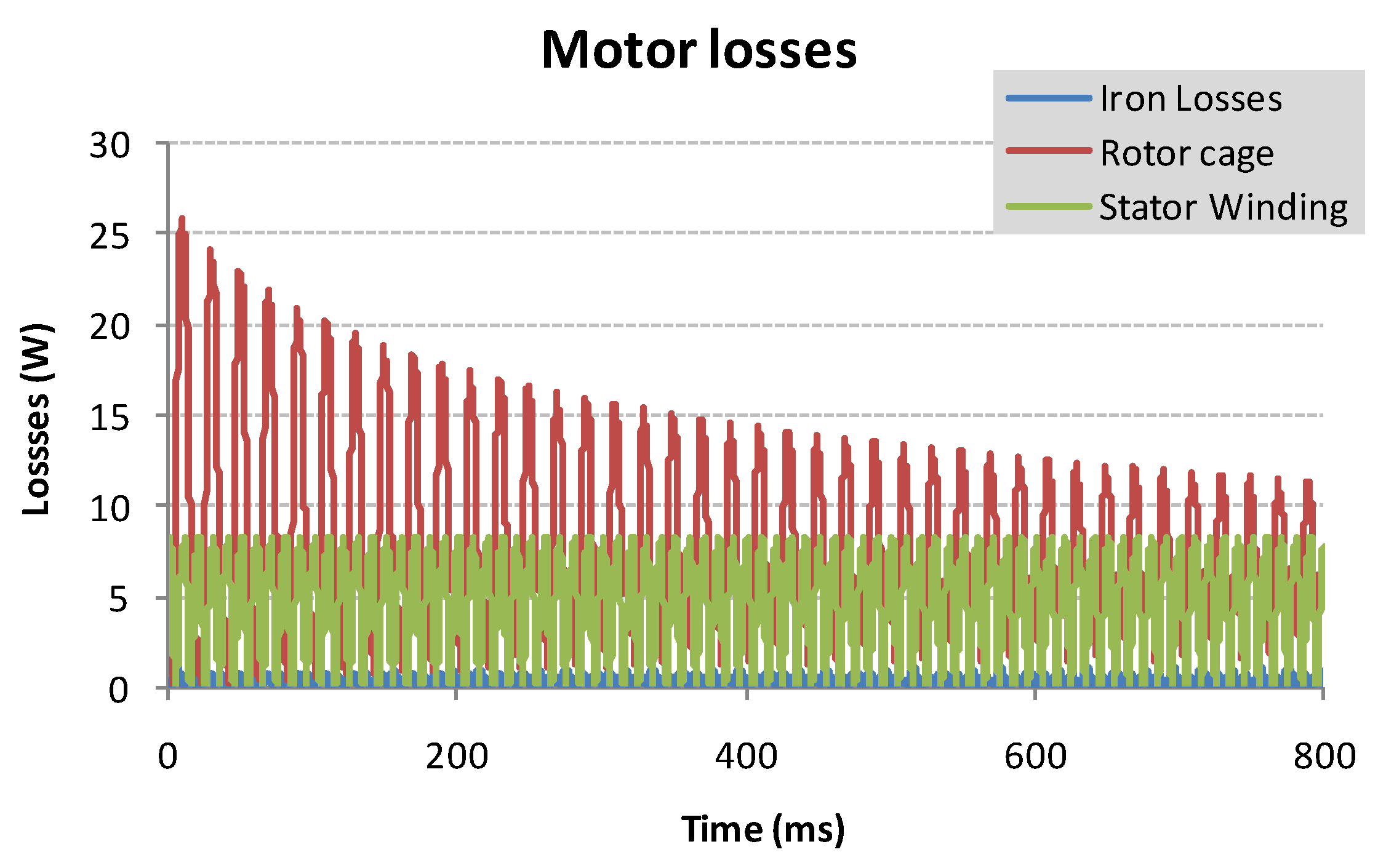
4.1. Charge Simulations
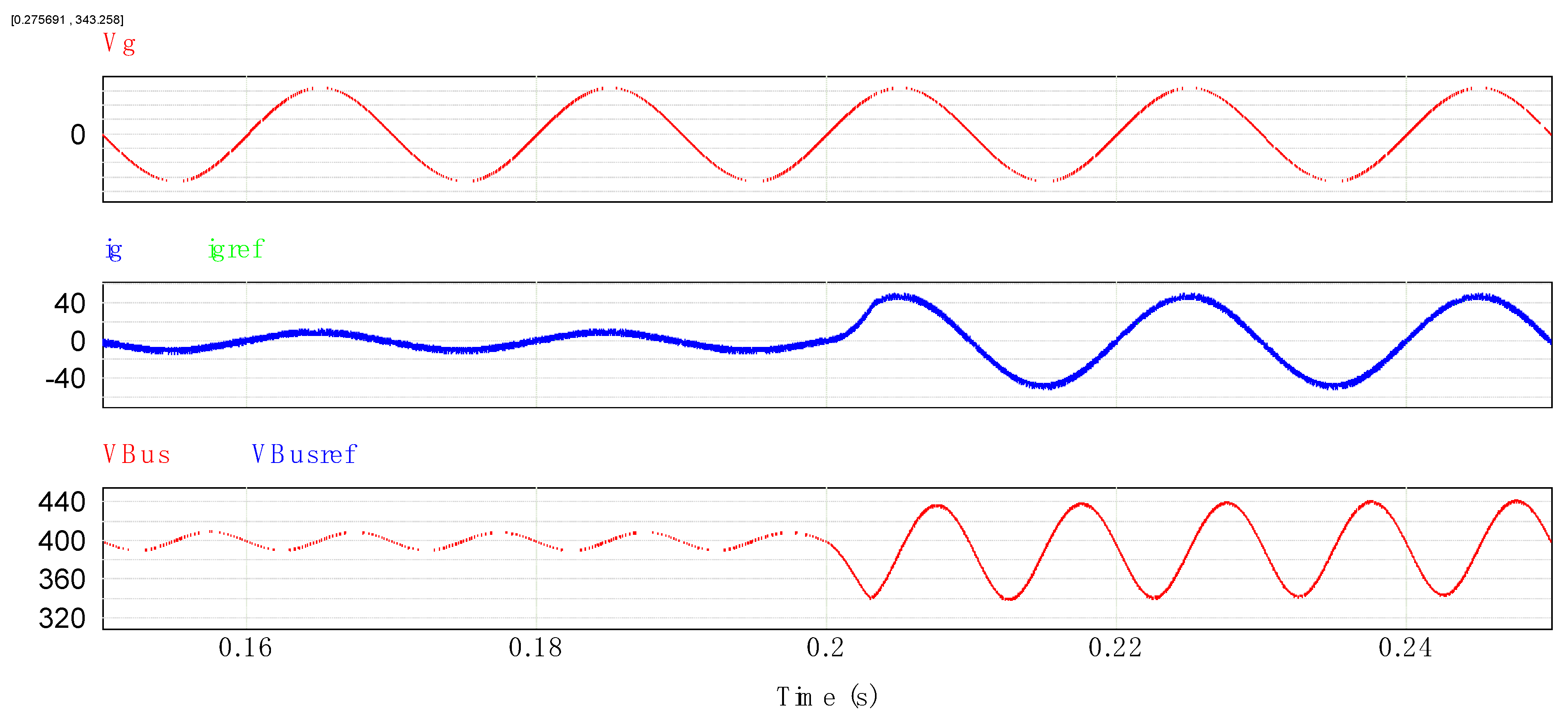
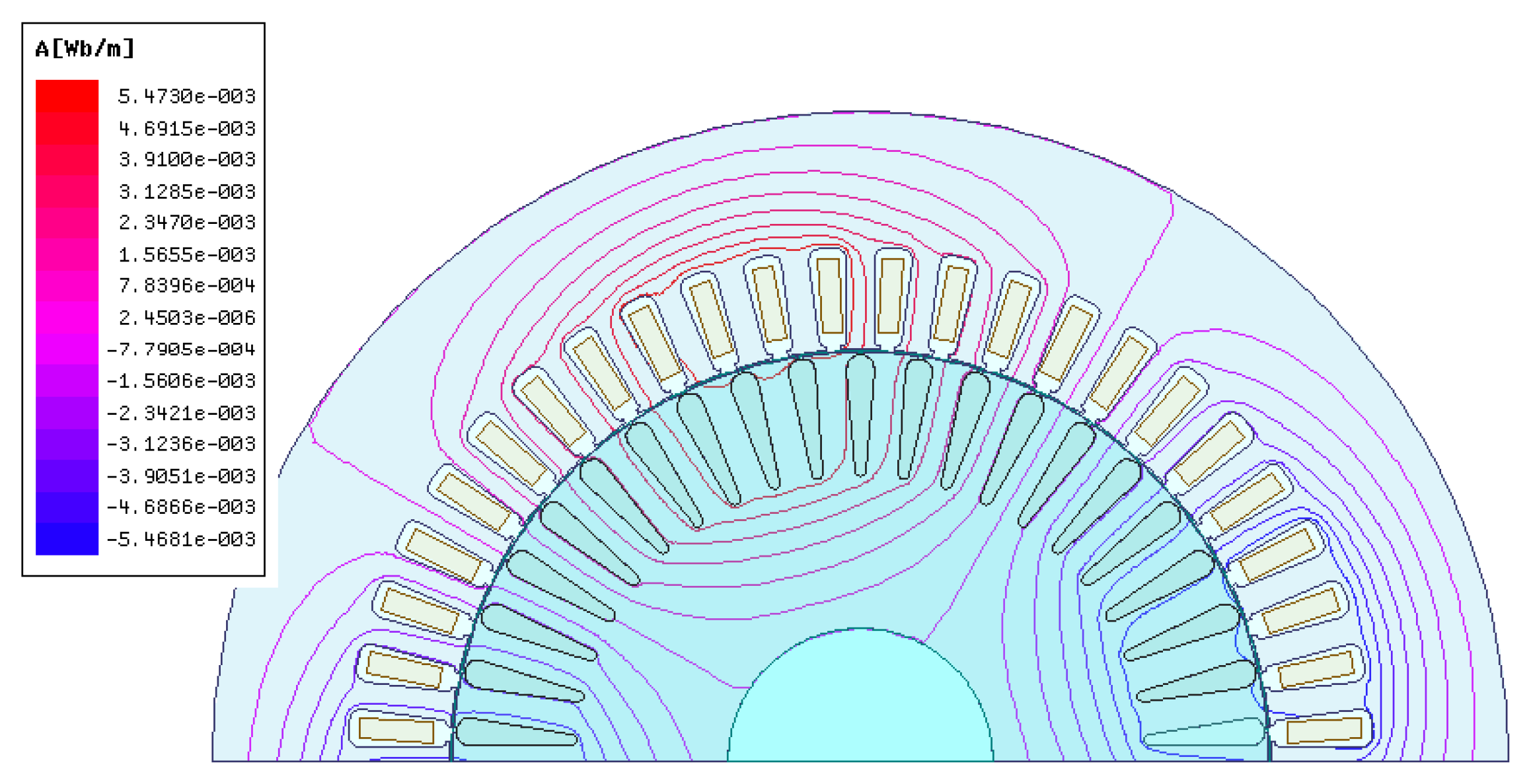
4.2. Electromagnetic Torque
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Drobnic, K.; Grandi, G.; Hammami, M.; Mandrioli, R.; Ricco, M.; Viatkin, A.; Vujacic, M. An Output Ripple-Free Fast Charger for Electric Vehicles Based on Grid-Tied Modular Three-Phase Interleaved Converters. IEEE Trans. Ind. Appl. 2019, 55, 6102–6114. [Google Scholar] [CrossRef]
- Patil, D.; Agarwal, V. Compact Onboard Single-Phase EV Battery Charger with Novel Low-Frequency Ripple Compensator and Optimum Filter Design. IEEE Trans. Ind. Appl. 2016, 65, 1948–1956. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Y.; Khaligh, A. A Three-Phase Integrated Onboard Charger for Plug-In Electric Vehicles. IEEE Trans. Power Electron. 2018, 33, 4716–4725. [Google Scholar] [CrossRef]
- Hatti, N.; Nuilers, S.; Chayopitak, N.; Somsiri, P. An integrated battery charger configuration for SRM drive in electric motorcycles. IEEJ Trans. Electr. Electron. Eng. 2018, 13, 295–302. [Google Scholar] [CrossRef]
- Subotic, I.; Bodo, N.; Levi, E. Single-Phase On-Board Integrated Battery Chargers for EVs Based on Multiphase Machines. IEEE Trans. Power Electron. 2016, 31, 6511–6523. [Google Scholar] [CrossRef]
- Shi, C.; Tang, Y.; Khaligh, A. A Single-Phase Integrated Onboard Battery Charger Using Propulsion System for Plug-in Electric Vehicles. IEEE Trans. Veh. Technol. 2017, 66, 10899–10910. [Google Scholar] [CrossRef]
- Cheng, H.; Wang, Z.; Yang, S.; Huang, J.; Ge, X. An Integrated SRM Powertrain Topology for Plug-In Hybrid Electric Vehicles with Multiple Driving and Onboard Charging Capabilities. IEEE Trans. Transp. Electrif. 2020, 6, 578–591. [Google Scholar] [CrossRef]
- Bodo, N.; Levi, E.; Subotic, I.; Espina, J.; Empringham, L.; Johnson, C.M. Efficiency Evaluation of Fully Integrated On-Board EV Battery Chargers with Nine-Phase Machines. IEEE Trans. Energy Convers. 2017, 32, 257–266. [Google Scholar] [CrossRef]
- Metwly, M.Y.; Abdel-Majeed, M.S.; Abdel-Khalik, A.S.; Hamdy, R.A.; Hamad, M.S.; Ahmed, S. A Review of Integrated On-Board EV Battery Chargers: Advanced Topologies, Recent Developments and Optimal Selection of FSCW Slot/Pole Combination. IEEE Access 2020, 8, 85216–85242. [Google Scholar] [CrossRef]
- Kataoka, R.; Shichi, A.; Yamada, H.; Iwafune, Y.; Ogimoto, K. Comparison of the Economic and Environmental Performance of V2H and Residential Stationary Battery: Development of a Multi-Objective Optimization Method for Homes of EV Owners. World Electr. Veh. J. 2019, 10, 78. [Google Scholar] [CrossRef]
- Subotic, I.; Jones, M.; Levi, E. A fast on-board integrated battery charger for four-motor EVs. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 2066–2072. [Google Scholar]
- Thimmesch, D. An SCR inverter with an integral battery charger for electric vehicles. IEEE Trans. Ind. Appl. 1985, IA-21, 1023–1029. [Google Scholar] [CrossRef]
- Tang, L.; Su, G.-J. Control scheme optimization for a low-cost, digitally-controlled charger for plug-in hybrid electric vehicles. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 12–16 September 2010; pp. 3604–3610. [Google Scholar]
- Matsuhashi, D.; Matsuo, K.; Okitsu, T.; Ashikaga, T.; Mizuno, T. Comparison study of various motors for EVs and the potentiality of a ferrite magnet motor. IEEJ J. Ind. Appl. 2015, 4, 173–179. [Google Scholar] [CrossRef][Green Version]
- Tuan, V.T.; Kreuawan, S.; Somsiri, P.; Tungpimolrut, K.; Huy, P.N. Switched Reluctance Motor and Induction Machine for E-Scooter Based on Driving Cycles Design Comparisons. IEEJ Trans. Electr. Electron. Eng. 2020, 15, 931–938. [Google Scholar] [CrossRef]
- Vosswinkel, M.; Lohner, A.; Platte, V.; Hirche, T. Design, Production, and Verification of a Switched-Reluctance Wheel Hub Drive Train for Battery Electric Vehicles. World Electr. Veh. J. 2019, 10, 82. [Google Scholar] [CrossRef]
- Na, T.; Zhang, Q.; Tang, J.; Wang, J. Active power filter for single-phase Quasi-Z-source integrated on-board charger. CPSS Trans. Power Electron. Appl. 2018, 3, 197–201. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, C.; Yu, F. An Effective Charging-Torque Elimination Method for Six-Phase Integrated On-Board EV Chargers. IEEE Trans. Power Electron. 2020, 35, 2776–2786. [Google Scholar] [CrossRef]
- Gavagsaz-Ghoachani, R.; Saublet, L.; Phattanasak, M.; Martin, J.; Nahid-mobarakeh, B.; Pierfederici, S. Active stabilisation design of DC–DC converters with constant power load using a sampled discrete-time model: Stability analysis and experimental verification. IET Power Electron. 2018, 11, 1519–1528. [Google Scholar] [CrossRef]
- Gavagsaz-Ghoachani, R.; Phattanasak, M.; Martin, J.; Nahid-Mobarakeh, B.; Pierfederici, S. A Fixed-Frequency Optimization of PWM Current Controller—Modeling and Design of Control Parameters. IEEE Trans. Transp. Electrif. 2018, 4, 671–683. [Google Scholar] [CrossRef]
- Das, P.; Pahlevaninezhad, M.; Moschopoulos, G. Analysis and Design of a New AC–DC Single-Stage Full-Bridge PWM Converter with Two Controllers. IEEE Trans. Ind. Electron. 2013, 60, 4930–4946. [Google Scholar] [CrossRef]
- Ferrieux, J.P.; Forest, F. Alimentations à Découpage Convertisseurs à Résonance, 3rd ed.; Dunod: Malakoff, France, 2006. [Google Scholar]
- Nussbaumer, T.; Raggl, K.; Kolar, J.W. Design Guidelines for Interleaved Single-Phase Boost PFC Circuits. IEEE Trans. Ind. Electron. 2009, 56, 2559–2573. [Google Scholar] [CrossRef]
- Shenai, K. WBG Power Converters for Hybrid & EV Applications. Auto Tech. Rev. 2016, 5, 42–47. [Google Scholar]
- Robert, E.; Dragan, M.; Khurram, A.; David, J.; Daniel, F.; Hyeokjin, K.; Usama, A.; Jianglin, Z.; Kraig, O.; Brandon, P.; et al. A Disruptive Approach to Electric Vehicle Power Electronics Final Report; Univ. of Colorado: Boulder, CO, USA, 2017. [Google Scholar]


| Manufacturer/Reference | Specific Power (kW/kg) | Power Density (kW/L) | Cost Per kW (USD/kW) |
|---|---|---|---|
| 2012 Nissan Leaf 6.6 kW OBC [24] | 0.41 | 0.66 | N/A |
| Tier one OBC 3.3 kW [24] | N/A | N/A | 83 |
| Eton (1) | N/A | 2 | N/A |
| Ovartech 6.6 kW Water-cool (2) | 1.1 | 0.61 | N/A |
| Manufacturer/Reference | Weight (kg) | Volume (L) | Cost (USD) |
|---|---|---|---|
| S2 (40 A, 450 V DC contactor) (3) | 0.15 | 0.11 | 30 |
| S3 (10 A, 250 Vac 3-pole relay) (4) | 0.03 | 0.02 | 10 |
| Lb (estimated) | 1 | 0.5 | 30 |
| Co (3 uF, 450 V) (5) | 0.0085 | 0.0074 | 5 |
| Total | 1.19 | 0.64 | 75 |
| Manufacturer/Reference | Specific Power (kW/kg) | Power Density (kW/L) | Cost Per kW (USD/kW) |
|---|---|---|---|
| Proposed ICI 7.7 kW | 5.88 | 10.93 | 10.71 |
| ICI 6.6 kW from [25] | 4 | N/A | N/A |
| Parameters (Unit) | |
|---|---|
| Grid voltage, | Vrms |
| Grid frequency, | 50 Hz |
| Switching frequency, | 20 kHz |
| Output voltage, | 400 V |
| Maximum battery power, | 7 kW |
| PFC inductor (phase a winding) | 1.3 mH, 0.015 Ω |
| Charger inductor (additional inductor) | 10 mH, 0.015 Ω |
| Capacitor, | 640 μF |
| Capacitor, | 2.2 μF |
| Battery full voltage of 48 cells | 201.6 V |
| Parameters (Unit) | |
|---|---|
| PFC | |
| - , | 0.11, 0.5 ms |
| - | 0.707, rad/s |
| - , | 212.10, 22,500 |
| Charger | |
| - | rad/s |
| - , | 0.01, 0.1 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tuan, V.T.; Phattanasak, M.; Kreuawan, S. Integrated Charger-Inverter for High-Performance Electric Motorcycles. World Electr. Veh. J. 2021, 12, 19. https://doi.org/10.3390/wevj12010019
Tuan VT, Phattanasak M, Kreuawan S. Integrated Charger-Inverter for High-Performance Electric Motorcycles. World Electric Vehicle Journal. 2021; 12(1):19. https://doi.org/10.3390/wevj12010019
Chicago/Turabian StyleTuan, Vu Tran, Matheepot Phattanasak, and Sangkla Kreuawan. 2021. "Integrated Charger-Inverter for High-Performance Electric Motorcycles" World Electric Vehicle Journal 12, no. 1: 19. https://doi.org/10.3390/wevj12010019
APA StyleTuan, V. T., Phattanasak, M., & Kreuawan, S. (2021). Integrated Charger-Inverter for High-Performance Electric Motorcycles. World Electric Vehicle Journal, 12(1), 19. https://doi.org/10.3390/wevj12010019





