Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics
Abstract
1. Introduction
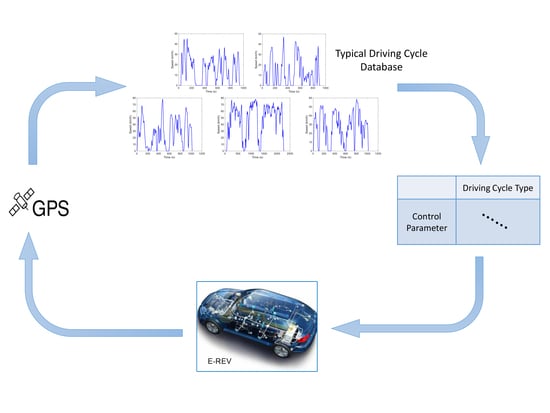
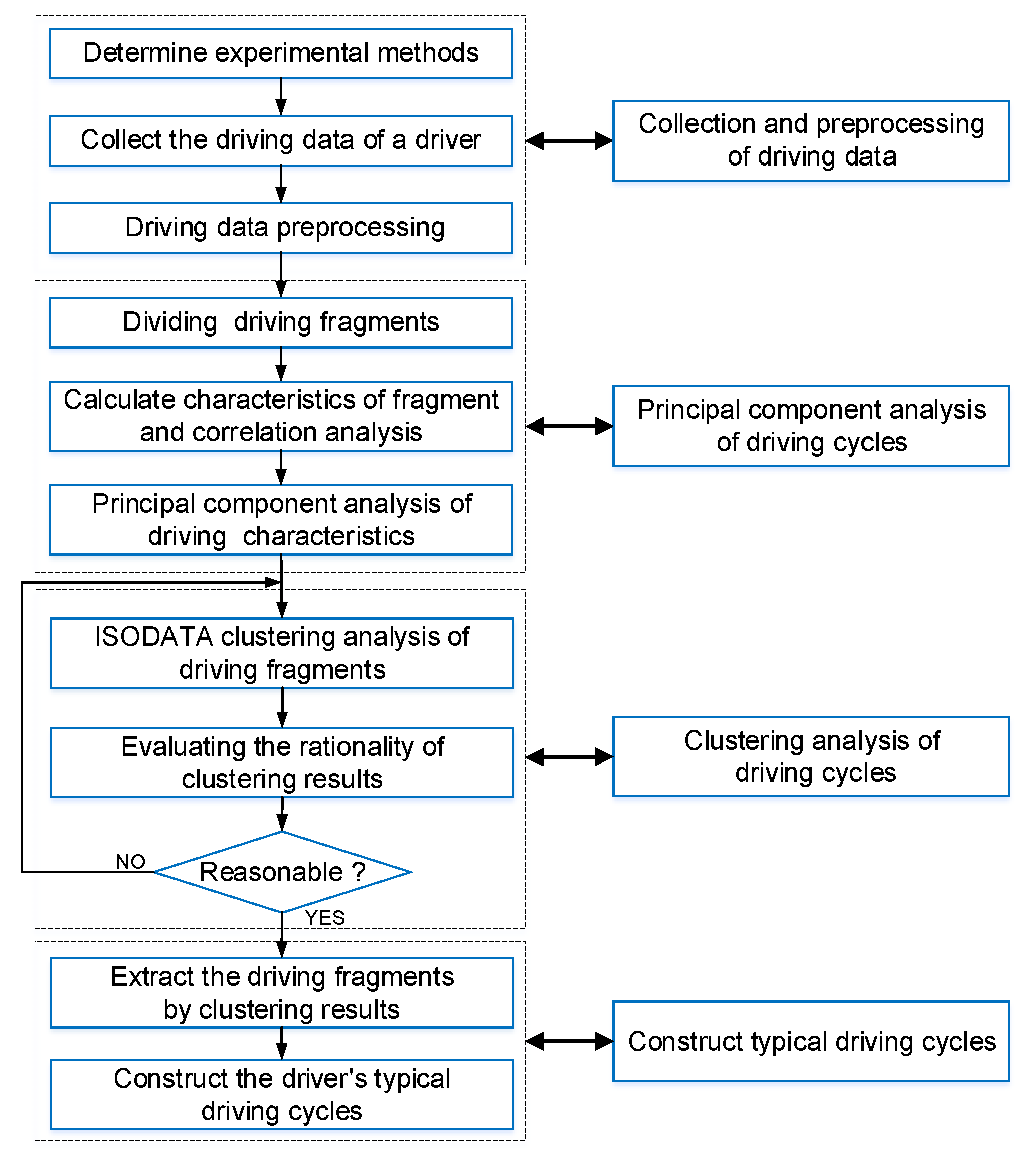
2. Driving Cycles Clustering and Recognition
- Collection and preprocessing driver’s driving data.
- Selection and principal component analysis of driving characteristics.
- Cluster analysis and verification of driving characteristics.
- Construction typical driving cycles for the driver.
2.1. Driving Data Preprocessing
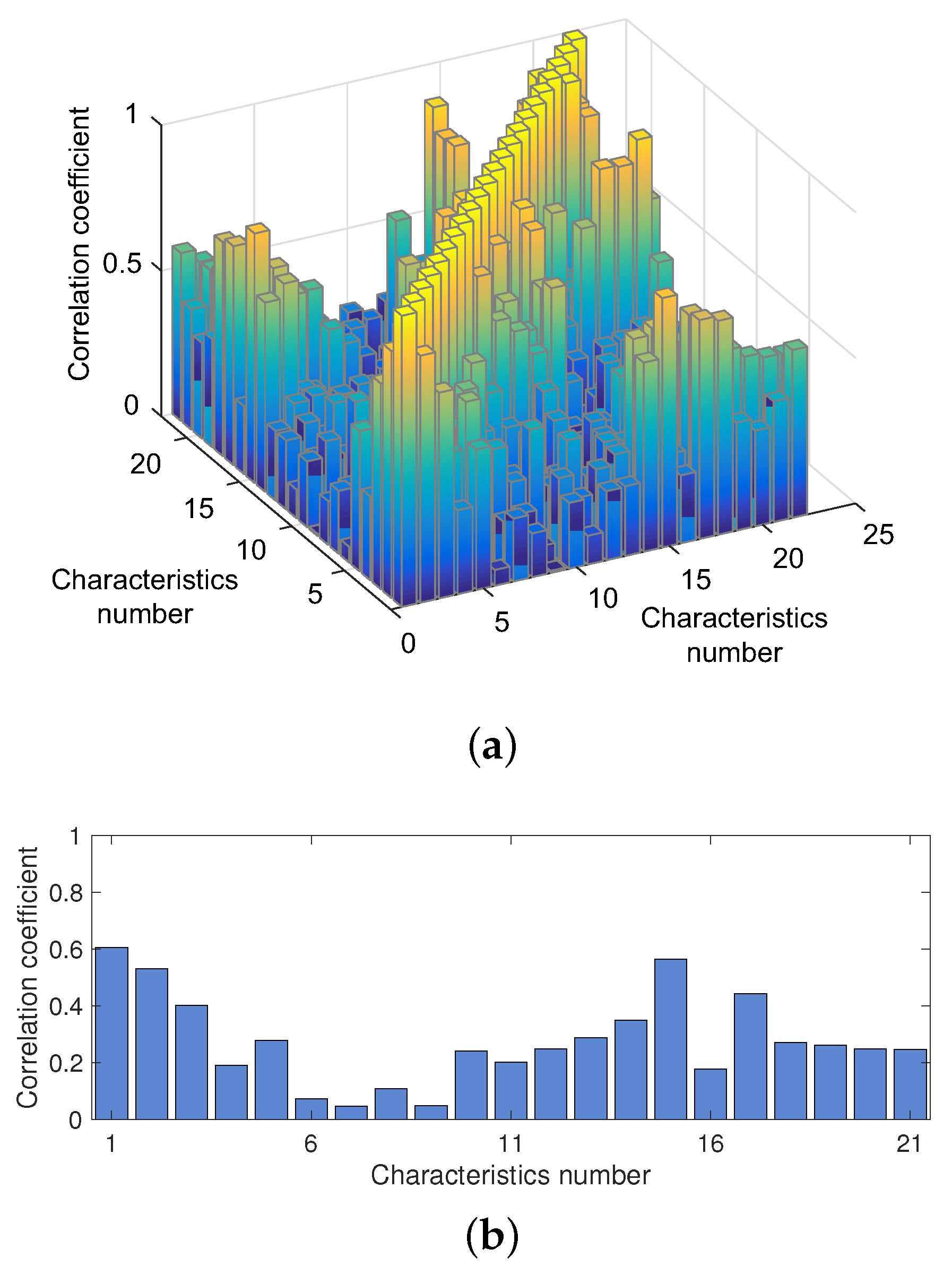
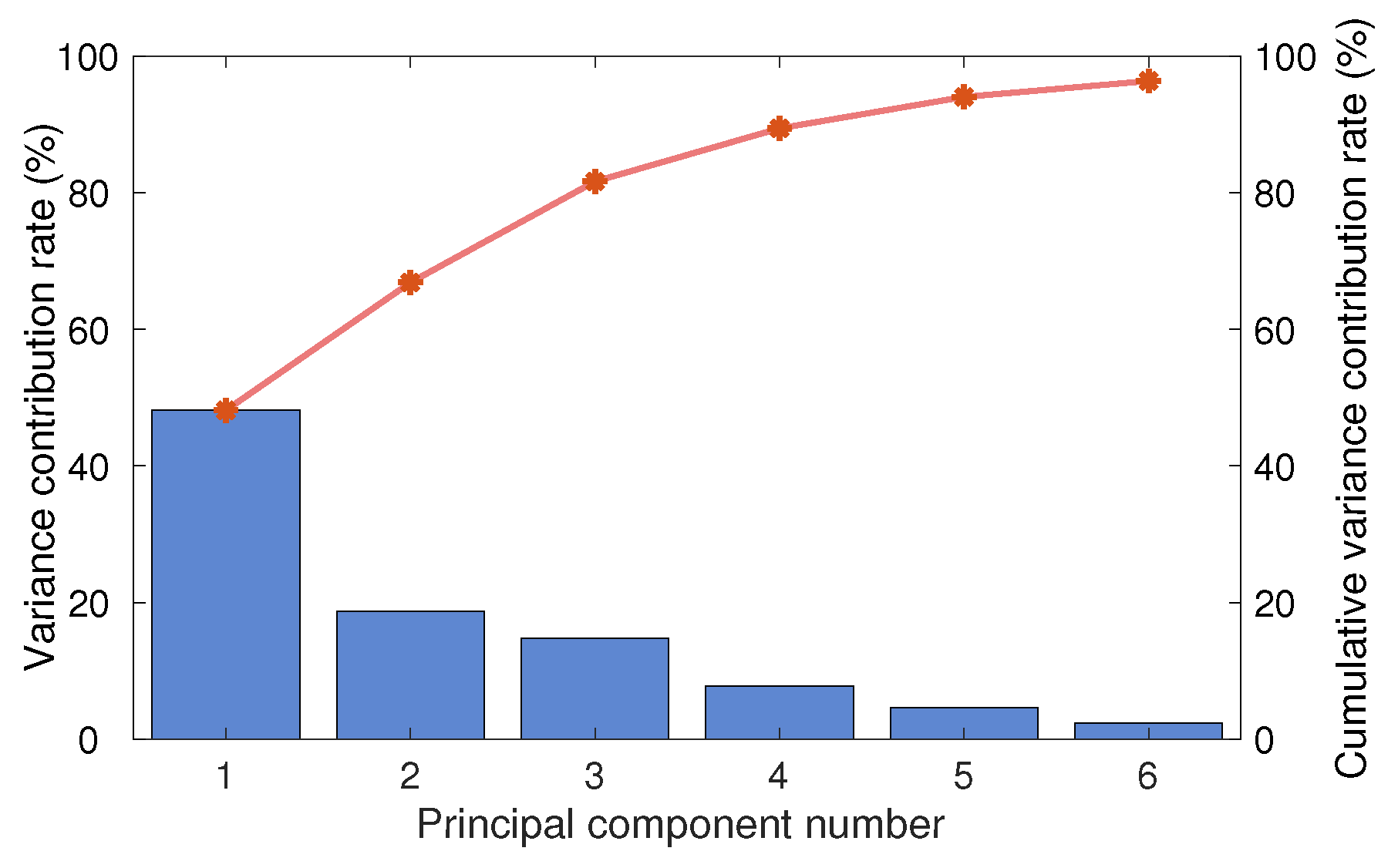
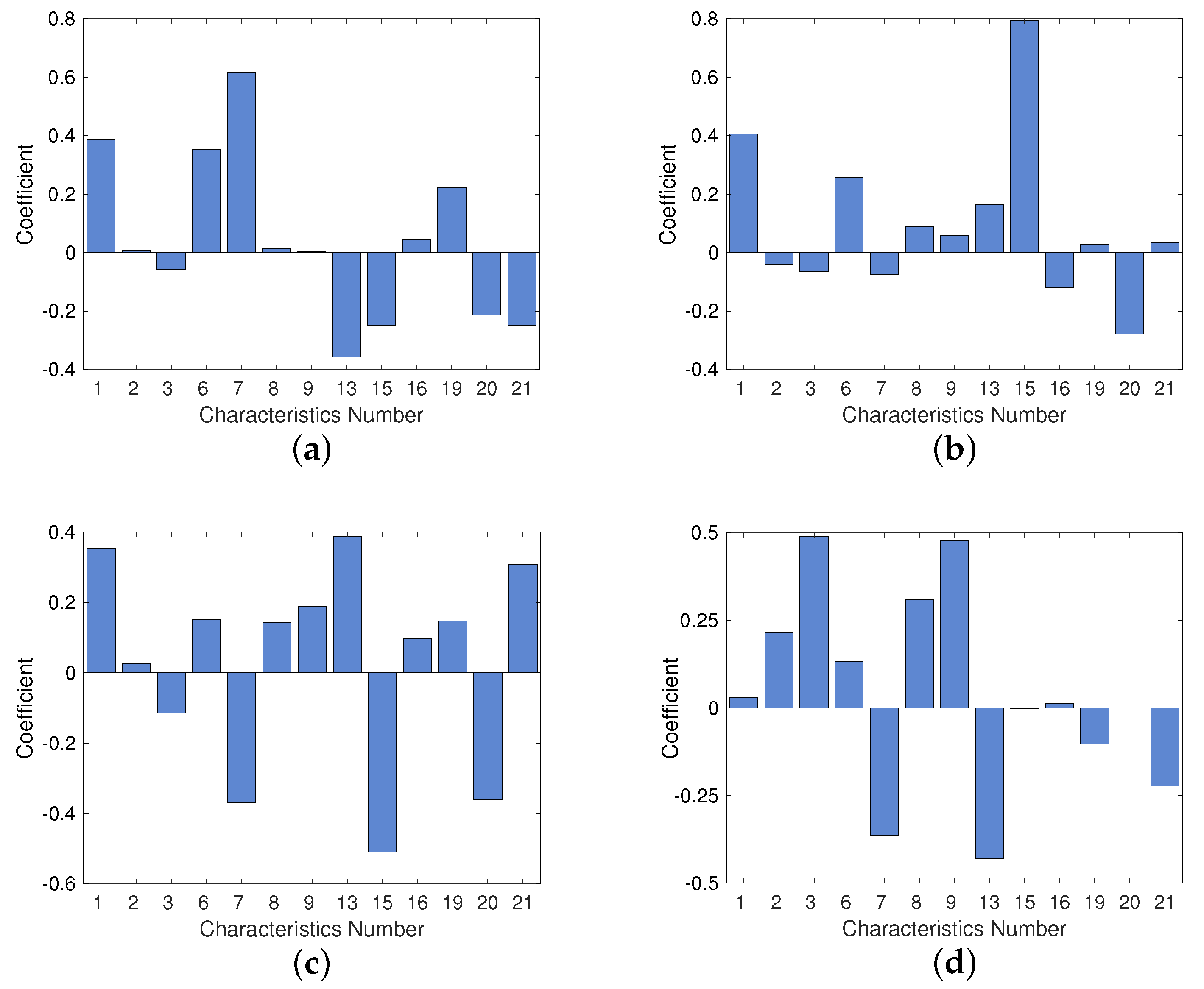
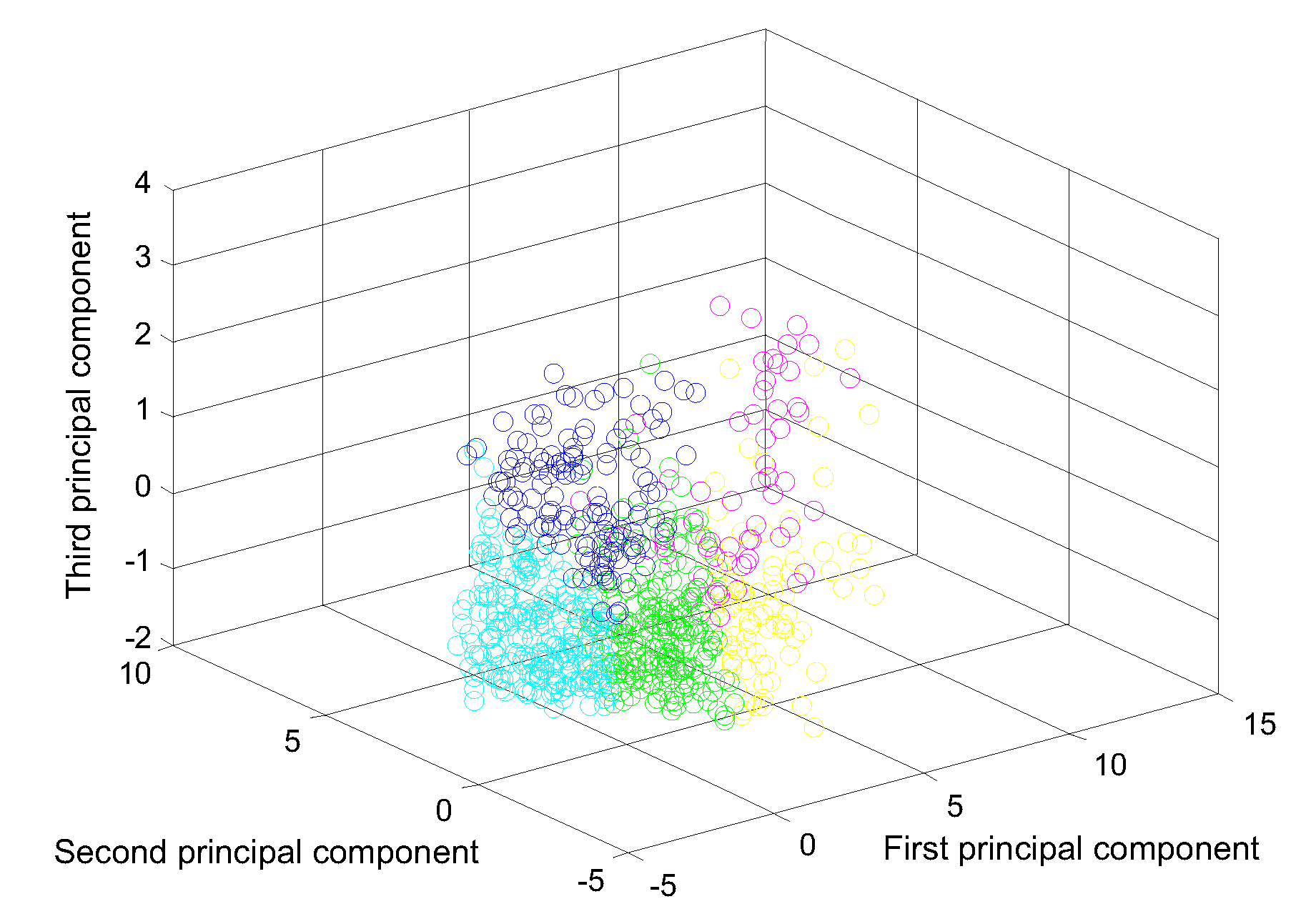
2.2. Characteristics Selection and Principal Component Analysis
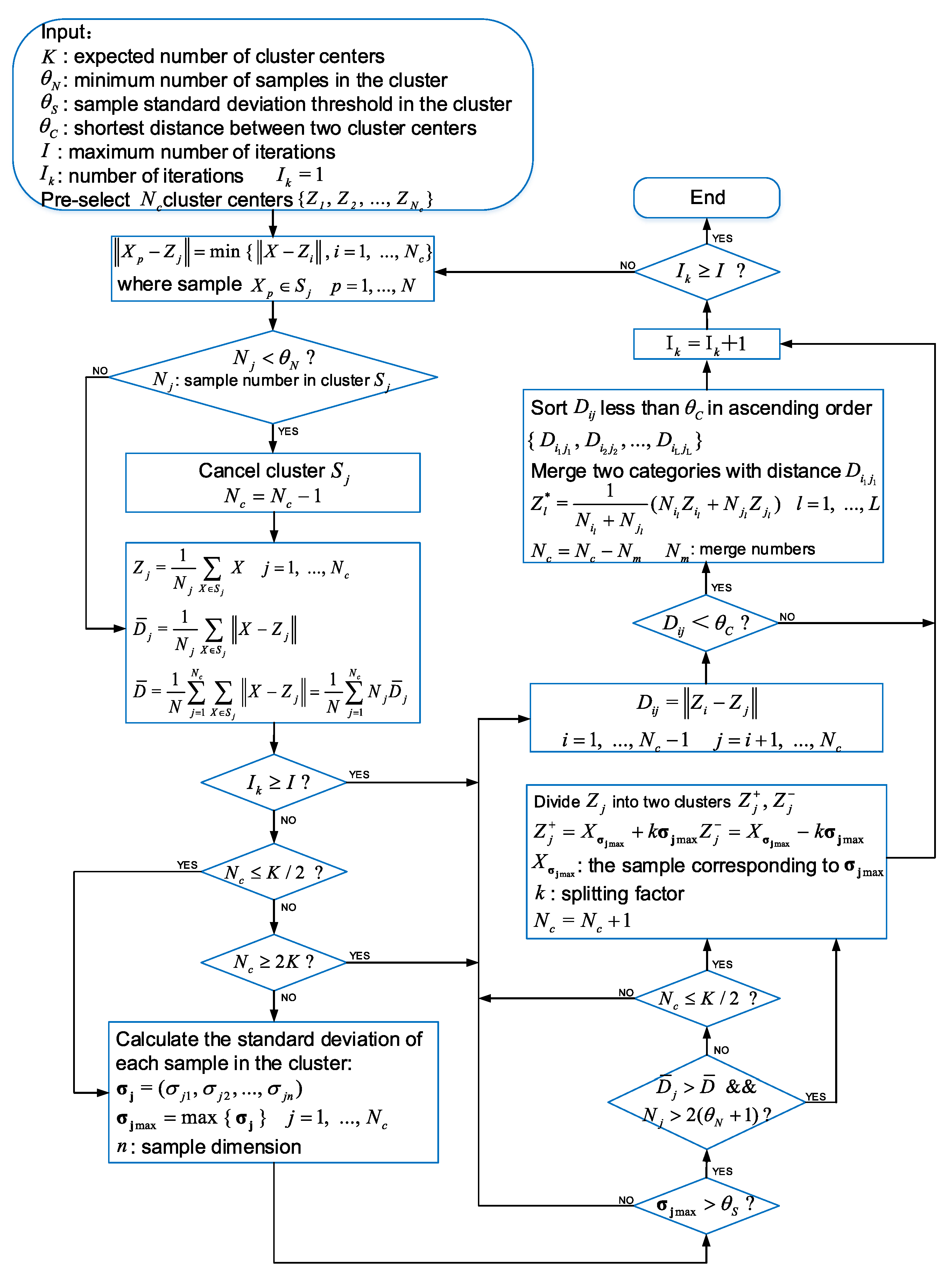
2.3. Cluster Analysis of Driving Cycle
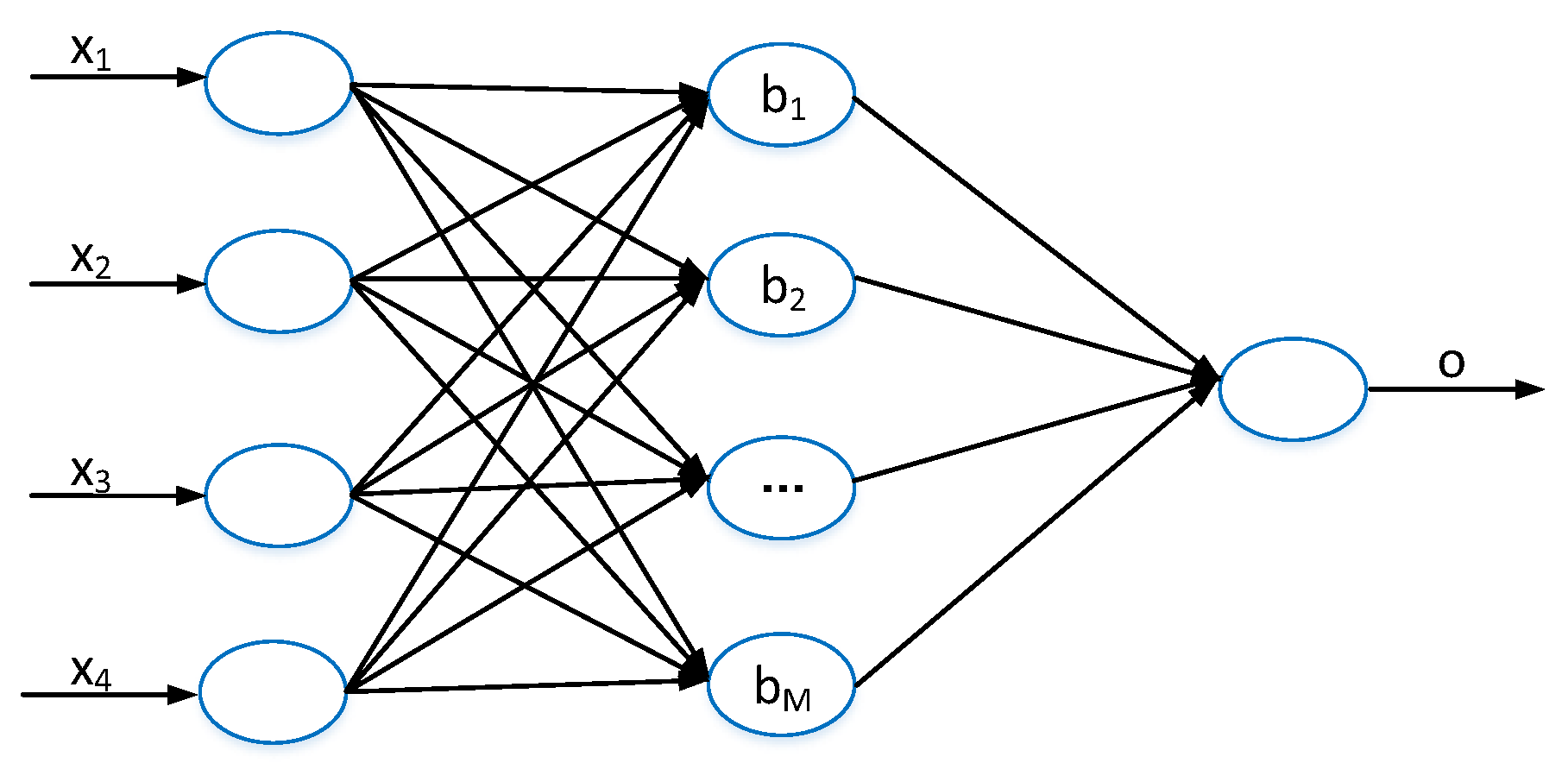
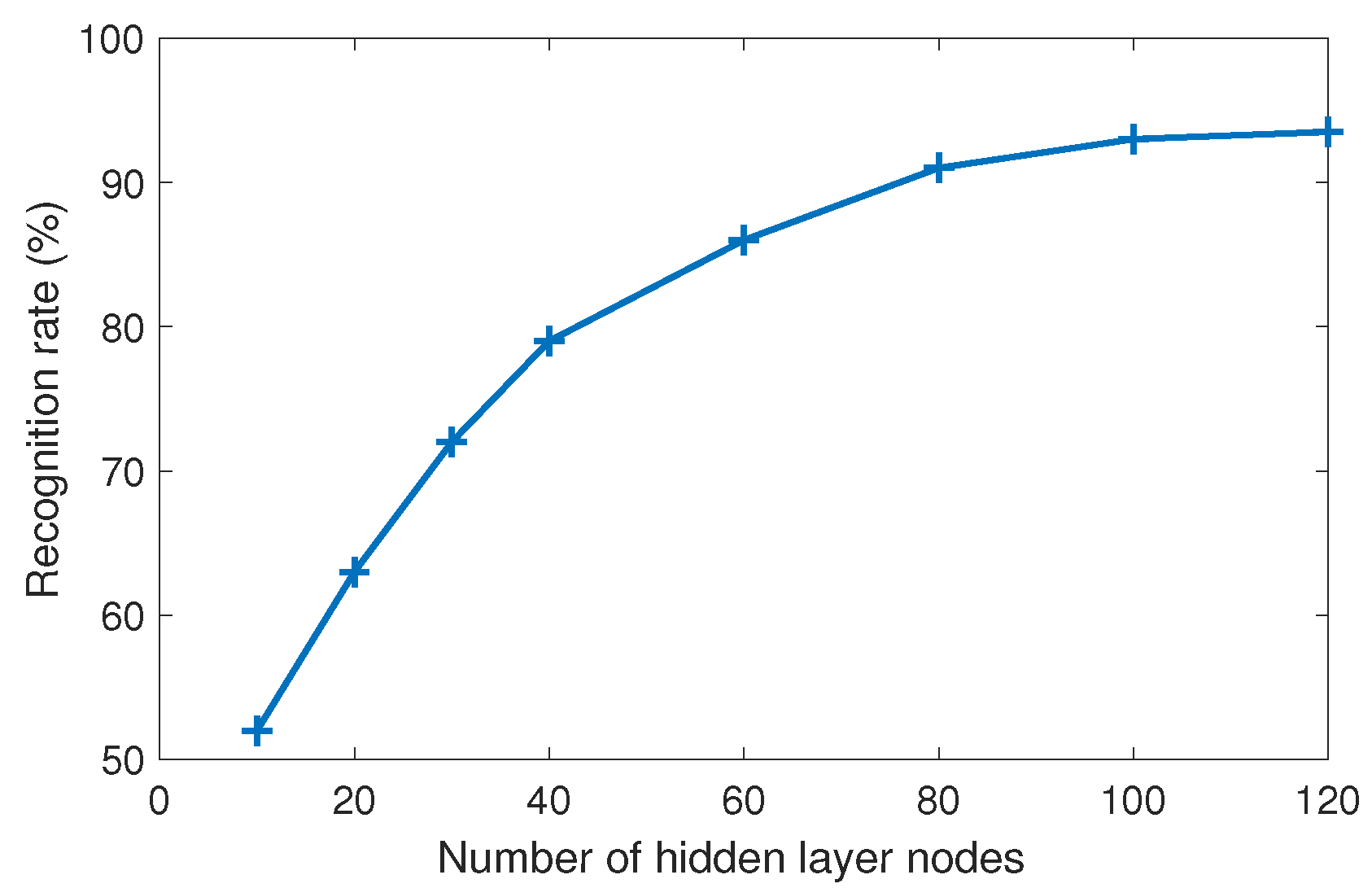
2.4. Driving Condition Recognition Based on Extreme Learning Machine
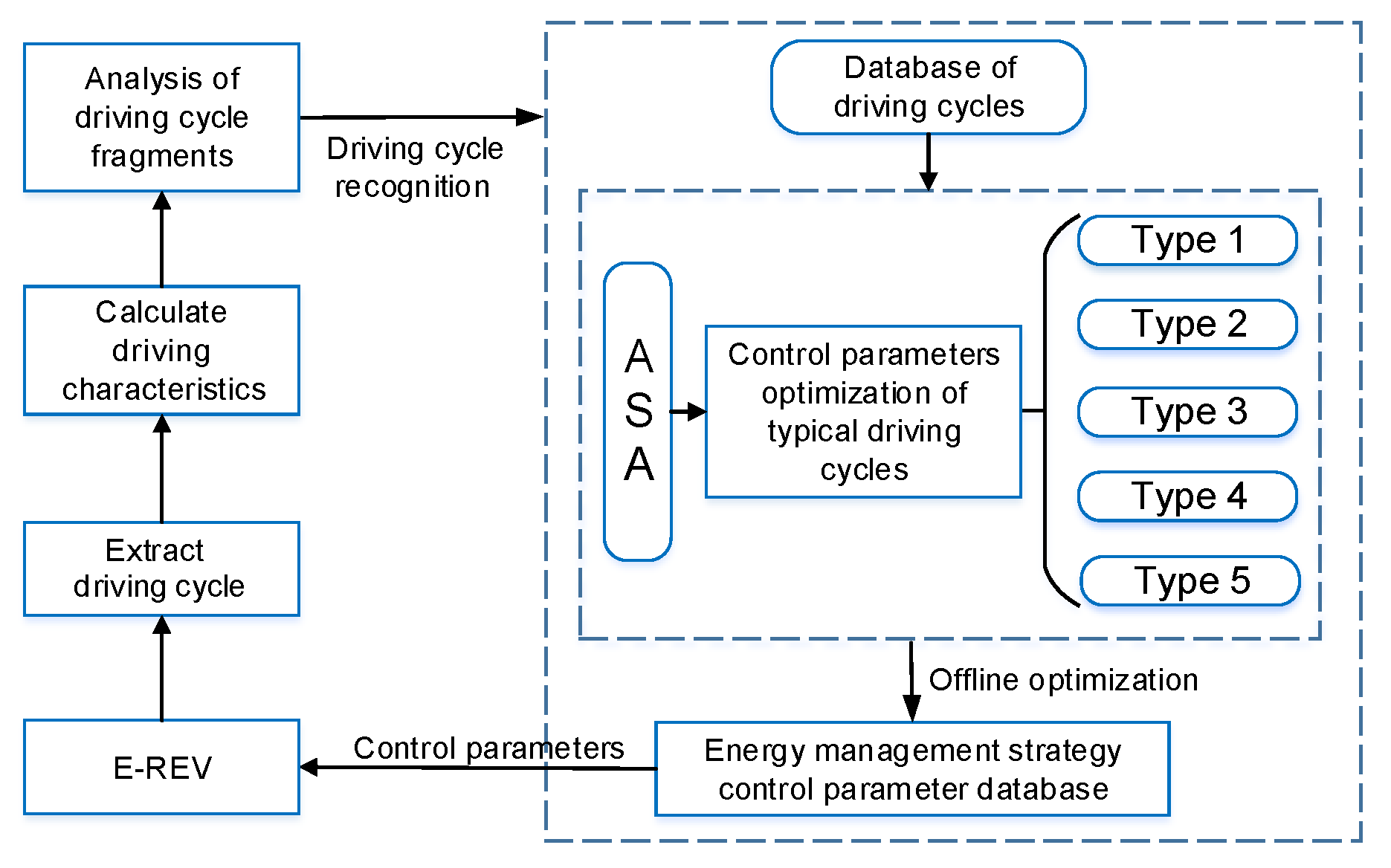
3. Energy Management Strategy for E-REV Based on Driving Characteristics
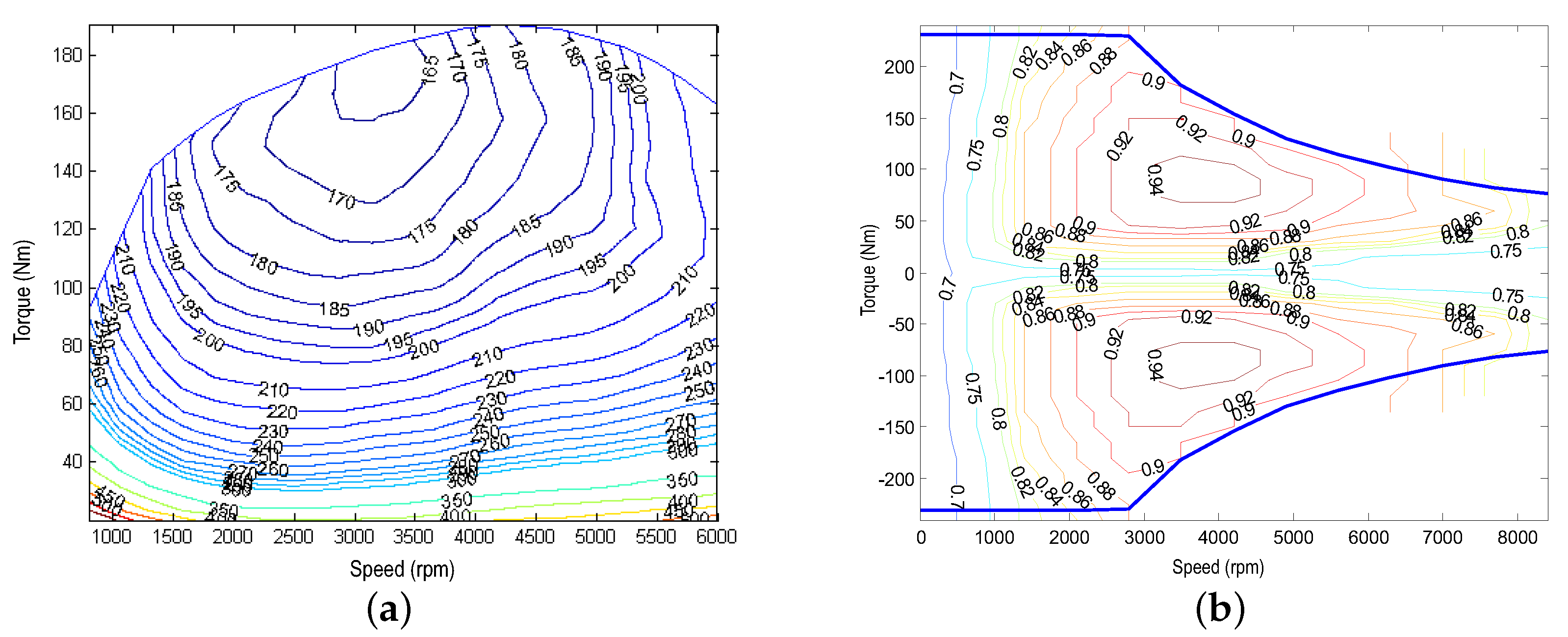
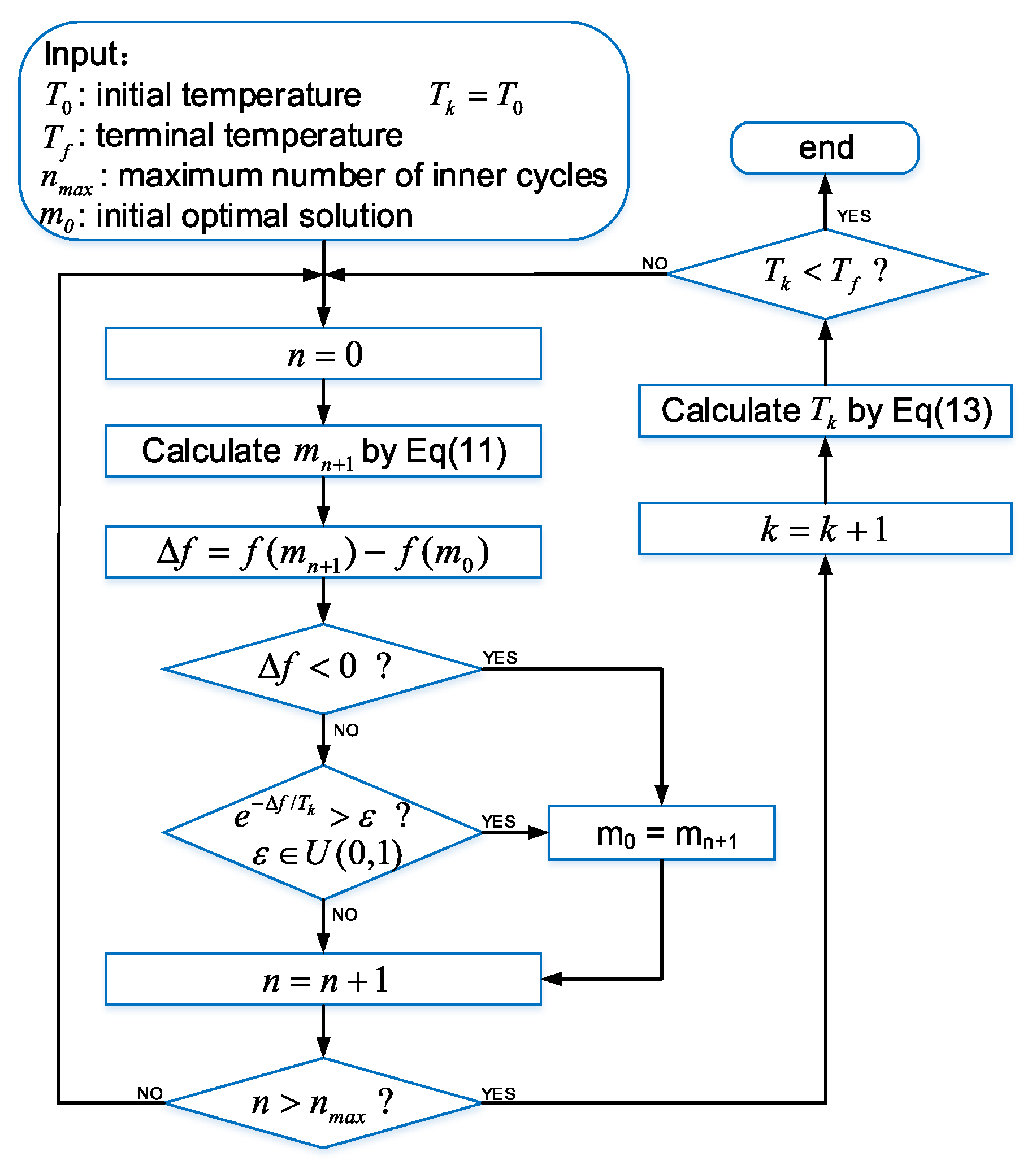
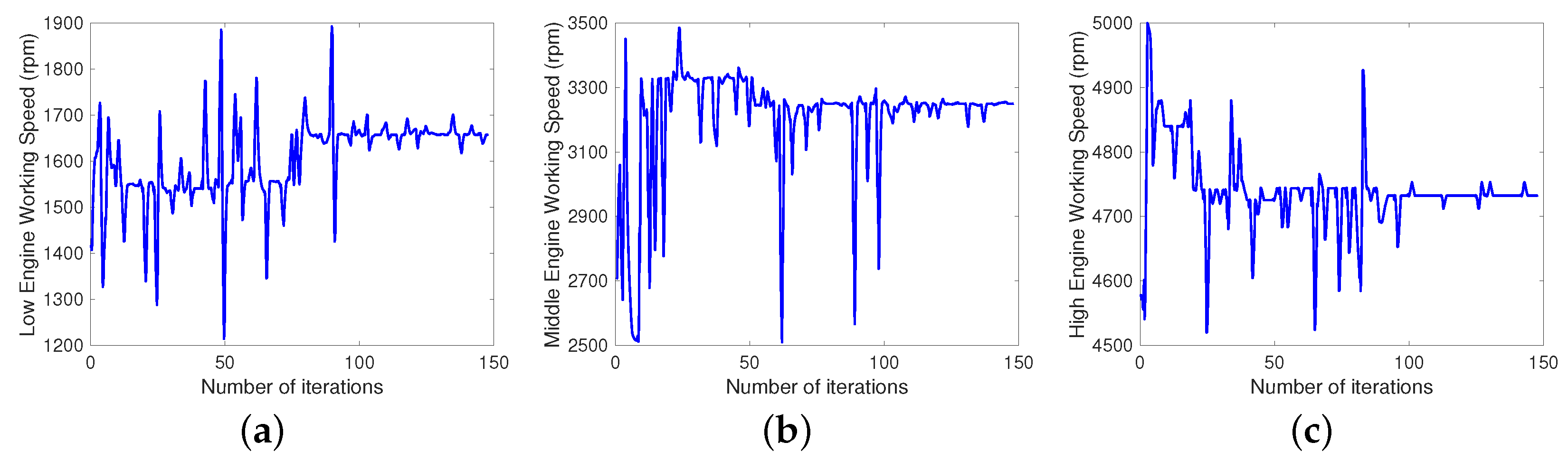
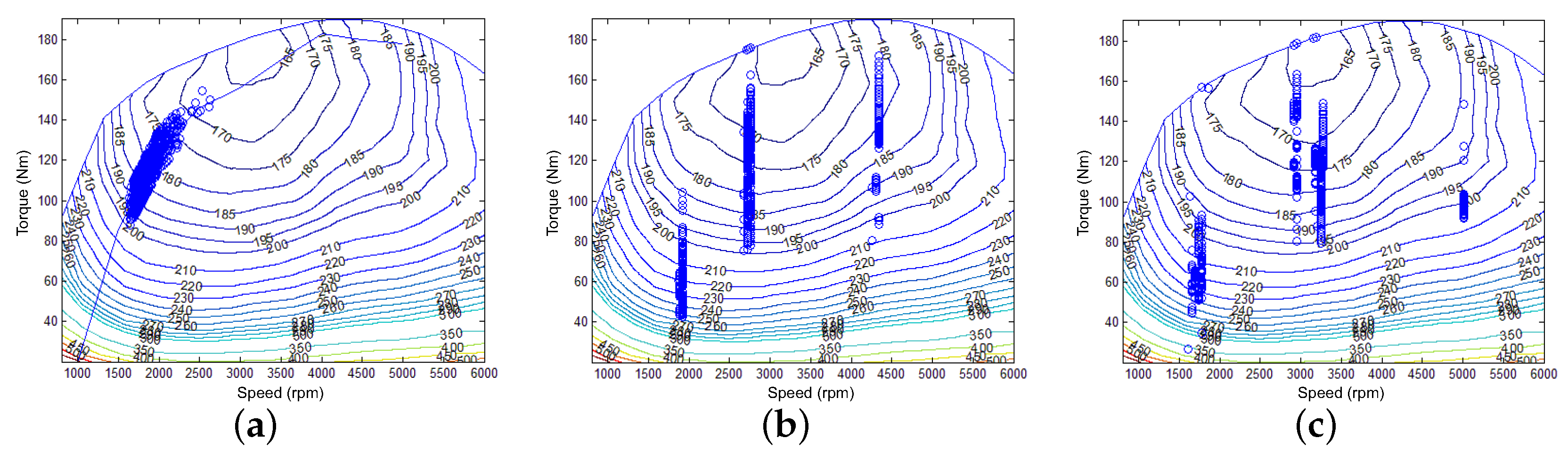
3.1. Multi-Objective Optimization for Typical Driving Conditions
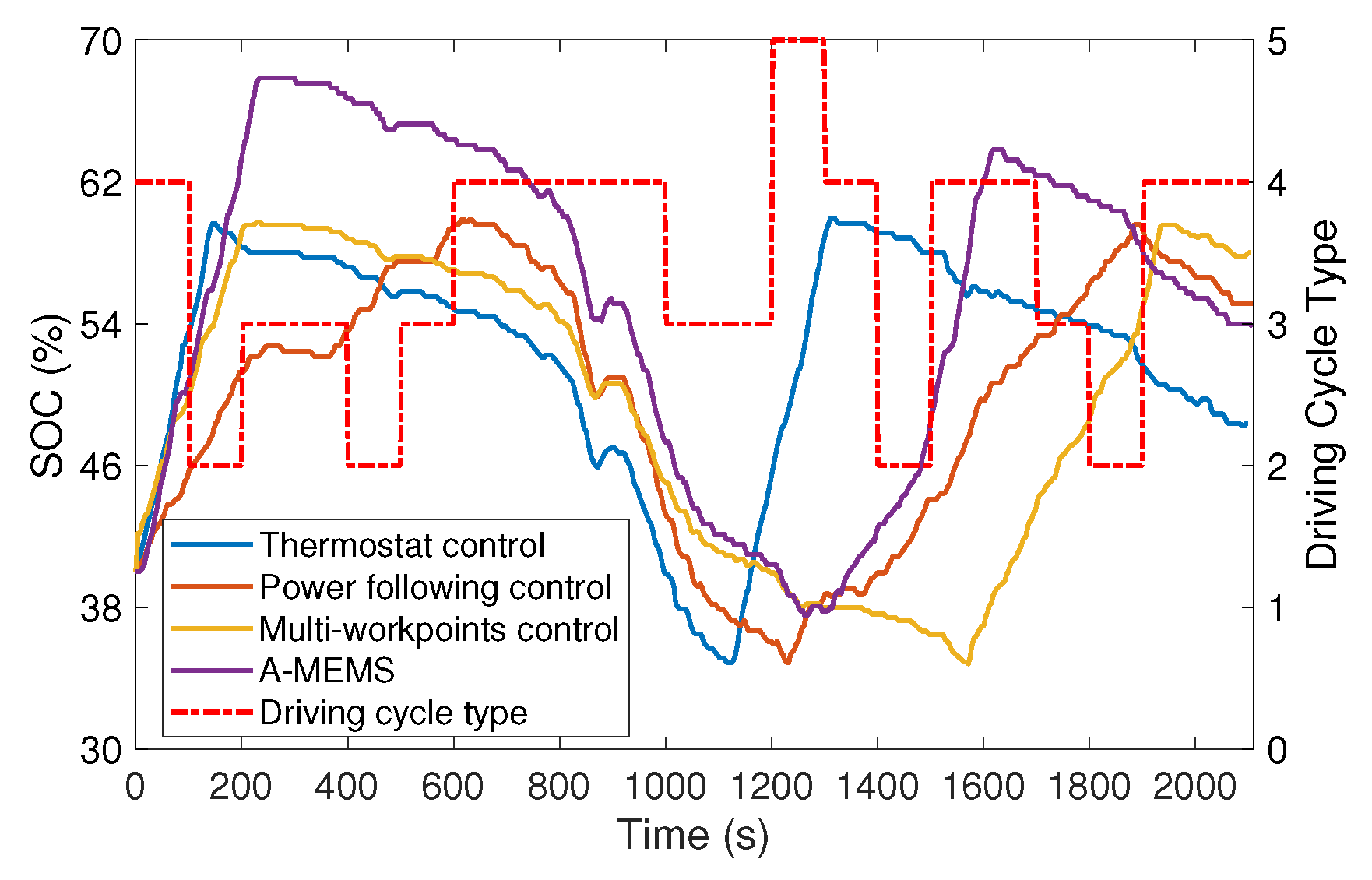
- Thermostat control: when the State of Charge (SOC) of battery is between and , the engine maintains the working state; when is more than , the engine is turned off and runs on pure electric power; when SOC is less than , the engine works at the highest efficiency point, and the excess energy charges the battery. This strategy can effectively avoid engine start and stop frequently, but batteries often charge and discharge with a large current which is extremely bad for battery life.
- Power following control: this strategy determines the working state of the engine according to the power demand of the vehicle and SOC of the battery. Only when SOC more than and the power demand is less than , the engine will turn off. Under this control strategy, the battery can maintain the best performance state, but frequent engine fluctuations are detrimental to the economy and fuel consumption.
- Multi-workpoints control: the strategy is to make the engine work at different working points according to the vehicle’s power demand and battery SOC. Too many working points will cause the engine fluctuation to become larger, and too few working points will not avoid the power battery work with large current. This strategy can not only ensure the life of the power battery but also reduce the fluctuation of the engine.
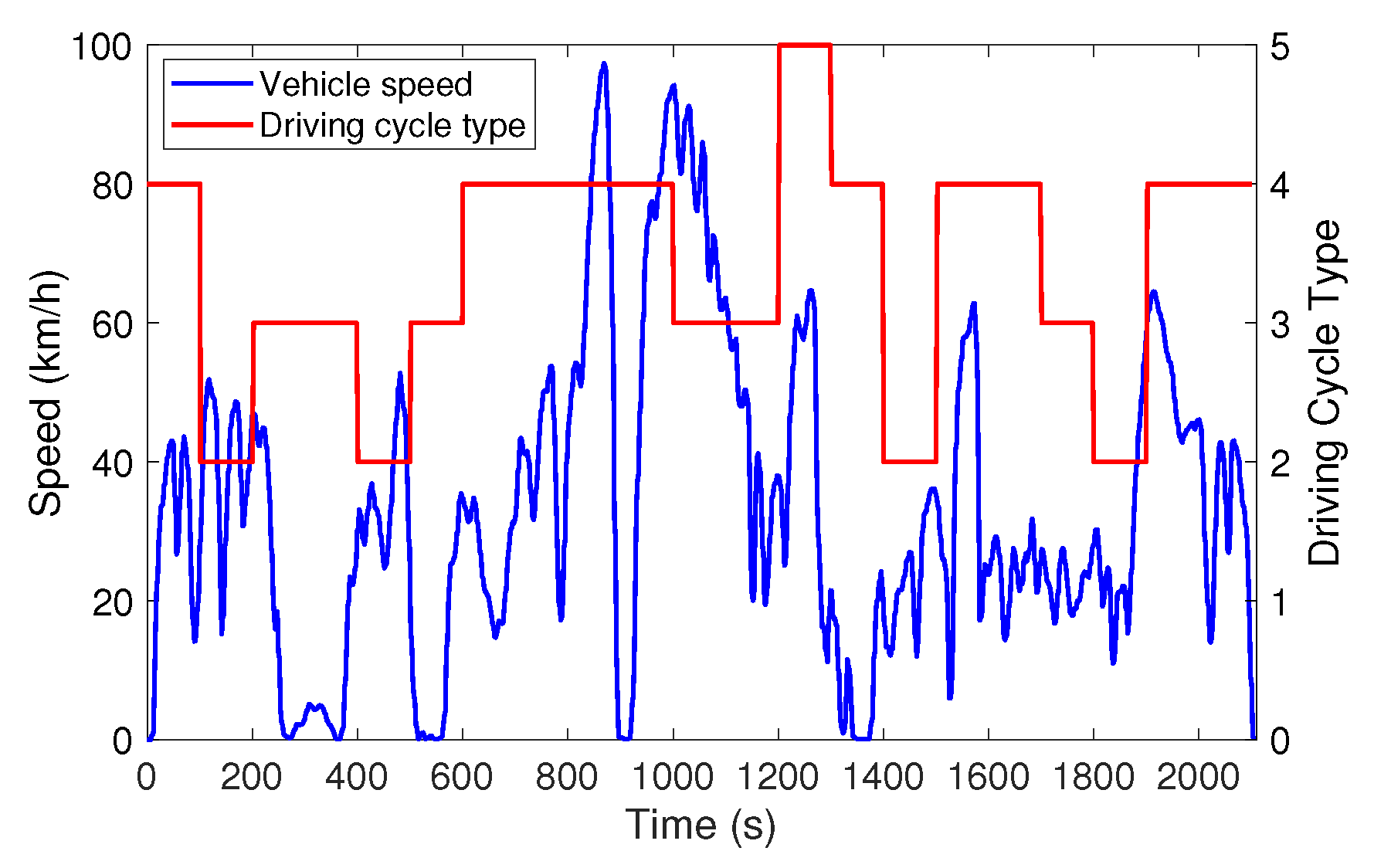
3.2. Real-Time Energy Management Strategy Based on Driving Cycle Recognition
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| E-REV | Extended-Range Electric Vehicle |
| EMS | Energy Management Strategy |
| CLTC-P | China Light-duty vehicles Test Cycle-Passenger |
| GPS | Global Positioning System |
| MSE | Mean Square Error |
| SNR | Signal-to-Noise Ratio |
| PCA | Principal Component Analysis |
| ISODATA | Iterative Self-Organizing Data Analysis Techniques Algorithm |
| CH | Calinski-Harabaz index |
| DBI | Davies-Bouldin index |
| ELM | Extreme Learning Machine |
| SOC | State of Charge |
| ASA | Adaptive Simulated Annealing |
| A-MEMS | Adaptive Multi-workpoints Energy Management Strategy |
References
- Xie, H.; Tian, G.; Chen, H.; Wang, J.; Huang, Y. A distribution density-based methodology for driving data cluster analysis: A case study for an extended-range electric city bus. Pattern Recognit. 2018, 73, 131–143. [Google Scholar] [CrossRef]
- Chrenko, D.; Gan, S.; Gutenkunst, C.; Kriesten, R.; Moyne, L.L. Novel Classification of Control Strategies for Hybrid Electric Vehicles. In Proceedings of the 2015 IEEE Vehicle Power and Propulsion Conference (VPPC), Montreal, QC, Canada, 19–22 October 2015; pp. 1–6. [Google Scholar]
- Yang, Y.; Zhang, Y.; Tian, J.; Li, T. Adaptive real-time optimal energy management strategy for extender range electric vehicle. Energy 2020, 197, 117237. [Google Scholar] [CrossRef]
- Tong, H.Y.; Hung, W.T. A Framework for Developing Driving Cycles with On-Road Driving Data. Transp. Rev. 2010, 30, 589–615. [Google Scholar] [CrossRef]
- Fotouhi, A.; Yusof, R.; Rahmani, R.; Mekhilef, S.; Shateri, N. A review on the applications of driving data and traffic information for vehicles’ energy conservation. Renew. Sustain. Energy Rev. 2014, 37, 822–833. [Google Scholar] [CrossRef]
- Shi, Q.; Zheng, Y.; Wang, R.; Li, Y. The study of a new method of driving cycles construction. Procedia Eng. 2011, 16, 79–87. [Google Scholar] [CrossRef]
- Ashtari, A.; Bibeau, E.; Shahidinejad, S. Using Large Driving Record Samples and a Stochastic Approach for Real-World Driving Cycle Construction: Winnipeg Driving Cycle. Transp. Sci. 2014, 48, 170–183. [Google Scholar] [CrossRef]
- Si, L.; Hirz, M.; Brunner, H. Big Data-Based Driving Pattern Clustering and Evaluation in Combination with Driving Circumstances; SAE Technical Papers; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Lee, J.; Li, J.; Liu, L.; Chen, C. A Novel Driving Pattern Recognition and Status Monitoring System; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2006; pp. 504–512. [Google Scholar]
- Yu, H.; Tseng, F.; Mcgee, R.A. Driving pattern identification for EV range estimation. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–7. [Google Scholar]
- Xie, L.; Tao, J.; Zhang, Q.; Zhou, H. CNN and KPCA-Based Automated Feature Extraction for Real Time Driving Pattern Recognition. IEEE Access 2019, 7, 123765–123775. [Google Scholar] [CrossRef]
- Berzi, L.; Delogu, M.; Pierini, M. Development of driving cycles for electric vehicles in the context of the city of Florence. Transp. Res. Part D Transp. Environ. 2016, 47, 299–322. [Google Scholar] [CrossRef]
- Donateo, T.; Giovinazzi, M. Building a cycle for Real Driving Emissions. Energy Procedia 2017, 126, 891–898. [Google Scholar] [CrossRef]
- China Automotive Driving Cycle-Part1: Light-Duty Vehicles, GB/T 38146.1-2019; National Technical Committee of Auto Standardization: Tianjin, China, 2019. (In Chinese)
- Zhang, J.; Yang, Y.; Zhou, Y. Parameter closed-loop optimization for pure electric vehicles unified design of power system and control parameters. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 229. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, X.; Langari, R.; Cao, D. Energy management strategies of connected HEVs and PHEVs: Recent progress and outlook. Prog. Energy Combust. Sci. 2019, 73, 235–256. [Google Scholar] [CrossRef]
- Kopczyński, A.; Krawczyk, P.; Lasocki, J. Parameters selection of extended-range electric vehicle supplied with alternative fuel. E3S Web Conf. 2018, 44, 00073. [Google Scholar] [CrossRef]
- Romaus, C.; Gathmann, K.; Bocker, J. Optimal energy management for a hybrid energy storage system for electric vehicles based on Stochastic Dynamic Programming. In Proceedings of the 2010 IEEE Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–6. [Google Scholar]
- Xie, S.; Li, H.; Xin, Z.; Liu, T.; Wei, L. A Pontryagin Minimum Principle-Based Adaptive Equivalent Consumption Minimum Strategy for a Plug-in Hybrid Electric Bus on a Fixed Route. Energies 2017, 10, 1379. [Google Scholar] [CrossRef]
- Zhou, M.; Jin, H. Development of a transient fuel consumption model. Transp. Res. Part D Transp. Environ. 2017, 51, 82–93. [Google Scholar] [CrossRef]
- Chang, F.L.Z. Research on Nissan e-Power Hybrid Power System. Autom. Dig. 2018, 5, 13–18. (In Chinese) [Google Scholar]
- Wang, H.; Huang, Y.; Khajepour, A.; He, H.; Lv, C. MPC-based power management strategy for a series hybrid electric tracked bulldozer. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 1403–1408. [Google Scholar]
- Li, Y.; Chen, B. Development of integrated rule-based control and equivalent consumption minimization strategy for HEV energy management. In Proceedings of the 12th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications (MESA), Auckland, New Zealand, 29–31 August 2016; pp. 1–6. [Google Scholar]
- Qi, X.; Luo, Y.; Wu, G.; Boriboonsomsin, K.; Barth, M. Deep reinforcement learning enabled self-learning control for energy efficient driving. Transp. Res. Part C Emerg. Technol. 2019, 99, 67–81. [Google Scholar] [CrossRef]
- Lian, R.; Peng, J.; Wu, Y.; Tan, H.; Zhang, H. Rule-interposing deep reinforcement learning based energy management strategy for power-split hybrid electric vehicle. Energy 2020, 197, 117297. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Chang, N.; Zhu, Q.; Lin, X. A deep reinforcement learning framework for optimizing fuel economy of hybrid electric vehicles. In Proceedings of the 2018 23rd Asia and South Pacific Design Automation Conference (ASP-DAC), Jeju, Korea, 22–25 January 2018; pp. 196–202. [Google Scholar]
- Panday, A.; Bansal, H.O. Energy management strategy for hybrid electric vehicles using genetic algorithm. J. Renew. Sustain. Energy 2016, 8, 741–746. [Google Scholar] [CrossRef]
- Lei, Z.; Cheng, D.; Liu, Y.; Qin, D.; Zhang, Y.; Xie, Q. A Dynamic Control Strategy for Hybrid Electric Vehicles Based on Parameter Optimization for Multiple Driving Cycles and Driving Pattern Recognition. Energies 2017, 10, 54. [Google Scholar] [CrossRef]
- Yanting, Z.; Qingfeng, W. Constant work-point control for parallel hybrid system with capacitor accumulator in hydraulic excavator. Chin. J. Mech. Eng. 2006, 19, 505–508. [Google Scholar]
- Joud, L.; Chrenko, D.; Keromnes, A.; Silva, R.D.; Moyne, L.L. Predictive Energy Management for Hybrid Vehicles Based on Driving Cycle Recognition. In Proceedings of the 2017 IEEE Vehicle Power and Propulsion Conference (VPPC), Belfort, France, 11–14 December 2017. [Google Scholar]
- Zhang, N.; Cao, C.; Yu, H. The cycle recognition algorithm based on Daubechies wavelet and fuzzy C-means clustering. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; pp. 4836–4840. [Google Scholar]
- Therrien, C.W. Discrete Random Signals and Statistical Signal Processinga; Prentice Hall PTR: Upper Saddle River, NJ, USA, 1992. [Google Scholar]
- Zhao, X.; Ma, J.; Wang, S.; Ye, Y.; Wu, Y.; Yu, M. Developing an electric vehicle urban driving cycle to study differences in energy consumption. Environ. Sci. Pollut. Res. 2018, 26, 13839–13853. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Zhang, G. Determination of Best Grading of Wavelet Transform in Deformation Measurement Data Filtering. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 285–288. (In Chinese) [Google Scholar]
- Changjun, Z.; Yuzong, C.; Wei, C. The real time classification of vehicle by combination of GA, PCA and Improved SVM. In Proceedings of the 6th InternationalConference on Advanced Information Management and Service, Seoul, Korea, 30 November–2 December 2010; pp. 414–419. [Google Scholar]
- Kalsoom, R.; Halim, Z. Clustering the driving features based on data streams. In Proceedings of the International Multi Topic Conference, Lahore, Pakistan, 19–20 December 2013; pp. 89–94. [Google Scholar]
- Du, B.; Jian, Q. An ISODATA approach to the estimation of atomistic definition for continuum stress. Mater. Sci. Forum 2017, 909, 293–299. [Google Scholar] [CrossRef]
- Duro, N.; Dormido, R.; Vega, J.; Dormidocanto, S.; Farias, G.; Sanchez, J.; Vargas, H.; Murari, A. Automated recognition system for ELM classification in JET. Symp. Fusion Technol. 2009, 84, 712–715. [Google Scholar] [CrossRef]
- Ingber, L. Very fast simulated re-annealing. Math. Comput. Model. 1989, 12, 967–973. [Google Scholar] [CrossRef]
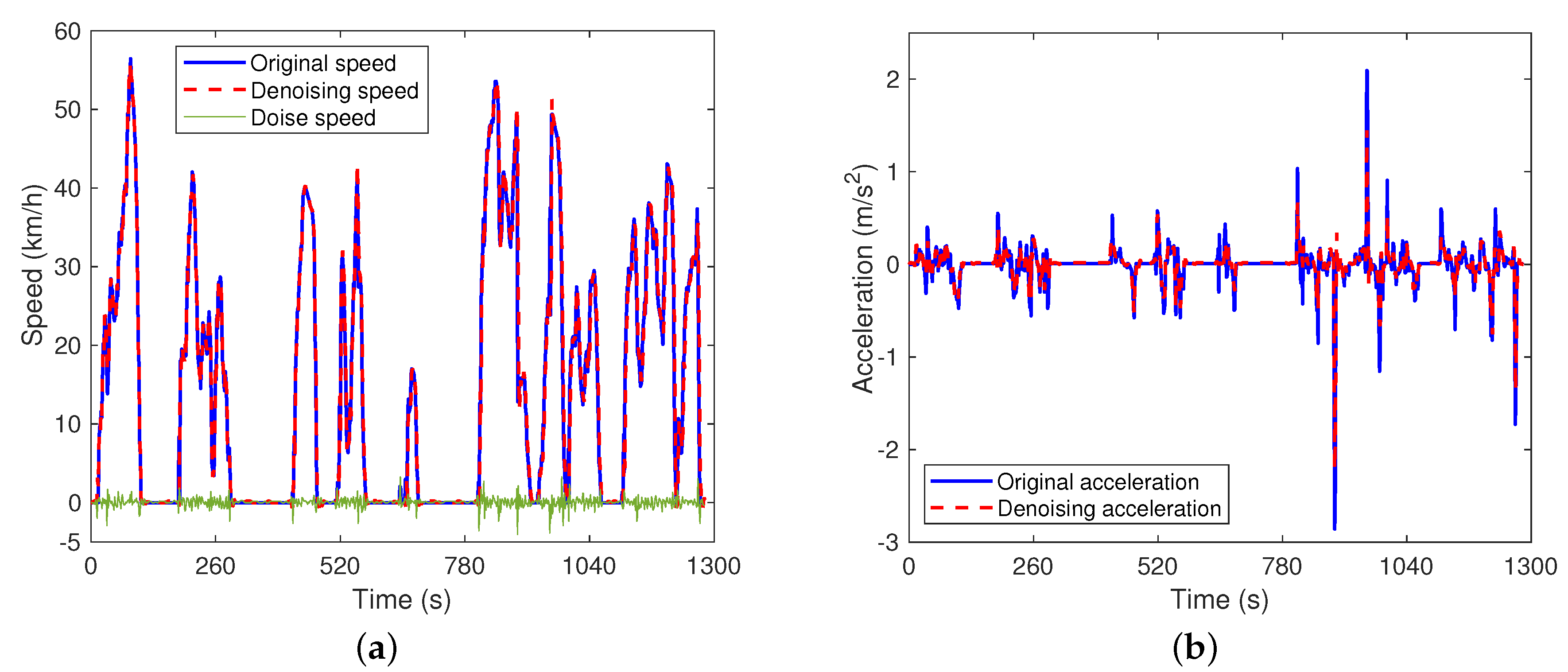
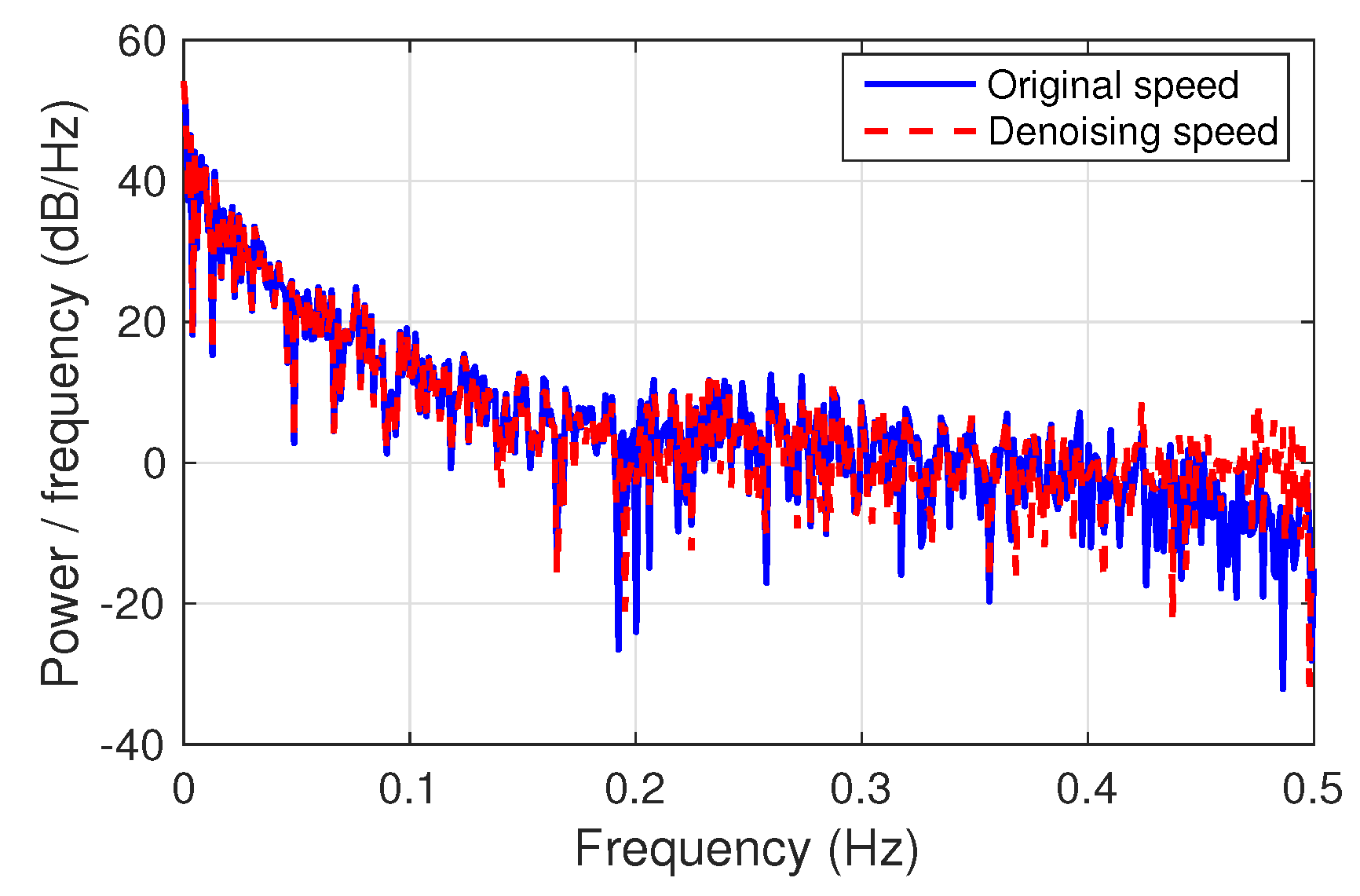
| Decomposition Scale | SNR | MSE | Smoothness |
|---|---|---|---|
| 3 | 30.683 | 0.6210 | 0.9705 |
| 4 | 30.649 | 0.6239 | 0.9247 |
| 5 | 30.587 | 0.6341 | 0.7052 |
| 6 | 30.543 | 0.6342 | 0.4434 |
| 7 | 28.348 | 0.6681 | 0.3980 |
| 8 | 27.261 | 0.6617 | 0.4567 |
| Number | Characteristics | Unit |
|---|---|---|
| 1 | Average speed | km/h |
| 2 | Maximum speed | km/h |
| 3 | Standard deviation of speed | km/h |
| 4 | Maximum acceleration | m/s |
| 5 | Maximum deceleration | m/s |
| 6 | Average acceleration | m/s |
| 7 | Average deceleration | m/s |
| 8 | Standard deviation of acceleration | m/s |
| 9 | Standard deviation of deceleration | m/s |
| 10 | Acceleration time ratio | % |
| 11 | Deceleration time ratio | % |
| 12 | Even speed time ratio | % |
| 13 | Idle speed time ratio | % |
| 14 | Mileage | km |
| 15 | Proportion in speed range of 0–20 km/h | % |
| 16 | Proportion in speed range of 20–40 km/h | % |
| 17 | Proportion in speed range of 40–60 km/h | % |
| 18 | Proportion in speed range of 60–80 km/h | % |
| 19 | Accelerating time | s |
| 20 | Decelerating time | s |
| 21 | Even speed time | s |
| BEGIN | Input clustering samples and number of cluster centers, search clustering center . |
| DO | Divide each sample into the nearest cluster center. |
| UNTIL | Cluster centers no longer change |
| END |
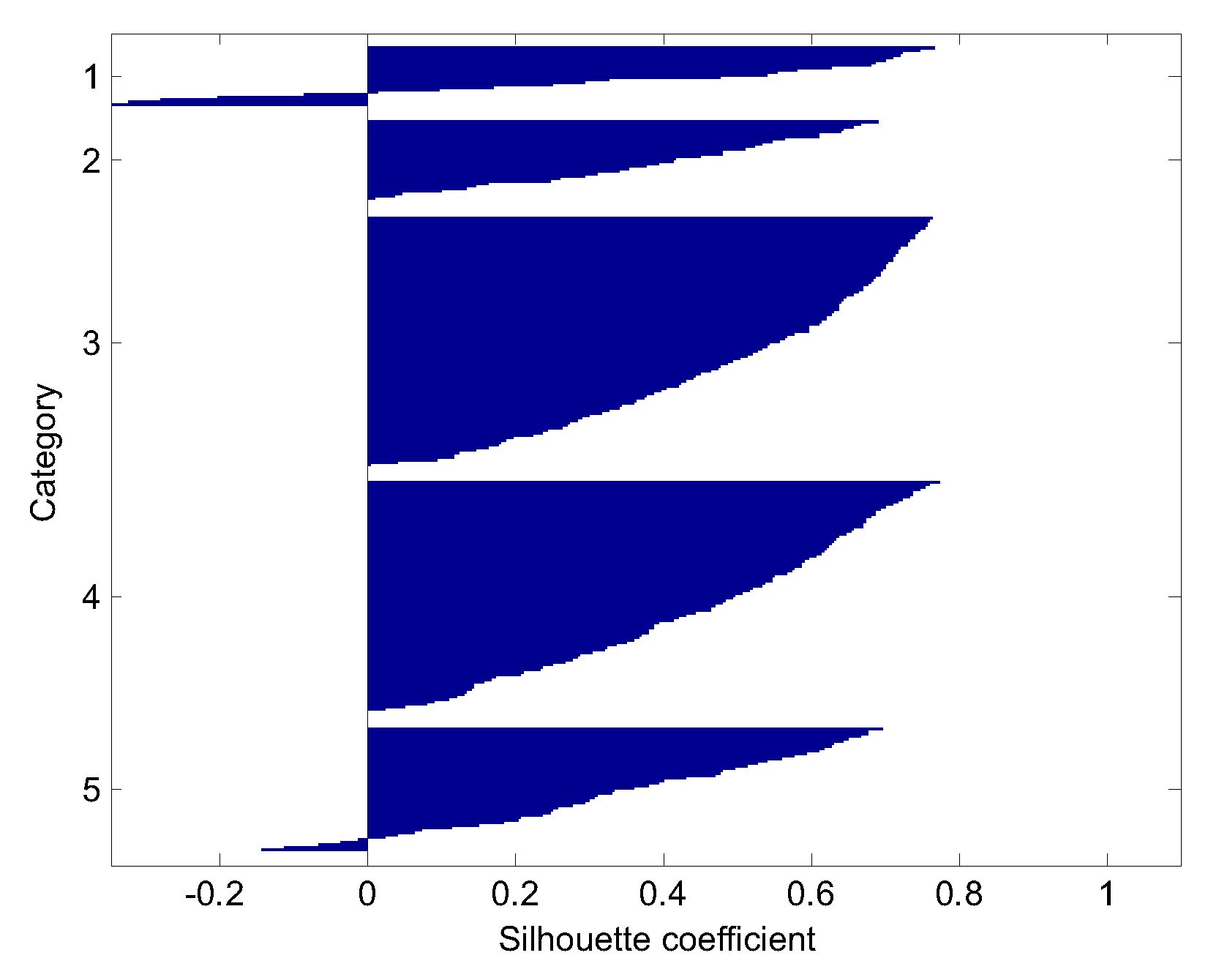
| Clustering Algorithm | Contour Coefficient | CH | DBI |
|---|---|---|---|
| K-means (3 categories) | 0.4859 | 595.12 | 0.9180 |
| K-means (4 categories) | 0.4612 | 582.02 | 1.0425 |
| K-means (5 categories) | 0.4771 | 552.93 | 0.9935 |
| K-means (6 categories) | 0.4883 | 549.37 | 0.9561 |
| K-means (7 categories) | 0.4400 | 531.24 | 0.9938 |
| ISODATA | 0.4907 | 597.11 | 0.9235 |
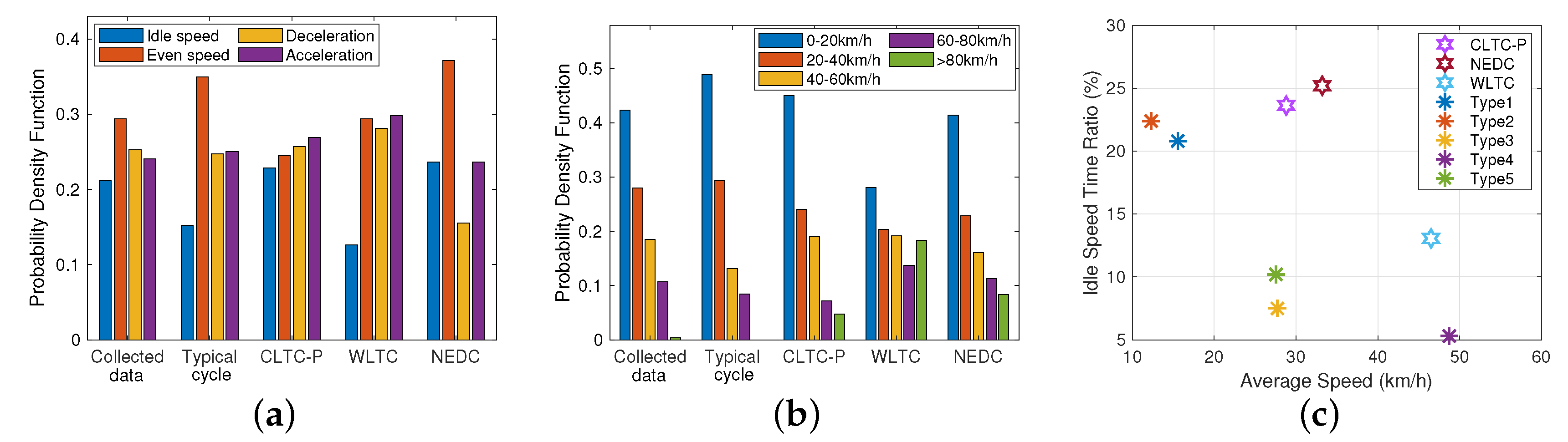
| Characteristics Number | 1 | 2 | 3 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|
| Type 1 | 15.548 | 45.293 | 12.091 | 0.432 | −0.409 | 0.314 | 0.273 |
| Type 2 | 12.289 | 46.993 | 12.563 | 0.404 | −0.423 | 0.236 | 0.294 |
| Type 3 | 27.722 | 78.285 | 20.226 | 0.462 | −0.467 | 0.293 | 0.340 |
| Type 4 | 48.732 | 78.209 | 22.735 | 0.389 | −0.418 | 0.256 | 0.320 |
| Type 5 | 27.536 | 58.340 | 16.260 | 0.466 | −0.492 | 0.340 | 0.302 |
| Characteristics Number | 13 | 15 | 16 | 19 | 20 | 21 | |
| Type 1 | 20.8 | 59.5 | 38.5 | 224 | 238 | 283 | |
| Type 2 | 22.4 | 75.1 | 22.0 | 251 | 237 | 222 | |
| Type 3 | 7.5 | 39.0 | 32.3 | 320 | 315 | 310 | |
| Type 4 | 5.3 | 17.1 | 11.5 | 423 | 397 | 1323 | |
| Type 5 | 10.2 | 30.2 | 42.8 | 269 | 260 | 389 |
| Vehicle Parameter | Value | Unit |
|---|---|---|
| Weight | 1300 | |
| Wheelbase | 2.46 | |
| Generator maximum power | 56 | |
| Motor maximum power | 82 | |
| Battery capacity | 2.88 | |
| Main reduction ratio | 6.24 | − |
| Control Parameters | Symbol | Value Range | Unit |
|---|---|---|---|
| Battery SOC lower limit | % | ||
| Battery SOC upper limit | % | ||
| Minimum switching speed | |||
| Maximum switching speed | |||
| Low engine working speed | |||
| Middle engine working speed | |||
| High engine working speed |
| Dynamic Index | Value |
|---|---|
| Max speed | >150 km/h |
| Max grade ability at 30 km/h | >20% |
| Acceleration time from 0 to 100 km/h | <15 s |
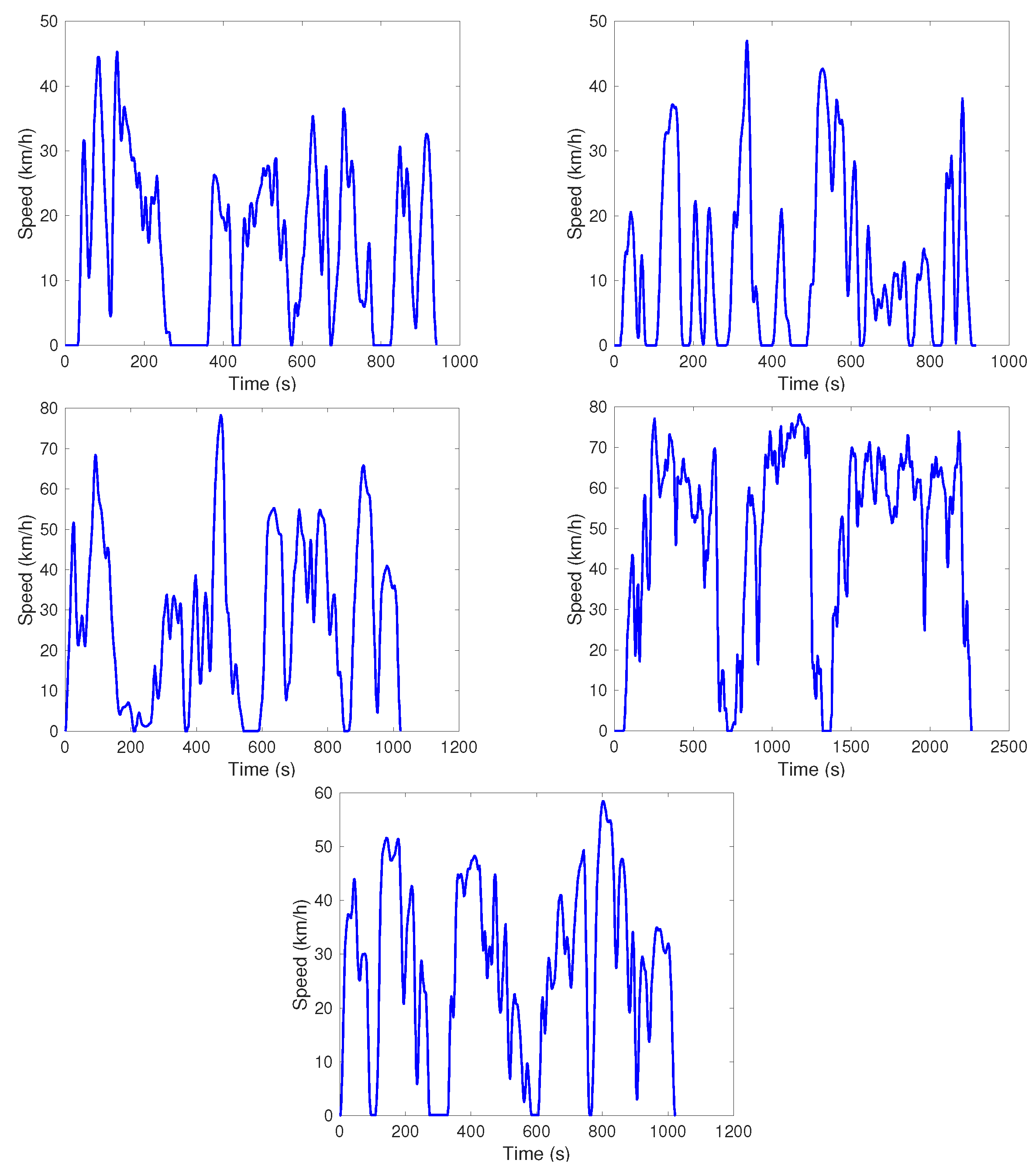
| Driving Cycle Type | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 36 | 45 | 35 | 46 | 33 | |
| 59 | 68 | 68 | 64 | 64 | |
| 36 | 46 | 43 | 39 | 43 | |
| 73 | 65 | 66 | 65 | 71 | |
| 1752 | 1656 | 1496 | 1741 | 1557 | |
| 3029 | 3246 | 3183 | 2920 | 2649 | |
| 4891 | 4727 | 4018 | 4985 | 4840 |
| Energy Management Strategy | Thermostat Control | Power Following Control | Multi-Workpoints Control | A-MEMS |
|---|---|---|---|---|
| Equivalent fuel consumption | 5.44 | 5.68 | 4.92 | 4.48 |
| 42.34 | 56.76 | 33.14 | 28.7 | |
| HC | 11.22 | 14.11 | 9.06 | 8.34 |
| CO | 97.53 | 104.83 | 81.76 | 70.3 |
| Max speed | 180 | 174 | 177 | 175 |
| Max grade ability | 35.4 | 33.7 | 34.8 | 34.3 |
| Acceleration time from 0 to 100 km/h | 9.94 | 10.08 | 10.52 | 10.68 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Y.; Jiang, J.; Min, Z.; Wang, P.; Shen, W. Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics. World Electr. Veh. J. 2020, 11, 54. https://doi.org/10.3390/wevj11030054
Yu Y, Jiang J, Min Z, Wang P, Shen W. Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics. World Electric Vehicle Journal. 2020; 11(3):54. https://doi.org/10.3390/wevj11030054
Chicago/Turabian StyleYu, Yuanbin, Junyu Jiang, Zhaoxiang Min, Pengyu Wang, and Wangsheng Shen. 2020. "Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics" World Electric Vehicle Journal 11, no. 3: 54. https://doi.org/10.3390/wevj11030054
APA StyleYu, Y., Jiang, J., Min, Z., Wang, P., & Shen, W. (2020). Research on Energy Management Strategies of Extended-Range Electric Vehicles Based on Driving Characteristics. World Electric Vehicle Journal, 11(3), 54. https://doi.org/10.3390/wevj11030054