A Consideration on Maximum Efficiency of Resonant Circuit of Inductive Power Transfer System with Soft-Switching Operation
Abstract
1. Introduction
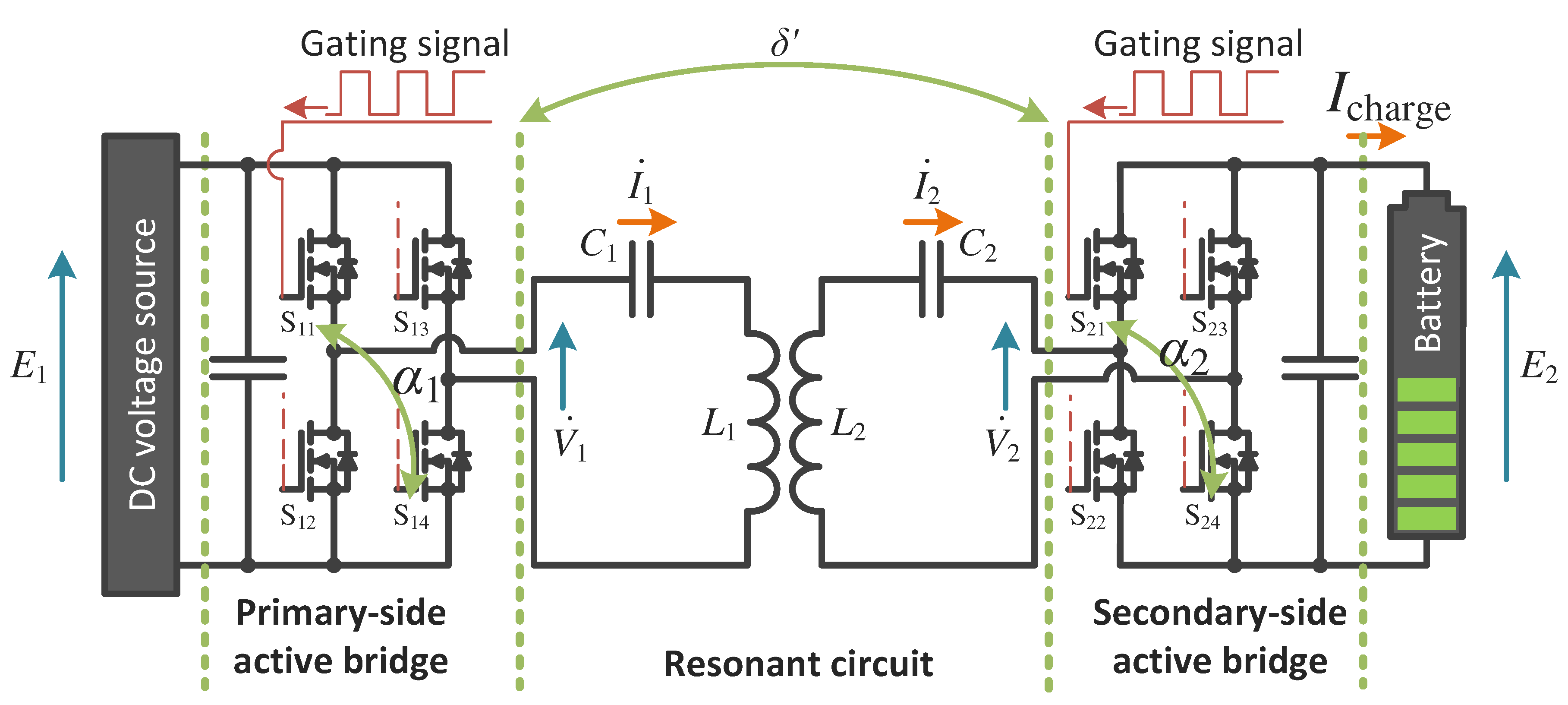
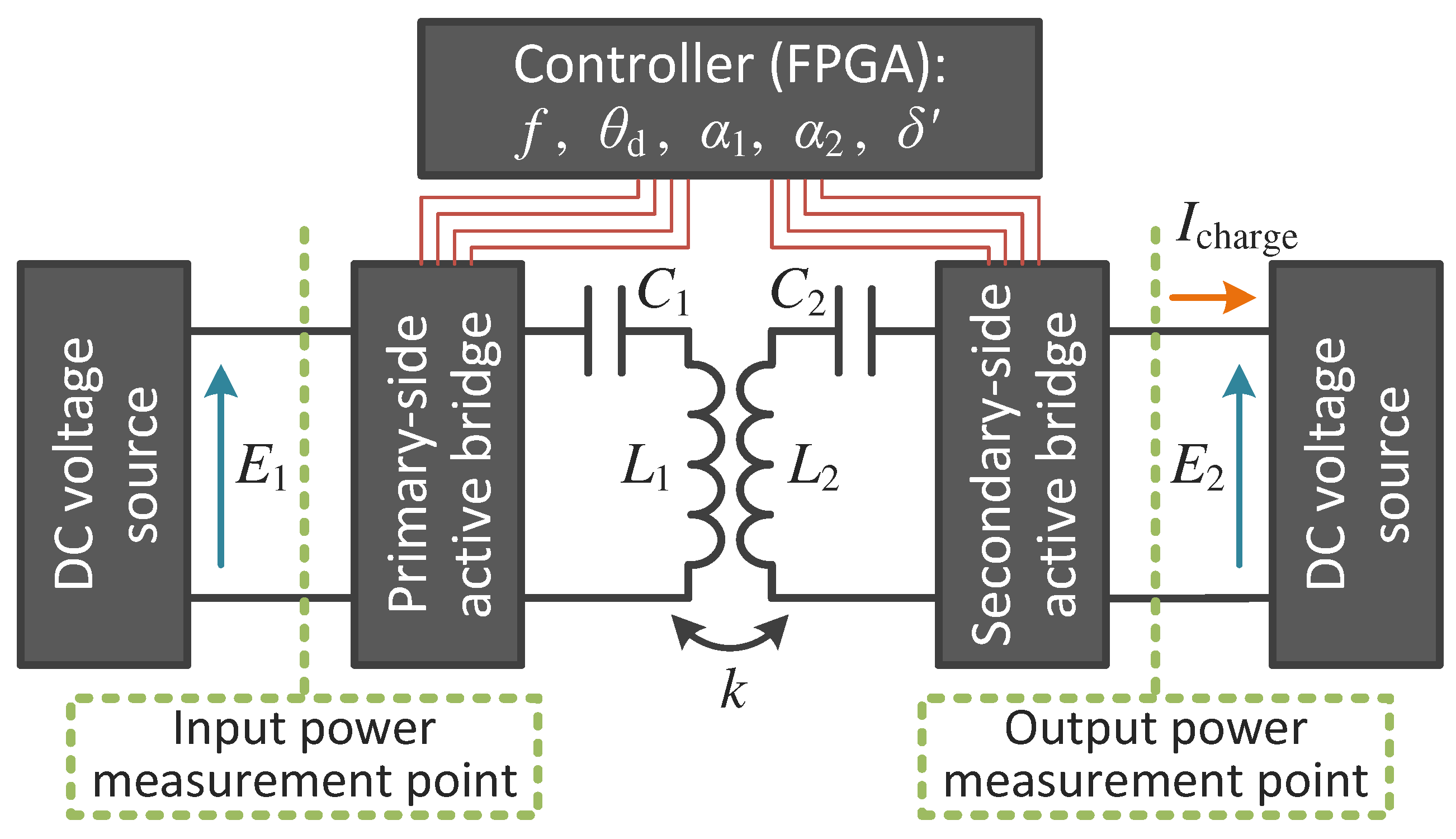
2. System Overview
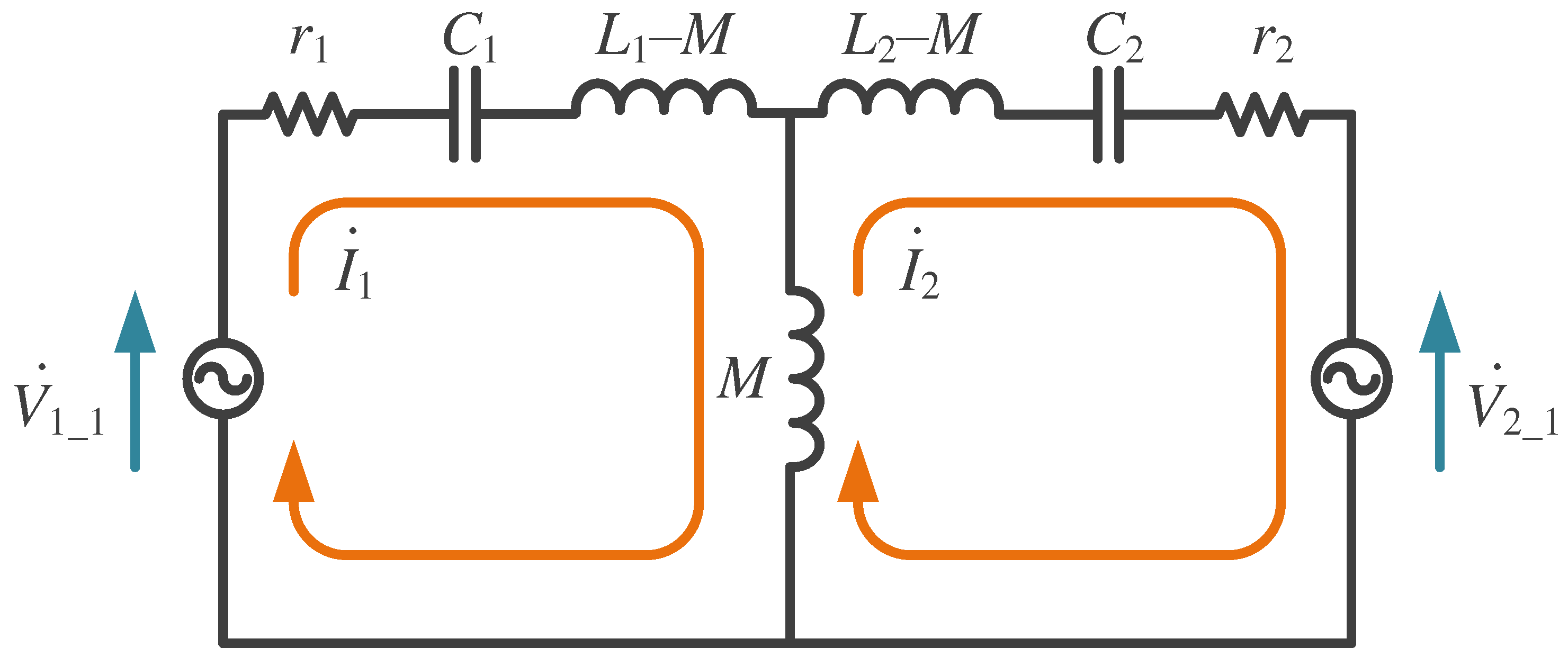
2.1. Derivation of Voltage and Current in a Bi-Directional inductive power transfer (IPT) System
2.2. Transmission Power and Efficiency
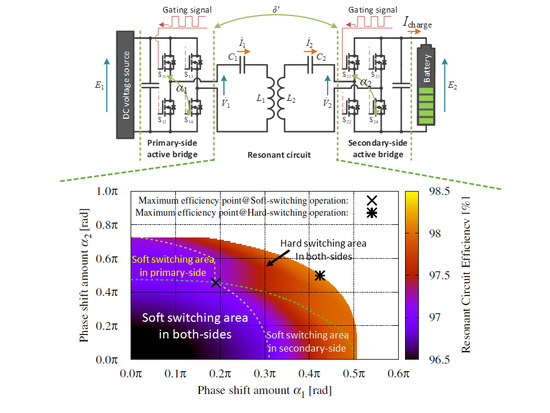
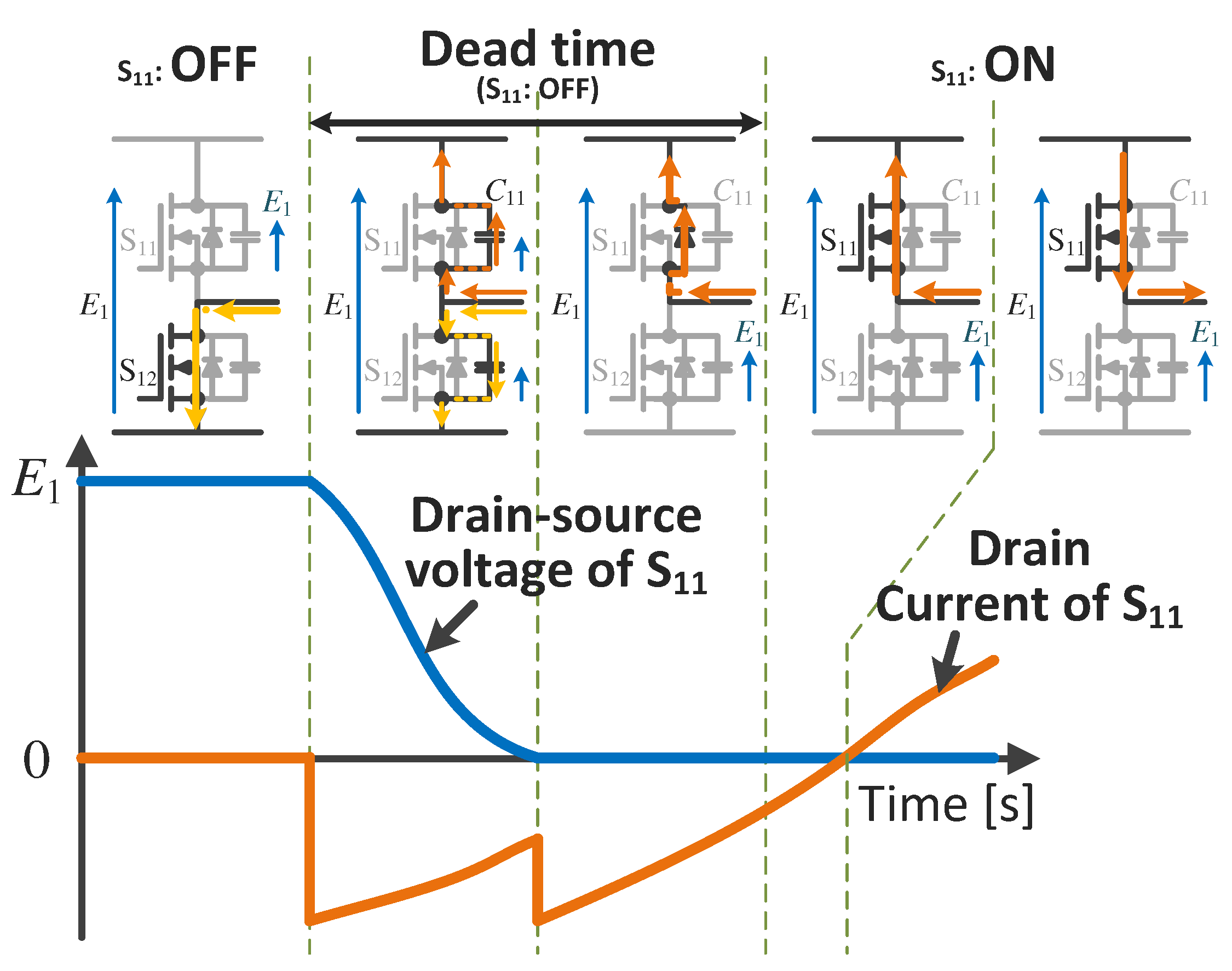
3. Influences of Soft-Switching Operation
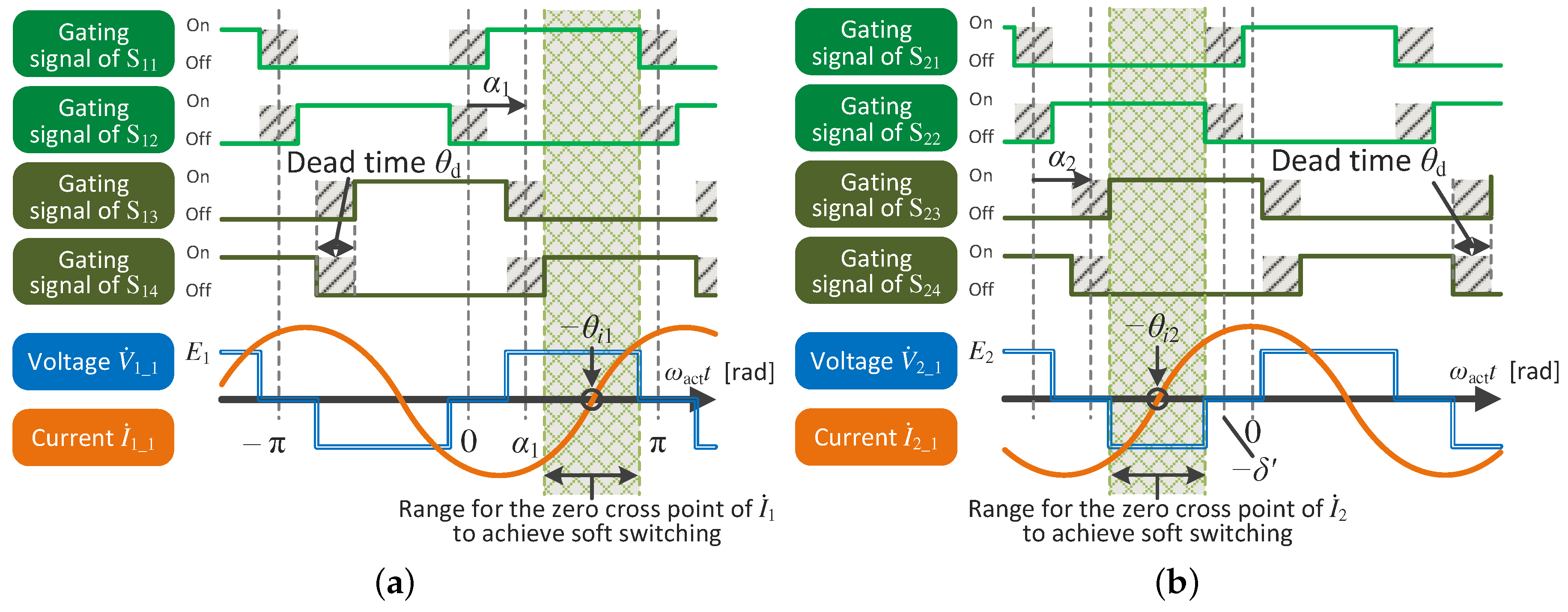
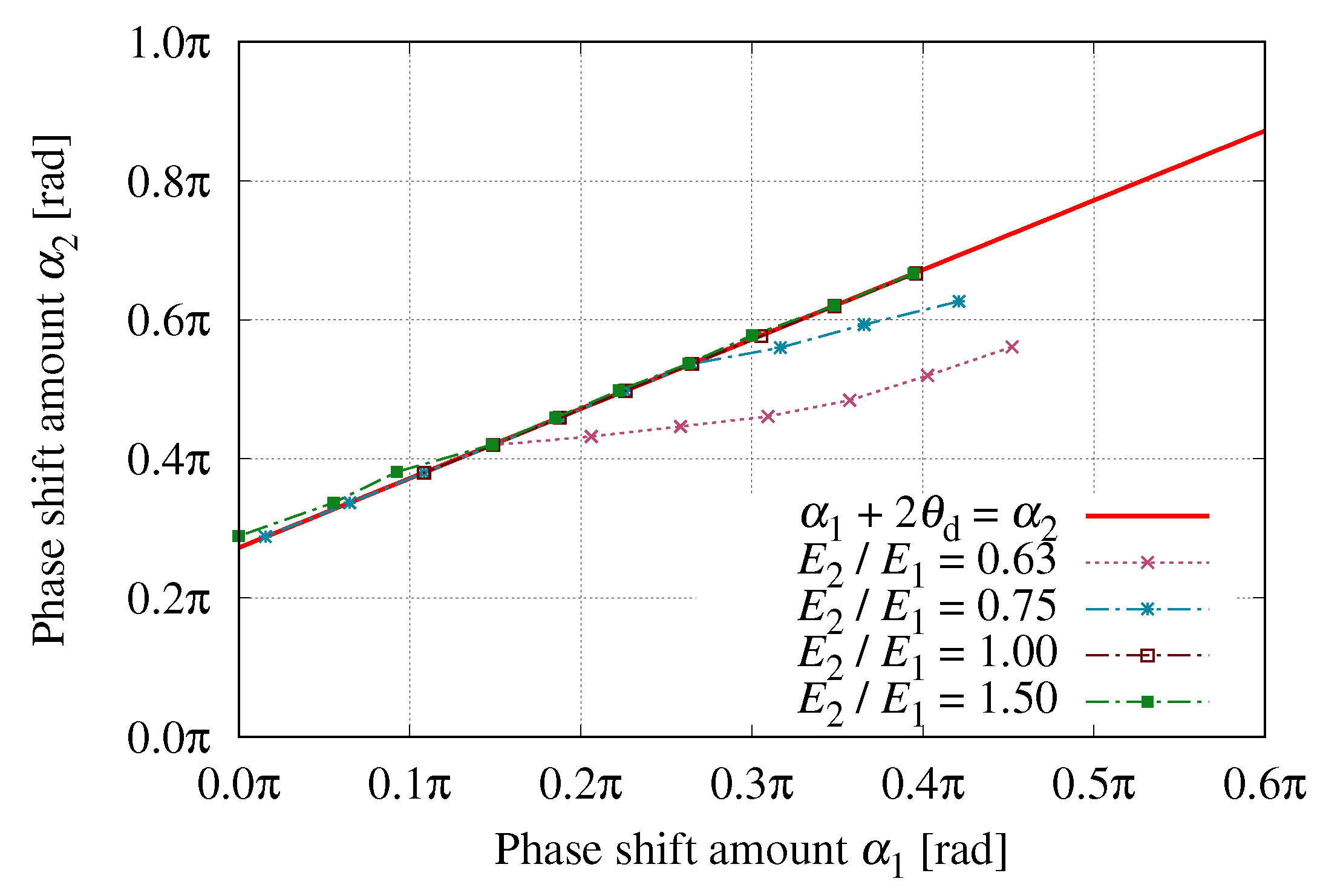
3.1. Requirement for Soft-Switching Operation
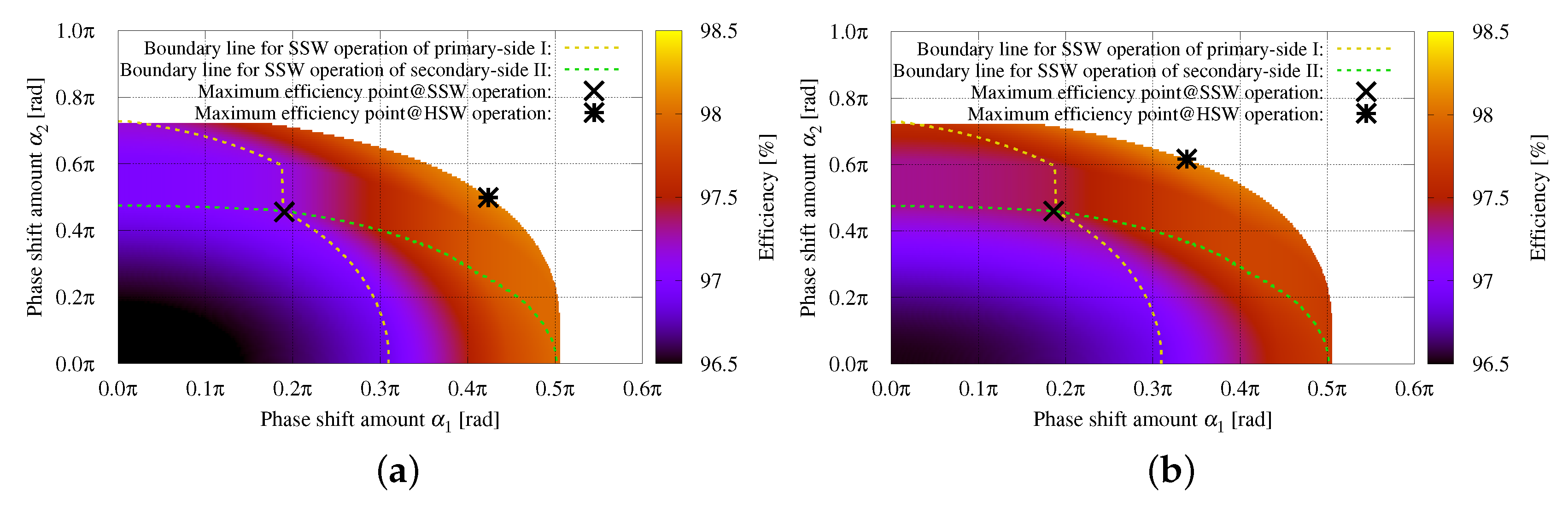
3.2. Analysis for Efficiency of the Resonant Circuit
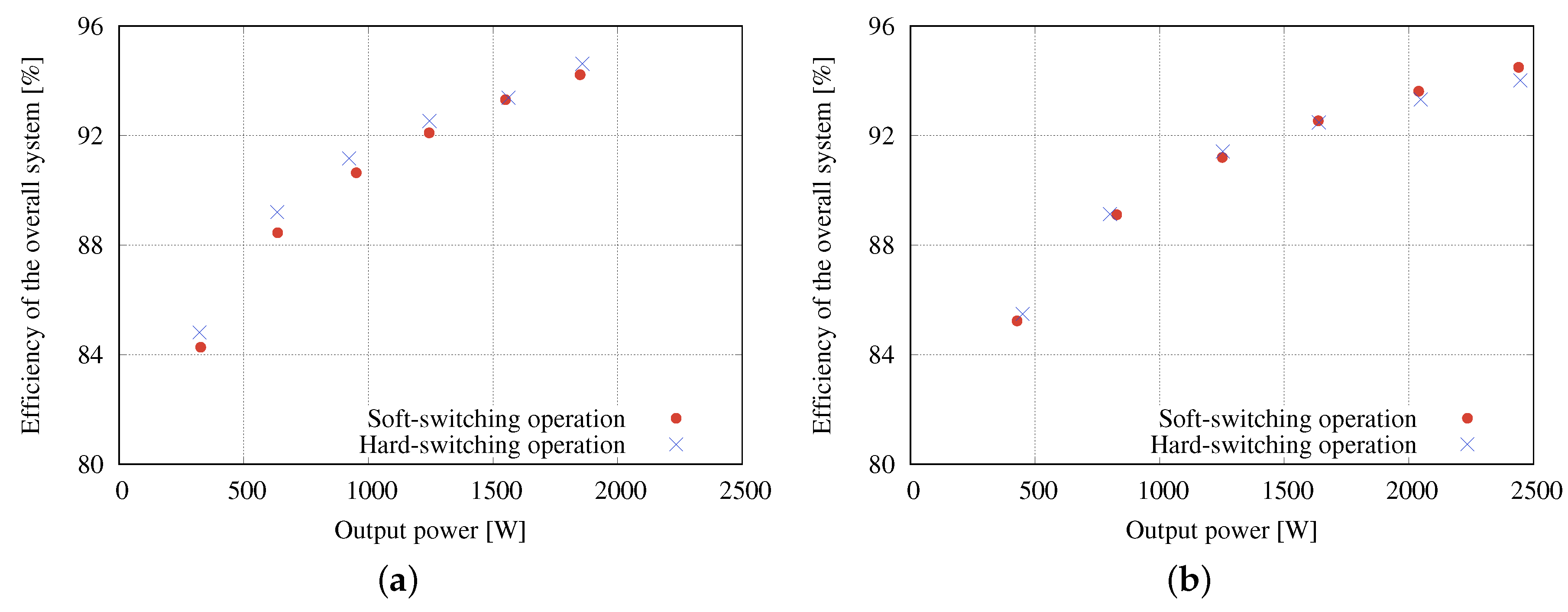
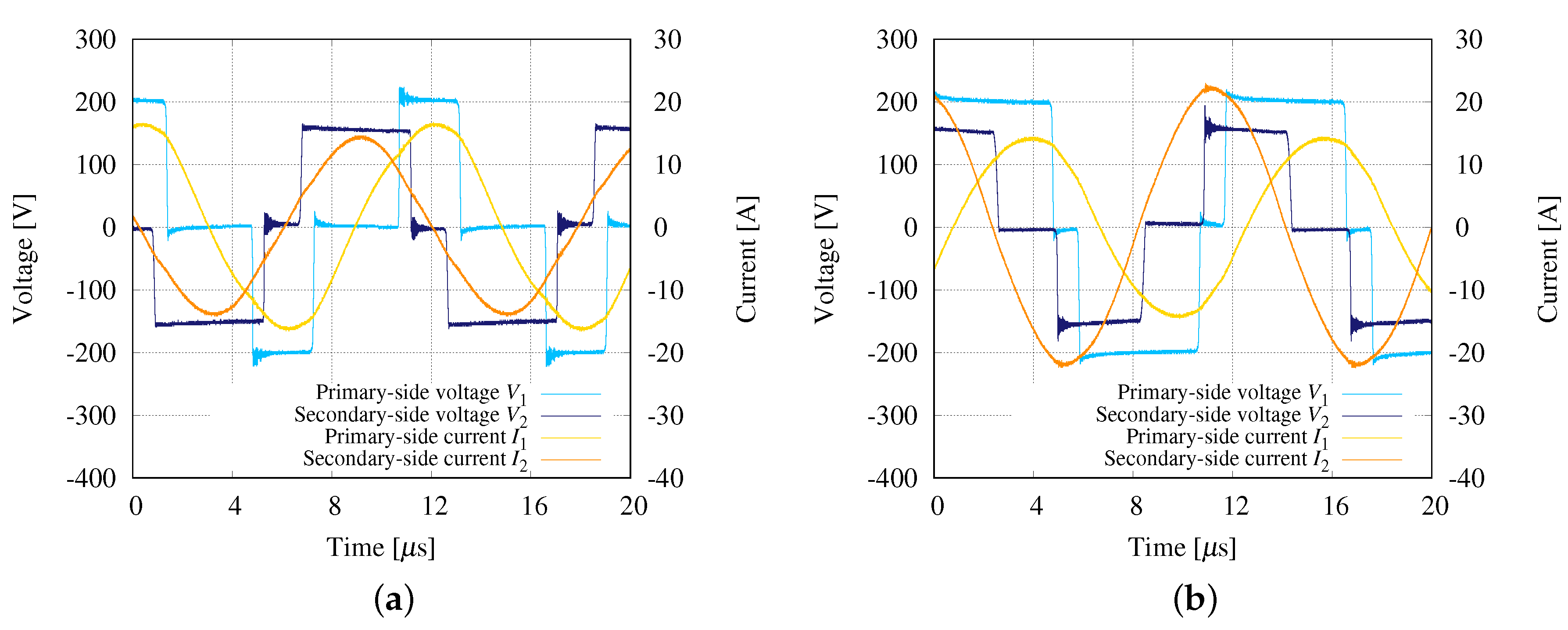
4. Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EV | Electric vehicle |
| IPT | Inductive power transfer |
References
- Cabrera, A.T.; Sanchez, J.A.A.; Longo, M.; Foiadelli, F. Sensitivity analysis of a bidirectional wireless charger for EV. In Proceedings of the 2016 IEEE International Conference on Renewable Energy Research and Applications (ICRERA), Birmingham, UK, 20–23 November 2016; pp. 1113–1116. [Google Scholar] [CrossRef]
- Ota, R.; Kakomura, K.; Hoshi, N.; Sato, D.; Transfer, C.E. Maximum Efficiency Control Scheme and Design Method for Resonant Circuit of Bi-directional Inductive Power Transfer System. In Proceedings of the 2017 European Power Electronics and Drives Association & the Institute of Electrical and Electronics Engineers, Warsaw, Poland, 11–14 September 2017; pp. 1–9. [Google Scholar]
- Khaki, B.; Sharaf, A. A hybrid multi-loop controlled facts-based smart v2g battery charger. Int. J. Renew. Energy Res. 2013, 3, 155–160. [Google Scholar]
- Kirmani, S.; Jamil, M.; Akhtar, I. Bi-directional power control mechanism for a microgrid hybrid energy system with power quality enhancement capabilities. Int. J. Renew. Energy Res. 2017, 7, 1962–1965. [Google Scholar]
- Gori, P.A.; Sadarnac, D.; Caillierez, A.; Loudot, S. Sensorless inductive power transfer system for electric vehicles: strategy and control for automatic dynamic operation. In Proceedings of the 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017. [Google Scholar] [CrossRef]
- Madawala, U.K.; Neath, M.; Thrimawithana, D.J. A power-frequency controller for bidirectional inductive power transfer systems. IEEE Trans. Ind. Electron. 2013, 60, 310–317. [Google Scholar] [CrossRef]
- Pellitteri, F.; Boscaino, V.; Di Tommaso, A.O.; Miceli, R. Efficiency optimization in bi-directional inductive power transfer systems. In Proceedings of the 2015 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles (ESARS), Aachen, Germany, 3–5 March 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Diekhans, T.; De Doncker, R.W. A Dual-Side Controlled Inductive Power Transfer System Optimized for Large Coupling Factor Variations and Partial Load. IEEE Trans. Power Electron. 2015, 30, 6320–6328. [Google Scholar] [CrossRef]
- Samanta, S.; Rathore, A.K. A New Inductive Power Transfer Topology Using Direct AC-AC Converter with Active Source Current Waveshaping. IEEE Trans. Power Electron. 2017, 30, 5565–5577. [Google Scholar] [CrossRef]
- Swain, A.K.; Neath, M.J.; Madawala, U.K.; Thrimawithana, D.J. A dynamic multivariable state-space model for bidirectional inductive power transfer systems. IEEE Trans. Power Electron. 2012, 27, 4772–4780. [Google Scholar] [CrossRef]
- Huang, Z.; Wong, S.C.; Tse, C.K. Design of a Single-Stage Inductive-Power-Transfer Converter for Efficient EV Battery Charging. IEEE Trans. Veh. Technol. 2017, 66, 5808–5821. [Google Scholar] [CrossRef]
- Koyama, T.; Umetani, K.; Hiraki, E. Design Optimization Method for the Load Impedance to Maximize the Output Power in Dual Transmitting Resonator Wireless Power Transfer System. IEEJ J. Ind. Appl. 2018, 7, 49–55. [Google Scholar] [CrossRef]
- Lovison, G.; Kobayashi, D.; Sato, M.; Imura, T.; Hori, Y. Secondary-side-only Control for High Efficiency and Desired Power with Two Converters in Wireless Power Transfer Systems. IEEJ J. Ind. Appl. 2017, 6, 473–481. [Google Scholar] [CrossRef]
- Ota, R.; Nugroho, D.S.; Hoshi, N. Efficiency Maximization of Inductive Power Transfer System by Impedance and Switching Frequency Control in Secondary-side Converter. In Proceedings of the 2018 International Power Electronics Conference (IPEC), Niigata, Japan, 20–24 May 2018; pp. 3855–3862. [Google Scholar] [CrossRef]
- Moghaddami, M.; Sarwat, A. Single-Phase Soft-Switched AC-AC Matrix Converter with Power Controller for Bidirectional Inductive Power Transfer Systems. IEEE Trans. Ind. Appl. 2018, 9994, 3760–3770. [Google Scholar] [CrossRef]
- Ota, R.; Hoshi, N.; Junnosuke, H. Design of Compensation Capacitor in S/P Topology of Inductive Power Transfer System with Buck or Boost Converter on Secondary Side. IEEJ J. Ind. Appl. 2015, 4, 476–485. [Google Scholar] [CrossRef]
- Ota, R.; Hoshi, N.; Uchida, K. Improving the Efficiency by Controlling the Switching Frequency for Secondary-Side Converter of an Inductive Power Transfer System. Electr. Eng. Jpn. 2018, 202, 33–43. [Google Scholar] [CrossRef]
- Iwata, Y.; Suzuki, K.; Takeshita, T.; Hayashi, Y.; Iyasu, S. Isolated bidirectional single-phase AC/DC converter using a soft-switching technique. In Proceedings of the 2017 IEEE 6th International Conference on Renewable Energy Research and Applications (ICRERA), San Diego, CA, USA, 5–8 November 2017; pp. 383–388. [Google Scholar] [CrossRef]
- Ota, R.; Nugroho, D.S.; Hoshi, N. A Capacitance Design Guideline of Snubber Capacitors for Soft Switching in Bi-directional Inductive Power Transfer System Considering Battery Charging Cycle. In Proceedings of the 7th International Conference on Renewable Energy Research and Applications (ICRERA), Paris, France, 14–17 October 2018; pp. 1080–1085. [Google Scholar] [CrossRef]
- Diekhans, T.; Stewing, F.; Engelmann, G.; Van Hoek, H.; De Doncker, R.W. A systematic comparison of hard- and soft-switching topologies for inductive power transfer systems. In Proceedings of the 4th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 30 September–1 October 2014. [Google Scholar] [CrossRef]
- Liu, C.; Hu, A.P.; Wang, B.; Nair, N.K.C. A capacitively coupled contactless matrix charging platform with soft switched transformer control. IEEE Trans. Ind. Electron. 2013, 60. [Google Scholar] [CrossRef]

| Switching frequency of the active bridges f | 85 kHz |
| Angle equivalent to dead-time length | 0.427 rad (@ ns) |
| Primary-side direct current (DC) voltage | 200 V |
| Secondary-side DC voltage | 150 V, 200 V |
| Charging DC current for battery | 8 A |
| Inductance of primary-side coil , secondary-side coil | 67.7 uH, 68.6 uH |
| ESR of primary-side coil , secondary-side coil | 95 m, 103 m |
| Coupling coefficient k | 0.3 |
| Software programing language | C++ language |
| Switching frequency of the active bridges f | 85 kHz |
| Angle equivalent to dead-time length | 0.427 rad (@ ns) |
| Primary-side DC voltage | 200 V |
| Secondary-side DC voltage | 150 V, 200 V |
| Inductance of primary-side coil , secondary-side coil | 67.7 uH, 68.6 uH |
| ESR of primary-side coil , secondary-side coil | 95 m, 103 m |
| Snubber capacitor | None (parasitic) |
| Coupling coefficient k | 0.3 |
| Switching devices | ROHM BSM080D12P2C008 |
| Oscilloscope | Tektronix MDO4034C |
| Power meter | HIOKI PW6001 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ota, R.; Sudarmo Nugroho, D.; Hoshi, N. A Consideration on Maximum Efficiency of Resonant Circuit of Inductive Power Transfer System with Soft-Switching Operation. World Electr. Veh. J. 2019, 10, 54. https://doi.org/10.3390/wevj10030054
Ota R, Sudarmo Nugroho D, Hoshi N. A Consideration on Maximum Efficiency of Resonant Circuit of Inductive Power Transfer System with Soft-Switching Operation. World Electric Vehicle Journal. 2019; 10(3):54. https://doi.org/10.3390/wevj10030054
Chicago/Turabian StyleOta, Ryosuke, Dannisworo Sudarmo Nugroho, and Nobukazu Hoshi. 2019. "A Consideration on Maximum Efficiency of Resonant Circuit of Inductive Power Transfer System with Soft-Switching Operation" World Electric Vehicle Journal 10, no. 3: 54. https://doi.org/10.3390/wevj10030054
APA StyleOta, R., Sudarmo Nugroho, D., & Hoshi, N. (2019). A Consideration on Maximum Efficiency of Resonant Circuit of Inductive Power Transfer System with Soft-Switching Operation. World Electric Vehicle Journal, 10(3), 54. https://doi.org/10.3390/wevj10030054