Research on the Anti-Disturbance Control Method of Brake-by-Wire Unit for Electric Vehicles
Abstract
:1. Introduction
2. Structure and Model of the DDEHB
2.1. Structure and Principle of the DDEHB
2.2. Model of the DDEHB
3. Control Method of the DDEHB
3.1. State Observer
3.2. Anti-Disturbance Controller
3.2.1. Outer Controller
3.2.2. Inner Controller
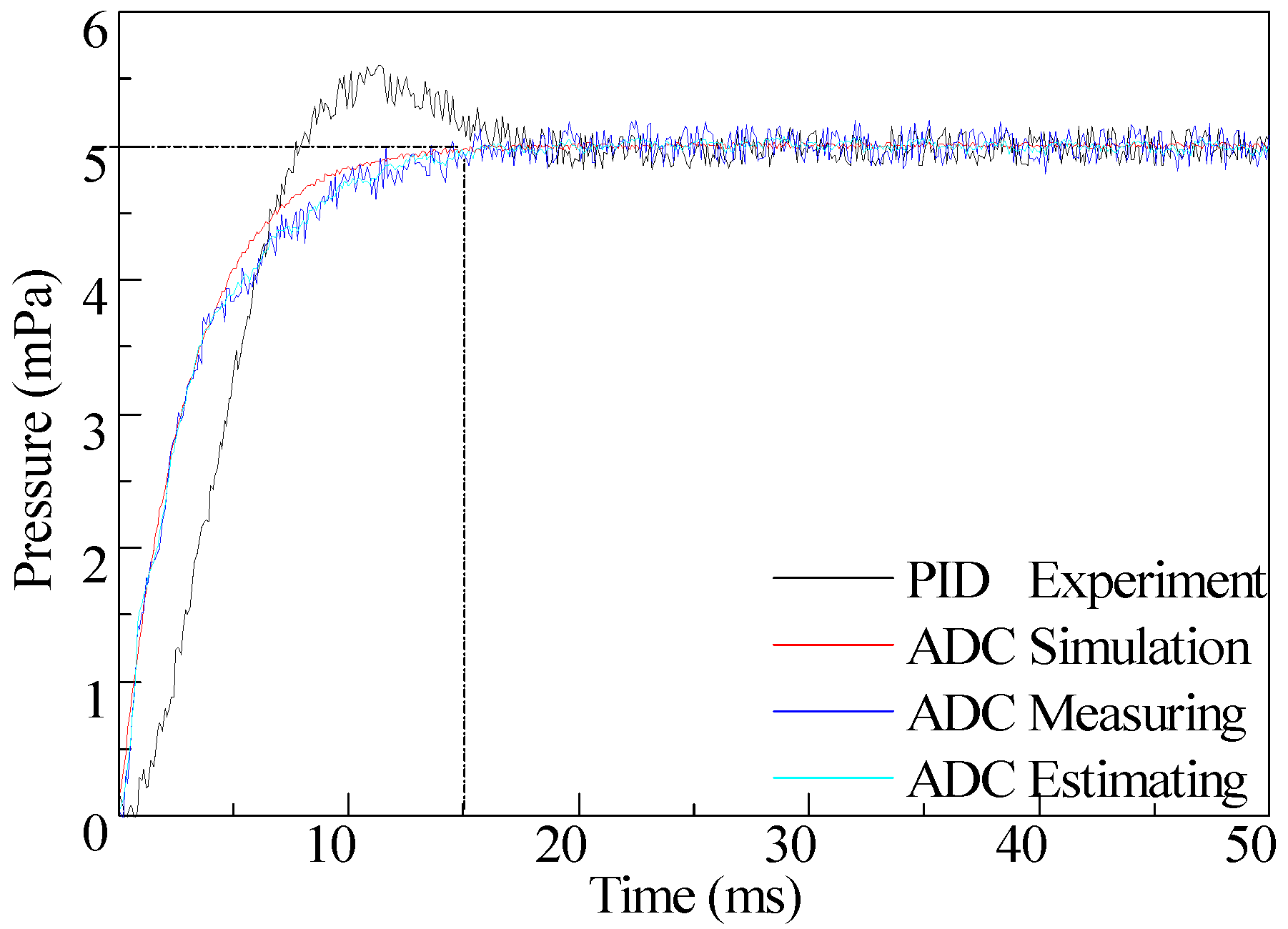
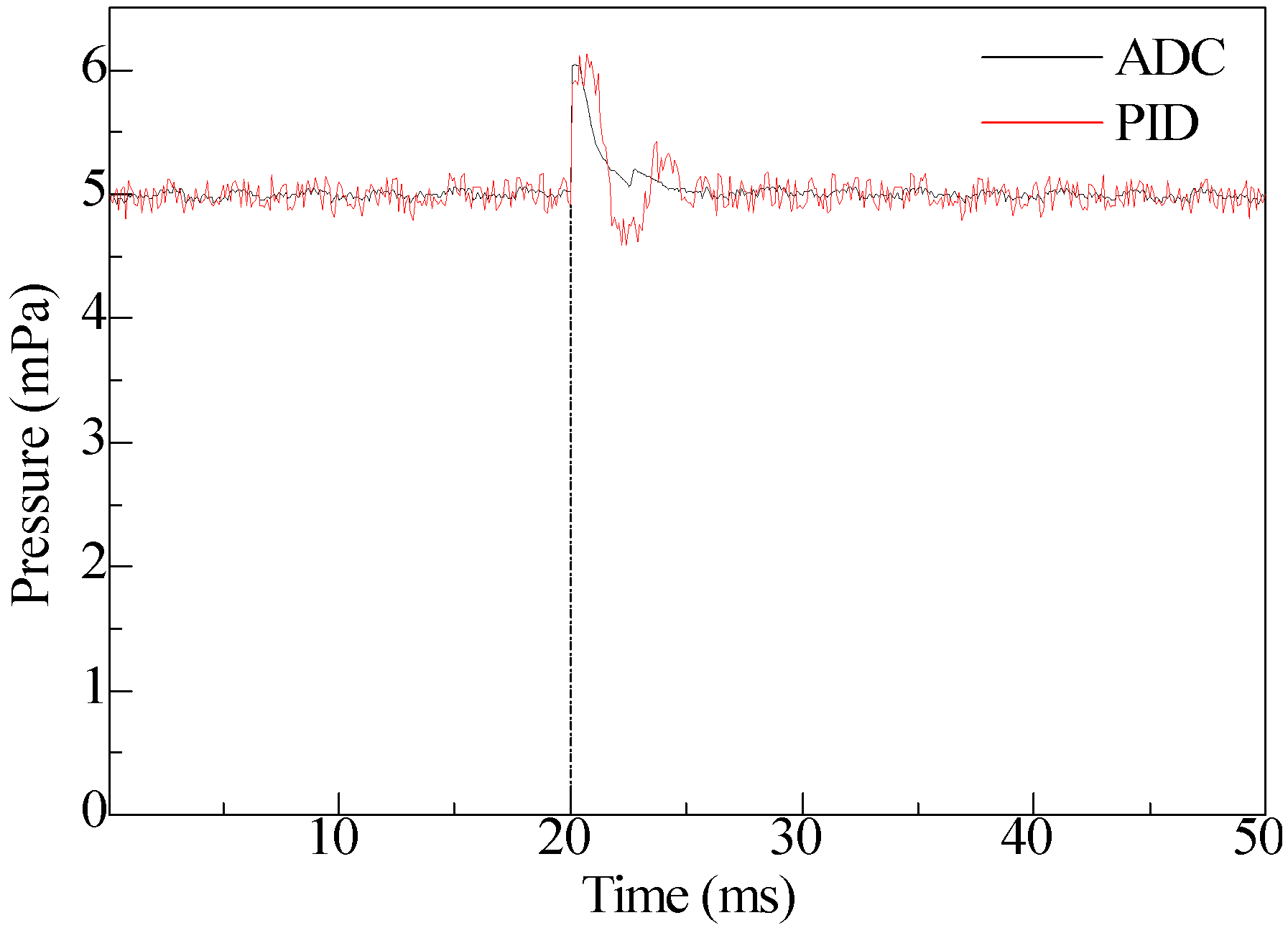
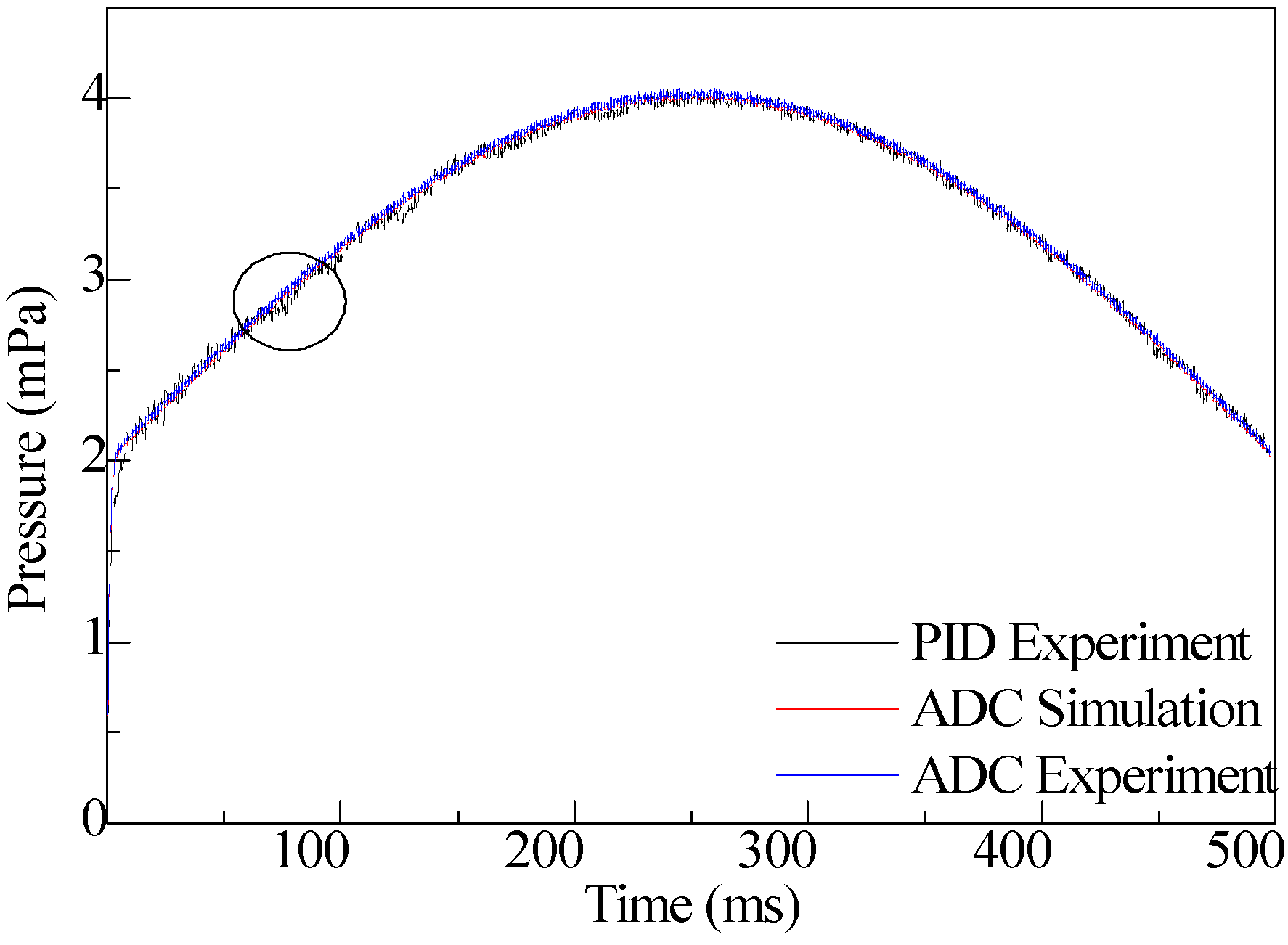
4. Simulation and Experimental Test
4.1. Simulation and Experimental Test of the DDEHB
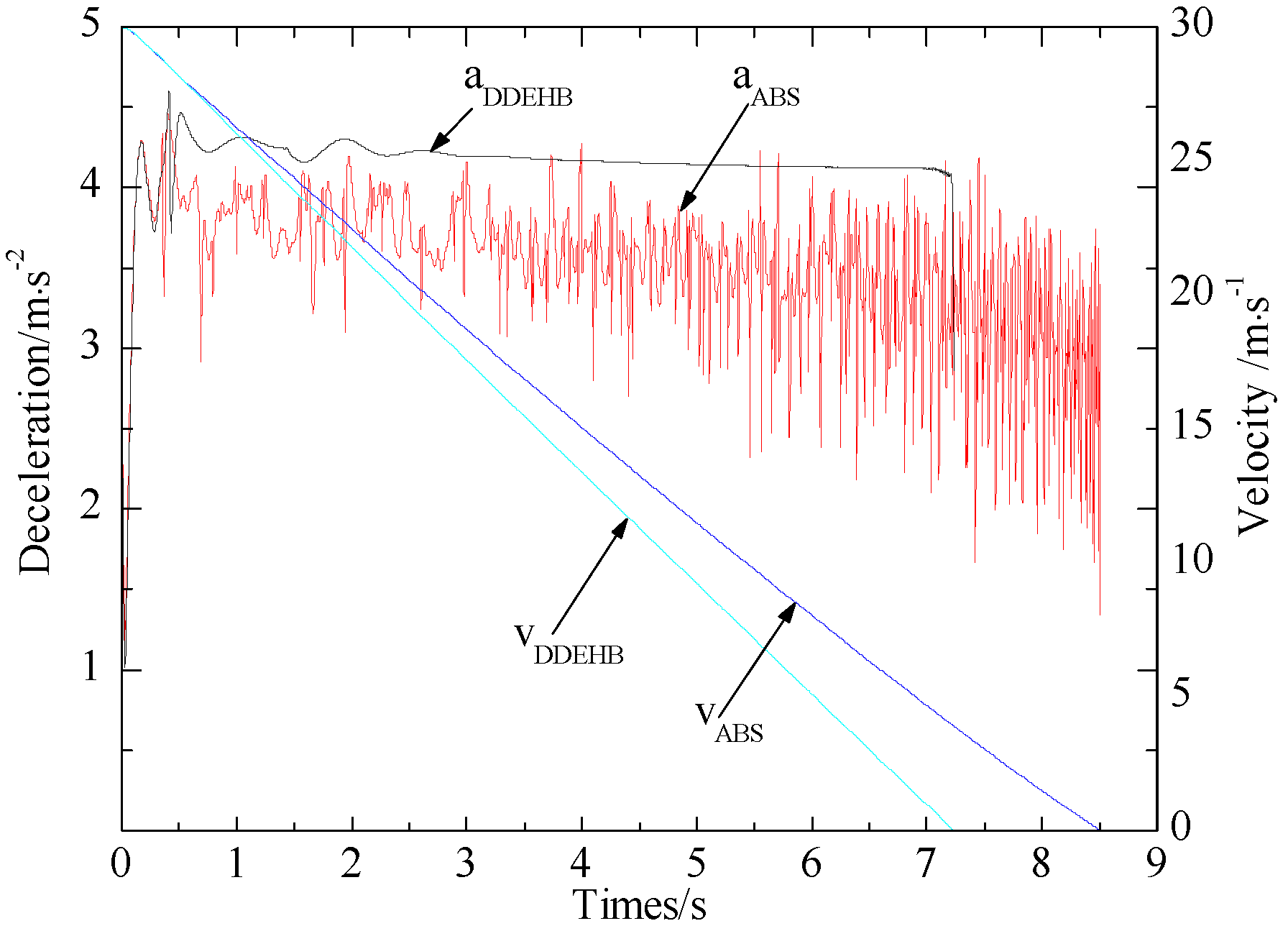
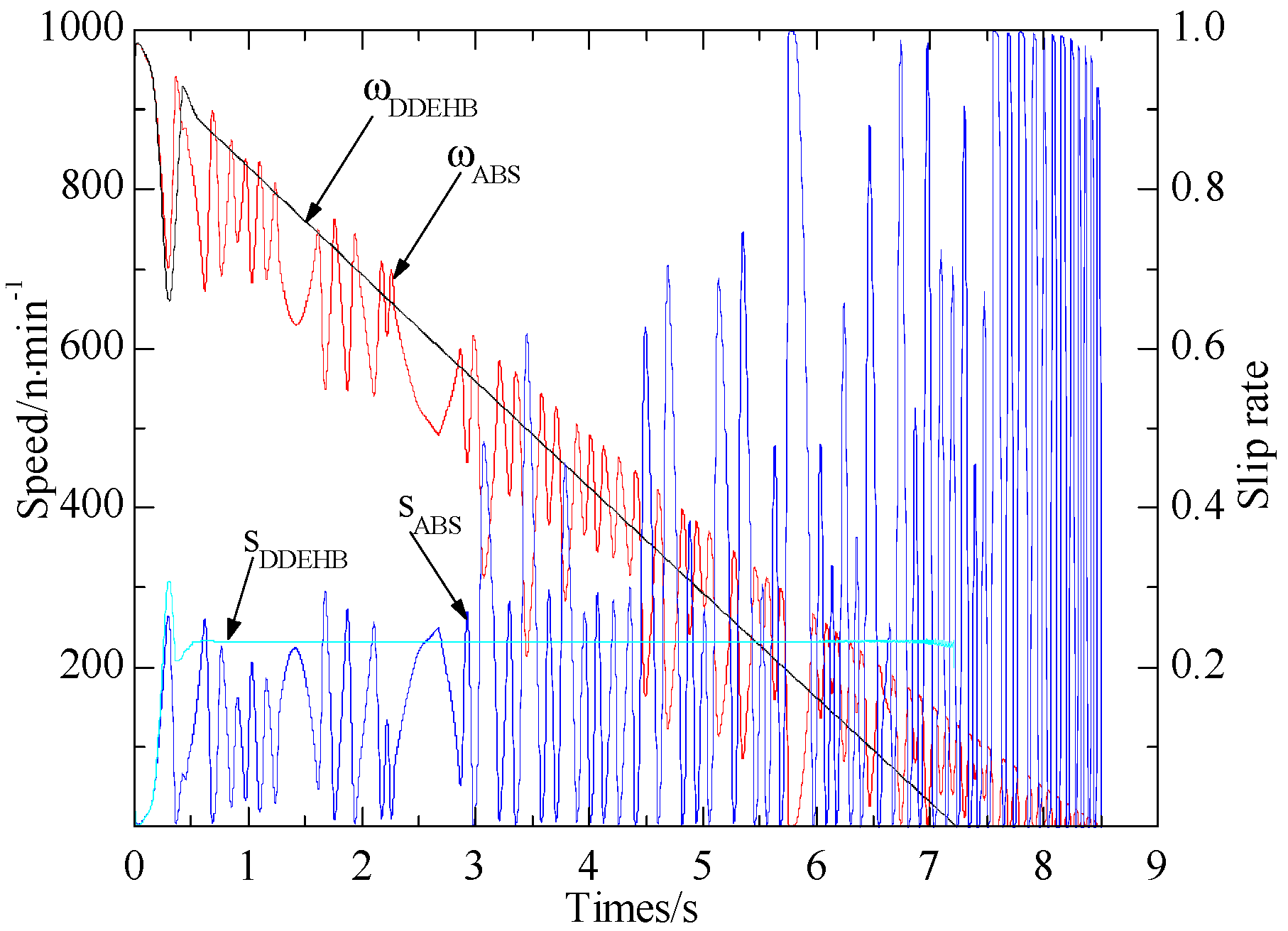
4.2. Simulation of Vehicle Performance
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, Y.; Lu, C.; Shen, J.; Yuan, C. Design and analysis of output feedback constraint control for antilock braking system with time-varying slip ratio. Math. Probl. Eng. 2019, 2019, 1–11. [Google Scholar] [CrossRef]
- Radac, M.-B.; Precup, R.-E. Data-driven model-free slip control of anti-lock braking systems using reinforcement q-learning. Neurocomputing 2018, 275, 317–329. [Google Scholar] [CrossRef]
- Sardarmehni, T.; Heydari, A. Sub-optimal switching in anti-lock brake systems using approximate dynamic programming. IET Control Theory Appl. 2019, 13, 1413–1424. [Google Scholar] [CrossRef]
- Ma, B.; Lin, M.; Chen, Y.; Wang, L.-X. Investigation of energy efficiency for electro-hydraulic composite braking system which is based on the regenerated energy. Adv. Mechan. Eng. 2016, 8, 1687814016666449. [Google Scholar] [CrossRef]
- Yong, J.; Gao, F.; Ding, N.; He, Y. Design and validation of an electro-hydraulic brake system using hardware-in-the-loop real-time simulation. Int. J. Automot. Technol. 2017, 18, 603–612. [Google Scholar] [CrossRef]
- Park, G.; Choi, S.; Hyun, D. Clamping force estimation based on hysteresis modeling for electro-mechanical brakes. Int. J. Automot. Technol. 2017, 18, 883–890. [Google Scholar] [CrossRef]
- Jo, C.H.; Lee, S.M.; Song, H.L.; Cho, Y.S.; Kim, I.; Hyun, D.Y.; Kim, H.S. Design and control of an upper-wedge-type electronic brake. Proc. Inst. Mechan. Eng. Part D 2010, 224, 1393–1405. [Google Scholar] [CrossRef]
- Hui, L.; Weida, W.; Jiao, H.; Changle, X. Modeling and simulation of the regenerative braking system in a hev based on fuzzy control. Automot. Eng. 2012, 34, 51–56. [Google Scholar]
- Benine-Neto, A.; Moreau, X.; Lanusse, P. Robust control for an electro-mechanical anti-lock braking system: The crone approach. IFAC-PapersOnLine 2017, 50, 12575–12581. [Google Scholar] [CrossRef]
- Peng, X.; Jia, M.; He, L.; Yu, X.; Lv, Y. Fuzzy sliding mode control based on longitudinal force estimation for electro-mechanical braking systems using bldc motor. CES Trans. Electr. Mach. Syst. 2018, 2, 142–151. [Google Scholar]
- Han, K.; Kim, M.; Huh, K. Modeling and control of an electronic wedge brake. Proc. Inst. Mechan. Eng. Part C 2012, 226, 2440–2455. [Google Scholar] [CrossRef]
- Lee, C.F.; Manzie, C. Active brake judder attenuation using an electromechanical brake-by-wire system. IEEE/ASME Trans. Mechatron. 2016, 21, 2964–2976. [Google Scholar] [CrossRef]
- Todeschini, F.; Formentin, S.; Panzani, G.; Corno, M.; Savaresi, S.M.; Zaccarian, L. Nonlinear pressure control for bbw systems via dead-zone and antiwindup compensation. IEEE Trans. Control Syst. Technol. 2016, 24, 1419–1431. [Google Scholar] [CrossRef]
- Shin, D.-H.; Lee, S.; Jeong, C.-P.; Kwon, O.-S.; Park, T.-S.; Jin, S.-H.; Ban, D.H.; Yang, S.-H. Analytic approaches for keeping high braking efficiency and clamping efficiency of electro wedge brakes. Int. J. Prec. Eng. Manuf. 2015, 16, 1609–1615. [Google Scholar] [CrossRef]
- Lindvai-Soos, D.; Horn, M. Modelling, Control & Implementation of an Electro-Mechanic Braking Force Actuator for HEV and EV; IFAC Proceedings Volumes Series; Elsevier: Amsterdam, The Netherlands, 2013; pp. 620–625. [Google Scholar]
- Wang, C.; Zhao, W.; Li, W. Braking sense consistency strategy of electro-hydraulic composite braking system. Mechan. Syst. Signal Process. 2018, 109, 196–219. [Google Scholar] [CrossRef]
- Li, J.; Ding, M.; Yong, W.; Li, C. Evaluation and optimization of the nonlinear flow controllability of switch valve in vehicle electro-hydraulic brake system. IEEE Access 2018, 6, 31281–31293. [Google Scholar] [CrossRef]
- Xiaoxiang, G.; Siqing, C.; Lichen, J.; Xiaopan, L. Research on regenerative brake technology of electric vehicle based on direct-drive electric-hydraulic brake system. Int. J. Veh. Design 2016, 70, 1–28. [Google Scholar]
- Cheon, J.S. Brake by Wire System Configuration and Functions Using Front EWB (Electric Wedge Brake) and Rear EMB (Electro-Mechanical Brake) Actuators; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Gong, X.; Chang, S.; Jiang, L.; Li, X. Braking method of electric vehicle based on direct drive electro- hydraulic brake unit. Open Mechan. Eng. J. 2015, 9, 351–360. [Google Scholar] [CrossRef]
- Zhiyuan, L.; Zhaodu, L.; Haifeng, C.; Renguang, W. Experimental study on change rate model of brake pressure of abs wheel cylinder. Trans. Chin Soc. Agric. Mach. 2007, 38, 6–9. [Google Scholar]
- Jingqing, H. Auto disturbances rejection control technique. Front. Sci. 2007, 1, 24–31. [Google Scholar]
- Zeng-Qiang, C.; Ming-Wei, S.; Rui-Guang, Y. On the stability of linear active disturbance rejection control. Acta Autom. Sin. 2013, 39, 574–580. [Google Scholar]
- Tan, S. Research on actuator of electromechanical brake and hardware in-the-loop test bench for light vehicle. Ph.D. Thesis, Jilin University, Changchun, China, 2008. [Google Scholar]
- Zhuoping, Y.; Jianling, Z.; Hui, C. Tire-road friction coefficient estimation with four wheel in-wheel-motor drive vehicle. Automot. Eng. 2007, 29, 141–145. [Google Scholar]







| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Value | −0.73 | 0.69 | 3.74 | 3 | 6.3 | 3.4 | 0.04 |
| Parameter | Value |
|---|---|
| EMLA diameter/mm | 60 |
| EMLA length/mm | 70 |
| EMLA voltage/V | 24 |
| Coil resistance/Ω | 0.7615 |
| Coil inductance/μH | 279.8 |
| Peak current/A | 25 |
| Parameter | Value |
|---|---|
| Piston diameter/mm | 38 |
| Plunger diameter/mm | 6 |
| Max pressure/mPa | 10 |
| Max braking force/N | 10,343 (μ = 0.38) |
| Max piston pressure/N | 27219 |
| Electromagnetic force/N | 339 |
| Parameter | Symbol/Unit | Value |
|---|---|---|
| Vehicle mass | M/kg | 1367 |
| Center of gravity | Hg/mm | 375 |
| Axle base | l/mm | 2400 |
| Front axle base | lf/mm | 1056 |
| Rear axle base | lr/mm | 1344 |
| Brake System | Brake Distance/m | Brake Time/s |
|---|---|---|
| Conventional ABS | 123.85 | 8.56 |
| DDEHB | 108.75 | 7.23 |
| Performance improvement | 12.19% | 15.54% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, X.; Qian, L.; Ge, W.; Wang, L. Research on the Anti-Disturbance Control Method of Brake-by-Wire Unit for Electric Vehicles. World Electr. Veh. J. 2019, 10, 44. https://doi.org/10.3390/wevj10020044
Gong X, Qian L, Ge W, Wang L. Research on the Anti-Disturbance Control Method of Brake-by-Wire Unit for Electric Vehicles. World Electric Vehicle Journal. 2019; 10(2):44. https://doi.org/10.3390/wevj10020044
Chicago/Turabian StyleGong, Xiaoxiang, Lixia Qian, Weiguo Ge, and Lifeng Wang. 2019. "Research on the Anti-Disturbance Control Method of Brake-by-Wire Unit for Electric Vehicles" World Electric Vehicle Journal 10, no. 2: 44. https://doi.org/10.3390/wevj10020044
APA StyleGong, X., Qian, L., Ge, W., & Wang, L. (2019). Research on the Anti-Disturbance Control Method of Brake-by-Wire Unit for Electric Vehicles. World Electric Vehicle Journal, 10(2), 44. https://doi.org/10.3390/wevj10020044





