Hierarchical Coordinated Control Method of In-Wheel Motor Drive Electric Vehicle Based on Energy Optimization
Abstract
:1. Introduction
2. Driving Architecture and Dynamic Model of an Electric Vehicle
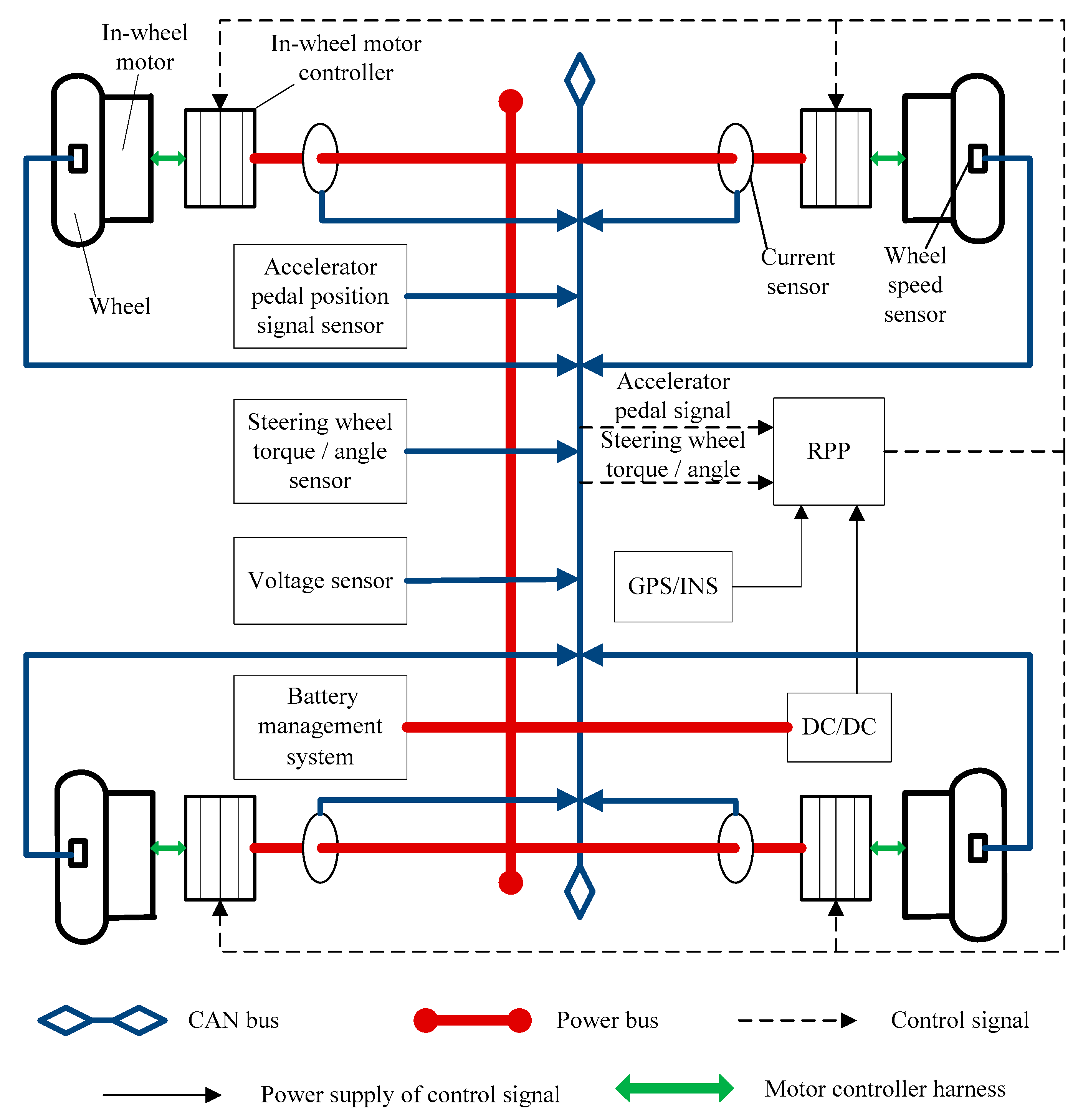
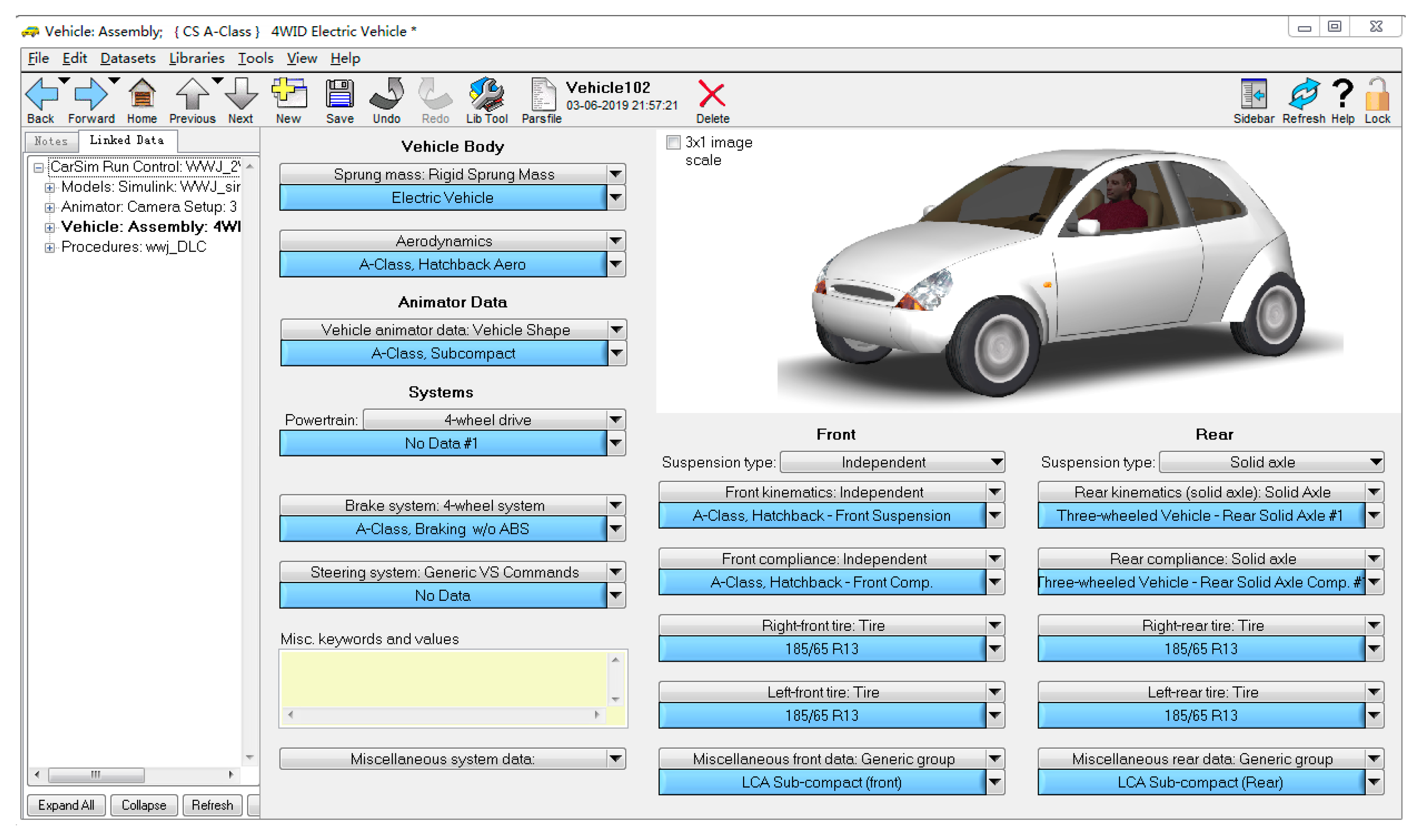
2.1. Driving Architecture and Simulation Modeling
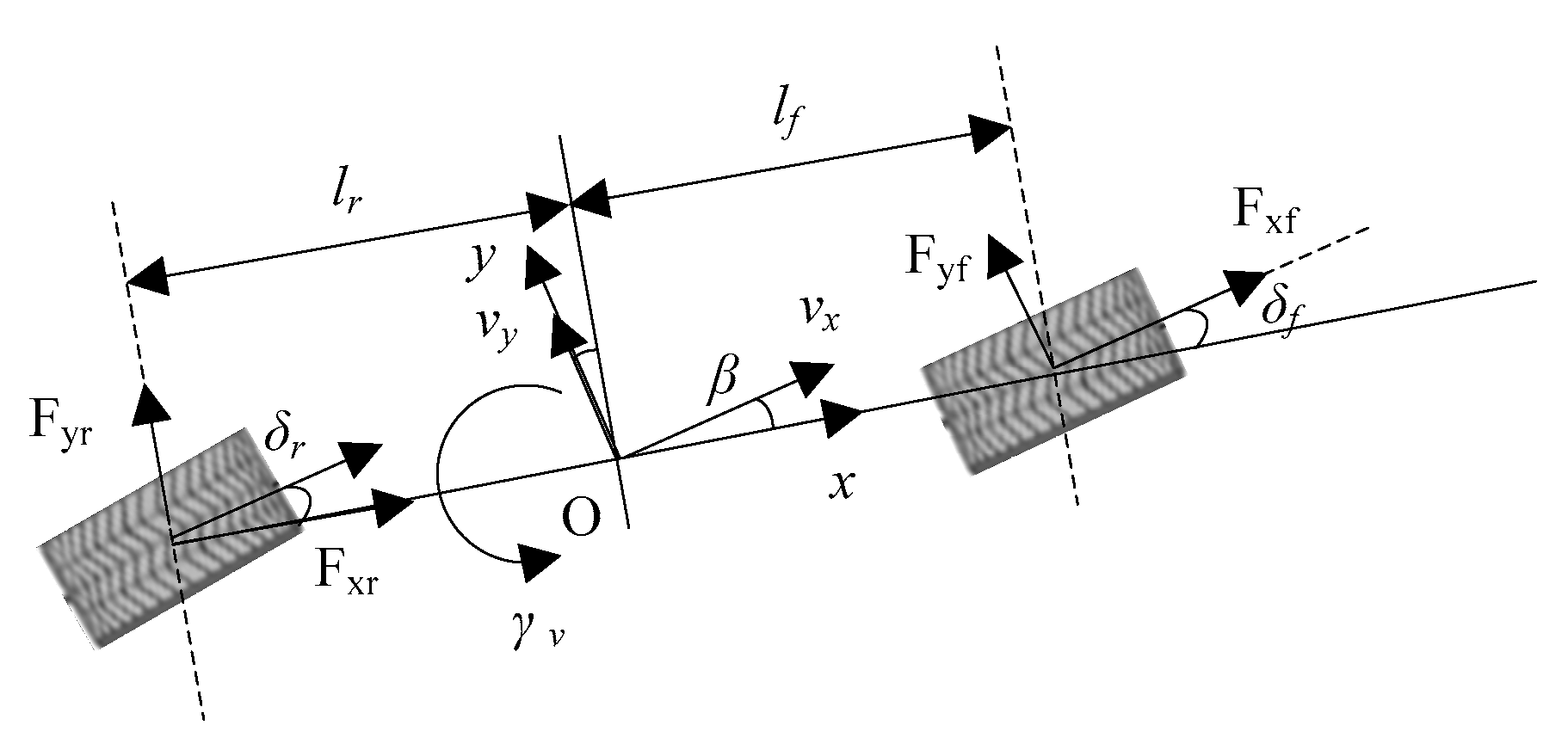
2.2. Vehicle Dynamic Model
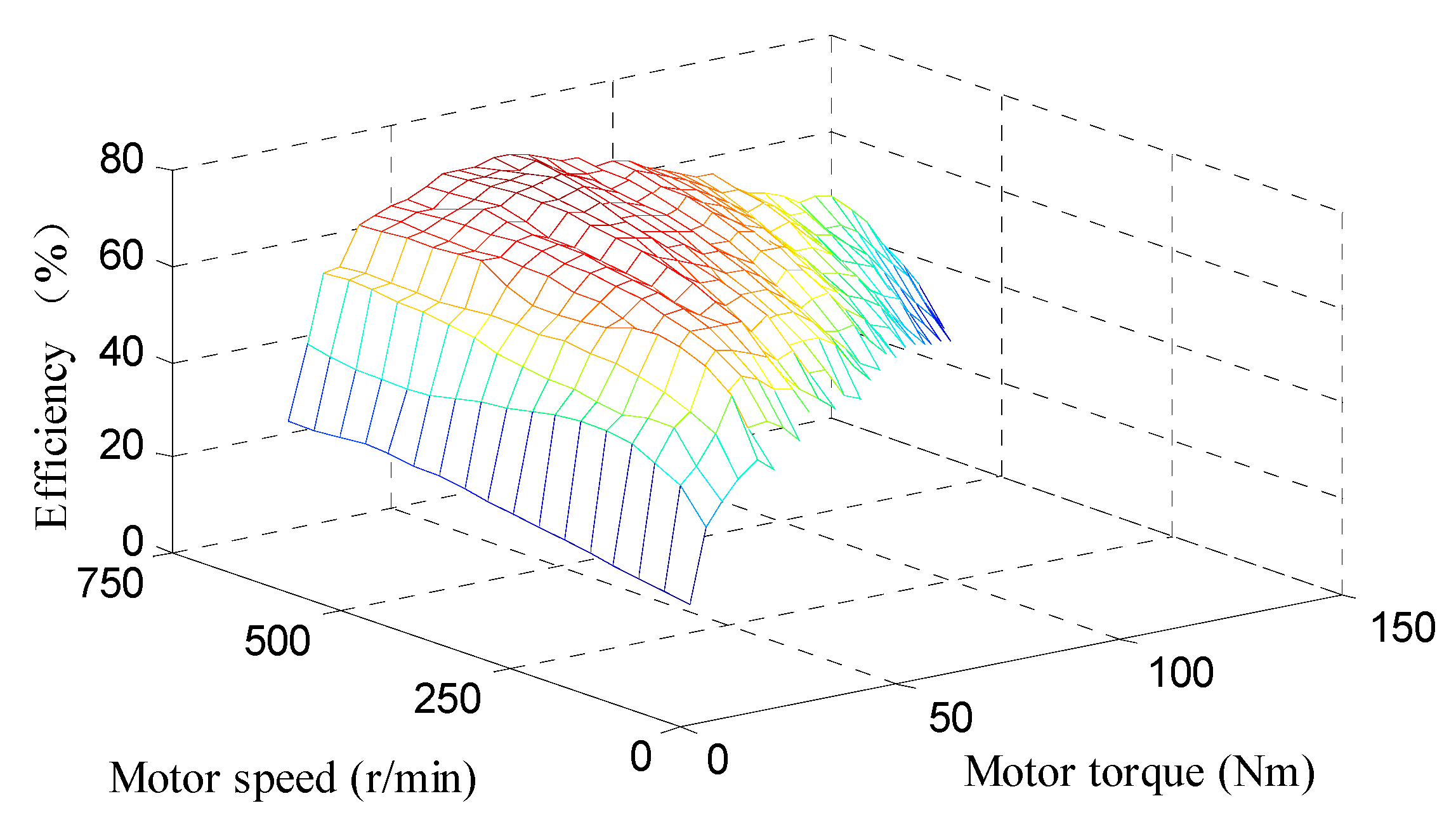
3. Analysis of Energy-Saving Feasibility
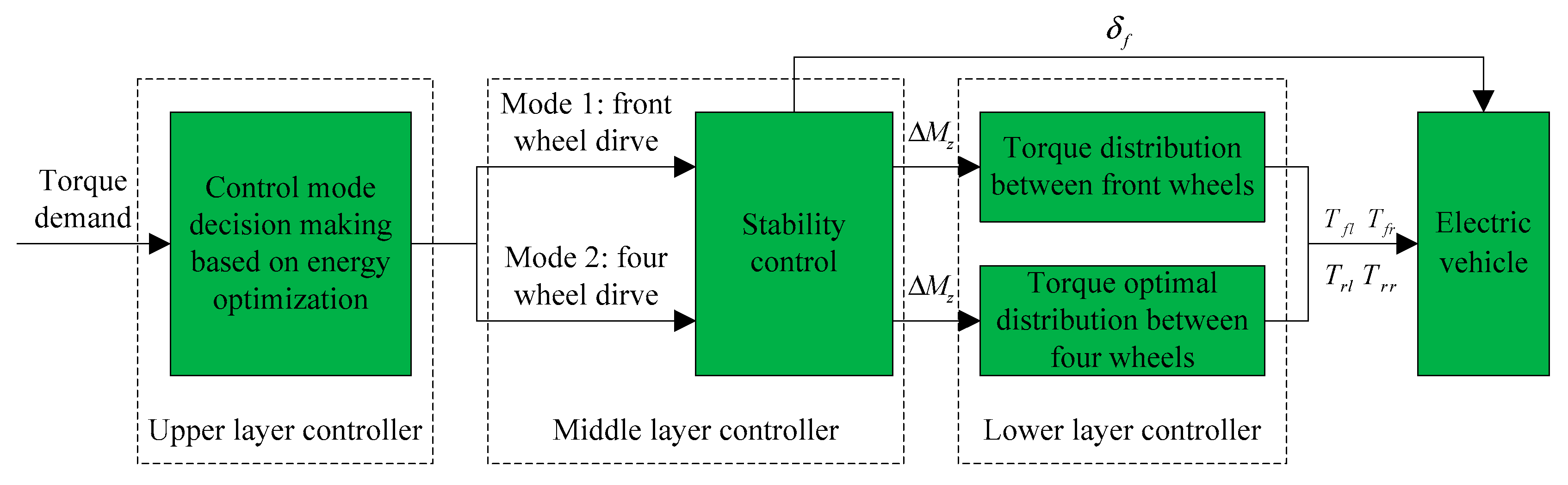
4. Hierarchical Coordinated Control Method Based on Energy Optimization
4.1. Overall Control Strategy
4.2. Upper Layer Controller: Driving Mode Decision
4.3. Middle Layer Controller: Vehicle Stability Control
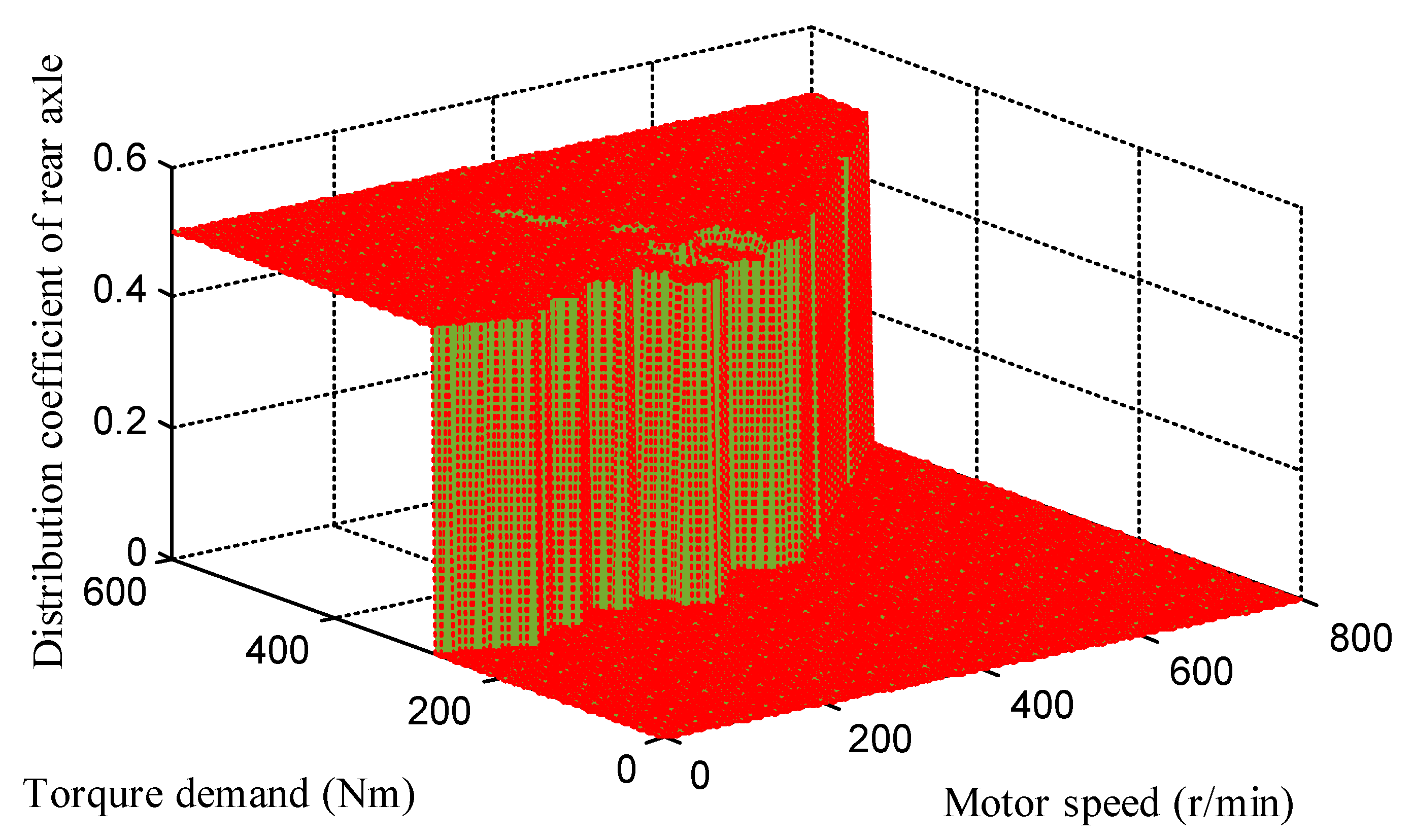
4.4. Lower Layer Controller: Optimal Torque Distribution Method in Different Driving Modes
5. Simulation Results
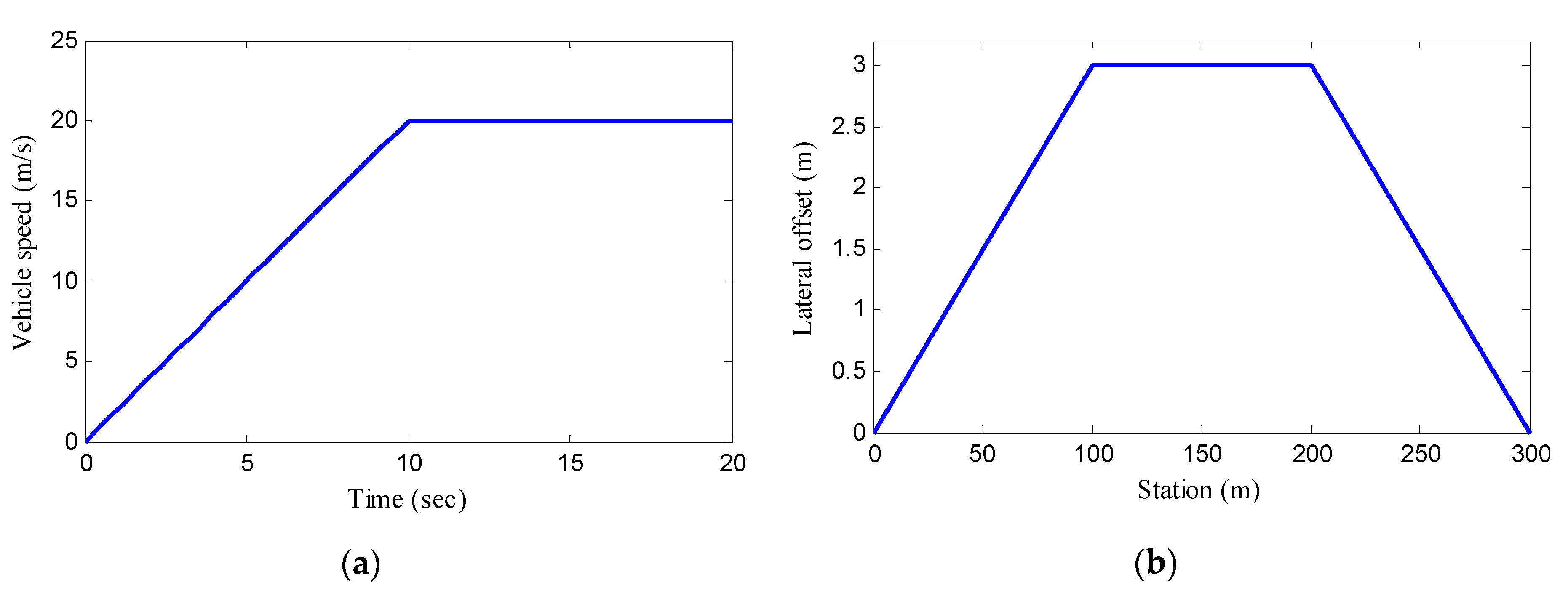
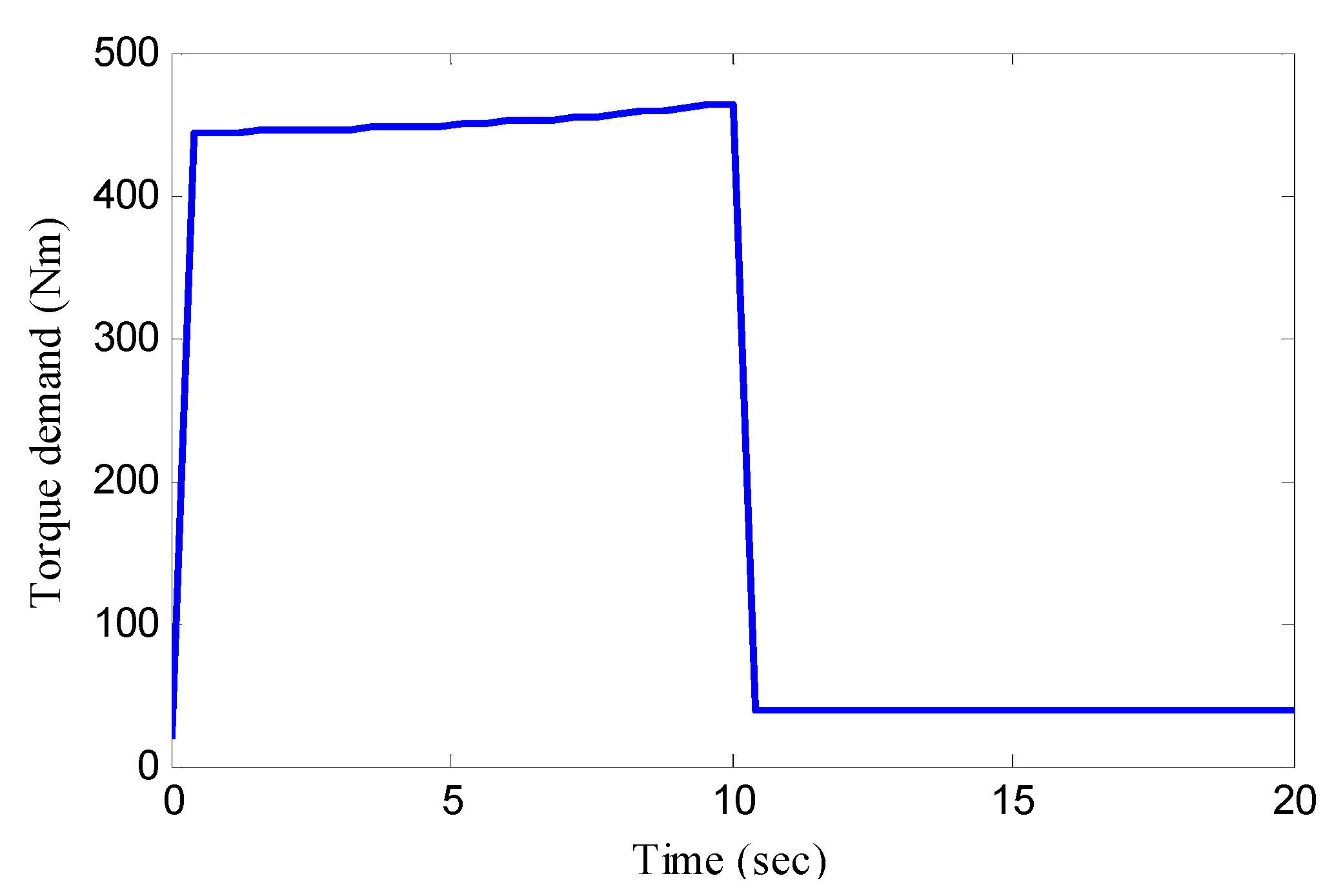
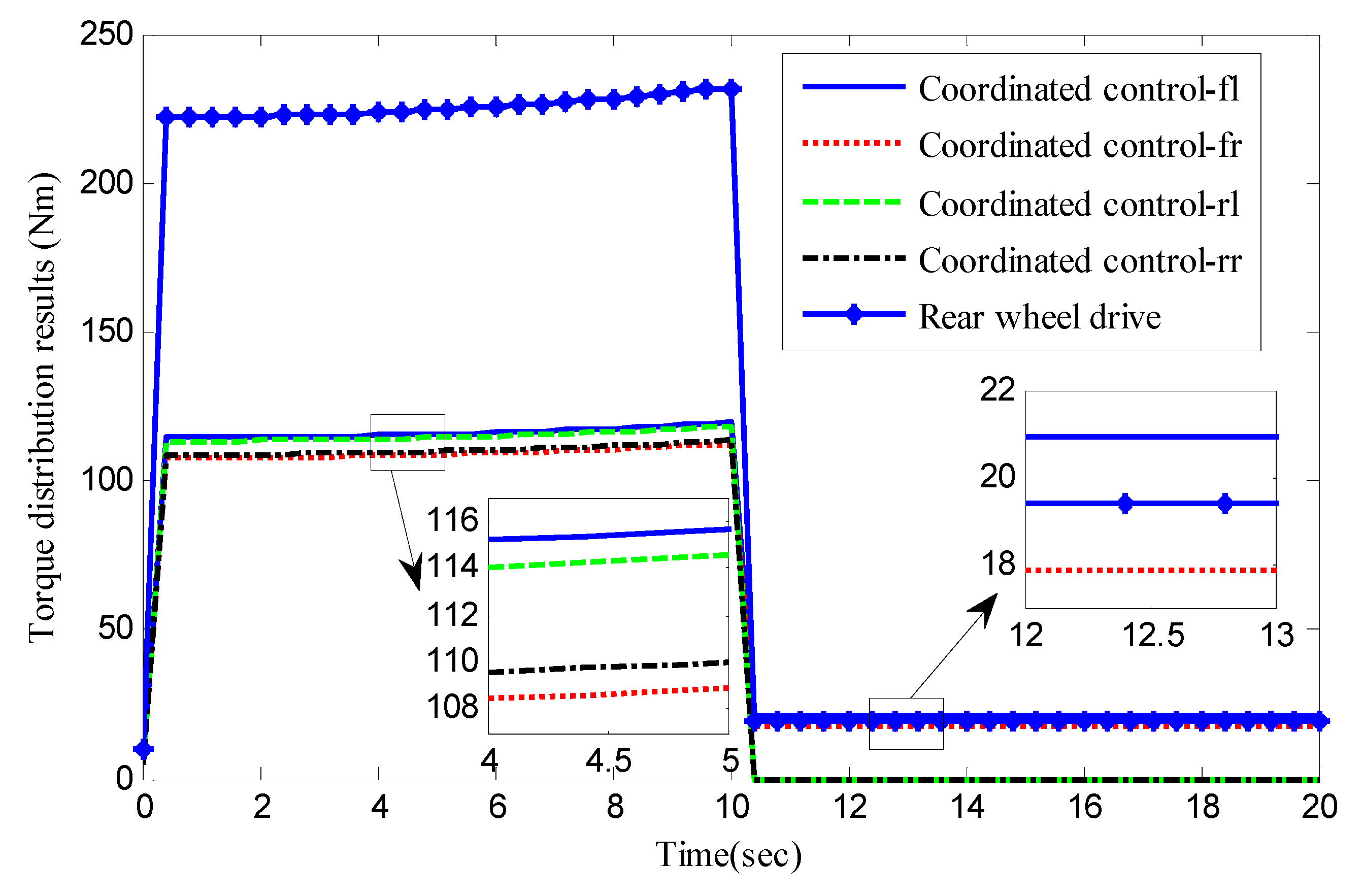
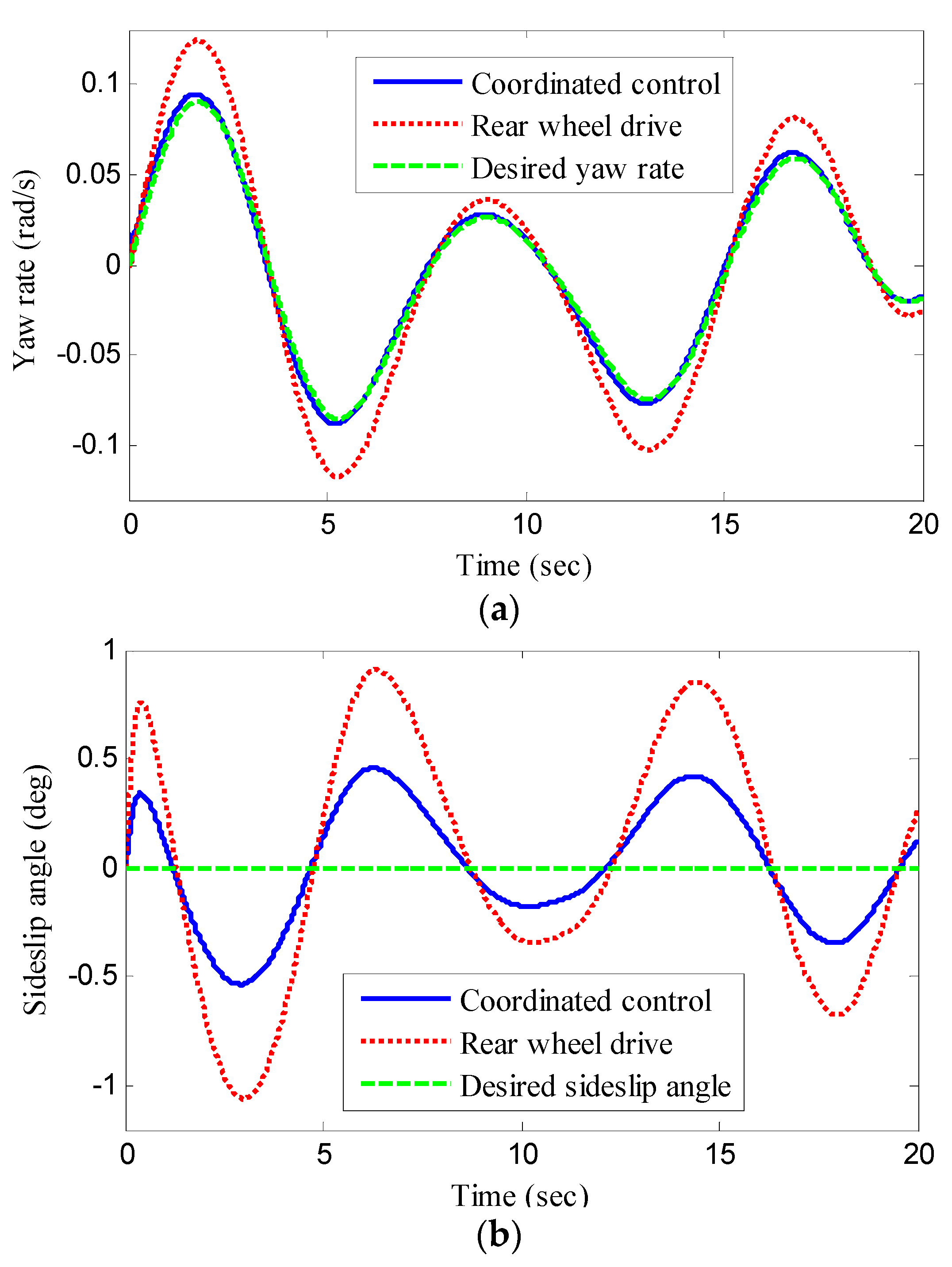
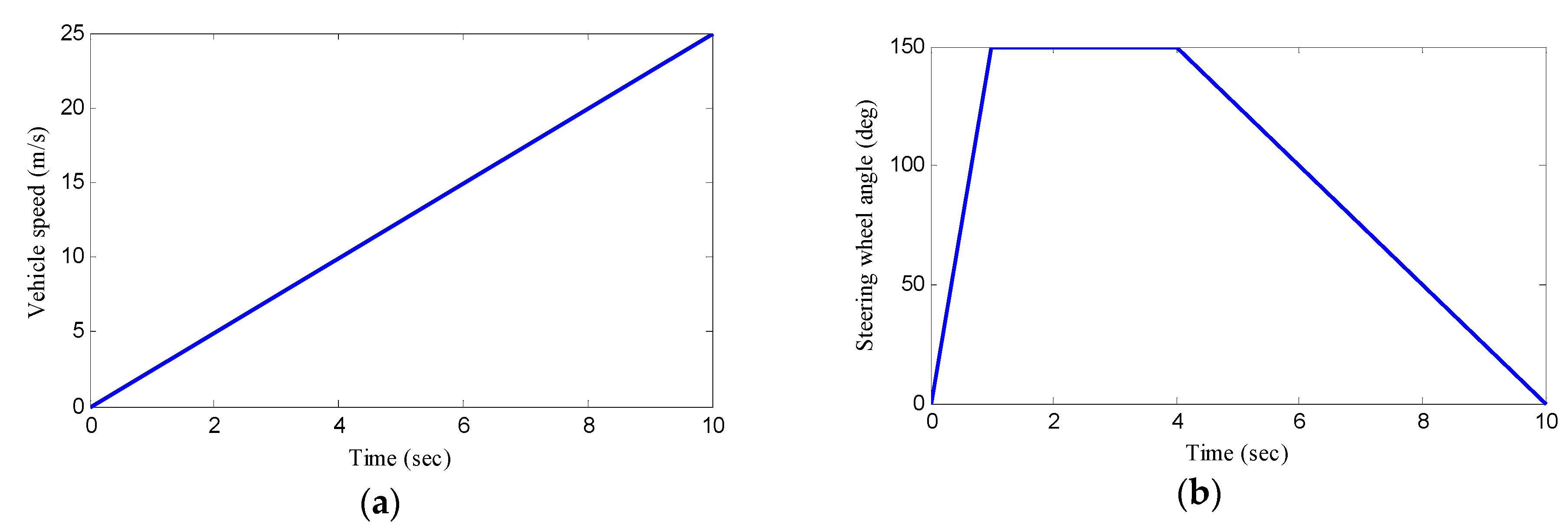
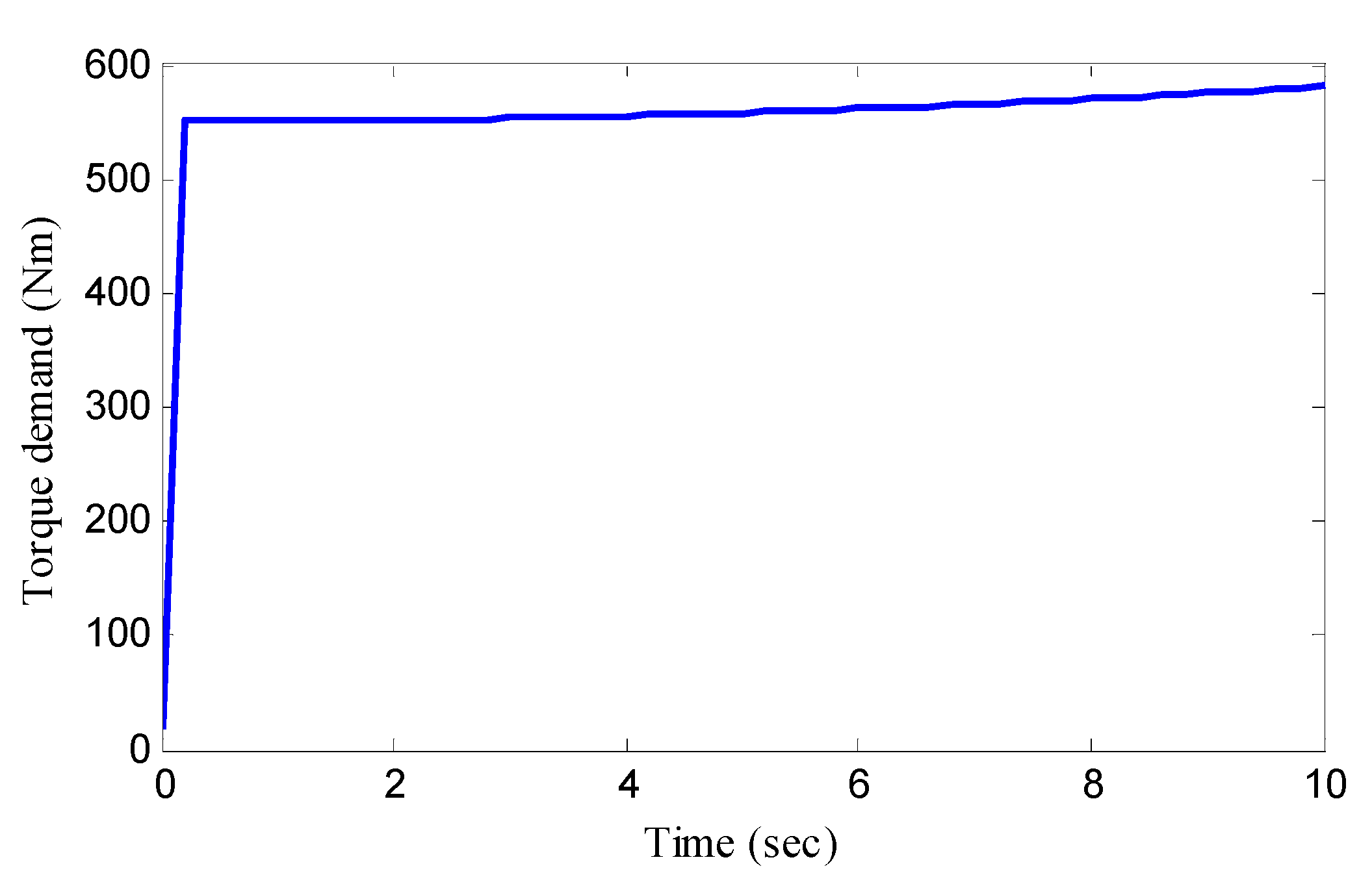
5.1. Double Lane Change Manoeuvre
5.2. J-Turn Manoeuver
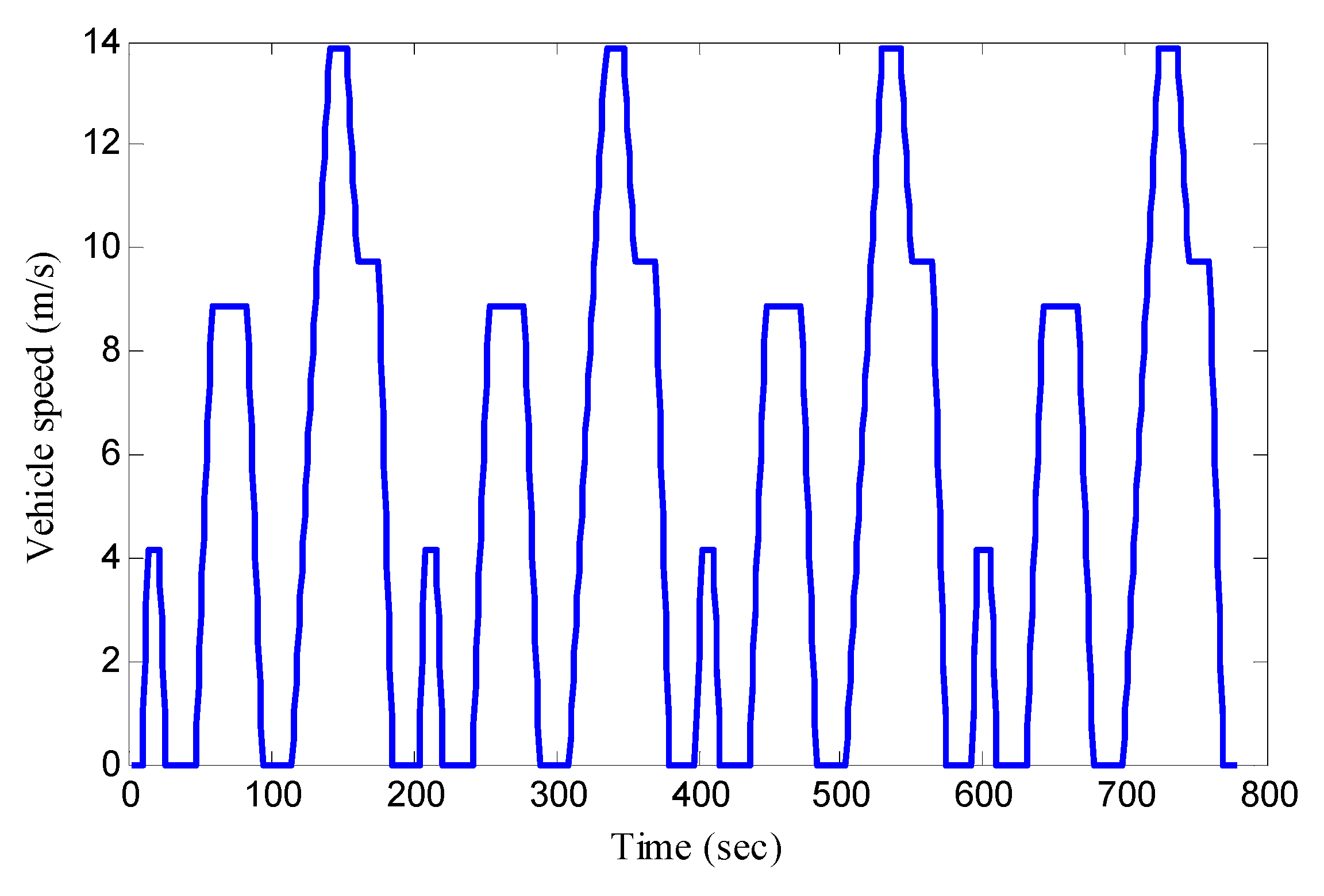
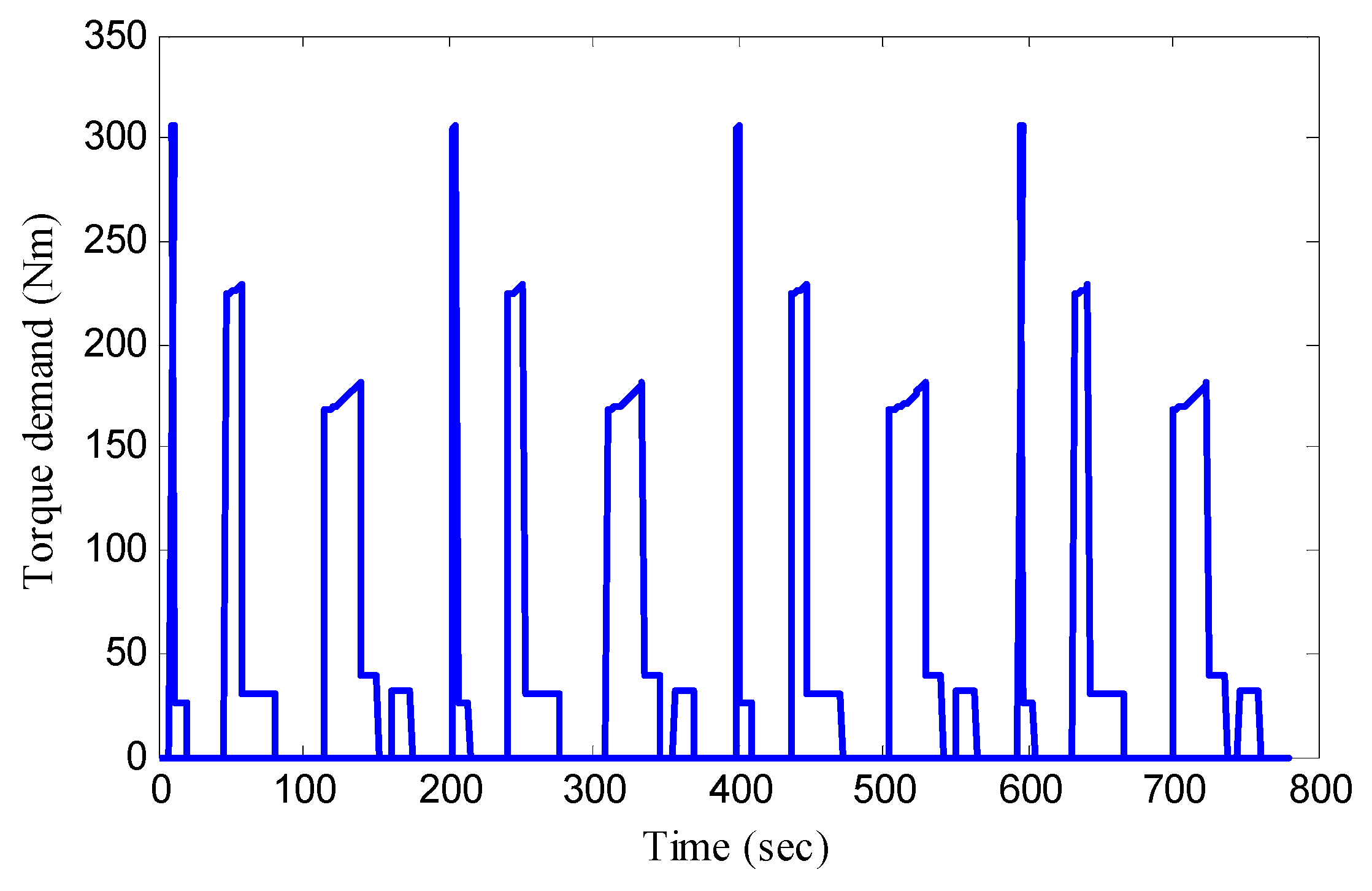
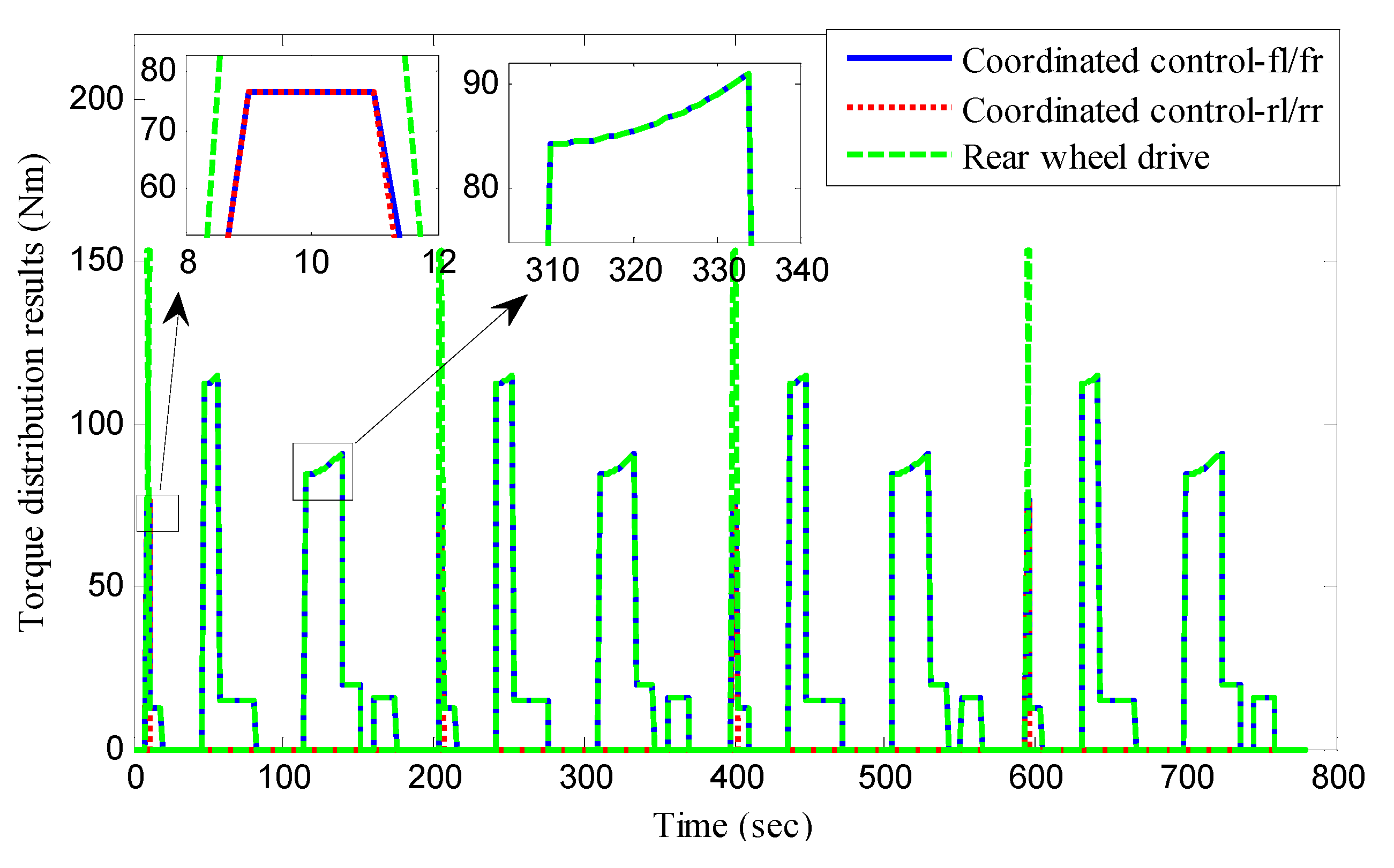
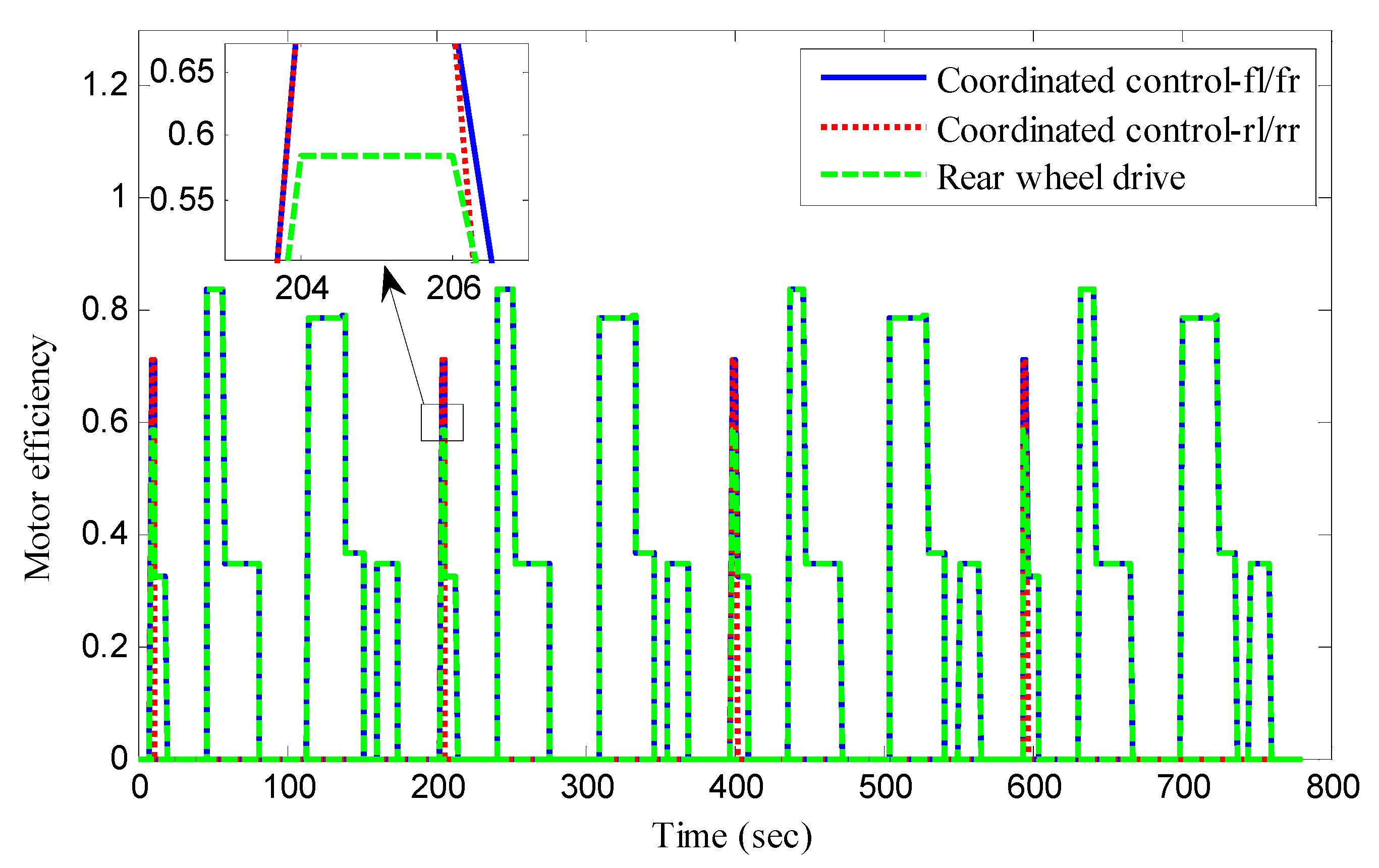
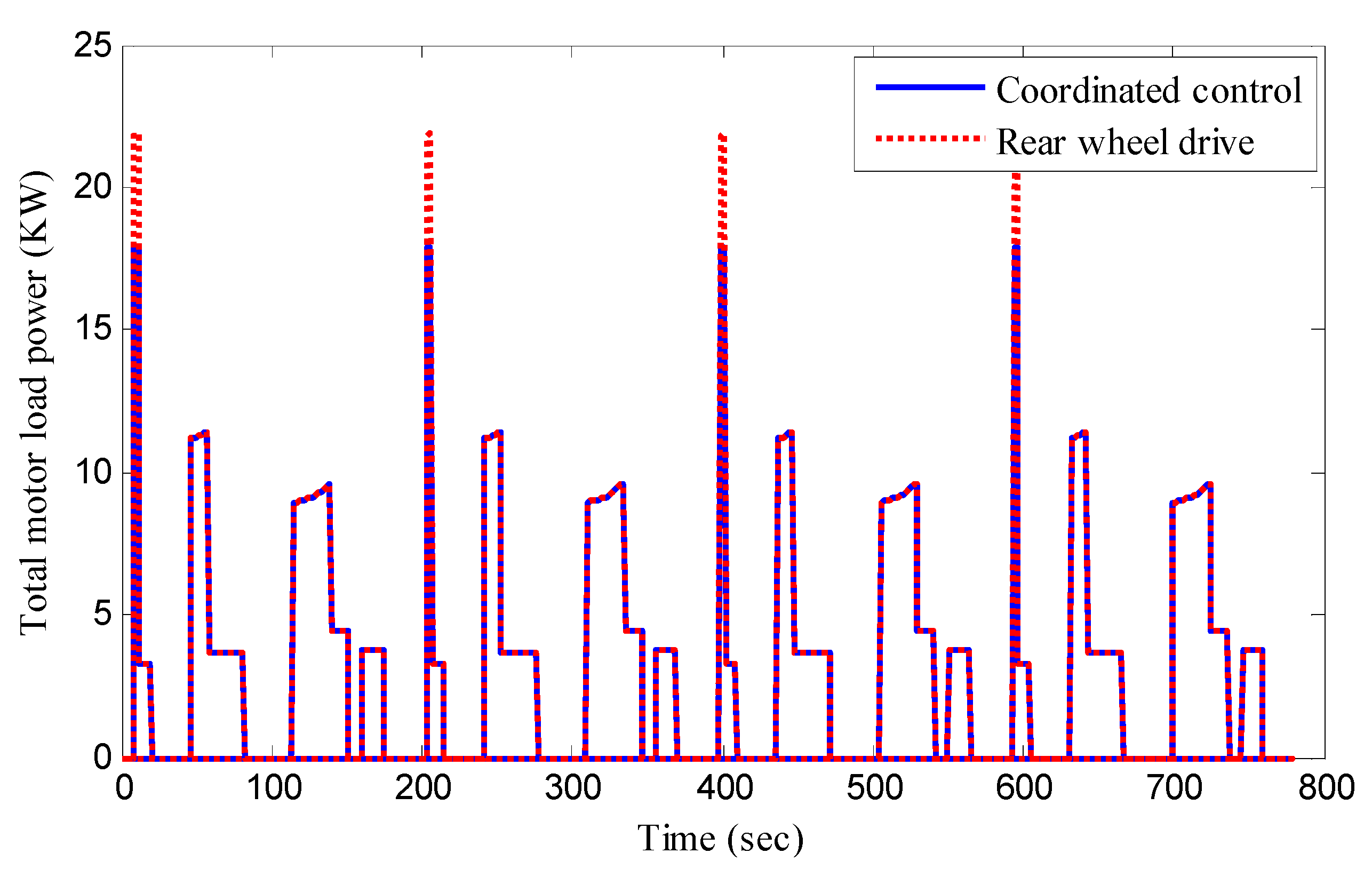
5.3. ECE Manoeuver
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khaligh, A.; Li, Z.H. Battery, Ultracapacitor, Fuel Cell, and Hybrid Energy Storage Systems for Electric, Hybrid Electric, Fuel Cell, and Plug-In Hybrid Electric Vehicles: State of the Art. IEEE Trans. Veh. Technol. 2010, 59, 2806–2814. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, Z.; Chai, J.; Kan, Z. Risk Identification and Analysis for PPP Projects of Electric Vehicle Charging Infrastructure Based on 2-Tuple and the DEMATEL Model. World Electr. Veh. J. 2019, 10, 4. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Chen, L.; Jiang, H.B.; Cai, Y.F.; Li, Y. Estimation of longitudinal force, lateral vehicle speed and yaw rate for four-wheel independent driven electric vehicles. Mech. Syst. Signal Process 2018, 101, 377–388. [Google Scholar] [CrossRef]
- Wang, R.; Chen, Y.; Feng, D.; Huang, X.; Wang, J. Development and performance characterization of an electric ground vehicle with independently actuated in-wheel motors. J. Power Sources 2011, 196, 3962–3971. [Google Scholar] [CrossRef]
- Iora, P.; Tribioli, L. Effect of ambient temperature on electric vehicles’ energy consumption and range: model definition and sensitivity analysis based on nissan leaf data. World Electr. Veh. J. 2019, 10, 2. [Google Scholar] [CrossRef]
- Zhai, L.; Hou, R.F.; Sun, T.M.; Kavuma, S. Continuous steering stability control based on an energy-saving torque distribution algorithm for a four in-wheel-motor independent-drive electric vehicle. Energies 2018, 11, 350. [Google Scholar] [CrossRef]
- Lin, C.; Xu, Z.F. Wheel torque distribution of four-wheel-drive electric vehicles based on multi-objective optimization. Energies 2015, 8, 3815–3831. [Google Scholar] [CrossRef]
- Fiori, C.; Ahn, K.; Rakha, H.A. Power-based electric vehicle energy consumption model: Model development and validation. Appl. Energy 2016, 168, 257–268. [Google Scholar] [CrossRef]
- Laurikko, J.; Granström, R.; Haakana, A. Realistic estimates of EV range based on extensive laboratory and field tests in Nordic climate conditions. World Electr. Veh. J. 2013, 6, 192–203. [Google Scholar] [CrossRef]
- Wang, Y.; Fujimoto, H.; Hara, S. Torque distribution-based range extension control system for longitudinal motion of electric vehicles by LTI modeling with generalized frequency variable. IEEE/ASME Trans. Mechatron. 2016, 21, 443–452. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Wiet, C.; Wang, J. Energy management and driving strategy for in-wheel motor electric ground vehicles with terrain profile preview. IEEE. Trans. Ind. Inf. 2014, 10, 1938–1947. [Google Scholar] [CrossRef]
- Wang, D.; Yang, F.; Gan, L.; Li, Y. Fuzzy prediction of power lithium ion battery state of function based on the fuzzy c-means clustering algorithm. World Electr. Veh. J. 2019, 10, 1. [Google Scholar] [CrossRef]
- Gogoana, R.; Pinson, M.B.; Bazant, M.Z.; Sarma, S.E. Internal resistance matching for parallel-connected lithium-ion cells and impacts on battery pack cycle life. J. Power Sources 2014, 252, 8–13. [Google Scholar] [CrossRef]
- Campestrini, C.; Keil, P.; Schuster, S.F.; Jossen, A. Ageing of lithium-ion battery modules with dissipative balancing compared with single-cell ageing. J. Energy Storage 2016, 6, 142–152. [Google Scholar] [CrossRef]
- Wang, R.R.; Hu, C.; Wang, Z.J.; Yan, F.J.; Chen, N. Integrated optimal dynamics control of 4WD4WS electric ground vehicle with tire-road frictional coefficient estimation. Mech. Syst. Signal Process 2015, 60–61, 727–741. [Google Scholar] [CrossRef]
- Chen, T.; Xu, X.; Li, Y.; Wang, W.J.; Chen, L. Speed-dependent coordinated control of differential and assisted steering for in-wheel motor driven electric vehicles. Proc IMechE Part D: J Auto. Eng. 2018, 232, 1206–1220. [Google Scholar] [CrossRef]
- Chen, T.; Chen, L.; Xu, X.; Cai, Y.; Jiang, H.; Sun, X. Estimation of longitudinal force and sideslip angle for intelligent four-wheel independent drive electric vehicles by observer iteration and information fusion. Sensors 2018, 18, 1268. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.J.; Yin, G.D.; Chen, N. Gain-scheduled robust control for lateral stability of four-wheel-independent-drive electric vehicles via linear parameter-varying technique. Mechatronics 2015, 30, 286–296. [Google Scholar] [CrossRef]
- Wang, R.R.; Zhang, H.; Wang, J.M.; Yan, F.J.; Chen, N. Robust lateral motion control of four-wheel independently actuated electric vehicles with tire force saturation consideration. J. Frankl. Inst. 2015, 352, 645–668. [Google Scholar] [CrossRef]
- Nam, K.; Fujimoto, H.; Hori, Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors. IEEE Trans. Veh. Technol. 2012, 61, 1972–1985. [Google Scholar]
- Li, B.Y.; Du, H.P.; Li, W.H.; Zhang, Y.J. Side-slip angle estimation based lateral dynamics control for omni-directional vehicles with optimal steering angle and traction/brake torque distribution. Mechatronics 2015, 30, 348–362. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Fast and global optimal energy-efficient control allocation with applications to over-actuated electric ground vehicles. IEEE Trans. Control Syst. Technol. 2012, 20, 1202–1211. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, J. Adaptive energy-efficient control allocation for planar motion control of over-actuated electric ground vehicles. IEEE Trans. Control Syst. Technol. 2014, 22, 1362–1373. [Google Scholar]
- Dizqah, A.; Lenzo, B.; Sorniotti, A.; Gruber, P.; Fallah, S.; Smet, J. A fast and parametric torque distribution strategy for four-wheel-drive energy-efficient electric vehicles. IEEE Trans. Ind. Electron. 2016, 63, 4367–4376. [Google Scholar] [CrossRef]


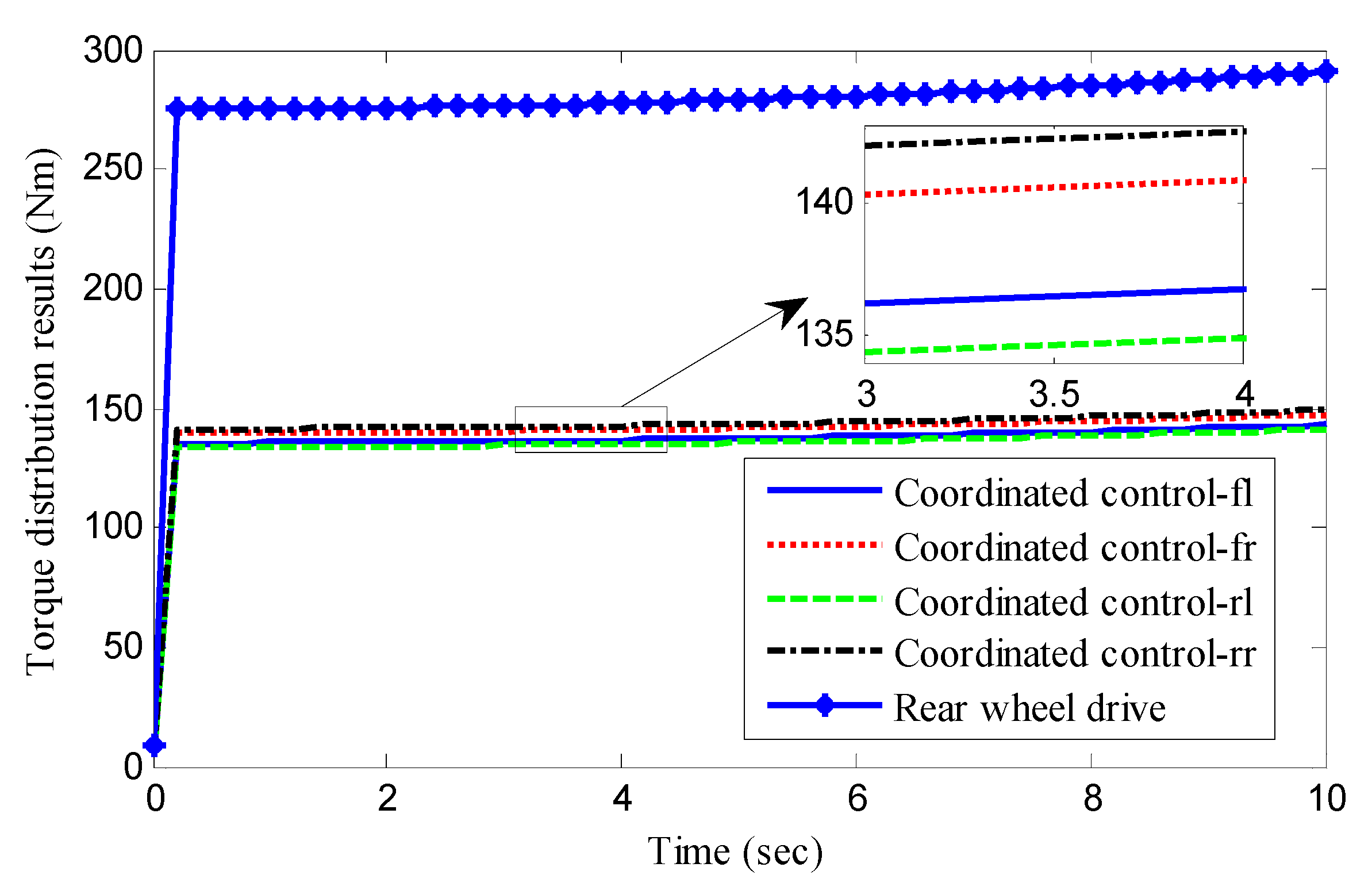
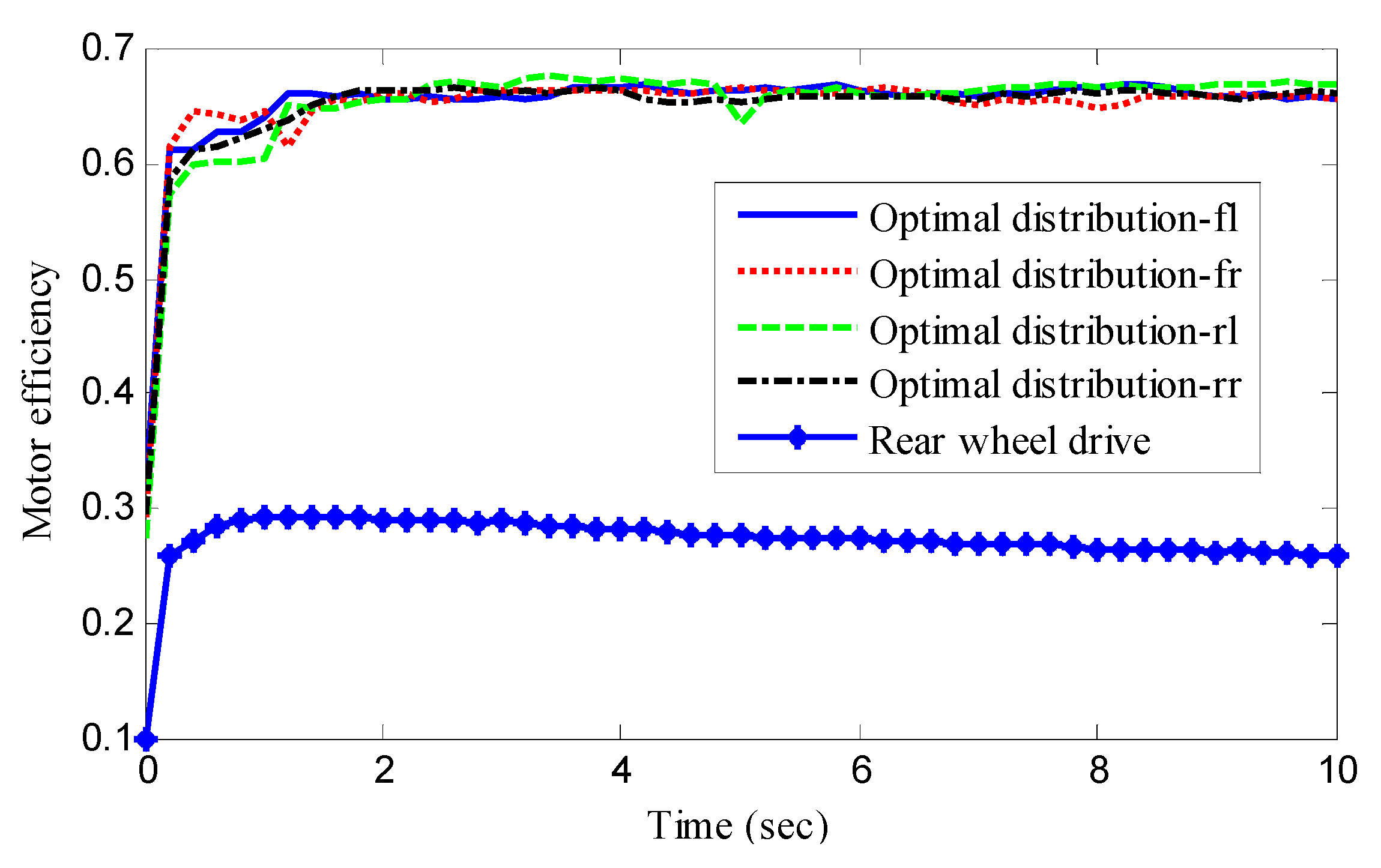
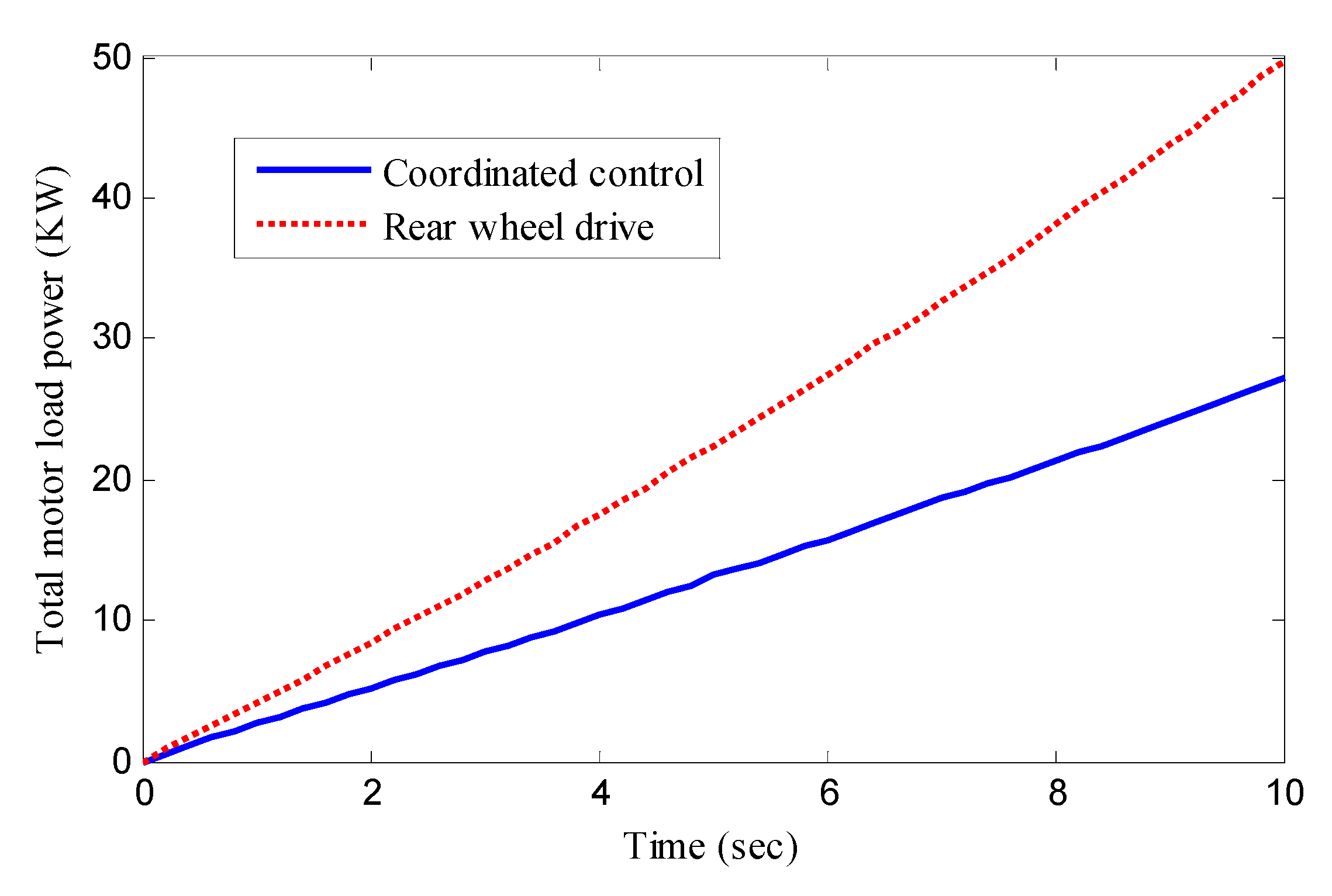
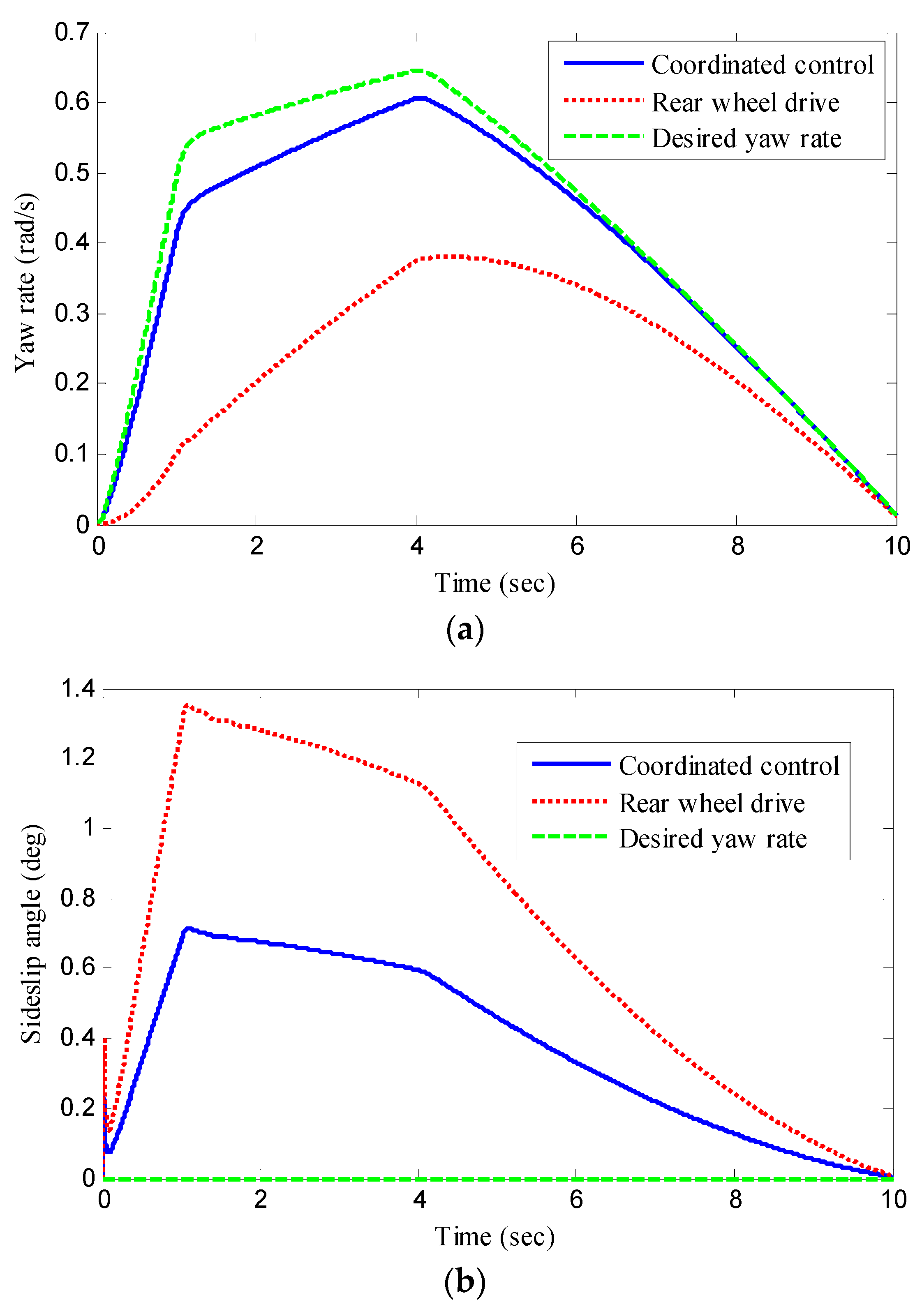
| Symbol | Parameters | Value and Units |
|---|---|---|
| m | Vehicle mass | 850 kg |
| r | Effective radius of wheel | 0.25 m |
| lf | Distances from vehicle gravity center to the front axle | 0.815 m |
| lr | Distances from vehicle gravity center to the rear axle | 0.985 m |
| bf, br | Half treads of the front(rear) wheels | 0.78 m |
| Cf | Equivalent cornering stiffness of front wheel | 65,000 N/rad |
| Cr | Equivalent cornering stiffness of rear wheel | 45,000 N/rad |
| Iz | Moment of inertia | 1000 kg·m2 |
| R | Equivalent resistance of winding | 0.675 Ω |
| Ka | Inverse electromotive force coefficient | 0.065 Nm/A |
| Kt | Motor torque constant | 11.425 Nm/A |
| J | Sum of inertia moment of wheel and motor | 7.165 kg·m2 |
| b | Damping coefficient | 0.645 Nm·sec/rad |
| L | Equivalent inductance of winding | 0.125H |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, J. Hierarchical Coordinated Control Method of In-Wheel Motor Drive Electric Vehicle Based on Energy Optimization. World Electr. Veh. J. 2019, 10, 15. https://doi.org/10.3390/wevj10020015
Wang J, Li J. Hierarchical Coordinated Control Method of In-Wheel Motor Drive Electric Vehicle Based on Energy Optimization. World Electric Vehicle Journal. 2019; 10(2):15. https://doi.org/10.3390/wevj10020015
Chicago/Turabian StyleWang, Junchang, and Junmin Li. 2019. "Hierarchical Coordinated Control Method of In-Wheel Motor Drive Electric Vehicle Based on Energy Optimization" World Electric Vehicle Journal 10, no. 2: 15. https://doi.org/10.3390/wevj10020015
APA StyleWang, J., & Li, J. (2019). Hierarchical Coordinated Control Method of In-Wheel Motor Drive Electric Vehicle Based on Energy Optimization. World Electric Vehicle Journal, 10(2), 15. https://doi.org/10.3390/wevj10020015




