Abstract
This paper proposes a method for analyzing and simulating the time-dependent flexibility of electric vehicle (EV) demand. This flexibility is influenced by charging power, which depends on the charging stations, the EV characteristics, and several environmental factors. Detailed charging station data from a Dutch case study have been analysed and used as input for a simulation. In the simulation, the interdependencies between plug-in time, connection duration, and required energy are respected. The data analysis of measured data reveals that 59% of the aggregated EV demand can be delayed for more than 8 h, and 16% for even more than 24 h. The evening peak shows high flexibility, confirming the feasibility of congestion management using smart charging within flexibility constraints. The results from the simulation show that the average daily EV demand increases by a factor 21 between the ‘Present-day’ and the ‘High’ scenario, while the maximum EV demand peak increases only by a factor 6, as a result of the limited simultaneity of the transactions. Further, simulations using the average charging power of individual measured transactions yield more accurate results than simulations using a fixed value for charging power. The proposed method for simulating future EV flexibility provides a basis for testing different smart charging algorithms.
1. Introduction
Over the past years, the number of electric vehicles (EVs) has rapidly increased in the Netherlands. The total number of Dutch electric passenger cars was about 143,000 by the end of December 2018 [1], which is 1.7% of the Dutch passenger car stock. Of these EVs, 31.5% were battery electric vehicles (BEVs) and 68.4% plug-in hybrid electric vehicles (PHEVs) [1]. The Dutch government aims at 50% of the new passenger cars sold being equipped with an electrical drive train in 2025, and 100% of all new passenger cars sold being zero-emission in 2030 [1]. The increase in number of EVs goes hand in hand with an increase in the number of EV charging stations. By the end of December 2018, there were 35,894 public and semi-public charging points in the Netherlands, and about 100,000 private charging points [1].
Previous studies have shown that, in residential areas, the EV demand peaks are likely to coincide with household demand peaks in the case of uncontrolled charging [2,3,4,5]. Uncontrolled charging means that EVs start charging at full power as soon as they are plugged in to a charging station, continuing until the battery is fully charged. Currently, this is the common way of charging in the Netherlands. Considering that by far the largest share of charging stations (99.4%) is currently connected to low-voltage (LV) networks [6], uncontrolled charging is expected to cause grid congestion for increased EV fleet sizes [5]. Smart charging is the redistribution of the charging demand over the period during which the EV is connected to the charging station. Apart from avoiding grid congestion caused by EV demand, smart charging can serve multiple other goals, for example, to provide ancillary services, to minimize charging costs, or to maximize the utilization of local renewable energy sources [5,7,8,9,10,11,12].
One of the requirements for smart charging is the availability of sufficient EV demand flexibility. We define a transaction as one charging session with connection duration including the entire process between connecting and disconnecting the EV charging cable to/from the charging point. Then, the maximum available flexibility during a transaction is determined by the difference between the connection duration () and the charging duration (), with being the period needed to charge the required energy (Ereq) into the EV battery. In previous studies on smart charging, the maximum available EV demand flexibility was often assessed in a simplified way, not investigating the diversity in connection durations and charging durations for the different transactions. Lopes et al. [11] used three types of EVs, with charging powers of 1.5, 3, and 6 kW, respectively, and an average value of 4 h for . The study assumed that all existing vehicles plugged in at 21:00 in the evening. Clement-Nyns et al. [12] divided the day into different time slots and assumed that all EVs had a maximum charging power of 4 kW. The EVs plugged in during a certain time slot and had to be fully charged by the end of the time slot, thereby underestimating the flexibility of EV demand, as in reality, the connection durations are expected to exceed the durations of the time slots used. Claessen et al. [9] used a normal distribution of charging start and end times around a fixed mean, a maximum power flow of 3.7 kW, and discrete values for Ereq per transaction (3, 6, or 12 kWh). Wu et al. [7] used a plug-in time between 07:00 and 08:00 and a plug-out time between 18:00 and 19:00, the (dis)charging power was flexible between −10 and 10 kW, and Ereq was assumed to be 12 kWh for each transaction. Jian et al. [13] used a chi-squared distribution for arrival times and a normal distribution for the simulation of , with a fixed mean of 10 h and a fixed standard deviation of 3 h, and a maximum charging power of 4 kW for all EVs. In the study by Van der Kam & Van Sark, a uniform distribution between 3 and 6 h was used for trip durations, and it was assumed that the EV was always connected when it was not on a trip, thereby overestimating the available flexibility [8]. The maximum charging power was set at 6.6 kW or 22 kW in that study, depending of the type of EV that was simulated. Scharrenberg et al. [14] used hourly frequency distributions of arrival and departure times from the Dutch national mobility study [15] for defining the availability of EVs for smart charging. This is more realistic than using predefined distributions, yet the study did not consider connection durations of individual transactions nor the diversity of charging durations for different transactions. Further, a charging power of 3.7 kW was used for all EVs. Liu et al. [16] used National Travel Surveys in the Nordic region to assess the availability of EVs for smart charging, but did not link this availability with charging durations. So far, only a few studies have been found that assessed the available EV demand flexibility by combining and . By taking into account the plug-in time () as well, the changes of available flexibility over time can be investigated. A study by D’Hulst et al. (2015) investigates time-dependent flexibility of several appliances, among which are EVs. The EV flexibility was based on a pilot in which seven EVs were monitored over a period of 10 weeks [17]. The charging power of the EVs in the study was limited to 2.3 kW. To achieve a realistic assessment of the maximum potential flexibility of EV demand and the time dependency of the available flexibility, it is necessary to investigate the differences between and for a large number of transactions. The earliest study found in which this was done was published in 2017 and examines a Dutch and a Flamish dataset [18]. The authors present a time-varying response potential in kW for different charging locations. A more recent study by Flammini et al. provides an extensive statistical analysis of EV behavior based on Dutch charging station data, including idle times [19]. However, the authors give no clear results on how idle time, and thus the flexibility, varies over the time of the day. Another recent study analysed one year of Dutch present-day public charging station data, including the flexibility and its time-dependency [20].
The purpose of this study is to analyse the maximum available flexibility of EV demand in a residential area, including the time-dependency of this flexibility, and to propose a method for the stochastic simulation of EV demand including detailed flexibility constraints. The results enable making accurate estimations of the maximum value of different smart charging schemes in residential areas, for example, in terms of reduced charging costs, reduced impacts on the low voltage network, and increased self-consumption of local photovoltaic (PV) generated electricity. In this study, an EV user participation rate of 100% and perfect forecast is assumed. In reality, perfect forecast is of course not feasible. However, in the pilot considered in this study, a certain amount of information on the flexibility constraints is available beforehand—the EV users that take part in the smart charging system communicate their estimated departure time and amount of energy needed to an aggregator when they connect their EV to the charging station. Besides, the aggregator is able to forecast future charging behavior based on historical data. The real-time user data in combination with the forecasted EV charging behavior enables the aggregator to plan the charging schedule in advance, taking into account the flexibility constraints. The charging stations in the pilot are owned and controlled by one company, but are accessible to everyone. Therefore, these charging stations are referred to as public charging stations in this study.
Most studies mentioned above use one value for charging power for all EVs. However, the available flexibility depends on , which in turn depends on the charging power. Charging power is influenced by several factors such as outside temperature, battery state-of-charge (SoC), and battery age [21,22,23]. Therefore, variations in charging power between different EVs and different transactions are investigated in this study as well.
Further, the paper proposes a method for simulating charging behavior of future EV fleet sizes, to investigate the future flexibility of EV demand. In previous studies, Markov Chain Monte Carlo has been used to simulate EV behavior [24,25]. In the present study, this method was not used because mobility patterns in general do not fulfill the Markov property as they are not memoryless—the time of departure from a location is dependent from the time of arrival at that location, which is in turn influenced by the departure time from the previous location [26]. Also, in reality, the variables , , and are statistically dependent [24,27], which is not reflected in Markov Chain Monte Carlo analysis. For these reasons, in this study, a stochastic Monte Carlo simulation was used in which the interdependencies between and , between and , and between and are respected. This simulation was used to examine the availability of EV demand flexibility and its variation over time for future EV fleets. Three different methods for simulating the charging power were compared. The first one uses a fixed charging power based on the maximum power that the charging point can deliver or the maximum power that the EV is able to charge with. The other two methods both use charging power values that vary per simulated transaction. The values for charging power are randomly selected from the transaction-specific maximum and average values from the measured charging power profiles.
The method for investigating EV demand flexibility was used to analyse available flexibility for a case study in a residential area in the city of Utrecht, the Netherlands. In this project, 21 charging stations were logged over one year. The outcomes from the flexibility analysis are used as input for the simulation of charging behavior of future EV fleets and the time-dependent flexibility of the resulting EV demand. The case study is performed to illustrate the proposed method for assessing EV demand flexibility.
The paper is structured as follows. In Section 2, the method for the analysis of EV demand flexibility and the method for the simulation of future EV demand flexibility are described. In Section 3, the case study is described. Then, in Section 4, the results are presented. The methods and results are discussed in Section 5. In Section 6, a conclusion and pointers for future work are given.
2. Methods
In this section, first the data analysis is described. Section 2.1 describes the analysis of the time-dependent flexibility of EV demand, and Section 2.2 explains the division of the EVs into different categories. Then, we explain the method used for the EV simulation. In Section 2.3, the method for setting up the simulated EV fleet size scenarios is given. Section 2.4 describes the data preparation for the simulation, and in Section 2.5, the simulation steps are explained. All data analyses and the simulations have been performed using Python 3.7 on Spyder 3.3.1.
The minimum data requirements to carry out the proposed flexibility assessment are, for each EV transaction i, as follows:
- : the plug-in time for transaction i.
- : the plug-out time for transaction i.
- : power charged at each time t during transaction i, with a sufficiently high time resolution ( ≤ 15 min). In this study, this data is referred to as the ‘measured charging profile’.
- Possibly also [kWh], which is the total charged energy during each transaction. However, this metric can also be derived from if is sufficiently small.
- A unique anonymous identity for each EV j that occurs in the dataset. For each transaction i in the dataset, the identity of the charging EV j must be known.
2.1. Analysis of Time-Dependent Flexibility of EV Demand
The connection duration for transaction i ( is the period of time during which an EV charging cable is connected to the charging point, which is calculated using Equation (1).
[h] can be derived by counting the number of non-zero values for during transaction i, as expressed in Equation (2), in which is the timestep of the charging power data. For uncontrolled transactions, there will be a continuous series of non-zero values starting at for each transaction i.
The difference between [h] and [h] defines the available flexibility, in hours, during transaction i, and is referred to as . This is expressed in Equation (3).
By aggregating the values of for all transactions i, the aggregated EV demand, defined as [kW], is derived. Using Equation (3), for each transaction i, it is calculated for how many hours the demand could be delayed. On the basis of this information, the available flexibility of aggregated EV demand at each moment in time is calculated. The definitions of , , and are illustrated in Figure 1.
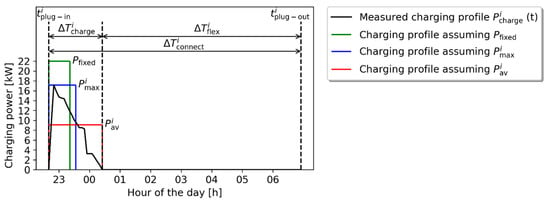
Figure 1.
Example of measured and constant charging power profiles using a typical transaction i by a battery electric vehicle (BEV). The measured charging power profile of this example transaction i, which is is shown in black. Like any realistic charging profile, this profile is not constant. The black arrows on top illustrate the definitions of , , and for the measured transaction i. Further, the three corresponding constant charging power profiles (green, blue, and red) are depicted for this transaction i, using three different constant charging powers: , , and . For all profiles, the energy charged during the transaction is kept equal to the measured value ().
In this study, the measured charging power profiles of each separate transaction i are analysed. For each measured charging power profile, three approximated constant charging power profiles are defined. An example of a measured charging power profile of a BEV and the corresponding three different constant charging power profiles is illustrated in Figure 1. For all four profiles, is kept the same, meaning that the area under the measured charging power profile and all three constant charging power profiles is equal. For the green profile shown in Figure 1, a fixed charging power ( [kW]) is used. is chosen depending on the type of EV or the type of charging station. In the example in Figure 1, it is 22 kW, which is the maximum power output of a 3 × 32 A AC 230 V charging point. The second and third constant charging power profiles are based on the maximum (blue profile in Figure 1) and average charging power (red profile in Figure 1) during , respectively. As the average and maximum charging power during differ for each transaction i, these charging powers are referred to as ‘transaction-specific’. Below, the characteristics of the three constant charging power profiles based on the three different values for charging power are described:
- Fixed constant charging power, [kW], which can be chosen depending on the type of car or the type of charging station. The charging duration for this fixed constant charging power profile is , which is calculated using Equation (4).
- Transaction-specific maximum constant charging power [kW], is the maximum value of charging power that occurs during transaction i. The charging duration is calculated using Equation (5).
- Transaction-specific average constant charging power, [kW], is the average power of transaction i, which is calculated using Equation (6).is equal to the measured charging duration .
2.2. EV Categories
To obtain more insight into the charging behavior of the EVs and to provide a basis for the simulation of future scenarios, the EVs are categorized, resulting in four different categories. It is usually not possible to link the identity of the users to the EV identities (IDs) because of privacy reasons. Therefore, the categorization is based on a unique anonymous identity for each EV j that occurs in the measured dataset, , where is the number of unique EV IDs in the measured dataset. For each transaction i, the identity of the charging EV j is known.
First, the EV IDs are split into two main categories, namely BEVs and PHEVs. This is done because charging behavior is different between these types of EVs and because the share of BEVs in the total EV fleet is expected to grow in the future [28]. The division between BEVs and PHEVs is based on the maximum charging power at which each EV j charged during the measurement period ( [kW]). For the top five best sold PHEVs in the Netherlands, which cover 66% of the total number of Dutch PHEVs, the maximum charging power is 3.7 kW [1,29]. Therefore, an EV is considered a BEV if ≥ 5 kW and a PHEV if < 5 kW. Further, as EVs owned by people living in the area were expected to charge more frequently and have longer connection times, a division between local and visiting EVs is made. A BEV is considered to be local (i.e., owned by residents) if its average daily charging demand ( [kWh·EV−1·day−1]), averaged over the year, exceeds a certain threshold. The demarcation is set at 3.45 kWh·day−1, which is 50% of the average daily energy demand of a Dutch electric passenger car, based on an average daily distance of 34.6 km [30,31] and a driving efficiency of 5 km·kWh−1 [32]. This assumption was found to yield meaningful results (see Section 4.1). For PHEVs, is less informative as the share of electricity demand in their total energy demand is unknown. Therefore, for PHEVs, the frequency of long transactions ( [week−1]) is used as a decision parameter, in which a long transaction was defined as a transaction with a connection duration of over 6 h. The division of EVs is illustrated in Figure 2. Using this division, the available flexibility can also be expressed per EV category by selecting only transactions by EVs from a certain category.
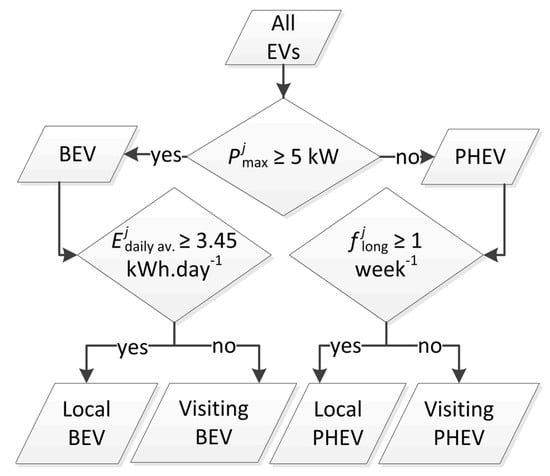
Figure 2.
Categorization of electric vehicles (EVs), in which is the maximum charging power of EV j, is the average amount of energy charged for EV j per day, and is its frequency of transactions with a duration >6 h.
2.3. Scenarios EV Fleet Size
In this section, the method for deriving the scenarios for future EV fleets charging in the simulated area is described. For this study, three scenarios are set up, namely, ‘Present-day’, ‘Medium’, and ‘High’.
To derive the number of unique EVs charging in the ‘Present-day’ scenario, the number of unique EVs charging in the measured data is multiplied by the ratio of the number of charging points in the simulated area to the number of charging points in the total area in which the charging data were measured. This is expressed in Equation (7), assuming that the EV density in the simulated area is equal to that in the total area. This step is only needed if the simulated area is smaller than the total area for which the charging data were collected.
In Equation (7), is the present-day number of simulated unique EV IDs in a certain category associated with the simulated area, is the number of unique EV IDs in that category occurring in the total measured dataset, is the number of charging stations in the simulated area, and is the total number of charging stations in the dataset. The outcome is rounded to the nearest integer. Note that the number of charging stations in the area is only used to define ; in the simulation, it is assumed that the number of charging stations is perfectly demand driven, meaning that the number of simultaneously charging EVs is left unconstrained.
Further, the following assumptions are made:
- The car possession rate (CPR [HH−1]), which is the number of passenger cars per household (both EV and non-electric), is the same in all scenarios.
- In the ‘High’ scenario, all passenger cars will be BEVs, based on the Dutch governmental target of 100% of the passenger cars sold in 2030 being emission free [1].
- In the ‘High’ scenario, the maximum number of unique visiting BEVs per month is limited to 50 times the current number of charging stations in the area.
- The difference in number of EVs between the ‘Current’ and the ‘Medium’ scenario is half the difference between the ‘Current’ and the ‘High’ scenario for each EV category.
- The lifetime (LT) of an EV is assumed to be 15 years [33].
Applying assumptions 1, 2, and 5, the number of local BEVs in the ‘High’ scenario is calculated using Equation (8).
In Equation (8), is the number of simulated local BEVs in the ‘High’ scenario, is the number of households, [HH−1] is the car possession rate, LT [year] is the lifetime of an EV, and is the number of days in the measured dataset. By combining this with the current number of EVs occurring in the dataset, the size of the different EV categories can be derived for each scenario. The scenarios are not associated with specific years, as it is uncertain when a 100% EV market share will be reached in the Netherlands [34].
2.4. Simulation: Preparation Input Data
In this section, the preparation of the input data for the EV simulation is explained. The aim of the simulation is to investigate the maximum available flexibility of future EV fleet sizes using available measured charging station data. Because the simulation of the maximum available flexibility is desired, EV demand peaks and flexibility are simulated assuming uncontrolled charging.
As explained in Section 2.2, four different EV categories are distinguished. These categories have to be considered in the simulation because the composition of the EV fleet is expected to change in the future, in other words, the different categories’ shares of the total fleet size will not remain constant. Further, the energy charged and the connection duration of transactions probably varies during the course of a day. For example, the probability of high values for and might be higher for a transaction starting in the evening than for one starting in the morning. The time-dependency of these parameters has to be accounted for in the simulation as it defines the intra-daily changes of EV demand impact and flexibility. Lastly, the charging behavior also differs between week and weekend days.
For these reasons, the measured transactions are split into different subsets. The first division is made based on the EV categories, resulting in four sets with size , as depicted in Figure 3. Then, these sets are divided into transactions during the week and transactions during the weekends. Each of these eight sets has size (see Figure 3). To take into account the variation of transaction properties with the time of the day, each of the 8 sets with size is further split into 24 sets based on starting hour of the transaction, resulting in 8 groups of 24 sets, each containing a number of transactions equal to (the bottom row of Figure 3). The distributions of and in each of these sets were tested on similarity with the distributions in the other 23 sets from the same group, that is, using a non-parametric two-sample Kolmogorov–Smirnov test [35,36]. The set with size is considered similar to another set if the frequency distributions of both and showed no significant (p ≤ 0.05) differences between the two compared sets. This way, each set with size is associated with similar sets in the same group.
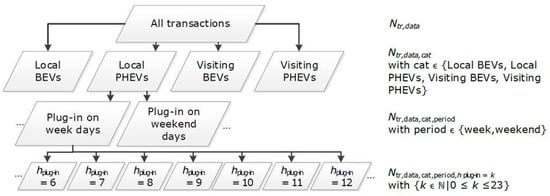
Figure 3.
Division of transactions. The dots indicate parts of the division tree that are not shown. The corresponding number of transactions in each set is given at the right of the figure.
2.5. Simulation Steps
For each of the simulated EVs m in a certain EV category, the following steps are taken during the simulation:
- From the available data, for each EV j in the dataset the number of transactions is normalized to the simulation period using Equation (9).In Equation (9), is the average number of transactions that EV j has during a period with the same length as the simulation period. is the number of transactions within the measured dataset for a certain EV j, is the number of days in the simulation period, and is the number of days in the measured dataset.
- A number of simulated transactions was assigned to each simulated EV m in a certain category using the measured number of transactions by a randomly chosen EV j from that category, as expressed by Equation (10).
- Next, all transactions for this EV m are simulated. To each separate simulated transaction q of this EV m, a day within the simulation period is assigned, taking into account the ratio between the number of transactions on weekdays and on weekend days as it is in the measured data, using Equations (11) and (12):In these equations, and are the probabilities that the simulated transaction q takes place on a week or weekend day, respectively; is the number of weekday transactions by EVs in a certain EV category in the measured dataset; and is the total number of transactions by EVs in this category in the measured dataset.
- The starting hour () of the simulated transaction q is stochastically chosen based on the number of transactions in each set with size (bottom row Figure 3). The probability that a simulated transaction q starts within a certain hour for transactions starting at week days, for example, is calculated using Equation (13). For weekend days, the method is analogous.In Equation (13), is the probability that the simulated transaction q starts within hour k. Using the probability distribution resulting from Equation (13), is stochastically simulated for each transaction q. After assigning , the exact simulated plug in time for each transaction q is derived by assigning a number of minutes within . This number of minutes is a randomly chosen multiple of .
- One measured transaction i is chosen randomly from the union of the set of transactions for which and the associated similar sets (see Section 2.4). Both and from this transaction were assigned to the simulated transaction q, as expressed in Equations (14) and (15). This way both the dependency of and to and the dependency of and are respected.
- All EVs in the simulation charge uncontrolled at constant power, starting at and ending when is reached for each simulated transaction q. To determine the constant charging power [kW] that the simulated EV m uses during simulated transaction q, the three different constant charging powers (see Section 2.1 and Figure 1) are used in the simulation and compared:
- 1.
- Fixed constant charging power: is set equal to . If the simulated EV m is a BEV, is assigned to each simulated transaction q as expressed in Equation (16).
- 2.
- Transaction-specific maximum constant charging power: is set equal to [kW], as expressed in Equation (17). By using this method, it is assumed that EVs charge constantly at .
- 3.
- Transaction-specific average constant charging power: is set equal to [kW], which is defined using Equation (6). The assignment is expressed in Equation (18).These three charging power methods result in three different simulated charging power profiles for each simulated transaction q. Using transaction-specific average constant charging power, the simulation is expected to yield most realistic results, as the simulated charging duration is equal to the measured charging duration (see Figure 1).
- As the plug-in times are chosen independent from each other, a constraint has to be set in order to ensure that, for a single EV, the interval between plugging out and then plugging in again for the next transaction is large enough. The constraint ensures that the EV theoretically has enough time to use the charged amount of energy during the period that the EV was not connected to the charging station. If all transactions of a simulated EV m are put in chronological order, the constraint used in this study is given by Equation (19).
- The maximum EV discharge power during a trip, , is assumed to be 20 kW for all EVs, based on an average speed during the trip of 100 km·h−1 and a driving efficiency of 5 km·kWh−1 [32,37]. After the simulation of every transaction, it is checked whether this constraint is met. If violated, the last simulated transaction is removed and re-simulated.
The abovementioned simulation steps are carried out for each EV m. Repeating this for all EVs in a certain EV scenario results in a simulated charging behavior of all EVs over the simulation period, which is 30 days in this study. For each EV scenario, the charging behavior of all EVs was aggregated to retrieve the simulated EV demand over the simulation period, including the simulated EV demand flexibility. A Monte Carlo simulation was performed by simulating the aggregated EV demand in this manner 50 times for each of the three different EV scenarios described in Section 2.2. The Monte Carlo simulation was carried out to investigate the spreading of the aggregated EV demand peak height and flexibility of the aggregated EV demand among different simulation runs.
3. Case Study Description
The Lombok district in the city of Utrecht, The Netherlands, has been considered as a case study. The studied area is a residential area in which a small amount of commercial activities also take place. Using the Dutch Basisregistratie Adressen en Gebouwen (BAG), the following information was retrieved: 89% of the addresses is registered as purely residential; 4% has a residential function combined with another function; and the remaining 7% of the addresses are shops, offices, or other [38]. The current car possession rate (CPR) is 0.4 HH−1 [39].
The EV charging data used in this study were logged at 21 charging stations located in the Lombok district over one year, from 1 August 2017 up to and including 31 July 2018. Each charging station was equipped with two charging points, both equipped with a 3 × 32 A connection on a 230 V network, so Pmax,CP is 22 kW. This value of 22 kW is used as for BEVs in the simulation. For PHEVs, in the simulation, is set equal to 3.7 kW, which is the maximum charging power for the top five best sold PHEVs in the Netherlands, as mentioned in Section 2.2. For each transaction i, the following data are available:
- : the plug-in time
- : the plug-out time
- : power charged at each time t during transaction i, with = 5 min
- [kWh]: the total charged energy
- An identity-key of each unique charging EV
Data cleaning steps included removing transactions with obvious faulty data: all transactions with = 0 s, all transactions for which > 73 h, and all transactions for which 125 kWh. The resulting dataset consists of 8223 transactions.
The area used for the simulation included 6 charging stations and 340 households. This corresponds to an area that is connected to one transformer converting medium voltage (MV) to low voltage (LV). The MV/LV-transformer in this area has a capacity limit of 400 kW.
4. Results
This section first presents key parameters from the data analysis in Section 4.1, then in Section 4.2, the time-dependent flexibility in the measured data is described. In Section 4.3, the scenarios for the simulated EV fleet sizes are given, followed by Section 4.4 presenting the results of the simulation.
4.1. Measured Data: EV Fleet and Transaction Parameters
Key figures from the data logged by the 21 EV charging stations are given in Table 1. It is shown that local BEVs have a relatively high impact on the aggregated EV demand in comparison with the other EV categories. During the measurement period, 13 different local BEVs used one or more of the 21 charging stations. These local BEVs charge with an average frequency of 0.47 transactions EV−1·day−1. The number of visiting BEVs in the dataset is 21 times higher than the number of local BEVs, but the average daily charging frequency for visiting BEVs is only 0.01 transactions EV−1·day−1. This difference is also reflected in the average daily volume charged per EV, , which is 8.41 kWh·EV−1·day−1 for local BEVs and 0.17 kWh·EV−1·day−1 for visiting BEVs. The number of different local PHEVs in the dataset is 20, while 617 unique visiting PHEV IDs were charging during the measurement period. The transaction frequencies differ by a factor 1.3 for BEVs and PHEVs. is around a factor 3.5 lower for local PHEVs compared with local BEVs. For visiting EVs, this difference is around a factor 3.

Table 1.
Key figures of electric vehicle (EV) charging station measured data analysis over the measurement period 1 August 2017 to 31 July 2018, covering 21 charging stations within the Lombok district in the city of Utrecht.
To shed more light on the distributions of the transaction parameters in this case study, Figure 4 shows histograms of key parameters for the different EV categories. The normality of these distributions was tested using the Shapiro–Wilk test; the test results showed that none of the distributions in Figure 4 follow a normal distribution (p-values << 0.001). The upper histograms show the distribution of over the hours of the day for EVs in the different categories, illustrating that local BEVs tend to plug in mostly in the evening, while the histogram for local PHEVs shows peaks in the evening as well as in the morning. This indicates that the local PHEV category also includes EVs from commuters that are working in the area and thus were not excluded by the selection criteria used in this study (see Figure 2). For visiting EVs, the arrival times are more evenly distributed over the period between 08:00 and 00:00. The distributions of , depicted in the second row of Figure 4, show that local BEVs mostly leave in the morning, whereas local PHEVs plug out mostly in the mornings or the early evenings. The third row in Figure 4 shows connection durations There is a cut-off in measured connection durations at 72 h: to transactions with h, a of 72 h is assigned. As expected, local EVs show longer connection durations than visiting EVs. For local BEVs, is frequently between 0 and 4 h or 12 and 14 h, while local PHEVs are most often plugged in during a period of 10–16 h. For visiting BEVs and PHEVs, values for below 2 h are most common. The fourth row of Figure 4 shows the distributions of [kWh]. The distribution for local BEVs shows a decreasing number of transactions for increasing values of , with a maximum of 60 kWh. One outlier, 105 kWh, is not included in the graph for reasons of clarity. For both local and visiting PHEVs, is often lower, showing a maximum of 22 kWh due to the criteria presented in Section 2.2. The bottom row in Figure 4 depicts the histograms for the transaction-specific average charging power (see Equation (6)). The measured transaction-specific average charging power varies largely between EV categories and between transactions within each EV category, especially for BEVs.
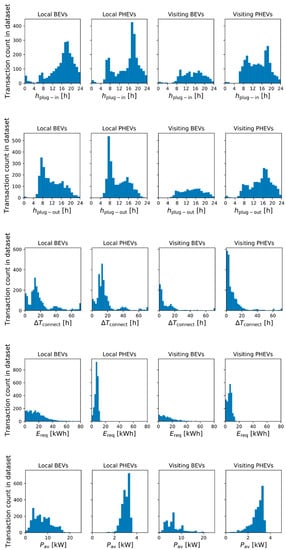
Figure 4.
From top to bottom, the histograms for , , , , and the average transaction power are given for all transactions in the measured data, per EV category.
In Figure 5, the maximum and average charging power per transaction in the measured data, and respectively, are given for BEVs (upper figure) and PHEVs (lower figure). Further, the green line depicts the value of the fixed charging power, which is explained in Section 2.5 and Equation (16). The graphs show that the average transaction power is often significantly lower than the maximum charging power during a transaction. For BEVs, the mean of the average transaction-specific power over all measured transactions is 7.3 kW with a standard deviation of 4 kW, while the maximum transaction power ± 5.5 kW. For PHEVs, is on average 2.9 ± , while is on average 3.4 ± 0.4 kW. Relatively spoken, for BEVs, is 23% ± 18% lower than . For PHEVs, this difference is smaller: 14% ± 10%. For BEVs, and are on average 55% ± 25% and 67% ± 18% lower, respectively, than , which is 22 kW for BEVs, and 9% ± 11% and 21% ± 13% lower, respectively, than (3.7 kW) for PHEVs.
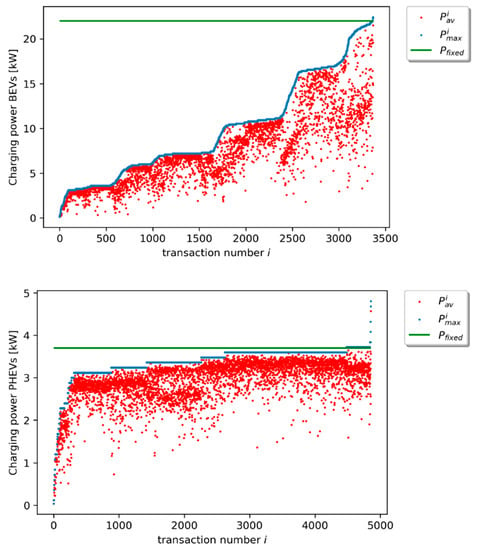
Figure 5.
Analysis of the measured charging power profiles per transaction for BEVs (top) and PHEVs (bottom). For each transaction i, two points are plotted: a red one depicting , and a blue one depicting . The transactions are sorted in order of increasing . The green line shows the value of (see Section 2.1).
4.2. Measured Data: Time-Dependent Flexibility
In order to assess the time-dependent flexibility of the EV demand, of each measured transaction i is linked to , after which the demand is aggregated, as described in Section 2.1. In Figure 6, the aggregated EV demand is averaged over the whole dataset for each time of the day with 5 min resolution. Figure 6a represents the time-dependent flexibility of the aggregated demand of all EVs in the dataset. In Figure 6b, the time-dependent flexibility is presented per EV category. The different colors indicate the possible [h] for different parts of the average measured aggregated EV demand at each time of the day. Note that was defined as the number of hours over which the demand could be shifted within the connection duration of an EV (see Figure 1). The results show that, given this maximum available flexibility, there are ample opportunities to shift the EV demand over time given the present-day plug-in and -out times and measured charging profiles. For all EVs together (Figure 6a), 59% of the aggregated EV demand can be delayed for more than 8 h, 25% over more than 16 h, and 16% even more than 24 h. This suggests that there is sufficient flexibility available to charge part of the EVs during the PV generation peak of the next day. This could increase local PV self-consumption and alleviate generation congestion. For both local BEVs and local PHEVs (upper row in Figure 6b), we see a clear peak in evening demand that shows a relatively high flexibility in comparison with other moments during the day. In contrast, the average demand profiles of the visiting EVs show both less pronounced peaks and reduced flexibility. Local BEVs have highest impact on the evening peak, but also show the highest flexibility. The difference between BEVs and PHEVs is mainly in the height of the evening peak of the aggregated charging profile, while the shape of the average daily charging profiles is similar between BEV and PHEVs.
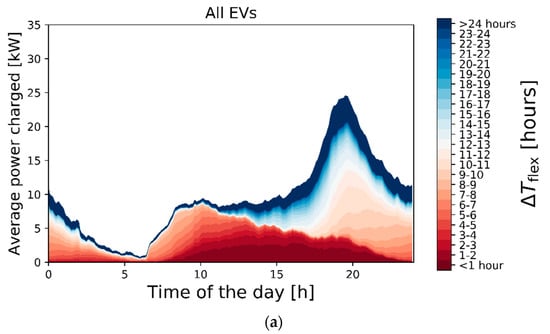
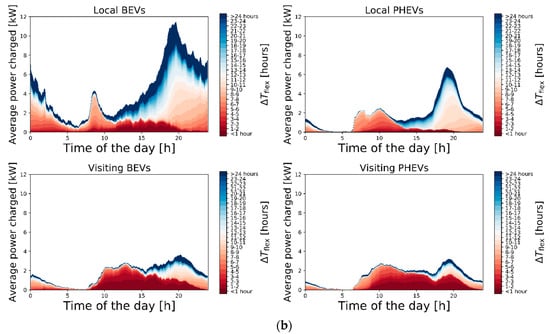
Figure 6.
(a) Available flexibility of aggregated EV demand in measured data, average values for each time of the day (5 min resolution). The demand profile shows a peak in the evening that is highly flexible, while the flexibility of the EV demand during the day is limited. (b) Aggregated demand profiles and available flexibility per EV category in measured data; average values for each time of the day (5 min resolution).
4.3. Simulation: Scenarios EV Fleet Size
In order to investigate the effect of different EV growth scenarios on the transformer level, the simulated EV fleet size was based on a smaller area than the total area for which the charging data were collected. In this area, 6 charging stations (12 charging points) and 340 households are connected to one MV/LV-transformer with a capacity limit of 400 kW. For the ‘Present-Day’ scenario, Equation (6) was used to define the number of simulated EVs for each EV category. Next, the numbers of simulated EVs in the other two scenarios were based on the assumptions mentioned in Section 2.3. According to assumption 1 and given that the current CPR is 0.4 HH−1, it will be 0.4 HH−1 in the ‘High’ scenario as well. Using a LT of 15 years and taking into account that is 365, and applying Equation (7), is calculated to be 145. The future EV fleet size scenarios are given in Table 2.

Table 2.
Number of unique EV identities (IDs) occurring in the simulation for the different EV categories and scenarios for EV fleet size, per EV category.
4.4. Simulation: Scenario Results
A Monte Carlo simulation was run 50 times for each of the EV scenarios over a simulation period of 30 days. The boxplots in Figure 7 show the results of the simulation for the three different EV scenarios. The average daily aggregated demand for all EVs is 58 kWh·day−1, 643 kWh·day−1, and 1227 kWh·day−1 for the ‘Present-day’, ‘Medium’, and ‘High’ scenarios, respectively (left graph in Figure 7). Given that in the simulated area, the average daily baseload was 4013 kWh·day−1 in December 2017 and 3254 kWh·day−1 in June 2017, the EV demand in the ‘High’ scenario would cause roughly an increase in electricity demand of one-third compared with present-day household demand. The maximum peaks in aggregated EV demand occurring in the simulated month are shown in the right graph in Figure 7. In the ‘High’ scenario, maximum peaks range from 286 kW to 393 kW when is used, while this range is from 214 kW to 301 kW for and 194 kW to 284 kW for . Relatively speaking, the simulated highest peak using is on average 33% higher than the simulated highest peak using . This difference is lower than the average relative difference between and for the separate transactions in the original data, which is 67% ± 18% for BEVs, as mentioned in Section 4.1. This is explained by the fact that is shorter when the simulated charging power is higher (see Figure 1), and thus the different transactions are less likely to overlap each other in the simulation, that is, the transactions show a lower simultaneity.
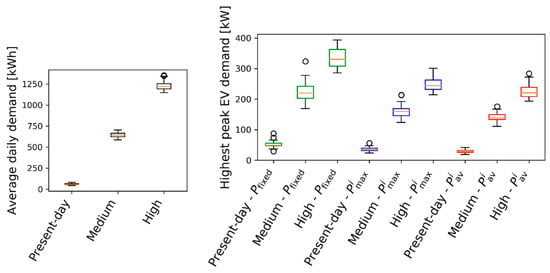
Figure 7.
Boxplots of average daily aggregated EV demand (left) and highest peak in EV demand (right) on the medium voltage (MV)/low voltage (LV)-transformer under study are given. The highest peaks in EV demand are given for the three different charging powers used, showing that peaks are largely overestimated when is used as EV charging power.
In Figure 8, the simulated EV demand and its time-dependent flexibility are given for the ‘Medium’ and ‘High’ scenario, averaged over all 50 simulation runs and over the time of the day. In Figure 8a, the results for the fixed constant charging power method are shown, while Figure 8b shows the results for the transaction-specific average constant power method for the same simulation run. Comparing these figures with the measured data shows that the shape is similar to the demand profile for local BEVs (upper left graph in Figure 6b), thus reflecting the high impact of local BEV penetration rate in the ‘Medium’ and ‘High’ scenario. As mentioned in Section 4.1, for BEVs, is 67% ± 18% lower than . These differences have two implications for the results concerning the simulated EV peak demand and the simulated available flexibility. Firstly, the average evening peak is lower and more spread out for the transaction-specific average power method than for the fixed charging power method, which is shown in Figure 7 as well. Secondly, the observed time-dependent flexibility is lower for the transaction-specific power compared with the fixed power method, as a lower charging power implicates larger values for and, therefore, lower values for , given that is the same for both methods. For comparison, using the fixed power method, 77% ± 1% of the EV demand could be delayed for more than 8 h. Using the transaction-specific average power method, this figure is 64% ± 2%.
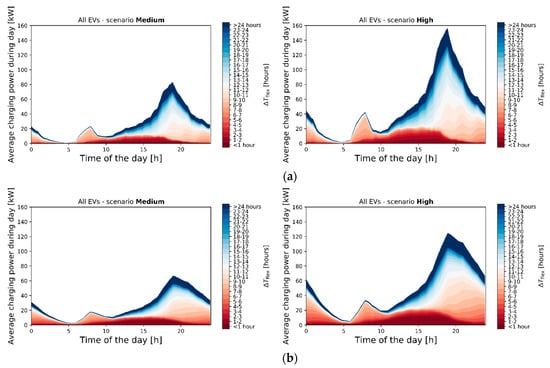
Figure 8.
(a) Presentation of the simulated time-dependent flexibility, averaged over the day over all 50 simulation runs, for ‘Medium’ (left) and ‘High’ (right) scenarios, using (22 kW for BEVs and 3.7 kW for PHEVs). (b) Presentation of the simulated time-dependent flexibility, averaged over the day over all 50 simulation runs, for ‘Medium’ and ‘High’ scenarios, using (see Equation (18)).
In conclusion, these results indicate that the fixed power method, using 22 and 3.7 kW for BEVs and PHEVs, respectively, produces inaccurate results for peak impacts of both future EVs and available flexibility of EV demand.
5. Discussion
In this section, the methods and results will be discussed.
Firstly, differentiating local and visiting BEVs by setting the average energy demand at half of the average energy demand of the present Dutch BEV fleet is an arbitrary choice. However, the results show that this choice leads to a clear, and in our view realistic, approximation of the distinction between local and visiting BEVs.
Secondly, there are uncertainties in the future development of residential EV demand and the number of charging stations. Besides, the scenarios for future numbers of EVs are uncertain. This especially counts for the number of visiting EVs. However, the number of visiting EVs is expected to have a limited impact on aggregated EV demand as the charging frequency of the visiting BEVs and PHEVs is low compared with that of local ones. Further, the future number of fast charging stations, mostly next to highways or close to main roads, is difficult to predict, and will also depend on developments in EV battery capacity, which is expected to increase [28]. A relatively large growth in the number of fast charging stations will cause the EV demand on residential networks to be lower than expected. Also, the rise of self-driving cars may result in a larger share of the EV demand being fulfilled outside residential areas, thereby decreasing the impact on residential networks.
Thirdly, there are uncertainties regarding the flexibility of the EV demand. To start with, for smart charging, active participation of EV users and their willingness to share information are of key importance. In this study, a participation of 100% is assumed. This was chosen because the target was to investigate the maximum potential flexibility and the influence of different simulation methods on estimations of future flexibility. In reality, the participation rate will be lower if the EVs are owned by individual users, causing a lower availability of the flexibility of EV demand. However, if the EVs are owned by a company, for example, a car-sharing company or leasing company, high participation rates are realistic. Further, the future charging behavior is likely to deviate from the historic measured charging data, which would influence the flexibility available. For example, the flexibility potential on residential networks may increase as a result of larger average charging power for future EVs, resulting in lower values for . Apart from this, user preferences that influence the charging scheme, such as charging part of the required energy in an uncontrolled manner and treating only the remaining energy demand as flexible load, could seriously reduce the available flexibility of EV demand. Note that user behavior may be steered if financial benefits are offered. Also, as perfect forecast is not realistic, part of the real driving behavior will deviate from the scheduled behavior. In order to avoid compromising the user comfort, ‘safety margins’ should be accounted for in the load scheduling, such as making sure that the car is fully charged a certain period before the scheduled or estimated departure time. This reduces the flexibility that can be used compared with the theoretical maximum amount of flexibility available when perfect forecast is assumed. Finally, the flexibility is influenced by the ratio between the number of EVs and the number of charging points, because charging durations are expected to decrease if charging points are more scarce. On the one hand, a high number of charging points increases the number of EVs that can charge simultaneously, which increases the maximum peak demand. On the other hand, however, a large number of charging points increases the flexibility of the EV demand, as EVs are expected to have longer connection durations when charging points are abundant compared with the situation in which charging points are scarce. In the simulation, the number of EVs charging simultaneously is left unconstrained, as it was assumed that the number of charging points is perfectly demand-driven. This was chosen because the target was to find the maximum available EV demand flexibility. In reality, the number of charging points available can be smaller, thereby limiting the available EV demand flexibility.
Fourthly, for the constraint on minimum trip duration, the maximum EV discharge power during a trip was assumed to be 20 kW, based on an average speed of 100 km·h−1 during the trip and a driving efficiency of 5 km·kWh−1 [32,37]. These numbers are uncertain as they depend on multiple variables such as the characteristics of the driving cycle and the battery technology. Yet, the exact value of the constraint is not expected to have a major impact on the results, as the constraint is not binding for most of the simulated transactions.
Fifthly, in this study, no data on home charging were available, but from our experience, this is not common in this pilot area. However, if home charging would have been included, this might have resulted in a higher demand of the current EV fleet, as well as a higher available flexibility, assuming that EVs charging at home would also be able to participate in smart charging schemes.
Further, we demonstrated that distributions of plug-in time, plug-out time, connection duration, and amount of energy charged per transaction do not follow normal distributions, suggesting that the proposed simulation method, which takes this into account, yields more realistic results compared with previous studies that use normal distributions for the simulation of one or more of these parameters.
Lastly, the different charging power simulation methods are discussed. If realistic charging profiles are not available, making a simulation using fixed constant charging power profiles is the most straightforward way to simulate EV demand flexibility. The introduction shows that many studies did indeed use a fixed constant charging power to simulate EV charging power profiles, for example, the works of [8,9,11,12,13,14,16]. In this study, for BEVs, the maximum power output of the charging points of 22 kW was used as fixed constant charging power, while 3.7 kW was used for PHEVs. The results were compared to transaction-specific charging power, in the data analysis as well as in the simulation. As the fixed constant charging power was relatively high, most EVs charge with lower power in reality. Therefore, both EV peak demand and EV demand flexibility are overestimated when the maximum charging power output of the charging stations is used in simulations of future EV demand profiles. The data analysis in this study shows that for BEVs, the maximum charging power occurring during a transaction is 55% ± 25% lower than the maximum output power of the charging station of 22 kW. The average charging power during a transaction is even 67% ± 18% lower than 22 kW. Further, a large variation in transaction-specific average charging power among different transactions is observed. The battery management systems of specific EVs influence the charging power profile, as well as other factors such as outside temperature, state of charge, and battery age [21,22,23]. These variations are ignored when a fixed charging power is used in simulations. To use transaction-specific average charging power for simulating the flexibility of EV demand, measured charging profiles or values for and must be available for each transaction and be used as exogenous input in the simulation. The advantage of this method over using the real time-varying charging profiles in the simulation, or in the EV demand scheduling, is that the computational time remains limited, while the resulting EV demand peak and flexibility closely approximate reality. For these reasons, operators of smart charging systems might require information on average charging power for each transaction, in addition to information on connection duration and required energy per transaction.
6. Conclusions
This study proposes a method for analyzing and simulating the time-dependent flexibility of EV demand. In our definition, the flexibility of EV demand is the difference between the time that the EV needs to charge, that is, the charging duration, and the time that the EV is connected to the charging station, that is, the connection duration, during a certain transaction. As a case study, we analysed the flexibility of EV charging demand using one year of measured data from charging stations located in the Lombok district, a residential area in the city of Utrecht (the Netherlands). Further, a method to simulate the future time-dependent flexibility of EV demand was proposed. Using this simulation, the differences in EV peak demand and flexibility were investigated for different scenarios and the effects of using a varying transaction-specific charging power instead of a fixed constant charging power in the simulation were tested.
The results of the analysis of the demand flexibility in the measured transaction data show that local BEVs have a relatively high impact on the aggregated EV demand in comparison with the other EV categories, but the demand flexibility of local BEVs is also high, especially during the evening peak that occurs in the case of uncontrolled charging. The analysis shows that 59% of the present-day EV demand could be delayed over more than 8 h. Even stronger, 16% of the aggregated EV demand is flexible over more than 24 h. This suggests that there is sufficient flexibility available to charge part of the EVs during the PV generation peak of the next day.
The time-dependent flexibility is lower for the average transaction-specific constant charging power method compared with the fixed constant charging power method: 77% ± 1% of the EV demand could be delayed for more than 8 h using the fixed constant charging power method, while this figure is 64% ± 2% for the average transaction-specific constant charging power method. Further, the maximum peak demand was on average 33% lower when the transaction-specific average constant charging power method was used in the simulation instead of the fixed constant charging power method.
In future work, the results produced by the proposed methods for the analysis and simulation of EV demand flexibility can be used by smart charging models that take into account detailed flexibility constraints. A recommendation for further research is to compare different smart charging optimization algorithms, based on local photovoltaic electricity generation or electricity day-ahead and imbalance markets, while considering the flexibility constraints as described in this paper. This could shed more light on the techno–economic feasibility of different smart charging schemes. Also, it would be interesting to apply the proposed methods to investigating the flexibility of EV demand to non-residential areas, such as parking lots in the city center or near offices. Finally, the influence of charging station availability on the flexibility of EV demand could be further investigated.
Author Contributions
M.K.G. designed the method, analyzed the data, and performed the simulation. T.A.A. and W.G.J.H.M.v.S. supervised the work and contributed to the design and implementation of the study. H.A.F. was involved in the data collection and also gave input on the research design. M.K.G. wrote the paper with input from all authors.
Funding
This study was supported by the European Regional Development Fund (ERDF) ‘EFRO Kansen voor West II’ in the framework of the project ‘Smart Solar Charging regio Utrecht’.
Acknowledgments
We would like to thank Robin Berg (Lomboxnet), Eric van Voorden (Last Mile Solutions), Bart van der Ree, and Carolien van Hemel (Utrecht Sustainability Institute) for their various contributions to this work. This study was supported by the European Regional Development Fund (ERDF) ‘EFRO Kansen voor West II’ in the framework of the project ‘Smart Solar Charging regio Utrecht’.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Indices | Description | |
| i | index of transaction in measured dataset | |
| j | index of EV in measured dataset | |
| q | index of transaction in simulated dataset | |
| m | index of EV in simulated dataset | |
| k | hour of the day | |
| Symbols | Description | Units |
| plug-in hour of transaction i | [-] | |
| average daily energy charged by EV j | [kWh·EV−1·day−1] | |
| energy required during transaction i | [kWh] | |
| number of charging stations in simulation area | [-] | |
| number of charging stations in total area | [-] | |
| number of days in measurement period | [-] | |
| number of days in simulation period | [-] | |
| number of simulated unique EV IDs in category ‘cat’ and scenario ‘scen’ | [-] | |
| number of unique EV IDs in category ‘cat’ in measured dataset | [-] | |
| number of unique EV IDs in measured dataset | [-] | |
| number of households | [-] | |
| number of transactions in measured dataset by EVs in category ‘cat’ during period ‘period’ for which the plug-in hour is k | [-] | |
| number of transactions in measured dataset by EVs in category ‘cat’ during ‘period’ (week or weekend) | [-] | |
| number of transactions in measured dataset by EVs in category ‘cat’ | [-] | |
| total number of transactions in measured dataset | [-] | |
| number of transactions by EV j during simulation period | [-] | |
| average charging power during transaction i | [kW] | |
| power charged at each time t during transaction i | [kW] | |
| maximum discharge power during a trip of simulated EV m | [kW] | |
| fixed charging power | [kW] | |
| maximum charging power during transaction i | [kW] | |
| maximum power charged by the EV | [kW] | |
| maximum power delivered by the charging point | [kW] | |
| maximum charging power occurring over all transactions by EV j in measured dataset | [kW] | |
| maximum charging power for simulated EV m | [kW] | |
| charging power for simulated transaction q | [kW] | |
| frequency of transactions with a duration > 6h for EV j | [week−1] | |
| average daily transaction frequency of EV j | [EV−1·day−1] | |
| probability that = k | [-] | |
| probability that a simulated transaction of simulated EV m in category ‘cat’ falls in ‘period’ (week or weekend) | [-] | |
| plug-in moment of transaction i | [-] | |
| plug-out moment of transaction i | [-] | |
| time step in measured charging profiles | [h] | |
| CPR | car possession rate | [HH−1] |
| LT | lifetime of an EV | [year] |
| charging duration during transaction i based on | [h] | |
| charging duration during transaction i based on | [h] | |
| measured charging duration during transaction i | [h] | |
| connection duration of transaction i | [h] | |
| available flexibility during transaction i | [h] | |
| Acronyms | Description | |
| BEV | battery electric vehicle | |
| EV | electric vehicle | |
| ID | identity | |
| LV | low voltage | |
| MV | medium voltage | |
| PHEV | plug-in hybrid electric vehicle |
References
- Netherlands Enterprise Agency. Statistics Electric Vehicles in the Netherlands (up to and Including December 2018); Ministry of Infrastructure and Water Management: The Hague, The Netherlands, 2019; pp. 1–7.
- Dallinger, D.; Schubert, G.; Wietschel, M. Integration of intermittent renewable power supply using grid-connected vehicles—A 2030 case study for California and Germany. Appl. Energy 2013, 104, 666–682. [Google Scholar] [CrossRef]
- Yong, J.Y.; Ramachandaramurthy, V.K.; Tan, K.M.; Mithulananthan, N. A review on the state-of-the-art technologies of electric vehicle, its impacts and prospects. Renew. Sustain. Energy Rev. 2015, 49, 365–385. [Google Scholar] [CrossRef]
- Sundström, O.; Binding, C. Flexible charging optimization for electric vehicles considering distribution grid constraints. IEEE Trans. Smart Grid 2012, 3, 26–37. [Google Scholar] [CrossRef]
- Verzijlbergh, R. The Power of Electric Vehicles—Exploring the Value of Flexible Electricity Demand in a Multi-Actor Context; Technische Universiteit Delft: Delft, The Netherlands, 2013. [Google Scholar]
- Netherlands Enterprise Agency. Vision on the Charging Infrastructure for Electric Transport; Ministry of Economic Affairs: The Hague, The Netherlands, 2017. [Google Scholar]
- Wu, X.; Hu, X.; Moura, S.; Yin, X.; Pickert, V. Stochastic control of smart home energy management with plug-in electric vehicle battery energy storage and photovoltaic array. J. Power Sources 2016, 333, 203–212. [Google Scholar] [CrossRef]
- Van der Kam, M.; van Sark, W. Smart charging of electric vehicles with photovoltaic power and vehicle-to-grid technology in a microgrid; a case study. Appl. Energy 2015, 152, 20–30. [Google Scholar] [CrossRef]
- Claessen, F.N.; Claessens, B.; Hommelberg, M.P.F.; Molderink, A.; Bakker, V.; Toersche, H.A.; van den Broek, M.A. Comparative analysis of tertiary control systems for smart grids using the Flex Street model. Renew. Energy 2014, 69, 260–270. [Google Scholar] [CrossRef]
- Liu, L.; Kong, F.; Liu, X.; Peng, Y.; Wang, Q. A review on electric vehicles interacting with renewable energy in smart grid. Renew. Sustain. Energy Rev. 2015, 51, 648–661. [Google Scholar] [CrossRef]
- Lopes, J.A.P.; Soares, F.J.; Almeida, P.M.R. Integration of electric vehicles in the electric power system. Proc. IEEE 2011, 99, 168–183. [Google Scholar] [CrossRef]
- Clement-Nyns, K.; Haesen, E.; Driesen, J. The impact of charging plug-in hybrid electric vehicles on a residential distribution grid. IEEE Trans. Power Syst. 2010, 25, 371–380. [Google Scholar] [CrossRef]
- Jian, L.; Zheng, Y.; Xiao, X.; Chan, C.C. Optimal scheduling for vehicle-to-grid operation with stochastic connection of plug-in electric vehicles to smart grid. Appl. Energy 2015, 146, 150–161. [Google Scholar] [CrossRef]
- Scharrenberg, R.; Vonk, B.; Nguyen, P.H. EV stochastic modelling and its impacts on the Dutch distribution network. In Proceedings of the 13th International Conference on Probabilistic Methods Applied to Power Systems, Durham, UK, 7–10 July 2014. [Google Scholar]
- CBS. Onderzoek Verplaatsingen in Nederland (OViN). 2018. Available online: https://www.cbs.nl/nl-nl/onze-diensten/methoden/onderzoeksomschrijvingen/korte-onderzoeksbeschrijvingen/onderzoek-verplaatsingen-in-nederland--ovin-- (accessed on 2 July 2018).
- Liu, Z.; Wu, Q.; Christensen, L.; Rautianen, A.; Xue, Y. Driving pattern analysis of Nordic region based on national travel surveys for electric vehicle integration. J. Mod. Power Syst. Clean Energy 2015, 3, 180–189. [Google Scholar] [CrossRef]
- D’hulst, R.; Labeeuw, W.; Beusen, B.; Claessens, S.; Deconinck, G.; Vanthournout, K. Demand response flexibility and flexibility potential of residential smart appliances: Experiences from large pilot test in Belgium. Appl. Energy 2015, 155, 79–90. [Google Scholar] [CrossRef]
- Develder, C.; Sadeghianpourhamami, N.; Strobbe, M.; Refa, N. Quantifying flexibility in EV charging as DR potential: Analysis of two real-world data sets. In 5th International Workshop of the Armand Peugeot Chair about Electric Vehicles and Electromobility Analysis; IEEE: Piscataway, NJ, USA, 2017; pp. 600–605. [Google Scholar]
- Flammini, M.G.; Prettico, G.; Julea, A.; Fulli, G.; Mazza, A.; Chicco, G. Statistical characterisation of the real transaction data gathered from electric vehicle charging stations. Electr. Power Syst. Res. 2018, 166, 136–150. [Google Scholar] [CrossRef]
- Sadeghianpourhamami, N.; Refa, N.; Strobbe, M.; Develder, C. Quantitive analysis of electric vehicle flexibility: A data-driven approach. Int. J. Electr. Power Energy Syst. 2018, 95, 451–462. [Google Scholar] [CrossRef]
- Mies, J.; Helmus, J.; van den Hoed, R. Estimating the charging profile of individual charge sessions of electric vehicles in the Netherlands. Electr. Veh. Symp. Exhib. 2017, 30, 17. [Google Scholar] [CrossRef]
- Panchal, S.; Mcgrory, J.; Kong, J.; Fraser, R.; Fowler, M.; Dincer, I.; Agelin-Chaab, M. Cycling degradation testing and analysis of a LiFePO4 battery at actual conditions. Int. J. Energy Res. 2017, 41, 2565–2575. [Google Scholar] [CrossRef]
- Panchal, S.; Mathew, M.; Dincer, I.; Agelin-Chaab, M.; Fraser, R.; Fowler, M. Thermal and electrical performance assessments of lithium-ion battery modules for an electric vehicle under actual drive cycles. Electr. Power Syst. Res. 2018, 163, 18–27. [Google Scholar] [CrossRef]
- Wang, Y.; Infield, D. Markov Chain Monte Carlo simulation of electric vehicle use for network integration studies. Int. J. Electr. Power Energy Syst. 2018, 99, 85–94. [Google Scholar] [CrossRef]
- Iversen, E.B.; Moller, J.K.; Morales, J.M.; Madsen, H. Inhomogeneous Markov models for describing driving patterns. IEEE Trans. Smart Grid 2017, 8, 581–588. [Google Scholar] [CrossRef]
- Vayá, M.G.; Andersson, G. Smart charging of plug-in electric vehicles under driving behavior uncertainty. In Reliability Modeling and Analysis of Smart Power Systems; Springer: New Delhi, India, 2014. [Google Scholar]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; Van Der Sluis, L. Stochastic modeling of power demand due to EVs. IEEE Trans. Power Syst. 2012, 27, 1–8. [Google Scholar] [CrossRef]
- Bunsen, T.; Cazzola, P.; Gorner, M.; Paoli, L.; Scheffer, S.; Schuitmaker, R.; Tattini, J.; Teter, J. Global EV Outlook 2018: Towards Cross-Modal Electrification; International Energy Agency: Paris, France, 2018. [Google Scholar]
- EVBox. Bekijk Alle Laadspecificaties. 2018. Available online: https://www.evbox.nl/elektrische-autos (accessed on 5 November 2018).
- CBS StatLine. Verkeersprestaties Personenauto’s; Kilometers, Brandstofsoort, Grondgebied. 2017. Available online: http://statline.cbs.nl/Statweb/publication/?DM=SLNL&PA=80428NED&D1=a&D2=0&D3=0&D4=0&D5=l&HDR=T&STB=G1,G2,G3,G4&VW=T (accessed on 1 June 2018).
- CBS StatLine. Motorvoertuigenpark; Inwoners, Type, Regio. 1 January 2017. Available online: http://statline.cbs.nl/Statweb/publication/?DM=SLNL&PA=7374hvv&D1=2-11&D2=0&D3=26&HDR=T&STB=G2,G1&VW=T (accessed on 1 June 2018).
- Seddig, K.; Jochem, P.; Fichtner, W. Integrating renewable energy sources by electric vehicle fleets under uncertainty. Energy 2017, 141, 2145–2153. [Google Scholar] [CrossRef]
- Simpson, A. Cost-benefit analysis of plug-in hybrid electric vehicle technology. In Proceedings of the 22nd International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium and Exhibition, Pacifico Yokohama, Yokohama, Japan, 23–28 October 2006. [Google Scholar]
- Van der Kam, M.J.; Meelen, A.A.H.; van Sark, W.G.J.H.M.; Alkemade, F. Diffusion of solar photovoltaic systems and electric vehicles among Dutch consumers: Implications for the energy transition. Energy Res. Soc. Sci. 2018, 46, 68–85. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. Foundations of the Theory of Probability; Chelsea Publishing Company: New York, NY, USA, 1956. [Google Scholar]
- Li, G.; Zhang, X.-P. Modeling of plug-in hybrid electric vehicle charging demand in probabilistic power flow calculations. Smart Grid IEEE Trans. 2012, 3, 492–499. [Google Scholar] [CrossRef]
- Canals Casals, L.; Martinez-Laserna, E.; Amante García, B.; Nieto, N. Sustainability analysis of the electric vehicle use in Europe for CO2 emissions reduction. J. Clean. Prod. 2016, 127, 425–437. [Google Scholar] [CrossRef]
- Kadaster. Basisregistratie Adressen en Gebouwen (BAG). 2018. Available online: https://bagviewer.kadaster.nl/lvbag/bag-viewer/index.html#?searchQuery=Utrecht&resultOffset=0&objectId=3295&geometry.x=135216.84&geometry.y=455756.208&zoomlevel=5&detailsObjectId=3295 (accessed on 15 June 2018).
- CBS StatLine. Motorvoertuigen van Particulieren; Wijken en Buurten. 2016. Available online: http://statline.cbs.nl/Statweb/publication/?DM=SLNL&PA=83603NED&D1=4,9-10&D2=14422&HDR=T&STB=G1&VW=T (accessed on 15 June 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).