Abstract
One of the most emblematic theorems in the theory of distributed databases is Eric Brewer’s CAP theorem. It stresses the tradeoffs between Consistency, Availability, and Partition and states that it is impossible to guarantee all three of them simultaneously. Inspired by this, we introduce the new CAP theorem for autonomous consensus systems, and we demonstrate that, at most, two of the three elementary properties, Consensus achievement (C), Autonomy (A), and entropic Performance (P) can be optimized simultaneously in the generic case. This provides a theoretical limit to Blockchain systems’ decentralization, impacting their scalability, security, and real-world adoption. To formalize and analyze this tradeoff, we utilize the IoT micro-Blockchain as a universal, minimal, consensus-enabling framework. We define a set of quantitative functions relating each of the properties to the number of event witnesses in the system. We identify the existing mutual exclusions, and formally prove for one homogenous system consideration, that (A), (C), and (P) cannot be optimized simultaneously. This suggests that a requirement for concurrent optimization of the three properties cannot be satisfied in the generic case and reveals an intrinsic limitation on the design and the optimization of distributed Blockchain consensus mechanisms. Our findings are formally proved utilizing the IoT micro-Blockchain framework and validated through the empirical data benchmarking of large-scale Blockchain systems, i.e., Bitcoin, Ethereum, and Hyperledger Fabric.
1. Introduction
In an ideal world, unanimity is always given: everyone agrees on whether an event took place or not by default. The mechanism for reaching a decision is also common and divine, and works in the same way for all: true is true and false is false always and for everyone. Seen under the Aristotelean perspective, the “harmony of true” prevails and is always treasured and guarded by all [1]. Autonomy and consensus are absolute, with no effort.
In the real world though, unanimity is not always given. Even if everyone carries the same mechanism for telling true from false, and even if everyone always acts rationally, consistently, and in good faith, the fact of the atoms’ finiteness suggests that subjectivity is not guaranteed [2]. Someone might eventually reach a contradictory conclusion, even upon a commonly observed event (e.g., while I see a cup, you see a pot). However true for others, things may escape his view due to limitations in memory, power, processing capacity, communication latencies, and deficiencies [3].
The process of reaching and proving consensus in Blockchain systems is known to be significantly resources-demanding: intensive processing, information exchange, and storage has to take place among and within the peer nodes. Reaching and proving consensus comes at a considerable cost [4,5,6,7].
In the world of Blockchain systems, the process of consensus semantically coincides with that of common witnessing [8]. An event-witnessing node is responsible for validating and recording the event data. With respect to each system, event witnesses are usually addressed under various names, as validators, verifiers, committers, or merely as full nodes. The number of event witnesses that are required every time also varies with the details of the architecture of each system. It largely defines the consensus dynamics of the system as well as its overall performance traits. To reach the desired level of consensus, without compromising the availability and without overburdening the resources, the Blockchain systems increasingly tend to adopt probabilistic over absolute finality and eventual over strong consistency practices [9].
As we demonstrate in this work, irrespective of the details of each Blockchain system, there are fundamental and universal tradeoffs between Consensus achievement (C), Autonomy (A) and entropic Performance (P) which prohibit their concurrent optimization.
1.1. Motivation
During the early stages of the evolution of cloud computing, a number of significant traits and constraints were revealed. One of the most definitive ones is described in the E. Brewer’s CAP theorem [10,11], which highlights the tradeoff between Consistency, Availability, and Partition in distributed database systems.
In our time, Blockchain incarnates the dream of modern technologists for autonomous peer and inclusive system operation of virtually infinite distribution capability. The limits and the constraints of Blockchain consensus mechanisms though, are beginning to reveal and set boundaries on the decentralization potential of the Blockchain systems [12,13].
Up to now, consensus mechanisms are typically studied within specific Blockchain systems. Recently, however, consensus has started to be considered as a distinct self-contained process evaluated under the prism of entropy [14].
Consensus mechanisms come with significant constraints. This is extensively discussed in the literature and highlighted in Dwork [3], Vogels [9], Brewer [10], Gilbert [11], and Rožman [12]. Blockchain researchers and engineers are inevitably balancing between the highly desirable need for autonomy, availability, and power efficiency on the one side and the consensus robustness and universality on the other [15,16,17,18].
This is also realized by observing the heterogeneity of the nodes in the prevailing Blockchain architectures, like, for example, the Bitcoin [16], the Ethereum [17], and the Hyperledger Fabric [18]: Irrespective of the details of the consensus mechanisms, i.e., Proof of Work, Proof of Stake, PBFT, and Raft [16,17,18,19], light nodes and mobile wallets are designed to deliver high availability and power efficiency, while the more intensive consensus achievement tasks are delegated to heavier duty full nodes. This by itself constitutes an early disruption to peerness and decentralization, and an early indication of the inherent limitations of the consensus process.
In this work, we explore the intrinsic tradeoffs among the fundamental properties of Autonomy (A), Consensus achievement (C) and entropic Performance (P) in peer autonomous consensus systems.
1.2. Contribution
In this work we introduce the new CAP theorem in the context of distributed consensus engineering.
In direct semantic analogy to the Eric Brewer’s CAP theorem, which formalizes the tradeoff between Consistency, Availability, and Partition tolerance in database systems, the new CAP theorem highlights the fundamental constraints existing between Autonomy (A), Consensus achievement (C), and entropic Performance (P) in Blockchain consensus systems.
In this work we study the process of consensus as a distinct self-containing process. We introduce a set of novel quantitative definitions:
- -
- Autonomy is defined in the atomic scale as the fraction of the memory of each node reserved to serve local operations.
- -
- Consensus achievement is defined at the system scale as the fraction of nodes required to reach agreement, i.e., to consent on new events for the system to function.
- -
- Entropic Performance is introduced, following [14], as a metric for the efficiency of the consensus process. It is given as the overall reduction in the information entropy of the system per unit of consumed energy. It measures how efficiently a Blockchain consensus system reduces uncertainty, in the sense of data disorder, relative to the energy it consumes.
A witnessing node is responsible for recording and validating the event data. Throughout this work, we recognize the notion of witness as the essential link among the Autonomy (A), the Consensus (C), and the entropic Performance (P) of the system.
- -
- We prove that of these three essential properties, two at the most can be optimized simultaneously at any given time in the generic case. For this, we formally prove that there exists at least one peer system consideration for which (C), (A), and (P) cannot be simultaneously optimal, and we validate the results through empirical real-world Blockchain systems data benchmarking.
- -
- We demonstrate that this trait comes in a direct analogy and has the same semantic origins as Eric Brewer’s CAP theorem.
The new CAP theorem, as presented in this work, establishes a fundamental theoretical constraint on distributed consensus mechanisms. Just like Brewer’s CAP theorem in distributed databases, the new CAP theorem in blockchain consensus holds independently of the specific blockchain architectures and considerations.
The main focus of this paper is on proving the intrinsic limitations of blockchain consensus mechanisms. The impact of the revealed limitations on the prevailing Blockchain systems is also studied in Section 5.2 and Section 5.3. This further reinforces the generality of the findings in this work, which is semantically based on the foundations of the common perception and witnessing that takes place among the consenters and lies beneath every consensus mechanism, irrespective of architectural considerations and system implementation details [2,14,15,16,17,18].
2. Materials and Methods
In this work we demonstrate that a requirement for concurrent optimization of the properties of Consensus achievement, Autonomy, and entropic Performance in Blockchain consensus systems cannot be satisfied in the generic case. We formally prove that there is at least one homogenous system consideration for which the three cannot be simultaneously optimized. The results are further validated through empirical data benchmarking analysis in Section 5.2.
To keep our approach universal and architecture agnostic, our formal analysis relies on two major pillars:
- -
- The deployment of the IoT micro-Blockchain, defined in [8], as a peer, distributed and architecture agnostic consensus-enabling framework.
- -
- The quantitative representation of (A), (C), and (P), with respect to the number of event witnesses in the system.
Following in this section, we quote their basic traits.
2.1. The IoT Micro-Blockchain Framework
The IoT micro-Blockchain implements a neutral universal consensus-achievement framework that operates in every node of the system. In this framework, Blockchain is considered in its most simple and generic form as the aggregation of interconnected atomic hash chains which are stored in the finite local memory of each node. Its source code can be found in https://github.com/arianagnostakis/IoT_Blockchain (accessed on 12 February 2025).
Our system is self-inclusive, and new events are only taking place inside the nodes. Consensus relies on common event witnessing. The process of witnessing is illustrated in Figure 1, which is given here after [8]. It depicts a new local event which is raised and stored locally in node , as well as transmitted to and witnessed by two other peer nodes.
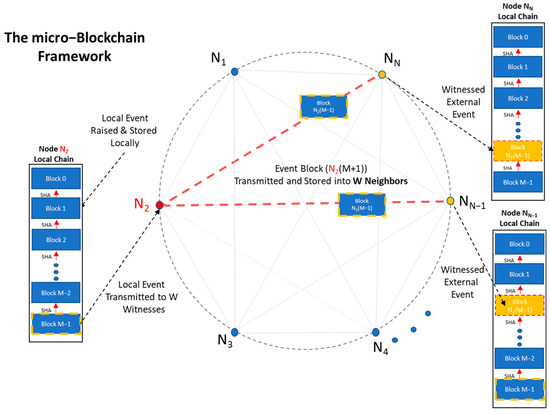
Figure 1.
The process of witnessing in the IoT micro-Blockchain network, published after [8]. In this example, the local event Block raised in is transmitted P2P (red dashed lines) to two neighbors.
Generally, in the light of a new event, W peer nodes are being contacted to validate and record it in their local memories. The whole consensus process relies on this simple witnessing function: every witness of an event agrees with every other witness of the same event. This way the collective agreement mechanism that governs the consensus process in its generality is formed.
The desired number of event witnesses W varies with respect to the needs of each application. In absolute-finality Blockchain systems, for example, the ones that are developed exclusively to facilitate monetary transactions, like the early-stages Bitcoin Blockchain [16], an absolutistic requirement of W = N at all times is usually raised, where N is the number of the peer nodes in a system. In this case, the content of the memories of all nodes becomes identical; the redundancy of the Blockchain as well as the consensus over it becomes absolute and maximum.
In a system consisting of finite capacity entities, and consequently in every digital system, this absolutistic requirement cannot always be guaranteed. This induces the consideration of consensus its generality as a scalar attribute [14]. A distributed world of finite-capacity entities has often got to work with W << N.
The memory of the autonomous node can be abstractly modeled as in Figure 2. It consists of two logical parts: (a) The ROM-like part in which the inherited code implementing the common consensus process is stored. (b) The active RAM-like part in which the events’ data are stored and has the form of hash chain. The active memory (b) can be further logically divided into two parts, storing either local or external events’ data. The events that are validated and stored in each node are either local, if the event was raised within the node, or external, if the node witnesses an event that came from another peer node.
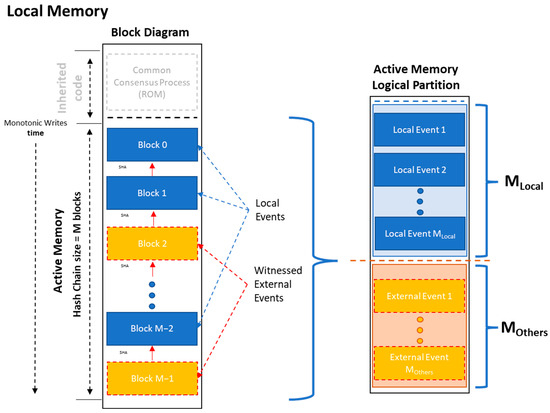
Figure 2.
A simple model of the memory of the autonomous node (M = MLocal + MOthers). The local event blocks are colored blue, and the witnessed external events orange.
We utilize this simple model to define the Autonomy of the node as the fragment of the local memory utilized by the node to store its local events (M_Local) to the total active memory of the node (M) later in Section 3. At a fundamental level, this also reflects the fraction of the total resources of the node dedicated to processing the local events.
The logical fragmentation of the memory of the node is depicted in Figure 2.
2.2. Consensus, Autonomy, and Entropic Performance
The basic traits of Consensus (C), Autonomy (A), and entropic Performance (P) in the consideration of a universal consensus mechanism are given here to facilitate their formal definition later in Section 3.
- -
- Consensus (C): Constitutes a collective attribute and can thus be defined only within a system of nodes. In its essence, consensus is a binary function: in the end, each node may either agree or disagree with the others over an observable event.
In its general form, consensus constitutes a metric of the awareness of “how close” the separate perceptions of the atoms in a realm are upon an observable event. If only infinitesimal events are considered, i.e., single-bit events like the opening of a door, the crossing of a temperature threshold, or the validity of a monetary transaction, then it is easy to identify consensus as “a count of ‘1’s”. Consensus is identified as the fraction of the population that witnesses a specific event, meaning they are aware of and agree on it. In every case though, the outcome of consensus remains a binary agreement/disagreement flag: e.g., “Does the hash produced in block X with nonce Y start with 5 zeros in a row?” (yes/no). This is analyzed in [14].
- -
- Autonomy (A): Autonomy is a metric of the independence of the node. It constitutes an atomic trait, defined here as the fraction of its memory each node can dedicate to serving itself. Atomic traits refer to properties defined in each individual node within the system. As mentioned earlier, at a fundamental level Autonomy generally reflects the fraction of the resources dedicated to processing and storing the node’s local events.
At an abstract level, in a peer-distributed system, every peer node operates in conformity with its siblings. To achieve this, part of its resources is contributed to serving the others, the community. Conceptually seen, the existence and the coherency of the community itself rely on this tribute from the part of each peer node.
In a peer, collective-consensus environment, autonomy is expected to increase when the required number of per event witnesses (W) is reduced. A fully independent node should operate consistently without the necessity of any event-sharing with the others.
In a fully autonomous system, as witnessing tends to zero (W- > 0), the node tends towards absolute autonomy (A- > 1) allocating all its resources to serve itself. Still, to comply with the notion of system, W, however small, can never be equal to zero, since this would lead to a system of totally isolated nodes with zero external awareness: a set of unconnected, lonely nodes.
- -
- Entropic Performance (P): At the cost of running the consensus mechanism, the observed information entropy of an isolated autonomous system decreases as W increases. As the number of witnesses increases, nodes store more uniform information, reducing the overall system entropy. This effect is strongest when the number of witnesses is low, meaning that even a small increase in witnesses leads to a sharp drop in entropy as discussed in detail in [14].
In this work, we introduce the entropic performance of the system as the ratio of the observed information entropy reduction to the overall energy consumed to achieve it, with respect to W.
A literature review of the relevant works is presented in the next section.
2.3. Related Work: Blockchain Consensus Tradeoffs
Eric Brewer’s CAP theorem in distributed systems has guided research in balancing Consistency, Availability, and Partition tolerance [10,11]. However, the existing studies on blockchain consensus mechanisms often focus on specific aspects rather than on the inherent tradeoffs between them.
While some works are addressing performance, security, and autonomy, this is often done fragmentally, in a KPI-specific approach, and does not focus on the interdependencies upon the attributes. Many of them are focusing on security and resilience issues, while others present comparative numeric analyses on KPIs.
Wan et al. in [15] provide a systematic review of blockchain consensus mechanisms, categorizing them based on their development and application requirements. The study of Mssassi and Abou El Kalam in [19] emphasizes that no single mechanism can simultaneously optimize decentralization, security, and scalability, as “the blockchain trilemma”. They formally analyze these, proving that different blockchain architectures must prioritize specific properties depending on the intended use case.
In the context of Blockchain systems for the Internet of Things (IoT), Auhl et al. in [20] examine the suitability of various consensus mechanisms under resource-constrained environments. Their findings suggest that lightweight mechanisms, such as lightweight Byzantine Fault Tolerant (BFT) algorithms, enhance energy efficiency, but often sacrifice decentralization. Oyinloye et al. in [21] provide an overview of alternative consensus protocols, including hybrid approaches. Merrad et al. in [22] explore key performance indicators for blockchain consensus, evaluating their tradeoffs in computational complexity, security, and scalability. Their work underscores that the selection of a consensus mechanism depends on the application context, as different mechanisms exhibit strengths and weaknesses in different domains. Guru et al. [23] focus on security vulnerabilities and attack vectors in blockchain consensus mechanisms, particularly in permissionless networks, where energy-intensive consensus can be more resilient against attacks.
Zhou et al. in [24] proposed a reputation-based consensus mechanism built on information-centric networking to address fairness and efficiency concerns. Their findings suggest that incorporating reputation models can improve network security while maintaining consensus efficiency.
From a sustainability perspective, Pineda et al. in [25] present a systematic literature review on energy-efficient blockchain consensus mechanisms, discussing strategies to reduce the environmental impact of blockchain networks. Lepore et al. in [26] present a comparative study of Proof-of-Work (PoW), Proof-of-Stake (PoS), and Hybrid consensus models.
From the security perspective Deirmentzoglou et al. in [27] examine Long-range attacks in PoS protocols, emphasizing the need for robust mitigation techniques. Faber et al. [28] present a review of Blockchain consensus mechanisms in search of strong Sybil attack resistance, while Sayeed et al. in [29] are assessing Blockchain consensus and security mechanisms against the 51% attack.
Sapra et al. [30] evaluated the energy consumption of PoW-based blockchain networks, offering a comprehensive analysis of their environmental impact. Their findings highlight the ongoing debate regarding the sustainability of Blockchain technology.
Several studies explore Blockchain efficiency. Entropy reduction in Blockchain consensus is investigated in [14], while Khosravi et al. in [5] and Pagone et al. in [6] analyze the environmental impacts of the large-scale popular Blockchain systems rather than focusing on inherent constraints.
This work differs by explicitly proving a fundamental tradeoff between Autonomy (A), Consensus (C), and entropic Performance (P) in the Blockchain consensus process. Unlike previous studies, which focus on improving individual metrics (e.g., PoW energy efficiency or BFT scalability), we show that optimizing all three properties simultaneously is fundamentally constrained.
Following in Section 3, we formalize the definitions, and we highlight the intrinsic constraints existing between the Autonomy (A), the Consensus achievement (C), and the entropic Performance (P).
3. Analysis and Results
In this section we intend to highlight the principles. We formally demonstrate that there exists a peer system consideration, for which (C), (A), and (P) cannot be simultaneously optimized. This holding constitutes a solid mathematical proof of the initial intuitive assertion that (C), (A), and (P) cannot be simultaneously optimized in the generic case. The findings are further validated through real-world empirical data benchmarking in Section 5.2.
To keep our mathematical analysis simple, we consider the average node as the representative unit of our system in the sense that the nodes in the system are equivalent, peer, and following the same principles. Building on the definitions in [8], we consider that the nodes in our system exhibit uniform behavior. The probabilities of new events’ occurrences and witnessing are also evenly distributed among the nodes.
While our model assumes uniform node behavior for simplicity, real-world Blockchain environments often exhibit diversity in node capacities and connectivity. Still, the principles remain intact. As discussed in detail in Section 5.3, the heterogeneity of the nodes observed in many large-scale Blockchain systems has the same origins as the new CAP theorem. The need for heterogeneity itself constitutes inherent evidence of the validity of the theorem.
3.1. Formal Definitions
Autonomy (A): Autonomy describes the fraction of resources each node dedicates exclusively to managing its own transactions rather than validating external ones. Autonomy is formally defined here as the fraction of the memory of the node reserved for local events relative to its total memory, given by:
where M is the active memory of the node, the memory dedicated to the local events, and the memory used to store external events, as it is defined through Figure 2 and discussed in detail in [8].
With respect to the witnessing requirements of the system, every event in the local memory of the node must be witnessed by W siblings for the system to function. With respect to the uniformity of the nodes, this as well suggests that every node in the system witnesses on average the events existing in W local memories of other nodes, leading to:
This quantifies the witnessing requirement and defines the fragment of to within each node with respect to the number of event witnesses W in our system.
Since
we get
where again, M is the total active memory in a node and W the number of witnesses on each event.
By substituting and in the Autonomy Formula (1) we get:
where N is the total number of nodes in the realm.
Equation (4) expresses Autonomy (A) as a function of the memory allocation with respect to W. It follows from the prerequisite that every event must be witnessed by W peers, thereby occupying a fraction of the node’s memory. By substituting the witnessing requirement into the autonomy function in Equation (1), we derive the relationship between W and A. Equation (4) indicates that as W increases, A decreases. This suggests that higher participation in consensus reduces node independence.
Consensus (C): We define the quantity of consensus as the proportion of the autonomous nodes that agree over an observable event every time. This corresponds to the average number of witnesses of each new event (W), with respect to the overall population of the nodes (N). It takes the form of a scalar ranging 1/N, where no one but the introducer of the event witnesses it, to 1 where every node witnesses every event. This is analyzed in depth in [14].
Consensus (C) quantifies the agreement among nodes, measured as the proportion of nodes in the system actively witnessing each event, given by:
where again, W is the number of witnesses of each event and N the total number of nodes in the system. This equation macroscopically reflects the level of agreement among the nodes. The ‘+1’ in the numerator accounts for the originating node, which always participates in consensus. As the number of witnesses W increases, the fraction approaches to 1, indicating a highly coherent network where a large number of nodes agree. C maximizes approaching 1 as W approaches N−1, i.e., when all nodes that participate in the consensus process agree for every new event. C becomes minimal () when , indicating a system tending to zero consensus, i.e., a system of isolated nodes.
Substituting W in Equation (4) with respect to Equation (5), leads us to:
which relates the Autonomy (A) with the collective Consensus (C) in a reverse analogy and reveals the constraint between A and C. This equation expresses a fundamental tradeoff: if the system prioritizes high consensus, it inherently sacrifices node autonomy. If every node is required to participate in the witnessing process of every event (), then autonomy (A) is diminished, meaning that no node can dedicate its resources wholly to its own operations. Conversely, if a node fully prioritizes autonomy (A = 1), then it does not contribute at all to the consensus process leading to (), which practically denotes a system of isolated nodes.
Entropic Performance (P): This is defined here as the entropy drop (bits) occurring per unit of energy consumed in the system (Wh). The consensus process, while seen as a distinct mechanism from the perspective of the second thermodynamic law, is an entropy conversion mechanism.
Information entropy H describes the uncertainty or disorder existing in a Blockchain system. Lower entropy means that the nodes have more similar information and comes with increased information redundancy. The entropic traits of the consensus process in peer-distributed systems have been discussed in detail in [14]. There, the information entropy in the system with respect to W is defined as:
which simplifies to:
where N is the number of peer nodes in the realm, M the active memory capacity of each node, and W the number of per-event witnesses.
These equations illustrate how increasing the number of witnesses lowers the entropy of the system. As W increases, more nodes align their records, reducing the overall disorder and uncertainty, thereby decreasing the observable information entropy in the system. Equation (7) derives from the definition of Shannon information entropy, and is discussed in detail in [14]. Equation (8) connects the information entropy of the system to the number of per-event witnesses W and highlights that increasing the number of witnesses, proportionally reduces the information entropy of the system.
The rate of the information entropy reduction with respect to W is also given in [14] by the derivative of H over W. The entropy reduction rate indicates the rate at which uncertainty decreases as more nodes witness each event. It is given by:
where again, N is the number of the nodes, M the active memory of each node, and W the number of per-event witnesses in the system. Equation (9) designates that the information entropy reduction in our system is steepest for low (still >0) values of W.
Let us now consider the energy required for introducing an additional witness of an event ().
The exact value of the energy consumption does not affect the findings, the results, and the conclusions of this work.
The total energy invested in the system to acquire W event witnesses is given by:
This corresponds to the total amount of energy consumed in the system per event in order to support the consensus process and is equal to the energy consumed by all W witnesses of the event. Consequently, the smaller the energy consumption in a node per event witnessing (, the more efficient the system is overall.
Entropic Performance (P) measures how effectively the consensus mechanism reduces the uncertainty in the system per unit of energy consumed. Higher performance means more efficient use of energy in achieving consensus. Following, the entropic Performance of the consensus mechanism is defined as the occurring entropy drop dH in the system per unit of energy consumed:
where again, E is the energy consumption per event witnessing, M the active memory of the node, N the number of nodes in the system, and W the number of per-event witnesses. This corresponds to the observed information entropy reduction occurring in the system per unit of energy consumed.
Equation (10) highlights the efficiency of consensus mechanisms from an energy perspective. Systems with high achieve significant entropy reduction while consuming minimal energy, whereas lower values of indicate inefficiencies where high energy expenditure does not lead to a proportionate reduction in entropy. This becomes particularly significant if we aim to compare different Blockchain consensus mechanisms such as, for example, Proof-of-Work (PoW) versus Proof-of-Stake (PoS), versus Byzantine Fault Tolerance (BFT)-based systems.
The above formal analysis is based on the thorough consideration of the IoT micro-Blockchain framework. Still the same principles undergo every Blockchain consensus system. To illustrate the implications of the new CAP theorem to the large-scale Blockchain systems, an empirical analysis based on real-life macroscopic benchmarking data is presented in Section 5.2.
Following in Section 4, we present the formal definition of the new CAP theorem and its proof, followed by graphical illustrations of the outcomes of our analysis.
4. The New CAP Theorem
Theorem 1.
Of the three elementary properties of the autonomous systems, Consensus achievement (C), node Autonomy (A), and entropic Performance (P), two at the most can be optimized at any given time in the generic case.
Proof of Theorem 1.
To prove the assertion, following we investigate the traits of the properties. In Section 4.2 and Section 4.3 we illustrate the two mutual exclusions holding among the properties in the presence of a requirement for concurrent optimization.
4.1. Autonomy and Consensus as Functions of W
Figure 3a,b depict Consensus and Autonomy as defined in Equations (4) and (5), respectively, with respect to W in a dynamic system of 100 nodes.
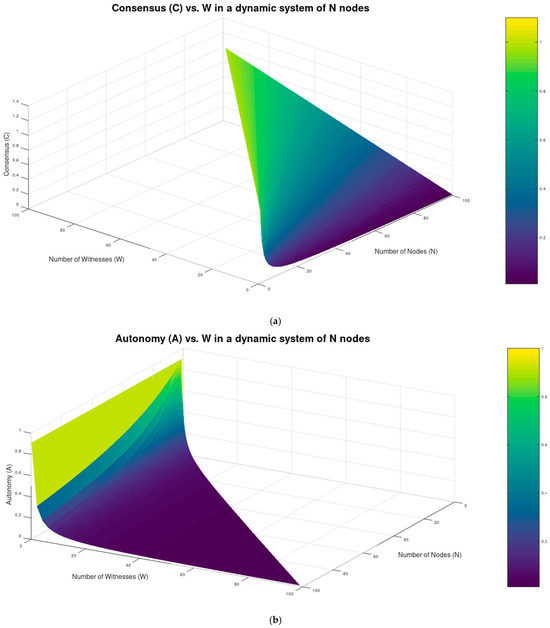
Figure 3.
(a) Consensus as a function of W in a dynamic system of 100 Nodes, W varying from 0.1 to N − 1. Consensus increases with the number of witnesses, illustrating that broader node participation leads to increased agreement in the system. (b) Autonomy as a function of W in a dynamic system of 100 Nodes, W varying from 0.1 to N − 1. Autonomy sharply decreases with increasing numbers of event witnesses (W), reflecting reduced independence of the nodes as they spend more resources to validating external events.
The macroscopic behavior of C and A as demonstrated in Figure 3a,b, is in strict conformance with the definitions: as expected, Consensus increases monotonically with W, while Autonomy declines rapidly. In Figure 3a,b the axes are left on their original scale to demonstrate the boundaries as well. It is noted that the same behavior is exhibited by the system for N ranging up to thousands of nodes, restrained in this section to 100 in order to facilitate the comparative illustration of the findings.
Based on Equations (4) and (5), we have , respectively.
Both the Consensus and the Autonomy become optimal as they approach 1 (see definitions in the previous section).
Still, as we demonstrate below in Section 4.2 this cannot happen simultaneously for both.
4.2. Autonomy (A) vs. Consensus (C)
The tradeoff between (A) and (C) is evident through Equation (6). This imposes a condition of mutual exclusion among them as a requirement for the concurrent optimization of the two properties.
Figure 4 shows the existing tradeoff between C and A with respect to the number of event witnesses (W).
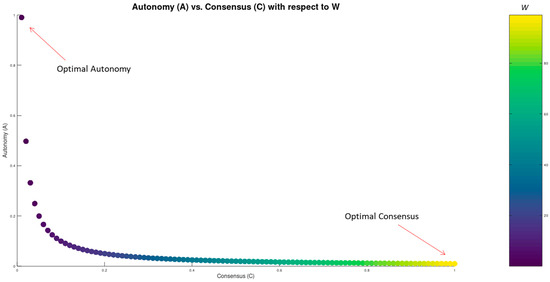
Figure 4.
Autonomy (A) vs. Consensus (C) as functions of W. As consensus requirements increase rightward, node autonomy reduces downward and vice versa, illustrating an intrinsic limitation.
The scatter plot in Figure 4 depicts the outcome of Equations (4) and (5) with respect to W and demonstrates that Autonomy and Consensus cannot be optimized simultaneously in our system: while consensus increases with W, the resources remaining to serve the local events in the nodes decrease, and along with them, the Autonomy of the node declines as well.
Figure 4 clearly demonstrates this mutual exclusion condition and constitutes the first proof of the initial assertion (the new CAP Theorem).
Still, this is not the only one. As we demonstrate following in Section 4.3, neither Consensus and entropic Performance (P) can be optimized simultaneously, raising the second mutual exclusion condition.
The constraint between Autonomy (A) and Consensus achievement (C) is also validated through the empirical analysis of real-world large-scale Blockchain system benchmarking data in Section 5.2. As it is clearly presented there, in the case of Bitcoin, the Autonomy (A) is fully sacrificed in favor of maximum Consensus achievement ( requirement). In the case of Hyperledger Fabric, the achievement of catholic Consensus is compromised, since only a pre-defined set of nodes out of the whole are invoked in the consensus process, requiring in the default case, leading nodes to higher Autonomy (A) and the system to high availability. In the case of Ethereum 2.0 (PoS), an elegant tradeoff between (C) and (A) is committed, keeping W from 128 verifiers initially, to validators in order to reach finality secondarily.
4.3. Consensus (C) vs. Entropic Performance (P)
The entropic Performance (P) is defined in Equation (10) as the observable reduction in the information entropy of the system per unit of consumed energy, and extends the definitions of [14].
The scatter plot in Figure 5 depicts the tradeoff between the entropic Performance (P) as defined in Equation (10) vs. Consensus (C) as defined in Equation (5), both as functions of W.
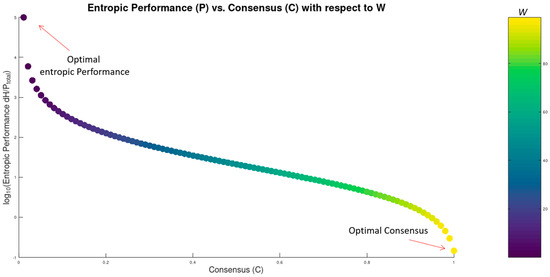
Figure 5.
Consensus (C) vs. entropic Performance (P) given as functions of W. Increasing consensus rightward, decreases energy efficiency in entropy reduction downward and vice-versa.
As demonstrated in Figure 5, Consensus and entropic Performance cannot be optimized simultaneously. While the higher Consensus occurs for high values of W, the entropic Performance is optimal (maximum) for low values. This also constitutes a conditional proof of the generic intuitive assertion that “higher consensus mandates higher power consumption”.
The relation of the entropic performance with respect to the degree of replication in a system was first revealed in [14] and raises here a mutual exclusion condition among C and P in a request for concurrent optimization. Again, this by itself also constitutes solid proof of Theorem 1.
It also mandates that in order to maximize the efficiency of the Consensus mechanisms, the systems need to operate on the lower possible number of per-event witnesses, with respect, of course, to the overall stability and consensus requirements every time.
Again, the constraint between Consensus achievement (C) and entropic Performance (P) in large-scale systems is also demonstrated through the empirical benchmarking data analysis in Section 5.2. In the case of Bitcoin, the consensus is absolute () leading to the worst entropic Performance (P) recorded in the benchmark. In the case of Hyperledger Fabric, Consensus (C) is moved from maximum since consenters are required in the default case, leading to higher entropic Performance. In the case of Ethereum, (C) is also moved from maximum: W varies from 128 verifiers to validators, while the benchmarks indicate rank better entropic Performance (P) in comparison to Bitcoin (discussed later in Section 5.2).
4.4. Autonomy (A) vs. Entropic Performance (P)
The entropic performance of the system increases with the increment of the autonomy in the system. This is depicted in Figure 6.
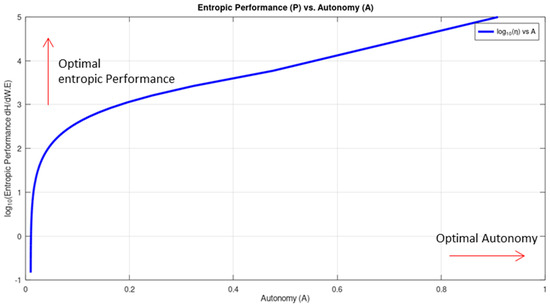
Figure 6.
Entropic Performance (P) vs. Autonomy (A). Entropic Performance improves with higher Autonomy, illustrating elevated efficiency for low number of witnesses.
The Autonomy of the system increases decreasing the number of per-event witnesses, while at the same time the entropic performance of the system becomes optimal. Figure 6 demonstrates that both Autonomy (A) and entropic Performance (P) can be simultaneously optimal. □
4.5. Entropic Performance (P) as a Function of W
In Figure 7, we see the entropic Performance in a dynamic peer system of 100 nodes. As noted earlier, the same behavior is exhibited by the system for N ranging up to thousands of nodes and is left at 100 to better facilitate the comparative illustration.
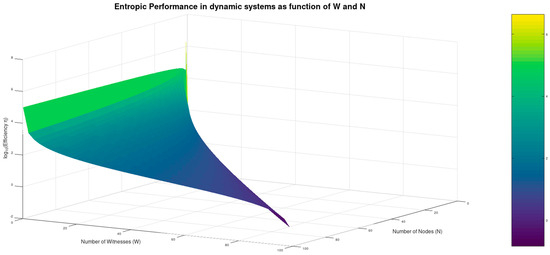
Figure 7.
Three-dimensional plot of the entropic Performance (efficiency) of a dynamic system of N nodes for N = 1:100, W = 0.1:N−1, E = 1, and M = 1000 bit. Maximum efficiency at low witness participation is illustrated.
It presents the outcome of Equation (10) and demonstrates once more that the steepest entropy reduction per energy unit paid occurs for low values of W. This also highlights that the entropic Performance tends to optimal (maximizes) as .
As it is proved in [14], the steepest decline in the information entropy of the system occurs for low values of W, meaning that the act of witnessing is more efficient in terms of information entropy reduction per unit of consumed energy while fewer witnesses exist in the system.
This also suggests that diversity in a system increases its overall entropic Performance.
4.6. Scalability and Performance Implications in Large-Scale Systems
The theorem has direct implications for Blockchain scalability and performance. In decentralized networks, increasing node involvement in the agreement process, i.e., higher W, improves Consensus (C) but inherently hurts Autonomy (A) and entropic Performance (P). This explains why large-scale fully permissionless systems like Bitcoin experience high confirmation times and energy costs, while hybrid or permissioned consensus systems such as Ethereum PoS and Hyperledger Fabric introduce optimizations at the expense of decentralization as discussed in Section 5.2.
Transaction Finality: As W increases, the time required to finalize transactions also increases in the generic case. Bitcoin’s block time, which is dynamically adjusted to 10 min, ensures high consensus at the cost of throughput and entropic performance, while Ethereum’s PoS finality mechanism speeds up transactions and reduces decentralization.
Scalability: Large-scale systems must carefully balance W to maintain their efficiency. Empirical studies of Ethereum and Hyperledger Fabric show that consensus participation thresholds significantly impact overall network performance [17,18].
Network overhead: In peer networks, higher W results in non-linear data traffic increment, leading to congestion and increased latencies. The exponential relationship of W to the latency is recorded [8].
In the next section, the findings and the broader implications of the new CAP theorem are discussed. The practical ways in which the large-scale Blockchain systems balance (C), (A), and (P) are also analyzed through empirical data benchmarking.
5. Discussion
Seemingly independent properties in nature often come with inherent constraints. This principle is elegantly captured in the great conservation laws where it relates to the existence of underlying symmetries [31,32]. These laws, fundamental to theoretical physics and mathematics, highlight an intrinsic truth: some properties are constrained and cannot vary without affecting others. Distributed Blockchain systems are no exception to this trait.
One of the most influential theorems in the field of distributed database systems, Eric Brewer’s CAP theorem, reveals such a constraint among the properties of Consistency, Availability, and Partition tolerance: it asserts that these cannot be simultaneously optimal. This assertion was initially introduced by Brewer as a conjecture in a keynote speech in 2000 [10] and was formally proved by S. Gilbert and N. Lynch two years after [11].
5.1. Revealing the Intrinsic Constraints
Building on these concepts, in this work we introduce the new CAP theorem for distributed Blockchain systems. Through a uniform distributed consensus system consideration, we formally demonstrate that Consensus achievement (C), Autonomy (A), and entropic Performance (P) cannot be optimized simultaneously in the generic case.
Our findings are further validated by the empirical benchmarking data from the prominent large-scale Blockchain systems, presented in Section 5.2.
In this work, the theorem is formally proved through two inherent mutual exclusions:
- (a)
- Between Autonomy (A) and Consensus achievement (C)In an attempt to optimize one of two, the other is sacrificed. This derives from Equations (4)–(6) in Section 3.1 and is demonstrated in Figure 4, Section 4.2. An attempt to optimize Autonomy, i.e., moving , would leave the nodes without any resources to serve the community: W moves close to 0, leading Consensus achievement to minimum, and the system degrades down to a set of isolated nodes. Again, trying to optimize Consensus (, we would have to withhold resources from the atoms to serve the system, sacrificing Autonomy.This intrinsic constraint was revealed in this work by starting from two apparently independent starting points: while we define Autonomy in the micro-scale of the node, Consensus is defined in macro, with respect to the properties of the realm. This strengthens even more our initial hypothesis for the existence of an inherent intrinsic constraint among (A) and (C).
- (b)
- Between Consensus achievement (C) and entropic Performance (P)Consensus achievement is an energy-consuming process: it relies on data transmission, processing, and storage, all of which are known to be energy-consuming tasks. The constraint between (C) and (P) is revealed in Section 3.1 through Equations (5) and (10) and is demonstrated in Figure 5, Section 4.3. Again, trying to optimize one of the two, the other is forced away from optimal. Our consideration for the two properties has independent starting points as well: while C is defined with respect to the macroscopic traits of the system, P is defined based on Shannon information entropy principles. This further strengthens the finding of the inherent constraint among C and P. The entropic traits of distributed consensus systems are studied extensively in [14].
In this work, we extend the scope of [14] by applying the notion of energy consumption to our considerations. We treat Consensus achievement as a distinct, self-contained process, and we exploit its entropic features to introduce a new metric on its efficiency, as the entropy reduction it induces to the system per unit of consumed energy. This paves the way for further research and development aimed at Blockchain optimization.
Throughout this work, we acknowledge event witnessing as the core feature of the consensus process in its entirety [2,8,14]. Across the different architectures, event witnesses take various forms and names, i.e., validators, solvers, verifiers, pruned or full nodes, etc. Regardless of the terminology, the witnessing process underlies every consensus mechanism, reflecting the Aristotelian notions of true and existent [1].
In this work, we exploit the architectural neutrality of the IoT micro-Blockchain framework to formalize (A), (C), and (P) with respect to the primitive traits of the distributed autonomous systems.
Throughout this work, we prioritized simplicity and generality, focusing on fundamental universal principles rather than on the implementation details of the various systems. To keep the focus, in several points we opted for the simpler applicable approach.
In this work, the new CAP theorem is formally proved through the thorough analysis of a universal consensus system and validated through real-life systems’ empirical data benchmarking.
In the next section, we include empirical benchmarks based on real-world data from the prominent Blockchain systems, i.e., Bitcoin PoW, Ethereum 2.0 PoS, and Hyperledger Fabric 3.0. The findings further fortify the validity of the new CAP theorem and come to explain the decisions made by their architects and engineers.
5.2. Empirical Validation Through Real-World Data
Here we consider and compare the Bitcoin (PoW), the Ethereum 2.0 (PoS), the Hyperledger Fabric 3.0 (Raft, PBFT), and the IoT micro-Blockchain 1.0.
It is noted that neither the actual per-transaction consumption values nor the scale of the Blockchain system affect the results and the conclusions of this work, and even though the findings of the empirical analysis fortify the universal validity of the theorem, the data are given here as a mere reference to the reader.
In our reference system, i.e., the IoT micro-Blockchain 1.0 framework running on a setup of Arduino Nano 33 IoT devices for N = 100 and events’ frequency ~10−2 Hz, the recorded energy consumption per event witnessing is approximately 55 μWh., and the time needed for a single event to be processed is ~16 ms. This considers the energy and the time required for one event block to be transmitted, validated, and stored in the IoT network. The benchmarks of the framework are given in detail in [8], while the technical specifications of the reference hardware can be found in [33].
Bitcoin and Ethereum 1.0 PoW Blockchains mandate . In these, every peer node acquires and validates every event and is expected to participate in the competitive new-event verification process [16]. At the time of writing, an average per-transaction consumption of ~1.200 kWh is recorded in the Bitcoin Blockchain. The average per-transaction size in the network is ~512 bytes and the network occupies a total of approximately 16.754 accessible full and pruned nodes [34]. These given, this yields an overall entropic performance (P) of the bitcoin network of approximately 7.4 × 104 kbit/kWh. It corresponds to the data bits that are inserted into the entire bitcoin Blockchain per kWh of electricity consumed. Macroscopically seen, the overall entropy of the system is reduced by this amount for every kWh spent [14].
The Bitcoin Blockchain constitutes the most inefficient consensus approach in terms of entropy reduction per energy unit in our benchmark.
PoS-based Ethereum 2.0 introduces a far more sophisticated node hierarchy, initially invoking verifiers per transactional event, ending up to of the total body of the validators for the event to be considered as finalized [17]. This approach realizes the pros of scalability and delivers a more efficient architecture in terms of entropy conversion. At the time of the writing, average per-transaction consumption of ~0.03 kWh is recorded for processing and finalizing a single transaction of an average ~256 Bytes size on the Ethereum 2.0 Blockchain network. The network occupies approximately 8.900 accessible full nodes. This yields an observable information entropic performance of 4.5 × 108 kbit/kwh. Compared to the Bitcoin, the Ethereum Blockchain appears to be rank 104 times more efficient. Macroscopically seen, the rigid requirement “everyone knows everything at all times” is relaxed. This corresponds to lower values of W and has a positive impact to the entropic Performance (P) of the system.
Hyperledger Fabric 3.0 adopts a trusted-node policy. It empowers adaptable strategies, relying on a fixed leader–follower hierarchy. It can deploy various consensus policies, from the default Raft where , to Practical Byzantine Fault Tolerant with , to total endorsement requiring [18]. The energy consumption and consequently the efficiency of the system varies and is subject to each implementation. In Table 1 we considered the default Raft case.

Table 1.
Benchmarking the entropic Performance of large-scale Blockchain systems *.
Please note that all the above are estimations based on macroscopic metrics of the networks at the time of the writing, susceptible to further in-depth analysis and refinement. Still, this falls out of the scope of this work and remains a subject for future work.
The above considerations are summarized in Table 1 below.
In Table 1, we see the Number of reachable peer Nodes (N), the Nodes Participating in the initial Consensus requirement (W), the target Transaction Time and the time to Finality, the Average Transaction size, and the Energy Consumption per Transaction (kWh), of Bitcoin (PoW), Ethereum 2.0 (PoS), Hyperledger Fabric 3.0 (Raft, PBFT), and IoT micro-Blockchain at the time of the writing. The estimation of the Entropic Performance (P) bit/kWh is based on macroscopic benchmarking data [18,34,35]. In every transaction, ( bits are entering finality, at the cost of Energy Consumption per Transaction kWh.
As we see, the Bitcoin Blockchain, which mandates the maximum W, also presents the higher Transaction time and the lowest entropic Performance of all. On the contrary, the Ethereum and the Hyperledger Fabric, which operate in lower W, are significantly faster and present much higher entropic Performance (ranking 104 and 103 less than Bitcoin, respectively).
The considerations of the above empirical analysis are summarized and presented in Table 2 with respect to (A), (C), and (P).

Table 2.
(A), (C), and (P) implications as observed on heterogenous real-world Blockchain systems *.
In Table 2, a comparison of the large real-world systems (Bitcoin (PoW), Ethereum 2.0 (PoS), and Hyperledger Fabric 3.0 (Raft, PBFT) with respect to Autonomy (A), Consensus achievement (C), and entropic Performance (P) is presented).
As we see, the high consensus achievement requirement of Bitcoin (high W) leads to low entropic Performance, while the low Consensus achievement requirement of the Hyperledger Fabric results in a significantly high entropic Performance. The Ethereum 2.0 balances (A) and (C) to achieve high entropic Performance (P).
In all cases, the new CAP theorem holds strong: of the (A), (C), and (P), two at the most are optimized. The real-data benchmarks fully comply with the new CAP theorem.
Given the above, someone may easily conclude that the calculation of the precise entropic Performance of the various Blockchain systems is subject to a vast number of factors, and architectural- and implementation-specific considerations, as well as to the co-evaluation of the dynamic real-world conditions. These are susceptible to further thorough refinement through in-depth modeling and analysis of each Blockchain system.
Still, as illustrated, the revealed mutual exclusions persist firmly in massive scale systems of thousands of nodes. In large-scale Blockchain systems with thousands or millions of peer nodes, the relationships between (A), Consensus (C), and (P) are expected to exhibit non-linear behaviors. The detailed formal analysis of the large-scale Blockchain systems is out of the core scope of this work and remains a subject for future works.
Following in the next sections, we discuss the implications of the theorem in the large-scale real-world systems.
5.3. Large-Scale Heterogenous Blockchain Systems Implications
The findings of this work do not depend on the actual scale or the absolute energy consumption of the systems. This work focuses on revealing the intrinsic constraints between Autonomy (A), Consensus achievement (C), and entropic Performance (P). The constraints among the three properties hold strong while considering large-scale heterogenous systems as well. To highlight their implications to the non-uniform, large-scale Blockchain systems, in Section 5.2 and Section 5.4 we present benchmarks and real-world empirical validation data using Ethereum, Bitcoin, and Hyperledger datasets.
The intrinsic constraints among Autonomy (A), Consensus achievement (C), and entropic Performance (P) in the practical performance of the Blockchain systems in terms of latency, throughput, and energy consumption, have been shaping the architectures of the Blockchain systems since their very beginning. They affect every aspect of the consensus mechanisms’ performance, including the transaction finality time, and the scalability capability of the systems.
The implications of the new CAP theorem are immense. They drive fundamental design decisions of the Blockchain consensus architectures, like, for example, the heterogeneity of the nodes and the adoption of node hierarchies:
- -
- Light nodes and digital wallets are introduced to deliver increased autonomy and energy efficiency.
- -
- Larger capacity full nodes usually undertake the heavier duties of running the more demanding core of the consensus process.
This understanding constitutes an additional practical demonstration of the intrinsic constraints existing among (A), (C), and (P) and further fortifies the validity of the theorem. The new CAP theorem constrains the ‘somehow illusionary’ vision of the early Blockchain technologists for absolute peerness, autonomy, and infinite decentralization for zero cost.
Acknowledging the adverse impact of high values of W to the efficiency of the system, many contemporary large-scale Blockchain architectures intentionally limit the number of required per-event witnesses. They tend to operate with W << N and they adopt scalable witnessing solutions and probabilistic-over-absolute-finality policies [9,25,26].
Benchmarks presented in Table 1 and Table 2 in Section 5.2 clearly show how the number of witnesses (W) impact the transaction finality time, the information entropy performance, and the scalability of the system.
In addition, high values of W induce exponential network overheads. As is shown in [8], in a pure peer-to-peer network, increasing the consensus requirement exponentially increases latencies, communication bottlenecks, and processing overheads deriving (a) from network congestions, conflicts, and retransmissions, and (b) from the consequent higher processing demands.
In the next section, the implications of the constraints between Autonomy (A), Consensus achievement (C), and entropic Performance (P) to the resilience of the systems is discussed.
5.4. Security and Finality Implications
The new CAP theorem also has substantial security implications for Blockchain consensus mechanisms. The balance between Autonomy (A), Consensus achievement (C), and entropic Performance (P) directly relates to the system’s resilience to the various forms of adversarial attacks [36,37]. Macroscopically seen, high Consensus achievement generally delivers increased resilience in most of the cases, as illustrated in Table 2. The exception is the Denial of Service attack, for which elevated Autonomy (A) and reduced Consensus requirements (C) minimize the risk.
5.4.1. Sybil and 51% Attacks Resilience and the Role of Autonomy (A)
A Sybil attack occurs when a single adversary creates multiple fake identities (nodes) to gain disproportionate impact over the system [27]. A 51% attack has its roots in BFT and relies on the existence of a critical mass of malicious nodes to take control of the system [38]. They usually take place at the network level. While autonomy (A) is maximized by reducing W, the system becomes more vulnerable: an adversary who can introduce a large number of fake nodes may gain control of the system.
PoW-based consensuses, like in Bitcoin and Ethereum 1.0, mitigate Sybil attacks by keeping Consensus (C) high, pushing the Autonomy (A) far from optimal. In addition, utilizing competitive mining, Consensus participation is bound to computational workload, making it immensely costly for an attacker to control a significant portion of the network. PoS-Based systems like Ethereum 2.0 generally resist Sybil attacks by directly increasing the cost for the introduction of a new node, i.e., economic staking. Yet, the fact that Autonomy (A) is relatively elevated, and thus Consensus is moved from optimum, makes the system more susceptible to attacks [38].
5.4.2. Denial of Service (DoS), Long-Range Attacks and the Role of Consensus (C)
Beyond Sybil and 51% attacks, Blockchain systems are susceptible to denial-of-service (DoS) and long-range attacks, both of which target different aspects of the consensus process [27,39].
In Denial-of-Service attacks, higher Autonomy (A) reduces risk, as nodes depend less on external validation. Considering the Denial-of-Service case, increased Autonomy (A) reduces the exposure to the attack. While Autonomy (A) is maximized, the DoS attacks become more irrelevant. On the other hand, increased Consensus achievement (C) requirements expose the nodes more: higher W implies that the nodes depend more on the others, increasing the vulnerability surface of the system.
In Long-range attacks, which are mostly relevant for PoS-based systems, the attacker attempts to gain control of old validator keys in order to rewrite the history of the chain. If Consensus achievement (C) is high, the risk is reduced. Having more validators to confirm history, the Long-range must be combined with intense Sybil or 51% for the attack to become relevant. On the contrary, increased Autonomy (A) increases the exposure, since statistically fewer nodes are guarding the system every time, making it more susceptible to combined Long range mild Sybil attacks.
5.4.3. Practical Security Implications of the New CAP Theorem Tradeoffs
In Bitcoin, maximizing Consensus by requiring all nodes to validate transactions strengthens the resistance against Sybil and 51% attacks but significantly increases energy consumption. Ethereum 2.0 balances Autonomy and Consensus, reducing the risks of delayed transaction finality and improving the energy efficiency compared to systems like Bitcoin, while Hyperledger Fabric employs limited Consensus participation, which enhances Autonomy and reduces energy consumption but introduces potential vulnerabilities to Byzantine failures.
The intrinsic tradeoffs between Autonomy (A), Consensus achievement (C), and Entropic Performance (P) significantly affect Blockchain system security, as presented in Table 2. Summarizing the above, we have the following:
- -
- High Autonomy/Low Consensus: Increases the risk of Sybil attacks and 51% attacks. Fewer nodes validate each event, making it easier for malicious attackers to dominate the system. For example, systems with minimal node consensus, such as sparce and lightweight IoT Blockchains, can easily become targets of Sybil and 51% attacks. A malicious attacker may deploy multiple compromised nodes without being noticed.
- -
- High Consensus/Low Autonomy: Enhances the resilience against Sybil and Byzantine attacks. The requirement of broad validation, though, increases the system vulnerability to denial-of-service (DoS) attacks. As nodes become highly interdependent, the attacker can infuse congestion to the network more easily. For example, Bitcoin requires all nodes to validate all transactions, providing strong security against fraudulent consensus but also making the network more susceptible to congestion attacks.
- -
- Balanced Consensus and Autonomy: Partially sacrificing absolute consensus and autonomy offers better scalability and resistance to DoS attacks while still maintaining the desired resilience levels against Sybil and Byzantine threats. As a practical example, Ethereum 2.0 uses a set number of validators for consensus. This approach improves resilience against DoS balancing the hazard of Sybil attacks as well. Still, it increases the vulnerability to long-range attacks through the potential historical key compromise in certain nodes. These tradeoffs highlight once more the practical necessity of designing scalable Blockchain systems that adjust W dynamically to mitigate security risks while maintaining the desired traits in terms of entropic Performance every time.
6. Conclusions
In this paper, we introduce the new CAP theorem for Blockchain consensus systems.
We demonstrate that from the three essential properties Autonomy (A), Consensus achievement (C), and entropic Performance (P), two at the most can be optimized at any given time in the generic case. This finding imposes an intrinsic limitation on the design and the optimization of distributed consensus mechanisms.
Our results formally prove two fundamental mutual exclusions:
- (a)
- Between Autonomy (A) and Consensus achievement (C): A Blockchain consensus system that maximizes the one inherently compromises the other.
- (b)
- Between Consensus achievement (C) and Entropic Performance (P): The achievement of high levels of Consensus requires significant energy and resource commitments, lowering the observed entropic efficiency of the system.
This theorem provides an inherent theoretical foundation that explains the major tradeoffs observed in the real-world Blockchain architectures.
Systems like Bitcoin are based on pure and competitive PoW and often prioritize absolute consensus: at the cost of autonomy and entropic efficiency, the homogeneity of the peer nodes of the system is absolute. On the other hand, systems like Ethereum 2.0 and Hyperledger Fabric balance efficiency and decentralization by making explicit tradeoffs in consensus achievement.
How far can the decentralization of Blockchain systems practically go?
This work sets a formal conceptual framework for the understanding of the limits of the distributed consensus mechanisms. It emphasizes the need for scalable and adaptive consensus processes that can dynamically balance (A), (C), and (P) to optimize the desired traits every time, whether the priority is the achievement of high consensus levels, autonomous operation, or high energy performance. The new CAP theorem provides essential guidance for future Blockchain research, inspiring researchers to pursue innovative consensus algorithms that dynamically balance these fundamental properties, opening paths towards more efficient and scalable Blockchain solutions. It highlights fundamental tradeoffs that future Blockchain consensus mechanisms must explicitly consider, through practical designs balancing security, decentralization, and efficiency.
This work lays the foundation for more scalable and efficient Blockchain consensus design, challenging the traditional understanding of decentralization and offering a new theoretical framework to future research and development in Blockchain engineering.
Author Contributions
Conceptualization, A.G.A.; methodology, A.G.A. and E.G.; software, A.G.A.; validation, E.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Aristoteles (284~322 B.C.) “Hθικά Νικομάχεια” Book 1, p. VII. Available online: https://www.greek-language.gr/digitalResources/ancient_greek/library/browse.html?text_id=78&page=8Last (accessed on 10 May 2024).
- Anagnostakis, A.G.; Naxakis, C.; Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Glavas, E. Scalable Consensus over Finite Capacities in Multiagent IoT Ecosystems. IEEE Internet Things J. 2022, 10, 6673–6688. [Google Scholar] [CrossRef]
- Dwork, C.; Lynch, N.; Stockmeyer, L. Consensus in the Presence of Partial Synchrony. J. ACM 1988, 35, 288–323. [Google Scholar] [CrossRef]
- Alon, N.; Benjamini, I.; Lubetzky, E.; Sodin, S. Communication Cost of Consensus for Nodes with Limited Memory. Proc. Natl. Acad. Sci. USA 2019, 116, 1912980117. [Google Scholar] [CrossRef]
- Khosravi, A.; Säämäki, F. Beyond Bitcoin: Evaluating Energy Consumption and Environmental Impact across Cryptocurrency Projects. Energies 2023, 16, 6610. [Google Scholar] [CrossRef]
- Pagone, E.; Hart, A.; Salonitis, K. Carbon Footprint Comparison of Bitcoin and Conventional Currencies in a Life Cycle Analysis Perspective. Procedia CIRP 2023, 116, 468–473. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, H.; Sun, X. Concerning Consensus Fairness and Efficiency with Uncertain Costs. Mathematics 2023, 12, 1266. [Google Scholar] [CrossRef]
- Anagnostakis, A.G.; Giannakeas, N.; Tsipouras, M.G.; Glavas, E.; Tzallas, A.T. IoT Micro-Blockchain Fundamentals. Sensors 2021, 21, 2784. [Google Scholar] [CrossRef]
- Vogels, W. Eventually Consistent. Commun. ACM 2009, 52, 40–44. [Google Scholar] [CrossRef]
- Brewer, E.A. Towards Robust Distributed Systems. In Proceedings of the Annual ACM Symposium on Principles of Distributed Computing (PODC), Portland, OR, USA, 16–19 July 2000. [Google Scholar] [CrossRef]
- Gilbert, S.; Lynch, N. Brewer’s Conjecture and the Feasibility of Consistent, Available, Partition-Tolerant Web Services. ACM SIGACT News 2002, 33, 51–59. [Google Scholar] [CrossRef]
- Rožman, N.; Corn, M.; Škulj, G.; Berlec, T.; Diaci, J.; Podržaj, P. Exploring the Effects of Blockchain Scalability Limitations on Performance and User Behavior in Blockchain-Based Shared Manufacturing Systems: An Experimental Approach. Appl. Sci. 2023, 13, 4251. [Google Scholar] [CrossRef]
- Bulgakov, A.L.; Aleshina, A.V.; Smirnov, S.D.; Demidov, A.D.; Milyutin, M.A.; Xin, Y. Scalability and Security in Blockchain Networks: Evaluation of Sharding Algorithms and Prospects for Decentralized Data Storage. Mathematics 2024, 12, 3860. [Google Scholar] [CrossRef]
- Anagnostakis, A.G.; Glavas, E. Entropy and Stability in Blockchain Consensus Dynamics. Information 2025, 16, 138. [Google Scholar] [CrossRef]
- Wan, S.; Lu, Q.; Li, Y.; Lai, C.; Wang, X. A Systematic Review of Consensus Mechanisms in Blockchain. Mathematics 2023, 11, 2248. [Google Scholar] [CrossRef]
- Nakamoto, S. Bitcoin: A Peer-to-Peer Electronic Cash System. Bitcoin.org. 2008. Available online: https://bitcoin.org/bitcoin.pdf (accessed on 15 May 2024).
- Buterin, V. Ethereum Whitepaper. Ethereum Foundation, 2015. Available online: https://ethereum.org/en/whitepaper/ (accessed on 10 January 2025).
- Hyperledger Fabric Documentation. Available online: https://hyperledger-fabric.readthedocs.io/ (accessed on 10 January 2025).
- Mssassi, S.; Abou El Kalam, A. The Blockchain Trilemma: A Formal Proof of the Inherent Trade-Offs Among Decentralization, Security, and Scalability. Appl. Sci. 2023, 15, 19. [Google Scholar]
- Auhl, Z.; Chilamkurti, N.; Alhadad, R.; Heyne, W. A Comparative Study of Consensus Mechanisms in Blockchain for IoT Networks. Electronics 2022, 11, 2694. [Google Scholar] [CrossRef]
- Oyinloye, D.P.; Teh, J.S.; Jamil, N.; Alawida, M. Blockchain Consensus: An Overview of Alternative Protocols. Symmetry 2021, 13, 1363. [Google Scholar] [CrossRef]
- Merrad, Y.; Habaebi, M.H.; Elsheikh, E.A.A.; Suliman, F.E.M.; Islam, M.R.; Gunawan, T.S.; Mesri, M. Blockchain: Consensus Algorithm Key Performance Indicators, Trade-Offs, Current Trends, Common Drawbacks, and Novel Solution Proposals. Mathematics 2022, 10, 2754. [Google Scholar] [CrossRef]
- Guru, A.; Mohanta, B.K.; Mohapatra, H.; Al-Turjman, F.; Altrjman, C.; Yadav, A. A Survey on Consensus Protocols and Attacks on Blockchain Technology. Appl. Sci. 2023, 13, 2604. [Google Scholar] [CrossRef]
- Zhou, Y.; Han, R.; Li, Y. Reputation Consensus Mechanism for Blockchain Based on Information-Centric Networking. Electronics 2025, 14, 1099. [Google Scholar] [CrossRef]
- Pineda, M.; Jabba, D.; Nieto-Bernal, W.; Pérez, A. Sustainable Consensus Algorithms Applied to Blockchain: A Systematic Literature Review. Sustainability 2024, 16, 10552. [Google Scholar] [CrossRef]
- Lepore, C.; Ceria, M.; Visconti, A.; Rao, U.P.; Shah, K.A. A Survey on Blockchain Consensus with a Performance Comparison of PoW, PoS, and Pure PoS. Mathematics 2020, 8, 1782. [Google Scholar] [CrossRef]
- Deirmentzoglou, E.; Papakyriakopoulos, G.; Patsakis, C. A Survey on Long-Range Attacks for Proof of Stake Protocols. IEEE Access 2019, 7, 28712–28725. [Google Scholar] [CrossRef]
- Faber, S.; Osterrieder, J.; Putz, L.M. Sybil in the Haystack: A Comprehensive Review of Blockchain Consensus Mechanisms in Search of Strong Sybil Attack Resistance. Algorithms 2023, 16, 34. [Google Scholar] [CrossRef]
- Sayeed, S.; Marco-Gisbert, H. Assessing Blockchain Consensus and Security Mechanisms against the 51% Attack. Appl. Sci. 2019, 9, 1788. [Google Scholar] [CrossRef]
- Sapra, N.; Shaikh, I.; Dash, A. Impact of Proof of Work (PoW)-Based Blockchain Applications on the Environment: A Systematic Review and Research Agenda. J. Risk Financ. Manag. 2023, 16, 218. [Google Scholar] [CrossRef]
- Noether, E. Invariante Variationsprobleme. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1918, 235–257. Available online: https://eudml.org/doc/59024 (accessed on 14 February 2025).
- Noether, E. Invariant Variation Problems. Transp. Theory Stat. Phys. 1971, 1, 186–207. Available online: https://arxiv.org/pdf/physics/0503066.pdf (accessed on 14 February 2025). [CrossRef]
- Arduino. Arduino ABX00027 Datasheet. Available online: https://docs.arduino.cc/resources/datasheets/ABX00027-datasheet.pdf (accessed on 1 February 2025).
- Mempool Space. Bitcoin Explorer and Blockchain Analytics Platform; Available online: https://mempool.space/ (accessed on 13 March 2025).
- Ethernodes. Ethereum Mainnet Node Explorer. Available online: https://ethernodes.org (accessed on 13 March 2025).
- Ismail, L.; Materwala, H. A Review of Blockchain Architecture and Consensus Protocols: Use Cases, Challenges, and Solutions. Symmetry 2019, 11, 1198. [Google Scholar] [CrossRef]
- Dwivedi, K.; Agrawal, A.; Bhatia, A.; Tiwari, K. A Novel Classification of Attacks on Blockchain Layers: Vulnerabilities, Attacks, Mitigations, and Research Directions. arXiv 2024, arXiv:2404.18090. [Google Scholar]
- Park, S.; Mun, B.; Lee, S.; Jeong, W.; Lee, J.; Eom, H.; Jang, H. Impact of EIP-4844 on Ethereum: Consensus Security, Ethereum Usage, Rollup Transaction Dynamics, and Blob Gas Fee Markets. arXiv 2024, arXiv:2405.03183. [Google Scholar]
- Ali, S.; Nicer, C.; Beschastnikh, I.; Feng, C. One Bad Apple Spoils the Bunch: Transaction DoS in MimbleWimble Blockchains. arXiv 2021, arXiv:2112.13009. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).