1. Introduction
Fifth- and sixth-generation (5G/6G) networks promise higher data rates for more connected devices than previously possible on cellular networks. Multiple industries are taking advantage of these benefits, including the energy sector and the applications this enables, by pushing for vastly more connected devices for Smart Grid, Smart Homes, Smart Manufacturing, Smart Cities, and other areas, collectively often referred to as the Internet of Things (IoT). Many of these application domains also intersect with Critical Infrastructure sectors, elevating the importance of longevity and reliability in these connected devices. With their rapidly growing number and the advantages provided by OFDM, such as reduced impact from Intersymbol Interference (ISI), more robust signal equalization, or ease of implementation, OFDM receivers are of vital importance and interest.
A drawback of these receivers being implemented on resource-constrained devices, however, is two-fold: the relatively high power requirement for signal transmission, and their computational complexity. This paper proposes a deep learning-based architecture for channel estimation, demodulation, and subsequent channel decoding. The motivation of this work is to improve OFDM receiver accuracy and facilitate reliable communications at lower signal quality while progressing towards a fully Machine Learning-based OFDM receiver architecture. Researchers are continuing to propose new applications of ML in 5G and 6G implementations [
1], with our research showing significant promise for replacing traditional receivers with deep learning architectures.
Our models utilize a CNN for channel estimation and demodulation and a GNN for LDPC-based channel decoding. CNNs of varying sizes ranging from 200 k to 1.2 M parameters are compared against a traditional receiver’s performance, with significant gains achieved by the DL-based approach with respect to the achieved BER. For the GNN, both a 20 k and 80 k parameter model were compared against standard LDPC decoders, showing comparable BER compared to standard belief propagation (BP) and Min-Sum algorithms. Our models are then combined in an end-to-end architecture, which shows significant improvement over the decoded output of a traditional receiver.
The remainder of the paper is organized as follows:
Section 2 will provide a review of related works, and
Section 3 outlines the methodology of this work, including subsections for our CNN and GNN model designs.
Section 4 presents the results for each model and compares them to traditional approaches.
Section 5 outlines our future work, and
Section 6 concludes the paper.
2. Related Works
The application of machine-learning models for various parts of OFDM receivers has gained increasing interest in recent years. The authors of [
2] proposed a Convolutional Neural Network (CNN) for symbol synchronization, channel estimation, demodulation, and channel decoding in channels utilizing BPSK and QPSK modulation. In [
3], the authors proposed the use of a Residual Neural Network (ResNet) with depthwise convolutions [
4] for channel estimation and demodulation in OFDM channels operating up to 64-QAM, which showed particular promise for a single model against multiple modulation schemes. However, a drawback of utilizing CNNs for these applications is the computational complexity and large number of parameters.
Graph Neural Networks (GNNs) have also been proposed for various receiver applications to combat this. The authors of [
5] proposed a GNN for symbol detection combined with expectation propagation to improve performance in multi-user Multiple-Input Multiple-Output (MU-MIMO) systems. GNNs have also been proposed for use in channel tracking of MIMO systems; for example, in [
6]. However, the trade-off for fewer parameters with these models is the requirement for multiple iterations and message passing within the GNN. Other approaches have also been proposed utilizing Long-Short Term Memory (LSTM) models in [
7], which show promising results in channel estimation and demodulation in Rician and 3GPP models.
Although each model mentioned has shown promise for different portions of an OFDM receiver, other approaches implement deep learning, utilizing multiple separate models to progress toward a completely ML-based receiver. The authors of [
8] propose different time domain and frequency domain models to improve an OFDM receiver’s response to increased Error Vector Magnitude while still utilizing traditional receiver components.
For channel decoding, GNNs were applied to BCH and Low-Density Parity Check (LDPC) codes in [
9], which utilized the generation matrix for these codes to ensure valid codewords were generated, rather than focusing solely on BER. The results from this work were promising even for Quasi-Cyclic (QC) LDPC codes and 5G LDPC codes. A shared GNN approach was proposed in [
10], where the authors reduced the parameter size of the GNN with limited impact on BER. Other work has focused on augmenting current LDPC decoders with trainable parameters to improve the performance of existing Belief Propagation (BP) algorithms [
11,
12]. This approach utilizes fewer parameters than the GNN approach by augmenting the BP algorithm with trainable parameters and improving algorithm performance. CNNs with specially crafted butterfly layers have been shown to perform well in learning linear codes [
13] and have also been shown to work well on 1D datasets [
14].
These efforts illustrate the potential for augmenting or replacing traditional wireless receiver functionalities with deep learning implementations. However, we observed a relative lack of consideration for resource-constrained devices and how this device class could benefit from such transformations. Additionally, previously published research provides limited results for DL architectures combining the functionalities of channel estimation, symbol demodulation, and channel decoding. To address this shortcoming, we outline the individual results of our separate functional models along with the results of our combined DL architecture.
3. Methodology
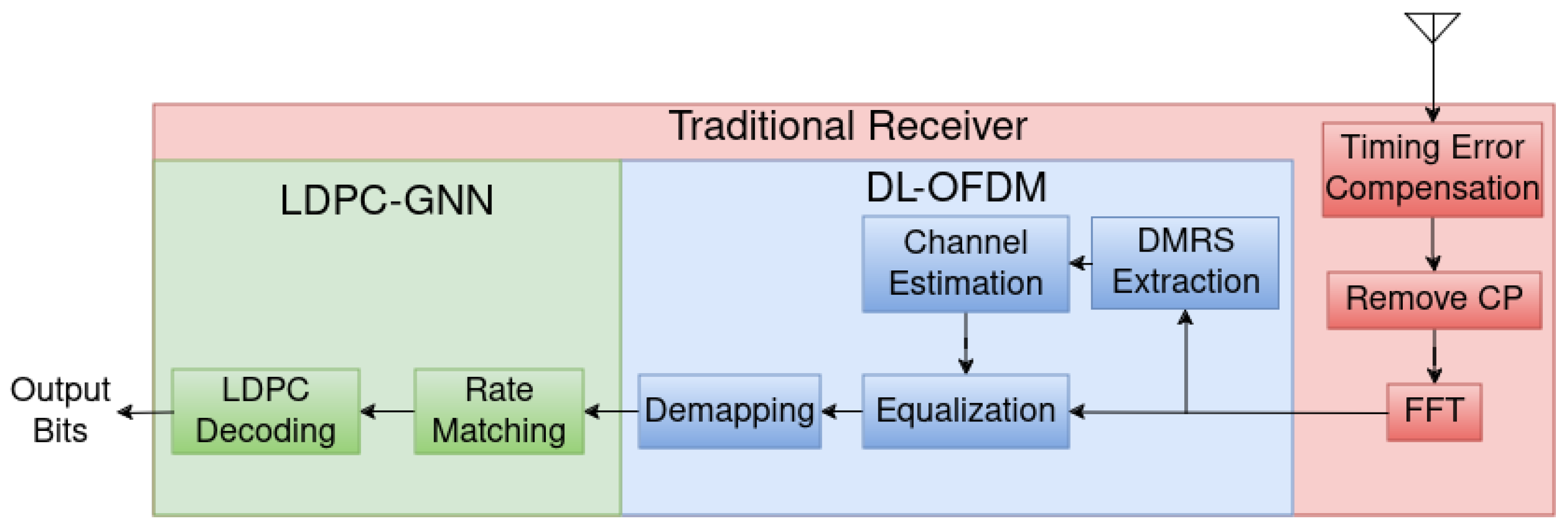
The methodology of this work is to expand the capabilities of currently proposed machine-learning receivers in OFDM systems by completing a Traditional Receiver’s channel estimation, equalization, demodulation, and decoding, all with machine-learning models. Our approach is presented in
Figure 1 and is organized into two separate blocks, DL-OFDM, utilized for all aspects from channel estimation through demodulation, and LDPC-GNN, which is utilized for rate matching and LDPC Decoding. Thus, in this paper, we explore a predominantly DL-driven architecture for resource-constrained devices, with potential applications ranging from IoT to mobile and vehicular communications.
Our proposed method differs from other current published research efforts due to the inclusion of additional traditional receiver functions within the DL architecture. Current research focuses on improvements to specific sections of receiver performance, whereas our research aims to expand joint machine-learning capabilities within OFDM receivers. This change is outlined in
Table 1.
The evaluation method chosen for our architecture is the BER for each SNR, modulation scheme, and channel model. Since this DL architecture evaluates the performance of an LDPC channel decoder, using BER allows us to compare and contrast the output of the demodulation compared to the final output of the receiver. With this in mind, we perform BER evaluations on both DL-OFDM and LDPC-GNN models compared to their traditional receiver counterparts. This process was then completed with the DL architecture compared to a traditional receiver to show end-to-end performance gains.
3.1. CNN-Based Joint Channel Estimation, Equalization, and Demodulation
The model we designed for OFDM symbol handling was inspired by a CNN with depthwise convolutions [
4]. Our model takes the place of a traditional receiver’s channel estimation, equalization, and OFDM demodulation blocks by taking the output of the Fast Fourier Transform as input and then generating each coded bit’s Log-Likelihood Ratio (LLR) as an output. The model input is similar to that outlined in [
3], with the real and imaginary matrices for the received signal
Y, received pilot signals
H, and expected pilots
X stacked along the third dimension. For this paper, we examine different model sizes to show the merits of not only the achievable performance gains but also the potential for reduced complexity.
The model architecture is comprised of only four layer types: 2D convolution, 1 × 1 2D convolution, Batch Normalization, and Rectified Linear Unit (ReLU). These layers combined together perform a Depthwise Separable Convolution in the convolutional block. For this paper, three different models of varying sizes are evaluated for our comparative analysis, with their fundamental architecture shown in
Figure 2.
In this study, we use an OFDM transceiver system with 64 subcarriers, out of which 11 are for the guardband regions and 1 is the DC subcarrier, plus 6 subcarriers used for pilots in a comb pattern, leaving 46 data subcarriers, with a frame comprised of a variable number of OFDM symbols to closely match the bits of the encoded LDPC code. We used QPSK, 16-QAM, and 64-QAM for data modulation, in a SISO system, tested with the Rician channel model as well as the four different LOS models provided by 3GPP TR 38.900 (CDL-D/E, TDL-D/E) [
15]. Matlab’s 5G toolbox was utilized to generate the dataset, with each test constituting a dataset of 500,000 frames for each modulation scheme and channel model for training. The train, test, and validation split was configured to be 40%, 10%, and 50%, respectively, to ensure a sufficiently sized validation set for the purposes of this evaluation. Three models were trained to compare the parameter size against the achieved BER performance, and show the feasibility of this implementation on resource-constrained devices.
Hyper-Parameter Tuning
For hyper-parameter tuning, layer channels were tested for values {4, 16, 64, 128, 256}, and dilation values were tested with values {(1, 1), (2, 3), and (3, 6)}, and the number of convolutional blocks was selected between 1, 3, and 5. Each model was tested for convergence against a 4-QAM AWGN dataset. Convergence occurred on most models with 3 and 5 convolutional blocks. Thus, the smallest, largest, and a representative mid-sized model were selected for comparative evaluation. The model overview of the highest-performing models is shown in
Table 2.
The model output represents the bit LLRs, obtained as a 3-dimensional array of dimensions
I × J × K, where
I is the number of data+pilot subcarriers,
J is the number of OFDM symbols, and
K is the number of bits per subcarrier. Pilot signals are discarded from the output of the demodulator deep learning model, as they are not considered in the final data bit array and do not have the same modulation as the data subcarriers. Each output data bit
is then translated from the LLR to a probability utilizing the Sigmoid function
. We use a Binary Cross-Entropy loss function for model training (Equation (
1)), where
B is the number of bits per subcarrier,
R is the set of data subcarriers in a transmitted frame, and
are the target coded bits.
3.2. GNN-Based LDPC Decoding
The LDPC-GNN model proposed in this paper utilizes message passing for node classification, with each iteration utilizing a graph convolutional layer, outlined in [
16]. (
N,
K) LDPC codes can be viewed as a bipartite graph, with the variable nodes
representing
N coded bits, and factor nodes
representing
K. As shown in
Figure 3, the variable nodes are utilized as inputs, feeding six graph convolutional layers that output the decoded factor nodes. The adjacency matrix
defines directional messages between
V and
F.
For each convolutional layer, Equation (
2) summarizes each layer update, as outlined in [
16], where
, with
being the identity matrix
, the count of input nodes to a specific variable node being represented by
, and where
Wl is the matrix of weights of layer
l,
Hl is the input array into the
lth layer, and
H0 is the input array
V, shown in
Figure 3. Since we require the last layer to update the factor nodes of the LDPC code, the output will always be a single channel of length
N.
For updating the factor nodes from the output of the graph convolutional layer, the adjacency matrix
A is utilized to ensure that only variable nodes that correspond to the updates of a factor node are considered. The inverse is true for updating the variable nodes, as shown in Equation (
3), with the mean value taken for each node. Given that
, we define
, producing a vector containing the number of input factor nodes to each variable node
. We define the inverse for factor nodes as well, with
.
Hyper-Parameter Tuning
For the purpose of this paper, we utilize the proposed (1998, 1512) QC-LDPC code, outlined in [
17] and utilized in [
11]. This code was chosen due to its high coding rate and Quasi-Cyclic nature. The tested models can also be seen in
Table 3.
Since the models tested for this application began converging before the search space maxima, two separate GNNs were evaluated for this paper, consisting of the smallest and largest converging models that we tested. The first model is comprised of six convolutional layers and 20 k parameters, with the set of channels for each layer being {32, 64, 128, 64, 32, 1}. The second model utilizes 80 k parameters, with the set of channels for each layer being {32, 64, 128, 256, 128, 64, 32, 1}. The impact of the number of iterations for message passing was evaluated for 3, 5, and 7 iterations, with 7 producing the best result. The same number of 500,000 frames was generated for training, with a train, test, and validation split of 40%, 10%, and 50%, respectively.
4. Results
To test the feasibility of our deep learning receiver approach, each model was evaluated for their respective receiver operations effectiveness, for both Rician and 3GPP LOS models, before also being evaluated jointly for the achievable end-to-end performance. This section will thus be divided into subsections focusing on the coded bit LLR extraction via OFDM demodulation, the LDPC decoding, and finally the end-to-end performance.
As mentioned in the previous section, each modulation scheme utilizes a variable number of OFDM symbols to reduce the number of padding bits required when varying the employed subcarrier modulation scheme and its associated bits per subcarrier. QPSK utilizes 22 symbols, 16-QAM utilizes 14 symbols, and 64-QAM utilizes 8 OFDM symbols. A comparison of the computational complexity regarding other proposed models can be seen in
Table 4. The latency and throughput of the models will be reliant on the optimization of the processor completing the ML accuracy, so BER and model complexity are the reported comparative results.
4.1. Coded Bit LLR Extraction Comparison
For coded bit LLR extraction, each CNN consumes the output from the FFT and produces as output the corresponding number of bit LLRs. To measure the BER for each model independently of any error correction coding benefits, the sigmoid of each LLR was calculated for the probability of each bit being a 1. Therefore, any sigmoid output larger than 0.5 would be interpreted as a 1, with a 0 corresponding to any value less than 0.5, which is subsequently compared against the coded bits utilized at the transmitter just prior to the transmitter’s modulation stage. Each test was conducted over an SNR range of 5–35 dB. The combined results for the Rician channel are shown in
Figure 4.
These results show an improved performance for all tested models against the traditional receiver. For QPSK, all models show a performance improvement of at least 1 dB over the traditional receiver, with the 200 k-parameter model requiring higher SNR to eliminate errors compared to the other tested models. However, three models for 16-QAM and 64-QAM, respectively, once again exhibit similar model performance, while retaining a bit error plateau, albeit at a much improved BER level compared to their traditional receiver counterparts. This is likely due to the models performing well, but not perfectly, when encountering the distortions resulting from the scattered path signal energies resulting in the Rician fading model. A surprising insight resulting from these tests is the relative lack of improvement achieved by the 1.2 M parameter model compared to the 800 k parameter model, which may be caused by the 800 k parameter model learning up to the theoretical limit for the noise on the channel. From these results, we can see that a relatively modest CNN model can achieve significant performance improvements compared to other, far larger models.
Each model was subsequently trained and evaluated for each modulation scheme against the previously outlined 3GPP LOS channel models, with our evaluation conducted and completed in the same manner as for the Rician channel model. These results, shown in
Figure 5, outline a much larger performance gain than what we observed in the Rician channel models, with the CNN models converging to 0 bit errors at 16 dB SNR, whereas the traditional receiver plateaus around a BER of 4 × 10
−4 16-QAM and 64-QAM begin to show the advantages of the larger models compared to the 200 k parameter model, with 800 k and 1.2 M parameter model’s BER plateauing at a much better BER value. All of these results, however, are very promising, as even the worst-performing model still far outperforms the traditional receiver across all of our tests.
4.2. LDPC Decoding Results
For the LDPC decoding, the LDPC-GNN was evaluated using the same channel models as we utilized for the CNN-based OFDM receiver demodulation evaluation. The inputs for this GNN are the LLR outputs of the traditional receiver, with the LLRs presenting the log-ratio of the probability of the demodulated bit being a 1 versus a 0. LDPC rate matching is performed on the input to the model. The largest axis of the adjacency matrix is utilized for rate matching to trim padding bits before inference. Similar to the previous CNN model, a hard decision was made for the probability of 0.5 or larger being designating a 1. For evaluation of the LDPC model, the 16-QAM dataset was generated for the BP, Layered-BP, Normalized Min-Sum, and Offset Min-Sum decoding algorithms, the results of which can be seen in
Figure 6.
From these results, we can observe that the Min-Sum algorithms perform worse at SNRs between 5 and 10 dB compared to the Belief Propagation algorithms and our GNN models, but slightly outperform both in the SNR range of 12–25 dB. The algorithms are on par in the range above 25 dB. We can observe that the GNN operation closely matches the BP algorithms, and varying the parameter size of the model does not appear to impact the BER performance. This matches previously reported results, showing increased performance of BP algorithms up to 10 iterations, and improvement with increasing SNR [
18]. Regarding training time, the larger 80 k parameter model converged faster than the 20 k model, but both produced these results after 2 epochs of training.
4.3. End-to-End Results
With promising results from both the DL-OFDM and LDPC-GNN models, we then completed an end-to-end evaluation of our overall deep learning receiver architecture, by feeding the output of the DL-OFDM into the LDPC-GNN. We refer to this end-to-end model as DL-WholeRx for simplicity. This test was completed on both Rician Fading and 3GPP LOS channel models shown in the previous sections, with our obtained results shown in
Figure 7 and
Figure 8.
The LDPC-GNN was retrained on the LLR output from the DL-OFDM model, as the amplitude for a given LLR was not guaranteed to fall in the same range as a traditional receiver. The DL-OFDM model did not need to be retrained, as the input signal from the FFT was the same.
The Rician channel results show similar results to those in the DL-OFDM section, with the deep learning receiver performing better across all modulation schemes. An interesting observation for the traditional receiver when utilizing the BP algorithm with 10 iterations is the degradation of 16-QAM BER, as the achieved BER is closer to 64-QAM results than the coded bits BER. This is likely due to the high rate of the LDPC code, combined with the relatively poor channel conditions. Compared to the traditional receiver, we observe that our deep learning receiver performs better for all modulation schemes, and reports significantly better BER at higher SNR for both 16-QAM and 64-QAM, with 16-QAM BER improving by 5 decades, and 64-QAM improving by 3.5 decades.
When examining the 3GPP LOS model results shown in
Figure 8, we see a dramatic increase in performance between the traditional and deep learning receiver, as 16-QAM shows a two-decade BER improvement, and 64-QAM shows a three-decade BER improvement. When compared against the coded bits BER in
Figure 5, a marginal BER performance increase is shown for our deep learning receiver and similar performance for the traditional receiver.
Given the maintained convergence of the QPSK model and improvement for 16-QAM and 64-QAM, we can conclude that our architecture manages to significantly outperform traditional receivers in adverse channel conditions. Our work expands on existing research by combining channel estimation, symbol demodulation, and channel decoding into a single deep-learning architecture.
5. Future Work
This paper provides a deep learning architecture for replacing most components of a traditional OFDM receiver. Research remains on exploring the replacement of the remaining components for error compensation, cyclic prefix removal, and performing the FFT utilizing deep learning. Some work in that regard has been proposed that may complete this at a lower modulation scheme [
2], but the architecture relies on CNN layers, which have difficulty learning linear codes, such as LPDC codes. This research is limited by the utilized carrier frequency and implemented channel models. The research can be expanded in the future to include additional channel models. Our team aims to continue this work to further harness the potential to significantly improve the BER performance achieved by such DL-driven receiver architectures and to leverage these gains to optimize energy consumption in resource-constrained devices, such as IoT. We also plan to further study parameter and model size reductions and approaches to unify the various DL models within the receiver chain into a single unified DL model. Finally, research remains to study approaches for reducing the latency resulting from GNN model iterations for LDPC decoding.
6. Conclusions
As the demand for IoT solutions grows, especially in areas such as Smart Grid applications and the energy sector, the number of resource-constrained or even battery-powered devices connecting to next-generation cellular networks also increases. By improving the achievable BER for these receivers through the use of a deep learning architecture, we aim to facilitate resource efficiency improvements for these devices by being able to reduce the transmit power requirements while maintaining or improving their BER performance. In this paper, we presented a deep learning approach to channel estimation, equalization, demodulation, and error correction decoding for OFDM-based receivers. CNN models were evaluated for 200 k, 800 k, and 1.2 M parameters, showing improvement with each model over a traditional receiver. A GNN architecture with 20 k and 80 k parameters was trained and evaluated against standard LDPC BP and Min-Sum algorithms, showing similar performance to that of standard algorithms. Finally, by combining both deep learning components into the proposed architecture, we could demonstrate the capabilities and benefits of an end-to-end deep learning-driven approach to OFDM receiver operations, showing not only the feasibility of this approach but also its tremendous benefits in the form of a much lower BER than a standard OFDM receiver for comparable transmit power usage. These results show significant promise for the future work of implementing a complete OFDM receiver through deep learning, with additional model optimizations to further improve resource efficiency. From this work, we observe the benefits this can provide to critical infrastructure sectors, such as the energy grid, by making device connectivity more robust and more energy efficient at the same time.
Author Contributions
Investigation, M.B., M.H. and H.S.; writing—original draft preparation, M.B. and M.H.; writing—review and editing, M.B., M.H. and H.S.; supervision, H.S. and M.H.; project administration, H.S. and M.H.; funding acquisition, H.S. and M.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the University of Nebraska-Lincoln’s Nebraska Center for Energy Sciences Research (NCESR) under Cycle 16 Grant# 20-706.
Data Availability Statement
The data can be shared upon request. The data are not publicly available due to being a part of an ongoing study.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| BP | Belief Propagation |
| BER | Bit Error Rate |
| CNN | Convolutional Neural Network |
| GNN | Graph Neural Network |
| IoT | Internet of Things |
| ISI | Intersymbol Interference |
| LDPC | Low-Density Parity Check |
| LOS | Line of Sight |
| LLR | Log-Likelihood Ratio |
| MU-MIMO | Multi-User Multiple-Input Multiple-Output |
| OFDM | Orthogonal Frequency Division Multiplexing |
| QC | Quasi-Cyclic |
| ReLU | Rectified Linear Unit |
| ResNet | Residual Neural Network |
References
- Scalise, P.; Boeding, M.; Hempel, M.; Sharif, H.; Delloiacovo, J.; Reed, J. A Systematic Survey on 5G and 6G Security Considerations, Challenges, Trends, and Research Areas. Future Internet 2024, 16, 67. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, S.; Yang, X. DeepReceiver: A Deep Learning-Based Intelligent Receiver for Wireless Communications in the Physical Layer. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 5–20. [Google Scholar] [CrossRef]
- Honkala, M.; Korpi, D.; Huttunen, J.M.J. DeepRx: Fully Convolutional Deep Learning Receiver. IEEE Trans. Wirel. Commun. 2021, 20, 3925–3940. [Google Scholar] [CrossRef]
- Chollet, F. Xception: Deep Learning with Depthwise Separable Convolutions. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1800–1807. [Google Scholar] [CrossRef]
- Kosasih, A.; Onasis, V.; Miloslavskaya, V.; Hardjawana, W.; Andrean, V.; Vucetic, B. Graph Neural Network Aided MU-MIMO Detectors. IEEE J. Sel. Areas Commun. 2022, 40, 2540–2555. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, S.; Gao, F.; Ma, J.; Dobre, O.A. Graph Neural Network-Based Channel Tracking for Massive MIMO Networks. IEEE Commun. Lett. 2020, 24, 1747–1751. [Google Scholar] [CrossRef]
- Mohammed, A.S.M.; Taman, A.I.A.; Hassan, A.M.; Zekry, A. Deep learning channel estimation for OFDM 5G systems with different channel models. Wirel. Pers. Commun. 2023, 128, 2891–2912. [Google Scholar] [CrossRef]
- Pihlajasalo, J.; Korpi, D.; Honkala, M.; Huttunen, J.M.J.; Riihonen, T.; Talvitie, J.; Brihuega, A.; Uusitalo, M.A.; Valkama, M. Deep Learning OFDM Receivers for Improved Power Efficiency and Coverage. IEEE Trans. Wirel. Commun. 2023, 22, 5518–5535. [Google Scholar] [CrossRef]
- Cammerer, S.; Hoydis, J.; Aoudia, F.A.; Keller, A. Graph neural networks for channel decoding. In Proceedings of the 2022 IEEE Globecom Workshops (GC Wkshps), Rio de Janeiro, Brazil, 4–8 December 2022; IEEE: Amsterdam, The Netherlands, 2022; pp. 486–491. [Google Scholar]
- Wu, Q.; Ng, B.K.; Lam, C.T.; Cen, X.; Liang, Y.; Ma, Y. Shared Graph Neural Network for Channel Decoding. Appl. Sci. 2023, 13, 12657. [Google Scholar] [CrossRef]
- Chu, L.; He, H.; Pei, L.; Qiu, R.C. NOLD: A neural-network optimized low-resolution decoder for LDPC codes. J. Commun. Netw. 2021, 23, 159–170. [Google Scholar] [CrossRef]
- Li, G.; Yu, X. A recipe of training neural network-based LDPC decoders. arXiv 2022, arXiv:2205.00481. [Google Scholar]
- Dao, T.; Gu, A.; Eichhorn, M.; Rudra, A.; Ré, C. Learning fast algorithms for linear transforms using butterfly factorizations. In Proceedings of the International Conference on Machine Learning (PMLR), Long Beach, CA, USA, 9–15 June 2019; pp. 1517–1527. [Google Scholar]
- Hariyanto, H.L.; Septyanto, A.W.; Sumpena, H.D. Split-Conv: 1HD Depth Estimation Deep Learning Model. In Proceedings of the 2023 Eighth International Conference on Informatics and Computing (ICIC), Zhengzhou, China, 10–13 August 2023; pp. 1–6. [Google Scholar] [CrossRef]
- 3GPP. Technical Specification Group Radio Access Network; Channel Model for Frequency Spectrum above 6 GHz (Release 14). 2016. Available online: http://www.3gpp.org/DynaReport/38900.htm (accessed on 22 February 2024).
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- UCLA CSL Published Codes and Design Tools. Available online: http://www.seas.ucla.edu/csl/#/publications/publishedcodes-and-design-tools (accessed on 22 February 2024).
- Casado, A.I.V.; Griot, M.; Wesel, R.D. Informed Dynamic Scheduling for Belief-Propagation Decoding of LDPC Codes. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 932–937. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).