Research on Blockchain Data Availability and Storage Scalability

Abstract

Blockchain adopts a chain data structure, and the characteristics of blocks that can only be added and cannot be deleted make the total number of blocks accumulate over time, forcing resource-constrained nodes to become degraded nodes in order to alleviate increasingly severe storage pressure. Degraded nodes only store partial blocks, although improving the scalability of blockchain storage and reducing data redundancy will lead to a decrease in data availability. To address the problem of storage scalability, quantitative research is needed on data availability. Based on a summary of the existing definitions of data availability, we propose a definition of data availability for blockchain. By analyzing the data synchronization process and the transaction lifecycle, key factors affecting data availability were extracted, and a data availability measurement model was constructed based on node types. On this basis, a relationship model linking data availability and storage scalability was constructed to find the range of data redundancy that meets the target data availability. The experimental results indicate that the data availability measurement model for blockchain can measure the data availability levels of different scalable storage schemes. The model of the relationship between data availability and storage scalability can guide the setting of data redundancy in scalable storage schemes.

1. Introduction

Blockchain is a distributed database that relies on P2P (Peer-to-Peer) networks and has the characteristics of being decentralized, secure, reliable, and traceable [1]. To ensure its characteristics, blockchain adopts a highly redundant data storage method wherein each node stores all blocks as a Full Node. The characteristics of blocks that can only be added and cannot be deleted make the total number of blocks accumulate over time, and nodes face increasingly severe storage pressure. Resource-constrained nodes have to choose to either become degraded nodes or exit the system, leading to a decrease in data availability and causing the problem of storage scalability in blockchain. Full nodes store complete block data and have full verification functions. Degraded nodes store partial block data and have partial verification functions.

Currently, solving the problem of storage scalability is carried out on two levels: (1) proposing scalable storage schemes based on experience, such as data sharding, data reduction, and multi-node-type collaborative storage [2], and (2) building a scalable storage model to guide the development of scalable storage solution schemes [1]. The Scalable Model for Blockchain Storage System (SMBSS) utilizes the transaction verification characteristics of UTXO (Unspent Transaction Outputs) and account type data, storing only some key data and storing it in the form of data sharding and thereby reducing data redundancy while giving nodes full functionality. However, none of the previous relevant studies have provided guarantees of data availability.

One important reason for the problem of blockchain storage scalability is the contradiction between data redundancy and data availability. On the one hand, blockchain utilizes P2P networks to achieve node communication and data sharing. To ensure high data availability, nodes need to store as much block data as possible, resulting in high data redundancy and poor storage scalability. On the other hand, lower data redundancy can improve storage scalability, but it will reduce data availability and ultimately affect the normal operation of blockchain.

According to the above analysis, when improving the scalability of blockchain storage while also considering data availability, it is necessary to establish a relationship model linking data redundancy and data availability. So far, no measurement model for blockchain data availability has been found in the collected literature. Therefore, this article first proposes a data availability definition for blockchain based on the existing definition of data availability in P2P networks. Then, by analyzing the data synchronization process and the transaction lifecycle, a Data Availability Measurement Model for Blockchain (DAMMB) is constructed, and the data availability levels of different storage schemes are measured. Finally, a model of the relationship between data availability and storage scalability is constructed to guide the setting of data redundancy in scalable storage schemes. The contributions of this article are as follows:

• It proposes a definition of data availability for blockchain;
• It summarizes the key factors that affect data availability during the data synchronization process and the transaction lifecycle;
• Based on the key factors affecting data availability, combined with information on node types, it proposes a Data Availability Measurement Model for Blockchain (DAMMB).
• It builds a model of the relationship between data availability and storage scalability to find the range of data redundancy that meets the target data availability.

2. Related Work

To solve the problem of blockchain storage scalability, it is necessary to resolve the contradiction between data redundancy and data availability. This section mainly discusses the scalable optimization of blockchain storage and data availability in P2P networks.

2.1. Scalable Optimization of Blockchain Storage

The solutions for optimizing the scalability of blockchain storage are mainly divided into three categories: data sharding, data reduction, and multi-node-type collaborative storage.

• Data sharding: The data is divided so that each node stores partial data. The ZILLIQA model [3] implements network sharding, transaction sharding, and smart contract sharding, with different shards stored on different nodes. The ElasticChain [4] model divides the blockchain into multiple segments and backs up data on different nodes on a segment-by-segment basis.
• Data reduction: Based on the consideration of the importance of block data, by deleting some block data, the storage pressures of full nodes are alleviated. The Block File Pruning [5,6] allows all nodes to discard block files while preserving the UTXO index. Dennis [7] proposed the rolling block method—requiring miners to add checkpoints in the block—in which all blocks older than 30 days are deleted.
• Multi-node-type collaborative storage: Multiple types of nodes work together to maintain blockchain operations. Examples of such storage include Storage Scheme with Full Nodes and Lightweight Nodes (SSFL) [8,9], Storage Scheme with Full Nodes and Enhanced Lightweight Nodes (SSFE) [10,11,12], etc.

The blockchain scalable storage model is a summary of and improvement on blockchain scalable storage schemes. On the basis of ensuring that nodes have verification functions, it uses data sharding to store block data, reducing data redundancy while giving nodes complete functionality. For example, it uses the Jigsaw-like Data Reduction [13]. Adopting the Efficient Block Validation method, which is based on state data reduction, it effectively reduces the amount of data that nodes need to store while ensuring node verification capability, significantly reducing the amount of saved data, and improving the scalability of blockchain storage.

Although the above studies can effectively improve the storage scalability of blockchain, they do not explicitly guarantee the availability of data.

2.2. Data Availability in P2P Networks

Improving the scalability of blockchain storage while also considering data availability requires research on data availability. Within the currently collected literature, there has been no research measuring the data availability in blockchain. Blockchain is a distributed database that relies on P2P networks. This section discusses data availability in P2P networks and identifies research ideas for blockchain data availability.

The definition of data availability in P2P networks can be divided into three aspects:

• The ratio of the online time of a node or system to the total time [14,15].
• A combination of time-varying functions that reflect the activity characteristics of nodes [16]. Since data is stored on nodes, and the opening and closing of nodes change over time, the activity characteristics of nodes can be represented by a series of functions that change over time.
• The probability of data being accessed within a specified time limit [17,18,19,20].

The diverse application scenarios of P2P networks result in different application scenarios for the three definitions. Definition 1 is applicable to non-real-time scenarios and is suitable for measuring the performance of nodes or systems at coarse granularity, such as when examining the online status of nodes or systems during a certain period of time. Definition 2 is applicable to real-time scenarios, such as real-time video streaming transmission, wherein the availability of nodes is related to factors such as bandwidth, delay, and packet loss rate. These factors can be expressed as bandwidth functions, delay functions, and packet loss rate functions over time. The availability of nodes is expressed as a combination of these time-varying functions, but the complexity of time-varying functions is high. Definition 3, which describes data availability as the probability that data can be obtained, applies to data storage in P2P networks and is applicable to most application scenarios in P2P networks.

Blockchain relies on P2P networks, and in order to ensure the characteristics of decentralization and transparency, consensus mechanisms are introduced, with higher requirements for data redundancy. Therefore, it is possible to learn from the research methods used to measure data availability in P2P networks, integrate the characteristics of blockchain, and propose a definition and measurement model for blockchain data availability.

3. Definition of Blockchain Data Availability

The main activities of blockchain can be summarized into two parts: establishing data synchronization processes between nodes and the full transaction lifecycle from creation to uplink. This section introduces the data synchronization process and the full transaction lifecycle, analyzes the specific manifestations of data availability, and proposes a definition of blockchain data availability.

The data synchronization process refers to the process that a node needs in order to obtain the latest data in the initialization phase, either when it is newly added to the blockchain or after it is offline and brought online again. It mainly includes five stages: the initiation of a request, the establishment of a connection, data transmission, data validation, and data storage, as shown in Figure 1.

• The initiation of a request: A node sends a request to other nodes in the blockchain to obtain the block data.
• The establishment of a connection: After receiving the request, other nodes establish a connection with the requesting node.
• Data transmission: Once the node establishes a connection, data can be synchronized. Data, typically including block data, transaction data, etc., is synchronized between nodes by sending and receiving messages. Data needs to be transmitted within a certain time, and therefore, data availability is reflected.
• Data verification: When the node receives data, it needs to first verify the data to ensure its correctness and legitimacy. For block data, the node needs to verify whether the hash value of a received block is correct and whether the transactions in the block are legal. For transaction data, the node needs to verify whether the signature of the transaction is correct and whether the transaction complies with rules. Data validation needs to obtain relevant data within a certain time; therefore, data availability is reflected.
• Data storage: When data validation is completed, the node stores the data in its local database.

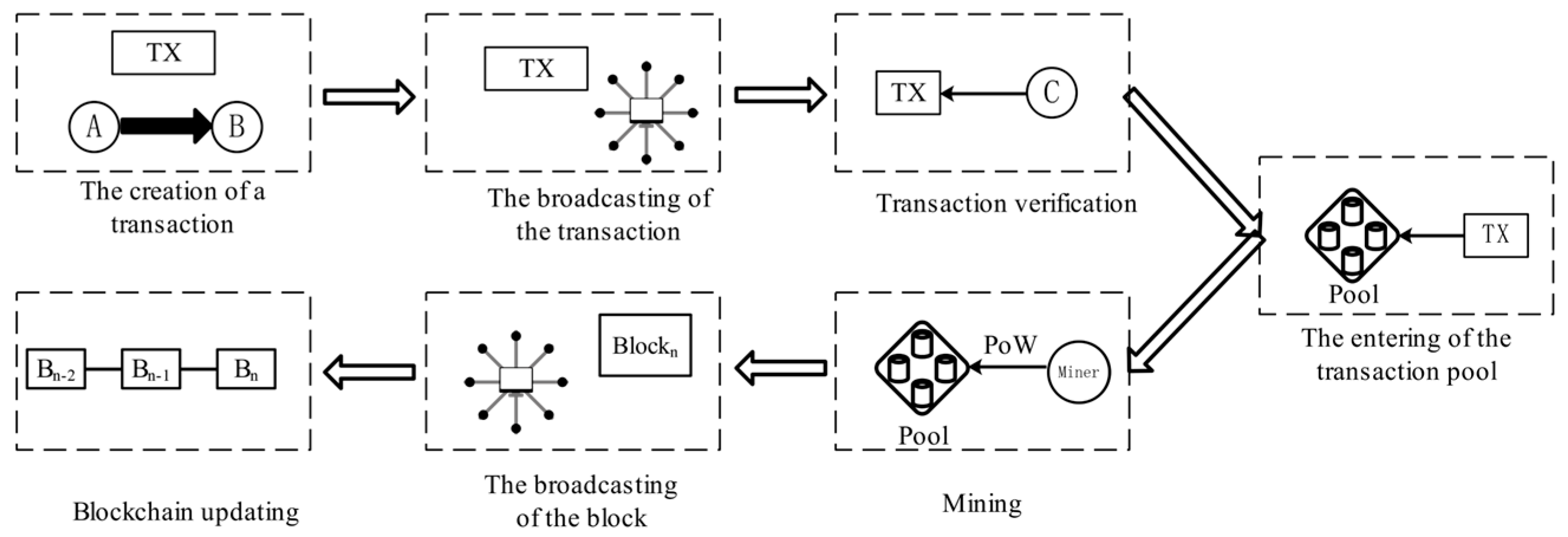
The full transaction lifecycle of blockchain includes seven stages: the creation of a transaction, the broadcasting of the transaction, transaction verification, the entering of the transaction pool, mining, the broadcasting of the block, and blockchain updating, as shown in Figure 2.

• The creation of a transaction: The creator of the transaction uses a private key to sign the transaction information, proving its authenticity and validity.
• The broadcasting of the transaction: The signed transaction information is broadcast to the network.
• Transaction verification: The node obtains relevant data to verify the signature, the legitimacy of the transaction content, whether there is double spending, and other abnormal conditions. The node needs to obtain data within a certain time; therefore, data availability is reflected.
• The entering of the transaction pool: Verified transactions enter the transaction pool and wait to be packaged into blocks.
• Mining: Miners select some transactions from the transaction pool and pack them into a new block.
• The broadcasting of the block: Miners broadcast the newly generated block to the network, and other nodes verify and confirm it.
• Blockchain updating: Verified and confirmed blocks are added to the blockchain, and transactions are permanently recorded on the blockchain.

Based on the above analysis, it is clear that the data availability of blockchain is mainly reflected in the data transmission stage and transaction verification stage. In the data transmission stage, each node has a data acquisition time limit [21,22], and it is necessary to obtain the target data within this time limit. In the transaction verification stage, nodes need to obtain target data within a time limit. Full nodes need to obtain locally stored target data within a time limit, while degraded nodes need to obtain target data from other nodes within a time limit. Combining related work analysis, the probability description method, which accounts for the probability of data being accessed within a specified time limit, is suitable for a definition of blockchain data availability. Its steps are to:

• Define the data acquisition time: The time interval between when a node makes a data request and when it receives all target data, represented by T.
• Define the time limit: The expected time for the node to obtain the target data—that is, the expected time that the node will take to obtain all the target data, represented by t.
• Define the data availability for blockchain: the probability that a node will obtain the target data within the time limit t, represented by A.

In blockchain, most often, there are multiple node types that are used simultaneously. For full nodes, data availability refers to the probability of obtaining locally stored target data within a time limit; for degraded nodes, data availability refers to the probability of obtaining target data from other nodes within a time limit.

The definition of data availability for blockchain aims at the probability of obtaining the target data within a time limit. The reliability not only needs to ensure that the data can be obtained within the time limit, but also needs to ensure the integrity and security of the data, such as by ensuring there is no double-spending problem, no sybil attack, etc.

4. Data Availability Measurement Model for Blockchain

This section summarizes the factors that affect data availability during the data synchronization process and the full transaction lifecycle and combines node types to construct the Data Availability Measurement Model for Blockchain (DAMMB).

4.1. Factors Affecting Data Availability

Based on the data synchronization process and the full transaction lifecycle, it can be seen that the factors affecting data availability mainly include the following four aspects:

• Node type: In the transaction verification stage, the data acquisition time of a full node refers to the time taken for the target data to be retrieved locally; the data acquisition time of a degraded node is the time interval between the time the data synchronization request is made and the receipt of all target data. The probability of obtaining target data varies with different node types and data acquisition times.
• Network transmission performance: The target data obtained by degraded nodes needs to be transmitted through P2P networks, and factors such as bandwidth, latency, and network congestion during the data transmission process affect the probability of obtaining target data within a time limit.
• Data redundancy: Data redundancy refers to the number of copies of data stored. The higher the data redundancy, the greater the probability of obtaining the target data within a time limit, and vice versa.
• Other factors: These include the failure of the node storing the target data, high frequency of target data requests requiring waiting, and different routing algorithms causing data transmission paths to become longer, all of which can prevent the target data from being obtained within a time limit.

4.2. DAMMB

The performance of data availability varies with different node types, and so, there are also differences in the DAMMBs constructed. Below, the nodes are divided into full nodes and degraded nodes, and a DAMMB is constructed separately for each type.

(1)

Full nodes store complete block data, and only need to obtain the target data locally within a time limit. When the data acquisition time T is less than or equal to the time limit t, a full node obtains all target data, making the data availability 100%; when the data acquisition time T is more than the time limit t, the data availability is expressed as the ratio of the already retrieved target data volume to the expected target data volume. The expected target data volume is N and the local data retrieval speed is v, and so, the target data volume retrieved within the time limit t is v × t, accounting for the expected target data volume, which is $\frac{v\times t}{N}\times 100\%$. In summary, the data availability of full nodes A_fnode is represented thus:

$$A_{fnode}=\left\{\begin{array}{cc}100\%& T\le t\\ \frac{v\times t}{N}\times 100\%& T>t\\ 0& \mathrm{not}\mathrm{obtained}\end{array}\right.$$

(1)

when the full node only obtains a single block, there are two kinds of acquisition cases: obtained (100%) and not obtained (0).

(2)

Degraded nodes store partial block data, and their data availabilities depend on other nodes. Therefore, a DAMMB for degraded nodes should not only consider the availability of target data, but also consider the impact of P2P network performance on the probability of obtaining target data. In P2P networks, the online behavior of nodes is independent. Assuming that a node is online with probability p, the target data availability A_files stored on it is denoted thus:

$$A_{files}={\displaystyle \sum _{i=m}^n{C}_n^i{p}^i{(1-p)}^{n-i}}$$

(2)

where n is the number of nodes and m is generally taken as 1, meaning that at least one node storing the target data can be obtained when it is online. This formula assumes that nodes are online with probability p at any time [23].

A degraded node’s acquisition of target data is mainly divided into three stages: (1) Requesting information to be transmitted in the network, (2) retrieving target data across full nodes, and (3) having data transmitted in the network. If the required times for these three stages are t1, t2, and t3, then the data acquisition time T = t1 + t2 + t3.

When a degraded node requests data, the request information is broadcasted to the network, and other nodes receive the request information and search for the target data. If the node stores the target data, it returns the data; if not, it continues to send the request information to other nodes until the data is found or the request times out. The nodes that continue to send request information to other nodes are called routing nodes, and the number of routing nodes is called hops.

During the data transmission process, when the data passes through a routing node and the routing node is online, the data transmission can be completed. If the online probability density of a routing node r is $f_r(t)$, then the online probability of routing node r during data transmission is:

$${\displaystyle {\int }_{{\alpha }_r(t)}^{{\alpha }_r(t)+\mathsf{\Delta }{t}_r}{f}_r(t)}$$

(3)

where ${\alpha }_r(t)$ represents the time when the data arrives at the routing node r and $\mathsf{\Delta }{t}_r$ represents the time interval at the routing node r from the moment the data is received to the moment it is forwarded.

The online probability of all routing nodes is:

$${\displaystyle \prod _{r=1}^s{\displaystyle {\int }_{{\alpha }_r(t)}^{{\alpha }_r(t)+\mathsf{\Delta }{t}_r}{f}_r(t)}}$$

(4)

In addition to the online probabilities of routing nodes, network performance metrics also include reliability, network topology, and network security. Among these, reliability refers to whether the data transmitted by the network accurately reaches the target node, network topology refers to the mode of connections between nodes in the network, and network security refers to whether the data transmitted on the network is secure or vulnerable to attacks or theft. The research object of this paper is blockchain. The network topology in blockchain is fixed and the network security is guaranteed compared with one might find in a traditional P2P network, and so these indicators are not suitable for analyzing and measuring network performance. Therefore, when the data acquisition time T is less than or equal to the time limit t, the data availability of degraded node A_lnode is represented thus:

$$\begin{array}{cc}{A}_{{}_{lnode}}=({\displaystyle \sum _{i=m}^n{C}_n^i{p}^i{(1-p)}^{n-i}})\times ({\displaystyle \prod _{r=1}^s{\displaystyle {\int }_{{\alpha }_r(t)}^{{\alpha }_r(t)+\mathsf{\Delta }{t}_r}{f}_r(t)}})& T\le t\end{array}$$

(5)

when the data acquisition time T is greater than the time limit t, the data availability is expressed as the ratio of the target data amount that has been transmitted within the time limit t to the expected target data amount. The expected target data amount is assumed to be N and the data transmission speed is uniformly v. When the routing node is offline and a backup node is selected to complete data transmission, the total delay of the process is ${\displaystyle \sum delay}$ and the ratio of the target data transmitted within the time $t_3-{\displaystyle \sum delay}-{\displaystyle \sum _{r=1}^s\mathsf{\Delta }{t}_r}$ to the expected target data obtained is:

$$\frac{v\times (t_3-{\displaystyle \sum delay}-{\displaystyle \sum _{r=1}^s\mathsf{\Delta }{t}_r})}{N}\times 100\%$$

(6)

In summary, the data availability of a degraded node is represented as A_lnode.

$$A_{lnode}=\left\{\begin{array}{cc}\begin{array}{l}({\displaystyle \sum _{i=m}^n{C}_n^i{p}^i{(1-p)}^{n-i}})\times ({\displaystyle \prod _{r=1}^s{\displaystyle {\int }_{{\alpha }_r(t)}^{{\alpha }_r(t)+\mathsf{\Delta }{t}_r}{f}_r(t)}})\\ \end{array}& \begin{array}{l}T\le t\\ \end{array}\\ \frac{v\times (t_3-{\displaystyle \sum delay}-{\displaystyle \sum _{r=1}^s\mathsf{\Delta }{t}_r})}{N}\times 100\%& T>t\\ \begin{array}{l}\\ \\ \\ 0\end{array}& \begin{array}{l}\\ \\ \\ \mathrm{not}\mathrm{obtained}\end{array}\end{array}\right.$$

(7)

5. Model Validation

An experiment was run on a device with an Intel (R) Core (TM) i7-10700 CPU @ 2.90 GHz, 16 GB of memory, and 1 T HDD server. Using existing Bitcoin data for simulation experiments, 10,000 blocks ranging in height from 718,560 to 728,559 were saved, totaling approximately 10.87 GB. The Bitcoin ETL tool was used to process block data and retain the required field information. The processed data was written in JSON format into a text file. A simulated blockchain network was built using VMware Workstation v16.0.0 and Docker. The tested network was Bitcoin Testnet, where 10 seed nodes and 1000 node objects were created. The node bandwidth was set between 1 Mbps and 20 Mbps, and the probability of having full nodes online was 0.9, while the probability of having degraded nodes online was 0.1. Backup routing nodes with an online probability of 1 were added. Each routing node stored information about adjacent routing nodes and backup routing nodes, and a delay of 20 ms was added when selecting backup routing nodes for transmission.

The scalable storage schemes selected for the experiment were Storage Scheme with Full Nodes (SSF), Storage Scheme with Full Nodes and Lightweight Nodes (SSFL), and Storage Scheme with Full Nodes and Enhanced Lightweight Nodes (SSFE). SSFL, which is a relatively traditional scheme, has the characteristics of full-node storage of complete data and fast response of SPV nodes; SSFE is a relatively new scheme. ESPV nodes extend the capabilities of SPV nodes and can provide better performance than SPV nodes.

More abbreviations are used in the following papers, and the abbreviations that appear more frequently in this paper, and their full names, are presented in Appendix A 

Table A1. List of abbreviations and full names.

Abbreviation	Full Name
SMBSS	The Scalable Model for Blockchain Storage System
UTXO	Unspent Transaction Outputs
DAMMB	Data Availability Measurement Model for Blockchain
SSF	Storage Scheme with Full Nodes
SSFL	Storage Scheme with Full Nodes and Lightweight Nodes
SSFE	Storage Scheme with Full Nodes and Enhanced Lightweight Nodes
SPV	Simplified Payment Verification
ESPV	Enhanced SPV

.

5.1. The Impact of Node Type on Data Availability

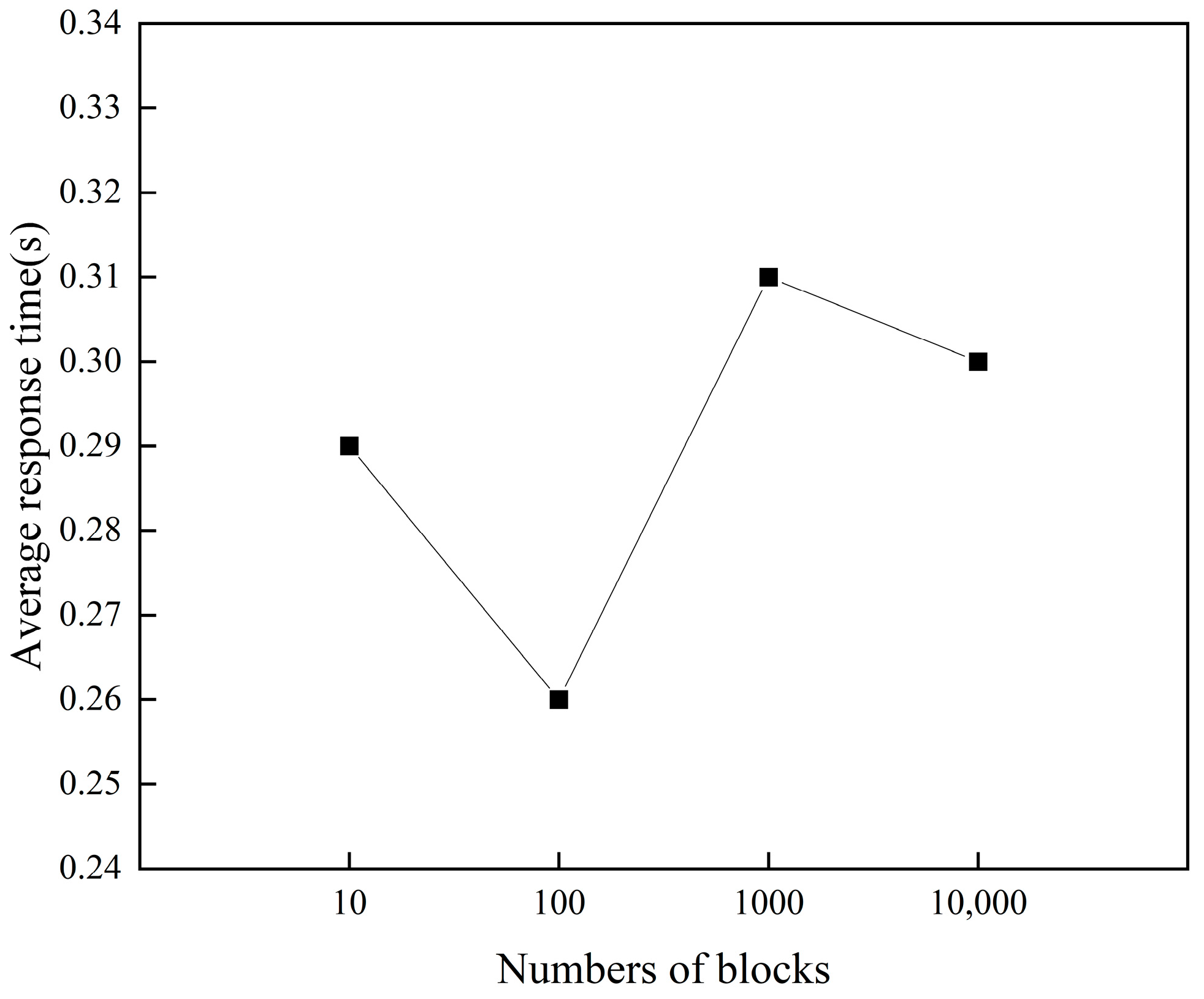
We constructed SSF and randomly requested block data with lengths of 10, 100, 1000, and 10,000 from full nodes, resulting in an average response time as shown in Figure 3.

As depicted in Figure 3, in the simulated blockchain network, a full node could obtain target data within 0.31 s irrespective of the number of target blocks acquired. The actual time limit t was set much higher than the duration required for full nodes to obtain data locally. Thus, full nodes had a 100% probability of acquiring data locally within the time limit.

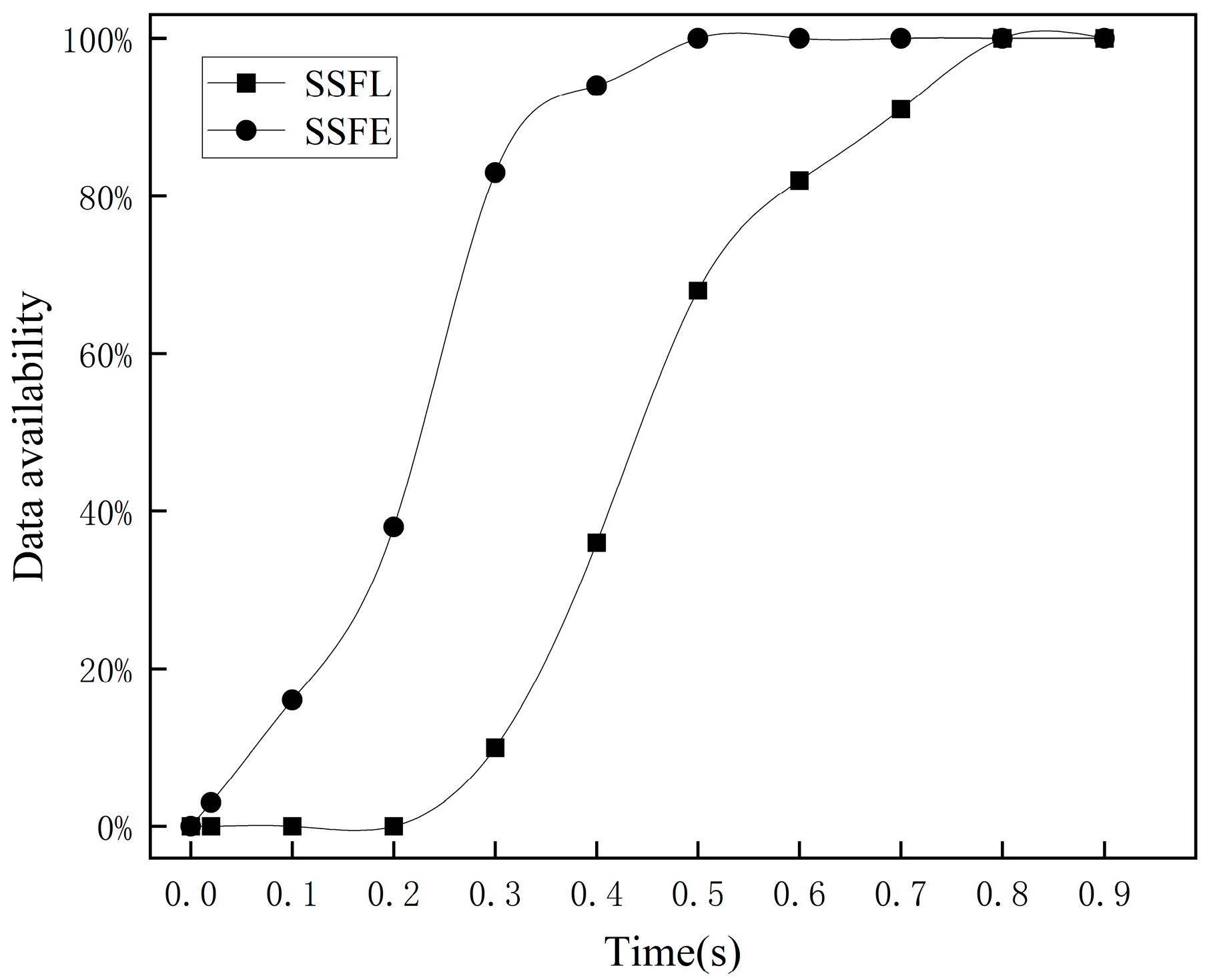
We built SSFL and SSFE with the proportion of SPV nodes and ESPV nodes set at 10% each. The SPV node requested block data with a length of 1000 from full nodes, while the ESPV node verified the block data with a length of 1000. Figure 4 depicts the change in data availability.

The experimental results indicate that in SSFL, during the initial stage, SPV nodes send data requests to full nodes, which process the requests and retrieve the data. During this phase, the data availability is 0. However, with time, SPV nodes gradually receive data from the full nodes, leading to a steady increase in data availability and ultimately reaching 100%. In SSFE, the simulation system completes most of the verification work within 0.3 s, after which the data availability slowly improves, eventually reaching 100% at 0.5 s.

According to the experimental results in Figure 4, the time limits t in SSFL and SSFE were set to 0.8 s and 0.5 s respectively. If any data received by the node exceeded the time limit, it was deemed unavailable. The proportion of SPV nodes and ESPV nodes was continuously changed, and the changes in data availability are summarized in Figure 5.

The experimental results indicate that in SSFL, when the proportion of SPV nodes is relatively low, the data availability level is higher. However, as the proportion of SPV nodes increases, data availability sharply declines. This is because a large number of data requests flow to full nodes, causing more requests to be processed and increasing the data response time. The response time for a large amount of data exceeds the time limit, rendering it unavailable and thus leading to a decrease in the data availability level. Conversely, in SSFE, even though the proportion of ESPV nodes continues to increase, data availability remains high.

The times taken for the system to achieve 100% data availability under different proportions of degraded nodes are shown in Figure 6.

The experimental results demonstrate that in SSFL, as the proportion of SPV nodes increases, the time taken to achieve 100% data availability significantly increases. An excessive number of SPV nodes means that a full node needs to handle a greater number of requests, greatly prolonging data response time and leading to an increasingly longer time to achieve 100% data availability. Conversely, in SSFE, as the proportion of ESPV nodes increases, the trend of the increase in time to reach 100% data availability is relatively mild. A full node does not need to handle too many requests from ESPV nodes, and the data response time is not significantly prolonged.

From the above experimental results, it can be concluded that node types have an impact on the data availability of blockchain within a time limit. If there are multiple node types, the proportion of their numbers can also affect data availability.

5.2. The Impact of Network Transmission Performance on Data Availability

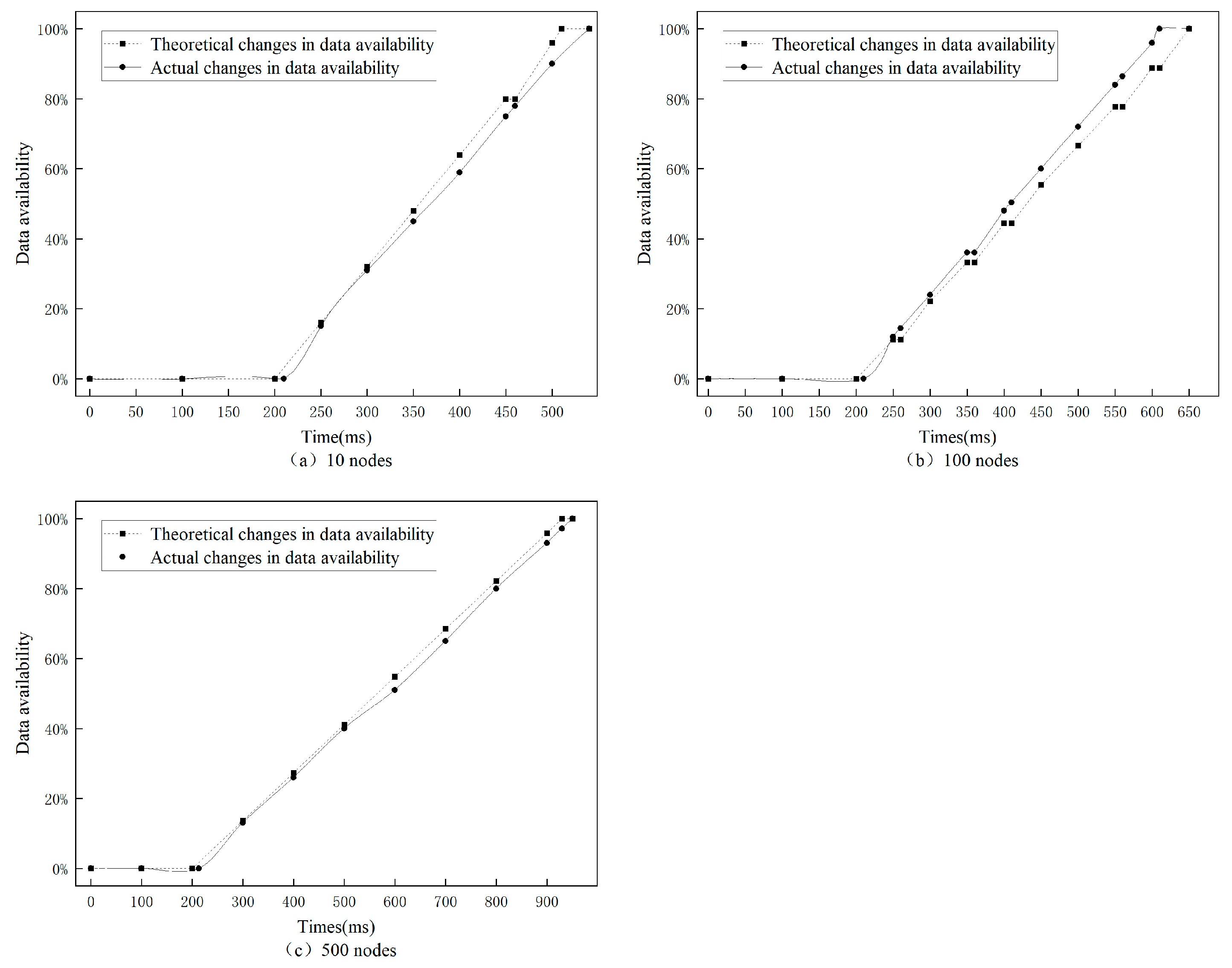
Firstly, we verified the applicability of the DAMMB for degraded nodes. We select SSFL, with a 10% proportion of SPV nodes and total numbers of nodes set to 10, 100, and 500, consecutively. The number of routing nodes was set to 5, and the offline probability was $e^{-0.01t}$. Then, we requested 1000 blocks and plotted the theoretical and practical curves of data availability under different numbers of nodes, as shown in Figure 7.

The experimental results suggest that the theoretical data availability is in good agreement with the actual changes. When the number of nodes is small, the data availability remains unchanged due to the failure to obtain target data. However, as the number of nodes increases, the number of situations where data availability remains unchanged due to not obtaining target data diminishes. It is worth noting that the theoretical change curve of data availability only represents the most likely trend of change, and that there may be some differences in the theoretical change curve due to actual probability differences. The time when the actual data availability reaches 100% in Figure 7b is advanced, and the reason for this situation is that the frequency of not obtaining the target data is relatively low. As the number of nodes increases, the theoretical change curve of data availability gradually matches the actual change curve, and thus, the DAMMB for degraded nodes has certain applicability for measuring data availability.

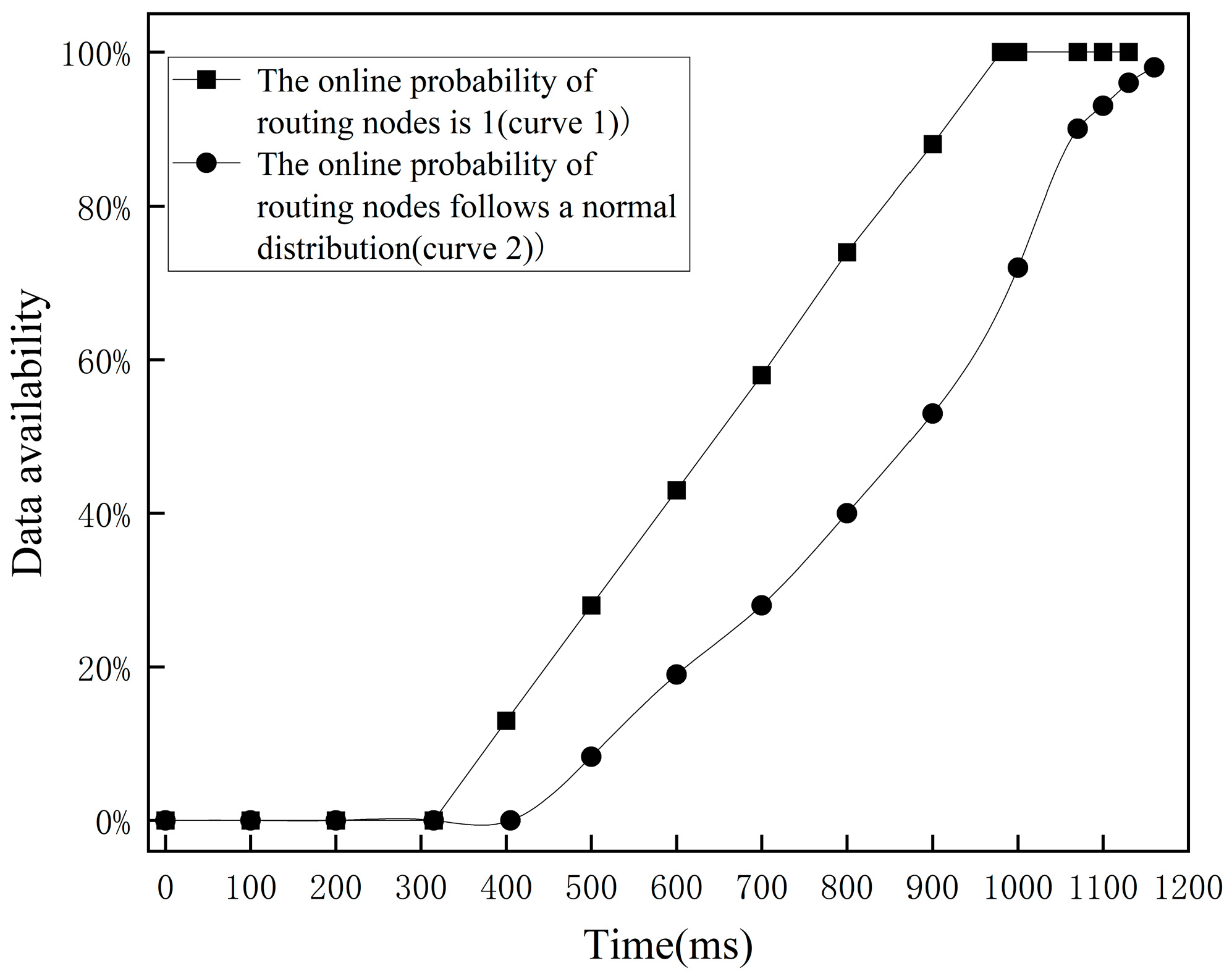
According to BitcoinVisuals [24], the average number of hops from one node to another in Bitcoin networks in the past three months was 9. We set the number of hops in the simulated blockchain to 9 and the online probability of routing nodes to 1, and used the normal distribution N (0,0.64). We then requested 1000 blocks and obtained the changes in data availability as shown in Figure 8.

The experimental results illustrate that curve 1 represented the control group. The addition of a routing node prolonged the time from requesting information to receiving data. The data availability increased linearly after receiving data. Curve 2 represents the routing nodes that conformed to the actual online situation. The trend of curve 2 shows that the routing node initially went offline, causing data to be transmitted through the backup routing node and resulting in a delay time. Horizontally, when receiving data, curve 2 experiences a certain time delay when it reaches the same data availability as curve 1. Vertically, at the same time, the data availability level represented by curve 2 is lower than that represented by curve 1.

Based on the experimental results above, it can be concluded that network transmission performance in blockchain has a significant impact on the level of data availability. In actual blockchain systems, it is not possible to guarantee that full nodes are always online. Therefore, when aiming to achieve a certain data availability level without considering the offline situations of nodes, it is necessary to consider the impact of delay time and adjust the time limit accordingly.

6. Research on Data Availability and Storage Scalability

To solve the problem of blockchain storage scalability is to reduce the data redundancy as much as possible under the premise of ensuring data availability. This section proposes a model of the relationship between data availability and storage scalability, guiding the setting of data redundancy in different scalable storage schemes.

6.1. Data Redundancy Metrics

Different blockchain networks have different data redundancy scales. To eliminate the impact of network scale on data redundancy comparison and analysis, it is necessary to normalize data redundancy and convert it into the same benchmark value or range.

Full nodes store complete block data with complete verification capability. The ratio of stored data to total data is 1, and the verification capability is 1. Degraded nodes store partial block data and have partial verification capabilities. For example, SPV nodes only store block headers, and the stored data accounts for approximately 0.008% of the total data volume; the verification function in SPV nodes relies on full nodes, and have a verification capability of 0. ESPV nodes store the latest 1800 blocks and have 90% verification capability. Data availability refers to the probability of obtaining target data, and is not specific to transaction verification capabilities. Assuming that nodes of the same type store the same amounts of data, storage redundancy is defined as follows:

Definition of storage redundancy: Storage redundancy, which is the normalized data redundancy, is the accumulation of the proportion of data stored by different node types and the proportion of each node type in the blockchain network. The calculation formula to calculate it is:

$$R={\displaystyle \sum _{i=1}^l{c}_i\times q_i}$$

(8)

where R represents the storage redundancy of the blockchain, l represents the number of different node types in the blockchain, $c_i$ represents the ratio of the data stored by node type i to the total data, and $q_i$ represents the proportion of the number of node type i in the blockchain.

Therefore, the storage redundancy of SSFL and SSFE can be obtained when the number of degraded nodes has different proportions, as shown in

Table 1. Storage redundancy of SSFL and SSFE.

The Proportion of Degraded Nodes	Storage Redundancy
	SSFL	SSFE
0%	1	1
10%	0.9	0.918
20%	0.8	0.836
30%	0.7	0.754
40%	0.6	0.672
50%	0.5	0.59
60%	0.4	0.508
70%	0.3	0.426
80%	0.2	0.344
90%	0.1	0.262
100%	——	0.18

.

When the proportion of degraded nodes is 0, these two storage schemes are called SSF, with a storage redundancy of 1. When the proportion of SPV nodes is 100%, the blockchain is full of SPV nodes without full nodes, and there is no usable data, it is determined that this situation does not exist, it is indicated by “——” in the table.

From Table 1, it can be seen that with the same proportion of degraded nodes, the storage redundancy of SSFE is higher than that of SSFL. From the experimental results in Figure 5, it can be seen that within a time limit, under the same proportion of degraded nodes, the data availability of SSFE is higher than that of SSFL.

6.2. Storage Scalability Metrics

Data availability and storage redundancy are mutually constrained. With an increase of storage redundancy, the possibility of data single-point failure is reduced, the data response delay is reduced, and the data availability level is increased, but the storage scalability becomes poor; the reduction of storage redundancy improves storage scalability, but the increase in target data acquisition time results in a decrease in the data availability level. We define the storage scalability coefficient as follows:

Definition of the storage scalability coefficient: It is the ratio of data availability to storage redundancy for scalable storage schemes within a time limit. It is calculated as follows:

$$S=\frac{A}{R}$$

(9)

where S represents the storage scalability coefficient, A represents the level of data availability within the time limit, and R represents storage redundancy. Storage scalability is directly reflected by the storage scalability coefficient.

From an intuitive perspective, the above definition compares data availability and storage redundancy and uses it as a measurement index of storage scalability with strong readability; from a comprehensive perspective, the definition takes into account both data availability and storage redundancy; from the perspective of comparability, the definition can compare and evaluate different scalable storage schemes, therefore providing reference for the selection and optimization of schemes. Therefore, the definition has strong rationality and applicability, and can provide support for the evaluation and optimization of different scalable storage schemes.

According to Figure 5 and Table 1, the storage scalability coefficients of SSFL and SSFE can be obtained under different proportions of degraded nodes, as shown in

Table 2. Storage scalability coefficient of SSFL and SSFE.

The Proportion of Degraded Nodes	Storage Scalability Coefficient
	SSFL	SSFE
0%	1	1
10%	1.11	1.09
20%	1.15	1.15
30%	1.20	1.25
40%	1.25	1.37
50%	1.32	1.53
60%	1.45	1.73
70%	1.43	2.02
80%	1.30	2.47
90%	1.20	3.21
100%	——	4.56

.

When the proportion of degraded nodes is 0, these two storage schemes are SSF, and the storage scalability coefficients are both equal to 1. When the proportion of SPV nodes is 100%, storage redundancy does not exist, and the storage scalability coefficients also do not exist, it is indicated by “——” in the table.

Storage scalability, data availability, and storage redundancy are interrelated and mutually influential. When evaluating any one indicator, it is necessary to comprehensively consider the other two indicators. Although the storage scalability coefficient is not necessarily as high as possible, this value can guide the optimal ratio between the numbers of full nodes and degraded nodes in different scalable storage schemes. Figure 9 shows the changes in the storage scalability coefficient and data availability after normalization in the same coordinate system.

As illustrated in Figure 9, in SSFL, the normalized storage scalability coefficient exhibits a trend of initially increasing and then decreasing with the proportion of SPV nodes. The reason for this trend is that when the proportion of SPV nodes is too high, full nodes are required to handle a large volume of data requests, resulting in longer data response times, significantly reduced data availability, and a decreasing trend in the storage scalability coefficient after it reaches its maximum value.

The solution to addressing blockchain storage scalability involves minimizing data redundancy and maximizing storage scalability while ensuring a certain level of data availability. In Figure 9, the intersection point of the data availability and storage scalability coefficient curves represents a balance between the three factors. For SSFL and SSFE, when the number of SPV nodes accounts for 46% and the number of ESPV nodes accounts for 67%, storage scalability, data availability, and storage redundancy reach a state of equilibrium.

7. Conclusions

Based on a summary of existing definitions of data availability, this article has proposed a definition of blockchain data availability. The article has also introduced the Data Availability Measurement Model for Blockchain (DAMMB) by analyzing the primary activities of blockchain and combining node types. The model’s applicability was verified through simulation experiments, and the data availability levels of different scalable storage schemes were obtained. Furthermore, we developed a model of the relationship between data availability and storage scalability that can be used to compare the storage scalabilities of different storage schemes and guide the setting of data redundancy in various storage schemes. The model has certain universality to different blockchain networks because different blockchains have similar characteristics, such as approximate data structures, and need a certain consensus mechanism to maintain data consistency and integrity.

This article does not take into account the time-dependent online probability of storing target data nodes when degraded nodes request target data. In P2P networks, factors that influence data availability include not only the online probabilities of routing nodes but also bandwidth, throughput, latency, and other factors. These factors are not currently reflected in the DAMMB, but they can impact data availability. Incorporating these factors into the model is a future direction for improvement.

In summary, the blockchain storage scalability needs to be continuously explored, and theoretically solving the problem of storage scalability remains a huge challenge.