Securing Critical User Information over the Internet of Medical Things Platforms Using a Hybrid Cryptography Scheme
Abstract
1. Introduction
- Cloud service providers may not have privacy protection that is strong enough to protect the data that are put in their care [28];
- If cryptography algorithms alongside authentication techniques are used to preserve the privacy of data on the cloud, searching for information from the encrypted data becomes an issue, as encryption conceals the relationships among the data [31];
- Apart from breaching the security of the data, performing decryption of the data before searching for particular information in the data stored on the cloud is not efficient, especially when dealing with a huge amount of encrypted data or resource starve devices.
- The existing Caesar cipher was modified to improve its security by extending the character set of the existing Caesar cipher from 26 to 256 (0–255), reshuffling the extended character set using an encryption key, and determining the ciphertext characters based on the location of each plaintext character in the plaintext and the location of the character on the character set using modulus 256 addition. The modulus 256 subtraction was used for recovering the plaintext characters from the ciphertext based on the position of each character on the ciphertext and on the character set. This was conducted to replace the mere shifting of characters by a constant value in the classical Caesar cipher;
- An efficient algorithm for searching through the encrypted files based on B+ file organization was proposed, and;
- The two innovations were combined to form a secure IoMT model which has the ability to secure and preserve the privacy of the patient medical records on the cloud.
2. Related Work
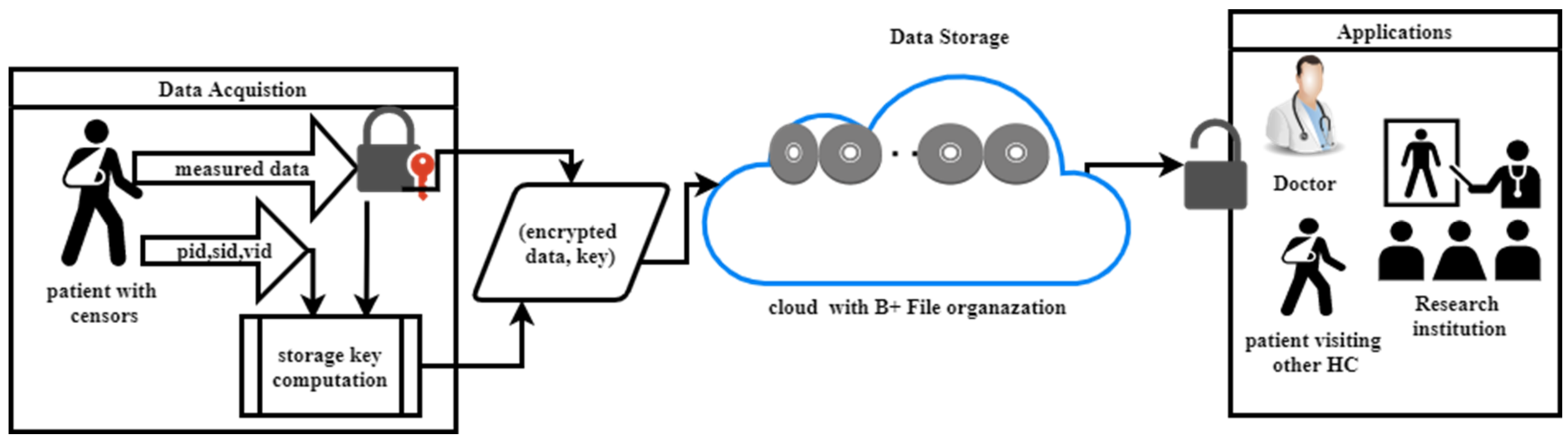
3. The Proposed IoMT Model
- Each healthcare centre has a cloud where information about patients is stored, and various clouds of different healthcare centres are networked together;
- Patients are embedded with different wireless sensors capable of communicating data to a central sensor connected to the healthcare cloud where the patient has registered;
- The central sensor is loaded, among other things, with encryption and decryption applications;
- Information from patients is stored in a central database through the help of a cloud network;
- A timestamp named “T” that is included in every message sent and received ensures the accuracy of the data;
- No two clients can communicate privately on the IoMT platform. The communication is between the HC and the clients;
- The architectural design of the proposed IoMT model is depicted in Figure 1.
3.1. Generation of Initialization Parameters
- ▪
- The HC assigns an identification number to itself, to each patient, and to each guest’s healthcare;
- ▪
- HC, the central sensor in each patient, and each GHC are preloaded with encryption and decryption algorithms.
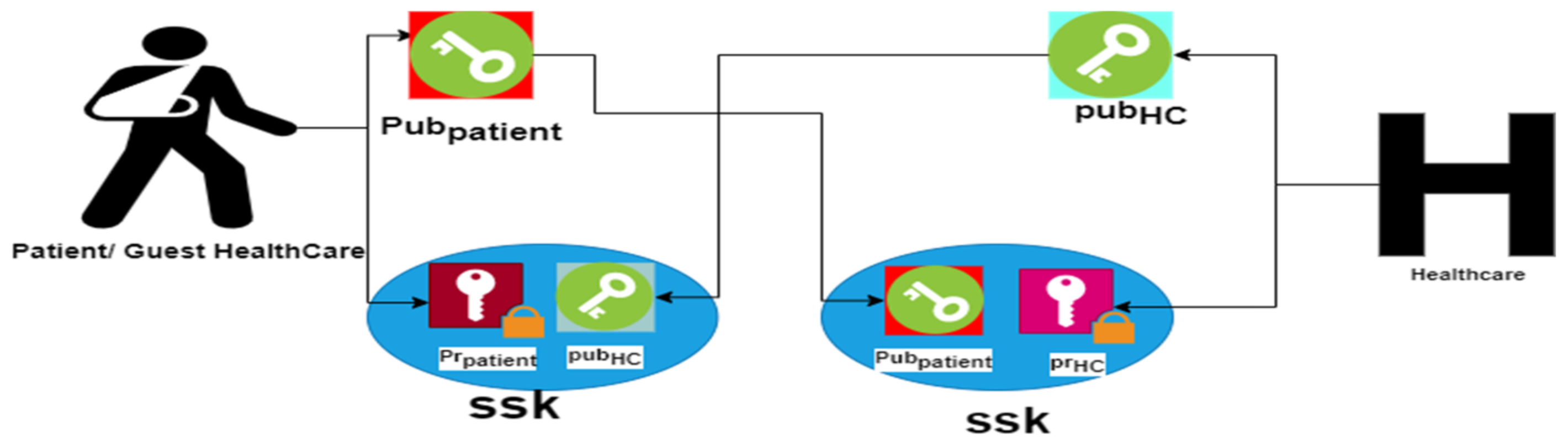
3.2. Creation of Initial Shared Secret Keys
| Algorithm 1: Initial shared secret key creation |
| Input: ,, PRK Output: ssk ssk = ( |
3.3. Registration of Patients and Guest Healthcare Centres
3.4. Updating the Shared Key in the Proposed IoMT Model
| Algorithm 2: Procedure for updating ssk, SNP, and nList when a client joins the HC network |
| Input: , , ssk Output: Updated ssk, snp and nList
|
| Algorithm 3: Procedure for updating ssk, snp, and nList when a node leaves WSN |
| Input: , ssk Output: Updated ssk, snp and nList
|
3.5. Secure Data Transmission and Storage
- Encryption of the message
| Algorithm 4: Conversion of plaintext into blocks of an equal number of characters |
| Input: Ptext Output: blocks // a set of strings with equal number of characters
|
- The generation of a key for rearranging ASCII characters from the ssk key;
- The introduction of confusion property into ciphertext by reshuffling of ASCII characters using Modified Columnar Transposition technique;
- The introduction of diffusion and confusion property through the modification of bits of the mixture of the plaintext and secrete key, and;
- The determination of ciphertext characters based on the location of the character in the plaintext and the location in the character set in the reshuffled ASCII characters. This makes the character set a lookup table for the modified Caesar cipher instead of the mere shifting of alphabets in the traditional Caesar cipher. The lookup table is based on modular addition and subtraction in modulus 256. During the encryption process, an ASCII character found at location i on the block of plaintext and at location j on the lookup table (the reshuffled ASCII characters table) will be represented by an ASCII character at location of the lookup table to form ciphertext character. During the decryption process, an ASCII character found at location j on the ciphertext block and location t on the lookup table will be represented by an ASCII character at location .
| Algorithm 5a: Modified Caesar Encryption Module (HMCC) |
| Input: set of Blocktext, Binkey Output: a set of encryptedblocktext: Variables: caesarchar: 1D array of ASCII characters as reshuffled
|
| Algorithm 5b: Encryption bit manipulation process |
| Module encmanipulatedbits = Encbitmanipulation(binarystr, randomseed) Output: encmanipulatedbits 1. START 2. randb = CHANGE randomseed to string of bits 3. rseeds = COUNT the number of bits in randb 4. Randkeys = ARRAY [1.. rseeds] of random seeds // geerated using randomseed 5. nibbleleft = ‘’ 6. nibbleright = ‘’ 7. sizeofbit = LENGTH (binarystr) 8. FOR i = 1 to sizeofbit, STEP 1byte i. onebyte = binarystr(i:i + 7) ii. nibbleleft = CONCATENATE (nibbleleft, onebyte(1:4)) iii. nibbleright = CONCATENATE(nibbleright, onebyte(5:8)) END FOR 9. FOR j = 1 to rseeds i. Seed1 = Randkeys(j) ii. nibblexor = nibbleleft XOR nibbleright iii. Fbyte = CONCATENATE(nibblexor, nibbleright) iv. confusionkey = GENERATE sizeofbit random integers from Seed1 v. manipbit = CALL Reshuffleforencryption(Fbyte, confusionkey) vi. nibbleleft = manipbit(1: sizeofbit/2) vii. nibbleright = manipbit(sizeofbit/2 + 1: sizeofbit) END FOR 10. encmanipulatedbits = manipbit 11. STOP |
| Algorithm 5c: Pseudocode for reshuffling ASCII characters |
| Module encryptionreshufflement (pblocktext, ckey) Output rearrangedtext [1…C]: array of characters Variables t, col, a, C message[1 C]: arrays of characters
|
| Algorithm 5d: Pseudocode for random number generation |
| Module Randgen (seed, n) Output: R[1…n]: Array of randomly generated integers
|
- ii.
- The signing of the Encrypted Message
| Algorithm 6: Appending signature of the sending node to the encrypted message |
| INPUT: encrypted points OUTPUT: Signed message
|
- iii.
- Signature Verification of the signed and encrypted message
| Algorithm 7: Verification of received signed message |
| Input: , , ciphertextsignature (c,d) Output: Verified ciphertexts
|
- iv.
- The decryption of the verified received message
| Algorithm 8a: Modified Caesar Decryption Module |
| Module DMCaesar (Blocktext, Binkey) Output: decryptedblocktext: string of characters Variables: caesarchar: 1D array of ASCII characters as reshuffled
|
| Algorithm 8b: Decryption Reverse Bit Modification Process |
| Module blockbits = DecReversebitmodification(binarystr, radseed) Input: binarystr, randomseedOutput: reversebinarystr
END FOR
END FOR
|
3.6. Privacy Preservation in the proposed IoMT Model
| Algorithm 9: Storing encrypted file on cloud storage using B+ file organisation |
Input: HC private key (ssk, Cm)
|
| Algorithm 10: Searching for a particular file on the cloud with B+ file organization |
Input: ssk, patientid
component of the key
|
- The space on the cloud is preserved as there is no need to store encrypted data redundantly, contrary to the approach in [59];
- Access to the data on cloud is based on B+ file organization which can be done both sequentially and randomly. Hence, search time is greatly reduced;
- There is no need for intensive computation on the encrypted data for searching purposes. This is an improvement to the existing FHE implementations;
- B+ tree is a self-balancing data structure for executing accurate and faster searching, inserting, and deleting procedures on data;
- B+ trees do not waste space;
- It takes an equal number of disk accesses to fetch records;
- B+ trees have redundant search keys, and storing search keys repeatedly is not possible;
- Faster search queries as the data are stored only on the leaf nodes.
3.7. Analysis of the Proposed IoMT Model
- Some samples of plaintext were carefully used as input into HMCC. The output ciphertexts obtained were analysed by examining how the cryptosystem handled these known plaintexts. Samples of plaintext used were plaintext with the same characters all through, plaintext with repetitive terms, and plaintext with non-repetitive terms. Analysis of the output ciphertexts from HMCC were carried out using the following procedure:
- Encrypt a block of plaintext P1 that contains the same characters throughout;
- Encrypt a block of plaintext P2 that contains repetitive characters;
- Encrypt block of plaintext P3 that contains distinct characters;
- Examine the ciphertext of each block obtained from steps 1 and 3.
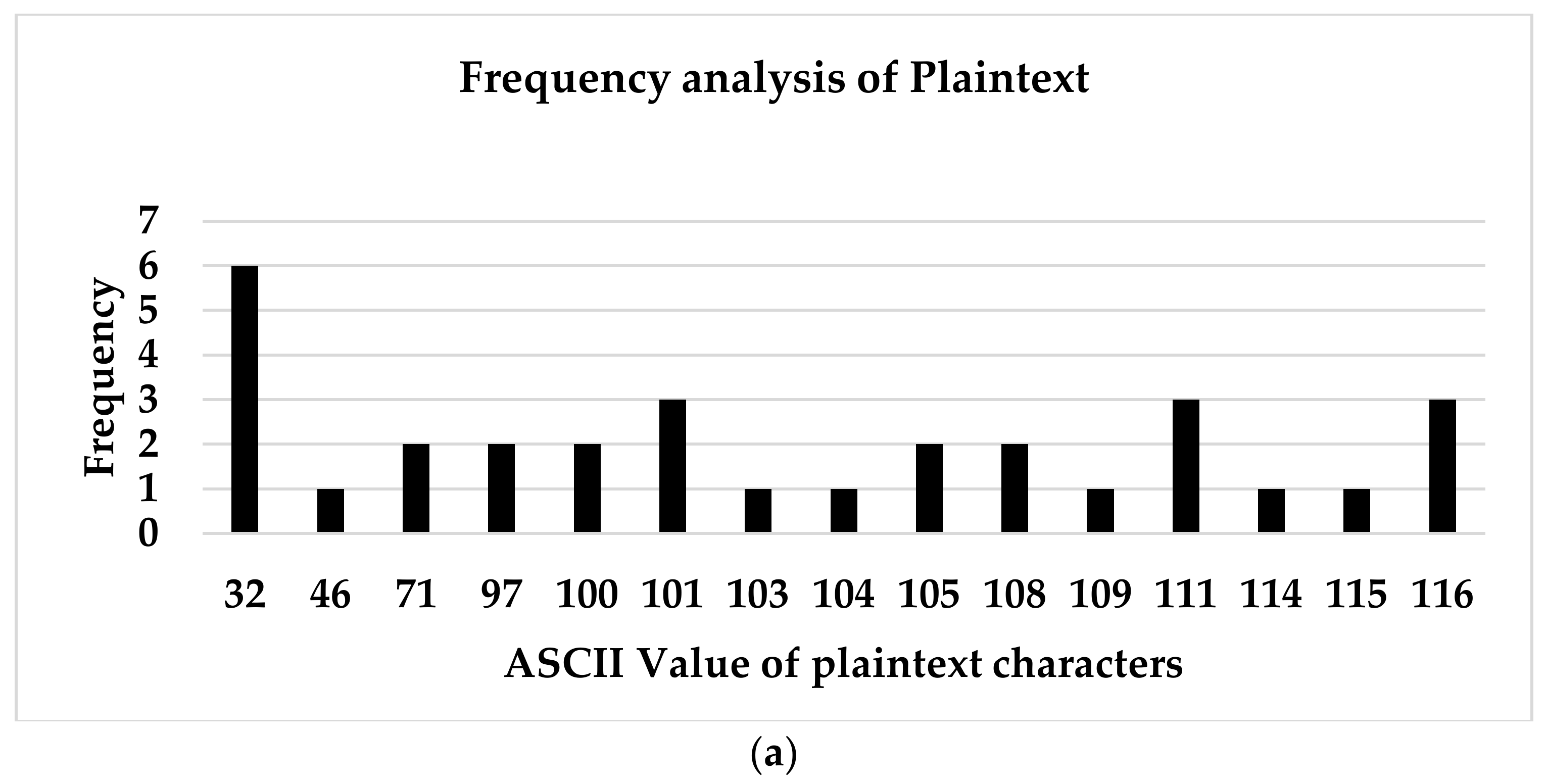
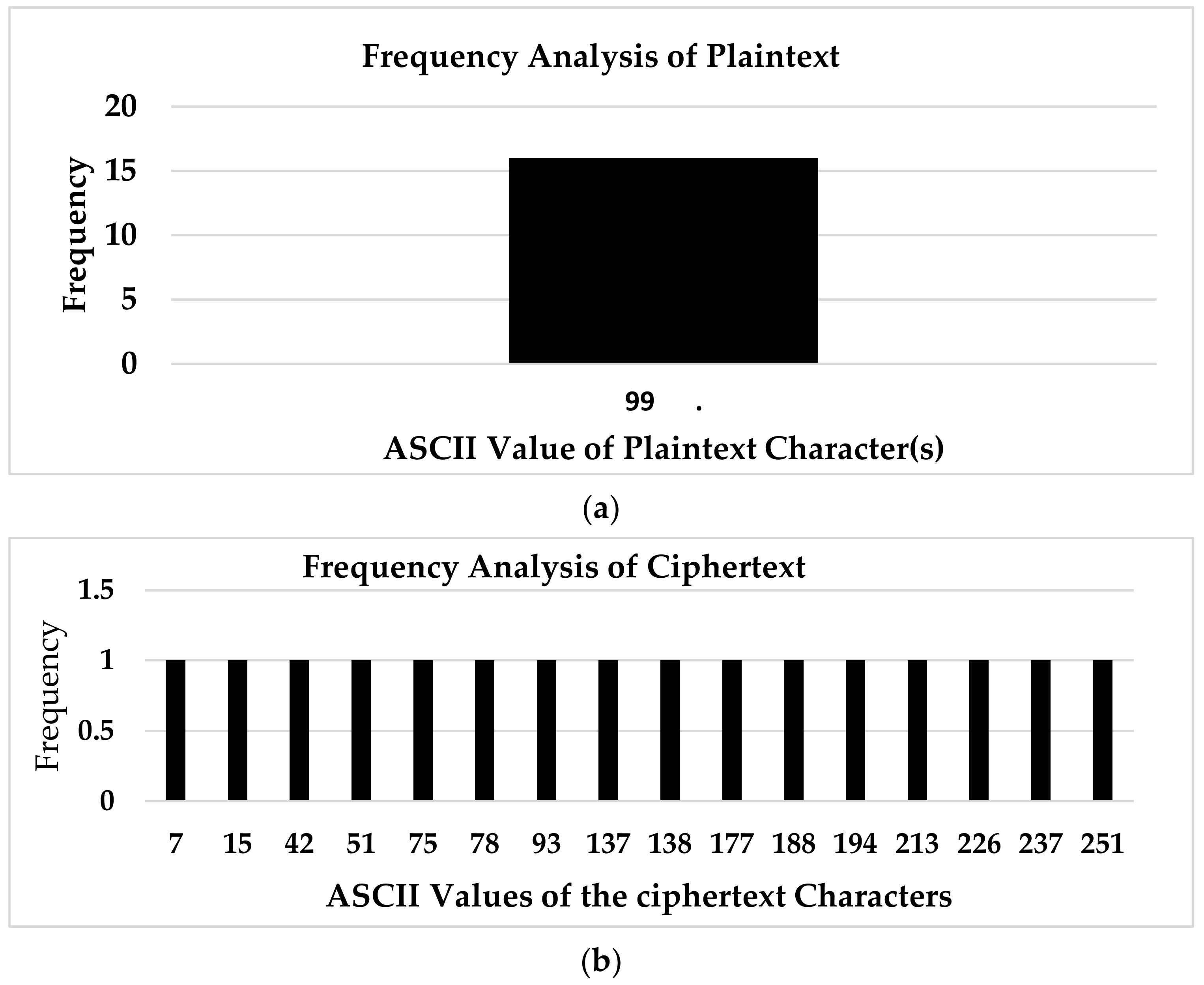
- Spectral Frequency Analysis of Modified Caesar Cipher: Information regarding plaintext, key, or both can be obtained by cryptanalysts by making use of frequency analysis of ciphertexts. HMCC resistance to frequency analysis attacks was carried out using spectral frequency analysis. Frequency analysis of some samples of plaintext and of the ciphertext produced when the plaintext passed through the encryption algorithm of HMCC were examined by plotting the histogram of the frequencies of the characters in the plaintext and ciphertext.
- Differential Cryptanalysis of HMCC: HMCC resistance to differential attacks was evaluated. The encryption results when two plaintexts that differ only by one bit were encrypted with the same key were analysed. Net Pixel Change Rate (NPCR) and Unified Average Changing Intensity (UACI) were used as metrics for measuring HMCC’s resistance to cryptanalysis attack. The NPCR and UACI were determined using the formula in Equations (3) and (4), respectively, for two ciphertexts C1 and C2 of length l.
- Encrypt a sample of plaintext P using MCC encryption module to obtain ciphertext C1;
- Change a symbol of P to another character to obtain a new plaintext P1;
- Encrypt the plaintext P1 using MCC encryption module to obtain ciphertext C2;
- Determine where ;
- Determine ;
- iv.
- HMCC Information Entropy Analysis: All of the 256 ASCII symbols are used by HMCC, so the expected maximum entropy is 8 when the formula in Equation (5) is used for entropy calculation.
- Encrypt a sample of plaintext P using HMCC encryption module to obtain ciphertext C;
- Find distinct unique ASCII characters Ptext and Ctext from P and C, respectively;
- Determine the frequency of each of the unique characters in Ptext and Ctext from P and C to respectively obtain pfrequency and cfrequency;
- Determine the probability of each unique character in P and C, respectively, using the formula pcharprobability [i] = pfrequency[i]/LENGTH(P) for I = 1 to LENGTH(P) and ccharprobability [i] = cfrequency[i]/LENGTH(C) FOR i = 1 to LENGTH(C);
- Determine the entropies of the plaintext and ciphertext by applying Equation (5):
- i.
- ii.
- Compare H(P) and H(C) with the maximum entropy value.
- v.
- Autocorrelation Analysis of HMCC: The autocorrelation function is used to define the resemblance of two sequences. Cryptanalysts use autocorrelation to calculate secret key length in classical ciphers. A cipher that is resistant to autocorrelation attacks will produce ciphertext that has more uniform and lower autocorrelation than plaintext. The following steps were taken in order to carry out autocorrelation analysis:
- Encrypt a sample plaintext P to obtain ciphertext C;
- Find distinct unique ASCII characters Ptext and Ctext from P and C, respectively;
- Determine the frequency of each of the unique characters in Ptext and Ctext from P and C to respectively obtain pfrequency and cfrequency;
- Plot the graph of the ASCII values of characters in Ptext against pfrequency and the ASCII values of Ctext against cfrequency;
- Compare the two graphs.
- vi.
- Strict Avalanche Criterion of HMCC
- vii.
- Comparative Security Analysis of the HMCC with Existing Ciphers
4. Results and Discussion
4.1. Results of Security Analysis
- Man-in-the-Middle, replay, and denial-of-service attacks: An attacker in MIMA is capable of impersonating both the sender and receiver [63]. If this attack succeeds, the attacker can send information to the receiver and also respond to the sender. An attacker in MIMA is also capable of resending the original message sent by a legitimate node to deceive the receiver. The activities of a MIMA attacker can also lead to denial-of-service attacks if such an attacker decides to regularly transmit false signals to deny authorized network users access to resources or services to which they are entitled. The proposed scheme is resistant to MIMA attacks of any form. A MIMA attacker that intercepts messages being transmitted between a client and the healthcare centre does not have enough information to compute a shared secret key between the two because it depends on the private keys of both, which were not shared. Because the delivered message contains a timestamp T that identifies the precise instant when the message was sent, a MIMA attack that resolves to engage in replay assaults will fail. This establishes the timing difference used to identify any attack during the replay phase. A MIMA attacker who resolves to launch denial-of-service attacks is incapacitated because the attacker needs a shared secret key to encrypt the data, which is only possible through stealing IDs or becoming a legitimate user.
- Analysis of Encryption algorithm of HMCC: Table 3 shows plaintext samples and the corresponding resulting ciphertexts when plaintexts are submitted to the HMCC encryption technique.
| Plaintext | Ciphertext |
|---|---|
| aaaaaaaaaaaaaaaa | \x8b5§\x82j\x99h¿®JÞØ\x9f\x943\x01 |
| aaaaaaaabbbbbbbbddddwwwww | \x97¡ÞFöWès}±eÎ×{\x9b9\xad×ó\x8b!ð\x8b1»\x15ÀÑyç\x8aÎ |
| God is good all the time. Great | 1\x95\x01èk\x00ÜätR\x116\x1f-Ô\x7fNnZ¢Ö\x19\x86_jÉQó\x83ê’¾ |
- iii.
- Spectral Frequency Analysis of Modified Caesar Cipher: The result of the frequency analysis of the plaintexts and their corresponding ciphertexts are given in Table 4 labelled serial number 1–3, and the frequency analysis of the sampled plaintexts and the corresponding obtained ciphertexts are respectively shown by the histograms in Figure 4, Figure 5 and Figure 6.
- iv.
- Differential Cryptanalysis of HMCC: Table 5 displays some plaintext samples, the obtained ciphertexts from HMCC, and estimated NPCR and UACI.
- v.
- HMCC Information Entropy Analysis
- vi.
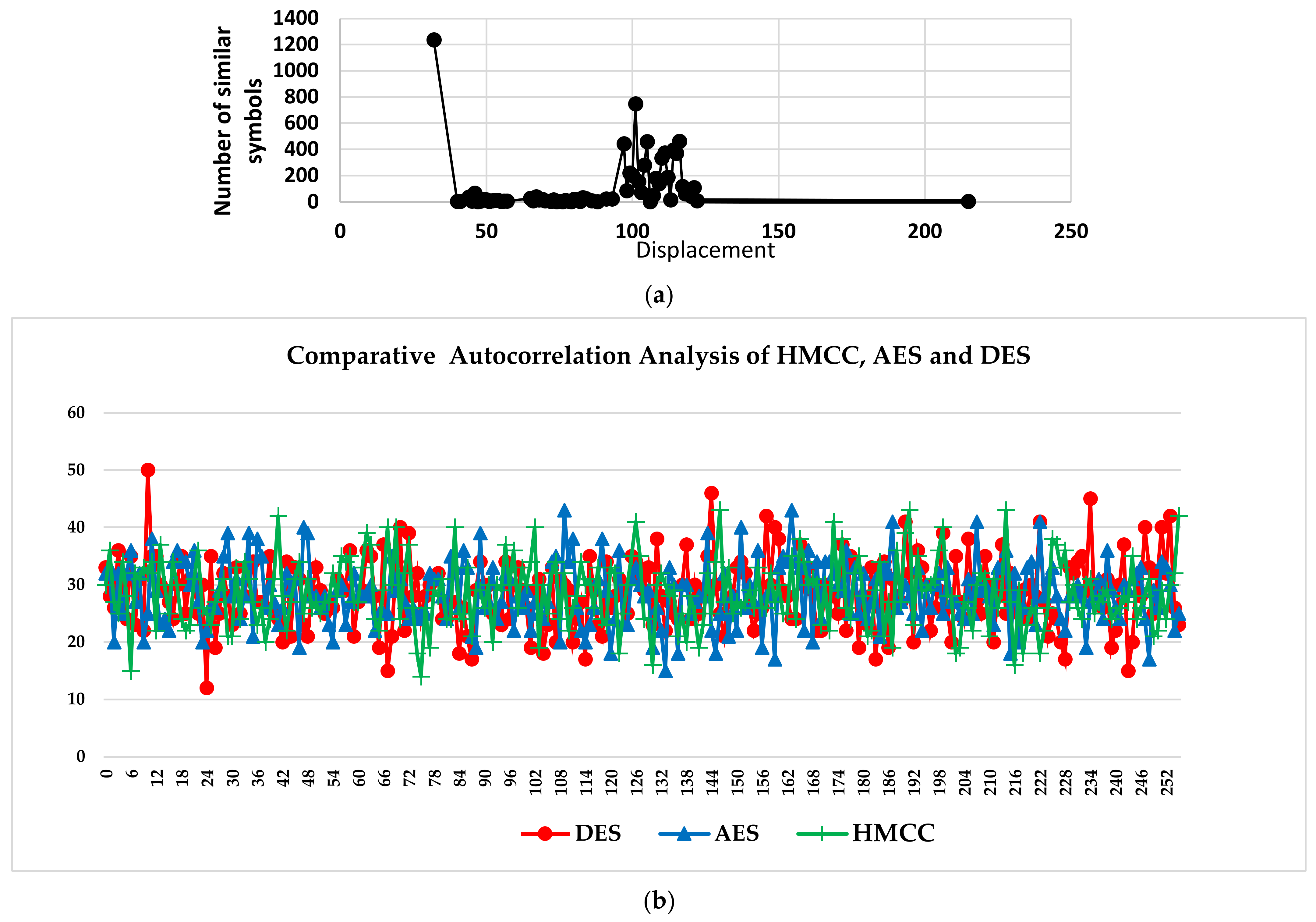
- Autocorrelation Analysis of HMCC: The autocorrelation function is used to define the resemblance of two sequences. Cryptanalysts use autocorrelation to calculate secret key length in classical ciphers. A cipher that is resistant to autocorrelation attacks produces ciphertext that has more uniform and lower autocorrelation than plaintext. Figure 7 depicts the graph of the autocorrelation of a sample of plaintext and the autocorrelation of the ciphertext generated after the sample plaintext was encrypted using the HMCC cipher.
- vii.
- Resistance of HMCC against Brute-Force Attack: To be immune to a brute-force attack, the secret key space of a cryptosystem that is relevant for modern-day information security should be larger than 2100 [66]. Although the size of the key in HMCC varies, the minimum key size is 128 bits; therefore, the key size is 2128. The key size can be increased to any number of bits by specifying the block size to be used when encryption is to be done. More entropy implies a broader and more unpredictable key search space, with smaller and more difficult-to-identify repetitions and correlations. In HMCC, all the 256 ASCII characters can be randomly used in the formation of the encryption keys. Hence, the entropy of the keys can be calculated using the formula in Equation (6).
- viii.
- Resistance of HMCC Against Classical Cryptanalysis attack: Kirchhoff’s principle states that the attacker has access to the encryption algorithms but no access to the secret key. With the encryption algorithm in the hand of a cryptanalyst, differential attacks such as cipher text-only and known/chosen plaintext attacks can be carried out [68]. In HMCC, the confusion and diffusion process is realized by modifying the bits of the encrypted text; in addition, the encryption of each block of plaintext is done such that each block is encrypted with a unique key. Again, the character set from where the ciphertext characters are obtained is determined by the key so each block uses a different character set. If a plaintext spans more than one block and the blocks are of the same characters, each block will be encrypted differently as different keys, and different character sets are used to determine the ciphertext characters. A sample output where the block size is 16 and the number of characters to be encrypted is 32 is given in Table 7.
- ix.
- Strict Avalanche Criterion of HMCC
4.2. Encryption and Decryption Time Analysis
4.3. Comparative Security Analysis of the HMCC with Existing System
- i.
- Comparative Analysis of Entropies of MCC, AES, and DES
- ii.
- Comparative Analysis of MCC, AES, and DES based on NPCR and UACI Values of Differential Cryptanalysis
- iii.
- Comparative analysis of MCC, AES, and DES based on Autocorrelation Analysis
- iv.
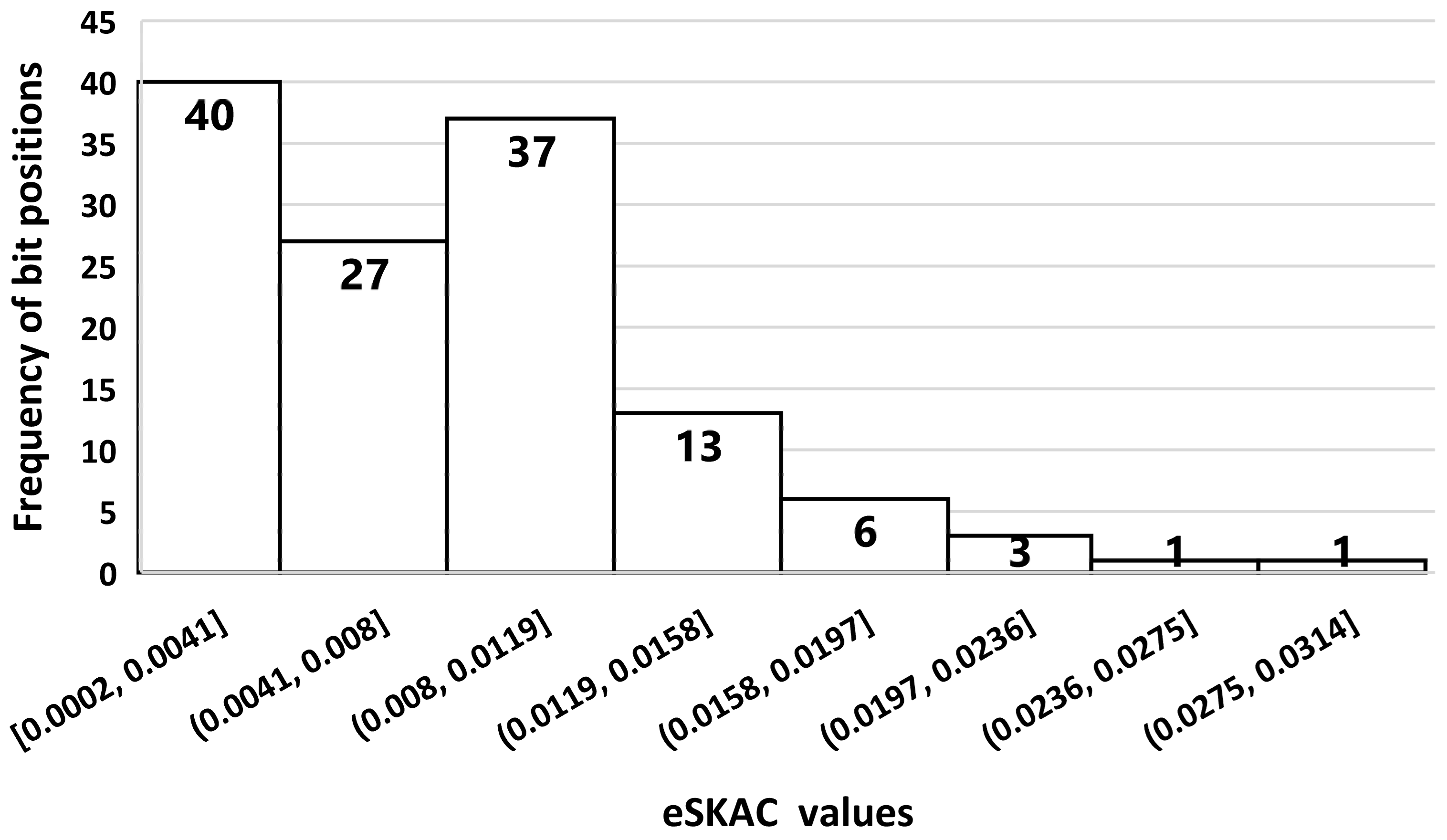
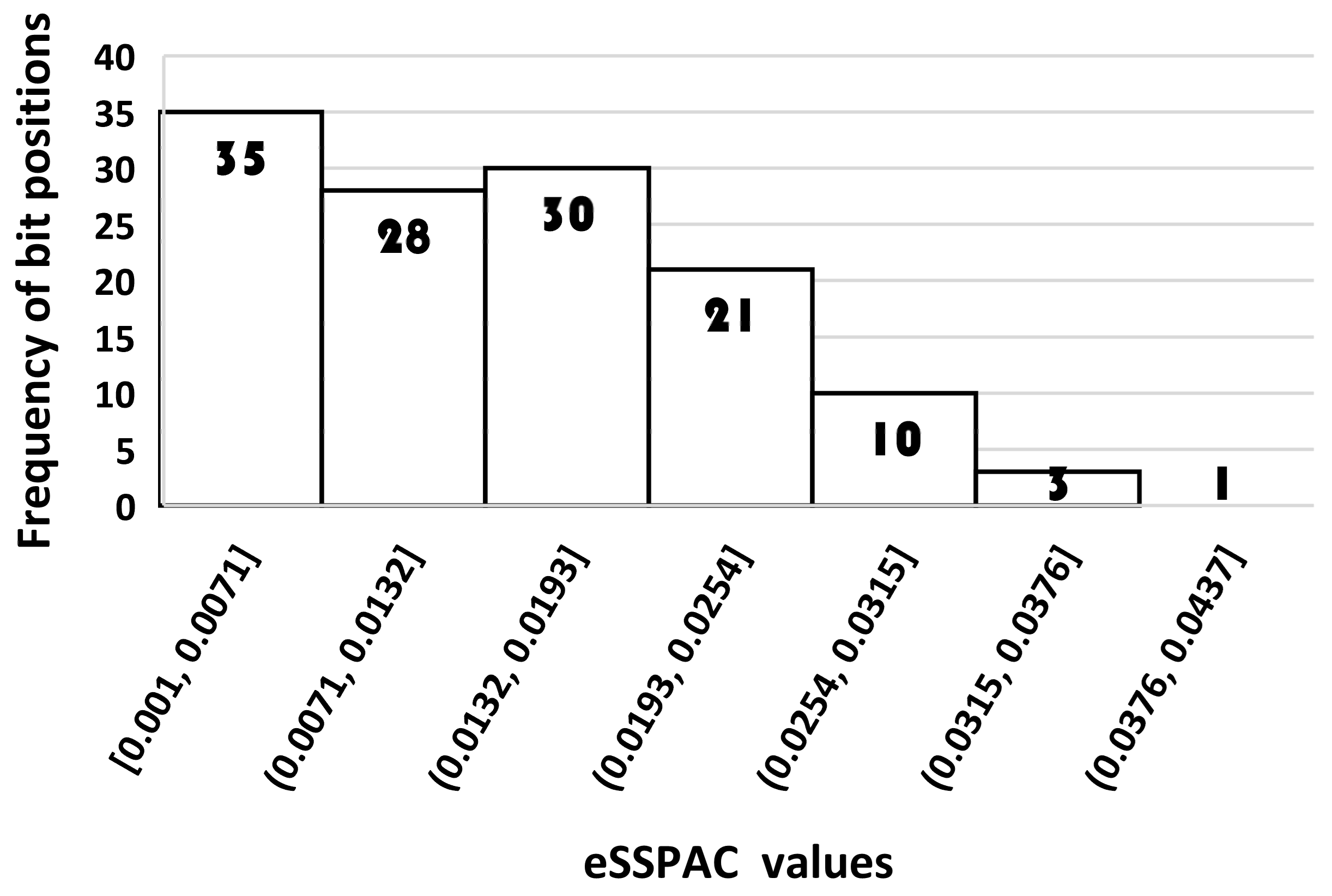
- Comparative Analysis of HMCC, AES, and DES based on SKAC and SPAC
5. Limitations and Areas of Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dhillon, P.K.; Kalra, S. Secure and efficient ECC based SIP authentication scheme for VoIP communications in internet of things. Multimed. Tools Appl. 2019, 78, 22199–22222. [Google Scholar] [CrossRef]
- Jagadeeswari, V.; Subramaniyaswamy, V.; Logesh, R.; Vijayakumar, V. A study on medical internet of things and big data in personalized healthcare system. Health Inf. Sci. Syst. 2018, 6, 14. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, D.; Novak, T. Consumer and object experience in the internet of things: An assemblage theory approach. J. Consum. Resour. 2018, 44, 1178–1204. [Google Scholar] [CrossRef]
- Borgia, E. The internet of things vision: Key features, applications and open issues. Comput. Commun. 2014, 54, 1–31. [Google Scholar] [CrossRef]
- Botta, A.; de Donato, W.; Persico, V.; Pescap, A. Integration of cloud computing and internet of things: A survey. Future Gener. Comput. Syst. 2016, 56, 684–700. [Google Scholar] [CrossRef]
- Sharma, M.; Siddiqui, A. RFID based mobiles: Next generation Applications. In Proceedings of the 2nd IEEE International Conference on Information Management and Engineering (ICIME), Chengdu, China, 16–18 April 2010; pp. 523–526. [Google Scholar]
- Matin, M.A.; Islam, M.M. Overview of Wireless Sensor Network. In Wireless Sensor Networks–Technology and Protocols; INTECH: Hong Kong, China, 2012; pp. 3–24. [Google Scholar]
- Al-kahtani, M.S.; Khan, F.; Taekeun, W. Application of Internet of Things and Sensors in Healthcare. Sensor 2022, 22, 5738. [Google Scholar] [CrossRef]
- Samaila, M.G.; Neto, M.; Fernandes, D.A.B.; Freire, M.M.; Inácio, P.R.M. Security Challenges of the Internet of Things. In Beyond the Internet of Things, Internet of Things; Batalla, J.M., Mastorakis, G., Mavromoustakis, C., Pallis, E., Eds.; Springer International Publishing AG: Berlin, Germany, 2017; pp. 53–82. ISBN 9783319507583. [Google Scholar]
- Mosenia, A.; Jha, N.K. A comprehensive study of security of Internet-of-Things. IEEE Trans. Emerg. Top. Comput. 2017, 5, 586–602. [Google Scholar] [CrossRef]
- Granjal, J.; Monteiro, E.; Silva, J.S. Security for the Internet of Things: A Survey of Existing Protocols and Open Research Issues. IEEE Commun. Surv. Tutor. 2015, 17, 1294–1312. [Google Scholar] [CrossRef]
- Ogundokun, R.O.; Awotunde, J.B.; Adeniyi, E.A.; Ayo, F.E. Crypto-Stegno based model for securing medical information on IOMT platform. Multimed. Tools Appl. 2021, 80, 31705–31727. [Google Scholar] [CrossRef]
- Darma, D.; Ilmi, Z.; Darma, S.; Syaharuddin, Y. COVID-19 and its impact on education: Challenges from industry 4.0. AQUADEMIA 2020, 4, ep20025. [Google Scholar]
- Ilmi, Z.; Darma, D.C.; Azis, M. Independence in learning, education management, and industry 4.0: Habitat indonesia during COVID-19. J. Anthr. Sport Phys. Educ. 2020, 4, 63–66. [Google Scholar]
- Kumar, K.; Kumar, N.; Shah, R. Role of IoT to avoid spreading of COVID-19. Int. J. Intell. Netw. 2020, 1, 32–35. [Google Scholar] [CrossRef]
- Celesti, A.; Fazio, M.; Galan, F.; Arquez, M.; Glikson, A.; Mauwa, H.; Bagula, A. How to develop IoT ’cloud e-health systems based on fiware: A lesson learnt. J. Sens. Actuator Netw. 2019, 8, 7. [Google Scholar] [CrossRef]
- Debdas, S.; Panigrahi, C.K.; Kundu, P.; Kundu, S.; Jha, R. IoT application in interconnected hospitals. Mach. Learn. Healthc. Appl. 2021, 225–247. [Google Scholar] [CrossRef]
- Swaroop, K.N.; Chandu, K.; Gorrepotu, R.; Deb, S. A health monitoring system for vital signs using IoT. Internet Things 2019, 5, 116–129. [Google Scholar] [CrossRef]
- Zamanifar, A. Remote patient monitoring: Health status detection and prediction in IoT-based health care. In iIoT in Healthcare and Ambient Assisted Living; Spinger: Berlin/Heidelberg, Germany, 2021; pp. 89–102. [Google Scholar]
- Rose, K.; Eldridge, S.; Chapin, L. The Internet of Things: An Overview-Understanding the Issues and Challenges of a More Connected World. Internet Soc. Pages 2015, 80, 1–50. [Google Scholar]
- Gamundani, A.M. An Impact Review on Internet of Things Attacks. In Proceedings of the 2015 International Conference on Emerging Trends in Networks and Computer Communications (ETNCC), Windhoek, Namibia, 17–20 May 2015. [Google Scholar]
- Rahman, A.; Rahman, M.; Kundu, D.; Karim, R.; Shahab, S. Study on IoT for SARS-CoV-2 with healthcare: Present and future perspective. Math. Biosci. Eng. 2021, 18, 9697–9726. [Google Scholar] [CrossRef]
- Yin, M.; Chen, X.; Wang, Q.; Wang, W.; Wang, Y. Dynamics on hybrid complex network: Botnet modeling and analysis ofmedical IoT. Secur. Commun. Netw. 2019, 2019, 6803801. [Google Scholar] [CrossRef]
- Din, I.U.; Guizani, M.; Kim, B.S.; Hassan, S.; Khan, M.K. Trust management techniques for the internet of things: A survey. IEEE Access 2018, 7, 29763–29787. [Google Scholar] [CrossRef]
- Din, I.U.; Almogren, A.; Guizani, M.; Zuair, M. A decade of internet of things: Analysis in the light of healthcare applications. IEEE Access 2019, 7, 89967–89979. [Google Scholar] [CrossRef]
- Slam, S.U.; Khattak, H.A.; Pierson, J.M.; Din, I.U.; Almogren, A.; Guizani, M.; Zuair, M. Leveraging utilization as performance metric for CDN enabled energy efficient internet of things. Measurement 2019, 147, 106814. [Google Scholar]
- Khan, S.; Sikandar, M.; Almogren, A.; Din, I.U.; Fortino, G.; Guerrieri, A. IoMT-based computational approach for detecting brain tumor. Future Gener. Comput. Syst. 2020, 109, 360–367. [Google Scholar] [CrossRef]
- Manasrah, A.M.; Shannaq, M.A.; Nasir, M.A. An Investigation Study of Privacy Preserving in Cloud Computing Environment. In Handbook of Computer Networks and Cyber Security; Springer Nature AG: Cham, Switzerland, 2020; ISBN 978-3-030-22276-5. [Google Scholar]
- Nabeel, M.; Bertino, E. Privacy preserving delegated access control in public clouds. IEEE Trans. Knowl. Data Eng. 2013, 26, 2268–2280. [Google Scholar] [CrossRef]
- Dong, X.; Yu, J.; Luo, Y.; Chen, Y.; Xue, G.; Li, M. Achieving an effective, scalable and privacy-preserving data sharingservice in cloud computing. Comput. Secur. 2014, 42, 151–164. [Google Scholar] [CrossRef]
- Joseph, N.M.; Daniel, E.; Vasanthi, N. Survey on privacy-preserving methods for Computing storage in cloud computing. In Proceedings of the IAmrita International Conference of Women in Computing, Coimbatore, India, 9–11 January 2013. [Google Scholar]
- Jogade, S.; Sharma, R.; Kadam, R. Partitioning data and domain integrity checking for storage-improving cloud storage security using data partitioning technique. Int. J. Emerg. Res. Manag. Technol. 2014, 3, 133–137. [Google Scholar]
- Chen, F.; Liu, A.X. Privacy and integrity preserving multi dimensional range queries for cloud computing. In Proceedings of the Networking Conference, Trondheim, Norway 2–4 June 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Ku, W.S.; Hu, L.; Shahabi, C.; Wang, H. A query integrity assurance scheme for accessing outsourced spatial databases. Geoinformatica 2013, 17, 97–124. [Google Scholar] [CrossRef]
- Hu, L.; Ku, W.S.; Bakiras, S.; Shahabi, C. Spatial query integrity with Voronoi neighbors. Knowl. Data Eng. 2013, 26, 863–876. [Google Scholar] [CrossRef]
- Naruchitparames, J.; Güneş, M.H. Enhancing data privacy and integrity in the cloud. In Proceedings of the International Conference on High Performance Computing and Simulation (HPCS), Istanbul, Turkey, 4–8 July 2011; IEEE: Piscataway, NJ, USA, 2011. [Google Scholar]
- Gentry, C.; Halevi, S. Implementing Gentry’s fully-homomorphic encryption scheme. In Proceedings of the Advances in Cryptology–EUROCRYPT 2011: 30th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Tallinn, Estonia, 15–19 May 2011; pp. 129–148. [Google Scholar]
- Gentry, C.; Halevi, S.; Smart, N. Better bootstrapping in fully homomorphic encryption. In Proceedings of the Public Key Cryptography–PKC 2012: 15th International Conference on Practice and Theory in Public Key Cryptography, Darmstadt, Germany, 21–23 May 2012; pp. 1–16. [Google Scholar]
- Gentry, C.; Halevi, S.; Smart, N. Fully homomorphic encryption with polylog overhead. Eurocrypt 2012, 7237, 465–482. [Google Scholar]
- Gentry, C.; Halevi, S.; Smart, N.P. Homomorphic evaluation of the AES circuit. In Proceedings of the Advances in Cryptology–CRYPTO 2012: 32nd Annual Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2012; pp. 850–867. [Google Scholar]
- Chavan, P.; More, P.; Thorat, N.; Yewale, S.; Dhade, P. ECG-Remote patient monitoring using cloud computing. Imp. J. Interdiscip. Res. 2016, 2, 368–372. [Google Scholar]
- Arbat, H.; Choudhary, S.; Bala, K. IoT smart health band. Imp. J. Interdiscip. Res. 2016, 2, 300–311. [Google Scholar]
- Islam, S.R.; Kwak, D.; Kabir, M.H.; Hossain, M.; Kwak, K.S. The internet of things for health care: A comprehensive survey. IEEE Access 2015, 3, 678–708. [Google Scholar] [CrossRef]
- Huiyeh, K.A. secure IoT-based healthcare system with body sensor networks. IEEE Access 2016, 4, 10288–10299. [Google Scholar]
- Rayappan, D.; Pandiyan, M. Lightweight Feistel structure based hybrid-crypto model for multimedia data security over uncertain cloud environment. Wirel. Netw. 2021, 27, 981–999. [Google Scholar] [CrossRef]
- Elhoseny, M.; Shankar, K.; Lakshmanaprabu, S.K.; Maseleno, A.; Arunkumar, N. Hybrid optimization with cryptography encryption for medical image security in Internet of Things. Neural Comput. Appl. 2020, 32, 10979–10993. [Google Scholar] [CrossRef]
- Chhabra, S.; Lata, K. Obfuscated AES cryptosystem for secure medical imaging systems in IoMT edge devices. Health Technol. 2022, 12, 971–986. [Google Scholar] [CrossRef]
- Song, D.X.; Wagner, D.; Perrig, A. Practical techniques for searches on encrypted data. In Proceedings of the Security and Privacy, 2000. S&P 2000, Berkeley, CA, USA, 14–17 May 2000; IEEE: Piscataway, NJ, USA, 2000. [Google Scholar]
- Goh, E.-J. Secure Indexes for Efficient Searching on Encrypted Compressed Data 2003. Available online: https://eprint.iacr.org/2003/216.pdf (accessed on 3 January 2023).
- Chang, Y.-C.; Mitzenmacher, M. Privacy preserving keyword searches on remote encrypted data. In Applied Cryptography and Network Security; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Li, J.; Wang, Q.; Wang, C.; Cao, N.; Ren, K.; Lou, W. Fuzzy keyword search over encrypte d data in cloud computing. In Proceedings of the INFOCOM, San Diego, CA, USA, 14–19 March 2010; IEEE: Piscataway, NJ, USA, 2010. [Google Scholar]
- Adjedj, M.; Bringer, J.; Chabanne, H.; Kindarji, B. Biometric identification over encrypted data made feasible. In Information Systems Security; Springer: Berlin/Heidelberg, Germany, 2009; pp. 86–100. [Google Scholar]
- Kuzu, M.; Islam, M.S.; Kantarcioglu, M. Efficient similarity search over encrypted data. In Proceedings of the 28th International Conference on Data Engineering (ICDE), Arlington, VA, USA, 1–5 April 2012; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Lu, Y.; Privacy-preserving logarithmic-time search on encrypted data in cloud. NDSS 2012. Available online: https://www.ndss-symposium.org/wp-content/uploads/2017/09/04_1.pdf (accessed on 3 January 2023).
- Wang, J.; Ma, H.; Tang, Q.; Li, J.; Zhu, H.; Ma, S.; Chen, X. A new efficient verifiable fuzzy keyword search scheme. JoWUA 2012, 3, 61–71. [Google Scholar]
- Boneh, D.; Di Crescenzo, G.; Ostrovsky, R.; Persiano, G. Public key encryption with keyword search. In Proceedings of the Advances in Cryptology-EUROCRYPT 2004: International Conference on the Theory and Applications of Cryptographic Techniques, Interlaken, Switzerland, 2–6 May 2004; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Bellare, M.; Boldyreva, A.; O’Neill, A. Deterministic and efficiently searchable encryption. In Proceedings of the Advances in Cryptology-CRYPTO 2007: 27th Annual International Cryptology Conference, Santa Barbara, CA, USA, 19–23 August 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 535–552. [Google Scholar]
- Subramaniyaswamy, V.; Jagadeeswari, V.; Indragandhi, V.; Jhaveri, R.H.; Vijayakumar, V.; Kotecha, K.; Ravi, L. Somewhat Homomorphic Encryption: Ring Learning with Error Algorithm for Faster Encryption of IoT Sensor Signal-Based Edge Devices. Secur. Commun. Netw. 2022, 2022, 2793998. [Google Scholar] [CrossRef]
- Kocabaş, Ö.; Soyata, T. Towards Privacy-Preserving Medical Homomorphic Encryption. In Virtual and Mobile Healthcare: Breakthroughs in Research and Practice; IGI Global: Hershey, PA, USA, 2015. [Google Scholar]
- Fahrnberger, G. Editing Encrypted Messages without Decrypting or Understanding Them. Ph.D Thesis, University of Hagen, Hagen, Germany, 2019. [Google Scholar]
- Goyal, T.K.; Sahula, V. Lightweight Security Algorithm for Low Power IoT Devices. In Proceedings of the Intl. Conference on Advances in Computing, Communications and Informatics (ICACCI), Jaipur, India, 21–24 September 2016; pp. 1725–1729. [Google Scholar]
- Sulak, F. Statistical Analysis of Block Cipher and Hash Function. Middle East Tech. Univ. 2011. [Google Scholar]
- Gupta, S.; Verma, H.K.; Sangal, A.L. Security attacks & prerequisite for wireless sensor networks. Int. J. Eng. Adv. Technol. 2013, 2, 558–566. [Google Scholar]
- Patidar, V.; Pareek, N.; Sud, K. A New Substitution-Diffusion Based Image Cipher Using Chaotic Standard and Logistic Maps. Commun. Nonlinear Sci. Number Simul. 2009, 14, 3056–3075. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, B.; Huang, L. Quantum Image Encryption Scheme Using Arnold Transform and S-box Scrambling. Entropy 2019, 21, 343. [Google Scholar] [CrossRef] [PubMed]
- Álvarez, G.; Li, S. Some basic cryptographic requirements for chaos-based cryptosystems. Int. J. Bifurc. Chaos 2006, 2129–2151. [Google Scholar] [CrossRef]
- Murillo-Escobar, M.A.; Meranza-Castillón, M.O.; López-Gutiérrez, R.M.; Cruz-Hernández, C. Suggested Integral Analysis for Chaos-Based Image Cryptosystems. Entropy 2019, 21, 815. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Wu, C. Compression-unimpared batch-image Encryption Combining Vector Quantization and Index Compression. Inf. Sci. 2010, 18, 1690–1701. [Google Scholar] [CrossRef]
- Matter, W.; Cauteruccio, F.; Stamile, C.; Ursino, D.; Sappey, D.; Cauteruccio, F.; Stamile, C.; Terracina, G.; Ursino, D.; Sappey-marinier, D. An automated string-based approach to extracting and characterizing White Matter fiber-bundle. Comput. Biol. Med. 2016, 77, 64–75. [Google Scholar] [CrossRef]
- Baldassarre, G.; Giudice, P.L.; Musarella, L.; Ursino, D. A paradigm for the cooperation of objects belonging to different IoTs. In Proceedings of the International Database Engineering & Applications Symposium, IDEAS 2018, Villa San Giovanni, Italy, 18–20 June 2018; pp. 157–164. [Google Scholar]
- Ursino, D.; Virgili, L. Humanizing IoT: Defining the profile and the reliability of a thing in a Multi-IoT scenario. In iTowards Social Internet of Things: Enabling Technologies, Architectures and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Baldassarre, G.; Giudice, P.L.; Musarella, L.; Ursino, D. The MIoT paradigm: Main features and an ‘“ad-hoc”’ crawler. Future Gener. Comput. Syst. 2019, 92, 29–42. [Google Scholar] [CrossRef]
- Giudice, P.L.; Nocera, A.; Ursino, D.L. Virgili Building topic-driven virtual IoTs in a multiple IoTs scenario. Sensors 2019, 19, 2956. [Google Scholar] [CrossRef]
- Cauteruccio, F.; Cinelli, L.; Fortino, G.; Savaglio, C.; Terracina, G.; Ursino, D.; Virgili, L. An approach to compute the scope of a social object in a Multi-IoT scenario. Pervasive Mob. Comput. 2020, 67, 101223. [Google Scholar] [CrossRef]




| Reference | Title | Method | Strength | Weakness |
|---|---|---|---|---|
| [44] | Secure IoT-based healthcare system with body sensor networks | Proposed body sensor network capable of proficiently and continually communicating data to a public IoT-based system | A secure IoT system was developed | Privacy issue was not addressed |
| [45] | Lightweight Feistel structure-based hybrid crypto model for multimedia data security over uncertain cloud environment | Feistel structure and substitution permutation cryptography | Higher attack resilience | The cipher has low entropy In addition, privacy issue was not addressed |
| [46] | Hybrid optimization with cryptography encryption for medical image security in the Internet of Things | Elliptic curve cryptography’s grasshopper and particle swarm optimization techniques | High peak signal to noise ratio and structural similarity of 1 | Only security of the data was addressed; the issue of privacy was not addressed |
| [47] | Obfuscated AES cryptosystem for secure medical imaging systems in IoMT edge devices | Adaptable medical imaging processing system that incorporates authentication-based methods of the AES cryptosystem on ZedBoard | A secured scalable hardware/software cryptosystem was built | The issue of privacy was not addressed |
| [48,49,50] | Practical techniques for searches on encrypted dataSecure indices for efficient searching on encrypted compressed dataPrivacy-preserving keyword searches on remote encrypted data | Symmetric cryptography algorithm and searchable encryption techniques | Both security and privacy issues were addressed | The system’s efficiency reduces as the number of distinct keywords in the document increases |
| [51,52,53,54,55] | Fuzzy keyword search over encrypted data in cloud computingBiometric identification over encrypted data made feasible | Fuzzy Searchable Encryption-based (FSE) systems | Searchable encryption technique that is tolerant to some typo errors | Vulnerable to MIMA They are not suitable for systems that need constant updating |
| [56,57] | Public key encryption with keyword searchDeterministic and efficiently searchable encryption | Searchable encryption technique that is based on public key encryption (PkSE) | Addresses the problem of MIMA faced by SE and FSE | Cannot protect keyword privacy in public, and the scheme only provides privacy to text drawn from a space of large min-entropy |
| [59] | Towards Privacy-Preserving Medical Homomorphic Encryption | Fully Homomorphic Encryption | Addresses both security and privacy issues | The scheme is both computationally and memory-intensive |
| Notation | Description |
|---|---|
| Healthcare identification number | |
| Patient identification number | |
| Guest healthcare identification number | |
| EC equation | |
| p | The large prime number obtained from chosen EC |
| a,b | |
| G | The base point which produces the subgroup of the elliptic curve that has a large prime as its order |
| n | Order (number of a point) of the subgroup. nG = 0, prime n is large |
| h | . h should be small , preferably, h = 1 |
| Healthcare private key | |
| Patient private key | |
| Guest healthcare private key | |
| ) | |
| ) | |
| ) | |
| The hash function used by healthcare | |
| nList | ) |
| HASH | Signing cipher message Cm hash function |
| ssk | Shared secret key |
| SNP | Share node point = (ssk × G) |
| PRK | Private random key (bit size is dependent on the type of EC) |
| K | A random integer is chosen from (1, p − 1) |
| CM | The ciphertext (all encrypted points) |
| ⊕ | Exclusive OR operation |
| + | Addition operation used for the ECC encryption process |
| T | Timestamp |
| S/N | Plaintext | Encrypted Text from HMCC |
|---|---|---|
| 1 | Plaintext: God is good all the time. Great ASCII Values: [71, 111, 100, 32, 105, 115, 32, 103, 111, 111, 100, 32, 97, 108, 108, 32, 116, 104, 101, 32, 116, 105, 109, 101, 46, 32, 71, 114, 101, 97, 116] | Ciphertext: hýa95×ó¾öí›?r”’·&TZô÷ýBÉe©Pz» ASCII Values: [104, 253, 97, 57, 6, 53, 215, 243, 190, 246, 237, 155, 63, 4, 114, 34, 16, 180, 183, 38, 84, 90, 244, 247, 253, 66, 201, 101, 169, 80, 122, 187] |
| 2 | Plaintext: Aaabbbbcccccddde ASCII Values: [97, 97, 97, 98, 98, 98, 98, 99, 99, 99, 99, 99, 100, 100, 100, 101] | Ciphertext: î×-E†}}Pð+GÌWÿ ASCII values: [238, 215, 30, 69, 134, 125, 125, 80, 240, 43, 71, 204, 3, 4, 87, 255] |
| 3 | Plaintext: cccccccccccccccc ASCII Values: [99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99, 99] | Ciphertext: âûKÕŠ±‰3]¼N*í ASCII Values: [226, 251, 75, 213, 7, 138, 177, 137, 15, 51, 93, 194, 188, 78, 42, 237] |
| Plaintext 1 | Plaintext 2 | C1 | C2 | NPCR (%) | UACI (%) |
|---|---|---|---|---|---|
| cccccccccccccccc | ccccccccãccccccc | BEÄÏpBr\n¬Ú$\r\x12\x89>‘“ | §Ã\x83\x7f4A>\x11§öÄòCt\x80î | 100 | 30.61 |
| God is good all | God is gïod all | \x7fYös\x90\x82\x04äÙx¿íà¥\x08¤ | es§ª\x16wú\x17¤ûÚÈO¤ma | 100 | 32.64 |
| Text Type | Entropy |
|---|---|
| Plaintext | 4.5009 |
| Ciphertext | 7.9773 |
| Block | Plaintext | Ciphertext |
|---|---|---|
| 1 | áaaaaaaaaaaaaaaa | cM9¶\x19ßq\x10àìi\x9aÜÿÕy |
| 2 | áaaaaaaaaaaaaaaa | \\\x1dßñ]Qê\x84±aweGÆZ |
| i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.4954 | 0.5019 | 0.4977 | 0.4942 | 0.4959 | 0.4966 | 0.4924 | 0.4975 | 0.502 | 0.5056 | 0.5056 | 0.4945 | 0.4964 | 0.4977 | 0.4995 | 0.4977 |
| 1 | 0.5031 | 0.4944 | 0.507 | 0.4994 | 0.506 | 0.4987 | 0.5049 | 0.4986 | 0.4888 | 0.5004 | 0.5026 | 0.5049 | 0.4973 | 0.4983 | 0.499 | 0.5059 |
| 2 | 0.5049 | 0.494 | 0.5039 | 0.4997 | 0.4937 | 0.5027 | 0.4973 | 0.5049 | 0.5008 | 0.5023 | 0.5084 | 0.5005 | 0.5005 | 0.5027 | 0.5002 | 0.4957 |
| 3 | 0.5036 | 0.4985 | 0.502 | 0.4973 | 0.5006 | 0.5031 | 0.4984 | 0.5047 | 0.5027 | 0.5077 | 0.4952 | 0.4941 | 0.4929 | 0.4973 | 0.4998 | 0.5073 |
| 4 | 0.4986 | 0.4889 | 0.499 | 0.4952 | 0.5059 | 0.4952 | 0.508 | 0.5038 | 0.5005 | 0.4951 | 0.4951 | 0.4988 | 0.4942 | 0.4961 | 0.4923 | 0.4946 |
| 5 | 0.4999 | 0.4948 | 0.5021 | 0.497 | 0.4966 | 0.4941 | 0.5052 | 0.4942 | 0.4945 | 0.5072 | 0.4948 | 0.4963 | 0.4921 | 0.4957 | 0.498 | 0.5012 |
| 6 | 0.5047 | 0.4858 | 0.5002 | 0.4933 | 0.4981 | 0.5012 | 0.5061 | 0.4909 | 0.4967 | 0.4875 | 0.502 | 0.4973 | 0.5064 | 0.4905 | 0.5047 | 0.4994 |
| 7 | 0.5004 | 0.4992 | 0.5059 | 0.4984 | 0.4943 | 0.4991 | 0.4952 | 0.4919 | 0.501 | 0.4941 | 0.4996 | 0.4982 | 0.4991 | 0.5009 | 0.5102 | 0.4945 |
| i/j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.4913 | 0.4879 | 0.4975 | 0.4977 | 0.4898 | 0.5041 | 0.4987 | 0.5055 | 0.4928 | 0.4938 | 0.4877 | 0.4938 | 0.4957 | 0.4946 | 0.4896 | 0.5059 |
| 1 | 0.4881 | 0.4927 | 0.5088 | 0.4891 | 0.4934 | 0.5011 | 0.4926 | 0.4971 | 0.4925 | 0.4891 | 0.486 | 0.4982 | 0.4891 | 0.4993 | 0.4969 | 0.4988 |
| 2 | 0.4887 | 0.4931 | 0.4873 | 0.4933 | 0.4969 | 0.4921 | 0.498 | 0.4929 | 0.4934 | 0.4859 | 0.487 | 0.4876 | 0.4993 | 0.4941 | 0.5038 | 0.4933 |
| 3 | 0.4926 | 0.4906 | 0.4963 | 0.4965 | 0.4941 | 0.4952 | 0.4916 | 0.4881 | 0.4922 | 0.4968 | 0.4895 | 0.4986 | 0.4878 | 0.4961 | 0.4933 | 0.5012 |
| 4 | 0.4946 | 0.4995 | 0.491 | 0.4975 | 0.4904 | 0.497 | 0.4828 | 0.4941 | 0.4839 | 0.4938 | 0.4852 | 0.4861 | 0.4982 | 0.4983 | 0.5012 | 0.4974 |
| 5 | 0.5007 | 0.4827 | 0.5023 | 0.4933 | 0.5081 | 0.4918 | 0.4931 | 0.4977 | 0.4895 | 0.492 | 0.4951 | 0.495 | 0.4896 | 0.4962 | 0.4802 | 0.491 |
| 6 | 0.492 | 0.4956 | 0.4943 | 0.4916 | 0.4864 | 0.4861 | 0.4943 | 0.4961 | 0.4966 | 0.4893 | 0.499 | 0.4908 | 0.488 | 0.4988 | 0.4849 | 0.4978 |
| 7 | 0.4984 | 0.4869 | 0.4891 | 0.4956 | 0.4911 | 0.4893 | 0.5012 | 0.4926 | 0.4958 | 0.4918 | 0.4986 | 0.4962 | 0.4888 | 0.4968 | 0.4867 | 0.4992 |
| HMCC | AES | DES |
|---|---|---|
| 7.9438 | 7.9302 | 7.94 |
| 7.9236 | 7.9345 | 7.9129 |
| 7.9662 | 7.966 | 7.962 |
| 7.8762 | 7.8831 | 7.8726 |
| 7.9667 | 7.9685 | 7.9613 |
| 7.952 | 7.9594 | 7.9533 |
| 7.9766 | 7.9748 | 7.971 |
| NPCR (%) | UACI (%) | ||||
|---|---|---|---|---|---|
| HMCC | AES | DES | HMCC | AES | DES |
| 100 | 100 | 57.0312 | 27.549 | 27.6471 | 0.2237 |
| 100 | 100 | 46.875 | 32.549 | 43.6029 | 0.1838 |
| 100 | 100 | 51.5625 | 27.402 | 32.0588 | 0.2022 |
| 93.75 | 100 | 50 | 23.0147 | 44.951 | 0.1961 |
| 100 | 100 | 51.5625 | 30.4412 | 32.3284 | 0.2022 |
| 100 | 100 | 51.5625 | 23.7745 | 24.9755 | 0.2022 |
| 100 | 100 | 57.0312 | 38.7255 | 32.8431 | 0.2237 |
| 100 | 93.75 | 48.4375 | 34.5343 | 26.7647 | 0.19 |
| 100 | 100 | 27.1569 | 42.1814 | ||
| 100 | 100 | 38.5784 | 31.9118 | ||
| 100 | 100 | 36.4951 | 30.8088 | ||
| 100 | 100 | 24.9755 | 40.3922 | ||
| 100 | 93.75 | 26.8382 | 28.0637 | ||
| 100 | 100 | 26.8627 | 32.7206 | ||
| 100 | 100 | 26.1029 | 26.9608 | ||
| 100 | 100 | 31.3725 | 34.5343 |
| CIPHER | MEAN | STD | CV |
|---|---|---|---|
| HMCC | 0.498977 | 0.004795 | 0.009609 |
| AES | 0.499663 | 0.00397 | 0.007945 |
| DES | 0.438242 | 0.005367 | 0.012248 |
| CIPHER | MEAN | STD | CV |
|---|---|---|---|
| MCC | 0.493714 | 0.005331 | 0.010799 |
| AES | 0.500483 | 0.004301 | 0.008594 |
| DES | 0.499297 | 0.00602 | 0.012056 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abikoye, O.C.; Oladipupo, E.T.; Imoize, A.L.; Awotunde, J.B.; Lee, C.-C.; Li, C.-T. Securing Critical User Information over the Internet of Medical Things Platforms Using a Hybrid Cryptography Scheme. Future Internet 2023, 15, 99. https://doi.org/10.3390/fi15030099
Abikoye OC, Oladipupo ET, Imoize AL, Awotunde JB, Lee C-C, Li C-T. Securing Critical User Information over the Internet of Medical Things Platforms Using a Hybrid Cryptography Scheme. Future Internet. 2023; 15(3):99. https://doi.org/10.3390/fi15030099
Chicago/Turabian StyleAbikoye, Oluwakemi Christiana, Esau Taiwo Oladipupo, Agbotiname Lucky Imoize, Joseph Bamidele Awotunde, Cheng-Chi Lee, and Chun-Ta Li. 2023. "Securing Critical User Information over the Internet of Medical Things Platforms Using a Hybrid Cryptography Scheme" Future Internet 15, no. 3: 99. https://doi.org/10.3390/fi15030099
APA StyleAbikoye, O. C., Oladipupo, E. T., Imoize, A. L., Awotunde, J. B., Lee, C.-C., & Li, C.-T. (2023). Securing Critical User Information over the Internet of Medical Things Platforms Using a Hybrid Cryptography Scheme. Future Internet, 15(3), 99. https://doi.org/10.3390/fi15030099










