A Multi-Agent Approach to Binary Classification Using Swarm Intelligence
Abstract
1. Introduction
2. Materials and Methods
2.1. System Design
2.1.1. Interaction Period
2.1.2. Swarm Aggregation
- Very High Confidence: All presenting agents agree on a prediction class immediately following fitness proportionate selection,
- High Confidence: of presenting agents agree on a prediction class within 100 iterations of the swarming process,
- Medium Confidence: of presenting agents agree on a prediction class after 100–150 additional iterations of the swarming process,
- Low Confidence: Weighted vote of presenters and watchers if above thresholds are not met.
2.1.3. Additional Features
2.1.4. Meta-Swarm
2.1.5. System Distributability
2.2. Datasets
2.2.1. Breast Cancer Metastasis Status
- Cellular mean area
- Cellular mean circularity
- Cellular mean eccentricity
- Cellular mean intensity
- Standard area
- Standard circularity
- Standard eccentricity
- Standard intensity
| Feature | % | |
|---|---|---|
| Age | ||
| ≤45 | 103 | 21.3 |
| >45 | 380 | 78.7 |
| PT Max size (mm) | ||
| ≥200 | 5 | 1.0 |
| 100–199 | 15 | 3.1 |
| 50–99 | 51 | 10.6 |
| 25–49 | 125 | 25.9 |
| 0–24 | 271 | 56.1 |
| unknown | 16 | 3.3 |
| Angio Lymphatic Invasion | ||
| Absent | 127 | 26.3 |
| Present | 200 | 41.4 |
| Unknown | 156 | 32.3 |
| pT Stage | ||
| Unknown | 36 | 7.5 |
| pT1 | 210 | 43.5 |
| pT2 | 173 | 35.9 |
| pT3/pT4 | 64 | 13.3 |
| Histologic Grade | ||
| Unknown | 33 | 6.8 |
| 1 | 53 | 11.0 |
| 2 | 164 | 34.0 |
| 3 | 233 | 48.2 |
| Tubule Formation | ||
| Unknown | 30 | 6.2 |
| 1 (>75%) | 13 | 2.7 |
| 2 (10–75%) | 98 | 20.3 |
| 3 (<10%) | 342 | 70.8 |
| Nuclear Grade | ||
| Unknown | 29 | 6.0 |
| 1 | 20 | 4.1 |
| 2 | 151 | 31.3 |
| 3 | 283 | 58.6 |
| Lobular Extension | ||
| Unknown | 202 | 41.8 |
| Absent | 147 | 30.4 |
| Present | 134 | 27.7 |
| Pagetoid Spread | ||
| Unknown | 213 | 44.1 |
| Absent | 177 | 36.6 |
| Present | 93 | 19.3 |
| Perineureal Invasion | ||
| Unknown | 267 | 55.3 |
| Absent | 186 | 38.5 |
| Present | 30 | 6.2 |
| Calcifications | ||
| Unknown | 115 | 23.8 |
| Absent | 126 | 26.1 |
| Present | 176 | 36.4 |
| Present w/ DCIS | 66 | 13.7 |
| ER Status | ||
| Unknown | 51 | 10.6 |
| Negative | 155 | 32.1 |
| Positive (>10%) | 277 | 57.3 |
| PR Status | ||
| Unknown | 54 | 11.2 |
| Negative | 201 | 41.6 |
| Positive (>10%) | 228 | 47.2 |
| P53 Status | ||
| Unknown | 81 | 16.8 |
| Negative | 255 | 52.8 |
| Positive (>5%) | 147 | 30.4 |
| Ki67 Status | ||
| Unknown | 56 | 11.6 |
| Negative | 114 | 23.6 |
| Positive (>14%) | 313 | 64.8 |
| Her2 Score | ||
| Unknown | 83 | 17.2 |
| 0 | 119 | 24.6 |
| 1 | 169 | 35.0 |
| 2 | 54 | 11.2 |
| 3 | 58 | 12.0 |
2.2.2. Hollywood Movie
- Cast, top 5 listed
- Crew, top 5 listed
- Production company
- Director
| Features | Description |
|---|---|
| budget | given to all agents, reported budget for movie |
| tmdb_popularity | dynamic variable from TMDb API attempting to represent interest in movie |
| revenue | used for sanity checks, reported revenue |
| runtime | unreliable metric for success without including genre information |
| tmdb_vote_average | average score from TMDb, can be combined with ML average |
| tmdb_vote_count | total votes for a movie from TMDb, can be combined with ML count |
| ml_vote_average | average score from ML, can be combined with TMDb average |
| ml_vote_count | total votes for a movie from ML, can be combined with TMDb count |
| ml_tmdb_genres | combined genre information from TMDb and ML; first 2 listed genres used |
| vote_average | combined tmdb_vote_average and ml_vote_average |
| vote_count | combined tmdb_vote_count and ml_vote_count |
2.2.3. Airline Satisfaction
2.2.4. Sports Betting
3. Results
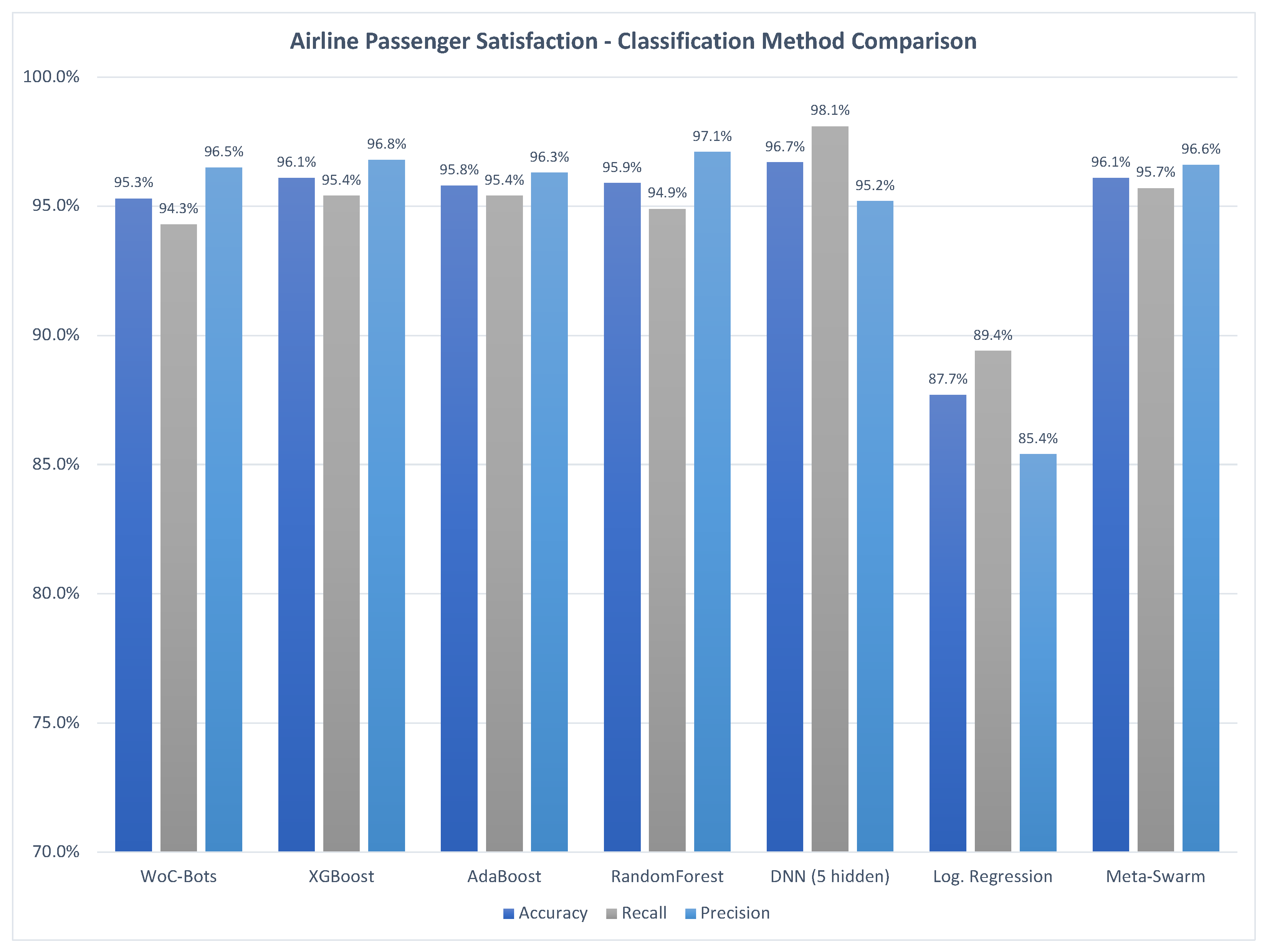
3.1. Classification Method Comparison
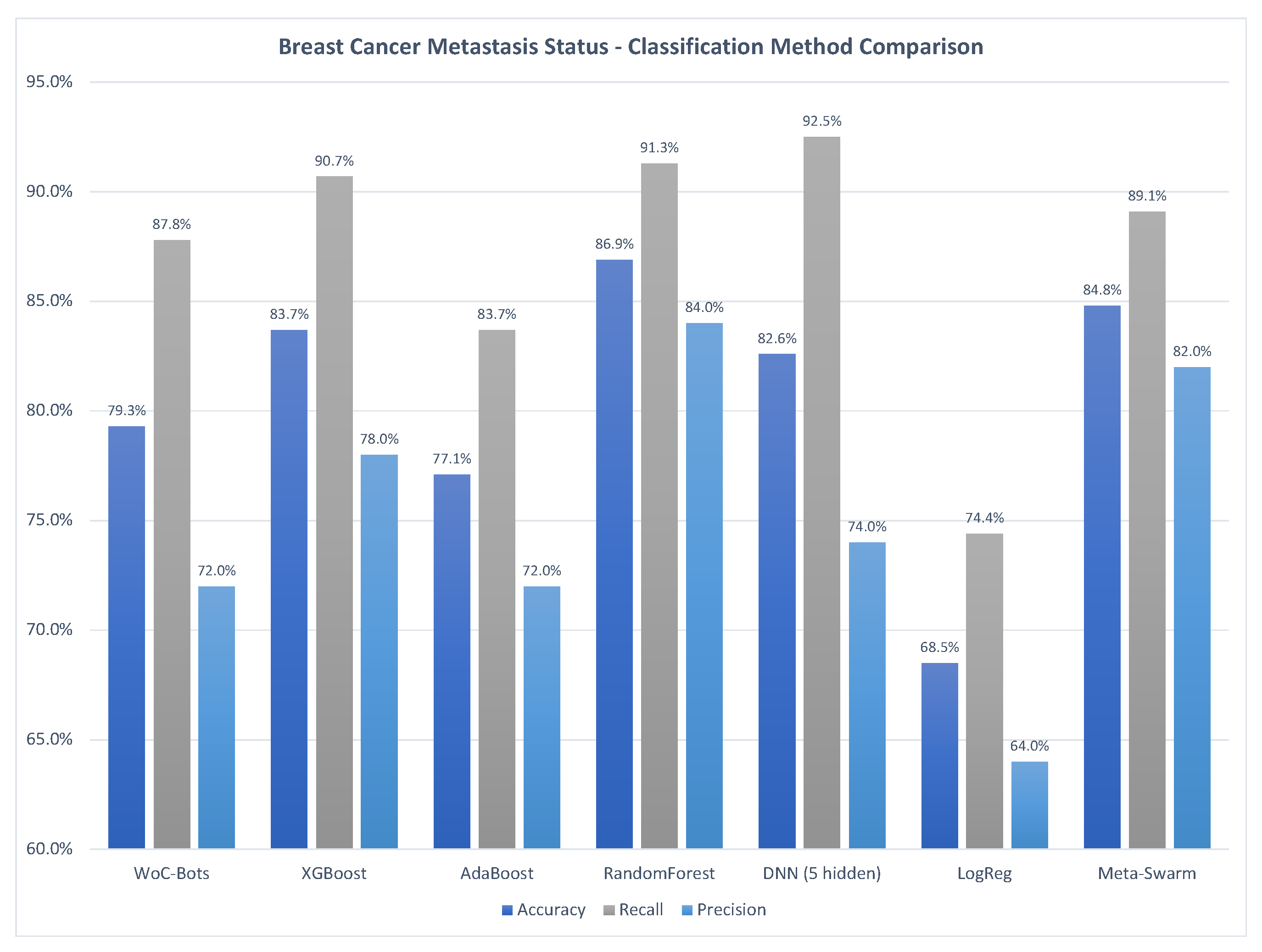
3.1.1. Breast Cancer Metastasis
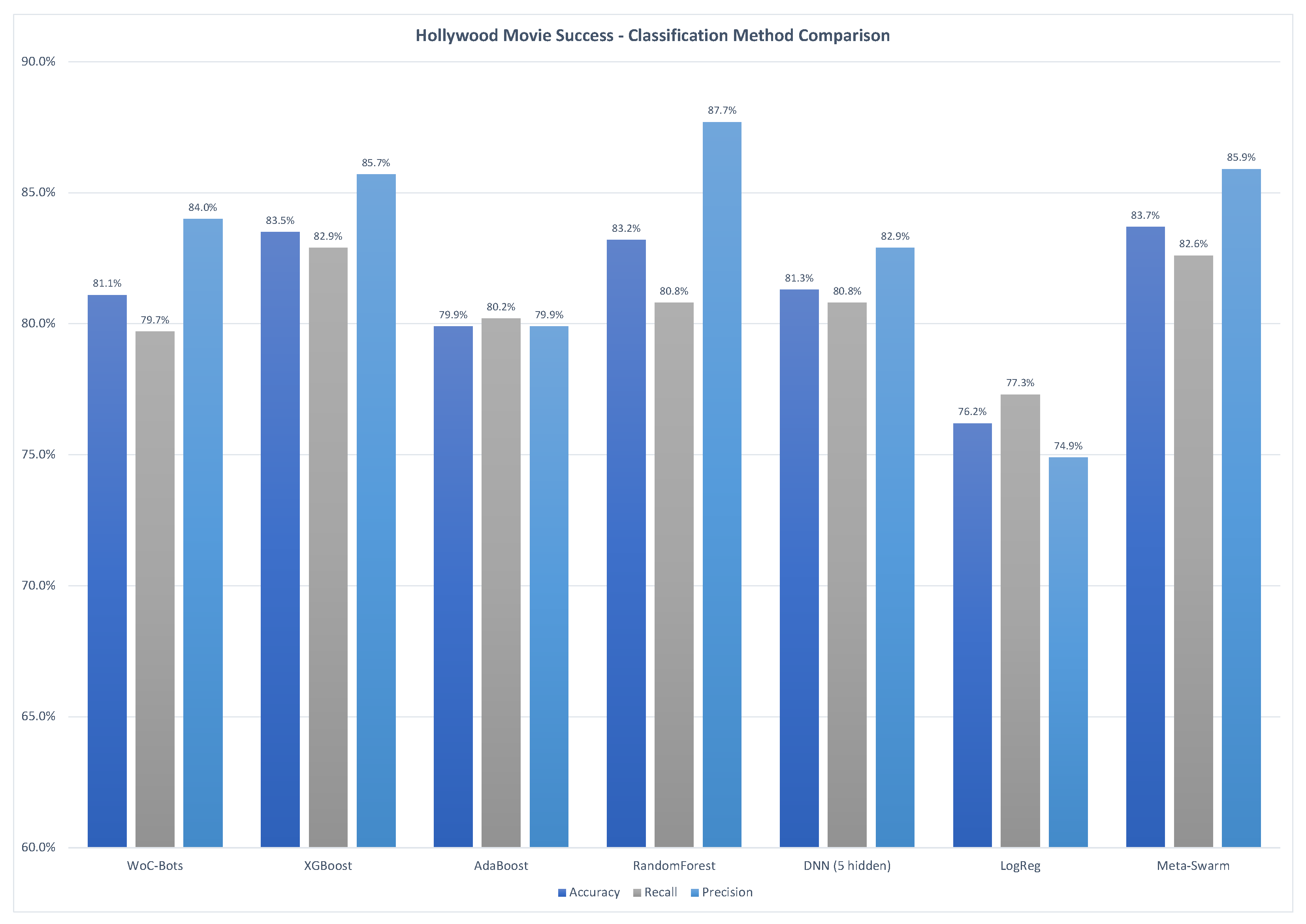
3.1.2. Hollywood Movie Success
3.1.3. Airline Passenger Satisfaction
3.2. Additional Features
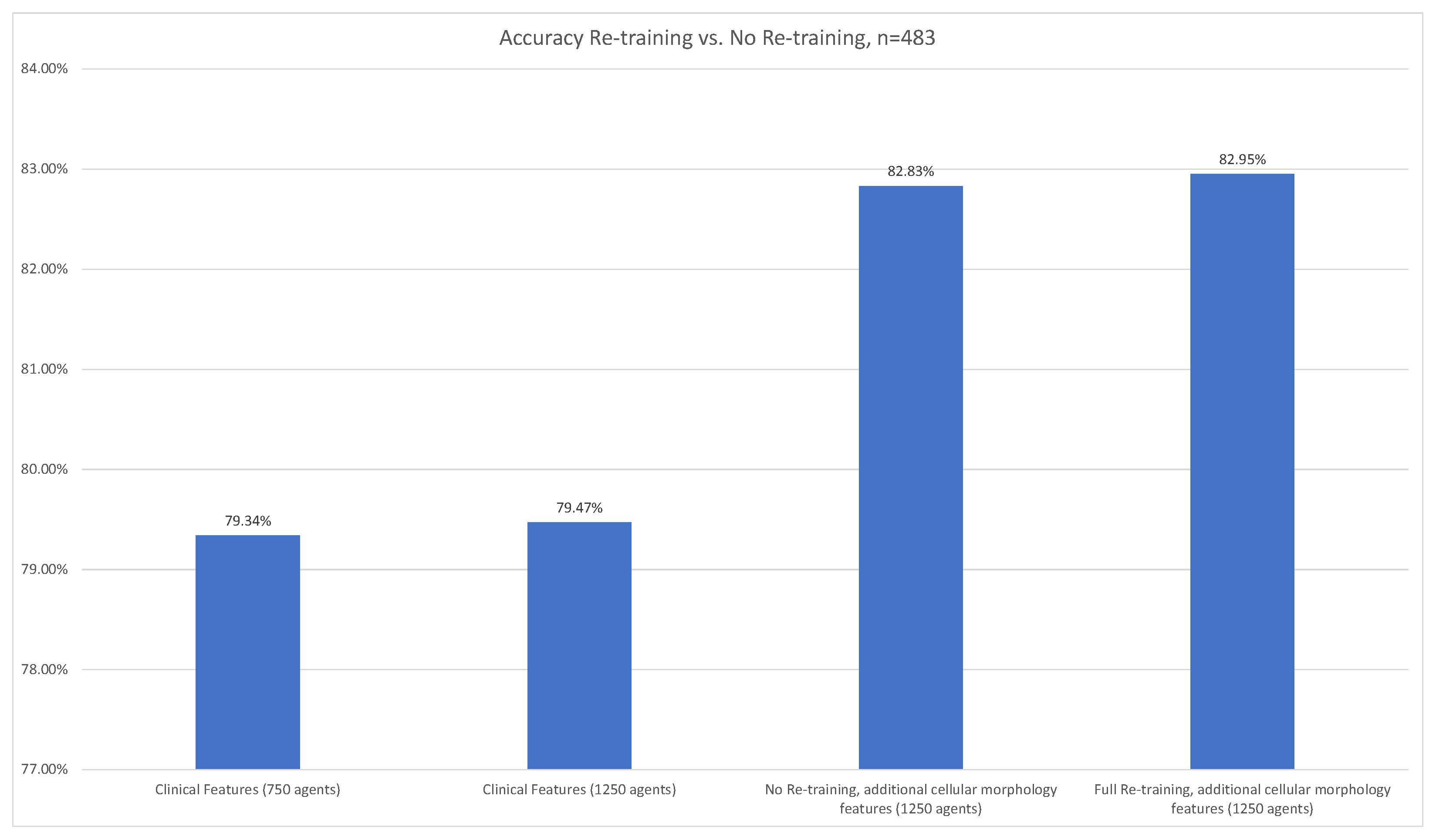
3.2.1. Breast Cancer Metastasis
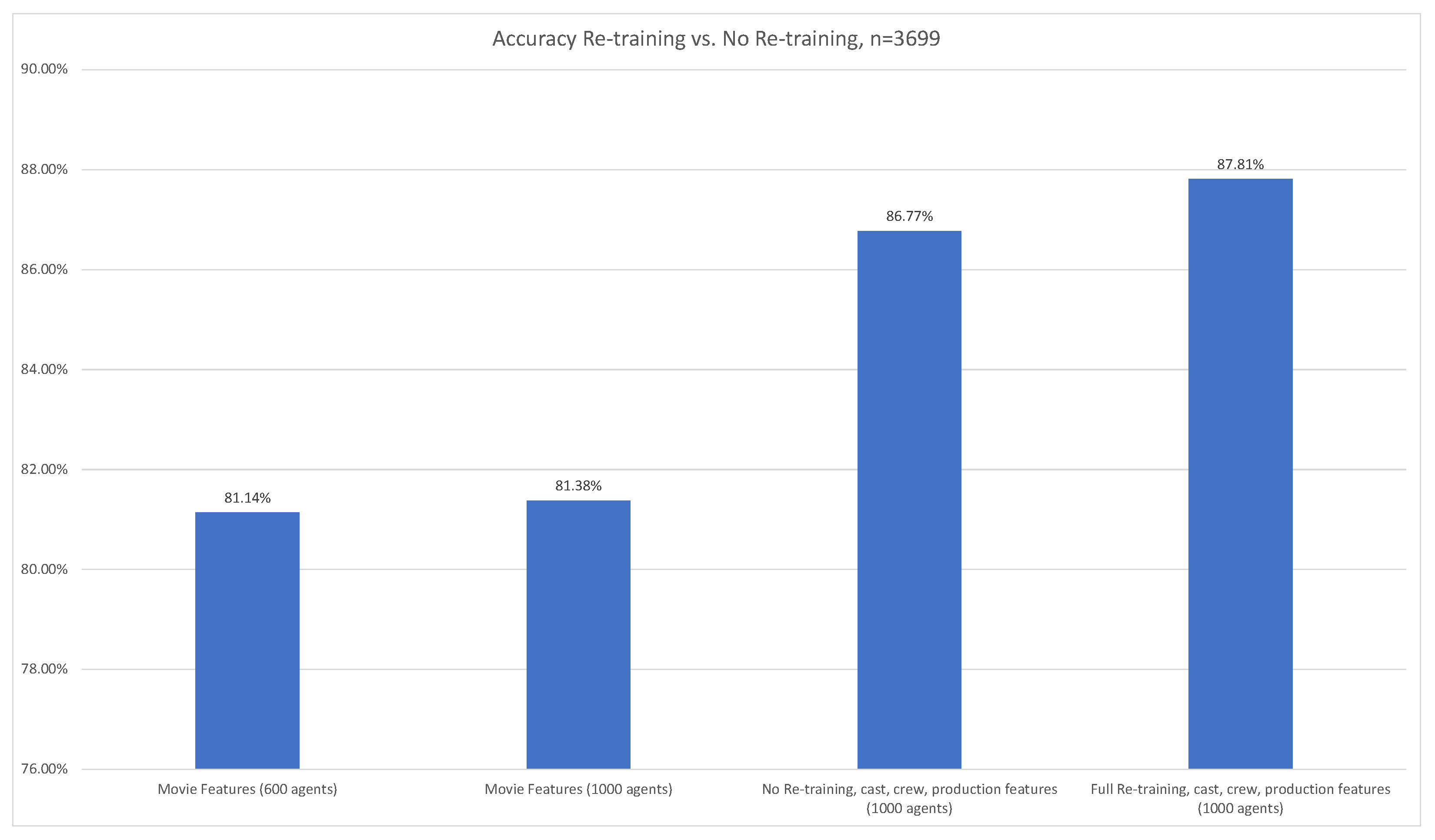
3.2.2. Hollywood Movie Success
3.3. System Distributability
- CPU: AMD Opteron 6376 (Released November 2012); four virtual CPU (vCPU) cores per virtual machine
- RAM: 12 GB DDR3 per virtual machine
- Ceph-based network storage,
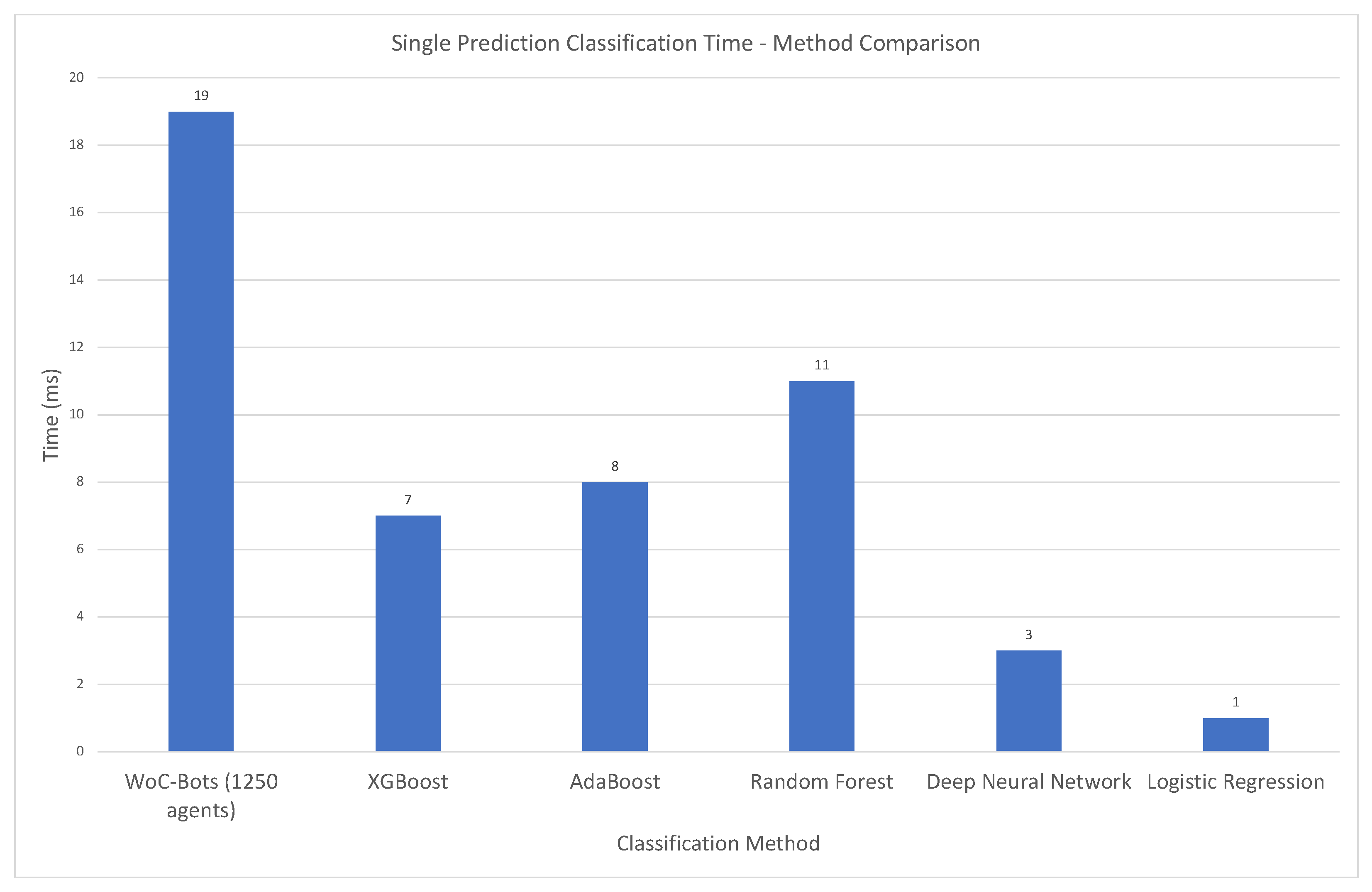
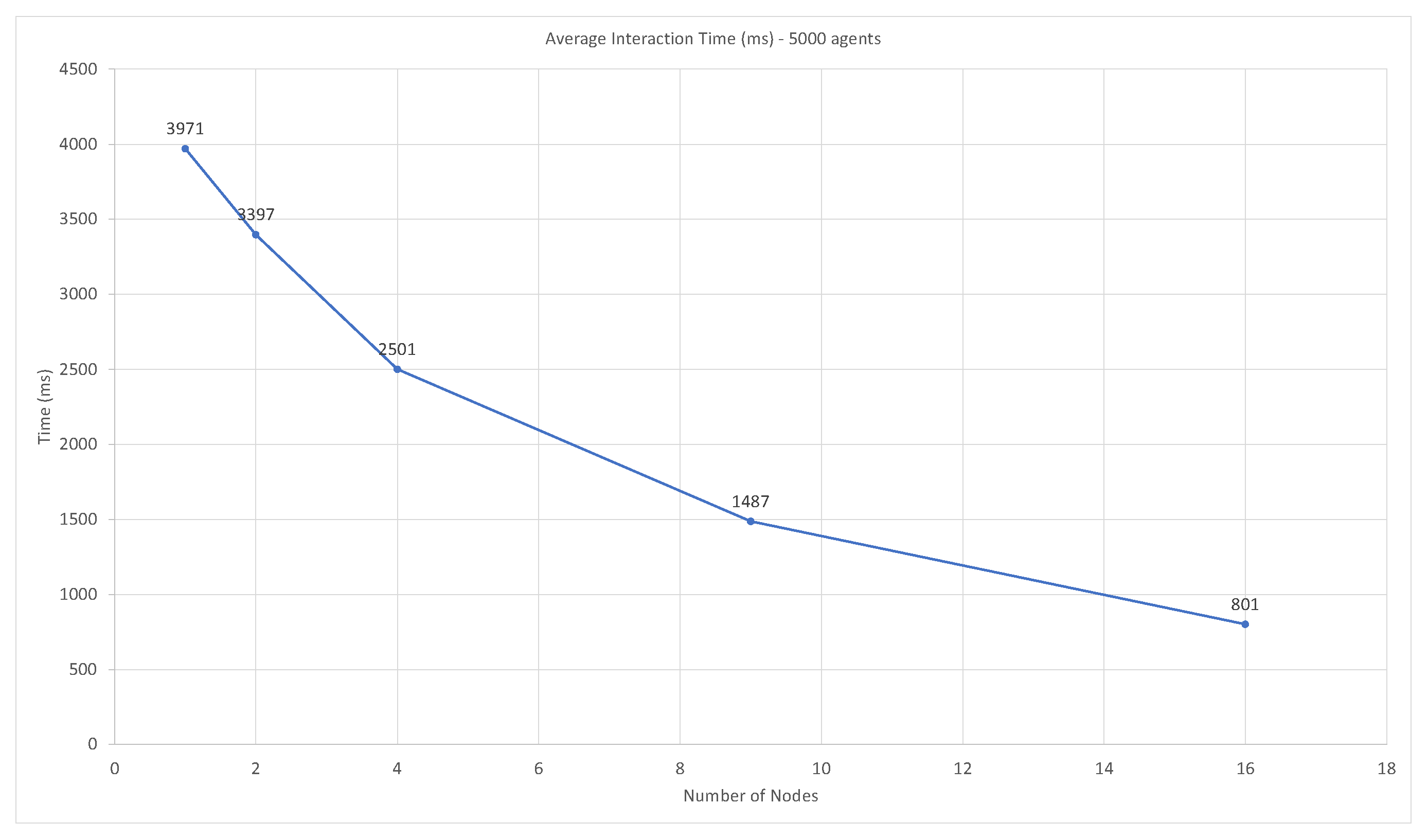
3.3.1. Runtime Performance
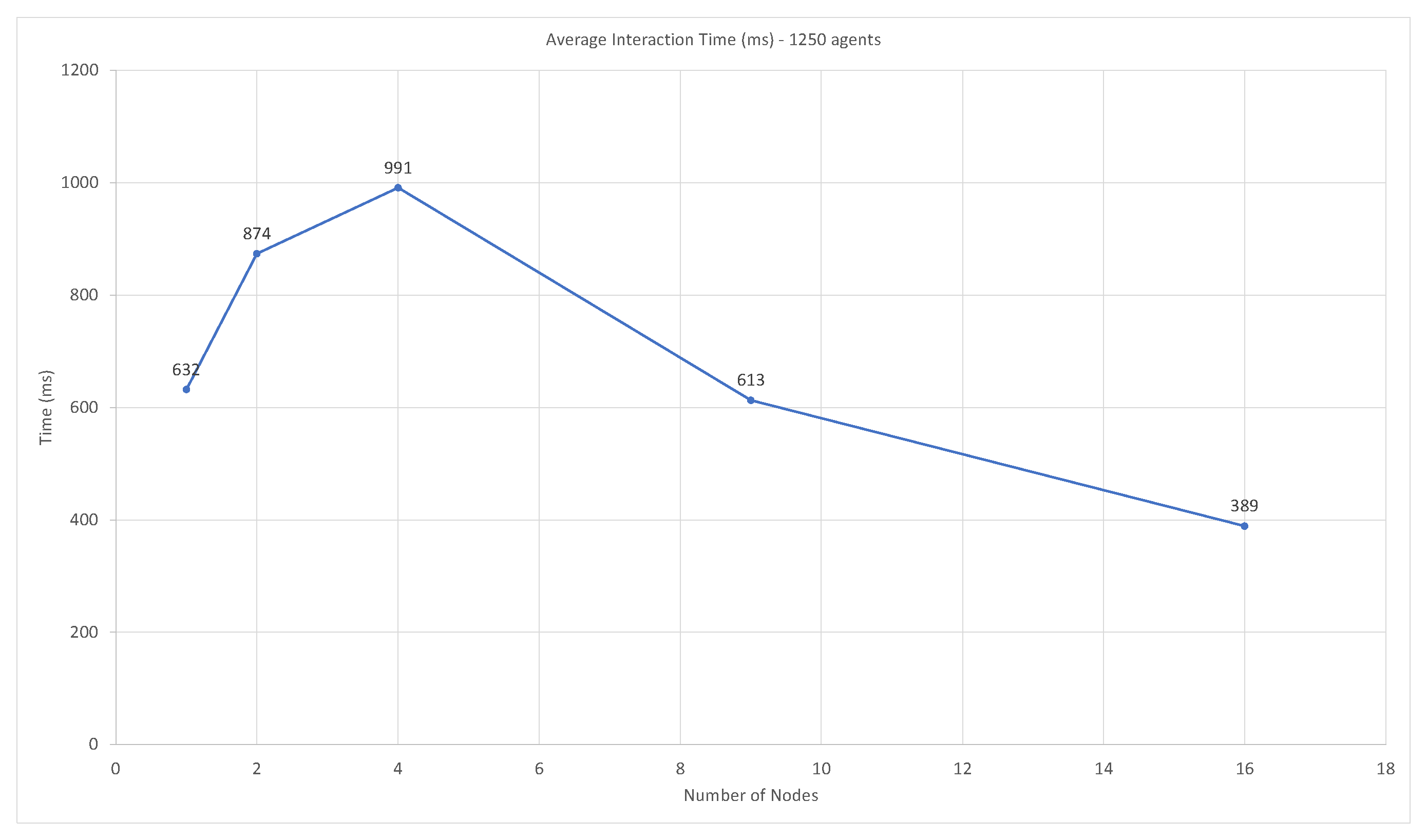
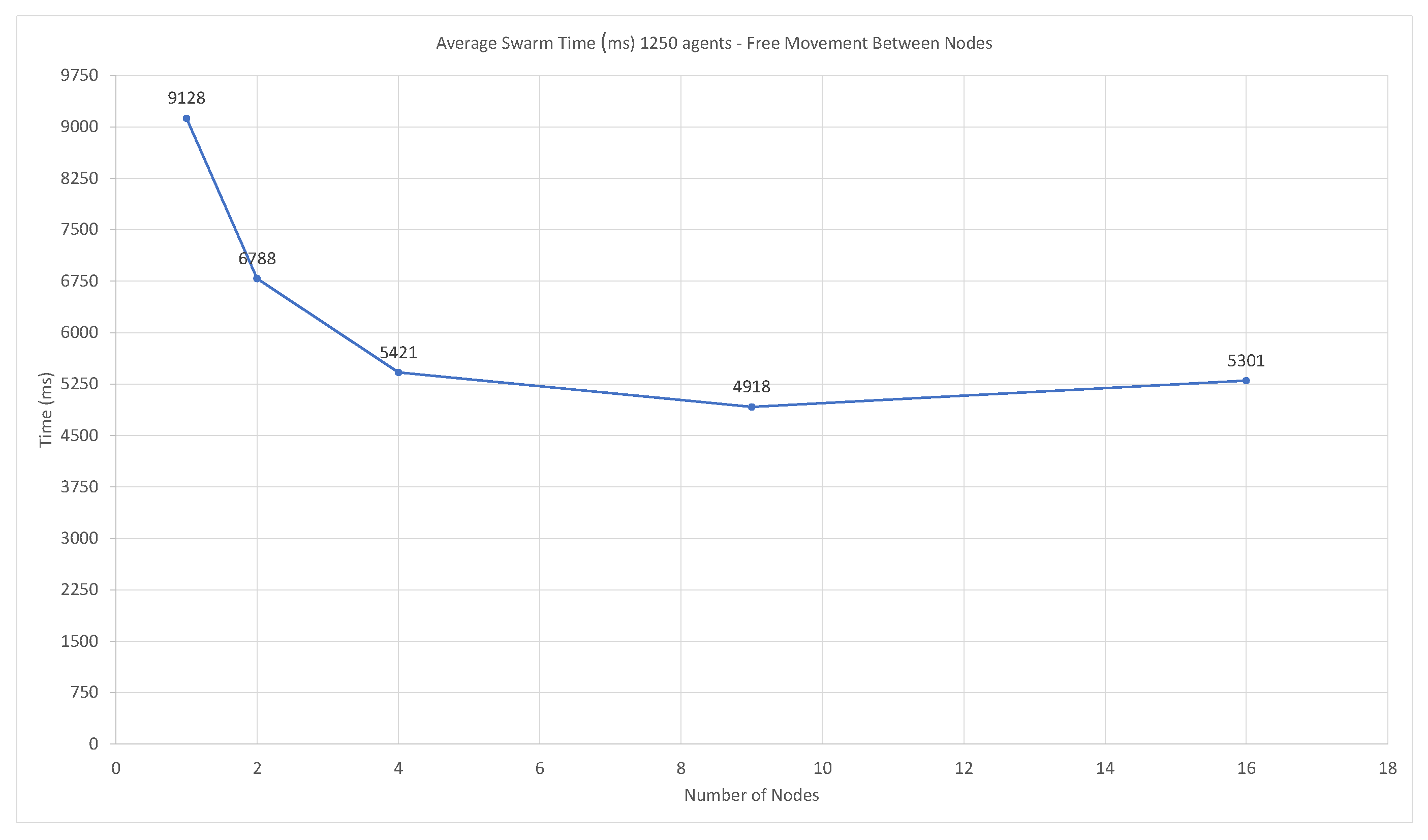
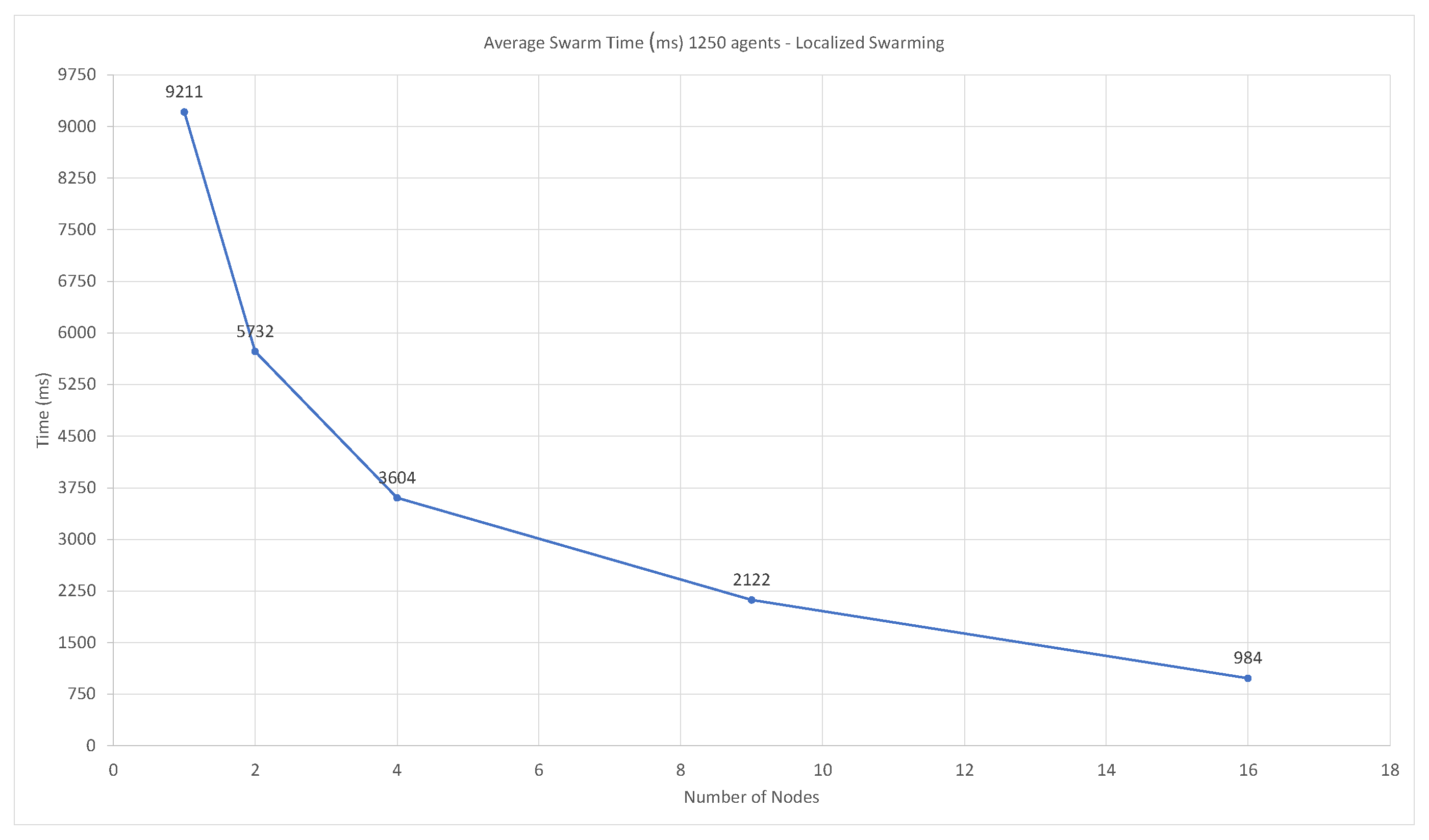
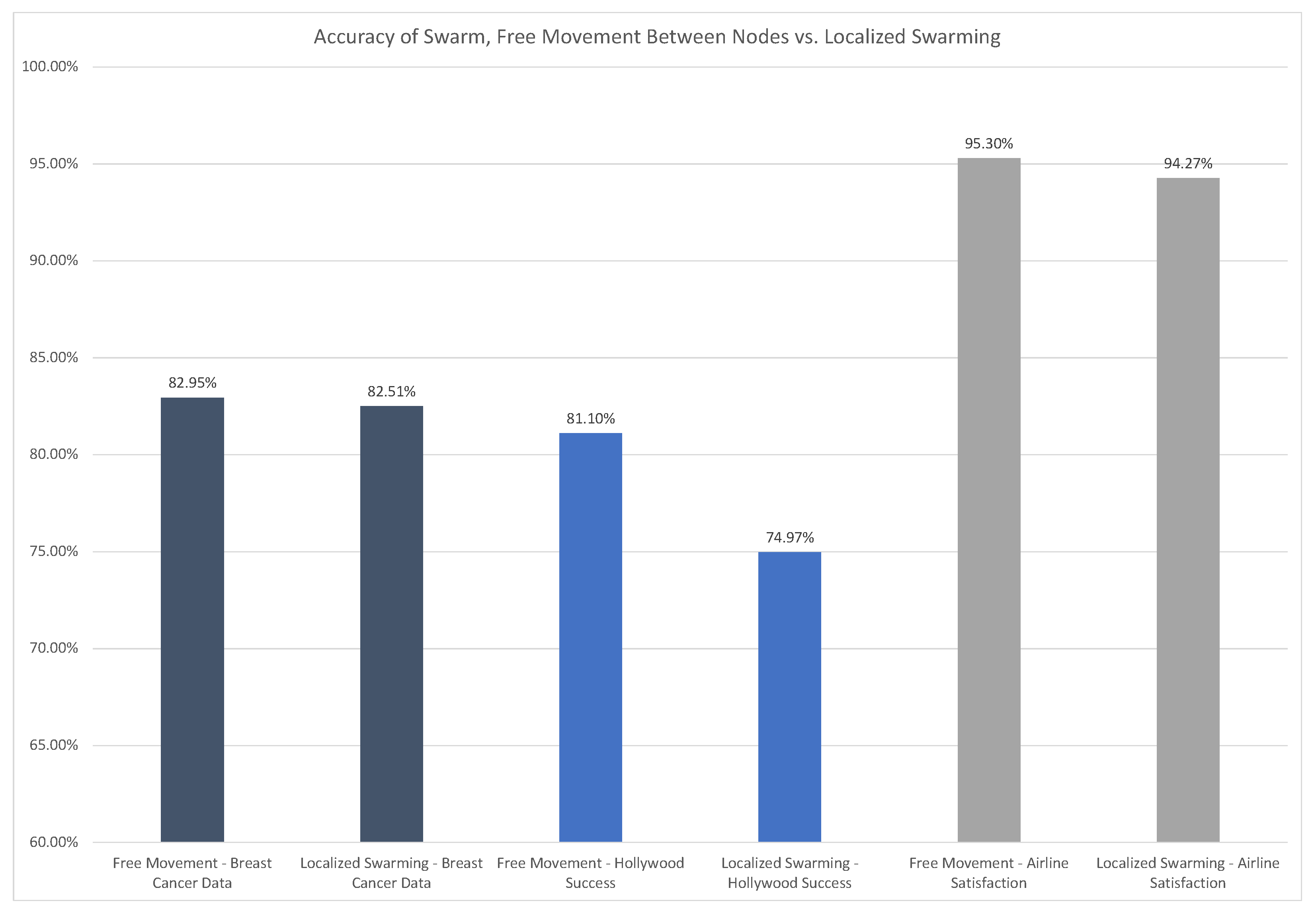
3.3.2. Swarm Performance—Timing and Accuracy
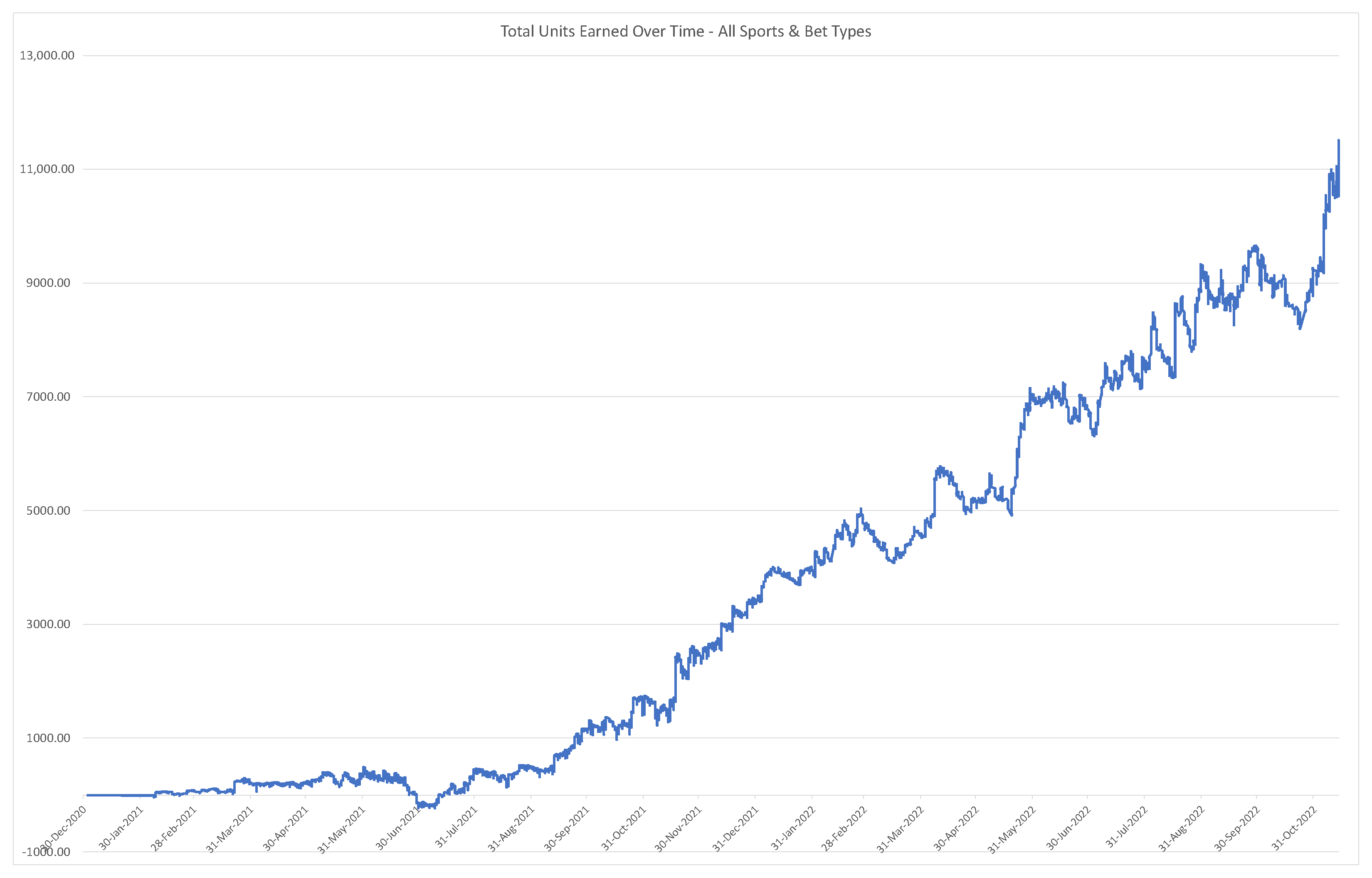
3.4. Sports Betting
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| WoC | Wisdom of Crowd |
| MLP | Multi-layer Perceptron |
| ANN | Artificial Neural Network |
| DNN | Deep Neural Network |
| CNN | Convolutional Neural Network |
| RNN | Recurrent Neural Network |
| PM | Prediction Market |
| API | Application Programming Interface |
| DL4J | DeepLearning4j |
| JVM | Java Virtual Machine |
| UWM | Unweighted Mean Model |
| WVM | Weighted Voter Model |
| TMDb | The Movie Database |
| NCAA | National Collegiate Athletic Association |
| FBS | Football Bowl Subdivision |
| NFL | National Football League |
| NBA | National Basketball Association |
| NHL | National Hockey League |
| MLB | Major League Baseball |
| MLS | Major League Soccer |
| ROI | Return on Investment |
References
- Zhang, C.; Liu, C.; Zhang, X.; Almpanidis, G. An up-to-date comparison of state-of-the-art classification algorithms. Expert Syst. Appl. 2017, 82, 128–150. [Google Scholar] [CrossRef]
- Hashemi, M. Enlarging smaller images before inputting into convolutional neural network: Zero-padding vs. interpolation. J. Big Data 2019, 6, 1–13. [Google Scholar] [CrossRef]
- Kim, E.; Cho, S.; Lee, B.; Cho, M. Fault detection and diagnosis using self-attentive convolutional neural networks for variable-length sensor data in semiconductor manufacturing. IEEE Trans. Semicond. Manuf. 2019, 32, 302–309. [Google Scholar] [CrossRef]
- Naul, B.; Bloom, J.S.; Pérez, F.; van der Walt, S. A recurrent neural network for classification of unevenly sampled variable stars. Nat. Astron. 2018, 2, 151–155. [Google Scholar] [CrossRef]
- Torrey, L.; Shavlik, J. Transfer learning. In Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques; IGI Global: Hershey, PA, USA, 2010; pp. 242–264. [Google Scholar]
- Olivas, E.S.; Guerrero, J.D.M.; Martinez-Sober, M.; Magdalena-Benedito, J.R.; Serrano, L. Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques: Algorithms, Methods, and Techniques; IGI Global: Hershey, PA, USA, 2009. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? arXiv 2014, arXiv:1411.1792. [Google Scholar]
- Grimes, S.; Zarella, M.D.; Garcia, F.U.; Breen, D.E. An agent-based approach to predicting lymph node metastasis status in breast cancer. In Proceedings of the 2021 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Houston, TX, USA, 9–12 December 2021; pp. 1315–1319. [Google Scholar]
- Yi, S.K.M.; Steyvers, M.; Lee, M.D.; Dry, M.J. The wisdom of the crowd in combinatorial problems. Cogn. Sci. 2012, 36, 452–470. [Google Scholar] [CrossRef]
- Othman, A. Zero-intelligence agents in prediction markets. In Proceedings of the 7th International Joint Conference on Autonomous Agents and Multiagent Systems: Volume 2, Estoril, Portugal, 12–16 May 2008; pp. 879–886. [Google Scholar]
- Ostrom, E. The Difference: How the Power of Diversity Creates Better Groups, Firms, Schools, and Societies. By Scott E. Page. Princeton: Princeton University Press, 2007. 448p. 19.95 paper. Perspect. Politics 2008, 6, 828–829. [Google Scholar] [CrossRef]
- Hastie, R.; Kameda, T. The robust beauty of majority rules in group decisions. Psychol. Rev. 2005, 112, 494. [Google Scholar] [CrossRef]
- Valentini, G.; Hamann, H.; Dorigo, M. Self-organized collective decision making: The weighted voter model. In Proceedings of the International Conference on Autonomous Agents and Multi-Agent Systems, Paris, France, 5–9 May 2014; pp. 45–52. [Google Scholar]
- Grimes, S.; Breen, D.E. Woc-Bots: An Agent-Based Approach to Decision-Making. Appl. Sci. 2019, 9, 4653. [Google Scholar] [CrossRef]
- Team, D. Deeplearning4j: Open-source distributed deep learning for the JVM. Apache Softw. Found. Licens. 2018, 2. Available online: http://deeplearning4j.org/ (accessed on 27 June 2022).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: http://www.deeplearningbook.org (accessed on 10 October 2022).
- Du, Q.; Hong, H.; Wang, G.A.; Wang, P.; Fan, W. CrowdIQ: A New Opinion Aggregation Model. In Proceedings of the 50th Hawaii International Conference on System Sciences, Hilton Waikoloa Village, HI, USA, 4–7 January 2017. [Google Scholar]
- Rosenberg, L.; Pescetelli, N.; Willcox, G. Artificial Swarm Intelligence amplifies accuracy when predicting financial markets. In Proceedings of the IEEE 8th Annual Conference on Ubiquitous Computing, Electronics and Mobile Communication, New York City, NY, USA, 19–21 October 2017; pp. 58–62. [Google Scholar]
- Rosenberg, L. Artificial Swarm Intelligence, a Human-in-the-loop approach to AI. In Proceedings of the 13th AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Tereshko, V.; Loengarov, A. Collective decision making in honey-bee foraging dynamics. Comput. Inf. Syst. 2005, 9, 1. [Google Scholar]
- Von Frisch, K. The Dance Language and Orientation of Bees; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Beekman, M.; Ratnieks, F. Long-range foraging by the honey-bee, Apis mellifera L. Funct. Ecol. 2000, 14, 490–496. [Google Scholar] [CrossRef]
- Lipowski, A.; Lipowska, D. Roulette-wheel selection via stochastic acceptance. Phys. A Stat. Mech. Its Appl. 2012, 391, 2193–2196. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, D.; Sun, J.; Zou, G.; Li, W. Adaptive convolutional neural network and its application in face recognition. Neural Process. Lett. 2016, 43, 389–399. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K. Xgboost: Extreme gradient boosting. R Package Version 0.4-2 2015, 1, 1–4. [Google Scholar]
- Schapire, R.E. Explaining adaboost. In Empirical Inference; Springer: Berlin/Heidelberg, Germany, 2013; pp. 37–52. [Google Scholar]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Wright, R.E. Logistic regression. In Reading and Understanding Multivariate Statistics; APA Publishing: Washington, DC, USA, 1995; pp. 217–244. [Google Scholar]
- Van Zee, K.J.; Manasseh, D.M.E.; Bevilacqua, J.L.; Boolbol, S.K.; Fey, J.V.; Tan, L.K.; Borgen, P.I.; Cody, H.S.; Kattan, M.W. A nomogram for predicting the likelihood of additional nodal metastases in breast cancer patients with a positive sentinel node biopsy. Ann. Surg. Oncol. 2003, 10, 1140–1151. [Google Scholar] [CrossRef]
- Kohrt, H.E.; Olshen, R.A.; Bermas, H.R.; Goodson, W.H.; Wood, D.J.; Henry, S.; Rouse, R.V.; Bailey, L.; Philben, V.J.; Dirbas, F.M.; et al. New models and online calculator for predicting non-sentinel lymph node status in sentinel lymph node positive breast cancer patients. BMC Cancer 2008, 8, 66. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. arXiv 2017, arXiv:1706.02275. [Google Scholar]
| Variable | Description |
|---|---|
| current_prediction | Binary, class 0 or class 1. |
| trust_score | Updated during interaction based on agreement and performance. |
| features | A list of features used by the agent’s classifier. |
| prior_performance | Long-term history of agent performance, varied between 0.7 and 1.3 where 1.0 is average performance. |
| certainty | Initialized to MLP classifier performance, updated during interaction period. Represents how strongly the agent believes in the current prediction. |
| eval_accuracy | Initial classification accuracy. |
| eval_precision | Initial classification precision. |
| eval_recall | Initial classification recall. |
| confidence | Biased value based on accuracy, precision, and recall. |
| Features | Description |
|---|---|
| Gender | Passenger gender: male, female, other |
| Customer type | Loyal or disloyal |
| Age | Customer age |
| Type of travel | Personal or business |
| Seat class | First, business, eco+, eco |
| Flight distance | Distance of journey |
| In-flight WiFi satisfaction | 0 (N/A) 1–5 |
| Flight time convenience | Satisfied with departure/arrival time |
| Ease of online booking | 0 (N/A) 1–5 |
| Gate location satisfaction | 1–5 |
| Food/drink satisfaction | 1–5 |
| Online boarding satisfaction | 0 (N/A) 1–5 |
| Seat comfort | 1–5 |
| In-flight entertainment | 0 (N/A) 1-5 |
| On-board service satisfaction | 0 (N/A) 1–5 |
| Leg room satisfaction | 0 (N/A) 1-5 |
| Baggage handling satisfaction | 0 (N/A) 1–5 |
| Check-in service satisfaction | 1–5 |
| Cleanliness | 1–5 |
| Departure delay | in minutes |
| Arrival delay | in minutes |
| Interval | % of n | Accuracy (%) | |
|---|---|---|---|
| Very High Confidence | 3 | 0.62 | 100 |
| High Confidence | 154 | 31.9 | 93.1 |
| Medium Confidence | 224 | 46.4 | 82.3 |
| Low Confidence | 102 | 21.1 | 64.7 |
| Very High + High + Medium | 381 | 78.9 | 86.8 |
| Interval | % of n | Accuracy (%) | |
|---|---|---|---|
| Very High Confidence | 51 | 1.4 | 96.1 |
| High Confidence | 958 | 25.9 | 91.6 |
| Medium Confidence | 1261 | 34.1 | 84.5 |
| Low Confidence | 1428 | 38.6 | 77.3 |
| Very High + High + Medium | 2271 | 61.4 | 87.8 |
| Interval | 129,882 | % of n | Accuracy (%) |
|---|---|---|---|
| Very High Confidence | 19,797 | 15.24 | 95.7 |
| High Confidence | 92,125 | 70.93 | 96.2 |
| Medium Confidence | 9109 | 7.01 | 95.9 |
| Low Confidence | 8851 | 6.81 | 95.7 |
| Values | Spread Bets | Moneyline Bets |
|---|---|---|
| Units Risked | 8212 | 18,532 |
| Units Returned | 628.5 | 668 |
| ROI | 9.5% | 3.6% |
| Total Bets | 1161 | 3282 |
| Winning Bets | 572 | 1481 |
| Win Rate | 49.06% | 45.12% |
| Values | Spread Bets | Moneyline Bets |
|---|---|---|
| Units Risked | 48,159 | 80,408 |
| Units Returned | 4863.5 | 5364.5 |
| ROI | 10.1% | 6.7% |
| Total Bets | 2376 | 3225 |
| Winning Bets | 1174 | 1296 |
| Win Rate | 49.33% | 40.19% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grimes, S.; Breen, D.E. A Multi-Agent Approach to Binary Classification Using Swarm Intelligence. Future Internet 2023, 15, 36. https://doi.org/10.3390/fi15010036
Grimes S, Breen DE. A Multi-Agent Approach to Binary Classification Using Swarm Intelligence. Future Internet. 2023; 15(1):36. https://doi.org/10.3390/fi15010036
Chicago/Turabian StyleGrimes, Sean, and David E. Breen. 2023. "A Multi-Agent Approach to Binary Classification Using Swarm Intelligence" Future Internet 15, no. 1: 36. https://doi.org/10.3390/fi15010036
APA StyleGrimes, S., & Breen, D. E. (2023). A Multi-Agent Approach to Binary Classification Using Swarm Intelligence. Future Internet, 15(1), 36. https://doi.org/10.3390/fi15010036









