This section analyzes the algorithms mentioned above from a mathematical perspective, including the overall computation complexity of the algorithm, the computational pressure of a single node, and the average path delay of the algorithm.
3.1. Algorithm Complexity Analysis
Greedy algorithm: For the source node, it only needs to find the next jump node with the shortest path in each step until it reaches the target node. At most,
nodes are passed through from the source node to the target node, and the average expectations are
nodes. Every time the information arrives at one node to find the next node, N nodes need to be traversed to calculate the locally optimal path [
17].
Its computational complexity is:
Flooding and backtracking algorithm: Its computational complexity is:
In this formula,
is the number of satellite nodes to be traversed when the source node passes m forwarding satellites. It can be deduced that finding the routing path from the source node to the destination node takes
calculations. There are
paths to calculate here.
is a positive number tending to be infinitesimally small, which represents the backtracking part of the flooding algorithm. Only when more than one path with the same distance is founded during traversal, backtracking is performed to compare the number of nodes that pass through and select the path with fewer nodes. However, this situation is very rare and can almost be ignored [
18,
19].
Partition routing algorithm: For the source node, the destination node has a chance of
being in the same group and a chance of
being outside the group [
20].
For stars nodes within the same group, its computational complexity is:
For stars nodes outside the group, its computational complexity is:
Both partial flooding algorithms and greedy algorithms are used to calculate the path within the group.
refers to the overhead of the backtracking part of the flooding algorithm.
represents the overhead of the greedy algorithm. Compared with the huge calculation time cost of the flooding algorithm, the time cost of the greedy algorithm and backtracking can almost be ignored [
21].
Hence, the average computational complexity of the total algorithm is:
Balanced partition routing algorithm: In contrast to the partition routing algorithm, a balanced partition routing algorithm adds the process of dynamically calculating communication nodes between the groups.
So its computational complexity is:
The computational complexity of the balanced partition routing algorithm and flooding algorithm is compared below:
It is easy to derive from the above equation:
It can be proved that the balanced partition routing algorithm is much lower than the flooding algorithm in terms of algorithm complexity. A balanced partition routing algorithm adds the process of calculating communication nodes between groups dynamically. Therefore its algorithm complexity is greater than that of the partition routing algorithm.
In terms of the partition routing algorithm and the flooding and backtracking algorithm:
Therefore, the computation complexity of the partition routing algorithm is higher than the greedy algorithm. In conclusion, the flooding and backtracking algorithm has the highest computational complexity, followed by the balanced partition routing algorithm and the partition routing algorithm, and the greedy algorithm has the lowest computational complexity.
3.3. Algorithm Validity Analysis
It is assumed that the direct distance between any two star nodes satisfies .
It is easy to know that the flooding and backtracking algorithm compares all possible paths between two star nodes and finds the shortest path among them. If there is more than one shortest path, the path with the least number of inter-star nodes will be selected. Therefore, the flooding and backtracking algorithm is definitely optimal [
23].
For greedy algorithms, the average expected route path distance is:
is an undetermined parameter. For greedy algorithms, in principle, the larger is, the smaller its expected distance is. The average expected path distance is proportional to and inversely proportional to .
For the balanced partition routing algorithm:
Further, it can be concluded that:
The greater the value of N, the more likely the greedy algorithm is to be less efficient than the balanced partition routing algorithm. When the number of inter-star nodes is small, specific variance and average step size should be considered for specific analysis.
3.4. Simulation and Analysis
Firstly, the computational complexity of the above algorithm is simulated.
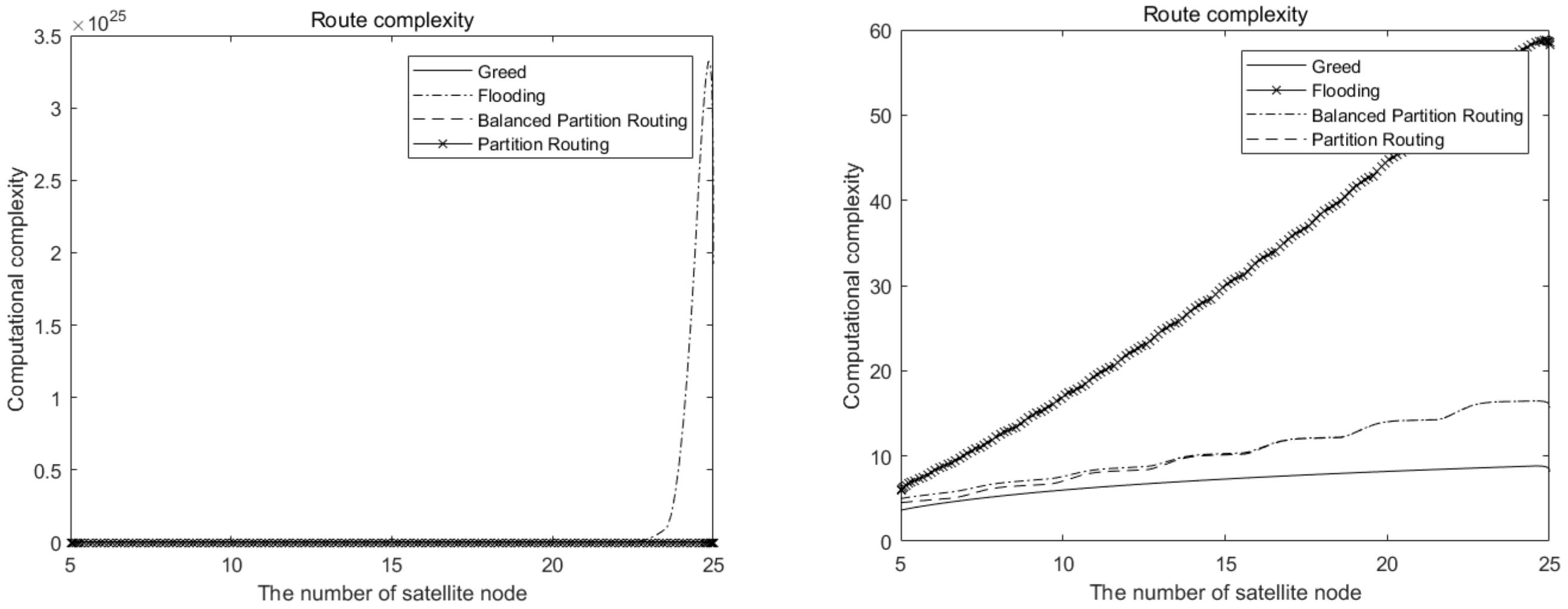
Figure 1 on the left is an actual simulation, and the data on the right are the logarithmic processing. As can be seen from the left figure, with the increase in the number of satellites, the computational complexity of the flooding and backtracking algorithm increases exponentially, while other algorithms increase slowly. From the figure on the right, in general, the flooding and backtracking algorithm has the highest computational complexity, followed by the two partition routing algorithms, and the greedy algorithm has the lowest computational complexity. When the number of inter-star nodes is not very large, the computational complexity of the balanced partition routing algorithm is slightly higher than that of an ordinary partition algorithm.
The computation force of a single star node under different algorithms is simulated:
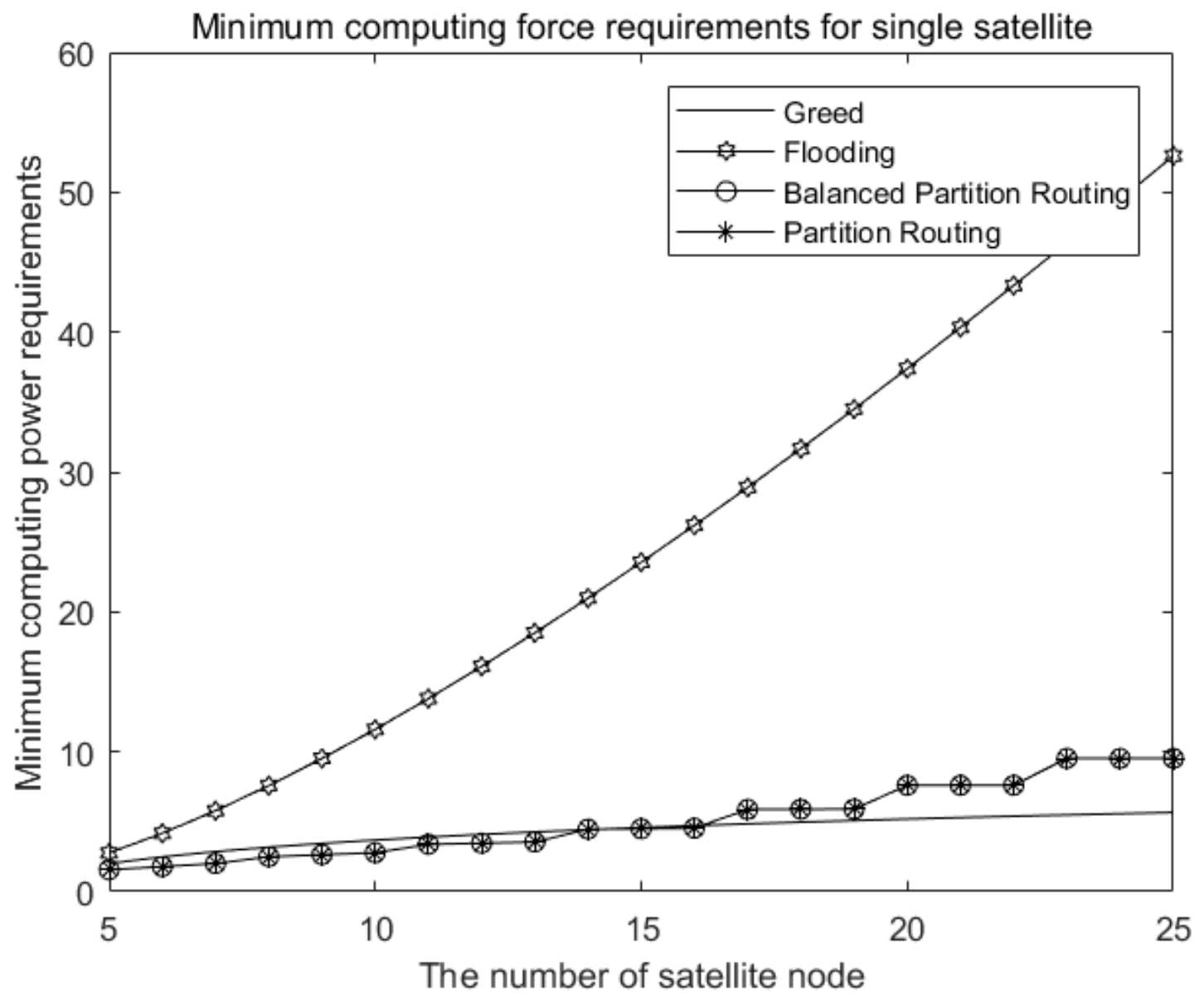
As can be seen from the analysis of
Figure 2, with the increase in the number of star nodes in the system, the requirement of the flooding and backtracking algorithm on the computing capacity of a single star node increases rapidly. However, the computing capacity of the two partition routing algorithms increases slowly for a single star node, even approaching the level of a greedy algorithm. This shows that a balanced partition routing algorithm can well distribute computing pressure to multiple star nodes, with stronger destruction resistance and better scalability.
Next, the efficiency of the above algorithms is simulated, and the inter-satellite node number is set to 15.
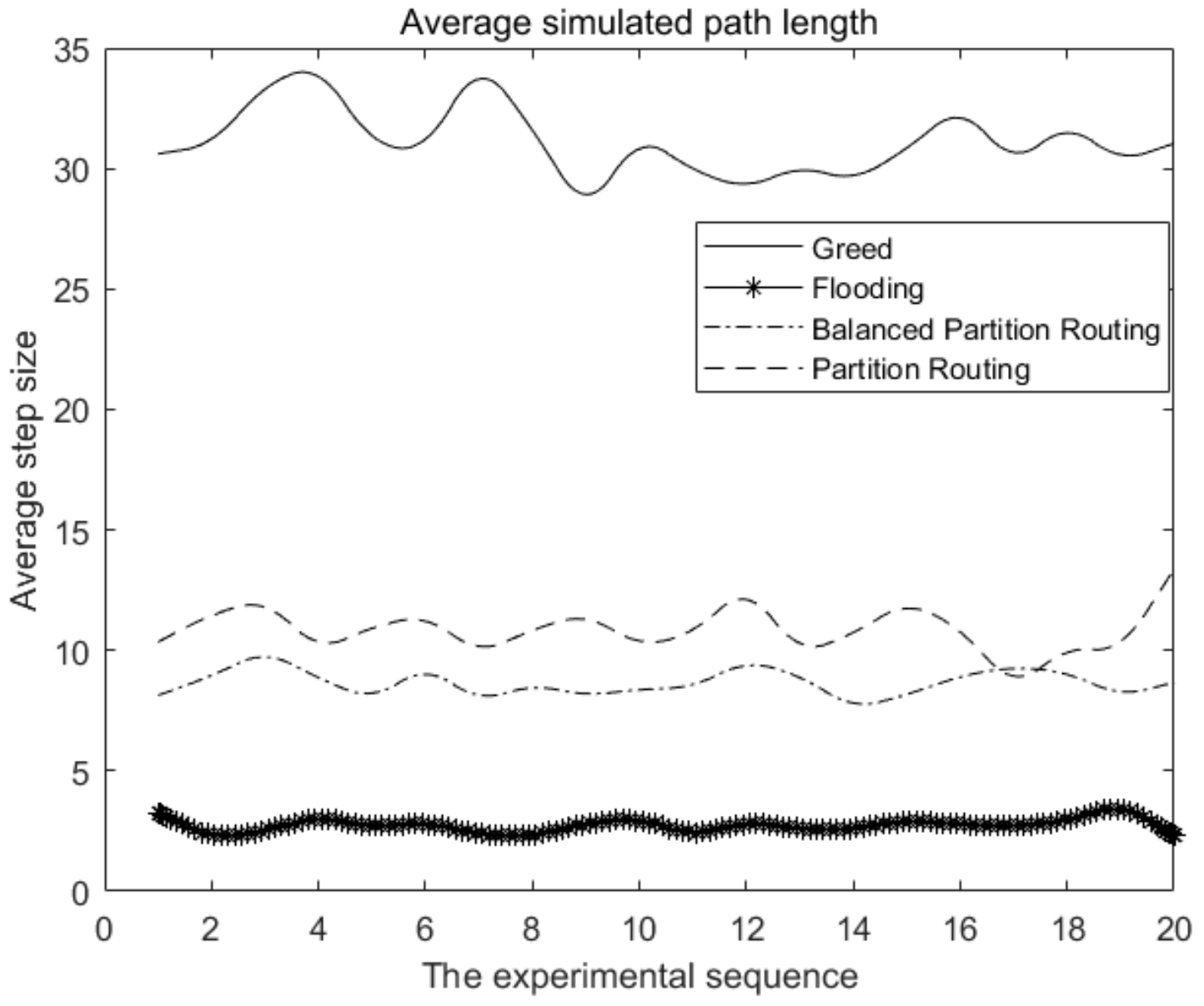
There were a total of 20 simulations. The average path delay of the greedy algorithm is the highest, and the variance of the average delay in each experiment is large. However, the efficiency of the flooding and backtracking algorithm is relatively stable, and the average delay calculated by this algorithm is significantly less than that of the two partition routing algorithms.
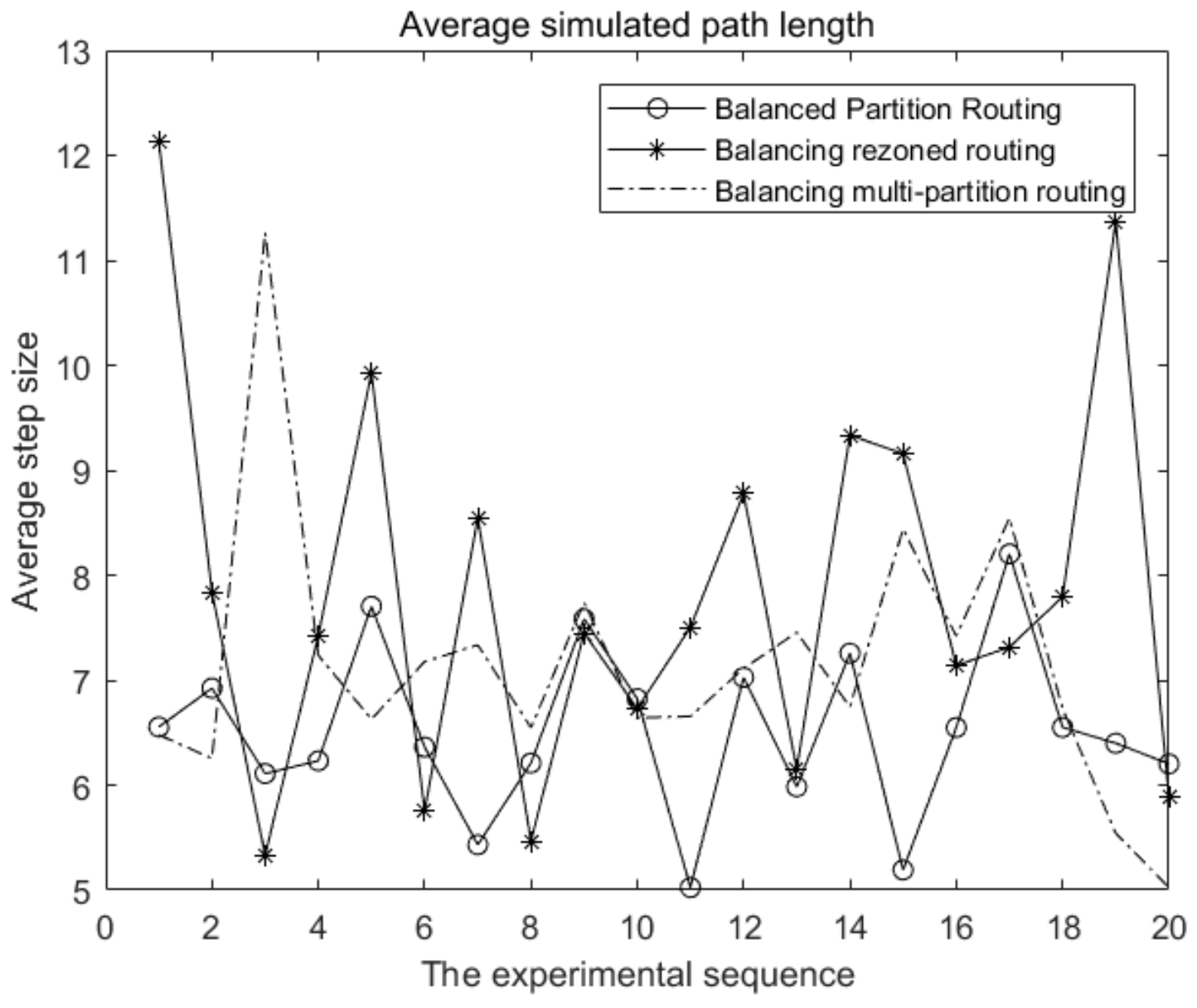
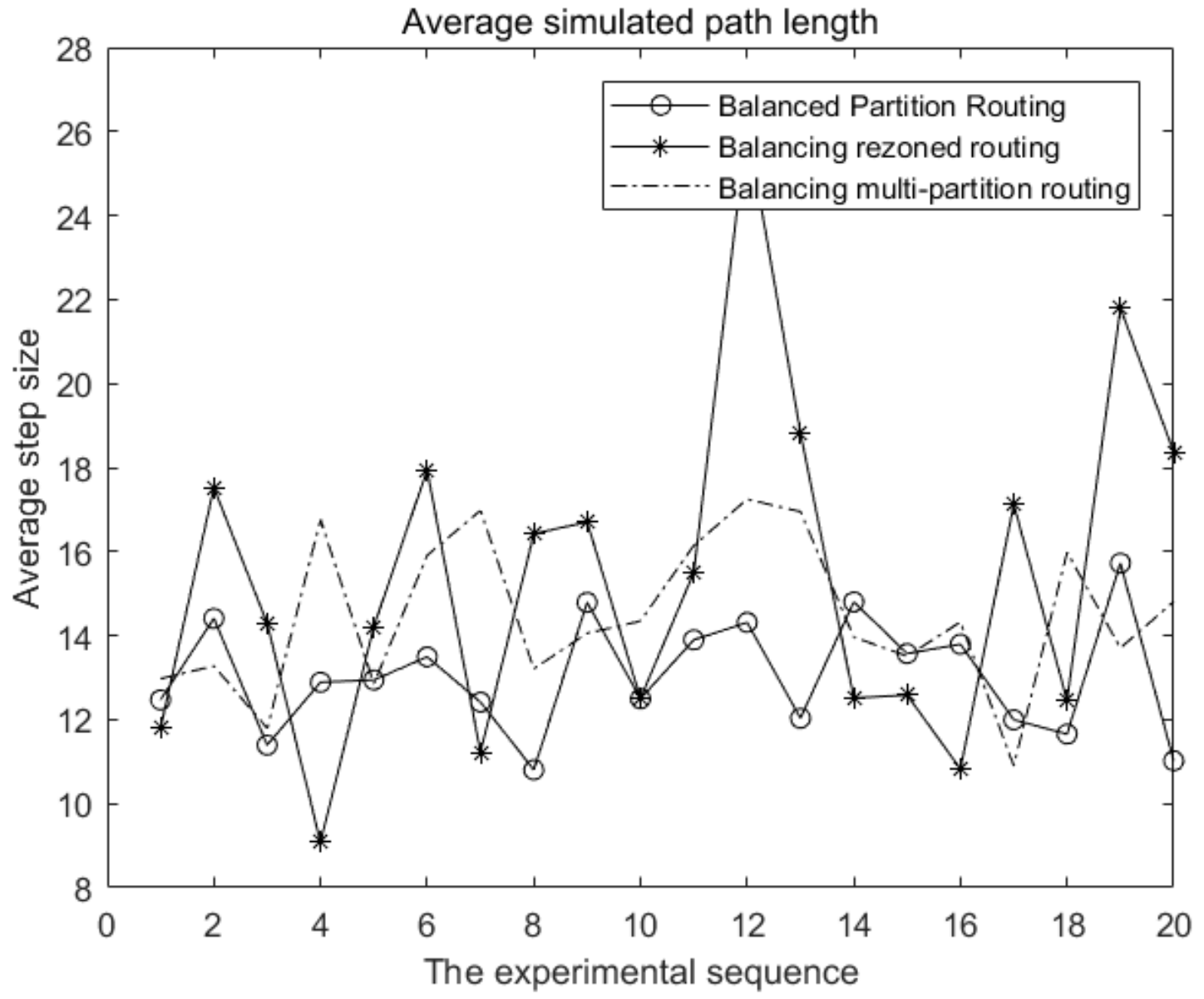
Figure 3 shows that the average route length of the balanced partition routing algorithm is shorter than that of the classical partition routing algorithm. In other words, the path calculated by the balanced partition algorithm is better than that of the classical partition routing algorithm.
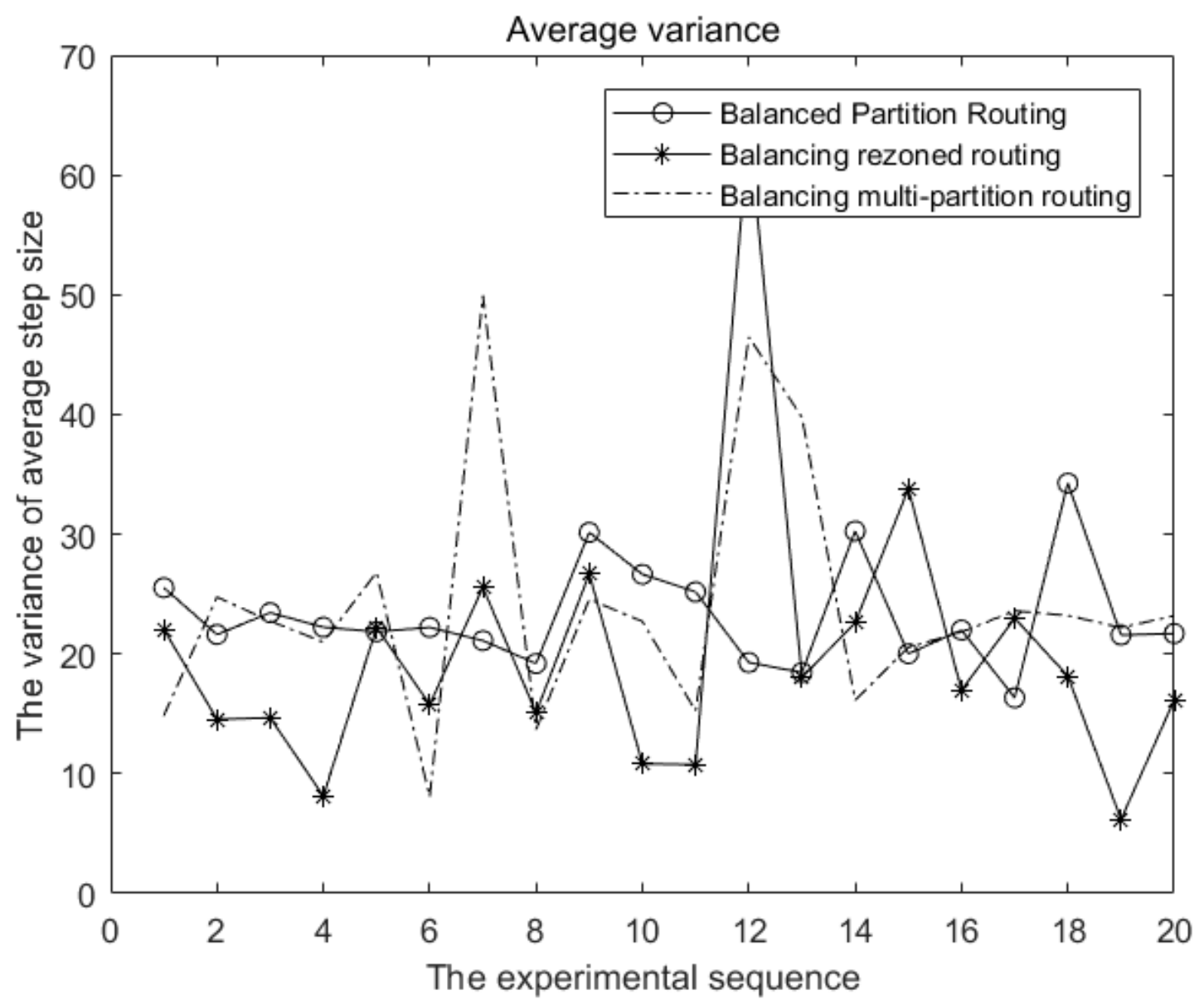
Twenty simulation experiments were conducted here. It can be seen from
Figure 4 that the variance of each shortest path length calculated by the flooding and backtracking algorithm is nearly 0, followed by the two partition routing algorithms. The variance calculated by the greedy algorithm is the largest and the stability is the worst. However, considering that the computation complexity of the balanced partition routing algorithm is much lower than that of the flooding and backtracking algorithm, the balanced partition routing algorithm still has high application significance.
3.5. Analysis of Hardware Architecture Cost
The inter-star model is composed of nine star nodes. We randomly conducted 1000 communication missions among these star nodes. We only considered the calculation power consumption of these nodes in calculating the routing path, and the energy consumption of the nodes is positively correlated with the calculation amount. In the actual space environment, the payload of the satellite relies on solar panels to collect solar energy to provide energy.
Table 1 shows the calculation amount for the routing calculation for each node under different algorithms in a simulation experiment. Something that looks like
or
is an order of magnitude. The amount of computation here is expressed only in numbers, not in units. The larger the value is here, the greater the amount of computation performed on this node. This means that this node will consume more power and require higher hardware costs. According to the principle of reliability, since we do not know the calculation pressure of each node in advance, the design index of each node should refer to the node with the largest calculation pressure. For example, in this experiment, the design index of the satellite nodes should refer to the No. 1 star under the flooding algorithm, and the No. 6 star under the greedy algorithm. In other words, the actual hardware design cost of satellite nodes is mainly determined by which node bears the most computational pressure.
In order to increase the reliability of the experiment, we conducted a total of 10 experiments. In
Table 2, we omit the computation amount of each star node under various algorithms and only show the numerical value of the node with the most computation in each experiment.
It can be seen from this table that the computing capacity requirements of the flooding algorithm for the nodes are not in the same order of magnitude as those of the other three algorithms. If the flooding algorithm is used, the hardware cost for the star nodes will be very large. In theory, the average calculation pressure of each node of the greedy algorithm should be far less than that of the partition routing algorithm and balanced partition routing algorithm. However, each route calculation of the greedy algorithm can only be completed by one node independently and cannot be dispersed to multiple nodes. It leads to great calculation pressure on some nodes. According to our simulation results, the node with the greatest computational pressure of the greedy algorithm is the same order of magnitude as that of the two partition routing algorithms, and the hardware cost among them is also close. From this point of view, on the premise of obtaining extremely high algorithm effectiveness, the hardware cost of a balanced partition routing algorithm is much lower than the flooding algorithm and the cost is close to the greedy algorithm and partition routing algorithm, which have good economic benefits.