The Car-Following Model and Its Applications in the V2X Environment: A Historical Review

Abstract

The application of vehicle-to-everything (V2X) technology has resulted in the traffic environment being different from how it was in the past. In the V2X environment, the information perception ability of the driver–vehicle unit is greatly enhanced. With V2X technology, the driver–vehicle unit can obtain a massive amount of traffic information and is able to form a connection and interaction relationship between multiple vehicles and themselves. In the traditional car-following models, only the dual-vehicle interaction relationship between the object vehicle and its preceding vehicle was considered, making these models unable to be employed to describe the car-following behavior in the V2X environment. As one of the core components of traffic flow theory, research on car-following behavior needs to be further developed. First, the development process of the traditional car-following models is briefly reviewed. Second, previous research on the impacts of V2X technology, car-following models in the V2X environment, and the applications of these models, such as the calibration of the model parameters, the analysis of traffic flow characteristics, and the methods that are used to estimate a vehicle’s energy consumption and emissions, are comprehensively reviewed. Finally, the achievements and shortcomings of these studies along with trends that require further exploration are discussed. The results that were determined here can provide a reference for the further development of traffic flow theory, personalized advanced driving assistance systems, and anthropopathic autonomous-driving vehicles.

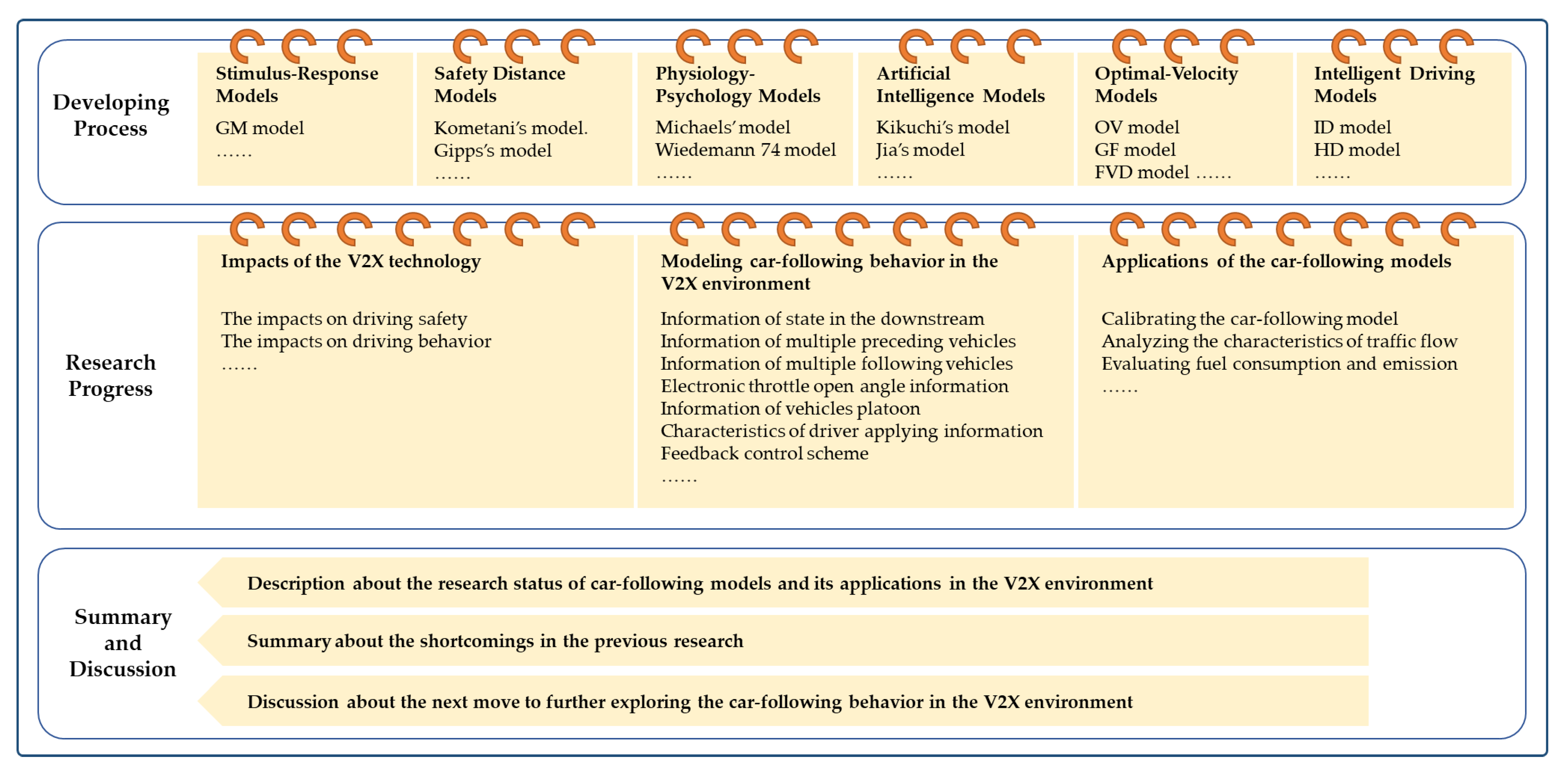
1. Introduction

Traffic accidents and congestion are common problems for both those who manage and use transportation systems. Further developments in technology will be able to effectively improve the poor state of the present situation. Relevant intelligent transportation system (ITS) technologies that are represented by the V2X have been developing rapidly in the last few years. The V2X is the general name that has been given to a series of technologies that have been developed, are developing, and will be developed, which are currently represented by Dedicated Short-Range Communication (DSRC)-based and Cellular Network-based technologies, i.e., the C–V2X. V2X technologies enable a vehicle to exchange information with the other elements that are involved in the system, providing the basis for intellectualization. These technologies have been regarded as being an effective way to solve problems such as traffic accidents, congestion and pollution. The informatization level of transportation systems has been greatly improved with the application of V2X technology, which has made the present-day traffic environment different from that of the past. Information is the basis of decision making. In the V2X environment, the driver–vehicle unit can obtain massive amounts of traffic information and understand the traffic situation more comprehensively. Based on this better understanding, car-following behavior can be optimized. Thus, the characteristics of car-following behavior and traffic flow, which is the macroscopic result of microcosmic car-following behavior, are significantly different from the previous traffic environment without V2X technology. In the traditional car-following models, only the dual-vehicle interaction between the object vehicle and its preceding vehicle was considered. This defect means that these models cannot be directly employed to describe the car-following behavior in the V2X environment, nor can they be implemented to form the theoretical basis for the analysis of traffic flow characteristics or for the estimation of vehicle energy consumption and its emission. Under these conditions, car-following models need to be further extended or updated.

Considering these limitations, studies conducted on the car-following model and its applications in the V2X environment were comprehensively reviewed in this paper in order to provide a reference for further exploration. The review that is presented in this paper is organized into three parts:

• An introduction of the development process of traditional car-following models;
• A description of the current status of research on the car-following model and its applications in the V2X environment;
• A discussion of the achievements and shortcomings of the previous studies along with future research trends.

The framework of the review that is provided in this paper is as shown in Figure 1.

The following contents of this paper are organized as follows: the development process of traditional car-following models is introduced in Section 2; the studies on the car-following model and its applications in the V2X environment are reviewed in Section 3; the achievements, shortcomings, and the trends that require further exploration are discussed in Section 4; the conclusion is given in Section 5.

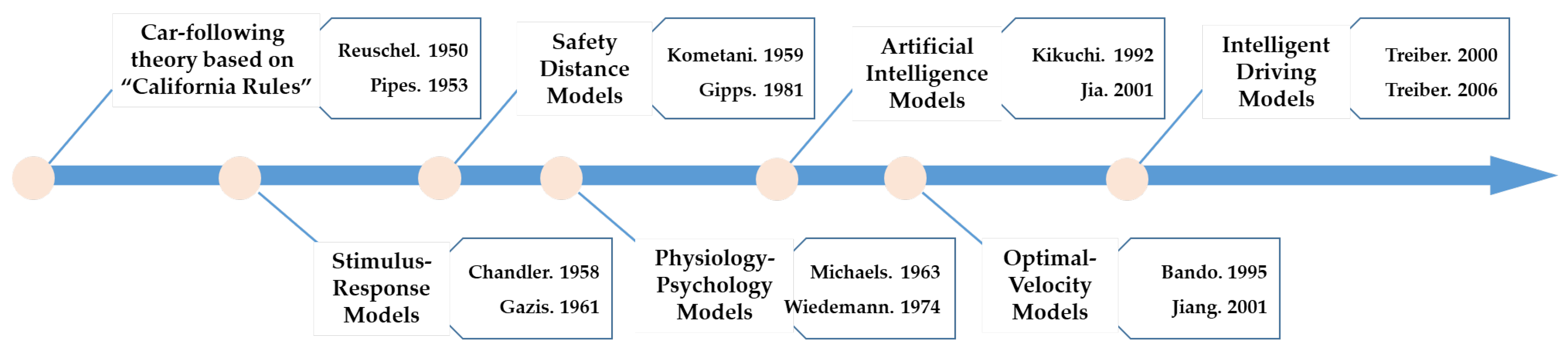
2. Development Process of the Traditional Car-Following Models

As the most basic driving behavior, car following is the behavior of an object vehicle as it follows its preceding vehicle and maintains the current lane, which describes the longitudinal movement characteristics of the object vehicle. The research of car-following behavior began with the car-following theory based on “California Rules” in the 1950s. In the “California Rules”, it is assumed that the driver will maintain a prescribed safe distance between his/her vehicle and the preceding vehicle. To be specific, when the preceding vehicle accelerates per 4.47 m/s, the safe distance will enlarge by 4.57 m. After a nearly 70-year development, a large number of car-following models have been proposed. Among them, the representative ones can be classified into six types, which are the stimulus–response models, the safety distance models, the physiology–psychology models, the artificial intelligence models, the optimal velocity models, and the intelligent driving models, according to the modeling ideas. The GM model, which establishes the foundation for study on the car-following models, is the first model of the stimulus–response type [1,2]. In the GM model, the relative velocity of the object vehicle and its preceding vehicle was regarded as the stimulus, and the acceleration of the object vehicle was regarded as the response to the stimulus. Generally, in the stimulus–response models, the car-following behavior is modeled as the response to external changes that usually refer to the movement changes in (multi-)preceding vehicle(s). After the first stimulus–response model proposed by Chandler et al., Kometani et al. established the first safety distance model [3]. Then, the classical safety distance model that is the Gipps model was proposed by Gipps [4]. In the safety distance models, the car-following behavior is modeled as a process that the driver tries to reach and to maintain the desired headway, i.e., the safety distance. There are some unique advantages in the safety distance models, including Newton’s laws of motion-based, concise structure and collision avoidance, making these models widely used to control vehicle longitudinal movement in the microcosmic traffic flow simulation software [5]. With the development of cognitive psychology, the researchers realized that the car-following behavior was not just a kinetic process, but also the results of the driver’s physiology and psychology characteristics. Considering this, Michaels proposed the first physiology–psychology model [6]. Later, the most well-known physiology–psychology model, the Wiedemann 74 model, was established by Wiedemann [7] and then developed as the core of Vissim, which is one of the most famous traffic flow simulation programs. In the Wiedemann 74 model, of which the major innovation is that the stimulus is modeled physiologically and psychologically, there are two psychology following distances. The driver will recognize the risk and decelerate when the headway is smaller than the first psychology following distance, and he/she will recognize the safety and accelerate when the headway is larger than the second psychology following distance. At the turn of the century, computing hardware and artificial intelligence technology were rapid developing, making possible the discovery of the laws of car-following behavior directly from the trajectory data and, based on this, the formation of a model. The first artificial intelligence model was proposed by Kikuchi [8]. Since then, many car-following models of the artificial intelligence type based on different methods have been constructed. Among them, the common artificial intelligence methods employed to establish the model are fuzzy logic [9] and artificial neural network [10]. The artificial intelligence models based on fuzzy logic can describe the fuzziness of drivers’ decision-making processes in car-following behavior. These models were usually established by fuzzifying one or multiple parameters in the previous car-following models. The artificial intelligence models based on the neural network can directly discover the laws of drivers’ car-following behavior from the field data measured in various environments, such as the widely used Next-Generation Simulation (NGSIM) data. In the same period, the attention of researchers in the field of physics was attracted to the car-following behavior because of the unique movement characteristics of vehicles in the car-following process. Based on the theory and method of statistical physics, Bando et al. established the first of the optimal velocity models, the optimal velocity (OV) model [11]. Subsequently, the negative velocity difference was introduced into the OV model to form the generalized force (GF) model by Helbing et al. [12]. Jiang et al. further integrated the positive velocity difference and proposed the full velocity difference (FVD) model [13]. These three models are the basic ones of optimal velocity models, and their core is the optimal velocity function. Due to the unique characteristics of this function, the optimal velocity models can describe the behavior of drivers pursuing higher speed but being unable to accelerate unlimitedly because of the constraints of vehicle and road. The last type of car-following model is intelligent driving, and the first model of this type, the intelligent driver (ID) model, was established by Treiber and Helbing [14]. Later, Treiber et al. further considered the reaction delay and estimation error and formed an extended model, the human driver (HD) model [15]. The intelligent driving models contains two vital items, which, respectively, represent the acceleration and deceleration trend. This kind of structure makes these models suitable to describe the car-following behavior of the vehicle(s) equipped the automatic controller such as the Adaptive Cruise Control (ACC) system and the Collaborative Adaptive Cruise Control (CACC) system.

The above models constitute the main body of research on modeling car-following behavior. In this paper, they are collectively named as traditional car-following models, and their developing process is as shown in Figure 2.

The traditional models have shown the ability to describe the driver’s car-following behavior under different conditions. Different types of traditional car-following models have distinct performance characteristics. For example, the optimal velocity models can reproduce nonlinear and complex traffic phenomena such as phase transition, stop-and-go. However, as mentioned above, only the dual-vehicle interaction was considered in these models, and thus they cannot be directly employed to describe the car-following behavior or to be the basis for analyzing traffic flow characteristics, estimating vehicle(s) energy consumption and emission in the V2X environment. Nevertheless, considering their distinct performance characteristics, the traditional car-following models are suitable to be the basic model and to be extended or improved to form new models for the V2X environment.

3. Research on Car-Following Behavior in the V2X Environment

In the V2X environment, the driver–vehicle unit can obtain massive amounts of traffic information of various units, including multiple vehicles, in the system. Based on this, the connection and interaction relationship between the object vehicle and other units will be established. With this relationship, characteristics of the object vehicle’s car-following behavior will differ from that in the previous traffic environment without V2X technology. These changes should be considered in modeling car-following behavior to make the results suitable for the V2X environment. As the core of traffic flow theory, the car-following model is the basis of theory applications such as analyzing the characteristics of traffic flow, evaluating the energy consumption and emission. In other words, the car-following model is the basis for comprehensively understanding the traffic flow in the V2X environment. Considering this, the relevant studies are reviewed from three aspects, that are the impacts of V2X technology, modeling the car-following behavior in the V2X environment, and the applications of the car-following models in this section.

3.1. Impacts of V2X Technology

As an emerging technology, the system reliability, social acceptance, and especially the impacts after the application of V2X technology have received a large amount of attention from academics and people from all walks of life. With V2X technology, the informatization level of the transportation system has been significantly improved. Utilizing V2X technology, drivers can obtain massive amounts of traffic information, and parts of the information were hard to obtain in the past without V2X technology, which will influence the drivers to a certain extent. How and to what extent drivers will be affected are the questions that should be answered before the large-scale practical application of V2X technology. Based on the virtual driving experiment and Gipps model, the impacts of the Intelligent Speed Adaptation (ISA) system on drivers’ car-following behavior and the key indicators restricting the system to exert this influence were explored by Spyropoulou et al. [16]. The results suggest that the application of the ISA system will reduce the average velocity as well as maximum velocity in the car-following process, and the extents of this influence on various types of drivers are different. The field driving experiment was employed by Farah et al. to study the impacts of the vehicle-to-infrastructure (V2I) system on the safety of the car-following process [17]. The results reveal that the V2I system can reduce the acceleration and deceleration deviations between different drivers and decrease the driver’s delay. The results also suggest that these effects are deeper for the older driver. Navarro et al. explored the stare characteristics of the driver when he/she is driving a vehicle equipped with the Advanced Driving Assistance System (ADAS) in a car-following process [18]. The results show that the driver will stare more into the distance when using the ADAS. However, are these effects essentially to liberate the drivers from the heavy driving task and enter a relatively relaxing driving state, or to cause them to enter a distraction state? To explain this, Calvi et al. carried out a serial of virtual driving experiments, and the results suggest that the drivers who have used the ADAS before will find it easier to enter a distraction state [19].

The above works focus on the discussion of the impacts of V2X technology on driving safety in a car-following process, which could help us better design, deploy, utilize V2X technology to achieve the “Re-evolution” of the transportation system. The results can also provide a reference for modeling the car-following behavior in the V2X environment. However, more detailed discussion about the impacts of V2X technology on car-following behavior needs to be carried out.

As mentioned above, when the driver accepts V2X technology and then utilizes it, a kind of human–machine interaction relationship is formed. With this relationship, the characteristics of driver’s car-following behavior will differ from the past. Tang et al. explored the characteristics of driver’s car-following behavior with and without the V2X information [20]. The results suggest that the starting/braking process and fuel consumption and emission in the car-following process are optimized with V2X technology. Considering that V2X technology can help the driver react in advance with the information, Hua et al. introduced a parameter into the Newell model [21] to represent this effect and, based on this, analyzed the positive impacts of V2X technology on car-following behavior [22]. Based on the virtual driving experiment, Chang et al. explored the impacts of vehicle-to-vehicle (V2V) onboard devices on car-following behavior [23]. The results reveal that the V2V device has an obvious positive impact on car-following behavior, which is reflected in the indicators including the lasting time of steady-state, and the extent of this positive effect varies for different drivers. Additionally, based on the virtual driving experiment, Ali et al. analyzed the impacts of two types of information, that are, respectively the continuous information such as velocity and the incident-based discrete information such as traffic accidents [24]. The results reveal that these two types of information have a positive influence on car-following behavior. To be special, affected by the information, the driver has a larger time-to-collision (TTC) and smaller deceleration, but a more intense tendency to continue driving when the traffic signal has turned to “yellow”.

The impacts of V2X technology on drivers in the car-following process were explored in the aforementioned works, and the results show that there are certain positive influences of V2X technology on car-following behavior in aspects such as safety, efficiency, comfort level, energy consumption, and emission. These improvements are essentially the expression of new characteristics of car-following behavior affected by V2X technology. Although the above works can provide an important reference for modeling the car-following behavior in the V2X environment, the specific impacts of V2X technology in the different development stages on car-following behavior and traffic flow along with the modeling efforts have become the research priority in the field of traffic flow theory currently and in the future.

3.2. Modelling the Car-Following Behavior

Constructing an accurate model is the basis for understanding, describing, and analyzing the car-following behavior in the V2X environment. Utilizing V2X technology, the information perception ability of the driver–vehicle units will be significantly improved, making it possible to obtain massive traffic information conveniently and in real-time. Affected by various information sources in the V2X environment, the new characteristics of car-following behavior and the model considering them have been the major research subjects.

3.2.1. Information of State in the Downstream

With the V2X technologies, especially the V2I technology, the information of state in the downstream can be collected and transmitted to the driver. Thus, drivers can understand the operating situation of the front traffic from the system level, and, based on this, they can take appropriate measures to adjust and optimize their car-following behavior. Among the information of state in the downstream provided by the V2X (V2I) technology, Tang et al. updated the parameters in the FVD model, introduced a new item to form an extended model, and analyzed the car-following behavior affected by the information about disturbance (represented by a traffic accident) in the downstream [25]. The results suggest that this kind of information can optimize the decelerating process, enhance driving safety and improve accessing efficiency. Later, they further introduced the lane-changing rules, proposed by Kurata and Tang [26,27], and extended the model for the two-lane scenario [28]. Based on analyzing the field data, Yu et al. proposed an extended FVD model with consideration of the remaining time of green traffic signal [29]. Based on similar ideas and methods, Tang et al. further extended the FVD model by updating the parameters and introducing a new item, and analyzed the car-following behavior affected by the information of real-time traffic signals, including the remaining duration of green light [30]. An FVD-based piecewise car-following model was proposed by Zhao et al. to explore the car-following behavior with consideration of the speed guidance information under four signal control conditions [31]. The results reveal that this kind of information of state in the downstream will exert a positive influence on drivers’ car-following behavior and the degree of this influence is positively correlated with the transmission range and the proportion of connected vehicles. Soon after, they further studied the impacts of speed guidance information on drivers’ car-following behavior in conflicting traffic flows in intersections without signal control [32]. Based on the above works, Ci et al. further discussed the impacts of speed guidance information on drivers’ car-following behavior in the signalized intersection with consideration of the number of vehicles in the queue [33]. The results suggest that the aforementioned information can help with optimizing the braking-to-stop access and improving the traffic efficiency of the interaction.

The results of the above research reveal that the information on traffic incidents, traffic signals, speed guidance, and other information regarding traffic state in the downstream can assist drivers with taking appropriate measures to optimize their car-following behavior in advance before they realize the situation through visual contact, which was the way in the previous traffic environment without V2X technology. These positive effects are mainly embodied in the following:

• The vehicles can decelerate to lower speed within a shorter time and take larger headway, which will enhance driving safety;
• The accelerating and decelerating processes, and especially the braking-to-stop process, are optimized;
• The traffic efficiency of the road or interaction is improved, which means that the number of vehicles passing by the road or interacting within per time unit increase.

These results also confirm that utilizing V2X technology to provide the information of state in the downstream, which reflects the operating or control situation, for the driver is of great significance for optimizing the traffic flow.

In addition to the information reflecting the downstream state of the transportation system, the driver–vehicle unit can obtain abundant microscopic traffic information of multiple vehicles in the system including the motion state (position, velocity, acceleration, etc.) and adjust the car-following behavior according to the information. In the various information-based interaction relationships, the new characteristics of car-following behavior need to be comprehensively explored.

3.2.2. Information of Multiple Preceding Vehicles

In the previous traffic environment without V2X technology, the drivers could only rely on themselves to obtain parts of the microscopic traffic information (position, velocity, vehicle type, etc.). The obtained information is usually qualitative or inaccurate. For example, the preceding vehicle is “close” and its velocity is “slow”. Furthermore, limited by the ability of human perception organs, the drivers can only obtain information of vehicles within their field of vision. However, in the new environment with V2X technology, the drivers can obtain quantitative, accurate, abundant information of all units in the system under ideal conditions. For example, the values of the position, velocity, and acceleration of the arbitrary number of preceding vehicles. In particular, the driver–vehicle unit can obtain the aforementioned information with very low delay, utilizing V2X technology based on 5G–LTE, which has been applied, and the 6G–LTE, which is to be applied. In fact, a kind of interaction relationship is formed between the vehicles that are connected and exchange information with others. As mentioned above, information is the basis of decision making. Thus, there will be new characteristics of car-following behavior affected by various pieces of information in the V2X environment, which requires new models to describe. Lenz et al. first extended the car-following model from dual-vehicle interaction to multi-vehicle interaction [34]. Considering the position of the arbitrary number of preceding vehicles in the current lane, Lenz et al. proposed an extended OV model by calculating the headway between each preceding vehicle and the object vehicle and, respectively, substituting the headways into optimal velocity functions. Lenz et al. pioneered the research on the multi-vehicle interaction car-following model. Since then, researchers have been extending and improving the traditional car-following models by considering various pieces of motion state information from multiple preceding vehicles in the current lane from different perspectives. Ge et al. also proposed an extended OV model with consideration of the position of the arbitrary number of preceding vehicles in the current lane [35]. Unlike Lenz’s approach, Ge et al. introduced the weighted sum of calculated headway into one optimal velocity function. The difference between these two kinds of optimal-function-based approaches to process the information is that in the corresponding model; it is assumed that the driver determines the car-following behavior according to multiple pieces of information, or determines that according to the overall situation represented by multiple pieces of information. Two extended OV models [34,36] considering the motion state information of multiple preceding vehicles were compared and analyzed by Wilson et al. [37]. The results reveal that the information can effectively enhance the stability of traffic flow and improve the performance of the OV model through solving the problem that the model will output unrealistic acceleration and deceleration under some conditions. Later, Li et al. replaced the velocity difference item with the relative velocity of the arbitrary number of preceding vehicles to form an extended model, i.e., the Forward Looking Relative Velocity (FLRV) model [38]. In the same period, Wang et al. proposed a similar FVD-based model [39]. After them, Yu et al. constructed an extended FVD model [40]. In Yu’s model, the weighted sum of the headway between the arbitrary number of preceding vehicles and their preceding vehicle was calculated and imputed into one optimal velocity function. Based on the above models with consideration of relative velocity or headway, Xie et al. proposed an extended OV model, i.e., the Multiple Headway and Velocity Difference (MHVD) model, which contains the relative velocity and headway mentioned above [41]. Then, Peng et al. incorporated the headway between the arbitrary number of preceding vehicles and their preceding vehicle by imputing the headway into multiple optimal velocity functions and then calculating the weighted sum of these functions to extend the FVD model [42]. Additionally, the linear and nonlinear stability of traffic flow affected by the information were analyzed based on this extended FVD model in another study [43]. Soon after, Li et al. comprehensively incorporated the headway, relative velocity, and acceleration difference and proposed an extended model considering the motion state information (position, velocity, and acceleration) of the arbitrary number of preceding vehicles in the current lane [44]. The optimal velocity function in the OV and FVD model represents the desired velocity of the driver. Thus, comparing the optimal velocity of the vehicle with that of the preceding vehicle can help with predicting the relative motion state of the two vehicles and adjusting the car-following behavior. According to this, Peng et al. added the relative optimal velocity between the object vehicle and its preceding vehicle in the FVD model to form an extended model, i.e., the Forward Optimal Velocity Difference (FOVD) model [45]. Cao et al. further extended the FOVD model by incorporating the relative optimal velocity of multiple preceding vehicles and proposed an extended model [46]. The incorporated information and the expressions of the above models, which consider the motion state of the arbitrary number of preceding vehicles in the current lane, are as shown in

Table 1. Incorporated information in the above models and their expression.

Research	Information 1	Expression 2
[34]	position	$\frac{d^2{x}_n(t)}{d{t}^2}={\displaystyle \sum _{j=1}^m{\alpha }_j}\left\{V\left(\frac{x_{n+j}(t)-x_n(t)}{j}\right)-v_n(t)\right\}$
[35]	position	$\frac{d{x}_n(t+\tau )}{dt}=V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+j-1}(t)\right)$
[38]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t)\right)-v_n(t)\right]+\kappa {\displaystyle \sum _{l=0}^n{\beta }_l}\Delta v_{n+l}(t)$
[39]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t)\right)-v_n(t)\right]+{\displaystyle \sum _{j=1}^m{\kappa }_j}{\Delta }_{V_{n+j-1}}(t)$
[40]	position	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+j-1}(t)\right)-v_n(t)\right]+\kappa \Delta v_n(t)$
[41]	position, velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t),\Delta x_{n+1}(t),\cdots ,\Delta x_{n+p-1}(t)\right)-v_n(t)\right]+{\displaystyle \sum _{j=1}^q{\kappa }_j}\Delta v_{n+j-1}(t)$
[42]	position, velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+m-1}(t)\right)-v_n(t)\right]+\lambda G\left(\Delta v_n(t),\Delta v_{n+1}(t),\dots ,\Delta v_{n+m-1}(t)\right)$
[44]	position, velocity acceleration	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left({\displaystyle \sum _{j=1}^q{\beta }_j}\Delta x_{n+j-1}(t)\right)-v_n(t)\right]+\lambda {\displaystyle \sum _{j=1}^q{\varsigma }_j}\Delta v_{n+j-1}(t)+\kappa {\displaystyle \sum _{j=1}^q{\zeta }_j}\Delta a_{n+j-1}(t-1)$
[46]	position	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& \alpha \left[V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+j-1}(t)\right)-v_n(t)\right]+\kappa \Delta v_n(t)\hfill \\ \hfill & +\mu [V\left(\Delta x_{n+1}(t),\Delta x_{n+2}(t),\dots ,\Delta x_{n+j}(t)\right)-V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+j-1}(t)\right)]\hfill \end{array}$

¹ The type of incorporated information is determined by the information directly imputed into the model’s expression. For instance, in the model with consideration of optimal velocity, the directly imputed information is the position, and the headway is calculated based on the position. After this, the optimal velocity can be calculated based on the headway. Thus, the incorporated information is the position rather than the headway. These are the same in the following tables. ² $x_n\left(t\right)$, $v_n\left(t\right)$, and $a_n\left(t\right)$ are, respectively, the position, velocity, and acceleration of the vehicle $n$ at the time $t$. $x_n\left(t\right)$, $v_n\left(t\right)$, and $a_n\left(t\right)$ are, respectively, the relative position, velocity, and acceleration, and ${\overline{x}}_n\left(t\right)$, ${\overline{v}}_n\left(t\right)$, and ${\overline{a}}_n\left(t\right)$ are, respectively, the mean ones. $V(.)$ is the optimal velocity function, and $G(.)$, as well as $H(.)$, are functions employed in the relevant works. The specific form of these three functions can be found in the references. $\alpha$, $\beta$, $\kappa$, $\zeta$, and $\rho$ are parameters corresponding to the attached items. $\tau$ is the time delay item. $s^{*}$ is the desired headway between the corresponding vehicles. $m$, $q$, and $j$ are the constants to represent the number of considered vehicles in the models. These are the same in the following tables.

.

In the above research, the car-following behavior affected by the motion state information of the arbitrary number of preceding vehicles, which are in the current lane, in the V2X environment, was stepwise explored. In part, the impacts of the values of incorporated preceding vehicles $n$ on car-following behavior were analyzed. The results show that the increment in the positive impacts will continuously decrease with an increase in $n$ when the $n$ continuously increases, which conforms to the “Marginal Effect”. It is pointed out by the results that when $n=2$, the positive influence exerted by the information is considerable. Considering this, some researchers modeled car-following behavior incorporating the two preceding vehicles rather than the arbitrary number of preceding vehicles in the current lane. Nagatani et al. incorporated the position of the two preceding vehicles and replaced the single headway in the Newell model with the dual headway that is calculated by the position to form the extended model [36]. In Nagatani’s model, the object vehicle is controlled by the first headway of the object vehicle and its preceding vehicle and the difference between the first headway and the second headway, which is of the preceding vehicle and its preceding vehicle. Sawada also introduced dual headway into the Newell model [47]. Different from Nagatani’s model, the object vehicle is controlled directly by the second headway. Later, the second headway was imputed into the optimal velocity function in the FVD model by Jin et al. to form an extended model [48]. In Jin’s model, the velocity difference item in the FVD model was also replaced with two velocity differences which, respectively, are the first one between the object vehicle and its preceding vehicle and the second one between the preceding vehicle and its preceding vehicle. Yu et al. identified the relationship between the dual velocity difference mentioned above and the acceleration of the object vehicle from field data and then introduced the item of dual velocity difference into the FVD model to propose an extended model [49]. Sun et al. imputed the dual headway into the optimal velocity function and proposed an extended OV model with consideration of the position of two preceding vehicles [50]. In the same period, Zhu et al. also proposed an extended OV model with consideration of the position of two preceding vehicles [51]. Unlike Sun’s approach, Zhu et al. imputed the dual headway into two optimal velocity functions rather than the single one used in Sun’s model. Recently, Cheng et al. proposed an extended model by introducing the mixed maximum velocity of the two preceding vehicles [52].

The results of the above works reveal that the motion state information, such as position, velocity, acceleration, and the ones calculated by those of preceding vehicles in the current lane can effectively assist the drivers with optimizing their car-following behavior and thus contribute to the traffic flow in the V2X environment. For the preceding vehicles in the current lane, the more preceding vehicles incorporated, the better the optimization effects exerted. However, these positive impacts conform to the marginal effect. It was verified that incorporating two preceding vehicles could produce considerable positive effects.

3.2.3. Information of Multiple Following Vehicles

Driving experience suggests that drivers will pay attention to the motion state of vehicle(s) in the back when they are in the car-following process. Keeping focus on the vehicle(s) in the back while driving in the car-following process, it is much easier to obtain the motion state information of vehicle(s) in the back with the V2X environment. Nakayama et al. firstly considered the following vehicle of the object vehicle, defined the behavior of the driver paying attention to the vehicle(s) in the back during car-following as the “Back Looking Effect”, and extended the OV model to the Black Looking Optimal Velocity (BLOV) model [53].

Limited by attention and energy, it is hard for drivers to keep focusing on the motion state of vehicle(s) in the back. In the V2X environment, the driver of the object vehicle can not only obtain the motion state information of preceding vehicles in the current lane but can also obtain some kinds of information which are difficult to obtain or successively obtain without V2X technology, such as the information of backward vehicles. Thus, it is much easier to obtain information about the motion state of vehicle(s) in the back with V2X technology.

Based on Nakayama’s model, Hasede et al. further introduced the headway between the two successive ones of the arbitrary number of vehicles in the front and back of the object vehicle into one optimal velocity function and proposed an extended OV model [54]. Then, Ge et al. constructed a Heavyside function to describe the drivers’ behavior of tending to accelerate to avoid the possible collision caused by the too-small headway between them and the following vehicle, and, based on this, established an extended OV model with consideration of the headway between the arbitrary number of preceding vehicles and the Back Looking Effect [55]. Yu et al. extended the FLRV model into a new one that incorporated the relative velocity between the two successive vehicles of the arbitrary number of vehicles in the front and back of the object vehicle [56]. Sun et al. extended their previous research [42] with consideration of the Back Looking Effect and proposed a new extended OV model that incorporated the headway and relative velocity of the two successive ones in the arbitrary number of preceding vehicles and the headway between the object vehicle and its following vehicle [57]. Soon after, Sun et al. introduced the Back Looking Effect into the FVD model to form an extended model, the Black Looking Full Velocity Difference (BLFVD) model [58].The Back Looking Effect was introduced into Peng’s extended OV model [42] by Yang et al. with consideration of the headway and relative velocity between the object vehicle and its following vehicle [59]. Like Yang’s approach, Zeng et al. further introduced the relative velocity into the BLFVD model and formed a new extended model [60]. Based on this model, they discussed the impacts of the following vehicle information on traffic flow, and the results show that the headway information or the relative velocity information along with the headway can effectively enhance the stability of traffic flow. However, single relative velocity information will produce negative effects on the stability of traffic flow. Considering the marginal effect discussed in the previous section, Li et al. proposed a three cooperated vehicles extended FVD model [61]. In this model, the car-following behavior of the object vehicle is determined by the difference between the velocity of itself and the re-defined optimal velocity of all three vehicles. The re-defined optimal velocity is the output of optimal velocity function about the headway between the vehicle and the other two vehicles. Recently, Ma et al. extended the BLFVD model by introducing the relative velocity of two preceding vehicles [62], and Zong et al. proposed an extended ID model with consideration of the velocity and acceleration of multiple vehicles in the front and back of the object vehicle, as well as the headway and relative velocity between these vehicles and the object vehicle [63]. The incorporated information and the expressions of the above models considering the motion state of following vehicles in the current lane are as shown in

Table 2. Incorporated information in the above models and their expression.

Research	Information	Expression
[53]	position	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[\left\{V_F\left(x_{n+1}(t)-x_n(t)\right)+V_B\left(x_n(t)-x_{n-1}(t)\right)\right\}-v_n(t)\right]$
[54]	position	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_{n+k_{+}}(t),\dots ,\Delta x_{n+1}(t),\Delta x_n(t),\Delta x_{n-1}(t),\dots ,\Delta x_{n-k_{-}}(t)\right)-v_n(t)\right]$
[55]	position	$\frac{d{x}_j(t+\tau )}{dt}=p{V}_F\left(\Delta x_j(t),\Delta x_{j+1}(t),\dots ,\Delta x_{j+n-1}(t)\right)+(1-p)H\left(h_c-\Delta x_{j-1}(t)\right)V_B\left(\Delta x_{j-1}(t)\right)$
[56]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\kappa \left[V\left(\Delta x_n(t)\right)-v_n(t)\right]+\kappa \left({\displaystyle \sum _{l=1}^{n_1}{\alpha }_l}\Delta v_{n+l-1}(t)+{\displaystyle \sum _{l=1}^{n_2}{\beta }_l}\Delta v_{n-l}(t)\right)$
[57]	position, velocity	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& \alpha \left[V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+m}(t);\Delta x_{n-1}(t)\right)-v_n(t)\right]\hfill \\ \hfill & +\kappa G\left(\Delta v_n(t),\Delta v_{n+1}(t),\dots ,\Delta v_{n+m}(t);\Delta v_{n-1}(t)\right)\hfill \end{array}$
[58]	position	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha [p{V}_F\left(\Delta x_n(t)\right)+(1-p)V_B\left(\Delta x_{n-1}(t)\right)-v_n(t)]+\kappa \Delta v_n(t)$
[61]	position, velocity	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& {\kappa }_l\left[V\left(\Delta x_{n-1,n-2}(t),\Delta x_{n-1,n-3}(t)\right)-v_{n–1}(t)\right]\hfill \\ \hfill & +{\kappa }_c\left[V\left(\Delta x_{n,n-1}(t),\Delta x_{n,n-2}(t)\right)-v_n(t)\right]\hfill \\ \hfill & +{\kappa }_f\left[V\left(\Delta x_{n+1,n}(t),\Delta x_{n+1,n-1}(t)\right)-v_{n+1}(t)\right]\hfill \end{array}$
[59]	position, velocity	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& \alpha \left[V\left(\Delta x_n(t),\Delta x_{n+1}(t),\dots ,\Delta x_{n+m}(t);\Delta x_{n-1}(t)\right)-v_n(t)\right]\hfill \\ \hfill & +\kappa G\left(\Delta v_n(t),\Delta v_{n+1}(t),\dots ,\Delta v_{n+m}(t);\Delta v_{n-1}(t)\right)\hfill \end{array}$
[60]	position, velocity	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& \alpha [\left(1-p^x\right)V\left(\Delta x_n(t)\right)+p^x\left(-V\left(\Delta x_{n-1}(t)\right)\right)-v_n(t)]\hfill \\ \hfill & +r\left(1-p^v\right)\Delta v_n(t)+r{p}^v\left(-\Delta v_{n-1}(t)\right)\hfill \end{array}$
[62]	position, velocity	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& \alpha \left[p{V}_F\left(\Delta x_n(t)\right)+(1-p)\left(V_B\left(\Delta x_{n-1}(t)\right)\right)-v_n(t)\right]\hfill \\ \hfill & +\lambda \left[q\Delta v_n(t)+(1-q)\Delta v_{n+1}(t)\right]\hfill \end{array}$
[63]	velocity, acceleration	$\begin{array}{l}\frac{d^2{x}_n(t+t_d)}{d{t}^2}=a_n^0\left[1-{\left(\frac{v_n(t)}{v_n^0}\right)}^4\right]-[{\tau }_f{\displaystyle \sum _{l_r=1}^{Q_f}\xi s^{*}\left(v_{n-l_f+1}(t),\Delta v_{n-l_f+1}(t)\right)}\times {\lambda }_{l_f}{a}_{n-l_f+1}^0{\left(\frac{s_{n-l_f+1}^{*}}{s_{n-l_f+1}}\right)}^2\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+{\tau }_r{\displaystyle \sum _{l_r=1}^{Q_r}\xi }{s}^{*}\left(v_{n+l_r-1}(t),\Delta v_{n+l_r-1}(t)\right)\times {\lambda }_{l_r}{a}_{n+l_r-1}^0{\left(\frac{s_{n+l_r-1}^{*}}{s_{n+l_r-1}}\right)}^2]\end{array}$

.

The results of the above studies confirm that the drivers will pay attention to their following vehicle(s) in the car-following process. With the results of this and the previous section, one can obtain that among all preceding and following vehicles in the current lane, the driver’s primary concern is the motion state of the vehicles in the front, especially the preceding vehicle and its preceding vehicle. Based on this, the driver will take into account the motion state of vehicles in the back. The results also suggest that there are positive effects exerted by the information of vehicles in the back on the object vehicle’s car-following behavior. Among various kinds of information on the vehicles in the back, the headway between the object vehicle and its following vehicle produces the most intense positive influence on the car-following behavior. Additionally, it is noteworthy that the single relative velocity between the object vehicle and its following vehicle may exert negative impacts on the car-following behavior. The studies incorporating the following vehicles, especially ones incorporating the following and the preceding vehicles, have a certain significance for understanding the characteristics of car-following behavior, constructing the cooperative car-following model, and the corresponding control methods for the V2X environment.

3.2.4. Electronic Throttle Open Angle Information

The throttle is a key component that controls the intake of the engine to determine its power output. When the driver decides to accelerate and depress the accelerator pedal, firstly, the throttle opening angle increases. Then, the engine starts to output more power to drive the vehicle to accelerate. Due to this, the accelerating state of the vehicle can be represented by the throttle opening angle. More importantly, the throttle opening angle can also describe the motion tendency that other indexes, including the value of acceleration, can hardly represent. For instance, the instantaneous acceleration when the vehicle starts at rest is about zero, which represents the current motion state. However, at the same time, the throttle opening angle is not zero and can describe the vehicle motion tendency to accelerate. Thus, applying the throttle opening angle information along with other motion state information can better assist the driver with understanding the current situation and its changing tendency. Furthermore, with the application of electronic throttle, information on the opening angle can be easily collected through the Controller Area Network (CAN) and other devices. This avoids the problem that the acceleration and its changing tendency are not only difficult to be perceived by the drivers themselves but also difficult to be measured directly by the onboard sensors, such as radar. To describe the relationship between the electronic throttle opening angle(ETOA) and the motion state of the vehicle, Ioannou et al. proposed a model that is as follows [64]:

$$a_n(t)=-b\left(v_n(t)-v_0\right)+c{\overline{\theta }}_n+d_n$$

(1)

where $a_n(t)$ is the acceleration of the vehicle, $v_0$ is the velocity in steady state, $b$ and $c$ are parameters depending on $v_0$, ${\overline{\theta }}_n$ is the ETOA, and $d_n$ is an adjustment item.

In the traditional traffic environment without the V2X environment, the driver can only obtain the information about ETOA of his/her own vehicle. However, like other kinds of information that are difficult to obtain or successively obtain, the ETOA information can be collected and then exchanged with other units in the V2X environment. According to this, some researchers modeled the car-following behavior with consideration of the ETOA information based on Ioannou’s model. Li et al. incorporated the ETOA information and proposed an extended FVD model, i.e., the throttle-based FVD (T-FVD) model [65]. Soon after, based on the T-FVD model, Li et al. further incorporated the headway and relative velocity of two preceding vehicles and the influence exerted by the preceding vehicles not driving on the center of the lane, and proposed a new model, i.e., the Non-Lane-Based Car-following (NLBCF) model [66]. Jiao et al. introduced the ETOA information of the preceding vehicle into the BLFVD model and established an extended model considering multiple kinds of information of the preceding vehicle and the Back Looking Effect [67]. In the same period, Qin et al. incorporated the ETOA information of multiple preceding vehicles to extend the FVD model [68]. Recently, Chen et al. further introduced the mean headway of multiple preceding vehicles into the T-FVD model and proposed a new extended model [69].

The results of the above works reveal that the ETOA information can further optimize the car-following behavior along with other kinds of motion state information, which would contribute to the operation of traffic flow. With the increase in correlation coefficients, the positive influence of ETOA information will increase accordingly. Although parts of vehicles are no longer equipped with throttle due to the replacement of the internal combustion engine, the ETOA information can still be applied in the future. This is because the vehicles with or without the internal combustion engine all have the accelerator pedal, and the ETOA information or equivalent can be collected through CAN or other vehicle control units. Considering this, the ETOA information will contribute to controlling and optimizing the vehicle motion and should be considered in modeling the car-following behavior in the V2X environment.

3.2.5. Information of Vehicles Platoon

In the aforementioned exploring process, it is pointed out that the motion state information of two preceding vehicles can produce considerable positive effects on car-following behavior and traffic flow. In contrast, considering the motion state information of more vehicles will lead to a surge in resource consumption, such as communication bandwidth and computing power. The positive effects that they produce are relatively less and subject to the marginal effect. Furthermore, it is difficult for human drivers to receive and effectively process a large amount of information at the same time, and there is a distinct primary and secondary priority for drivers when processing information. According to this, some researchers assumed that the drivers pay attention to the overall motion state of multiple preceding vehicles, which are not close to them, rather than the individual motion state of these vehicles. This assumption is based on the actual characteristics of the drivers, in that they utilize the information of vehicles not close to them to acquire the traffic state in the front segment of the road, and do not focus on the value of the individual motion state of these vehicles. Therefore, the researchers employed the average motion state of the platoon to represent the overall motion state of the vehicles that are not close to the object vehicle and incorporated it to extend or improve the car-following model. Sun et al. incorporated the average velocity of the arbitrary number of preceding vehicles, which can represent the overall operating state of vehicles ahead, and, based on this, extended the velocity difference item to improve the FVD model [70]. Considering that the average headway of the arbitrary number of preceding vehicles can assist the driver with acquiring the congestion degree of the road ahead, Kuang et al. incorporated the average headway and proposed an extended FVD model [71]. Guo et al. introduced the average field velocity of the arbitrary number of preceding vehicles and established an extended FVD model [72]. In the same period, Zhu et al. constructed an extended FVD model with consideration of the average optimal velocity of those vehicles [73]. Soon after, based on the previous research [70,73], Kuang et al. comprehensively incorporated average velocity and average optimal velocity of the arbitrary number of preceding vehicles and further extended the FVD model [74]. In the above research, multiple kinds of average motion state information were incorporated. However, the individual motion state of the vehicles close to the object vehicle was not considered comprehensively. According to this, Cao et al. further extended Kuang’s model [71] by introducing the acceleration of the preceding vehicle [75].

The results of the above research reveal that the overall motion state of the vehicles platoon can assist the driver with understanding the traffic operating state in the front segment of the road, and thus contribute to the optimization of car-following behavior as well as the traffic flow. In fact, with driving experience, not only the overall motion state of vehicles in the current lane but also the overall motion state of vehicles in the adjacent lanes can represent the traffic operating state and thus contribute to the car-following behavior of the object vehicle in the current lane. For instance, when the average velocity of the vehicles in the adjacent lane is lower than that of the current lane, the driver is likely to decelerate according to their judgment, which is that the traffic state in the front segment is poor and the vehicles in the adjacent lane decelerated due to this, even if the (average) velocity of the vehicles in the current lane is relatively high. According to this, Yu et al. incorporated the average velocity of multiple preceding vehicles in the adjacent lane and introduced the difference between this average velocity and the velocity of the preceding vehicle to form an extended model, i.e., the Lane Velocity Difference (LVD) model [76]. In the work, they also proposed an average intensity coefficient to describe the relationship between the disturbance in the current lane and that in the adjacent lane and, based on this, analyzed the stability of traffic flow. Later, Gao et al. extended the LVD model from a two-lane scenario to a three-lane scenario and formed the Left and Right Velocity Difference (LRVD) model [77]. The LRVD model also can be considered as an extended FVD model by introducing two items, which are the velocity difference between the current lane and the adjacent lanes. Recently, Yu et al. also extended the LVD model based on the approach of Wen et al. [78] to incorporate the driver heterogeneity and formed an improved model with consideration of the heterogeneity and the honk effect [79]. In this model, driver heterogeneity was considered and relative velocity information of different time steps was provided for various drivers. The results of the above research confirm that there are positive effects of the motion state of vehicles in the adjacent lanes on the car-following behavior and traffic flow. According to this, Han et al. further considered that information on the two preceding vehicles in the current lane can exert a considerable positive influence, as pointed out in the works reviewed in the previous sections, defined the two preceding vehicles in the current lane and the left/right preceding vehicles in the adjacent lanes, which contribute greatly to the car-following behavior, as the generalized preceding vehicle (GPV), and proposed an extended FVD model, i.e., the GPV model, by employing the average velocity of GPV to represent its overall motion state [80]. The incorporated information and the expressions of the above models considering the overall state of the vehicle platoon are shown in

Table 3. Incorporated information in the above models and their expression.

Research	Information	Expression
[70]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t)\right)-v_n(t)\right]+\lambda \left[{\overline{v}}_n(t)-v_n(t)\right]$
[71]	position	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t),\overline{\Delta x_n}(t)\right)-v_n(t)\right]+\lambda \Delta v_n(t)$
[72]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left(V_e\left(\Delta x_n(t)\right)-v_n(t)\right)+\alpha \kappa \left(\frac{1}{n}{\displaystyle \sum _{l=0}^{n-1}{v}_{n+l}(t)}-v_n(t)\right)$
[73]	position	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t)\right)+\beta \left(\frac{1}{\gamma }{\displaystyle \sum _{l=1}^{\gamma }V}\left(\Delta x_{n+l}(t)\right)-V\left(\Delta x_n(t)\right)\right)-v_n(t)\right]$
[74]	position, velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[(1-p)V\left(\Delta x_n(t)\right)+p{V}_{mf}\left(\Delta x_n(t)\right)-v_n(t)\right]+\lambda \left[{\overline{v}}_n(t)-v_n(t)\right]$
[75]	position, acceleration	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left\{(1-p)V\left[\Delta x_n(t)\right]+pV\left[\frac{1}{m}{\displaystyle \sum _{j=0}^{m-1}\Delta }{x}_{n+j}(t)\right]-v_n(t)\right\}+\beta a_{n+1}(t)+\lambda \Delta v_n(t)$
[76]	position	$\begin{array}{cc}\hfill \Delta x_n(t+2\tau )=& \Delta x_n(t+\tau )+\tau \left[V\left(\Delta x_{n+1}(t)\right)-V\left(\Delta x_n(t)\right)\right]\hfill \\ \hfill & +{\lambda }_1(\Delta x_{n+1}(t+\tau )-\Delta x_{n+1}(t)-\Delta x_n(t+\tau )+\Delta x_n(t))+{\lambda }_2\tau \hfill \end{array}$
[77]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=\alpha \left[V\left(\Delta x_n(t)\right)-v_n(t)\right]+{\kappa }_1\Delta v_n(t)+{\lambda }_2\Delta v_n{}^{\mathrm{LVD}}(t)+{\lambda }_3\Delta v_n^{\mathrm{RVD}}(t)$
[79]	velocity	$\begin{array}{cc}\hfill \frac{d^2{x}_n(t)}{d{t}^2}=& \frac{1}{\tau }[V\left(\Delta x_n(t)\right)+p\mu {\displaystyle \sum _{l=1}^{P_1}{\alpha }_l}\left(v_1-v_n(t)-l\tau \frac{d{v}_n(t)}{dt}\right)\hfill \\ \hfill & +(1-p)\mu {\displaystyle \sum _{j=1}^{P_2}\beta }\left(v_2-v_n(t)+j\tau \frac{d{v}_n(t)}{dt}\right)+\lambda \Delta v_n^{LVD}(t)-v_n(t)]\hfill \end{array}$
[80]	velocity	$\frac{d^2{x}_n(t)}{d{t}^2}=p\left\{\alpha \left[V\left(\Delta x_n(t)\right)-v_n(t)\right]+\lambda v_n(t)\right\}+(1-p)\left(\overline{v_n}(t)-v_n(t)\right)$

.

The results of the studies in this and previous sections reveal that various kinds of information in the V2X environment can contribute various positive effects to optimize the car-following behavior. This kind of optimization effect referring to the system level is the enhancement of traffic flow stability. In part of the aforementioned works, the neutral stability conditions and the nonlinear evolution characteristics were derived based on the theory and methods of linear stability and nonlinear analysis. The derivation and analysis results suggest that the stability of the traffic flow is significantly enhanced with the various kinds of information in the V2X environment, which is reflected in the sinking of the neutral stability curves and the expanding of the stable region in the sensitivity-headway phase space. In general, the stability of the traffic flow will be enhanced continuously with the increasing value of the sensitivity coefficient to the information, which means the car-following behavior determined based on paying more attention to the information is better. However, the increase in sensitivity to some kinds of information, such as the motion state of following vehicles, could produce negative effects on the traffic flow stability when the value is beyond the critical value. It is of great significance for alleviating traffic congestion and guiding the development of V2X technology that systematical discussion, especially the comparison analysis, takes place on the impacts of various information sources on traffic flow stability in different scenarios.

3.2.6. Characteristics of Driver Applying Information

In the V2X environment, the impacts of various kinds of information on car-following behavior and traffic flow have been widely discussed. The positive effects of the information have been acknowledged. However, the assumptions about the affecting mode of information on car-following behavior are usually too ideal, which is reflected in that the characteristics of the driver applying the information were not considered. On the one hand, there is a certain amount of time for drivers to react according to the information after they received it, which is defined as the “reaction delay”. On the other hand, drivers determine their car-following behavior according to not only the information of the current time $t$ but also the historical information in the past period $\left[t-\tau ,t\right]$, which is defined as the “memory effect”.

Reaction Delay

In the previous sections, the car-following models with consideration of the information of preceding and following vehicles in the current and adjacent lanes were comprehensively reviewed. In these models, the drivers will instantly adjust their car-following behavior when they receive the information, which is inconsistent with the actual characteristics of the drivers’ behavior. For the drivers, they need some time to determine and then conduct the adjustment according to the received information. In other words, there is a certain “reaction delay” in the adjusting process of car-following behavior. To explore the delay in detail, some researchers re-defined the delay as the “reaction delay”, which is the delay due to drivers’ decision-making process, and the “action delay” which is the acting time for drivers to carry out the decision. In most scenarios, it is difficult to accurately classify these two kinds of delay, and the impacts of regarding the two kinds of delay as one when modeling car-following behavior are small. Thus, we apply the first definition, that the time for drivers to finish the adjustment of their car-following behavior after they received the information is the reaction delay (RD). Based on this definition, we review and discuss the corresponding studies in the following contents. Chen et al. extended Wilson’s model [37] by introducing the RD corresponding to the information of preceding vehicles considered in Wilson’s model [81]. Hu et al. extended Lenz’s model [34] by incorporating the relative velocity and the RD corresponding to it, as well as the headway [82]. Soon after, Ngoduy et al. extended the OV and ID model with consideration of the information of preceding vehicles and their RD [83]. In the same period, Yu et al. introduced the RD into the extended FVD model, which incorporated the relative velocity of the two preceding vehicles [49]. Then, Chen et al. proposed an extended OV model with consideration of the optimal velocity, desired following headway, and the RD [84]. Sun et al. established an extended FVD model with consideration of the RD corresponding to velocity, headway, and relative velocity and discussed the impacts of various kinds of RD on car-following behavior and traffic flow stability [85]. In the above studies incorporated in the RD, drivers’ RD was set as a constant, making these models unable describe the drivers’ heterogeneity. According to this, Cao et al. proposed an extended OV model by differentiating the RD to describe the characteristic of RD varying due to different conditions or various drivers [86]. Based on Cao’s approach, Zhang et al. further incorporated the differentiated RD corresponding to the velocity of preceding vehicles to extend the OV model [87].

The results of the above achievements confirm that incorporating the RD is important to accurately model the car-following behavior and reproduce the complex traffic phenomenon in the simulation using the car-following model. As one of the most important behavioral characteristics, RD should be considered in modeling car-following behavior and analyzing traffic flow in the environment, with or without V2X technology, although the automatic controller, such as the ACC and CACC, can assist or even replace the driver in the car-following process. Limited by the vehicle dynamics and communication delay, the car-following behavior cannot alter instantly when the traffic situation changes. Thus, there will still be a “reaction” delay in the future, and it is of great significance to incorporate the delay for exploring the car-following behavior and traffic flow in the V2X environment.

Memory Effect

In the traditional car-following models, along with its most extended models, the motion state at the next time step $t+1$, which is the model output, is determined by various kinds of information at the current time step $t$. Nevertheless, drivers determine their car-following behavior at the next time step $t+1$ not only based on the information at the current time step $t$ but also considering the historical information in the past period $\left[t-\tau ,t\right]$. This behavioral characteristic is the so-called “memory effect”. The correlation between the historical information and car-following behavior was identified from the field data [88,89,90,91]. Tang et al. introduced a memory item about the headway into the OV model and formed the first extended model incorporating the memory effect [92]. Considering that drivers memorize the historical information over the past period rather than at a specific time, Cao constructed a desired-velocity function based on an integral form to describe the drivers’ continuous memory of the historical headway over the past period and proposed the first extended OV model that incorporated continuous memory [86]. Utilizing the Grey correlation analysis method, the correlation between the memory of the historical headway and the car-following behavior was identified by Yu et al., and, based on this, they introduced a new item, the difference between the headway and its historical value into the FVD model to form an extended model [88]. Unlike Yu’s approach, Peng et al. introduced the difference between the optimal velocity calculated by the headway and the historical optimal velocity calculated by the historical headway into the FVD model [93]. Considering that drivers determine the optimal velocity based on short-term memory of the historical headway, Liu et al. replaced the optimal velocity item in the FVD model with a new one based on short-term memory and the correction index [94]. Soon after, Li et al. also explored the correlation between the car-following behavior and the historical headway using the grey correlation analysis method based on a field data set and proposed an extended FVD model [90]. Unlike the previous research, Li et al. introduced an item describing the memory of headway and incorporated this kind of memory in the optimal velocity function. In the same period, Wang et al. proposed an extended OV model with consideration of drivers’ desire to maintain a steady state, which was represented by the difference between the optimal velocity and its historical value [95]. Wang et al. further incorporated an integral item to represent the continuous memory of optimized velocity information over a period in the BLFVD model and constructed a new extended model [96]. Yu et al. explored the correlation between the memory of relative velocity with different time steps and the car-following behavior based on the grey correlation analysis method and field data [89]. Based on this, they introduced an item about the difference between the relative velocity and its historical values with different time steps. Like Yu’s approach, Zhang et al. also employed the grey correlation analysis method based on the field data and explored the correlation between the memory of acceptable risk and car-following behavior [91]. Based on this, they proposed an extended Desired Safety Margin (DSM) model considering the drivers’ memory of the historical acceptable risk. Later, Ma et al. replaced the items about optimal velocity and velocity difference, respectively, with the integral items about the continuous memory of optimized velocity and velocity difference over a period in the FVD model, and established a new extended model [97]. Jafaripournimchahi et al. extended the FVD model by incorporating items about the memory, its velocity and the headway between the object vehicles and the preceding vehicle over the last time period m [98]. At the same time, the hysteresis in the traffic flow was recognized based on the field data, and its causes were discussed by employing a deep learning model, of which the input was various pieces of historical information with different time steps, by Wang et al. [99]. The results reveal that considering the long memory is important for reproducing the hysteresis in the simulation of traffic flow. Then, Zhang et al. extended the previous research [100] with consideration of the availability and ease-of-storage of information in the V2X environment and proposed a new model incorporating the historical information of each one of the preceding vehicles [101]. Recently, Ma et al. incorporated the drivers’ memory of the second headway with the preceding and following vehicle, respectively, to further extend the BLFVD model [102].

Differences between the vehicle’s current and historical motion state can present the varying tendency in the motion state. It is obvious that the drivers will consider the varying motion state tendency in other vehicles in the car-following process. The results of the above studies confirm that there is a correlation between the car-following behavior in the time $t+1$ and the historical information over the last period $\left[t-\tau ,t\right]$. The impacts of the memory of various information sources, whether continuous or not, on car-following behavior were discussed, although it was not pointed out in part of the works that they were for the V2X environment. The results of these achievements can all contribute to the research on car-following behavior in the V2X environment and construction, as well as the improvement of V2X technology.

3.2.7. Feedback Control Scheme

Among the research on modeling car-following behavior affected by various kinds of information in the V2X environment, there is a special kind of model, i.e., the Coupled Map (CM) model. The CM model is essentially a discrete form of the OV model. Compared with the normal OV models, there are some unique advantages in the CM model and its extended models in combination with control items and the simplicity of their simulation algorithm. The CM model was proposed, and the validity of the feedback control item for alleviating the traffic jams was confirmed by Konishi et al. [103]. The CM model and its extended models can be subdivided into the chaotic CM models and the non-chaotic CM models. In the chaotic ones, the optimal velocity function is regarded as a chaotic map, and each vehicle in the system has its own chaotic state. In the non-chaotic CM models, the optimal velocity function remains the same form as that in the OV model. The first CM model proposed by Konishi et al. is one of the non-chaotic CM models, and it adopts the same time-delay feedback as the control scheme. Based on Konishi’s work, Zhao and Gao adopted the relative velocity between the object vehicle and its preceding vehicles as the feedback control item [104], which is widely used in the following studies. Later, Han et al. incorporated the velocity of multiple preceding vehicles to improve the control scheme proposed by Zhao and Gao and formed an extended CM model suitable for the V2X environment [105]. Specifically, from the perspective of collaborative control for a vehicle platoon, Han et al. designed a one-way feedback scheme, in which the vehicles in turn are controlled based on the information of their preceding vehicle. Later, Shen et al. designed a control scheme based on the relative velocity between the two preceding vehicles and the object vehicle and, based on this, proposed an extended CM model [106]. Yu et al. incorporated the Back Looking Effect and established an extended CM model with consideration of the following vehicle [107]. Based on the optimal velocity of the two preceding vehicles, Ge et al. extended the optimal velocity function in the CM model and formed an improved CM model [107]. Then, Sun et al. further introduced the headway and difference in optimal velocity between the object vehicle and its preceding vehicle into the control scheme to extend the CM model [108]. Considering that the penetration and reliability of V2X technology cannot be maintained at 100% all the time, Yao et al. constructed a matrix to represent the communication connection state between vehicles in the system and, based on this, proposed an extended model with consideration of the headway and velocity information of multiple preceding vehicles [109]. The impacts of V2X technology penetration on car-following behavior were also explored by Shi and Yang, utilizing numerical simulation based on the extended CM model considering the velocity fluctuation information of multiple preceding vehicles proposed by themselves [110]. As discussed in the previous sections, the delay exists in the system of which the vehicles are automatically or manually controlled. Considering this, Zheng et al. proposed an improved CM model with consideration of various safe headways and the corresponding delays [111]. Later, Peng et al. considered the velocity of two preceding vehicles as well as the corresponding delay and further extended the CM model [112].

The results of the above research reveal that the control scheme designed based on various sources of information in the V2X environment can effectively alleviate traffic congestion by keeping the vehicle(s) operating at a relative steady state. From the perspective of traffic flow theory, the essence of traffic congestion is the generation and further evolution of disturbance. Under the ideal conditions, all vehicles in the system will maintain the initial steady state, and, thus, congestion never occurs. However, disturbance exists and is common in realistic transportation systems. In the CM model and its extended models, the control scheme will work when the object vehicle operates away from the steady state. Then, the deviation between the current operating state and the steady state is narrowed due to the control effects, and the system will return to the steady state. The traffic congestion can be prevented or alleviated by one-by-one or cooperatively controlling all vehicles in the system. To sum up, in alleviating traffic jams and improving transportation efficiency, there is significance to research on extending or improving the CM model with the consideration of various sources of information and, especially, the characteristics of the driver applying the information in the V2X environment.

3.3. Applications of the Car-Following Models

As the core of traffic flow theory, the significance of car-following models is determined by their important cornerstone role in traffic flow theory. To be specific, understanding and then describing the car-following behavior in the right way are the basis for analyzing the operation and stability characteristics of traffic flow and evaluating the energy consumption and emission. Before these applications, the car-following model needs to be calibrated to make it suitable for describing the specific traffic system. In the V2X environment, with the development of relevant technologies and devices, it is easier to obtain field data sets with larger scale and higher precision, which creates new requirements for the model calibration methods. Based on these, the calibration of car-following models is first reviewed in this section. Then, applications of the car-following model are reviewed from two aspects: analyzing the traffic flow characteristics and evaluating the energy consumption and emission.

3.3.1. Calibrating the Car-Following Model

In the V2X environment, the informatization degree of units in the system will be greatly enhanced. This presents in that the various kinds of information of other vehicles (such as the velocity and position) can be detected based on the onboard sensors, the detected information can be transmitted or exchanged based on the onboard and system communication components, and the information can be stored, processed, analyzed based on the system data center, computing cloud and edge computing devices. Under this condition, the calibration methods for car-following models need to be updated to make them suitable for the V2X environment. The updated goals focus on how to rapidly and accurately calibrate the car-following model based on the larger-scale field dataset. Although the traditional calibration methods such as the genetic algorithm can achieve relatively satisfied effects, there are some defects in these methods. Due to enlarging the scale of the data set in the V2X environment, the time consumption of traditional calibration methods will be significantly increased, and rapid calibration methods with high accuracy need to be constructed. To achieve this goal, researchers explored each composition in the whole chain of the calibrating process.

Calibration Algorithm

In the V2X environment, connected vehicles are usually equipped with multi-sensors. The data detected by these sensors along with the data obtained from the V2X technologies form a typical heterogeneous data set with multiple sources. How to utilize this kind of data set to calibrate the car-following model is a key problem to be solved in the research field of modeling car-following behavior in the V2X environment. Aiming at this, Hoogendoorn and Hoogendoorn proposed an improved calibration algorithm based on the maximum likelihood estimation method and a cross-comparison method of calibration results with the indexes, including the standard errors [113].

The time consumption and accuracy of the calibration process are directly determined by the performance of the calibration algorithm itself. Improvement of the calibration algorithm will contribute significantly to the development of the whole process of calibrating car-following models. Aiming at this, Hoogendoorn and Hoogendoorn constructed a general calibration algorithm for parameters in the car-following model based on the extended maximum likelihood estimation algorithm [114]. With Hoogendoorn’s algorithm, the joint estimation of multiple parameters in the model can be carried out, and statistical analysis results such as standard error can be obtained. Considering that the error may accumulate in the calibrating process with previous calibration algorithms, Jin et al. proposed an improved error control method based on the correlation between the parameters and the model stability [115]. Utilizing the genetic algorithm and a field data set, Jin et al. verified their method with the Mean Absolute Error (MAE) index in calibrating typical car-following models, such as the GM, OV, Gipps, FRESIM, and ID model. It was proved by Li et al. that the objective function in the calibrating process is Lipschitz continuous and around the global optimal solution [116]. Based on this, they proposed a global optimization rapid calibration algorithm by combining the global direct search and the local gradient search and verified this algorithm utilizing the NGSIM data set based on the comparison with the Nelder–Mead algorithm, sequential quadratic programming algorithm, genetic algorithm, and simultaneous perturbation stochastic approximation algorithm. Keane and Gao derived the gradient of the optimization problem using the adjoint method and, based on this, proposed an improved quasi-newton algorithm for rapidly calibrating parameters in the car-following model [117]. The results confirm that the calibrating process with this algorithm is significantly faster than that with the genetic algorithm.

As mentioned in the previous sections, there is heterogeneity in the car-following behavior with the consideration of various kinds of information, drivers, and traffic conditions. This heterogeneity makes the calibration difficult to “once for all”, and re-calibration needs to be carried out when these conditions change, which will greatly increase the workload. Considering this, Papathanasopoulou et al. proposed an online calibration algorithm for parameters in the models for micro traffic simulation based on the dynamic multi-step prediction of traffic measures [118]. Pop et al. proposed an online calibration algorithm for parameters in the car-following models based on the Kalman filtering method and Takagi–Sugeno Fuzzy Reasoning System [119].

Model to be Calibrated

The parameters in parts of the car-following models are not all independent of each other, which means that there is a kind of relevance. Based on this, Kim et al. discussed the relevance of parameters in the car-following models and evaluated the impacts of this relevance on the calibration results [120]. Later, Punzo et al. proposed a method to simplify the parameters in car-following models based on the sensitivity analysis and Monte Carlo framework and verified this method employing the FVD model [121]. The results suggest that the FVD model simplified by Punzo’s method is easier to calibrate and the performance of the calibrated model is still relatively high. Then, employing the factor fixation and variance sensitivity method, Punzo et al. proposed a robust calibration method for simplifying parameters in the car-following models and verified the proposed method with the ID model and NGSIM data set [122]. The results reveal that the proposed method can reduce the parameters in the ID model from 6 to 3 on the basis of not decreasing the model’s performance, which will significantly improve the calibrating efficiency.

Data Set Used in Calibrating

The calibrating process is essentially the process of calculating the undetermined parameters in the model using the data set. Thus, the quality of the data set can significantly influence the performance of the model calibrated with the data set. To be specific, the detecting error, the trajectory length as well as trajectory integrity are the key indexes that determine the quality of the data set. In the V2X environment, the multi-advanced sensors can relatively reduce the detecting error. However, there still are some defects. On the one hand, using more advanced sensors means more cost, making this approach unacceptable in many conditions. On the other hand, no matter how advanced the sensors are, the errors cannot all be eliminated. Considering this, Shao et al. proposed a two-step calibration algorithm with consideration of the detecting error of the data set and verified the algorithm employing the Van-Aerde model along with the data set collected from field experiments organized by themselves [123]. In the same work, Punzo et al. pointed out that the large length of the trajectory in the data set can improve the performance of models calibrated with this data set [122]. Complete and accurate trajectory data are the basis of effective calibration. However, the data set collected from the field experiments, especially the natural driving experiments, are not all about car-following behavior. Considering this, Sharma et al. proposed a recognition method for extracting complete car-following trajectory data from the driving data set and a method to evaluate the integrity of extracted data [124].

Evaluating Method of the Calibration Results

When the calibration is finished, the evaluation of the calibration results and the comparison between the calibrated model and other representative models are the following key steps in the whole calibration process. However, the previous evaluation methods are usually suitable for only one specific type of model, making it difficult to conduct the comparison. Aiming at this, Valero-Mora et al. proposed a general calibration method based on the Bayesian framework for most kinds of car-following models, and the relatively good performance of this method was verified by them based on seven typical car-following models [125]. However, for most researchers, they would like to use the traditional but widely used calibration methods, such as the genetic algorithm. To compare and analyze the calibration results using these traditional methods, the general evaluation method needs to be constructed. Considering this, Punzo et al. proposed an evaluation method using the calibration results of the car-following model based on the Spider Web Graph in the work mentioned above [121].

From data collection to results evaluation, the whole process of calibrating the car-following model is continuous and complex. The before and after steps are connected in this process, and there are a series of scientific and technological issues. Several scholars discussed these issues based on their experience and typical car-following models. Valero-More et al. discussed the challenges in the process of utilizing natural driving experiments to collect data and then storing, processing, and using the data based on the experience of research centers in three countries [125]. Considering that the calibration process of car-following models is an essential solving process for optimization problems, Monteil et al. discussed the impacts of data filtering, the correlation between parameters, sampling technique, and objective function on robust calibration, and derived the confidence interval near the minimum [126].

Calibration is a necessary step before applying the car-following model. The performance of the model is greatly affected by the performance of the calibrating method. In the aforementioned works, the vital compositions, including the algorithm, model itself, data set, and evaluating method in the whole calibration process of the car-following model were discussed. The research results can provide a reference for improving aspects of calibration performance, such as the calibrating speed. The calibrated model can be utilized in simulating traffic flow and then analyzing the characteristics of traffic flow, as well as other applications such as evaluating energy consumption and emission.

3.3.2. Analyzing the Characteristics of Traffic Flow

Generally, traffic flow characteristics include all features of the traffic flow when operating. In traffic flow theory, the traffic flow characteristics usually refer to the stability characteristics and operation characteristics. Among them are described the stability characteristics and the resistance characteristics of traffic flow to disturbance, which are usually represented by the neutral stability condition and density wave equations. The operating performance of traffic flow is described with the operation characteristics, which is usually represented by the traffic flow three-parameter (i.e., volume, velocity, and density) and the space–time graph. The traffic flow characteristics are essentially the macroscopic aggregation of microscopic characteristics of units in the system. In the V2X environment, the changes in car-following behavior will cause the traffic flow characteristics to be different from the past. The traffic flow characteristics in the V2X environment were analyzed in parts of the aforementioned studies based on approaches such as stability analysis and numerical simulation. Among these works, the optimal velocity models and the intelligent driving models were widely employed, which is because of their unique advantages in performance and, more importantly, the convenience to analyze stability characteristics using (non)linear analysis methods based on these two types of models. In [43,48,56,65,70,71,72,74,127,128,129,130,131,132,133], the researchers derived the neutral stability condition and nonlinear characteristics of traffic flow and analytical solutions of traffic flow stability affected by various kinds of information in the V2X environment, utilizing the (non)linear analysis methods based on the car-following models proposed by themselves.

The analytical solutions of traffic flow stability are the vital theoretical basis for preventing or alleviating traffic congestion. As the quantitative expression of traffic flow, the operation characteristics also should be given importance. In the previous studies on car-following behavior in the V2X environment, the operation characteristics of traffic flow were explored by constructing virtual scenarios and employing numerical simulation based on the proposed car-following models. Shi et al. analyzed the operation characteristics of traffic flow with different penetrations of connected vehicles in the system based on the extended CM model, which is incorporated with the velocity fluctuation information of multiple preceding vehicles, proposed by themselves [110]. Zhu et al. employed the OV model and the extended OV model, which incorporated the headway of two preceding vehicles, to, respectively, describe the car-following behavior of traditional and connected vehicles, and explored the operation characteristics with different penetrations [51]. Based on the extended FVD model with consideration of the ETOA information of multiple preceding vehicles and the Back Looking Effect, Jiao et al. explored the characteristics of traffic flow when operation was affected by the information in the V2X environment [67]. In the same period, Qin et al. analyzed the characteristics of traffic flow when operation was affected by various sources of motion state information, including the ETOA, of multiple preceding vehicles based on the extended FVD model [68].

In traffic flow theory, there is a mathematical relationship between aspects of the microscopic motion state, such as velocity and position described by the car-following models, and the macroscopic operating indexes of traffic flow. Thus, the corresponding macro traffic flow model can be derived based on this mathematical relationship and the corresponding car-following model. Considering this, Zhang derived a second-order continuous medium model based on the improved car-following model with consideration of drivers’ memory effect to explore the macro characteristics of traffic flow [134]. The results reveal that there is a direct relationship between the macro viscosity effect in traffic flow and the micro memory effect in car-following behavior. Tang et al. constructed a macro traffic flow model considering the drivers’ forecast effect based on the micro–macro relationship and a car-following model with consideration of this effect [135]. Later, Tao et al. further derived a macro model based on the extended car-following model incorporating drivers’ reaction delay to explore the traffic flow characteristics analytically [136]. It is also confirmed with these studies that it is necessary to introduce the drivers’ memory effect, forecast effect, and reaction delay in modeling their car-following behavior from the macro perspective of the system level, which is consistent with the conclusion given in the previous reviews. After the above works, more studies were carried out. Kang et al. derived a macro model utilizing the micro–macro relation based on Sun’s model [137] to explore the traffic flow characteristic affected by information about the average velocity of multiple preceding vehicles in the current lane [70]. Jiao et al. derived a macro model for describing characteristics of traffic flow with slope based on the extended car-following model with consideration of the ETOA information [138]. Sun et al. derived a macro model to analyze how the traffic flow affected the information of two preceding vehicles based on the extended model incorporating the same information [139]. Yu constructed a continuous medium macro model based on the car-following model with consideration of the drivers’ reaction delay, using the headway and relative velocity information [140]. Different from the above works, Wang et al. proposed a simulation framework to combine the car-following model into the cellular automata model, and analyzed the traffic flow affected by information about the average velocity of the GPV based on the framework [141].

The results of the studies on traffic flow stability along with their meaning are summarized in Section 3.2.5. As another core content of traffic flow characteristics, the operation characteristics were discussed from various perspectives based on numerical simulation or theoretical analysis in the aforementioned works. Generally speaking, the various sources of information mentioned above in the V2X environment can exert positive effects on traffic flow with different degrees in the operation and stability characteristics. On the one hand, the traffic flow can maintain a steady state in resisting larger disturbance. On the other hand, as the representation of better stability characteristics in the operation characteristics, the efficiency of traffic flow can be improved, which means an increase in volume, velocity, and critical density. It is also pointed out that with the increase in the penetration of connected vehicles in the system, the optimization effects caused by these vehicles on traffic flow will increase.

Noteworthy is that the positive effects caused by each increase in the penetration are not all increasing linearly. There are some results we would like to further discuss, which are that the connected vehicles may exert negative effects on traffic flow when their penetration is low. When the penetration of connected vehicles is low, only a small proportion of the vehicles in the system can obtain V2X information and adjust their car-following behavior according to the information. However, for most vehicles in the system, they cannot obtain the information and gain knowledge on the adjustment of connected vehicles (if they are not close enough to be recognized by the drivers) without the V2X environment. Thus, for these vehicles, the adjustment of car-following behavior conducted by the connected vehicles according to the V2X information equals a disturbance, which would exert negative effects on traffic flow.

To sum up, the discussion based on a comprehensive comparison of traffic flow in which the vehicles are controlled by various car-following models is vital for providing a reference for planning, constructing, and managing the transportation system with the V2X environment. According to this, works such as the simulation framework which can combine with various car-following models to simulate the traffic flow [141] are important for further research.

3.3.3. Evaluating Energy Consumption and Emission

It is very hard to directly measure the energy consumption and emission of the transportation system. Thus, the energy consumption and emission were usually estimated based on the car-following and evaluating model along with the numerical simulation approach in previous works. According to vehicle dynamics theory, the energy consumption and emission of the vehicle are determined by the acceleration and its changing rate. Most of the car-following models essentially calculate the object vehicle’s acceleration, and are marked as second-order models. The non-second-order models can be derived into the second-order form based on the differential or integral approach. Based on these second-order models, the energy consumption and emission can be conveniently estimated through numerical methods. Ahn et al. proposed a model for estimating vehicle energy consumption and its emission [142], and the equation is as follows:

$$\ln (MO{E}_e)={\displaystyle \sum _{i=0}^3{\displaystyle \sum _{j=0}^3\left[K_{i,j}^e\times v^i\times {\left(\frac{dv}{dt}\right)}^j\right]}}$$

(2)

where the $MO{E}_e$ is the instantaneous rate of energy consumption or emission of the vehicle $n$; $i$ is the velocity power of the vehicle $n$; $j$ is the acceleration power of the vehicle $n$; and $K_{i,j}^e$ is the regression coefficient. Applying different values of the regression coefficient, Equation (2) can be used to estimate the energy consumption or emission of CO/HC/NO_x. The values of $K_{i,j}^e$ to estimate the above items are given in [142].

This estimation model has been widely used to estimate the energy consumption and emission of vehicles controlled by various car-following models. Among these approaches, Yu Shaowei and his team contributed much. Based on the field driving experiments conducted with vehicles equipped with the ACC system, Yu et al. explored the fuel consumption and emission characteristics of vehicles with consideration of the headway fluctuation, utilizing Ahn’s method and the extended car-following models proposed by themselves [88]. Later, Yu et al. analyzed the fuel consumption and emission characteristics of vehicles affected by the velocity fluctuation of the preceding vehicle with different lengths of time window [143]. In the same period, Yu et al. further analyzed the impacts of relative velocity fluctuation information on the fuel consumption and emission characteristics of vehicles [144]. On the basis of the aforementioned research, Guo et al. discussed the fuel consumption and emission characteristics of vehicles affected by the relative velocity fluctuation information of multiple preceding vehicles equipped with the CACC system [145]. Li et al. also explored the impacts of headway fluctuation on fuel consumption and emission from a different perspective [90]. Then, Yu et al. analyzed the impacts of relative velocity and its fluctuation on fuel consumption and emission [89]. Besides the above works based on the ACC or CACC systems, Tang et al. explored the impacts of information about traffic accidents that occurred downstream on fuel consumption and emission based on their extended car-following model [20]. Tang et al. also analyzed the impacts of information about the remaining time of green light in the signalized intersection on the fuel consumption and emission of the vehicles approaching the intersection based on their extended car-following model [30]. Later, Qin et al. discussed the fuel consumption and emission characteristics affected by the information about ETOA of multiple preceding vehicles [68]. Based on the extended car-following model, Jiao et al. explored the impacts of driver’s characteristics on fuel consumption and emission [146]. Recently, Xiao et al. discussed the fuel consumption and emission characteristics of a Connected and Automated Vehicle (CAV) based on the improved car-following model for the CAV [147].

With the results of the above works, the positive effects of various sources of information on energy consumption and emission in the V2X environment have been confirmed. These effects are caused by the optimization exerted by the information on the car-following behavior, as we discussed in the previous sections. These results also prove that it is vital to further develop the V2X technologies and incorporate the information in modeling the car-following behavior in the V2X environment. Furthermore, it should be pointed out that the car-following models are the theoretical basis of the aforementioned works. Thus, modeling the car-following behavior is key and basic.

4. Discussion

Safety, congestion, and pollution, etc., are very common in transportation systems around the world. With the development of the economy and urbanization, this present situation is likely to become worse. In recent years, the relevant technologies represented by the V2X have been regarded as an effective means to solve or alleviate the above problems. The penetration of V2X technologies has made the present-day traffic environment different from that of the past, and thus significantly influenced the car-following behavior and traffic flow. Due to these factors, the car-following model and its applications have been one of the hot and frontline topics in the field of traffic flow theory.

In this paper, we first reviewed the development process of traditional car-following models and the research on the impacts of the V2X environment. In the V2X environment, the most obvious changes caused by the penetration of relevant technologies are the informatization level of units in the system, including the driver–vehicle unit, which are significantly improved. Thus, the driver–vehicle unit can obtain massive amounts of traffic information. Considering this, the information in the V2X environment was divided into the forward and backward information based the variable attention of the driver in this paper. Based on this, research on the impact of various sources of information on car-following behavior along with the corresponding models were reviewed according to their development process. The results of these works reveal that the characteristics of car-following behavior and traffic flow affected by various sources of information in the V2X environment are different from the past, which is mainly reflected at:

• The micro-level. The car-following process of vehicle(s) has been significantly optimized. In other words, the motion state of the vehicle(s) in all three stages (i.e., the normal car-following stage, the start-accelerating stage, and the braking-stop stage) has been improved. Specifically, the motion state of the vehicle(s) in the normal car-following stage is steadier and approximates the optimal state within less deviation. In the other two stages, the starting/braking process needs less time, and the safety, as well as the comfort of these processes, have been improved. Meanwhile, the headway and velocity of vehicle(s) during the car-following process are different from the past environment without V2X technology.
• The macro-level. Generally, the traffic flow can operate in a better state. Specifically, for the disturbance with the same scale, it can be absorbed by the traffic flow in the V2X environment in less time, and the deviation between the current state and the optimized state of traffic flow in the environment when resisting the disturbance is smaller than that in the traditional environment. For the disturbance with different scales, the traffic flow in the V2X environment can maintain a steady-state when encountering larger disturbance. When operating at the steady-state, the efficiency of the traffic flow of the road segment or intersection in the V2X environment is much higher than that in the previous environment, which is the expression of the aforementioned optimization at the micro-level. When the traffic flow is operating out of the steady-state, the deviation can be kept in a smaller range. It is more difficult for the traffic flow to reach the completely blocked state, and the traffic flow will show the different propagating and evolving characteristics of the density wave.

The impacts of various sources of information on car-following behavior were explored and the corresponding car-following models were established in the studies reviewed in this paper. Based on the normal form of traditional car-following models [148], the normal form of these extended or improved car-following models for the V2X environment can be summarized as

$$\frac{d^2{x}_n\left(T^j\right)}{d{t}^2}=f\left[X\left(x_{n,m}^i\right),V\left(v_{n,m}^i\right),a_{n,m}^i,Z_{n,m}^i,\hspace{0.17em}\cdots \hspace{0.17em}\right]$$

(3)

where $T^j$ is a function of $t$, which is used to express the consideration (if there is one) of the memory effect or time delay; $j$ is the identification symbol of $T^j$, when there is more than one $T^j$; $x_{n,m}^i$, $v_{n,m}^i$, $a_{n,m}^i$ and $Z_{n,m}^i$ are, respectively, the position, velocity, acceleration and other kinds of information (i.e., ETOA) of the vehicle $n$ or $m$; $i$ is the identification symbol to express which lane the considered vehicle is in; $n$ is the number of considered vehicles in the current lane; $m$ is the number of considered vehicles in other lanes; $\cdots$ is the information that was not incorporated in the previous research; and $X\left(x_{n,m}^i\right)$ and $V\left(v_{n,m}^i\right)$ are the functions, respectively, of $x_{n,m}^i$ and $v_{n,m}^i$, which are to express the detailed way of incorporating the information in the model. For instance, the optimal velocity function $V\left(\Delta x_n\left(t\right)\right)$ is a typical one of the $x_{n,m}^i$.

In the works modeling car-following behavior in the V2X environment, the optimal velocity models have been widely employed, for the following reasons:

• As the core of optimal velocity models, the unique performance of the optimal velocity function contributes much. As a kind of velocity–headway function, the optimal velocity function is monotonically increasing, with an upper bound and inflection point. Those models established based on the optimal velocity function can describe the actual characteristics of human drivers, which are that they will pursue their desired car-following state. They will use a higher speed when conditions permit in the pursuing process, but they cannot unlimitedly accelerate with the constraints of vehicle and road conditions.
• The optimal velocity models, especially the FVD model, can avoid collisions in simulations such as the safety distance models, and they can also reproduce several nonlinear traffic phenomena such as the stop-and-go, which the safety distance models can hardly achieve. Meanwhile, compared with other types of traditional car-following models, these optimal velocity function-based models are much easier to combine with the (reduced) perturbation method and other methods of linear stability analysis or nonlinear analysis, which is mainly contributed by the unique performance of the optimal velocity function, especially the inflection point, when they are employed in exploring the traffic flow. Based on this, the neutral stability conditions, which describe the ability of traffic flow to maintain a steady state, and the density wave, which describes the evolution characteristics of traffic flow when it operates away from the steady state, can be derived and analyzed.
• The structure of optimal velocity models is concise and easier to extend. This kind of unique structure enables the optimal velocity models to conveniently incorporate various kinds of information, such as position, velocity, acceleration, and ETOA in the V2X environment. Meanwhile, the incorporation will not impact the ability of these models, including fitting the characteristics of actual car-following behavior at the micro-level and reproducing nonlinear traffic phenomena, as well as analyzing the stability characteristics of traffic flow.

Furthermore, studies on the characteristics of the driver applying the information and the feedback control scheme were also systematically reviewed in this paper. For the characteristics of the driver applying the information, attention was paid to the time delay and memory effect. On the one hand, the time delay cannot be totally eliminated in the traditional or the V2X environment, and thus it is necessary to incorporate the time delay in exploring the car-following behavior. On the other hand, the memory effect is one of the main actual characteristics of human drivers, and the models with consideration of the memory effect will better fit the actual car-following behavior and be able to re-produce several nonlinear traffic phenomena. Especially considering that the automatic controller cannot fully replace the human drivers in the foreseeable future, it is necessary to incorporate these two effects in modeling the car-following behavior. For the feedback control scheme, a series of CM-based models has moved the research on modeling car-following behavior into a new field by combining it with the control scheme. Considering the development and popularization of the automatic controller, such as the ACC/CACC system, it is of great significance to research modeling car-following behavior through combining it with the control scheme.

The applications of car-following models are the direct embodiment of their value. As the core of traffic flow theory, the car-following models are the theoretical basis for many traffic flow studies. These studies are essentially the applications of the car-following models, and calibration of the model needs to be carried out before being used in these applications. Accordingly, the works on the applications of car-following models were reviewed from three aspects, which are the model calibration, traffic flow characteristics analysis, and estimating the energy consumption and the emission.

With the aforementioned review contents in the previous sections, we can obtain that the core of research on car-following behavior in the V2X environment is modeling the behavior. In the previous works, the impact of information about aspects of the motion state of vehicles in the front or back, such as position, velocity, acceleration and ETOA, information about the motion state of the vehicles platoon, such as average velocity, and the driver’s characteristics of applying information, such as the time delay and the memory effect, on car-following behavior were explored within a process. The results reveal that the characteristics of car-following behavior are affected by various sources of information and consider the information applying characteristics, and can provide an important reference for further updating traffic flow theory, the planning/designing/constructing/managing of the transportation system, and developing next-generation vehicles equipped with personalized ADAS or quasi-human automatic controller. However, there are still some imperfections in these previous works. To solve these problems, further exploration needs to be carried out. Meanwhile, the development of big data, cloud computing, autonomous driving, and other emerging technologies provides development opportunities for further efforts on the car-following model and its applications. The imperfections of previous studies and the trends that require further exploration will be discussed in the following sections.

4.1. The Existing Shortcomings

Idealized Assumptions in Modeling Car-following Behavior

Among the previous works, the traffic flow in most of the models was set as uniform flow, which means the penetration of V2X technology in the system is 100%. However, as is well known, the development of anything is not achieved overnight, and the V2X technologies are no exception. As a typical kind of advanced informatization technology, the development of V2X technologies certainly is a process by which the equipment will gradually become common, functions will become gradually comprehensive, and performance will continuously improve. In this development process of V2X technology, the penetration of connected vehicles with different equipment will certainly increase from low to high. Considering the unbalanced economical development in different regions, the penetration may never reach 100%. However, the impacts of the penetration of connected vehicles were not considered in most of the previous studies.

Incomplete Considerations in Modeling Car-following Behavior

Along with the penetration of connected vehicles, the attributes of drivers and vehicles were also not incorporated in most of the previous works. The drivers’ car-following behavior is essentially the implementation of their subjective driving will, which is time-varying and easily affected by factors internal and external. There are significant differences in the physical and dynamic characteristics of various vehicles, which could affect the driving behavior, such as the car-following one to a considerable extent. In the V2X environment, the driver can obtain massive amounts of traffic information, including about the attributes of drivers and vehicles in the system. However, there are few works incorporating these attributes when modeling car-following behavior in the V2X environment.

Absence of Global Perspective in Modeling the Car-following Behavior

In the V2X environment, the informatization degree of transportation systems has been significantly improved, which theoretically enables the drivers to obtain massive amounts of information of all units in the system. In the previous works, the impacts of various sources of information, such as headway, relative velocity, and acceleration, on car-following behavior were discussed, and there is a small number of works that explored the impacts of information about vehicles in the adjacent lanes. However, the aforementioned works only incorporated one or several kinds of information in isolation, and research incorporating information about all relevant units in the system is still absent.

Scarcity of General Modeling Method/Framework

The models constructed based on various theories in the previous studies are able to describe the car-following behavior under specific conditions. However, due to the differences in basic theory and hypothetical conditions, the generality of these models is poor, which is mainly reflected in two aspects. On the one hand, the performance of these models to describe the car-following behavior beyond the initial hypothetical conditions is upset, meaning these models can only be employed in the environment within their hypothetical conditions. These conditions are a limitation. On the other hand, it is hard to effectively compare these models to discuss the differences in car-following behavior affected by various sources of information. General models or modeling frameworks, which are suitable for all development phases of V2X technology and that can describe the car-following behavior under various conditions, along with the corresponding evaluating methods for cross comparison, should attract more attention in future works.

Destitution of Large-scale Open-source Data Set for the V2X Environment

It is obvious that large-scale open-source data sets such as the NGSIM play a great role in promoting research on car-following behavior and even traffic flow theory as a whole; although, it is easier to collect large-scale and high-precision data sets with the penetration of V2X technology in transportation systems. Most of the previous works were carried out based on numerical simulation without using field data or were only based on small-scale data sets collected in exclusive experiment roads by the corresponding researchers themselves. It is certain that the results of these studies contribute much to understanding the car-following behavior in the V2X environment. However, there are some limitations in this way. On the one hand, due to the limitations of exclusive experiment roads and the experiment scale, there are deviations between the data collected in the experiment roads and the normal roads in transportation systems, which will negatively impact the performance of models in fitting actual car-following behavior. On the other hand, compared with works based on the open-source data set, the comparability and portability of those studies based on the exclusive data set are poor. It is no exaggeration to say that the lack of data sets such as the NGSIM in the V2X environment has restricted the further development of car-following behavior research to a considerable extent. The key issue for researchers and traffic management institutions is how to organize and effectively collect large-scale and high-precision data sets corresponding to different development stages of the V2X environment and formulate the unified data standards and evaluation methods.

Adaptation of the Estimation Methods of Energy Consumption and Emission for Future Transportation Systems

It is hard to measure the energy consumption and especially the emission of vehicle(s) when driving. Thus, the estimation methods, along with the numerical simulation based on the car-following models, has been widely employed to assess the energy consumption and emission affected by various sources of information in the V2X environment. With the development of V2X technology, there is also the upgrading of the vehicle and energy industry. Driven by national policies, the energy consumption and emission performance of newly manufactured vehicles, whether using non-fossil fuels or not, have been effectively improved by technological updating. The energy industry is also continuously improving the environmental performance of its products such as gas, which means less emissions caused by per unit energy consumption. Due to these factors, there is a certain deviation between the output of the previous widely used estimation method and the actual values of vehicle(s) energy consumption and emission. Thus, the estimation method needs to be updated and then calibrated based on the instrument vehicle driving experiments at a large scale under various traffic conditions.

4.2. Research Trends

Incorporating the Development Laws of V2X Technology

The development of things is a process. As the application of emerging informatization technologies in transportation systems, V2X technology cannot achieve its development overnight. However, the penetration and reliability of V2X technology were assumed as 100% in most of the previous studies, which deviates from the objective development laws of things. To further develop and enrich the traffic flow, it is necessary to incorporate the penetration and the reliability of V2X technology in future research on car-following behavior. Specifically, further works should pay more attention to the impacts of various V2X technologies and the penetration/reliability/performance/availability of the devices on car-following behavior and traffic flow in the different development stages of the V2X environment.

Considering the Driver/Vehicle Attribute in Modeling Car-following Behavior

The drivers’ car-following behavior is essentially the implementation of their subjective driving will, and the vehicle is the specific carrier to implement the will. Thus, the attributes of driver and vehicle will exert significant impacts on car-following behavior. To be specific, drivers with different attributes may exhibit different car-following behavior under the same conditions, and the same driver may also exhibit different car-following behavior under the same conditions when driving vehicles with different attributes. In addition to the attributes of the object vehicle and its driver, the attributes of other vehicles and their drivers will also impact the car-following behavior of the object vehicle, which has been confirmed in several previous studies. In the V2X environment, it is possible to collect and exchange information about the attributes of the connected vehicles in the system and their drivers. However, the impacts of this kind of information have not been explored. Considering that the automatic controller cannot fully replace the human driver in the foreseeable future, it is necessary to conduct research on the impacts of the attributes of the vehicles and their drivers on car-following behavior and traffic flow in the V2X environment.

Comprehensively Incorporating the Various Information Sources

It is very limited for human drivers to obtain information by relying on themselves. However, in the V2X environment, the driver can theoretically obtain information on all vehicles in the system by utilizing the relevant devices. However, the exploration of the impacts of different information on car-following behavior and traffic flow in the previous works is isolated. Thus, it is necessary to discuss these impacts comprehensively and comparatively. Based on this, the impacts of various information sources and their aggregation on car-following behavior and traffic flow under different conditions can be analyzed. Further considering the limitation of a driver’s energy and attention, personalized information schemes can be established for different drivers under different conditions, which has significance for the development of V2X technology.

Focus on the Car-following Behavior Mechanism Affected by Various Information Sources

The majority of attention in the previous works was paid to the external characteristics of car-following behavior, although the extended/improved models based on the traditional car-following models such as the FVD model can describe the car-following behavior characteristics under special conditions with considerable high accuracy. The nature, i.e., the internal mechanism, of car-following behavior has not received enough attention. Human behavior, including that of car-following, is the result of the interaction of the person’s internal subjective will, emotion, personality, and other factors. “All conscious actions of human beings are to enhance their own happiness and satisfaction”, as pointed out by Mises. Corresponding with car-following behavior, it is the process by which drivers pursue their desired car-following state. Based on the characteristics of car-following behavior affected by various sources of information, it will be a major and significant issue of future research to explore in depth the drivers’ decision-making and behavior mechanisms in the car-following process in the V2X environment.

Updating the Application Methods of Car-following Models

Application of the theoretical models is a necessary process to achieve their value. As the core of traffic flow theory, the status of car-following models is determined by their role as the theoretical basis in most traffic flow studies. In the V2X environment, the improved informatization degree makes the present-day traffic environment different from that of the past, which has made profound changes in the application of car-following models. The first issue in future works is to construct a large-scale open-source data set collected from the V2X environment. On the one hand, widely used data sets such as the NGSIM cannot be employed in the V2X environment, and there is an urgency to construct a large-scale high-precision open-source data set about the car-following process in the V2X environment, which is vital for applying the established models. On the other hand, when dealing with emerging technologies, opportunities and challenges usually coexist. With the application of V2X technology, it is easier to collect massive amounts of information, especially under the natural driving condition, about the units in the system to form the data set. In addition, there are other new technologies, such as the intellectualization and the new energy technology, along with the V2X, that will significantly influence the transportation system. Application of the intellectualization technology will further impact the operating and stability characteristics of traffic flow, and applications of the new energy technology will change the characteristics of energy consumption and emission. It is another major issue in future research to update the research on car-following models’ applications, represented by analyzing the operating and stability characteristics of traffic flow, and estimating energy consumption and emission, which may combine with the industry standard with the penetration of the aforementioned technology.

5. Conclusions

The informatization and intellectualization degree of the transportation systems will be significantly improved with the application of V2X and other relevant technologies. In the new traffic environment, there are changes in the characteristics of drivers’ car-following behavior. A certain number of studies on the car-following models and their applications have been carried out by many scholars, and achievements have been made. In this paper, we first briefly reviewed the development process of traditional car-following models. Second, the relevant and representative studies were reviewed by dividing them into three aspects, which, respectively, are the impacts of V2X technology, the car-following models considering the impacts of V2X technology, and the applications of these models. Finally, the achievements, as well as the existing shortcomings, were summarized, and, based on this, the major issues in the further exploration were discussed. We hope the results of this paper can provide a reference for further research on the car-following model and its applications in the V2X environment, and contribute to updating and enriching traffic flow theory.