Abstract
Numerous middleware application programming interfaces (APIs) and protocols were introduced in the literature in order to facilitate the application development of the Internet of Things (IoT). Such applications are built on reliable or even unreliable protocols that may implement different quality-of-service (QoS) delivery modes. The exploitation of these protocols, APIs and QoS modes, can satisfy QoS requirements in critical IoT applications (e.g., emergency response operations). To study QoS in IoT applications, it is essential to leverage a performance analysis methodology. Queueing-network models offer a modeling and analysis framework that can be adopted for the IoT interactions of QoS representation through either analytical or simulation models. In this paper, various types of queueing models are presented that can be used for the representation of various QoS settings of IoT interactions. In particular, we propose queueing models to represent message-drop probabilities, intermittent mobile connectivity, message availability or validity, the prioritization of important information, and the processing or transmission of messages. Our simulation models demonstrate the significant effect on delivery success rates and response times when QoS settings are varied.
1. Introduction
The Internet of Things (IoT) promises the integration of the physical world into computer-based systems. IoT devices, featuring sensing capabilities, are deployed in many application domains, including community spaces, smart buildings, and intelligent transportation. By exploiting the information that IoT devices can provide, peoples’ quality of life and safety can be substantially improved. For instance, in [1,2], IoT devices are exploited to monitor offices or homes for possible seismic activity. Such an application provides critical information, and it is anticipated to function timely and reliably. Hence, identifying a methodology for the analysis and performance modeling of IoT applications is of great significance. IoT devices can be inexpensive, low-powered, and mobile; regarding their deployment environment, applications that utilize them have different characteristics.
More precisely, the following quality-of-service (QoS) constraints can be identified: (i) limited memory of low-cost devices, (ii) limited data availability or validity, (iii) intermittent (mobile) device connectivity, and (iv) urgent data delivery. Furthermore, IoT applications are built on application programming interfaces (APIs) and reliable or unreliable protocols that introduce additional QoS constraints [3,4]. Hence, these constraints pose important challenges for IoT performance analysis.
Existing efforts [5,6,7] concerning both the design and the evaluation of mobile systems under particular constraints (e.g., limited resources or intermittent availability) rely on queueing theory [8]. Key IoT protocols were evaluated with regard to metrics such as delivery success rates and response times [9,10]. However, such efforts are protocol-specific; thus, the research community analyzed the performance of well-known interaction paradigms [11,12] that may abstract different IoT protocols. The publish/subscribe paradigm was analyzed using formal models [13] and evaluated using queueing networks [14] or queueing Petri nets [15]. Queueing networks can be considered as networks of connected service centers that provide simulation or analytical solutions for various performance measures (e.g., response time).
Combining separate service centers in order to form a queueing network enables us to model an IoT interaction. Some of the queueing models presented in this paper were investigated in the context of previous works. In particular, in [16,17,18,19], we identified a framework where various middleware protocol nodes (e.g., clients, servers, and brokers) are analyzed as queues while exchanged messages are represented as served jobs. To model QoS settings such as the intermittent connectivity [20] of mobile things, a separated queueing model was investigated with the aid of an ON/OFF queueing model [16,17]. The applicability of our models was demonstrated in [16,17,18,21,22,23] for the performance of publish/subscribe and data-streaming systems, respectively. In [19], we applied our approach to analyze the performance of IoT devices with heterogeneous QoS settings.
This paper expands upon our previous work [24] that provides a summary of queueing models that represent the aforementioned QoS constraints of IoT applications. In this paper, we include two queueing systems that model the processing or transmission of diverse IoT messages (e.g., video data vs. temperature data) and the prioritization of urgent data in critical IoT applications (e.g., structural fire scenarios). The key contributions of this paper are:
- Description of a generalized ON/OFF model that includes message losses and message join probabilities.
- Introduction of two queueing systems that model diverse message transmission, processing, and prioritization on the basis of delivery urgency requirements.
- Description of additional features for queueing models that represent message availability and resource-constrained devices.
- Comparison of different queueing models in terms of delivery success rate and response time through simulation-based experiments.
The rest of this paper is organized as follows: related work is discussed in Section 2. In Section 3, we describe the queueing models that represent various QoS settings of IoT interactions and applications. In Section 4, we compare the performance of queueing models when message availabilities, message join probabilities, and finite buffer capacities are considered. In addition, we show how the presented queueing models can be leveraged to properly configure and tune an IoT system. We conclude this paper and provide possible future extensions in Section 5.
2. Related Work
Today’s IoT applications consist of IoT devices that employ existing APIs and (IP-based) IoT protocols such as CoAP, MQTT, DPWS, XAMPP, and ZeroMQ [10,25] to exchange data. To guarantee specific response times and data delivery success rates between things, each protocol provides several quality-of-service (QoS) features. Initially, it inherits different characteristics from the underlying transport (TCP/UDP) mechanisms. Subsequently, it supports different modes of message delivery. For instance, CoAP offers a choice between “confirmable” and “nonconfirmable”, whereas MQTT support three choices (“fire and forget”,“delivered at least once”, and “delivered exactly once”) [4]. Furthermore, devices that employ such protocols can be mobile (e.g, wearable devices), while IoT applications may need to guarantee the freshness of provided information dropping (possibly less important) messages (e.g., mission-critical information for public safety [2]).
In [3,9,10] the trade-off between response times and delivery success rates by using key IoT protocols is evaluated. However, such methods are protocol-specific and limit the application designer upon the introduction of a new IoT protocol. Regarding middleware protocols, queueing Petri nets (QPNs) were used in [15] for accurate performance prediction. However, QPNs, while highly expressive in representing parallelism, are suited for small-to-moderate size systems and intake considerable computational resources [26]. Several existing efforts concerning the design and evaluation of mobile systems aim at guaranteeing QoS requirements under several constraints (e.g., intermittent availability and limited resources) [27,28,29]. The used evaluation methods were mainly derived from the field of queueing theory.
Several existing efforts support message dropping such as RabbitMQ, ActiveMQ, and mosquitto message brokers via maximum queue capacity [30]. To ensure message timeliness, message losses occur due to the validity or availability periods that can be assigned to every message through pub/sub protocols and APIs (e.g., the JMS API). More sophisticated approaches support semiprobabilistic delivery [31] or take into account subscriber preferences [32,33,34]. To allow for the reliable and timely data exchange, existing solutions manipulate data at both the middleware and network layers. Early middleware-based solutions [35,36,37] support prioritization or bandwidth allocation based on available system capacity, data relevance, and data importance. More recent solutions assign priorities on the basis of the validity span of published data and subscriptions [38], or on the basis of delay and reliability requirements [39]. Currently, standardized message brokers such as RabbitMQ and ActiveMQ support the assignment of priorities at the publisher side prior to the emission of a message.
In this paper, we model the performance of data exchange in the IoT by relying on queueing-network models (QNMs) [14,40]. QNMs have been extensively applied to represent and analyze communication and computer systems, and proven to be simple and powerful tools for application designers with regard to system performance evaluation and prediction. While in [27,28] the authors evaluated the performance of WiFi mobile users via an ON/OFF queue, this work leverages and adapts this queue as part of a QNM that represents the mobile behavior of IoT devices. To represent the maximal capacity of IoT system components such as pub/sub message brokers (RabbitMQ, ActiveMQ), a specific buffer size can be applied to any queue of the QNM. In addition, to represent message losses occurring in such brokers via APIs or protocols (e.g., JMS), a validity or availability (lifetime) period can be applied to each message entering the QNM. To represent losses occurring due to the protocol leveraged for data exchange (e.g., CoAP deployed over UDP [25]), the ON/OFF loss model can be used, which drops messages when the queueing server is not active. We also introduce a model for message dropping by relying on probabilistic techniques. Lastly, to represent IoT systems that consider the data recipients’ preferences [32,33,34] to deliver different types of data (message sizes, important, etc.) [35,36,38,39], multiclass and priority queues are introduced where different classes of messages can be assigned with different priorities. To summarize, application designers are able to analyze and configure certain system aspects (middleware QoS delivery modes, network and user connectivity, message dropping rates, system resources, priority levels, message sizes) by combining the provided queueing models in order to tune and guarantee the appropriate response time and delivery success rate between IoT devices.
3. Queueing Models
In this section, we provide some necessary definitions of the queueing models that were adopted in our simulation-based methodology.
3.1. M/M/1 Model
This queue is used to model uninterrupted service of messages (transmission, reception or processing) as part of an (end-to-end) IoT interaction. It corresponds to the classical M/M/1 queue (Figure 1a) where Poisson arrivals are serviced by a single server for an exponentially distributed service time.
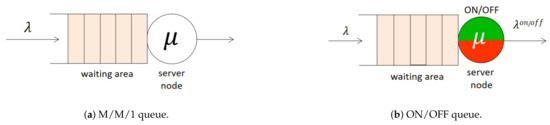
Figure 1.
M/M/1 and ON/OFF queues.
An M/M/1 queue () can be defined via the tuple:
where is the message arrival rate to the queue and is the service rate of messages. Let D = 1/ be the service demand for the processing delay (service time) of a message. On the basis of [14], the time that a message remains in a M/M/1 system (corresponding to queueing time + service time; we also call it mean response time) is determined via
3.2. ON/OFF Model
In Figure 1b, we introduce the intermittent (ON/OFF) queue, so as to capture the mobile peer’s connections and disconnections. Messages arrive in the system following a Poisson process with rate > 0, and are placed in a queue waiting to be “served” with rate > 0 (also exponentially distributed).
With regard to the server, we assumed that its operation followed an on–off procedure. More specifically, the server remains for an exponentially distributed time, with parameter , in the ON state. While in that state, the server provides service to messages. Let be the time during which the server is ON. Upon the expiration of this time, the server enters the OFF state for an exponentially distributed period with rate . While in that state, the server stops providing service to messages. Let be the time during which the server is OFF. Similar to the M/M/1 queue, an ON/OFF queue can be defined via the tuple:
where is the messages’ arrival rate, is the messages’ output rate, and is the service rate for the messages’ processing during . Output process is intermittent since, during intervals, no messages depart from the queue. Regarding the case where expires while a message is still under service, we assumed that the server stops the processing of the message and continues in the next period.
We denote by the mean response time for the queue, i.e., the time that a message spends in the system.
In [16,17,19], we provided the following formula for the estimation of :
where refers to the average number of messages that exist in the system (both in the server and the queue) [17].
3.3. Probabilistic ON/OFF Model
The reduction in queueing delays that may appear in the ON/OFF model can be addressed via the probabilistic ON/OFF model (Figure 2a).

Figure 2.
Probabilistic and loss ON/OFF queues.
In this model, the arrival process remains Poisson, and messages wait to be served while the server is ON. However, when the server is OFF, messages may leave the system with probability or enter the queue with probability . The probabilistic ON/OFF queue can be defined via the tuple:
where refers to the messages’ arrival rate, refers to the probability of entering the queue, is the messages’ output rate, and is the service rate (during ) for the message transmission. When = 1, we have the ON/OFF model of Section 3.2 (i.e., during OFF periods, all messages enter the queue).
is the mean response time (the time during which a message remains in the system) for the queue. In [41], we provided the following formula for the estimation of :
where is the rate of messages served in the probabilistic ON/OFF queue .
Such a probabilistic ON/OFF model aids system designers in improving or tuning delays of components that transmit messages during period , but also may disconnect for a period . More specifically, such a component can represent an IoT sensor (which is resource-constrained as far as memory and energy are concerned) that can periodically be on sleep mode, while its probabilistic behavior can be defined via the application layer.
3.4. ON/OFF Loss Model
The ON/OFF models presented in the previous subsections do not consider the case of message losses (or message drops). All messages are either buffered before service or immediately served if the server is empty.
In order to model message losses, we consider the case of the ON/OFF loss queue where messages still arrive in the system according to a Poisson process (Figure 2b). Regarding the server function, we consider the following: while the server is ON, messages enter the queue and wait to be served with rate . When the server OFF, messages enter the queue, are served with rate > , and exit the system (i.e., messages are lost).
The assumption that messages are “served” with rate > was adopted because the ON/OFF loss queue is used for the performance analysis of an IoT mobile device that employs a middleware protocol. The latter introduces (message) losses since it builds atop UDP and does not install a logical sender/receiver session (i.e., there is QoS guarantee for messages). Regarding the value of , it can be based on the network transmission delay of the end-to-end interaction. Regarding , we identify the network’s point where message losses occur. As an example, if the ON/OFF loss queue is used to model the intermittent connectivity of a wireless receiver, then we parameterize via the corresponding transmission delay of the network. The definition of such a delay can be based on how the sender interacts with the access point that the receiver connects or disconnects.
An ON/OFF loss queue can be defined according to the tuple:
where is the messages’ arrival rate; and are the messages’ output and processing rates during ON periods, respectively; and are the lost and processing rates during OFF periods. Both / rates were exponential since new messages split according to the / intervals.
3.5. Multiclass Model
This queue model’s uninterrupted serving (transmission, reception, or processing) of messages belonging to different classes. Such classes are used to categorize messages of IoT interactions that have different characteristics. For example, sensor data, video streaming services and transnational messaging require different transmission and processing resources. Each class corresponds to the common M/M/1 queue (see Figure 1a), featuring Poisson arrivals and exponential service times; thus, multiple M/M/1 queues are used to form the multiclass queue (see Figure 3a).

Figure 3.
Multiclass and priority queues.
A multiclass queue () is defined by the tuple:
where is the input rate of messages to the queue of each class and is the service rate for the processing of messages of . On the basis of standard solutions [14] for the multiclass queue, and given a message that belongs to a class , its time that remains in the system is given by
3.6. Nonpreemptive Priority and Multiclass Model
The multiclass queue (see Figure 3a) serves messages on the basis of a first-come first-served policy regardless of the class to which each message belongs. However, IoT systems handle the data of different application types such as emergency response, real-time, and video streaming. The nonpreemptive priority and multiclass (NPPM) enables the prioritization of messages belonging to different classes when being served (transmitted or processed). The NPPM is different from the nonpreemptive priority (NPP) queue, where classes of messages are created on the basis of the priority assigned to each message. As depicted in Figure 3b, messages belonging to n classes arrive according to Poisson processes and are then classified to different queues on the basis of their assigned priority. At the exit of each priority queue, messages are classified to be served (on the basis of exponential service times) depending on the class to which they belong (video-streaming data vs sensor data).
A nonpreemptive priority and multiclass queue () is defined by the tuple:
where is the input rate of messages to the queue of each class , is the service rate for the processing of messages of and is the assigned priority to each class . Given a message that belongs to a class and is assigned with priority , the time that it remains is given by:
where is the number of messages classified to and assigned with priority in the system (queue + server) of . We omitted the proof of (11) due to space constraints, but analysis is similar to that in Section 3.4.2 in [8] (provided in [23]).
3.7. Additional Features
Up to this point, we considered queueing models of which the buffers have infinite capacity, and arriving messages simultaneously have an infinite lifetime. This affects both the ratio of successfully served messages and the response time. However, it may be unrealistic to model IoT interactions with such characteristics. As an example, in the case of the long disconnection period of an IoT sensor (e.g., 30 min), the produced messages may well exceed the buffer capacity of the IoT sensor, and some of the oldest messages (data) may simultaneously become obsolete. We now describe the features that can consider such constraints and apply them to the already defined queueing models.
3.7.1. Lifetime Messages in Queueing Networks
As already discussed, a queueing network consists of a network of (connected) queues used for the performance modelling of a system. As an example, in the context of this paper, IoT interactions can be modeled via the creation of queueing networks that consist of queueing models already described in previous subsections. According to Figure 4a, messages that have an arrival rate are processed in the first queue of a queueing network. Such messages have a lifetime period attributed to them upon their creation which expresses the validity of the message inside the (queueing) network. Hence, as soon as the lifetime of a message elapses, the message leaves the queueing network and is said to be expired.
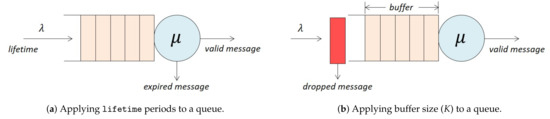
Figure 4.
Queues with event expirations and finite capacity.
To take into account the case of an expired message, we consider the time that a message spends in both server and queue. By assuming that a queueing network includes only one M/M/1 queue, a message reneges when a certain lifetime period passes without its service having started. According to the literature, such a model is the M/M/1 queue with reneging or impatient customers [42,43,44]. In this paper, we present the simulation of such a model via our simulator and incorporate the case of reneging in our ON/OFF models. Hence, it is possible for system designers to create networks of queues, including various queueing models enriched with the feature of the lifetime period.
3.7.2. Queues of Finite Capacity
According to this feature, a specific buffer size is considered for each queue that prevents the system from handling more than K messages (in both queue and server). Such a feature prevents the system from storing messages for a long period of time in devices of limited capacity. More specifically, consider Figure 4b, where messages arrive in the queue with a rate . If condition + > K is true when a new message arrives in the system, then the message is dropped. Otherwise, the message joins the queue and waits to be served. According to the literature, an M/M/1 queue with a limited buffer size is notated as M/M/1/K [8]. In the case of our model, we incorporated system size K in the M/M/1 and the ON/OFF queues by adding it to corresponding Tuples (1),(3), (5), and (7).
4. Experiment Results
For our experiments, we considered our simulator (MobileJINQS) that was presented in [17] and is an extension of the Java implementation of the JINQS simulator [45]. In this paper, we extended our simulator to include the ON/OFF models of Section 3. In our experiments, we assumed that each ON/OFF model represented a mobile sender that uses various QoS settings for the transmission of messages. Such a mobile sender generates 7,500,000 messages so as to accurately determine the mean response times and success rates per message. Then, we let the mobile peer connect and disconnect in the time scale of seconds.
4.1. ON–OFF Model
We set the ON/OFF mode parameters as follows: (i) the server remains in the ON and OFF states for exponentially distributed time periods = = 20/40/60 s; thus, the server changes its state every 20, 40, and 60 s, respectively; (ii) messages are processed with a mean service demand D = 0.125 s; (iii) there is sufficient buffer capacity so that no messages are dropped; and (iv) messages arrive to the queue with a mean rate varying from 0.05 to 4 messages per sec ( = 4 messages/s). By applying rates greater than 4 messages/sec, the system saturates. Using the above settings in our simulator, we ran the system and derived the simulated curve of the mean response time for several rates as depicted in Figure 5.
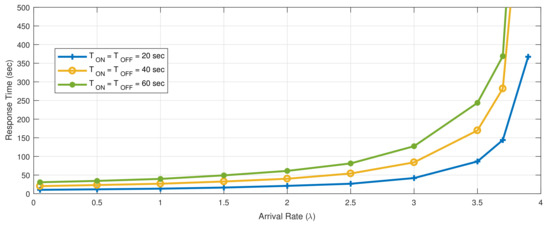
Figure 5.
Response time for various , parameters.
4.2. ON/OFF Model with QoS Features
We then set the following parameters to the ON/OFF model: (i) the server remains in states ON and OFF for time periods = = 20 s (exponentially distributed); (ii) the mean service demand for message processing is D = 0.125 s; and (iii) message arrival rate varies from 0.05 to the maximal value of 3.9 messages/s. On the above basis, we set up four experiments (which correspond to different ON/OFF models) by considering the following QoS features: (1) = 1, lifetime = ∞ and K = ∞; (2) = 1, lifetime = 30 s, K = ∞; (3) = 0.75, lifetime = ∞, K = ∞; and (4) = 1, lifetime = ∞, K = 100.
Response times: For each of the four experiments above, we ran the corresponding ON/OFF model 10 times and derived the curves of Figure 6 on the basis of the average values of these runs. According to Figure 6, the highest values of mean response times (∼10–360 s) were observed in the first experiment where messages were buffered and served (i.e., no message losses occurred). On the other hand, the lowest values of mean response times (∼5–10 s) were observed in the fourth experiment, where we considered the application of lifetime periods in messages. In the third experiment, where a certain buffer capacity was considered, mean response time varied from 10 to 16 s. Lastly, the fourth experiment provided low mean response times (∼8–14 s) for = 0.05–2 and higher response times (∼17–49 s) for = 2.5–3.9.
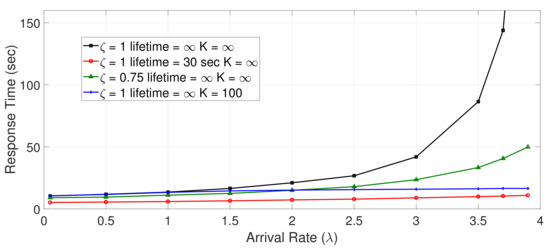
Figure 6.
Response time for various ON/OFF model parameters.
Success rate vs. response time: In order to investigate the trade-off between success rates and response times, the rates of successful message service are presented in Figure 7 for the same set of experiments. In the first experiment, there was a 100% message success rate since no messages were lost. Lowest rates were observed in the case of lifetime periods and increased arrival rates. In the third experiment, low arrival rates led to high message success rates (in the range of ∼90–100%), while higher arrival rates led to a decrease (∼87–77%). Lastly, the fourth experiment led to a stable message success rate (75%).
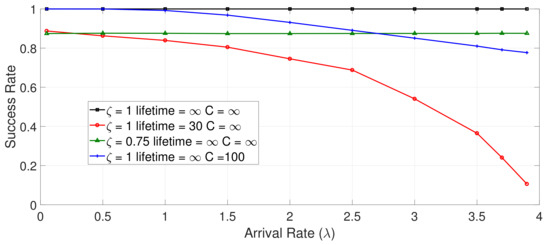
Figure 7.
Success rates for various ON/OFF model parameters.
4.3. Message Classes Assigned with Priorities
We then leveraged the nonpreemptive priority and multiclass simulation model to compare response times of different classes assigned with priorities. As depicted in Figure 8a, we defined 19 classes (i.e., ) with different arrival () and service () rates for each class . Depending on the values of , the queue (or IoT system that it represents) can be saturated. Let be server utilization (i.e., probability that the server is busy) of the nonpreemptive priority and multiclass queue. The queue remains unsaturated (i.e., queue stability is ensured) when . In Figure 8a, we defined ; thus, queue stability was ensured. As expected, lower priorities present higher response times. experienced a lower response time than that of despite the fact that was assigned with a lower priority. This is because our model enables system designers to assign different arrival or service rates to different classes (e.g., different groups of IoT data sizes to be transmitted with diverse importance).
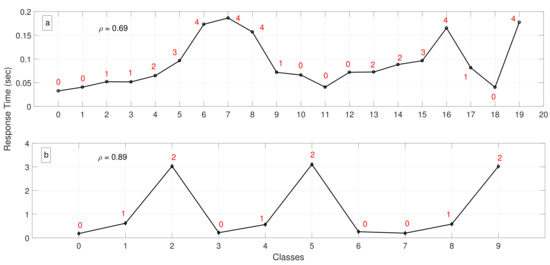
Figure 8.
Response time for various classes of messages assigned with different priority parameters.
In Figure 8b, we define 9 classes (i.e., ) but with the server utilization defined as . Therefore, the system was close to the saturation point, and classes assigned with lower priorities thereby experienced high response times. On the other hand, despite the fact that the system was almost saturated, high-priority classes experienced low response times.
4.4. IoT System Tuning
The queueing models presented in this paper can be employed to properly configure and tune an IoT system. For instance, suppose that an IoT designer is willing to deploy occupancy counters in a smart building. Such a sensor remains inactive (sleep mode) for a certain period; right afterwards, it becomes active to count people in the covered space. IoT designers can leverage the obtained results in Section 4.1 to either configure the inactive period or to estimate the response time for a default inactive period. For example, given min as the inactive period, s as the active period to count people and s as the service time required to count people, IoT designers can estimate the resulting response time. Now, suppose that data flowing from IoT sources are collected via a message broker to be disseminated to interested recipients. To guarantee the freshness of the occupancy data, IoT designers can apply dropping parameters K, , or lifetime to ensure that obsolete data are dropped. The presented methodology in Section 4.2 can be exploited to evaluate the trade-off between the resulting response time and delivery success rate, thereby guiding an IoT designer to select the most appropriate dropping mechanism. Lastly, suppose that the smart building hosts an IoT application for the creation of evacuation plans in case of an emergency by leveraging occupancy data and the building’s floor plans. To ensure that occupancy data flow quicker than other flows of data do, different classes with assigned priorities can be defined. The obtained results in Section 4.3 can help in this direction for evaluating the expected response times.
5. Conclusions
Modeling the performance of IoT applications is a tedious task. IoT messaging may lead to message losses or delays due to various QoS settings such as resource-constrained devices, message availability, and intermittent connectivity. In this paper, we summarized simulation-based queueing models that represent such QoS settings. Some of the presented models were investigated in the context of previous articles where their validation and evaluation has been performed in realistic application settings and using real data traces. Using the simulator we have developed, the trade-off between message success rates and response times can be evaluated for various queueing models. The latter may help system designers to create queueing networks that represent IoT interactions and analyze (or tune) their performance.
In future work, we will consider analytical models for queueing networks that include finite capacity buffers, lifetime periods, losses, ON/OFF probability, and message prioritization (via dropping probability).
Author Contributions
Conceptualization, G.B., I.M., N.G., and V.I.; formal analysis, G.B., I.M., N.G., and V.I.; investigation, G.B.; methodology, G.B. and I.M.; resources, I.M.; validation, G.B.; writing—original draft, G.B., I.M., N.G., and V.I.; writing—review and editing, G.B., I.M., N.G., and V.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable, the study does not report any data.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| IoT | Internet of Things |
| QoS | Quality of service |
| APIs | Application programming interfaces |
| NPP | Nonpreemptive priority |
| NPPM | Nonpreemptive priority and multiclass |
| JINQS | Network-of-queues = simulation |
| QPNs | Queueing Petri nets |
| QNMs | Queueing network models |
References
- Community Seismic Network. Available online: http://www.communityseismicnetwork.org (accessed on 1 May 2015).
- Cochran, E.; Lawrence, J.; Christensen, C.; Chung, A. A novel strong-motion seismic network for community participation in earthquake monitoring. IEEE Instrum. Meas. Mag. 2009, 12, 8–15. [Google Scholar] [CrossRef]
- De Caro, N.; Colitti, W.; Steenhaut, K.; Mangino, G.; Reali, G. Comparison of two lightweight protocols for smartphone-based sensing. In Proceedings of the IEEE 20th Symposium on Communications and Vehicular Technology in the Benelux (SCVT), Namur, Belgium, 21 November 2013. [Google Scholar]
- Lee, S.; Kim, H.; Hong, D.k.; Ju, H. Correlation analysis of MQTT loss and delay according to QoS level. In Proceedings of the International Conference on Information Networking (ICOIN), Bangkok, Thailand, 28–30 January 2013. [Google Scholar]
- Mehmeti, F.; Spyropoulos, T. Performance analysis of “on-the-spot” mobile data offloading. In Proceedings of the 2013 IEEE Global Communications Conference (GLOBECOM), Atlanta, GA, USA, 9–13 December 2013. [Google Scholar]
- Lee, K.; Lee, J.; Yi, Y.; Rhee, I.; Chong, S. Mobile Data Offloading: How Much Can WiFi Deliver? Available online: https://conferences.sigcomm.org/co-next/2010/CoNEXT_papers/26-Lee.pdf (accessed on 27 March 2021).
- Wu, H.; Wolter, K. Tradeoff analysis for mobile cloud offloading based on an additive energy-performance metric. In Proceedings of the 8th International Conference on Performance Evaluation Methodologies and Tools, Bratislava, Slovakia, 9–11 December 2014. [Google Scholar]
- Gross, D.; Shortle, J.; Thompson, J.; Harris, C. Fundamentals of Queueing Theory; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Durkop, L.; Czybik, B.; Jasperneite, J. Performance evaluation of M2M protocols over cellular networks in a lab environment. In Proceedings of the 18th International Conference on Intelligence in Next Generation Networks (ICIN), Paris, France, 17–19 February 2015. [Google Scholar]
- Fysarakis, K.; Askoxylakis, I.; Soultatos, O.; Papaefstathiou, I.; Manifavas, C.; Katos, V. Which IoT protocol? Comparing standardized approaches over a common M2M application. In Proceedings of the IEEE Global Communications Conference (GLOBECOM), Washington, DC, USA, 4–8 December 2016. [Google Scholar]
- Aldred, L.; van der Aalst, W.M.; Dumas, M.; ter Hofstede, A.H. On the notion of coupling in communication middleware. In Proceedings of the OTM Confederated International Conferences on the Move to Meaningful Internet Systems, Agia Napa, Cyprus, 31 October–4 November 2005. [Google Scholar]
- Kattepur, A.; Georgantas, N.; Bouloukakis, G.; Issarny, V. Analysis of timing constraints in heterogeneous middleware interactions. In Proceedings of the International Conference on Service-Oriented Computing, Goa, India, 16–19 November 2015. [Google Scholar]
- He, F.; Baresi, L.; Ghezzi, C.; Spoletini, P. Formal analysis of publish-subscribe systems by probabilistic timed automata. In Proceedings of the International Conference on Formal Techniques for Networked and Distributed Systems, Tallinn, Estonia, 27–29 June 2007. [Google Scholar]
- Lazowska, E.D.; Zahorjan, J.; Graham, G.S.; Sevcik, K.C. Quantitative System Performance: Computer System Analysis Using Queueing Network Models; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1984. [Google Scholar]
- Kounev, S.; Sachs, K.; Bacon, J.; Buchmann, A. A methodology for performance modeling of distributed event-based systems. In Proceedings of the 11th IEEE International Symposium on Object Oriented Real-Time Distributed Computing (ISORC), Orlando, FL, USA, 5–7 May 2008. [Google Scholar]
- Bouloukakis, G.; Georgantas, N.; Kattepur, A.; Issarny, V. Timeliness Evaluation of Intermittent Mobile Connectivity over Pub/Sub Systems. In Proceedings of the 8th ACM/SPEC on International Conference on Performance Engineering, L’Aquila, Italy, 22–26 April 2017. [Google Scholar]
- Bouloukakis, G.; Moscholios, I.; Georgantas, N.; Issarny, V. Performance Modeling of the Middleware Overlay Infrastructure of Mobile Things. In Proceedings of the IEEE International Conference on Communications, Paris, France, 21–25 May 2017. [Google Scholar]
- Bouloukakis, G.; Agarwal, R.; Georgantas, N.; Pathak, A.; Issarny, V. Leveraging cdr datasets for context-rich performance modeling of large-scale mobile pub/sub systems. In Proceedings of the IEEE 11th International Conference on Wireless and Mobile Computing, Networking and Communications (WiMob), Abu Dhabi, United Arab Emirates, 19–21 October 2015. [Google Scholar]
- Bouloukakis, G. Enabling Emergent Mobile Systems in the IoT: From Middleware-layer Communication Interoperability to Associated QoS Analysis. Ph.D. Thesis, Inria Paris, Paris, France, August 2017. [Google Scholar]
- Bajaj, G.; Bouloukakis, G.; Pathak, A.; Singh, P.; Georgantas, N.; Issarny, V. Toward enabling convenient urban transit through mobile crowdsensing. In Proceedings of the IEEE 18th International Conference on Intelligent Transportation Systems (ITSC), Gran Canaria, Spain, 15–18 September 2015. [Google Scholar]
- Gomes, R.; Bouloukakis, G.; Costa, F.; Georgantas, N.; da Rocha, R. Qos-aware resource allocation for mobile iot pub/sub systems. In Proceedings of the 8th International Conference on Internet of Things, Santa Barbara, CA, USA, 15–18 October 2018. [Google Scholar]
- Benson, K.; Bouloukakis, G.; Grant, C.; Issarny, V.; Mehrotra, S.; Moscholios, I.; Venkatasubramanian, N. Firedex: A prioritized iot data exchange middleware for emergency response. In Proceedings of the 19th International Middleware Conference, Rennes, France, 10–14 December 2018. [Google Scholar]
- Bouloukakis, G.; Benson, K.; Scalzotto, L.; Bellavista, P.; Grant, C.; Issarny, V.; Mehrotra, S.; Moscholios, I.; Venkatasubramanian, N. PrioDeX: A Data Exchange Middleware for Efficient Event Prioritization in SDN-based IoT Systems. Available online: https://hal.archives-ouvertes.fr/hal-03171358/ (accessed on 27 March 2021).
- Bouloukakis, G.; Moscholios, I.; Georgantas, N.; Issarny, V. Simulation-based queueing models for performance analysis of IoT applications. In Proceedings of the 2018 11th International Symposium on Communication Systems, Networks and Digital Signal Processing (CSNDSP), Budapest, Hungary, 18–20 July 2018. [Google Scholar]
- Karagiannis, V.; Chatzimisios, P.; Vazquez-Gallego, F.; Alonso-Zarate, J. A survey on application layer protocols for the internet of things. Trans. Iot Cloud Comput. 2015, 3, 11–17. [Google Scholar]
- Vernon, M.; Zahorjan, J.; Lazowska, E.D. A Comparison of Performance Petri Nets and Queuing Network Models; Technical Report; University of Wisconsin-Madison: Madison, WI, USA, 1986. [Google Scholar]
- Mehmeti, F.; Spyropoulos, T. Performance analysis of mobile data offloading in heterogeneous networks. IEEE Trans. Mob. Comput. 2016, 16, 482–497. [Google Scholar] [CrossRef]
- Lee, K.; Lee, J.; Yi, Y.; Rhee, I.; Chong, S. Mobile Data Offloading: How Much Can WiFi deliver? IEEE/ACM Trans. Netw. 2012, 21, 536–550. [Google Scholar] [CrossRef]
- Phung-Duc, T.; Masuyama, H.; Kasahara, S.; Takahashi, Y. A simple algorithm for the rate matrices of level-dependent QBD processes. In Proceedings of the 5th International Conference on Queueing Theory and Network Applications, Beijing, China, 1 June 2010. [Google Scholar]
- John, V.; Liu, X. A Survey of Distributed Message Broker Queues. Available online: https://arxiv.org/pdf/1704.00411.pdf (accessed on 27 March 2021).
- Gian, P.C.; Costa, P.; Picco, G.P. Publish-Subscribe on Sensor Networks: A Semi-probabilistic Approach. In Proceedings of the 2nd IEEE International Conference on Mobile Adhoc and Sensor Systems, Washington, DC, USA, 7–10 November 2005. [Google Scholar]
- Diallo, M.; Fdida, S.; Sourlas, V.; Flegkas, P.; Tassiulas, L. Leveraging caching for Internet-scale content-based publish/subscribe networks. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar]
- Pripuzic, K.; Zarko, I.P.; Aberer, K. Top-k/w publish/subscribe: Finding k most relevant publications in sliding time window w. In Proceedings of the second international conference on Distributed event-based systems, Rome, Italy, 1–4 July 2008. [Google Scholar]
- Salehi, P.; Zhang, K.; Jacobsen, H.A. Popsub: Improving resource utilization in distributed content-based publish/subscribe systems. In Proceedings of the 11th ACM International Conference on Distributed and Event-based Systems, Barcelona, Spain, 19–23 June 2017. [Google Scholar]
- Chakravarthy, S.; Vontella, N. A publish/subscribe based architecture of an alert server to support prioritized and persistent alerts. In Proceedings of the International Conference on Distributed Computing and Internet Technology, Bhubaneswar, India, 22–24 December 2004. [Google Scholar]
- Maheshwari, P.; Tang, H.; Liang, R. Enhancing web services with message-oriented middleware. In Proceedings of the IEEE International Conference on Web Services 2004, San Diego, CA, USA, 6–9 June 2004. [Google Scholar]
- Zhang, R.; Lu, C.; Abdelzaher, T.F.; Stankovic, J.A. Controlware: A middleware architecture for feedback control of software performance. In Proceedings of the 22nd International Conference on Distributed Computing Systems, Vienna, Austria, 2–5 July 2002. [Google Scholar]
- Saghian, M.; Ravanmehr, R. Publish/subscribe middleware for resource discovery in MANET. In Proceedings of the 2015 15th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing, Shenzhen, China, 4–7 May 2015. [Google Scholar]
- Wang, Y.; Zhang, Y.; Chen, J. Pursuing differentiated services in a sdn-based iot-oriented pub/sub system. In Proceedings of the 2017 IEEE International Conference on Web Services (ICWS), Honolulu, HI, USA, 25–30 June 2017. [Google Scholar]
- Baskett, F.; Chandy, K.M.; Muntz, R.R.; Palacios, F.G. Open, closed, and mixed networks of queues with different classes of customers. J. ACM (JACM) 1975, 22, 248–260. [Google Scholar] [CrossRef]
- Bouloukakis, G.; Moscholios, I.; Georgantas, N. Probabilistic Event Dropping for Intermittently Connected Subscribers over Pub/Sub Systems. In Proceedings of the IEEE International Conference on Communications (ICC), Shanghai, China, 21–23 May 2019. [Google Scholar]
- Montazer-Haghighi, A.; Medhi, J.; Mohanty, S.G. On a multiserver Markovian queueing system with balking and reneging. Comput. Oper. Res. 1986, 13, 421–425. [Google Scholar] [CrossRef]
- Abou-El-Ata, M.; Hariri, A. The M/M/c/N queue with balking and reneging. Comput. Oper. Res. 1992, 19, 713–716. [Google Scholar] [CrossRef]
- Yue, D.; Zhang, Y.; Yue, W. Optimal performance analysis of an M/M/1/N queue system with balking, reneging and server vacation. Int. J. Pure Appl. Math. 2006, 28, 101–115. [Google Scholar]
- Field, T. JINQS: An Extensible Library for Simulating Multiclass Queueing Networks, v1.0 User Guide. Available online: http://www.doc.ic.ac.uk/~ajf/Software/manual.pdf (accessed on 27 March 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).