Abstract
Network tomography has emerged as one of the lean approaches for efficient network monitoring, especially aiming at addressing the ever-increasing requirements for scaling and efficiency in modern network architectures and infrastructures. In this paper, we explore network coding and compressed sensing as enabling technologies in the context of network tomography. Both approaches capitalize on algebraic tools for achieving accuracy while allowing scaling of operation as the size of the monitored network increases. Initially, a brief overview of the tomographic problems and the related classification of methods is provided to better comprehend the problems encountered and solutions provided to date. Subsequently, we present representative approaches that employ either one of the aforementioned technologies and we comparatively describe their fundamental operation. Eventually, we provide a qualitative comparison of features and approaches that can be used for further research and technology development for network monitoring in future Internet infrastructures.
1. Introduction
Modern communication network infrastructures exhibit the tendency of more heterogeneous and larger topologies, larger volumes of transferred data, and faster transmission rates. Traditional management and monitoring frameworks require reconsideration and, in some cases, clean-slate approaches in order to cope with the emerging scales of operation. Network monitoring is one of the prominent functions that needs to be revisited under the aforementioned perspective and will be a determinant factor for creating advanced communication infrastructures in the future Internet. Towards this direction, in this review, we focus specifically on network tomography.
Network tomography (NT) is a network-monitoring technique that involves estimating network performance and Quality of Service (QoS) parameters based on traffic measurements at a limited subset of the network’s nodes (where each node may represent an end-system, a router, or a subnetwork) [1,2]. The goal is to infer desired characteristics, which are not easily measured directly, by their aggregate values. These values are possible to obtain through measurements collected at accessible nodes/links under the administrative responsibility of the network authority. Among other benefits, such an approach mitigates the need for special purpose cooperation and participation from the various network elements while reducing the associated traffic-overhead footprint to the network load compared to well-known tools such as traceroute and ping, which require Internet Control Message Protocol (ICMP) responses from routers. Furthermore, this approach avoids the current problem of an increasing number of Internet routers blocking traceroute requests due to privacy and security concerns (such routers are referred to as anonymous routers).
Network tomography can be realized in many different ways, each focusing on different goals. Three main categories can be identified: (1) link-level parameter estimation, (2) path-level traffic intensity estimation, and (3) topology inference, which are elaborated on in Section 2.2. These goals can be achieved by means of various approaches such as hierarchical clustering, Expectation-Maximization (EM) algorithm, Markov Chain Monte Carlo (MCMC) sampling, Method of Moments (MoM) estimation, and other classical and Bayesian statistical methods. In this review, we focus on two families of approaches, namely network coding and compressed sensing, due to the fact that (a) they were recently introduced in the field of NT, (b) they exhibit great potential for designing highly accurate schemes with low complexity, and( c) they form two independent methods, which can be used in a broader spectrum of problems and in a complementary fashion.
Network coding (NC) has received considerable attention in recent years due to its potential of maximizing network resource utilization up to the theoretical upper bound (i.e., max-flow/min-cut) and its promising applications in the context of ad hoc networks, overlay infrastructures, and sensor networks. The basic concept of network coding is that the intermediate nodes of the network (i.e., not sources and destinations) are able to linearly combine, i.e., perform additions and multiplications of the packets they receive, and to send out the resulted linear combinations on their outgoing links [3,4]. The packets received eventually at the destination(s) can be written as a linear combination of the packets sent out by the source(s). This broadcasting nature of network coding ensures that a transmitted probe will traverse almost every path between the two boundary nodes (located at the network edge) and can be exploited in the context of network tomography. In particular, the observations obtained at the end-hosts depend on the underlying network topology and can be used to deterministically recover it. Furthermore, in the presence of packet losses, one successfully received probe per end-to-end path is sufficient (there is no need for extensive packet loss statistics), leading to rapid topology discovery. Compared with the traditional methods that are based on measuring monotonic properties of shared paths that do not decrease as the number of traversed links increases (e.g., loss rates, mean delay, delay covariance, link utilization, etc.), the number of required probes under network coding is significantly smaller. Additionally, the complexity of the local additions and multiplications at the node level is not particularly high.
Compressed sensing (CS) is a signal-processing technique for efficiently acquiring and reconstructing a signal, which has demonstrated a wide applicability in communications systems [5]. More precisely, it is a method to obtain a unique solution from an under-determined linear system (when the number of measurements is less than that of unknowns, the system is under determined and its solution is no longer unique) by taking advantage of the prior knowledge that the true solution is sparse [6]. A signal is said to be sparse (or exactly sparse), when most of its components are exactly equal to zero. It is said to be k-sparse, when it has at most k nonzero elements. The signals that can be well approximated by sparse signals are called compressible (approximately sparse or relatively sparse). The basic principle of compressed sensing is that, through -optimization (i.e., minimization of the -norm), the sparsity of a signal can be exploited to recover it from far fewer samples than required by the Nyquist–Shannon sampling theorem [7]. The goal is to reconstruct a finite-dimensional sparse vector based on its linear measurements of dimension smaller than the size of the unknown sparse vector. The application of compressed sensing in network tomography stems from the observation that, usually in typical networks, only a limited number of links exhibit large delays or high loss rates. If the focus is on the identification of those bottleneck links, one can reasonably assume that the vector of the unknown parameters of interest will be sparse (or in other words, compressible).
In this article, we explore in more detail network coding and compressed sensing as enabling technologies that can be applied in tomographic approaches from the whole range of network tomography taxonomy, with the goal of improving the estimation accuracy, the time and computational complexity, the probing and operational cost, as well as facilitating link identifiability. The rest of this review is organized as follows. Section 2 presents the fundamental concepts of network tomography and some interesting classifications of relevant approaches. Section 3 presents approaches in the class of network coding, while Section 4 presents works belonging in the class of compressed sensing. Section 5 provides some overall qualitative discussion on the presented techniques, and finally, Section 6 concludes the paper.
2. Network Tomography Model and Classification Overview
2.1. Linear Measurement Model and Basic Definitions
Network tomography falls in the category of statistical inverse problems. More precisely, network tomography problems can be approximately described by the linear model , where is an I-dimensional vector of measurements taken at a specific time t at various sites/nodes, is the routing matrix (with I rows corresponding to measurement paths and J columns corresponding to links of which the unknown parameters are of interest) that represents the topology of the network, is a J-dimensional vector of time-dependent performance parameters like mean delays and logarithms of loss probabilities, and is a noise vector. In some cases, the random vector has an underlying parameterized distribution, and we are interested in those parameters. The routing matrix is usually binary (entries are 0 or 1, indicating the participation of a particular link—denoted by column index—in a routing/measurement path—denoted by row index), but its entries can also be probabilities in the case of multiple paths in a network due to load balancing considerations.
Network inference refers to the inverse problem of estimating the statistics of the unobserved random vector given the linear measurements model and a set of assumptions regarding the statistical distribution of the noise or the introduction of some form or regularization to induce identifiability. From the perspective of linear algebra, the components of are uniquely identifiable if and only if the number of linear independent measurement paths equals the number of -components. The challenge lies in the fact that is usually an ill-posed matrix (i.e., the number of observations I is much smaller than the number of variables J) and, hence, non-invertible. Thus, the number of variables to be estimated is much larger than the number of equations, resulting in the non-uniqueness of solutions.
Network tomography problems require the estimation of a possibly large number of instances of parameters such as link loss rates, delay distributions, and traffic intensity, which are spatially distributed. To face these estimation tasks, researchers nowadays abandon intricate and complex statistical models of network traffic and adopt simpler models that do not introduce significant estimation errors and reduce the complexity. The most common relevant assumptions made are the spatial independence of the link states (Assumption 1) and the stationary behavior of network traffic (Assumption 2).
Assumption 1 (Spatial Independence).
The link states are independent from each other (but not identically distributed).
Assumption 2 (Temporal Stationarity).
The link states are stationary during the measurement period.
Although the aforementioned simpler models are not suitable for studying network queuing dynamics and for making detailed analyses of the network behavior, they are sufficient for the inference of general performance statistics.
2.2. Network Tomography Classification Overview
Network tomography can be classified into various categories depending on the type of the observed data (measurements) and the performance parameters of interest [1,2]. More precisely, we can distinguish the following three wide classes of tomographic approaches (Figure 1):
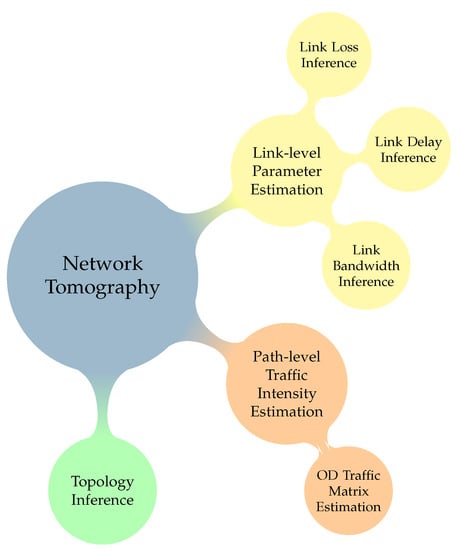
Figure 1.
Network tomography classes.
- Link-level parameter estimation: vector consists of end-to-end traffic measurements such as accounts of delivered/lost packets and time delays (differences) between packet transmissions and receptions. The unknown variables (i.e., vector ) are the link metrics, which are typically additive, meaning that the path metric obtained by combining multiple serial links is the sum of the individual link metrics. Time delays are a good example of an additive metric, whereas a multiplicative metric, such as loss rates, can be expressed in an additive form by using the logarithmic function. Since these end-to-end path measurements are carried out between pairs of nodes with monitoring capabilities, the decision of which nodes will be chosen as monitors becomes a key problem. This category can be further divided based on the different application contexts and the specific link metric used (e.g., loss tomography [8,9,10], delay tomography [11,12,13], bandwidth tomography [14], etc.)
- Path-level traffic intensity estimation [15,16,17]: the goal is to estimate the traffic volume (or to infer the distribution of the flowing traffic) of end-to-end routes between all pairs of nodes in the network based on the observed traffic volumes on individual links. At a practical level, the involved link aggregate data are acquired by monitoring the total number of packets traversing the respective nodes. The combination of the traffic intensities of all these origin–destination pairs forms the origin–destination (OD) traffic matrix. Hence, this category aims at the inference of OD traffic matrices () based on (aggregated) link traffic counts (). This is the original NT problem studied in [18].
- Topology inference [19,20,21,22,23]: the network topology, which is expressed by the routing matrix , is unknown. Hence, in this category, the goal is the inference of the topology based on end-to-end measurements conducted at the network edge and obtained without the cooperation and the participation of the internal nodes. These measurements evaluate the degree of correlation between receivers. Network topology is usually examined in terms of the logical topology, which is defined by the branching points between paths to different destination nodes. Internal nodes where no branching of traffic occurs do not appear in the logical topology. The central idea of the methods in this category is to obtain a measure of similarity between pairs of terminal nodes (i.e., source and destination) by means of end-to-end measurements that behave as a monotonically increasing function of the number of shared links or common queues between the two receiving nodes. Knowledge of the pairwise similarity metric values under an additive metric is sufficient to completely identify the logical topology by employing various statistical techniques such as hierarchical clustering, maximum likelihood, and Bayesian inference.
Similarly, network tomography can be further categorized based on the measurement methodology, i.e., the way in which the end-to-end or link-level measurements are acquired. In particular, the distinction is made between active network probing and passive traffic monitoring. Active techniques collect measurements by explicitly sending out probe packets between the participating nodes in order to measure a specific end-to-end characteristic. Passive techniques observe already existing network traffic and occurring packet sequences. Since they analyze the regular data flow, no extra network resources are consumed. However, because of exclusively observing existing communications, there is a negative impact in terms of flexibility. In either case, there exist development and administrative costs regarding the deployment of data collection and/or probing software, which directly affect scalability.
3. Network Coding Enabled Network Tomography
The operation of today’s communication network infrastructures relies on the fundamental assumption that, although independent information flows may share network resources, the data themselves are separated. Network coding is a new paradigm based on the idea that independent data streams can be linearly combined throughout the network in order to achieve benefits in terms of throughput and robustness. As demonstrated in [3,4], optimal multicast throughput (i.e., the min-cut/max-flow of the network to each receiver) can be achieved if intermediate nodes can perform local additions (i.e., Exclusive-Or (XOR) operations) on their incoming packets. Furthermore, network coding can be leveraged in the setting of packet erasure networks to achieve both optimal rate and optimal delay at the same time [24]. The basic premise of network coding is to make the network behave as a linear system with a transfer function that depends on the topology. Nodes are able to linearly combine (i.e., perform additions and multiplications on) the packets received on their incoming links and to broadcast the resulted packets on all of their outgoing links. The combined packets eventually observed at the end receivers can be leveraged to recover the original information by solving a set of linear equations over the employed finite field [25].
To provide a more educated overview of NC, assuming that each packet consists of L bits (shorter packets are padded with trailing zeros) and interpreting l consecutive bits of a packet as a symbol over the finite field with (each packet consists of a vector of symbols), under linear network coding, the outgoing packets are linear combinations of the incoming ones with addition and multiplication being performed over the field . Given the series of original packets that is generated by one or several sources, a combined/coded packet contains the encoding vector (i.e., the coefficients with ) and the information vector (i.e, the encoded data) , where the summation occurs for every symbol position (i.e., , with and as the kth symbol of and D, respectively). Encoding is performed recursively, over the original and/or previously encoded packets. An end receiver observing the sets , where and are the encoding and the information vectors of the i-th received packet, respectively, has to solve the system with unknowns . The coefficients over the field can be chosen uniformly at random by each node (Random Linear Network Coding—RLNC). Alternatively, network codes can be constructed by deterministic algorithms (e.g., the polynomial time algorithm presented in [26]).
In the next subsections, we present more particular approaches exploiting network coding in tomography, centered around specific problem areas.
3.1. Topology Inference
Among the first efforts to leverage network coding in order to improve network tomography was the one presented in [27]. In particular, the authors address the problem of topology inference of binary trees, where multiple sources and receivers are employed at the edge of the network and the intermediate nodes are equipped with simple network coding capabilities (i.e., local XOR operations). The basic idea of their approach is that the combination of the incoming information flows by the intermediate nodes reveals information about the network structure that can be utilized during the inference. To that end, they develop an algorithm that exploits these topology dependent correlations and can deterministically infer the underlying topology in one pass, when there are no packet losses. Furthermore, in the presence of packet losses, the rapid discovery of the network topology is still possible after a relatively small number of probes, since the only thing required is one successfully received probe packet per end-to-end path.
More precisely, the proposed algorithm starts by randomly choosing two of the tree leaves as sources ( and ) that send probe packets ( and , respectively) to the remaining nodes in the set of leaves. The intermediate nodes either receive one probe packet ( or ) and forward it to all their outgoing links or they receive both (within a predetermined time window W) and forward their linear (i.e., XOR) combination (). Eventually, each receiver observes one probe packet, either or or . The set of leaves is divided into three parts based on the observed probe at each node, and the way these parts are connected to each other is deducted. When one of the constituent parts has two or less leaves, its internal structure is also revealed given that the tree is binary. The algorithm then proceeds in iterations within each part, choosing two different sources and repeating the process, until all edges are inferred. At each iteration, every link is traversed by one probe packet (or linear combination). The algorithm terminates in a number of iterations that is less than the number of leaves, and the binary tree topology is exactly discovered.
The only difference in the presence of losses is that, in every iteration, each designated source sends probe packets instead of just one. In order to avoid the case of probe packets meeting at different nodes during the same iteration, the direction of the edges is set for each iteration according to the first probe packet that arrives at each intermediate node. More precisely, each intermediate node maintains a table of neighbors marked as sources or sinks based on the reception of probes within a time window W after the first probe arrival. After that window passes, the node accepts probes only if they originate from one of its source neighbors, whereas it rejects probes coming from sink neighbors and it does not forward probe packets to source neighbors. The probability of error due to a leaf not receiving the “correct” probe decreases very fast as K increases, since it is sufficient for each node to receive exactly one probe packet from each of the sources it is connected to.
The above hierarchical top-down approach is extended to full m-ary (intermediate nodes have a degree of , ) and general m-ary (the degree of intermediate nodes is between 3 and ) trees in [28]. For the former, assuming no probe packets are lost, the number of components that are revealed in every iteration is increased by applying one of the following modifications. Either the intermediate nodes deterministically generate different linear combinations when receiving probe packets from two different neighbors and forward each resulting packet to a different outgoing link (i.e., different neighbor) or up to m (more than two) sources are used per iteration sending distinct probe packets . In the first case, the leaves are partitioned into components in each iteration based on the probe packet they receive and, once a component has m or less nodes, its internal structure is revealed, given that the tree is assumed full m-ary. In the second case, the intermediate nodes (i.e., coding points) send the same linear combination of the k () probe packets they receive within a time window W to all of their remaining neighbors and the leaves are divided into or m components. For general m-ary trees, only the first modification can be applied. In the presence of packet losses, directions are assigned to edges at each iteration, as described before.
Furthermore, the authors propose a method for reconstructing the topology of directed acyclic graphs (DAGs) with a fixed set of M sources and N receivers and a predetermined routing scheme by decomposing them into a number of two-source, two-receiver (2-by-2) subnetwork components, which are then merged accordingly. The multiple-source multiple-destination tomography problem was first introduced in [29], where it was shown that any DAG can be decomposed into a collection of 2-by-2 topologies, each of which belongs to one of four distinct types of 2-by-2 subnetwork components (Types 1, 2, 3, and 4). However, contrary to the methods proposed in [29], the network coding enabled approach can uniquely distinguish among all those 2-by-2 subnetwork component types.
More precisely, the first step of the proposed method involves the identification of the type of every 2-by-2 component of the original DAG. In the second step, the identified 2-by-2 components are merged in order to reconstruct the M-by-N topology. To that end, the sources send multicast probe packets that are spaced apart by intervals of length T (duration of every experiment/iteration) to the receivers. In order to force the probe packets to meet at different points (or not meet at all) in different iterations, there is a per iteration randomly chosen time offset u between the sending times of the two sources. The intermediate nodes are divided into two categories: joining points that add and forward probe packets and branching points that forward the single received probe to all “interested” links (i.e., links that are the next hop for at least one source packet in the linearly combined packet).
Assuming that there are no packet losses, in every 2-by-2 component, sources and multicast probe packets and , respectively, to receivers and . Depending on the underlying 2-by-2 topology, the receivers observe variations of the linear combinations and . Types 2 and 3 result in unique observed combinations and can therefore be identified with the first observation. Types 1 and 4 are identified in subsequent iterations by forcing probes to meet at only one of the joining points through appropriately tuning the offset u. In particular, Type 4 is identified the first time the two receivers observe different linear combinations, whereas Type 1 is inferred if the receivers see the same combined (i.e., coded) packets after a specific number of iterations chosen suitably to ensure small probability of error. A similar procedure is followed in the presence of packet losses, according to which, after performing several independent experiments and collecting a number of observations (coded packets that have arrived at the receivers), the candidate topologies can be distinguished depending on whether and on the observed coefficient differences .
The described procedures can be applied to a 2-by-N network on every one of the possible pairs of receivers, inferring in this way (in parallel and independently) the type of all constituent 2-by-2 components. Two algorithms that merge the identified 2-by-2 components in order to recover the 2-by-N topology are provided. The first is suitable when the 1-by-N tree rooted at source and containing only branching points is known (e.g., it can be inferred using some tomographic method), and the second does not require any such prior knowledge. Both merging algorithms can localize every joining point between two branching points. Starting from a 2-by-N topology, the inference technique can be extended to the M-by-N topology by adding one source at a time in order to connect the 1-by-N (single source) trees of the remaining sources.
Another active tomography method for the logical topology inference of directed acyclic graphs with M sources, N receivers (M-by-N network) and maximum total degree is presented in [30]. Assuming the nodes in the network are capable of (scalar linear) network coding, the exact logical DAG topology is inferred with a single probing experiment during which each link is traversed by only one probe packet and synchronization between the sources is not required. The proposed approach comprises four stages. First, each of the M sources generates and transmits (asynchronously) a single probe packet. Every probe packet consists of two parts: the information field and the hop-length field (an integer up to the maximum number of possible intermediate nodes in the topology). The information field of the probe packet generated by source is set according to , and the hop-length field is set to 0.
In the second stage, every intermediate node u with k incoming and r outgoing links constructs the information fields of the outgoing probe packets according to a component-wise multiplication (provided in [30]). In the third stage, each receiver eventually gets the packet , where and the hop-length of is . The component can be expressed as a power of as with . Based on the above exponents, the hop lengths of the pairwise joining (between two sources and a receiver) and pairwise branching (between one source and two receivers) nodes can be computed. These hop lengths can be leveraged for calculating the path lengths of the three path segments of the 1-by-2 and 2-by-1 components that were proven to uniquely determine the DAG topology in [29]. A 2-step explicit algorithm that recovers the topology of the network from the determined hop lengths of the pairwise branching and joining nodes is provided and comprises the final stage of the proposed approach.
In [31], random linear network coding (RLNC) is explored in the context of passive network tomography in the presence of errors, both adversarial and random. The main idea is that the linear transformations produced by RLNC provide insights about the network structure that can significantly aid tomography. Furthermore, given that end-to-end network error-correcting codes are employed, no dedicated probe packets are necessary; hence, passive tomography is a suitable option. Assuming directed acyclic and delay-free networks where the capacity of each edge is normalized to one symbol of per unit time and there is a single source that communicates with a single receiver, both topology inference (the receiver wishes to correctly estimate the upstream network topology) and error localization (the receiver wishes to identify the locations of occurred network errors) are considered. Common randomness (i.e., all candidate local coding coefficients of node are chosen from its local random codebook and the set of all local random codebooks is a priori known to the receiver) is shown to be necessary and sufficient for recovering the topology under RLNC. Specifically, two types of common randomness are defined: (i) weak type for random errors, where each distinct element indexes a distinct element in the codebook of node and the local coding coefficient is chosen as the element , and (ii) strong type for adversarial errors, where each distinct element indexes a distinct element in the codebook of node and the coding coefficient is chosen as , with denoting the edge from node v to node and corresponding to the set of all outgoing edges of node v.
Topology inference in the presence of adversarial errors is based on the idea that, for strongly connected networks, the transform matrices generated by every pair of networks are very different. Hence, no matter what changes an adversary may perform, he/she is unable to make the transform matrix of one network resemble that of another. The proposed algorithm operates on the overall (polluted with the adversarial errors) transform matrix that is observed by the receiver and finds the closest (in terms of rank distance) matrix that corresponds to an error-free network. The topology is estimated as the one corresponding to this closest matrix. Furthermore, a polynomial time algorithm for inferring the topology under random errors is also provided. The algorithm proceeds in two stages. First, a set of candidate Impulse Response Vectors (IRVs—unit impulse responses, linear transformations from each edge to receiver) is recovered during several rounds of successful (i.e., the number of errors does not exceed the bound C-1, where C is the min-cut from source to receiver) source generations. Then, the obtained IRV information is leveraged to recover the topology after filtering out the fake candidate IRVs.
Regarding error localization, the detection of the edges where adversarial errors have been introduced is reduced to the problem of detecting IRVs in the error matrix. This detection is shown to be computationally intractable even when the receiver knows in advance the topology and the local encoding coefficients. A polynomial time algorithm is presented for the localization of random errors. Finally, a new type of RLNC called Network Reed-Solomon Coding (NRSC) that is based on Reed–Solomon codes and incorporates the use of virtual IRVs is proposed in order to improve the performance of tomographic algorithms in terms of computational efficiency and robustness to dynamicity. This applies especially to the adversarial error model, for which the previously presented schemes require exponential time in terms of network parameters. Under NRSC, a maximal number of adversarial errors can be localized in a computationally efficient manner even without knowing the network topology.
3.2. Loss Estimation
Any link statistic (e.g., loss rate or mean delay) can be mapped to a binary (good/bad) performance measure by setting a threshold above which the performance is classified as bad (otherwise, it is classified as good). The same classification can be extended to paths comprising multiple links, i.e., a path is considered bad if it contains at least one bad link. A class of network tomography in which links can have one of two states, namely good or bad, and that consists of observing the status of end-to-end paths and based on that inferring the status of individual network links has been introduced in [32]. In particular, the author presents a quick and simple inference algorithm that identifies with high likelihood the worst performing links using only uncorrelated end-to-end measurements. The author considers a logical routing tree network topology consisting of paths from a single source (the root) to multiple destinations (the leaves), assuming that this topology is accurately known. The proposed Smallest Consistent Failure Set (SCFS) algorithm infers the locations of bad links in a (logical) routing tree, using a single measurement (snapshot) of the good/bad status of each source-to-leaf path. It attributes a pattern of bad paths as being caused by the smallest possible set of bad interior links consistent with it. Specifically, it designates as bad only the links nearest the root that are consistent with the observed set of bad paths. A link is classified as bad when there are no good paths from the corresponding terminating node to its descendant leaves but a path through its parent is known to be good.
Adopting the previous formulation (i.e., assuming that the vector of the individual link attributes is binary with indicating if the corresponding link is congested or not), the authors in [33] focus on the case of a single congested link within the network, i.e., vector has only one nonzero component. Sufficient conditions on the network coding coefficients of the intermediate nodes and the training sequence under which 1-identifiability (congestion status of a single link can be inferred from the end-to-end measurements) is guaranteed for any logical network (i.e., a network in which the interior nodes have degrees greater than or equal to three) are derived. Based on these conditions, a lower bound for the probability of 1-identifiability under random network coding (i.e, nodes pick their network-coding coefficients randomly) is calculated. Furthermore, a way to construct a training sequence that allows identifying the location of a congested link inside the network is presented, and the trade-off between the length of training slots and the size of the network coding alphabet (i.e., the time needed to identify the congested link and the size of network coding packets) is established. Although the previous results are derived for networks with a single source-destination pair, they can be applied to a multiple-source multiple-destination network by considering the equivalent single-source single-destination network, where the set of sources and destinations have been substituted by a single super node source and destination, respectively.
In [34], a linear algebraic approach for developing consistent estimators of link loss rates in mesh topologies using network coding is presented. The network is modeled as a directed acyclic graph and represent the set of source nodes and the set of receiver nodes, respectively. A path-line matrix (usually denoted as routing matrix ) , whose rows correspond to the paths and columns correspond to the links, is defined as follows: the element is equal to 1 if the i-th path in includes the j-th link in and is equal to 0 otherwise. Furthermore, it is proven that the identifiability of a link, which only depends on the network topology, is a necessary and sufficient condition for the consistent estimation of link loss rates.
Building on the concept of identifiability, the authors refer to virtual links as the non-identifiable links that are included in the same paths. Therefore, a modified path-link matrix is defined as before, where is the set of identifiable links and is the set of virtual links. The packet losses on different links are modeled by a set of mutually independent Bernoulli processes; thus, spatial and temporal independence is assumed. Therefore, packet losses may be represented by the following system:
where is the success rate of the j-th link and is the success rate of the i-th path, which, using a logarithmic transformation, can be written in the following form:
In most cases, the system described by Equation (2) is under-determined; thus, the authors make use of the network coding technique in order to reveal the inherent correlation between packet losses on links and on different sets of paths, which results in increased bandwidth efficiency and reduced monitoring cost (when compared to multicast probing on trees). More precisely, they implement a framework in two phases. In the first phase, the probe coding scheme takes place. Specifically, n batches of probe packets are sent from the sources in a synchronized manner. The probe packets are binary vectors of length l, which can be interpreted as elements in a finite field with an alphabet of size . In each time window, the coding points (i.e., the intermediate nodes with multiple incoming links) linearly combine incoming probes according to the coding coefficients. The authors establish a lower bound on the probe size, which is necessary for a valid probe coding scheme, that is, a probe coding scheme that enables the identification of the paths that successfully transmitted a probe from the end-to-end observations. Within valid probe-coding schemes, the probe size l is desired to be as small as possible because it is directly related to bandwidth efficiency. It has been shown that, if one is given a directed acyclic graph with a set of monitored end-to-end paths , for valid probe coding schemes, the size l of the probes transmitted on the paths in (i.e., the set of end-to-end paths that include link (h,r) which is adjacent to receiver ) satisfies .
The second phase entails the inspection of the content of the received probe packets in order to estimate the success rate of all paths and combinations of paths, which increases the rank of the system, thus enabling the estimation of link loss rates. To that end, a modified path-link matrix, , is constructed, where is the power set of . is referred to as a type-2 modified path-link matrix, and the modified system is expressed as follows:
where , and denotes the success rate of the i-th path set in . For each path set in , the n probe batches sent can be considered as a binomial experiment with n trials; thus, a random variable can be defined as the number of received probes whose contents represent that a probe (or batch of probes) has been successfully transmitted on the path (or the paths) in the i-th path set. The sample proportion is a maximum likelihood estimator of , which gives the estimator of . Now that the above system described by Equation (3) is over-determined (), can be calculated by means of least squares.
Simulations comparing the proposed linear algebraic (LA) approach to the belief propagation (BP) approach showed that the former achieves better estimation accuracy after sending reasonably sufficient probes ( probe batches for a topology consisting of 10 nodes and 15 edges). Additionally, the proposed LA approach allows the use of a small number of sources, the locations of which in the network can be flexibly chosen.
The work in [35] extends [34] by addressing the problems that were not explored there. Firstly, an algorithm is developed in order to find a valid probe coding scheme such that the minimum probe size is achieved. To that end, the authors of [35] construct auxiliary tree topologies, , each associated with one particular end link to the root node, where the root node of corresponds to the destination node r in . The leaves of the auxiliary tree correspond to the sources of that use link e to relay packets to the root node. The number of leaves is equal to the number of paths that traverse link e. Each corresponds to the subgraph . Based on the auxiliary trees and, more specifically, based on the number of leaf nodes that correspond to the i-th incoming link of a coding point in , the coding coefficients are selected as , where is the number of incoming links to .
The size of the probe packets is decided by means of combining the different sets of subgraphs with overlapping links as one subgraph set, where the cardinality of the set of leaf nodes that corresponds to the combination of these subgraph sets is the maximum of the cardinalities of the sets of leaf nodes corresponding to each individual subgraph set. This extends the lower bound on probe size of [34] for a set of subgraphs with overlapping links, as follows: for the probes that are transmitted on subgraph set , the probe size should satisfy to obtain valid end-to-end observations. The minimum probe packet size is , where is the set of end links in the subgraph set and is the number of paths that contain link e.
Moreover, the authors select the method of normal equations in order to solve the full-rank least squares problem of Equation (3) (which is formulated based on their LA approach) and prove that the complexity of the LA approach when using this technique is , where , , n is the number of probe batches, and is the number of times that the calculations are repeated during a monitoring period. Given that the number of path sets () grows exponentially with the number of paths (), the previous method exhibits lack of scalability. To address this issue, the authors propose the use of the method of row selection in order to limit the number of monitoring path sets to a sufficient number for estimating all link loss rates ( is converted to a lower rank matrix by means of QR factorization). The complexity of applying the LA technique using the method of row selection is , which is lower than the complexity of the previous case. Ultimately, they implement an algorithm for efficiently updating and , when links are either deleted from or added to the network. Simulation results again showed that the proposed LA framework for network tomography achieves better estimation accuracy than the BP algorithm when the estimators converge.
A passive loss estimation method that employs random linear network coding for Wireless Sensor Networks (WSNs) is presented in [36]. More precisely, the authors use a slightly modified RLNC scheme according to which every intermediate node with more than one incoming links randomly selects two flows from two different incoming links and combines them. By leveraging the subspace property of NC, they propose estimators for the path loss rates from the sources and virtual sources (i.e., intermediate nodes with more than one incoming links) to the sink of the WSN. Furthermore, they characterize the conditions for the estimation of the loss rate of a particular link to be feasible (a link can be either identifiable, possibly identifiable, or not identifiable), and they propose an algorithm that leverages the aforementioned estimated path loss rates to infer the link loss rates that can be identified.
In [37], the authors present a loss tomography scheme for inferring link loss rates on both trees and general topologies by combining and extending all their previous work, like [38], where they proposed a low complexity algorithm to compute the MLEs of link loss rates in multiple-source tree networks with multicast and network-coding capabilities (corresponding to Algorithm 1 in [37] that will be presented later). Their contribution can be summarized into four main aspects: (a) designing an appropriate monitoring scheme (which affects the identifiability of network links and paths) in polynomial time using Linear Programming (LP), (b) describing the necessary and sufficient conditions for links and paths to be identifiable and reversible (they introduce the notion of the dual configuration), (c) designing the probes that are sent from the sources (size and content) as well as the coding that will be done from the intermediate nodes with multiple incoming links (coding points) based on appropriate coding coefficients (they introduce the notion of path monomials), and ultimately, (d) presenting techniques for accurate loss estimation while calculating errors and confidence intervals using the Fisher information matrix.
The network is again modeled as a graph , where corresponds to logical links and packet loss on link e is an independent and identically distributed (i.i.d.) Bernoulli variable with probability , where and is the success probability of link e. The observations at all receivers form a vector in the space , where is the number of sources and is the number of receivers in the network. The probability mass function for a single observation is . By letting denote the number of probes during n conducted experiments for which the observation is obtained, the authors obtain the probability of n independent observations analytically. In order to measure the per link estimation accuracy, they use the mean-squared error (MSE), while the estimation performance of all links is measured by means of an entropy measure and the covariance matrix is approximated using the Fisher information matrix .
Applying network coding in trees can be considered as combining probes from different incoming links (at the coding points) using the bitwise XOR operation. Hence, network coding increases bandwidth efficiency as well as the number of identifiable links, since a single packet carries information on more than one paths, which is a compressed way to carry enhanced information (taking advantage of the correlation between different links and paths). Based on the mild assumption that all coding points are located above all branching points, the authors propose an algorithm that efficiently computes the MLE of all links at the same time. They define the triplet as a configuration and as the dual configuration of on a graph that has the same nodes but reversed edges, i.e., if and only if , and success rate , associated with every edge . They select sources and receivers , noting that a multicast tree (MT) is the dual configuration of a reversed multicast tree (RMT) and that the MLE of those two has the same functional form. Algorithm 1 of [37] implements the above mentioned procedure. The estimates that this algorithm produces are the link loss rates of the original tree.
Additional heuristic approaches are presented for loss estimation. Firstly, subtree decomposition partitions the original tree into MTs separated by coding points and, in each of them, employs the Maximum Likelihood Estimator (MLE). Observations of the coding points are inferred from the observations of the leaves; therefore, this algorithm is suboptimal. In addition, a belief propagation (BP) approach is presented, which is based on creating a factor graph corresponding to the estimation problem. The factor graph is a bipartite graph: one set of nodes represents the links (variable nodes) of which the loss rates need to be estimated, while the other set of nodes represents paths (function nodes) that are observed by each received probe. An edge exists in the factor graph between a link and a path if the link belongs to this path in the original graph. This approach can be applied in general topologies as well, while the previous one is applied only on tree topologies.
In more general topologies, the benefits of network coding are more pronounced than in tree topologies but so are the challenges posed due to the presence of cycles. Subsequently, an orientation algorithm is proposed for the construction of DAGs. Additionally, the design of the probe coding schemes is modified: coding operations over a larger alphabet and coding coefficients satisfying specific constraints are introduced in order to ensure path identifiability, which refers to the ability of uniquely mapping each possible observation (received probes at all receivers) to the state of the paths (i.e., which paths operated during the measurement period and which failed).
Assuming a set of links, the goal is to estimate the success probability for all links in at the minimum bandwidth cost, given a set of nodes that can act as sources, a set of nodes that can act as receivers, and the set of links whose success rates are of interest. This optimization problem can be solved in polynomial time using linear programming (LP), whereas the minimum cost routing problem when performing tomography with multicast trees (MTs) is NP-hard. To ensure identifiability in that case, the notion of conceptual flows is introduced: each path corresponds to a flow of fixed rate . To ensure minimum cost, these flows have to use the minimum resources possible.
If the success rate of all links is to be estimated, then the scheme used is simpler and there is no need to solve the above LP problem: each source sends a probe, and each intermediate node forwards a combination of its incoming packets to its outgoing edges. Thus, each edge of the graph is utilized exactly once per time slot and the required total bandwidth is minimum. An orientation algorithm is proposed. It requires some flexibility regarding the selection of source nodes and receiver nodes, and it leads to the construction of an acyclic graph with a small number of receiver nodes (this is desired for efficient data collection), which can be represented as a factor graph where BP estimation algorithms can be applied. The proposed algorithm guarantees the identifiability of all links in a general undirected graph consisting of logical links, for any choice of sources.
Another challenge regarding general topologies besides the presence of cycles rises from the fact that the design of the code affects identifiability. Therefore, the authors present a result determining the lower size of the alphabet (i.e., probe size), which ensures path identifiability. However, having a large alphabet size is necessary but not sufficient to guarantee path identifiability. It is also crucial to assign coefficients so that the failure of every subset of paths leads to a distinct observable outcome (received probe content). Finally, the authors employ a low complexity algorithm that offers fast estimation of link loss rates, that is a suboptimal BP approach.
In the following section, we shift our focus on tomographic techniques based on compressed sensing, which, as already mentioned, constitute an independent family of network tomography that could be used in combination to other approaches.
4. Compressed Sensing Enabled Network Tomography
Compressed sensing is an emerging field in signal/image processing that has recently made its appearance in the field of network tomography, gaining more ground ever since. It is based on the assumption that only a few network links are responsible for the end-to-end delays and/or losses, which provides prior information that the solution, i.e., the vector of the linear measurement model, is sparse (the only nonzero components of the vector are those corresponding to these “bottleneck” links). According to compressed sensing theory, if a vector is k-sparse (i.e., has k nonzero value elements), then we can precisely recover it with only measurements, with n being the vector’s dimension [39,40]. In order to accurately estimate using LP optimization (or a variation of this method when synchronization errors are taken under consideration), the routing matrix (often termed measurement matrix in the context of CS) needs to be constructed following some desirable (and conflicting) properties:
- enable accurate reconstruction of from when is known to be sparse;
- use fast decoding algorithm; and
- make the least possible measurements (maximum achievable compression of ) [41].
In order to ensure that the measurement paths are selected such that they meet the k-identifiable condition, i.e., the ability to recover the k-sparse vector from the end-to-end measurements obtained over these measurement paths, different methods have been proposed.
According to [42], whether one can recover a sparse vector from by means of compressed sensing can be evaluated by the mutual coherence , which is defined as the largest absolute norm inner product between different columns of :
where is the i-th column of and represents norm defined as , with being the components of vector . The fact that the equation is ill-posed means that any vector satisfies the equation, where is the null space of and is defined as the true delay vector that needs to be obtained. If is (exactly) k-sparse and , then can be determined by the optimization:
where is the norm of .
A collaborative and distributed framework according to which nodes cooperate with each other in order to monitor the status of the entire network (i.e., efficiently recover any k-sparse networked data vector) is presented in [43]. Every node, apart from its own measurements utilizes measurements generated by the rest nodes, with the goal of reducing the number of overall required measurements. To that end, all nodes have their own independent measurement matrices consisting of random walks initiated by themselves as well as random walks generated by other peers. The authors derive an upper bound for the number of measurements that each node must generate, such that the collaborative global view of the entire network is achieved. Based on that upper bound, an optimization method is proposed to minimize the total number of measurements. The results of the performed simulations demonstrate that only low degree nodes are necessary to initiate random walks (measurements).
4.1. Delay Estimation
In [41], the authors apply concepts from compressed sensing and expander graphs to the link delay estimation problem. Specifically, they determine the conditions on the routing matrices under which the underlying networks are k-identifiable; that is, for every exactly k-sparse vector , the equation is uniquely solvable. By combining concepts from compressed sensing and expander graphs, the authors relax the k-identifiability expansion condition of a network, such that its routing matrix does not have to be the bi-adjacency matrix of a regular bipartite graph but the bi-adjacency matrix of the union of disjoint expander graphs with error parameter . Under this relaxed condition, the k-sparse link vector can be estimated via minimization. This relaxation expands the list of identifiable networks with bounded estimation error by 30%. Another work based on expander graphs is [44], where the authors demonstrate that the routing matrix corresponding to a full tree with q branches on each node excluding leaves can be used as a measurement matrix in CS for recovering k-sparse signals with and a bounded expected estimation error. If the tree is not full, they present a heuristic method that proceeds by adding virtual nodes. Therefore, -minimization can be employed for network topologies that can be interpreted as a series of trees, either full or not full.
In [45], the synchronization error is taken under consideration and it is treated as additive, zero-mean white Gaussian noise. In addition, link delays are assumed to follow an exponential distribution, whose parameter value reveals whether is sparse or not. Based on these two assumptions and in order to account for measurement errors too, a variation of - optimization using Maximum A-Posteriori (MAP) estimation is proposed. An unconstrained - optimization problem is defined:
where is a function of sparsity and noise. In particular, if vector is assumed to follow a Laplace prior distribution, the optimization problem of Equation (6) leads to a MAP estimator. Since link delay does not follow the Laplace distribution as it cannot be negative, the constraint that is positive leads to following the exponential distribution. Under the assumption that the components are independent, the authors look for the vector that maximizes the conditional probability of link delay vector given the measurement and noise. They apply the Bayes Rule and replace the by the weighted form . Thus, Equation (6) is transformed to the constrained - optimization problem:
where . Simulation experiments have shown that the constrained - optimization outperforms the original one, achieving smaller norm estimation error and higher detection probability. Yet, the need for an efficient algorithm to solve Equation (7) remains.
Since delay tomography depends on accurate end-to-end time measurements, clock synchronization is a requirement that restricts the number of suitable end-to-end paths over which the measurements can be made. In order to overcome this limitation, an approach called reflective network tomography is proposed in [46]. This method employs a single transceiver node that transmits probe packets along different predetermined paths and receives them after they traverse back from the network. In greater detail, there are the following two types of paths over which packet traveling time (PTT) measurements are made: fully loop paths (LPs) with nodes that do not appear more than once except for the transceiver and folded paths (FPs) with all nodes appearing twice except for the destination. The objective is the identification of a limited number of bottleneck links, whereas small link delays are approximated as zero. Therefore, compressed sensing based on minimization is utilized.
The routing matrix construction (i.e., the selection of measurement paths) is done in two steps. First, the set of measurement path candidates is constructed by connecting the node-disjoint paths and respective reverse paths from the transceiver s to every other node . We note that the set of node-disjoint paths from s to v signifies the shortest combination of paths among which no nodes are shared. Then, from this set of candidates, the path with the minimum cost (or the shortest path in case of a tie) is iteratively selected until the mutual coherence of the constructed routing matrix becomes less than one. The aforementioned cost is calculated based on the number of unused links in the path under examination.
Another method for removing the clock synchronization requirement is presented in [47] and involves the construction of the differential routing matrix, which preserves the 1-identifiability property of the original routing matrix, by selecting a path between the source and receiver measurements nodes as the reference path. More precisely, when the measured path delays are contaminated with synchronization errors, the measurement vector is defined as , where is the synchronization error vector and m is the number of paths between measurement nodes s and d. By defining the n-th component of as the reference component and the n-th row of as the reference row and by subtracting them from all other components and rows, the following new equation is formed: , where is the differential measurement vector and the differential routing matrix. Although still contains some synchronization errors, if with , then . In spite of the loss of an equation, given that the goal is the identification of a limited number of bottleneck links with large delays, optimization based compressed sensing is utilized to obtain a unique solution from the under-determined linear system.
In [48], a different approach on link delay inference at mobile networks is proposed. In order to apply compressed sensing, the authors ensure sparsity of vector by applying Graph Fourier Transform (GFT) at base stations’ delays that are assumed to be spatially dependent (the GFT f will be sparse if is spatially dependent), while servers’ delays are assumed to be sparse and delays at core routers are assumed to be negligibly small. This way, elements with different characteristics can be estimated in the same framework. All previously presented methods based on compressed sensing realized active measurements, whereas the current one employs a crowd-sourcing approach, which is considered as a kind of passive measurement method. More specifically, according to this approach voluntary mobile users implement a measurement tool in their terminals. When mobile users connect to servers (e.g., Web servers), RTTs (Round Trip Times) are measured and reported to a data collection center. Although the crowd-sourcing approach has several issues such as privacy protection, it is promising because no measurement nodes need to be deployed.
Each path of the given network can be identified by a pair of a base station and a server, so measurements referring to such a path are given by the following equation:
where , and where and are the number of base stations and servers, respectively. The rank of is proven to be strictly less than , so even if all possible paths are used, and cannot be uniquely determined by Equation (8). Therefore, the GFT of is calculated and approximated by a sparse vector.
In [49], the authors address the dynamic network tomography problem by extending the work of [50] to link delay estimation with dynamic link operations. In order to use the concept of compressed sensing, the authors, unlike all previously mentioned works, use a hub set to measure the links with “small” delays—the remaining links. The set of remaining links is selected randomly in order to ensure that the measurement matrix satisfies the restricted isometry property (RIP) that characterizes matrices which are nearly orthonormal, at least when operating on sparse vectors. Then, they adopt a line graph model and use the vertices of a connected dominated set (CDS—a set of vertices of the line graph of graph G, such that every vertex in either belongs to or is adjacent to a vertex in , and is connected) on that line graph model as the hub vertices that will be used for recovering the states of all others. A line graph model refers to a model where every vertex in corresponds to a link in , i.e., and two vertices are adjacent in if and only if their corresponding links in are incident, i.e., they share a common end vertex.
By assuming that a vertex subset of a graph can be measured together in one measurement if and only if the subgraph induced by is connected and that the measurement is an additive sum of values at the corresponding vertices, then in a graph, a maximal independent set (i.e., a set of vertices for which no pair of vertices are adjacent to each other and which is not a subset of any other set with the same property) is also a dominating set, namely every vertex is either in or has at least one neighbor in . This means that a matching (i.e., a set of edges without common vertices) in a graph corresponds to an independent set in the line graph of , which in turn allows the authors to reduce the computation cost of transforming the network tomography problem to a sparse recovery problem by means of achieving a better selection of hub vertices at time compared to time achieved in [50].
Eventually, they propose an algorithm for link insertion and deletion, thus adopting a dynamic strategy when dynamic link operations are taking place, instead of simply rerunning the original algorithm, which would mean that all data—even the unchanged parts—would be recomputed. Therefore, time complexity is significantly reduced, enabling the proposed technique to be applied in large-scale networks while maintaining similar recovery performance as the technique proposed in [50].
4.2. Loss Estimation
Building on [32], the authors in [51] claim that it is not necessary for all links to be equally likely to be congested, i.e., to have the same prior probability of being congested. They present a different approach consisting of two steps: (i) the congestion probabilities of the links are uniquely identified from a small set of full network measurements (snapshots) over a period of time by using properties of Boolean algebra, and (ii) the estimated link congestion probabilities are used as prior information, together with subsequent snapshots, to find the links that are actually congested at any time using a Maximum A-Posteriori (MAP) estimator.
Let be the set of all paths between the nodes of the overlay monitoring system, referred to as vantage points. The number of paths is , where is the number of vantage points. For a known topology and set of paths , the routing matrix is computed as follows: if the path , with , contains the link and otherwise. Therefore, each row of corresponds to a path and each column corresponds to a link. If a column has only zero entries, then the state of the corresponding link cannot be inferred from measurements of the paths in . Therefore, by dropping the columns that contain only zero entries, a matrix of dimensions , where is the number of links that are covered by at least one path in , is obtained.
If represents the state of the path (i.e., if is good and otherwise) and is the state of link ( if is good and otherwise), the following system of Boolean algebra linear equations between link and path states is established:
where “∨” denotes the binary max operation and each input is obtained from end-to-end measurements by comparing the path transmission rate to a threshold , with being the link threshold and h being the length of the path: if and otherwise. Although these equations have multiple solutions (since it is very rare in practice that all the columns of are linearly independent in Boolean algebra), the most probable solution can be found by using the additional information of the probability that link is congested. The vector of the link state probabilities can be uniquely identified from a small number of snapshots. The actual congested links can be estimated by using the resulting vector as prior link state probabilities. Assuming that the set of paths remains unchanged during the measurement period, that the link states are independent from each other, and that there are no disconnected links (i.e., ), the link state probability vector is identifiable if and only if the columns of the routing matrix are all distinct, i.e., the prior probabilities can be learned by a sufficient large number of snapshots.
Given the routing matrix and m measured snapshots , with denoting the t-th snapshot, the prior probabilities can be calculated. Then, given the routing matrix , a measured snapshot and the prior link state probabilities calculated in the previous step, the links that are currently congested (and not just simply their probabilities of congestion) can be located by solving Equation (9) for . Given that Equation (9) has multiple solutions, the goal is to find the most likely one. Let denote the set of paths measured as being good (i.e., ) and as the set of paths found to be congested (i.e., ). The reduced routing matrix is obtained by removing from all rows that correspond to good paths and all columns that correspond to links in the good paths. Therefore, each row of represents a congested path and each column is a link that belongs to at least one congested path. Let denote the set of links represented by columns of . Then, has dimensions . The congested link identification problem is simplified to finding a set of links , such that all congested paths are covered by at least one link in H and:
subject to for all , where is the probability measure on the set of network links when the link probability vector is .
Let denote the domain of the link , i.e., the set of paths that contain it. The optimization problem described by Equation (10) is an instance of the Weighted Set Cover Problem (WSCP), and the proposed CLINK algorithm [51] is a computationally effective heuristic algorithm (the best polynomial-time approximation algorithm, ) capable of constructing a feasible solution set by a sequence of steps, each of which consists of selecting a link (i.e., setting the variable to 1) that minimizes .
In order to localize congested links and infer loss rates, the authors in [52] connect compressed sensing theory with Bayesian theory, in the sense that they propose a variation of the minimization method, the weighted minimization method, and use MAP estimation based on the prior congestion probability to determine the weights. Prior probabilities of link congestion are determined from path congestion probabilities based on Boolean algebra. By taking the expectations and logarithms of Equation (9), n equations containing the prior probabilities are obtained. Nevertheless, more equations are needed in order to determine . To that end, by combining different paths, new independent equations can be created, containing the joint probabilities that two or more paths are congested. Now, can be determined.
In practice, since the Boolean random variable which represents link state follows the Bernoulli distribution, q can be updated based on former diagnostic results, thus easing the expensive time consumption of computing prior probabilities, using the maximum likelihood estimator for Bernoulli distribution:
Based on Equation (10), the weights that will be used in the formulation of the weighted minimization method can be calculated as follows:
Having computed the weights, , weighted minimization can be formulated and solved:
The convex problem of Equation (13) can be recast as a linear problem and can be solved by any LP optimizer. Assuming that the routing matrix can be represented as the adjacency matrix of an expander graph, the estimation that comes from Equation (13) can be upper bounded. We note that a (t, )-expander is a bipartite simple graph with left degree d such that, for any with , the following condition holds: , where is the set of neighbors of , t is the expansion factor, and is the error parameter.
Simulation results show that weighted minimization method performs better than both the unweighted counterpart and CLINK algorithm [51] in terms of estimation accuracy, detection rate (i.e., the fraction of links that are correctly identified as bad), and false positive rate (i.e., the fraction of links that are good but are diagnosed as bad).
Another method for the localization of the k-sparsely congested links (the rest links have packet loss rate near zero) with only a limited number of path measurements is presented in [53]. The authors propose a CS based method for estimating the congestion probabilities of the individual links based on the deficient (i.e., not full rank) measurement matrix (i.e., the historical deficient path measurements). These estimated congestion probabilities are then utilized in conjunction with the most recent measurement snapshot by a greedy iterative estimation algorithm that locates the most possible sparsely congested links.
In [54], a different approach to loss tomography is proposed. Based on compressed sensing, the proposed scheme consists of offline and online parts. The offline part is responsible for the measurement paths (or equivalently the routing matrix) construction when a network with only two monitoring nodes (a single source and a single destination) is considered. Moreover, it is assumed that an arbitrary number of bidirectional measurement paths can be established between the two monitoring nodes. The algorithm that constructs the measurement paths is combined with an algorithm that discovers if a set of low-quality links (where low-quality links correspond to the nonzero components of the link vector in the t-th time window) is a k-sparse-identifiable set or not in order to create a k-identifiable routing matrix that enables the solution of equation , when is k-sparse.
In greater detail, the construction of measurement paths from source s to destination d and vice versa (reverse paths) takes place in three steps by adding appropriate paths one at a time from the set of all possible paths between the two nodes. First, the maximum set of link-disjoint paths (i.e., no links are shared among the paths) is constructed. Then, the set of all existing acyclic paths from s to d and the respective reverse paths are given by a path enumeration algorithm. New measurement paths are selected one by one based on the minimization of a suitable cost function until the maximum number of k-sparse-identifiable sets corresponding to the potential use of all existing paths and reverse paths is reached.
The online part is responsible for low quality link detection. The authors consider practical situations in which link quality vector is approximately sparse and estimate the steady-state path loss rates (where refers to the i-th path and t refers to the t-th time window), which they subtract from both vector and the measurement vector , thus formulating modified vectors and . Via this procedure, the values of the elements of representing normal links are closer to 0 than the corresponding values of ; thus, is closer than to an exactly sparse vector. In order to estimate , the authors assume that all measurement paths are in the normal quality states and that the number of packets lost on each path, , follows a binomial distribution. Since constitute a proportion of total , the conjugate prior distribution of corresponds to the beta distribution. When at a certain time window t is measured, the posterior distribution of can be computed. Then, using the Exponentially Weighted Moving Average (EWMA), ’s posterior distribution is estimated by the mode in the posterior distribution of . After estimating , the authors subtract them from the path loss rates , where is the number of packets transmitted from the source node to its destination node during time window t. The modified measurement vector, , is set as follows:
where is a threshold. In order to classify estimated as a low or high quality link, the authors compare it to a threshold , which is set using Otsu’s binarization method [55]. This paper is the first to discuss measurement path construction based on compressed sensing.
A Graph Fourier Transform (GFT) based tomography approach for the estimation of packet loss rates at nodes in wireless multihop networks with spatially dependent channels is presented in [56]. The basic idea is similar to the previously described delay tomography method of [48] (see Section 4.1). Namely instead of estimating the node state vector (i.e., the vector whose components are the packet loss rates at the respective nodes) directly, the proposed scheme employs CS to first estimate the GFT of the node state vector (which has a few dominant components due to the spatially dependent channels) and then examines the network internal characteristics in the transformed domain.
In [57], the authors propose a scalable (the total number of measurements scales logarithmically with the number of links) adaptive CS based tomographic scheme for fault localization. The proposed approach consists of two stages. First, the network is monitored (with a few tomographic path measurements) for the detection of faults (the initial set of measurements although not sufficient for localizing the faults, it is indicative of their presence). Then, upon detection of one or more faults, the adaptive fault localization stage is initiated, during which further path measurements are iteratively carried out (each adaptive measurement covers a set of links that is identified based on the previous iteration) in order to localize the faults. Three conditions for convergence (termination) and two selection criteria for the adaptive measurements are determined, whereas the performed simulations demonstrate that the proposed scheme achieves a very high detection rate and a very low false positive rate.
5. Discussion
The traffic overhead footprint on the total network load and the need for special purpose cooperation from the network elements involved in network monitoring motivates approaches of network tomography as a fast and lightweight alternative to traditional techniques. In this review, we focused on two families of algebraic-based approaches, namely network coding and compressed sensing, which capitalize on concepts from linear algebra for building more advanced tomographic techniques. Network coding, although developed for different goals (i.e., improving the throughput of networks), can be exploited in network tomography due to the introduced topology-dependent correlations and information that are implicitly present in the obtained measurements. Classic tomography problems such as link loss inference and topology recovery can be revisited with approaches that leverage the network coding capabilities of the intermediate nodes in order to improve the estimation accuracy and to reduce the probing cost and the complexity of selecting measurement/monitoring paths.
On the other hand, compressed sensing enables the recovering of sparse signals from lower-dimensional linear measurements (i.e., the inference of the sparse vector from measurements , where the dimension of is smaller than the dimension of ). Furthermore, it can be applied in cases where measurements are noisy (noise is usually assumed to be Gaussian distributed) and hard/expensive to collect directly from the sources. Although it is a flexible and data-efficient method, its application has been restricted by the stringent assumption of sparsity. However, in the context of network tomography, this sparsity assumption is not so restrictive as in other fields and it is in fact appropriate, since often path-level performance characteristics (e.g., delays, packet losses, etc.) can be attributed to a few “bottleneck” links. Therefore, the unknown vector can be considered sparse with only a few nonzero elements (the components corresponding to the “bottleneck” links) and it can be recovered nearly perfectly with high probability from the ill-posed routing matrix (or measurement matrix in CS terminology) and measurement vector based on CS theory [58,59].
Figure 2 illustrates the classification of some of the examined tomographic methods based on the network tomography category in which they belong and the enabling technology they employ. It can be used for a quick overview of positioning of each included approach in the state-of-the-art and as a potential guidance for the novice reader who wants to start becoming acquainted with the field.
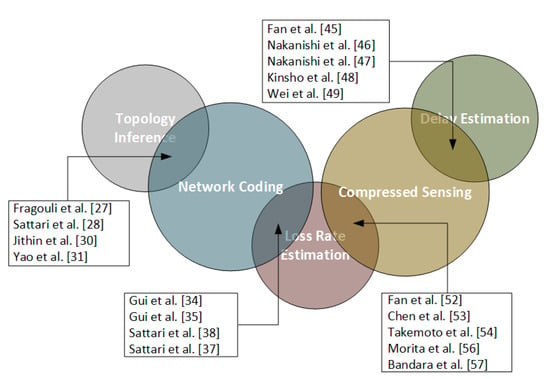
Figure 2.
Classification of selected tomographic methods.
Similarly, Table 1 summarizes the key features of the approaches. It can be used as a quick reference for each approach separately, providing succinctly the key features of each method while at the same time providing the overall bigger picture at a glance in terms of features. A more educated overview of the key ideas, strong points, and performance of the presented approaches is provided in Table 2, in a comparative manner when possible. This table can be used for choosing among the available approaches, weighing the pros and cons of the included techniques and identifying the most appropriate for more specific applications and operational objectives.

Table 1.
Key features of selected tomographic methods.

Table 2.
Overview of key points, advantages, and performance of selected tomographic methods.
Finally, Table 3 lists a selection of quantitative performance evaluation results, each in their relevant context, as compiled from the simulation-based evaluations presented in the respective original works that proposed them. This table can be used as a performance guide for selecting among the various approaches given performance operational requirements, i.e., the RMSE error, entropy, FPR and DR.

Table 3.
Quantitative performance evaluation of selected tomographic methods.
6. Conclusions
In this review, we presented some of the latest algebraic-based approaches for network tomography, which are expected to have considerable practical and theoretical merit in future communication network infrastructures. We focused on approaches adopting network coding and compressed sensing as their fundamental machinery for inferring various parameters of the network, such as delay and packet loss, or the topology of the network itself. We presented various aspects of some of the specific solutions that have been proposed already. Eventually, we provided a qualitative comparative discussion on the presented techniques, summarizing in tabular form the key features of the selected methods. The outcomes of this comparison can be used as basis for the selection of the most appropriate approach given specific application requirements. From such an analysis, the network coding based approaches seem to be the more appropriate in an idealized setting where network routers can be modified at bulk to execute network coding protocols, while compressed sensing emerged as the more pragmatic and efficient solution that could be realistically applied directly in today’s infrastructure, paving the way for more advanced network monitoring solutions.
Author Contributions
All authors have contributed in the conceptualization of the paper. G.K. and D.G. have outlined the structure of the paper and have performed extensive literature review. V.K. and S.P. have guided the development of the content. All authors have participated in the writing of the manuscript. G.K. and D.G. have performed the qualitative comparison and classification of approaches. V.K. and S.P. have participated in the classification of approaches and the overall consistency check. All authors have read and agree to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NT | Network Tomography |
| QoS | Quality of Service |
| ICMP | Internet Control Message Protocol |
| EM | Expectation-Maximization |
| MCMC | Markov Chain Monte Carlo |
| MoM | Method of Moments |
| NC | Network Coding |
| CS | Compressed Sensing |
| OD | Origin-Destination |
| RLNC | Random Linear Network Coding |
| XOR | Exclusive Or |
| IRV | Impulse Response Vector |
| NRSC | Network Reed-Solomon Coding |
| DAG | Directed Acyclic Graph |
| SCFS | Smallest Consistent Failure Set |
| LA | Linear Algebraic |
| LA-NE | Linear Algebraic with Normal Equations |
| LA-RS | Linear Algebraic with Row Selection |
| BP | Belief Propagation |
| WSN | Wireless Sensor Network |
| MLE | Maximum Likelihood Estimator |
| LP | Linear Programming |
| i.i.d. | independent and identically distributed |
| MSE | Mean Squared Error |
| MT | Multicast Tree |
| RMT | Reversed Multicast Tree |
| MAP | Maximum A-Posteriori |
| WSCP | Weighted Set Cover Problem |
| GFT | Graph Fourier Transform |
| BS | Base Station |
| RTT | Round Trip Time |
| CDS | Connected Dominating Set |
| RIP | Restricted Isometry Property |
| MIS | Maximal Independent Set |
| FPR | False Positive Rate |
| DR | Detection Rate |
| RMSE | Root Mean Square Error |
References
- Coates, A.; Hero, A.O., III; Nowak, R.; Yu, B. Internet tomography. IEEE Signal Process. Mag. 2002, 19, 47–65. [Google Scholar] [CrossRef]
- Castro, R.; Coates, M.; Liang, G.; Nowak, R.; Yu, B. Network Tomography: Recent Developments. Stat. Sci. 2004, 19, 499–517. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N.; Li, S.Y.; Yeung, R. Network information flow. IEEE Trans. Inf. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Li, S.Y.; Yeung, R.; Cai, N. Linear network coding. IEEE Trans. Inf. Theory 2003, 49, 371–381. [Google Scholar] [CrossRef]
- Rani, M.; Dhok, S.B.; Deshmukh, R.B. A Systematic Review of Compressive Sensing: Concepts, Implementations and Applications. IEEE Access 2018, 6, 4875–4894. [Google Scholar] [CrossRef]
- Hayashi, K.; Nagahara, M.; Tanaka, T. A User’s Guide to Compressed Sensing for Communications Systems. IEICE Trans. Commun. 2013, E96.B, 685–712. [Google Scholar] [CrossRef]
- Qaisar, S.; Bilal, R.M.; Iqbal, W.; Naureen, M.; Lee, S. Compressive sensing: From theory to applications, a survey. J. Commun. Netw. 2013, 15, 443–456. [Google Scholar] [CrossRef]
- Cascares, R.; Duffield, N.G.; Horowitz, J.; Towsley, D.F. Multicast-based inference of network-internal loss characteristics. IEEE Trans. Inf. Theory 1999, 45, 2462–2480. [Google Scholar] [CrossRef]
- Tsang, Y.; Coates, M.; Nowak, R. Passive network tomography using EM algorithms. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001. [Google Scholar] [CrossRef]
- Duffield, N.; Presti, F.L.; Paxson, V.; Towsley, D. Network loss tomography using striped unicast probes. IEEE/ACM Trans. Netw. 2006, 14, 697–710. [Google Scholar] [CrossRef][Green Version]
- Presti, F.L.; Duffield, N.; Horowitz, J.; Towsley, D. Multicast-based inference of network-internal delay distributions. IEEE/ACM Trans. Netw. 2002, 10, 761–775. [Google Scholar] [CrossRef]
- Nie, X.; Lu, C.; Zhai, S.; Li, L.; Wang, X. Research on End-to-End Delay Variation Feature Extraction Method for Nonstationary Network. In Proceedings of the 2017 4th International Conference on Information Science and Control Engineering (ICISCE), Changsha, China, 21–23 July 2017. [Google Scholar] [CrossRef]
- Rad, N.E.; Ephraim, Y.; Mark, B.L. Delay Network Tomography Using a Partially Observable Bivariate Markov Chain. IEEE/ACM Trans. Netw. 2017, 25, 126–138. [Google Scholar] [CrossRef]
- Dey, B.K.; Manjunath, D.; Chakraborty, S. Estimating network link characteristics using packet-pair dispersion: A discrete-time queueing theoretic analysis. Comput. Netw. 2011, 55, 1052–1068. [Google Scholar] [CrossRef]
- Zhang, Y.; Roughan, M.; Duffield, N.; Greenberg, A. Fast accurate computation of large-scale IP traffic matrices from link loads. ACM SIGMETRICS Perform. Eval. Rev. 2003, 31, 206. [Google Scholar] [CrossRef]
- Zhao, E.; Tan, L. A PCA based optimization approach for IP traffic matrix estimation. J. Netw. Comput. Appl. 2015, 57, 12–20. [Google Scholar] [CrossRef]
- Mardani, M.; Giannakis, G.B. Estimating Traffic and Anomaly Maps via Network Tomography. IEEE/ACM Trans. Netw. 2016, 24, 1533–1547. [Google Scholar] [CrossRef]
- Vardi, Y. Network Tomography: Estimating Source-Destination Traffic Intensities from Link Data. J. Am. Stat. Assoc. 1996, 91, 365–377. [Google Scholar] [CrossRef]
- Castro, R.; Coates, M.; Nowak, R. Likelihood Based Hierarchical Clustering. IEEE Trans. Signal Process. 2004, 52, 2308–2321. [Google Scholar] [CrossRef]
- Duffield, N.; LoPresti, F. Network Tomography from Measured End-to-End Delay Covariance. IEEE/ACM Trans. Netw. 2004, 12, 978–992. [Google Scholar] [CrossRef]
- Ni, J.; Xie, H.; Tatikonda, S.; Yang, Y. Efficient and Dynamic Routing Topology Inference from End-to-End Measurements. IEEE/ACM Trans. Netw. 2010, 18, 123–135. [Google Scholar] [CrossRef]
- Ni, J.; Tatikonda, S. Network Tomography Based on Additive Metrics. IEEE Trans. Inf. Theory 2011, 57, 7798–7809. [Google Scholar] [CrossRef]
- Eriksson, B.; Dasarathy, G.; Barford, P.; Nowak, R. Efficient Network Tomography for Internet Topology Discovery. IEEE/ACM Trans. Netw. 2012, 20, 931–943. [Google Scholar] [CrossRef]
- Lun, D.S.; Médard, M.; Koetter, R.; Effros, M. On coding for reliable communication over packet networks. Phys. Commun. 2008, 1, 3–20. [Google Scholar] [CrossRef]
- Fragouli, C.; Boudec, J.Y.L.; Widmer, J. Network coding. ACM SIGCOMM Comput. Commun. Rev. 2006, 36, 63. [Google Scholar] [CrossRef]
- Sanders, P.; Egner, S.; Tolhuizen, L. Polynomial time algorithms for network information flow. In Proceedings of the Fifteenth Annual ACM Symposium on Parallel Algorithms and Architectures—SPAA ’03, San Diego, CA, USA, 7–9 June 2003. [Google Scholar] [CrossRef]
- Fragouli, C.; Markopoulou, A.; Diggavi, S. Topology inference using network coding. In Proceedings of the 44th Annual Allerton Conference on Communication, Control and Computing, Monticello, IL, USA, 27–30 September 2006. [Google Scholar]
- Sattari, P.; Fragouli, C.; Markopoulou, A. Active topology inference using network coding. Phys. Commun. 2013, 6, 142–163. [Google Scholar] [CrossRef]
- Rabbat, M.; Coates, M.; Nowak, R. Multiple-Source Internet Tomography. IEEE J. Sel. Areas Commun. 2006, 24, 2221–2234. [Google Scholar] [CrossRef]
- Jithin, R.; Dey, B.K. Exact topology inference for DAGs using network coding. In Proceedings of the 2012 International Symposium on Network Coding (NetCod), Cambridge, MA, USA, 29–30 June 2012. [Google Scholar] [CrossRef]
- Yao, H.; Jaggi, S.; Chen, M. Passive Network Tomography for Erroneous Networks: A Network Coding Approach. IEEE Trans. Inf. Theory 2012, 58, 5922–5940. [Google Scholar] [CrossRef]
- Duffield, N. Network Tomography of Binary Network Performance Characteristics. IEEE Trans. Inf. Theory 2006, 52, 5373–5388. [Google Scholar] [CrossRef]
- Mohammad, H.F.; Roy, S.; Bai, L.; Lydick, C. Link failure monitoring via network coding. In Proceedings of the IEEE Local Computer Network Conference, Denver, CO, USA, 10–14 October 2010. [Google Scholar] [CrossRef]
- Gui, J.; Shah-Mansouri, V.; Wong, V.W.S. A Linear Algebraic Approach for Loss Tomography in Mesh Topologies Using Network Coding. In Proceedings of the 2010 IEEE International Conference on Communications, Cape Town, South Africa, 23–27 May 2010. [Google Scholar] [CrossRef]
- Gui, J.; Shah-Mansouri, V.; Wong, V.W.S. Accurate and Efficient Network Tomography Through Network Coding. IEEE Trans. Veh. Technol. 2011, 60, 2701–2713. [Google Scholar] [CrossRef][Green Version]
- Shah-Mansouri, V.; Wong, V.W.S. Link Loss Inference in Wireless Sensor Networks with Randomized Network Coding. In Proceedings of the 2010 IEEE Global Telecommunications Conference GLOBECOM 2010, Miami, FL, USA, 6–10 December 2010. [Google Scholar] [CrossRef]
- Sattari, P.; Markopoulou, A.; Fragouli, C.; Gjoka, M. A Network Coding Approach to Loss Tomography. IEEE Trans. Inf. Theory 2013, 59, 1532–1562. [Google Scholar] [CrossRef]
- Sattari, P.; Markopoulou, A.; Fragouli, C. Maximum Likelihood Estimation for Multiple-Source Loss Tomography with Network Coding. In Proceedings of the 2011 International Symposium on Networking Coding, Beijing, China, 25–27 July 2011. [Google Scholar] [CrossRef]
- Berinde, R.; Gilbert, A.C.; Indyk, P.; Karloff, H.; Strauss, M.J. Combining geometry and combinatorics: A unified approach to sparse signal recovery. In Proceedings of the 2008 46th Annual Allerton Conference on Communication, Control, and Computing, Urbana-Champaign, IL, USA, 23–26 September 2008. [Google Scholar] [CrossRef]
- Xu, W.; Hassibi, B. Efficient Compressive Sensing with Deterministic Guarantees Using Expander Graphs. In Proceedings of the 2007 IEEE Information Theory Workshop, Tahoe City, CA, USA, 2–6 September 2007. [Google Scholar] [CrossRef]
- Firooz, M.H.; Roy, S. Link Delay Estimation via Expander Graphs. IEEE Trans. Commun. 2014, 62, 170–181. [Google Scholar] [CrossRef]
- Donoho, D.L.; Elad, M. Optimally sparse representation in general (nonorthogonal) dictionaries via ℓ1 minimization. Proc. Natl. Acad. Sci. USA 2003, 100, 2197–2202. [Google Scholar] [CrossRef]
- Fattaholmanan, A.; Rabiee, H.R.; Siyari, P.; Soltani-Farani, A.; Khodadadi, A. Peer-to-Peer Compressive Sensing for Network Monitoring. IEEE Commun. Lett. 2015, 19, 38–41. [Google Scholar] [CrossRef]
- Wang, W.; Gan, X.; Bai, W.; Wang, X.; Tian, X. Compressed sensing based network tomography using end-to-end path measurements. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017. [Google Scholar] [CrossRef]
- Fan, X.; Li, X. Delay tomography via compressed sensing under exponential distribution. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017. [Google Scholar] [CrossRef]
- Nakanishi, K.; Hara, S.; Matsuda, T.; Takizawa, K.; Ono, F.; Miura, R. Reflective Network Tomography Based on Compressed Sensing. Procedia Comput. Sci. 2015, 52, 186–193. [Google Scholar] [CrossRef]
- Nakanishi, K.; Hara, S.; Matsuda, T.; Takizawa, K.; Ono, F.; Miura, R. Synchronization-Free Delay Tomography Based on Compressed Sensing. IEEE Commun. Lett. 2014, 18, 1343–1346. [Google Scholar] [CrossRef]
- Kinsho, H.; Tagyo, R.; Ikegami, D.; Matsuda, T.; Takahashi, A.; Takine, T. Heterogeneous delay tomography based on graph fourier transform in mobile networks. In Proceedings of the 2017 IEEE International Workshop Technical Committee on Communications Quality and Reliability (CQR), Naples, FL, USA, 16–18 May 2017. [Google Scholar] [CrossRef]
- Wei, H.T.; Hsieh, S.H.; Hwang, W.L.; Liao, C.S.; Lu, C.S. Link Delay Estimation Using Sparse Recovery for Dynamic Network Tomography. arXiv 2018, arXiv:1812.00369. [Google Scholar]
- Wang, M.; Xu, W.; Mallada, E.; Tang, A. Sparse Recovery With Graph Constraints. IEEE Trans. Inf. Theory 2015, 61, 1028–1044. [Google Scholar] [CrossRef]
- Nguyen, H.X.; Thiran, P. The Boolean Solution to the Congested IP Link Location Problem: Theory and Practice. In Proceedings of the IEEE INFOCOM 2007—26th IEEE International Conference on Computer Communications, Barcelona, Spain, 6–12 May 2007. [Google Scholar] [CrossRef]
- Fan, X.; Li, X.; Zhang, J. Compressed sensing based loss tomography using weighted ℓ1 minimization. Comput. Commun. 2018, 127, 122–130. [Google Scholar] [CrossRef]
- Chen, J.; Qi, X.; Wang, Y. An efficient solution to locate sparsely congested links by network tomography. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014. [Google Scholar] [CrossRef]
- Takemoto, K.; Matsuda, T.; Takine, T. Sequential Loss Tomography Using Compressed Sensing. IEICE Trans. Commun. 2013, E96.B, 2756–2765. [Google Scholar] [CrossRef]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Morita, T.; Matsuda, T.; Takine, T. Spatially dependent loss tomography for multihop wireless networks. In Proceedings of the 2016 International Conference on Information Networking (ICOIN), Kota Kinabalu, Malaysia, 13–15 January 2016. [Google Scholar] [CrossRef]
- Bandara, V.W.; Jayasumana, A.P.; Whitner, R. An adaptive compressive sensing scheme for network tomography based fault localization. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014. [Google Scholar] [CrossRef]
- Donoho, D. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Candès, E.J.; Romberg, J.K.; Tao, T. Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 2006, 59, 1207–1223. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A Fast Iterative Shrinkage-Thresholding Algorithm for Linear Inverse Problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).