A Comprehensive Physiologically Based Pharmacokinetic Framework of Ofloxacin: Predicting Disposition in Renal Impairment
Abstract
1. Introduction
2. Materials and Methods
2.1. Screening of Reported Pharmacokinetic Data
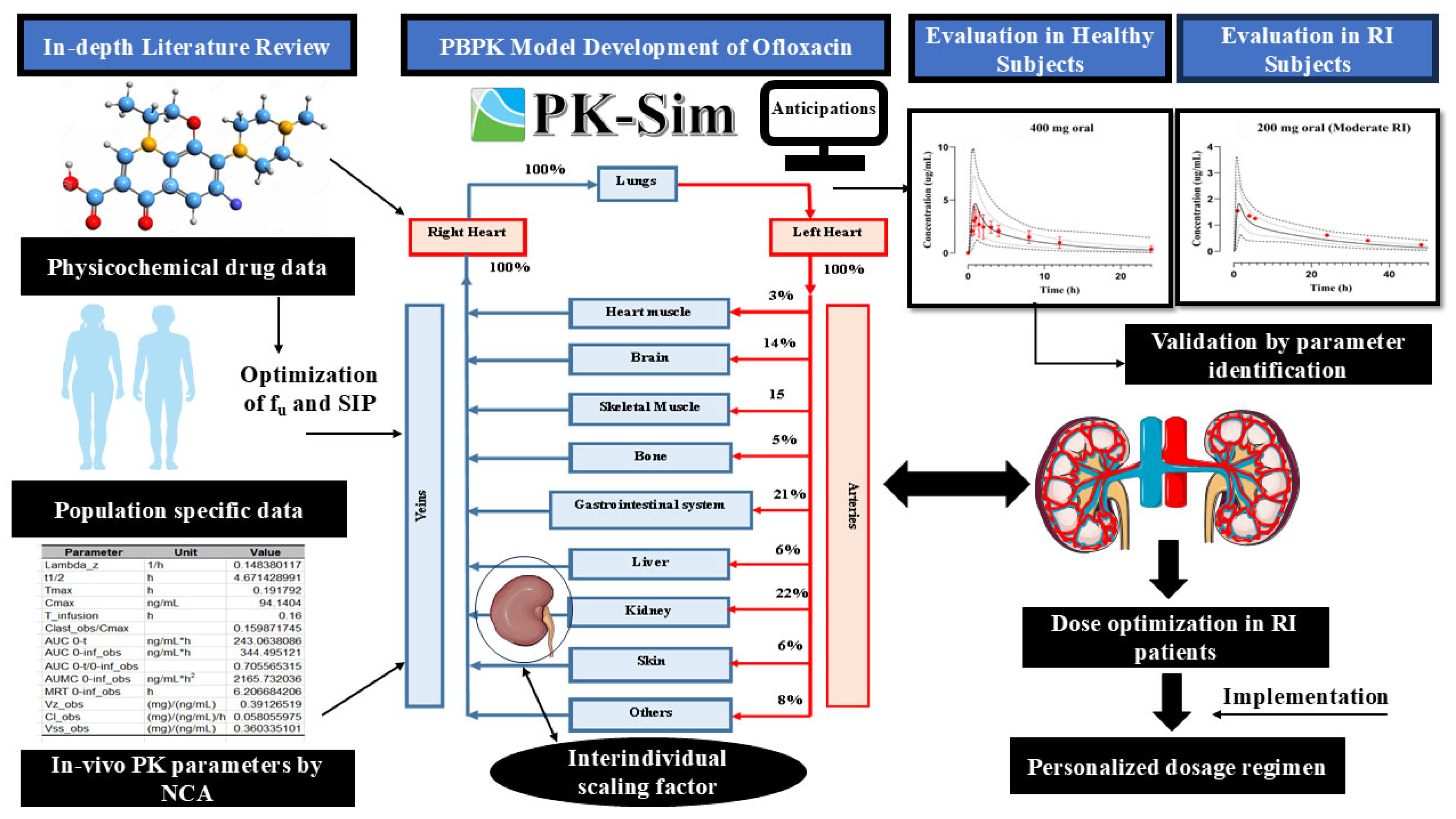
2.2. Description of PBPK Simulation Software
2.3. Creation of Building Blocks
2.4. Strategy for PBPK Model Building
2.5. Model Structure
2.6. PBPK Model Structure in a Diseased Population
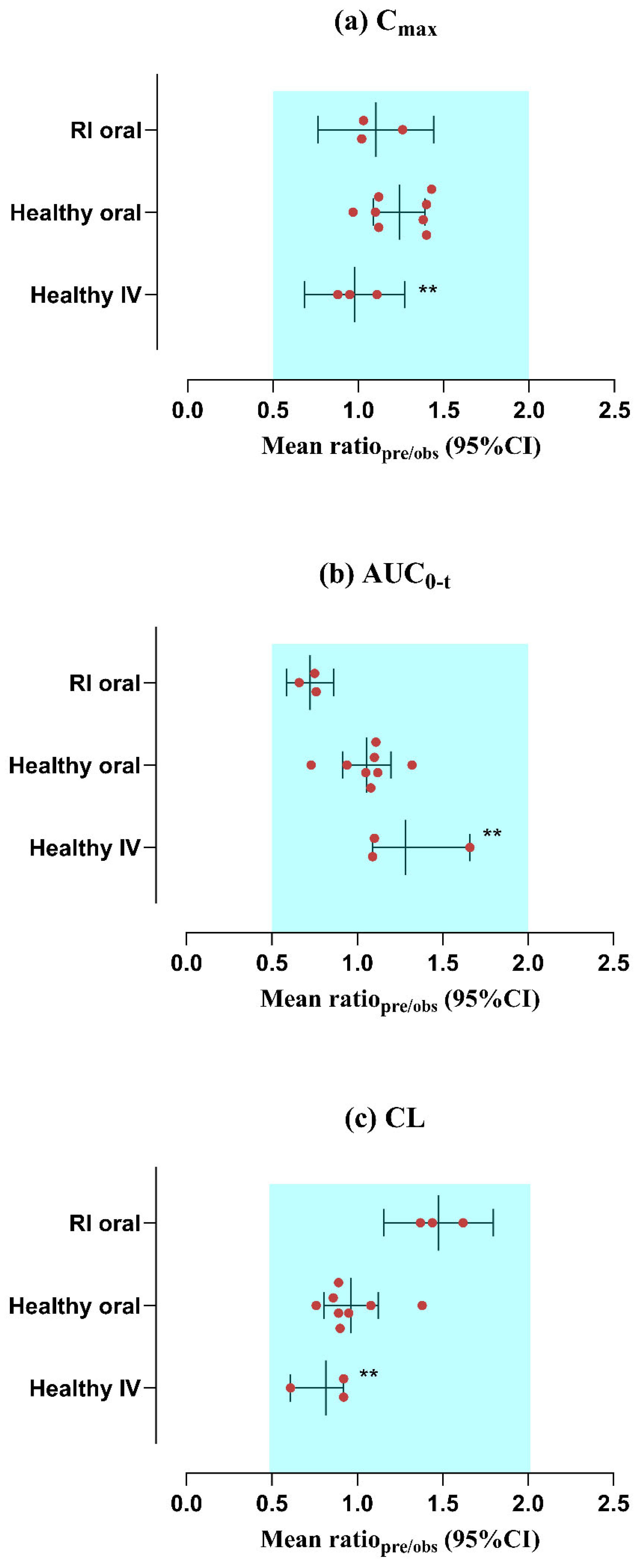
2.7. Evaluation of Model Predictions
3. Results
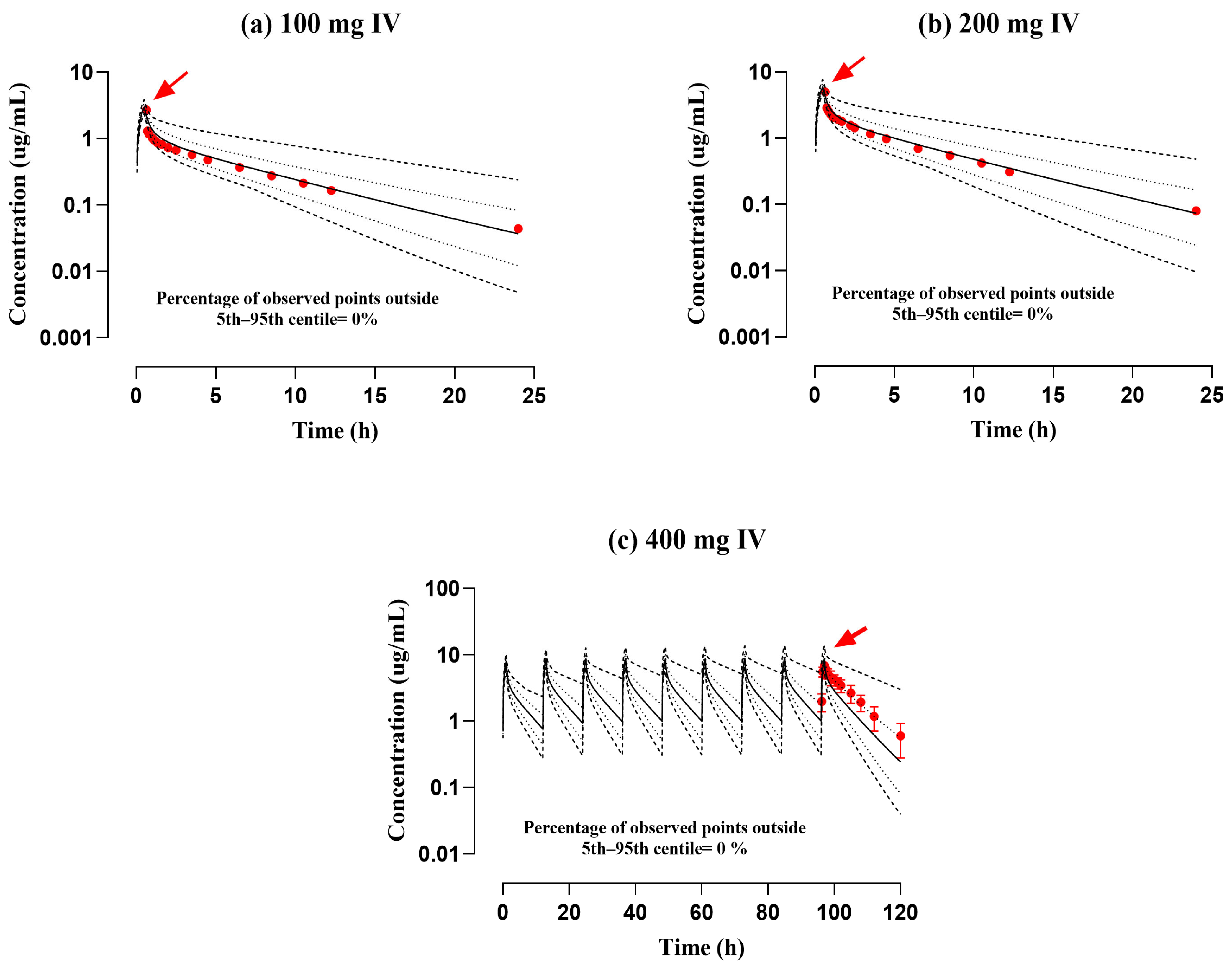
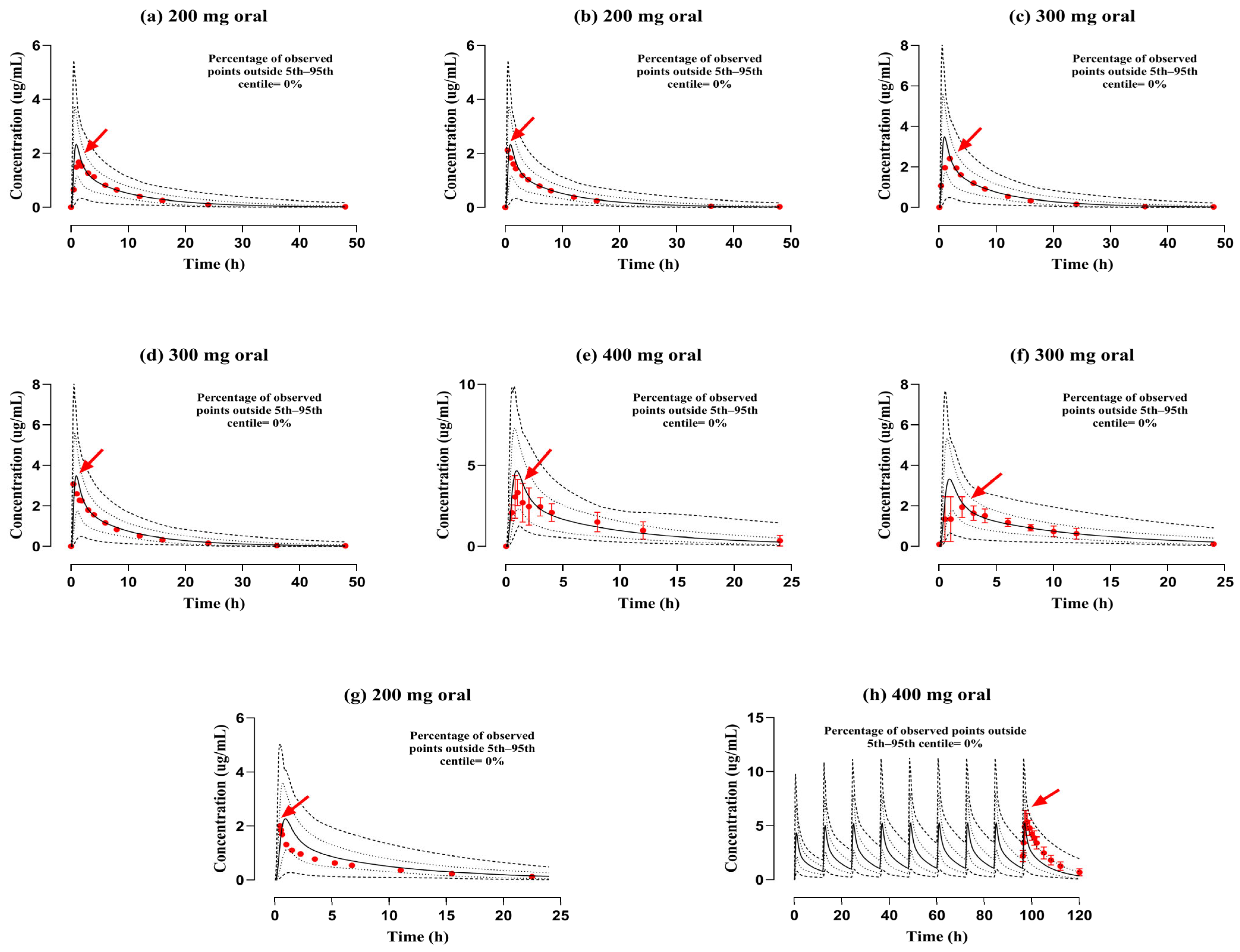
3.1. Assessment of the PBPK Model in a Healthy (IV and PO) Population
3.2. Evaluation of the PBPK Model in the Population with RI
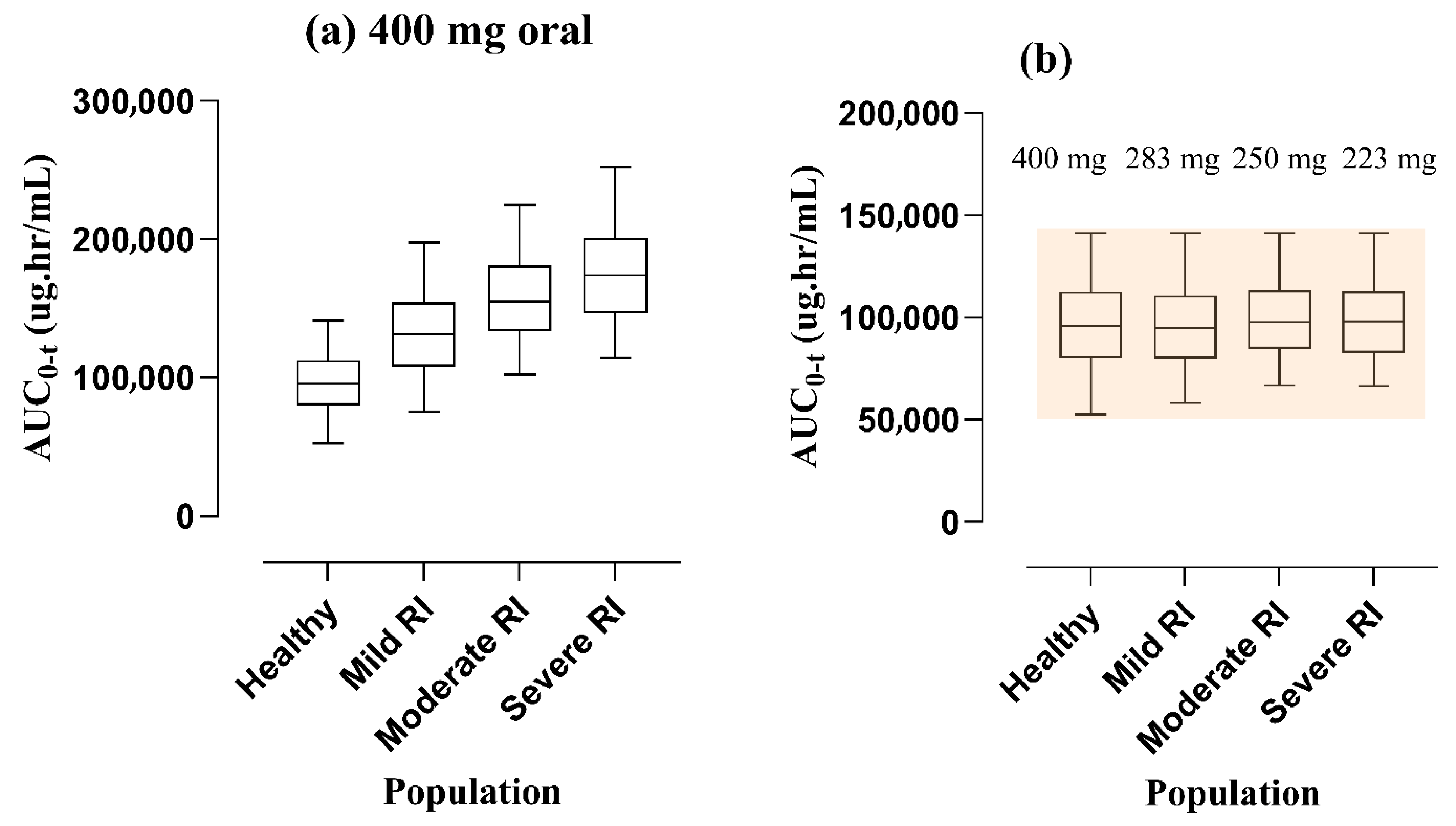
3.3. Dose Amendments in Subjects with RI
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Jin, J.Y.; Mukadam, S.; Malhi, V.; Kenny, J.R. Application of IVIVE and PBPK modeling in prospective prediction of clinical pharmacokinetics: Strategy and approach during the drug discovery phase with four case studies. Biopharm. Drug Dispos. 2012, 33, 85–98. [Google Scholar] [CrossRef]
- Heimbach, T.; Chen, Y.; Chen, J.; Dixit, V.; Parrott, N.; Peters, S.A.; Poggesi, I.; Sharma, P.; Snoeys, J.; Shebley, M.; et al. Physiologically-Based Pharmacokinetic Modeling in Renal and Hepatic Impairment Populations: A Pharmaceutical Industry Perspective. Clin. Pharmacol. Ther. 2021, 110, 297–310. [Google Scholar] [CrossRef] [PubMed]
- Hartmanshenn, C.; Scherholz, M.; Androulakis, I.P. Physiologically-based pharmacokinetic models: Approaches for enabling personalized medicine. J. Pharmacokinet. Pharmacodyn. 2016, 43, 481–504. [Google Scholar] [CrossRef] [PubMed]
- Rostami-Hodjegan, A. Physiologically based pharmacokinetics joined with in vitro-in vivo extrapolation of ADME: A marriage under the arch of systems pharmacology. Clin. Pharmacol. Ther. 2012, 92, 50–61. [Google Scholar] [CrossRef]
- Clewell, R.A.; Clewell, H.J., 3rd. Development and specification of physiologically based pharmacokinetic models for use in risk assessment. Regul. Toxicol. Pharmacol. RTP 2008, 50, 129–143. [Google Scholar] [CrossRef]
- Peters, S.A. Evaluation of a generic physiologically based pharmacokinetic model for lineshape analysis. Clin. Pharmacokinet. 2008, 47, 261–275. [Google Scholar] [CrossRef]
- Jones, H.M.; Chen, Y.; Gibson, C.; Heimbach, T.; Parrott, N.; Peters, S.A.; Snoeys, J.; Upreti, V.V.; Zheng, M.; Hall, S.D. Physiologically based pharmacokinetic modeling in drug discovery and development: A pharmaceutical industry perspective. Clin. Pharmacol. Ther. 2015, 97, 247–262. [Google Scholar] [CrossRef]
- Rowland, M.; Peck, C.; Tucker, G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu. Rev. Pharmacol. Toxicol. 2011, 51, 45–73. [Google Scholar] [CrossRef]
- Zamir, A.; Rasool, M.F.; Imran, I.; Saeed, H.; Khalid, S.; Majeed, A.; Rehman, A.U.; Ahmad, T.; Alasmari, F.; Alqahtani, F. Physiologically Based Pharmacokinetic Model To Predict Metoprolol Disposition in Healthy and Disease Populations. ACS Omega 2023, 8, 29302–29313. [Google Scholar] [CrossRef]
- Tan, S.P.F.; Wu, H.; Rostami-Hodjegan, A.; Scotcher, D.; Galetin, A. Evaluation of Adefovir PBPK Model to Assess Biomarker-Informed OAT1 Drug-Drug Interaction and Effect of Chronic Kidney Disease. CPT Pharmacomet. Syst. Pharmacol. 2025, 14, 964–974. [Google Scholar] [CrossRef] [PubMed]
- Rasool, M.F.; Ali, S.; Khalid, S.; Khalid, R.; Majeed, A.; Imran, I.; Saeed, H.; Usman, M.; Ali, M.; Alali, A.S.; et al. Development and evaluation of physiologically based pharmacokinetic drug-disease models for predicting captopril pharmacokinetics in chronic diseases. Sci. Rep. 2021, 11, 8589. [Google Scholar] [CrossRef]
- Ayub, A.; Zamir, A.; Rasool, M.F.; Arshad, U.; Alqahtani, F. A PBPK modeling approach for personalized dose optimization of nicardipine in renal and hepatic dysfunction. Sci. Rep. 2025, 15, 19752. [Google Scholar] [CrossRef]
- Dubinsky, S.; Malik, P.; Hajducek, D.M.; Edginton, A. Determining the Effects of Chronic Kidney Disease on Organic Anion Transporter1/3 Activity Through Physiologically Based Pharmacokinetic Modeling. Clin. Pharmacokinet. 2022, 61, 997–1012. [Google Scholar] [CrossRef]
- Monk, J.P.; Campoli-Richards, D.M. Ofloxacin. A review of its antibacterial activity, pharmacokinetic properties and therapeutic use. Drugs 1987, 33, 346–391. [Google Scholar] [CrossRef] [PubMed]
- Graham, D.B.; Tripp, J. Ofloxacin. In StatPearls; StatPearls Publishing LLC.: Treasure Island, FL, USA, 2025. [Google Scholar]
- Todd, P.A.; Faulds, D. Ofloxacin. A reappraisal of its antimicrobial activity, pharmacology and therapeutic use. Drugs 1991, 42, 825–876. [Google Scholar] [CrossRef] [PubMed]
- Lode, H.; Höffken, G.; Olschewski, P.; Sievers, B.; Kirch, A.; Borner, K.; Koeppe, P. Comparative pharmacokinetics of intravenous ofloxacin and ciprofloxacin. J. Antimicrob. Chemother. 1988, 22 (Suppl. C), 73–79. [Google Scholar] [CrossRef] [PubMed]
- Stein, G.E.; LeBel, M.; Flor, S.C.; Zinny, M. Bioavailability and pharmacokinetics of oral ofloxacin formulations in normal subjects. Curr. Med. Res. Opin. 1991, 12, 479–484. [Google Scholar] [CrossRef]
- Sánchez Navarro, A.; Martínez Cabarga, M.; Dominguez-Gil Hurlé, A. Oral absorption of ofloxacin administered together with aluminum. Antimicrob. Agents Chemother. 1994, 38, 2510–2512. [Google Scholar] [CrossRef]
- Molinaro, M.; Villani, P.; Regazzi, M.B.; Rondanelli, R.; Doveri, G. Pharmacokinetics of ofloxacin in elderly patients and in healthy young subjects. Eur. J. Clin. Pharmacol. 1992, 43, 105–107. [Google Scholar] [CrossRef]
- Jagdale, S.; Pawar, S. Gellified Emulsion of Ofloxacin for Transdermal Drug Delivery System. Adv. Pharm. Bull. 2017, 7, 229–239. [Google Scholar] [CrossRef]
- Ross, D.L.; Riley, C.M. Aqueous solubilities of some variously substituted quinolone antimicrobials. Int. J. Pharm. 1990, 63, 237–250. [Google Scholar] [CrossRef]
- Al-Omar, M.A. Chapter 6—Ofloxacin. In Profiles of Drug Substances, Excipients and Related Methodology; Brittain, H.G., Ed.; Academic Press: Cambridge, MA, USA, 2009; Volume 34, pp. 265–298. [Google Scholar]
- Kim, G.K. The Risk of Fluoroquinolone-induced Tendinopathy and Tendon Rupture: What Does The Clinician Need To Know? J. Clin. Aesthet. Dermatol. 2010, 3, 49–54. [Google Scholar] [PubMed]
- Rowland Yeo, K.; Aarabi, M.; Jamei, M.; Rostami-Hodjegan, A. Modeling and predicting drug pharmacokinetics in patients with renal impairment. Expert Rev. Clin. Pharmacol. 2011, 4, 261–274. [Google Scholar] [CrossRef]
- Malik, P.R.V.; Yeung, C.H.T.; Ismaeil, S.; Advani, U.; Djie, S.; Edginton, A.N. A Physiological Approach to Pharmacokinetics in Chronic Kidney Disease. J. Clin. Pharmacol. 2020, 60 (Suppl. S1), S52–S62. [Google Scholar] [CrossRef]
- Le Merdy, M.; AlQaraghuli, F.; Tan, M.-L.; Lukacova, V. Clinical Ocular Exposure Extrapolation Using PBPK Modeling and Simulation: Ofloxacin Ointment Case Study. Investig. Ophthalmol. Vis. Sci. 2024, 65, 3706. [Google Scholar]
- Utsey, K.; Gastonguay, M.S.; Russell, S.; Freling, R.; Riggs, M.M.; Elmokadem, A. Quantification of the impact of partition coefficient prediction methods on physiologically based pharmacokinetic model output using a standardized tissue composition. Drug Metab. Dispos. 2020, 48, 903–916. [Google Scholar] [CrossRef]
- Schlender, J.F.; Teutonico, D.; Coboeken, K.; Schnizler, K.; Eissing, T.; Willmann, S.; Jaehde, U.; Stass, H. A Physiologically-Based Pharmacokinetic Model to Describe Ciprofloxacin Pharmacokinetics Over the Entire Span of Life. Clin. Pharmacokinet. 2018, 57, 1613–1634. [Google Scholar] [CrossRef] [PubMed]
- Sadiq, M.W.; Nielsen, E.I.; Khachman, D.; Conil, J.M.; Georges, B.; Houin, G.; Laffont, C.M.; Karlsson, M.O.; Friberg, L.E. A whole-body physiologically based pharmacokinetic (WB-PBPK) model of ciprofloxacin: A step towards predicting bacterial killing at sites of infection. J. Pharmacokinet. Pharmacodyn. 2017, 44, 69–79. [Google Scholar] [CrossRef]
- Estradé, O.; Vozmediano, V.; Carral, N.; Isla, A.; González, M.; Poole, R.; Suarez, E. Key Factors in Effective Patient-Tailored Dosing of Fluoroquinolones in Urological Infections: Interindividual Pharmacokinetic and Pharmacodynamic Variability. Antibiotics 2022, 11, 641. [Google Scholar] [CrossRef]
- Flor, S.C.; Rogge, M.C.; Chow, A.T. Bioequivalence of oral and intravenous ofloxacin after multiple-dose administration to healthy male volunteers. Antimicrob. Agents Chemother. 1993, 37, 1468–1472. [Google Scholar] [CrossRef][Green Version]
- Fillastre, J.P.; Leroy, A.; Humbert, G. Ofloxacin pharmacokinetics in renal failure. Antimicrob. Agents Chemother. 1987, 31, 156–160. [Google Scholar] [CrossRef]
- Willmann, S.; Lippert, J.; Sevestre, M.; Solodenko, J.; Fois, F.; Schmitt, W. PK-Sim (R): A physiologically based pharmacokinetic‘whole-body’model. Biosilico 2003, 1, 121–124. [Google Scholar] [CrossRef]
- Varlan, A.; Ionescu, S.; Hillebrand, M. Study of the interaction between ofloxacin and human serum albumin by spectroscopic methods. Luminescence 2011, 26, 710–715. [Google Scholar] [CrossRef]
- Sakore, S.; Choudhari, S.; Chakraborty, B. Biowaiver monograph for immediate release solid oral dosage forms: Ofloxacin. Int. J. Pharm. Pharm. Sci. 2010, 2, 156–161. [Google Scholar]
- Takács-Novák, K.; Józan, M.; Hermecz, I.; Szász, G. Lipophilicity of antibacterial fluoroquinolones. Int. J. Pharm. 1992, 79, 89–96. [Google Scholar] [CrossRef]
- PubChem Compound Summary for CID 4583, Ofloxacin. Available online: https://pubchem.ncbi.nlm.nih.gov/compound/Ofloxacin (accessed on 11 July 2025).
- Ola, A.K.; Sandhu, H.S.; Dumka, V.K.; Ranjan, B. Pharmacokinetics, urinary excretion and plasma protein binding of ofloxacin in water buffalo calves (Bubalus bubalis). J. S. Afr. Vet. Assoc. 2013, 84, 1–5. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Khalil, F.; Läer, S. Physiologically based pharmacokinetic models in the prediction of oral drug exposure over the entire pediatric age range-sotalol as a model drug. AAPS J. 2014, 16, 226–239. [Google Scholar] [CrossRef]
- Rasool, M.F.; Khalil, F.; Läer, S. Optimizing the clinical use of carvedilol in liver cirrhosis using a physiologically based pharmacokinetic modeling approach. Eur. J. Drug Metab. Pharmacokinet. 2017, 42, 383–396. [Google Scholar] [CrossRef] [PubMed]
- Verbeeck, R.K.; Singu, B.S. Chapter 3—Pathophysiologic changes in chronic heart failure affecting drug pharmacokinetics. In Cardio-Hepatology; Taniguchi, T., Lee, S.S., Eds.; Academic Press: Cambridge, MA, USA, 2023; pp. 17–30. [Google Scholar]
- Zhang, Y.; Huo, M.; Zhou, J.; Xie, S. PKSolver: An add-in program for pharmacokinetic and pharmacodynamic data analysis in Microsoft Excel. Comput. Methods Programs Biomed. 2010, 99, 306–314. [Google Scholar] [CrossRef]
- Franchetti, Y.; Nolin, T.D. Dose optimization in kidney disease: Opportunities for PBPK modeling and simulation. J. Clin. Pharmacol. 2020, 60, S36–S51. [Google Scholar] [CrossRef]
- Dagrosa, E.E.; Verho, M.; Malerczyk, V.; de Looze, S.; Hajdú, P.; Toyodera, K. Multiple-dose pharmacokinetics of ofloxacin, a new broad-spectrum antimicrobial agent. Clin. Ther. 1986, 8, 632–645. [Google Scholar] [PubMed]
- Fabre, J.; Fox, H.M.; Dayer, P.; Balant, L. Differences in kinetic properties of drugs: Implications as to the selection of a particular drug for use in patients with renal failure with special emphasis on antibiotics and beta-adrenoceptor blocking agents. Clin. Pharmacokinet. 1980, 5, 441–464. [Google Scholar] [CrossRef] [PubMed]
- Floxin Tablets (Ofloxacin Tablets). Available online: https://www.accessdata.fda.gov/drugsatfda_docs/label/2008/019735s059lbl.pdf (accessed on 12 July 2025).
| Sr. No. | Study Reference | Target Population | No. of Enrolled Participants | Applied Dosage (mg) | Mode of Administration | Female Proportion (%) | Age (Years) | Weight (kg) |
|---|---|---|---|---|---|---|---|---|
| 1- | Lode et al. (1988) [17] a,b | Healthy | 10 | 100 | IV infusion | 50 | 25–46 | 54–74 |
| 200 | ||||||||
| 2- | Stein et al. (1991) [18] b | Healthy | 32 | 200 | PO | 0 | 18–37 | 59–99 |
| 300 | ||||||||
| 3- | Sanchez Sánchez et al. (1994) [19] a | Healthy | 10 | 400 | PO | 20 | 21–50 | 62.3 ± 13.2 |
| 4- | Molinaro et al. (1992) [20] a | Healthy | 12 | 300 | PO | 0 | 20–27 | 62–86 |
| 5- | Flor et al. (1993) [32] b | Healthy | 20 | 400 | IV infusion | 0 | 18–41 | 61–100 |
| PO | ||||||||
| 6- | Fillastre et al. (1987) [33] b | Healthy | 12 | 200 | PO | N/M | 27.7 ± 3.1 | 71 ± 6.2 |
| Mild RI | 58.0 ± 11.9 | 63.6 ± 11.5 | ||||||
| Moderate RI | 63.3 ± 8.2 | 72.4 ± 12.9 | ||||||
| Severe RI | 63.6 ± 13.3 | 74.4 ± 20.5 |
| Model Parameters | Incorporated Values | Reference ID |
|---|---|---|
| Physicochemical characteristics | ||
| Molecular mass (g/mol) | 361.388 | [23] |
| pKa | pKa1 6.05 | [22] |
| pKa2 8.22 | ||
| Plasma protein binding | Human serum albumin | [35] |
| Solubility in water (mg/mL) | 2.66 mg/mL @ pH 7 | [36] |
| Log P (log units) | Range (−0.39–2.1) a | [36,37,38] |
| Absorption | ||
| Specific intestinal permeability (cm/min) | 4.92 × 10−6 b | Optimized |
| Distribution | ||
| Cellular permeability model | PK Sim Standard | [34] |
| Partition coefficient model | Rodger and Rowland | [34] |
| Specific organ permeability (cm/min) | 1.29 × 10−4 | Calculated by PK-Sim |
| Fraction of unbound drug (fu) | 80%, 83% c | [16,39] |
| Metabolism and elimination | ||
| Total hepatic clearance (L/h/kg) | 0.04 | [33] |
| GFR fraction | 0.90 d | [33] |
| Tubular secretion (L/h) | 5.52 e | [33] |
| Sr. No. | Study ID | Administered Doses | Cmax (μg/mL) | AUC0–t (μg·h/mL) | CL (L/h) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| PRE | OBS | R Ratio | PRE | OBS | R Ratio | PRE | OBS | R Ratio | |||
| Healthy population (IV infusion route) | |||||||||||
| 1- | Lode et al. (1988) [17] | 100 | 2.39 | 2.7 | 0.88 | 7.94 | 7.19 | 1.1 | 12.16 | 13.19 | 0.92 |
| 2- | Lode et al. (1988) [17] | 200 | 4.78 | 4.98 | 0.95 | 15.81 | 14.47 | 1.09 | 12.21 | 13.23 | 0.92 |
| 3- | Flor et al. (1993) [32] | 400 | 7.74 | 6.92 | 1.11 | 253.68 | 152.05 | 1.66 | 1.56 | 2.52 | 0.61 |
| Healthy population (PO route) | |||||||||||
| 1- | Stein et al. (1991) [18] | 200 | 2.33 | 1.66 | 1.4 | 16.07 | 14.39 | 1.11 | 12.3 | 13.71 | 0.89 |
| 2- | Stein et al. (1991) [18] | 200 | 2.33 | 2.11 | 1.1 | 16.08 | 15.24 | 1.05 | 12.29 | 12.87 | 0.95 |
| 3- | Stein et al. (1991) [18] | 300 | 3.46 | 2.41 | 1.43 | 22.7 | 20.2 | 1.12 | 13.2 | 14.67 | 0.89 |
| 4- | Stein et al. (1991) [18] | 300 | 3.46 | 3.08 | 1.12 | 23.06 | 20.79 | 1.1 | 12.83 | 14.24 | 0.9 |
| 5- | Sanchez et al. (1994) [19] | 400 | 4.64 | 3.31 | 1.4 | 27.9 | 29.49 | 0.94 | 12.99 | 12 | 1.08 |
| 6- | Molinaro et al. (1992) [20] | 300 | 3.19 | 2.3 | 1.38 | 20.57 | 18.99 | 1.08 | 12.99 | 15.07 | 0.86 |
| 7- | Fillastre et al. (1987) [33] | 200 | 2.25 | 2 | 1.12 | 13.77 | 10.42 | 1.32 | 12.95 | 16.98 | 0.76 |
| 8- | Flor et al. (1993) [32] | 400 | 5.25 | 5.36 | 0.97 | 118.3 | 160.16 | 0.73 | 3.26 | 2.36 | 1.38 |
| Population/Route | PK Variable | AFE | RMSE | MAE |
|---|---|---|---|---|
| Healthy adults (IV) | Cmax | 0.98 | 0.51 | 0.44 |
| AUC0–t | 1.28 | 58.68 | 34.57 | |
| CL | 0.81 | 1 | 1 | |
| Healthy adults (Oral) | Cmax | 1.24 | 0.73 | 0.61 |
| AUC0–t | 1.05 | 14.93 | 6.95 | |
| CL | 0.96 | 1.89 | 1.6 | |
| RI (Oral) | Cmax | 1.1 | 0.22 | 0.16 |
| AUC0–t | 0.71 | 12.47 | 11.31 | |
| CL | 1.54 | 2.43 | 2.41 |
| Sr. No. | Study ID | Population | Administered Doses | Cmax (μg/mL) | AUC0–t (μg·h/mL) | CL (L/h) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PRE | OBS | R Ratio | PRE | OBS | R Ratio | PRE | OBS | R Ratio | ||||
| RI Population (PO Route) | ||||||||||||
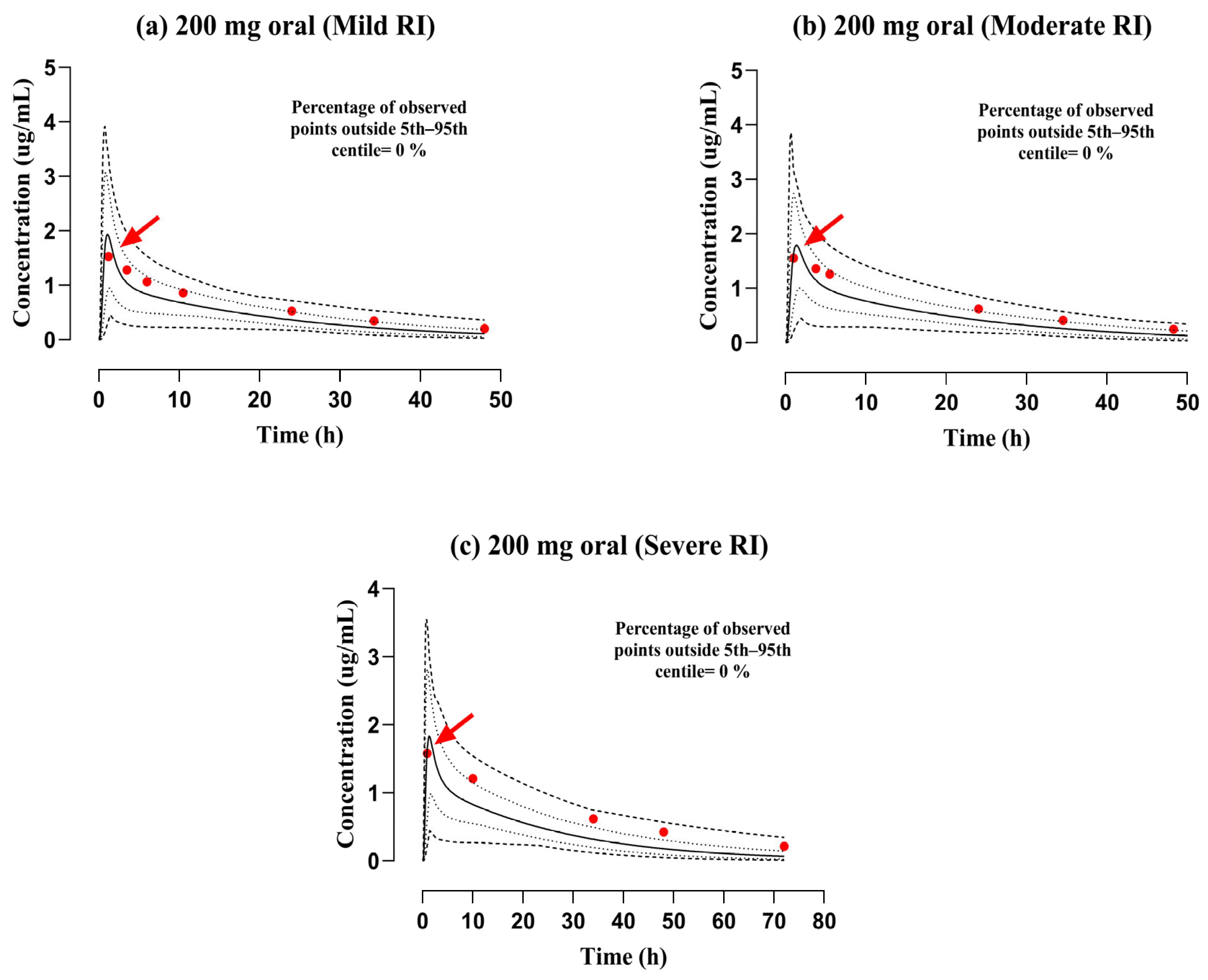
| 1- | Fillastre et al. (1987) [33] | Mild RI | 200 | 1.91 | 1.52 | 1.25 | 22.32 | 28.79 | 0.77 | 8.16 | 5.88 | 1.38 |
| 2- | Fillastre et al. (1987) [33] | Moderate RI | 200 | 1.59 | 1.55 | 1.02 | 25.50 | 34.33 | 0.74 | 7.01 | 4.9 | 1.43 |
| 3- | Fillastre et al. (1987) [33] | Severe RI | 200 | 1.64 | 1.57 | 1.04 | 31.49 | 50.12 | 0.63 | 6.32 | 3.46 | 1.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamir, A.; Rasool, M.F.; Hussain, I.; Alsanea, S.; Alhabardi, S.A.; Alqahtani, F. A Comprehensive Physiologically Based Pharmacokinetic Framework of Ofloxacin: Predicting Disposition in Renal Impairment. Pharmaceutics 2025, 17, 1224. https://doi.org/10.3390/pharmaceutics17091224
Zamir A, Rasool MF, Hussain I, Alsanea S, Alhabardi SA, Alqahtani F. A Comprehensive Physiologically Based Pharmacokinetic Framework of Ofloxacin: Predicting Disposition in Renal Impairment. Pharmaceutics. 2025; 17(9):1224. https://doi.org/10.3390/pharmaceutics17091224
Chicago/Turabian StyleZamir, Ammara, Muhammad Fawad Rasool, Iltaf Hussain, Sary Alsanea, Samiah A. Alhabardi, and Faleh Alqahtani. 2025. "A Comprehensive Physiologically Based Pharmacokinetic Framework of Ofloxacin: Predicting Disposition in Renal Impairment" Pharmaceutics 17, no. 9: 1224. https://doi.org/10.3390/pharmaceutics17091224
APA StyleZamir, A., Rasool, M. F., Hussain, I., Alsanea, S., Alhabardi, S. A., & Alqahtani, F. (2025). A Comprehensive Physiologically Based Pharmacokinetic Framework of Ofloxacin: Predicting Disposition in Renal Impairment. Pharmaceutics, 17(9), 1224. https://doi.org/10.3390/pharmaceutics17091224








