Modeling and Design of Chitosan–PCL Bi-Layered Microspheres for Intravitreal Controlled Release
Abstract
1. Introduction
2. Methods
2.1. Geometry
2.2. Mathematical Model
2.3. Numerical Methods
2.3.1. Finite Difference Approach in MATLAB
2.3.2. Finite Element Approach in COMSOL Multiphysics
2.4. Sensitivity Analysis
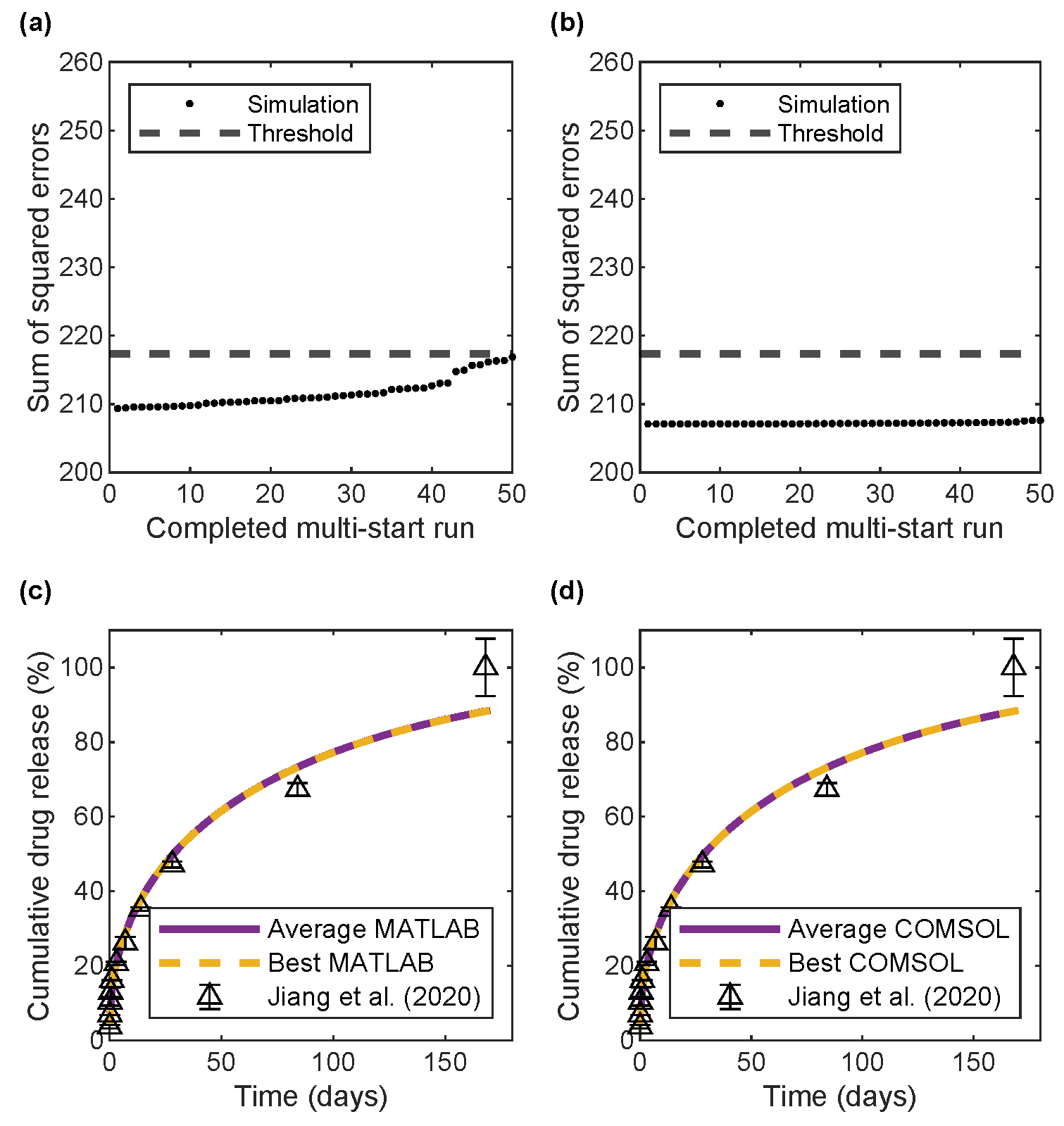
2.5. Parameter Estimation
2.6. Parameter Uncertainty Quantification
3. Results
3.1. Sensitivity Analysis
3.2. Parameter Estimation
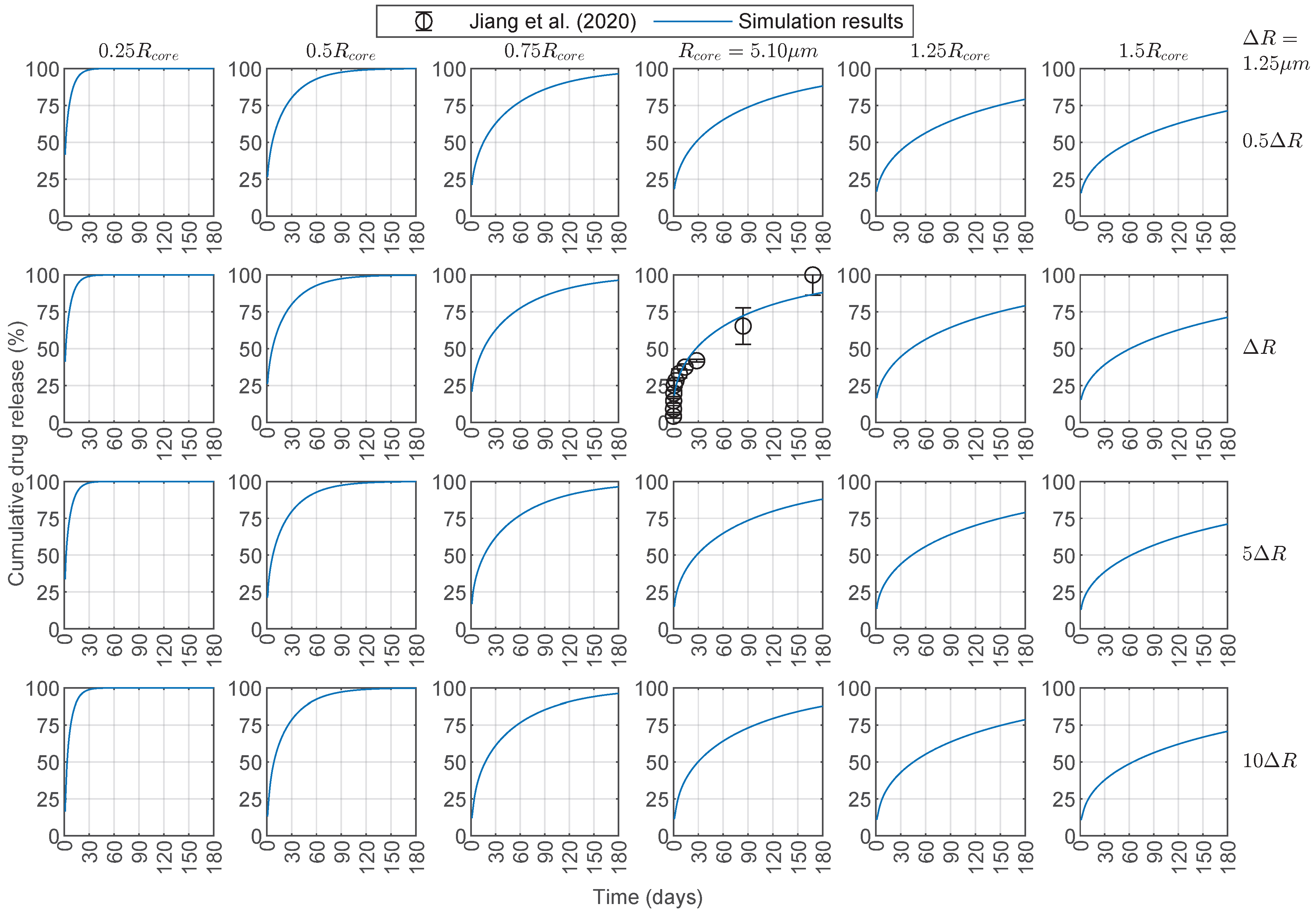
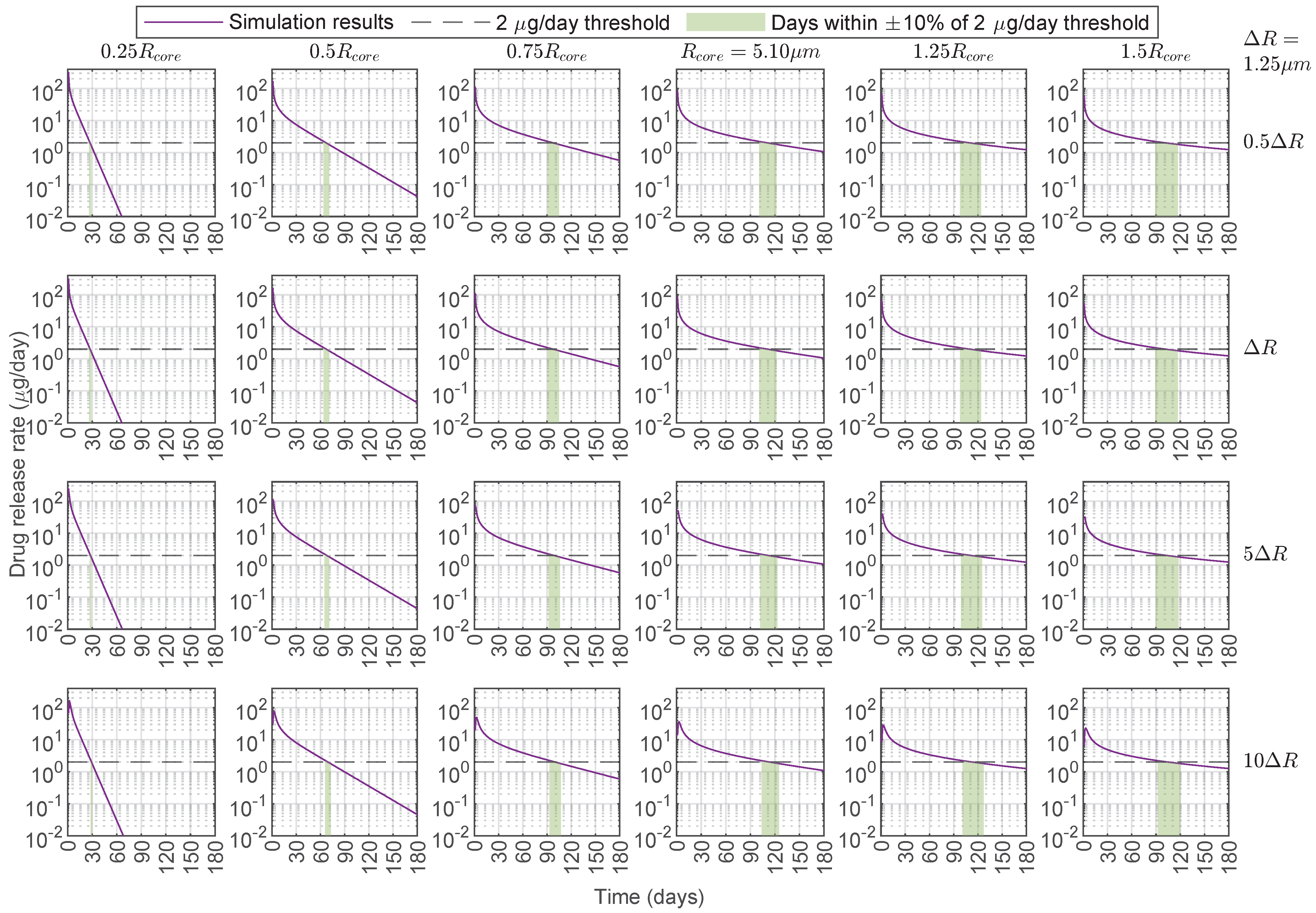
3.3. Predictive Capabilities
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kaur, I.P.; Kakkar, S. Nanotherapy for posterior eye diseases. J. Control. Release 2014, 193, 100–112. [Google Scholar] [CrossRef] [PubMed]
- Chacin Ruiz, E.A.; Swindle-Reilly, K.E.; Ford Versypt, A.N. Experimental and mathematical approaches for drug delivery for the treatment of wet age-related macular degeneration. J. Control. Release 2023, 363, 464–483. [Google Scholar] [CrossRef] [PubMed]
- Mi, F.L.; Tan, Y.C.; Liang, H.F.; Sung, H.W. In vivo biocompatibility and degradability of a novel injectable-chitosan-based implant. Biomaterials 2002, 23, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Cojocariu, A.; Profire, L.; Aflori, M.; Vasile, C. In vitro drug release from chitosan/Cloisite 15A hydrogels. Appl. Clay Sci. 2012, 57, 1–9. [Google Scholar] [CrossRef]
- Das, S.; Chaudhury, A.; Ng, K. Preparation and evaluation of zinc–pectin–chitosan composite particles for drug delivery to the colon: Role of chitosan in modifying in vitro and in vivo drug release. Int. J. Pharm. 2011, 406, 11–20. [Google Scholar] [CrossRef]
- Justin, R.; Chen, B. Characterisation and drug release performance of biodegradable chitosan–graphene oxide nanocomposites. Carbohydr. Polym. 2014, 103, 70–80. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, X.; Li, P.; He, Q.; Zhou, H. Chitosan and chitosan/ β-cyclodextrin microspheres as sustained-release drug carriers. J. Appl. Polym. Sci. 2007, 103, 1183–1190. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, L.; Chen, Z.; Sun, J.; Guo, X.; Wang, H.; Zhang, X.; Liu, Z.; Liu, J.; Zhang, K.; et al. Remineralization and bacterial inhibition of early enamel caries surfaces by carboxymethyl chitosan lysozyme nanogels loaded with antibacterial drugs. J. Dent. 2025, 152, 105489. [Google Scholar] [CrossRef]
- Nair, L.; Laurencin, C. Biodegradable polymers as biomaterials. Prog. Polym. Sci. 2007, 32, 762–798. [Google Scholar] [CrossRef]
- Astuti, S.; Rahma, W.A.; Budianto, E. Biodegradable Microcapsules from D,L–PLA/PCL as Controlled Nifedipine Drug Delivery Carrier. Macromol. Symp. 2020, 391, 1900132. [Google Scholar] [CrossRef]
- Gedik, B.; Erdem, M.A. Electrospun PCL membranes for localized drug delivery and bone regeneration. BMC Biotechnol. 2025, 25, 31. [Google Scholar] [CrossRef]
- Mirzaeei, S.; Mansurian, M.; Asare-Addo, K.; Nokhodchi, A. Metronidazole- and Amoxicillin-Loaded PLGA and PCL Nanofibers as Potential Drug Delivery Systems for the Treatment of Periodontitis: In Vitro and In Vivo Evaluations. Biomedicines 2021, 9, 975. [Google Scholar] [CrossRef]
- Mitxelena-Iribarren, O.; Riera-Pons, M.; Pereira, S.; Calero-Castro, F.J.; Castillo Tuñón, J.M.; Padillo-Ruiz, J.; Mujika, M.; Arana, S. Drug-loaded PCL electrospun nanofibers as anti-pancreatic cancer drug delivery systems. Polym. Bull. 2023, 80, 7763–7778. [Google Scholar] [CrossRef]
- Tabassi, S.A.S.; Tekie, F.S.M.; Hadizadeh, F.; Rashid, R.; Khodaverdi, E.; Mohajeri, S.A. Sustained release drug delivery using supramolecular hydrogels of the triblock copolymer PCL–PEG–PCL and α-cyclodextrin. J. Sol-Gel Sci. Technol. 2014, 69, 166–171. [Google Scholar] [CrossRef]
- Allyn, M.M.; Luo, R.H.; Hellwarth, E.B.; Swindle-Reilly, K.E. Considerations for polymers used in ocular drug delivery. Front. Med. 2022, 8, 787644. [Google Scholar] [CrossRef]
- Dias, J.R.; Sousa, A.; Augusto, A.; Bártolo, P.J.; Granja, P.L. Electrospun polycaprolactone (PCL) degradation: An in vitro and in vivo study. Polymers 2022, 14, 3397. [Google Scholar] [CrossRef] [PubMed]
- Bartnikowski, M.; Dargaville, T.R.; Ivanovski, S.; Hutmacher, D.W. Degradation mechanisms of polycaprolactone in the context of chemistry, geometry and environment. Prog. Polym. Sci. 2019, 96, 1–20. [Google Scholar] [CrossRef]
- Lam, C.X.F.; Savalani, M.M.; Teoh, S.H.; Hutmacher, D.W. Dynamics of in vitro polymer degradation of polycaprolactone-based scaffolds: Accelerated versus simulated physiological conditions. Biomed. Mater. 2008, 3, 034108. [Google Scholar] [CrossRef] [PubMed]
- Badiee, P.; Varshochian, R.; Rafiee-Tehrani, M.; Abedin Dorkoosh, F.; Khoshayand, M.R.; Dinarvand, R. Ocular implant containing bevacizumab-loaded chitosan nanoparticles intended for choroidal neovascularization treatment. J. Biomed. Mater. Res. Part A 2018, 106, 2261–2271. [Google Scholar] [CrossRef]
- Mihailovici, R.; Croitoriu, A.; Nedeff, F.; Nedeff, V.; Ochiuz, L.; Vasincu, D.; Popa, O.; Agop, M.; Moraru, A.; Costin, D.; et al. Drug-Loaded Polymeric Particulated Systems for Ophthalmic Drugs Release. Molecules 2022, 27, 4512. [Google Scholar] [CrossRef]
- Pandit, J.; Sultana, Y.; Aqil, M. Chitosan coated nanoparticles for efficient delivery of bevacizumab in the posterior ocular tissues via subconjunctival administration. Carbohydr. Polym. 2021, 267, 118217. [Google Scholar] [CrossRef] [PubMed]
- Ugurlu, N.; Asik, M.D.; Çakmak, H.B.; Tuncer, S.; Turk, M.; Çagil, N.; Denkbas, E.B. Transscleral Delivery of Bevacizumab-Loaded Chitosan Nanoparticles. J. Biomed. Nanotechnol. 2019, 15, 830–839. [Google Scholar] [CrossRef] [PubMed]
- Zamboulis, A.; Nanaki, S.; Michailidou, G.; Koumentakou, I.; Lazaridou, M.; Ainali, N.M.; Xanthopoulou, E.; Bikiaris, D.N. Chitosan and its Derivatives for Ocular Delivery Formulations: Recent Advances and Developments. Polymers 2020, 12, 1519. [Google Scholar] [CrossRef] [PubMed]
- de Souza, S.O.L.; Guerra, M.C.A.; Heneine, L.G.D.; de Oliveira, C.R.; Cunha Junior, A.D.S.; Fialho, S.L.; Oréfice, R.L. Biodegradable core-shell electrospun nanofibers containing bevacizumab to treat age-related macular degeneration. J. Mater. Sci. Mater. Med. 2018, 29, 173. [Google Scholar] [CrossRef]
- Iyer, S.; Lee, C.; Amiji, M.M. Biodegradable polymeric microsphere formulations of full-length anti-VEGF antibody bevacizumab for sustained intraocular delivery. Drug Deliv. Transl. Res. 2025, 15, 3149–3160. [Google Scholar] [CrossRef]
- Waterkotte, T.; He, X.; Wanasathop, A.; Li, S.K.; Park, Y.C. Long-Term Antibody Release Polycaprolactone Capsule and the Release Kinetics in Natural and Accelerated Degradation. ACS Biomater. Sci. Eng. 2022, 8, 4428–4438. [Google Scholar] [CrossRef]
- Meng, Y.; Sun, S.; Li, J.; Nan, K.; Lan, B.; Jin, Y.; Chen, H.; Cheng, L. Sustained release of triamcinolone acetonide from an episcleral plaque of multilayered poly-ε-caprolactone matrix. Acta Biomater. 2014, 10, 126–133. [Google Scholar] [CrossRef]
- Alkholief, M.; Kalam, M.A.; Raish, M.; Ansari, M.A.; Alsaleh, N.B.; Almomen, A.; Ali, R.; Alshamsan, A. Topical Sustained-Release Dexamethasone-Loaded Chitosan Nanoparticles: Assessment of Drug Delivery Efficiency in a Rabbit Model of Endotoxin-Induced Uveitis. Pharmaceutics 2023, 15, 2273. [Google Scholar] [CrossRef]
- Wu, Z.; Sun, W.; Wang, C. Clinical characteristics, treatment, and outcomes of pembrolizumab-induced uveitis. Investig. New Drugs 2024, 42, 510–517. [Google Scholar] [CrossRef]
- Jiang, P.; Jacobs, K.M.; Ohr, M.P.; Swindle-Reilly, K.E. Chitosan-polycaprolactone core-shell microparticles for sustained delivery of bevacizumab. Mol. Pharm. 2020, 17, 2570–2584. [Google Scholar] [CrossRef]
- Jiang, P.; Chaparro, F.J.; Cuddington, C.T.; Palmer, A.F.; Ohr, M.P.; Lannutti, J.J.; Swindle-Reilly, K.E. Injectable biodegradable bi-layered capsule for sustained delivery of bevacizumab in treating wet age-related macular degeneration. J. Control. Release 2020, 320, 442–456. [Google Scholar] [CrossRef]
- Ford Versypt, A.N.; Pack, D.W.; Braatz, R.D. Mathematical modeling of drug delivery from autocatalytically degradable PLGA microspheres–A review. J. Control. Release 2013, 165, 29–37. [Google Scholar] [CrossRef] [PubMed]
- Kanjickal, D.G.; Lopina, S.T. Modeling of drug release from polymeric delivery systems–a review. Crit. Rev. Ther. Drug Carr. Syst. 2004, 21, 345–386. [Google Scholar]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef] [PubMed]
- Baker, R. Controlled Release of Biologically Active Agents; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Higuchi, T. Rate of release of medicaments from ointment bases containing drugs in suspensions. J. Pharm. Sci. 1961, 50, 874–875. [Google Scholar] [CrossRef]
- Roseman, T.J.; Higuchi, W.I. Release of medroxyprogesterone acetate from a silicone polymer. J. Pharm. Sci. 1970, 59, 353–357. [Google Scholar] [CrossRef]
- Roseman, T.J. Release of steroids from a silicone polymer. J. Pharm. Sci. 1972, 61, 46–50. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Vergnaud, J. Controlled Drug Release of Oral Dosage Forms; Ellis Horwood: New York, NY, USA, 1993. [Google Scholar]
- Lu, S.M.; Chen, S.R. Mathematical analysis of drug release from a coated particle. J. Control. Release 1993, 23, 105–121. [Google Scholar] [CrossRef]
- Hadjitheodorou, A.; Kalosakas, G. Analytical and numerical study of diffusion-controlled drug release from composite spherical matrices. Mater. Sci. Eng. C 2014, 42, 681–690. [Google Scholar] [CrossRef]
- Kaoui, B.; Lauricella, M.; Pontrelli, G. Mechanistic modelling of drug release from multi-layer capsules. Comput. Biol. Med. 2018, 93, 149–157. [Google Scholar] [CrossRef]
- Carr, E.J.; Pontrelli, G. Modelling mass diffusion for a multi-layer sphere immersed in a semi-infinite medium: Application to drug delivery. Math. Biosci. 2018, 303, 1–9. [Google Scholar] [CrossRef]
- Wang, S.; Lou, X. Numerical methods for the estimation of effective diffusion coefficients of 2D controlled drug delivery systems. Optim. Eng. 2010, 11, 611–626. [Google Scholar] [CrossRef]
- Wang, S.; Mahali, S.M.; McGuiness, A.; Lou, X. Mathematical models for estimating effective diffusion parameters of spherical drug delivery devices. Theor. Chem. Acc. 2010, 125, 659–669. [Google Scholar] [CrossRef]
- Mohd-Mahali, S.; Wang, S.; Lou, X.; Pintowantoro, S. Numerical methods for estimating effective diffusion coefficients of three-dimensional drug delivery systems. Numer. Algebra Control Optim. 2012, 2, 377–393. [Google Scholar]
- Bielinski, C.; Kaoui, B. Numerical method to characterise capsule membrane permeability for controlled drug delivery. Int. J. Numer. Methods Biomed. Eng. 2021, 38, e3551. [Google Scholar] [CrossRef] [PubMed]
- Barchiesi, E.; Wareing, T.; Desmond, L.; Phan, A.N.; Gentile, P.; Pontrelli, G. Characterization of the shells in layer-by-layer nanofunctionalized particles: A computational study. Front. Bioeng. Biotechnol. 2022, 10, 888944. [Google Scholar] [CrossRef]
- Morton, K.W.; Mayers, D.F. Numerical Solution of Partial Differential Equations, 2nd ed.; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- LeVeque, R.J. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-State and Time-Dependent Problems; SIAM: Philadelphia, PA, USA, 2007. [Google Scholar]
- Axelsson, O.; Barker, V.A. Finite Element Solution of Boundary Value Problems: Theory and Computation; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2001. [Google Scholar]
- Dorfman, K.D.; Daoutidis, P. Numerical Methods with Chemical Engineering Applications; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Ozisik, M.N. Heat Conduction, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1993. [Google Scholar]
- Ford Versypt, A.N.; Braatz, R.D. Analysis of finite difference discretization schemes for diffusion in spheres with variable diffusivity. Comput. Chem. Eng. 2014, 71, 241–252. [Google Scholar] [CrossRef]
- Tosa, V.; Mercea, P. Solution of the diffusion equation for multilayer packaging. In Plastic Packaging: Interactions with Food and Pharmaceuticals, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2008; pp. 247–262. [Google Scholar]
- Sundqvist, H.; Veronis, G. A simple finite-difference grid with non-constant intervals. Tellus 1970, 22, 26–31. [Google Scholar] [CrossRef]
- Kalnay de Rivas, E. On the Use of Nonuniform Grids in Finite-Difference Equations. J. Comput. Phys. 1972, 10, 202–210. [Google Scholar] [CrossRef]
- Garcia, D. Simpson’s Rule for Numerical Integration. MATLAB Central File Exchange. 2025. Available online: https://www.mathworks.com/matlabcentral/fileexchange/25754-simpson-s-rule-for-numerical-integration (accessed on 24 March 2025).
- Moreno, E.; Larese, A.; Cervera, M. Modelling of Bingham and Herschel–Bulkley flows with mixed P1/P1 finite elements stabilized with orthogonal subgrid scale. J. Non-Newton. Fluid Mech. 2016, 228, 1–16. [Google Scholar] [CrossRef]
- Van Kampen, E.; Vandervelden, C.; Fakhari, A.; Qian, J.; Berkland, C.; Gehrke, S.H. Design of Hollow Hyaluronic Acid Cylinders for Sustained Intravitreal Protein Delivery. J. Pharm. Sci. 2018, 107, 2354–2365. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity estimates for nonlinear mathematical models. Mat. Model. 1990, 2, 112–118. [Google Scholar]
- Saltelli, A. Making best use of model valuations to compute sensitivity indices. Comput. Phys. Commun. 2002, 145, 280–297. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Variance-based methods. In Global Sensitivity Analysis. The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 155–182. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Campolongo, F.; Cariboni, J.; Saltelli, A. An effective screening design for sensitivity analysis of large models. Environ. Model. Softw. 2007, 22, 1509–1518. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Elementary effects method. In Global Sensitivity Analysis. The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 109–154. [Google Scholar] [CrossRef]
- COMSOL. Uncertainty Quantification Module Users Guide. 2021. Available online: https://doc.comsol.com/6.0/doc/com.comsol.help.uq/UncertaintyQuantificationModuleUsersGuide.pdf (accessed on 22 March 2025).
- Beck, J.; Arnold, K. Matrix analysis for linear parameter estimation. In Parameter Estimation in Engineering and Science; John Wiley and Sons: Hoboken, NJ, USA, 1977; pp. 213–326. [Google Scholar]
- Avery, R.L.; Pearlman, J.; Pieramici, D.J.; Rabena, M.D.; Castellarin, A.A.; Nasir, M.A.; Giust, M.J.; Wendel, R.; Patel, A. Intravitreal bevacizumab (Avastin) in the treatment of proliferative diabetic retinopathy. Ophthalmology 2006, 113, 1695–1705. [Google Scholar] [CrossRef]
- Carichino, L.; Guidoboni, G.; Kansara, V.; Ciulla, T.; Harris, A. Gene therapy bio-factory: Mathematical modeling of the human eye pharmacokinetics. In Applied Mathematical Analysis and Computations II; Wanduku, D., Zheng, S., Zhou, H., Chen, Z., Sills, A., Agyingi, E., Eds.; Springer Nature: Cham, Switzerland, 2024; pp. 47–64. [Google Scholar]
- Bölgen, N.; Menceloğlu, Y.Z.; Acatay, K.; Vargel, I.; Pişkin, E. In vitro and in vivo degradation of non-woven materials made of poly(ϵ-caprolactone) nanofibers prepared by electrospinning under different conditions. J. Biomater. Sci. Polym. Ed. 2005, 16, 1537–1555. [Google Scholar] [CrossRef]
- Chowdhury, J.M.; Chacin Ruiz, E.A.; Ohr, M.P.; Swindle-Reilly, K.E.; Ford Versypt, A.N. Computer modeling of bevacizumab drug distribution after intravitreal injection in rabbit and human eyes. J. Pharm. Sci. 2025, 114, 1164–1174. [Google Scholar] [CrossRef]
- Chacin Ruiz, E.A.; Carpenter, S.L.; Swindle-Reilly, K.E.; Ford Versypt, A.N. LayeredSpheres_DDSdesign. 2025. Available online: https://github.com/ashleefv/LayeredSpheres_DDSdesign (accessed on 25 July 2025).
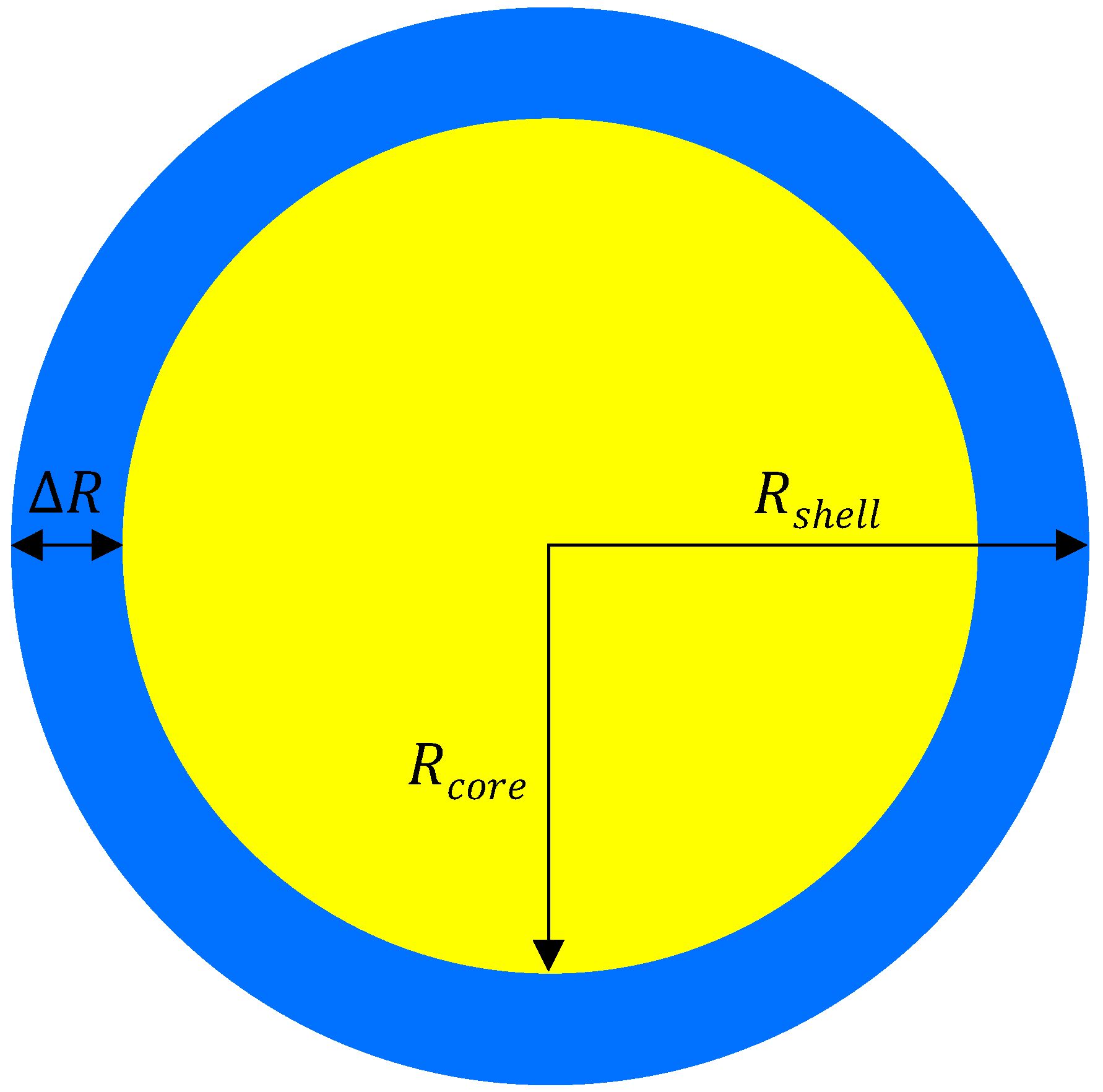




| Parameter | Lower Limit | Upper Limit | Units |
|---|---|---|---|
| B | 0 | 20 | % |
| cm2/s |
| BSA in MATLAB | |||||
|---|---|---|---|---|---|
| Average Model | Best Model | ||||
| Parameter | Value ± 95% C.I. | Units | Parameter | Value | Units |
| B | % | B | 4.72 | % | |
| cm2/s | cm2/s | ||||
| Error value | 211.62 | - | Error value | 209.34 | - |
| BSA in COMSOL | |||||
| Average Model | Best Model | ||||
| Parameter | Value | Units | Parameter | Value | Units |
| B | 4 | % | B | 3.86 | % |
| cm2/s | cm2/s | ||||
| Error value | 207.20 | - | Error value | 207.10 | - |
| Bevacizumab in MATLAB | |||||
| Average Model | Best Model | ||||
| Parameter | Value ± 95% C.I. | Units | Parameter | Value | Units |
| B | % | B | 10.3 | % | |
| cm2/s | cm2/s | ||||
| Error value | 435.60 | - | Error value | 435.06 | - |
| Bevacizumab in COMSOL | |||||
| Average Model | Best Model | ||||
| Parameter | Value | Units | Parameter | Value | Units |
| B | 9.6 | % | B | 9.56 | % |
| cm2/s | cm2/s | ||||
| Error value | 440.25 | - | Error value | 440.09 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chacin Ruiz, E.A.; Carpenter, S.L.; Swindle-Reilly, K.E.; Ford Versypt, A.N. Modeling and Design of Chitosan–PCL Bi-Layered Microspheres for Intravitreal Controlled Release. Pharmaceutics 2025, 17, 1174. https://doi.org/10.3390/pharmaceutics17091174
Chacin Ruiz EA, Carpenter SL, Swindle-Reilly KE, Ford Versypt AN. Modeling and Design of Chitosan–PCL Bi-Layered Microspheres for Intravitreal Controlled Release. Pharmaceutics. 2025; 17(9):1174. https://doi.org/10.3390/pharmaceutics17091174
Chicago/Turabian StyleChacin Ruiz, Eduardo A., Samantha L. Carpenter, Katelyn E. Swindle-Reilly, and Ashlee N. Ford Versypt. 2025. "Modeling and Design of Chitosan–PCL Bi-Layered Microspheres for Intravitreal Controlled Release" Pharmaceutics 17, no. 9: 1174. https://doi.org/10.3390/pharmaceutics17091174
APA StyleChacin Ruiz, E. A., Carpenter, S. L., Swindle-Reilly, K. E., & Ford Versypt, A. N. (2025). Modeling and Design of Chitosan–PCL Bi-Layered Microspheres for Intravitreal Controlled Release. Pharmaceutics, 17(9), 1174. https://doi.org/10.3390/pharmaceutics17091174









