Experimental and Numerical Study to Enhance Granule Control and Quality Predictions in Pharmaceutical Granulations
Abstract
1. Introduction
- -
- The mechanisms of wet agglomeration can be defined as the succession of three stages: (i) wetting and nucleation; (ii) coalescence, consolidation, and growth; and (iii) rupture and attrition. Predicting the dominance of one mechanism over others is challenging, with most studies focusing on a single predominant mechanism [1]. Advances in the field have emphasized the complexity of these mechanisms and their interactions with material properties and granulation kinetics, especially concerning binder interactions and granule formation dynamics [2].
- -
- Systematic studies have established links between operational parameters (such as filling rate and stirring speed, etc.), physicochemical characteristics of the binder (like wettability, angle of contact, and viscosity, etc.), and the quality of the final product (e.g., size distribution and flowability) [2,3,4,5,6]. However, the influence of these parameters on granule growth mechanisms varies with the raw materials and technologies employed, making it difficult to generalize the observed trends and hindering the overall optimization of the process.
- -
2. Materials and Methods
2.1. Experimental Study
2.1.1. Granulation Protocol
2.1.2. Particle and Granule Characterization
2.2. Numerical Study
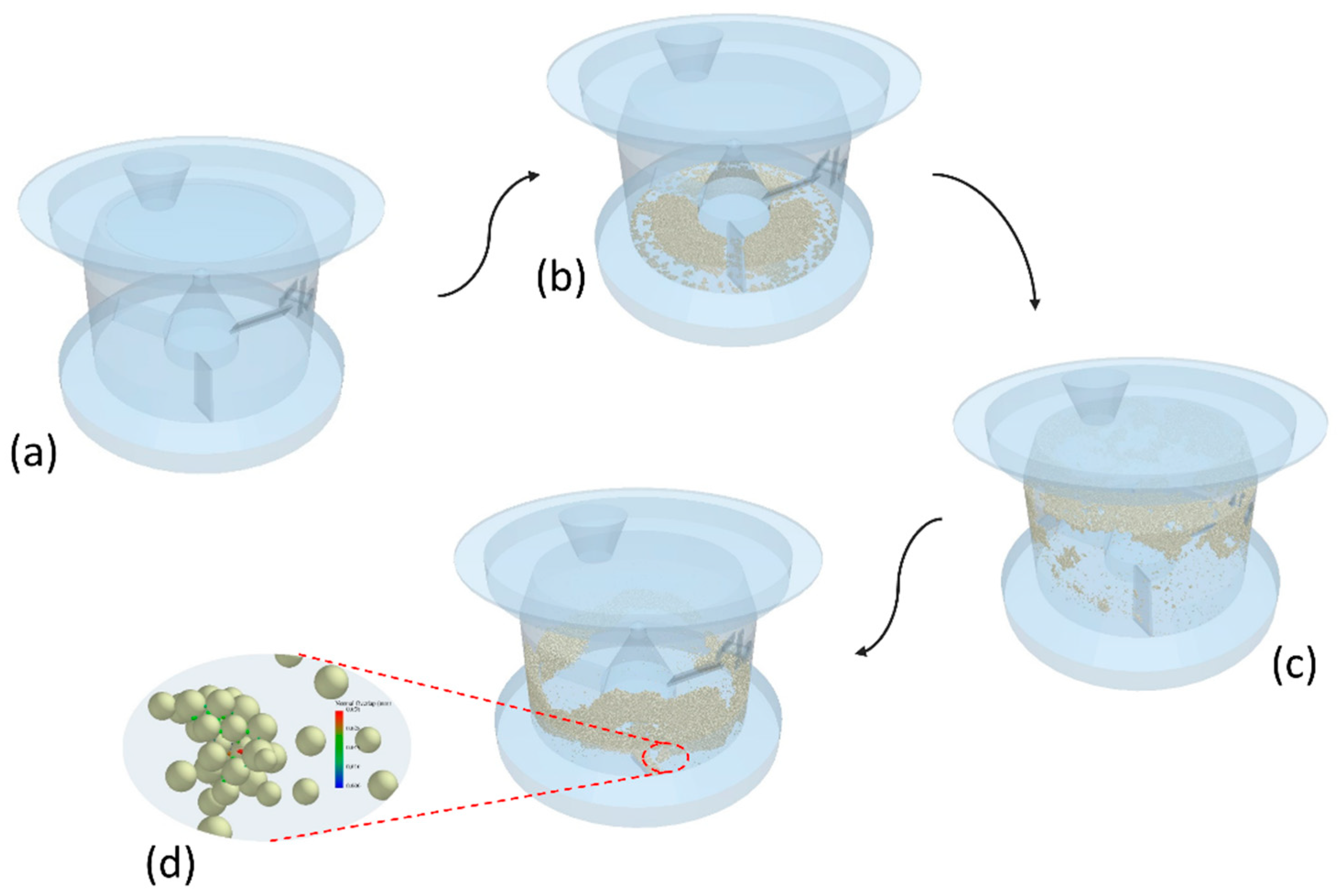
2.2.1. DEM Modeling
2.2.2. Numerical High-Shear Wet Granulation
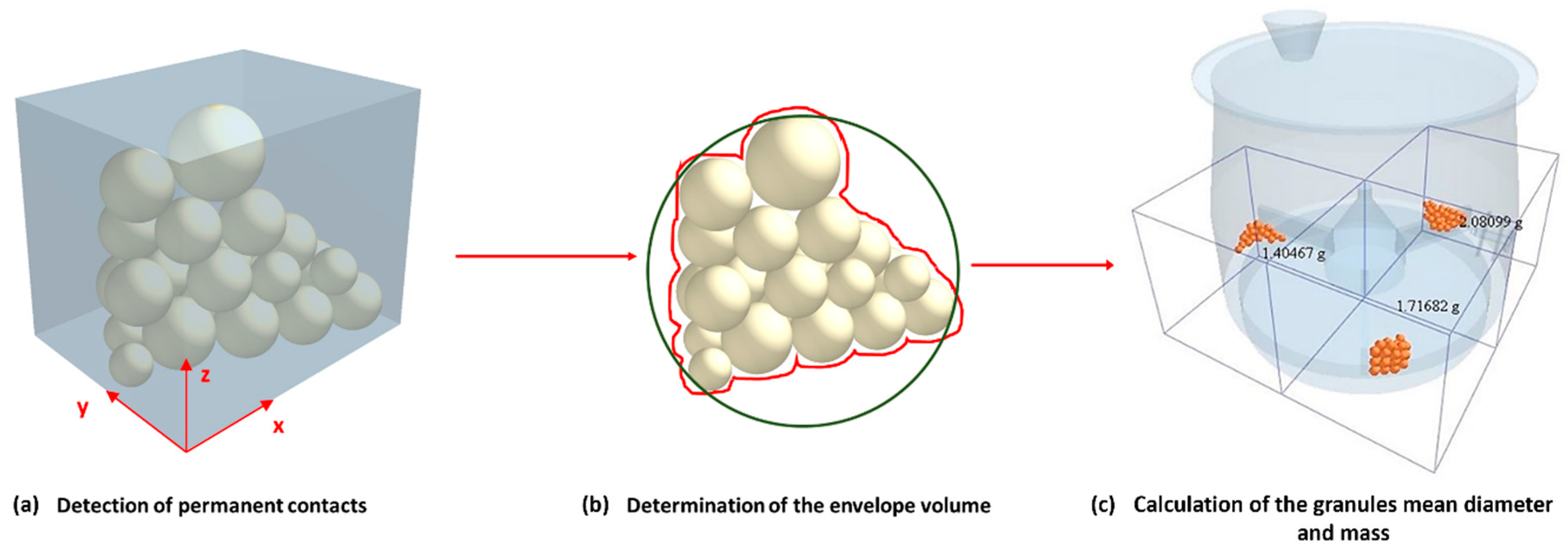
2.2.3. Posttreatment Developed Tool
3. Results and Discussion
3.1. Particle Generation and Numerical Limitations
3.2. Parametric Analysis
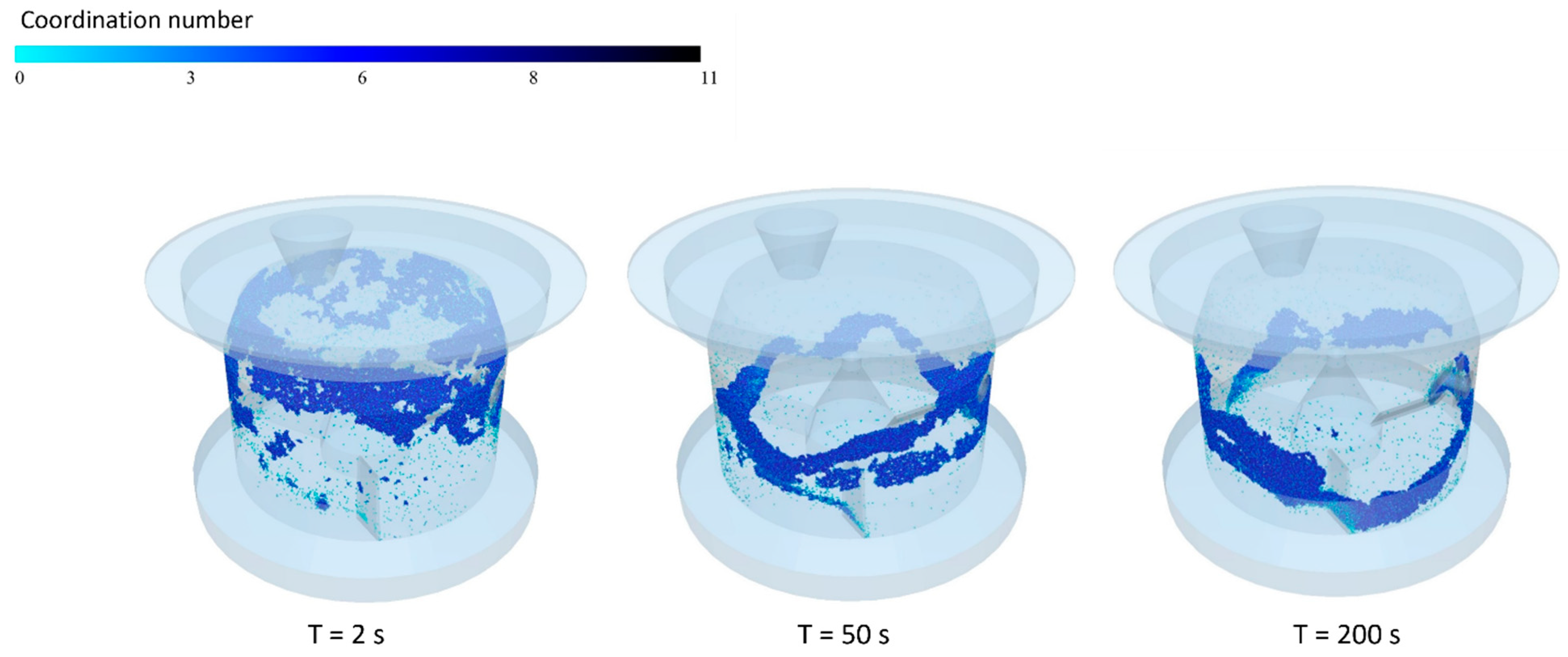
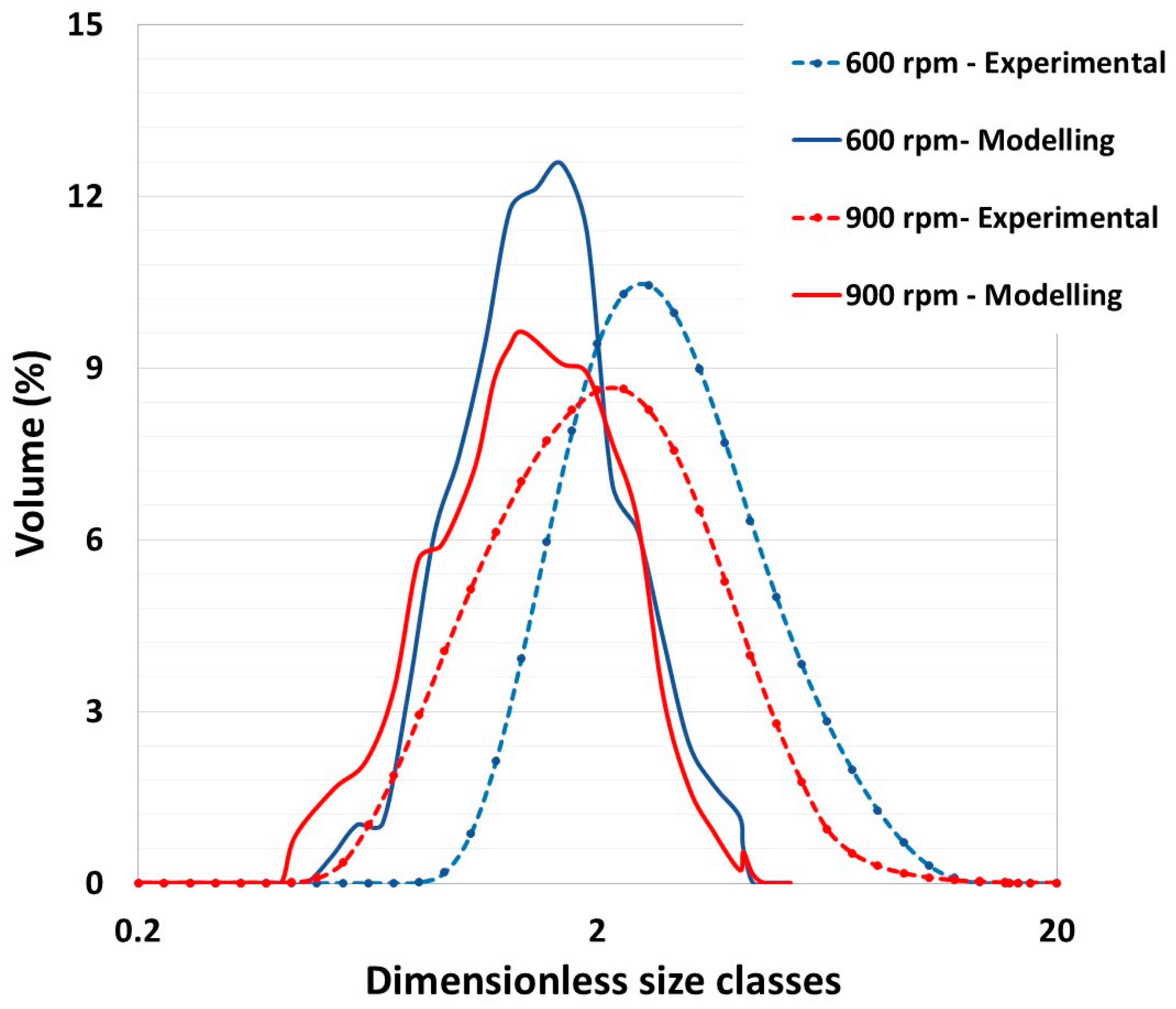
3.2.1. Influence of Impeller Velocity
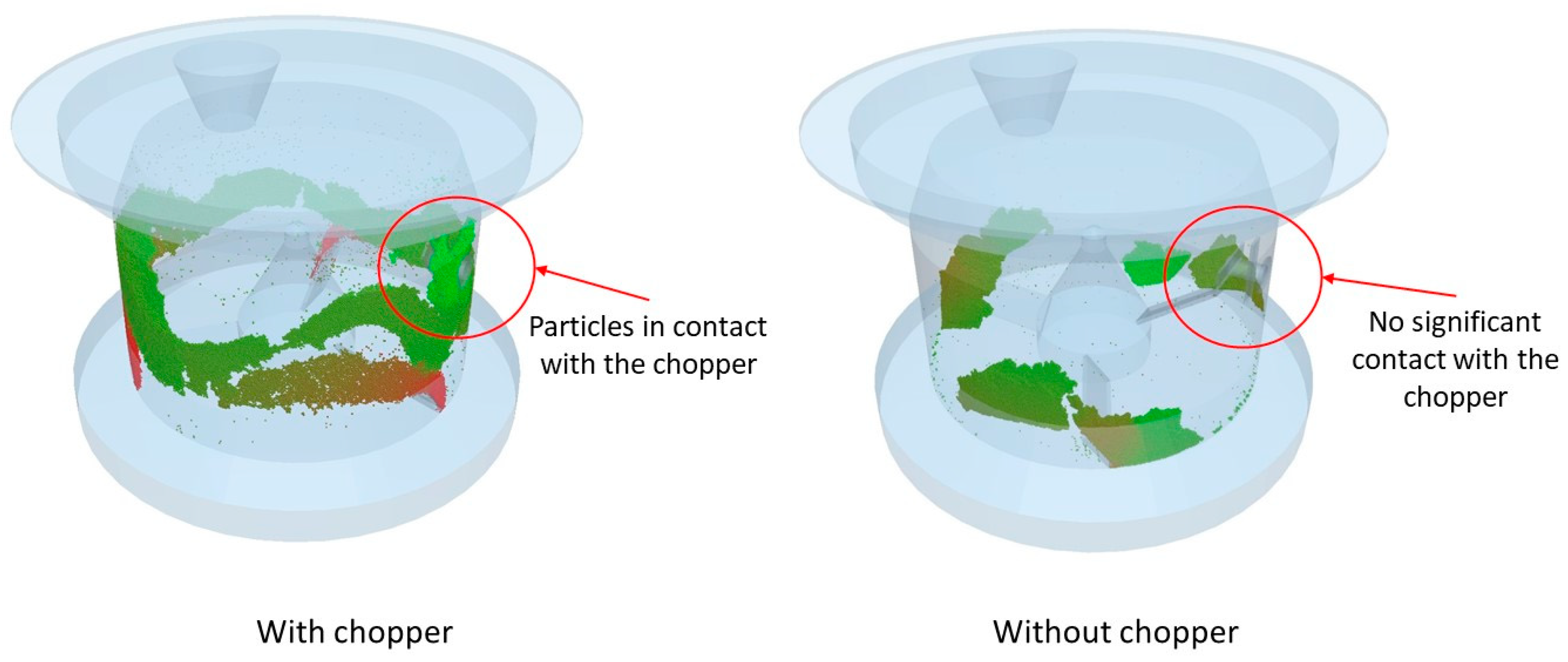
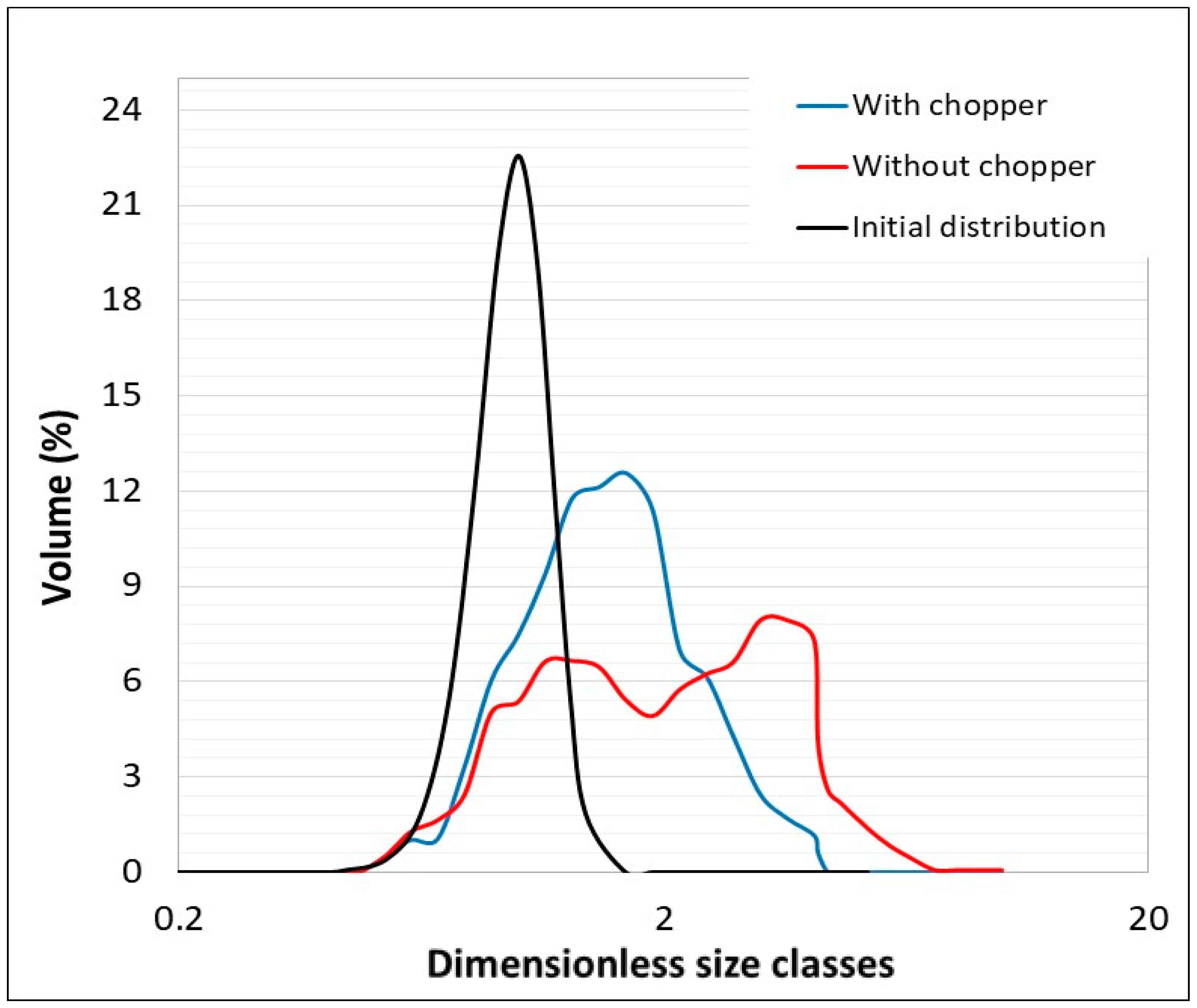
3.2.2. Influence of the Chopper
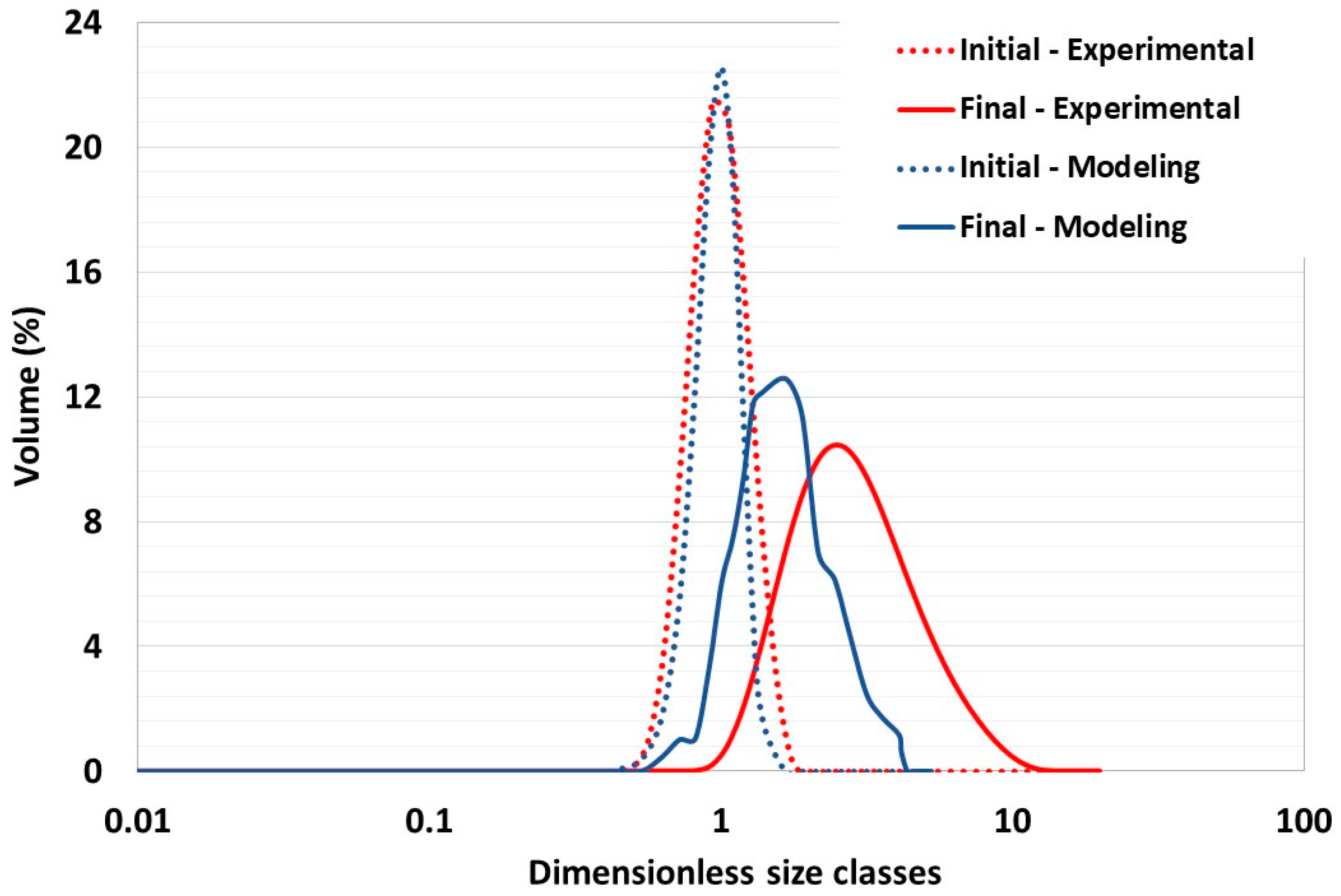
3.3. Numerical and Experimental Correlation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| AI | Artificial intelligence |
| DEM | Discrete element method |
| HSG | High shear granulator |
| JKR | Johnson–Kendall–Roberts |
| MCC | Microcrystalline cellulose |
| NIR | Near-infrared spectroscopy |
| PBM | Population balance modeling |
| PSD | Particle size distribution |
| PVP | Polyvinylpyrrolidone |
| RMSEP | Root Mean Square Error of Prediction |
| SEM | Scanning electron microscopy |
References
- Saleh, K.; Vialatte, L.; Guigon, P. Wet granulation in a batch high shear mixer. Chem. Eng. Sci. 2005, 60, 3763–3775. [Google Scholar] [CrossRef]
- Alves, A.R.; Simões, M.F.; Simões, S.; Gomes, J. A Review on the Scale-up of High-Shear Wet Granulation Processes and the Impact of Process Parameters. Particuology 2024, 92, 180–195. [Google Scholar] [CrossRef]
- Chitu, T.M.; Oulahna, D.; Hemati, M. Wet granulation in laboratory scale high shear mixers: Effect of binder properties. Powder Technol. 2011, 206, 25–33. [Google Scholar] [CrossRef]
- Chitu, T.M.; Oulahna, D.; Hemati, M. Wet granulation in laboratory-scale high shear mixers: Effect of chopper presence, design and impeller speed. Powder Technol. 2011, 206, 34–43. [Google Scholar] [CrossRef]
- Badawy, S.I.F.; Narang, A.S.; LaMarche, K.; Subramanian, G.; Varia, S.A. Mechanistic basis for the effects of process parameters on quality attributes in high shear wet granulation. Int. J. Pharm. 2012, 439, 324–333. [Google Scholar] [CrossRef]
- Narang, A.S.; Badawy, S.I.F. Handbook of Pharmaceutical Wet Granulation: Theory and Practice in a Quality by Design Paradigm; Academic Press: New York, NY, USA, 2018. [Google Scholar]
- Betz, G.; Bürgin, P.J.; Leuenberger, H. Power consumption profile analysis and tensile strength measurements during moist agglomeration. Int. J. Pharm. 2003, 252, 11–25. [Google Scholar] [CrossRef]
- Ly, A.; Achouri, I.E.; Gosselin, R.; Abatzoglou, N. Wet granulation end point prediction using dimensionless numbers in a mixer torque rheometer: Relationship between capillary and Weber numbers and the optimal wet mass consistency. Int. J. Pharm. 2021, 605, 120823. [Google Scholar] [CrossRef]
- Faure, A.; York, P.; Rowe, R.C. Process control and scale-up of pharmaceutical wet granulation processes: A review. Eur. J. Pharm. Biopharm. 2001, 52, 269–277. [Google Scholar] [CrossRef]
- Bouillon-Camara, A.-L. Extrapolation du Procédé de Granulation Humide en Mélangeur Haute Vitesse. Ph.D. Thesis, Institut National Polytechnique de Lorraine, Nancy, France, 2005. [Google Scholar]
- Iveson, S.M.; Litster, J.D.; Hapgood, K.; Ennis, B.J. Nucleation, growth and breakage phenomena in agitated wet granulation processes: A review. Powder Technol. 2001, 117, 3–39. [Google Scholar] [CrossRef]
- Hapgood, K.P.; Litster, J.D.; Smith, R. Nucleation regime map for liquid bound granules. AIChE J. 2003, 49, 350–361. [Google Scholar] [CrossRef]
- Plath, T.; Luding, S.; Weinhart, T. Population Balance Modelling and Reconstruction by Quadrature Method of Moments for Wet Granulation. Powder Technol. 2025, 449, 120374. [Google Scholar] [CrossRef]
- Suresh, P.; Sreedhar, I.; Vaidhiswaran, R.; Venugopal, A. A comprehensive review on process and engineering aspects of pharmaceutical wet granulation. Chem. Eng. J. 2017, 328, 785–815. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Mahoney, A.W. Population balance modeling. Promise for the future. Chem. Eng. Sci. 2002, 57, 595–606. [Google Scholar] [CrossRef]
- Barrasso, D.; Ramachandran, R. A comparison of model order reduction techniques for a four-dimensional population balance model describing multi-component wet granulation processes. Chem. Eng. Sci. 2012, 80, 380–392. [Google Scholar] [CrossRef]
- Poon, J.M.-H.; Immanuel, C.D.; Doyle, I.; Francis, J.; Litster, J.D. A three-dimensional population balance model of granulation with a mechanistic representation of the nucleation and aggregation phenomena. Chem. Eng. Sci. 2008, 63, 1315–1329. [Google Scholar] [CrossRef]
- Poon, J.M.-H.; Ramachandran, R.; Sanders, C.F.W.; Glaser, T.; Immanuel, C.D.; Doyle, F.J., III; Litster, J.D.; Stepanek, F.; Wang, F.-Y.; Cameron, I.T. Experimental validation studies on a multi-dimensional and multi-scale population balance model of batch granulation. Chem. Eng. Sci. 2009, 64, 775–786. [Google Scholar] [CrossRef]
- Watano, S.; Nakamura, H. Chapter 22—Numerical Modeling for Wet Granulation Processes. In Handbook of Pharmaceutical Wet Granulation; Narang, A.S., Badawy, S.I.F., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 737–763. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 1, 47–65. [Google Scholar] [CrossRef]
- Mesnier, A.; Rouabah, M.; Cogné, C.; Peczalski, R.; Vessot-Crastes, S.; Vacus, P.; Andrieu, J. Contact heating of bi-dispersed milli-beads in a rotary drum. Mechanical segregation impact on temperature distribution and on heating kinetic analyzed by DEM simulation. Powder Technol. 2019, 354, 240–246. [Google Scholar] [CrossRef]
- Mindlin, R.D. A Mathematical Theory of Photo-Viscoelasticity. J. Appl. Phys. 1949, 20, 206–216. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berûhrung fester elastischer KÖrper. J. Die Reine Angew. Math. 1882, 92, 156–171. [Google Scholar]
- Kendall, K. The adhesion and surface energy of elastic solids. J. Phys. D Appl. Phys. 1971, 4, 1186–1195. [Google Scholar] [CrossRef]
- Remy, B.; Khinast, J.G.; Glasser, B.J. Polydisperse granular flows in a bladed mixer: Experiments and simulations of cohesionless spheres. Chem. Eng. Sci. 2011, 66, 1811–1824. [Google Scholar] [CrossRef]
- Muguruma, Y.; Tanaka, T.; Tsuji, Y. Numerical simulation of particulate flow with liquid bridge between particles simulation of centrifugal tumbling granulator. Powder Technol. 2000, 109, 49–57. [Google Scholar] [CrossRef]
- Litster, J.D.; Hapgood, K.P.; Michaels, J.N.; Sims, A.; Roberts, M.; Kameneni, S.K. Scale-up of mixer granulators for effective liquid distribution. Powder Technol. 2002, 124, 272–280. [Google Scholar] [CrossRef]
- Terashita, K.; Nishimura, T.; Natsuyama, S.; Satoh, M. DEM Simulation of Mixing and Segregation in High-Shear Mixer. J. Jpn. Soc. Powder Powder Metall. 2002, 49, 638–645. [Google Scholar] [CrossRef]
- Reinhold, A.; Briesen, H. Numerical behavior of a multiscale aggregation model—Coupling population balances and discrete element models. Chem. Eng. Sci. 2012, 70, 165–175. [Google Scholar] [CrossRef]
- Song, Y.; Zhou, T.; Bai, R.; Zhang, M.; Yang, H. Review of CFD-DEM Modeling of Wet Fluidized Bed Granulation and Coating Processes. Processes 2023, 11, 382. [Google Scholar] [CrossRef]
- Barrasso, D.; Eppinger, T.; Pereira, F.E.; Aglave, R.; Debus, K.; Bermingham, S.K.; Ramachandran, R. A multi-scale, mechanistic model of a wet granulation process using a novel bi-directional PBM–DEM coupling algorithm. Chem. Eng. Sci. 2015, 123, 500–513. [Google Scholar] [CrossRef]
- Rouabah, M.; Bourgeois, S.; Briançon, S.; Cogné, C. A numerical tool to predict powder behaviour for pharmaceutical handling and processing. J. Drug Deliv. Sci. Technol. 2022, 70, 1773–2247. [Google Scholar] [CrossRef]
- Ramaker, J.S.; Jelgersma, M.A.; Vonk, P.; Kossen, N.W.F. Scale-down of a High-Shear Pelletisation Process: Flow Profile and Growth Kinetics. Int. J. Pharm. 1998, 166, 89–97. [Google Scholar] [CrossRef]


| Material Properties | Units | MCC |
|---|---|---|
| Poisson’s ratio (ν) | [-] | 0.25 |
| Density (ρ) | [kg/m3] | 460 |
| Young’s modulus (E) | [GPa] | 8.67 |
| Shear modulus (G) | [GPa] | 3.47 |
| Surface energy (γ) | [J/m2] | 1.7 |
| Particle–particle coefficients | ||
| Coefficient of static friction | [-] | 0.40 |
| Coefficient of restitution | [-] | 0.35 |
| Coefficient of rolling friction | [-] | 0.01 |
| Particle geometry coefficients | ||
| Coefficient of restitution | [-] | 0.50 |
| Coefficient of static friction | [-] | 0.45 |
| Coefficient of rolling friction | [-] | 0.15 |
| Number of Particles | Mass Calculation [g] | |||
|---|---|---|---|---|
| Manual Count | EDEM | EDEMpy AI Tool | ||
| Cluster 1 | 40 | 2.081 | 2.081 | 2.081 |
| Cluster 2 | 33 | 1.717 | 1.717 | 1.717 |
| Cluster 3 | 27 | 1.405 | 1.405 | 1.405 |
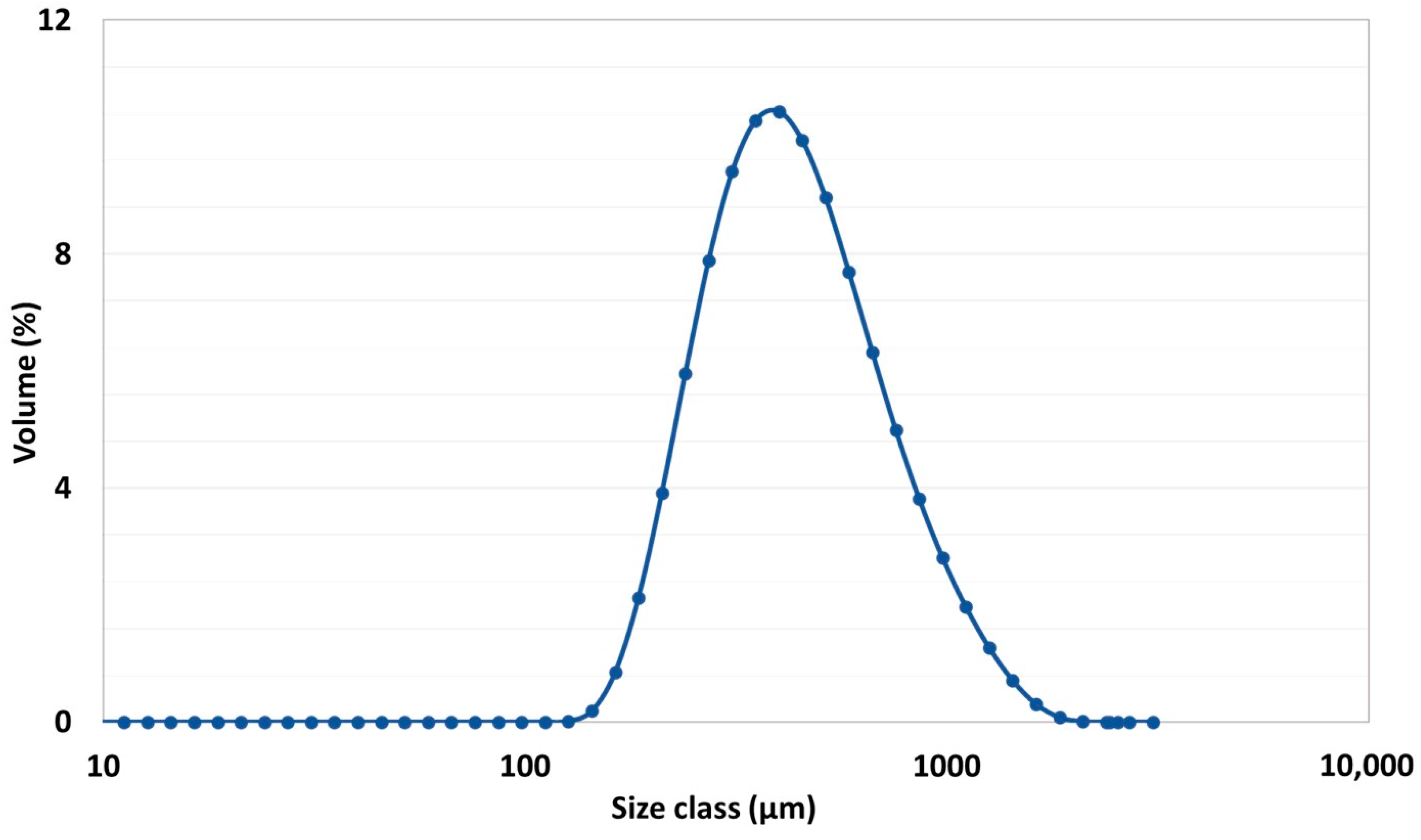
| PSD at 600 rpm (μm) | PSD at 900 rpm (μm) | |||
|---|---|---|---|---|
| Mean Average | Standard Deviation | Mean Average | Standard Deviation | |
| Experimental | 3.16 | 1.64 | 2.35 | 1.36 |
| Modeling | 1.66 | 0.71 | 1.50 | 0.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rouabah, M.; Achouri, I.E.; Bourgeois, S.; Briançon, S.; Cogné, C. Experimental and Numerical Study to Enhance Granule Control and Quality Predictions in Pharmaceutical Granulations. Pharmaceutics 2025, 17, 364. https://doi.org/10.3390/pharmaceutics17030364
Rouabah M, Achouri IE, Bourgeois S, Briançon S, Cogné C. Experimental and Numerical Study to Enhance Granule Control and Quality Predictions in Pharmaceutical Granulations. Pharmaceutics. 2025; 17(3):364. https://doi.org/10.3390/pharmaceutics17030364
Chicago/Turabian StyleRouabah, Maroua, Inès Esma Achouri, Sandrine Bourgeois, Stéphanie Briançon, and Claudia Cogné. 2025. "Experimental and Numerical Study to Enhance Granule Control and Quality Predictions in Pharmaceutical Granulations" Pharmaceutics 17, no. 3: 364. https://doi.org/10.3390/pharmaceutics17030364
APA StyleRouabah, M., Achouri, I. E., Bourgeois, S., Briançon, S., & Cogné, C. (2025). Experimental and Numerical Study to Enhance Granule Control and Quality Predictions in Pharmaceutical Granulations. Pharmaceutics, 17(3), 364. https://doi.org/10.3390/pharmaceutics17030364









