Living Together Apart: Quantitative Perspectives on the Costs and Benefits of a Multipartite Genome Organization in Viruses
Abstract
1. Introduction
2. Results and Discussion
2.1. The Transmission Cost of Multipartition
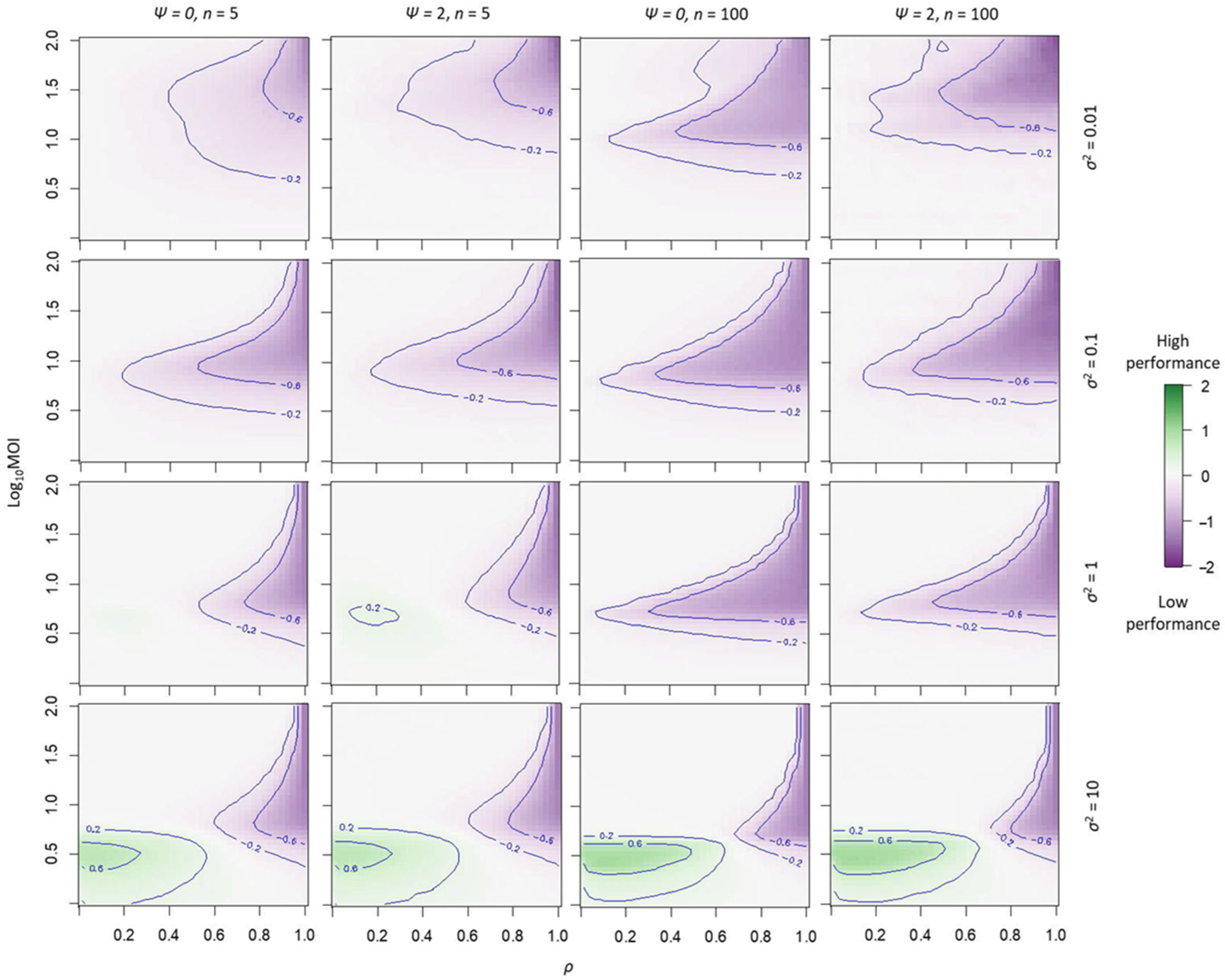
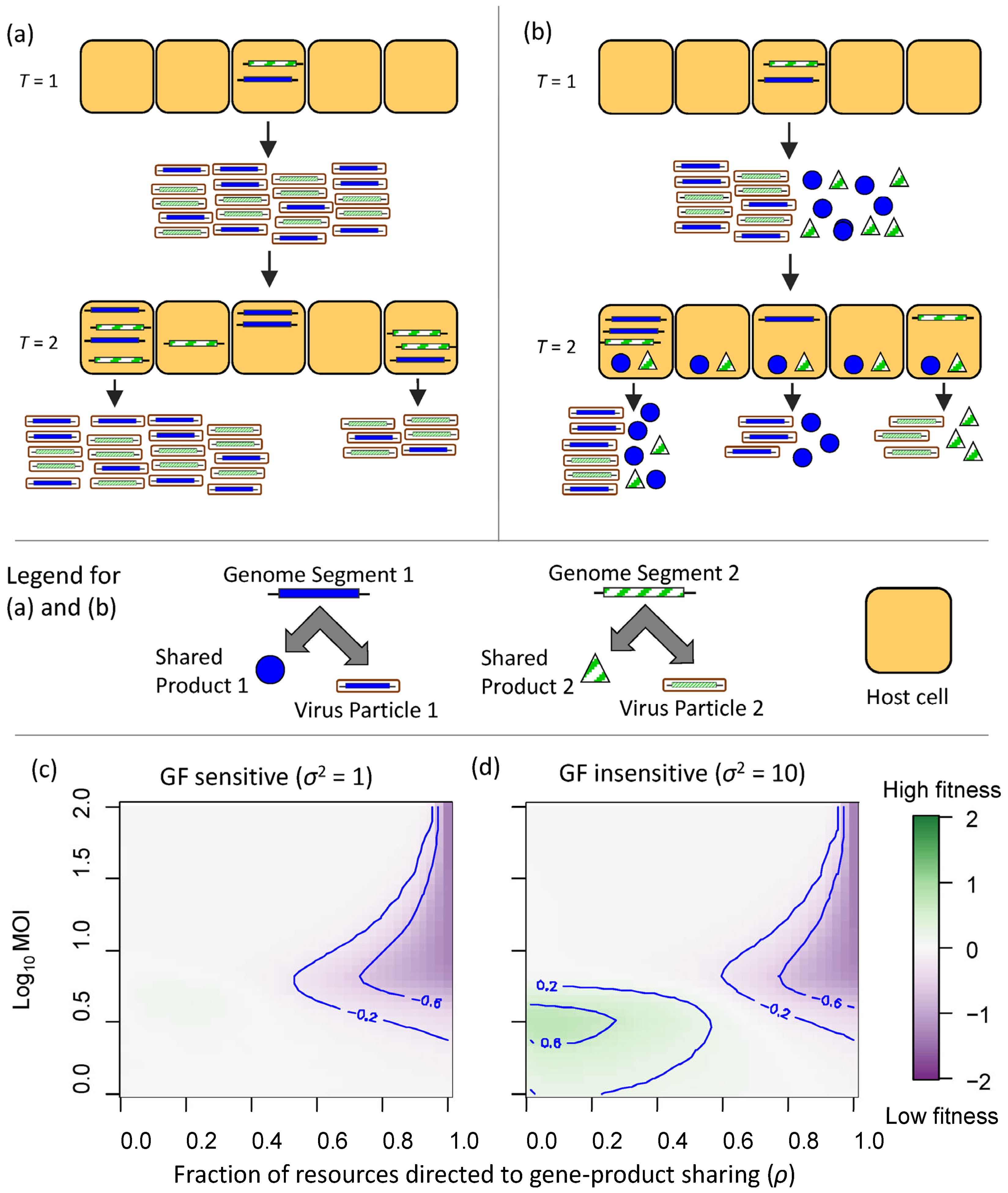
2.2. Reducing Multipartite Virus Transmission Costs by Gene-Product Sharing
2.3. Benefits of Genome Segmentation: Evidence for Extended Host Range?
3. Conclusions
4. Materials and Methods
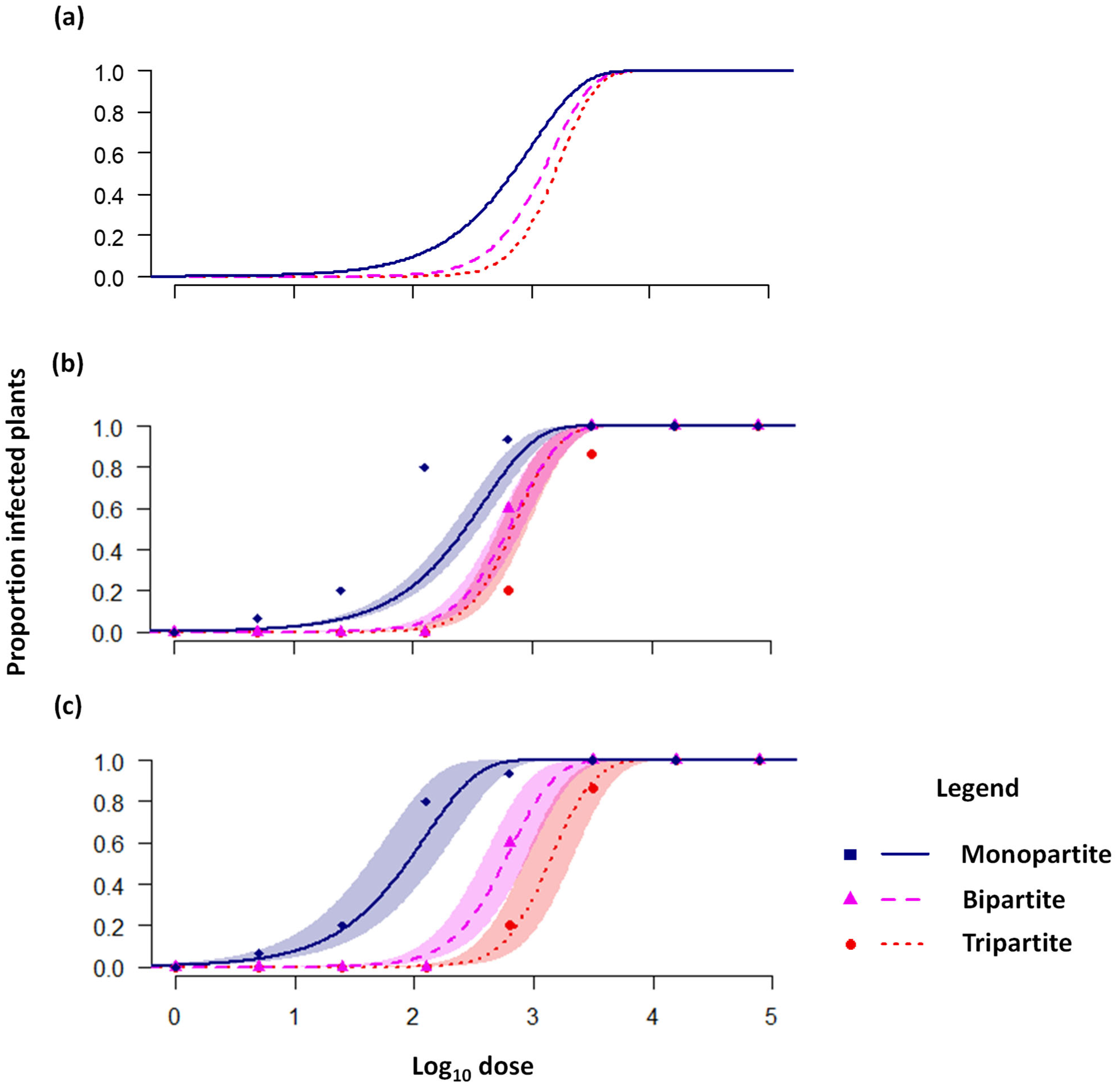
4.1. Re-Analysis of AMV Dose–Response Data
4.2. A Simulation Model to Explore Gene-Product Sharing in Multipartite Viruses
4.3. Estimates of Host Range Using Virus-Sequence Metadata
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
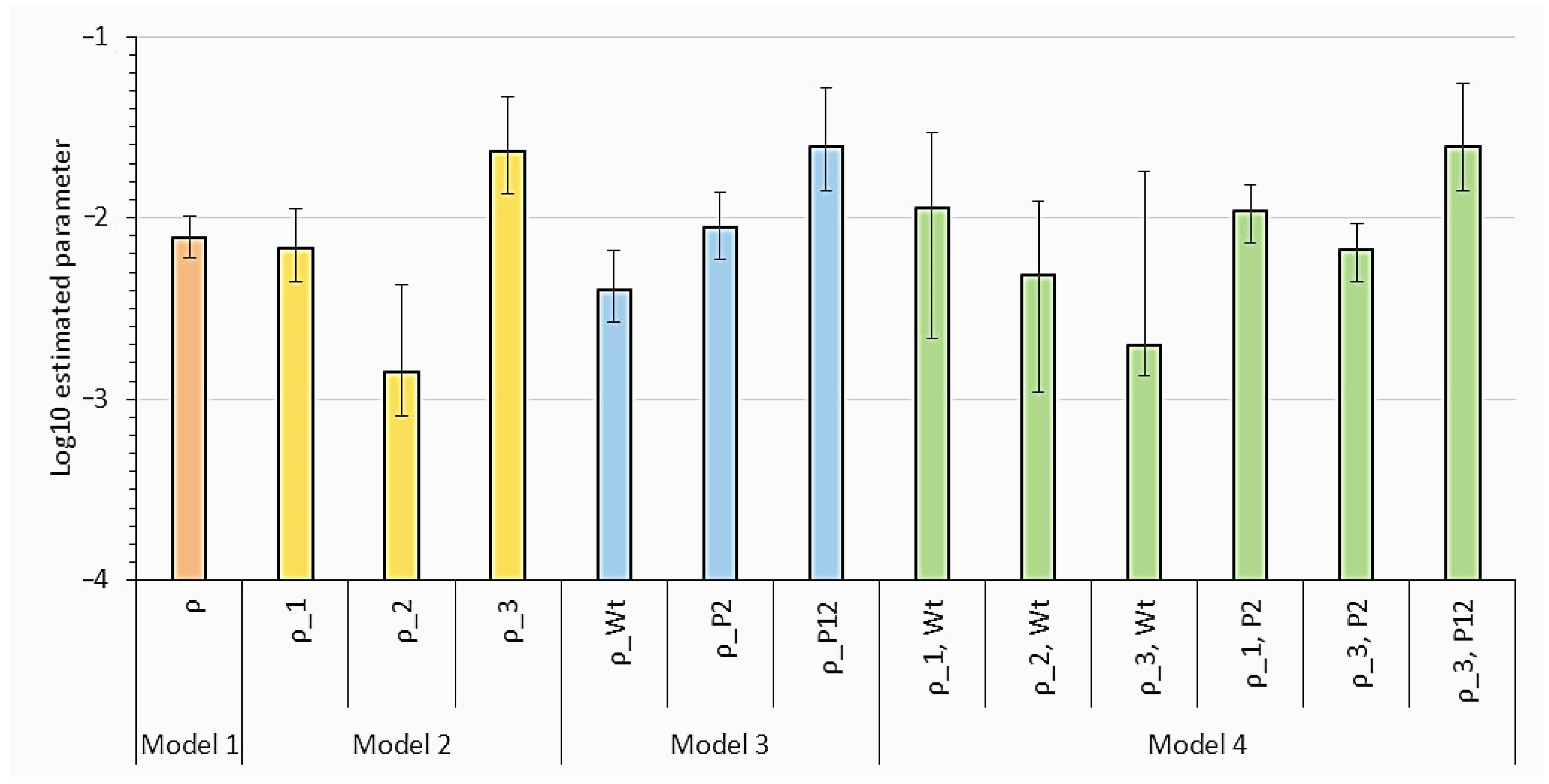
- Text A1: Dose Response Model Fitting and Model Selection Results
| Model | Parameter Estimates (95% Confidence Interval) |
|---|---|
| 1 | ρ = 7.82 × 10−3 (5.96 × 10−3–1.03 × 10−2) |
| 2 | ρ1 = 6.85 × 10−3 (4.42 × 10−3–1.13 × 10−2) ρ2 = 1.42 × 10−3 (8.09 × 10−4–4.29 × 10−3) ρ3 = 2.32 × 10−2 (1.35 × 10−2–4.62 × 10−2) |
| 3 | ρwt = 4.00 × 10−3 (2.64 × 10−3–6.58 × 10−3) ρP2 = 8.81 × 10−3 (5.87 × 10−3–1.37 × 10−2) ρP12 = 2.47 × 10−2 (1.42 × 10−3–5.20 × 10−3) |
| 4 | ρ1,wt = 1.14 × 10−2 (2.17 × 10−3–2.94 × 10−2) ρ2,wt = 4.81 × 10−3 (1.10 × 10−3–1.23 × 10−2) ρ3,wt = 2.00 × 10−3 (1.33 × 10−3–1.81 × 10−2) ρ1,P2 = 1.09 × 10−2 (7.29 × 10−3–1.52 × 10−2) ρ3,P2 = 6.71 × 10−3 (4.46 × 10−3–9.29 × 10−3) ρ3,P12 = 2.47 × 10−2 (1.41 × 10−2–5.50 × 10−2) |
| Model | NLL a | AIC b | ΔAIC c | AW d |
|---|---|---|---|---|
| 1 | 28.958 | 59.916 | 28.068 | 0.000 |
| 2 | 13.579 | 33.158 | 1.31 | 0.328 |
| 3 | 12.924 | 31.848 | - | 0.632 |
| 4 | 12.681 | 37.362 | 5.514 | 0.040 |
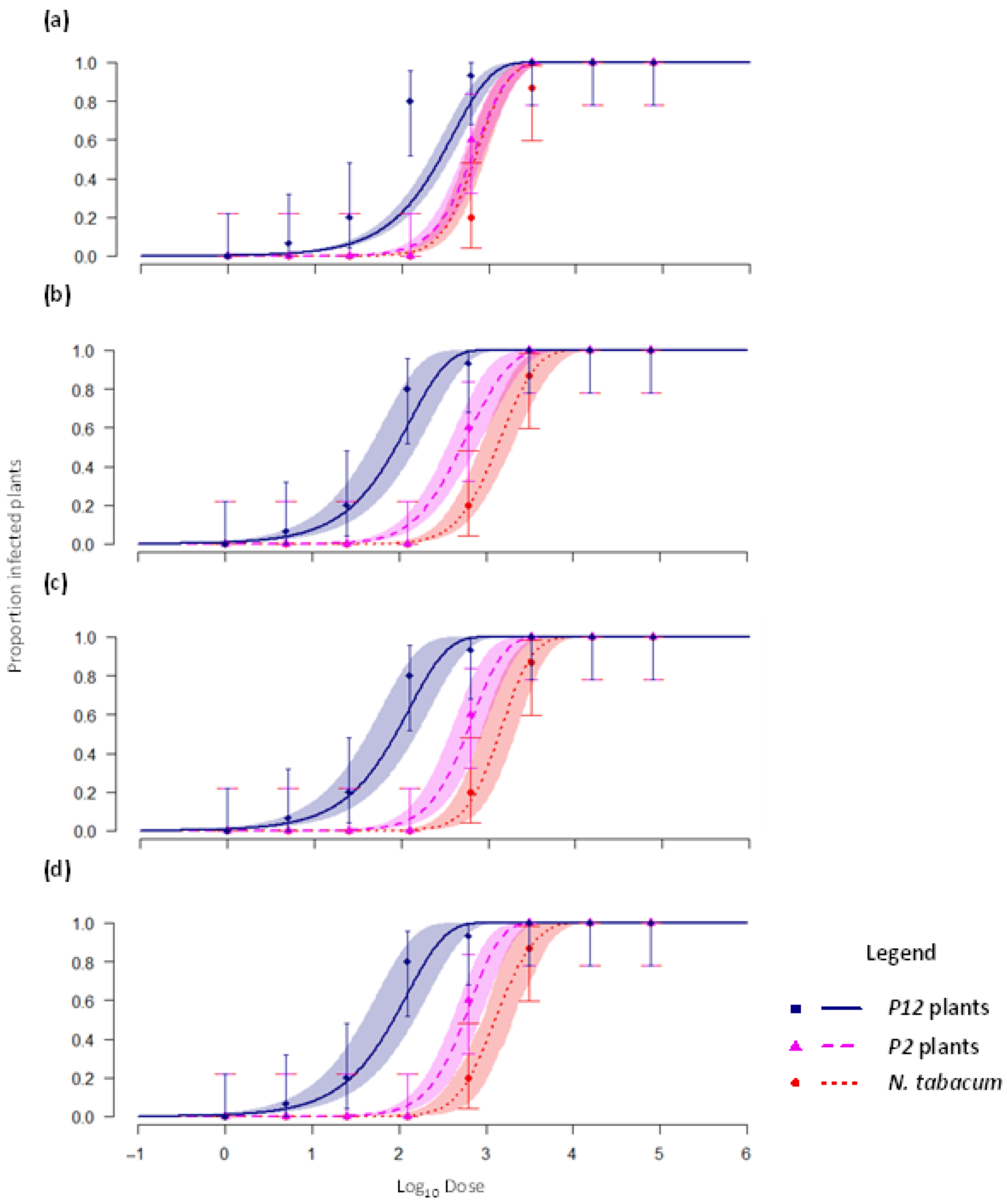
Appendix B
- Text A2: Overview of Results
Appendix C
| Model Parameter θ c | ||||||
|---|---|---|---|---|---|---|
| Group | Species a | Perm b | Range d | Estimate e | 95% CI f | NLL g |
| Monopartite | 869 | 103 | 0.01–0.99 | 0.42 | 0.34–0.45 | 1287.012 |
| 104 | 0.24–0.55 | 0.34 | 0.34–0.41 | 1350.753 | ||
| 105 | 0.28–0.50 | 0.33 | 0.31–0.38 | 1387.726 | ||
| Segmented | 196 | 103 | 0.01–0.99 | 0.19 | 0.13–0.43 | 175.981 |
| 104 | 0.03–0.53 | 0.18 | 0.11–0.29 | 196.808 | ||
| 105 | 0.05–0.40 | 0.15 | 0.08–0.28 | 216.413 | ||
| Multipartite | 67 | 103 | 0.01–0.99 | 0.32 | 0.22–0.35 | 400.789 |
| 104 | 0.12–0.45 | 0.25 | 0.20–0.33 | 446.624 | ||
| 105 | 0.12–0.40 | 0.24 | 0.16–0.30 | 484.343 | ||
| Begomovirus all h | 413 | 103 | 0.01–0.99 | 0.27 | 0.24–0.35 | 673.485 |
| 104 | 0.14–0.45 | 0.24 | 0.19–0.29 | 718.048 | ||
| 105 | 0.14–0.40 | 0.24 | 0.20–0.26 | 748.026 | ||
| Begomovirus monopartite | 245 | 103 | 0.01–0.99 | 0.37 | 0.33–0.46 | 382.287 |
| 104 | 0.20–0.60 | 0.31 | 0.26–0.40 | 403.375 | ||
| 105 | 0.20–0.45 | 0.30 | 0.23–0.40 | 413.076 | ||
| Begomovirus multipartite | 168 | 103 | 0.01–0.99 | 0.28 | 0.27–0.40 | 300.182 |
| 104 | 0.15–0.50 | 0.28 | 0.19–0.34 | 321.867 | ||
| 105 | 0.14–0.40 | 0.26 | 0.21–0.31 | 336.574 | ||
References
- Sicard, A.; Michalakis, Y.; Gutiérrez, S.; Blanc, S. The strange lifestyle of multipartite viruses. PLoS Pathog. 2016, 12, e1005819. [Google Scholar] [CrossRef]
- Diefenbacher, M.; Sun, J.; Brooke, C. The parts are greater than the whole: The role of semi-infectious particles in influenza A virus biology. Curr. Opin. Virol. 2018, 33, 42–46. [Google Scholar] [CrossRef]
- Wichgers Schreur, P.J.; Kortekaas, J. Single-molecule FISH reveals non-selective packaging of Rift Valley fever virus genome segments. PLoS Pathog. 2016, 12, e1005800. [Google Scholar] [CrossRef]
- Fulton, R.W. The effect of dilution on Necrotic ringspot virus infectivity and the enhancement of infectivity by noninfective virus. Virology 1962, 18, 477–485. [Google Scholar] [CrossRef] [PubMed]
- Iranzo, J.; Manrubia, S.C. Evolutionary dynamics of genome segmentation in multipartite viruses. Proc. R. Soc. B Biol. Sci. 2012, 279, 3812–3819. [Google Scholar] [CrossRef] [PubMed]
- Sánchez-Navarro, J.A.; Zwart, M.P.; Elena, S.F. Effects of the number of genome segments on primary and systemic infections with a multipartite plant RNA virus. J. Virol. 2013, 87, 10805–10815. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gutiérrez, S.; Zwart, M.P. Population bottlenecks in multicomponent viruses: First forays into the uncharted territory of genome-formula drift. Curr. Opin. Virol. 2018, 33, 184–190. [Google Scholar] [CrossRef]
- Michalakis, Y.; Blanc, S. The curious strategy of multipartite viruses. Annu. Rev. Virol. 2020, 7, 203–218. [Google Scholar] [CrossRef]
- Zwart, M.P.; Elena, S.F. Modeling multipartite virus evolution: The genome formula facilitates rapid adaptation to heterogeneous environments. Virus Evol 2020, 6, veaa022. [Google Scholar] [CrossRef]
- Lucía-Sanz, A.; Manrubia, S. Multipartite viruses: Adaptive trick or evolutionary treat? NPJ Syst. Biol. Appl. 2017, 3, 34. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, X.; Liu, W.; Zhou, Q.; Zhang, Q.; Li, G.; Yao, Q. Genome segments accumulate with different frequencies in Bombyx mori bidensovirus. J. Basic Microbiol. 2016, 56, 1338–1343. [Google Scholar] [CrossRef]
- Ladner, J.T.; Wiley, M.R.; Beitzel, B.; Kramer, L.D.; Tesh, R.B.; Palacios, G.; Auguste, A.J.; Dupuis Ii, A.P.; Lindquist, M.E.; Sibley, S.D.; et al. A multicomponent animal virus isolated from mosquitoes. Cell Host Microbe 2016, 20, 357–367. [Google Scholar] [CrossRef]
- Reanney, D.C. The evolution of RNA viruses. Annu. Rev. Microbiol. 1982, 36, 47–73. [Google Scholar] [CrossRef] [PubMed]
- Chao, L. Levels of selection, evolution of sex in RNA viruses, and the origin of life. J. Theor. Biol. 1991, 153, 229–246. [Google Scholar] [CrossRef] [PubMed]
- Ojosnegros, S.; García-Arriaza, J.; Escarmís, C.; Manrubia, S.C.; Perales, C.; Arias, A.; Mateu, M.G.; Domingo, E. Viral genome segmentation can result from a trade-off between genetic content and particle stability. PLoS Genet. 2011, 7, e1001344. [Google Scholar] [CrossRef]
- Neuman, B.W.; Smart, A.; Gilmer, O.; Smyth, R.P.; Vaas, J.; Böker, N.; Samborskiy, D.V.; Bartenschlager, R.; Seitz, S.; Gorbalenya, A.E.; et al. Giant RNA genomes: Roles of host, translation elongation, genome architecture, and proteome in nidoviruses. Proc. Natl. Acad. Sci. USA 2025, 122, e2413675122. [Google Scholar] [CrossRef] [PubMed]
- Sicard, A.; Yvon, M.; Timchenko, T.; Gronenborn, B.; Michalakis, Y.; Gutierrez, S.; Blanc, S. Gene copy number is differentially regulated in a multipartite virus. Nat. Commun. 2013, 4, 2248. [Google Scholar] [CrossRef]
- Wu, B.; Zwart, M.P.; Sánchez-Navarro, J.A.; Elena, S.F. Within-host evolution of segments ratio for the tripartite genome of alfalfa mosaic virus. Sci. Rep. 2017, 7, 5004. [Google Scholar] [CrossRef]
- Moreau, Y.; Gil, P.; Exbrayat, A.; Rakotoarivony, I.; Bréard, E.; Sailleau, C.; Viarouge, C.; Zientara, S.; Savini, G.; Goffredo, M.; et al. The genome segments of bluetongue virus differ in copy number in a host-specific manner. J. Virol. 2020, 95, e01834. [Google Scholar] [CrossRef]
- Gallet, R.; Fabre, F.; Thébaud, G.; Sofonea, M.T.; Sicard, A.; Blanc, S.; Michalakis, Y. Small bottleneck size in a highly multipartite virus during a complete infection cycle. J. Virol. 2018, 92, e00139-18. [Google Scholar] [CrossRef]
- Gilmer, D.; Ratti, C.; Michel, F. Long-distance movement of helical multipartite phytoviruses: Keep connected or die? Curr. Opin. Virol. 2018, 33, 120–128. [Google Scholar] [CrossRef]
- Sicard, A.; Pirolles, E.; Gallet, R.; Vernerey, M.-S.; Yvon, M.; Urbino, C.; Peterschmitt, M.; Gutierrez, S.; Michalakis, Y.; Blanc, S. A multicellular way of life for a multipartite virus. eLife 2019, 8, e00139-18. [Google Scholar] [CrossRef] [PubMed]
- Di Mattia, J.; Torralba, B.; Yvon, M.; Zeddam, J.L.; Blanc, S.; Michalakis, Y. Nonconcomitant host-to-host transmission of multipartite virus genome segments may lead to complete genome reconstitution. Proc. Natl. Acad. Sci. USA 2022, 119, e2201453119. [Google Scholar] [CrossRef] [PubMed]
- Nee, S. The evolution of multicompartmental genomes in viruses. J. Mol. Evol. 1987, 25, 277–281. [Google Scholar] [CrossRef]
- Leeks, A.; Young, P.G.; Turner, P.E.; Wild, G.; West, S.A. Cheating leads to the evolution of multipartite viruses. PLoS Biol. 2023, 21, e3002092. [Google Scholar] [CrossRef]
- Bald, J. The use of numbers of infections for comparing the concentration of plant virus suspensions I. Dilution experiments with purified suspensions. Ann. Appl. Biol. 1937, 24, 33–55. [Google Scholar] [CrossRef]
- Price, A.W.C.; Spencer, E.L. Accuracy of the local lesion method for measuring virus activity. II. Tobacco-necrosis, Alfalfa-mosaic and Tobacco-ringspot viruses. Am. J. Botary 1943, 30, 340–346. [Google Scholar] [CrossRef]
- Zwart, M.P.; Hemerik, L.; Cory, J.S.; De Visser, J.A.G.M.; Bianchi, F.J.J.A.; Van Oers, M.M.; Vlak, J.M.; Hoekstra, R.F.; Van Der Werf, W. An experimental test of the independent action hypothesis in virus-insect pathosystems. Proc. R. Soc. B Biol. Sci. 2009, 276, 2233–2242. [Google Scholar] [CrossRef]
- Zwart, M.P.; Elena, S.F. Matters of size: Genetic bottlenecks in virus infection and their potential impact on evolution. Annu. Rev. Virol. 2015, 2, 161–179. [Google Scholar] [CrossRef]
- Zwart, M.P.; Daròs, J.-A.; Elena, S.F. One is enough: In vivo effective population size is dose-dependent for a plant RNA virus. PLoS Pathog. 2011, 7, e1002122. [Google Scholar] [CrossRef]
- Regoes, R.R.; Hottinger, J.W.; Sygnarski, L.; Ebert, D. The infection rate of Daphnia magna by Pasteuria ramosa conforms with the mass-action principle. Epidemiol. Infect. 2003, 131, 957–966. [Google Scholar] [CrossRef] [PubMed]
- Taschner, P.E.M.; Van Der Kuyl, A.C.; Neeleman, L.; Bol, J.F. Replication of an incomplete alfalfa mosaic virus genome in plants transformed with viral replicase genes. Virology 1991, 181, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Johnson, J.B.; Omland, K.S. Model selection in ecology and evolution. Trends Ecol. Evol. 2004, 19, 101–108. [Google Scholar] [CrossRef] [PubMed]
- Whitfield, A.E.; Falk, B.W.; Rotenberg, D. Insect vector-mediated transmission of plant viruses. Virology 2015, 479–480, 278–289. [Google Scholar] [CrossRef]
- Brown, D.J.F.; Robertson, W.M.; Trudgill, D.L. Transmission of viruses by plant nematodes. Annu. Rev. Phytopathol. 1995, 33, 223–249. [Google Scholar] [CrossRef] [PubMed]
- Rochon, D.; Kakani, K.; Robbins, M.; Reade, R. Molecular aspects of plant virus transmission by olpidium and plasmodiophorid vectors. Annu. Rev. Phytopathol. 2004, 42, 211–241. [Google Scholar] [CrossRef]
- Mauck, K.E.; De Moraes, C.M.; Mescher, M.C. Deceptive chemical signals induced by a plant virus attract insect vectors to inferior hosts. Proc. Natl. Acad. Sci. USA 2010, 107, 3600–3605. [Google Scholar] [CrossRef]
- Watson, M.A. Transmission of plant viruses by aphids. In Principles and Techniques in Plant Virology; Kado, C.I., Agrawal, H.O., Eds.; Van Nostrand Reinhold Company: New York, NY, USA, 1972; pp. 131–167. [Google Scholar]
- Valdano, E.; Manrubia, S.; Gómez, S.; Arenas, A. Endemicity and prevalence of multipartite viruses under heterogeneous between-host transmission. PLoS Comput. Biol. 2019, 15, e1006876. [Google Scholar] [CrossRef]
- Bonnamy, M.; Brousse, A.; Pirolles, E.; Michalakis, Y.; Blanc, S. The genome formula of a multipartite virus is regulated both at the individual segment and the segment group levels. PLoS Pathog. 2024, 20, e1011973. [Google Scholar] [CrossRef]
- Matilla, A.J. The interplay between enucleated sieve elements and companion cells. Plants 2023, 12, 3033. [Google Scholar] [CrossRef]
- Savory, F.R.; Varma, V.; Ramakrishnan, U. Identifying geographic hot spots of reassortment in a multipartite plant virus. Evol. Appl. 2014, 7, 569–579. [Google Scholar] [CrossRef]
- Lowen, A.C. Constraints, drivers, and implications of Influenza A Virus reassortment. Annu. Rev. Virol. 2017, 4, 105–121. [Google Scholar] [CrossRef]
- Varsani, A.; Lefeuvre, P.; Roumagnac, P.; Martin, D. Notes on recombination and reassortment in multipartite/segmented viruses. Curr. Opin. Virol. 2018, 33, 156–166. [Google Scholar] [CrossRef]
- McDonald, S.M.; Nelson, M.I.; Turner, P.E.; Patton, J.T. Reassortment in segmented RNA viruses: Mechanisms and outcomes. Nat. Rev. Microbiol. 2016, 14, 448–460. [Google Scholar] [CrossRef] [PubMed]
- Gallet, R.; Di Mattia, J.; Ravel, S.; Zeddam, J.L.; Vitalis, R.; Michalakis, Y.; Blanc, S. Gene copy number variations at the within-host population level modulate gene expression in a multipartite virus. Virus Evol. 2022, 8, veac058. [Google Scholar] [CrossRef] [PubMed]
- Boezen, D.; Johnson, M.L.; Grum-Grzhimaylo, A.A.; van der Vlugt, R.A.; Zwart, M.P. Evaluation of sequencing and PCR-based methods for the quantification of the viral genome formula. Virus Res. 2023, 326, 199064. [Google Scholar] [CrossRef] [PubMed]
- Yu, N.T.; Xie, H.M.; Zhang, Y.L.; Wang, J.H.; Xiong, Z.; Liu, Z.X. Independent modulation of individual genomic component transcription and a cis-acting element related to high transcriptional activity in a multipartite DNA virus. BMC Genom. 2019, 20, 573. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, Q.; Xu, Z.; Liu, R.; Cui, F. Distinct replication and gene expression strategies of the Rice Stripe virus in vector insects and host plants. J. Gen. Virol. 2019, 100, 877–888. [Google Scholar] [CrossRef] [PubMed]
- Brooke, C.B.; Ince, W.L.; Wei, J.; Bennink, J.R.; Yewdell, J.W. Influenza A virus nucleoprotein selectively decreases neuraminidase gene-segment packaging while enhancing viral fitness and transmissibility. Proc. Natl. Acad. Sci. USA 2014, 111, 16854–16859. [Google Scholar] [CrossRef]
- Wichgers Schreur, P.J.; Kormelink, R.; Kortekaas, J. Genome packaging of the Bunyavirales. Curr. Opin. Virol. 2018, 33, 151–155. [Google Scholar] [CrossRef]
- Moury, B.; Fabre, F.; Hébrard, E.; Froissart, R. Determinants of host species range in plant viruses. J. Gen. Virol. 2017, 98, 862–873. [Google Scholar] [CrossRef]
- Morris, C.E.; Moury, B. Revisiting the concept of host range of plant pathogens. Annu. Rev. Phytopathol. 2019, 57, 63–90. [Google Scholar] [CrossRef]
- Hutchinson, G.E. Concluding remarks. Cold Spring Harb. Symp. Quant. Biol. 1957, 22, 415–427. [Google Scholar] [CrossRef]
- Rohde, K. Niche restriction in parasites: Proximate and ultimate causes. Parasitology 1994, 109, S69–S84. [Google Scholar] [CrossRef] [PubMed]
- Hatcher, E.L.; Zhdanov, S.A.; Bao, Y.; Blinkova, O.; Nawrocki, E.P.; Ostapchuck, Y.; Schaffer, A.A.; Rodney Brister, J. Virus Variation Resource-improved response to emergent viral outbreaks. Nucleic Acids Res. 2017, 45, D482–D490. [Google Scholar] [CrossRef] [PubMed]
- ICTV 2023. Virus Metadata Resource. Available online: https://ictv.global/vmr (accessed on 29 April 2024).
- Zwart, M.P.; Blanc, S.; Johnson, M.; Manrubia, S.; Michalakis, Y.; Sofonea, M.T. Unresolved advantages of multipartitism in spatially structured environments. Virus Evol. 2021, 7, veab004. [Google Scholar] [CrossRef] [PubMed]
- Hull, R.; Hills, G.J.; Markham, R. Studies on Alfalfa Mosaic Virus II. The structure of the virus components. Virology 1969, 37, 416–428. [Google Scholar] [CrossRef]
- Baltimore, D. Expression of animal virus genomes. Bacteriol. Rev. 1971, 35, 235–241. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2023. [Google Scholar]
- Wickham, H.; François, R.; Henry, L.; Müller, K. dplyr: A Grammar of Data Manipulation; R Package Version 1.1.1, 2023. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 1 May 2023).


| Group | N a | Host Range b [95% CI c] |
|---|---|---|
| Monopartite | 869 | 3.03 [2.63–3.23] |
| Multipartite | 196 | 4.17 [3.33–6.25] |
| Segmented | 67 | 6.67 [4.00–12.50] |
| Begomovirus | 413 | 4.17 [3.85–5.00] |
| Group | N a | Host Range b [95% CI c] |
|---|---|---|
| Monopartite | 245 | 3.33 [2.50–4.35] |
| Multipartite | 168 | 3.85 [3.23–4.76] |
| Parameter | Value | Explanation and Comments |
|---|---|---|
| λ | Cellular multiplicity of infection; maximum value that can decrease under suboptimal conditions. | |
| c | 5, 100 | Number of cells per round of infection. Unlike the previous model, c is not adjusted to maintain the same number of effectively infected cells per round of infection. |
| σ2 | 0.01, 0.1, 1, 10 | Variance of the normal probability function used to link virus gene products to the total production of viral resources |
| tfinal | 20 | Number of rounds of infection |
| ρ | 0, 0.05, 0.1, …, 1 | Proportion of virus resources dedicated to gene-product sharing, the remaining fraction is used for virus particles. |
| ψ | 0, 2 | Determines the range of values from which values of can be drawn from a uniform distribution, from to . When , is always 0. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Johnson, M.L.; Boezen, D.; Grum-Grzhimaylo, A.A.; van der Vlugt, R.A.A.; de Visser, J.A.G.M.; Zwart, M.P. Living Together Apart: Quantitative Perspectives on the Costs and Benefits of a Multipartite Genome Organization in Viruses. Viruses 2025, 17, 1275. https://doi.org/10.3390/v17091275
Johnson ML, Boezen D, Grum-Grzhimaylo AA, van der Vlugt RAA, de Visser JAGM, Zwart MP. Living Together Apart: Quantitative Perspectives on the Costs and Benefits of a Multipartite Genome Organization in Viruses. Viruses. 2025; 17(9):1275. https://doi.org/10.3390/v17091275
Chicago/Turabian StyleJohnson, Marcelle L., Dieke Boezen, Alexey A. Grum-Grzhimaylo, René A. A. van der Vlugt, J. Arjan G. M. de Visser, and Mark P. Zwart. 2025. "Living Together Apart: Quantitative Perspectives on the Costs and Benefits of a Multipartite Genome Organization in Viruses" Viruses 17, no. 9: 1275. https://doi.org/10.3390/v17091275
APA StyleJohnson, M. L., Boezen, D., Grum-Grzhimaylo, A. A., van der Vlugt, R. A. A., de Visser, J. A. G. M., & Zwart, M. P. (2025). Living Together Apart: Quantitative Perspectives on the Costs and Benefits of a Multipartite Genome Organization in Viruses. Viruses, 17(9), 1275. https://doi.org/10.3390/v17091275






