Quantifying Impact of HIV Receptor Surface Density Reveals Differences in Fusion Dynamics of HIV Strains
Abstract
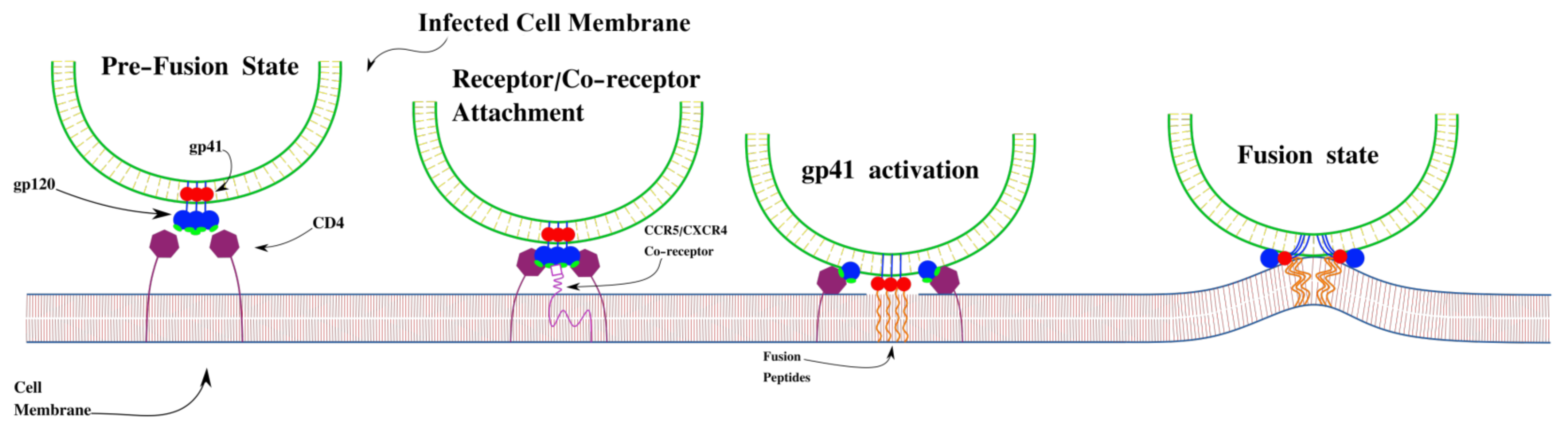
:1. Introduction
2. Materials and Methods
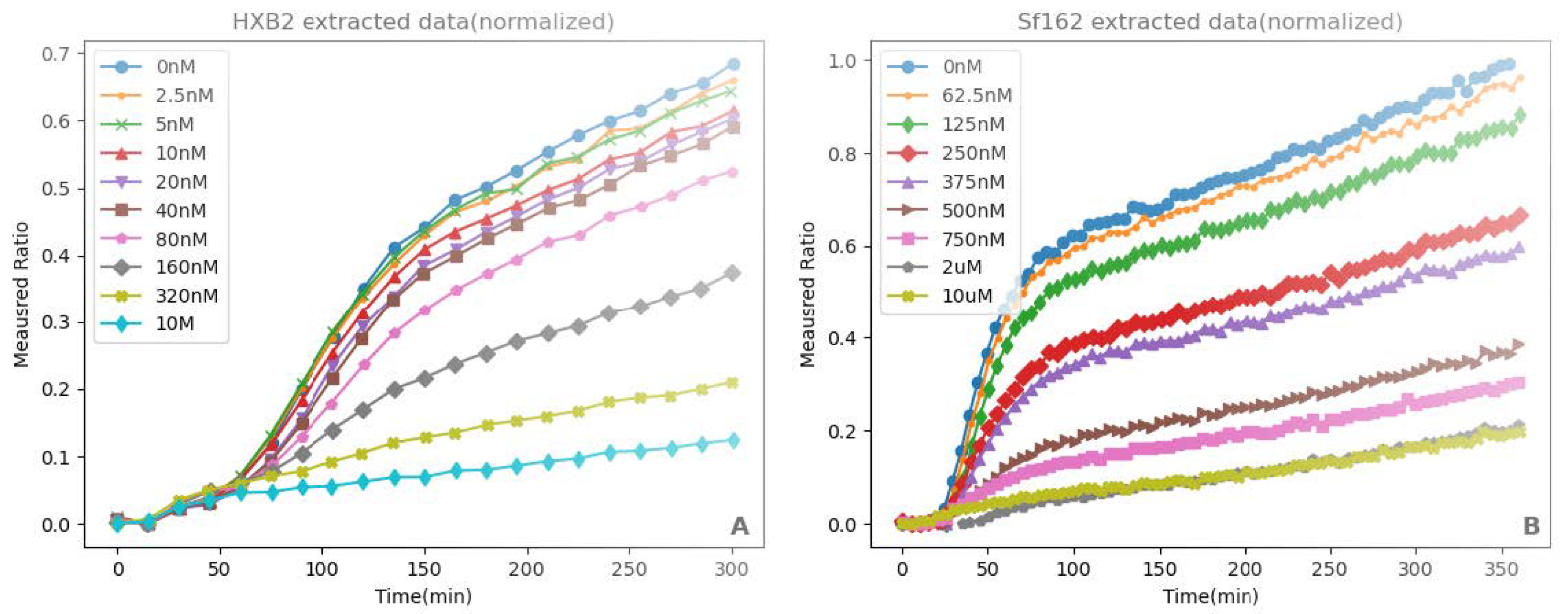
2.1. Experimental Data
2.2. Mathematical Models
2.3. Model Fitting
3. Results
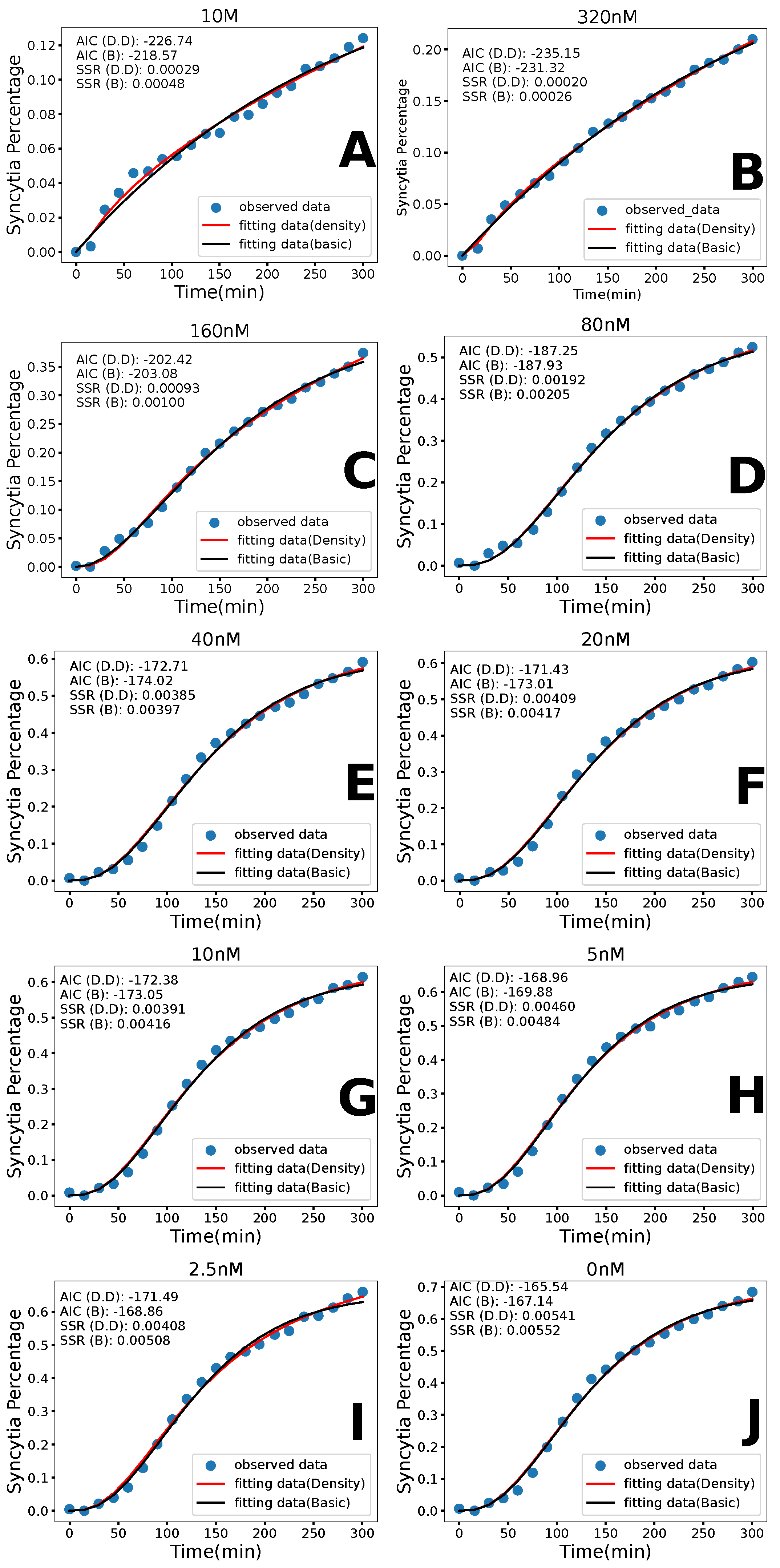
3.1. Basic Model
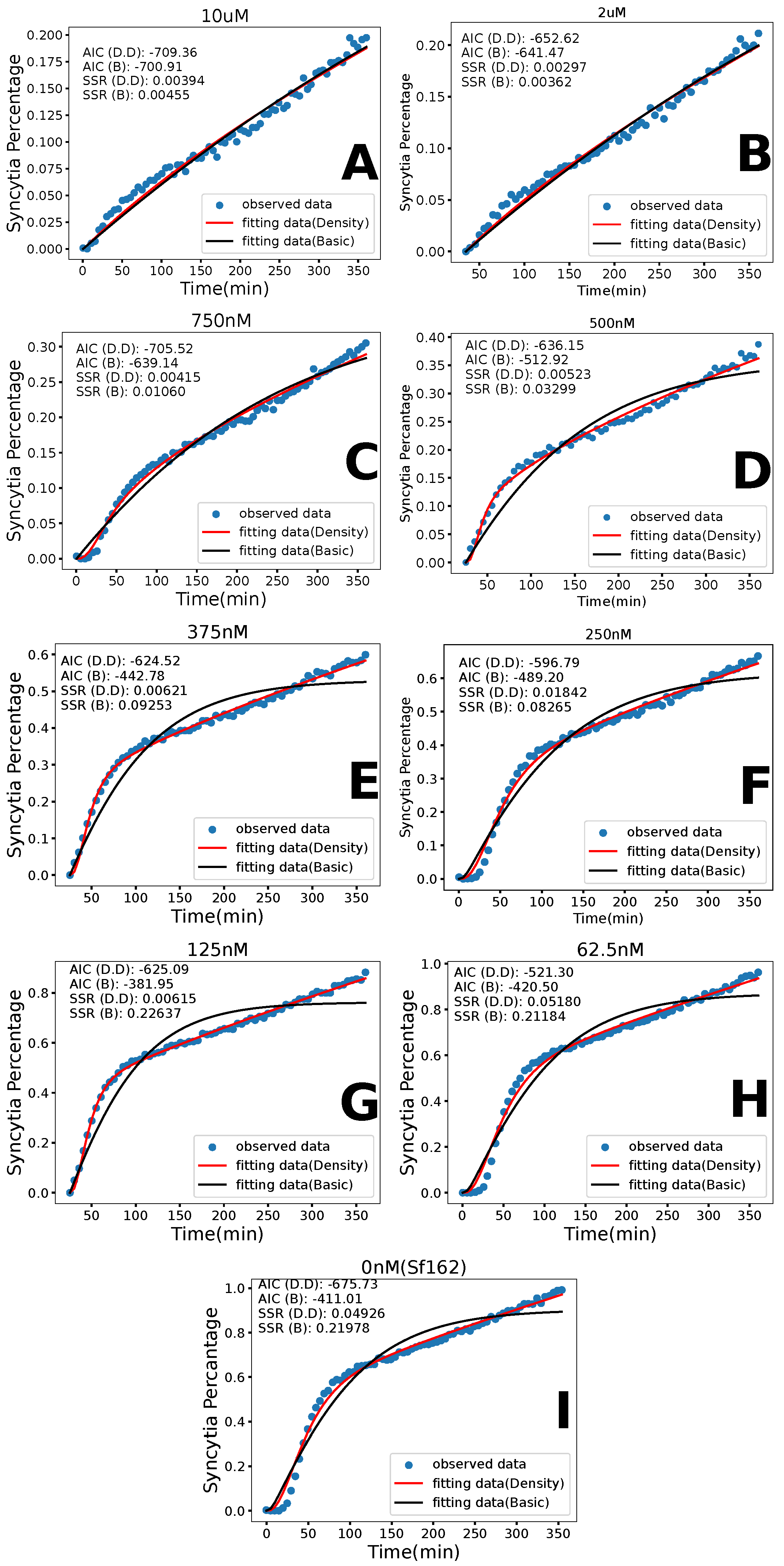
3.2. Density-Dependent Syncytia Formation
3.3. Model Comparison
3.4. Parameter Dose Dependence
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- van Heuvel, Y.; Schatz, S.; Rosengarten, J.F.; Stitz, J. Infectious RNA: Human Immunodeficiency Virus (HIV) Biology, Therapeutic Intervention, and the Quest for a Vaccine. Toxins 2022, 14, 138. [Google Scholar] [CrossRef] [PubMed]
- Douek, D.C.; Brenchley, J.M.; Betts, M.R.; Ambrozak, D.R.; Hill, B.J.; Okamoto, Y.; Casazza, J.P.; Kuruppu, J.; Kunstman, K.; Wolinsky, S.; et al. HIV preferentially infects HIV-specific CD4+ T cells. Nature 2002, 417, 95–98. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Kirschner, D.E.; De Boer, R. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef]
- Gendelrnan, H.E.; Orenstein, J.M.; Baca, L.M.; Weiser, B.; Burger, H.; Kalter, D.C.; Meltzer, M.S. The macrophage in the persistence and pathogenesis of HIV infection. AIDS 1989, 3, 475–495. [Google Scholar] [CrossRef]
- Eugenin, E.; Gaskill, P.; Berman, J. Tunneling nanotubes (TNT) are induced by HIV-infection of macrophages: A potential mechanism for intercellular HIV trafficking. Cell. Immunol. 2009, 254, 142–148. [Google Scholar] [CrossRef]
- Piguet, V.; Steinman, R.M. The interaction of HIV with dendritic cells: Outcomes and pathways. Trends Immunol. 2007, 28, 503–510. [Google Scholar] [CrossRef]
- Barroca, P.; Calado, M.; Azevedo-Pereira, J.M. HIV/dendritic cell interaction: Consequences in the pathogenesis of HIV infection. AIDS Rev. 2014, 16, 223–235. [Google Scholar] [PubMed]
- The HIV-CAUSAL Collaboration The effect of combined antiretroviral therapy on the overall mortality of HIV-infected individuals. AIDS 2010, 24, 123–137. [CrossRef]
- Nakagawa, F.; Lodwick, R.; Smith, C.; Smith, R.; Cambiano, V.; Lundgren, J.; Delpech, V.; Phillips, A. Projected life expectancy of people with HIV according to timing of diagnosis. AIDS 2012, 26, 335–343. [Google Scholar] [CrossRef]
- Zhu, P.; Liu, J.; Bess, J.; Chertova, E.; Lifson, J.D.; Grisé, H.; Ofek, G.A.; Taylor, K.A.; Roux, K.H. Distribution and three-dimensional structure of AIDS virus envelope spikes. Nature 2006, 441, 847–852. [Google Scholar] [CrossRef]
- Ganser-Pornillos, B.K.; Yeager, M.; Pornillos, O. Assembly and architecture of HIV. Adv. Exp. Med. Biol. 2012, 726, 441–465. [Google Scholar] [PubMed]
- Wilen, C.B.; Tilton, J.C.; Doms, R.W. HIV: Cell binding and entry. Cold Spring Harb. Perspect. Med. 2012, 2, a006866. [Google Scholar] [CrossRef] [PubMed]
- Doms, R.W.; Moore, J.P. HIV-1 Membrane Fusion: Targets of Opportunity. J. Cell Biol. 2000, 151, F9–F14. [Google Scholar] [CrossRef] [PubMed]
- Blumenthal, R.; Durell, S.; Viard, M. HIV Entry and Envelope Glycoprotein-mediated Fusion. J. Biol. Chem. 2012, 287, 40841–40849. [Google Scholar] [CrossRef]
- Leroy, H.; Han, M.; Woottum, M.; Bracq, L.; Bouchet, J.; Xie, M.; Benichou, S. Virus-Mediated Cell-Cell Fusion. Int. J. Mol. Sci. 2020, 21, 9644. [Google Scholar] [CrossRef]
- Koga, Y.; Nakamura, K.; Sasaki, M.; Kimura, G.; Nomoto, K. The Difference in gp160 and gp120 of HIV Type 1 in the Induction of CD4 Downregulation Preceding Single-Cell Killing. Virology 1994, 201, 137–141. [Google Scholar] [CrossRef]
- Compton, A.A.; Schwartz, O. They Might Be Giants: Does Syncytium Formation Sink or Spread HIV Infection? PLoS Pathog. 2017, 13, e1006099. [Google Scholar] [CrossRef]
- Sattentau, Q.J.; Moore, J.P.; Barclay, A.N.; Crumpton, M.J.; Weiss, R.A. The role of CD4 in HIV binding and entry. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 1993, 342, 59–66. [Google Scholar] [CrossRef]
- Guan, Y. The first structure of HIV-1 gp120 with CD4 and CCR5 receptors. Cell Biosci. 2019, 9, 2. [Google Scholar] [CrossRef]
- Huang, C.-C.; Tang, M.; Zhang, M.Y.; Majeed, S.; Montabana, E.; Stanfield, R.L.; Dimitrov, D.S.; Korber, B.; Sodroski, J.; Wilson, I.A.; et al. Structure of a V3-Containing HIV-1 gp120 Core. Science 2005, 310, 1025–1028. [Google Scholar] [CrossRef]
- Blaak, H.; VantWout, A.; Brouwer, M.; Hooibrink, B.; Hovenkamp, E.; Schuitemaker, H. In vivo HIV-1 infection of CD45RA+CD4+ T cells is established primarily by syncytium-inducing variants and correlates with the rate of CD4+ T cell decline. Proc. Natl. Acad. Sci. USA 2000, 97, 1269–1274. [Google Scholar] [CrossRef]
- van Rij, R.; Blaak, H.; Visser, J.; Brouwer, M.; Rientsma, R.; Broersen, S.; Husman, A.; Schuitemaker, H. Differential coreceptor expression allows for independent evolution of non-syncytium-inducing and syncytium-inducing HIV-1. J. Clin. Investig. 2000, 106, 1039–1052. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, L.; Verdejo, J.; Lahoz, J.; Gurbindo, D.; Hernandez-Sampelayo, T.; Moreno, E.; Azanedo, M.; Contreras, G.; Medrano, L.; Najera, R. Expression of different HIV-1 phenotypic subpopulations through the natural history of the infection. Med. Clin. 1998, 110, 441–445. [Google Scholar]
- van’t Wout, A.; Blaak, H.; Ran, L.; Brouwer, M.; Kuiken, C.; Schuitemaker, H. Evolution of syncytium-inducing and non-syncytium-inducing biological virus clones in relation to replication kinetics during the course of human immunodeficiency virus type 1 infection. J. Virol. 1998, 72, 5099–5107. [Google Scholar] [CrossRef] [PubMed]
- Todd, B.; Kedar, P.; Pope, J. Syncytium induction in primary CD4+ T-cell lines from normal donors by human immunodeficiency virus type-1 isolates with non-syncytium-unducing genotype and phenotype in MT-2 cells. J. Virol. 1995, 69, 7099–7105. [Google Scholar] [CrossRef]
- Connor, R.; Paxton, W.; Sheridan, K.; Koup, R. Macrophages and CD4(+) T lymphocytes from two multiply exposed, uninfected individuals resist infection with primary non-syncytium-inducing isolates of human immunodeficiency virus type 1. J. Virol. 1996, 70, 8758–8764. [Google Scholar] [CrossRef]
- Jurriaans, S.; Vangemen, B.; Weverling, G.; Vanstrijp, D.; Nara, P.; Coutino, R.; Koot, M.; Schuitemaker, H.; Goudsmit, J. The natural history of HIV-1 infection—Virus load and virus phenotype independent determinants of clinical course. Virology 1994, 204, 223–233. [Google Scholar] [CrossRef] [PubMed]
- Greco, G.; Fujimura, S.; Mourich, D.; Levy, J. Differential effects of human immunodeficiency virus isolates on β-chemokine and gamma interferon production and on cell proliferation. J. Virol. 1999, 73, 1528–1534. [Google Scholar] [CrossRef]
- Koot, M.; VantWout, A.; Kootstra, N.; DeGoede, R.; Tersmette, M.; Schuitemaker, H. Relation between changes in cellular load, evolution of viral phenotype, and the clonal composition of virus populations in the course of human immunodeficiency virus type 1 infection. J. Infect. Dis. 1996, 173, 349–354. [Google Scholar] [CrossRef]
- VantWout, A.; DeJong, M.; Kootstra, N.; Veenstra, J.; Lange, J.; Boucher, C.; Schuitemaker, H. Changes in Cellular Virus Load and Zidovudine Resistance of Syncytium-Inducing and Non-Syncytium-Inducing Human Immunodeficiency Virus Populations Under Zidovudine Pressure: A Clonal Analysis. J. Infect. Dis. 1996, 174, 845–849. [Google Scholar] [CrossRef]
- Locher, C.; Witt, S.; Kassel, R.; Dowell, N.; Fujimura, S.; Levy, J. Differential effects of R5 and X4 human immunodeficiency virus type 1 infection on CD4+ cell proliferation and activation. J. Gen. Virol. 2005, 86, 1171–1179. [Google Scholar] [CrossRef] [PubMed]
- Lineberger, J.E.; Danzeisen, R.; Hazuda, D.J.; Simon, A.J.; Miller, M.D. Altering Expression Levels of Human Immunodeficiency Virus Type 1 gp120-gp41 Affects Efficiency but Not Kinetics of Cell-Cell Fusion. J. Virol. 2002, 76, 3522–3533. [Google Scholar] [CrossRef] [PubMed]
- Mulampaka, S.N.; Dixit, N.M. Estimating the Threshold Surface Density of Gp120-CCR5 Complexes Necessary for HIV-1 Envelope-Mediated Cell-Cell Fusion. PLoS ONE 2011, 6, e19941. [Google Scholar] [CrossRef]
- Pugach, P.; Ray, N.; Klasse, P.J.; Ketas, T.J.; Michael, E.; Doms, R.W.; Lee, B.; Moore, J.P. Inefficient entry of vicriviroc-resistant HIV-1 via the inhibitor-CCR5 complex at low cell surface CCR5 densities. Virology 2009, 387, 296–302. [Google Scholar] [CrossRef]
- Colby, C.; Jurale, C.; Kates, J.R. Mechanism of Synthesis of Vaccinia Virus Double-Stranded Ribonucleic Acid In Vivo and In Vitro. J. Virol. 1971, 7, 71–76. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef] [PubMed]
- Canini, L.; Perelson, A.S. Viral kinetic modeling: State of the art. J. Pharmacokinet. Pharmacodyn. 2014, 41, 431–443. [Google Scholar] [CrossRef]
- Layden, T.J.; Layden, J.E.; Ribeiro, R.M.; Perelson, A.S. Mathematical modeling of viral kinetics: A tool to understand and optimize therapy. Clin. Liver Dis. 2003, 7, 163–178. [Google Scholar] [CrossRef]
- Beggs, N.F.; Dobrovolny, H.M. Determining drug efficacy parameters for mathematical models of influenza. J. Biol. Dyn. 2015, 9, 332–346. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S. Viral kinetics and mathematical models. Am. J. Med. 1999, 107, 49–52. [Google Scholar] [CrossRef]
- Jessie, B.; Dobrovolny, H.M. The role of syncytia during viral infections. J. Theor. Biol. 2021, 525, 110749. [Google Scholar] [CrossRef]
- Amidei, A.; Dobrovolny, H.M. Virus-mediated cell fusion of SARS-CoV-2 variants. Math. Biosci. 2024, 369, 109144. [Google Scholar] [CrossRef] [PubMed]
- Amidei, A.; Dobrovolny, H.M. Estimation of virus-mediated cell fusion rate of SARS-CoV-2. Virology 2022, 575, 91–100. [Google Scholar] [CrossRef]
- Iliopoulou, M.; Nolan, R.; Alvarez, L.; Watanabe, Y.; Coomer, C.A.; Jakobsdottir, G.M.; Bowden, T.A.; Padilla-Parra, S. A dynamic three-step mechanism drives the HIV-1 pre-fusion reaction. Nat. Struct. Mol. Biol. 2018, 25, 814–822. [Google Scholar] [CrossRef] [PubMed]
- Gruters, R.A.; Neefjes, J.J.; Tersmette, M.; de Goede, R.E.Y.; Tulp, A.; Huisman, H.G.; Miedema, F.; Ploegh, H.L. Interference with HIV-induced syncytium formation and viral infectivity by inhibitors of trimming glucosidase. Nature 1987, 330, 74–77. [Google Scholar] [CrossRef]
- DeSantis, M.C.; Kim, J.H.; Song, H.; Klasse, P.J.; Cheng, W. Quantitative Correlation between Infectivity and Gp120 Density on HIV-1 Virions Revealed by Optical Trapping Virometry. J. Biol. Chem. 2016, 291, 13088–13097. [Google Scholar] [CrossRef] [PubMed]
- Miranda, L.R.; Schaefer, B.C.; Kupfer, A.; Hu, Z.; Franzusoff, A. Cell surface expression of the HIV-1 envelope glycoproteins is directed from intracellular CTLA-4-containing regulated secretory granules. Proc. Natl. Acad. Sci. USA 2002, 99, 8031–8036. [Google Scholar] [CrossRef]
- Chojnacki, J.; Staudt, T.; Glass, B.; Bingen, P.; Engelhardt, J.; Anders, M.; Schneider, J.; Müller, B.; Hell, S.W.; Kräusslich, H.G. Maturation-Dependent HIV-1 Surface Protein Redistribution Revealed by Fluorescence Nanoscopy. Science 2012, 338, 524–528. [Google Scholar] [CrossRef]
- Roy, N.H.; Chan, J.; Lambelé, M.; Thali, M. Clustering and Mobility of HIV-1 Env at Viral Assembly Sites Predict Its Propensity To Induce Cell-Cell Fusion. J. Virol. 2013, 87, 7516–7525. [Google Scholar] [CrossRef]
- Dutch, R.; Joshi, S.; Lamb, R. Membrane fusion promoted by increasing surface densities of the paramyxovirus F and HN proteins: Comparison of fusion reactions mediated by simian virus 5 F, human parainfluenza virus type 3 F, and influenza virus HA. J. Virol. 1998, 72, 7745–7753. [Google Scholar] [CrossRef]
- Günther-Ausborn, S.; Schoen, P.; Bartoldus, I.; Wilschut, J.; Stegmann, T. Role of hemagglutinin surface density in the initial stages of influenza virus fusion: Lack of evidence for cooperativity. J. Virol. 2000, 74, 2714–2720. [Google Scholar] [CrossRef] [PubMed]
- Clague, M.; Schoch, C.; Blumenthal, R. Delay time for influenza virus hemagglutinin-induced membran fusion depends on hemagglutinin surface density. J. Virol. 1991, 65, 2402–2407. [Google Scholar] [CrossRef]
- Mohan, G.S.; Ye, L.; Li, W.; Monteiro, A.; Lin, X.; Sapkota, B.; Pollack, B.P.; Compans, R.W.; Yang, C. Less Is More: Ebola Virus Surface Glycoprotein Expression Levels Regulate Virus Production and Infectivity. J. Virol. 2015, 89, 1205–1217. [Google Scholar] [CrossRef] [PubMed]
- Graw, F.; Perelson, A.S. Spatial Aspects of HIV Infection. In Mathematical Methods and Models in Biomedicine; Springer: New York, NY, USA, 2013; pp. 3–31. [Google Scholar] [CrossRef]
- Fain, B.G.; Dobrovolny, H.M. GPU acceleration and data fitting: Agent-based models of viral infections can now be parameterized in hours. J. Comput. Sci. 2022, 61, 101662. [Google Scholar] [CrossRef]
- Durso-Cain, K.; Kumberger, P.; Schalte, Y.; Fink, T.; Dahari, H.; Hasenauer, J.; Uprichard, S.L.; Graw, F. HCV Spread Kinetics Reveal Varying Contributions of Transmission Modes to Infection Dynamics. Viruses 2021, 13, 1308. [Google Scholar] [CrossRef] [PubMed]
- Beauchemin, C.; Samuel, J.; Tuszynski, J. A simple cellular automaton model for influenza A viral infections. J. Theor. Biol. 2005, 232, 223–234. [Google Scholar] [CrossRef]
- Beauchemin, C. Probing the effects of the well-mixed assumption on viral infection dynamics. J. Theor. Biol. 2006, 242, 464–477. [Google Scholar] [CrossRef]
- Yuan, Y.; Allen, L.J.S. Stochastic models for virus and immune system dynamics. Math. Biosci. 2011, 234, 84–94. [Google Scholar] [CrossRef]


| Dosage | (/min) | (min) | SSR | |
|---|---|---|---|---|
| 10 M AraC | 0.924 | 1.02 | 4.76 | |
| CI | (0.889, 0.943) | (2.45, 7.30) | (0.00824, 16,300) | (3.67, 17.7) |
| 320 nM AraC | 0.871 | 1.14 | 2.59 | |
| CI | (0.860, 0.880) | (3.49, 4.41) | (0.223, 3650) | (2.01, 2.61) |
| 160 nM AraC | 0.852 | 0.499 | 87.0 | 9.96 |
| CI | (0.847, 0.859) | (0.0583, 1.00) | (73.2, 93.7) | (7.07, 22.2) |
| 80 nM AraC | 0.817 | 0.0433 | 64.6 | 0.00205 |
| CI | (0.813, 0.894) | (0.00847, 0.187) | (6.47 , 77.0) | (0.00139, 0.596) |
| 40 nM AraC | 0.807 | 0.0339 | 55.3 | 0.00397 |
| CI | (0.799, 0.864) | (0.0168, 1.42) | (6.47 , 76.2) | (0.00287, 0.484) |
| 20 nM AraC | 0.804 | 0.0333 | 54.5 | 0.00417 |
| CI | (0.796, 0.859) | (0.0158, 0.589) | (6.48 , 75.6) | (0.00286, 0.792) |
| 10 nM AraC | 0.804 | 0.0421 | 54.6 | 0.00416 |
| CI | (0.799, 0.859) | (0.0103, 0.910) | (6.47 , 69.3) | (0.00291, 0.809) |
| 5 nM AraC | 0.799 | 0.0411 | 51.2 | 0.00484 |
| CI | (0.793, 0.823) | (0.0182, 0.147) | (6.49 , 65.8) | (0.00335, 0.476) |
| 2.5 nM AraC | 0.796 | 0.0300 | 46.8 | 0.00508 |
| CI | (0.790, 0.799) | (0.0254, 0.105) | (40.1, 67.6) | (0.00369, 0.00579) |
| 0 nM AraC | 0.791 | 0.0364 | 51.8 | 0.00552 |
| CI | (0.784, 0.816) | (0.0186, 0.143) | (6.99, 53.7) | (0.00375, 0.502) |
| Dosage | (/min) | (min) | SSR | |
|---|---|---|---|---|
| 10 M AraC | 0.833 | 3.52 | 0.00455 | |
| CI | (0.576, 0.840) | (0.610, 1.97) | (0.140, 21.3) | (0.00425, 0.00689) |
| 2 M AraC | 0.831 | 6.53 | 0.00362 | |
| CI | (0.785, 0.834) | (1.59, 2.23) | (1.41, 25.3) | (0.00324, 0.00362) |
| 750 nM AraC | 0.859 | 5.88 | 0.0106 | |
| CI | (0.847, 0.887) | (4.33, 9.95) | (0.169, 176,000) | (0.00977, 0.0911) |
| 500 nM AraC | 0.857 | 7.10 | 0.03298 | |
| CI | (0.769, 0.864) | (3.32, 10.2) | (0.422, 152,000) | (0.0296, 0.190) |
| 375 nM AraC | 0.808 | 0.0147 | 8.79 | 0.0925 |
| CI | (0.804, 0.839) | (0.0131, 0.999) | (0.000544, 8.77) | (0.0847, 1.62) |
| 250 nM AraC | 0.788 | 0.0113 | 3.44 | 0.0826 |
| CI | (0.781, 0.793) | (0.000983, 0.0131) | (0.133, 6.83) | (0.0746, 0.0826) |
| 125 nM AraC | 0.753 | 0.0184 | 2.06 | 0.226 |
| CI | (0.749, 0.759) | (0.0165, 0.0202) | (0.802, 46.1) | (0.207, 0.226) |
| 62.5 nM AraC | 0.734 | 0.0141 | 0.300 | 0.212 |
| CI | (0.724, 0.735) | (0.0118, 0.0151) | (1.02 , 6.33) | (0.193, 0.232) |
| 0 nM AraC | 0.727 | 0.0144 | 2.99 | 0.219 |
| CI | (0.720, 0.735) | (0.0126, 0.0178) | (0.00330, 6.40) | (0.198, 0.243) |
| Dosage | (/min) | (min) | (/cell) | SSR | |
|---|---|---|---|---|---|
| 10 M AraC | 0.165 | 2.73 | 176 | 2.94 | |
| CI | (0.162, 0.169) | (5.75, 60.8) | (6.08 , 6.29) | (167, 185) | (2.27, 2.99) |
| 320 nM AraC | 0.119 | 3.43 | 104 | 1.97 | |
| CI | (0.118, 0.121) | (7.12, 8.21) | (0.880, 5.29) | (83.8, 115) | (1.52, 2.32) |
| 160 nM AraC | 0.779 | 19.9 | 4.08 | 9.35 | |
| CI | (0.0562, 0.783) | (1.17, 8.80) | (2.69 , 21.2) | (1.78, 417) | (6.57, 36.9) |
| 80 nM AraC | 0.795 | 42.1 | 5.57 | 1.92 | |
| CI | (2.70 , 0.815) | (0.0959, 36.5) | (6.29 , 48.0) | (1.84 , 16,300) | (1.47, 12.4) |
| 40 nM AraC | 0.790 | 43.0 | 4.89 | 3.85 | |
| CI | (8.89 , 0.808) | (0.115, 62.3) | (8.86 , 49.9) | (7.72 , 13,800) | (2.85, 184) |
| 20 nM AraC | 0.791 | 43.7 | 3.93 | 4.09 | |
| CI | (2.44 , 0.804) | (0.121, 57.2) | (7.46 , 69.4) | (1.28 , 8530) | (2.92, 333) |
| 10 nM AraC | 0.785 | 39.7 | 5.55 | 3.91 | |
| CI | (5.43 , 0.802) | (0.137, 74.7) | (7.21 , 46.9) | (0.608, 15,200) | (2.82, 147) |
| 5 nM AraC | 0.783 | 38.5 | 4.69 | 4.59 | |
| CI | (6.50 , 0.798) | (0.153, 99.9) | (6.11 , 48.3) | (2.76 , 13,600) | (3.31, 181) |
| 2.5 nM AraC | 0.755 | 38.4 | 9.51 | 4.08 | |
| CI | (4.02 , 0.784) | (0.138, 55.5) | (7.10 , 41.2) | (2.54, 11,300) | (2.98, 22.7) |
| 0 nM AraC | 0.778 | 41.2 | 3.42 | 5.41 | |
| CI | (0.00154, 0.789) | (0.152, 77.3) | (1.12 , 46.8) | (2.78 , 13,700) | (3.79, 204) |
| Dosage | (/min) | (min) | (/cell) | SSR | |
|---|---|---|---|---|---|
| 10 M AraC | 3.51 | 0.340 | 17,700 | 3.94 | |
| 95% CI | (3.33, 4.01) | (3.57, 4.00) | (0.0857, 7.54) | (16,200, 21,500) | (3.69, 4.93) |
| 2 M AraC | 1.87 | 0.0368 | 31,700 | 2.97 | |
| 95% CI | (1.73, 2.06) | (4.25, 4.66) | (0.0251, 0.0537) | (28,500, 37,900) | (2.77, 3.17) |
| 750 nM AraC | 7.41 | 9.16 | 3650 | 4.15 | |
| 95% CI | (7.34, 7.59) | (1.43, 1.58) | (6.69, 11.5) | (3500, 4360) | (3.87, 4.18) |
| 500 nM AraC | 0.0415 | 5.92 | 2380 | 5.23 | |
| 95% CI | (0.0369, 0.0455) | (6.16, 8.14) | (4.95, 7.03) | (1990, 2820) | (4.66, 5.22) |
| 375 nM AraC | 0.0497 | 9.15 | 3870 | 0.0621 | |
| 95% CI | (0.0480, 0.080) | (2.28, 26.5) | (0.945, 9.72) | (3310, 12,700) | (5.56, 92.5) |
| 250 nM AraC | 0.0320 | 18.8 | 2290 | 0.0184 | |
| 95% CI | (0.0298, 0.0354) | (9.24, 14.4) | (16.5, 20.6) | (2010, 3250) | (0.0165, 0.0381) |
| 125 nM AraC | 0.0653 | 9.49 | 4020 | 6.15 | |
| 95% CI | (0.0643, 0.0685) | (5.25, 5.84) | (9.11, 9.86) | (3610, 4300) | (5.49, 6.15) |
| 62.5 nM AraC | 0.0451 | 19.8 | 2210 | 0.0518 | |
| 95% CI | (0.0410, 0.0510) | (1.87, 2.37) | (17.6, 21.4) | (1860, 2960) | (0.0464, 0.0526) |
| 0 nM AraC | 0.0682 | 19.3 | 1470 | 0.0493 | |
| 95% CI | (0.0417, 0.0789) | (2.13, 31.8) | (1.43, 20.7) | (1250, 15,900) | (0.0443, 0.368) |
| HXB2 | Sf162 | ||||
|---|---|---|---|---|---|
| Dosage | Basic AIC | DD AIC | Dosage | Basic AIC | D.D AIC |
| 10 M | −219 | −227 | 10 M | −701 | −709 |
| 320 nM | −231 | −235 | 2 M | −641 | −653 |
| 160 M | −203 | −202 | 750 nM | −639 | −706 |
| 80 nM | −188 | −187 | 500 nM | −513 | −636 |
| 40 nM | −175 | −173 | 375 nM | −423 | −625 |
| 20 nM | −173 | −171 | 250 nM | −489 | −597 |
| 10 nM | −173 | −172 | 125 nM | −382 | −626 |
| 5 nM | −170 | −169 | 62.5 nM | −420 | −521 |
| 2.5 nM | −169 | −171 | 0 nM | −411 | −517 |
| 0 nM | −167 | −166 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gerg, A.; Dobrovolny, H.M. Quantifying Impact of HIV Receptor Surface Density Reveals Differences in Fusion Dynamics of HIV Strains. Viruses 2025, 17, 583. https://doi.org/10.3390/v17040583
Gerg A, Dobrovolny HM. Quantifying Impact of HIV Receptor Surface Density Reveals Differences in Fusion Dynamics of HIV Strains. Viruses. 2025; 17(4):583. https://doi.org/10.3390/v17040583
Chicago/Turabian StyleGerg, Anthony, and Hana M. Dobrovolny. 2025. "Quantifying Impact of HIV Receptor Surface Density Reveals Differences in Fusion Dynamics of HIV Strains" Viruses 17, no. 4: 583. https://doi.org/10.3390/v17040583
APA StyleGerg, A., & Dobrovolny, H. M. (2025). Quantifying Impact of HIV Receptor Surface Density Reveals Differences in Fusion Dynamics of HIV Strains. Viruses, 17(4), 583. https://doi.org/10.3390/v17040583







