Mathematical Modeling Finds Disparate Interferon Production Rates Drive Strain-Specific Immunodynamics during Deadly Influenza Infection
Abstract
:1. Introduction
2. Materials and Methods
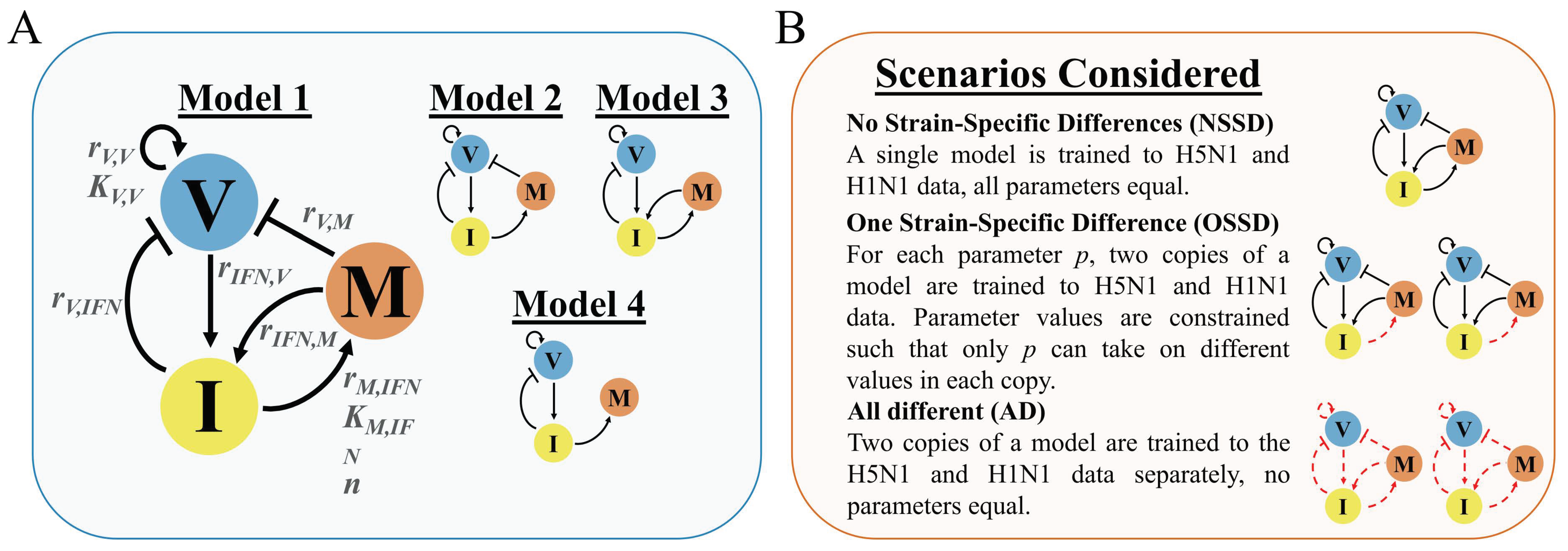
2.1. Model Development Rationale and Equations
2.2. Experimental Data Collected from Literature and Relating the Data to the Model
2.3. Parameter Training
2.4. Model and Scenario Prioritization
2.5. Sensitivity Analysis
3. Results
3.1. In Silico Screenings of Candidate Innate Immune Models Find That H5N1 and H1N1 Viruses Induce Interferon Production at Different Rates In Vivo
3.2. Strain-Specific Interferon Production Is Not an Artifact of Parameter Sensitivity
3.3. Deep Exploration of Model 4’s Parameter Space Using PT MCMC
3.4. MCMC-Based Parameter Exploration Again Finds That H5N1 and H1N1 Viruses Induce Interferon Production at Different Rates In Vivo
3.5. Independent Estimation of Virus Parameters per Strain Does Not Improve Model AIC
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Parameter | H1N1 | H5N1 | Unit |
|---|---|---|---|
| 1.22 | 1.21 | ||
| 3.65 × 101 | 7.80 × 102 | ||
| 1.20 × 10−1 | 1.07 × 10−1 | ||
| 1.61 × 10−1 | 1.10 × 10−5 | ||
| 7.70 × 10−1 | 3.06 | ||
| 9.59 × 10−1 | 3.22 | ||
| 2.16 × 107 | 9.71 × 103 | ||
| 1.90 × 105 | 1.04 × 109 | unitless | |
| 8.80 × 103 | 6.18 × 10−1 | ||
| 5.47 | 9.98 | unitless | |
| N/A | |||
| N/A | |||
References
- Shoemaker, J.E.; Fukuyama, S.; Eisfeld, A.J.; Zhao, D.; Kawakami, E.; Sakabe, S.; Maemura, T.; Gorai, T.; Katsura, H.; Muramoto, Y.; et al. An Ultrasensitive Mechanism Regulates Influenza Virus-Induced Inflammation. PLoS Pathog. 2015, 11, e1004856. [Google Scholar] [CrossRef] [Green Version]
- 2016–2017 Estimated Influenza Illnesses, Medical Visits, Hospitalizations, and Deaths Averted by Vaccination in the United States|CDC. Available online: https://www.cdc.gov/flu/vaccines-work/burden-averted-2016-17.htm (accessed on 2 March 2022).
- Kawaoka, Y. H5N1: Flu Transmission Work Is Urgent. Nature 2012, 482, 155. [Google Scholar] [CrossRef]
- CDC Highly Pathogenic Asian Avian Influenza A(H5N1) in People|Avian Influenza (Flu). Available online: https://www.cdc.gov/flu/avianflu/avian-in-humans.htm (accessed on 2 March 2022).
- Guarner, J.; Falcón-Escobedo, R. Comparison of the Pathology Caused by H1N1, H5N1, and H3N2 Influenza Viruses. Arch. Med. Res. 2009, 40, 655–661. [Google Scholar] [CrossRef] [PubMed]
- Boon, A.C.M.; Finkelstein, D.; Zheng, M.; Liao, G.; Allard, J.; Klumpp, K.; Webster, R.; Peltz, G.; Webby, R.J. H5N1 Influenza Virus Pathogenesis in Genetically Diverse Mice Is Mediated at the Level of Viral Load. mBio 2011, 2, e00171-11. [Google Scholar] [CrossRef] [Green Version]
- Hale, B.G.; Randall, R.E.; Ortin, J.; Jackson, D. The Multifunctional NS1 Protein of Influenza A Viruses. J. Gen. Virol. 2008, 89, 2359–2376. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Liu, S.; Chen, Z.J. SnapShot: Pathways of Antiviral Innate Immunity. Cell 2010, 140, 436–436.e2. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, W.; Wang, G.; Zhang, H.; Xin, G.; Zhang, D.; Zeng, J.; Chen, X.; Xu, Y.; Cui, Y.; Li, K. Effects of NS1 Variants of H5N1 Influenza Virus on Interferon Induction, TNFα Response and P53 Activity. Cell. Mol. Immunol. 2010, 7, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Mok, B.W.-Y.; Liu, H.; Chen, P.; Liu, S.; Lau, S.-Y.; Huang, X.; Liu, Y.-C.; Wang, P.; Yuen, K.-Y.; Chen, H. The Role of Nuclear NS1 Protein in Highly Pathogenic H5N1 Influenza Viruses. Microbes Infect. 2017, 19, 587–596. [Google Scholar] [CrossRef]
- Cheung, C.Y.; Poon, L.L.M.; Lau, A.S.; Luk, W.; Lau, Y.L.; Shortridge, K.F.; Gordon, S.; Guan, Y.; Peiris, J.S.M. Induction of Proinflammatory Cytokines in Human Macrophages by Influenza A (H5N1) Viruses: A Mechanism for the Unusual Severity of Human Disease? Lancet 2002, 360, 1831–1837. [Google Scholar] [CrossRef]
- van Riel, D.; Leijten, L.M.E.; van der Eerden, M.; Hoogsteden, H.C.; Boven, L.A.; Lambrecht, B.N.; Osterhaus, A.D.M.E.; Kuiken, T. Highly Pathogenic Avian Influenza Virus H5N1 Infects Alveolar Macrophages without Virus Production or Excessive TNF-Alpha Induction. PLoS Pathog. 2011, 7, e1002099. [Google Scholar] [CrossRef] [Green Version]
- Mochan, E.; Ackerman, E.; Shoemaker, J. A Systems and Treatment Perspective of Models of Influenza Virus-Induced Host Responses. Processes 2018, 6, 138. [Google Scholar] [CrossRef] [Green Version]
- Smith, A.M. Validated Models of Immune Response to Virus Infection. Curr. Opin. Syst. Biol. 2018, 12, 46–52. [Google Scholar] [CrossRef] [PubMed]
- Pawelek, K.A.; Huynh, G.T.; Quinlivan, M.; Cullinane, A.; Rong, L.; Perelson, A.S. Modeling Within-Host Dynamics of Influenza Virus Infection Including Immune Responses. PLoS Comput. Biol. 2012, 8, e1002588. [Google Scholar] [CrossRef] [Green Version]
- Price, I.; Mochan-Keef, E.D.; Swigon, D.; Ermentrout, G.B.; Lukens, S.; Toapanta, F.R.; Ross, T.M.; Clermont, G. The Inflammatory Response to Influenza A Virus (H1N1): An Experimental and Mathematical Study. J. Theor. Biol. 2015, 374, 83–93. [Google Scholar] [CrossRef] [Green Version]
- Gregg, R.W.; Sarkar, S.N.; Shoemaker, J.E. Mathematical Modeling of the CGAS Pathway Reveals Robustness of DNA Sensing to TREX1 Feedback. J. Theor. Biol. 2019, 462, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Pawelek, K.A.; Dor, D.; Salmeron, C.; Handel, A. Within-Host Models of High and Low Pathogenic Influenza Virus Infections: The Role of Macrophages. PLoS ONE 2016, 11, e0150568. [Google Scholar] [CrossRef]
- Weaver, J.J.A.; Shoemaker, J.E. Mathematical Modeling of Rna Virus Sensing Pathways Reveals Paracrine Signaling as the Primary Factor Regulating Excessive Cytokine Production. Processes 2020, 8, 719. [Google Scholar] [CrossRef]
- Smith, A.M.; Adler, F.R.; Ribeiro, R.M.; Gutenkunst, R.N.; McAuley, J.L.; McCullers, J.A.; Perelson, A.S. Kinetics of Coinfection with Influenza A Virus and Streptococcus Pneumoniae. PLoS Pathog. 2013, 9, e1003238. [Google Scholar] [CrossRef] [Green Version]
- Gregg, R.W.; Shabnam, F.; Shoemaker, J.E. Agent-Based Modeling Reveals Benefits of Heterogeneous and Stochastic Cell Populations during CGAS-Mediated IFNβ Production. Bioinformatics 2021, 37, 1428–1434. [Google Scholar] [CrossRef]
- Aponte-Serrano, J.O.; Weaver, J.J.A.; Sego, T.J.; Glazier, J.A.; Shoemaker, J.E. Multicellular Spatial Model of RNA Virus Replication and Interferon Responses Reveals Factors Controlling Plaque Growth Dynamics. PLoS Comput. Biol. 2021, 17, e1008874. [Google Scholar] [CrossRef]
- Hernandez-Vargas, E.A.; Wilk, E.; Canini, L.; Toapanta, F.R.; Binder, S.C.; Uvarovskii, A.; Ross, T.M.; Guzman, C.A.; Perelson, A.S.; Meyer-Hermann, M. Effects of Aging on Influenza Virus Infection Dynamics. J. Virol. 2014, 88, 4123–4131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peiris, J.S.M.; Cheung, C.Y.; Leung, C.Y.H.; Nicholls, J.M. Innate Immune Responses to Influenza A H5N1: Friend or Foe? Trends Immunol. 2009, 30, 574–584. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shinya, K.; Ito, M.; Makino, A.; Tanaka, M.; Miyake, K.; Eisfeld, A.J.; Kawaoka, Y. The TLR4-TRIF Pathway Protects against H5N1 Influenza Virus Infection. J. Virol. 2012, 86, 19–24. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neumann, G.; Chen, H.; Gao, G.F.; Shu, Y.; Kawaoka, Y. H5N1 Influenza Viruses: Outbreaks and Biological Properties. Cell Res. 2010, 20, 51–61. [Google Scholar] [CrossRef] [Green Version]
- Shinya, K.; Gao, Y.; Cilloniz, C.; Suzuki, Y.; Fujie, M.; Deng, G.; Zhu, Q.; Fan, S.; Makino, A.; Muramoto, Y.; et al. Integrated Clinical, Pathologic, Virologic, and Transcriptomic Analysis of H5N1 Influenza Virus-Induced Viral Pneumonia in the Rhesus Macaque. J. Virol. 2012, 86, 6055–6066. [Google Scholar] [CrossRef] [Green Version]
- Muramoto, Y.; Shoemaker, J.E.; Mai, L.T.Q.; Itoh, Y.; Tamura, D.; Sakai-Tagawa, Y.; Imai, H.; Uraki, R.; Takano, R.; Kawakami, E.; et al. Disease Severity Is Associated with Differential Gene Expression at the Early and Late Phases of Infection in Non-Human Primates Infected with Different H5N1 Highly Pathogenic Avian Influenza Viruses. J. Virol. 2014, 88, 8981–8997. [Google Scholar] [CrossRef] [Green Version]
- Kobasa, D.; Jones, S.M.; Shinya, K.; Kash, J.C.; Copps, J.; Ebihara, H.; Hatta, Y.; Kim, J.H.; Halfmann, P.; Hatta, M.; et al. Aberrant Innate Immune Response in Lethal Infection of Macaques with the 1918 Influenza Virus. Nature 2007, 445, 319–323. [Google Scholar] [CrossRef]
- Diamond, G.; Legarda, D.; Ryan, L.K. The Innate Immune Response of the Respiratory Epithelium. Immunol. Rev. 2000, 173, 27–38. [Google Scholar] [CrossRef]
- Koyama, S.; Ishii, K.J.; Coban, C.; Akira, S. Innate Immune Response to Viral Infection. Cytokine 2008, 43, 336–341. [Google Scholar] [CrossRef]
- Petes, C.; Odoardi, N.; Gee, K. The Toll for Trafficking: Toll-like Receptor 7 Delivery to the Endosome. Front. Immunol. 2017, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Rehwinkel, J.; Gack, M.U. RIG-I-like Receptors: Their Regulation and Roles in RNA Sensing. Nat. Rev. Immunol. 2020, 20, 537–551. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Zhang, L.; Joo, D.; Sun, S.C. NF-ΚB Signaling in Inflammation. Signal Transduct. Target. Ther. 2017, 2, e17023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rajsbaum, R.; Albrecht, R.A.; Wang, M.K.; Maharaj, N.P.; Versteeg, G.A.; Nistal-Villán, E.; García-Sastre, A.; Gack, M.U. Species-Specific Inhibition of RIG-I Ubiquitination and IFN Induction by the Influenza A Virus NS1 Protein. PLoS Pathog. 2012, 8, e1003059. [Google Scholar] [CrossRef] [PubMed]
- Gack, M.U.; Albrecht, R.A.; Urano, T.; Inn, K.S.; Huang, I.C.; Carnero, E.; Farzan, M.; Inoue, S.; Jung, J.U.; García-Sastre, A. Influenza A Virus NS1 Targets the Ubiquitin Ligase TRIM25 to Evade Recognition by the Host Viral RNA Sensor RIG-I. Cell Host Microbe 2009, 5, 439–449. [Google Scholar] [CrossRef] [Green Version]
- Koyama, S.; Ishii, K.J.; Kumar, H.; Tanimoto, T.; Coban, C.; Uematsu, S.; Kawai, T.; Akira, S. Differential Role of TLR- and RLR-Signaling in the Immune Responses to Influenza A Virus Infection and Vaccination. J. Immunol. 2007, 179, 4711–4720. [Google Scholar] [CrossRef]
- Zeng, H.; Goldsmith, C.; Thawatsupha, P.; Chittaganpitch, M.; Waicharoen, S.; Zaki, S.; Tumpey, T.M.; Katz, J.M. Highly Pathogenic Avian Influenza H5N1 Viruses Elicit an Attenuated Type I Interferon Response in Polarized Human Bronchial Epithelial Cells. J. Virol. 2007, 81, 12439–12449. [Google Scholar] [CrossRef] [Green Version]
- Channappanavar, R.; Fehr, A.R.; Zheng, J.; Wohlford-Lenane, C.; Abrahante, J.E.; Mack, M.; Sompallae, R.; McCray, P.B.; Meyerholz, D.K.; Perlman, S. IFN-I Response Timing Relative to Virus Replication Determines MERS Coronavirus Infection Outcomes. J. Clin. Investig. 2019, 129, 3625–3639. [Google Scholar] [CrossRef]
- Galani, I.E.; Rovina, N.; Lampropoulou, V.; Triantafyllia, V.; Manioudaki, M.; Pavlos, E.; Koukaki, E.; Fragkou, P.C.; Panou, V.; Rapti, V.; et al. Untuned Antiviral Immunity in COVID-19 Revealed by Temporal Type I/III Interferon Patterns and Flu Comparison. Nat. Immunol. 2021, 22, 32–40. [Google Scholar] [CrossRef]
- Lee, J.; Adler, F.R.; Kim, P.S. A Mathematical Model for the Macrophage Response to Respiratory Viral Infection in Normal and Asthmatic Conditions. Bull. Math. Biol. 2017, 79, 1979–1998. [Google Scholar] [CrossRef]
- Kumagai, Y.; Takeuchi, O.; Kato, H.; Kumar, H.; Matsui, K.; Morii, E.; Aozasa, K.; Kawai, T.; Akira, S. Alveolar Macrophages Are the Primary Interferon-Alpha Producer in Pulmonary Infection with RNA Viruses. Immunity 2007, 27, 240–252. [Google Scholar] [CrossRef] [Green Version]
- Weiss, J.N. The Hill Equation Revisited: Uses and Misuses. FASEB J. 1997, 11, 835–841. [Google Scholar] [CrossRef] [PubMed]
- Waldrop, S.L.; Davis, K.A.; Maino, V.C.; Picker, L.J. Normal Human CD4+ Memory T Cells Display Broad Heterogeneity in Their Activation Threshold for Cytokine Synthesis. J. Immunol. 1998, 161, 5284–5295. [Google Scholar] [PubMed]
- Itoh, Y.; Germain, R.N. Single Cell Analysis Reveals Regulated Hierarchical T Cell Antigen Receptor Signaling Thresholds and Intraclonal Heterogeneity for Individual Cytokine Responses of CD4+ T Cells. J. Exp. Med. 1997, 186, 757–766. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dawson, T.C.; Beck, M.A.; Kuziel, W.A.; Henderson, F.; Maeda, N. Contrasting Effects of CCR5 and CCR2 Deficiency in the Pulmonary Inflammatory Response to Influenza A Virus. Am. J. Pathol. 2000, 156, 1951–1959. [Google Scholar] [CrossRef] [Green Version]
- Lin, K.L.; Suzuki, Y.; Nakano, H.; Ramsburg, E.; Gunn, M.D. CCR2 + Monocyte-Derived Dendritic Cells and Exudate Macrophages Produce Influenza-Induced Pulmonary Immune Pathology and Mortality. J. Immunol. 2008, 180, 2562–2572. [Google Scholar] [CrossRef] [Green Version]
- Wales, D.J.; Doye, J.P.K. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef] [Green Version]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Geyer, C.J. Markov Chain Monte Carlo Maximum Likelihood, Computing Science and Statistics. In Proceedings of the 23rd Symposium Interface, Seattle, DC, USA, 21–24 April 1991; pp. 156–163. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef] [Green Version]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control. 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Saltelli, A.; Bolado, B. An Alternative Way to Compute Fourier Amplitude Sensitivity Test (FAST); Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A Methodology for Performing Global Uncertainty and Sensitivity Analysis in Systems Biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [Green Version]
- Herman, J.; Usher, W. SALib: An Open-Source Python Library for Sensitivity Analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Perrone, L.A.; Plowden, J.K.; García-Sastre, A.; Katz, J.M.; Tumpey, T.M. H5N1 and 1918 Pandemic Influenza Virus Infection Results in Early and Excessive Infiltration of Macrophages and Neutrophils in the Lungs of Mice. PLoS Pathog. 2008, 4, e1000115. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, W.C.L.; Chan, R.W.Y.; Wang, J.; Travanty, E.A.; Nicholls, J.M.; Peiris, J.S.M.; Mason, R.J.; Chan, M.C.W. Viral Replication and Innate Host Responses in Primary Human Alveolar Epithelial Cells and Alveolar Macrophages Infected with Influenza H5N1 and H1N1 Viruses. J. Virol. 2011, 85, 6844. [Google Scholar] [CrossRef] [Green Version]
- Mi, Z.; Ma, Y.; Tong, Y. Avian Influenza Virus H5N1 Induces Rapid Interferon-Beta Production but Shows More Potent Inhibition to Retinoic Acid-Inducible Gene i Expression than H1N1 in Vitro. Virol. J. 2012, 9, 145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cate, T.R. Clinical Manifestations and Consequences of Influenza. Am. J. Med. 1987, 82, 15–19. [Google Scholar] [CrossRef]
- Cromer, D.; van Hoek, A.J.; Jit, M.; Edmunds, W.J.; Fleming, D.; Miller, E. The Burden of Influenza in England by Age and Clinical Risk Group: A Statistical Analysis to Inform Vaccine Policy. J. Infect. 2014, 68, 363–371. [Google Scholar] [CrossRef] [Green Version]


| Scenario | Independent Parameter | Energy | DoF | AIC |
|---|---|---|---|---|
| NSSD | None | 15.04 | 10 | 50.08 |
| AD | All | 3.33 | 20 | 46.66 |
| OSSD | 10.83 | 11 | 43.66 | |
| 9.37 | 11 | 40.74 | ||
| 9.79 | 11 | 41.59 | ||
| 9.65 | 11 | 41.31 | ||
| 6.65 | 11 | 35.30 | ||
| 10.3 | 11 | 42.61 | ||
| 12.36 | 11 | 46.73 | ||
| 12.29 | 11 | 46.57 | ||
| 12.28 | 11 | 46.57 | ||
| 12.37 | 11 | 46.75 |
| Scenario | Independent Parameter | Energy | DoF | AIC |
|---|---|---|---|---|
| {V} | {V} | 9.34 | 14 | 46.68 |
| {V} + OSSD | 5.55 | 15 | 41.11 | |
| 8.38 | 15 | 46.75 | ||
| 8.86 | 15 | 47.72 | ||
| 8.89 | 15 | 47.79 | ||
| 8.92 | 15 | 47.85 | ||
| 8.89 | 15 | 47.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ackerman, E.E.; Weaver, J.J.A.; Shoemaker, J.E. Mathematical Modeling Finds Disparate Interferon Production Rates Drive Strain-Specific Immunodynamics during Deadly Influenza Infection. Viruses 2022, 14, 906. https://doi.org/10.3390/v14050906
Ackerman EE, Weaver JJA, Shoemaker JE. Mathematical Modeling Finds Disparate Interferon Production Rates Drive Strain-Specific Immunodynamics during Deadly Influenza Infection. Viruses. 2022; 14(5):906. https://doi.org/10.3390/v14050906
Chicago/Turabian StyleAckerman, Emily E., Jordan J. A. Weaver, and Jason E. Shoemaker. 2022. "Mathematical Modeling Finds Disparate Interferon Production Rates Drive Strain-Specific Immunodynamics during Deadly Influenza Infection" Viruses 14, no. 5: 906. https://doi.org/10.3390/v14050906
APA StyleAckerman, E. E., Weaver, J. J. A., & Shoemaker, J. E. (2022). Mathematical Modeling Finds Disparate Interferon Production Rates Drive Strain-Specific Immunodynamics during Deadly Influenza Infection. Viruses, 14(5), 906. https://doi.org/10.3390/v14050906







