Multiscale Model of Antiviral Timing, Potency, and Heterogeneity Effects on an Epithelial Tissue Patch Infected by SARS-CoV-2
Abstract
:1. Introduction
2. Materials and Methods
2.1. Remdesivir Physiologically Based Pharmacokinetic Model
2.2. Sego et al.’s Agent-Based Model
2.3. Viral Life Cycle Model
2.4. Remdesivir Mode of Action (MOA) Model
2.5. Heterogeneous Cellular Metabolism of Remdesivir Modeling
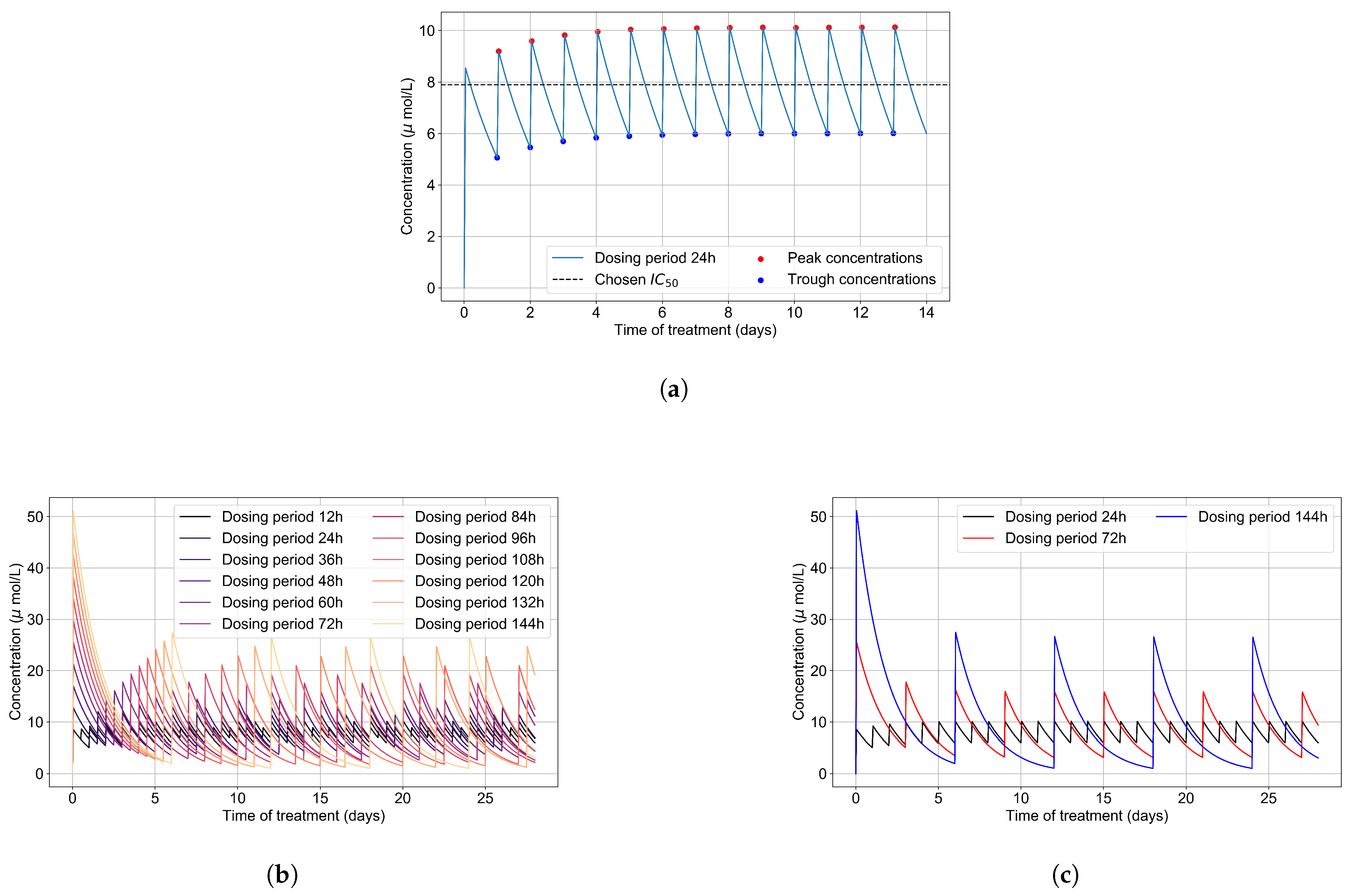
2.6. Simulating Antiviral Treatment Regimens and Treatment Classification Metrics
3. Results
3.1. Remdesivir PK Model
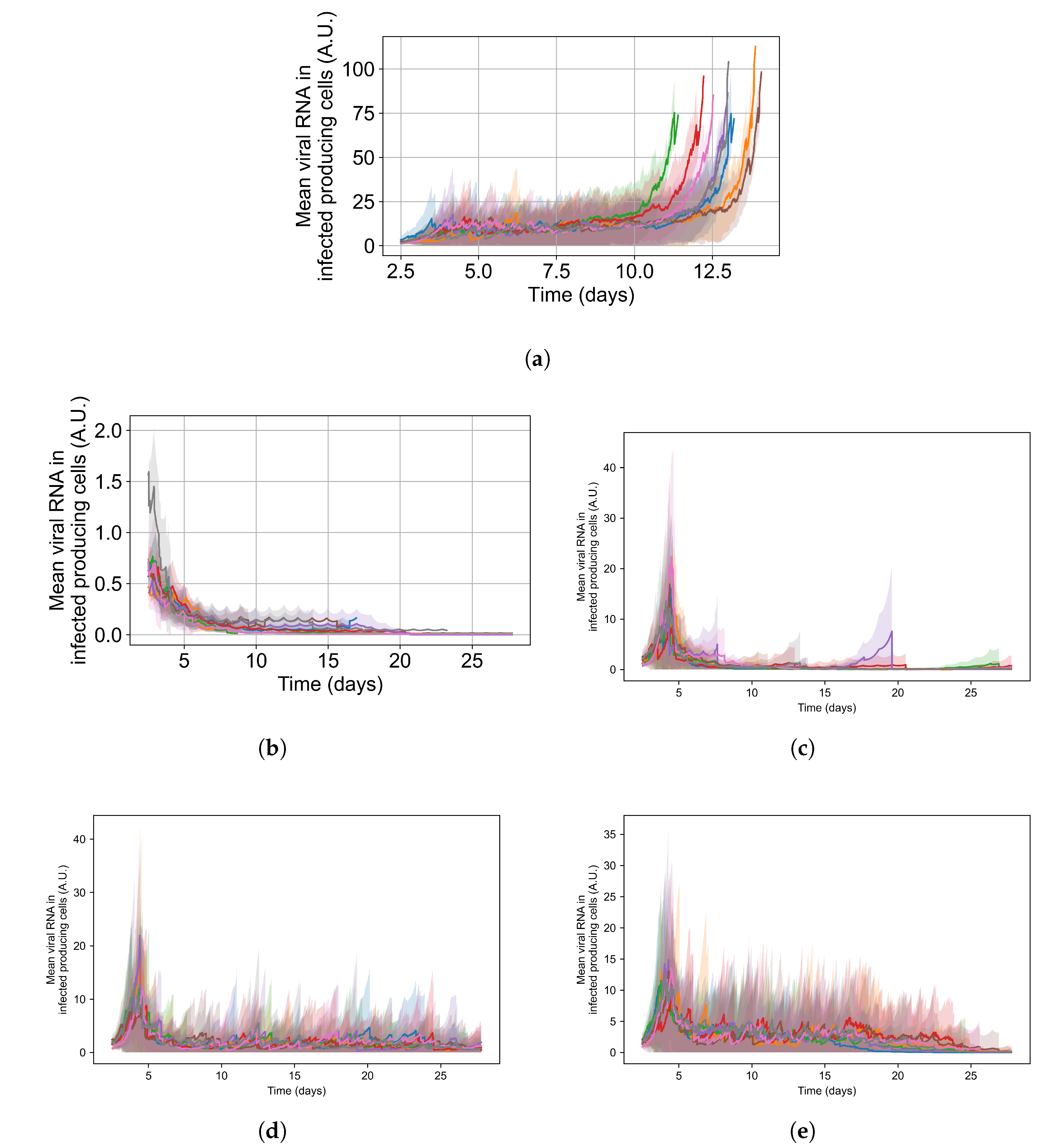
3.2. Variability of Outcomes in Sego’s Model
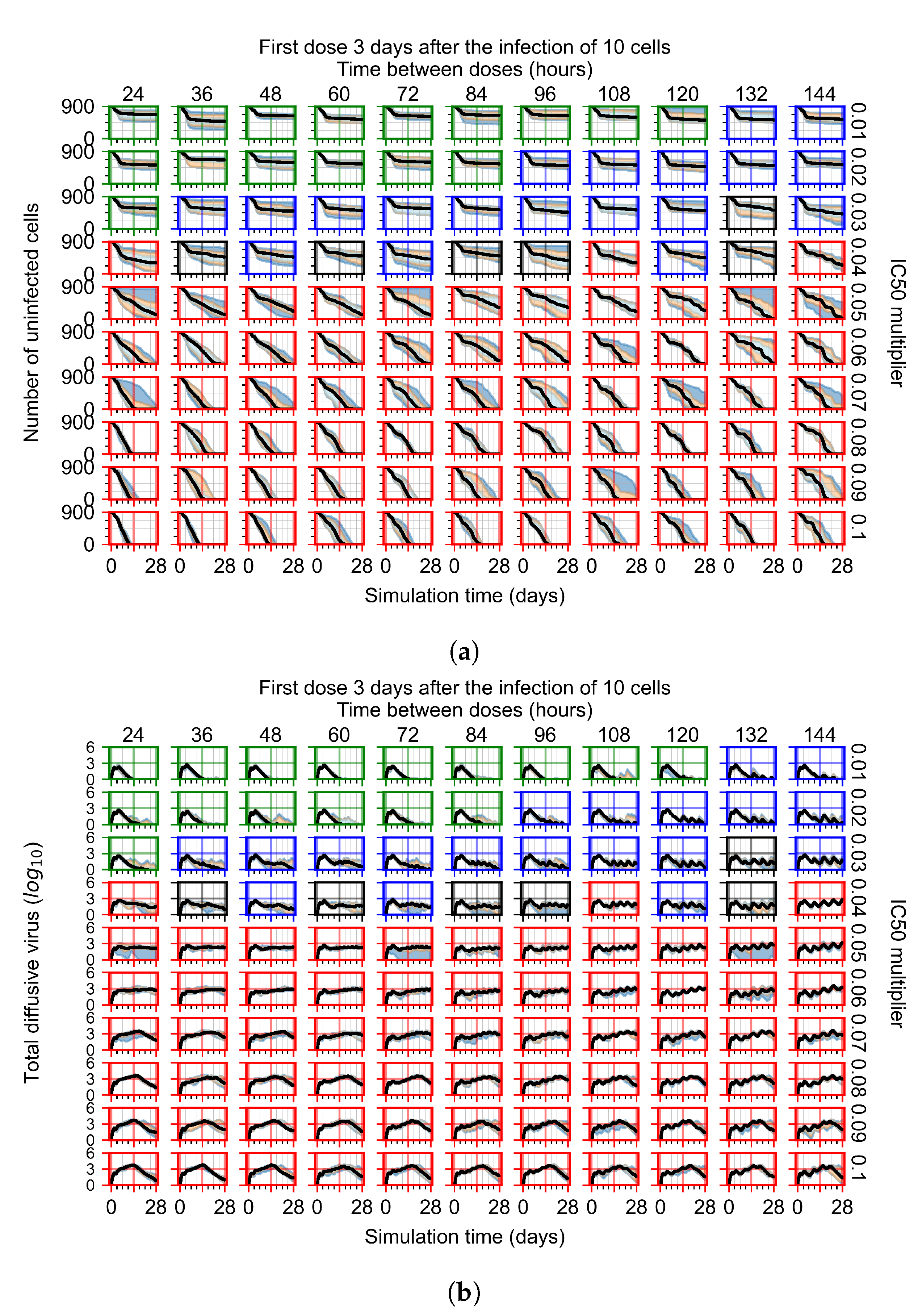
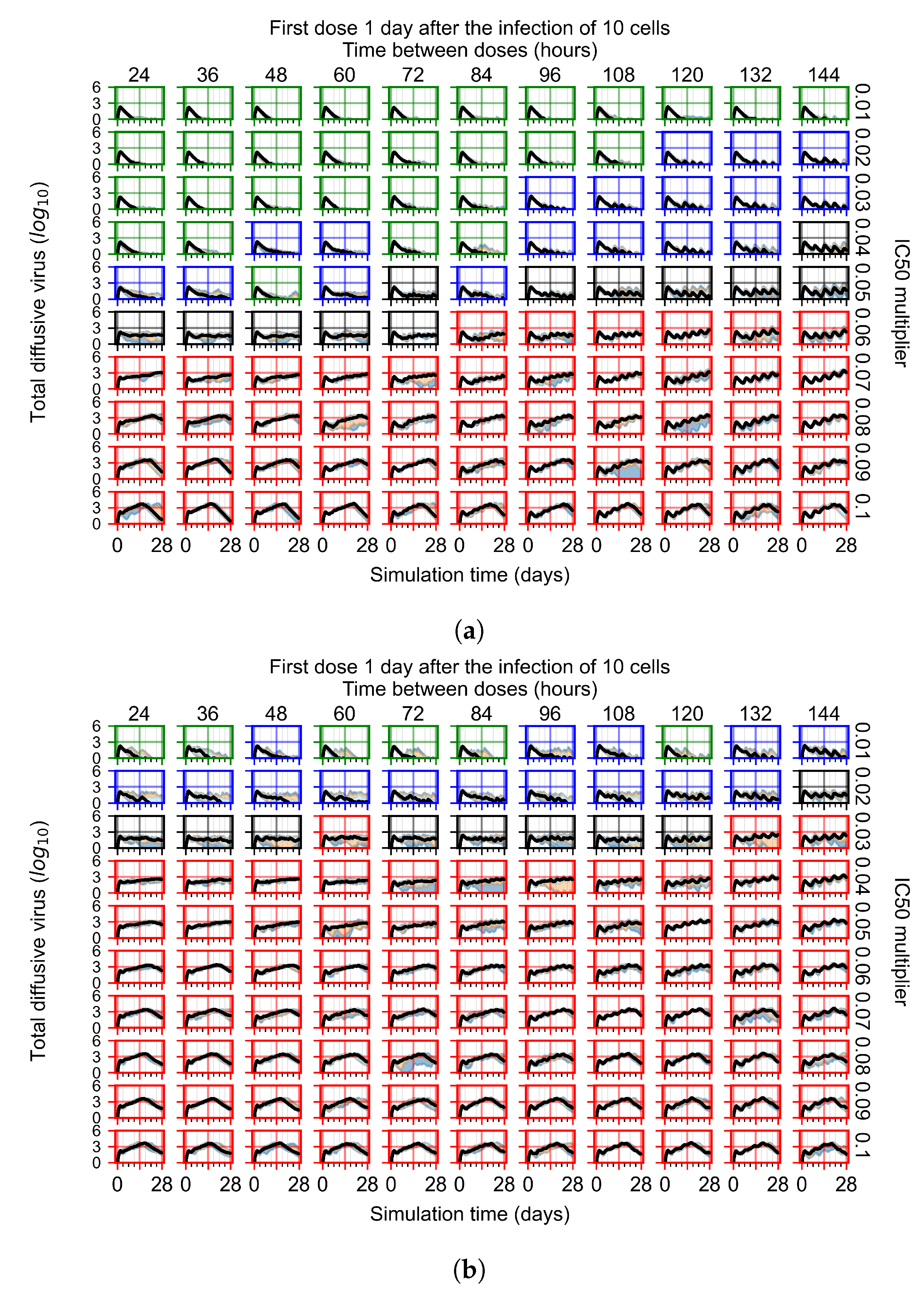
3.3. Predictive Treatment Outcomes
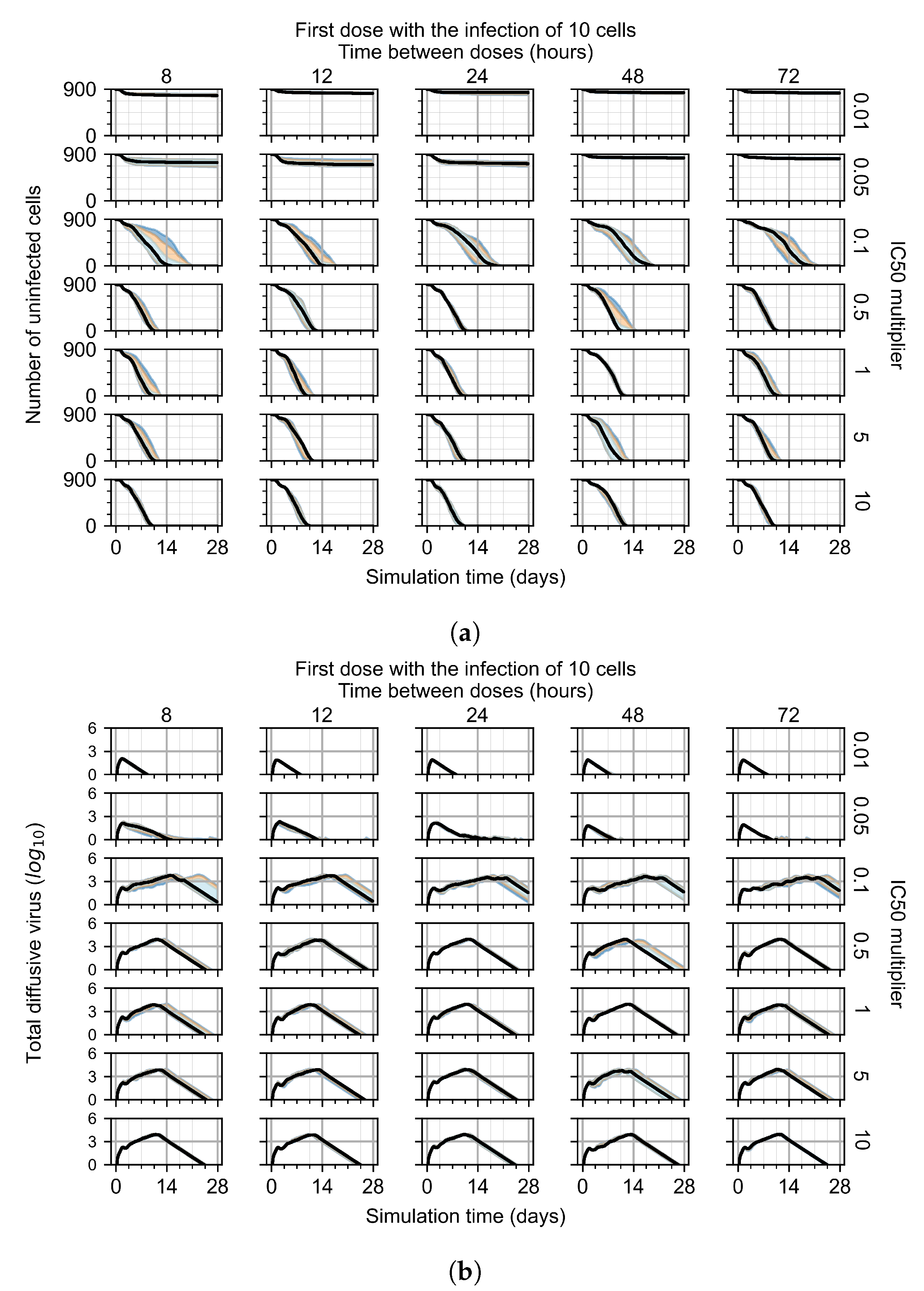
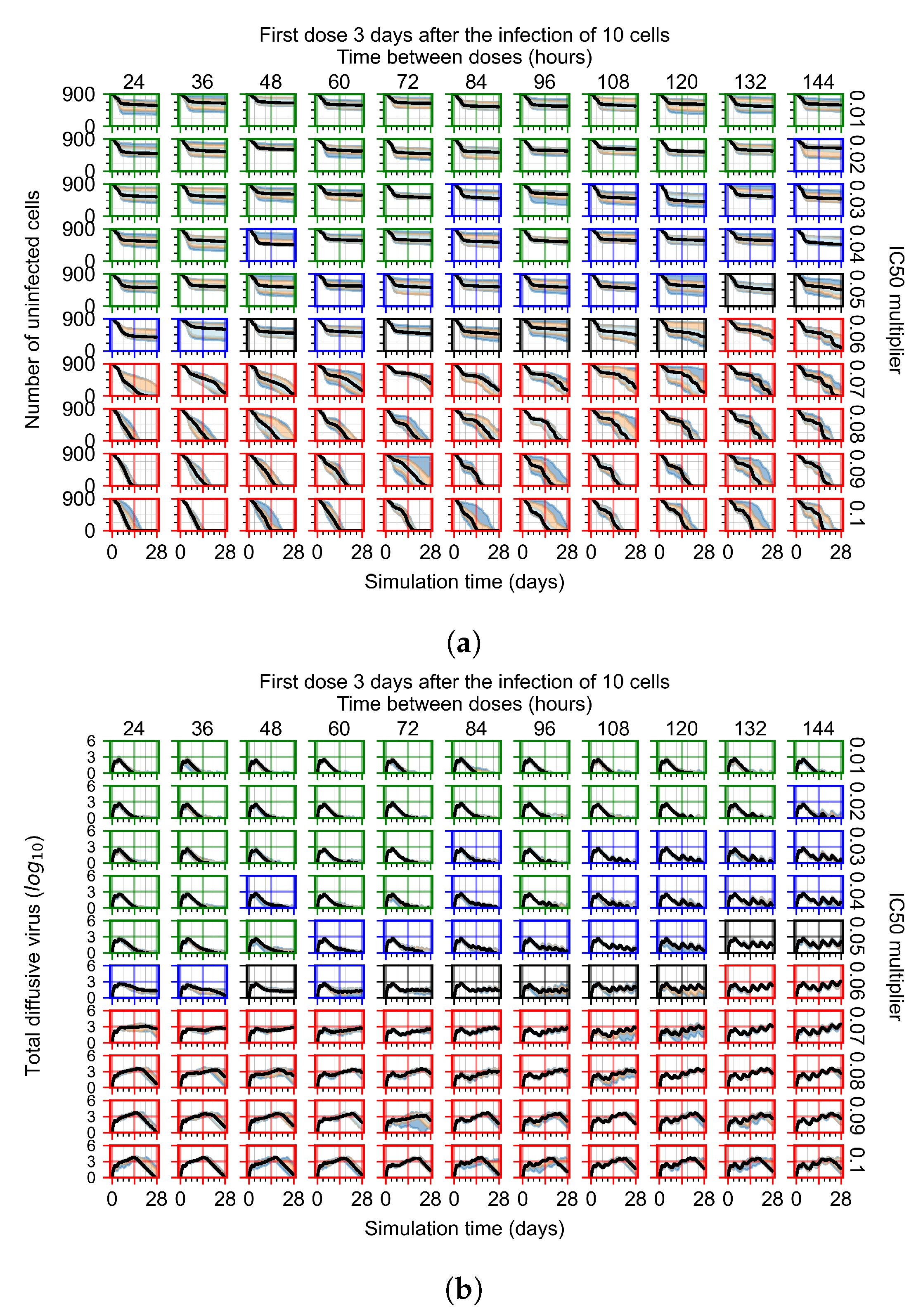
3.3.1. Coarse-Parameter Variation
3.3.2. Fine Parameter Variation
3.3.3. Faster Clearing Drug Necessitates More Potent Antiviral in Order to Contain the Infection
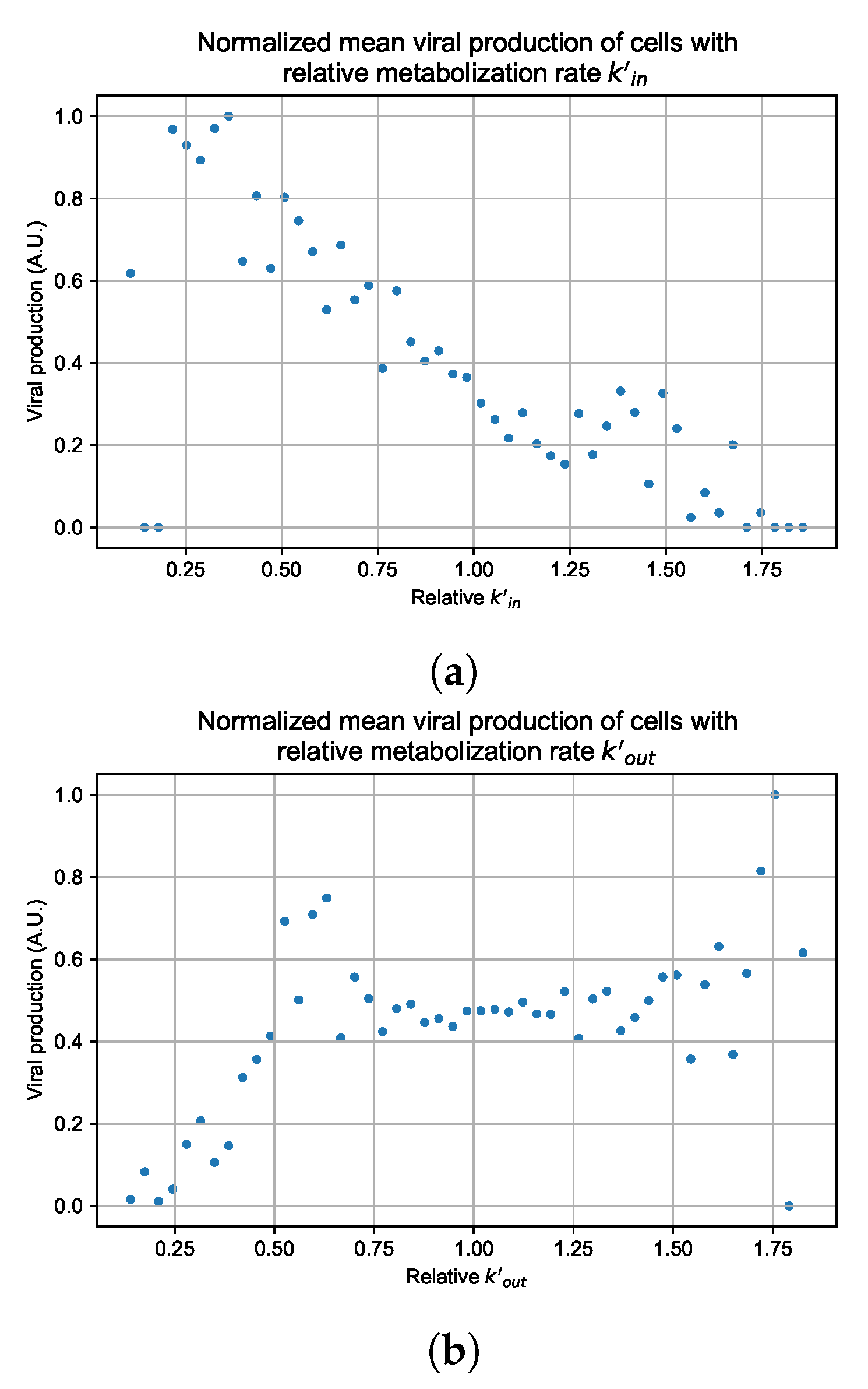
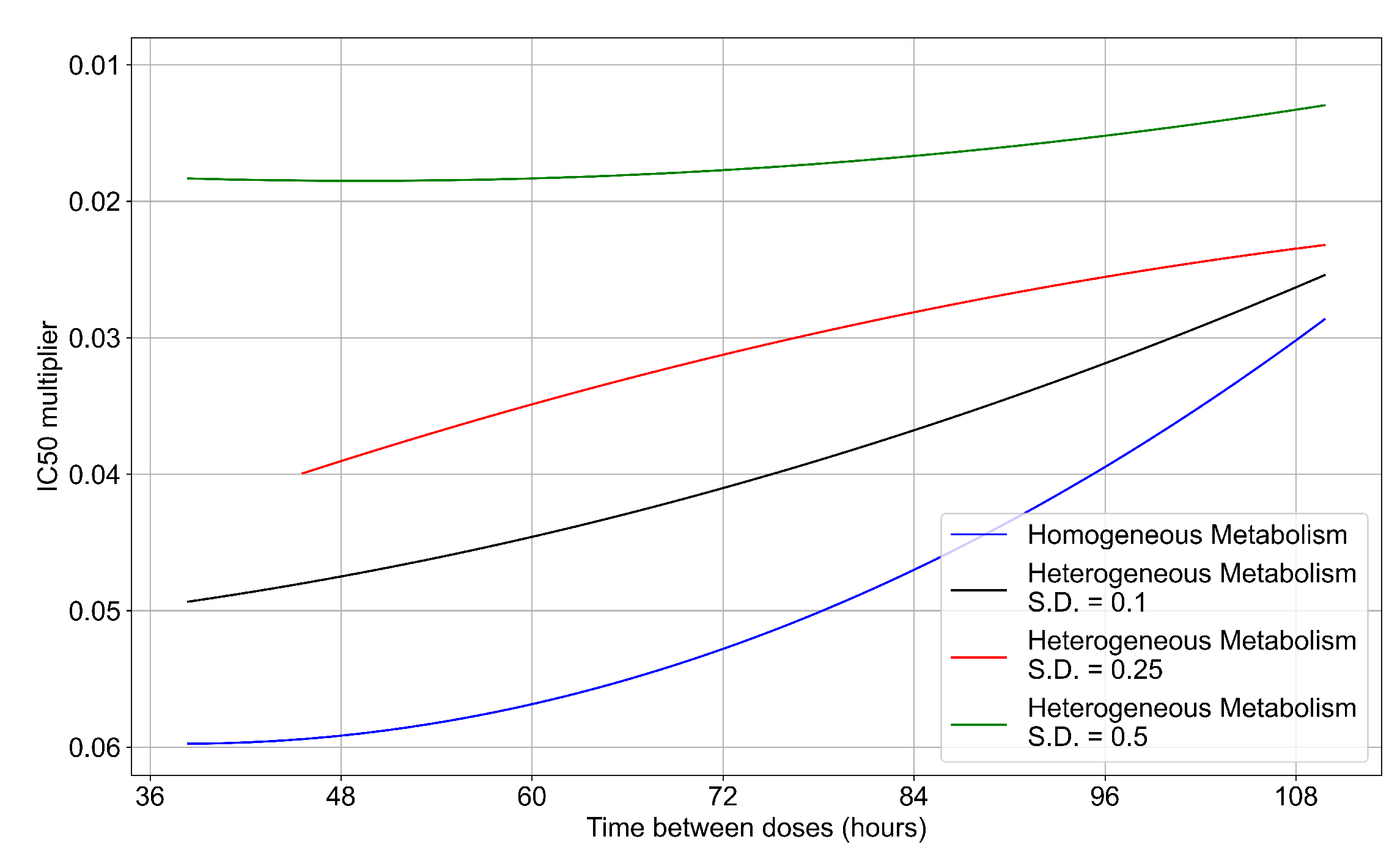
3.3.4. Heterogeneous Cellular Metabolism of Remdesivir Results
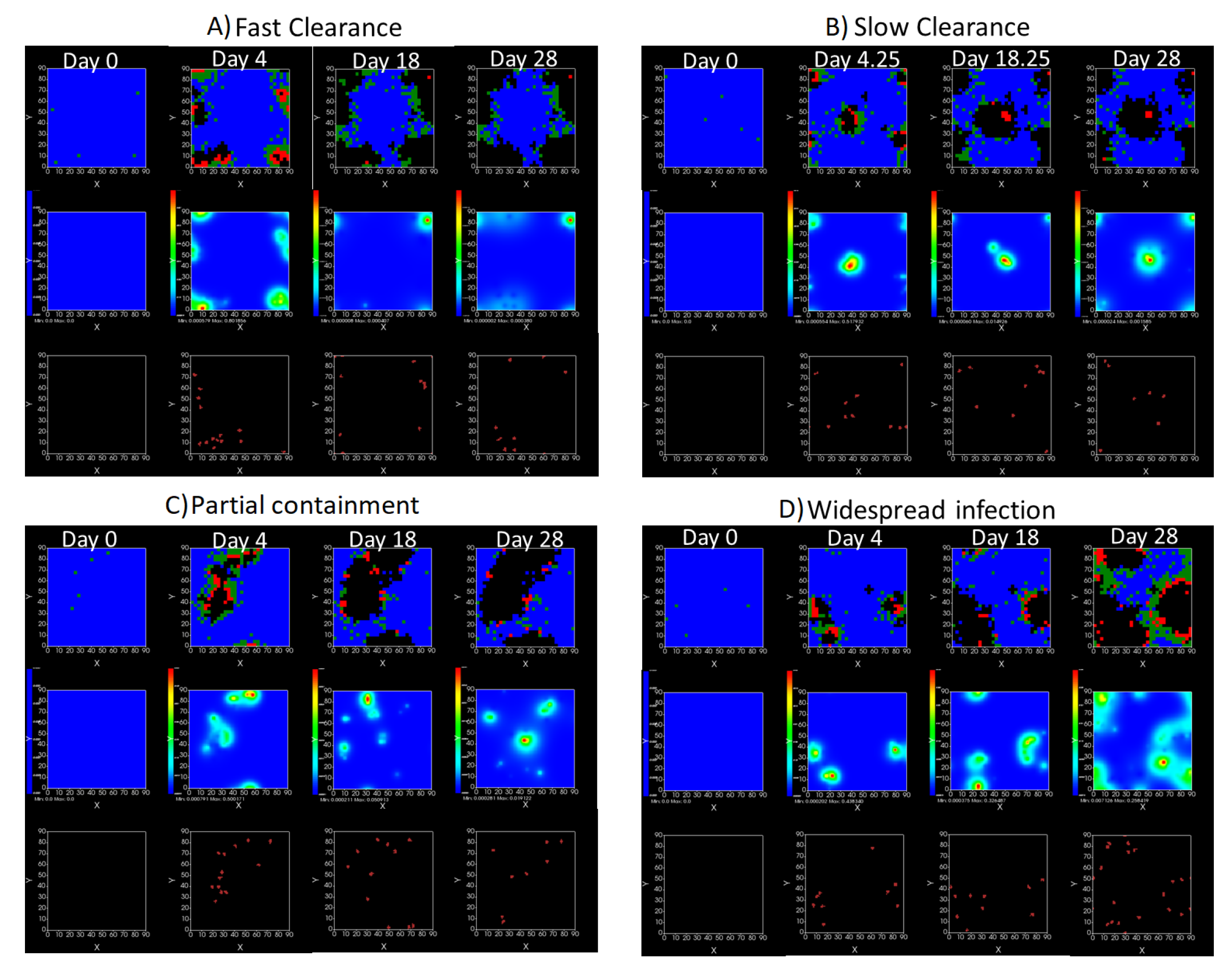
3.3.5. Factors Responsible for Negative Treatment Outcomes in the Heterogeneous Metabolism Model
- Rapid clearance: 24 h dose interval, 0.01 multiplier;
- Slow clearance: 120 h dose interval, 0.03 multiplier;
- Partial containment: 96 h dose interval, 0.06 multiplier;
- Widespread infection: 24 h dose interval, 0.1 multiplier.
3.3.6. Effects of Variability in Cellular Drug Metabolism on Treatment Outcomes
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABM | Agent-based model |
| COPASI | Complex Pathway Simulator |
| CPM | Cellular Potts model |
| EBOV | Ebola virus |
| GS-443902 | Remdesivir Triphosphate, CAS: 1355149-45-9, CHEBI:150869 |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MOA | Mechanism of action |
| ODE | Ordinary differential equation |
| PBMC | Peripheral blood mononuclear cells |
| PBPK | Physiological based pharmacokinetic model |
| PD | Pharmacodynamic model |
| PK | Pharmacokinetic model |
| RdRP | RNA-dependent RNA polymerase |
| SBML | Systems Biology Markup Language |
Appendix A. Simple PK Model for Remdesivir and GS-443902
| Parameter | Unit | Humeniuk * Cohort 7 | Humeniuk * Cohort 8 | EU Compassionate Use ** |
|---|---|---|---|---|
| Remdesivir Dose | mg | 150 | 75 | 200 |
| Infusion Duration | h | 2 | 0.5 | 1.0 *** |
| GS-443902 | uM | 6.0 | 5.9 | 9.8 |
| GS-443902 | uM | 3.7 | 3.3 | 6.9 |
| GS-443902 | 1/h | 36 | 49 | |
| GS-443902 | h × uM | 157.4 | ||
| GS-443902 | h × uM | 297 | 394 | |
| GS-443902 | h × uM | 272 | 340 |
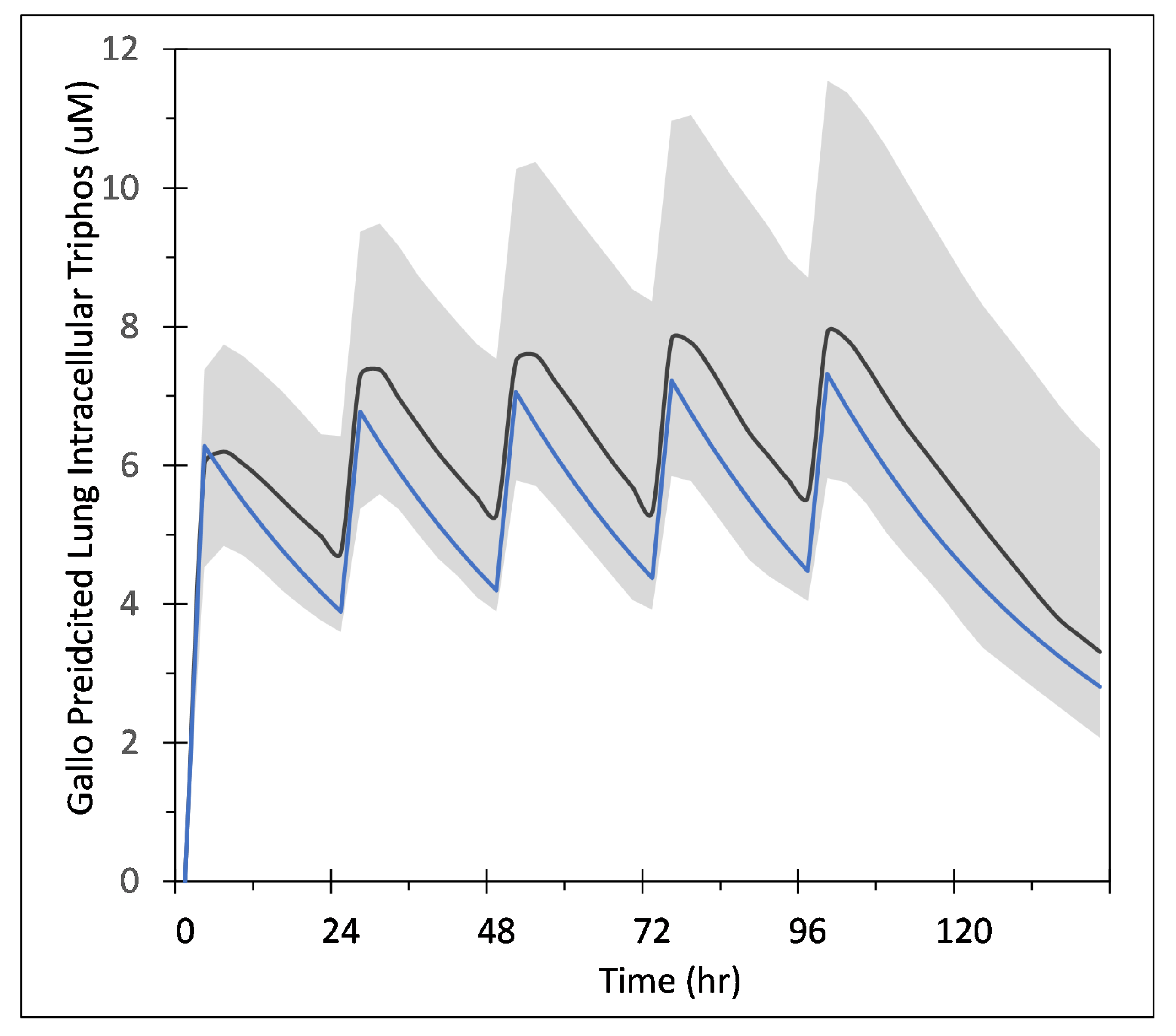
Appendix A.1. COPASI Codes
Appendix A.1.1. COPASI Model File for Parameter Fitting
- Humeniuk_PK_data_Europe_Table_16.txt
- Humeniuk_PK_data_Table_4_Cohort7.txt
- Humeniuk_PK_data_Table_4_Cohort8.txt
Appendix A.1.2. COPASI Model File for Calculating GS-443902 from Repetitive Remdesivir Doses
Appendix B. Table of Parameters from Sego et al.
| Conversion Factors | Value |
|---|---|
| Simulation step | 1200.0 s * (300.0 s) |
| Lattice width | 4.0 μm |
| Scale factor for concentration | mol |
| Simulation Parameter Name | Value | Simulation Parameter Name | Value |
|---|---|---|---|
| Cell diameter | 12.0 μm | Viral decay rate | 7.71 × 10−6 s−1 |
| Replication rate | (1/12)10−3 s−1 | Cytokine diffusion coefficient | 0.16 μm2 s−1 |
| Translating rate | (1/18)10−3 s−1 | Cytokine diffusion length | 100 μm |
| Unpacking rate | (1/6)10−3 s−1 | Cytokine decay rate | 1.32 × 10−5 s−1 |
| Packaging rate | (1/6)10−3 s−1 | Maximum cytokine immune secretion rate | 3.5 × 10−4 pMs−1 |
| Release rate | (1/6)10−3 s−1 | Immune secretion midpoint | 1 pM |
| Scale factor for number of mRNA per infected cell | 1000 cell−1 | Cytokine immune uptake rate | 3.5 × 10−4 pMs−1 |
| Viral dissociation coefficient | 2000 | Maximum cytokine infected cell secretion rate | 3.5 × 10−3 pMs−1 |
| Viral diffusion coefficient | 0.01 μm2 s−1 | Infected cell cytokine secretion mid-point , | 0.1 |
| Viral diffusion length | 36 μm | Cytokine secretion Hill coefficient | 2 |
| Immune cell cytokine activation | 10 pM | Virally-induced apoptosis dissociation coefficient | 100 |
| Immune cell equilibrium bound cytokine | 210 pM | Virally-induced apoptosis characteristic time constant | 20 min |
| Immune cell bound cytokine memory | 0.99998 s−1 | Immune cell activation Hill coefficient | 2 |
| Immune cell activated time | 10 h | Immune response add immune cell coefficient | 1/1200 s−1 |
| Oxidation Agent diffusion coefficient | 0.64 μm2 s−1 | Immune response subtract immune cell coefficient | 1/6000 cell−1 s−1 |
| Oxidation Agent diffusion length | 36 μm | Immune response delay coefficient | 1.2 × 106 s |
| Oxidation Agent decay rate | 1.32 × 10−5 s−1 | Immune response decay coefficient | 1/12,000 s−1 |
| Immune cell oxidation agent secretion rate | 3.5 × 10−3 pMs−1 | Immune response cytokine transmission coefficient | 0.5 |
| Immune cell threshold for Oxidation Agent release | 10 = 1.5625 pM | Immune response probability scaling coefficient | 0.01 |
| Tissue cell threshold for death | 1.5 = 0.234375 pM | Number of immune cell seeding samples | 10 |
| Simulation Parameter Name | Value | Simulation Parameter Name | Value |
|---|---|---|---|
| Initial density of unbound cell surface receptors | 200 cell−1 | Initial immune cell target volume | 64 μm3 |
| Virus–receptor association affinity | 1.4 × 104 M−1 s−1 | Immune cell lambda volume | 9 |
| Virus–receptor dissociation affinity | 1.4 × 104 s | Initial number of immune cells | 0 |
| Infection threshold | 1 | Immune cells lambda chemotaxis | 1 |
| Uptake Hill coefficient | 2 | Intrinsic Random Motility | 10 |
| Uptake characteristic time constant | 20 min | Contact coefficients J (all interfaces) | 10 |
| Virally-induced apoptosis Hill coefficient | 2 |
Appendix C. Quantitative Metrics of Treatment Outcome
Appendix D. Instructions for Running the Multiscale CompuCell3D Simulations and for Analyzing the Results
Appendix D.1. CompuCell3D Simulations
- mult_dict = treatment_starts_0, parameters varied in the fine investigation with treatment starting with the infection of 10 epithelial cells;
- mult_dict = treatment_starts_3_halved_half_life, parameters varied in the fine investigation with treatment starting3 days post the infection of 10 epithelial cells and with the half life of GS-443902 halved.
 the first set (set_0) uses first_dose=0, dose_interval=1, ic50_multiplier=0.01, and t_half_mult=1. The results for it will be in sweep_output_folder/set_0, each replica will be in sweep_output_folder/set_0/run_0, sweep_output_folder/ set_0/run_1, [...], sweep_output_folder/set_0/run_num_rep. The second set (set_1) then uses dose_interval=1.5 and ic50_multiplier=0.01; and so on.
the first set (set_0) uses first_dose=0, dose_interval=1, ic50_multiplier=0.01, and t_half_mult=1. The results for it will be in sweep_output_folder/set_0, each replica will be in sweep_output_folder/set_0/run_0, sweep_output_folder/ set_0/run_1, [...], sweep_output_folder/set_0/run_num_rep. The second set (set_1) then uses dose_interval=1.5 and ic50_multiplier=0.01; and so on.Appendix D.2. Results Analysis
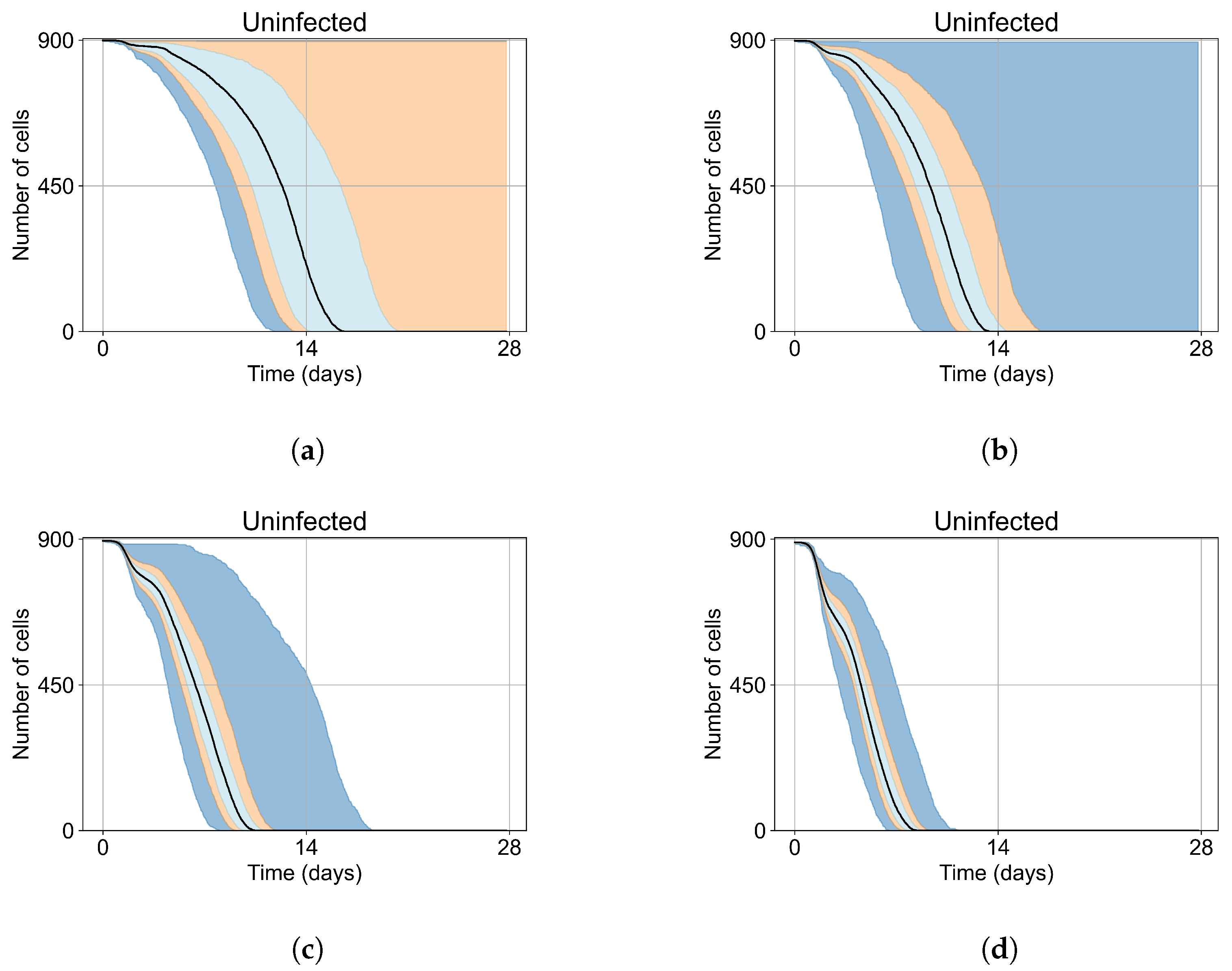
Appendix E. Supplementary Results for the Untreated Simulations with Different Initial Conditions
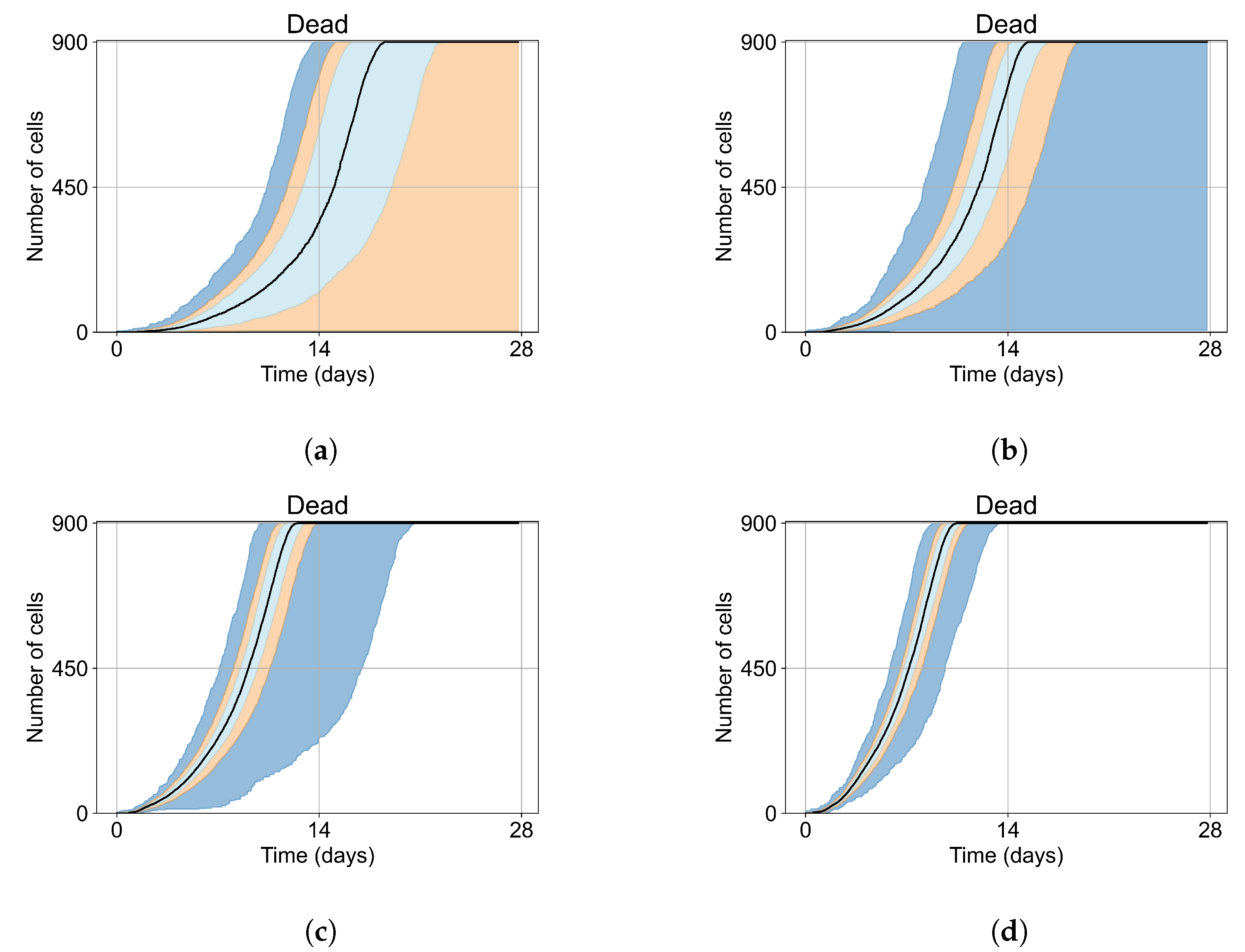
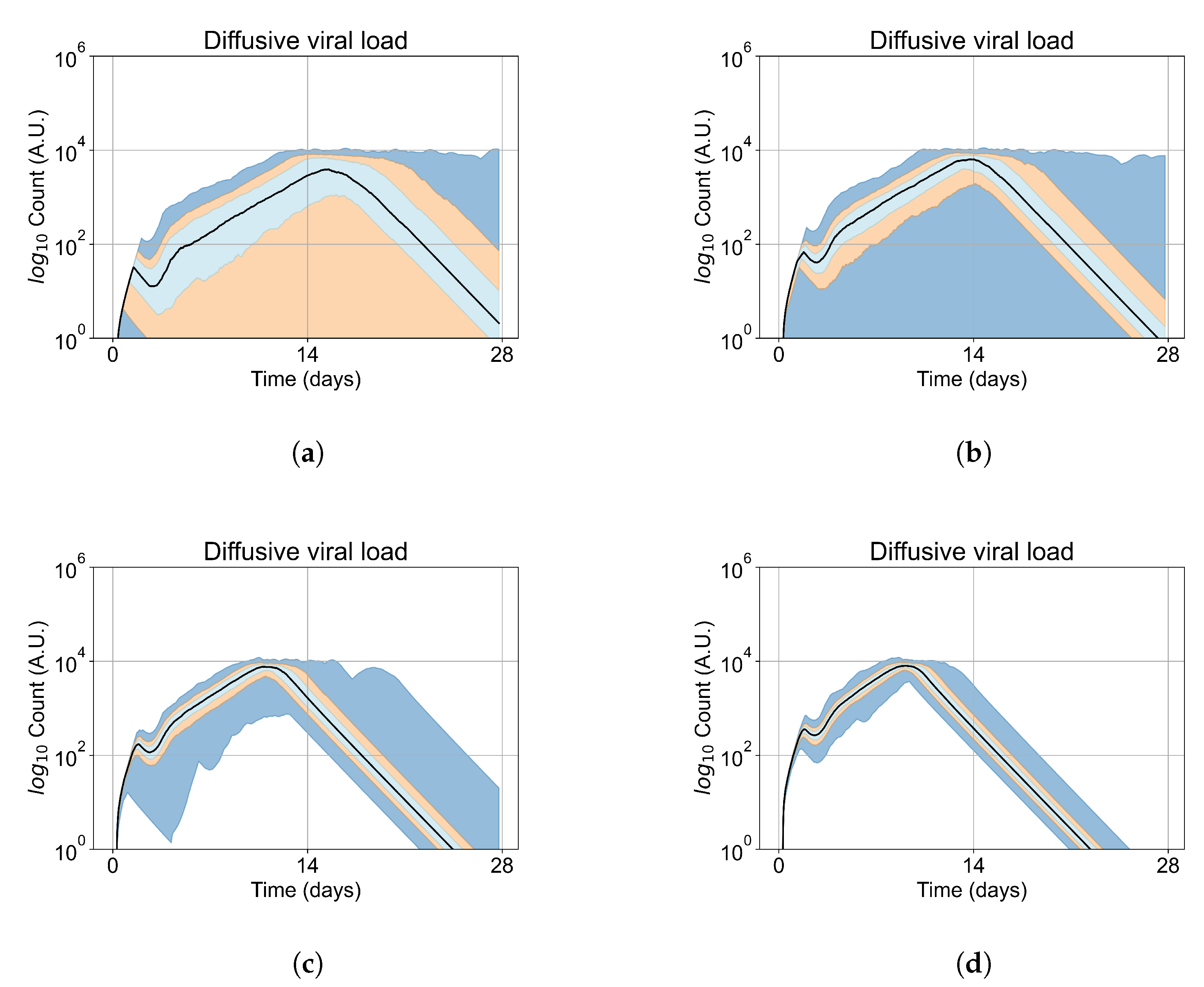
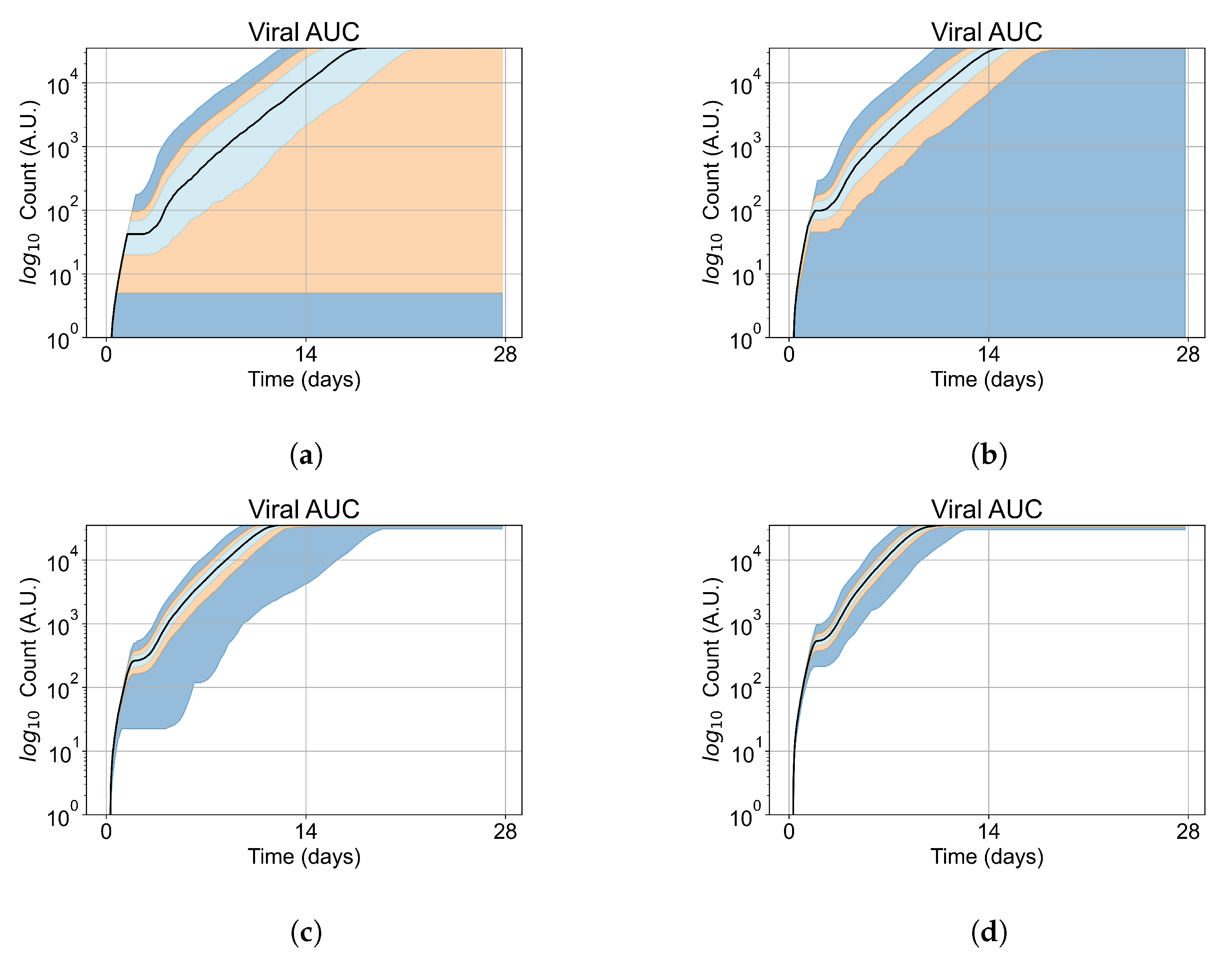
Appendix F. Supplementary Results from Treatment Initiation Delay, Antiviral Potency, and GS-443902 Half-Life Variation
Appendix F.1. Homogeneous Metabolism, Regular GS-443902 Half-Life
Appendix F.1.1. Treatment Initiation with Infection of Ten Epithelial Cells
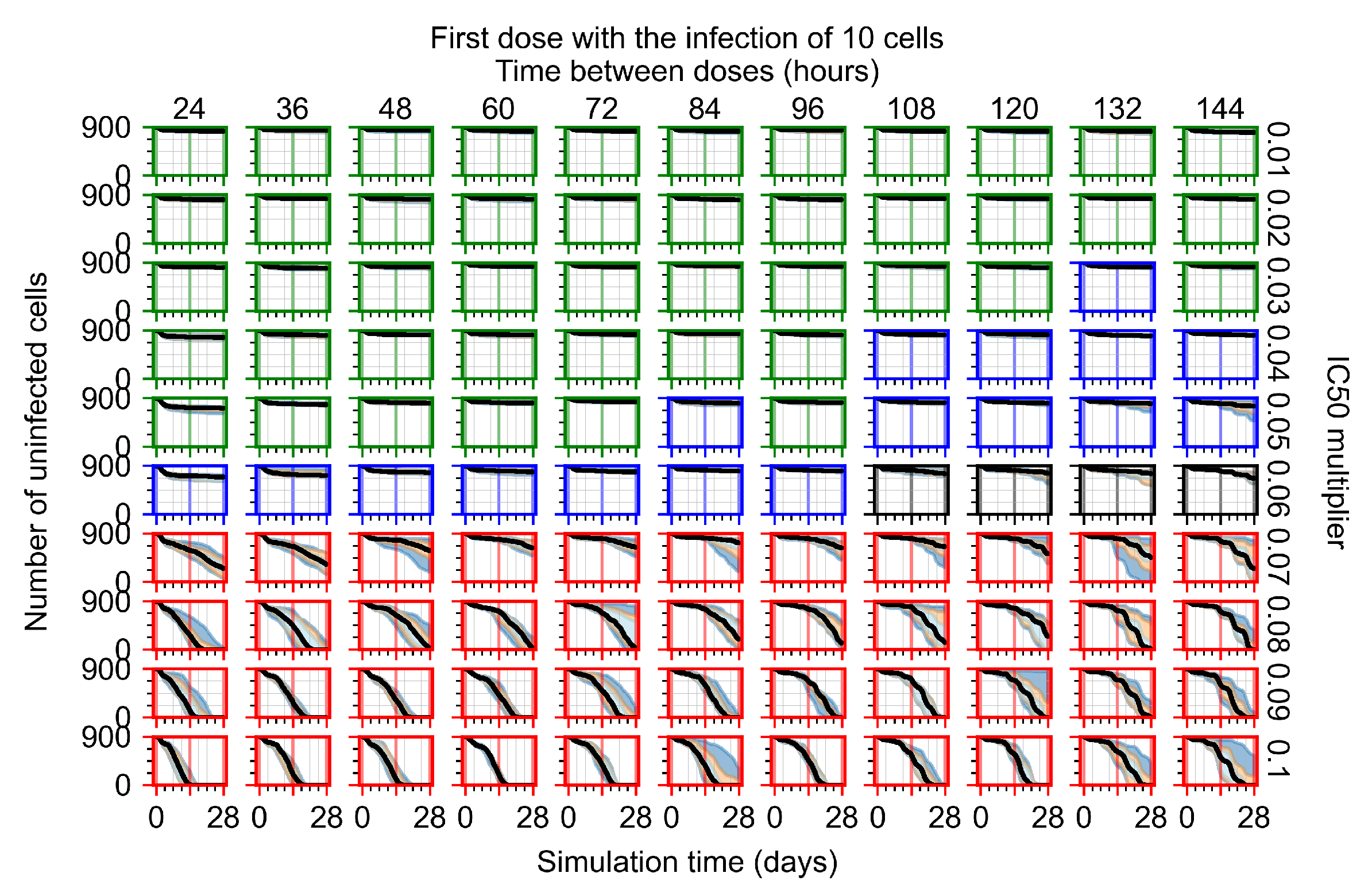
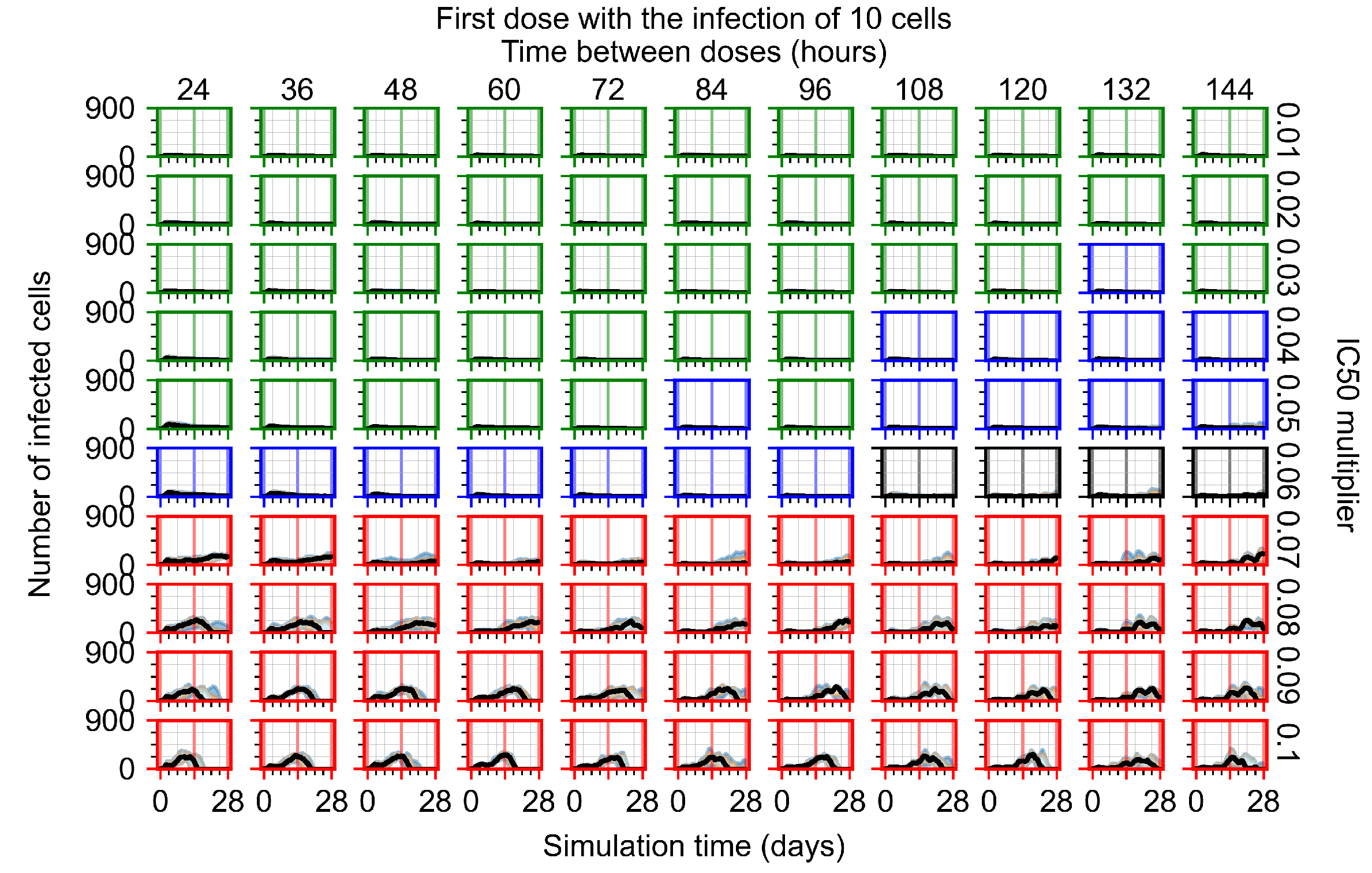

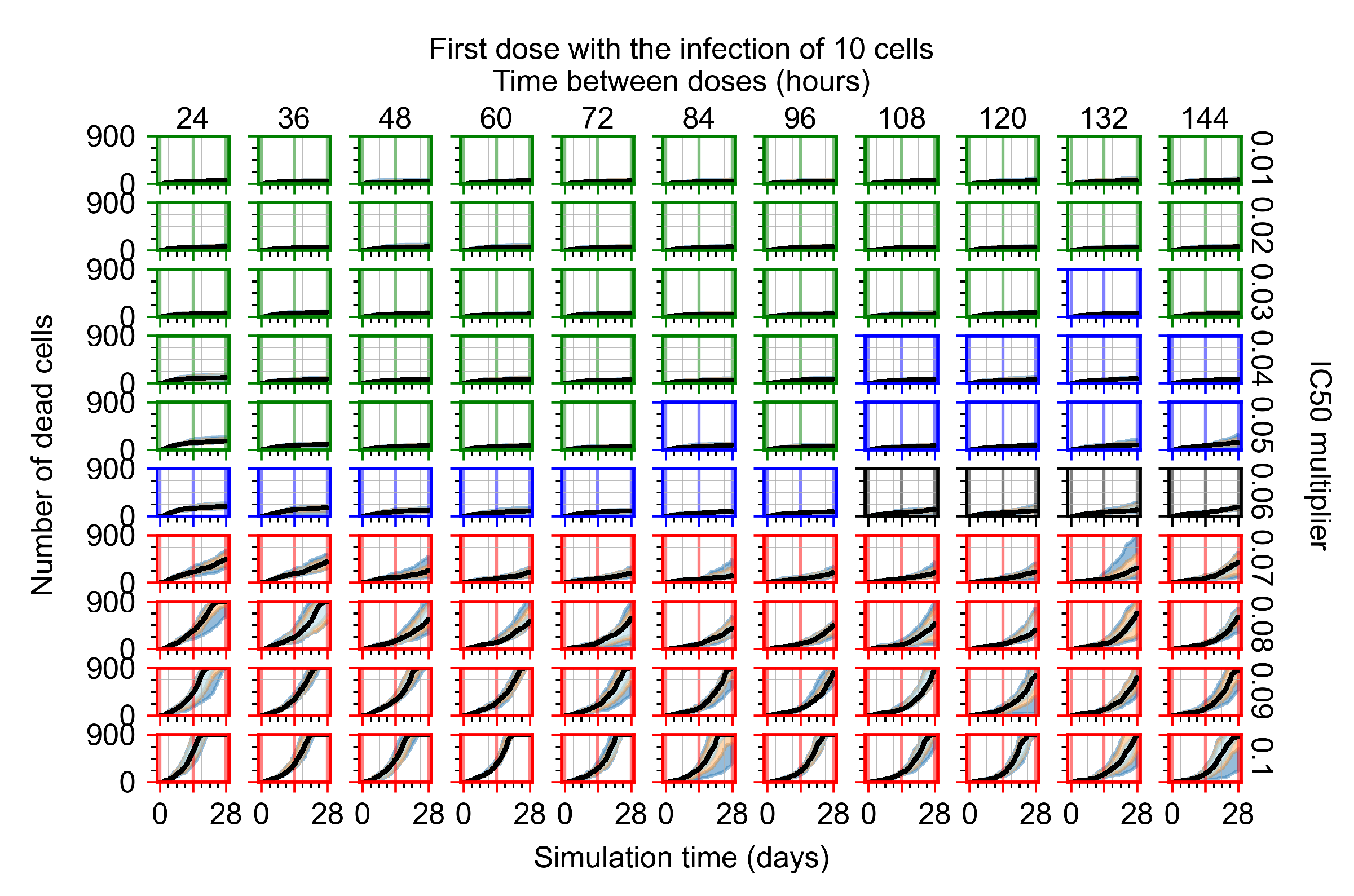
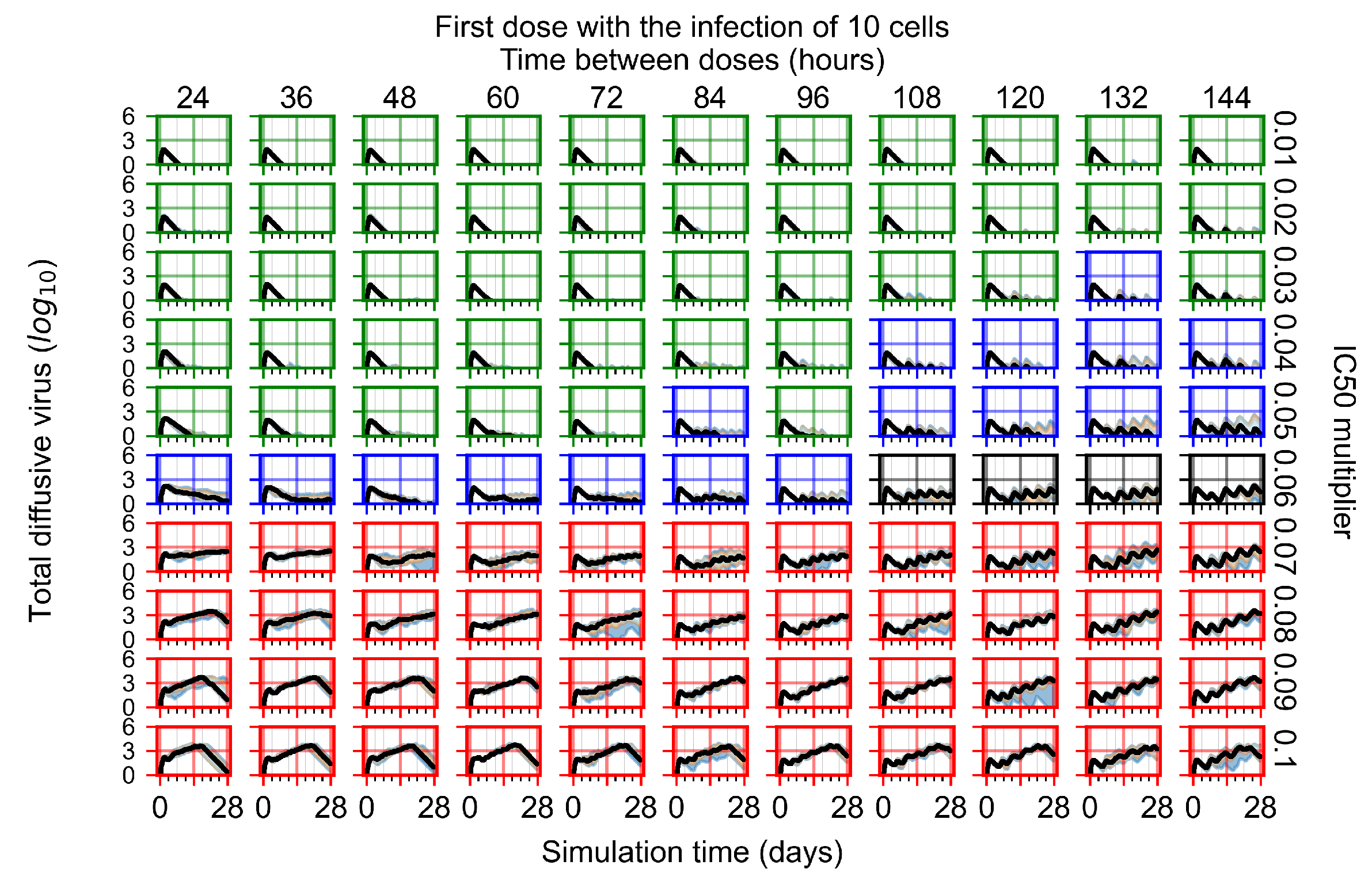
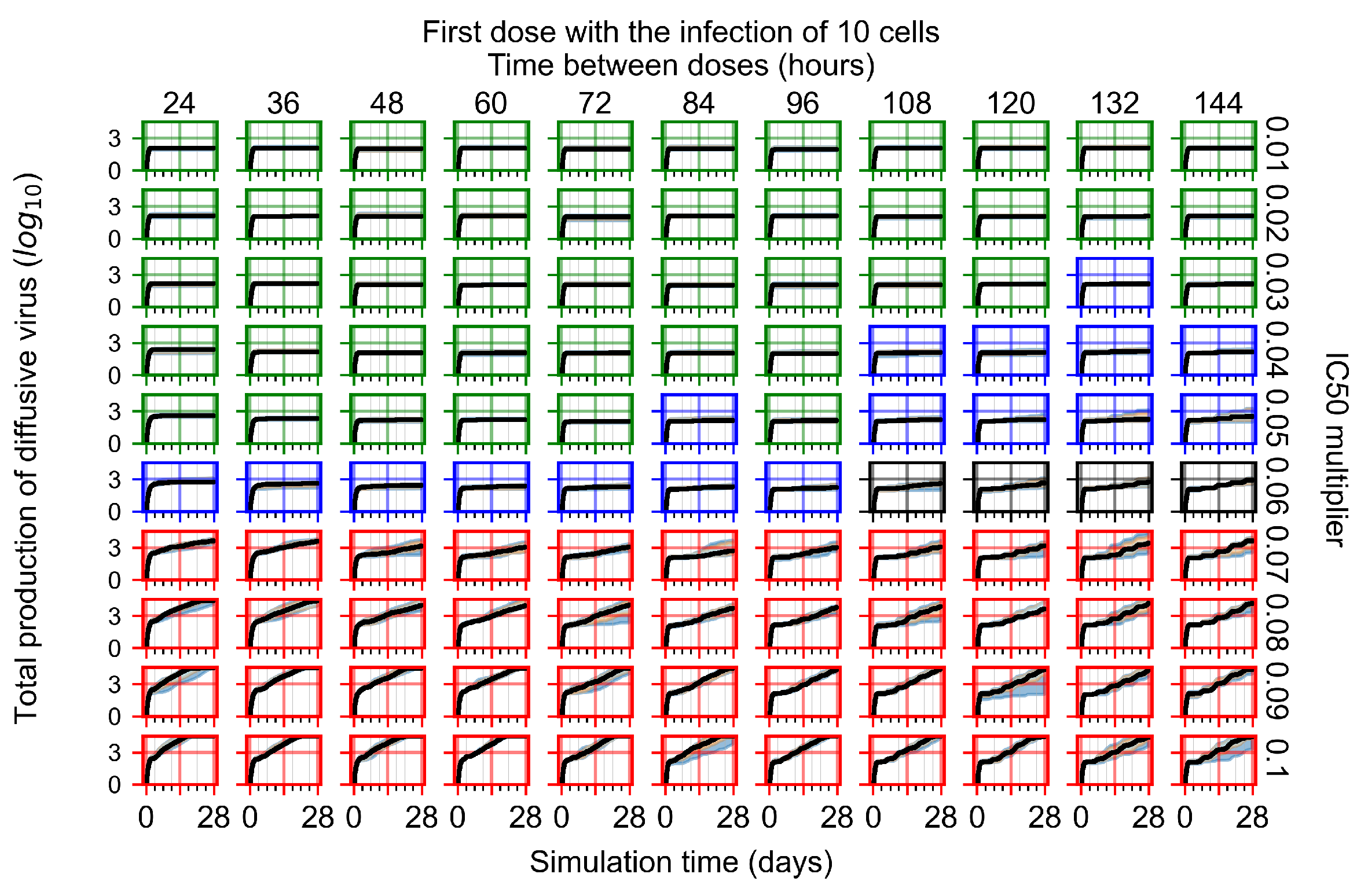
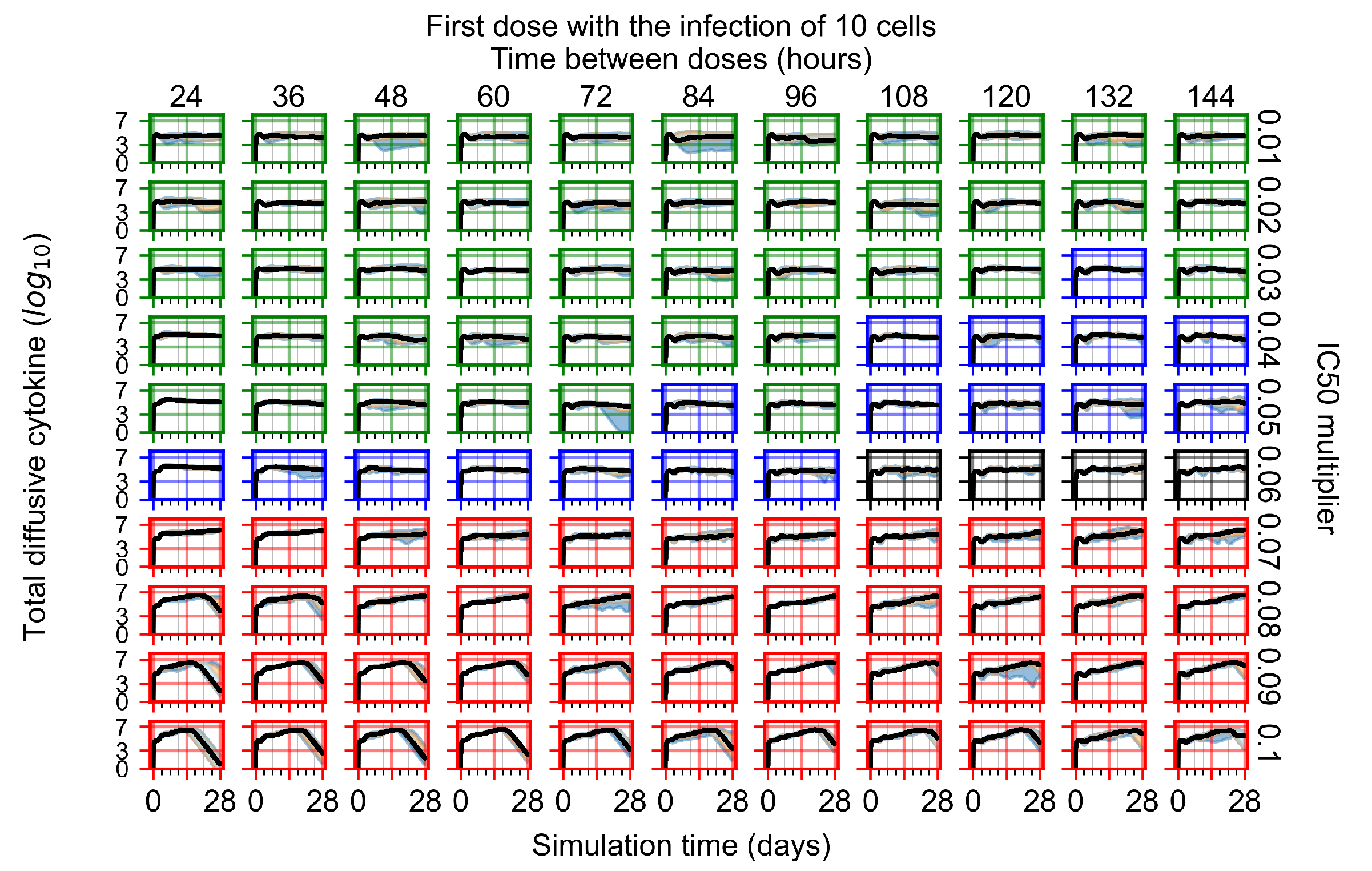

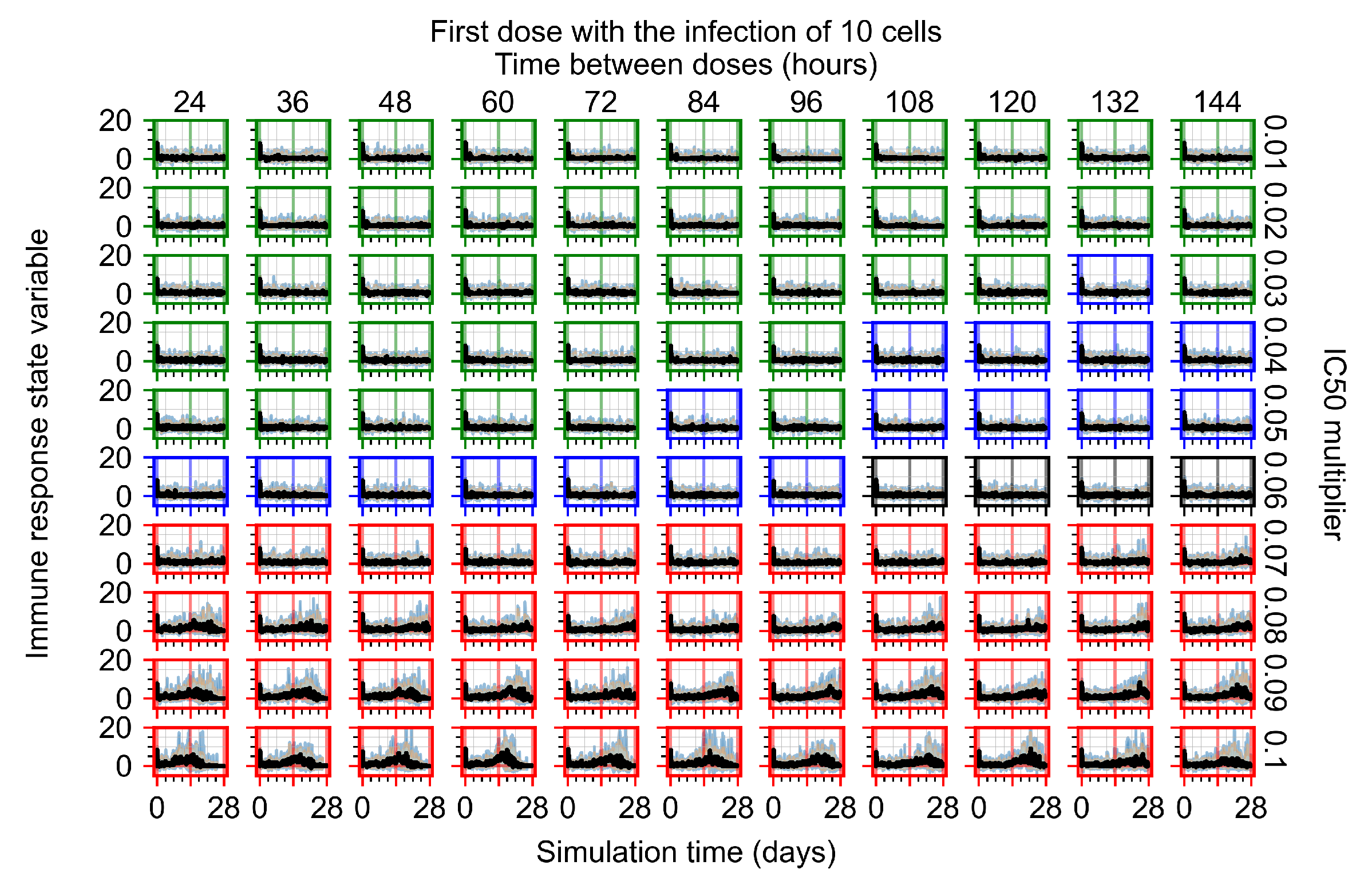
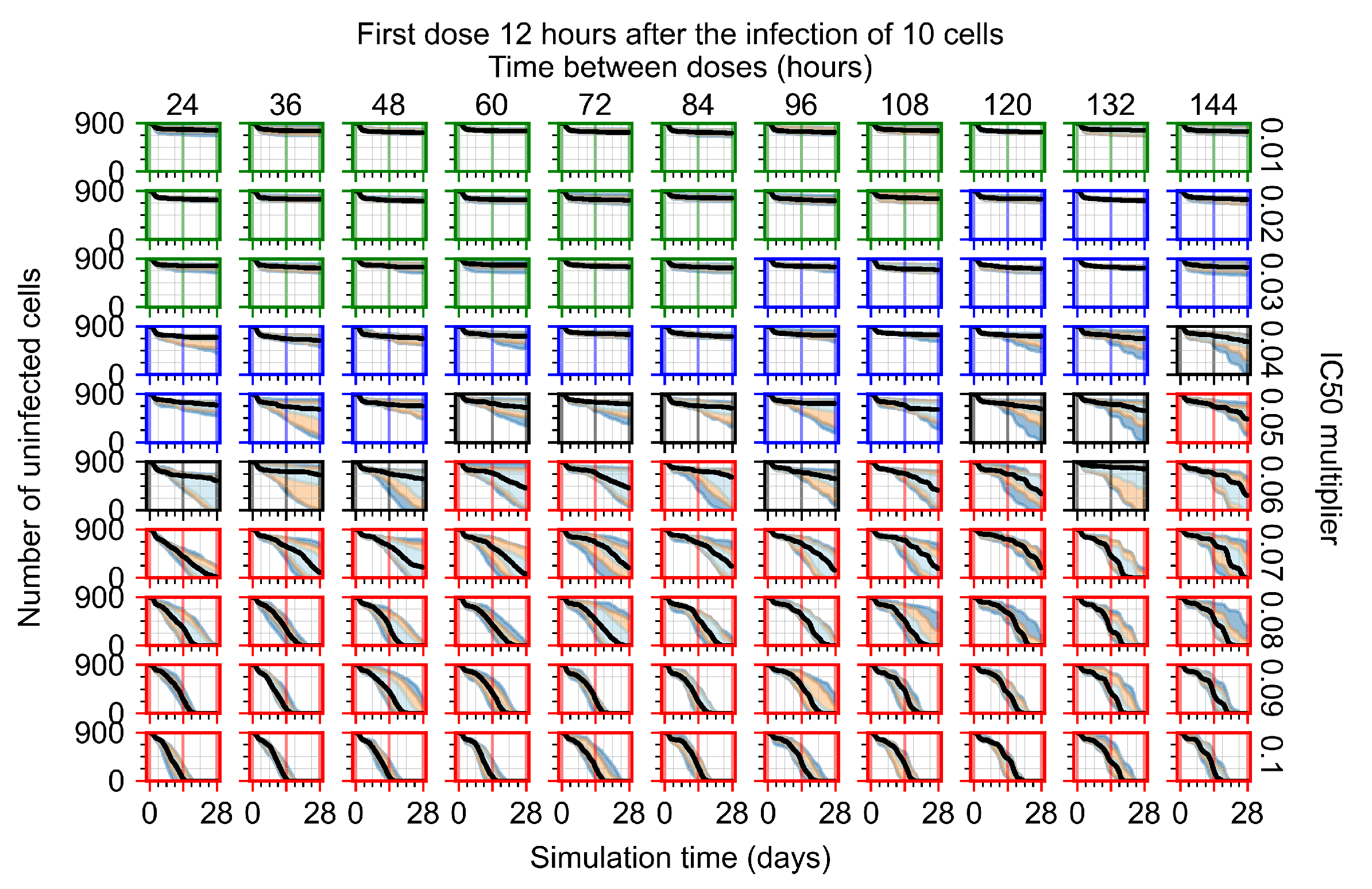
Appendix F.1.2. Treatment Initiation 12 h Post the Infection of Ten Epithelial Cells
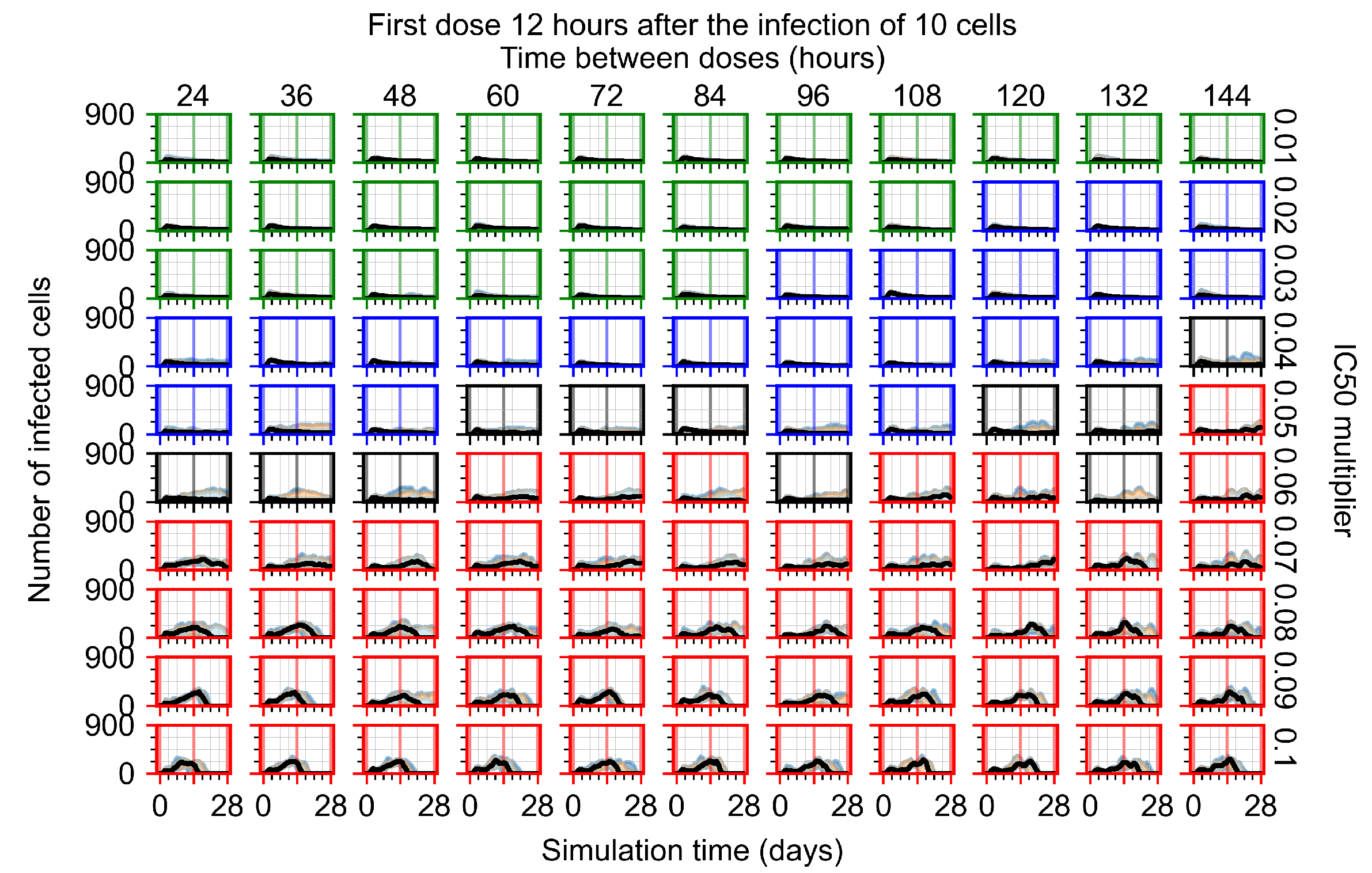
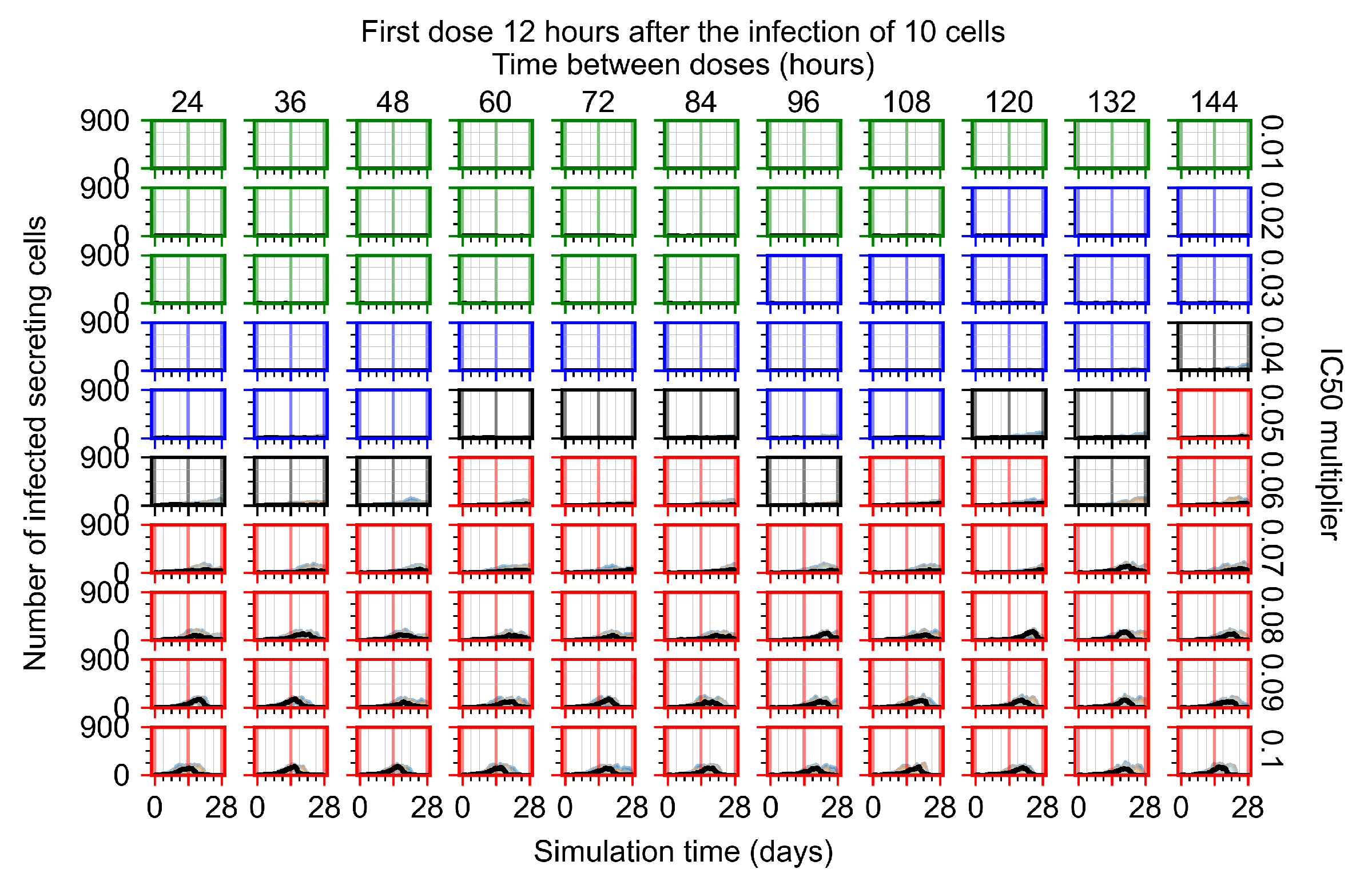

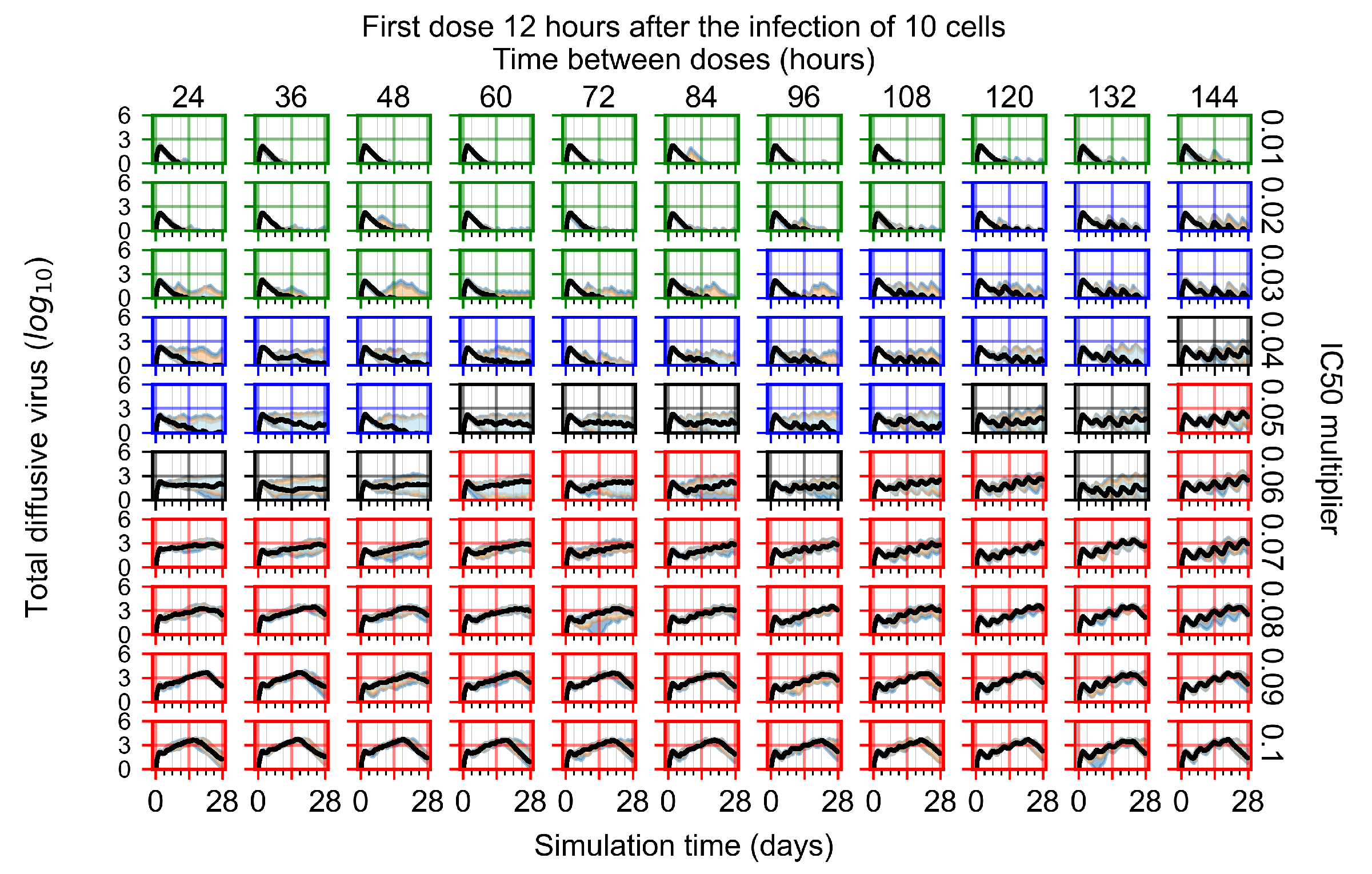
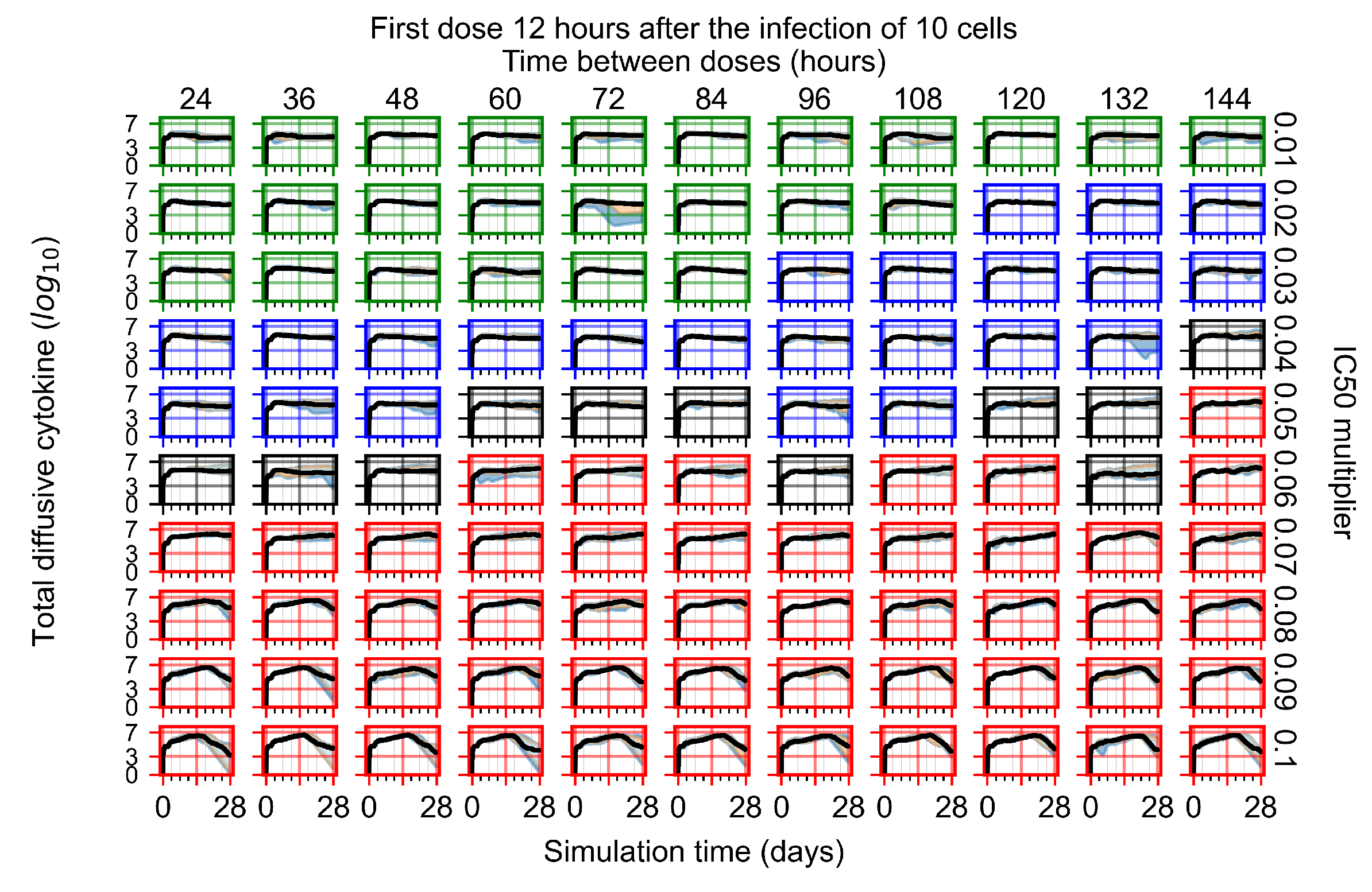
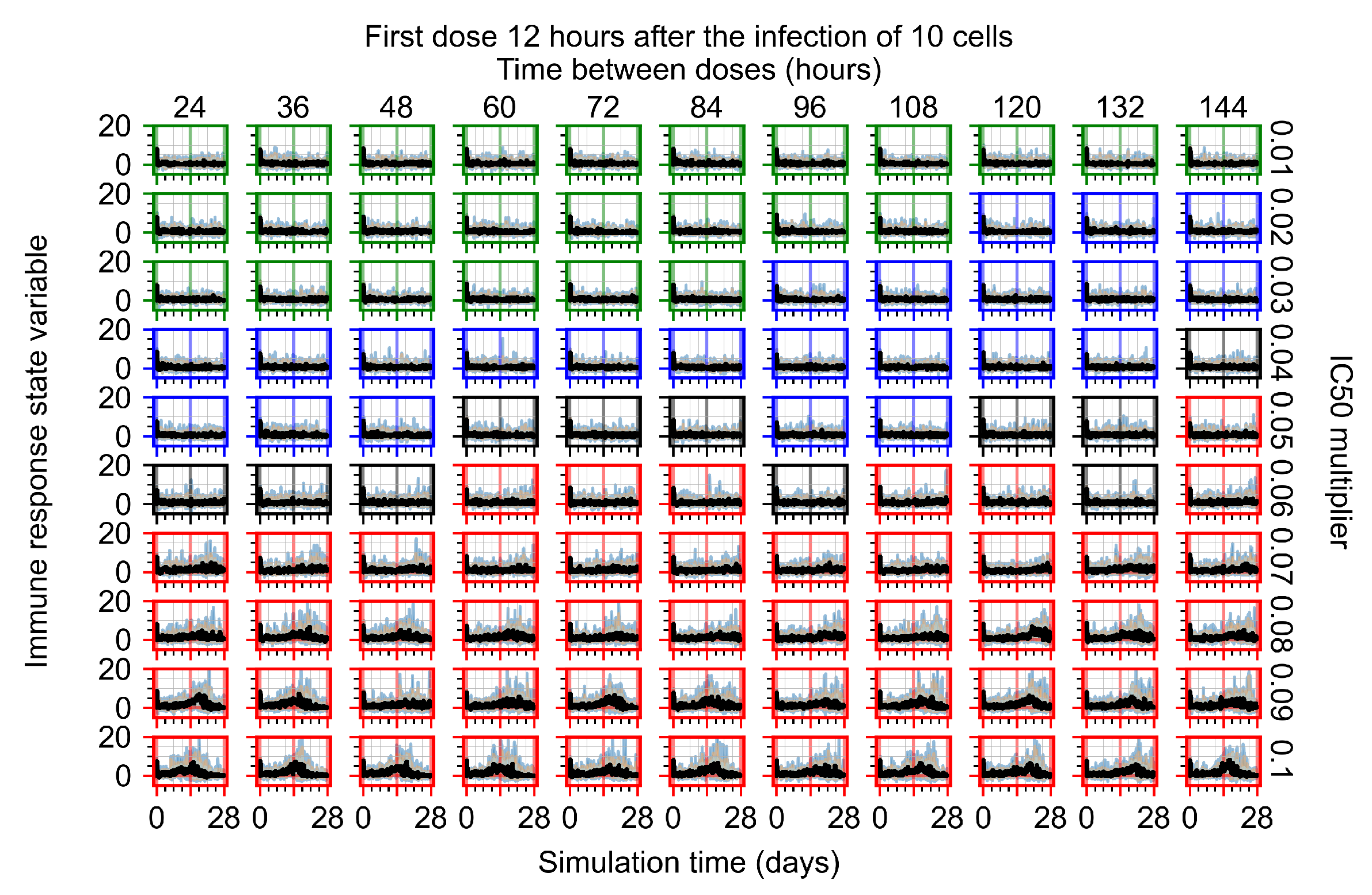
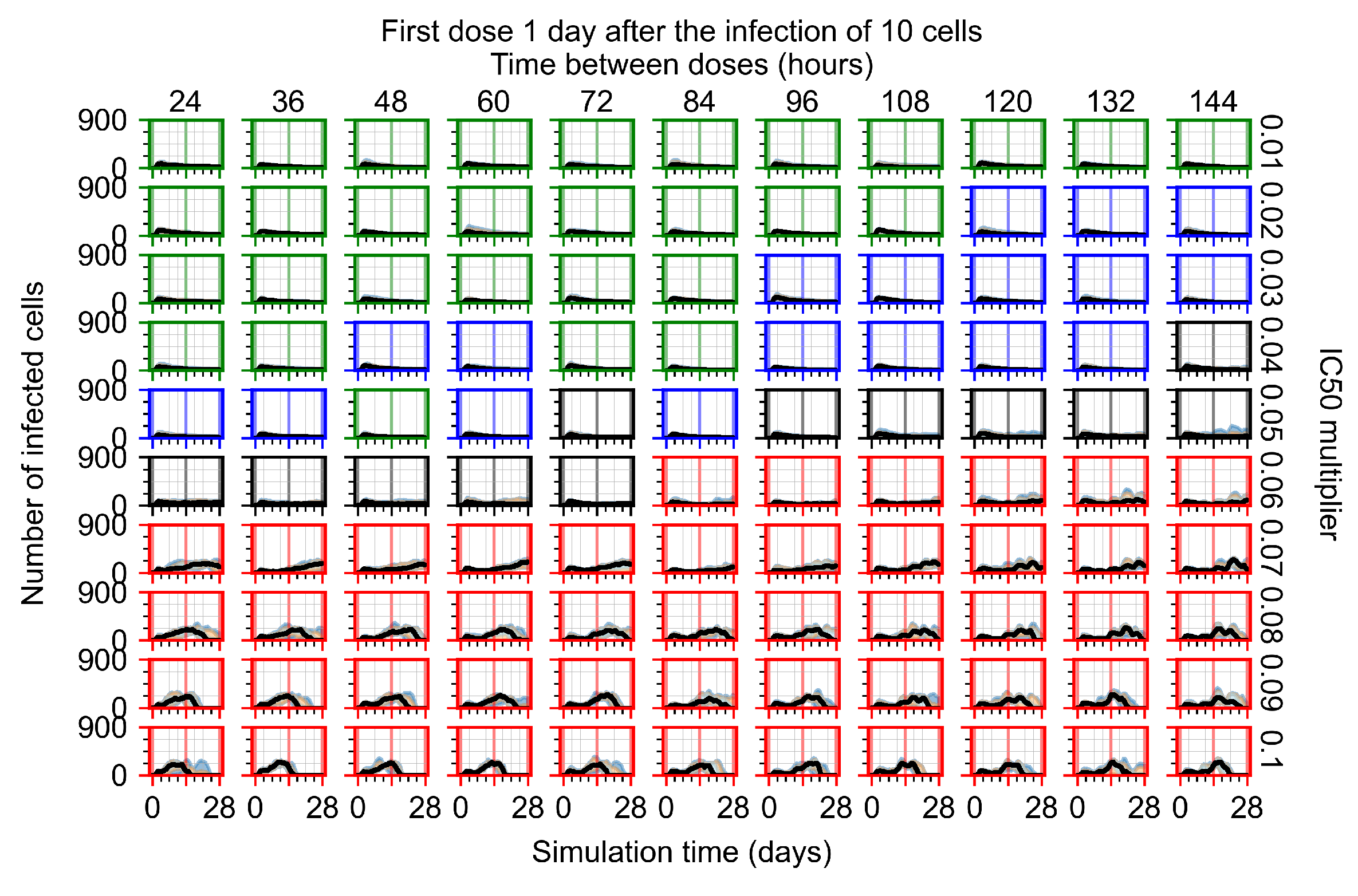
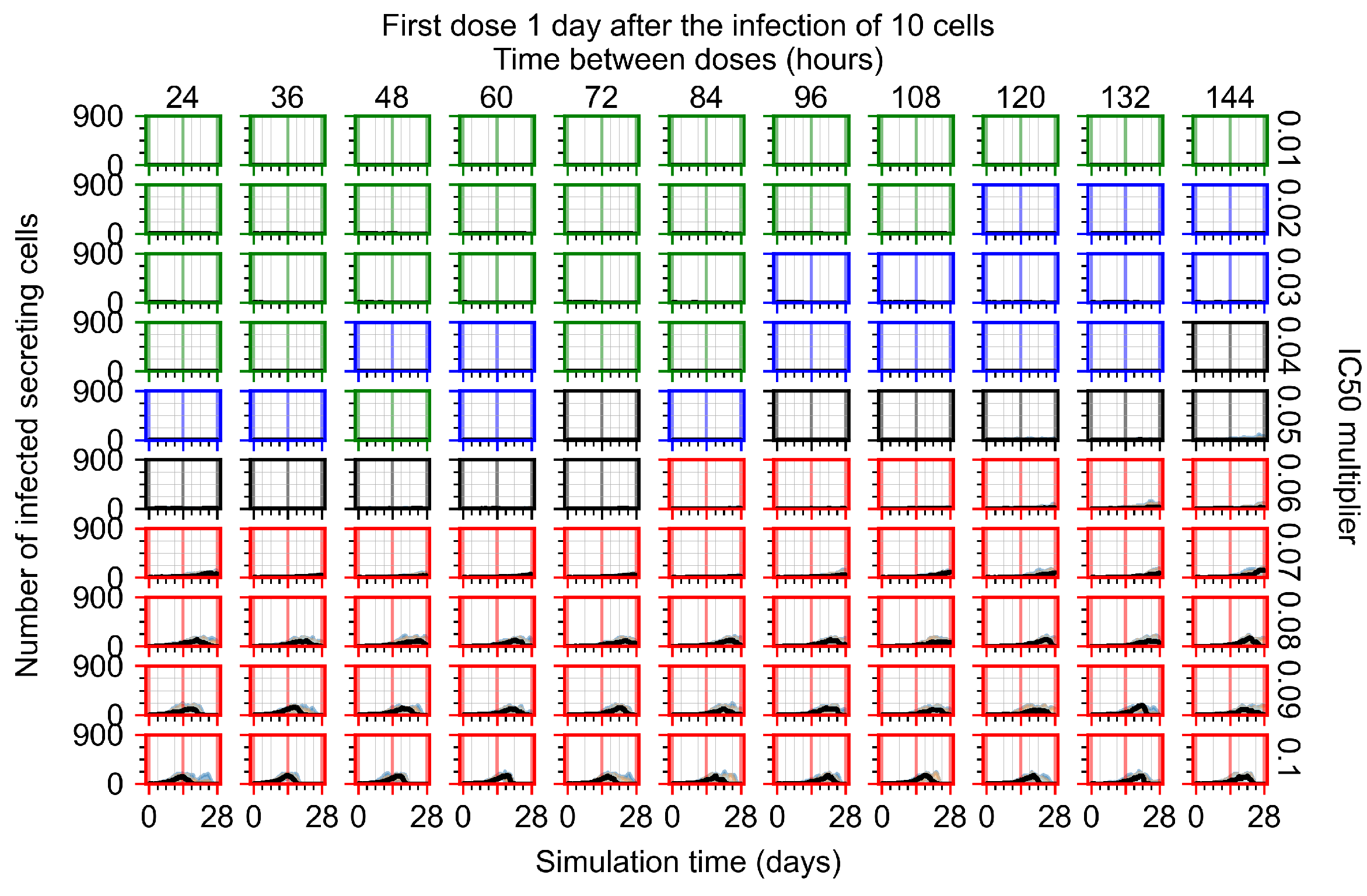
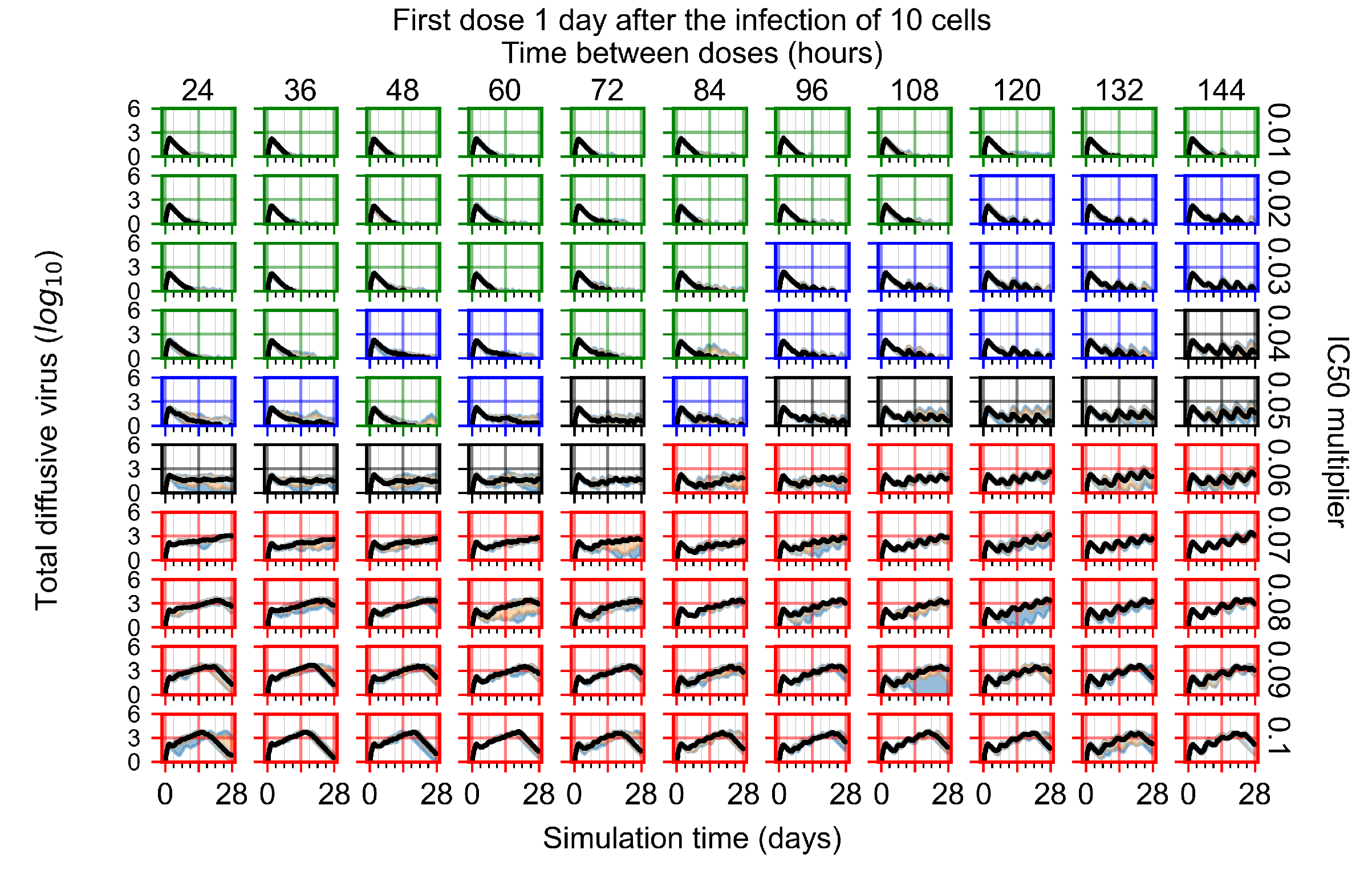
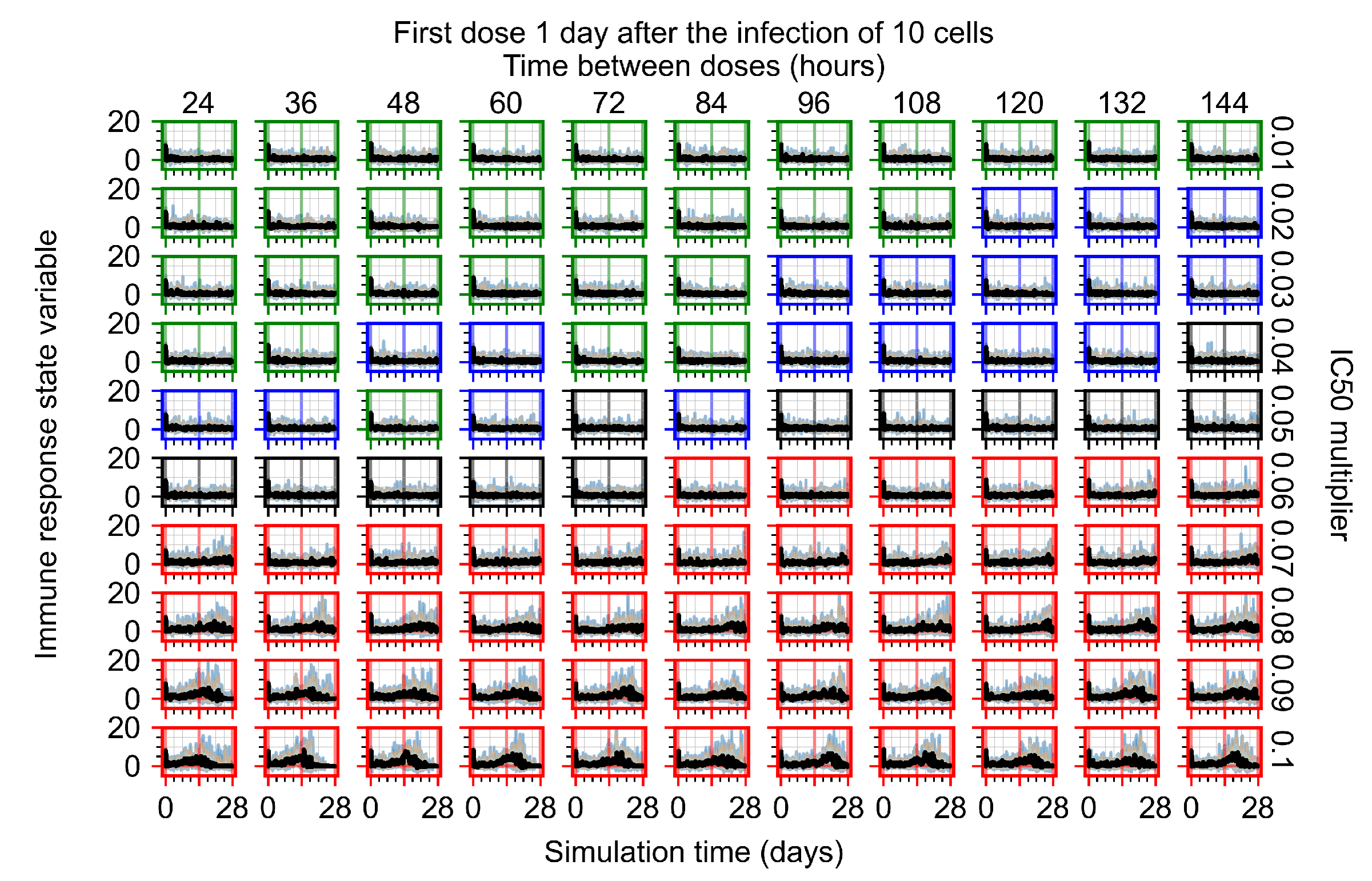
Appendix F.1.3. Treatment Initiation One Day Post the Infection of Ten Epithelial Cells
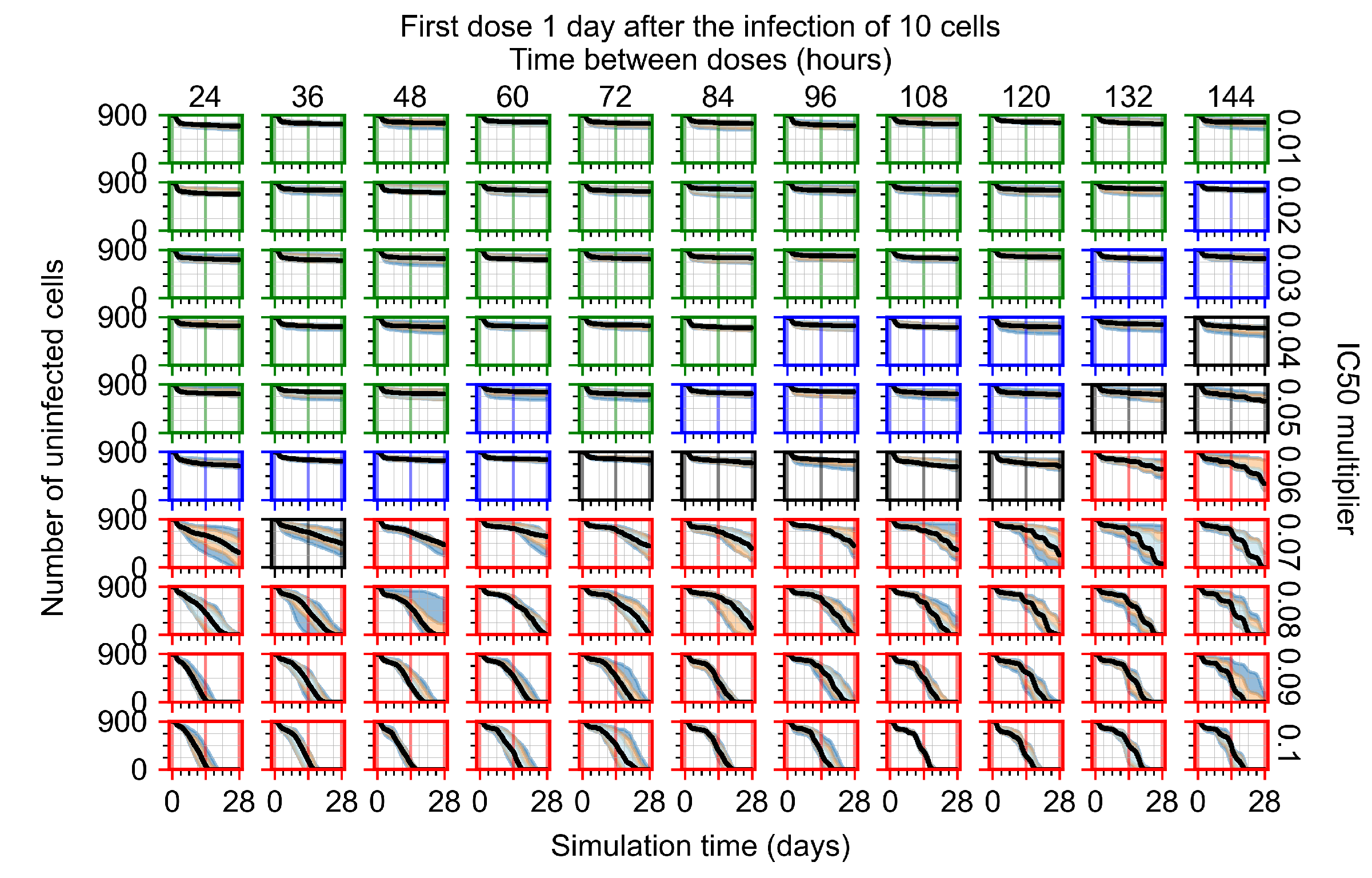
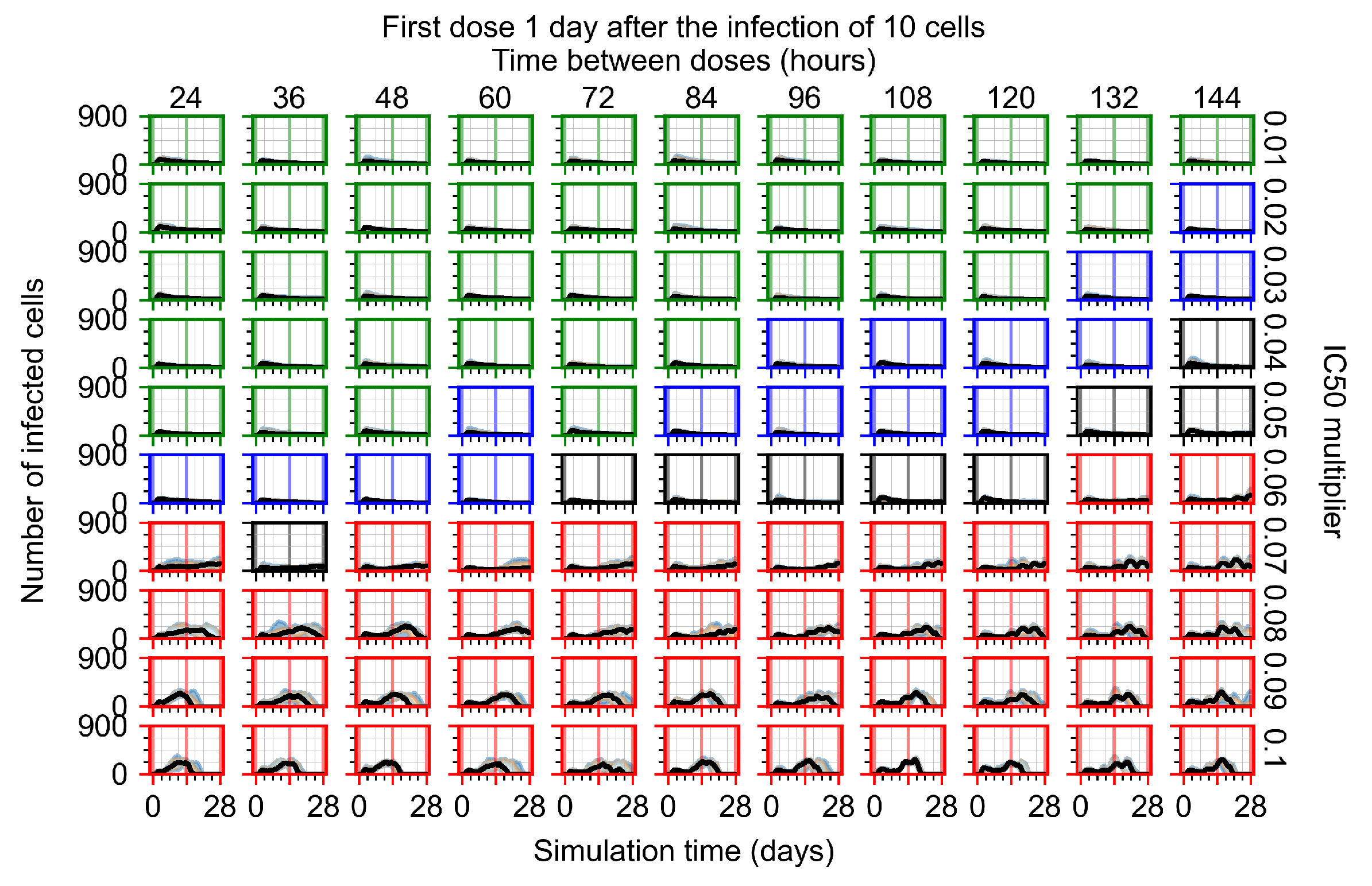


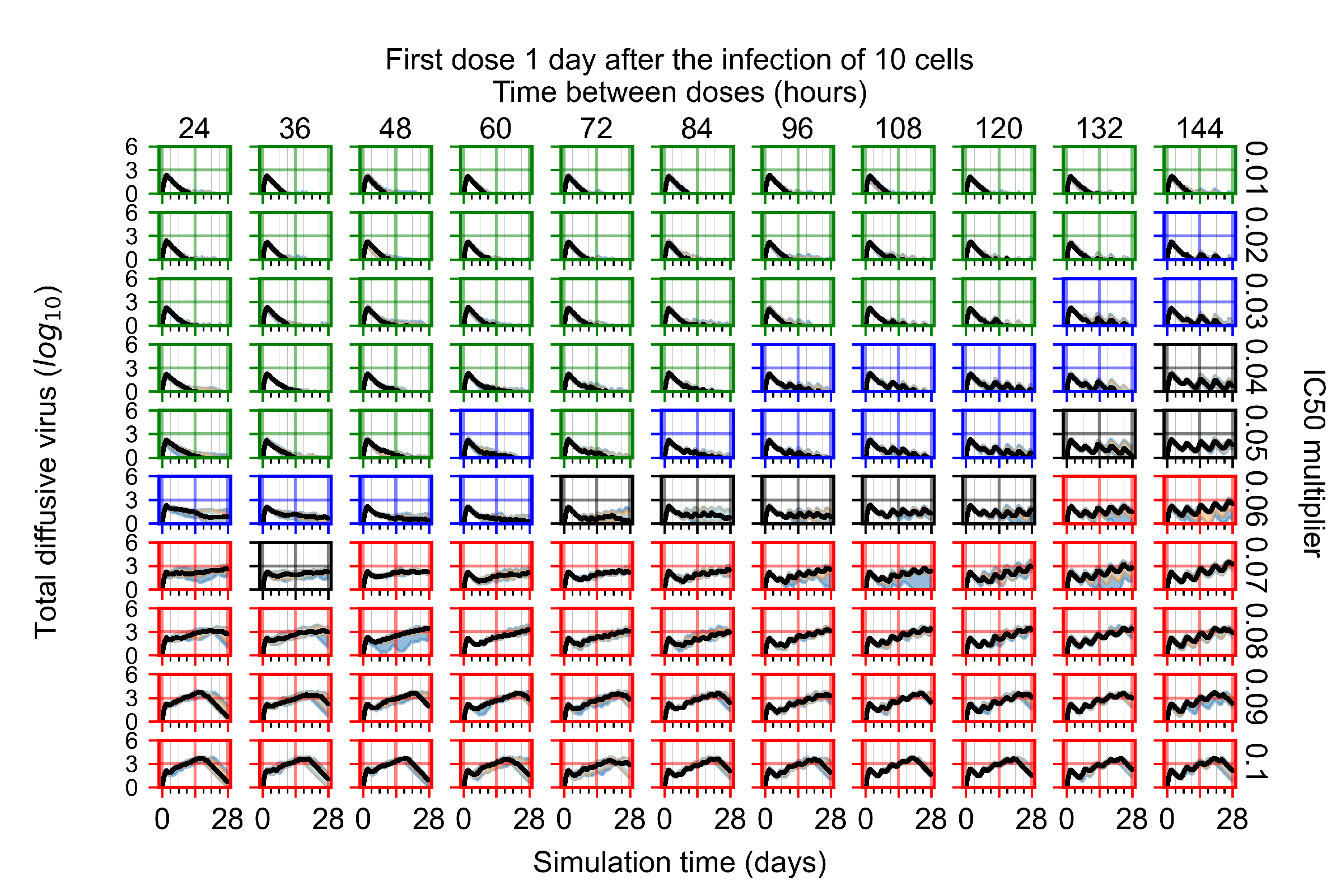

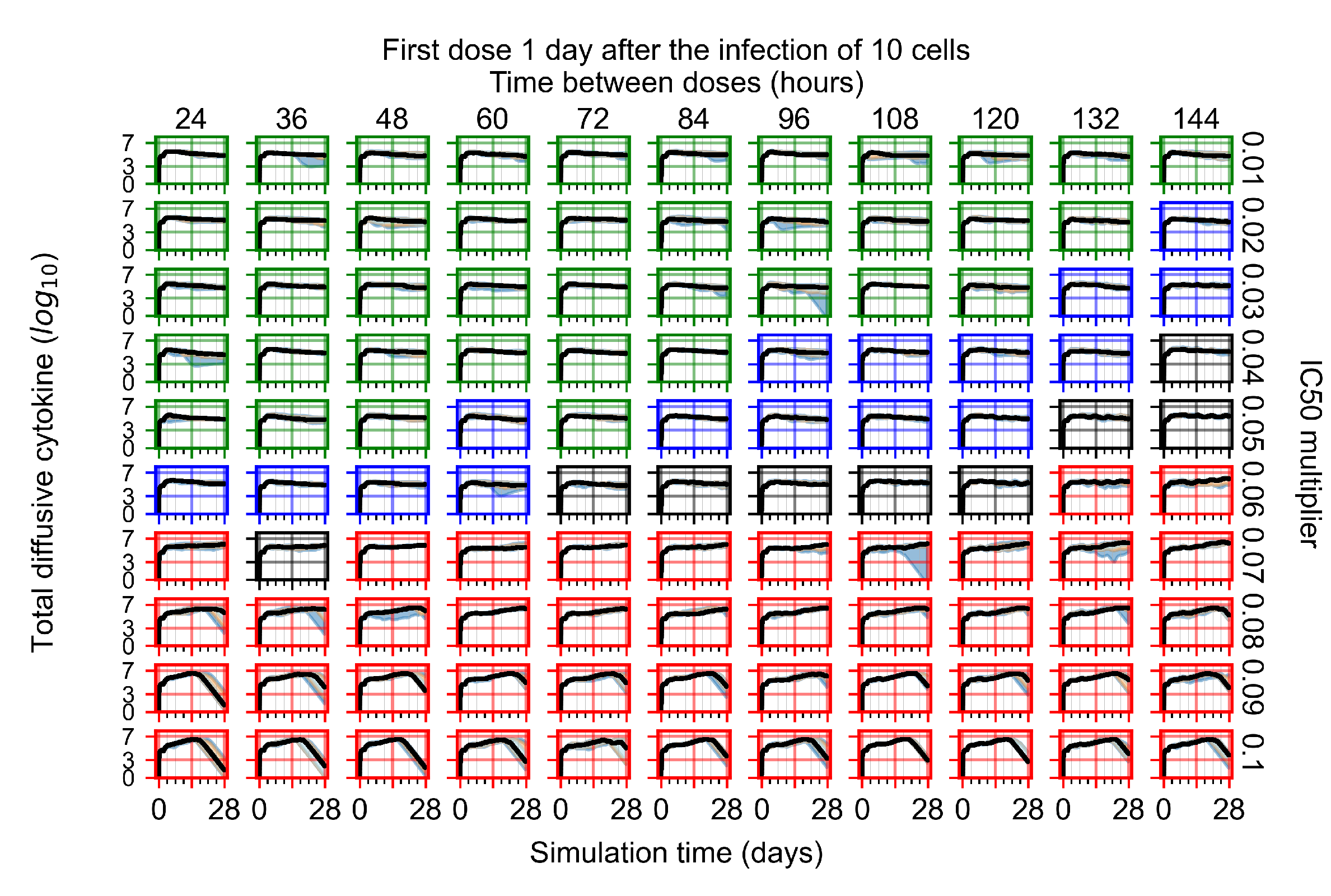
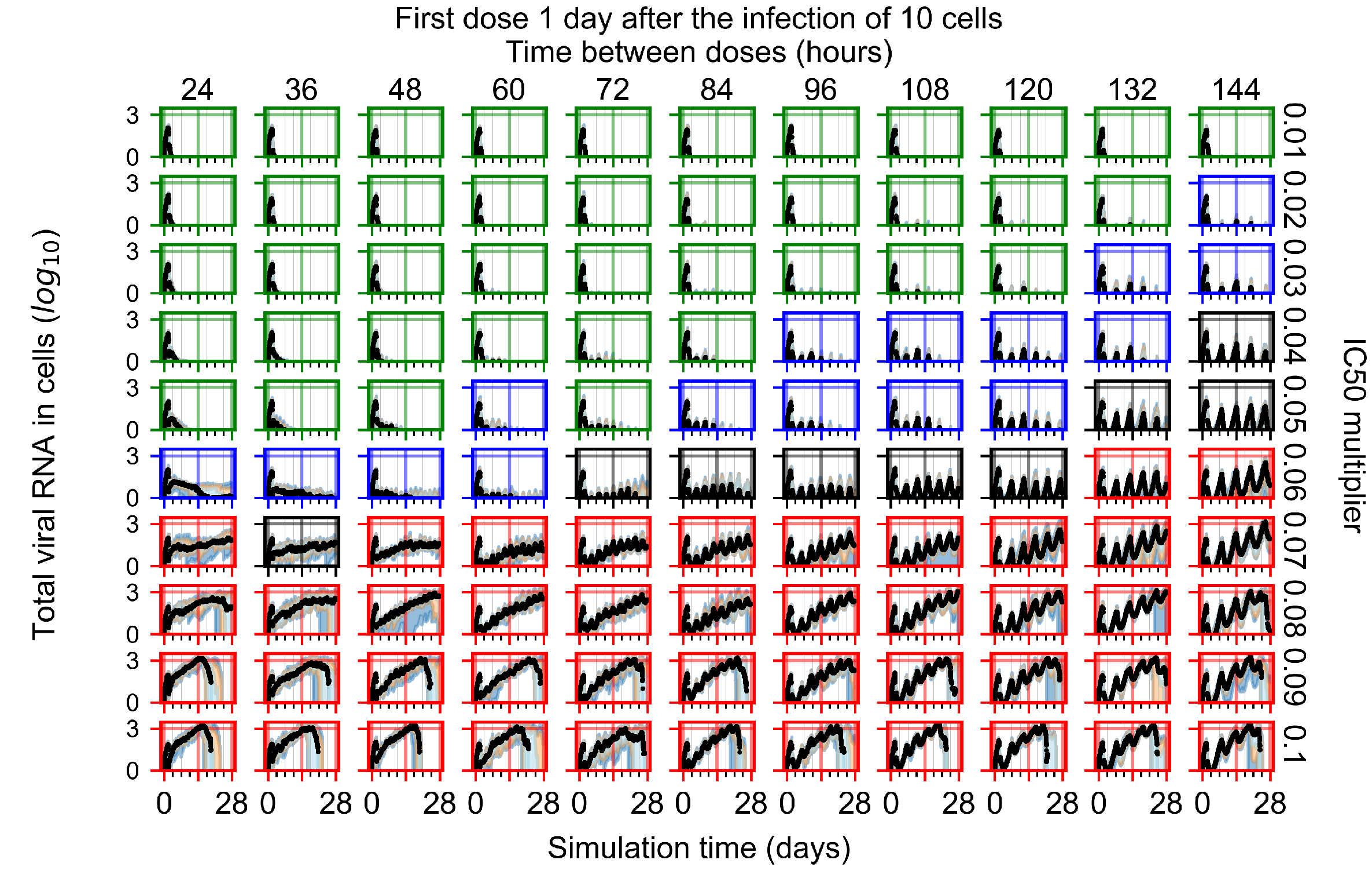

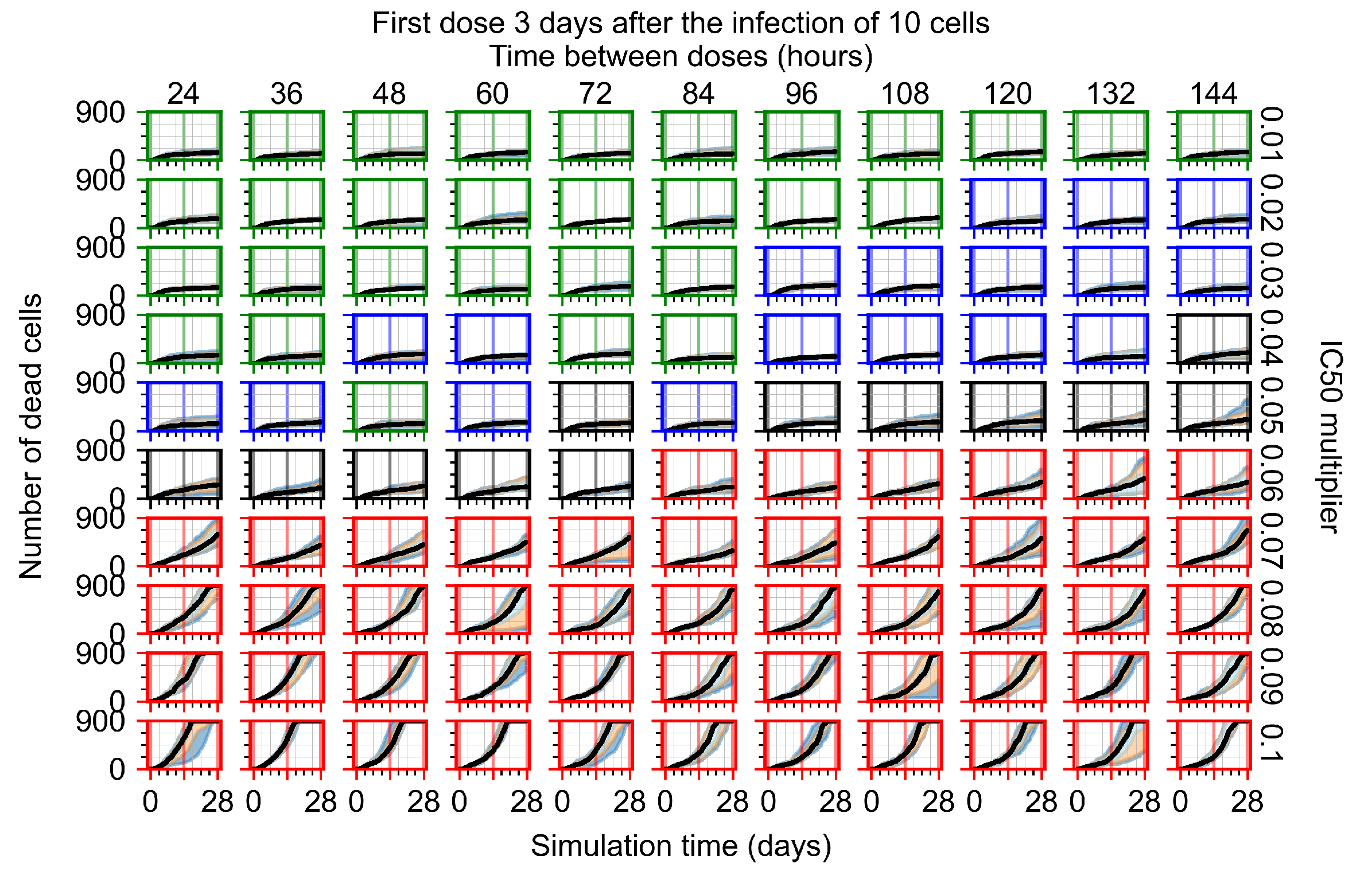
Appendix F.1.4. Treatment Initiation Three Days Post the Infection of Ten Epithelial Cells
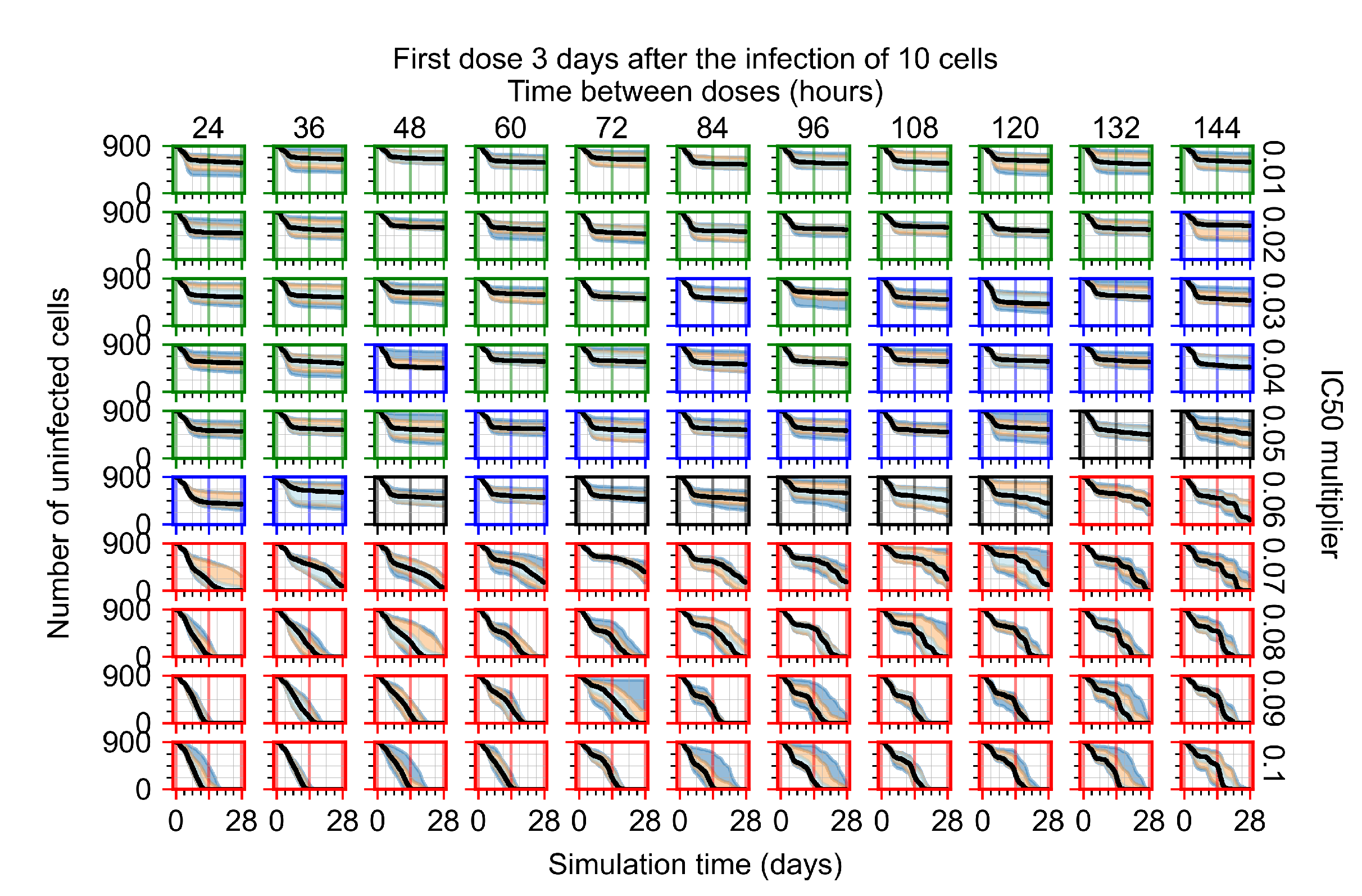
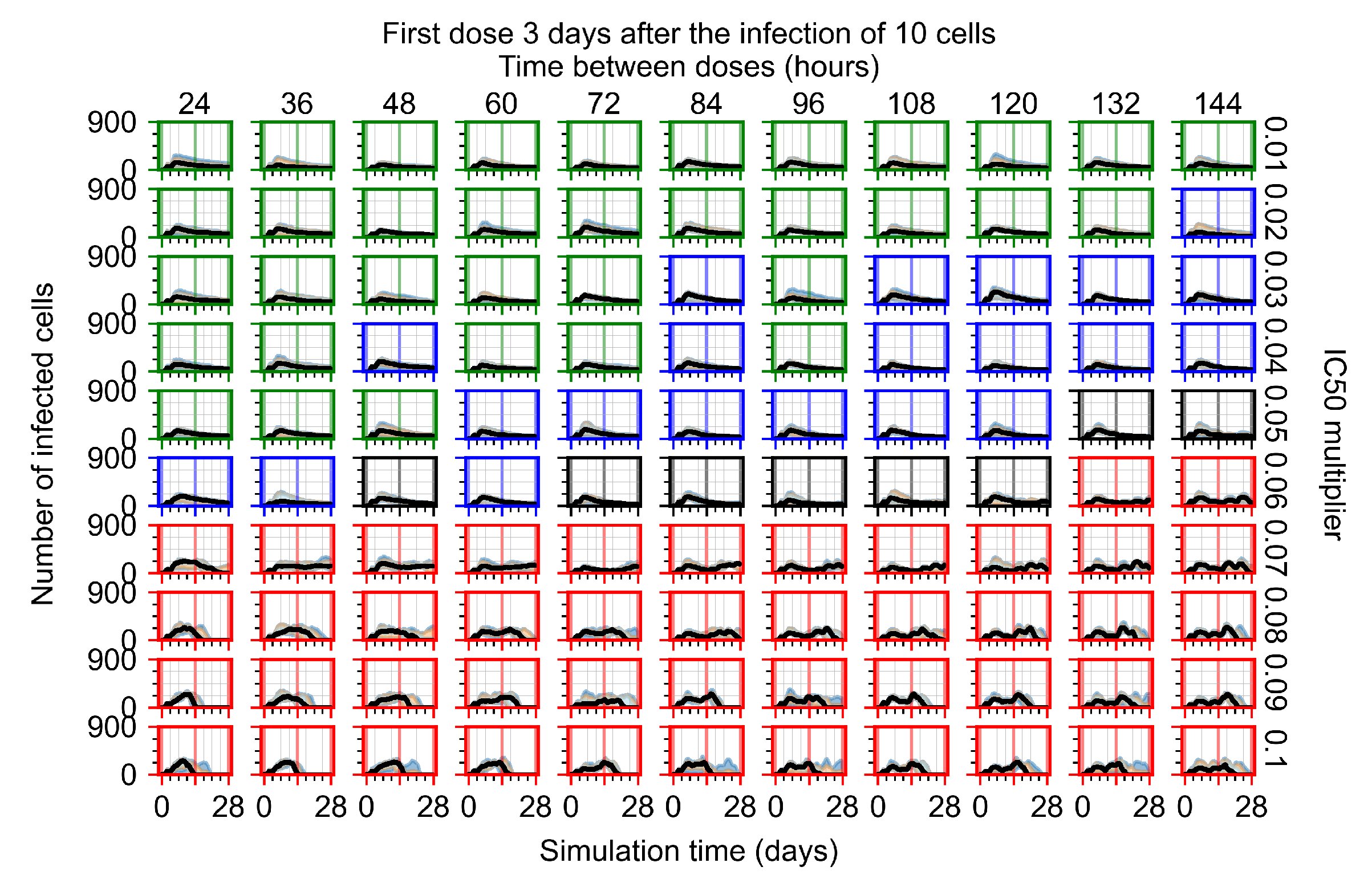

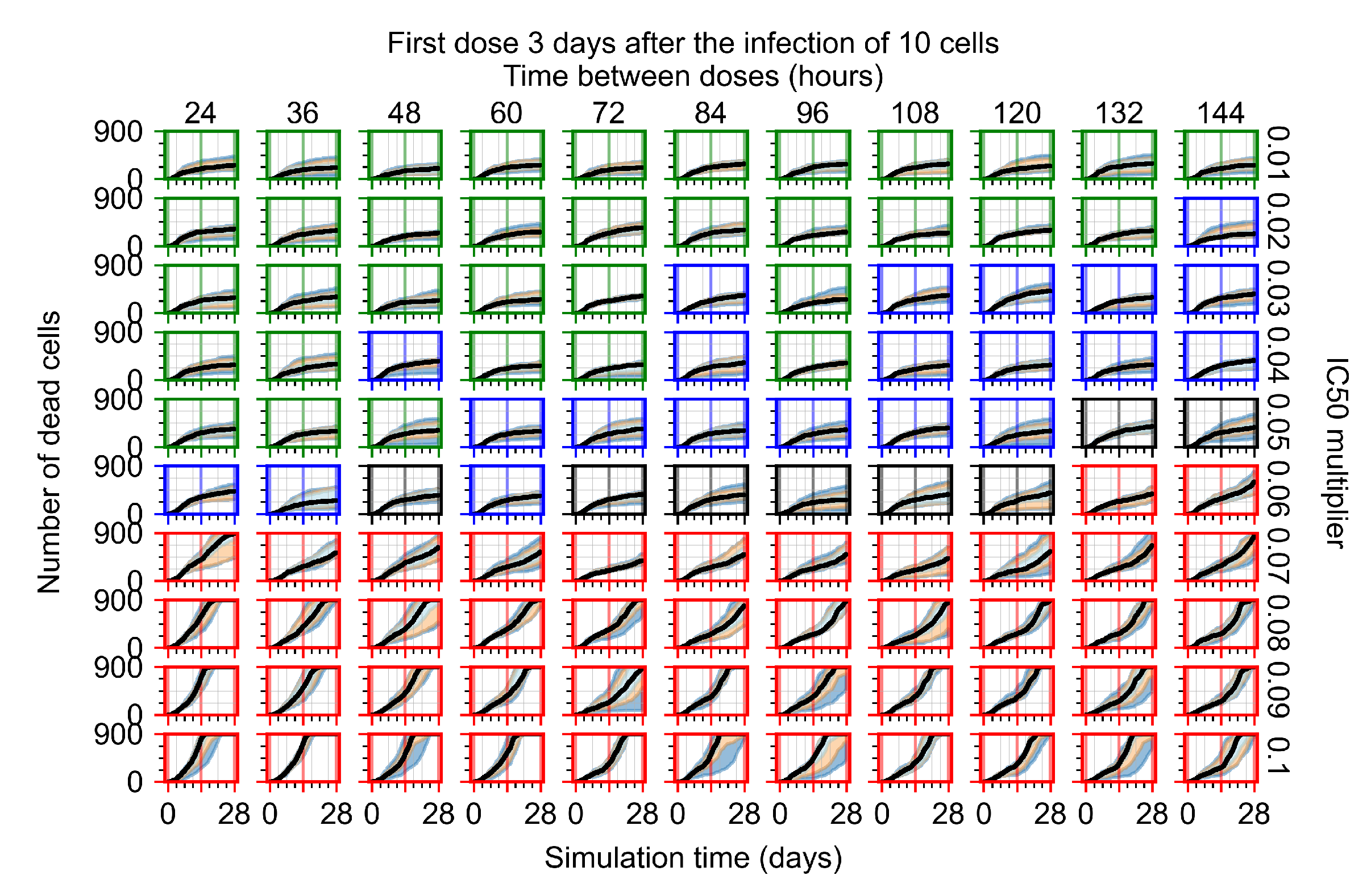
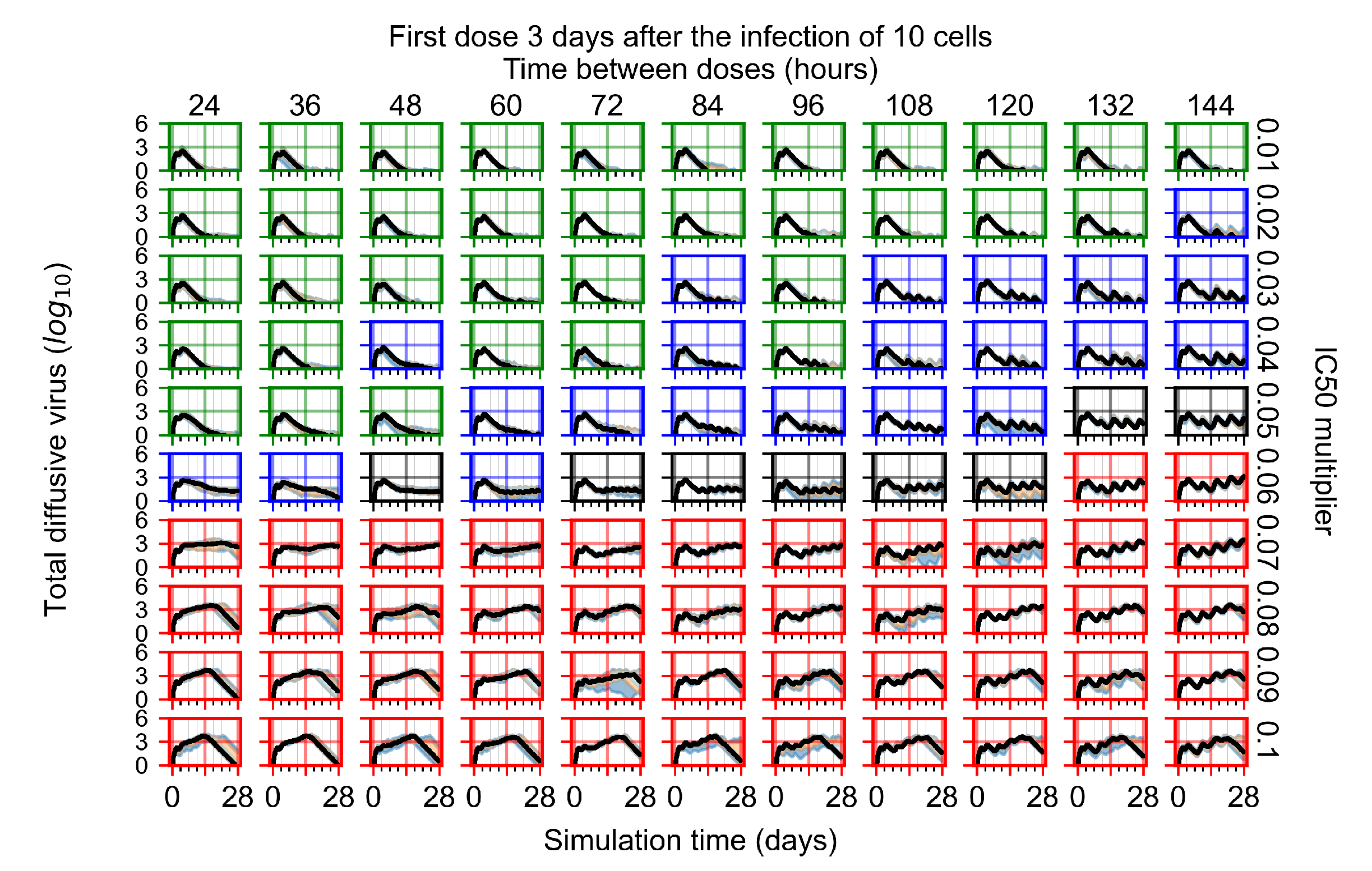


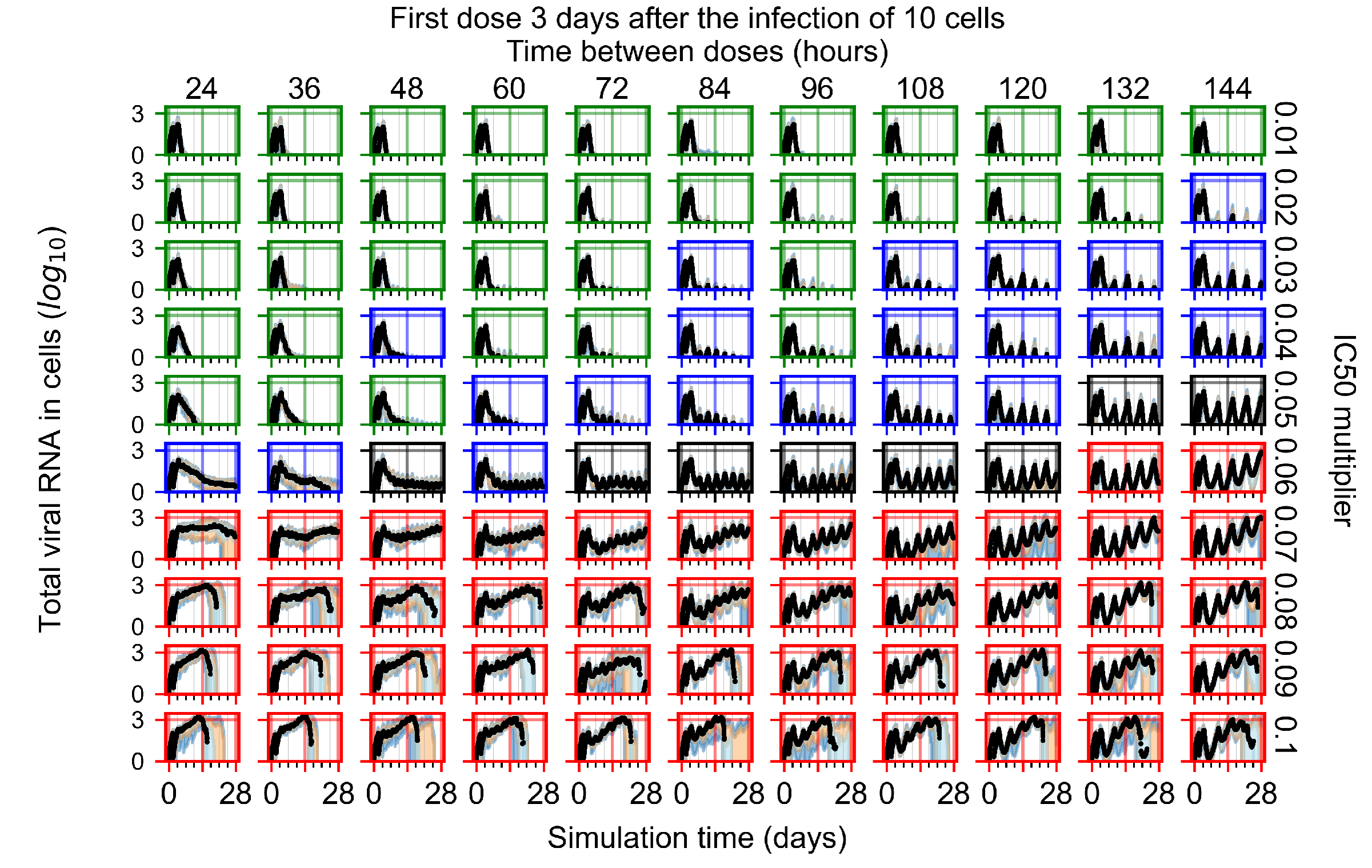
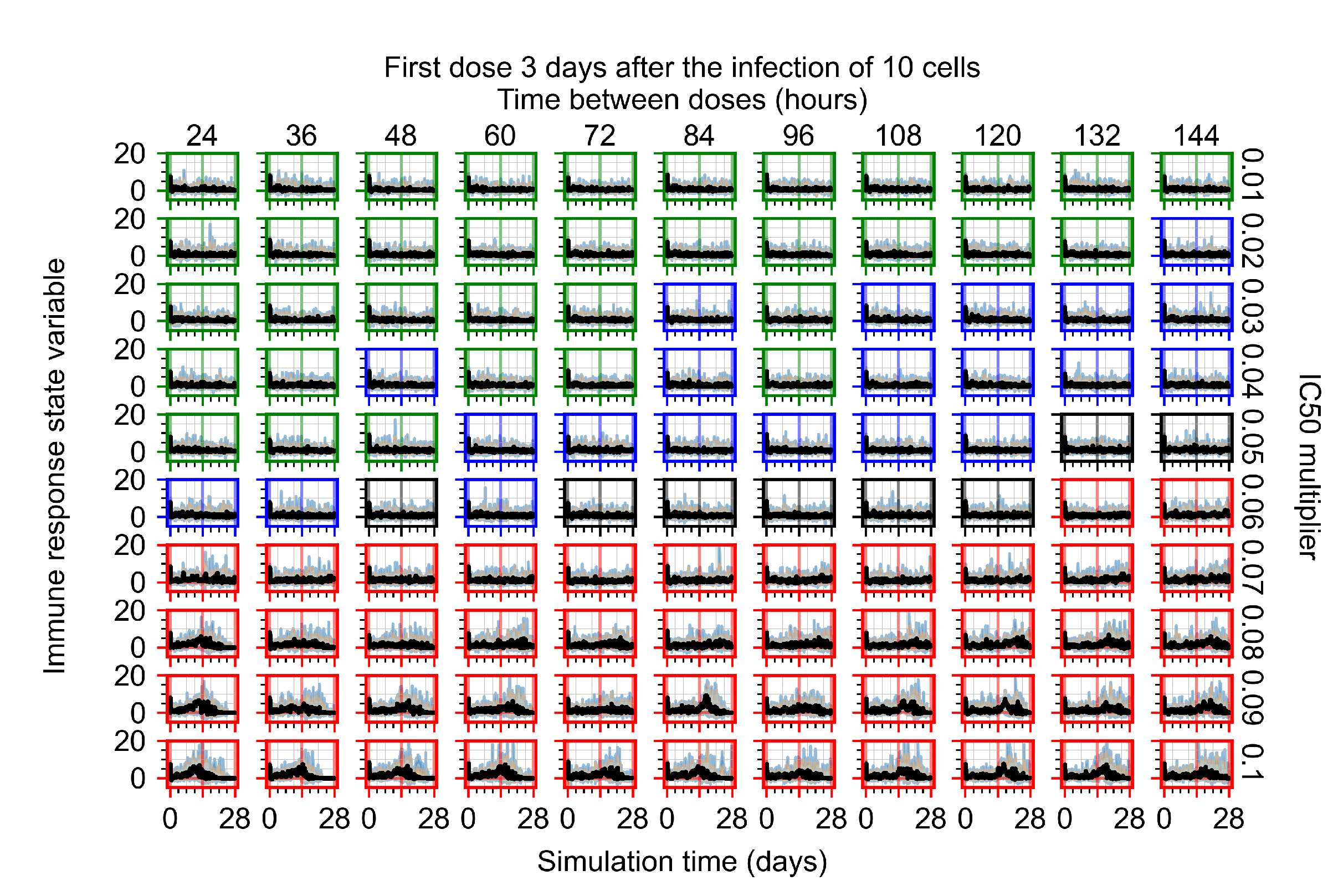
Appendix F.2. Homogeneous Metabolism, Halved GS-443902 Half-Life
Appendix F.2.1. Treatment Initiation with Infection of Ten Epithelial Cells

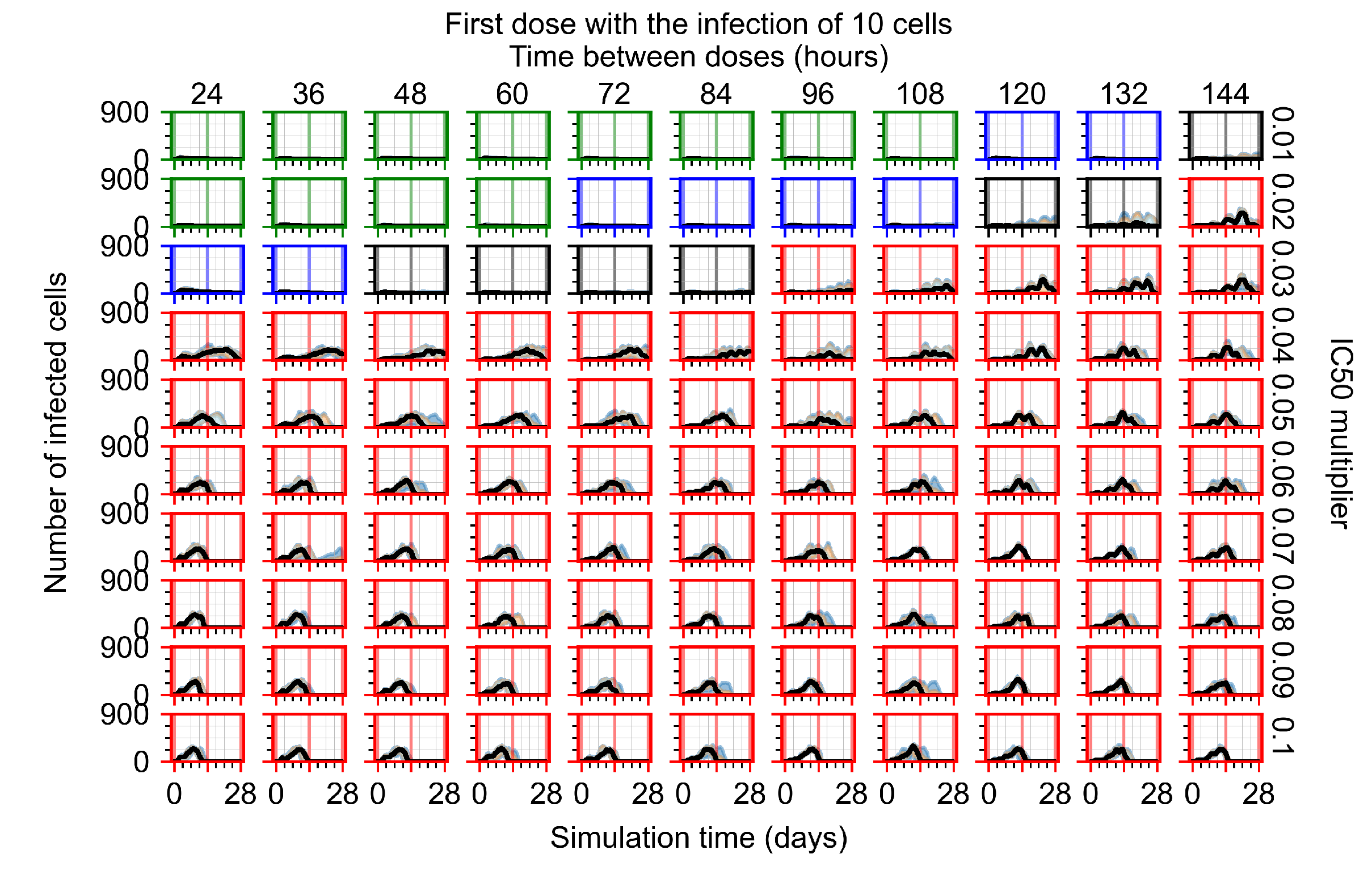
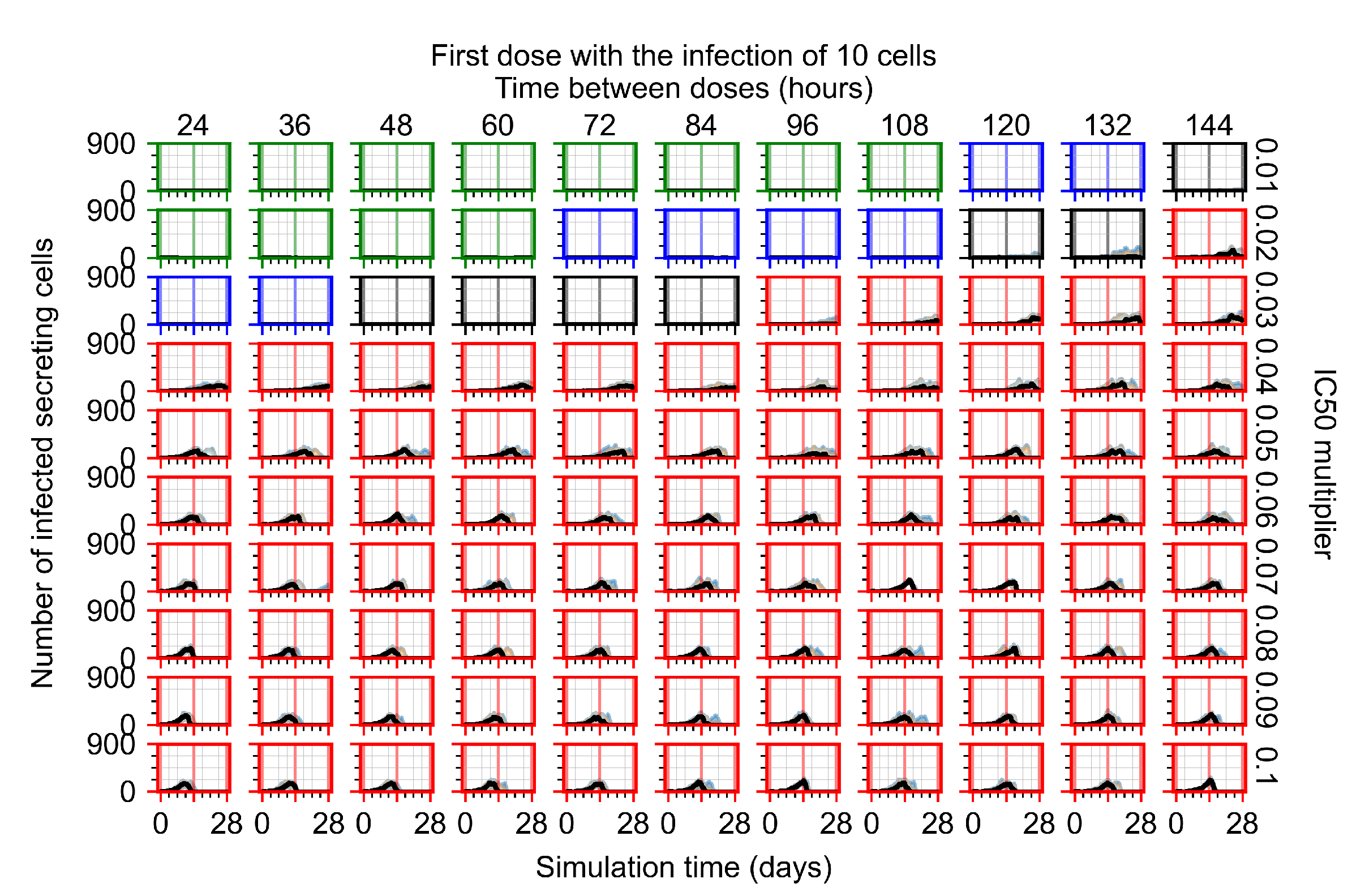
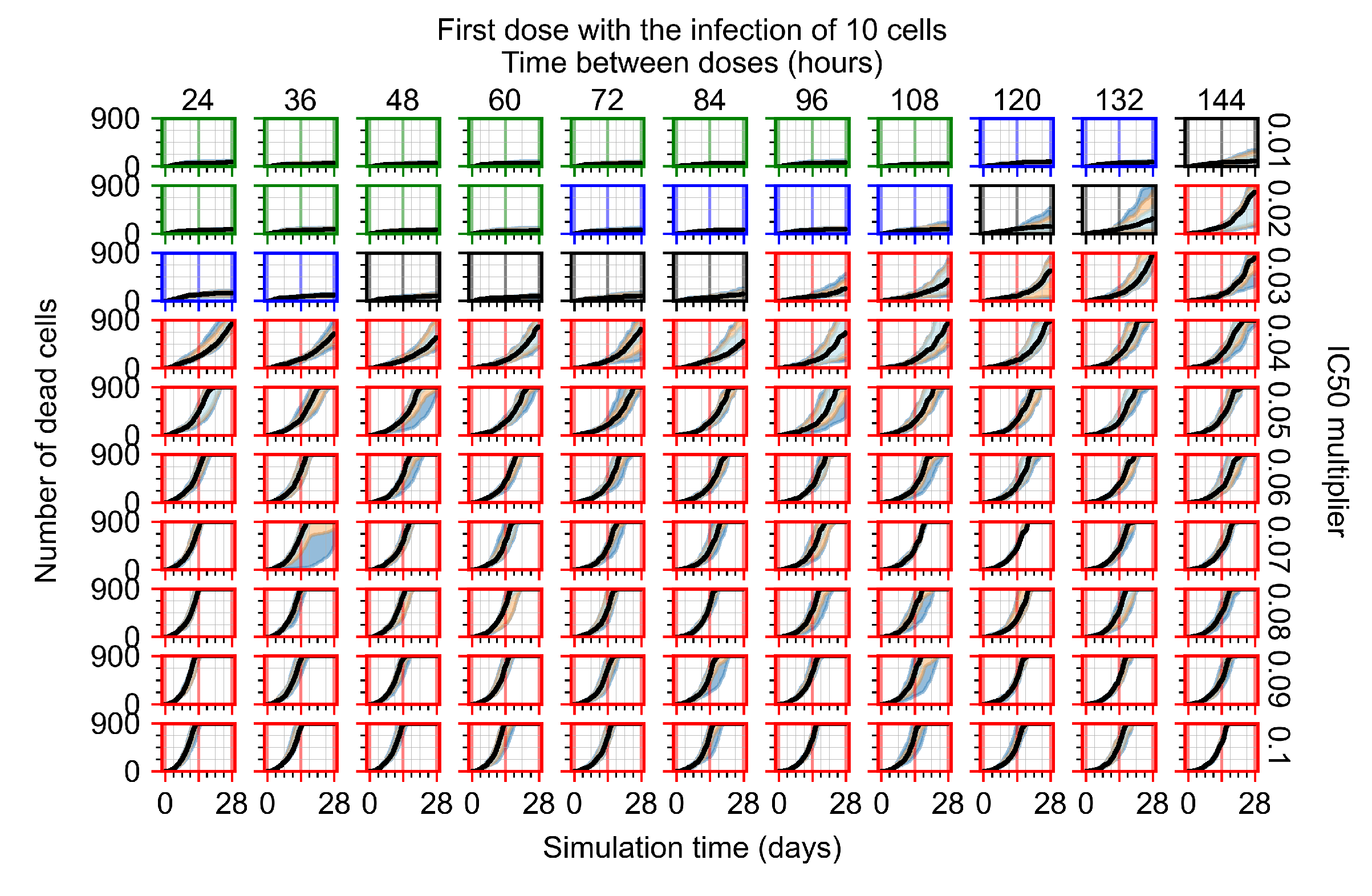
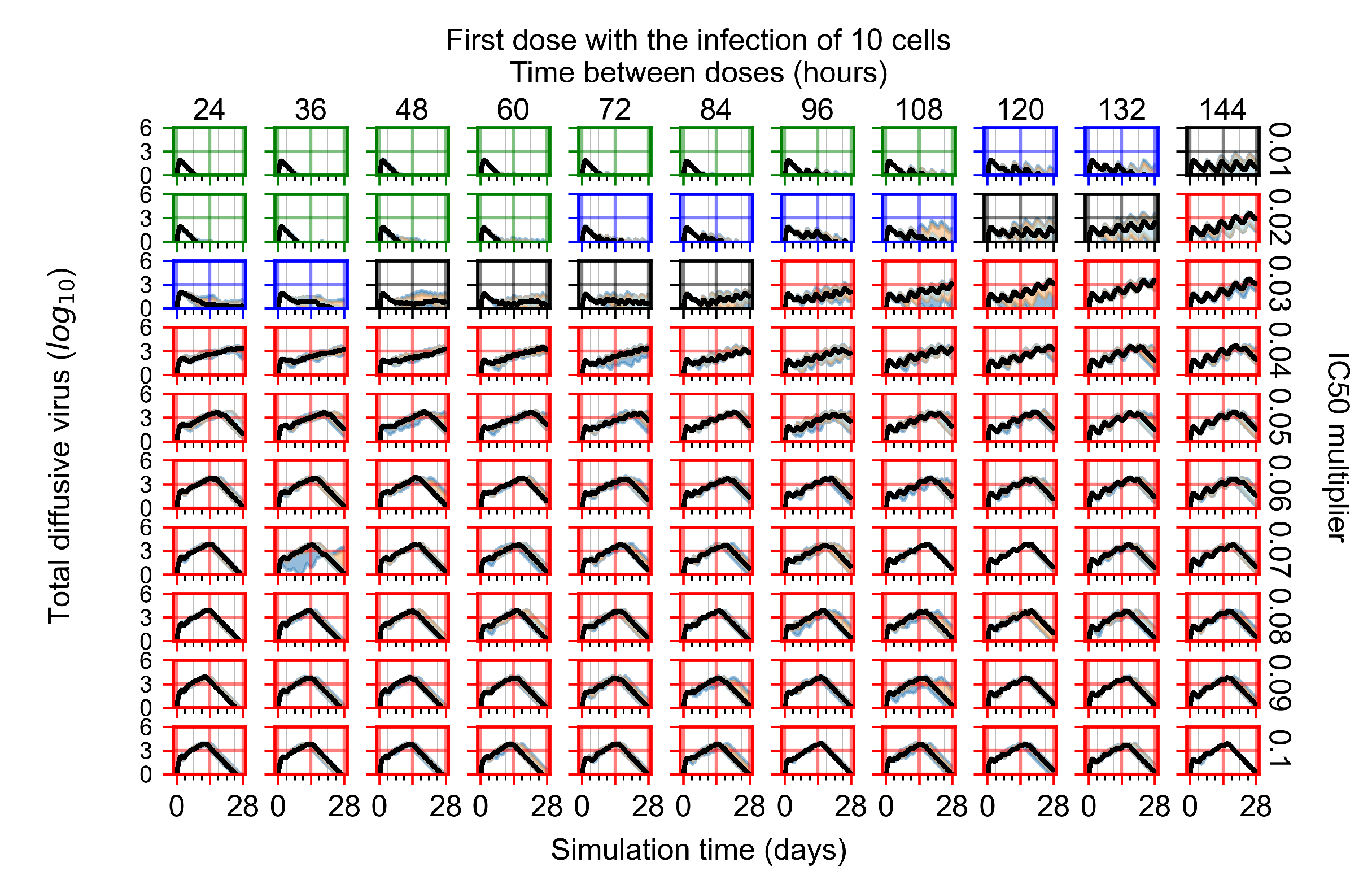
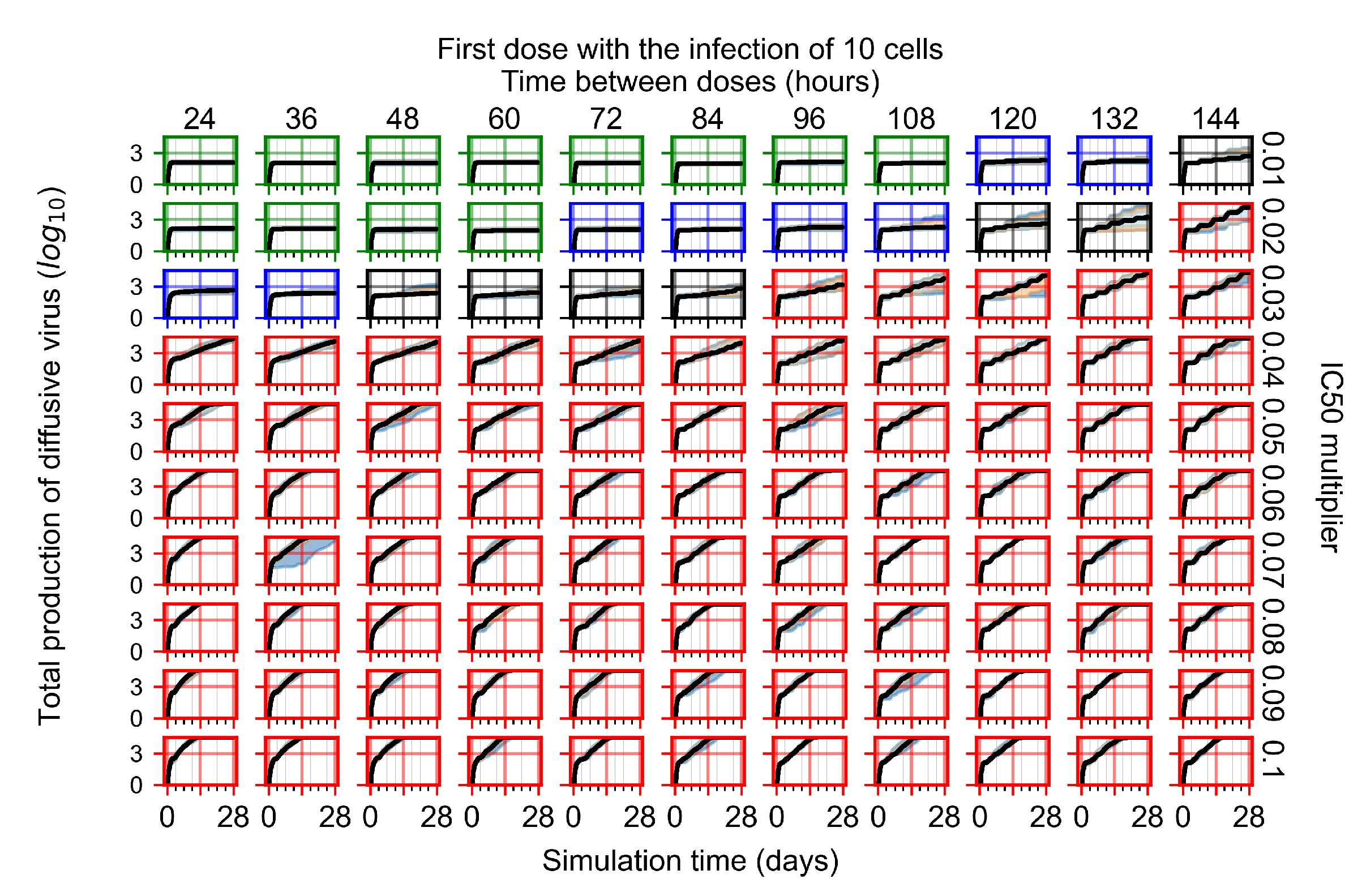
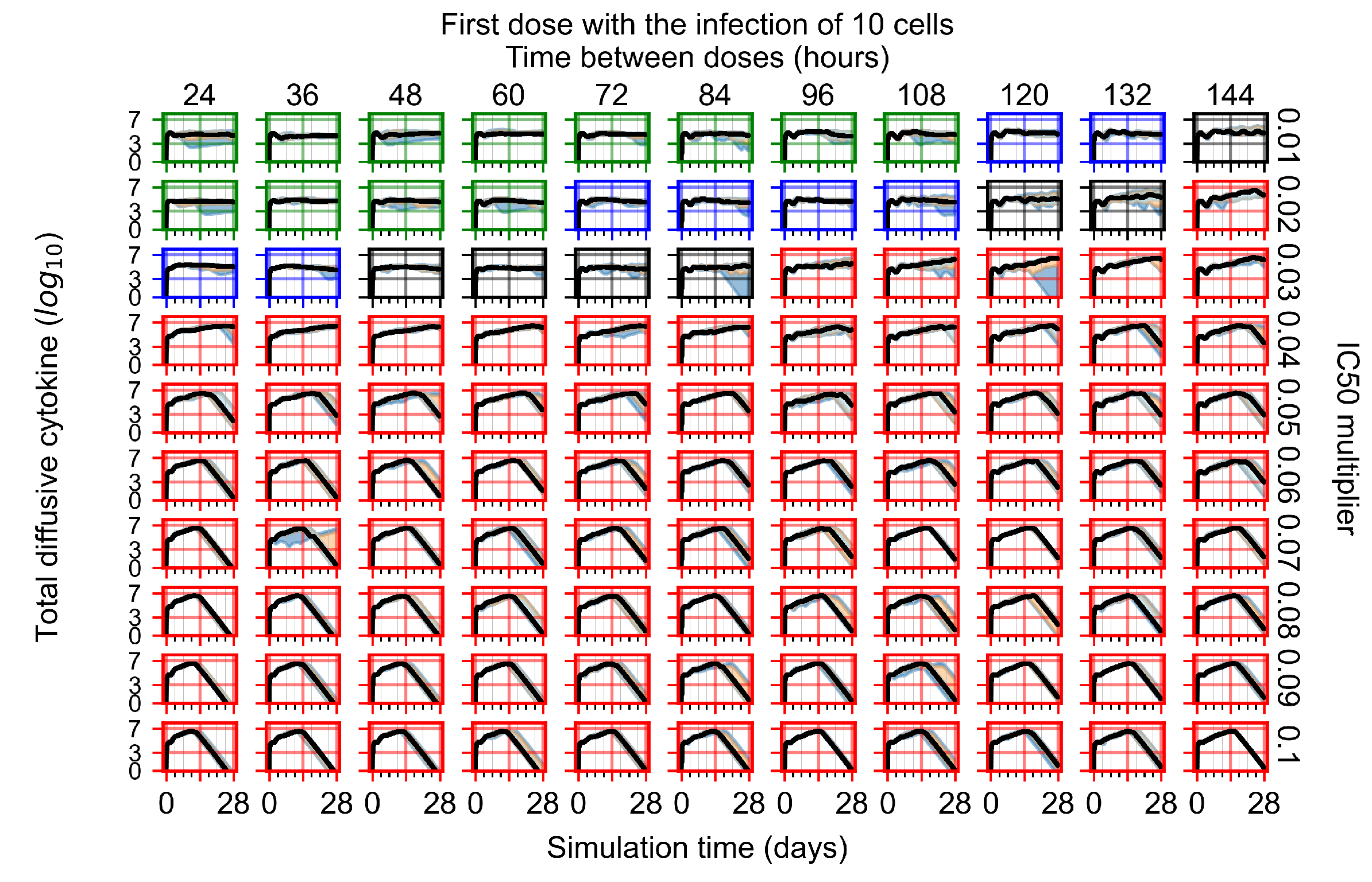
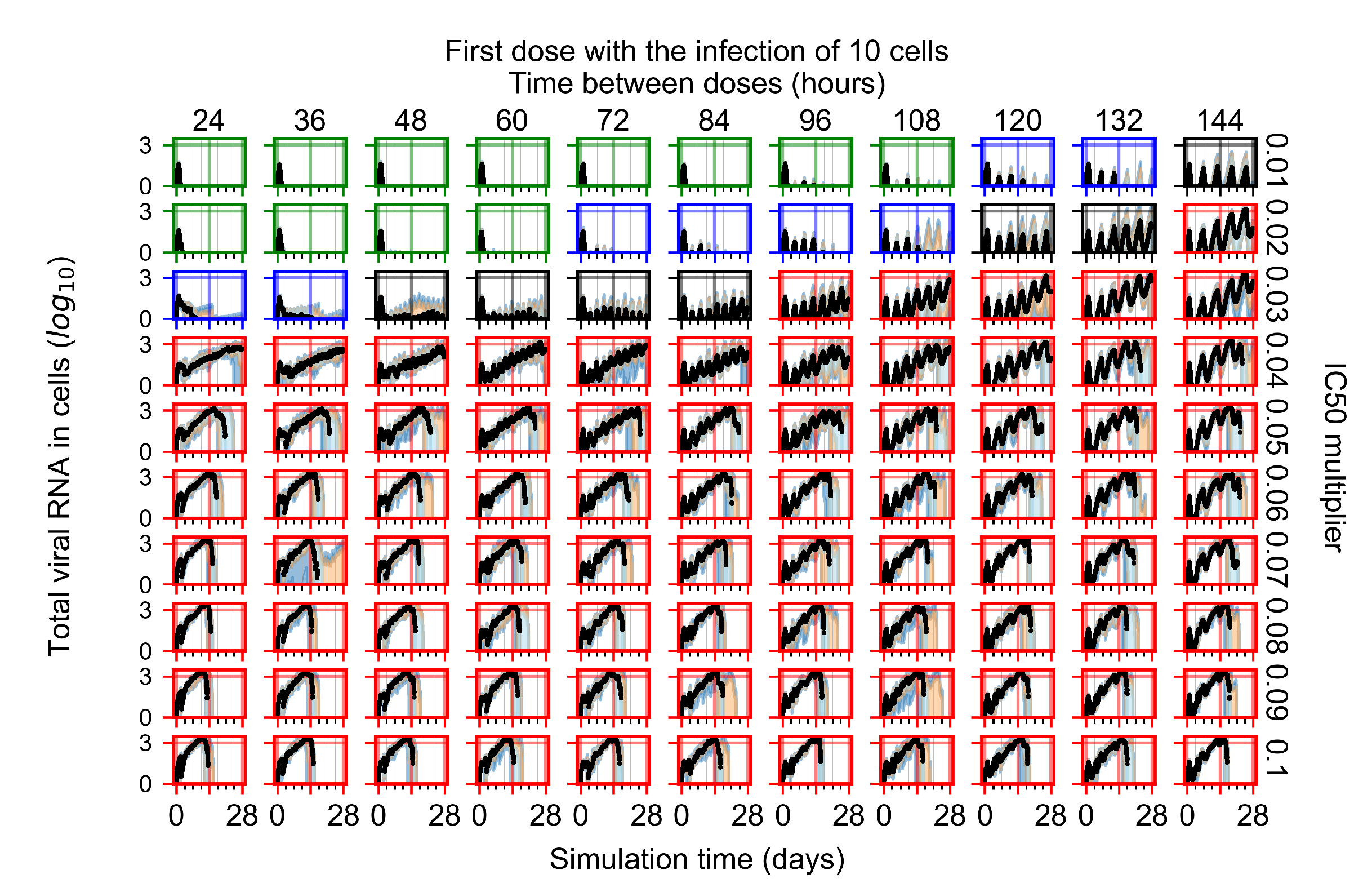
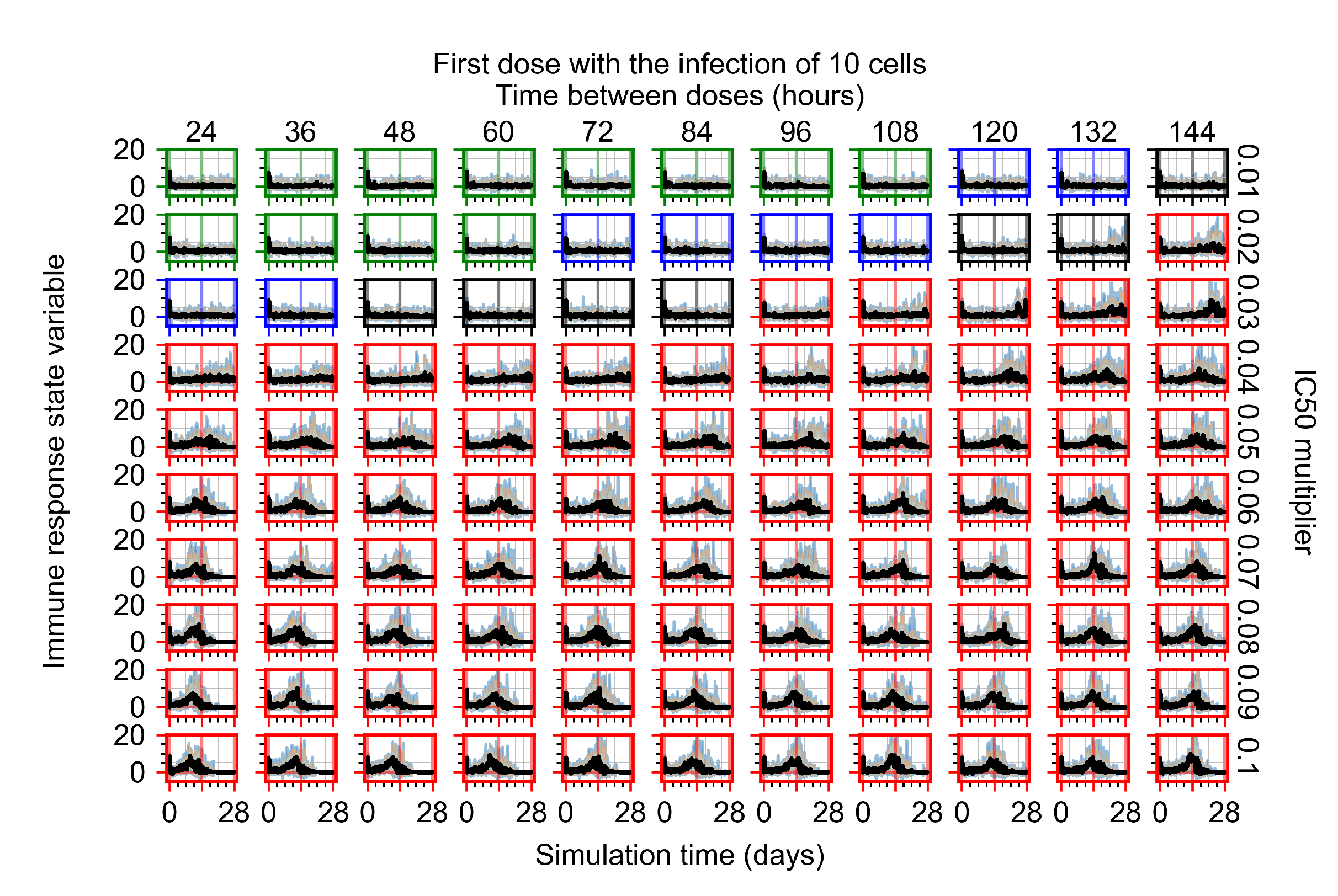
Appendix F.2.2. Treatment Initiation One Day Post Infection of Ten Epithelial Cells


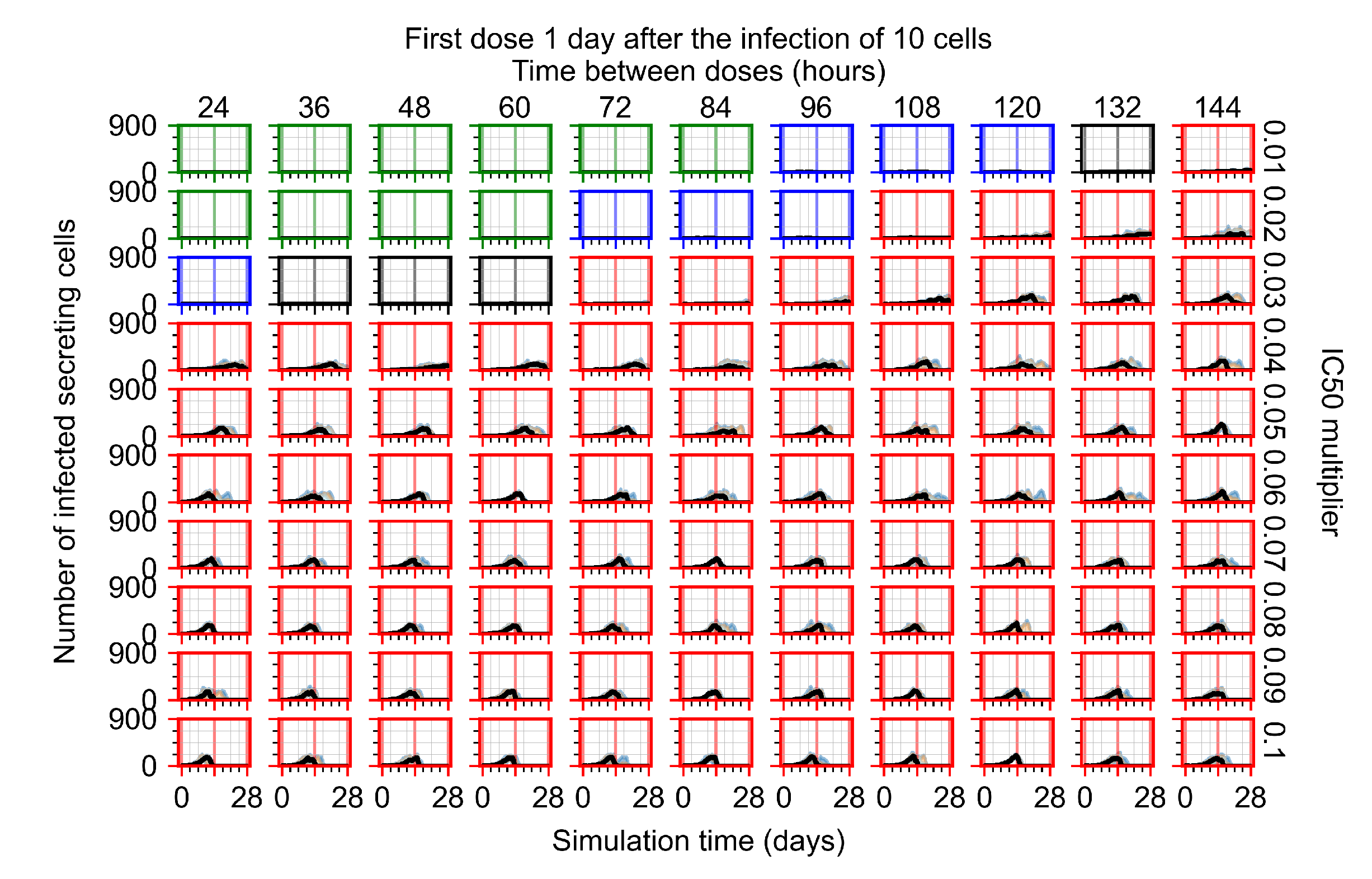
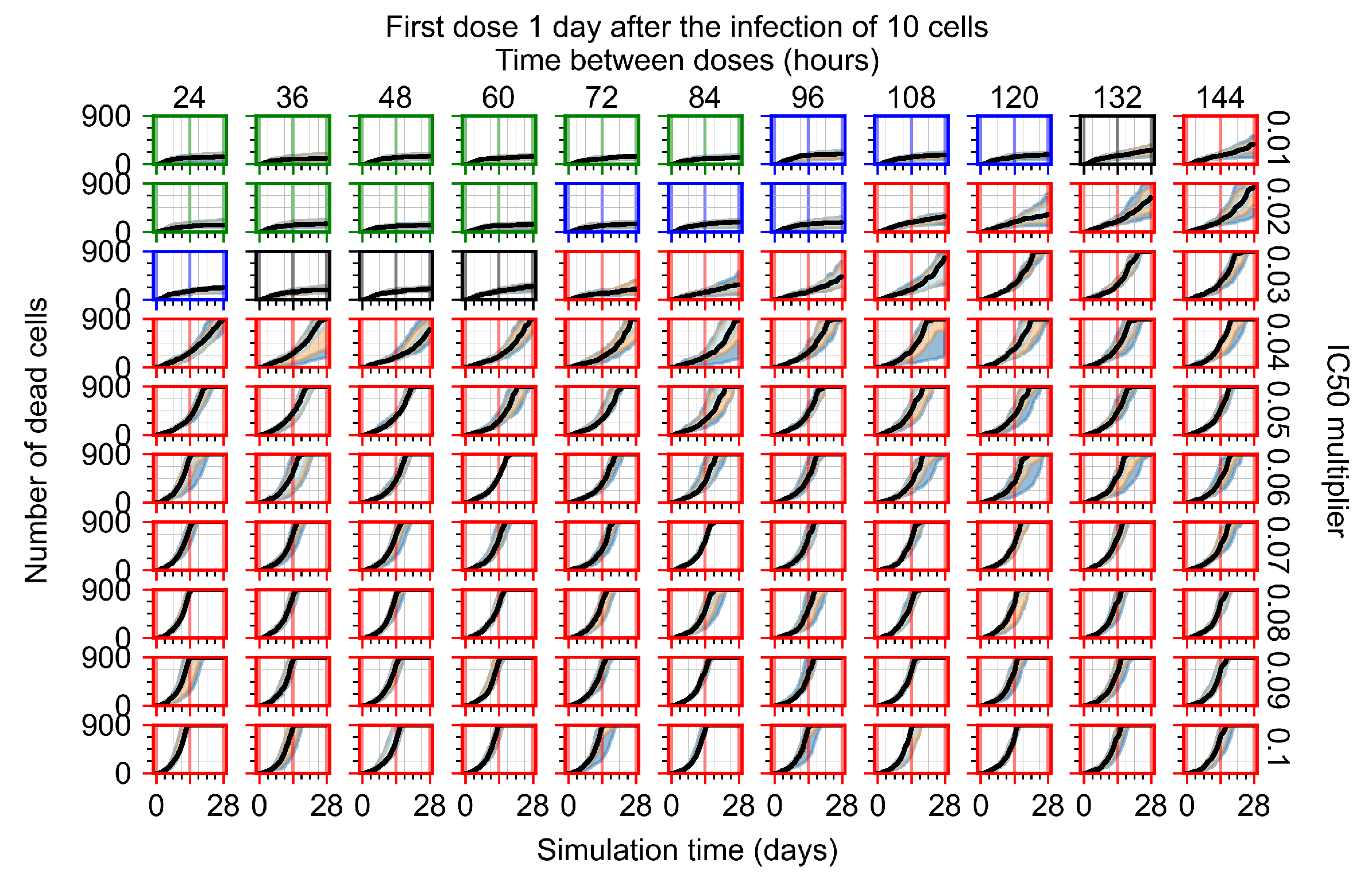
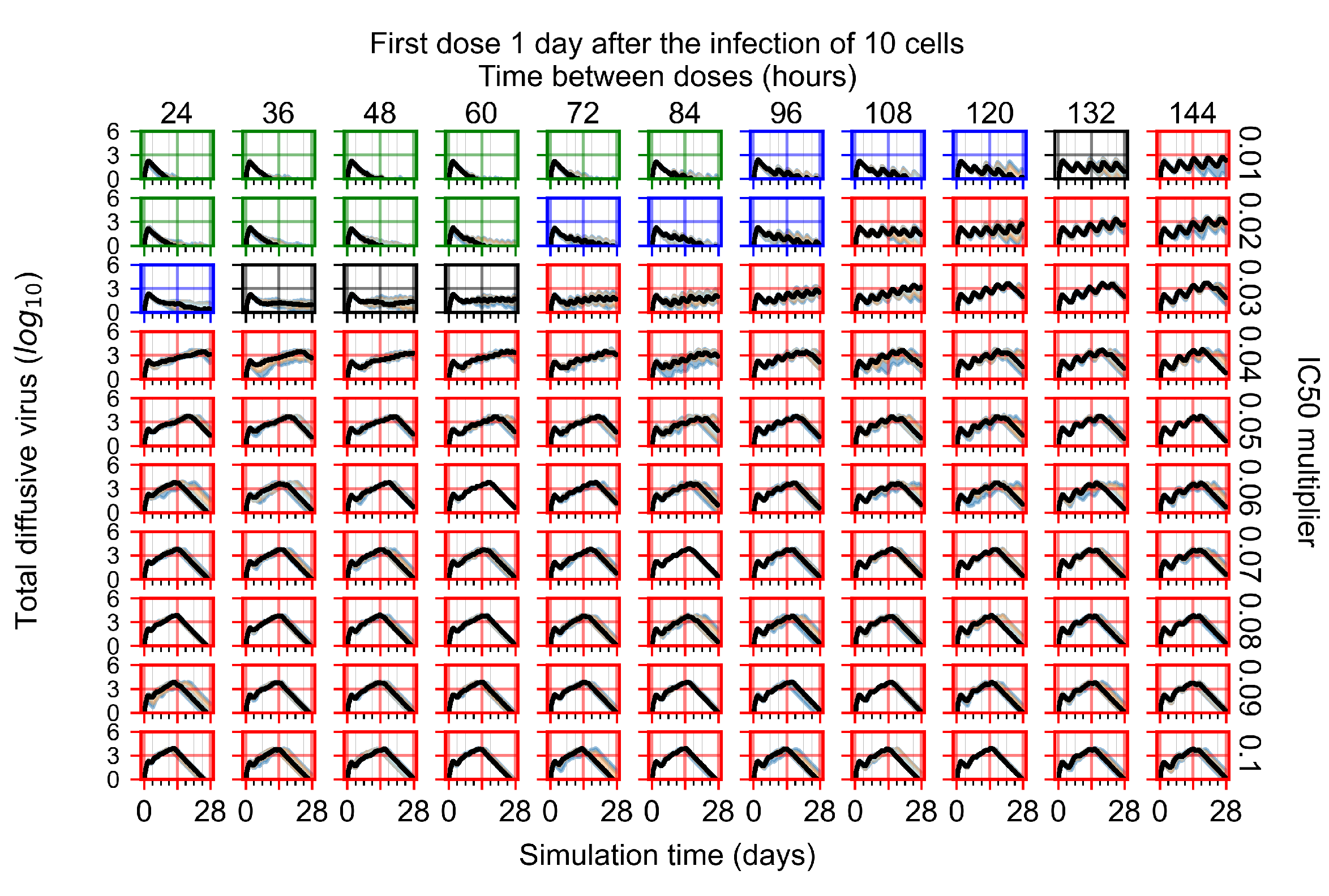
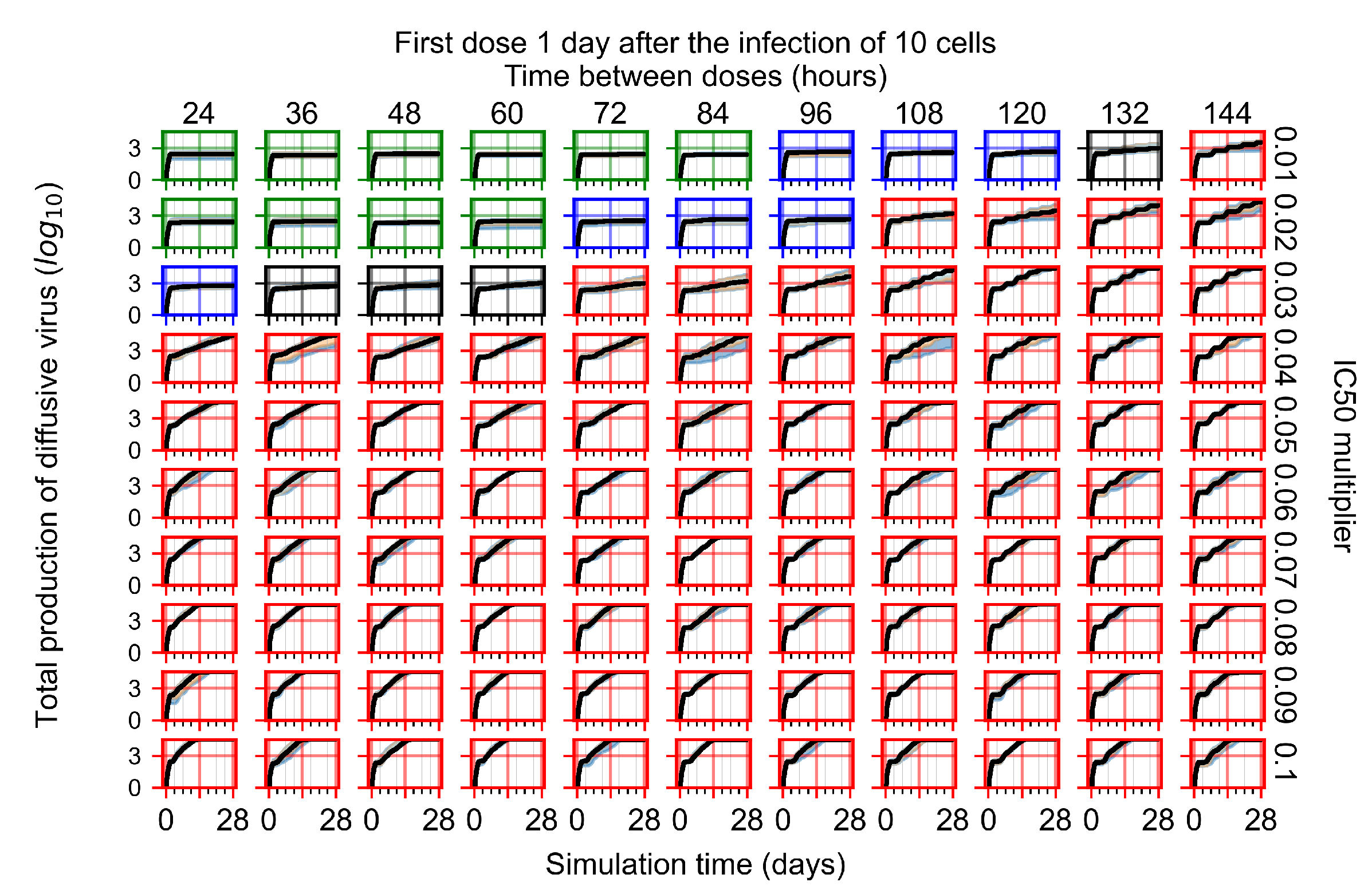


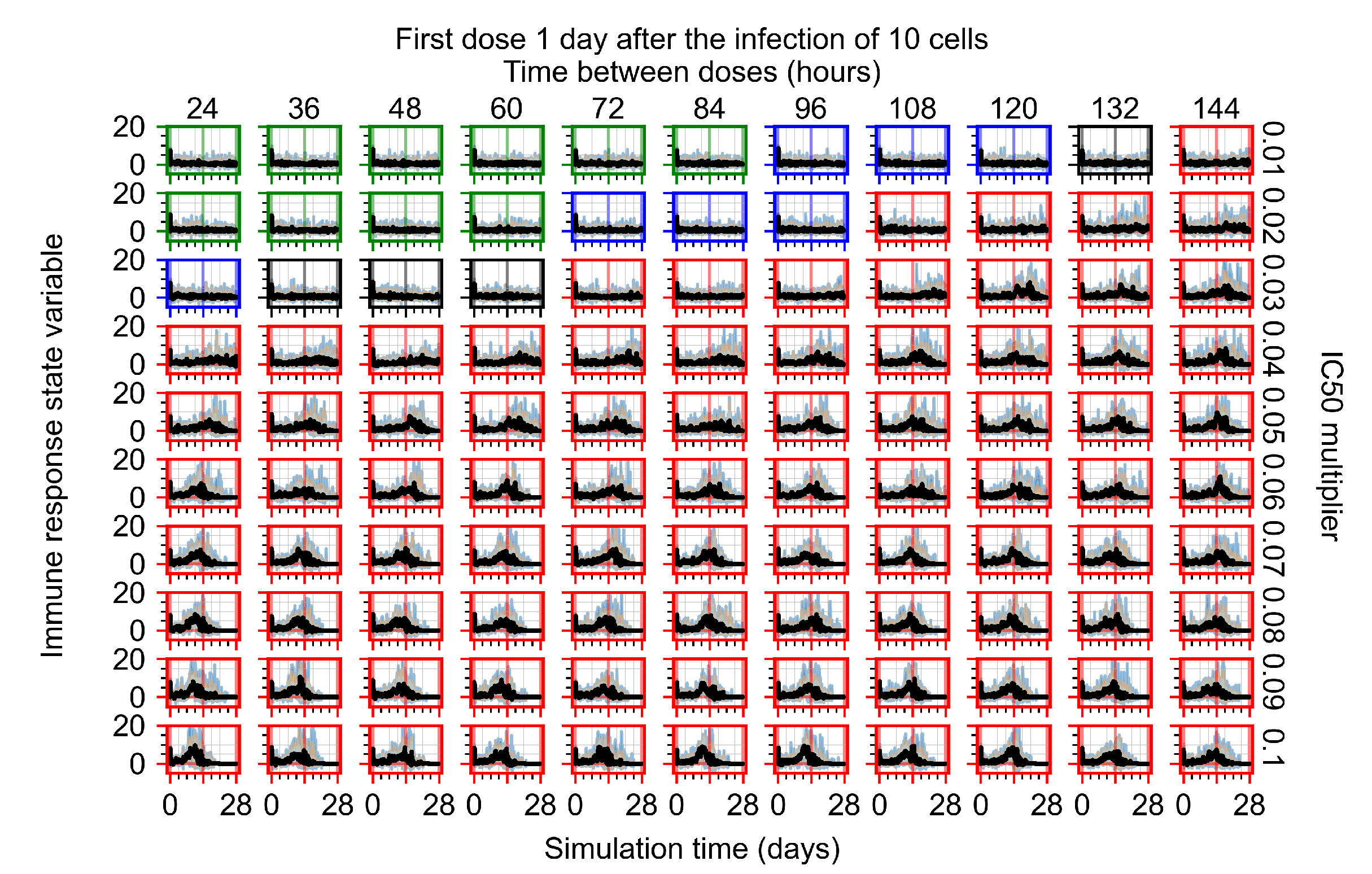
Appendix F.2.3. Treatment Initiation Three Days Post Infection of Ten Epithelial Cells

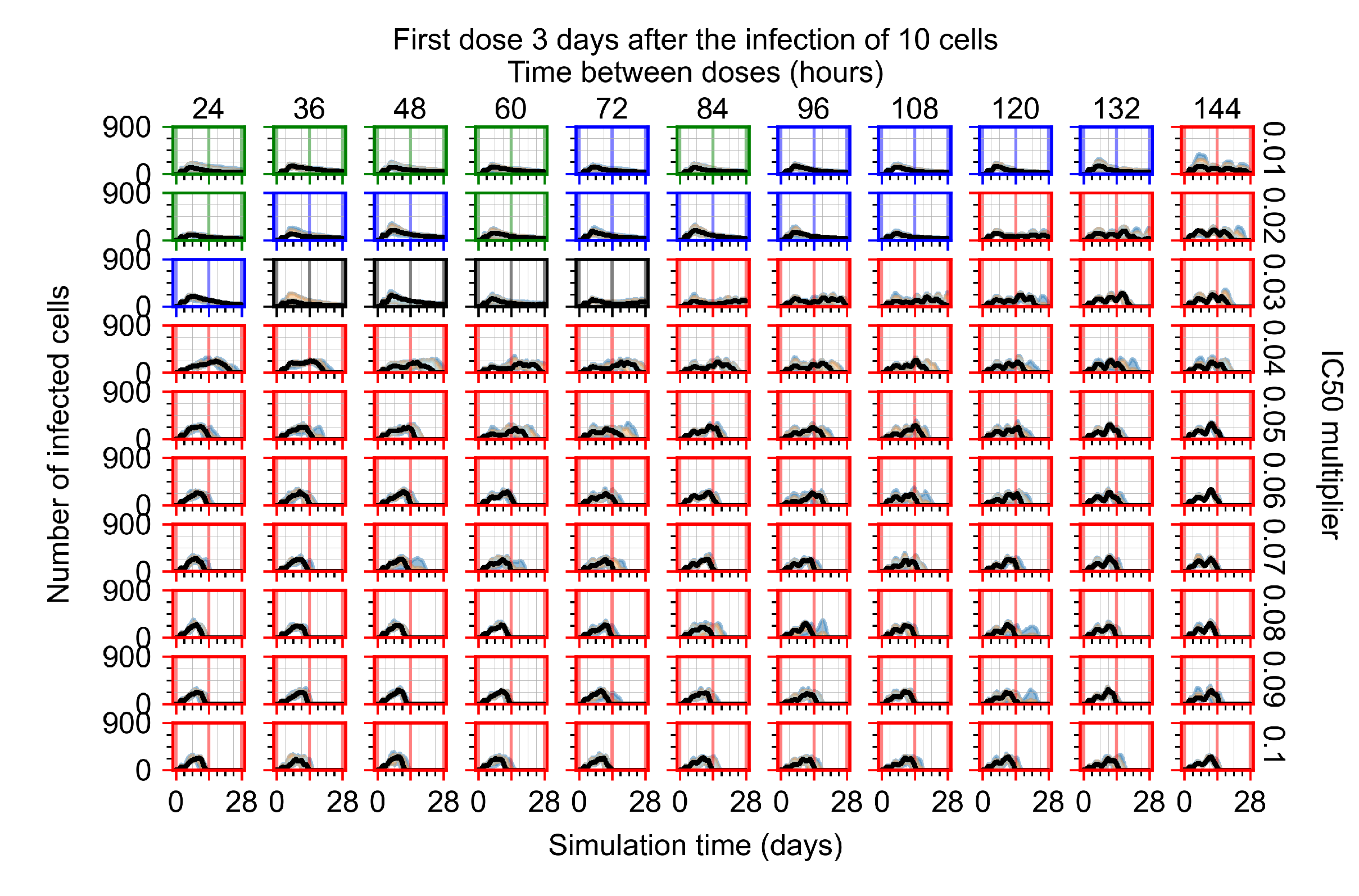
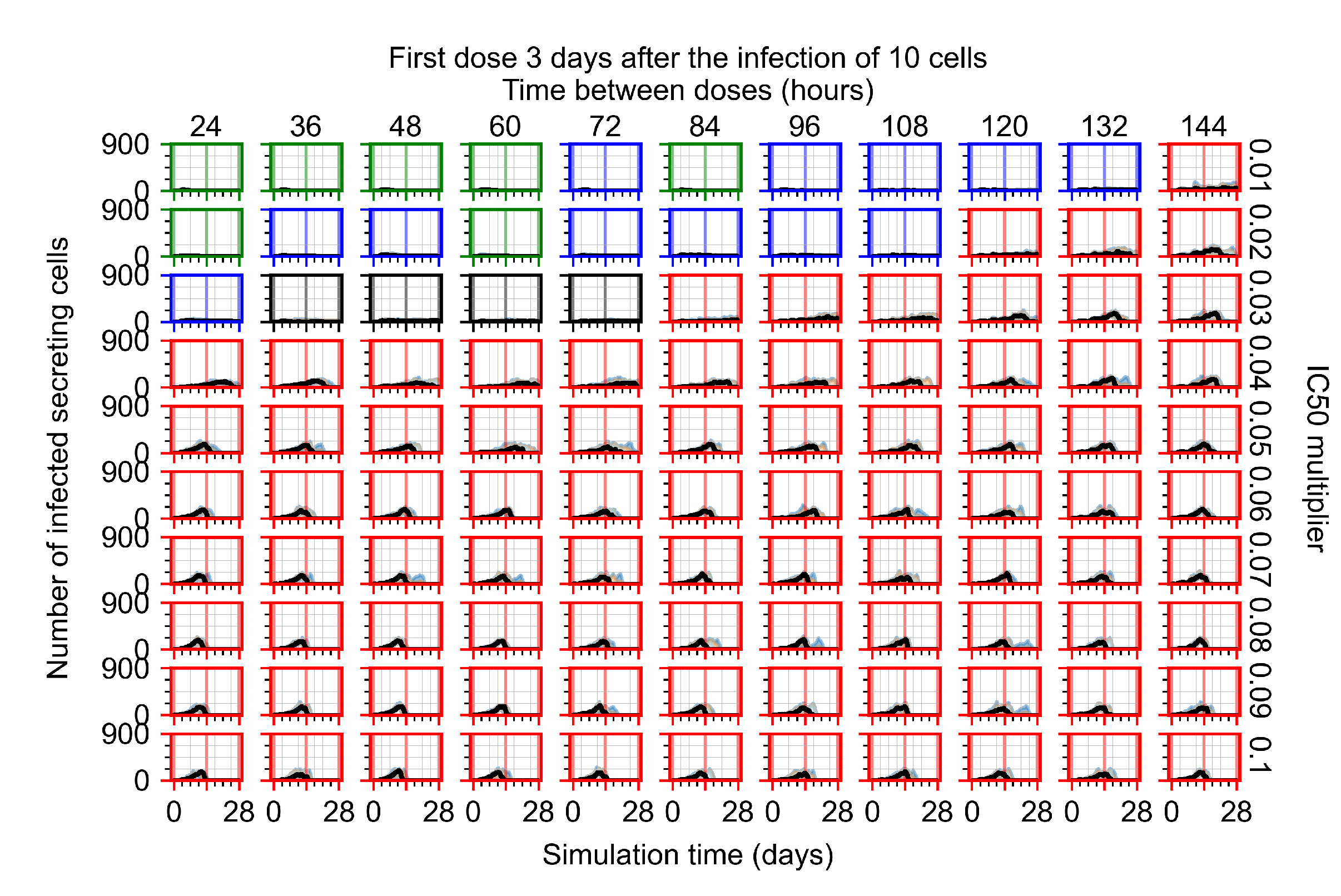
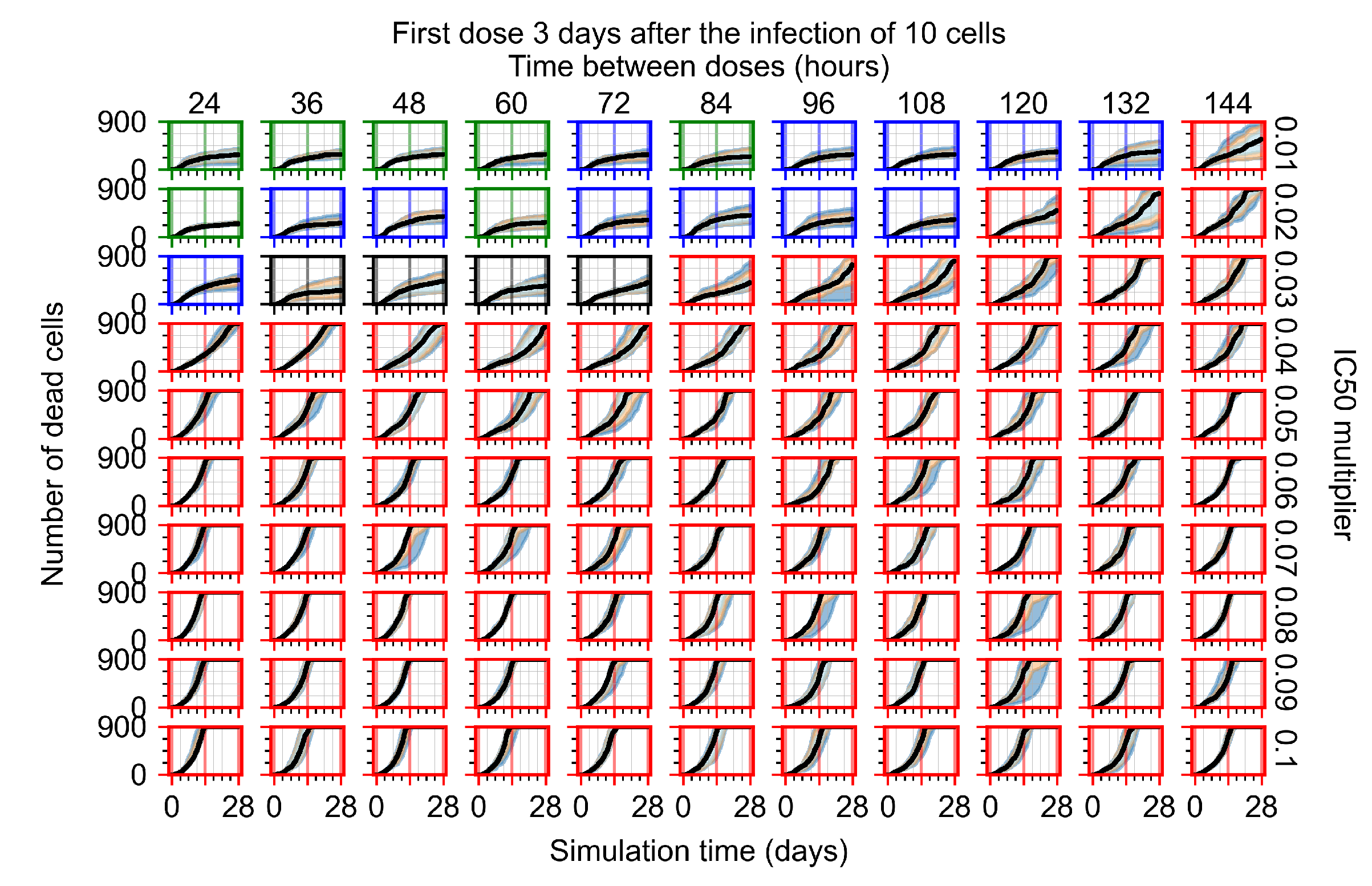


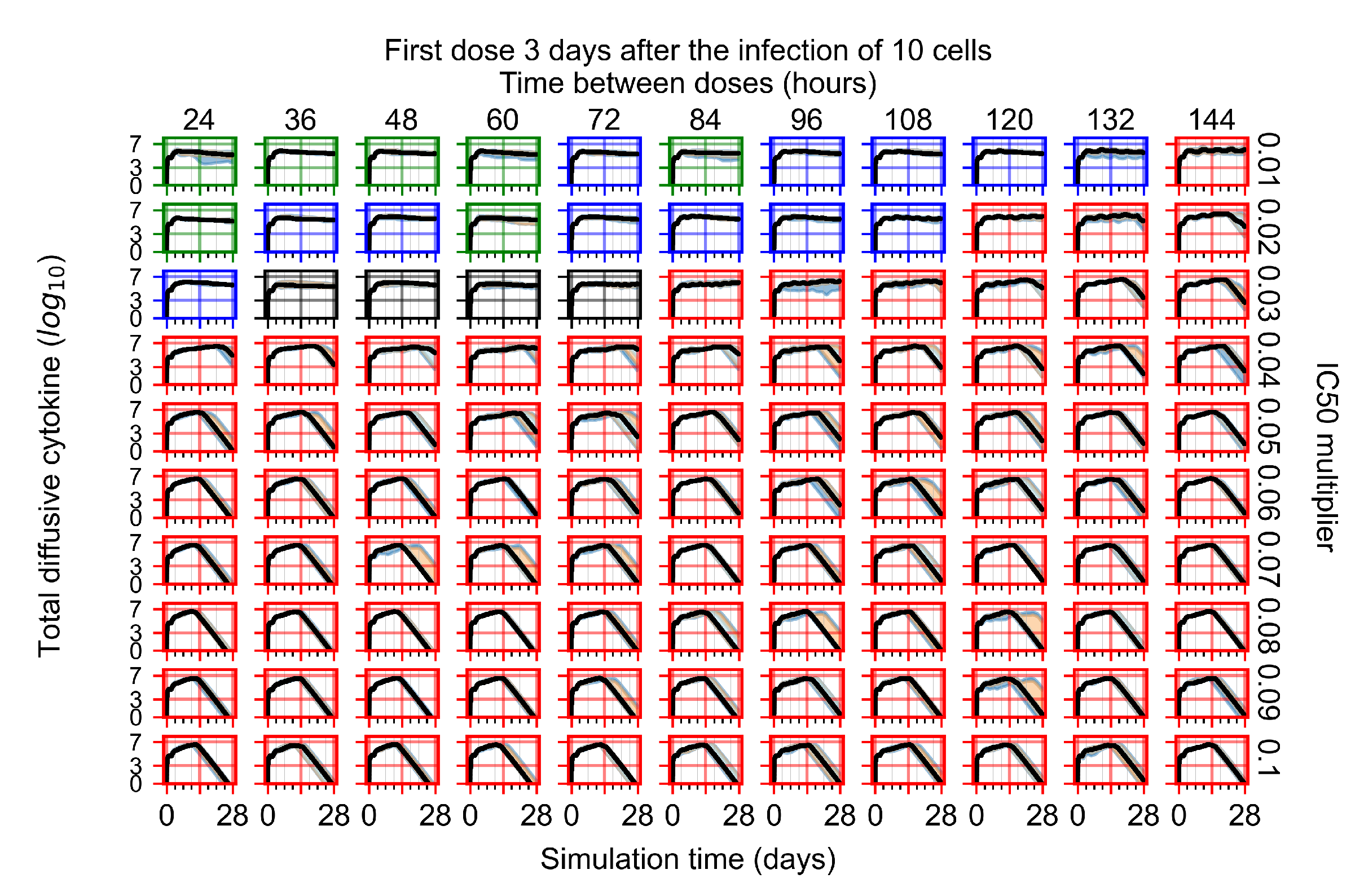
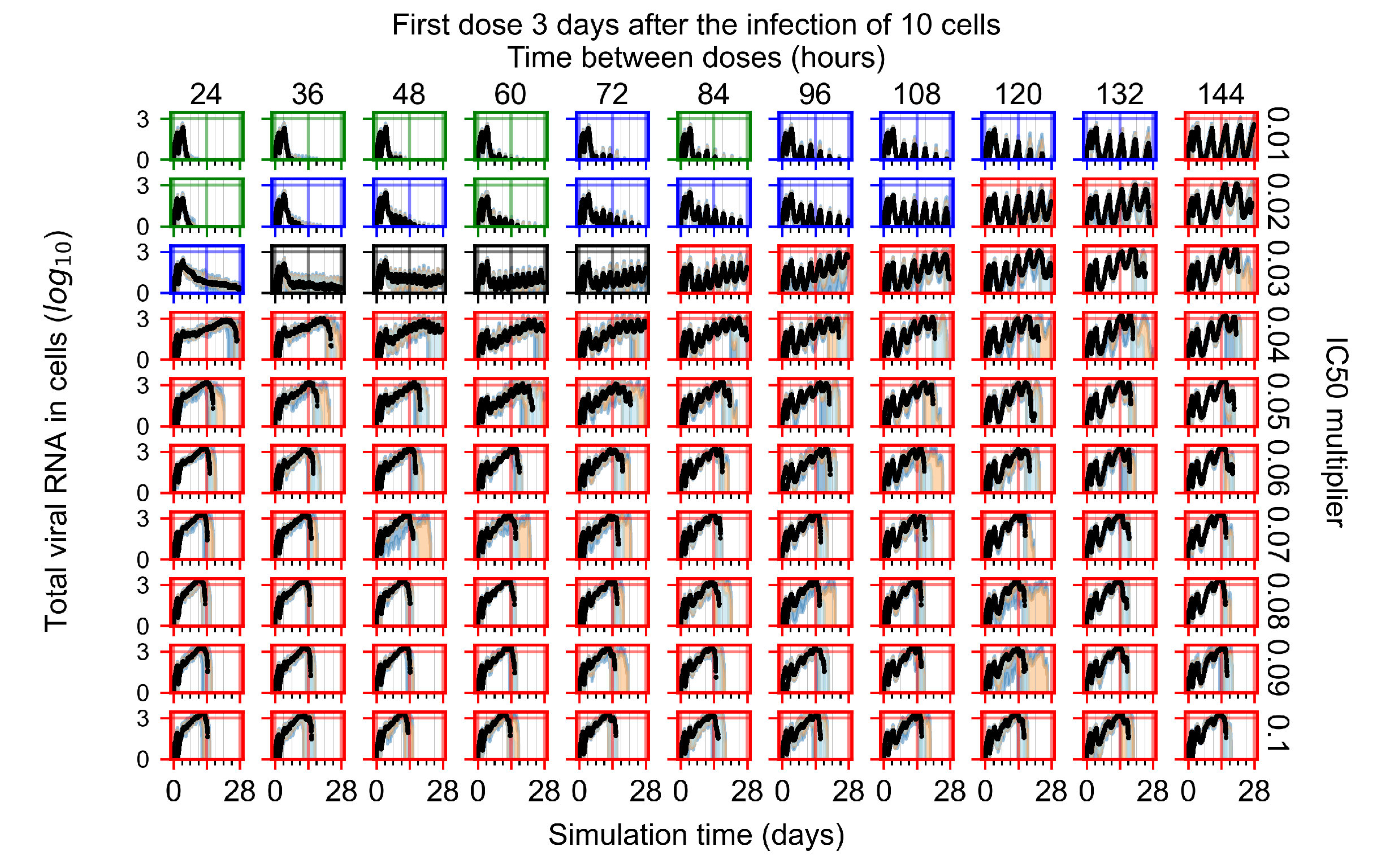
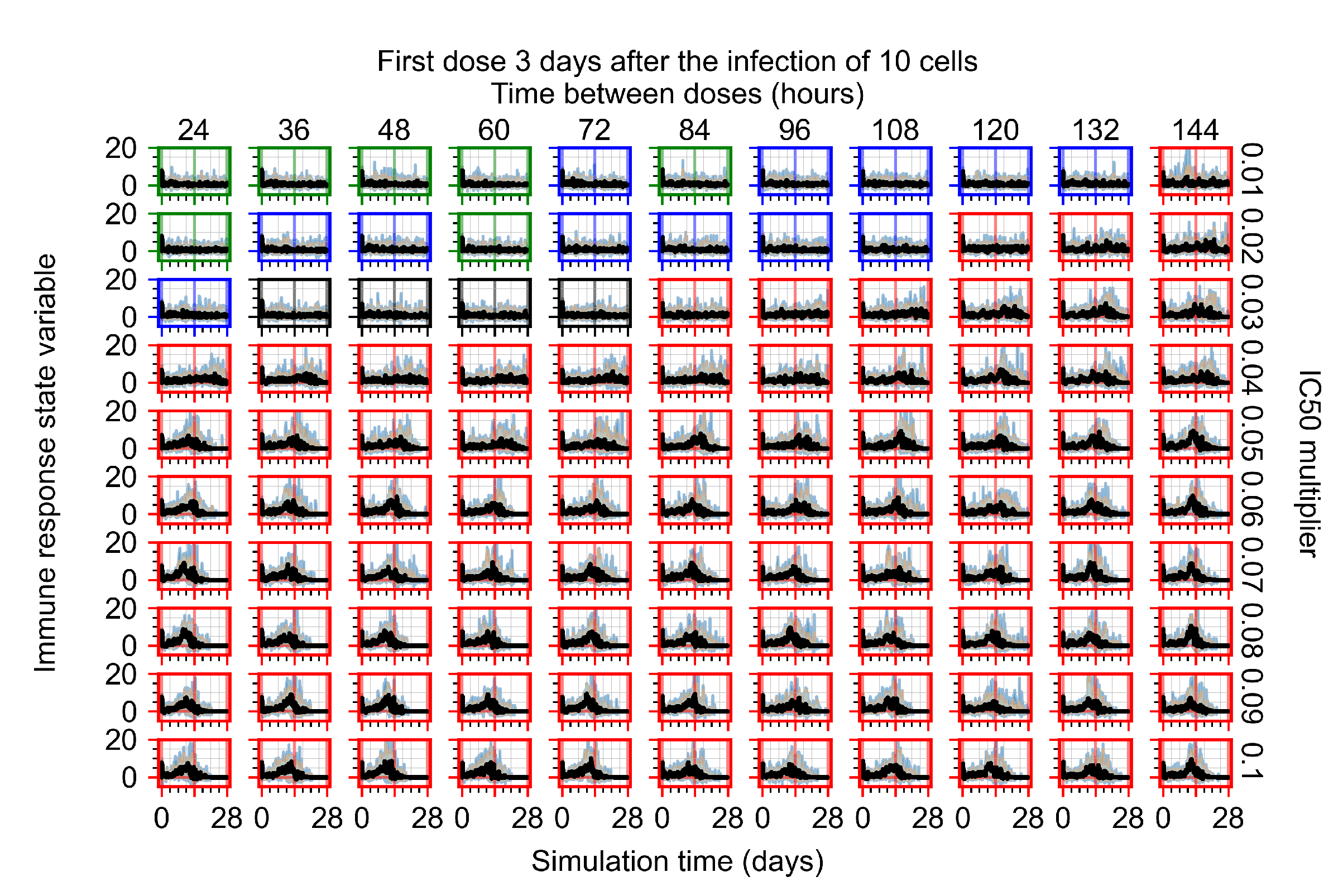
Appendix F.3. Homogeneous Metabolism, GS-443902 Half-Life Reduced by 75%
Treatment Initiation with Infection of Ten Epithelial Cells
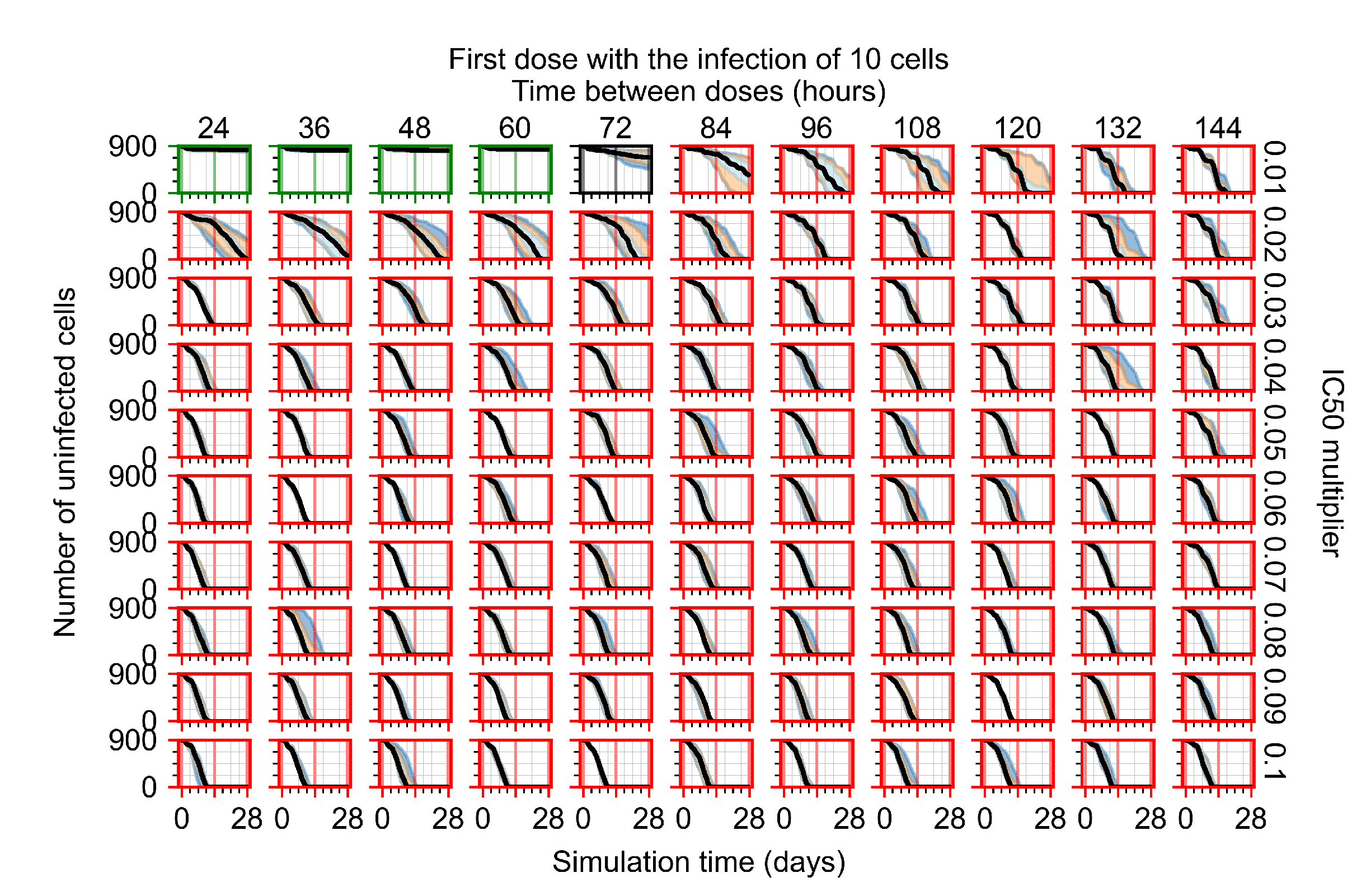



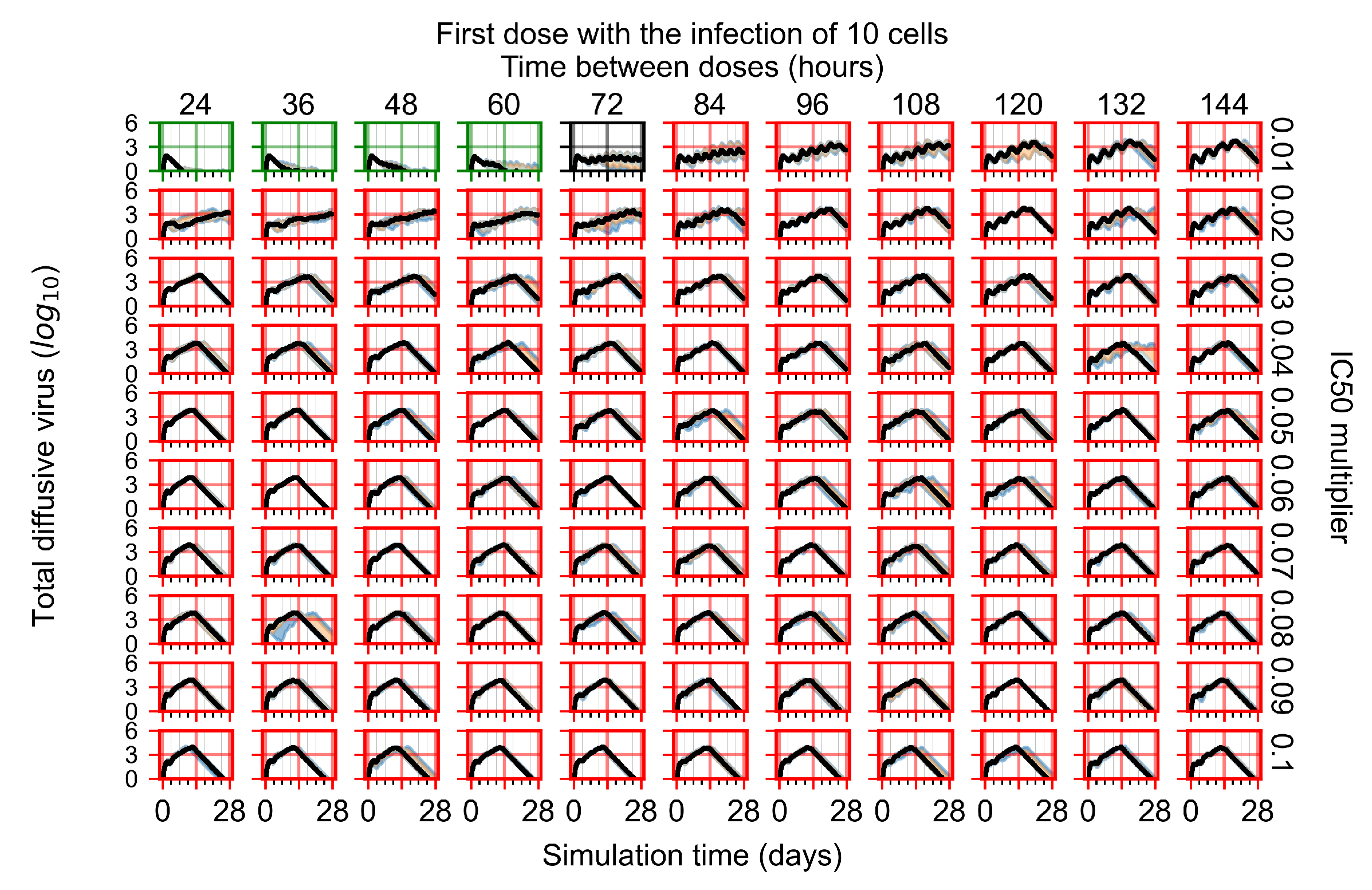
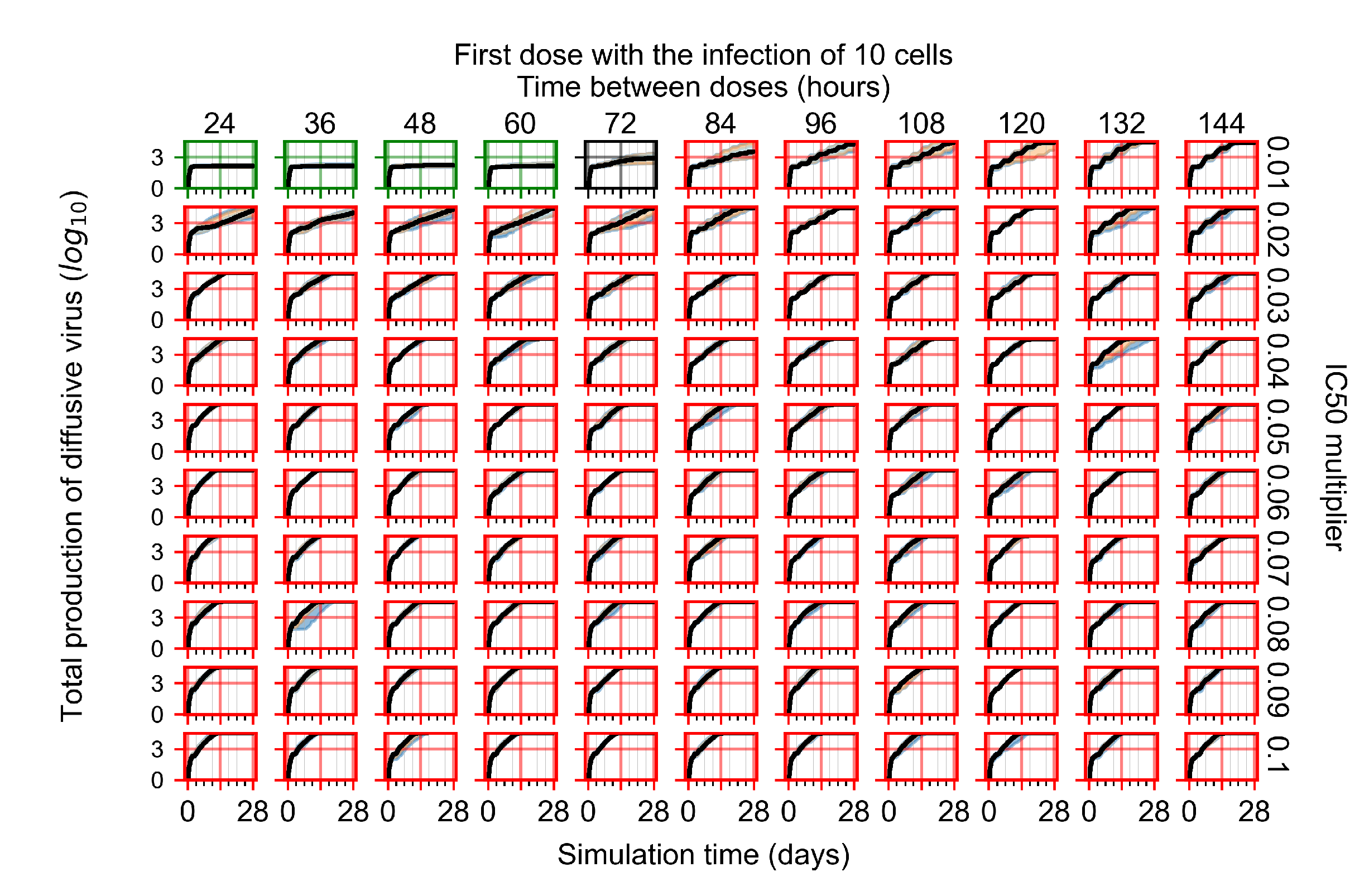
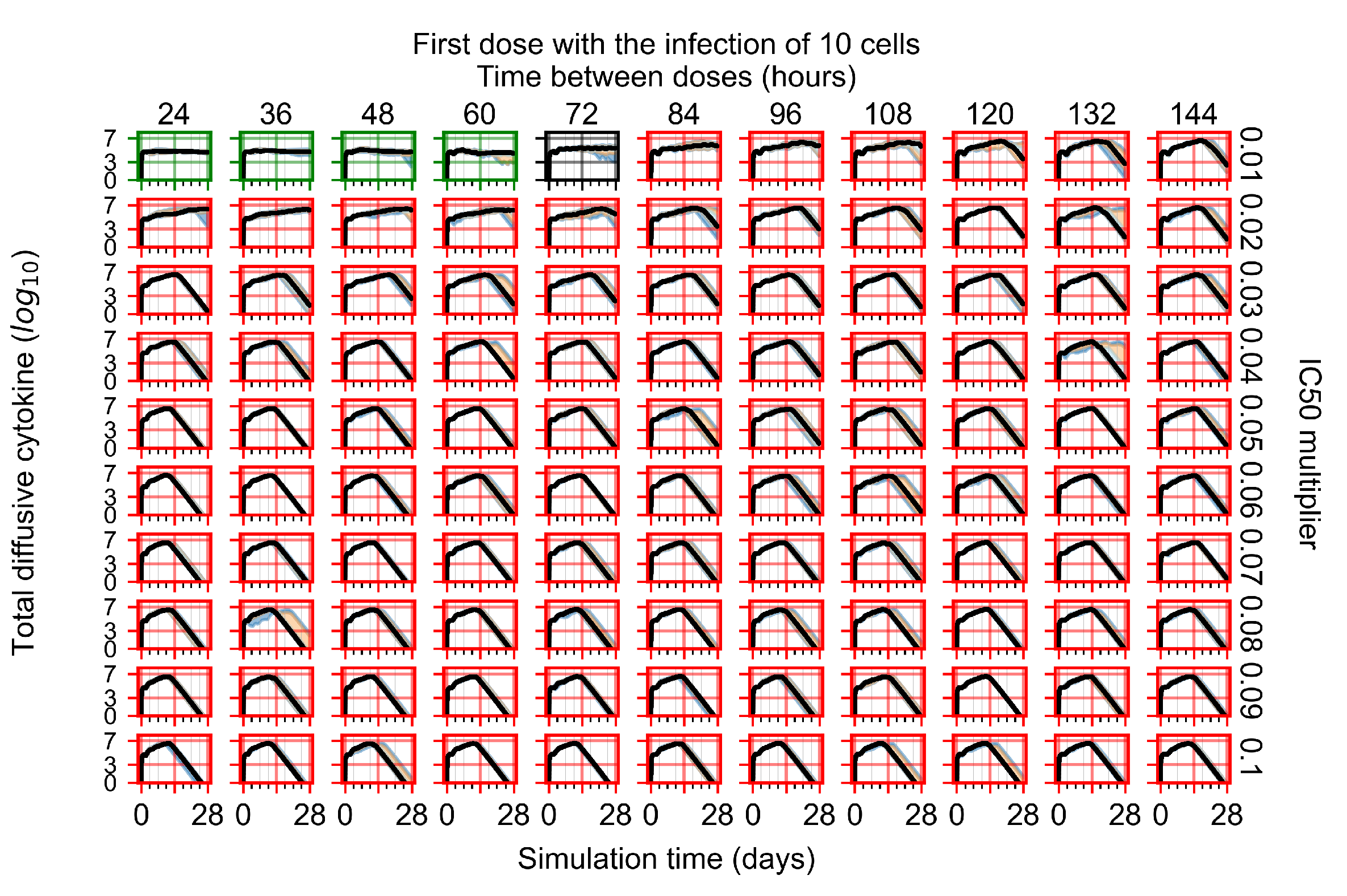
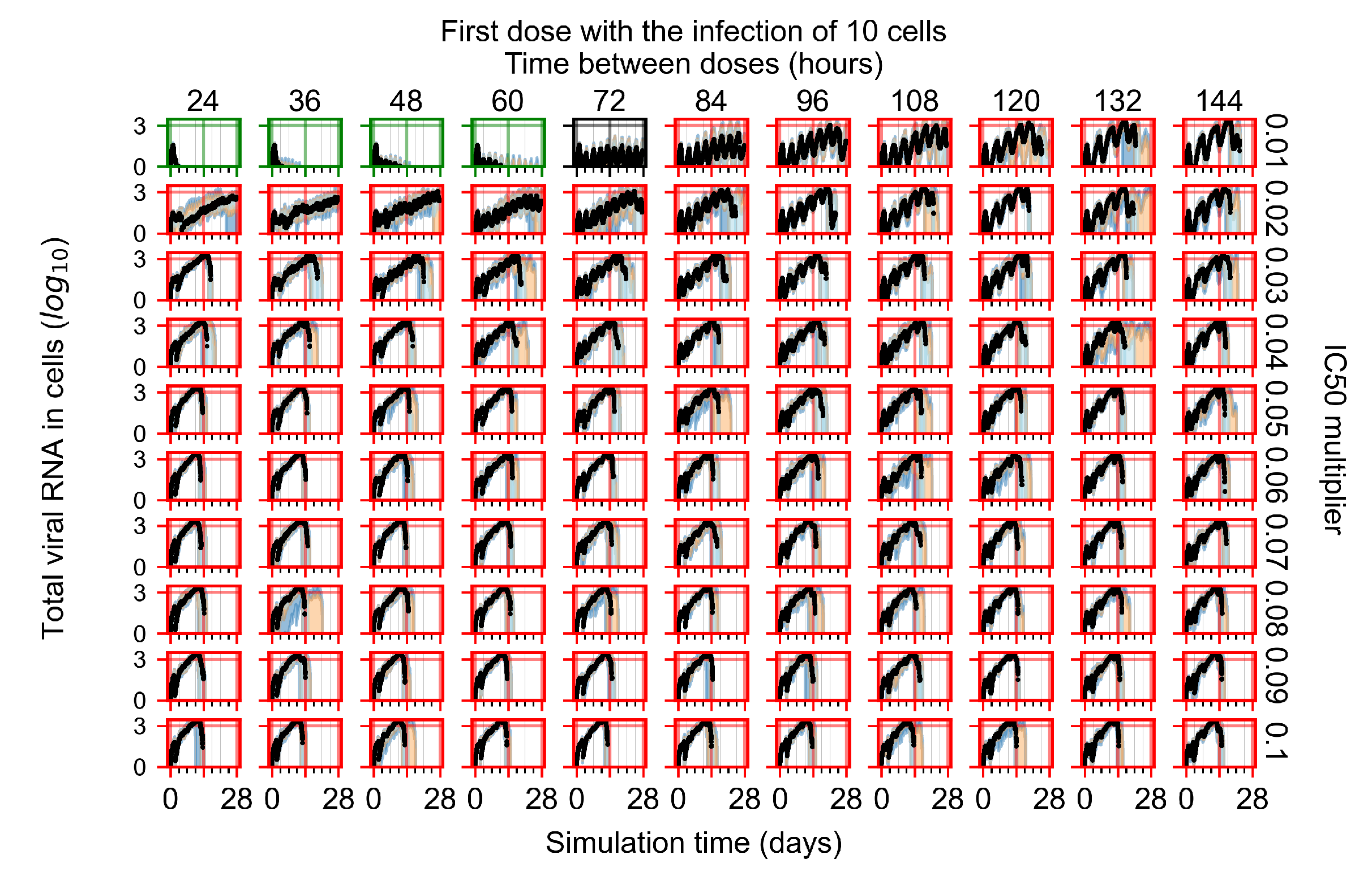

Appendix F.4. Heterogeneous Metabolism, Regular GS-443902 Half-Life
Appendix F.4.1. Treatment Initiation with Infection of Ten Epithelial Cells
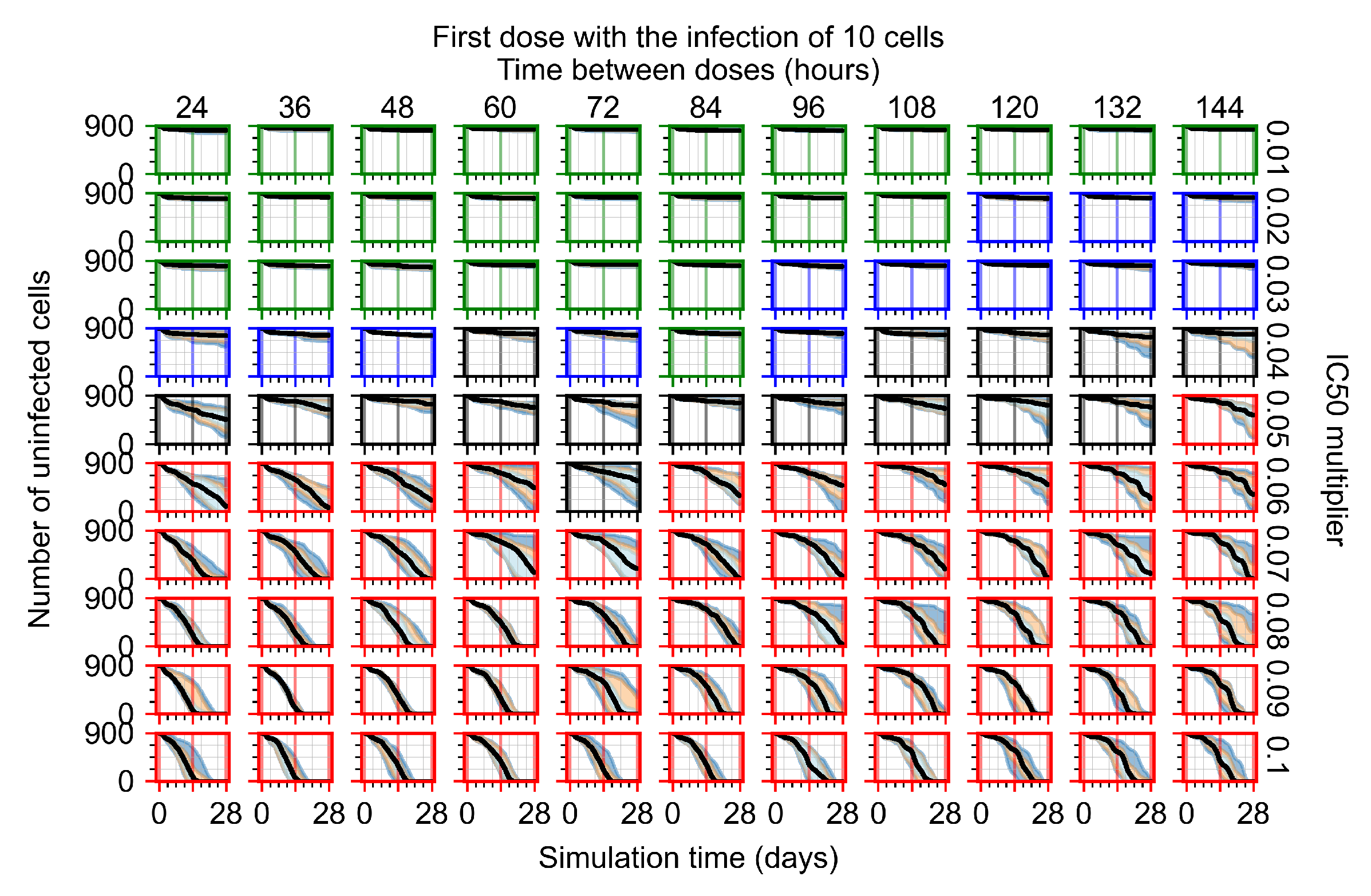

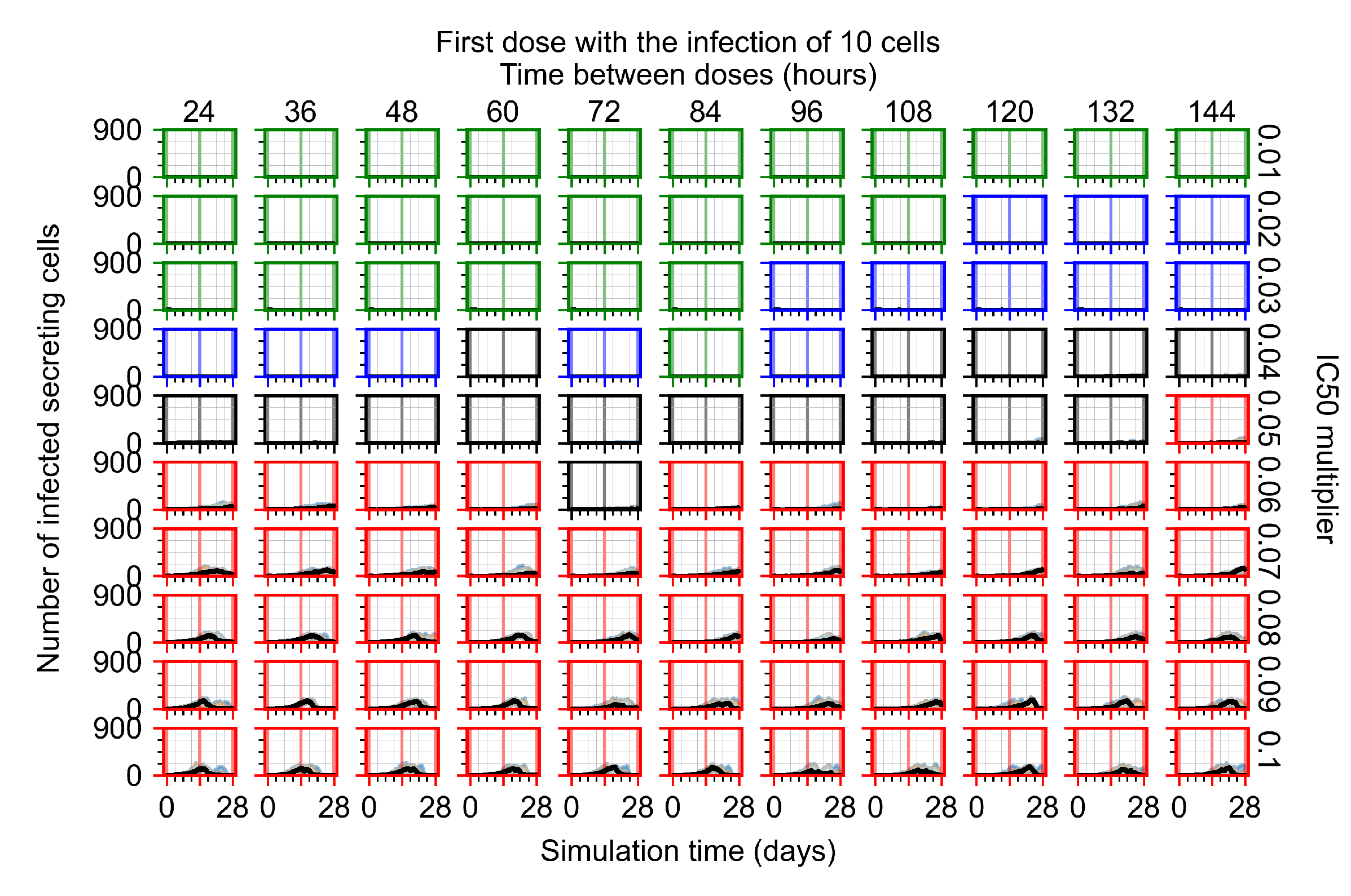
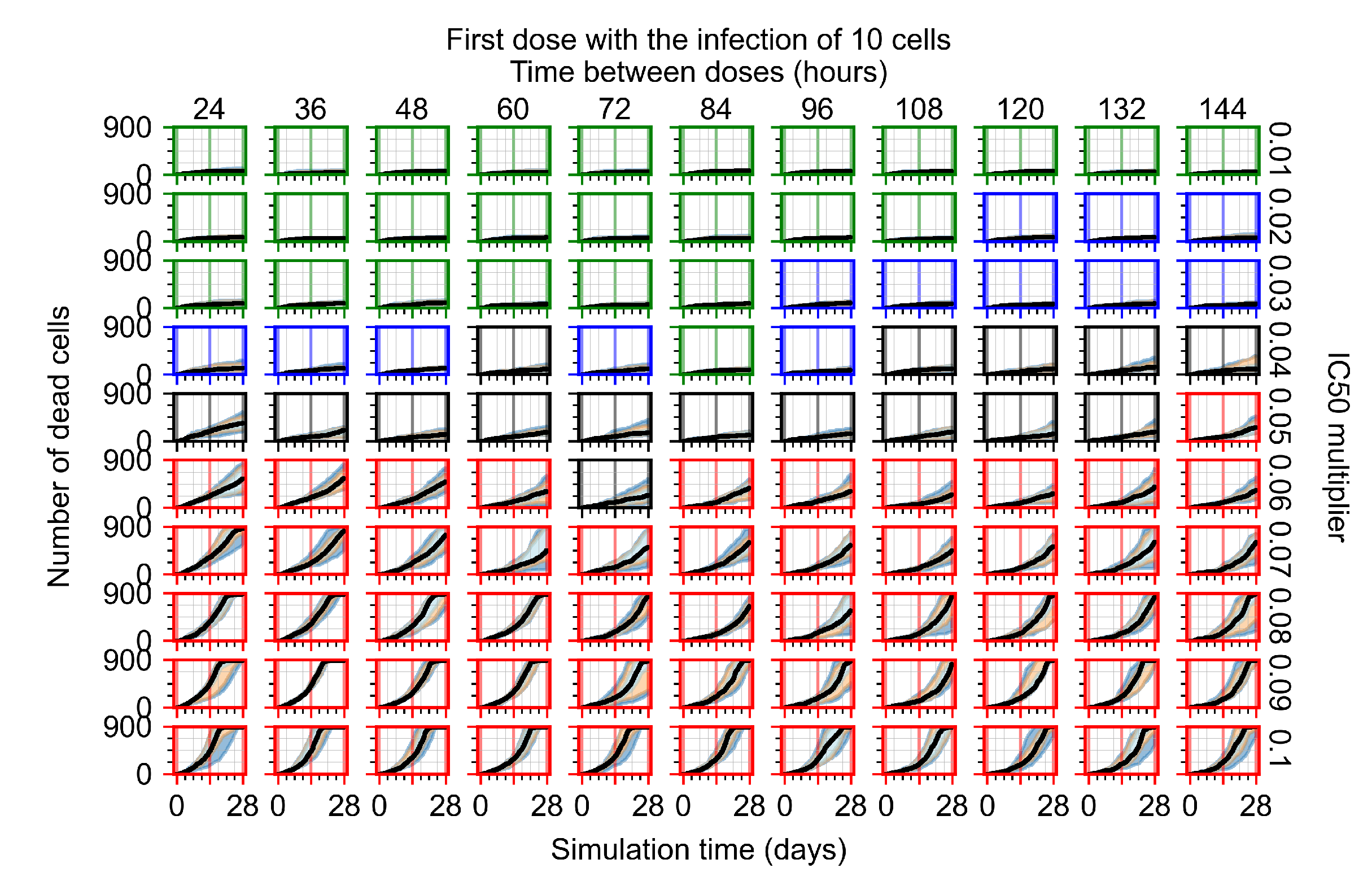
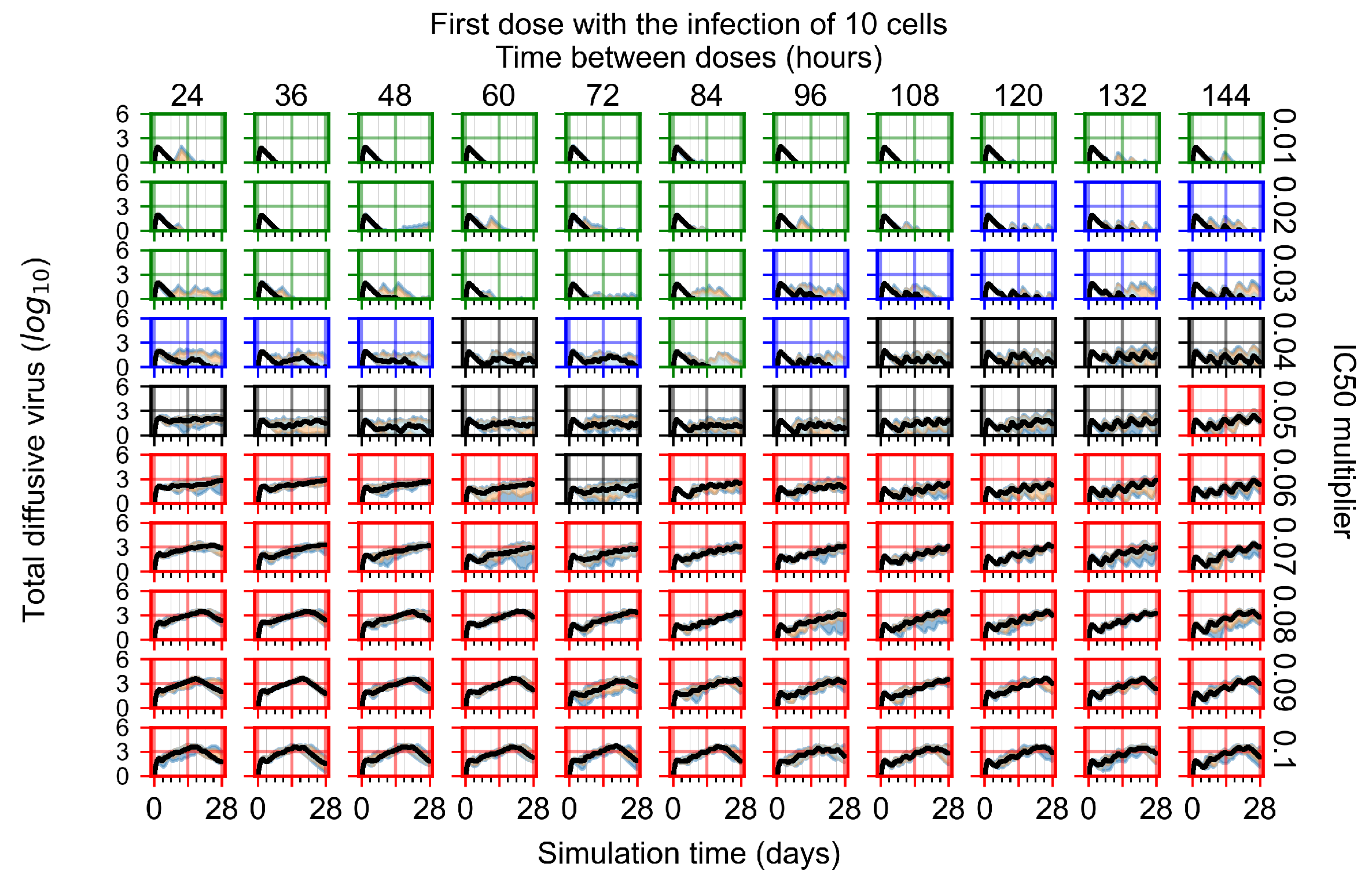
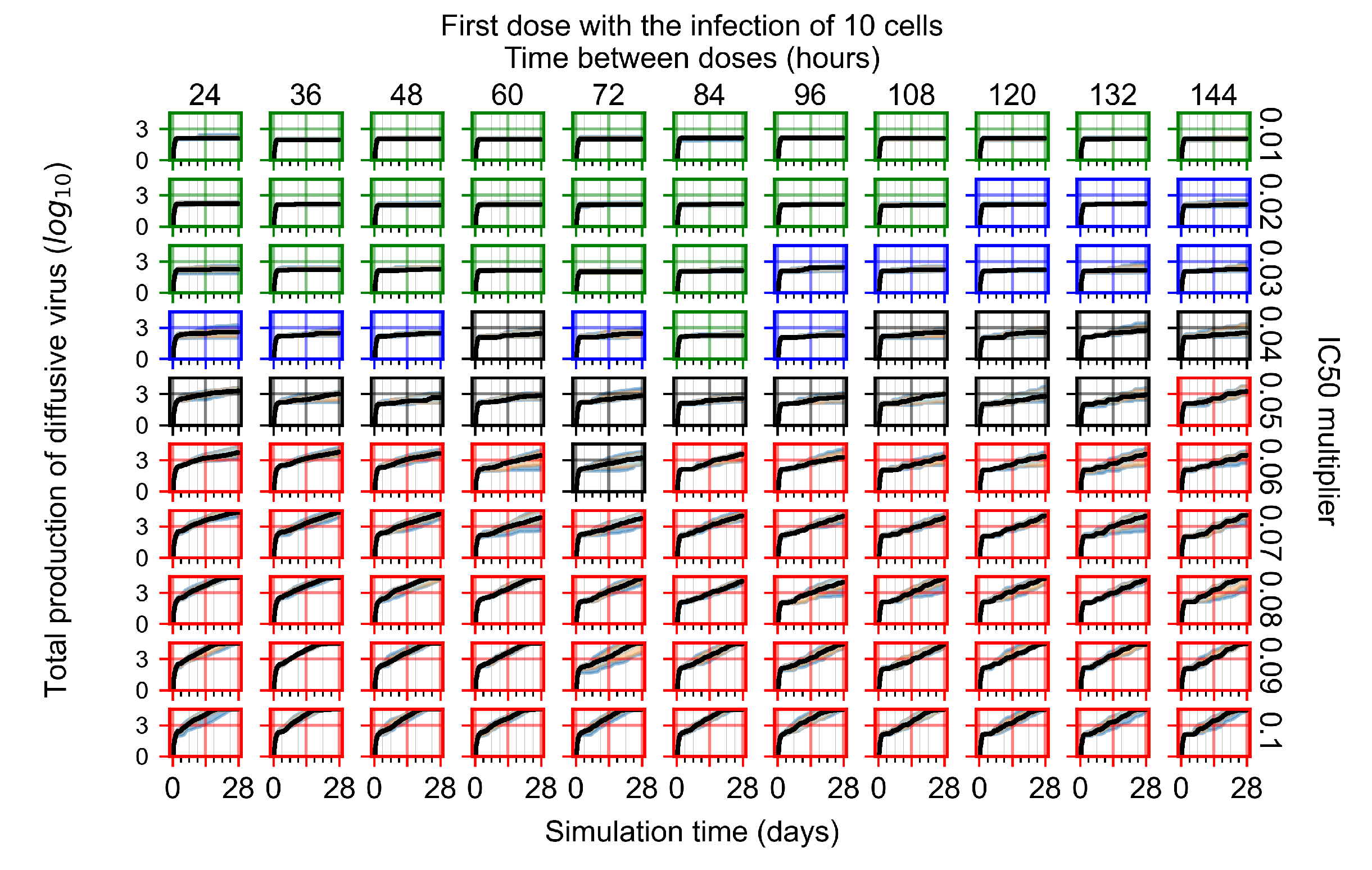
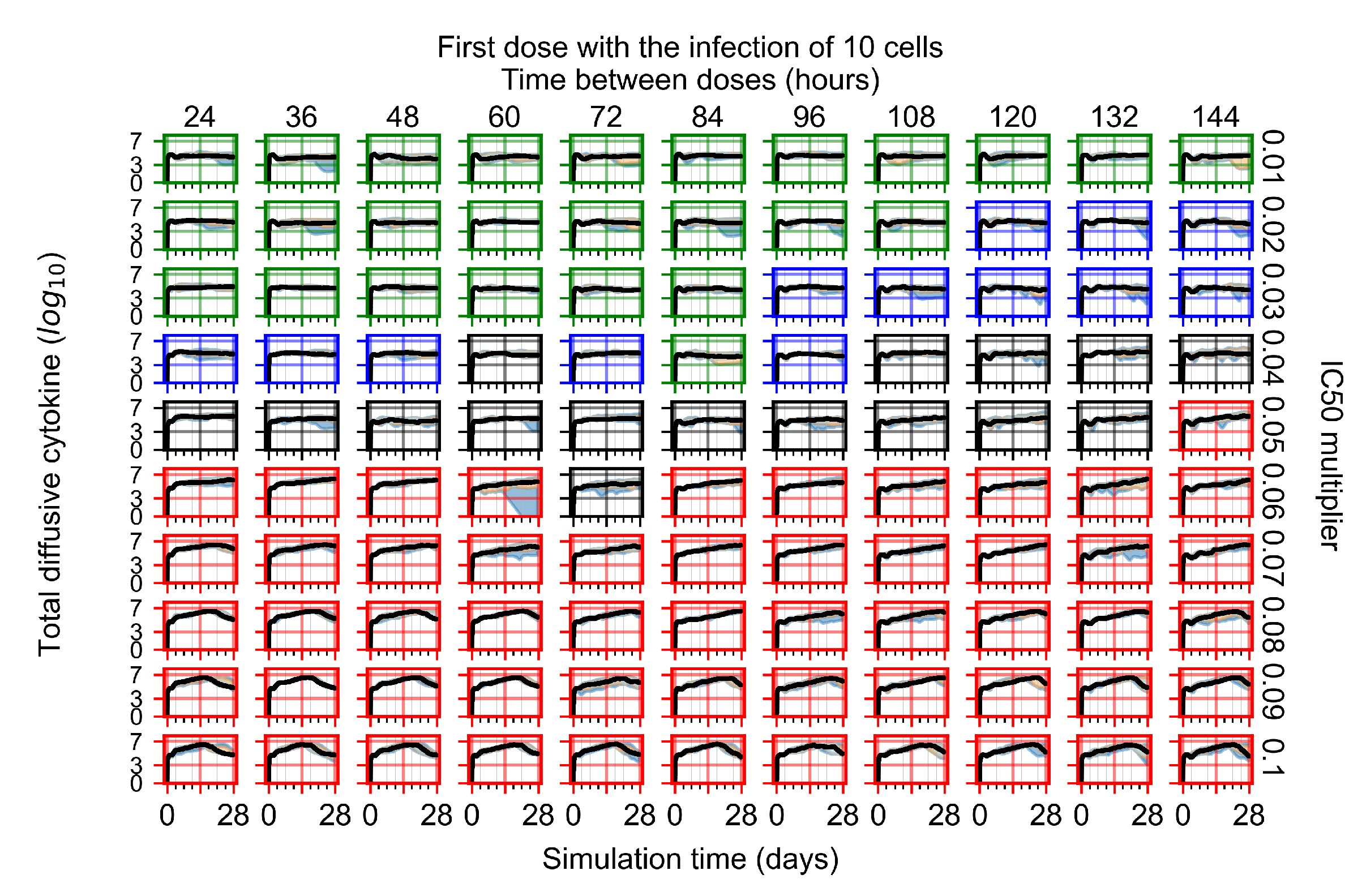

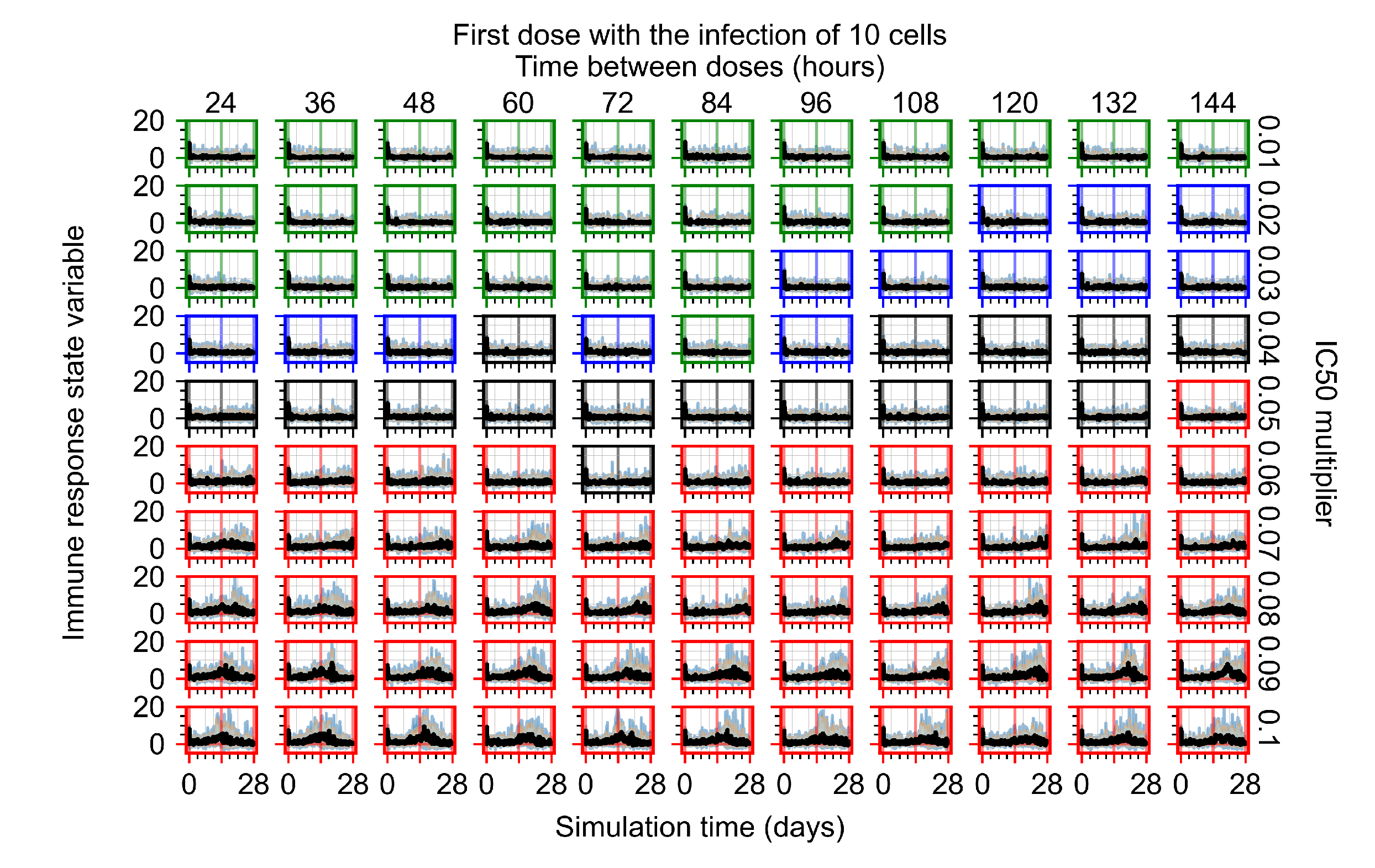
Appendix F.4.2. Treatment Initiation Twelve Hours Post the Infection of Ten Epithelial Cells
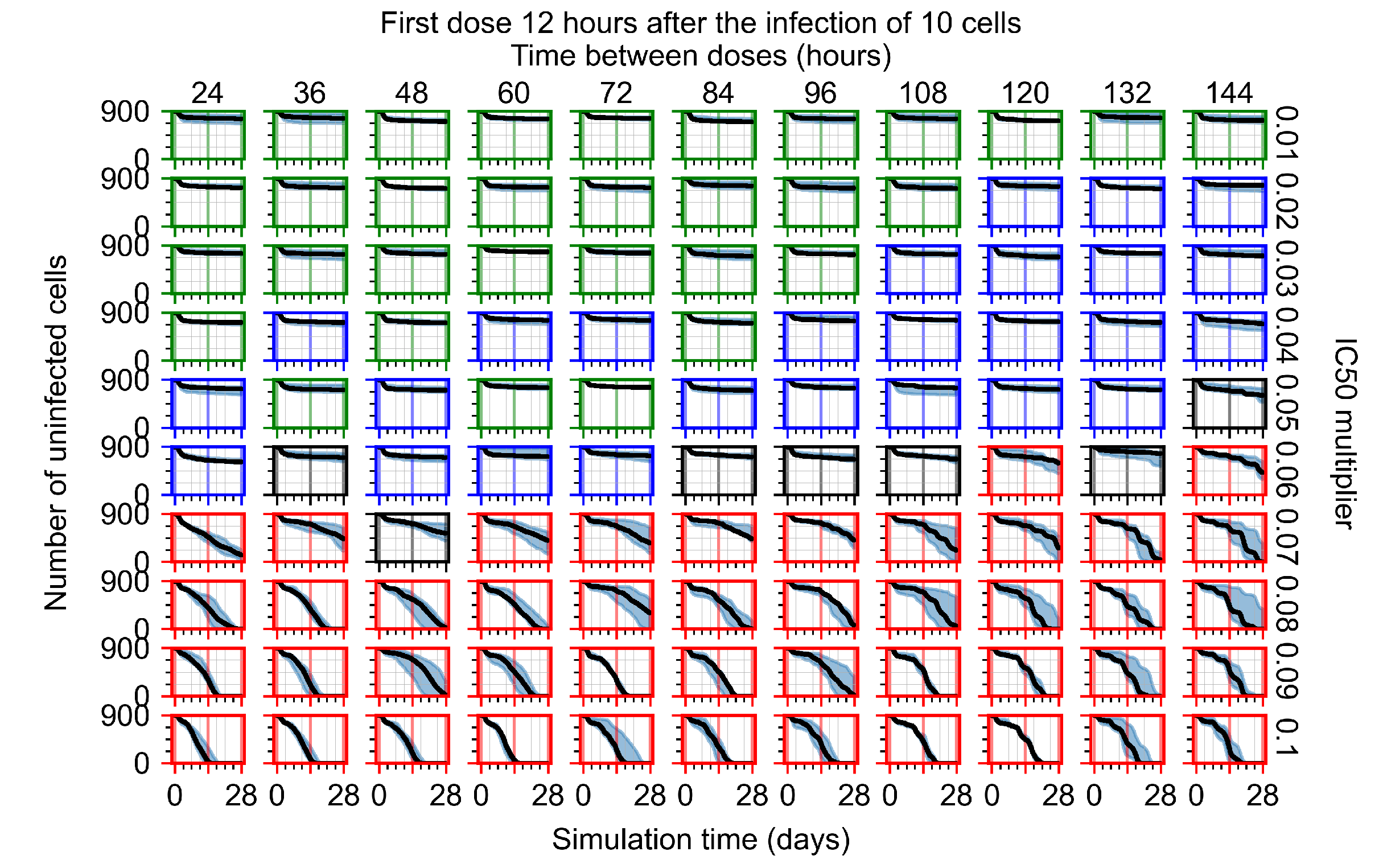

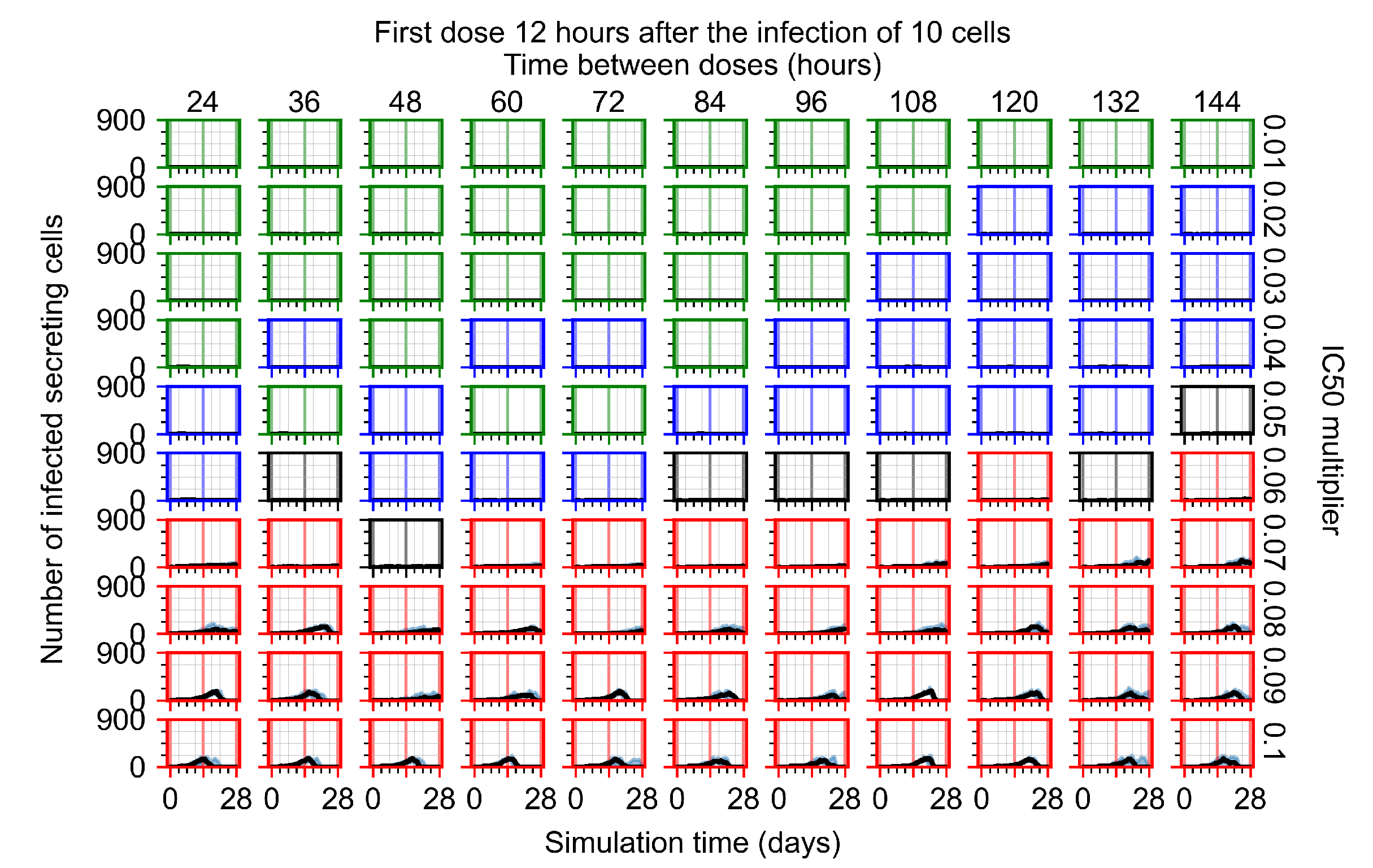
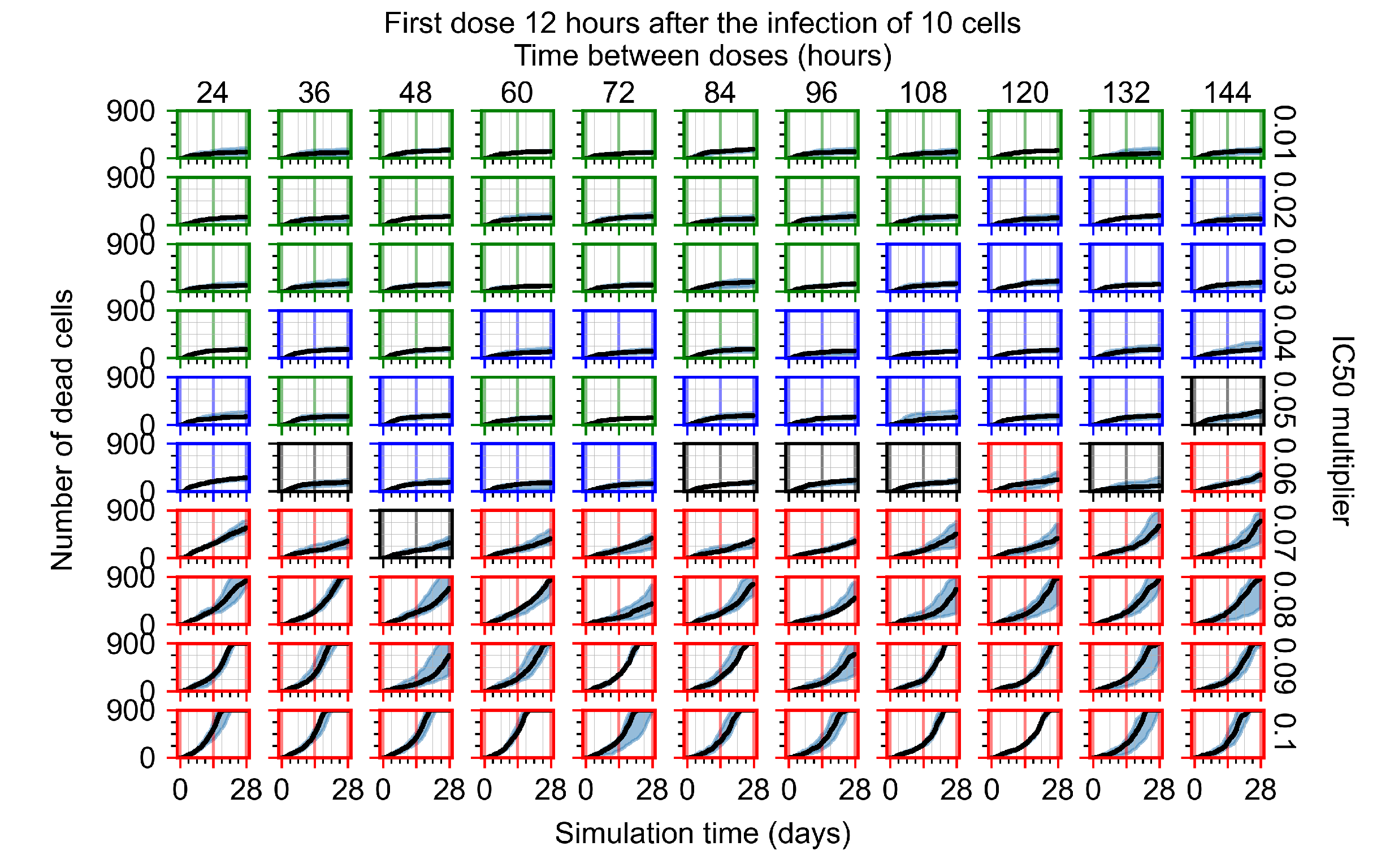
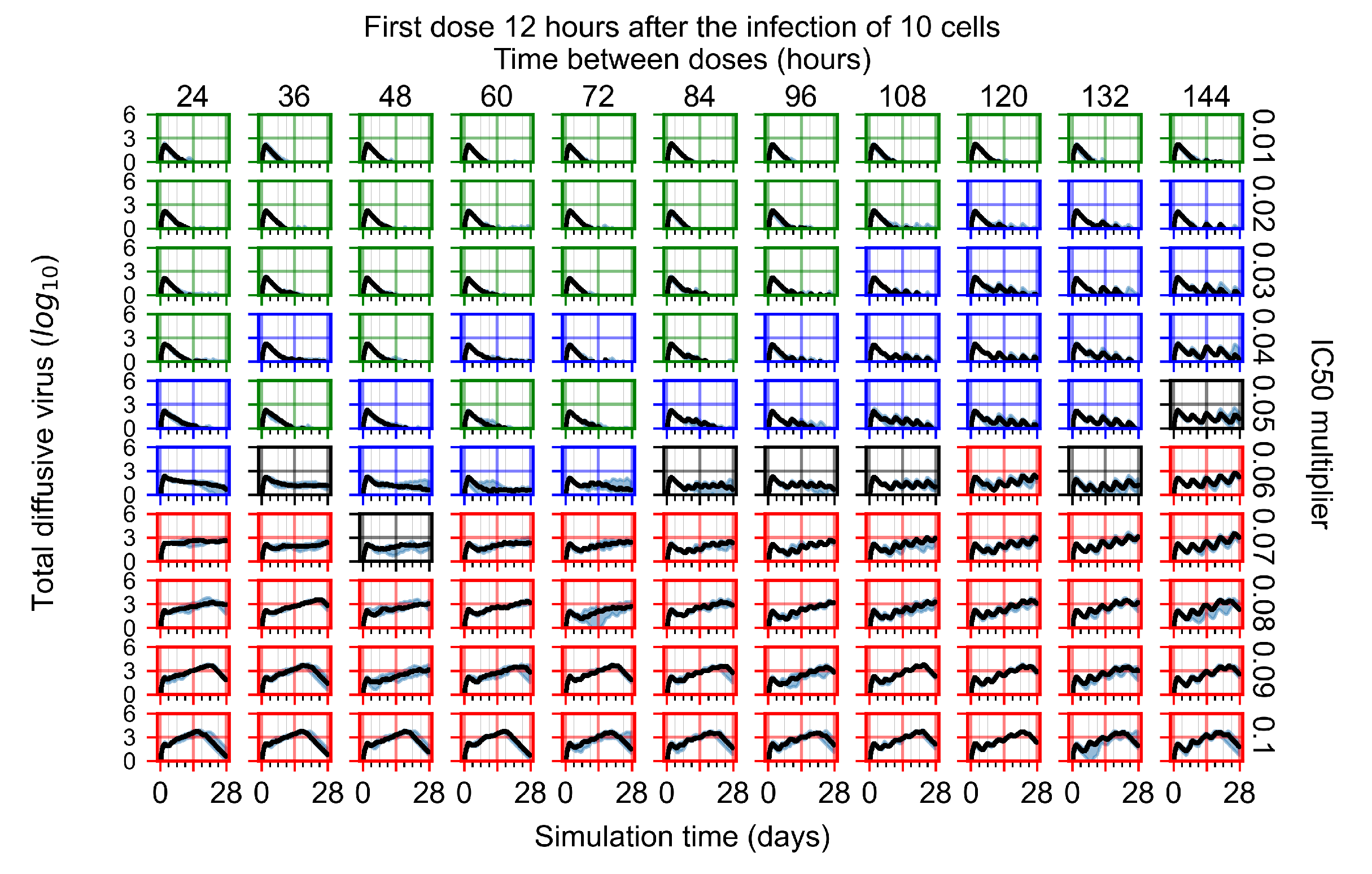
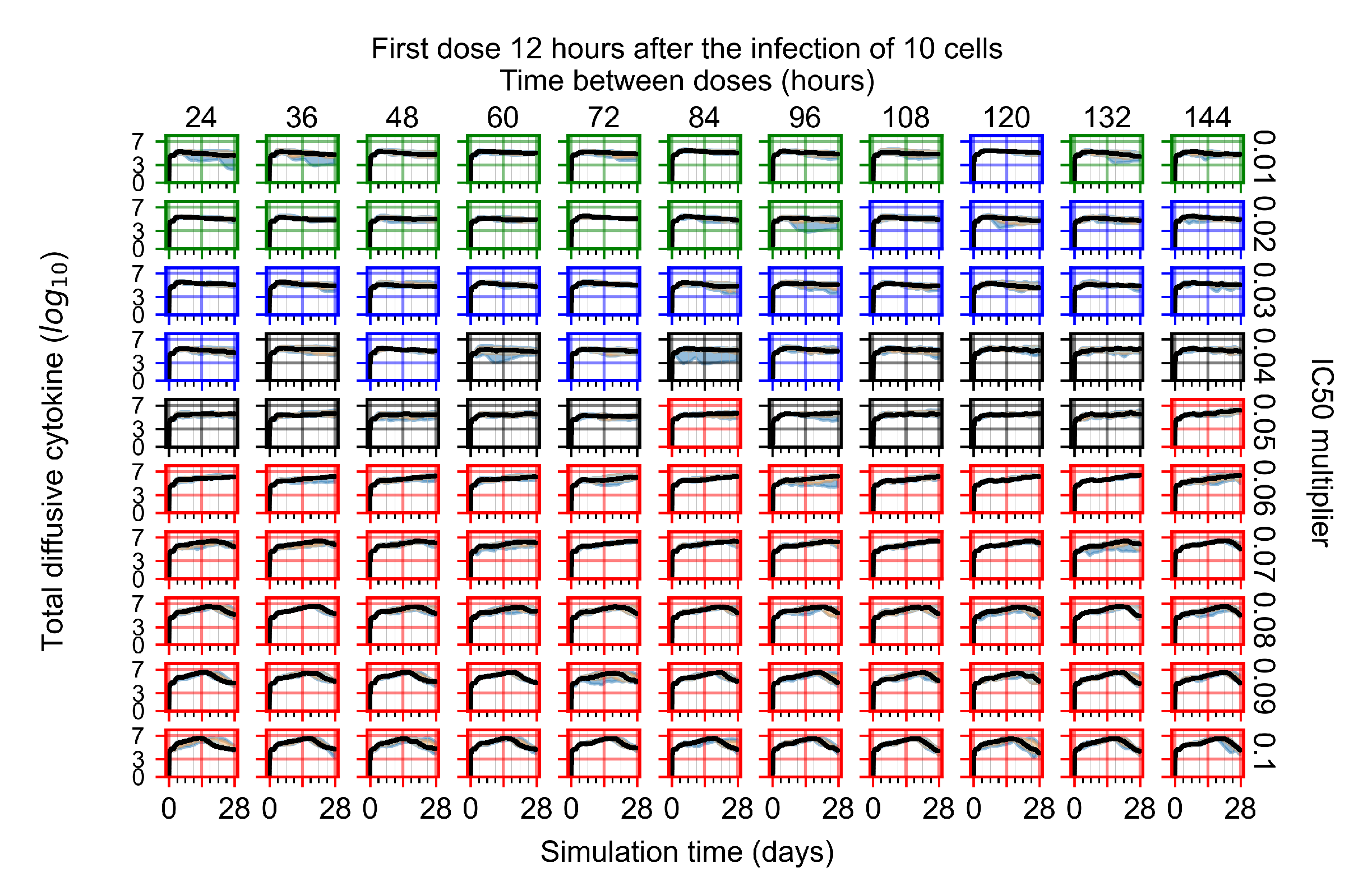

Appendix F.4.3. Treatment Initiation One Day Post the Infection of Ten Epithelial Cells
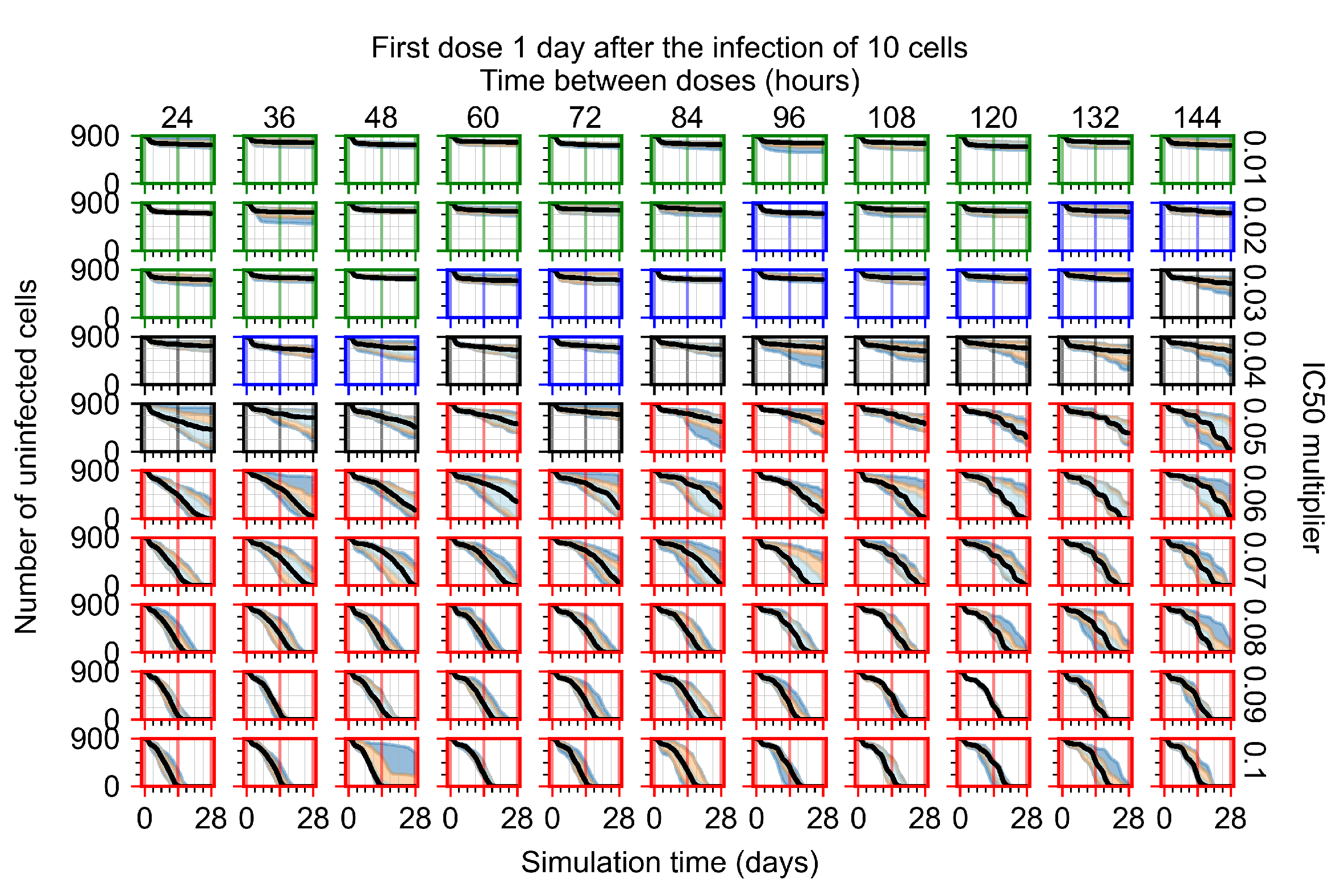
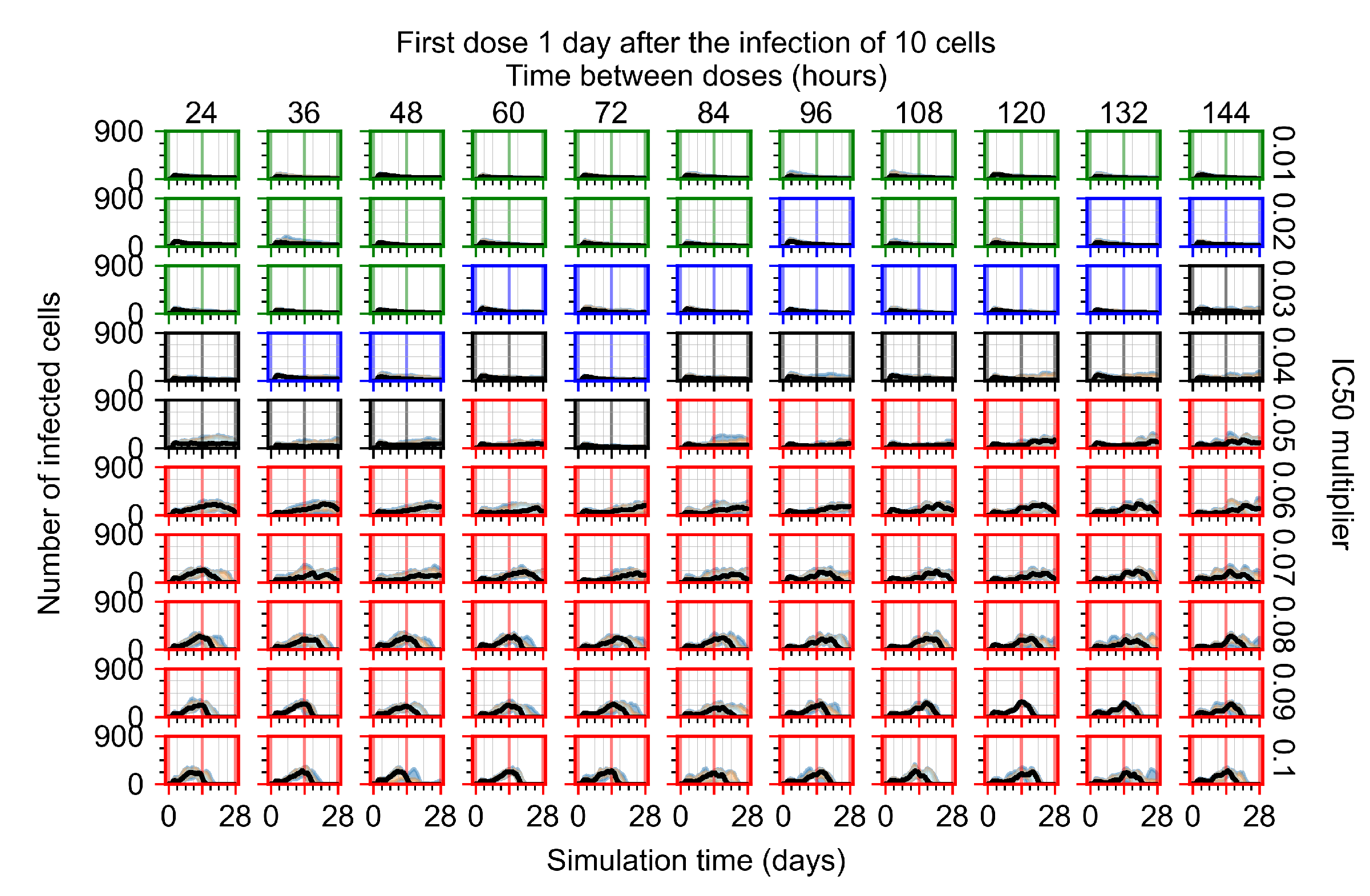
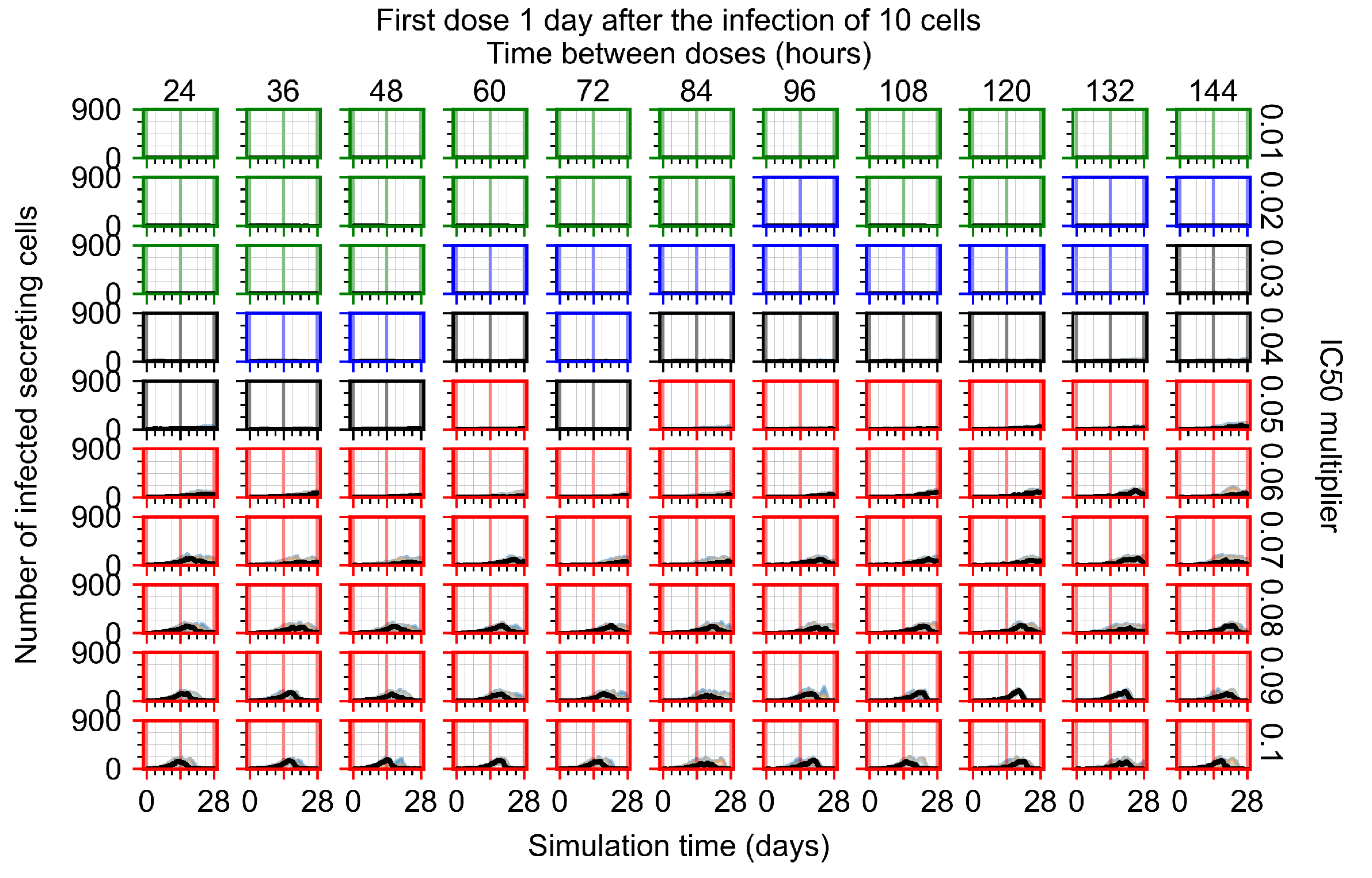
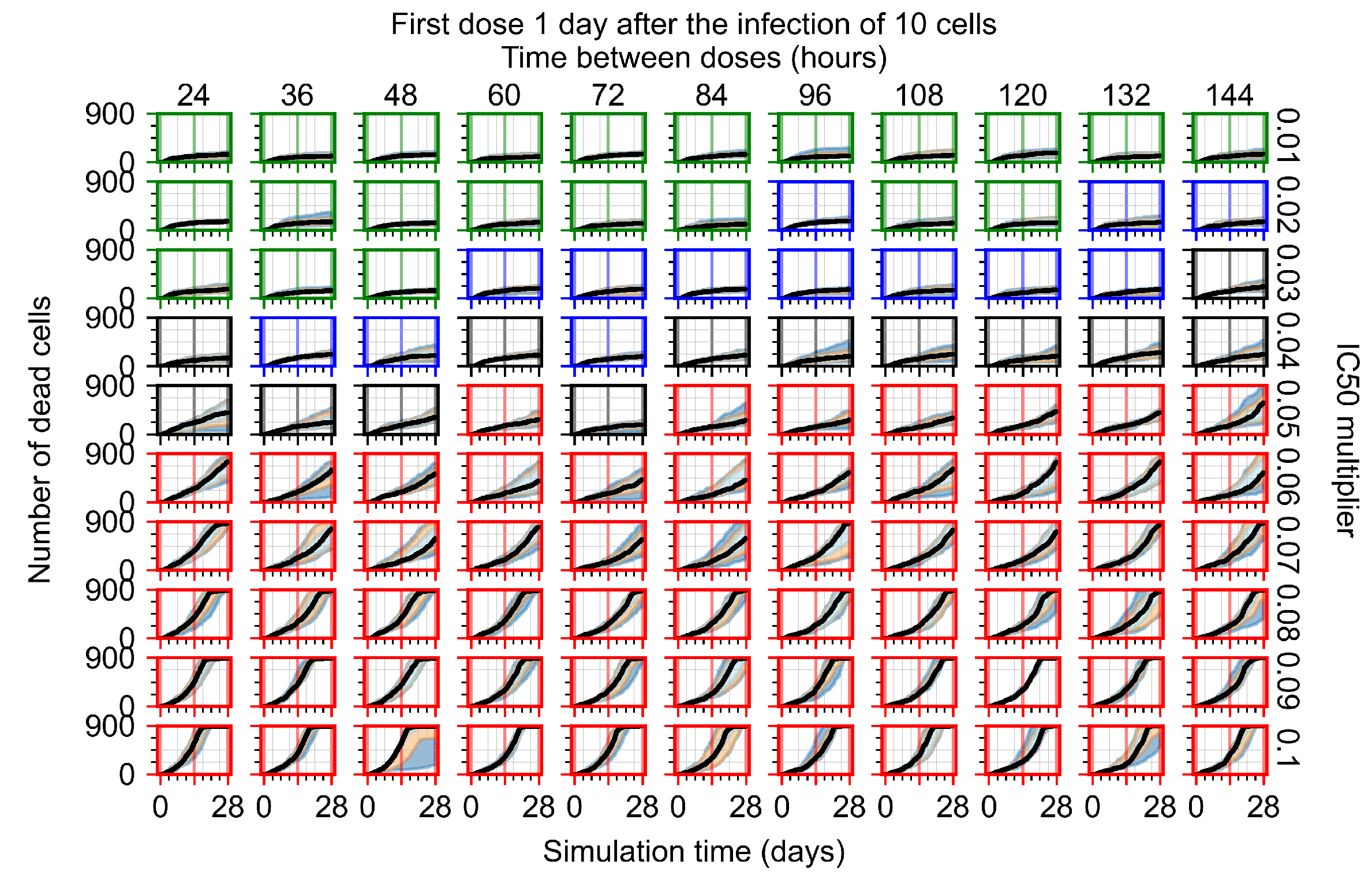
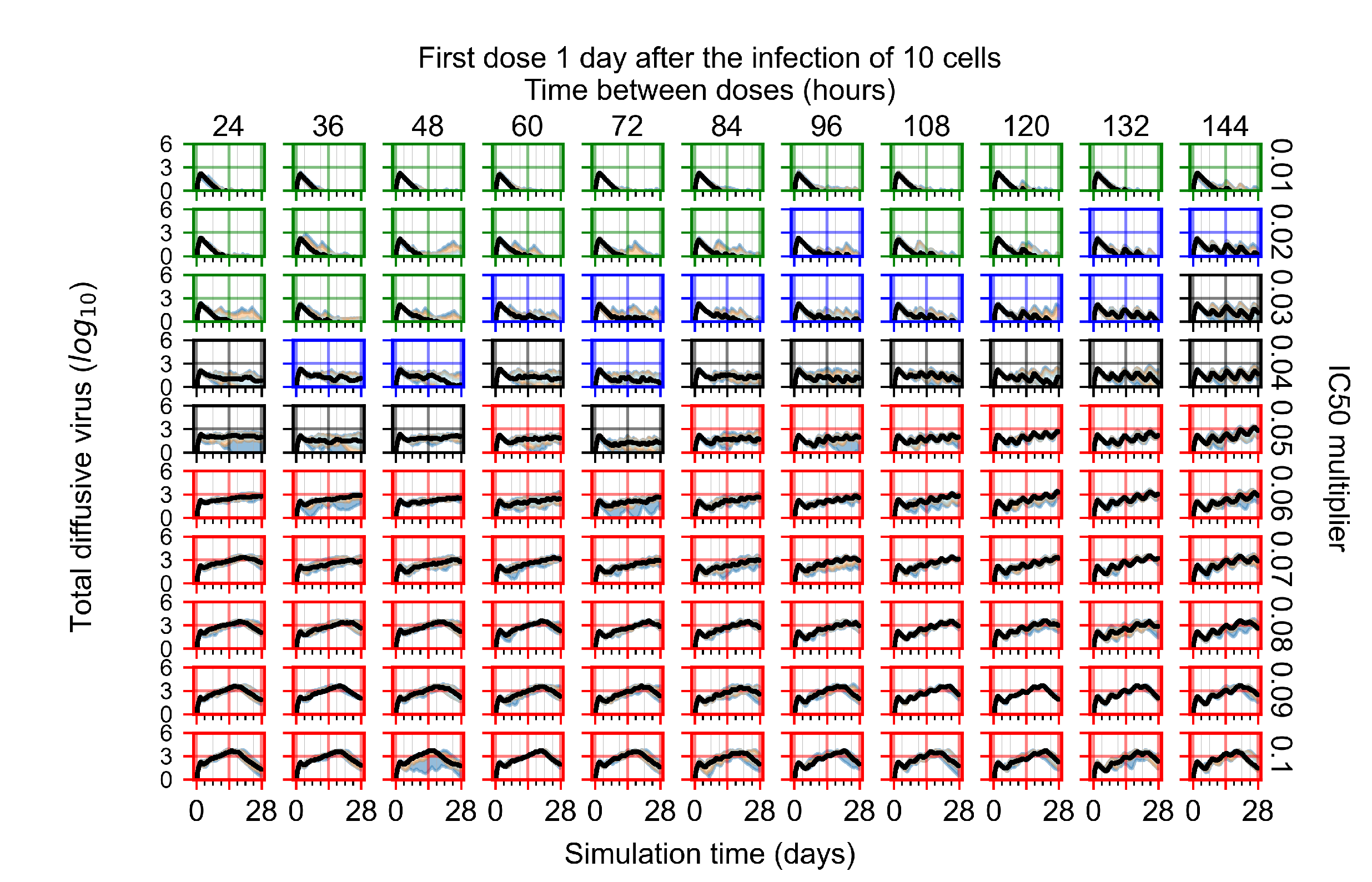
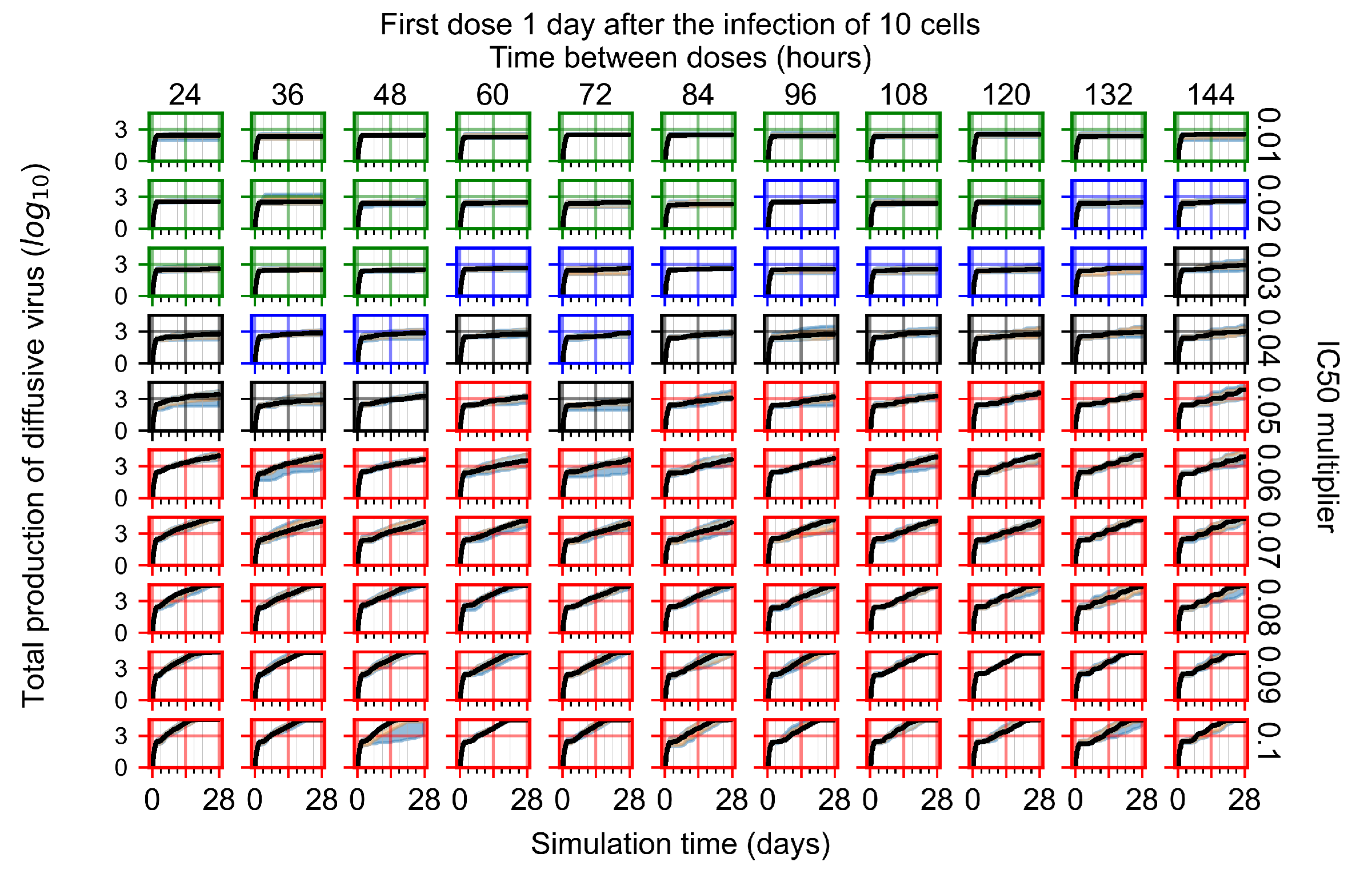
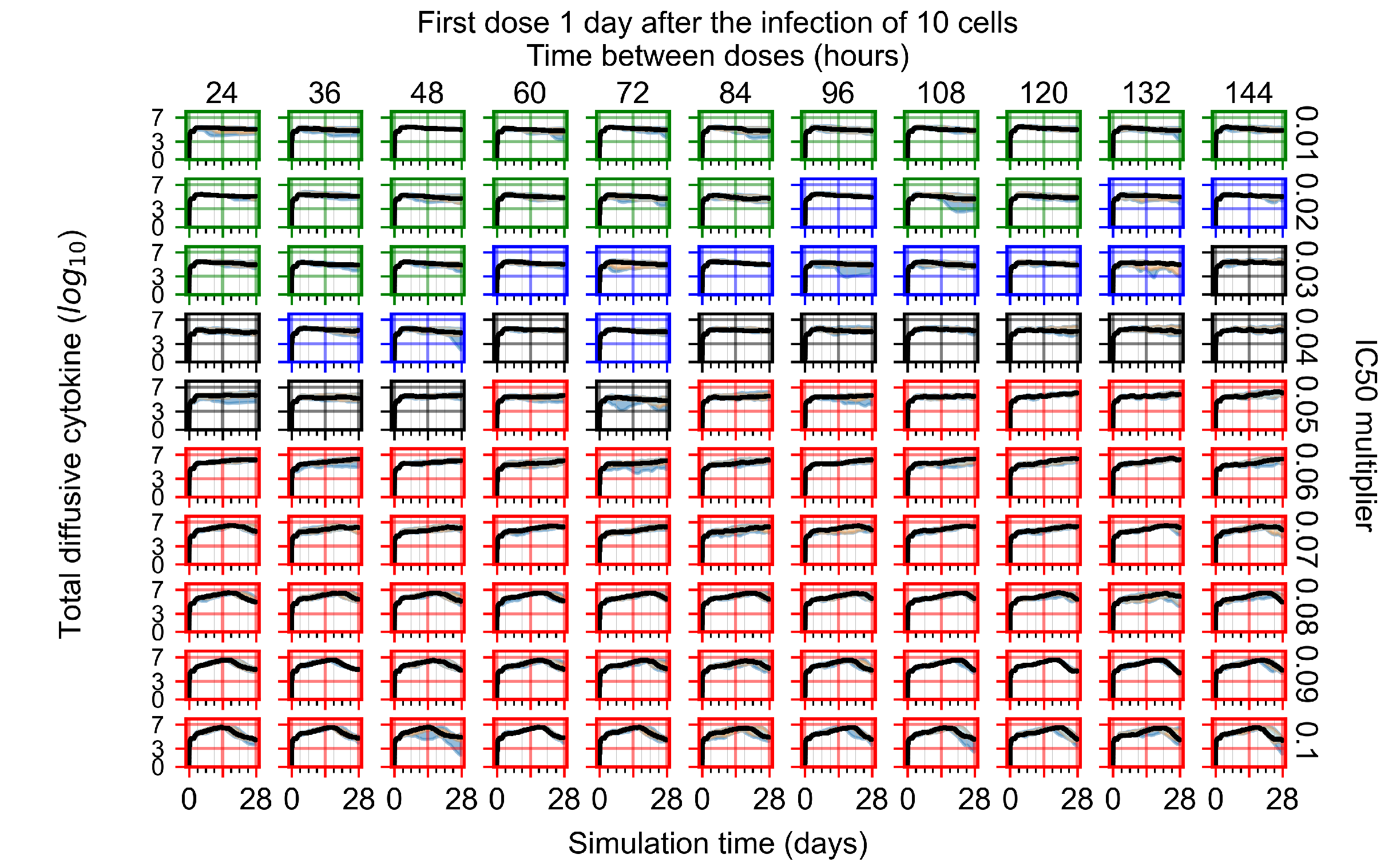

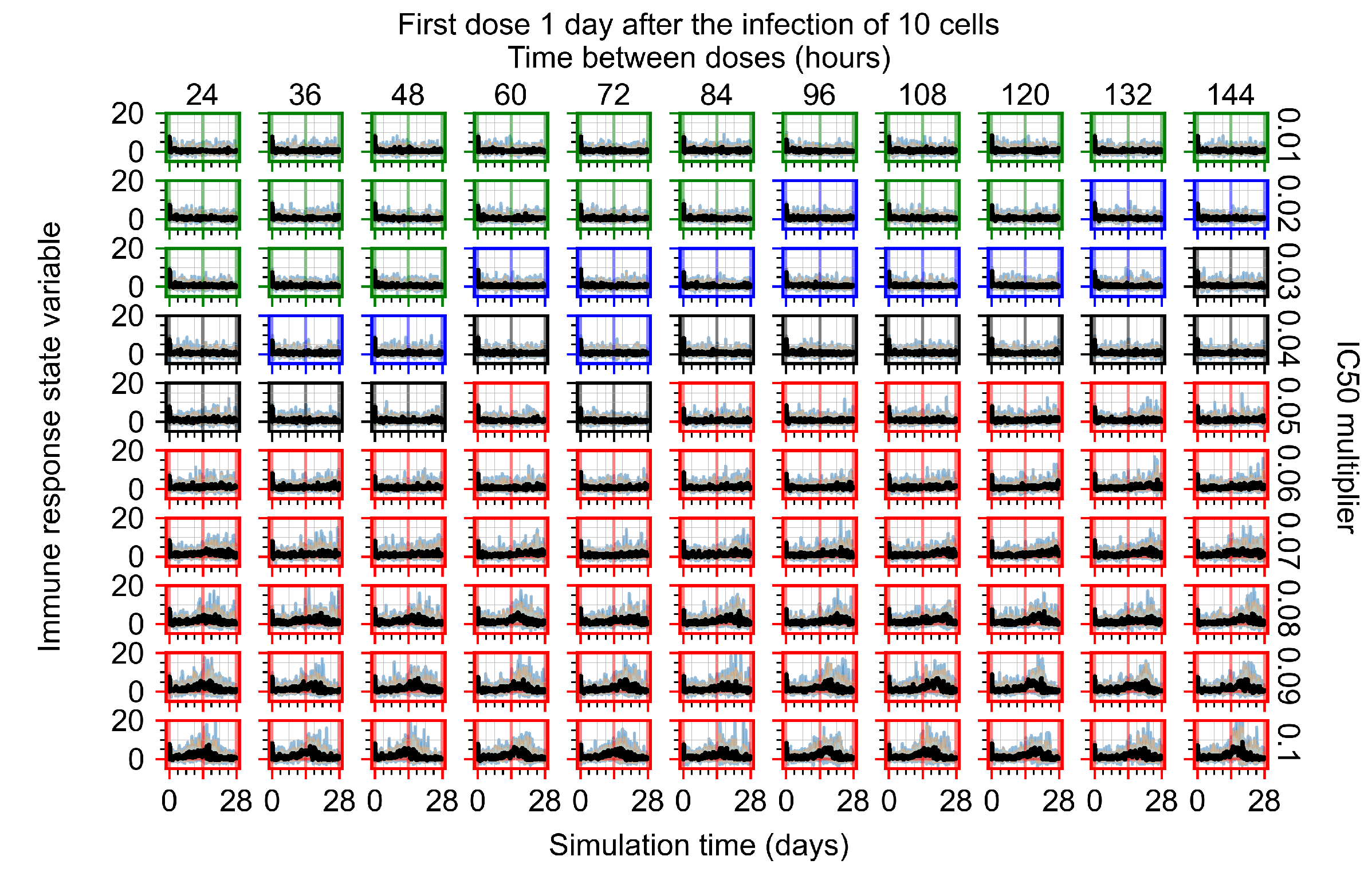
Appendix F.4.4. Treatment Initiation Three Days Post the Infection of Ten Epithelial Cells

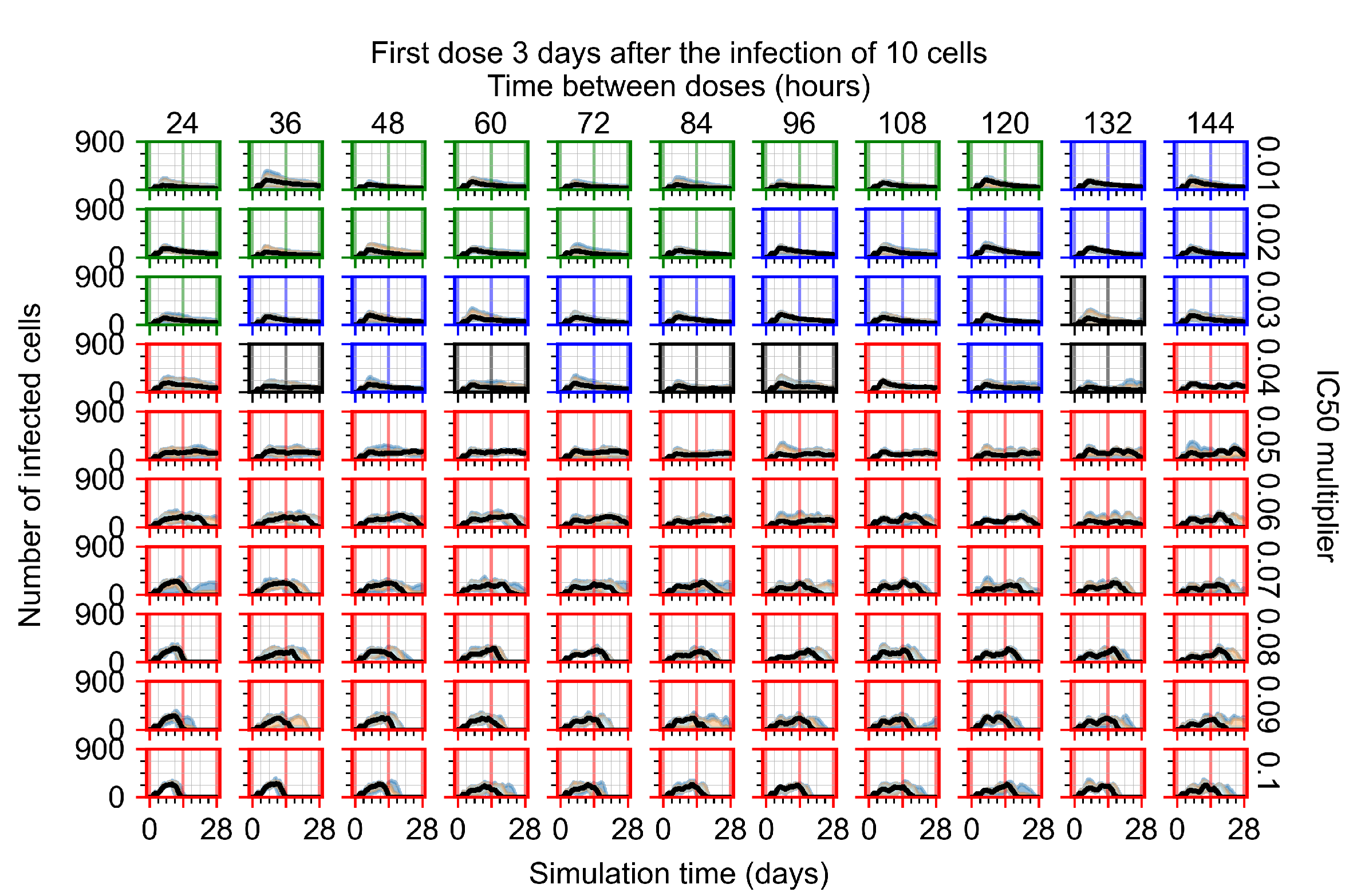

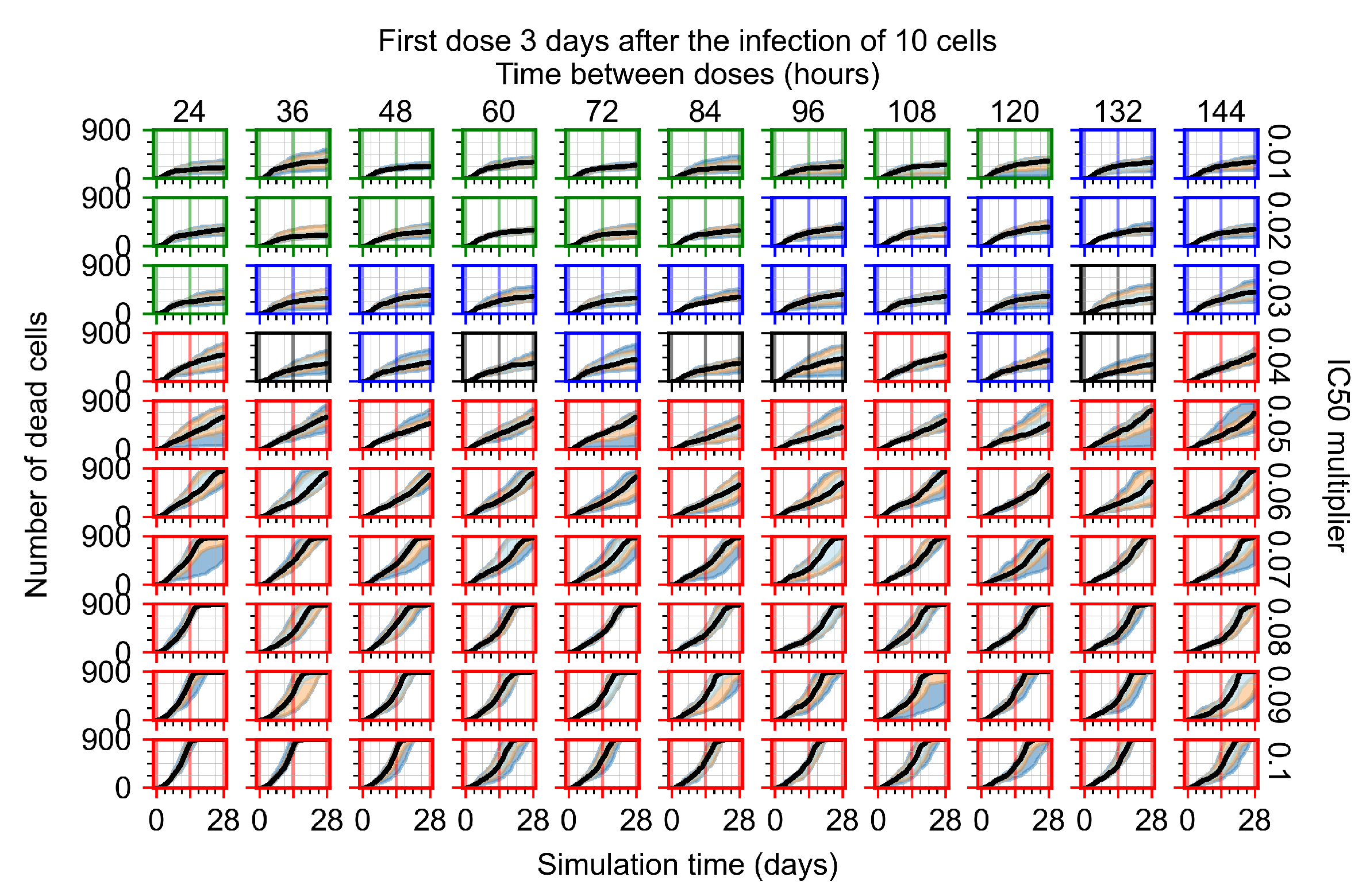
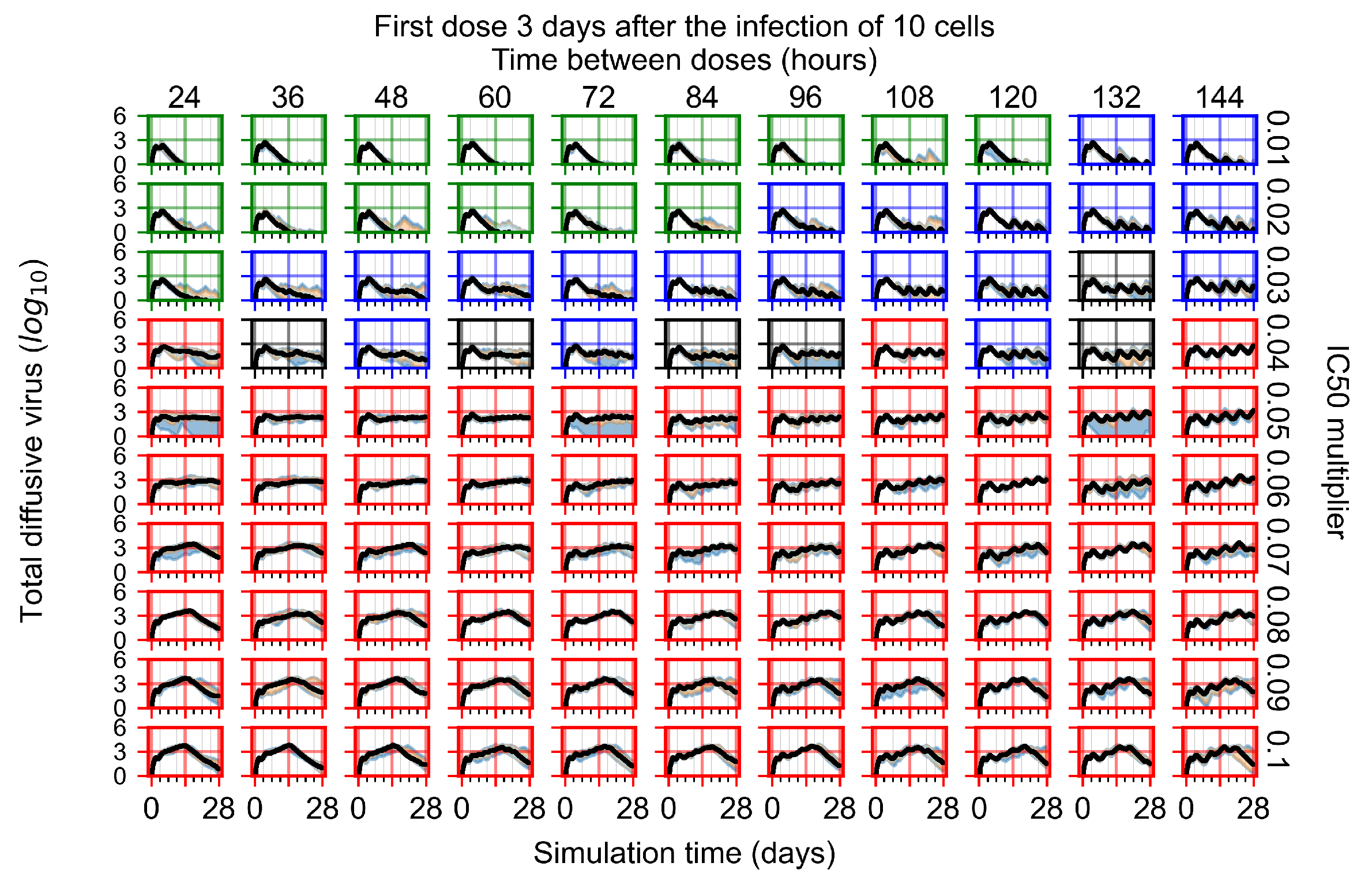
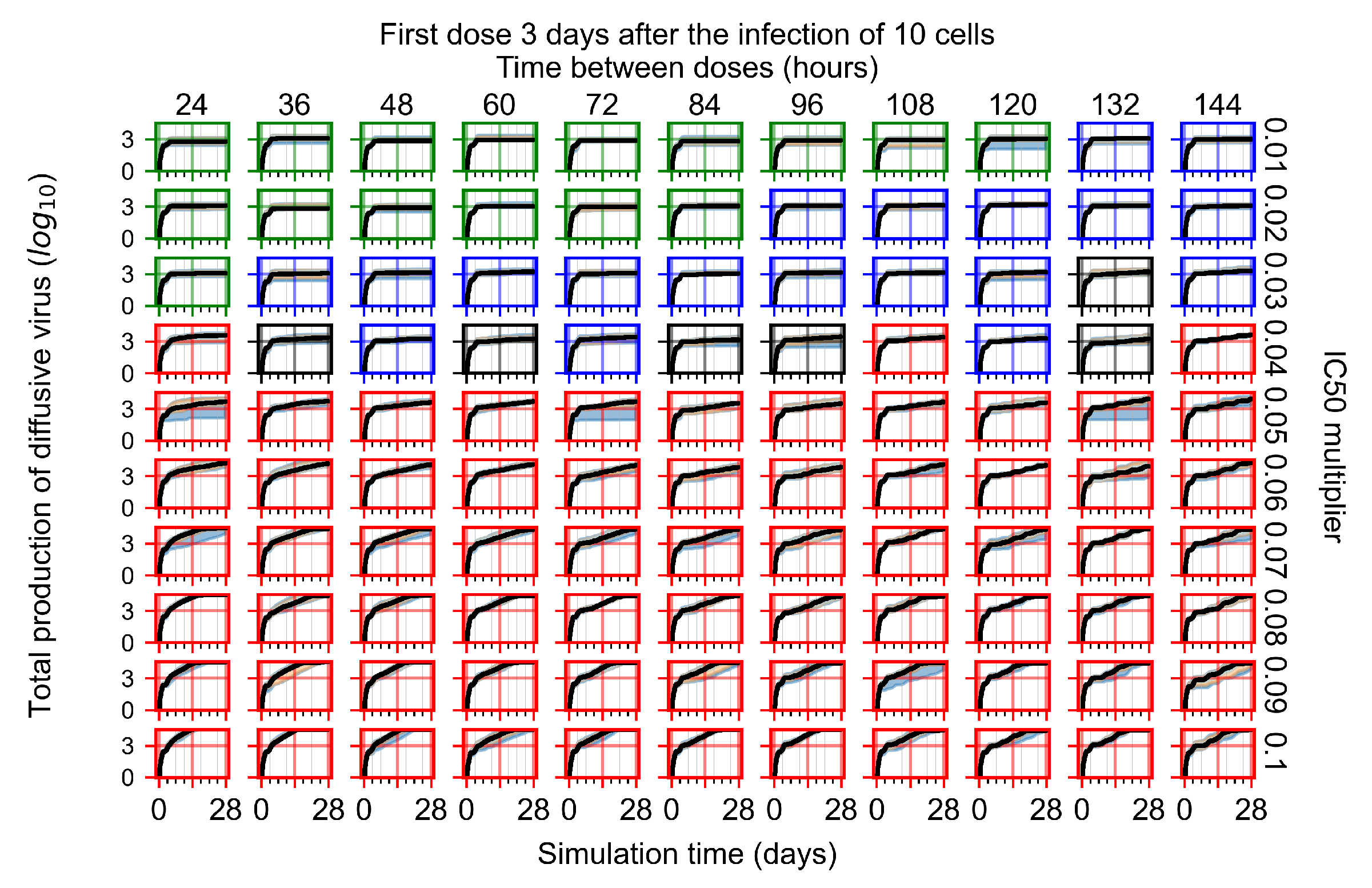
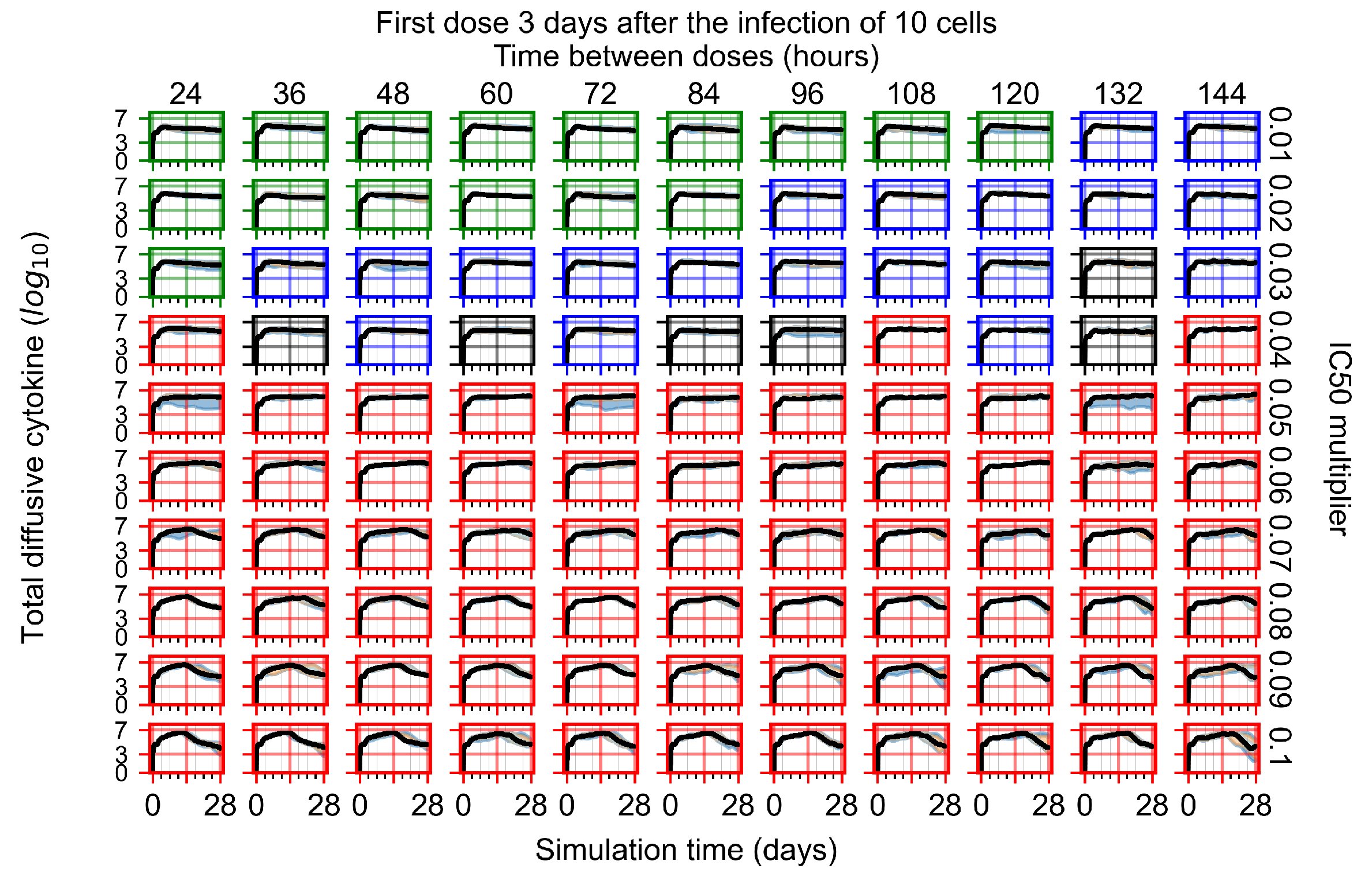
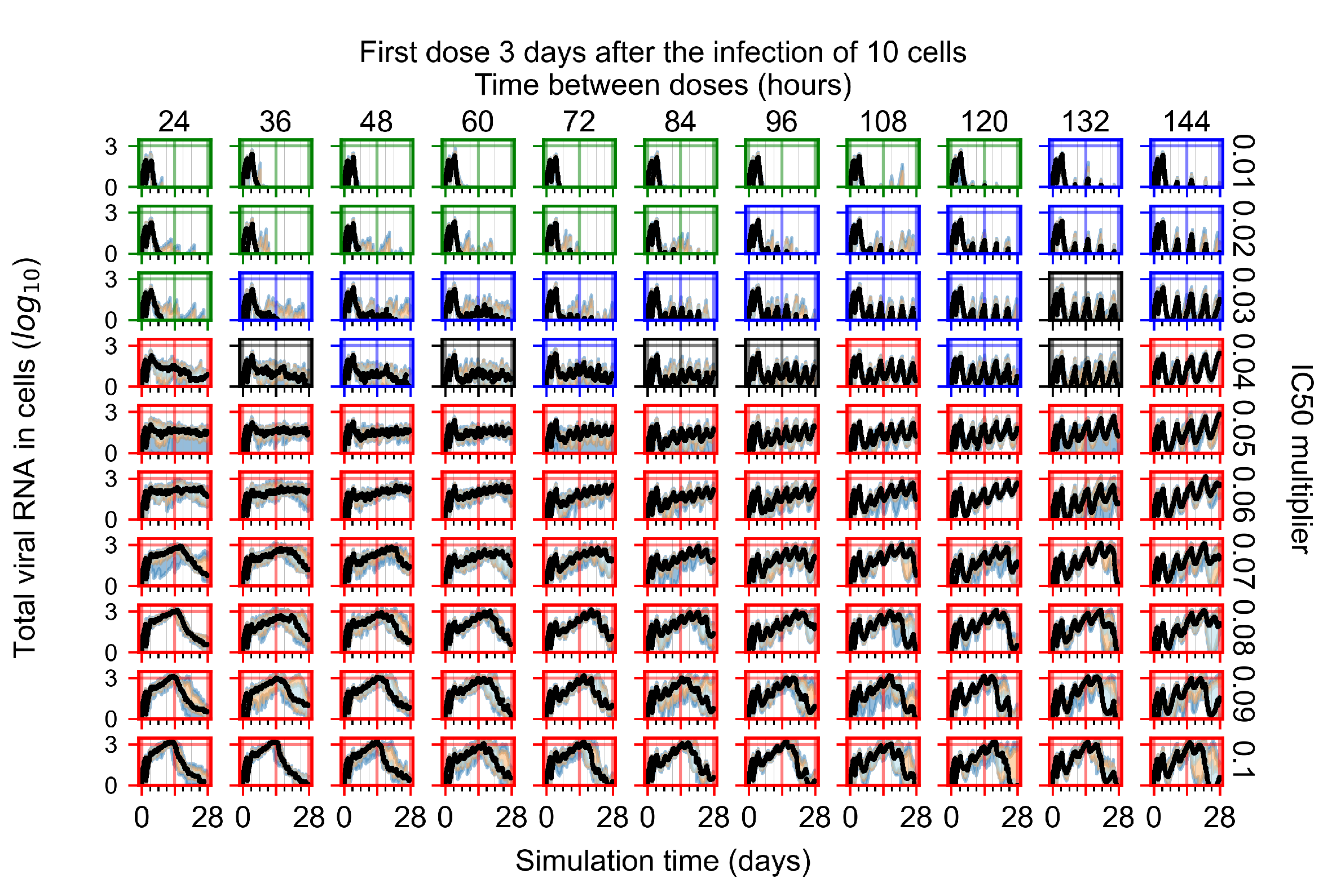
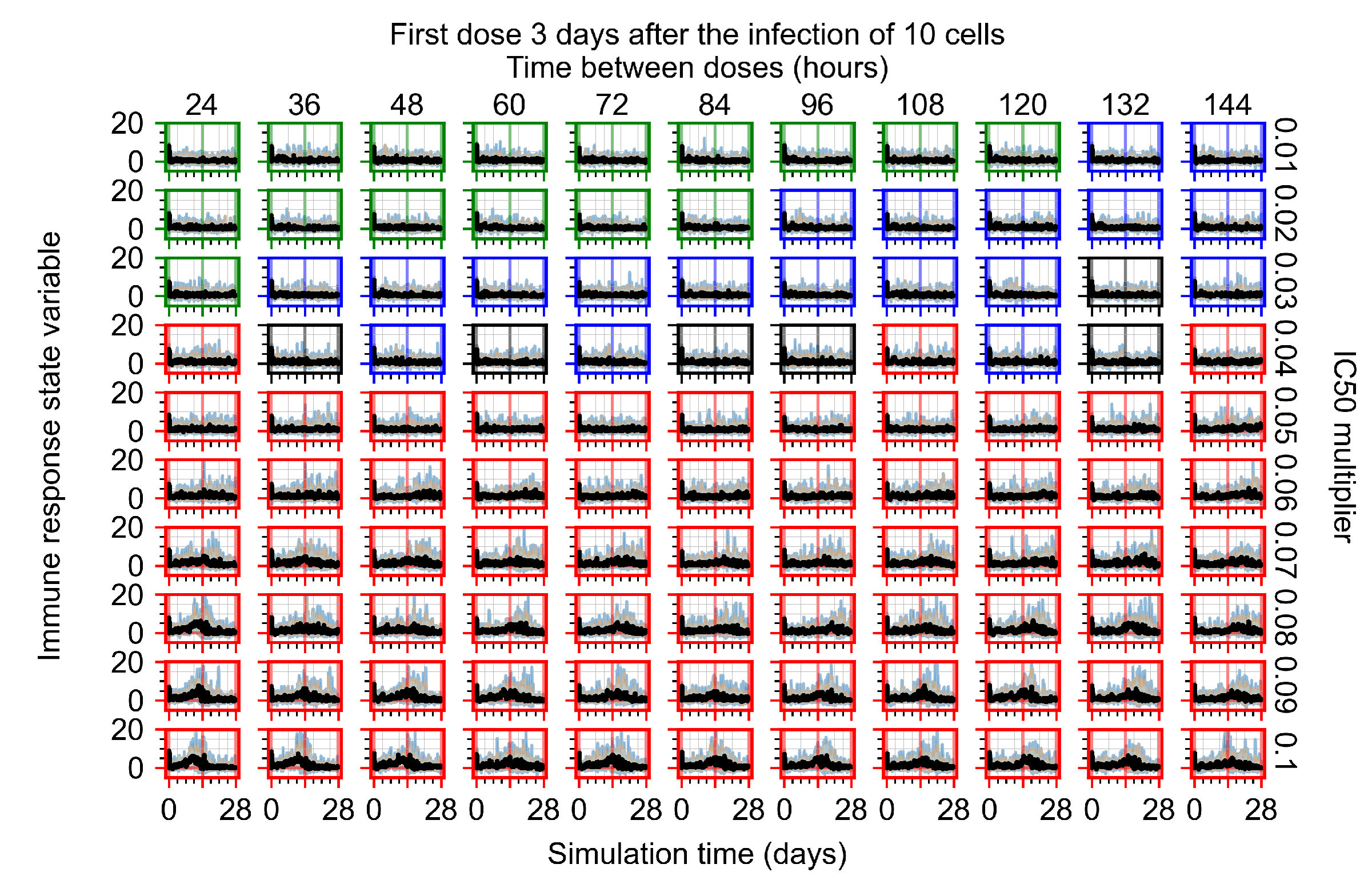
Appendix F.5. Heterogeneous Metabolism Using Other Standard Deviations
Appendix F.5.1. Standard Deviation Set to 0.1


Appendix F.5.2. Standard Deviation Set to 0.5
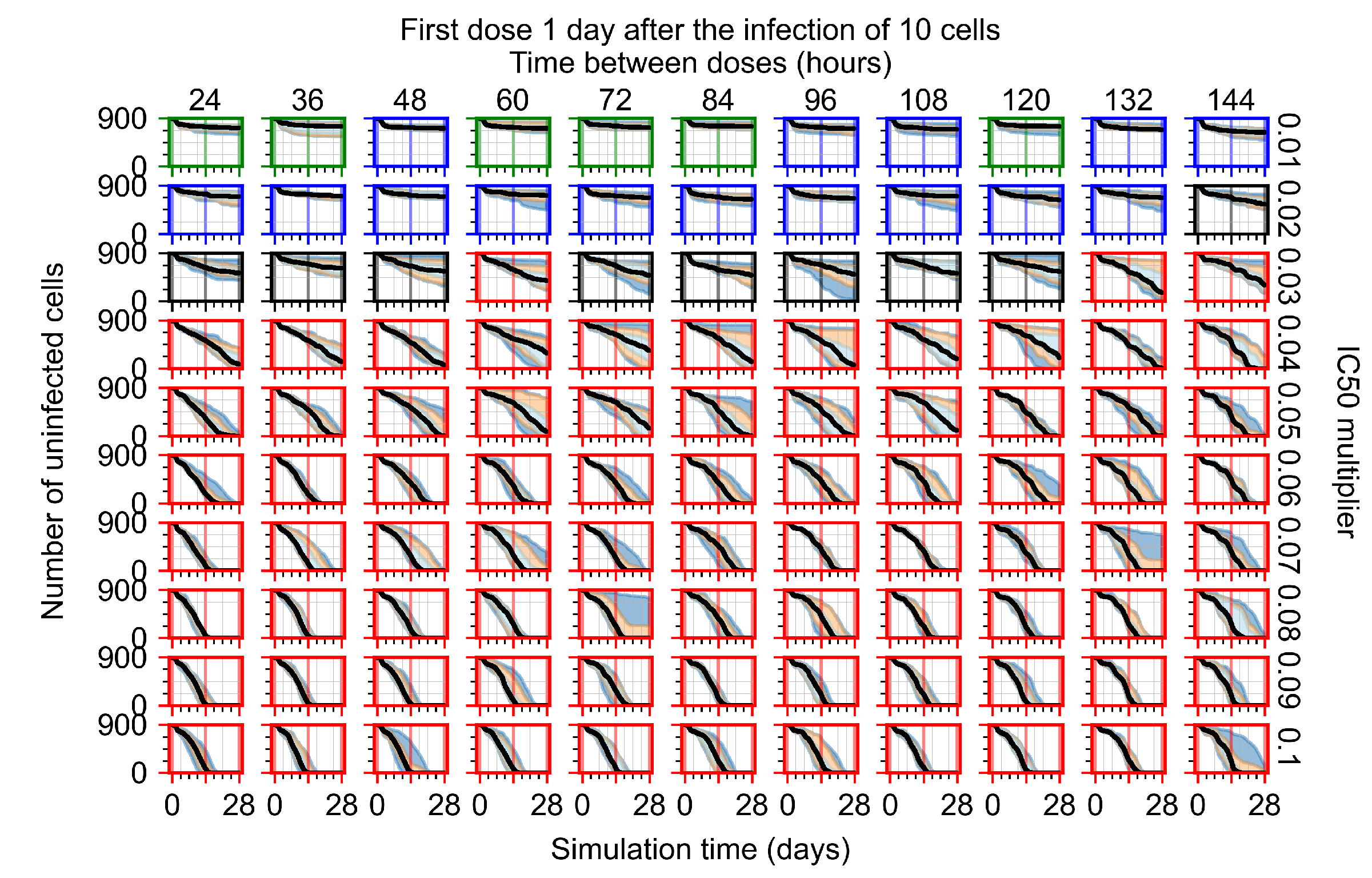
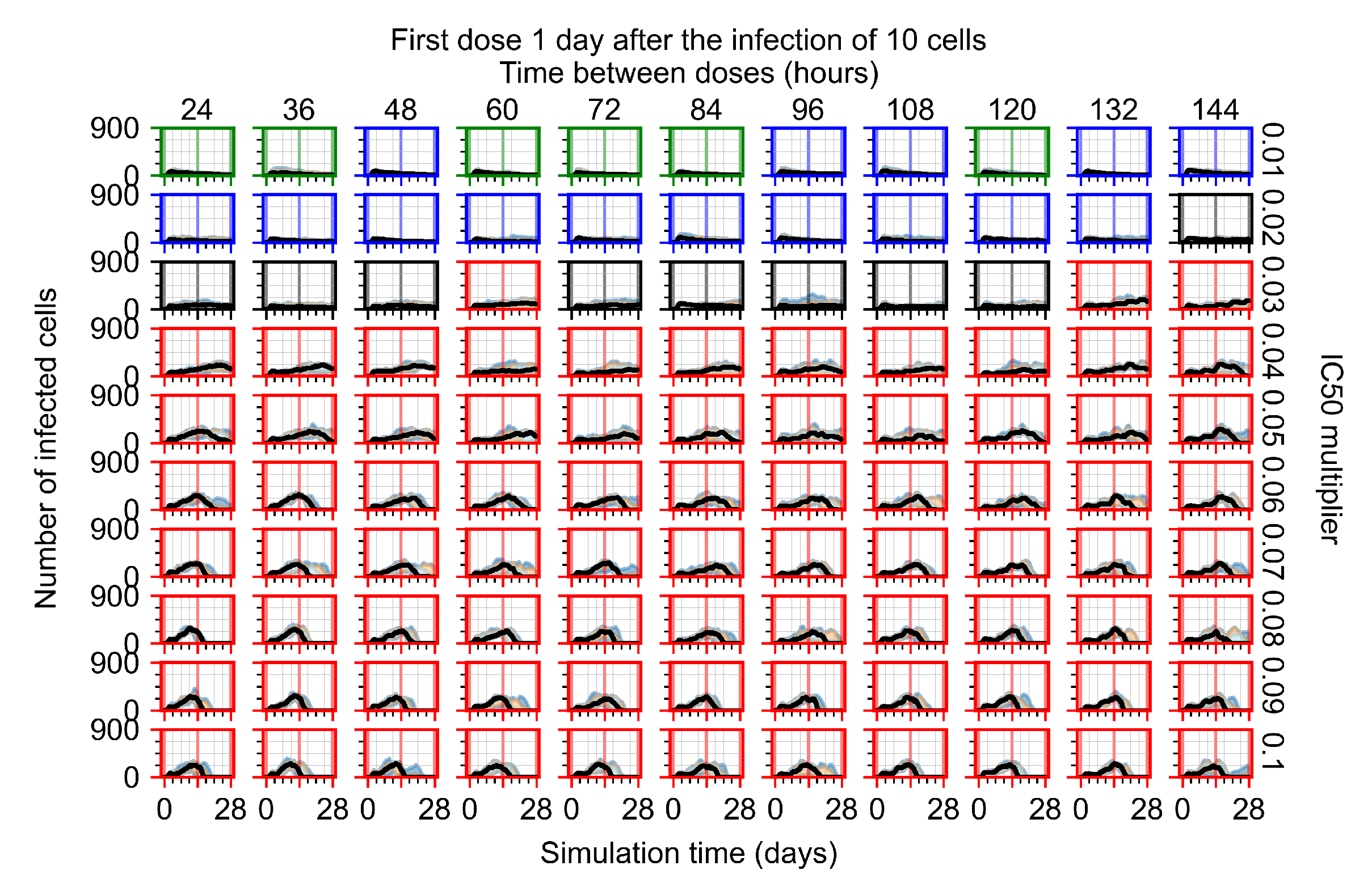
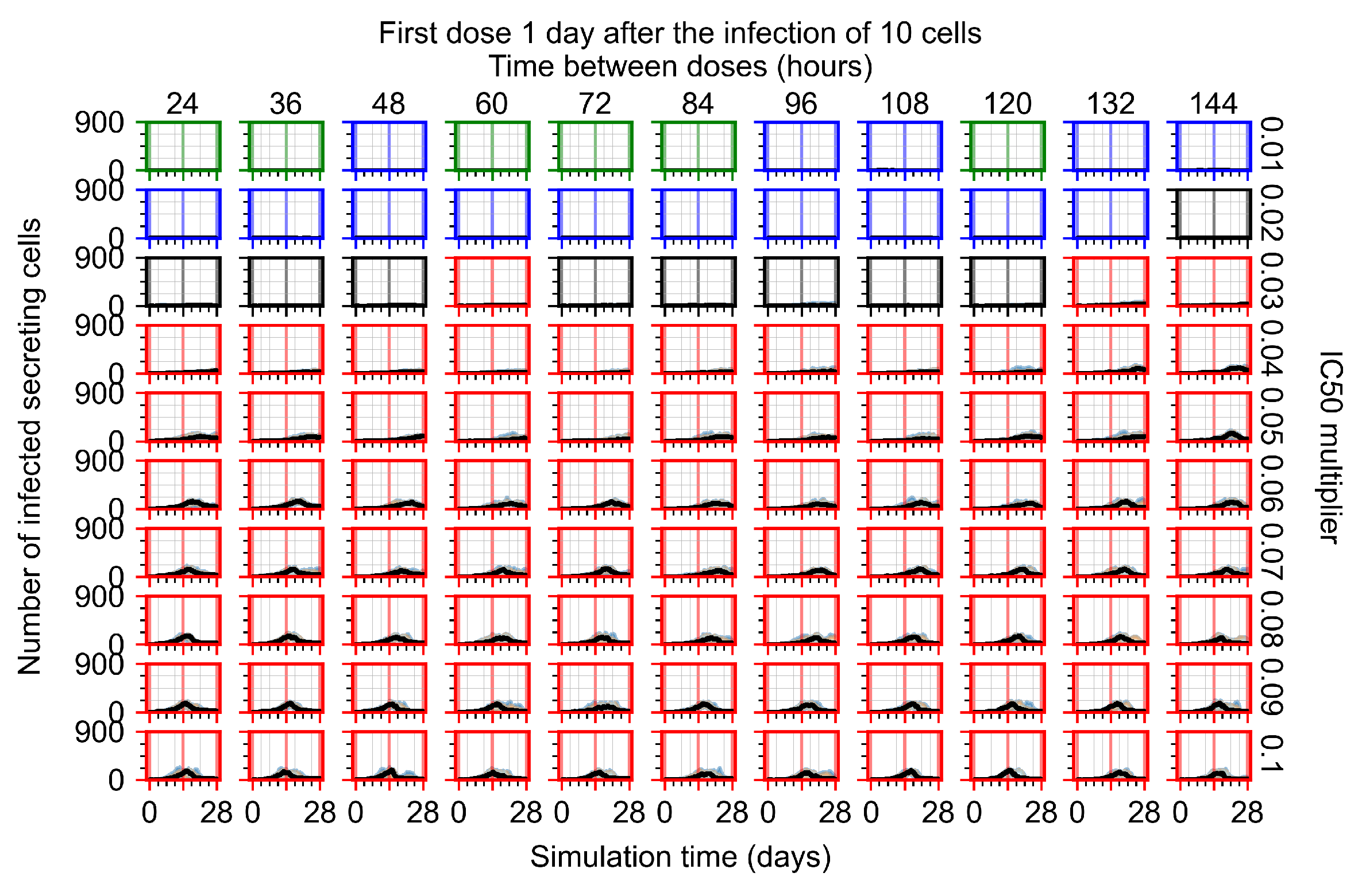


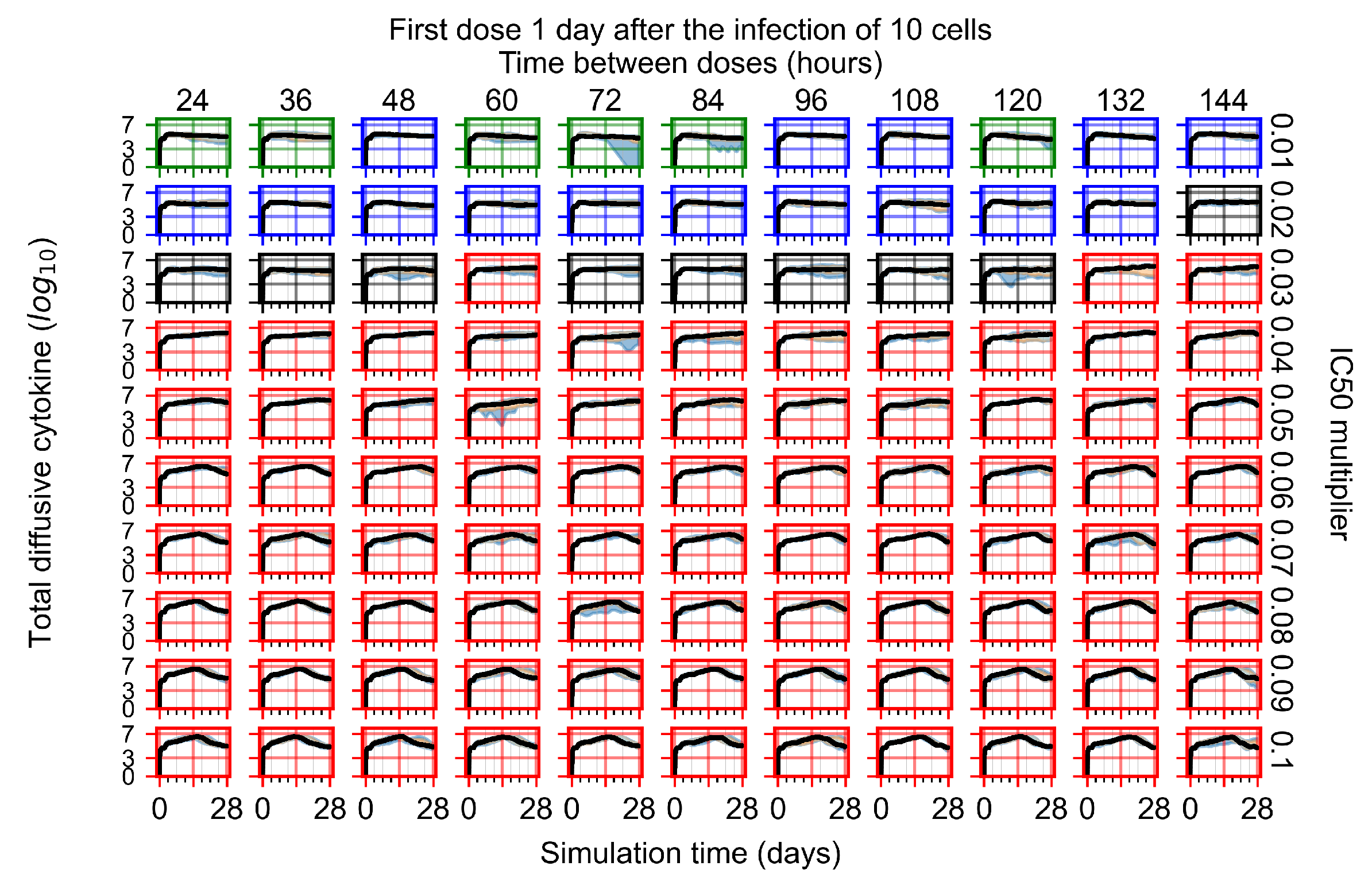
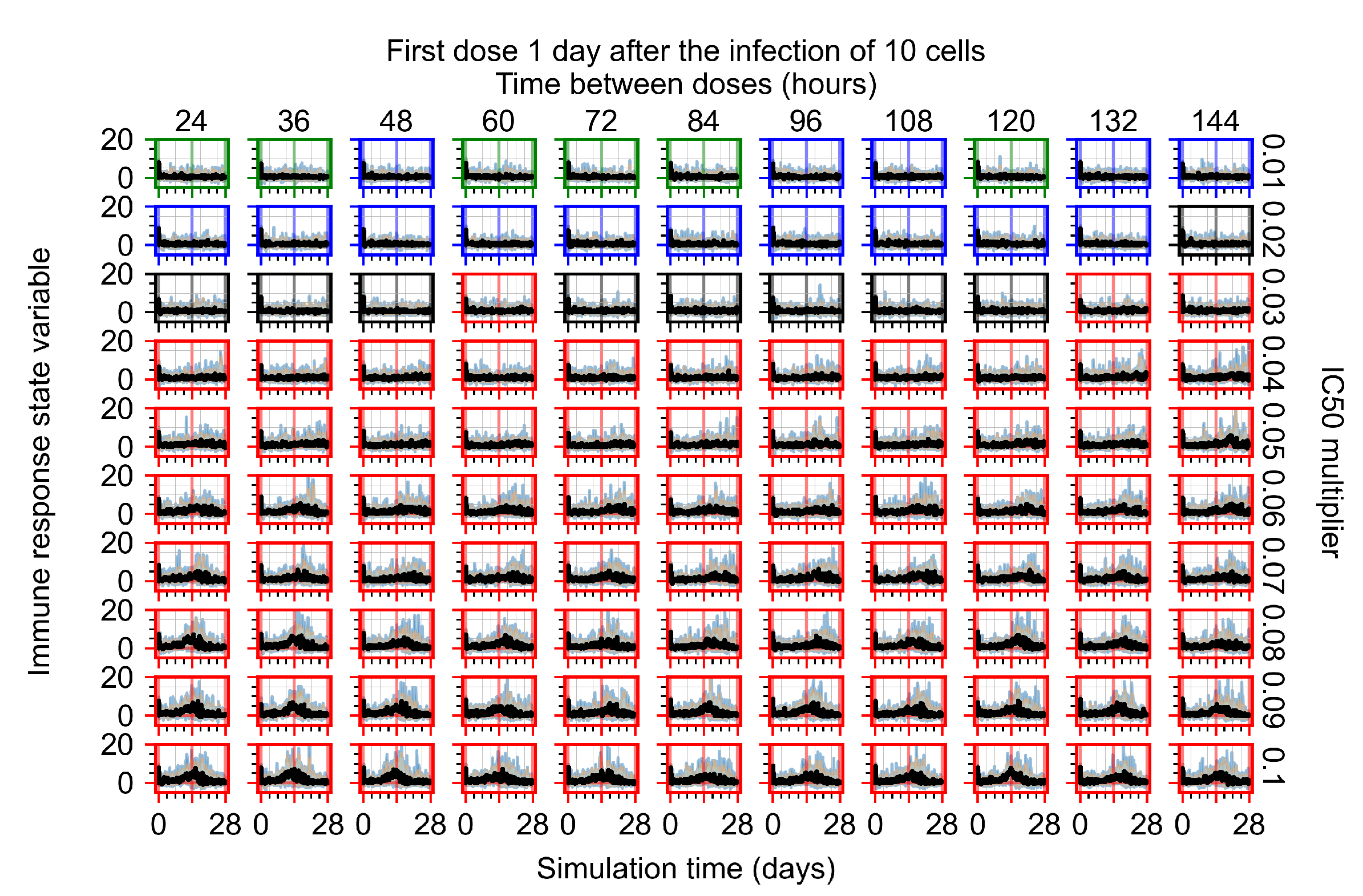
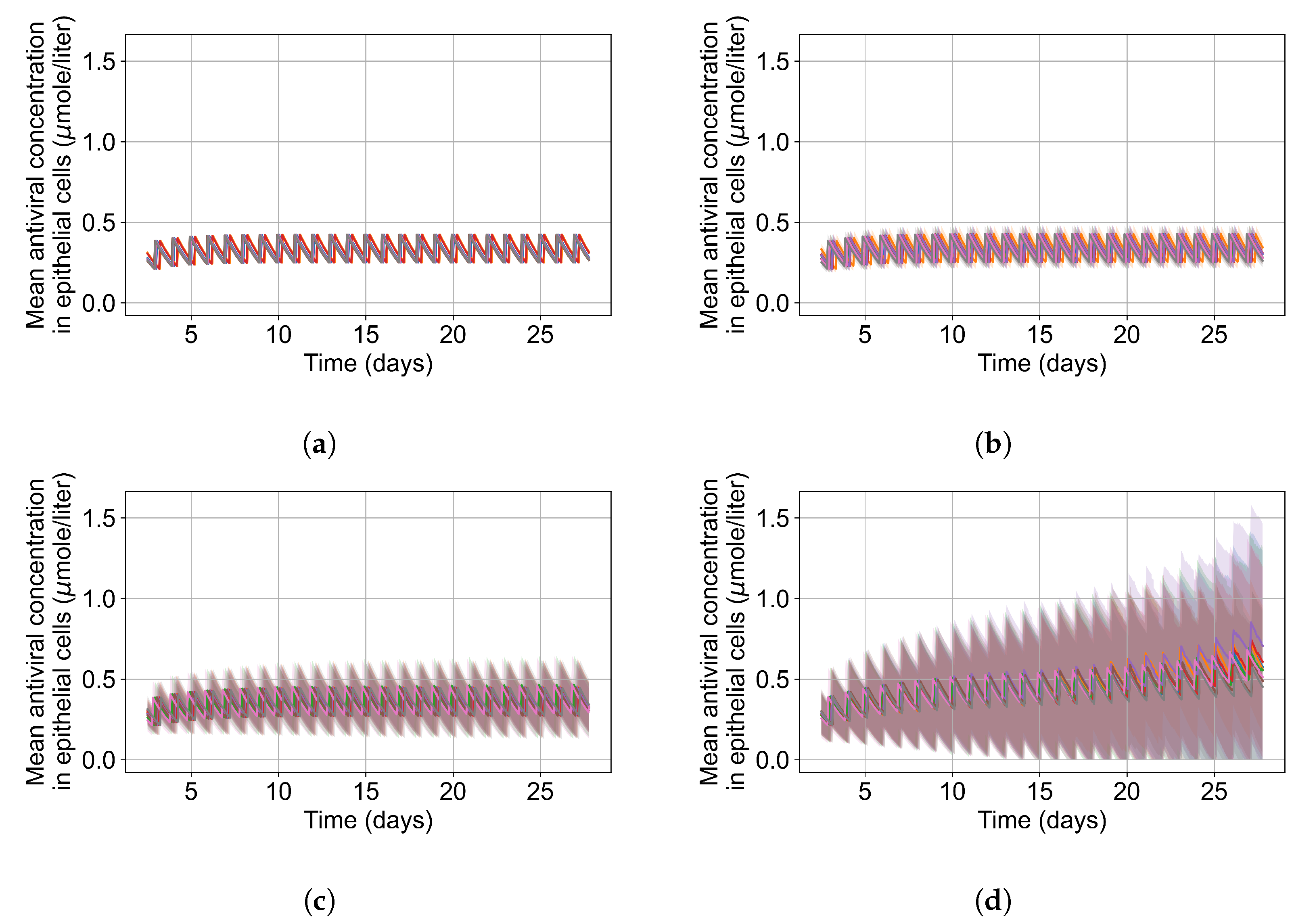
Appendix F.5.3. How Heterogeneity Affects Intracellular Drug Levels
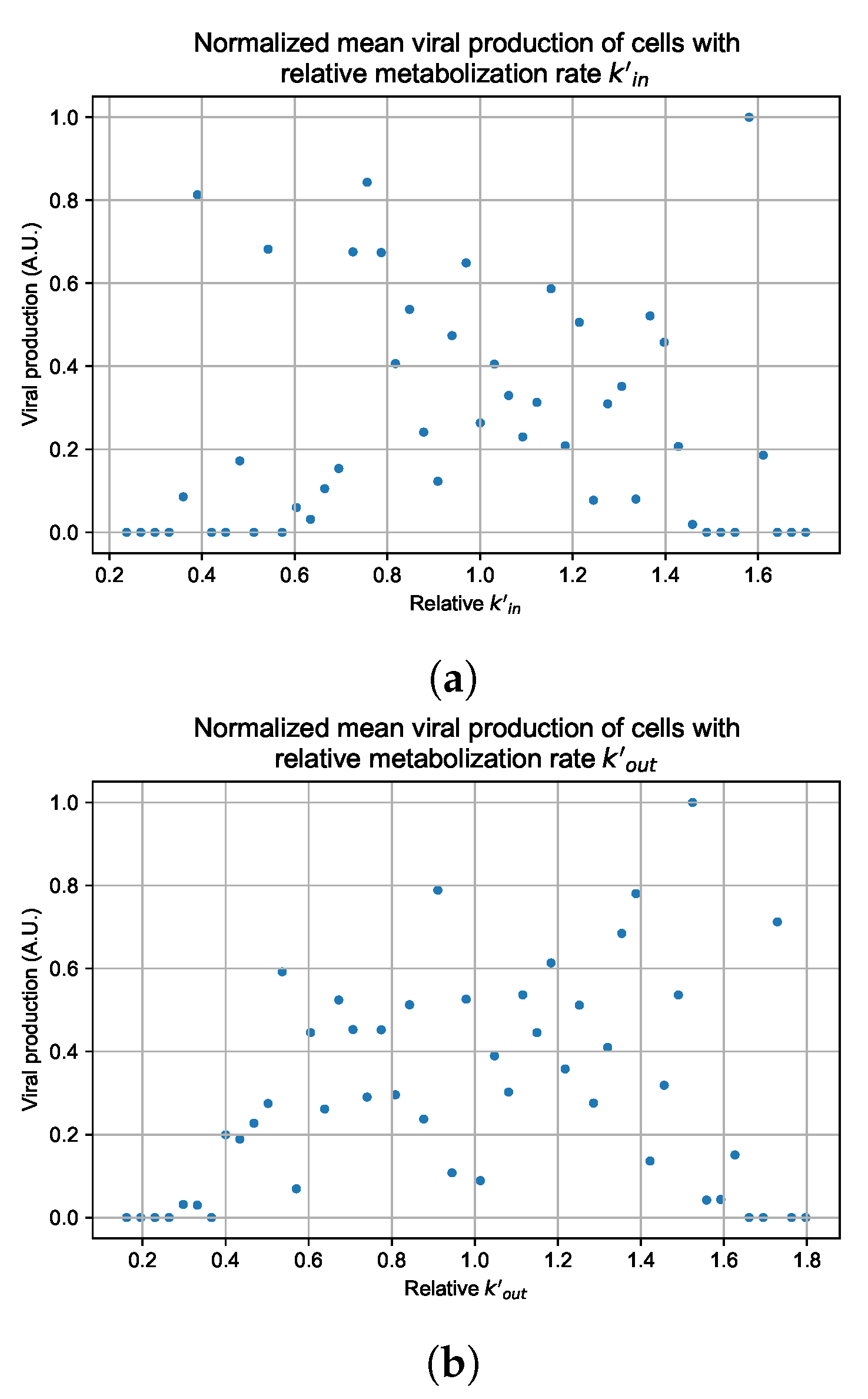
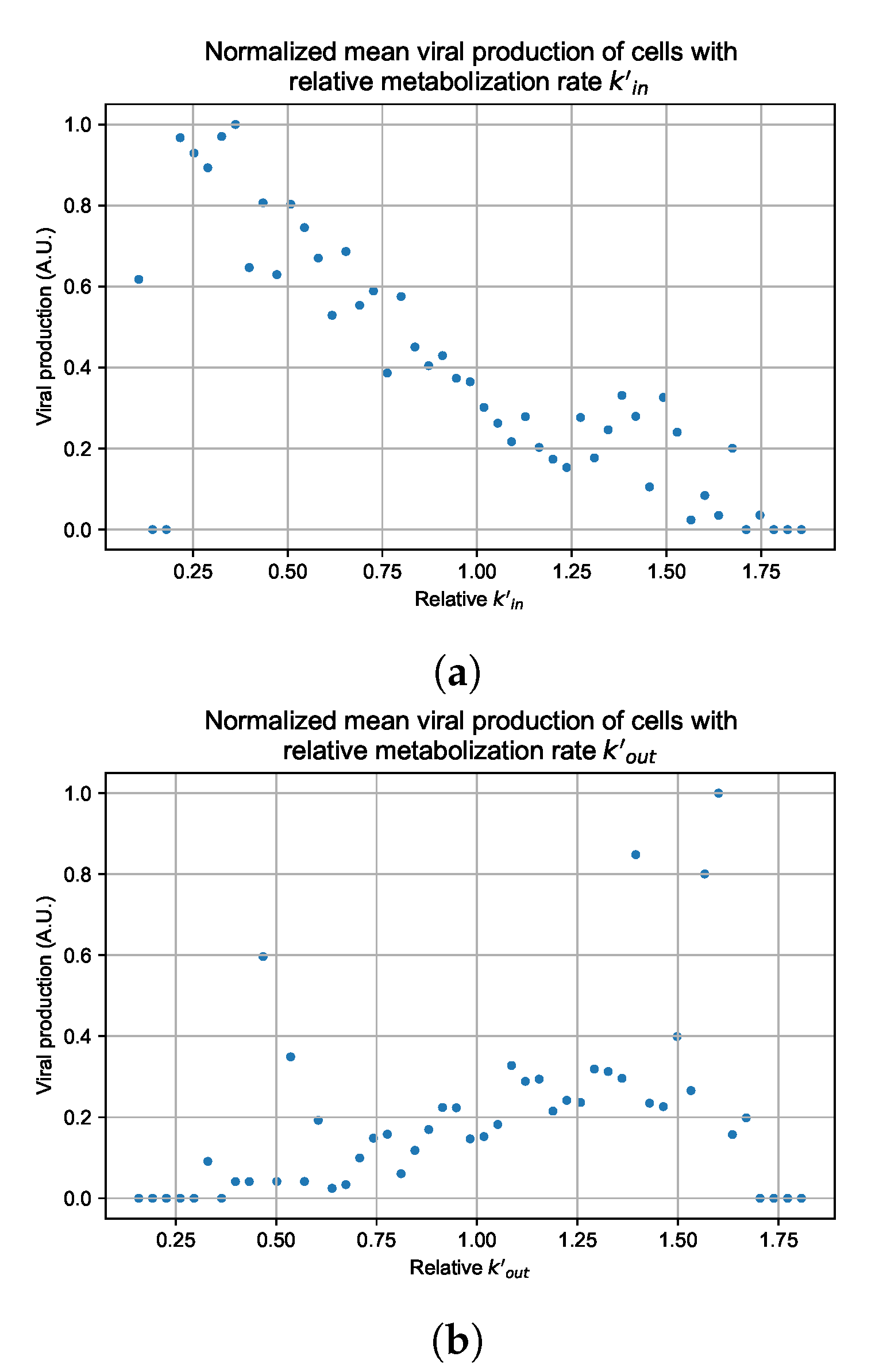
Appendix G. Supplementary Results for Viral Production Metabolism Rate Correlation


References
- Keshavarzi Arshadi, A.; Webb, J.; Salem, M.; Cruz, E.; Calad-Thomson, S.; Ghadirian, N.; Collins, J.; Diez-Cecilia, E.; Kelly, B.; Goodarzi, H.; et al. Artificial Intelligence for COVID-19 Drug Discovery and Vaccine Development. Front. Artif. Intell. 2020, 3, 65. [Google Scholar] [CrossRef] [PubMed]
- Jenner, A.L.; Aogo, R.A.; Davis, C.L.; Smith, A.M.; Craig, M. Leveraging Computational Modeling to Understand Infectious Diseases. Curr. Pathobiol. Rep. 2020, 8, 149–161. [Google Scholar] [CrossRef] [PubMed]
- Ciupe, S.M. Modeling the dynamics of hepatitis B infection, immunity, and drug therapy. Immunol. Rev. 2018, 285, 38–54. [Google Scholar] [CrossRef] [PubMed]
- Best, K.; Perelson, A.S. Mathematical modeling of within-host Zika virus dynamics. Immunol. Rev. 2018, 285, 81–96. [Google Scholar] [CrossRef] [PubMed]
- Schiffer, J.T.; Swan, D.A.; Prlic, M.; Lund, J.M. Herpes simplex virus-2 dynamics as a probe to measure the extremely rapid and spatially localized tissue-resident T-cell response. Immunol. Rev. 2018, 285, 113–133. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.C.; Deng, Q.X.; Dai, S.X. Remdesivir for severe acute respiratory syndrome coronavirus 2 causing COVID-19: An evaluation of the evidence. Travel Med. Infect. Dis. 2020, 35, 101647. [Google Scholar] [CrossRef] [PubMed]
- Humeniuk, R.; Mathias, A.; Cao, H.; Osinusi, A.; Shen, G.; Chng, E.; Ling, J.; Vu, A.; German, P. Safety, Tolerability, and Pharmacokinetics of Remdesivir, An Antiviral for Treatment of COVID-19, in Healthy Subjects. Clin. Transl. Sci. 2020, 13, 896–906. [Google Scholar] [CrossRef] [PubMed]
- Spinner, C.D.; Gottlieb, R.L.; Criner, G.J.; Arribas López, J.R.; Cattelan, A.M.; Soriano Viladomiu, A.; Ogbuagu, O.; Malhotra, P.; Mullane, K.M.; Castagna, A.; et al. Effect of Remdesivir vs Standard Care on Clinical Status at 11 Days in Patients With Moderate COVID-19: A Randomized Clinical Trial. JAMA 2020, 324, 1048–1057. [Google Scholar] [CrossRef] [PubMed]
- Kokic, G.; Hillen, H.S.; Tegunov, D.; Dienemann, C.; Seitz, F.; Schmitzova, J.; Farnung, L.; Siewert, A.; Höbartner, C.; Cramer, P. Mechanism of SARS-CoV-2 polymerase stalling by remdesivir. Nat. Commun. 2021, 12, 279. [Google Scholar] [CrossRef] [PubMed]
- Eastman, R.T.; Roth, J.S.; Brimacombe, K.R.; Simeonov, A.; Shen, M.; Patnaik, S.; Hall, M.D. Remdesivir: A Review of Its Discovery and Development Leading to Emergency Use Authorization for Treatment of COVID-19. ACS Cent. Sci. 2020, 6, 672–683. [Google Scholar] [CrossRef] [PubMed]
- Mitjà, O.; Clotet, B. Use of antiviral drugs to reduce COVID-19 transmission. Lancet Glob. Health 2020, 8, e639–e640. [Google Scholar] [CrossRef] [Green Version]
- De Clercq, E.; Li, G. Approved antiviral drugs over the past 50 years. Clin. Microbiol. Rev. 2016, 29, 695–747. [Google Scholar] [CrossRef] [Green Version]
- Zitzmann, C.; Kaderali, L. Mathematical analysis of viral replication dynamics and antiviral treatment strategies: From basic models to age-based multi-scale modeling. Front. Microbiol. 2018, 9, 1546. [Google Scholar] [CrossRef] [Green Version]
- Cao, P.; McCaw, J.M. The mechanisms for within-host influenza virus control affect model-based assessment and prediction of antiviral treatment. Viruses 2017, 9, 197. [Google Scholar] [CrossRef]
- Kim, K.S.; Iwanami, S.; Oda, T.; Fujita, Y.; Kuba, K.; Miyazaki, T.; Ejima, K.; Iwami, S. Incomplete antiviral treatment may induce longer durations of viral shedding during SARS-CoV-2 infection. Life Sci. Alliance 2021, 4. [Google Scholar] [CrossRef]
- Dobrovolny, H.M. Quantifying the effect of remdesivir in rhesus macaques infected with SARS-CoV-2. Virology 2020, 550, 61–69. [Google Scholar] [CrossRef]
- Williamson, B.N.; Feldmann, F.; Schwarz, B.; Meade-White, K.; Porter, D.P.; Schulz, J.; Van Doremalen, N.; Leighton, I.; Yinda, C.K.; Pérez-Pérez, L.; et al. Clinical benefit of remdesivir in rhesus macaques infected with SARS-CoV-2. Nature 2020, 585, 273–276. [Google Scholar] [CrossRef]
- Gallo, J.M. Hybrid physiologically-based pharmacokinetic model for remdesivir: Application to SARS-CoV-2. Clin. Transl. Sci. 2021, 14, 1082–1091. [Google Scholar] [CrossRef]
- Goyal, A.; Cardozo-Ojeda, E.F.; Schiffer, J.T. Potency and timing of antiviral therapy as determinants of duration of SARS-CoV-2 shedding and intensity of inflammatory response. Sci. Adv. 2020, 6, eabc7112. [Google Scholar] [CrossRef]
- Goyal, A.; Duke, E.R.; Cardozo-Ojeda, E.F.; Schiffer, J.T. Mathematical modeling explains differential SARS CoV-2 kinetics in lung and nasal passages in remdesivir treated rhesus macaques. bioRxiv 2020. [Google Scholar] [CrossRef]
- Zarnitsyna, V.I.; Gianlupi, J.F.; Hagar, A.; Sego, T.; Glazier, J.A. Advancing therapies for viral infections using mechanistic computational models of the dynamic interplay between the virus and host immune response. Curr. Opin. Virol. 2021, 50, 103–109. [Google Scholar] [CrossRef] [PubMed]
- Glazier, J.A.; Balter, A.; Popławski, N.J. Magnetization to morphogenesis: A brief history of the Glazier-Graner-Hogeweg mode. In Single-Cell-Based Models in Biology and Medicine; Springer: New York, NY, USA, 2007; pp. 79–106. [Google Scholar]
- Bonabeau, E. Agent-based modeling: Methods and techniques for simulating human systems. Proc. Natl. Acad. Sci. USA 2002, 99, 7280–7287. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sego, T.J.; Aponte-Serrano, J.O.; Gianlupi, J.F.; Heaps, S.R.; Breithaupt, K.; Brusch, L.; Crawshaw, J.; Osborne, J.M.; Quardokus, E.M.; Plemper, R.K.; et al. A modular framework for multiscale, multicellular, spatiotemporal modeling of acute primary viral infection and immune response in epithelial tissues and its application to drug therapy timing and effectiveness. PLoS Comput. Biol. 2020, 16, e1008451. [Google Scholar] [CrossRef] [PubMed]
- Sego, T.; Mochan, E.D.; Ermentrout, G.B.; Glazier, J.A. A multiscale multicellular spatiotemporal model of local influenza infection and immune response. J. Theor. Biol. 2022, 532, 110918. [Google Scholar] [CrossRef] [PubMed]
- Shirinifard, A.; Gens, J.S.; Zaitlen, B.L.; Popławski, N.J.; Swat, M.; Glazier, J.A. 3D Multi-Cell Simulation of Tumor Growth and Angiogenesis. PLoS ONE 2009, 4, e7190. [Google Scholar] [CrossRef] [Green Version]
- Gast, T.J.; Fu, X.; Gens, J.S.; Glazier, J.A. A computational model of peripheral photocoagulation for the prevention of progressive diabetic capillary occlusion. J. Diabetes Res. 2016, 2016, 2508381. [Google Scholar] [CrossRef] [Green Version]
- Getz, M.; Wang, Y.; An, G.; Asthana, M.; Becker, A.; Cockrell, C.; Collier, N.; Craig, M.; Davis, C.L.; Faeder, J.R.; et al. Iterative Community-driven development of a SARS-CoV-2 tissue simulator. BioRxiv 2021. [Google Scholar] [CrossRef] [Green Version]
- Cockrell, C.; An, G. Comparative computational modeling of the bat and human immune response to viral infection with the Comparative Biology Immune Agent Based Model. Viruses 2021, 13, 1620. [Google Scholar] [CrossRef]
- Zeng, Z.; Xu, L.; Xie, X.Y.; Yan, H.l.; Xie, B.J.; Xu, W.z.; Liu, X.A.; Kang, G.j.; Jiang, W.L.; Yuan, J.p. Pulmonary pathology of early-phase COVID-19 pneumonia in a patient with a benign lung lesion. Histopathology 2020, 77, 823–831. [Google Scholar] [CrossRef]
- Remmelink, M.; De Mendonça, R.; D’Haene, N.; De Clercq, S.; Verocq, C.; Lebrun, L.; Lavis, P.; Racu, M.L.; Trépant, A.L.; Maris, C.; et al. Unspecific post-mortem findings despite multiorgan viral spread in COVID-19 patients. Crit. Care 2020, 24, 495. [Google Scholar] [CrossRef]
- Fiege, J.K.; Thiede, J.M.; Nanda, H.A.; Matchett, W.E.; Moore, P.J.; Montanari, N.R.; Thielen, B.K.; Daniel, J.; Stanley, E.; Hunter, R.C.; et al. Single cell resolution of SARS-CoV-2 tropism, antiviral responses, and susceptibility to therapies in primary human airway epithelium. PLoS Pathog. 2021, 17, e1009292. [Google Scholar] [CrossRef]
- Ordonez, A.A.; Wang, H.; Magombedze, G.; Ruiz-Bedoya, C.A.; Srivastava, S.; Chen, A.; Tucker, E.W.; Urbanowski, M.E.; Pieterse, L.; Fabian Cardozo, E.; et al. Dynamic imaging in patients with tuberculosis reveals heterogeneous drug exposures in pulmonary lesions. Nat. Med. 2020, 26, 529–534. [Google Scholar] [CrossRef]
- Ben-Moshe, S.; Itzkovitz, S. Spatial heterogeneity in the mammalian liver. Nat. Rev. Gastroenterol. Hepatol. 2019, 16, 395–410. [Google Scholar] [CrossRef]
- Diaz Ochoa, J.G.; Bucher, J.; Péry, A.R.; Zaldivar Comenges, J.M.; Niklas, J.; Mauch, K. A multi-scale modeling framework for individualized, spatiotemporal prediction of drug effects and toxicological risk. Front. Pharmacol. 2013, 3, 204. [Google Scholar] [CrossRef] [Green Version]
- Dheda, K.; Lenders, L.; Magombedze, G.; Srivastava, S.; Raj, P.; Arning, E.; Ashcraft, P.; Bottiglieri, T.; Wainwright, H.; Pennel, T.; et al. Drug-penetration gradients associated with acquired drug resistance in patients with tuberculosis. Am. J. Respir. Crit. Care Med. 2018, 198, 1208–1219. [Google Scholar] [CrossRef]
- Swat, M.H.; Thomas, G.L.; Belmonte, J.M.; Shirinifard, A.; Hmeljak, D.; Glazier, J.A. Multi-Scale Modeling of Tissues Using CompuCell3D. Methods Cell Biol. 2012, 110, 325–366. [Google Scholar] [CrossRef] [Green Version]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—a COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [Green Version]
- European Medicines Agency. Summary on Compassionate Use. Remdesivir. EMA/178637/2020—Rev.2. Technical Report. 2020. Available online: https://www.ema.europa.eu/en/human-regulatory/research-development/compassionate-use (accessed on 4 November 2021).
- Hao, S.; Ning, K.; Kuz, C.A.; Vorhies, K.; Yan, Z.; Qiu, J. Long-Term Modeling of SARS-CoV-2 Infection of In Vitro Cultured Polarized Human Airway Epithelium. MBio 2020, 11, 17. [Google Scholar] [CrossRef]
- Choy, K.T.; Wong, A.Y.L.; Kaewpreedee, P.; Sia, S.F.; Chen, D.; Hui, K.P.Y.; Chu, D.K.W.; Chan, M.C.W.; Cheung, P.P.H.; Huang, X.; et al. Remdesivir, lopinavir, emetine, and homoharringtonine inhibit SARS-CoV-2 replication in vitro. Antivir. Res. 2020, 178, 104786. [Google Scholar] [CrossRef]
- Pizzorno, A.; Padey, B.; Dubois, J.; Julien, T.; Traversier, A.; Dulière, V.; Brun, P.; Lina, B.; Rosa-Calatrava, M.; Terrier, O. In vitro evaluation of antiviral activity of single and combined repurposable drugs against SARS-CoV-2. Antivir. Res. 2020, 181, 104878. [Google Scholar] [CrossRef]
- Hanafin, P.O.; Jermain, B.; Hickey, A.J.; Kabanov, A.V.; Kashuba, A.D.; Sheahan, T.P.; Rao, G.G. A mechanism-based pharmacokinetic model of remdesivir leveraging interspecies scaling to simulate COVID-19 treatment in humans. CPT Pharmacomet. Syst. Pharmacol. 2021, 10, 89–99. [Google Scholar] [CrossRef] [PubMed]
- Sun, D. Remdesivir for treatment of COVID-19: Combination of pulmonary and IV administration may offer aditional benefit. AAPS J. 2020, 22, 77. [Google Scholar] [CrossRef] [PubMed]
- Lew, Y.Y.; Michalak, T.I. In vitro and in vivo infectivity and pathogenicity of the lymphoid cell-derived woodchuck hepatitis virus. J. Virol. 2001, 75, 1770–1782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mateus, A.; Gordon, L.J.; Wayne, G.J.; Almqvist, H.; Axelsson, H.; Seashore-Ludlow, B.; Treyer, A.; Matsson, P.; Lundbäck, T.; West, A.; et al. Prediction of intracellular exposure bridges the gap between target- and cell-based drug discovery. Proc. Natl. Acad. Sci. USA 2017, 114, E6231–E6239. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhang, L.; Sang, L.; Ye, F.; Ruan, S.; Zhong, B.; Song, T.; Alshukairi, A.N.; Chen, R.; Zhang, Z.; et al. Kinetics of viral load and antibody response in relation to COVID-19 severity. J. Clin. Investig. 2020, 130, 5235–5244. [Google Scholar] [CrossRef]
- Wölfel, R.; Corman, V.M.; Guggemos, W.; Seilmaier, M.; Zange, S.; Müller, M.A.; Niemeyer, D.; Jones, T.C.; Vollmar, P.; Rothe, C.; et al. Virological assessment of hospitalized patients with COVID-2019. Nature 2020, 581, 465–469. [Google Scholar] [CrossRef] [Green Version]
- Reinharz, V.; Ishida, Y.; Tsuge, M.; Durso-Cain, K.; Chung, T.L.; Tateno, C.; Perelson, A.S.; Uprichard, S.L.; Chayama, K.; Dahari, H. Understanding Hepatitis B Virus Dynamics and the Antiviral Effect of Interferon Alpha Treatment in Humanized Chimeric Mice. J. Virol. 2021, 95, e00492-20. [Google Scholar] [CrossRef]
- Hu, W.j.; Chang, L.; Yang, Y.; Wang, X.; Xie, Y.c.; Shen, J.s.; Tan, B.; Liu, J. Pharmacokinetics and tissue distribution of remdesivir and its metabolites nucleotide monophosphate, nucleotide triphosphate, and nucleoside in mice. Acta Pharmacol. Sin. 2021, 42, 1195–1200. [Google Scholar] [CrossRef]
- RECOVERY Collaborative Group. Tocilizumab in patients admitted to hospital with COVID-19 (RECOVERY): A randomised, controlled, open-label, platform trial. Lancet 2021, 397, 1637–1645. [Google Scholar] [CrossRef]
- Chen, H.; Xie, J.; Su, N.; Wang, J.; Sun, Q.; Li, S.; Jin, J.; Zhou, J.; Mo, M.; Wei, Y.; et al. Corticosteroid Therapy Is Associated With Improved Outcome in Critically Ill Patients With COVID-19 With Hyperinflammatory Phenotype. Chest 2021, 159, 1793–1802. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.; Du, G.; Du, R.; Zhao, J.; Jin, Y.; Fu, S.; Gao, L.; Cheng, Z.; Lu, Q.; et al. Remdesivir in adults with severe COVID-19: A randomised, double-blind, placebo-controlled, multicentre trial. Lancet 2020, 395, 1569–1578. [Google Scholar] [CrossRef]





| Parameter | Value | Source |
|---|---|---|
| (unit-less) | 0 or 1 | Fit to [7] |
| GS-443902 observed Half-life, (h) | 30.2 | [7] |
| , GS-443902’s decay rate (1/h) | ||
| (mg/day) | 100 (200 for loading dose) | Doses used in clinical situations |
| (L) | 38.4 | Fit to [7,39] |
| (h) | 1 |
| Parameter | Values Used |
|---|---|
| Total epithelial population | 900 |
| Number of initially infected cells | 5 |
| Treatment initiation delay (day) | 0, 1, 3 |
| Time between antiviral doses | 8, 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144 |
| Remdesivir doses (rescaled to match the schedules) (mg) | 25, 50, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600 |
| Base (μmol/L) | 7.897 |
| Viral replication rate reduction (Equation (11)) Hill coefficient | 2 |
| multipliers | 0.01, 0.02, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.1, 0.5, 1, 5, 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrari Gianlupi, J.; Mapder, T.; Sego, T.J.; Sluka, J.P.; Quinney, S.K.; Craig, M.; Stratford, R.E., Jr.; Glazier, J.A. Multiscale Model of Antiviral Timing, Potency, and Heterogeneity Effects on an Epithelial Tissue Patch Infected by SARS-CoV-2. Viruses 2022, 14, 605. https://doi.org/10.3390/v14030605
Ferrari Gianlupi J, Mapder T, Sego TJ, Sluka JP, Quinney SK, Craig M, Stratford RE Jr., Glazier JA. Multiscale Model of Antiviral Timing, Potency, and Heterogeneity Effects on an Epithelial Tissue Patch Infected by SARS-CoV-2. Viruses. 2022; 14(3):605. https://doi.org/10.3390/v14030605
Chicago/Turabian StyleFerrari Gianlupi, Juliano, Tarunendu Mapder, T. J. Sego, James P. Sluka, Sara K. Quinney, Morgan Craig, Robert E. Stratford, Jr., and James A. Glazier. 2022. "Multiscale Model of Antiviral Timing, Potency, and Heterogeneity Effects on an Epithelial Tissue Patch Infected by SARS-CoV-2" Viruses 14, no. 3: 605. https://doi.org/10.3390/v14030605
APA StyleFerrari Gianlupi, J., Mapder, T., Sego, T. J., Sluka, J. P., Quinney, S. K., Craig, M., Stratford, R. E., Jr., & Glazier, J. A. (2022). Multiscale Model of Antiviral Timing, Potency, and Heterogeneity Effects on an Epithelial Tissue Patch Infected by SARS-CoV-2. Viruses, 14(3), 605. https://doi.org/10.3390/v14030605






