Combining Viral Genetics and Statistical Modeling to Improve HIV-1 Time-of-Infection Estimation towards Enhanced Vaccine Efficacy Assessment
Abstract
1. Introduction
- (1)
- Time-dependent marker correlates of risk (CoR) of HIV-1 infection: For studying the correlates of HIV-1 risk, a case-cohort or case-control study design can be used to measure a time-varying potential correlate (marker) of interest as near as possible prior to the time of HIV-1 acquisition for all HIV-1 infected cases. Moreover, for a random sample of participants who complete follow-up testing as HIV-1-negative, the marker(s) is measured at all longitudinal sample time points (e.g., this design was employed in the VaxGen HIV-1 VE trial [20,28] and the Partners in PrEP prevention efficacy trial [29] and is planned for the AMP prevention efficacy trials [27] as well as for the HVTN 702 and HVTN 705 VE trials). In AMP one key marker of interest is VRC01 serum concentration measured by ELISA or serum neutralization titer against a standard panel of viruses by a neutralization assay; population pharmacokinetics/pharmacodynamics (PK/PD) models can be used to provide low-error unbiased estimates for the VRC01 concentration in infected individuals [30], given an accurate estimate of the date of infection. An important goal of the AMP trials is to characterize the relationship between a person’s VRC01 concentration and their instantaneous risk of HIV-1 infection. Identification of a serum neutralization threshold associated with (very) low risk of HIV-1 infection would provide valuable guidance for future vaccine development. What makes it challenging to pinpoint a marker’s value at infection is uncertainty in the date of infection. Even with monthly HIV-1 testing with high adherence to the testing schedule, the estimation methodologies that we previously employed for evaluation of HIV-1 VE trials are inadequate for the requirements of the AMP studies. In Supplementary Section A we illustrate the amount of increase in statistical power to detect such a CoR in the AMP studies that we expect to result from reducing the error in the infection time estimator (Supplementary Figure S1) using our previously applied approach [31].
- (2)
- “Sieve analysis”: How the level of vaccine/prevention efficacy depends on genotypic characteristics of HIV-1 at the time of acquisition: Sieve analysis provides another tool to detect and evaluate correlates of vaccine protection, based on the comparison of viruses that infect placebo recipients with the viruses that infect vaccine recipients, despite the protective barrier induced by vaccination [32]. An ongoing challenge for sieve analysis is that the determination of HIV-1 genetics at the time of HIV-1 acquisition is of fundamental importance for discriminating true sieve effects from post-acquisition effects. That is, whether observed viral genetic differences (across treatment groups, vaccine vs. placebo) can be interpreted as differential blockage of acquisition of incoming variants (a true “sieve effect”) vs. as resulting from differential evolution post-infection of similar starting viruses, resulting for example from effects in which vaccine-induced anamnestic responses impact the early evolution of HIV-1 prior to diagnosis (and sampling for sequencing) [33]. This issue has been critically important in the interpretation of sieve effects for all HIV-1 sieve reports to date [34,35,36,37,38]. Statistical methods have been developed that require the ability to determine which HIV-1 infection events are diagnosed very early prior to significant post-infection evolution [39,40,41]; additional research is needed to ensure that the methods optimally incorporate state-of-the-art infection time estimators.
2. Materials and Methods
2.1. Studies, Participants, Diagnostic Testing and HIV-1 Sequencing
2.2. Sequence Data Pre-Processing, Hypermutation Detection, and Recombination Detection
2.3. Infection Time
2.4. True and Artificial Diagnostic Bounds on the Date of Infection
2.5. PFitter Estimate of Days Since Infection
2.6. Variations on the PFitter Estimator of t: (syn) and (w/in clusts)
2.7. Clustering Sequences for the Within-Clusters PFitter Method
2.8. PrankenBeast
2.9. Founder Multiplicity Characterization
2.10. Rolland HVTN Method for Determining Founder Multiplicity
2.11. Tests for Star-Like Phylogeny or Founder Multiplicity
2.12. Statistical Methods for Calibrating Predictors of the Indicator of a Multiple-Founder Infection
2.13. Statistical Methods for Calibrating Predictors of Infection Timing
2.14. Software Pipeline
3. Results
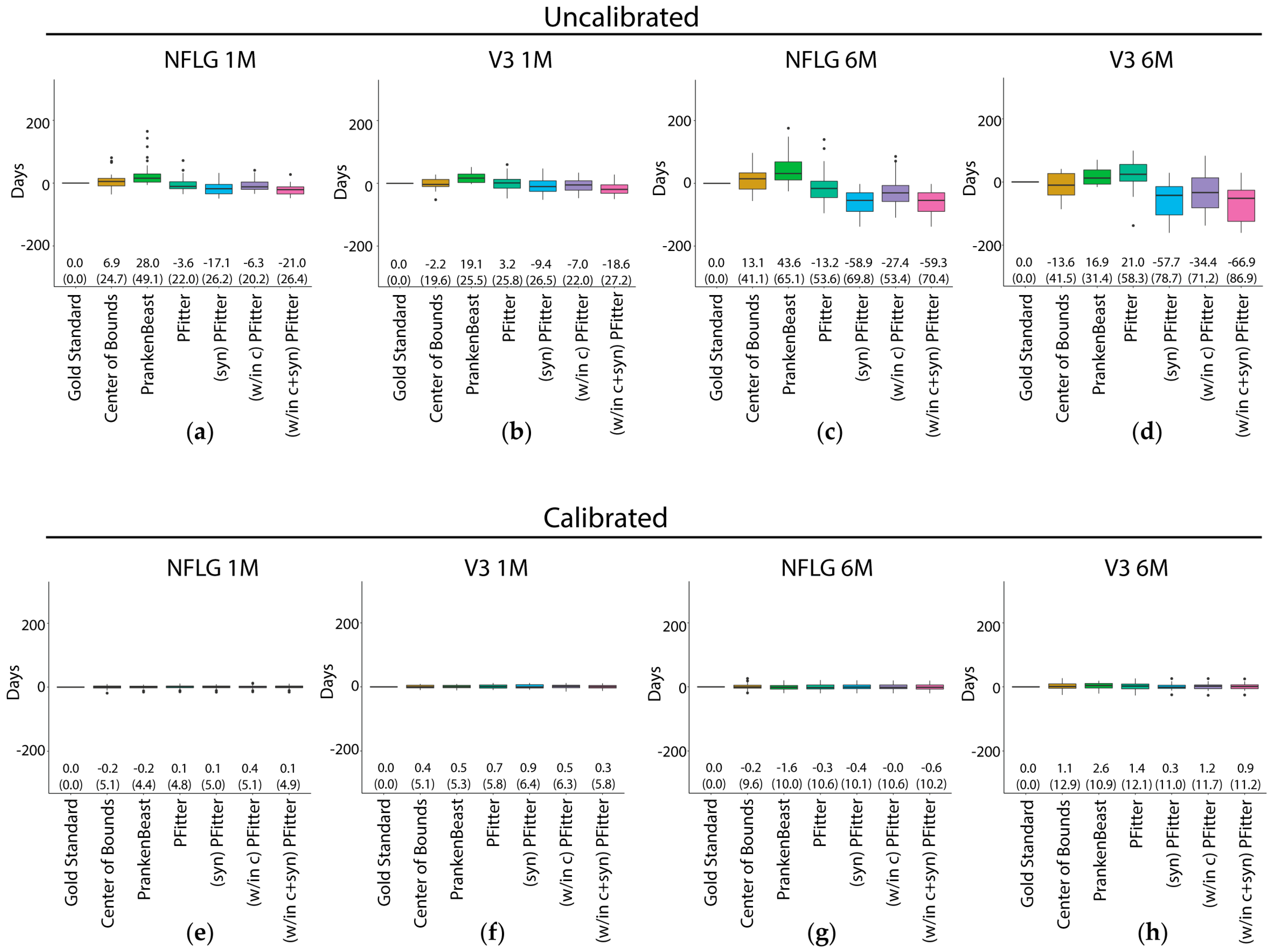
3.1. RMSE and Bias of Center-of-Bounds (COB) Estimates of Infection Time
3.2. Prediction Error of Sequence-Based Estimators of Time Since HIV-1 Infection is Improved with Calibration
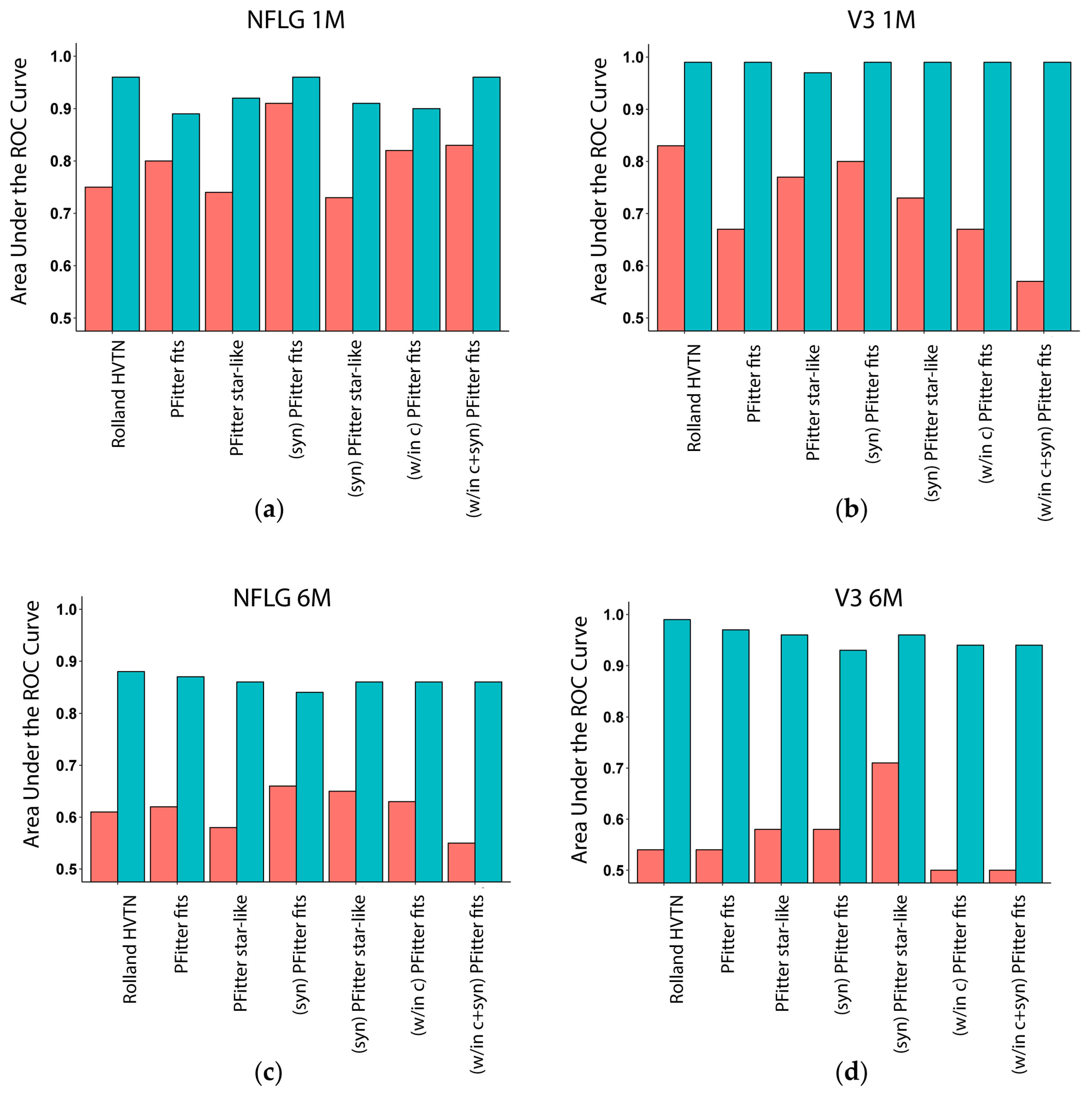
3.3. Multiplicity Assessment is Improved by Calibration with LASSO
3.4. Calibration, Considerations and Results Summary
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Fiebig, E.W.; Wright, D.J.; Rawal, B.D.; Garrett, P.E.; Schumacher, R.T.; Peddada, L.; Heldebrant, C.; Smith, R.; Conrad, A.; Kleinman, S.H.; et al. Dynamics of HIV viremia and antibody seroconversion in plasma donors: Implications for diagnosis and staging of primary HIV infection. AIDS 2003, 17, 1871–1879. [Google Scholar] [CrossRef]
- McMichael, A.J.; Borrow, P.; Tomaras, G.D.; Goonetilleke, N.; Haynes, B.F. The immune response during acute HIV-1 infection: Clues for vaccine development. Nat. Rev. Immunol. 2010, 10, 11–23. [Google Scholar] [CrossRef]
- Cohen, M.S.; Gay, C.L.; Busch, M.P.; Hecht, F.M. The detection of acute HIV infection. J. Infect. Dis 2010, 202 Suppl. 2, S270–S277. [Google Scholar] [CrossRef]
- Ananworanich, J.; Fletcher, J.L.; Pinyakorn, S.; van Griensven, F.; Vandergeeten, C.; Schuetz, A.; Pankam, T.; Trichavaroj, R.; Akapirat, S.; Chomchey, N.; et al. A novel acute HIV infection staging system based on 4th generation immunoassay. Retrovirology. 2013, 10, 56. [Google Scholar] [CrossRef]
- Le, T.; Wright, E.J.; Smith, D.M.; He, W.; Catano, G.; Okulicz, J.F.; Young, J.A.; Clark, R.A.; Richman, D.D.; Little, S.J.; et al. Enhanced CD4+ T-cell recovery with earlier HIV-1 antiretroviral therapy. N Engl. J. Med. 2013, 368, 218–230. [Google Scholar] [CrossRef]
- Sanders, E.J.; Okuku, H.S.; Smith, A.D.; Mwangome, M.; Wahome, E.; Fegan, G.; Peshu, N.; van der Elst, E.M.; Price, M.A.; McClelland, R.S.; et al. High HIV-1 incidence, correlates of HIV-1 acquisition, and high viral loads following seroconversion among men who have sex with men in coastal Kenya. AIDS (London, England) 2013, 27, 437–446. [Google Scholar] [CrossRef]
- Mlisana, K.; Werner, L.; Garrett, N.J.; McKinnon, L.R.; van Loggerenberg, F.; Passmore, J.A.; Gray, C.M.; Morris, L.; Williamson, C.; Abdool Karim, S.S.; et al. Rapid disease progression in HIV-1 subtype C-infected South African women. Clin. Infect. Dis. 2014, 59, 1322–1331. [Google Scholar] [CrossRef]
- Hoenigl, M.; Green, N.; Camacho, M.; Gianella, S.; Mehta, S.R.; Smith, D.M.; Little, S.J. Signs or symptoms of acute HIV infection in a cohort undergoing community-based screening. Emerg. Infect. Dis 2016, 22, 532–534. [Google Scholar] [CrossRef]
- Moyo, S.; Wilkinson, E.; Novitsky, V.; Vandormael, A.; Gaseitsiwe, S.; Essex, M.; Engelbrecht, S.; de Oliveira, T. Identifying recent HIV infections: From serological assays to genomics. Viruses 2015, 7, 5508–5524. [Google Scholar] [CrossRef]
- Gay, C.; Dibben, O.; Anderson, J.A.; Stacey, A.; Mayo, A.J.; Norris, P.J.; Kuruc, J.D.; Salazar-Gonzalez, J.F.; Li, H.; Keele, B.F.; et al. Cross-sectional detection of acute HIV infection: Timing of transmission, inflammation and antiretroviral therapy. PLoS ONE 2011, 6, e19617. [Google Scholar] [CrossRef]
- Ciccozzi, M.; Lo Presti, A.; Andreotti, M.; Mancinelli, S.; Ceffa, S.; Galluzzo, C.M.; Buonomo, E.; Luhanga, R.; Jere, H.; Cella, E.; et al. Viral sequence analysis of HIV-positive women and their infected children: Insight on the timing of infection and on the transmission network. AIDS Res. Hum. Retroviruses 2014, 30, 1010–1015. [Google Scholar] [CrossRef]
- Love, T.M.; Park, S.Y.; Giorgi, E.E.; Mack, W.J.; Perelson, A.S.; Lee, H.Y. Spmm: Estimating infection duration of multivariant HIV-1 infections. Bioinformatics 2016, 32, 1308–1315. [Google Scholar] [CrossRef]
- Poon, A.F.; McGovern, R.A.; Mo, T.; Knapp, D.J.; Brenner, B.; Routy, J.P.; Wainberg, M.A.; Harrigan, P.R. Dates of HIV infection can be estimated for seroprevalent patients by coalescent analysis of serial next-generation sequencing data. AIDS 2011, 25, 2019–2026. [Google Scholar] [CrossRef]
- Puller, V.; Neher, R.; Albert, J. Estimating time of HIV-1 infection from next-generation sequence diversity. PLoS Comput. Biol. 2017, 13, e1005775. [Google Scholar] [CrossRef]
- Shankarappa, R.; Margolick, J.B.; Gange, S.J.; Rodrigo, A.G.; Upchurch, D.; Farzadegan, H.; Gupta, P.; Rinaldo, C.R.; Learn, G.H.; He, X.; et al. Consistent viral evolutionary changes associated with the progression of human immunodeficiency virus type 1 infection. J. Virol. 1999, 73, 10489–10502. [Google Scholar]
- Kouyos, R.D.; von Wyl, V.; Yerly, S.; Boni, J.; Rieder, P.; Joos, B.; Taffe, P.; Shah, C.; Burgisser, P.; Klimkait, T. , et al. Ambiguous nucleotide calls from population-based sequencing of HIV-1 are a marker for viral diversity and the age of infection. Clin. Infect. Dis. 2011, 52, 532–539. [Google Scholar] [CrossRef]
- Ragonnet-Cronin, M.; Aris-Brosou, S.; Joanisse, I.; Merks, H.; Vallee, D.; Caminiti, K.; Rekart, M.; Krajden, M.; Cook, D.; Kim, J.; et al. Genetic diversity as a marker for timing infection in HIV-infected patients: Evaluation of a 6-month window and comparison with bed. J. Infect. Dis. 2012, 206, 756–764. [Google Scholar] [CrossRef]
- Andersson, E.; Shao, W.; Bontell, I.; Cham, F.; Cuong do, D.; Wondwossen, A.; Morris, L.; Hunt, G.; Sonnerborg, A.; Bertagnolio, S.; et al. Evaluation of sequence ambiguities of the HIV-1 pol gene as a method to identify recent HIV-1 infection in transmitted drug resistance surveys. Infect. Genet. Evol. 2013, 18, 125–131. [Google Scholar] [CrossRef]
- Flynn, N.M.; Forthal, D.N.; Harro, C.D.; Judson, F.N.; Mayer, K.H.; Para, M.F.; Rgp, H.I.V.V.S.G. Placebo-controlled phase 3 trial of a recombinant glycoprotein 120 vaccine to prevent HIV-1 infection. J. Infect. Dis 2005, 191, 654–665. [Google Scholar]
- Pitisuttithum, P.; Gilbert, P.; Gurwith, M.; Heyward, W.; Martin, M.; van Griensven, F.; Hu, D.; Tappero, J.W.; Choopanya, K.; Bangkok Vaccine Evaluation, G. Randomized, double-blind, placebo-controlled efficacy trial of a bivalent recombinant glycoprotein 120 HIV-1 vaccine among injection drug users in Bangkok, Thailand. J. Infect. Dis 2006, 194, 1661–1671. [Google Scholar] [CrossRef]
- Buchbinder, S.P.; Mehrotra, D.V.; Duerr, A.; Fitzgerald, D.W.; Mogg, R.; Li, D.; Gilbert, P.B.; Lama, J.R.; Marmor, M.; Del Rio, C.; et al. Efficacy assessment of a cell-mediated immunity HIV-1 vaccine (the Step study): A double-blind, randomised, placebo-controlled, test-of-concept trial. Lancet 2008, 372, 1881–1893. [Google Scholar] [CrossRef]
- Rerks-Ngarm, S.; Pitisuttithum, P.; Nitayaphan, S.; Kaewkungwal, J.; Chiu, J.; Paris, R.; Premsri, N.; Namwat, C.; de Souza, M.; Adams, E.; et al. Vaccination with ALVAC and AIDSVAX to prevent HIV-1 infection in Thailand. N Engl. J. Med. 2009, 361, 2209–2220. [Google Scholar] [CrossRef]
- Gray, G.E.; Allen, M.; Moodie, Z.; Churchyard, G.; Bekker, L.G.; Nchabeleng, M.; Mlisana, K.; Metch, B.; de Bruyn, G.; Latka, M.H.; et al. Safety and efficacy of the HVTN 503/Phambili study of a clade-B-based HIV-1 vaccine in South Arica: A double-blind, randomised, placebo-controlled test-of-concept phase 2b study. Lancet Infect. Dis. 2011, 11, 507–515. [Google Scholar] [CrossRef]
- Hammer, S.M.; Sobieszczyk, M.E.; Janes, H.; Karuna, S.T.; Mulligan, M.J.; Grove, D.; Koblin, B.A.; Buchbinder, S.P.; Keefer, M.C.; Tomaras, G.D.; et al. Efficacy trial of a DNA/rAd5 HIV-1 preventive vaccine. N Engl. J. Med. 2013, 369, 2083–2092. [Google Scholar] [CrossRef]
- Gray, G.E.; Laher, F.; Lazarus, E.; Ensoli, B.; Corey, L. Approaches to preventative and therapeutic HIV vaccines. Curr. Opin. Virol. 2016, 17, 104–109. [Google Scholar] [CrossRef]
- ClinicalTrials.gov. A study to assess the efficacy of a heterologous prime/boost vaccine regimen of ad26.Mos4.Hiv and aluminum phosphate-adjuvanted clade C gp140 in preventing human immunodeficiency virus (HIV)-1 infection in women in Sub-Saharan Africa. Available online: https://clinicaltrials.gov/ct2/show/NCT03060629 (accessed on 3 March 2019).
- Gilbert, P.B.; Juraska, M.; deCamp, A.C.; Karuna, S.; Edupuganti, S.; Mgodi, N.; Donnell, D.J.; Bentley, C.; Sista, N.; Andrew, P.; et al. Basis and statistical design of the passive HIV-1 Antibody Mediated Prevention (AMP) test-of-concept efficacy trials. Stat. Commun. Infect. Dis 2017, 9. [Google Scholar] [CrossRef]
- Gilbert, P.B.; Peterson, M.L.; Follmann, D.; Hudgens, M.G.; Francis, D.P.; Gurwith, M.; Heyward, W.L.; Jobes, D.V.; Popovic, V.; Self, S.G.; et al. Correlation between immunologic responses to a recombinant glycoprotein 120 vaccine and incidence of HIV-1 infection in a phase 3 HIV-1 preventive vaccine trial. J. Infect. Dis. 2005, 191, 666–677. [Google Scholar] [CrossRef]
- Baeten, J.M.; Donnell, D.; Ndase, P.; Mugo, N.R.; Campbell, J.D.; Wangisi, J.; Tappero, J.W.; Bukusi, E.A.; Cohen, C.R.; Katabira, E.; et al. Antiretroviral prophylaxis for HIV prevention in heterosexual men and women. N. Engl. J. Med. 2012, 367, 399–410. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, L.; Ledgerwood, J.; Grunenberg, N.; Bailer, R.; Isaacs, A.; Seaton, K.; Mayer, K.H.; Capparelli, E.; Corey, L.; et al. Population pharmacokinetics analysis of VRC01, an HIV-1 broadly neutralizing monoclonal antibody, in healthy adults. MAbs 2017, 9, 792–800. [Google Scholar] [CrossRef]
- Gilbert, P.B.; Zhang, Y.; Rudnicki, E.; Huang, Y. Assessing pharmacokinetic marker correlates of outcome, with application to antibody prevention efficacy trials. Stat. Med. 2019, in press. [Google Scholar]
- Gilbert, P.B. Interpretability and robustness of sieve analysis models for assessing HIV strain variations in vaccine efficacy. Stat. Med. 2001, 20, 263–279. [Google Scholar] [CrossRef]
- Edlefsen, P.T.; Gilbert, P.B.; Rolland, M. Sieve analysis in HIV-1 vaccine efficacy trials. Curr. Opin. HIV AIDS 2013, 8, 432–436. [Google Scholar] [CrossRef]
- Rolland, M.; Edlefsen, P.T.; Larsen, B.B.; Tovanabutra, S.; Sanders-Buell, E.; Hertz, T.; deCamp, A.C.; Carrico, C.; Menis, S.; Magaret, C.A.; et al. Increased HIV-1 vaccine efficacy against viruses with genetic signatures in Env V2. Nature 2012, 490, 417–420. [Google Scholar] [CrossRef]
- Rolland, M.; Tovanabutra, S.; deCamp, A.C.; Frahm, N.; Gilbert, P.B.; Sanders-Buell, E.; Heath, L.; Magaret, C.A.; Bose, M.; Bradfield, A.; et al. Genetic impact of vaccination on breakthrough HIV-1 sequences from the Step trial. Nat. Med. 2011, 17, 366–371. [Google Scholar] [CrossRef]
- Edlefsen, P.T.; Rolland, M.; Hertz, T.; Tovanabutra, S.; Gartland, A.J.; deCamp, A.C.; Magaret, C.A.; Ahmed, H.; Gottardo, R.; Juraska, M.; et al. Comprehensive sieve analysis of breakthrough HIV-1 sequences in the RV144 vaccine efficacy trial. PLoS Comput. Biol. 2015, 11, e1003973. [Google Scholar] [CrossRef]
- Hertz, T.; Logan, M.G.; Rolland, M.; Magaret, C.A.; Rademeyer, C.; Fiore-Gartland, A.; Edlefsen, P.T.; DeCamp, A.; Ahmed, H.; Ngandu, N.; et al. A study of vaccine-induced immune pressure on breakthrough infections in the Phambili phase 2b HIV-1 vaccine efficacy trial. Vaccine 2016, 34, 5792–5801. [Google Scholar] [CrossRef]
- deCamp, A.C.; Rolland, M.; Edlefsen, P.T.; Sanders-Buell, E.; Hall, B.; Magaret, C.A.; Fiore-Gartland, A.J.; Juraska, M.; Carpp, L.N.; Karuna, S.T.; et al. Sieve analysis of breakthrough HIV-1 sequences in HVTN 505 identifies vaccine pressure targeting the CD4 binding site of Env-gp120. PLoS ONE 2017, 12, e0185959. [Google Scholar] [CrossRef]
- Sun, Y.; Gilbert, P.B. Estimation of stratified mark-specific proportional hazards models with missing marks. Scand. Stat. Theory Appl. 2012, 39, 34–52. [Google Scholar] [CrossRef]
- Juraska, M.; Gilbert, P.B. Mark-specific hazard ratio model with missing multivariate marks. Lifetime Data Anal. 2016, 22, 606–625. [Google Scholar] [CrossRef]
- Gilbert, P.B.; Sun, Y. Inferences on relative failure rates in stratified mark-specific proportional hazards models with missing marks, with application to HIV vaccine efficacy trials. J. R Stat. Soc. Ser. C Appl. Stat. 2015, 64, 49–73. [Google Scholar] [CrossRef]
- Robb, M.L.; Eller, L.A.; Kibuuka, H.; Rono, K.; Maganga, L.; Nitayaphan, S.; Kroon, E.; Sawe, F.K.; Sinei, S.; Sriplienchan, S.; et al. Prospective study of acute HIV-1 infection in adults in east Africa and Thailand. N Engl. J. Med. 2016, 374, 2120–2130. [Google Scholar] [CrossRef]
- Salazar-Gonzalez, J.F.; Bailes, E.; Pham, K.T.; Salazar, M.G.; Guffey, M.B.; Keele, B.F.; Derdeyn, C.A.; Farmer, P.; Hunter, E.; Allen, S.; et al. Deciphering human immunodeficiency virus type 1 transmission and early envelope diversification by single-genome amplification and sequencing. J. Virol. 2008, 82, 3952–3970. [Google Scholar] [CrossRef]
- Van Loggerenberg, F.; Mlisana, K.; Williamson, C.; Auld, S.C.; Morris, L.; Gray, C.M.; Abdool Karim, Q.; Grobler, A.; Barnabas, N.; Iriogbe, I. , et al. Establishing a cohort at high risk of HIV infection in South Africa: Challenges and experiences of the CAPRISA 002 acute infection study. PLoS ONE 2008, 3, e1954. [Google Scholar] [CrossRef]
- Rose, P.P.; Korber, B.T. Detecting hypermutations in viral sequences with an emphasis on g --> a hypermutation. Bioinformatics 2000, 16, 400–401. [Google Scholar] [CrossRef]
- Los Alamos National Security, L. Hypermut: Analysis & detection of apobec-induced hypermutation. Available online: http://www.hiv.lanl.gov/content/sequence/HYPERMUT/hypermut.html (accessed on 28 February 2019).
- Abrahams, M.R.; Anderson, J.A.; Giorgi, E.E.; Seoighe, C.; Mlisana, K.; Ping, L.H.; Athreya, G.S.; Treurnicht, F.K.; Keele, B.F.; Wood, N.; et al. Quantitating the multiplicity of infection with human immunodeficiency virus type 1 subtype C reveals a non-poisson distribution of transmitted variants. J. Virol. 2009, 83, 3556–3567. [Google Scholar] [CrossRef]
- Song, H.; Giorgi, E.E.; Ganusov, V.V.; Cai, F.; Athreya, G.; Yoon, H.; Carja, O.; Hora, B.; Hraber, P.; Romero-Severson, E.; et al. Tracking HIV-1 recombination to resolve its contribution to HIV-1 evolution in natural infection. Nat. Commun. 2018, 15, 1928. [Google Scholar] [CrossRef]
- Konrad, B.P.; Taylor, D.; Conway, J.M.; Ogilvie, G.S.; Coombs, D. On the duration of the period between exposure to HIV and detectable infection. Epidemics 2017, 20, 73–83. [Google Scholar] [CrossRef]
- Busch, M.P.; Satten, G.A. Time course of viremia and antibody seroconversion following human immunodeficiency virus exposure. Am. J. Med. 1997, 102, 117–124; discussion 125–116. [Google Scholar] [CrossRef]
- Masciotra, S.; McDougal, J.S.; Feldman, J.; Sprinkle, P.; Wesolowski, L.; Owen, S.M. Evaluation of an alternative HIV diagnostic algorithm using specimens from seroconversion panels and persons with established HIV infections. J. Clin. Virol. 2011, 52 Suppl. 1, S17–S22. [Google Scholar] [CrossRef]
- Owen, S.M.; Yang, C.; Spira, T.; Ou, C.Y.; Pau, C.P.; Parekh, B.S.; Candal, D.; Kuehl, D.; Kennedy, M.S.; Rudolph, D.; et al. Alternative algorithms for human immunodeficiency virus infection diagnosis using tests that are licensed in the United States. J. Clin. Microbiol. 2008, 46, 1588–1595. [Google Scholar] [CrossRef]
- Giorgi, E.E.; Funkhouser, B.; Athreya, G.; Perelson, A.S.; Korber, B.T.; Bhattacharya, T. Estimating time since infection in early homogeneous HIV-1 samples using a poisson model. BMC Bioinformatics 2010, 11, 532. [Google Scholar] [CrossRef]
- Mansky, L.M.; Temin, H.M. Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J. Virol. 1995, 69, 5087–5094. [Google Scholar]
- Stafford, M.A.; Corey, L.; Cao, Y.Z.; Daar, E.S.; Ho, D.D.; Perelson, A.S. Modeling plasma virus concentration during primary hiv infection. J. Theoret. Biol. 2000, 203, 285–301. [Google Scholar] [CrossRef]
- Markowitz, M.; Louie, M.; Hurley, A.; Sun, E.; Di Mascio, M.; Perelson, A.S.; Ho, D.D. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J. Virol. 2003, 77, 5037–5038. [Google Scholar] [CrossRef]
- Lee, H.Y.; Giorgi, E.E.; Keele, B.F.; Gaschen, B.; Athreya, G.S.; Salazar-Gonzalez, J.F.; Pham, K.T.; Goepfert, P.A.; Kilby, J.M.; Saag, M.S.; et al. Modeling sequence evolution in acute HIV-1 infection. J. Theoret. Biol. 2009, 261, 341–360. [Google Scholar] [CrossRef]
- Sokal, R.R. A statistical method for evaluating systematic relationships. Uni. Kansas Scient. Bulletin 1958, 38, 1409–1438. [Google Scholar]
- Langfelder, P.; Zhang, B.; Horvath, S. Dynamictreecut: Methods for Detection of Clusters in Hierarchical Clustering Dendrograms. R Package Version 1.63–1. Available online: https://CRAN.R-project.org/package=dynamicTreeCut 2016 (accessed on 28 February 2019).
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. Rocr: Visualizing classifier performance in R. Bioinformatics 2005, 21, 3940–3941. [Google Scholar] [CrossRef]
- Mullins Lab. Divein. Available online: https://indra.mullins.microbiol.washington.edu/DIVEIN/insites.html (accessed on 28 February 2019).
- Deng, W.; Maust, B.S.; Nickle, D.C.; Learn, G.H.; Liu, Y.; Heath, L.; Kosakovsky Pond, S.L.; Mullins, J.I. Divein: A web server to analyze phylogenies, sequence divergence, diversity, and informative sites. Biotechniques 2010, 48, 405–408. [Google Scholar] [CrossRef]
- Dempster, A.P. The Dempster–Shafer calculus for statisticians. Int. J. Approx. Reason. 2008, 48, 365–377. [Google Scholar] [CrossRef]
- Geisser, S. Predictive inference; Chapman and Hall: New York, NY, USA, 1993. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction (Second Edition); Springer Series in Statistics; Springer Science+Business Media, LLC: New York, NY, USA, 2009. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. Royal Statist. Society Series B-Methodolog. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Gottlieb, G.S.; Heath, L.; Nickle, D.C.; Wong, K.G.; Leach, S.E.; Jacobs, B.; Gezahegne, S.; van’t Wout, A.B.; Jacobson, L.P.; Margolick, J.B.; et al. HIV-1 variation before seroconversion in men who have sex with men: Analysis of acute/early HIV infection in the Multicenter AIDS Cohort study. J. Infect. Dis 2008, 197, 1011–1015. [Google Scholar] [CrossRef]
- Haaland, R.E.; Hawkins, P.A.; Salazar-Gonzalez, J.; Johnson, A.; Tichacek, A.; Karita, E.; Manigart, O.; Mulenga, J.; Keele, B.F.; Shaw, G.M.; et al. Inflammatory genital infections mitigate a severe genetic bottleneck in heterosexual transmission of subtype A and C HIV-1. PLoS Pathog. 2009, 5, e1000274. [Google Scholar] [CrossRef]
- Keele, B.F.; Giorgi, E.E.; Salazar-Gonzalez, J.F.; Decker, J.M.; Pham, K.T.; Salazar, M.G.; Sun, C.; Grayson, T.; Wang, S.; Li, H.; et al. Identification and characterization of transmitted and early founder virus envelopes in primary HIV-1 infection. Proc. Natl. Acad. Sci. USA 2008, 105, 7552–7557. [Google Scholar] [CrossRef]
- LeDell, E.; Petersen, M.L.; van der Laan, M.J. Computationally efficient confidence intervals for cross-validated area under the roc curve estimates (in review). Available online: https://biostats.bepress.com/ucbbiostat/paper304 (accessed on 28 February 2019).
- Los Alamos National Laboratory. Available online: http://www.hiv.lanl.gov/. (accessed on 28 February 2019).
- Matsen Group at Fred Hutchinson Cancer Research Center. Available online: https://matsen.fhcrc.org/research.html. (accessed on 28 February 2019).
- Donnell, D.; Ramos, E.; Celum, C.; Baeten, J.; Dragavon, J.; Tappero, J.; Lingappa, J.R.; Ronald, A.; Fife, K.; Coombs, R.W.; et al. The effect of oral preexposure prophylaxis on the progression of HIV-1 seroconversion. AIDS 2017, 31, 2007–2016. [Google Scholar] [CrossRef]
- Sivay, M.V.; Li, M.; Piwowar-Manning, E.; Zhang, Y.; Hudelson, S.E.; Marzinke, M.A.; Amico, R.K.; Redd, A.; Hendrix, C.W.; Anderson, P.L.; et al. Characterization of HIV seroconverters in a TDF/FTC prep study: HPTN 067/adapt. J. Acquir. Immune Defic. Syndr. 2017, 75, 271–279. [Google Scholar] [CrossRef]
- Chaillon, A.; Samleerat, T.; Zoveda, F.; Ballesteros, S.; Moreau, A.; Ngo-Giang-Huong, N.; Jourdain, G.; Gianella, S.; Lallemant, M.; Depaulis, F.; et al. Estimating the timing of mother-to-child transmission of the human immunodeficiency virus type 1 using a viral molecular evolution model. PLoS ONE 2014, 9, e90421. [Google Scholar] [CrossRef]
- Giorgi, E.E.; Li, H. Estimating the timing of early SHIV infections: A comparison between Poisson Fitter and Beast. Bioinformatics 2019. manuscript in preparation. [Google Scholar]
- Gottlieb, G.S.; Nickle, D.C.; Jensen, M.A.; Wong, K.G.; Grobler, J.; Li, F.; Liu, S.L.; Rademeyer, C.; Learn, G.H.; Karim, S.S.; et al. Dual HIV-1 infection associated with rapid disease progression. Lancet 2004, 363, 619–622. [Google Scholar] [CrossRef]
- Herbeck, J.T.; Rolland, M.; Liu, Y.; McLaughlin, S.; McNevin, J.; Zhao, H.; Wong, K.; Stoddard, J.N.; Raugi, D.; Sorensen, S.; et al. Demographic processes affect HIV-1 evolution in primary infection before the onset of selective processes. J. Virol. 2011, 85, 7523–7534. [Google Scholar] [CrossRef]
- Janes, H.; Herbeck, J.T.; Tovanabutra, S.; Thomas, R.; Frahm, N.; Duerr, A.; Hural, J.; Corey, L.; Self, S.G.; Buchbinder, S.P.; et al. HIV-1 infections with multiple founders are associated with higher viral loads than infections with single founders. Nat. Med. 2015, 21, 1139–1141. [Google Scholar] [CrossRef]
- Rossenkhan, R.; Novitsky, V.; Sebunya, T.K.; Musonda, R.; Gashe, B.A.; Essex, M. Viral diversity and diversification of major non-structural genes vif, vpr, vpu, tat exon 1 and rev exon 1 during primary HIV-1 subtype C infection. PLoS ONE 2012, 7, e35491. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Li, H.; Bar, K.J.; Wang, S.; Decker, J.M.; Chen, Y.; Sun, C.; Salazar-Gonzalez, J.F.; Salazar, M.G.; Learn, G.H.; Morgan, C.J. High multiplicity infection by HIV-1 in men who have sex with men. PLoS Pathog. 2010, 6, e1000890. [Google Scholar] [CrossRef] [PubMed]
- Bar, K.J.; Li, H.; Chamberland, A.; Tremblay, C.; Routy, J.P.; Grayson, T.; Sun, C.; Wang, S.; Learn, G.H.; Morgan, C.J. Wide variation in the multiplicity of HIV-1 infection among injection drug users. J. Virol. 2010, 84, 6241–6247. [Google Scholar] [CrossRef] [PubMed]
- Novitsky, V.; Wang, R.; Margolin, L.; Baca, J.; Rossenkhan, R.; Moyo, S.; van Widenfelt, E.; Essex, M. Transmission of single and multiple viral variants in primary HIV-1 subtype C infection. PLoS ONE 2011, 6, e16714. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chaillon, A.; Gianella, S.; Little, S.J.; Caballero, G.; Barin, F.; Kosakovsky Pond, S.; Richman, D.D.; Smith, D.M.; Mehta, S.R. Characterizing the multiplicity of HIV founder variants during sexual transmission among MSM. Virus Evol. 2016, 2, vew012. [Google Scholar] [CrossRef][Green Version]
- Zanini, F.; Brodin, J.; Thebo, L.; Lanz, C.; Bratt, G.; Albert, J.; Neher, R.A. Population genomics of intrapatient HIV-1 evolution. Elife. 2015, 4, e11282. [Google Scholar] [CrossRef]
- Grebe, E.; Facente, S.N.; Bingham, J.; Pilcher, C.D.; Powrie, A.; Gerber, J.; Priede, G.; Chibawara, T.; Busch, M.P.; Murphy, G.; et al. Interpreting HIV diagnostic histories into infection time estimates: Analytical framework and online tool. bioRxiv 2018. [Google Scholar] [CrossRef]
| Study Feature | RV 217 (ECHO) | CAPRISA 002 |
|---|---|---|
| HIV-1 subtype(s) | CRF01_AE (MSM); A1/D/C and Recombinants (WSM) | C (WSM) |
| Sequencing strategy | Single genome amplification and sequencing | Next generation sequencing (Illumina w/PrimerID) |
| HIV-1 genomic region | Near full length genome (NFLG) | V3 variable loop of the gp120 envelope protein |
| Median bases per HIV-1 sequence (min, IQR, max) | NFLG: 8813 (8624, 8753-8841, 8891); LH:5057 (5027, 5051-5063, 5209); RH:5061 (4898, 5040-5092, 5141) | 498 (495, 498-498, 501) |
| Median HIV-1 sequences per participant after removing recombination and hypermutation (min, IQR, max) | 9.5 (2.6, 8.4-10, 11) NFLG: 10 (2, 8-10, 11) LH: 10 (2, 8-10,10) RH: 10 (3, 8-10, 11) | 352 (26, 142.3-640, 2764) |
| Median HIV-1 sequences removed per participant (min, IQR, max) | 0 (0, 0-1, 8) NFLG: 0 (0, 0-1.3, 8) LH: 0 (0, 0-0, 4) RH: 0 (0, 0-1, 4) | 0 (0, 0-1, 356) |
| Total number of participants | 36 | 21 |
| Number of MSM | 17 | 0 |
| Number of WSM | 19 | 21 |
| N participants with 1-2M sample | 36 | 20 |
| N participants with ~6M sample | 34 | 18 |
| Mean Gold days 1-2M (SD) | 47 (4.3) | 62 (4.9) |
| Mean Gold days ~6M (SD) | 184 (11.3) | 180 (12.1) |
| N Gold isMultiple 1-2M (%) | 10 (28%) | 5 (25%) |
| N Gold isMultiple ~6M (%) | 10 (29%) | 6 (33%) |
| Median bounds width in days 1-2M (min, IQR, max) | 48 (20, 34-76, 308) | 54 (27, 41-70, 108) |
| Median bounds width in days ~6M (min, IQR, max) | 146 (18, 91-195, 369) | 120 (30, 86-170, 183) |
| Mean lPVL 1-2M (SD) | 4.5 (0.8) | 4.9 (0.7) |
| Mean lPVL ~6M (SD) | 4.1 (1.0) | 4.5 (0.8) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rossenkhan, R.; Rolland, M.; Labuschagne, J.P.L.; Ferreira, R.-C.; Magaret, C.A.; Carpp, L.N.; Matsen IV, F.A.; Huang, Y.; Rudnicki, E.E.; Zhang, Y.; et al. Combining Viral Genetics and Statistical Modeling to Improve HIV-1 Time-of-Infection Estimation towards Enhanced Vaccine Efficacy Assessment. Viruses 2019, 11, 607. https://doi.org/10.3390/v11070607
Rossenkhan R, Rolland M, Labuschagne JPL, Ferreira R-C, Magaret CA, Carpp LN, Matsen IV FA, Huang Y, Rudnicki EE, Zhang Y, et al. Combining Viral Genetics and Statistical Modeling to Improve HIV-1 Time-of-Infection Estimation towards Enhanced Vaccine Efficacy Assessment. Viruses. 2019; 11(7):607. https://doi.org/10.3390/v11070607
Chicago/Turabian StyleRossenkhan, Raabya, Morgane Rolland, Jan P.L. Labuschagne, Roux-Cil Ferreira, Craig A. Magaret, Lindsay N. Carpp, Frederick A. Matsen IV, Yunda Huang, Erika E. Rudnicki, Yuanyuan Zhang, and et al. 2019. "Combining Viral Genetics and Statistical Modeling to Improve HIV-1 Time-of-Infection Estimation towards Enhanced Vaccine Efficacy Assessment" Viruses 11, no. 7: 607. https://doi.org/10.3390/v11070607
APA StyleRossenkhan, R., Rolland, M., Labuschagne, J. P. L., Ferreira, R.-C., Magaret, C. A., Carpp, L. N., Matsen IV, F. A., Huang, Y., Rudnicki, E. E., Zhang, Y., Ndabambi, N., Logan, M., Holzman, T., Abrahams, M.-R., Anthony, C., Tovanabutra, S., Warth, C., Botha, G., Matten, D., ... Edlefsen, P. T. (2019). Combining Viral Genetics and Statistical Modeling to Improve HIV-1 Time-of-Infection Estimation towards Enhanced Vaccine Efficacy Assessment. Viruses, 11(7), 607. https://doi.org/10.3390/v11070607





