Host Resistance, Genomics and Population Dynamics in a Salmonella Enteritidis and Phage System
Abstract
:1. Introduction
2. Materials and Methods
2.1. Microorganisms
2.2. Phages
2.3. Media
2.4. Lysate Preparation
2.5. S. Enteritidis and Phage φSan23 Evolutionary Dynamics
2.6. Genomic Analyses
2.7. DNA Extraction
2.8. BtuB, Colicin, Fhu Receptor Knockout
2.9. Bacterial Growth at Sublethal Chloramphenicol Concentration
2.10. Evolutionary Dynamics of S. Enteritidis with Phages and Antibiotic
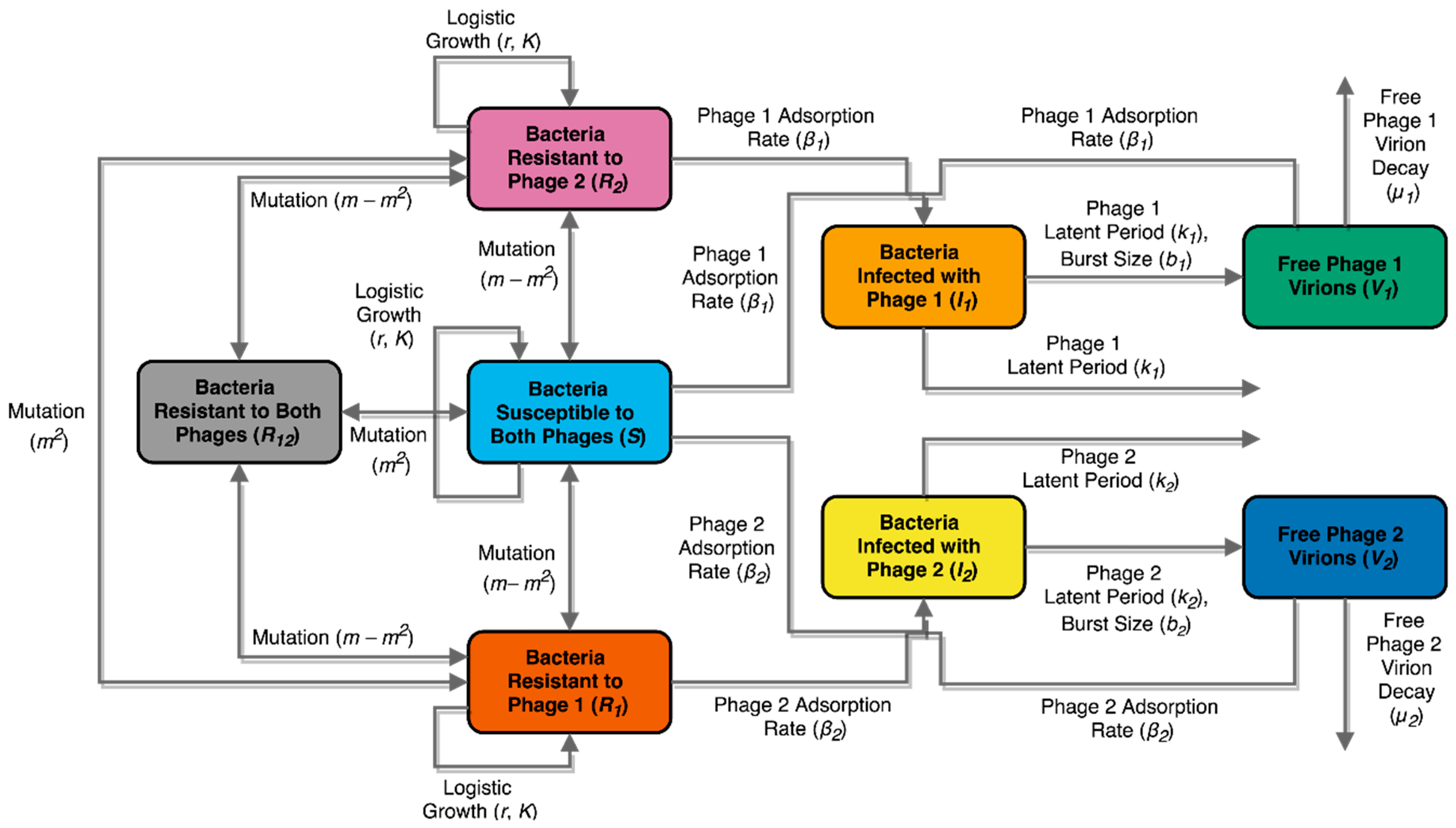
2.11. Mathematical Model: Compartment Model Design
3. Results
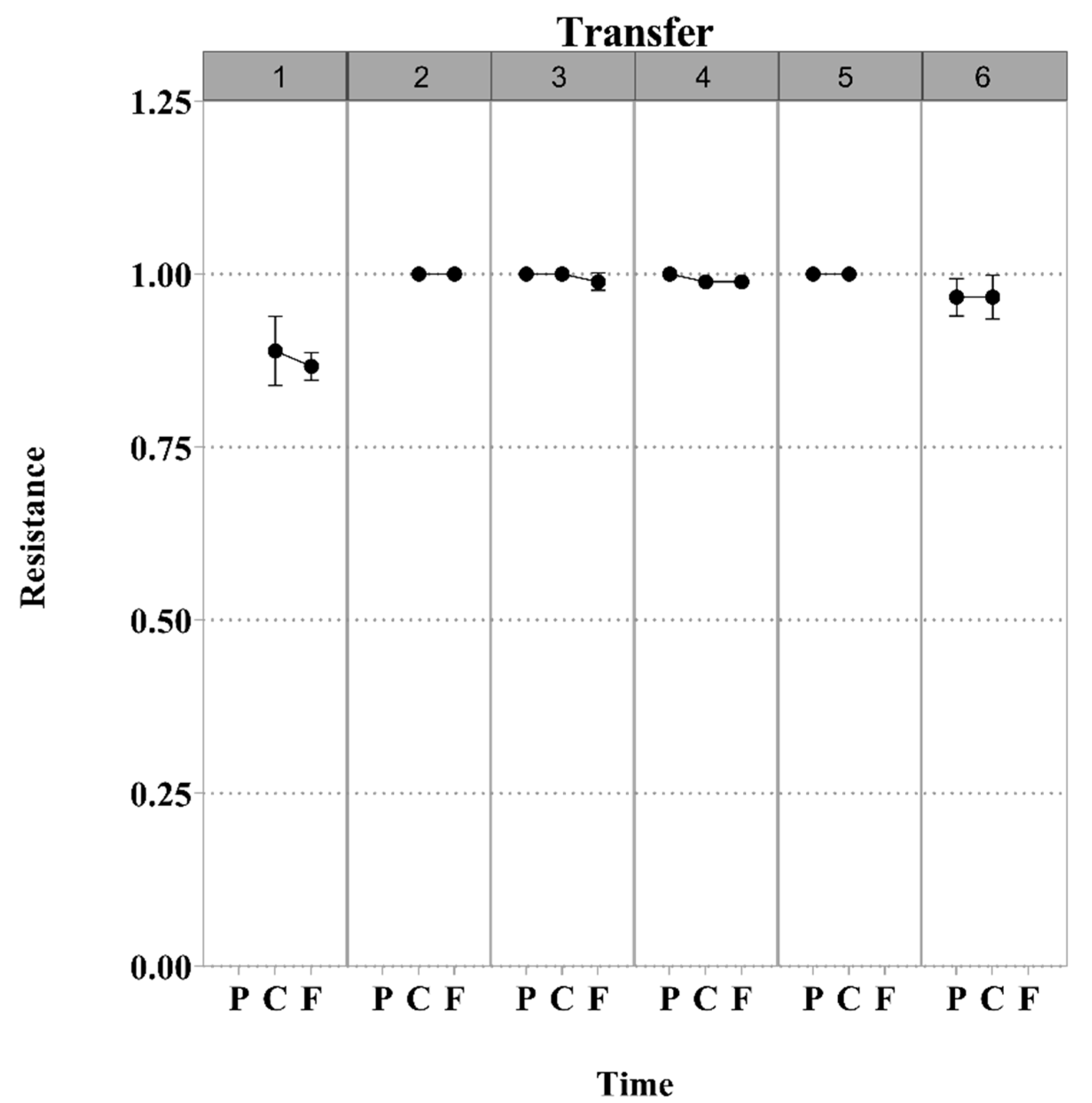
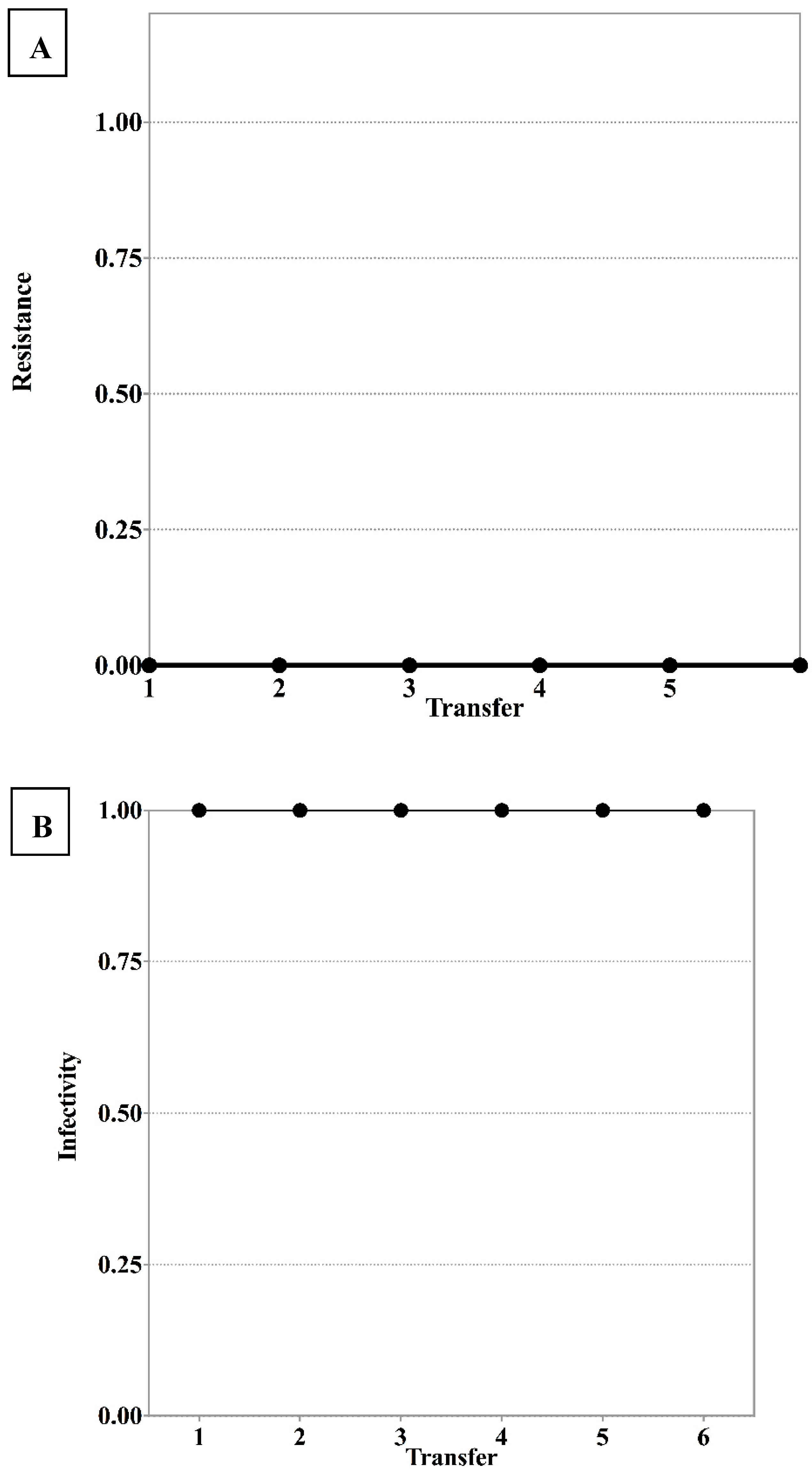
3.1. S. Enteritidis and Phage φSan23 Evolutionary Dynamics
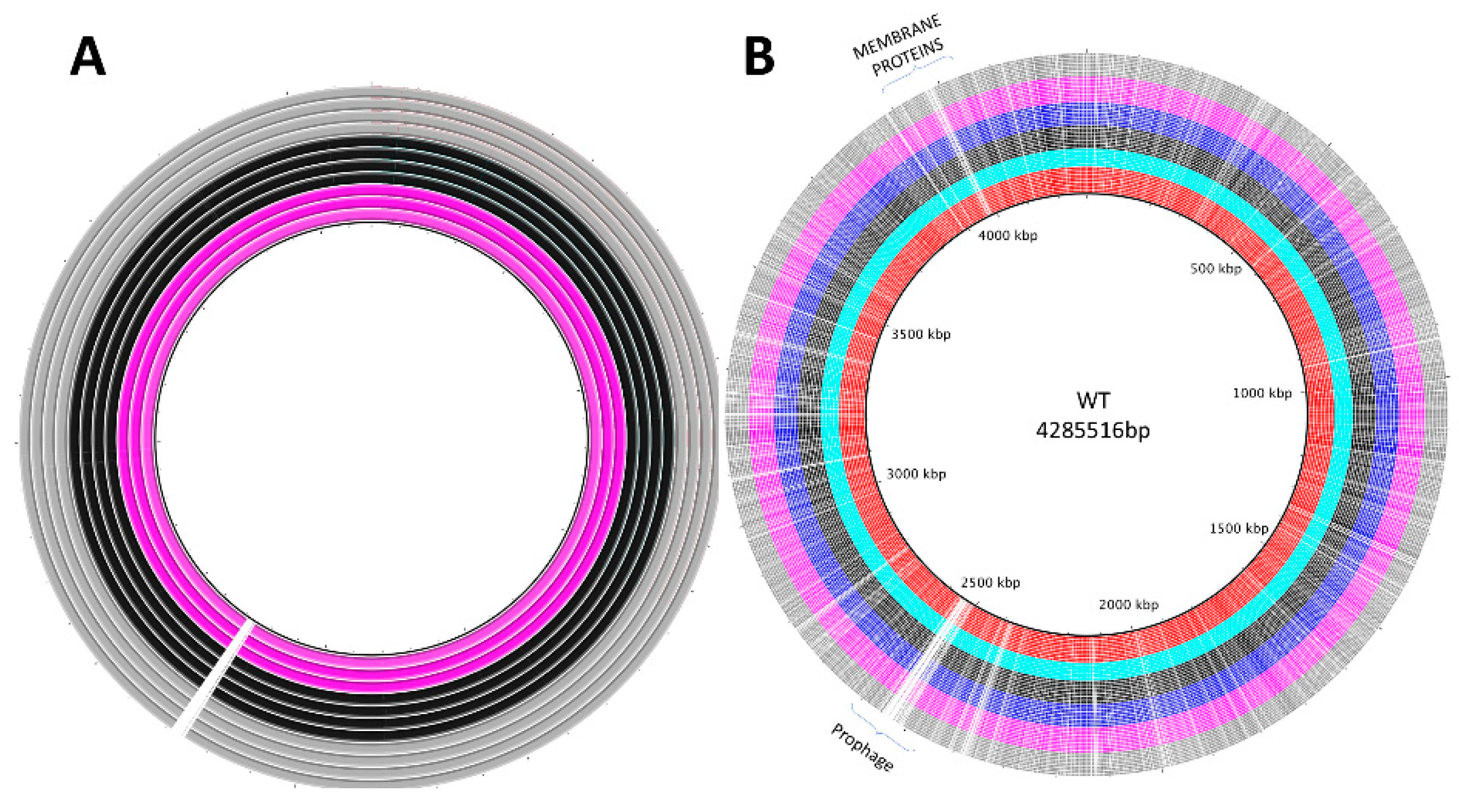
3.2. Genomic Analyses
3.3. BtuB, Colicin, Fhu Receptor knockout
3.4. Assessing Bacterial Growth at Sub-Lethal Chloramphenicol Concentration
3.5. Evolutionary Dynamics of S. Enteritidis with Phages and Antibiotic
4. Discussion
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Donado-Godoy, P.; Byrne, B.A.; Hume, M.; Leon, M.; Pérez-Gutiérrez, E.; Vives Flores, M.J.; Clavijo, V.; Holguin, A.; Romero-Zuñiga, J.J.; Castellanos, R.; et al. Molecular characterization of Salmonella Paratyphi B dT+ and Salmonella Heidelberg from poultry and retail chicken meat in Colombia by pulsed-field gel electrophoresis. J. Food Prot. 2015, 78, 802–807. [Google Scholar] [CrossRef] [PubMed]
- Crim, S.M.; Iwamoto, M.; Huang, J.Y.; Griffin, P.M.; Gilliss, D.; Cronquist, A.B.; Cartter, M.; Tobin-D’Angelo, M.; Blythe, D.; Smith, K.; et al. Incidence and trends of infection with pathogens transmitted commonly through food—Foodborne Diseases Active Surveillance Network, 10 US sites, 2006--2013. MMWR Morb. Mortal. Wkly. Rep. 2014, 63, 328–332. [Google Scholar] [PubMed]
- Scallan, E.; Hoekstra, R.M.; Angulo, F.J.; Tauxe, R.V.; Widdowson, M.-A.; Roy, S.L.; Jones, J.L.; Griffin, P.M. Foodborne illness acquired in the United States—Major pathogens. Emerg. Infect. Dis. 2011, 17, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Labrie, S.J.; Samson, J.E.; Moineau, S. Bacteriophage resistance mechanisms. Nat. Rev. Microbiol. 2010, 8, 317–327. [Google Scholar] [CrossRef] [PubMed]
- Milind, M.N.; Santosh, K.D. Lear resistant bacteria: Lead resistance mechanisms, their applications in lead bioremediation and biomonitoring. Ecotox Environ. Saf. 2013, 98, 1–7. [Google Scholar]
- Lambert, P.A. Bacterial resistance to antibiotics: Modified target sites. Adv. Drug Deliv. Rev. 2005, 57, 1471–1485. [Google Scholar] [CrossRef] [PubMed]
- Enright, M.C.; Robinson, D.A.; Randle, G.; Feil, E.J.; Grundmann, H.; Spratt, B.G. The evolutionary history of methicillin-resistant Staphylococcus aureus [MRSA]. Proc. Natl. Acad. Sci. USA 2002, 99, 7687–7692. [Google Scholar] [CrossRef]
- Chen, H.D.; Groisman, E.A. The biology of the PmrA/PmrB two-component system: The major regulator of lipopolysaccharide modifications. Annu. Rev. Microbiol. 2013, 67, 83–112. [Google Scholar] [CrossRef]
- Faridani, O.R.; Nikravesh, A.; Pandey, D.P.; Gerdes, K.; Good, L. Competitive inhibition of natural antisense Sok-RNA interactions activates Hok-mediated cell killing in Escherichia coli. Nucleic Acids Res. 2006, 34, 5915–5922. [Google Scholar] [CrossRef] [Green Version]
- Fineran, P.C.; Blower, T.R.; Foulds, I.J.; Humphreys, D.P.; Lilley, K.S.; Salmond, G.P.C. The phage abortive infection system, ToxIN, functions as a protein--RNA toxin--antitoxin pair. Proc. Natl. Acad. Sci. USA 2009, 106, 894–899. [Google Scholar] [CrossRef]
- Richter, C.; Chang, J.T.; Fineran, P.C. Function and regulation of clustered regularly interspaced short palindromic repeats [CRISPR]/CRISPR associated [Cas] systems. Viruses 2012, 4, 2291–2311. [Google Scholar] [CrossRef] [PubMed]
- Buckling, A.; Rainey, P.B. Antagonistic coevolution between a bacterium and a bacteriophage. Proc. R. Soc. Lond. B Biol. Sci. 2002, 269, 931–936. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barbosa, C.; Venail, P.; Holguin, A.V.; Vives, M.J. Co-evolutionary dynamics of the bacteria Vibrio sp. CV1 and phages V1G, V1P1, and V1P2: Implications for phage-therapy. Microb. Ecol. 2013, 66, 897–905. [Google Scholar] [CrossRef] [PubMed]
- Lenski, R.E.; Levin, B.R. Constraints on the coevolution of bacteria and virulent phage: A model, some experiments, and predictions for natural communities. Am. Nat. 1985, 125, 585–602. [Google Scholar] [CrossRef]
- Bohannan, B.J.M.; Lenski, R.E. Linking genetic change to community evolution: Insights from studies of bacteria and bacteriophage. Ecol. Lett. 2000, 3, 362–377. [Google Scholar] [CrossRef]
- Gómez, P.; Buckling, A. Bacteria-phage antagonistic coevolution in soil. Science 2011, 332, 106–109. [Google Scholar] [CrossRef]
- Koskella, B.; Parr, N. The evolution of bacterial resistance against bacteriophages in the horse chestnut phyllosphere is general across both space and time. Phil. Trans. R. Soc. B 2015, 370, 20140297. [Google Scholar] [CrossRef] [Green Version]
- Scanlan, P.D.; Hall, A.R.; Blackshields, G.; Friman, V.-P.; Davis Jr, M.R.; Goldberg, J.B.; Buckling, A. Coevolution with bacteriophages drives genome-wide host evolution and constrains the acquisition of abiotic-beneficial mutations. Mol. Biol. Evol. 2015, 32, 1425–1435. [Google Scholar] [CrossRef]
- Schwartz, D.A.; Lindell, D. Genetic hurdles limit the arms race between Prochlorococcus and the T7-like podoviruses infecting them. ISME J. 2017, 11, 1836–1851. [Google Scholar] [CrossRef]
- Holguín, A.V.; Universidad de los Andes, Bogotá, Colombia. Complementary experiments performed in the home lab to have a well understanding of the phage-bacteria dynamics. Unpublished work. 2014. [Google Scholar]
- Universidad de los Andes. Composition Comprising Bacteriophages for Reducing, Eliminating and/or Preventing Salmonella Enteritidis, Salmonella Typhimurium and Salmonella Paratyphi B. CO Patent 15281747759, 25 November 2015. [Google Scholar]
- Kropinski, A.M.; Mazzocco, A.; Waddell, T.E.; Lingohr, E.; Johnson, R.P. Enumeration of bacteriophages by double agar overlay plaque assay. Methods Mol. Biol. 2009, 501, 69–76. [Google Scholar] [PubMed]
- Pradel, E.; Pagès, J.-M. The AcrAB-TolC efflux pump contributes to multidrug resistance in the nosocomial pathogen Enterobacter aerogenes. Antimicrob. Agents Chemother. 2002, 46, 2640–2643. [Google Scholar] [CrossRef] [PubMed]
- Baucheron, S.; Tyler, S.; Boyd, D.; Mulvey, M.R.; Chaslus-Dancla, E.; Cloeckaert, A. AcrAB-TolC directs efflux-mediated multidrug resistance in Salmonella enterica serovar Typhimurium DT104. Antimicrob. Agents Chemother. 2004, 48, 3729–3735. [Google Scholar] [CrossRef] [PubMed]
- Du, D.; Zhao Wang, N.R.J.; Voss, J.E.; Klimont, E.; Ohene-Agyei, T.; Venter, H.; Chiu, W.; Luisi, B.F. Structure of the AcrAB-TolC multidrug efflux pump. Nature 2014, 509, 512–515. [Google Scholar] [CrossRef] [PubMed]
- Santos, S.B.; Carvalho, C.M.; Sillankorva, S.; Nicolau, A.; Ferreira, E.C.; Azeredo, J. The use of antibiotics to improve phage detection and enumeration by the double-layer agar technique. BMC Microbiol. 2009, 9, 148. [Google Scholar] [CrossRef] [PubMed]
- Petty, N.K.; Foulds, I.J.; Pradel, E.; Ewbank, J.J.; Salmond, G.P.C. A generalized transducing phage [$φ$IF3] for the genomically sequenced Serratia marcescens strain Db11: A tool for functional genomics of an opportunistic human pathogen. Microbiology 2006, 152, 1701–1708. [Google Scholar] [CrossRef] [PubMed]
- Kaas, R.S.; Leekitcharoenphon, P.; Aarestrup, F.M.; Lund, O. Solving the problem of comparing whole bacterial genomes across different sequencing platforms. PLoS ONE 2014, 9, e104984. [Google Scholar] [CrossRef]
- CSI Phylogeny software. Available online: https://cge.cbs.dtu.dk/services/CSIPhylogeny/ (accessed on 20 May 2015).
- Darling, A.C.E.; Mau, B.; Blattner, F.R.; Perna, N.T. Mauve: Multiple alignment of conserved genomic sequence with rearrangements. Genome Res. 2004, 14, 1394–1403. [Google Scholar] [CrossRef]
- Mauve alignment software. Available online: http://darlinglab.org/mauve/mauve.html (accessed on 3 April 2017).
- Alikhan, N.-F.; Petty, N.K.; Zakour, N.L.; Beatson, S.A. BLAST Ring Image Generator [BRIG]: Simple prokaryote genome comparisons. BMC Genom. 2011, 12, 402. [Google Scholar] [CrossRef]
- BLAST Ring Image Generator. Available online: https://sourceforge.net/projects/brig/ (accessed on 15 October 2016).
- Bikadi, Z.; Hazai, E. Application of the PM6 semi-empirical method to modeling proteins enhances docking accuracy of AutoDock. J. Cheminform. 2009, 1, 15. [Google Scholar] [CrossRef] [Green Version]
- Molecular Docking server. Available online: https://www.dockingserver.com/web (accessed on 20 November 2016).
- Quality assessment FastQC. Available online: https://www.bioinformatics.babraham.ac.uk/projects/download.html (accessed on 28 January 2017).
- Bolger, A.M.; Lohse, M.; Usadel, B. Trimmomatic: A flexible trimmer for Illumina sequence data. Bioinformatics 2014, 30, 2114–2120. [Google Scholar] [CrossRef] [PubMed]
- Trimmomatic. Available online: http://www.usadellab.org/cms/?page=trimmomatic (accessed on 2 February 2017).
- Larsen, M.V.; Cosentino, S.; Rasmussen, S.; Friis, C.; Hasman, H.; Marvig, R.L.; Jelsbak, L.; Pontén, T.S.; Ussery, D.W.; Aarestrup, F.M.; et al. Multilocus sequence typing of total genome sequenced bacteria. J. Clin. Microbiol. JCM 2012, 50, 1355–1361. [Google Scholar] [CrossRef] [PubMed]
- Assembler 1.0. Available online: https://cge.cbs.dtu.dk/services/Assembler/ (accessed on 15 May 2015).
- Bankevich, A.; Nurk, S.; Antipov, D.; Gurevich, A.A.; Dvorkin, M.; Kulikov, A.S.; Lesin, V.M.; Nikolenko, S.I.; Pham, S.; Prjibelski, A.D.; et al. SPAdes: A new genome assembly algorithm and its applications to single-cell sequencing. J. Comput. Biol. 2012, 19, 455–477. [Google Scholar] [CrossRef] [PubMed]
- SPAdes. Available online: http://cab.spbu.ru/software/spades/ (accessed on 15 November 2016).
- Langmead, B.; Salzberg, S.L. Fast gapped-read alignment with Bowtie 2. Nat. Methods 2012, 9, 357–359. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bowtie2. Available online: http://bowtie-bio.sourceforge.net/bowtie2/index.shtml (accessed on 15 January 2016).
- Delcher, A.L.; Bratke, K.A.; Powers, E.C.; Salzberg, S.L. Identifying bacterial genes and endosymbiont DNA with Glimmer. Bioinformatics 2007, 23, 673–679. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glimmer. Available online: https://ccb.jhu.edu/software/glimmer (accessed on 3 October 2016).
- Brettin, T.; Davis, J.J.; Disz, T.; Edwards, R.A.; Gerdes, S.; Olsen, G.J.; Olson, R.; Overbeek, R.; Parrello, B.; Pusch, G.D.; et al. RASTtk: A modular and extensible implementation of the RAST algorithm for building custom annotation pipelines and annotating batches of genomes. Sci. Rep. 2015, 5, 8365. [Google Scholar] [CrossRef]
- Rast. Available online: http://rast.theseed.org/FIG./rast.cgi (accessed on 25 July 2018).
- Götz, S.; Arnold, R.; Sebastián-León, P.; Martín-Rodríguez, S.; Tischler, P.; Jehl, M.-A.; Dopazo, J.; Rattei, T.; Conesa, A. B2G-FAR, a species-centered GO annotation repository. Bioinformatics 2011, 27, 919–924. [Google Scholar] [CrossRef]
- Blast2go. Available online: https://www.blast2go.com (accessed on 15 september 2017).
- Hyatt, D.; Chen, G.-L.; LoCascio, P.F.; Land, M.L.; Larimer, F.W.; Hauser, L.J. Prodigal: Prokaryotic gene recognition and translation initiation site identification. BMC Bioinform. 2010, 11, 119. [Google Scholar] [CrossRef]
- Prodigal. Available online: http://prodigal.ornl.gov (accessed on 28 September 2016).
- McNair, K.; Bailey, B.A.; Edwards, R.A. PHACTS, a computational approach to classifying the lifestyle of phages. Bioinformatics 2012, 28, 614–618. [Google Scholar] [CrossRef] [Green Version]
- PHACTS. Available online: http://www.phantome.org/PHACTS (accessed on 2 December 2015).
- Levin, B.R.; Stewart, F.M.; Chao, L. Resource-limited growth, competition, and predation: A model and experimental studies with bacteria and bacteriophage. Am. Nat. 1977, 111, 3–24. [Google Scholar] [CrossRef]
- Levin, B.R.; Bull, J.J. Phage-therapy revisited: The population biology of a bacterial infection and its treatment with bacteriophage and antibiotics. Am. Nat. 1996, 147, 881–898. [Google Scholar] [CrossRef]
- Sahani, S.K.; Gakkhar, S. A Mathematical Model for Phage-therapy with Impulsive Phage Dose. Differ. Equ. Dyn. Syst. 2016, 1–12. [Google Scholar] [CrossRef]
- Middelboe, M. Bacterial growth rate and marine virus--host dynamics. Microb. Ecol. 2000, 40, 114–124. [Google Scholar] [PubMed]
- Payne, R.J.H.; Jansen, V.A.A. Phage-therapy: The peculiar kinetics of self-replicating pharmaceuticals. Clin. Pharmacol. Ther. 2000, 68, 225–230. [Google Scholar] [CrossRef] [PubMed]
- Payne, R.J.H.; Jansen, V.A.A. Understanding bacteriophage-therapy as a density-dependent kinetic process. J. Theor. Biol. 2001, 208, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Weld, R.J.; Butts, C.; Heinemann, J.A. Models of phage growth and their applicability to phage-therapy. J. Theor. Biol. 2004, 227, 1–11. [Google Scholar] [CrossRef]
- Mudgal, P.; Breidt, F.; Lubkin, S.R.; Sandeep, K.P. Quantifying the significance of phage attack on starter cultures: A mechanistic model for population dynamics of phage and their hosts isolated from fermenting sauerkraut. Appl. Environ. Microbiol. 2006, 72, 3908–3915. [Google Scholar] [CrossRef]
- Cairns, B.J.; Timms, A.R.; Jansen, V.A.A.; Connerton, I.F.; Payne, R.J.H. Quantitative models of in vitro bacteriophage--host dynamics and their application to phage-therapy. PLoS Pathog. 2009, 5, e1000253. [Google Scholar] [CrossRef] [PubMed]
- Santos, S.B.; Carvalho, C.; Azeredo, J.; Ferreira, E.C. Population dynamics of a Salmonella lytic phage and its host: Implications of the host bacterial growth rate in modelling. PLoS ONE 2014, 9, e102507. [Google Scholar] [CrossRef]
- Volkova, V.V.; Lu, Z.; Besser, T.; Gröhn, Y.T. Modeling the infection dynamics of bacteriophages in enteric Escherichia coli: Estimating the contribution of transduction to antimicrobial gene spread. Appl. Environ. Microbiol. 2014, 80, 4350–4362. [Google Scholar] [CrossRef]
- Zwietering, M.H.; Jongenburger, I.; Rombouts, F.M.; Van’t Riet, K. Modeling of the bacterial growth curve. Appl. Environ. Microbiol. 1990, 56, 1875–1881. [Google Scholar] [PubMed]
- Wachenheim, D.E.; Patterson, J.A.; Ladisch, M.R. Analysis of the logistic function model: Derivation and applications specific to batch cultured microorganisms. Bioresour. Technol. 2003, 86, 157–164. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin, Germamy, 2001. [Google Scholar]
- Wiggins, B.A.; Alexander, M. Minimum bacterial density for bacteriophage replication: Implications for significance of bacteriophages in natural ecosystems. Appl. Environ. Microbiol. 1985, 49, 19–23. [Google Scholar] [PubMed]
- Payne, R.J.H.; Jansen, V.A.A. Pharmacokinetic principles of bacteriophage-therapy. Clin. Pharmacokinet. 2003, 42, 315–325. [Google Scholar] [CrossRef] [PubMed]
- Lind, P.A.; Andersson, D.I. Whole-genome mutational biases in bacteria. Proc. Natl. Acad. Sci. USA 2008, 105, 17878–17883. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Paepe, M.; Taddei, F. Viruses’ life history: Towards a mechanistic basis of a trade-off between survival and reproduction among phages. PLoS Biol. 2006, 4, e193. [Google Scholar] [CrossRef]
- Beale, G.H. A method for the measurement of mutation rate from phage sensitivity to phage resistance in Escherichia coli. Microbiology 1948, 2, 131–142. [Google Scholar] [CrossRef]
- Arias-Sánchez, F.I.; Hall, A.R. Effects of antibiotic resistance alleles on bacterial evolutionary responses to viral parasites. Biol. Lett. 2016, 12, 20160064. [Google Scholar] [CrossRef] [Green Version]
- Hughes, D.; Andersson, D.I. Carbon starvation of Salmonella typhimurium does not cause a general increase of mutation rates. J. Bacteriol. 1997, 179, 6688–6691. [Google Scholar] [CrossRef]
- Galhardo, R.S.; Hastings, P.J.; Rosenberg, S.M. Mutation as a stress response and the regulation of evolvability. Crit. Rev. Biochem. Mol. Biol. 2007, 42, 399–435. [Google Scholar] [CrossRef]
- Bjedov, I.; Tenaillon, O.; Gerard, B.; Souza, V.; Denamur, E.; Radman, M.; Taddei, F.; Matic, I. Stress-induced mutagenesis in bacteria. Science 2003, 300, 1404–1409. [Google Scholar] [CrossRef] [PubMed]
- Foster, P.L. Stress-induced mutagenesis in bacteria. Crit. Rev. Biochem. Mol. Biol. 2007, 42, 373–397. [Google Scholar] [CrossRef] [PubMed]
- Thomas, R.; Berdjeb, L.; Sime-Ngando, T.; Jacquet, S. Viral abundance, production, decay rates and life strategies [lysogeny versus lysis] in Lake Bourget [France]. Environ. Microbiol. 2011, 13, 616–630. [Google Scholar] [CrossRef] [PubMed]
- Hyman, P.; Abedon, S.T. Practical methods for determining phage growth parameters. Methods Mol. Biol. 2009, 501, 175–202. [Google Scholar] [PubMed]
- Moldovan, R.; Chapman-McQuiston, E.; Wu, X.L. On kinetics of phage adsorption. Biophys. J. 2007, 93, 303–315. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Wang, N. Bacteriophage adsorption rate and optimal lysis time. Genetics 2008, 180, 471–482. [Google Scholar] [CrossRef] [PubMed]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Springer: Berlin, Germany, 1978; pp. 105–116. [Google Scholar]
- Petzold, L. Automatic selection of methods for solving stiff and nonstiff systems of ordinary differential equations. SIAM J. Sci. Stat. Comput. 1983, 4, 136–148. [Google Scholar] [CrossRef]
- The R Project for Statistical Computing. Available online: https://www.r-project.org/ (accessed on 10 December 2018).
- Github. Available online: https://github.com/pablocarderam/PhageModel (accessed on 14 February 2019).
- Shultis, D.D.; Purdy, M.D.; Banchs, C.N.; Wiener, M.C. Outer membrane active transport: Structure of the BtuB: TonB complex. Science 2006, 312, 1396–1399. [Google Scholar] [CrossRef] [PubMed]
- Killmann, H.; Herrmann, C.; Wolff, H.; Braun, V. Identification of a new site for ferrichrome transport by comparison of the FhuA proteins of Escherichia coli, Salmonella paratyphi B, Salmonella typhimurium, and Pantoea agglomerans. J. Bacteriol. 1998, 180, 3845–3852. [Google Scholar] [PubMed]
- McKay, A.L.; Peters, A.C.; Wimpenny, J.W.T. Determining specific growth rates in different regions of Salmonella typhimurium colonies. Lett. Appl. Microbiol. 1997, 24, 74–76. [Google Scholar] [CrossRef]
- Rakhuba, D.V.; Kolomiets, E.I.; Dey, E.S.; Novik, G.I. Bacteriophage receptors, mechanisms of phage adsorption and penetration into host cell. Pol. J. Microbiol. 2010, 59, 145–155. [Google Scholar] [PubMed]
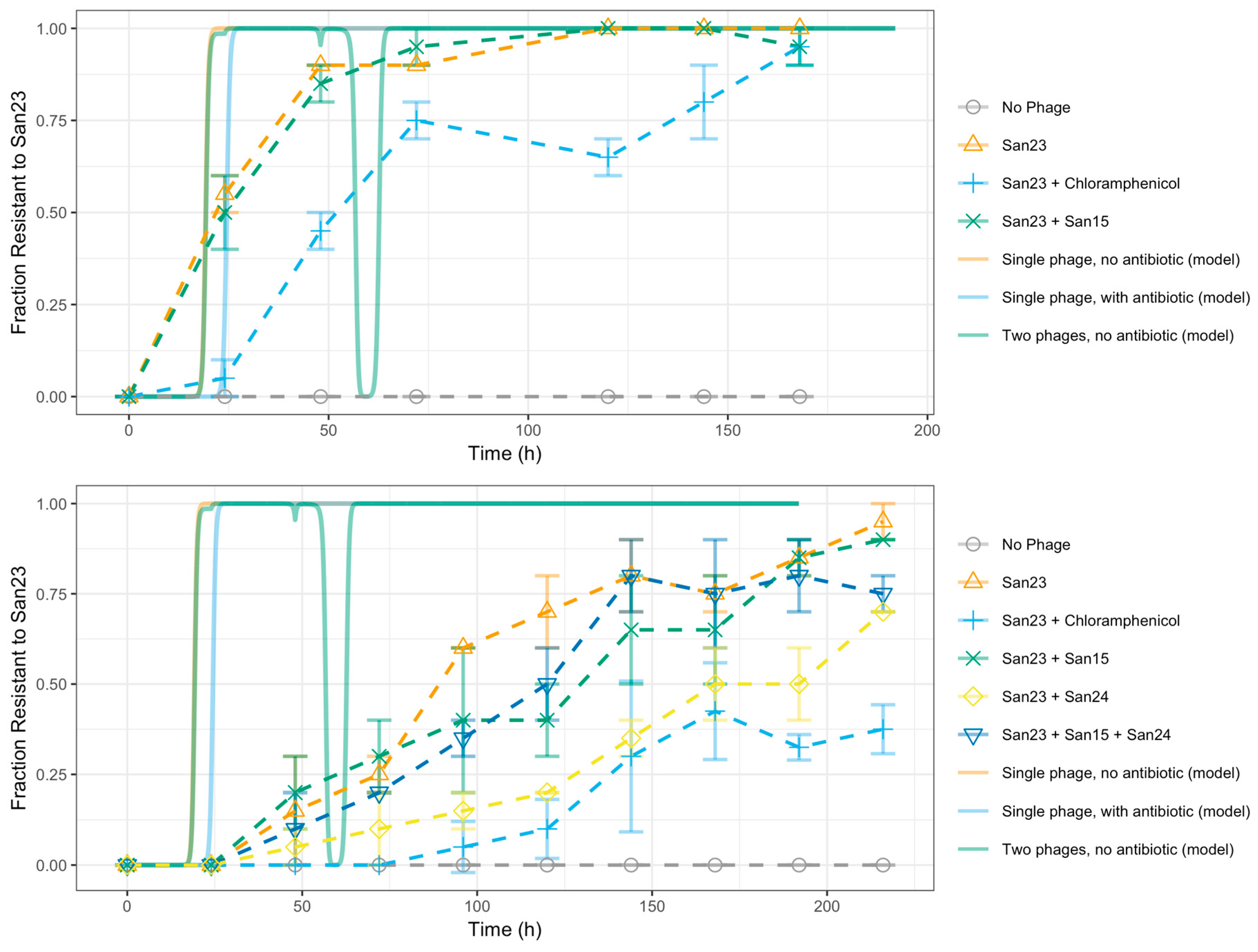
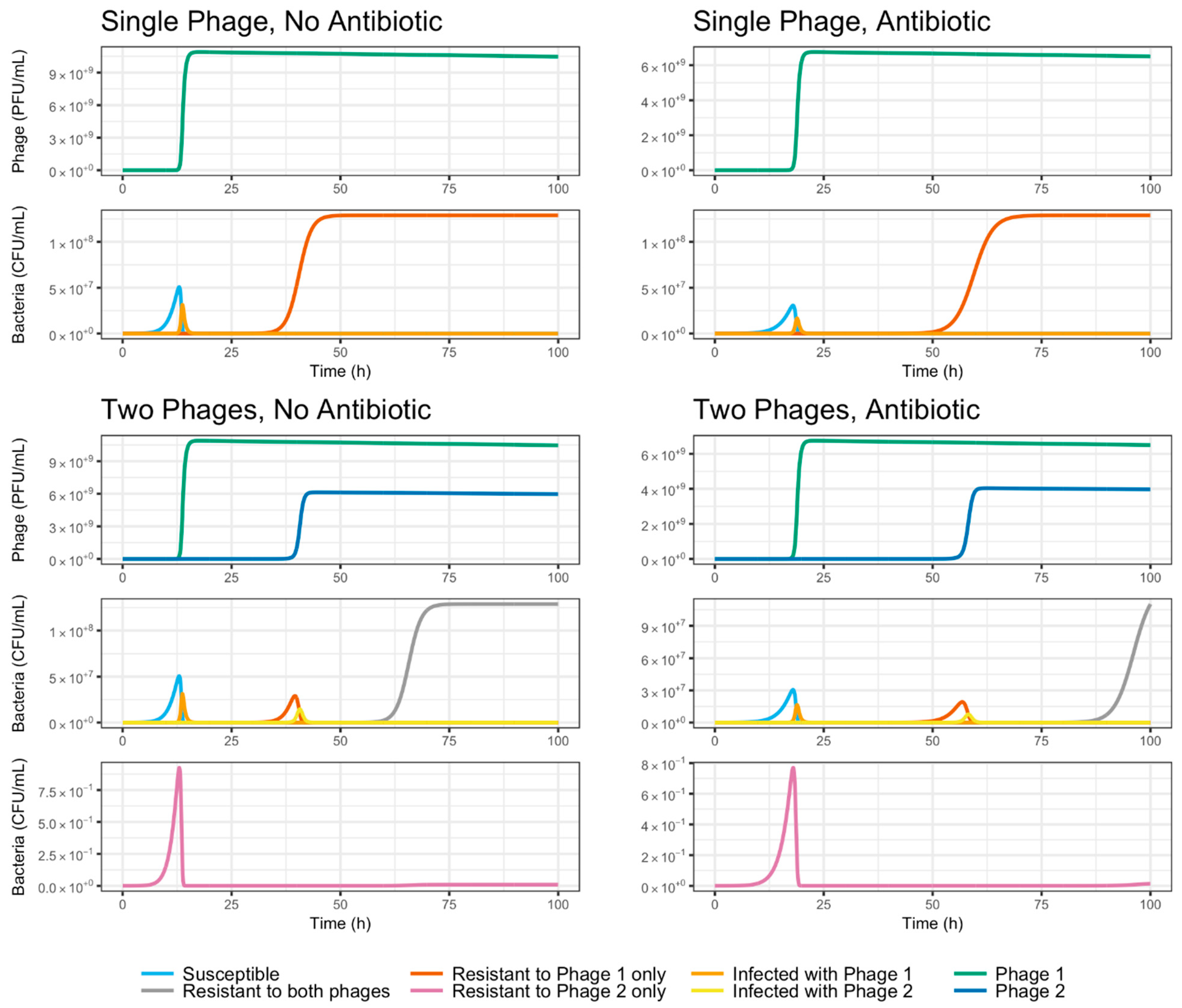
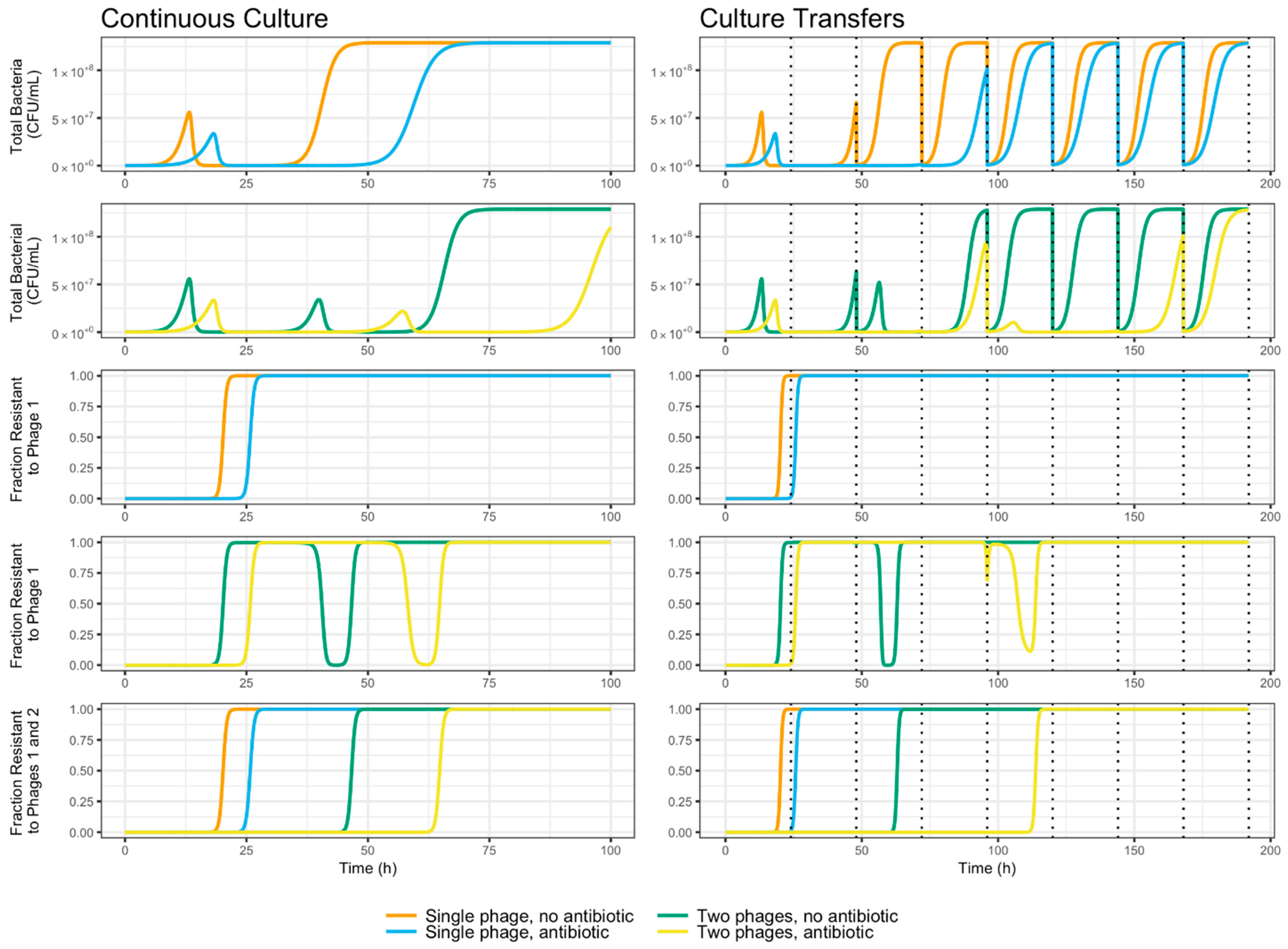
| Constant | Symbol | Value | Units | Reference |
|---|---|---|---|---|
| Intrinsic growth rate of bacteria | r | 0.68885 | h−1 | This study |
| Relative growth rate penalty of bacteria in presence of antibiotic | α | 0.33736 | -- | This study |
| Presence/absence of antibiotic | a | {1,0} | -- | -- |
| Bacterial carrying capacity | k | 1.2888 × 108 | CFU/mL | This study |
| Mutation probability | m | 1.4000 × 10−9 | -- | This study, [71] |
| Adsorption rate for phage 1 | β1 | 1.8000 × 10−9 | mL pfu−1 h−1 | * |
| Adsorption rate for phage 2 | Β2 | 1.0000 × 10−9 | mL pfu−1 h−1 | * |
| Burst size for phage 1 | b1 | 165 | PFU/mL | * |
| Burst size for phage 2 | b2 | 120 | PFU/mL | * |
| Phage 1 virion decay rate | µ1 | 4.7917 × 10−4 | h−1 | [63,64,72] |
| Phage 2 virion decay rate | µ2 | 4.7917 × 10−4 | h−1 | [63,64,72] |
| Phage 1 latent period | λ1 | 0.5 | h | * |
| Phage 2 latent period | Λ2 | 0.5 | h | * |
| Inoculation volume as a fraction of the culture volume | v | 6.000 × 10−3 | -- | -- |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Holguín, A.V.; Cárdenas, P.; Prada-Peñaranda, C.; Rabelo Leite, L.; Buitrago, C.; Clavijo, V.; Oliveira, G.; Leekitcharoenphon, P.; Møller Aarestrup, F.; Vives, M.J. Host Resistance, Genomics and Population Dynamics in a Salmonella Enteritidis and Phage System. Viruses 2019, 11, 188. https://doi.org/10.3390/v11020188
Holguín AV, Cárdenas P, Prada-Peñaranda C, Rabelo Leite L, Buitrago C, Clavijo V, Oliveira G, Leekitcharoenphon P, Møller Aarestrup F, Vives MJ. Host Resistance, Genomics and Population Dynamics in a Salmonella Enteritidis and Phage System. Viruses. 2019; 11(2):188. https://doi.org/10.3390/v11020188
Chicago/Turabian StyleHolguín, Angela Victoria, Pablo Cárdenas, Catalina Prada-Peñaranda, Laura Rabelo Leite, Camila Buitrago, Viviana Clavijo, Guilherme Oliveira, Pimlapas Leekitcharoenphon, Frank Møller Aarestrup, and Martha J. Vives. 2019. "Host Resistance, Genomics and Population Dynamics in a Salmonella Enteritidis and Phage System" Viruses 11, no. 2: 188. https://doi.org/10.3390/v11020188
APA StyleHolguín, A. V., Cárdenas, P., Prada-Peñaranda, C., Rabelo Leite, L., Buitrago, C., Clavijo, V., Oliveira, G., Leekitcharoenphon, P., Møller Aarestrup, F., & Vives, M. J. (2019). Host Resistance, Genomics and Population Dynamics in a Salmonella Enteritidis and Phage System. Viruses, 11(2), 188. https://doi.org/10.3390/v11020188





