Modelling Vector Transmission and Epidemiology of Co-Infecting Plant Viruses
Abstract
1. Introduction
2. Materials and Methods
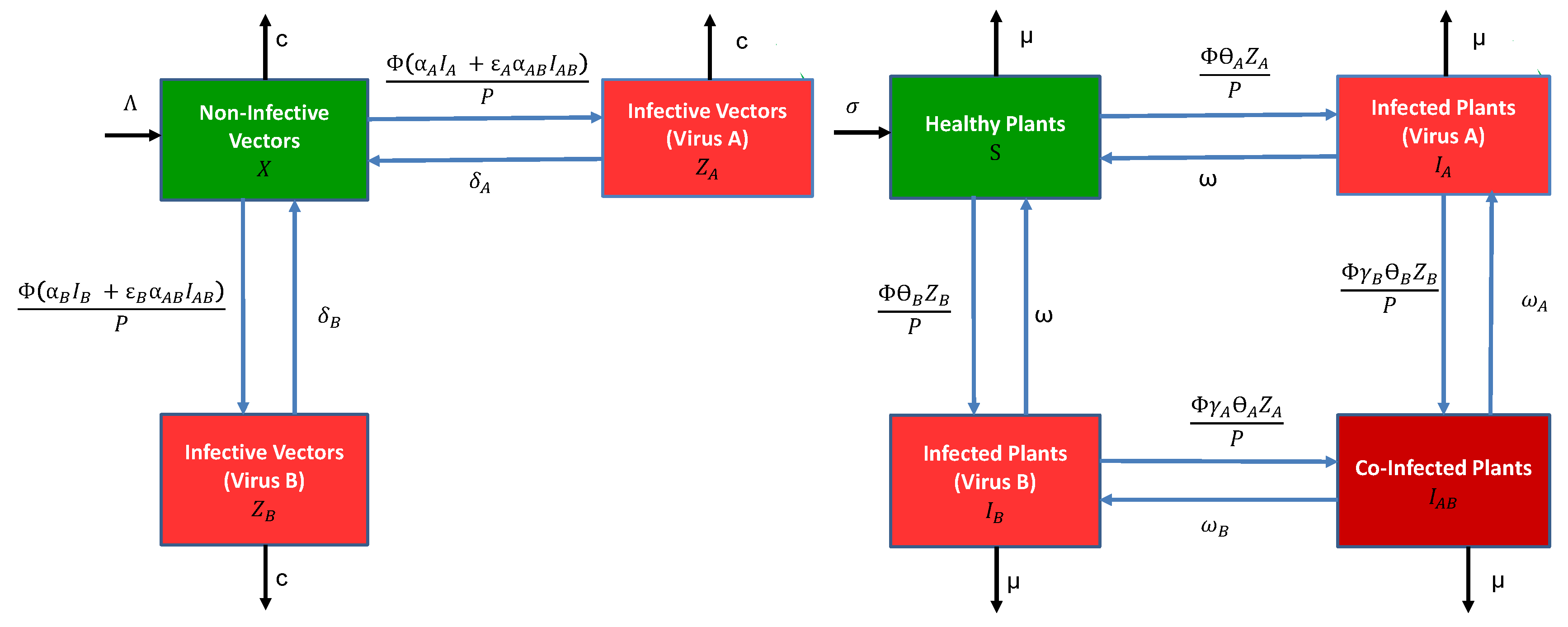
2.1. Modelling
2.2. Invasion Thresholds
2.3. Formal Reduction to a Model That Does Not Track Vectors Explicitly
3. Results
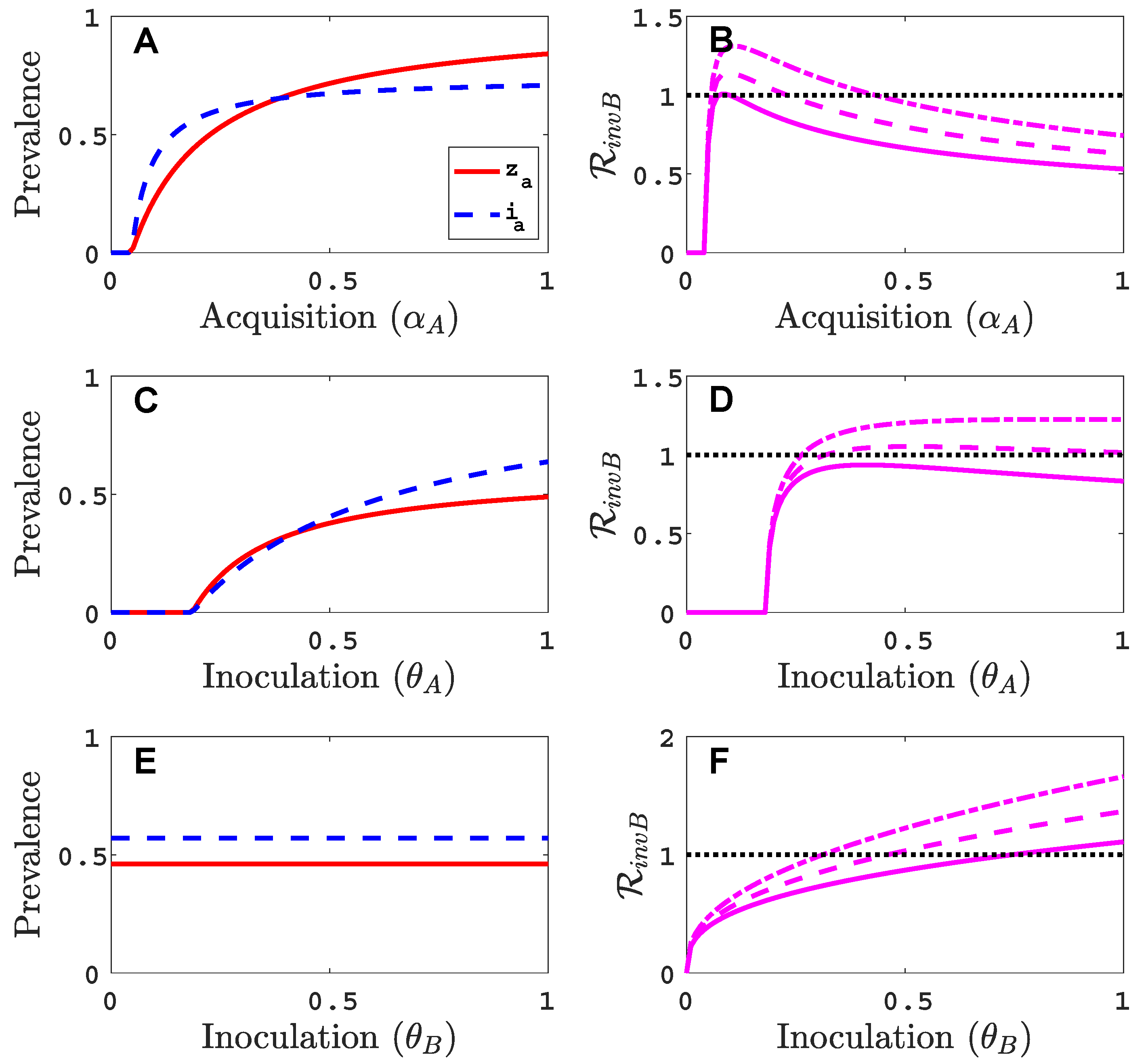
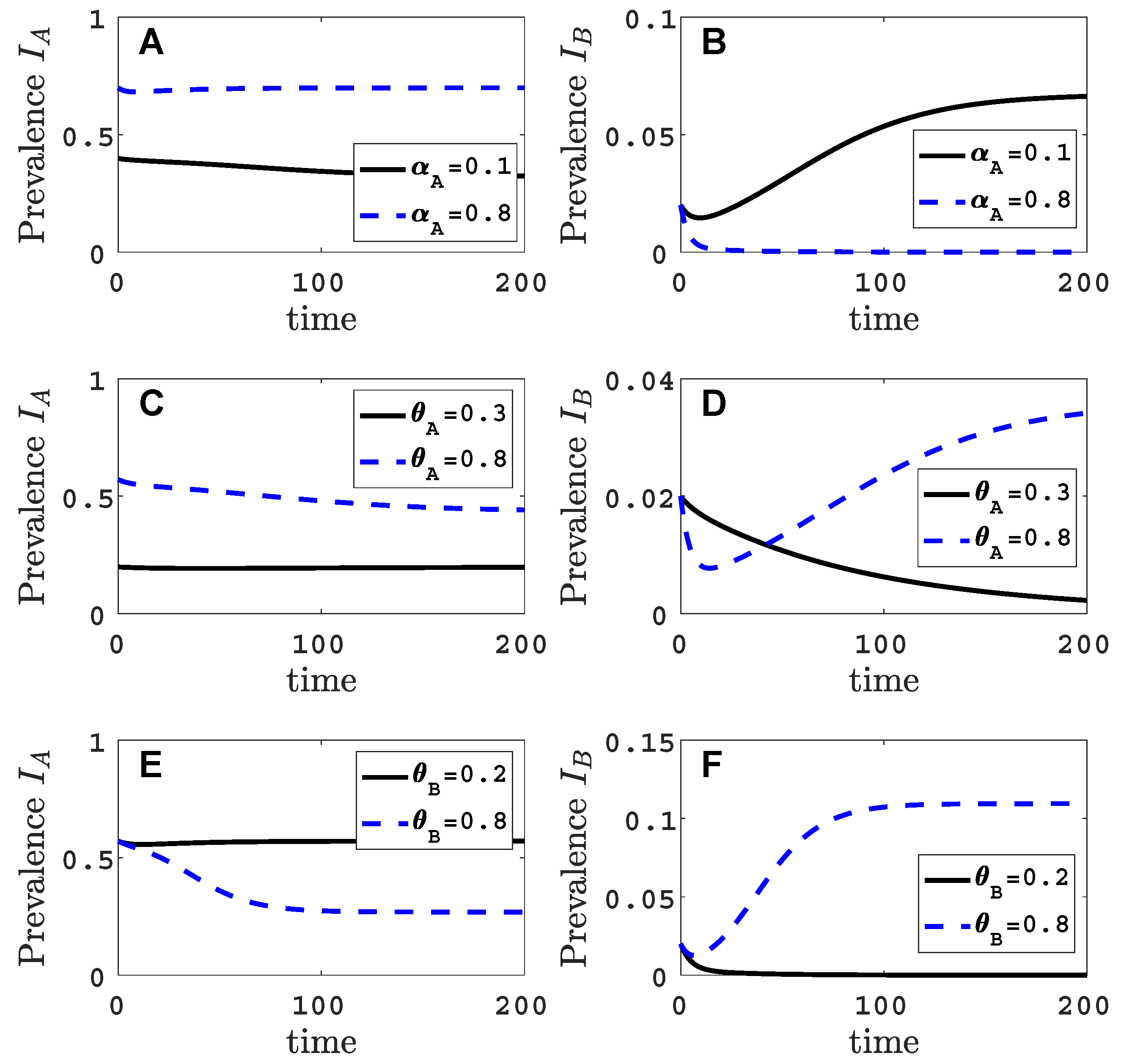
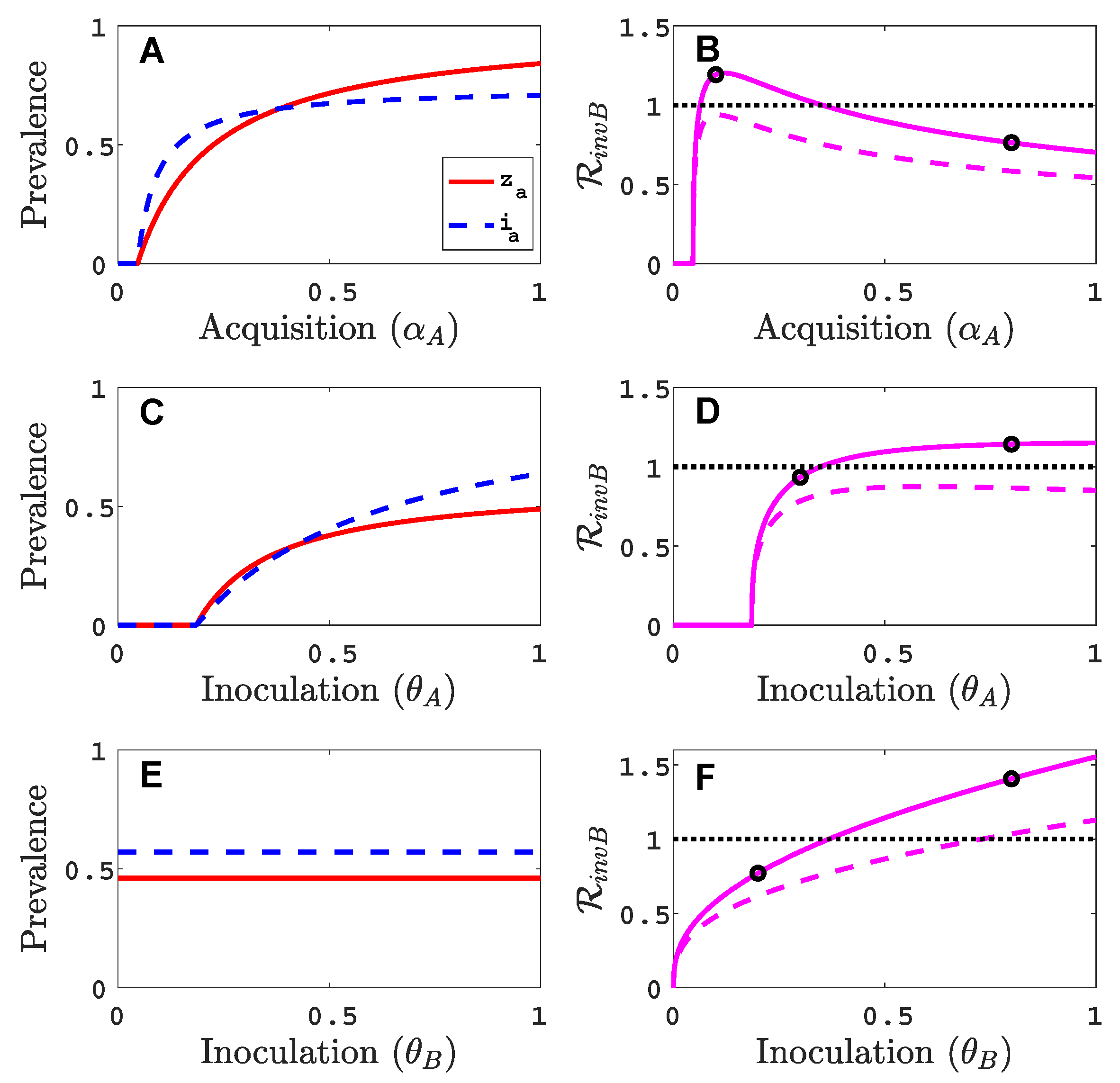
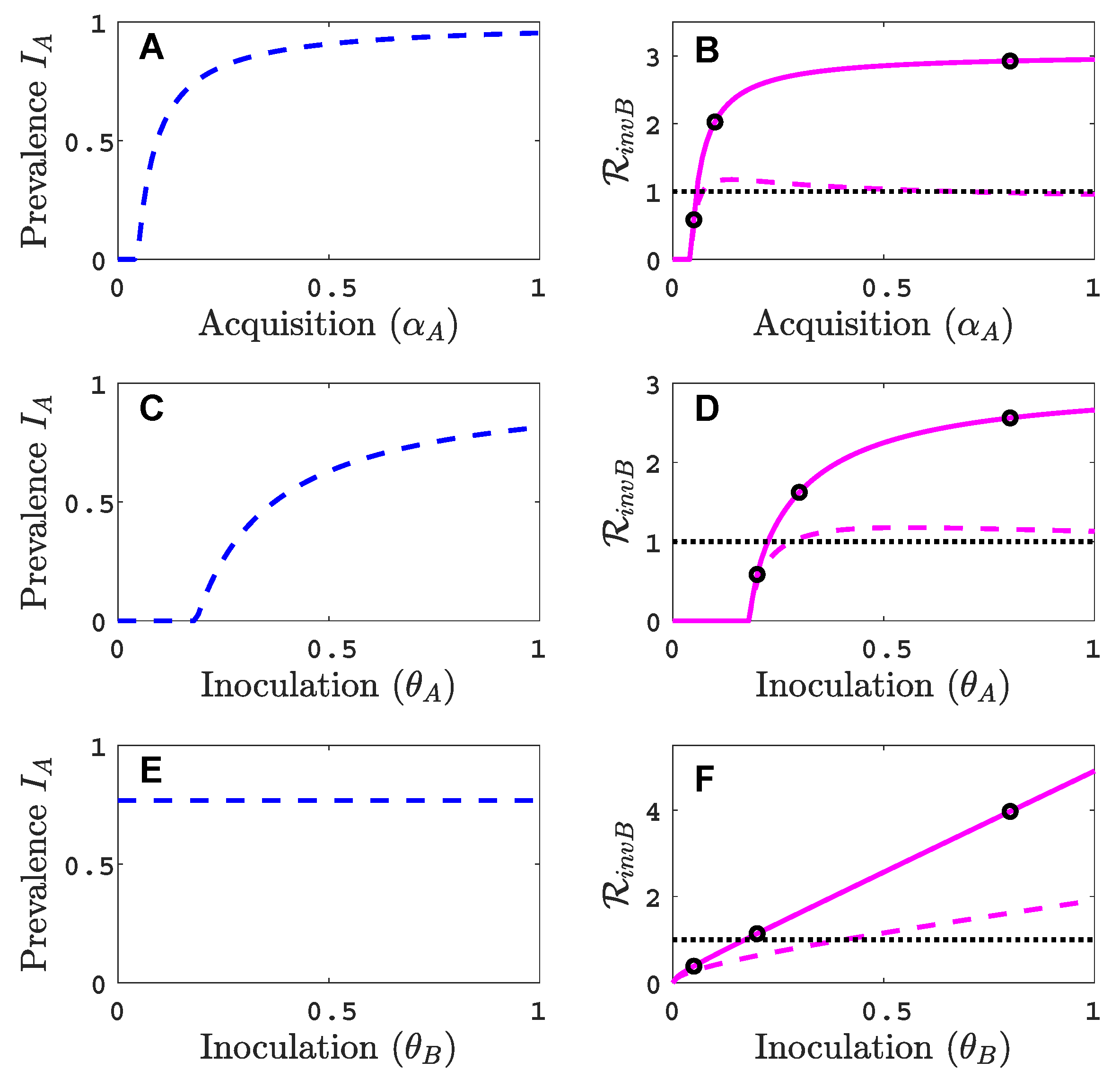
3.1. Only One Virus Can Invade in Absence of the Other
3.2. Comparison with Results of Model That Does Not Track Vectors Explicitly
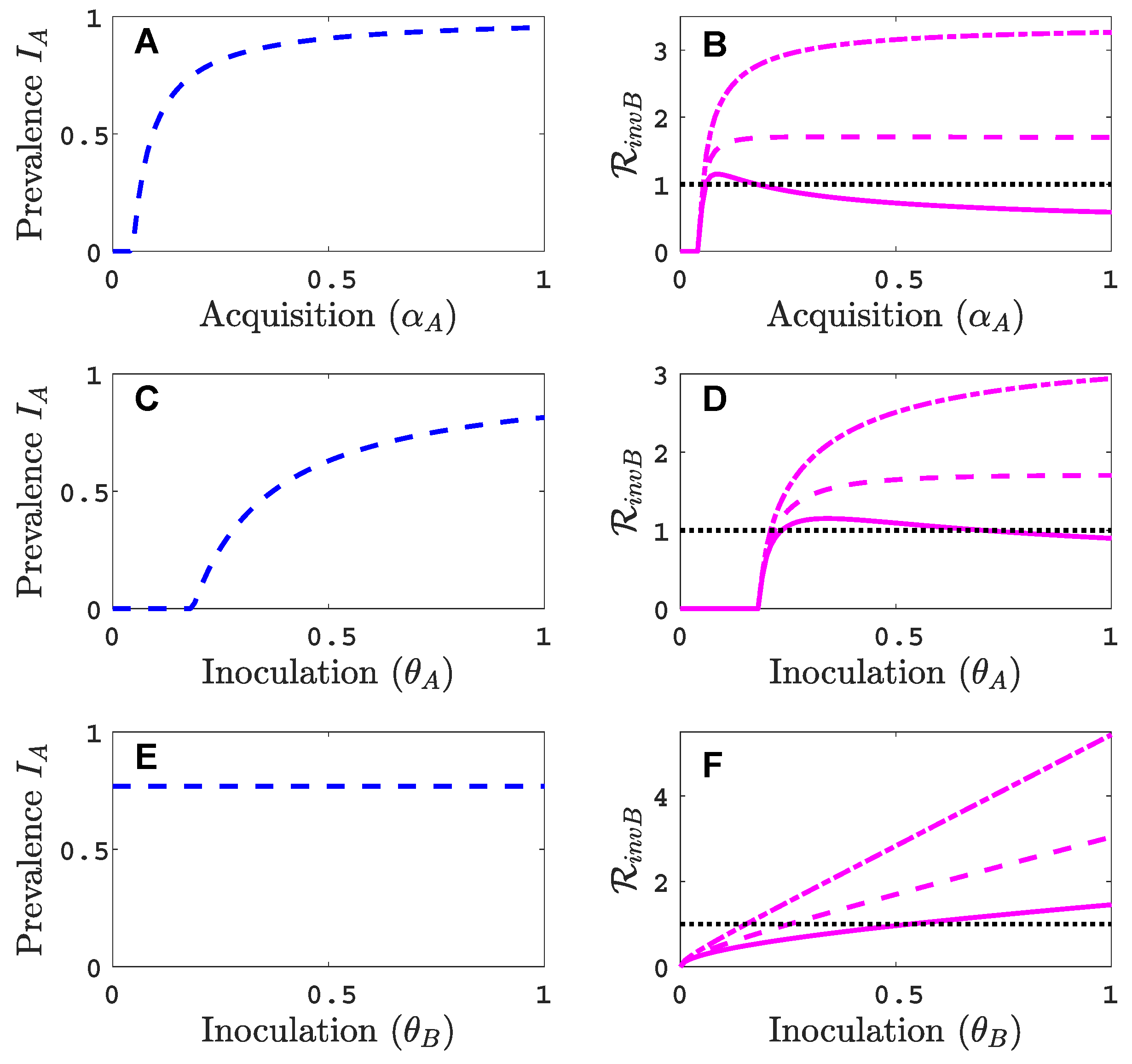
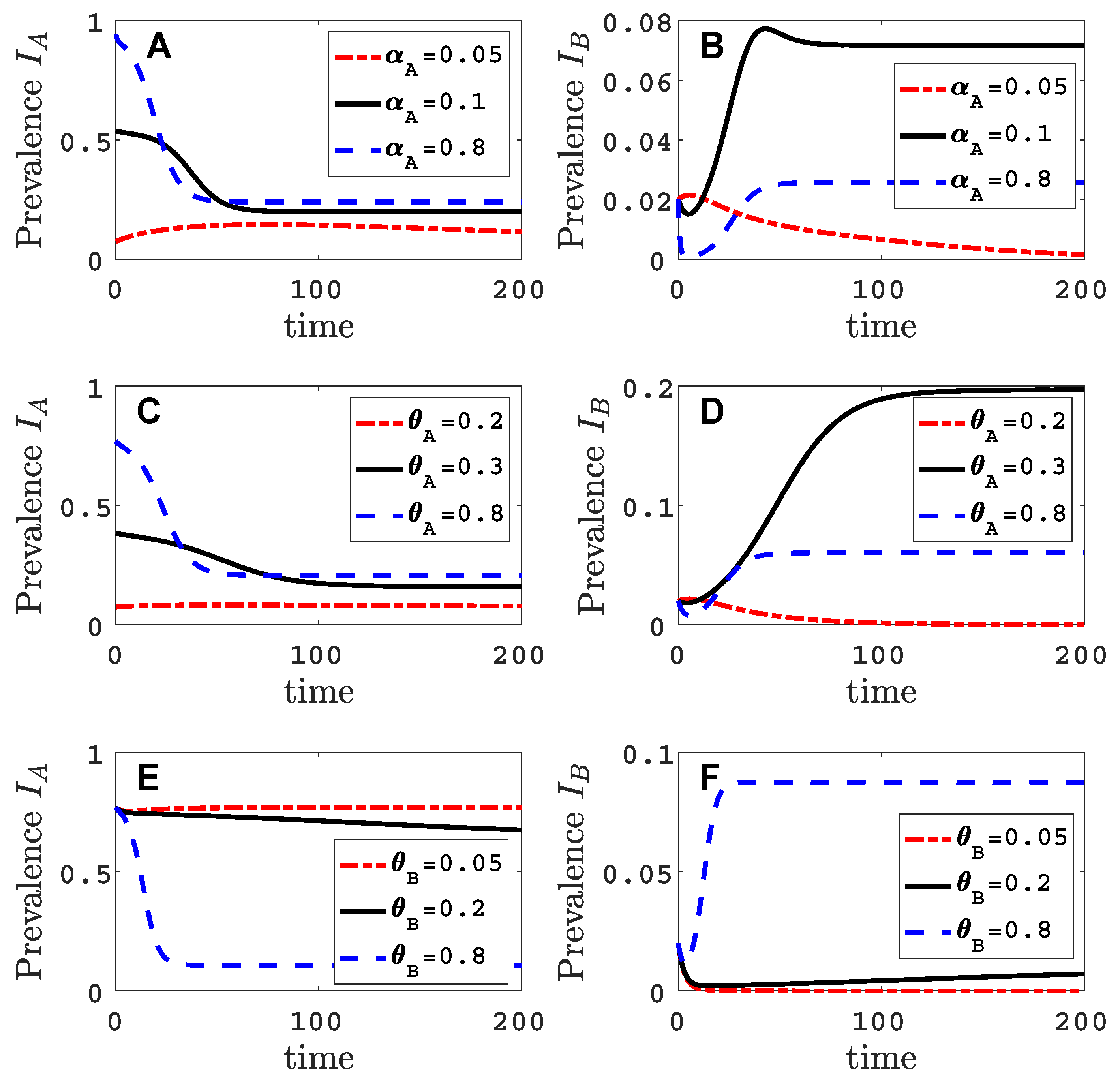
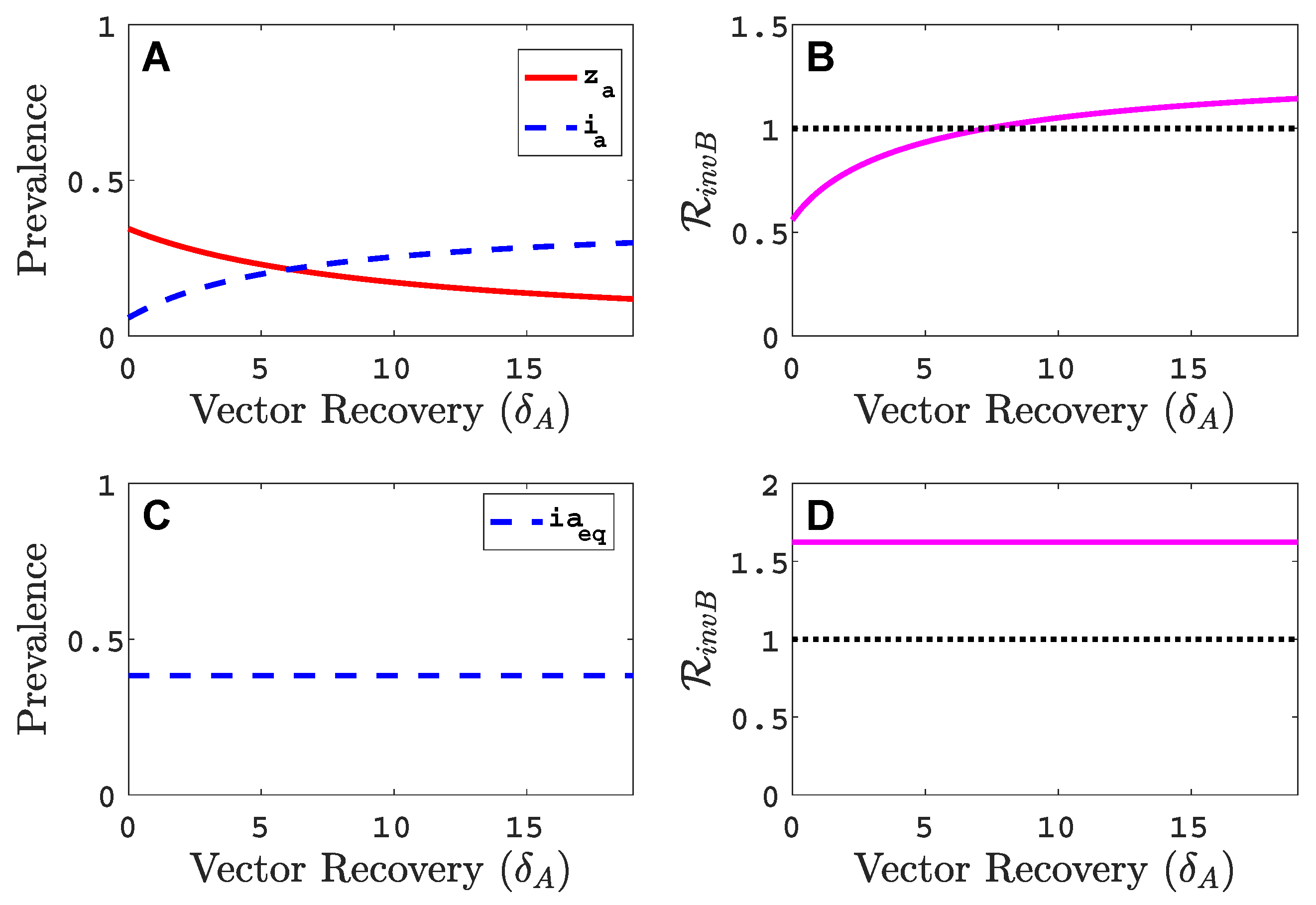
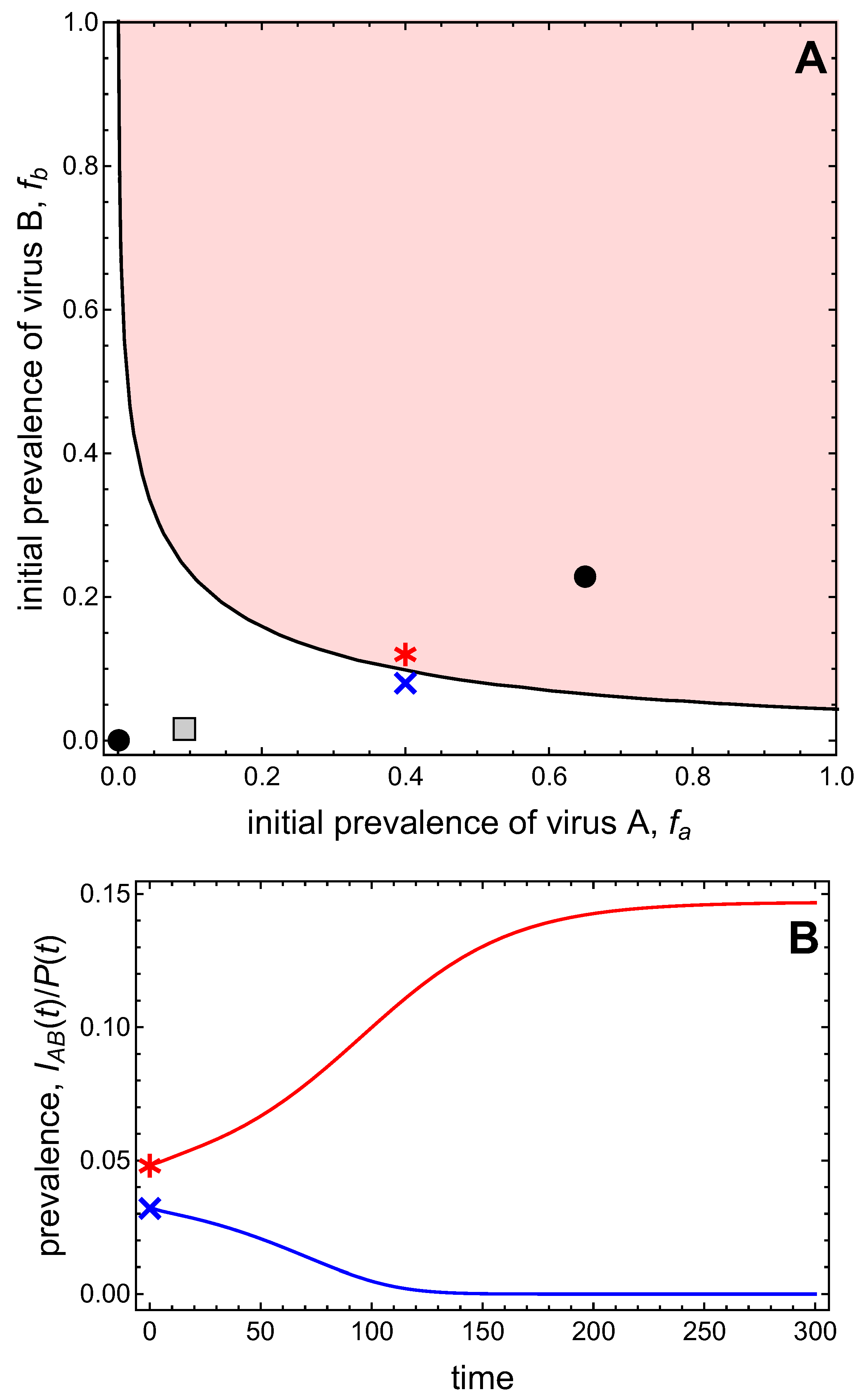
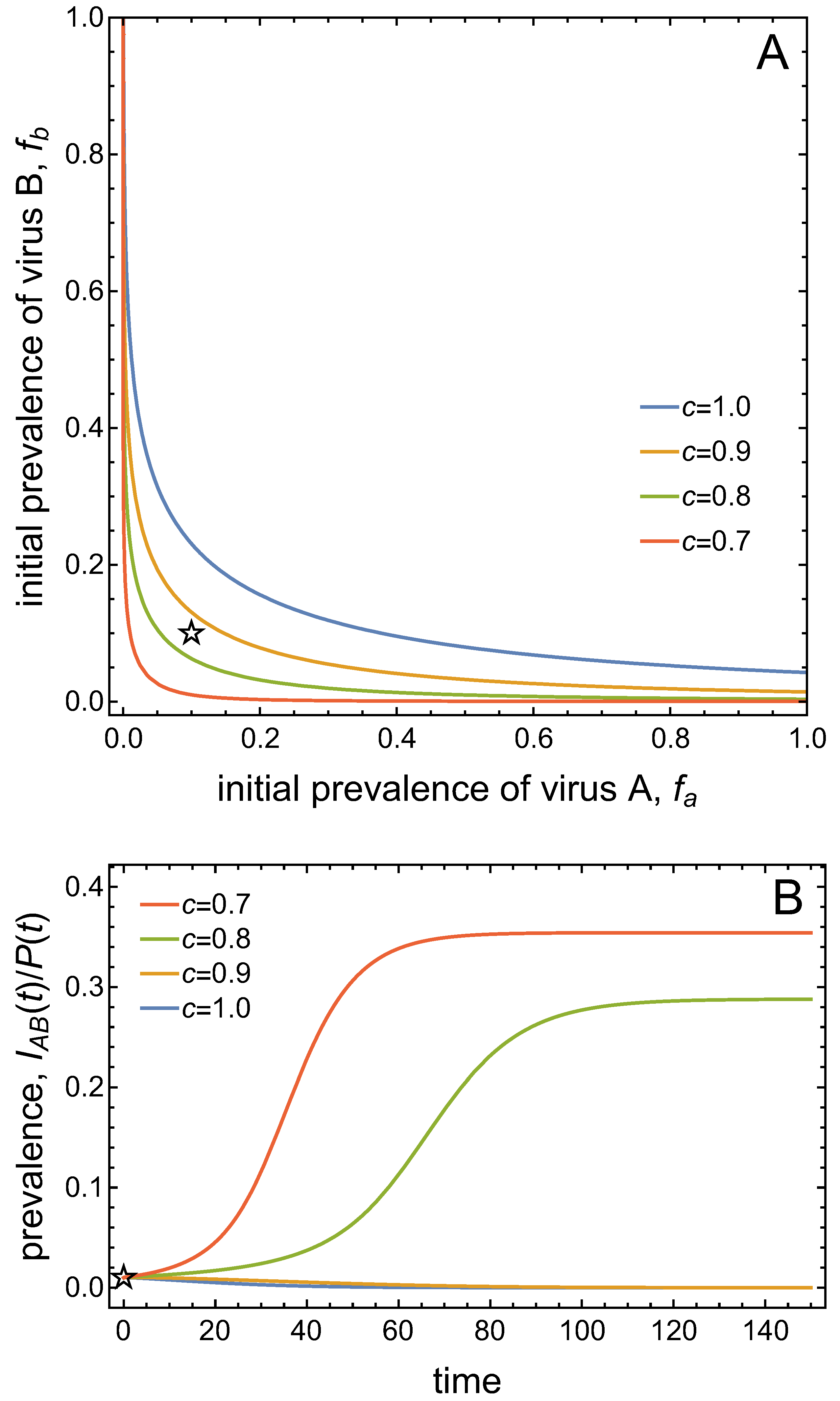
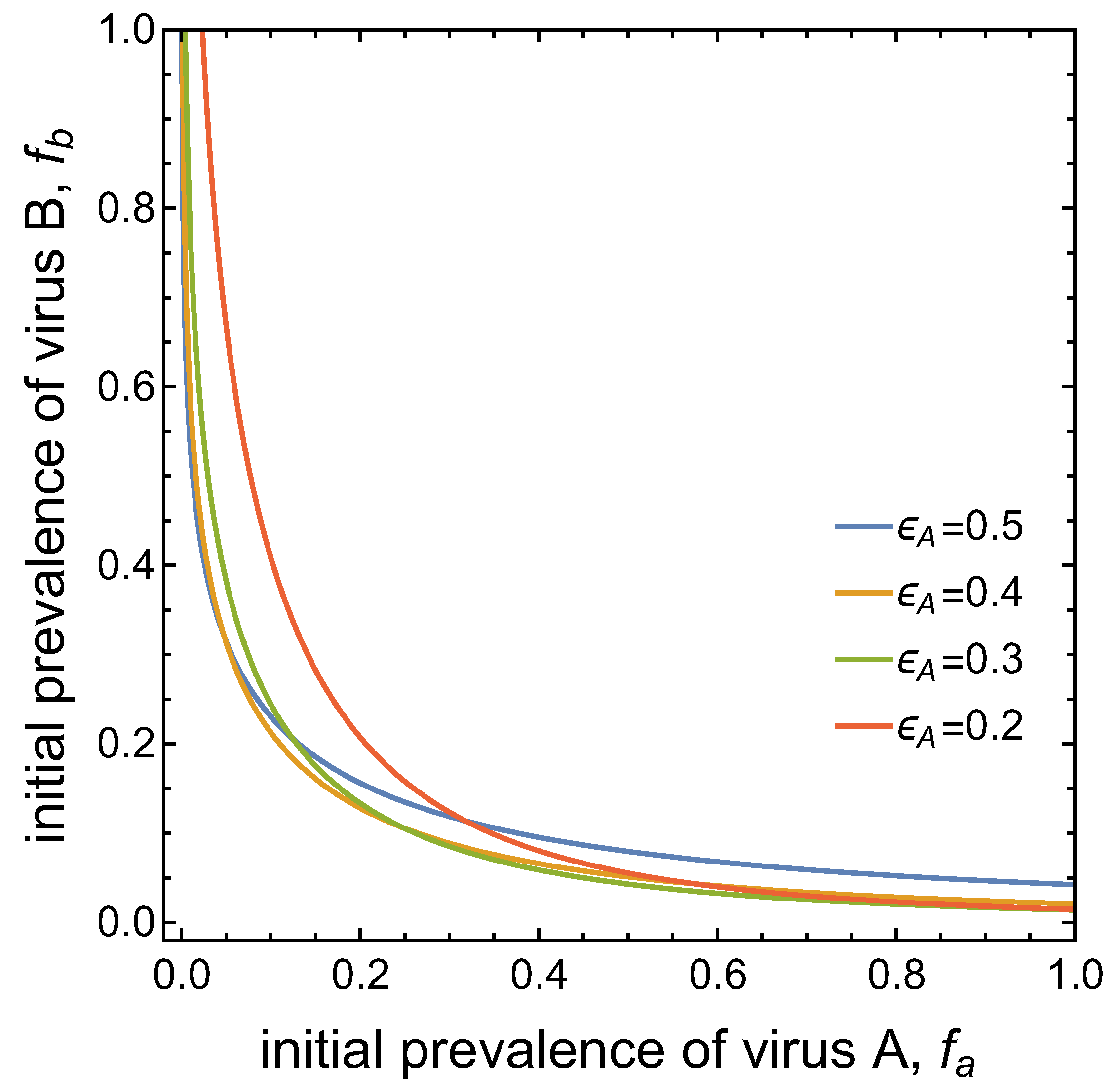
3.3. Neither Virus Can Invade in Absence of the Other
4. Discussion
- i
- Virus A is able to complete a full infection cycle, invade a disease-free population and settle at an endemic equilibrium in the absence of virus B. By contrast, virus B can systematically infect a plant but cannot be acquired by a vector in the absence of co-infection in the host plant. Successful invasion of virus B depends on a complex relation between vector acquisition and inoculation rates, the relative inoculation success of viruses A and B and the prevalence of infected hosts and infective vectors carrying virus A.
- ii
- Virus A and virus B can both complete their infection cycles but are unable to invade a disease-free population in the absence of the other virus. The only biologically feasible endemic equilibrium is a co-infection equilibrium. The system will approach the co-infection equilibrium if the initial prevalences of virus A and B are sufficiently large, i.e., if the initial condition is in the basin of attraction of the co-infection equilibrium. Otherwise, if the initial virus prevalences are so low that the initial condition is in the basin of attraction of the disease-free equilibrium, both viruses will disappear from the system. The separatrix between these two different outcomes represents a curve of tipping points. On either side of these tipping points, we have contrasting dynamics, namely a disease-free versus a co-infected system. We have seen that increased vector mortality rates (e.g., due to vector control programs) moves the separatrix by making the co-infection equilibrium less resilient. This could lead to an abrupt (rather than gradual) extinction of co-infection.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Basic Reproduction Number
Appendix B. Invasion Reproduction Number
Appendix C. Reduction to a Vector-Implicit Model
References
- Gray, S.M.; Banerjee, N. Mechanisms of arthropod transmission of plant and animal viruses. Microbiol. Mol. Biol. Rev. 1999, 63, 128–148. [Google Scholar] [PubMed]
- Blanc, S. Virus transmission–gettin. In Viral Transport in Plants; Springer: Berlin/Heidelberg, Germany, 2007; pp. 1–28. [Google Scholar]
- Brault, V.; Uzest, M.; Monsion, B.; Jacquot, E.; Blanc, S. Aphids as transport devices for plant viruses. C. R. Biol. 2010, 333, 524–538. [Google Scholar] [CrossRef] [PubMed]
- Bragard, C.; Caciagli, P.; Lemaire, O.; Lopez-Moya, J.; MacFarlane, S.; Peters, D.; Susi, P.; Torrance, L. Status and prospects of plant virus control through interference with vector transmission. Annu. Rev. Phytopathol. 2013, 51, 177–201. [Google Scholar] [CrossRef] [PubMed]
- Jeger, M.; Van Den Bosch, F.; Madden, L.; Holt, J. A model for analysing plant-virus transmission characteristics and epidemic development. Math. Med. Biol. A J. IMA 1998, 15, 1–18. [Google Scholar] [CrossRef]
- Verbeek, M.; van Bekkum, P.J.; Dullemans, A.M.; van der Vlugt, R.A. Torradoviruses are transmitted in a semi-persistent and stylet-borne manner by three whitefly vectors. Virus Res. 2014, 186, 55–60. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.S.; Holt, J.; Colvin, J. Mathematical models of host plant infection by helper-dependent virus complexes: Why are helper viruses always avirulent? Phytopathology 2000, 90, 85–93. [Google Scholar] [CrossRef][Green Version]
- Mahuku, G.; Lockhart, B.E.; Wanjala, B.; Jones, M.W.; Kimunye, J.N.; Stewart, L.R.; Cassone, B.J.; Sevgan, S.; Nyasani, J.O.; Kusia, E.; et al. Maize lethal necrosis (MLN), an emerging threat to maize-based food security in sub-Saharan Africa. Phytopathology 2015, 105, 956–965. [Google Scholar] [CrossRef]
- Legg, J.; Jeremiah, S.; Obiero, H.; Maruthi, M.; Ndyetabula, I.; Okao-Okuja, G.; Bouwmeester, H.; Bigirimana, S.; Tata-Hangy, W.; Gashaka, G.; et al. Comparing the regional epidemiology of the cassava mosaic and cassava brown streak virus pandemics in Africa. Virus Res. 2011, 159, 161–170. [Google Scholar] [CrossRef]
- Seabloom, E.W.; Hosseini, P.R.; Power, A.G.; Borer, E.T. Diversity and composition of viral communities: Coinfection of barley and cereal yellow dwarf viruses in California grasslands. Am. Nat. 2009, 173, E79–E98. [Google Scholar] [CrossRef]
- Susi, H.; Barrès, B.; Vale, P.F.; Laine, A.L. Co-infection alters population dynamics of infectious disease. Nat. Commun. 2015, 6, 5975. [Google Scholar] [CrossRef]
- Cunniffe, N.J.; Koskella, B.; Metcalf, C.J.E.; Parnell, S.; Gottwald, T.R.; Gilligan, C.A. Thirteen challenges in modelling plant diseases. Epidemics 2015, 10, 6–10. [Google Scholar] [CrossRef] [PubMed]
- Escriu, F.; Fraile, A.; García-Arenal, F. The evolution of virulence in a plant virus. Evolution 2003, 57, 755–765. [Google Scholar] [CrossRef]
- Syller, J. Biological and molecular events associated with simultaneous transmission of plant viruses by invertebrate and fungal vectors. Mol. Plant Pathol. 2014, 15, 417–426. [Google Scholar] [CrossRef] [PubMed]
- Moury, B.; Fabre, F.; Senoussi, R. Estimation of the number of virus particles transmitted by an insect vector. Proc. Natl. Acad. Sci. USA 2007, 104, 17891–17896. [Google Scholar] [CrossRef] [PubMed]
- Gallet, R.; Michalakis, Y.; Blanc, S. Vector-transmission of plant viruses and constraints imposed by virus–vector interactions. Curr. Opin. Virol. 2018, 33, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Syller, J.; Grupa, A. Antagonistic within-host interactions between plant viruses: Molecular basis and impact on viral and host fitness. Mol. Plant Pathol. 2016, 17, 769–782. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.S.; Holt, J.; Colvin, J. Synergism between plant viruses: A mathematical analysis of the epidemiological implications. Plant Pathol. 2001, 50, 732–746. [Google Scholar] [CrossRef]
- Zhang, X.S.; Holt, J. Mathematical models of cross protection in the epidemiology of plant-virus diseases. Phytopathology 2001, 91, 924–934. [Google Scholar] [CrossRef][Green Version]
- Mascia, T.; Gallitelli, D. Synergies and antagonisms in virus interactions. Plant Sci. 2016, 252, 176–192. [Google Scholar] [CrossRef]
- Srinivasan, R.; Hall, D.G.; Cervantes, F.A.; Alvarez, J.M.; Whitworth, J.L. Strain specificity and simultaneous transmission of closely related strains of a Potyvirus by Myzus persicae. J. Econ. Entomol. 2012, 105, 783–791. [Google Scholar] [CrossRef]
- Carroll, J.; Smith, D.; Gray, S. Preferential acquisition and inoculation of PVYNTN over PVYO in potato by the green peach aphid Myzus persicae (Sulzer). J. Gen. Virol. 2016, 97, 797. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Mondal, S.; Wenninger, E.J.; Hutchinson, P.J.; Whitworth, J.L.; Shrestha, D.; Eigenbrode, S.D.; Bosque-Pérez, N.A. Comparison of transmission efficiency of various isolates of Potato virus Y among three aphid vectors. Entomol. Exp. Et Appl. 2016, 158, 258–268. [Google Scholar] [CrossRef]
- Lacroix, C.; Seabloom, E.W.; Borer, E.T. Environmental nutrient supply alters prevalence and weakens competitive interactions among coinfecting viruses. New Phytol. 2014, 204, 424–433. [Google Scholar] [CrossRef] [PubMed]
- Salvaudon, L.; De Moraes, C.M.; Mescher, M.C. Outcomes of co-infection by two potyviruses: Implications for the evolution of manipulative strategies. Proc. R. Soc. B Biol. Sci. 2013, 280, 20122959. [Google Scholar] [CrossRef]
- Holt, J.; Chancellor, T. Simulation modelling of the spread of rice tungro virus disease: The potential for management by roguing. J. Appl. Ecol. 1996, 33, 927–936. [Google Scholar] [CrossRef]
- Peñaflor, M.F.G.; Mauck, K.E.; Alves, K.J.; De Moraes, C.M.; Mescher, M.C. Effects of single and mixed infections of Bean pod mottle virus and Soybean mosaic virus on host-plant chemistry and host–vector interactions. Funct. Ecol. 2016, 30, 1648–1659. [Google Scholar] [CrossRef]
- Naidu, R.A.; Maree, H.J.; Burger, J.T. Grapevine leafroll disease and associated viruses: A unique pathosystem. Annu. Rev. Phytopathol. 2015, 53, 613–634. [Google Scholar] [CrossRef]
- Blaisdell, G.K.; Cooper, M.L.; Kuhn, E.J.; Taylor, K.A.; Daane, K.M.; Almeida, R.P. Disease progression of vector-mediated Grapevine leafroll-associated virus 3 infection of mature plants under commercial vineyard conditions. Eur. J. Plant Pathol. 2016, 146, 105–116. [Google Scholar] [CrossRef]
- Untiveros, M.; Fuentes, S.; Salazar, L.F. Synergistic interaction of Sweet potato chlorotic stunt virus (Crinivirus) with carla-, cucumo-, ipomo-, and potyviruses infecting sweet potato. Plant Dis. 2007, 91, 669–676. [Google Scholar] [CrossRef]
- McLeish, M.; Sacristán, S.; Fraile, A.; García-Arenal, F. Coinfection Organizes Epidemiological Networks of Viruses and Hosts and Reveals Hubs of Transmission. Phytopathology 2019, 109, 1003–1010. [Google Scholar] [CrossRef]
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Diekmann, O.; Heesterbeek, J.A.P.; Metz, J.A. On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–382. [Google Scholar] [CrossRef] [PubMed]
- Roberts, M.; Heesterbeek, J. A new method for estimating the effort required to control an infectious disease. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2003, 270, 1359–1364. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P.; Watmough, J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002, 180, 29–48. [Google Scholar] [CrossRef]
- Ortega, J.M. Matrix Theory: A Second Course; Plenum Press: New York, NY, USA; London, UK, 1987. [Google Scholar]
- Hilker, F.M.; Allen, L.J.; Bokil, V.A.; Briggs, C.J.; Feng, Z.; Garrett, K.A.; Gross, L.J.; Hamelin, F.M.; Jeger, M.J.; Manore, C.A.; et al. Modeling virus coinfection to inform management of maize lethal necrosis in Kenya. Phytopathology 2017, 107, 1095–1108. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008. [Google Scholar]
- Hamelin, F.M.; Allen, L.J.; Prendeville, H.R.; Hajimorad, M.R.; Jeger, M.J. The evolution of plant virus transmission pathways. J. Theor. Biol. 2016, 396, 75–89. [Google Scholar] [CrossRef]
- Donnelly, R.; Cunniffe, N.J.; Carr, J.P.; Gilligan, C.A. Pathogenic modification of plants enhances long-distance dispersal of nonpersistently transmitted viruses to new hosts. Ecology 2019, e02725. [Google Scholar] [CrossRef]
- Gildow, F.E.; Rochow, W.F. Transmission interference between two isolates of barley yellow dwarf virus in Macrosiphum avenae. Phytopathology 1980, 70, 122–126. [Google Scholar] [CrossRef]
- Cohen, S.; Duffus, J.E.; Liu, H.Y. Acquisition, interference, and retention of cucurbit leaf curl viruses in whiteflies. Phytopathology 1989, 79, 109–113. [Google Scholar] [CrossRef]
- Ng, J.C.; Chen, A.Y. Acquisition of Lettuce infectious yellows virus by Bemisia tabaci perturbs the transmission of Lettuce chlorosis virus. Virus Res. 2011, 156, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Seabloom, E.W.; Borer, E.T.; Gross, K.; Kendig, A.E.; Lacroix, C.; Mitchell, C.E.; Mordecai, E.A.; Power, A.G. The community ecology of pathogens: Coinfection, coexistence and community composition. Ecol. Lett. 2015, 18, 401–415. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.J. Introduction to Mathematical Biology; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
| Pathosystem | Authors | Key Message | |
|---|---|---|---|
| Two virus strains | Potato virus Y (PYV)—Myzus persicae (host Capsicum annuum) | Moury et al. [15] | Two strains were equally transmissible and competition was studied to estimate the size of bottlenecks imposed by vector transmission. If there was a cost of virulence, modelling showed that virulent strains would go extinct. |
| compared with other strains—Myzus persicae | Srinivasan et al. [21] | Previous work had suggested some specificity in transmission of strains. The rate of infection for was higher than for other strains, a vector-related outcome as this was not observed with mechanical transmission. | |
| compared with —Myzus persicae | Carroll et al. [22] | The necrotic strain was transmitted more efficiently than the wild-type. Co-infection would more likely result from inoculation by multiple aphids feeding on plants infected with the different strains rather than by single aphids feeding on multiple plants infected with the different strains. | |
| Two virus species—common vector | Barley yellow dwarf virus/cereal yellow dwarf virus—Rhopalosiphum padi | Lacroix et al. [24] | The co-inoculation of BYDV-PAV lowered the CYDV-RPV infection rate but only at low nutrient supply rates. Broader environmental and nutritional factors can alter co-infection interactions and outcomes. |
| Watermelon mosaic virus/zucchini yellow mosaic virus—Aphis gossypii | Salvaudon et al. [25] | ZYMV accumulated at similar rates in single and mixed infections, whereas WMV was much reduced in the presence of ZYMV. ZYMV also induced host changes that gave strong vector preference for infected plants; whereas WMV did not, although it was still readily acquired from mixed infections. | |
| Rice tungro spherical virus/rice tungro bacilliform virus—Nephottetix virescens | Holt and Chancellor [26] | Infection by each virus alone results in less pronounced symptoms. RTBV is retained in the vector for a longer period. When a vector carries both viruses, co-inoculation is common. When inoculative with RSTV alone the infection probability is higher. | |
| Two virus species—multiple vector species | Bean pod mottle virus—Epilachna varivestis/soybean mosaic virus—Aphis glycines | Penaflor et al. [27] | Singly-infected plants with either BPMV or SMV increased soybean palatability, potentially enhancing acquisition of BPMV from BPMV plants and secondary infection of BPMV from SMV plants. BPMV infection had little effect on A. glycines, whereas SMV infection reduced aphid population growth but increased the preference for infected plants. With co-infection, effects on population growth were reversed and aphids showed a preference for co-infected plants. |
| Multiple virus species—multiple vector species | Grapevine leafroll-associated viruses (GLRaVs)—mealybugs/scale insects | Naidu et al. [28] | The exact role of GLRaVs in disease etiology remains unclear. With mealybugs, transmission is of a semi-persistent manner with a lack of vector-virus specificity. |
| Blaisdell et al. [29] | Co-infections of GLRaVs are frequent in grapevines although with some spatial separation with implications for transmission and epidemiology. | ||
| Sweet potato chlorotic stunt virus/sweet potato feathery mottle virus/multiple viruses—multiple vector species | Untiveros et al. [30] | Six viruses from the same or different virus families interacted synergistically with sweet potato virus disease, with increased disease symptoms, virus accumulation and movement in plants, and reduced yield of storage roots. All inoculations were made by grafting; no conclusions can be drawn on vector transmission effects. | |
| Multiple virus species—multiple vector species, multiple hosts | Ecological networks formed by multiple co-infecting viruses in multiple hosts | McLeish et al. [31] | Co-infection networks were found to lead to strong non-random associations compared with single infections. Single infections were mostly related to habitat parameters, whereas co-infections were more related to ecological heterogeneity and ecosystem-level processes. |
| Vector | Default Values | Default Values | |
|---|---|---|---|
| Parameters | Section 3.1 and Section 3.2, Appendix B and Appendix C | Section 3.3 | |
| vector birth rate | 10/month/area | 1/month/area | |
| c | per capita vector natural death rate | 1/month | 1/month |
| number of plants visited/time by a vector | 1/day | 8.33/day | |
| per capita infective vector recovery rate from virus A | 3/month | 0.66/day | |
| per capita infective vector recovery rate from virus B | 3/month | 1.33/day | |
| probability non-infective vector acquires virus A from per plant visit | 0.2 | 0.005 | |
| probability non-infective vector acquires virus B from per plant visit | 0 | 0.005 | |
| probability non-infective vector acquires a single virus, A or B, from per plant visit | 0.5 | 0.15 | |
| conditional probability of acquiring virus A from a co-infected plant , given a successful acquisition | 0.5 | 0.5 | |
| conditional probability of acquiring virus B from co-infected plant , given a successful acquisition () | 0.5 | 0.5 | |
| Plant | Default Values | Default Values | |
| Parameters | Section 3.1 and Section 3.2, Appendix B and Appendix C | Section 3.3 | |
| per capita mortality and or harvest of plants | 1/year | 1/year | |
| seeding or planting rate | 1000/year/area | 100/year/area | |
| probability an infective vector with virus A inoculates a healthy plant per visit | 0.8 | 0.8 | |
| probability an infective vector with virus B inoculates a healthy plant per visit | 0.5 | 0.5 | |
| relative inoculation success of virus A (as compared to a heathy plant) in a plant , infected with a single virus B | 0.9 | 0.5 | |
| relative inoculation success of virus B (as compared to a healthy plant) in a plant , infected with a single virus A | 0.25, 0.9 | 0.5 | |
| per-capita viral A or B loss rate in a plant infected with single virus | 0 | 0.001/day | |
| per-capita viral B loss rate (A is retained) from a co-infected plant | 0 | 0.001/day | |
| per-capita viral A loss rate (B is retained) from a co-infected plant | 0 | 0.001/day | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allen, L.J.S.; Bokil, V.A.; Cunniffe, N.J.; Hamelin, F.M.; Hilker, F.M.; Jeger, M.J. Modelling Vector Transmission and Epidemiology of Co-Infecting Plant Viruses. Viruses 2019, 11, 1153. https://doi.org/10.3390/v11121153
Allen LJS, Bokil VA, Cunniffe NJ, Hamelin FM, Hilker FM, Jeger MJ. Modelling Vector Transmission and Epidemiology of Co-Infecting Plant Viruses. Viruses. 2019; 11(12):1153. https://doi.org/10.3390/v11121153
Chicago/Turabian StyleAllen, Linda J. S., Vrushali A. Bokil, Nik J. Cunniffe, Frédéric M. Hamelin, Frank M. Hilker, and Michael J. Jeger. 2019. "Modelling Vector Transmission and Epidemiology of Co-Infecting Plant Viruses" Viruses 11, no. 12: 1153. https://doi.org/10.3390/v11121153
APA StyleAllen, L. J. S., Bokil, V. A., Cunniffe, N. J., Hamelin, F. M., Hilker, F. M., & Jeger, M. J. (2019). Modelling Vector Transmission and Epidemiology of Co-Infecting Plant Viruses. Viruses, 11(12), 1153. https://doi.org/10.3390/v11121153





