The Urban Environment Can Modify Drought Stress of Small-Leaved Lime (Tilia cordata Mill.) and Black Locust (Robinia pseudoacacia L.)
Abstract
:1. Introduction
- Can the average growth rates of the analyzed tree species be quantified in respect to their growing sites?
- How stable and sensitive is the growth of trees in urban environments?
- How does the urban climate (temperature and precipitation) and environment (light, open surface, neighboring trees, and close buildings) influence tree growth?
- What are the responses of urban tree species with varying drought tolerances to drought years?
- Do the urban environment and individual tree structure modify the drought stress of trees?
2. Materials and Methods
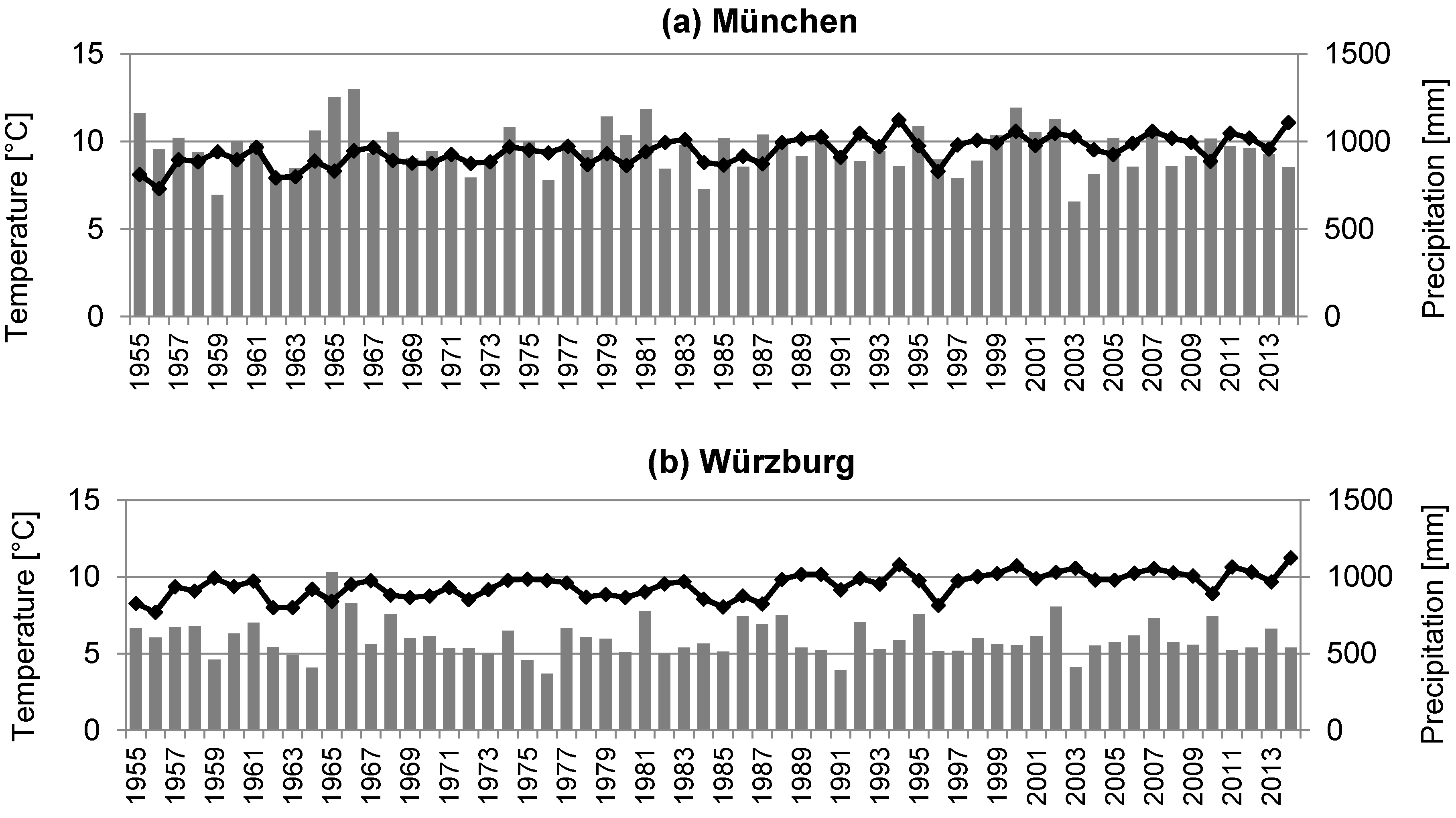
2.1. Site Description and Data Collection
2.2. Quantification of Urban Tree Growth in Relation to Growing Site Based on Tree Ring Analysis
2.3. Investigated Variables
2.4. Statistical Analyses
3. Results
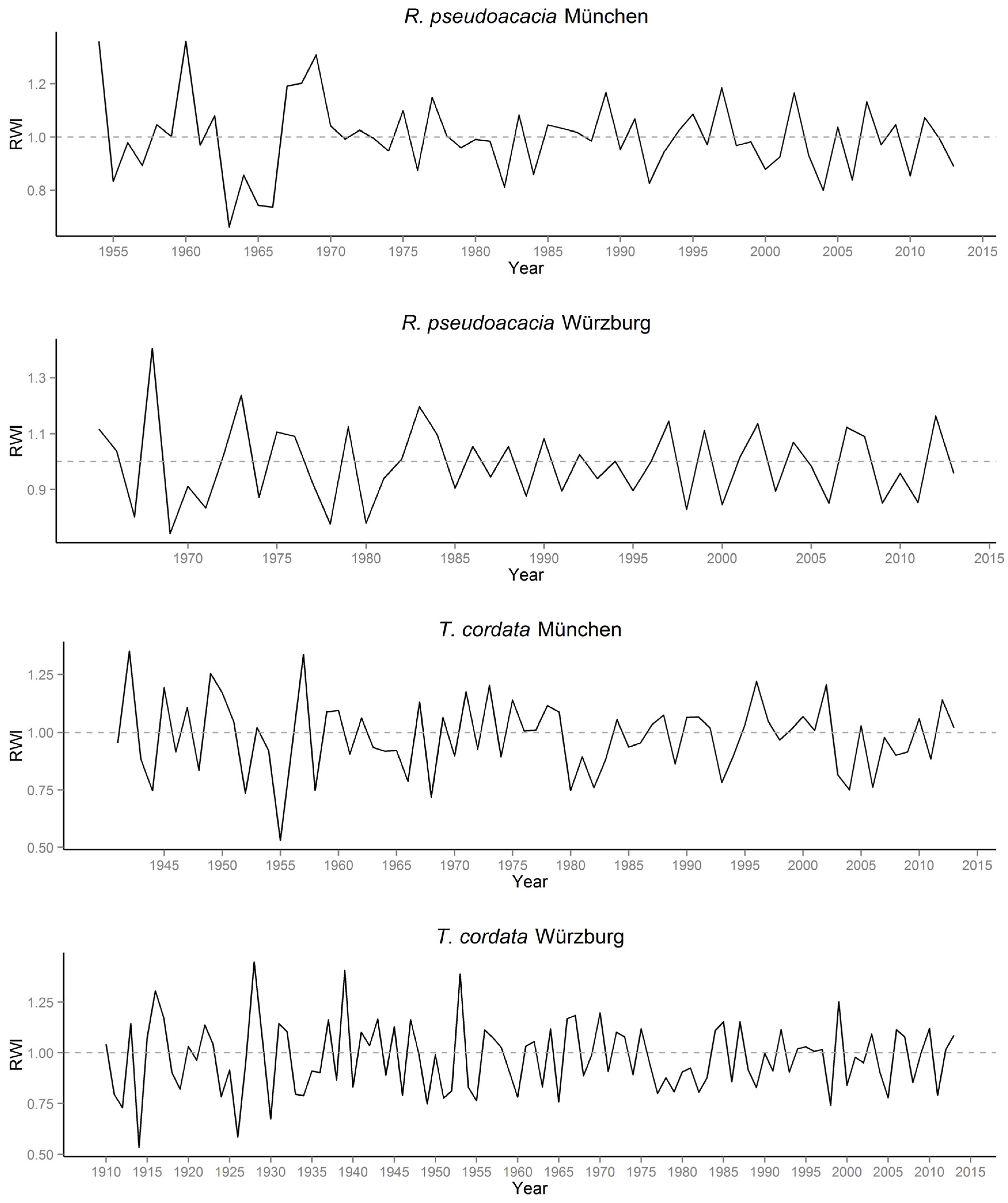
3.1. Quantification of Urban Tree Growth in Relation to Growing Site Based on Tree Ring Analysis
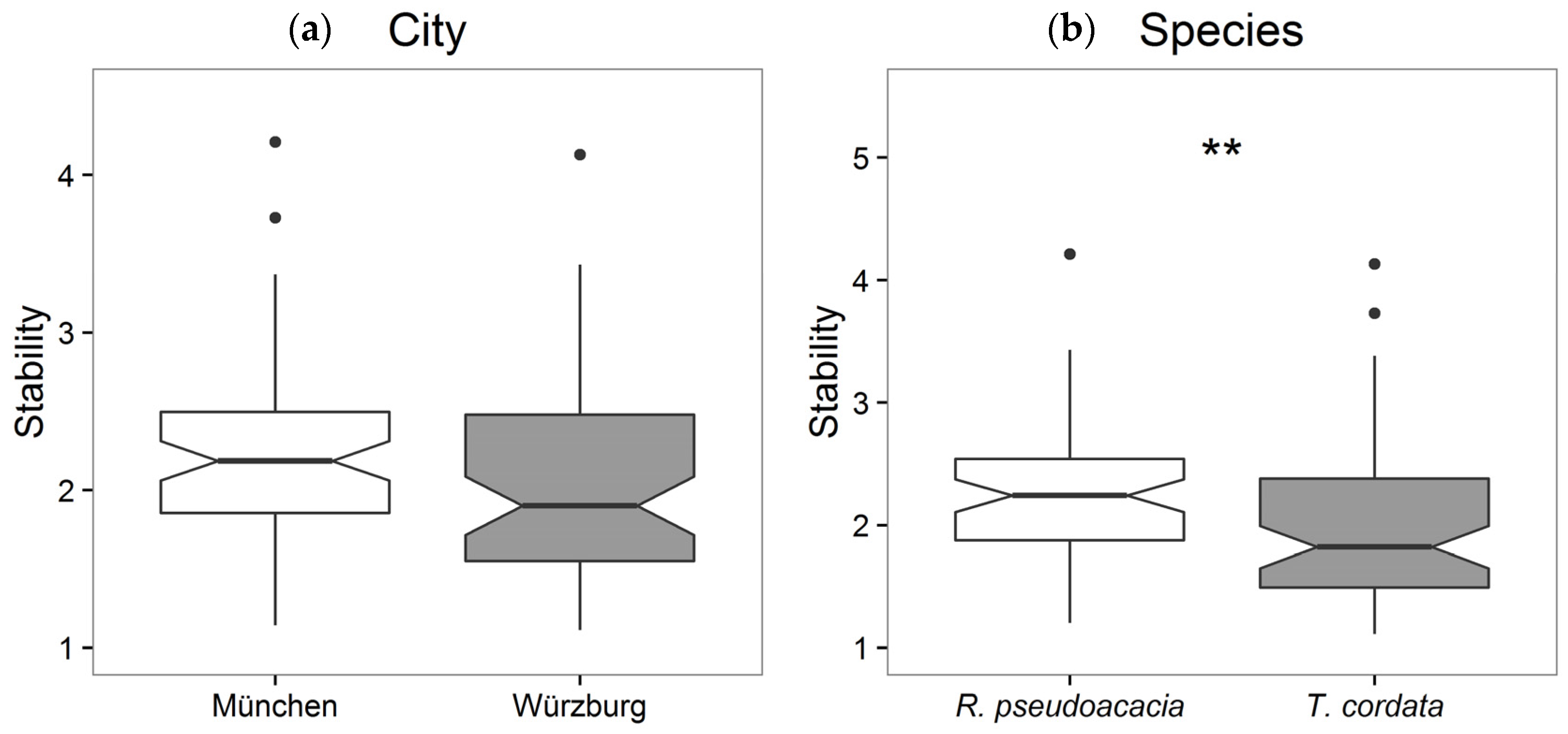
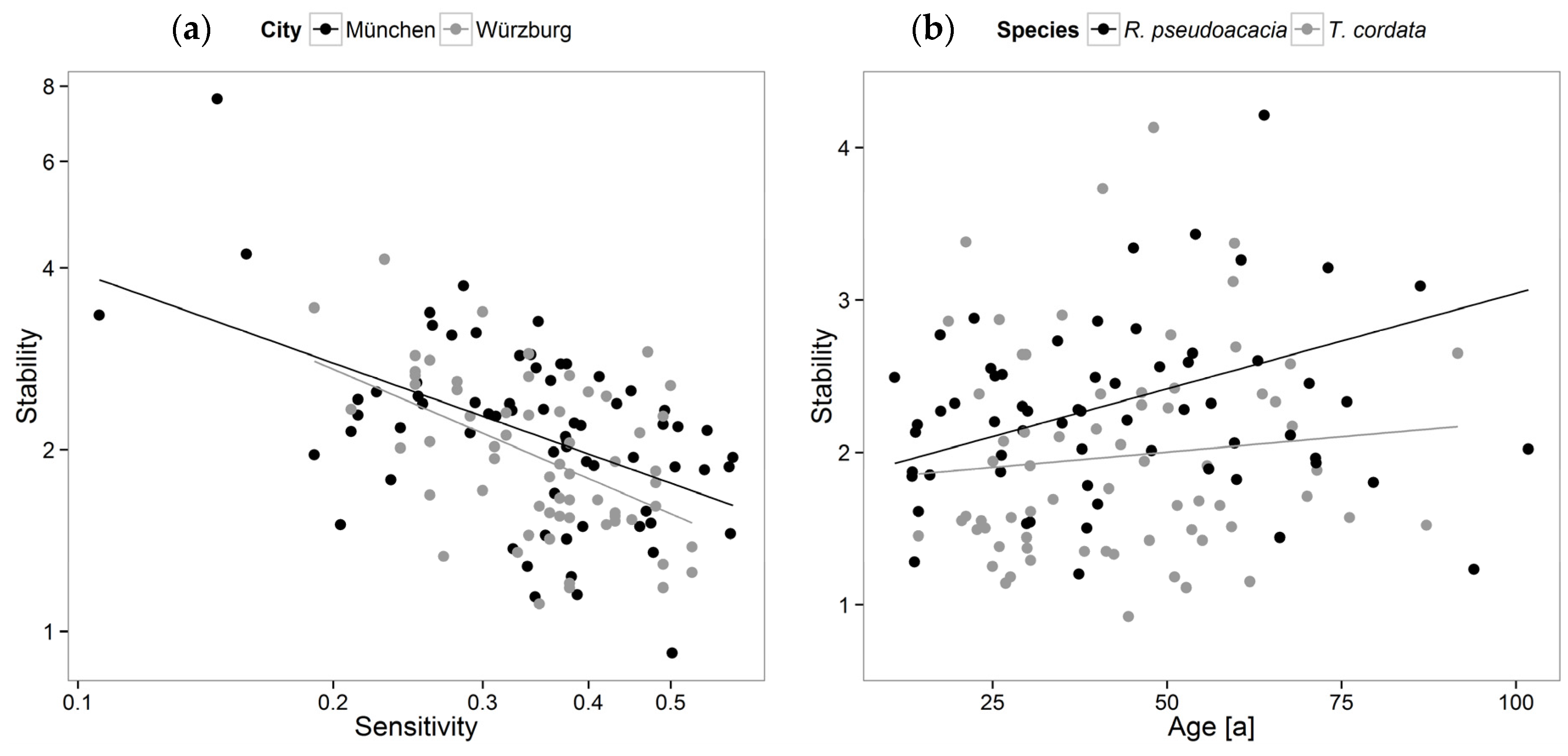
3.2. Stability, Sensitivity, and Modeling of Tree Growth in Relation to Their Environment
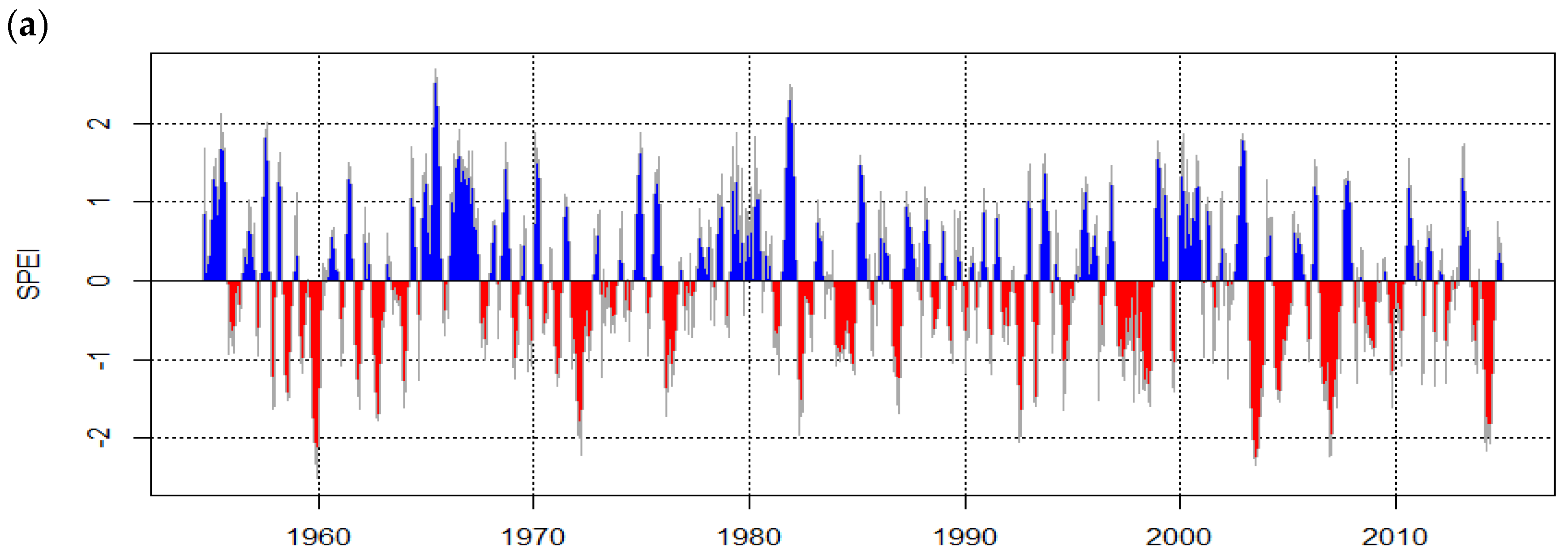
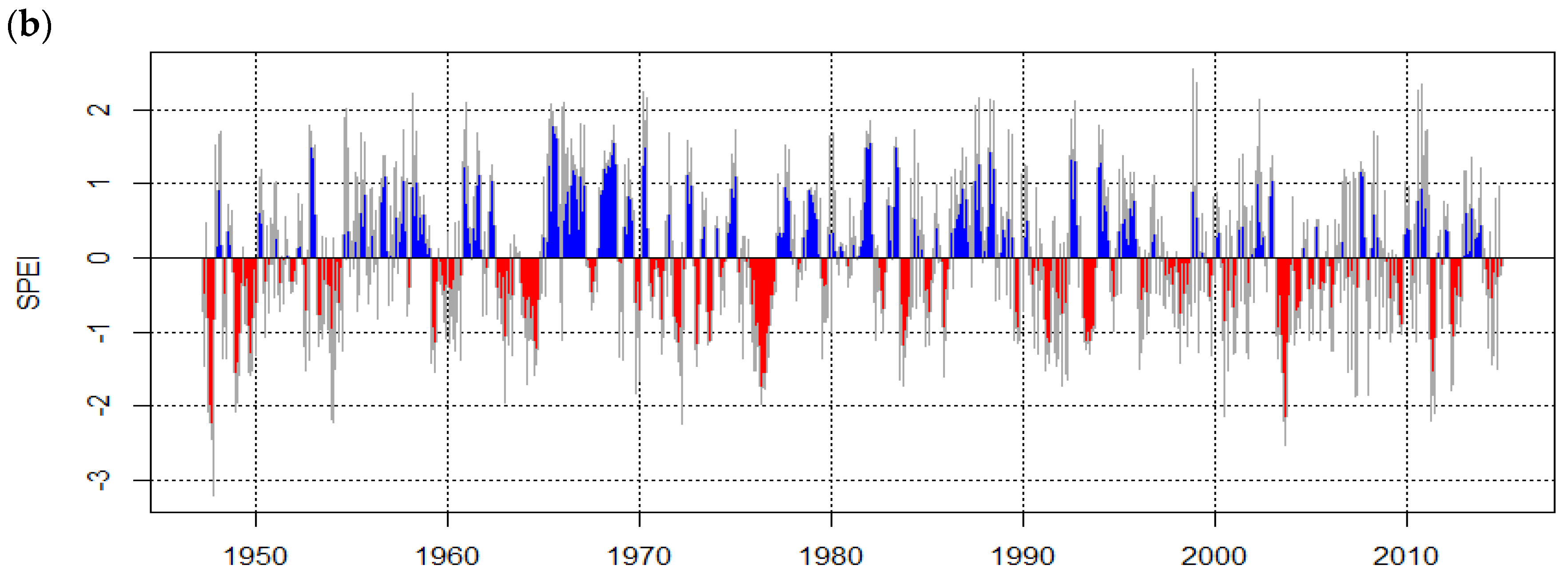
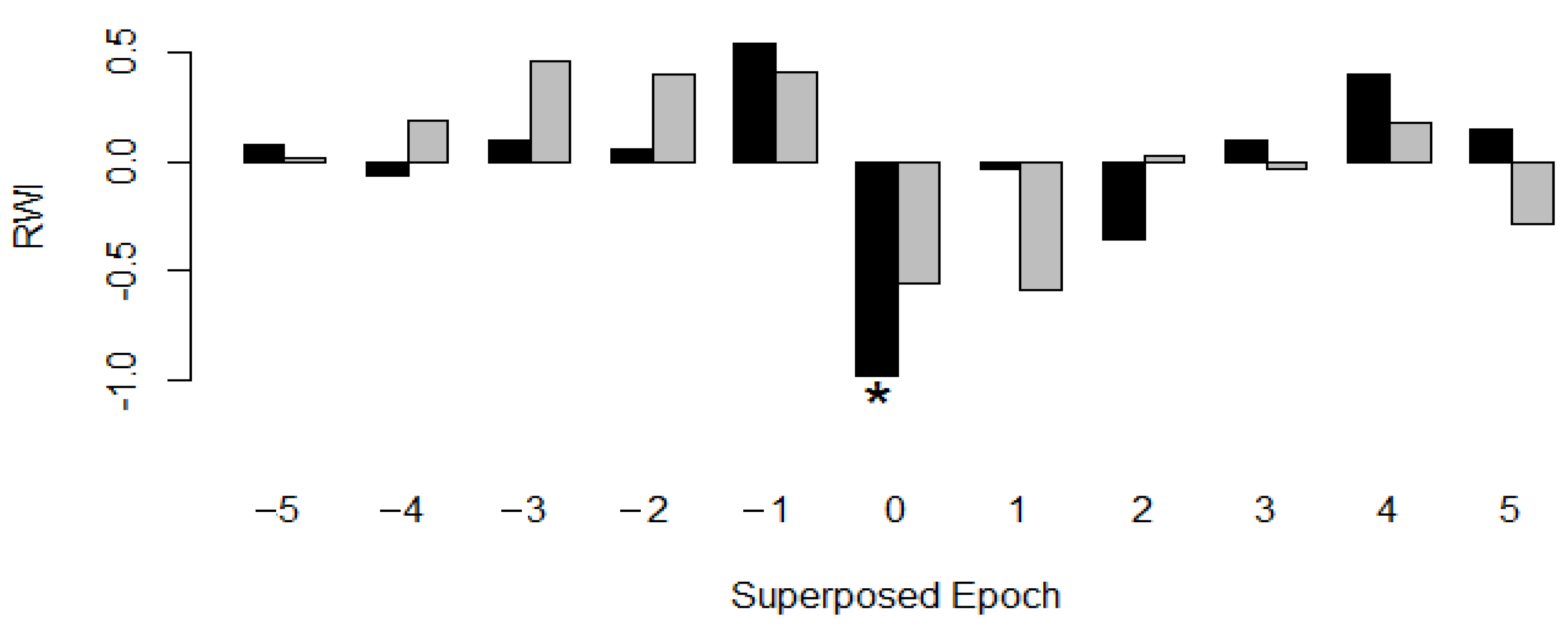
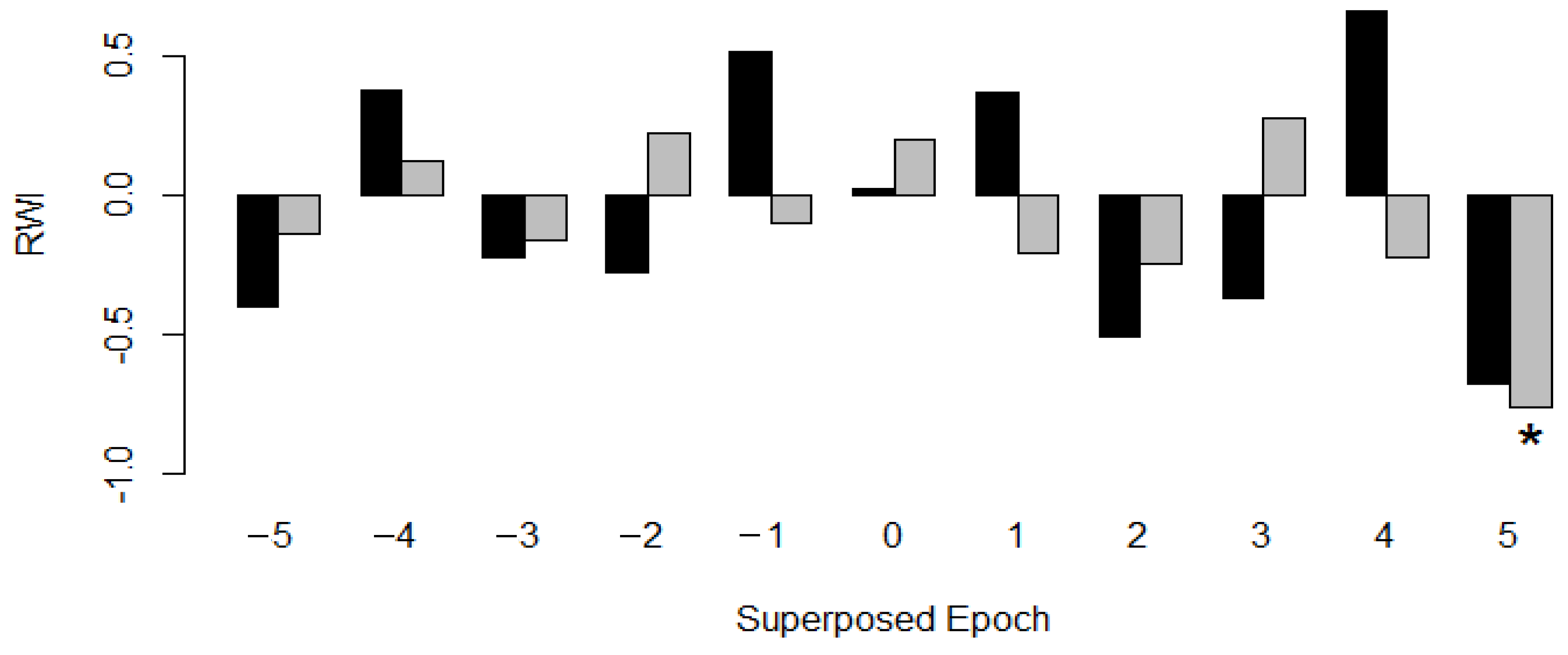
3.3. Growth of Urban Trees Under Drought Stress in Relation to the Tree Structure and Environment
4. Discussion
4.1. Tree Ring Analysis: Quantification of Growth of Urban Trees in Relation to the Growing Site
4.2. Stability, Sensitivity, and Modeling of Tree Growth in Relation to Their Environment
4.3. Growth of Urban Trees under Drought Stress in Relation to the Tree Structure and Environment
4.4. Effect of Urban Environment and Individual Tree Structure on the Drought Stress of Trees
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| AIC | Akaike’s information criterion |
| Dbh | diameter at breast height |
| EPS | expressed population signal |
| OSA | open surface area of the tree pit |
| PET | potential evapotranspiration |
| RSE | residual standard error |
| RWI | ring width index |
| SD | standard deviation |
| SE | standard error |
| SEA | superposed epoch analysis |
| SPEI | standardized precipitation-evapotranspiration index |
| SVF | sky view factor |
References
- Shashua-Bar, L.; Hoffman, M.E. Geometry and orientation aspects in passive cooling of canyon streets with trees. Energy Build. 2003, 35, 61–68. [Google Scholar] [CrossRef]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool surfaces and shade trees to reduce energy use and improve air quality in urban areas. Sol. Energy 2001, 70, 295310. [Google Scholar] [CrossRef]
- Gillner, S.; Vogt, J.; Roloff, A. Climatic response and impacts of drought on oaks at urban and forest sites. Urban For. Urban Green. 2013, 12, 597–605. [Google Scholar] [CrossRef]
- Leuzinger, S.; Vogt, R.; Körner, C. Tree surface temperature in an urban environment. Agr. For. Meteorol. 2010, 150, 56–62. [Google Scholar] [CrossRef]
- Mueller, E.C.; Day, T.A. The effect of urban ground cover on microclimate, growth and leaf gas exchange of oleander in Phoenix, Arizona. Int. J. Biometeorol. 2005, 49, 244–255. [Google Scholar] [CrossRef] [PubMed]
- Nowak, D.J.; Crane, D.E. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- Bolund, P.; Hunhammar, S. Ecosystem services in urban areas. Ecol. Econ. 1999, 29, 293–301. [Google Scholar] [CrossRef]
- Nowak, D.J.; Hirabayashi, S.; Bodine, A.; Hoehn, R. Modeled PM2.5 removal by trees in ten US cities and associated health effects. Environ. Pollut. 2013, 176, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Dimoudi, A.; Nikolopoulou, M. Vegetation in the urban environment: Microclimatic analysis and benefits. Energy Build. 2003, 35, 69–76. [Google Scholar] [CrossRef]
- Dobbs, C.; Kendal, D.; Nitschke, C.R. Multiple ecosystem services and disservices of the urban forest establishing their connections with landscape structure and sociodemographics. Ecol. Indic. 2014, 43, 44–55. [Google Scholar] [CrossRef]
- Dobbs, C.; Escobedo, F.J.; Zipperer, W.C. A framework for developing urban forest ecosystem services and goods indicators. Landsc. Urban Plan. 2011, 99, 196–206. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. A new approach to modeling tree rainfall interception. J. Geophys. Res. 2000, 105, 29–173. [Google Scholar] [CrossRef]
- Xiao, Q.; McPherson, E.G.; Ustin, S.L.; Grismer, M.E.; Simpson, J.R. Winter rainfall interception by two mature open-grown trees in Davis, California. Hydrol. Process. 2000, 14, 763–784. [Google Scholar] [CrossRef]
- Tyrväinen, L.; Pauleit, S.; Seeland, K.; Vries, S. Benefits and Uses of Urban Forests and Trees. In Urban Forests and Trees: A Reference Book; Konijnendijk, C., Nilsson, K., Randrup, T., Schipperijn, J., Eds.; Springer Berlin Heidelberg: Berlin, Germany, 2005; pp. 81–114. [Google Scholar]
- Fahey, R.T.; Bialecki, M.B.; Carter, D.R. Tree Growth and Resilience to Extreme Drought Across an Urban Land-use Gradient. Arboric. Urban For. 2013, 39, 279–285. [Google Scholar]
- Iakovoglou, V.; Thompson, J.; Burras, L.; Kipper, R. Factors related to tree growth across urban-rural gradients in the Midwest, USA. Urban Ecosyst. 2001, 5, 71–85. [Google Scholar] [CrossRef]
- Nowak, D.J.; Kuroda, M.; Crane, D.E. Tree mortality rates and tree population projections in Baltimore, Maryland, USA. Urban For. Urban Green. 2004, 2, 139–147. [Google Scholar] [CrossRef]
- Iakovoglou, V.; Thompson, J.; Burras, L. Characteristics of trees according to community population level and by land use in the U.S. Midwest. J. Arboric. 2002, 28, 59–69. [Google Scholar]
- Whitlow, T.H.; Bassuk, N.L. Trees in difficult sites. J. Arboric. 1986, 13, 10–17. [Google Scholar]
- Day, S.D.; Bassuk, N.L.; van Es, H. Effects of four compaction remediation methods for landscape trees on soil aeration, mechanical impedance and tree establishment. J. Arboric. 1995, 22, 144–150. [Google Scholar]
- Petersen, A.; Eckstein, D. Roadside trees in Hamburg-their present situation of environmental stress and their future chance for recovery. Arboric. J. 1988, 12, 109–117. [Google Scholar] [CrossRef]
- Beatty, R.A.; Heckman, C.T. Survey of urban tree programs in the United States. Urban Ecol. 1981, 5, 81–102. [Google Scholar] [CrossRef]
- Rhoades, R.W.; Stipes, R.J. Growth of trees on Virgina Tech campus in response to various factors. J. Arboric. 1999, 25, 211–217. [Google Scholar]
- IPCC. Climate Change 2007: The Physical Science Basis. In Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Kjelgren, R.K.; Clark, J.R. Microclimates and Tree Growth in Tree Urban Spaces. J. Environ. Hortic. 1992, 10, 139–145. [Google Scholar]
- Pretzsch, H.; Matthew, C.; Dieler, J. Allometry of Tree Crown Structure. Relevance for Space Occupation at the Individual Plant Level. In Growth and Defence in Plants; Matyssek, R.E.A., Ed.; Springer Verlag: Berlin, Germany, 2012. [Google Scholar]
- Rötzer, T.; Seifert, T.; Gayler, S.; Priesack, E.; Pretzsch, H. Effects of Stress and Defence Allocationon Tree Growth: Simulation Results at the Individual and Stand Level. In Growth and Defence in Plants, Ecological Studies; Al, R.M.E., Ed.; Springer-Verlag: Berlin, Germany, 2012; Volume 220, pp. 401–432. [Google Scholar]
- Pretzsch, H.; Dieler, J. The dependency of the size-growth relationship of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica [L.]) in forest stands on long-term size conditions, drought events, and ozone stress. Trees 2011, 25, 355–369. [Google Scholar] [CrossRef]
- Pretzsch, H.; Schütze, G.; Uhl, E. Resistance of European tree species to drought stress in mixed versus pure forests: Evidence of stress release by inter-specific faciliation. Plant Biol. 2013, 15, 483–495. [Google Scholar] [CrossRef] [PubMed]
- McDowell, N.; Pockman, W.T.; Allen, C.D.; Breshears, D.D.; Cobb, N.; Kolb, T.; Plaut, J.; Sperry, J.; West, A.; Williams, D.G.; et al. Mechanisms of plant survival and mortality during drought: Why do some plants survive while others succumb to drought? New Phytol. 2008, 178, 719–739. [Google Scholar] [CrossRef] [PubMed]
- Rais, A.; van de Kuilen, J.-W.G.; Pretzsch, H. Growth reaction patterns of tree height, diameter, and volume of Douglas-fir (Pseudotsuga menziesii [Mirb.] Franco) under acute drought stress in Southern Germany. Eur. J. For. Res. 2014, 133, 1043–1056. [Google Scholar] [CrossRef]
- Ryan, M.G.; Binkley, D.; Fownes, J.H. Age-Related Decline in Forest Productivity: Pattern and Process. Adv. Ecol. Res. 1997, 27, 213–262. [Google Scholar]
- Bartens, J.; Grissino-Mayer, H.D.; Day, S.D.; Wiseman, P.E. Evaluating the potential for dendrochronological analysis of live oak (Quercus virginiana Mill.) from the urban and rural environment—An explorative study. Dendrochronologia 2012, 30, 15–21. [Google Scholar] [CrossRef]
- Speer, J.H. Fundamentals of Tree-Ring Research; The University of Arizona Press: Tucson, AZ, USA, 2012. [Google Scholar]
- Cavin, L.; Mountford, E.P.; Peterken, G.F.; Jump, A.S. Extreme drought alters competitive dominance within and between tree species in a mixed forest stand. Funct. Ecol. 2013, 27, 1424–1435. [Google Scholar] [CrossRef]
- Orwig, D.A.; Abrams, D.A. Variation in radial growth responses to drought among species, site, and canopy strata. Trees 1997, 11, 474–484. [Google Scholar] [CrossRef]
- Rybníček, M.; Čermák, P.; Kolář, T.; Žid, T. Growth responses of Norway spruce (Picea abies (L.) Karst.) to the climate in the south-eastern part of the Českomoravská Upland (Czech Republic). Geochronometria 2012, 39, 149–157. [Google Scholar]
- Gillner, S.; Bräuning, A.; Roloff, A. Dendrochronological analysis of urban trees: Climatic response and impact of drought on frequently used tree species. Trees 2014, 28, 1079–1093. [Google Scholar] [CrossRef]
- He, X.; Chen, Z.; Chen, W.; Shao, X.; He, H.; Sun, Y. Solar activity, global surface air temperature anomaly and pacific decadal oscillation recorded in urban tree rings. Ann. For. Sci. 2007, 64, 743–756. [Google Scholar] [CrossRef]
- DWD. Deutscher Wetterdienst. Available online: http://www.dwd.de.
- Pauleit, S.; Jones, N.; Garcia-Marin, G.; Garcia-Valdecantos, J.-L.; Rivière, L.M.; Vidal-Beaudet, L.; Bodson, M.; Randrup, T.B. Tree establishment practice in towns and cities—Results from a European survey. Urban For. Urban Green. 2002, 1, 83–96. [Google Scholar] [CrossRef]
- Radoglou, K.; Dobrowolska, D.; Spyroglou, G.; Nicolescu, V.-N. A review on the ecology and silviculture of limes (Tilia cordata Mill., Tilia platyphyllos Scop. and Tilia tormentosa Moench.) in Europe. Die Bodenkult. 2009, 60, 9–19. [Google Scholar]
- Roloff, A.; Bonn, S.; Gillner, S. Klimawandel und Baumartenwahl in der Stadt—Entscheidungsfindung mit der Klima-Arten-Matrix (KLAM). Available online: http://www.frankfurt.de/sixcms/media.php/738/klam_stadt.pdf (accessed on 16 March 2016).
- Keresztesi, B. The Black Locust; Akadémiai Kiadó: Budapest, Hungary, 1988. [Google Scholar]
- Baker, F.S. A revised tolerance table. J. For. 1949, 47, 179–181. [Google Scholar]
- Niinemets, Ü.; Valladares, F. Tolerance to shade, drought, and waterlogging of temperate northern hemisphere trees and shrubs. Ecol. Monogr. 2006, 76, 521–547. [Google Scholar] [CrossRef]
- Moser, A.; Rötzer, T.; Pauleit, S.; Pretzsch, H. Structure and ecosystem services of small-leaved lime (Tilia cordata Mill.) and black locust (Robinia pseudoacacia L.) in urban environments. Urban For. Urban Green. 2015, 14, 1110–1121. [Google Scholar] [CrossRef]
- Matzarakis, A.; Rutz, F.; Mayer, H. Modelling radiation fluxes in simple and complex environments—Application of the RayMan model. Int. J. Biometeorol. 2007, 51, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Yamashita, S.; Sekine, K.; Shoda, M.; Yamashita, K.; Hara, Y. On relationships between heat island and sky view factor in the cities of Tama River Basin, Japan. Atmos. Environ. 1986, 20, 681–686. [Google Scholar] [CrossRef]
- Rinn, F. TSAP Reference Manual. Available online: http://www.rinntech.com/.
- TSAP-Win: Time Series Analysis and Presentation for Dendrochronology and Related Applications, version 0.55; Rinn Tech.: Heidelberg, Germany, 2010.
- R, A language and environment for statistical computing; R Core Team: Vienna, Austria, 2014.
- Bunn, A.; Korpela, M.; Biondi, F.; Campelo, F.; Mérian, P.; Qeadan, F.; Zang, C.; Buras, A.; Cecile, J.; Mudelsee, M.; et al. (Eds.) Package “dplR”, version 1.6.3; Dendrochronology Program Library in R. 2015.
- COFECHA and ARSTAN, Chronology Series VI. In Tree-Ring Chronologies of Western North America: California, Eastern Oregon and Northern Great Basin with Procedures Used in the Chronology Development Work Including Users Manuals; Laboratory of Tree-Ring Research: University of Arizona, Tuscon, AZ, USA, 1986.
- Cook, E.R.; Holmes, R.L. User manual for computer program ARSTAN. In Tree-Ring Chronologies of Western North America: California, Eastern Oregon and Northern Great Basi; Holmes, R.L., Adams, R.K., Fritts, H.C., Eds.; University of Arizona: Tucson, AZ, USA, 1986; Volume 6, pp. 50–57. [Google Scholar]
- Roloff, A. Baumkronen. Verständnis Und Praktische Bedeutung Eines Komplexen Naturphänomens; Ulmer: Stuttgart, Germany, 2001. [Google Scholar]
- Jucker, T.; Bouriaud, O.; Avacaritei, D.; Coomes, D.A. Stabilizing effects of diversity on aboveground wood production in forest ecosystems: linking patterns and processes. Ecol. Lett. 2014, 17, 1560–1569. [Google Scholar] [CrossRef] [PubMed]
- Fritts, H.C. Tree Rings and Climate; Academic Press: London, UK, 1976. [Google Scholar]
- Lukaszkiewicz, J.; Kosmala, M. Determining the Age of Streetside Trees with Diameter at Breast Height-based Multifactorial Model. Arboric. Urban For. 2008, 34, 137–143. [Google Scholar]
- Dwyer, J.F. How old is that tree? Illinois Trees 2009, 24, 13. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Defining and using reference evapotranspiration. J. Irrig. Drain. Eng. 1994, 120, 1132–1139. [Google Scholar] [CrossRef]
- Quinoa: Improvement and Sustainable Production; Wiley-Blackwell: Oxford, UK, 2015.
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team (Eds.) Nlme: Linear and Nonlinear Mixed Effects Models, 2015.
- Lough, J.M.; Fritts, H.C. An assessment of the possible effects of volcanic eruptions on North American climate using tree-ring data, 1602 to 1900 A.D. Clim. Chang. 1987, 10, 219–239. [Google Scholar] [CrossRef]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the Average Value of Correlated Time Series, with Applications in Dendroclimatology and Hydrometeorology. J. Clim. Appl. Meteor. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Schweingruber, F.H. Tree Rings and Environment; Swiss Federal Institute for Forest, Snow and Landscape Research: Birmensdorf, Switzerland, 1996. [Google Scholar]
- Beck, W.; Müller, J. Impact of heat and drought on tree and stand vitality─Dendroecological methods and first results from level II-plots in southern Germany. Schr. Forstl. Fak. Univ. Gött. Niedersächs. Forstl. Versanst. 2006, 142, 120–127. [Google Scholar]
- George, J.P.; Schueler, S.; Karanitsch-Ackerl, S.; Mayer, K.; Klumpp, R.T.; Grabner, M. Inter- and intra-specific variation in drought sensitivity in Abies spec. and its relation to wood density and growth traits. Agr. For. Meteorol. 2015, 214–215, 430–443. [Google Scholar] [CrossRef]
- Juday, G.P.; Alix, C. Consistent negative temperature sensitivity and positive influence of precipitation on growth of floodplain Picea glauca in Interior Alaska. Can. J. For. Res. 2012, 42, 561–573. [Google Scholar] [CrossRef]
- Pretzsch, H.; Dieler, J.; Seifert, T.; Rötzer, T. Climate effects on productivity and resource-use efficiency of Norway spruce (Picea abies [L.] Karst.) and European beech (Fagus sylvatica [L.]) in stands with different spatial mixing patterns. Trees 2012, 26, 1343–1360. [Google Scholar] [CrossRef]
- Gillner, S. Stadtbäume im Klimawandel—Dendrochronologische und physiologische Untersuchungen zur Identifikation der Trockenstressempfindlichkeit häufig verwendeter Stadtbaumarten in Dresden. Ph.D. Thesis, Universität Dresden, Dresden, Germany, 2012. [Google Scholar]
- Monteith, J.L. Climate and the efficiency of crop production in Britain. Philos. Trans. R. Soc. B 1977, 281, 277–294. [Google Scholar] [CrossRef]
- Walters, M.B.; Reich, P.B. Are shade tolerance, survival, and growth linked? Low light and nitrogen effects on hardwood seedlings. Ecology 1996, 77, 841–853. [Google Scholar] [CrossRef]
- Hasenauer, H. Dimensional relationship of open-grown trees in Austria. For. Ecol. Manag. 1997, 96, 197–206. [Google Scholar] [CrossRef]
- Uhl, E.; Metzger, H.G.; Seifert, T. Dimension und Wachstum von Solitären Buchen und Eichen, Sektion Ertragskunde, Jahrestagung, Staufen; Deutscher Verband Forstlicher Forschungsanstalten: Staufen, Germany, 2006. [Google Scholar]
- Río, M.D.; Schütze, G.; Pretzsch, H. Temporal variation of competition and facilitation in mixed species forests in Central Europe. Plant Biol. 2014, 16, 166–176. [Google Scholar] [PubMed]
- Pretzsch, H.; Rötzer, T.; Matyssek, R.; Grams, T.E.E.; Häberle, K.-H.; Pritsch, K.; Kerner, R.; Munch, J.-C. Mixed Norway spruce (Picea abies [L.] Karst) and European beech (Fagus sylvatica [L.]) stands under drought: From reaction pattern to mechanism. Trees 2014, 28, 1305–1321. [Google Scholar] [CrossRef]
- Peters, E.B.; McFadden, J.P.; Montgomery, R.A. Biological and environmental controls on tree transpiration in a suburban landscape. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
- Rahman, M.A.; Armson, D.; Ennos, A.R. A comparison of the growth and cooling effectiveness of five commonly planted urban tree species. Urban Ecosyst. 2015, 18, 371–389. [Google Scholar] [CrossRef]
- Rahman, M.A.; Smith, J.G.; Stringer, P.; Ennos, A.R. Effect of rooting conditions on the growth and cooling ability of Pyrus calleryana. Urban For. Urban Green. 2011, 10, 185–192. [Google Scholar] [CrossRef]
- Zaharah, S.S.; Razi, I.M. Growth, stomata aperture, biochemical changes and branch anatomy in mango (Mangifera indica) cv. Chokanan in response to root restriction and water stress. Sci. Hortic. 2009, 123, 58–67. [Google Scholar] [CrossRef]
- Prügl, B.J. Vegetationstechniken für Innerörtliche Baumstandorte; Bodeninstitut Johannes Prügl: Hallertau, Germany, 2016. [Google Scholar]
- Stadt Würzburg. STELLPLATZSATZUNG der Stadt Würzburg (SPS). Stellplatzsatzung vom 25. März 2014 (MP und VBl Nr. 73/2014 vom 28. März 2014)
| n | dbh min [cm] | dbh Avg [cm] | dbh Max [cm] | Avg Tree Height [m] | Avg OSA [m²] | Avg Age [a] | Growth Rate ± SD [mm·Year−1] | Mean Sensitivity | EPS 1 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Robinia pseudoacacia | ||||||||||
| München | 30 | 14.0 | 44.5 | 101.9 | 15.7 | 102.39 | 44.3 | 3.9 ± 1.7 | 0.33 | 0.90 |
| Würzburg | 32 | 11.0 | 44.3 | 102.2 | 15.1 | 109.55 | 44.1 | 4.0 ± 1.9 | 0.34 | 0.85 |
| Tilia cordata | ||||||||||
| München | 37 | 12.0 | 34.2 | 86.7 | 13.1 | 146.48 | 42.6 | 3.2 ± 1.6 | 0.38 | 0.89 |
| Würzburg | 30 | 14.0 | 33.1 | 71.5 | 12.5 | 123.34 | 44.0 | 2.9 ± 1.6 | 0.39 | 0.89 |
| Response Variable | Explanatory Variable | n | a ± SE | b ± SE | r2 | RSE | F | p |
|---|---|---|---|---|---|---|---|---|
| ln(Stability) | ln(Sensitivity) | 128 | 0.14 ± 0.09 | −0.54 ± 0.08 | 0.25 | 0.28 | 42.83 | <0.001 |
| Stability | Dbh | 128 | 1.68 ± 0.15 | 0.01 ± 0.003 | 0.09 | 0.77 | 12.85 | <0.001 |
| Stability | Age | 128 | 1.74 ± 0.16 | 0.01 ± 0.003 | 0.06 | 0.78 | 7.77 | 0.006 |
| Value ± SE | p | |
|---|---|---|
| Intercept | 8.46 ± 1.74 | <0.001 |
| Dbh | −0.27 ± 0.03 | <0.001 |
| Canopy openness | 0.10 ± 0.03 | <0.001 |
| OSA | −0.02 ± 0.01 | 0.03 |
| Species | −0.33 ± 1.90 | 0.86 |
| Water supply (SPEI) | 0.18 ± 0.04 | <0.001 |
| Dbh:OSA | 0.001 ± 2.1 × 10−4 | <0.001 |
| Canopy openness:Species | 0.09 ± 0.04 | 0.03 |
| SD Intercept | 5.72 | - |
| SD Dbh | 0.19 | - |
| ε | 1.18 | - |
| Value ± SE | p | |
|---|---|---|
| Intercept | 0.82 ± 0.04 | <0.001 |
| Water supply (SPEI) | 0.03 ± 0.01 | <0.001 |
| City | −0.01 ± 0.01 | 0.67 |
| Species | −0.05 ± 0.01 | <0.001 |
| Dbh | −0.001 ± 7.4 × 10−4 | 0.27 |
| Canopy openness | −0.002 ± 7.4 × 10−4 | 0.03 |
| Water supply (SPEI): City | −0.03 ± 0.01 | 0.009 |
| Canopy openness: Dbh | 0.0001 ± 1.7 × 10−5 | 0.002 |
| SD Intercept | 0.09 | - |
| SD Dbh | 0.001 | - |
| ε | 0.17 | - |
| Value ± SE | p | |
|---|---|---|
| Intercept | 1.24 ± 0.04 | <0.001 |
| Canopy openness | 0.002 ± 8.9 × 10−4 | 0.01 |
| Species | 0.05 ± 0.02 | 0.001 |
| Dbh | 0.001 ± 7.5 × 10−4 | 0.30 |
| Canopy openness: Dbh | −0.0001 ± 1.8 × 10−5 | 0.003 |
| SD Intercept | 0.11 | - |
| SD Dbh | 0.001 | - |
| ε | 0.22 | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moser, A.; Rötzer, T.; Pauleit, S.; Pretzsch, H. The Urban Environment Can Modify Drought Stress of Small-Leaved Lime (Tilia cordata Mill.) and Black Locust (Robinia pseudoacacia L.). Forests 2016, 7, 71. https://doi.org/10.3390/f7030071
Moser A, Rötzer T, Pauleit S, Pretzsch H. The Urban Environment Can Modify Drought Stress of Small-Leaved Lime (Tilia cordata Mill.) and Black Locust (Robinia pseudoacacia L.). Forests. 2016; 7(3):71. https://doi.org/10.3390/f7030071
Chicago/Turabian StyleMoser, Astrid, Thomas Rötzer, Stephan Pauleit, and Hans Pretzsch. 2016. "The Urban Environment Can Modify Drought Stress of Small-Leaved Lime (Tilia cordata Mill.) and Black Locust (Robinia pseudoacacia L.)" Forests 7, no. 3: 71. https://doi.org/10.3390/f7030071
APA StyleMoser, A., Rötzer, T., Pauleit, S., & Pretzsch, H. (2016). The Urban Environment Can Modify Drought Stress of Small-Leaved Lime (Tilia cordata Mill.) and Black Locust (Robinia pseudoacacia L.). Forests, 7(3), 71. https://doi.org/10.3390/f7030071






