Abstract
Understanding the distribution of forest aboveground biomass (AGB) is pivotal for carbon monitoring. Field-based inventorying is time-consuming and costly for large-area AGB estimations. The integration of multimodal remote sensing (RS) observations with single-year, field-based forest inventory analysis (FIA) data has the potential to improve the efficiency of large-scale AGB modeling and carbon monitoring initiatives. Our main objective was to systematically compare the AGB prediction accuracies of machine learning algorithms (e.g., random forest (RF) and support vector machine (SVM)) with those of conventional statistical methods (e.g., multiple linear regression (MLR)) using multimodal RS variables as predictors. We implemented a method combining AGB estimates of actual FIA subplot locations with airborne LiDAR, National Agriculture Imagery Program (NAIP) aerial imagery, and Sentinel-2 satellite images for model training, validation, and testing. The hyperparameter-tuned RF model produced a root mean square error (RMSE) of 27.19 Mgha−1 and an R2 of 0.41, which outperformed the evaluation metrics of SVM and MLR models. Among the 28 most important explanatory variables used to build the best RF model, 68% of variables were derived from the LiDAR height data. The hyperparameter-tuned linear SVM model exhibited an R2 of 0.10 and an RMSE of 32.17 Mgha−1. Additionally, we developed an MLR using eight explanatory variables, which yielded an RMSE of 22.59 Mgha−1 and an R2 of 0.22. The linear ensemble model, which was developed using the predictions of all three models, yielded an R2 of 0.79. Our results suggested that more field data are required to better generalize the ensemble model. Overall, our findings highlight the importance of variable selection methods, the hyperparameter tuning of ML algorithms, and the integration of multimodal RS data in improving large-area AGB prediction models.
1. Introduction
Forests play a fundamental role in the carbon cycle by serving as a significant carbon sink. Globally, forests sequester approximately 2.4 ± 0.4 Pg of carbon per year, which is equivalent to nearly one-third of the annual carbon emissions associated with fossil fuel usage [1]. In the United States, forests and associated harvested wood products offset about 10%–15% of nationwide CO2 emissions per annum [2]. Trees store carbon in belowground and aboveground components as biomass [3,4,5]. The accurate estimation of AGB is essential for effective forest management, biodiversity conservation, and climate change mitigation efforts [6,7]. Forest biomass estimates are based on both destructive and non-destructive methods [8]. Non-destructive methods use tree structural measurements, such as diameter at breast height (dbh) and tree height, that are extensively utilized in the forest management sector due to their efficiency and feasibility for large-area estimation [9,10]. Often, tree dendrometry data are combined with allometric equations [11,12] to estimate aboveground biomass (AGB) and forest carbon from sample plots, such as those from the US Forest Service (USFS)’s Forest Inventory and Analysis (FIA) network [13,14,15]. Hudak et al. [15] built a carbon monitoring system utilizing 3805 field-measured plots across the northwestern USA. Tang et al. [16] published a multi-state-level forest carbon map with an R2 of 0.38 that utilized 1986 FIA subplot locations with Light Detection and Ranging (LiDAR) and National Agriculture Imagery Program (NAIP) data. Sheridan et al. [14] used 177 FIA plots that resulted in 708 subplots. Johnson et al. [17] used FIA and non-forest inventory (NFI) data and FIA-like plots to estimate AGB with an R2 of 0.49.
Remote sensing (RS) provides a promising mechanism to assess AGB or carbon content in large-area estimations when coupled with field AGB estimations [3,15,18]. Often, FIA plot-level AGB values were used as the ground truth data. RS variables, such as LiDAR-derived metrics (e.g., height percentiles, height bins, and density), were incorporated as explanatory variables in prediction models [3,14,15,16,17,18]. Integrating the FIA data with the active and passive RS data, such as LiDAR [14,15,16], satellite (e.g., Landsat, Sentinel-2), and aerial imagery (e.g., National Agriculture Imagery Program—NAIP), can reduce the uncertainty of large-area AGB predictions [19]. RS observations provide a comprehensive characterization of forest structure, vertical profile, and forest health via LiDAR-derived height metrics and imagery-derived vegetation indices [17,20,21,22,23]. Remotely acquired data reduce the need for extensive fieldwork, manpower, and associated logistical complications in challenging landscape monitoring [24].
A variety of linear regression and machine learning (ML) algorithms have been developed and tested to predict AGB from RS data [8,25]. Sheridan et al. [14] and Li et al. [26] employed linear regression models, linear dummy variable models, and linear mixed-effects models. Shrestha [27] suggested that the utilization of LiDAR- and RS-derived variables requires treatments for multicollinearity to reach the assumptions of linear regression models. The variance inflation factor (VIF) is a common technique to reduce the multicollinearity of a set of predictor variables [28,29]. Two popular techniques of selecting variables in MLR models are stepwise regression and the best subset method [30]. In the realm of MLRs, assessing diagnostic plots and verifying underlying assumptions, such as linearity, normality, homoscedasticity, and independence of errors, are imperative to warrant the validity of MLR results [31]. However, the use of variable selection techniques can sometimes reduce model performance as influential variables might be excluded during the modeling process due to their multicollinearity. In contrast, recent studies indicate that ML optimization methods are more robust in handling multicollinearity compared to traditional statistical estimators [32].
ML algorithms have shown remarkable success in predictive analytics tasks across multiple domains, including AGB modeling efforts [8,25]. By design, ML models can utilize variables with multicollinearity and spatial autocorrelation, which are common challenges when using RS variables with the FIA subplot data [8]. One of the most popular ML approaches utilized in AGB research is the random forest (RF) algorithm due to its robustness and success in an array of domain applications [17,26]. Adaptive random forest (ARF) includes adaptive operators coupled with drift detectors, such as leveraging bagging [33], which can handle various types of variable drifts without requiring complex optimizations for different datasets [34]. In addition to RF models, Guo et al. [35] and Sivasankar et al. [36] incorporated a support vector machine (SVM), which utilizes a high-dimensional feature space. The SVM can reduce the generalized error and the common kernel functions, which effectively handle non-linear AGB distributions [36]. Johnson et al. [8] and Li et al. [37] proposed a novel method to develop linear stacked ensemble models to predict AGB, utilizing both ML and statistical models. Generally, ensemble models including RF and Gradient Boosting can unravel more localized variables and patterns [8,38], showing better performance in response prediction compared to their independent model counterparts [39].
In this study, we systematically examined potential strategies for integrating RS observations with the single-year FIA field data using ML and MLR algorithms, then combined ML and MLR approaches within an ensemble modeling framework. The central objective was to develop and compare the accuracy of ML and MLR models to estimate forest AGB across the state of Connecticut, USA. Our research includes an in-depth analysis of explanatory variable selection and hyperparameter tunning of ML models based on limited training datasets. We aimed to combine the accuracy of each modeling approach via a stacked linear ensemble modeling technique. In our analysis, we attempted to maximize the use of single-year FIA data to avoid and reduce the disadvantages of having limited access to the FIA data due to data privacy protocols of US Forest Service (USFS) or when the model needs to be run on off-site computers (i.e., USFS computing facilities). We aimed to build an open-access tool that multiple users can utilize to estimate AGB at the 30 m or 15 m level without direct access to the actual FIA plot locations.
2. Data and Method
2.1. Study Area
This study was conducted across the forested area of the state of Connecticut (41.6° N, 72.7° W), located in the northeastern United States (Figure 1). The forests of Connecticut are largely classified as oak-hickory forests but exhibit a diverse tree species composition. Nearly 58% of Connecticut’s land area falls under the FIA definition of forested areas. Connecticut had around 1.8 million acres of forest land, with 46% of this forest land categorized as family-owned in 2016 [40]. Connecticut has a statewide LiDAR coverage in 2016 [41], which facilitates the integration of RS data for large-area AGB modeling. FIA plot data are available for the region. The study area comprises mixed-deciduous, coniferous, and mixed forest stands, providing a relatively heterogeneous ecological space for AGB estimation with a small training dataset [42]. This diversity allows for robust testing of our models, even under the constraints of limited data availability.
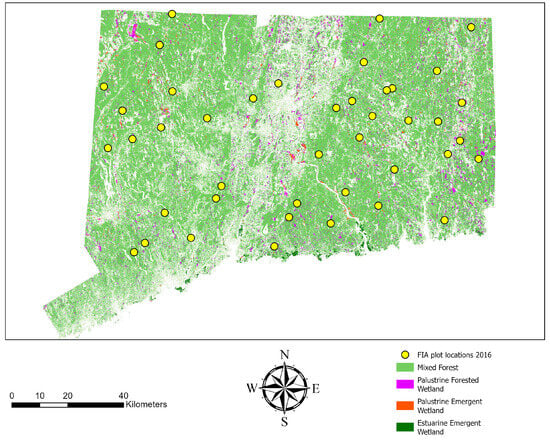
Figure 1.
The forested landcover derived from the 2016 Connecticut 1 m landcover map overlain with 2016 FIA plot locations used in this study.
2.2. Data
2.2.1. Forest Inventory and Analysis (FIA) Data
The Northern Research Station of USFS-FIA program is responsible for sampling a statewide network of field plots across Connecticut (CT). Placement of FIA plots follows a stratified random sampling technique, and each plot consists of a cluster of four 7.32 m (24ft) radius subplots. The original FIA plot locations in CT included 320 plots in total but only 10%–14% of plot locations are measured and reported annually [43]. We utilized 42 FIA plots (Figure 1) measured in 2016 to align with 2016 statewide Light Detection and Ranging (LiDAR) mission [40]. The northeast FIA program (NE-FIA) used Rockwell Precision Lightweight Global Positioning System (GPS) receivers; therefore, the plot locations were established with an average geolocation error of 8 m and a standard deviation of 2 m [44].
2.2.2. Aboveground Biomass Calculation
We used the true FIA plot locations (168 subplots), referring to the original geolocation readings recorded in the FIA database, which were not swapped or fuzzed due to privacy protection concerns. In our research, we were not permitted to directly access true FIA plot coordinates or run models directly on our computers due to the non-disclosure policy of private FIA plot coordinates. Therefore, we provided all codes and extracted rasters of 2.4 km (1.5 miles) buffer of public FIA locations and sent those to the FIA scientists, who executed the codes on USFS computers on our behalf. The FIA component ratio method (CRM) was used to compute AGB and recorded in megagrams per hectare (Mgha−1) for each subplot location [43]. We only considered the FIA-measured dendrometry data for the trees with ≥12 cm dbh for AGB calculations [17]. We excluded subplot locations in non-forested areas [45,46]. Outliers caused by FIA geolocation errors were removed by checking deviations from the expected biomass ranges of forested stands [17]. We removed locations where field biomass estimates were <50 Mgha−1, but LiDAR heights >30 m. Also, we excluded plots with LiDAR heights greater than 10 m, but a field biomass estimate of zero [45]. This plummeted the initial sample size from 168 subplots to 142 subplots for further analysis.
2.2.3. Remote Sensing Variables
We derived an array of explanatory variables (Table 1) from the 2016 leaf-off aerial LiDAR, Sentinel-2 (https://dataspace.copernicus.eu, accessed on 1 August 2022) satellite imagery, and 2016 leaf-on NAIP aerial images for the selected 142 FIA subplots. The 2016 LiDAR dataset was acquired at a 2 points/m2 point density [41]. We employed Sentinel-2 satellite images from spring 2016 (a cloud coverage of ≤10%) to coincide with the LiDAR data collection period. We derived a set of 65 raster layers within a 2.4 km (1.5 miles) buffer around the publicly available FIA plot locations. FIA scientists then masked and extracted the data corresponding to the true subplot locations to generate the explanatory variable pool of 65 predictors. A temporal composite approach was applied to obtain cloud-free imagery if the buffer zone was concealed by clouds. When level 2 images were heavily covered by clouds, we performed atmospheric correction using Sen2Cor v2.9 to convert cloud-free Sentinel-2 Level 1 products into bottom-of-atmosphere (BOA) reflectance [47]. Vegetation indices (VIs) and spectral band responses (Table 1) were then derived from the surface reflectance of the selected Sentinel-2 and NAIP images [48]. LiDAR and imagery-based secondary rasters were derived using ArcGIS Pro 3.1.2, FUSION/LDV processing software (4.40), R studio (4.3.0), and SNAP (9.0.0) software. We conducted variable importance analysis for explanatory variables (Table 1) using different selection criteria to identify the most influential predictors for each candidate model. The RF variable importance was assessed using the IncNodePurity metric [49]. For the SVM model, we applied the recursive feature elimination method [50]. We evaluated predictors using both best subset selection and stepwise regression approaches [51,52,53] for MLR models.

Table 1.
Full set of explanatory variables, which were the inputs of the ML model training and testing. For the RF regression, Group-1 consisted of sections 01–03 variables. Group-2 consisted of section 02 variables only and Group-3 consisted of section 03 variables. For other candidate models, only variable 01–65 was considered [54].
2.3. Model Training and Testing
The selected explanatory variables and corresponding AGB (response variable) were used as the inputs to train and test the RF, the SVM [35], and the MLR [14] models. We employed an 80:20 split strategy for training and testing [8]. The initial regression (MLR) and ML (SVM, RF) models were validated and hyperparameter-tuned using the K-fold cross-validation method. The multiple linear regression ensemble was validated using leave-one-out cross-validation (LOOCV) method due to a lack of sample plots [8,69] (Figure 2).
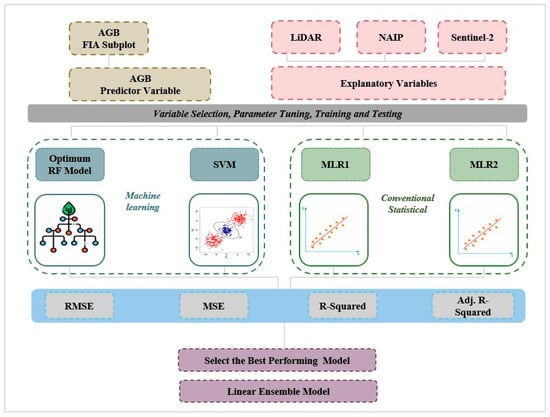
Figure 2.
Research workflow diagram.
2.3.1. Random Forest Regression
We used the “randomForest” package in the R environment, version (4.3.0), to train RF models [22,70]. We grouped explanatory variables as follows: (i) Group-1: all 65 variables combined; (ii) Group-2: LiDAR metrics; and (iii) Group-3: image metrics. This categorization allowed us to measure the contribution of different RS data inputs to AGB modeling [54]. We built three RF models including default parameters, only tuning two key parameters, i.e., Mtry (number of independent variables per split) and Ntree (number of regression trees), and a grid tuned RF model per group. The hyperparameter grid with a sequence of values was employed for tuning the RF model with 5-fold cross-validation [10,17]. We reduced the dimensionality of the variables by selecting the most important variables with respect to the increase in node purity (IncNodePurity) values to rank the colinear variables [49,71]. We trained a sequence of RF models based on IncNodePurity of each variable. This step helped to reduce the number multicollinear variables in RF variable selection [72]. The number of variables in the RF model with the highest mean cross-validation R2 was taken for tuning and testing the final model [10,22,48]. The grid search method was incorporated to tune the RF hyperparameters with 5-fold cross-validation [73]. We tuned ntree, mtry, max_depth, min_sample_leaf, and min_sample_split [54] to identify the best hyperparameter RF models (Table 2). These approaches enhanced the predictive performance of the RF model and mitigated issues related to multicollinearity and overfitting [10]. Beyond bagging, our RF implementation utilized hyperparameter tuning through grid search and incorporated variable selection, facilitating the construction of an adaptive random forest (ARF) model.

Table 2.
Hyperparameter sequence used for tuning RF models.
2.3.2. Support Vector Machine
We used the SVM as the second candidate ML algorithm to estimate forest AGB [35,74]. In the SVM regression, the initial step involves mapping input features onto an m-dimensional feature space through a predetermined mapping function. Subsequently, a linear model is established within this feature space [35]. The kernels of linear, polynomial, and radial basis functions (RBFs) were compared and evaluated to identify the best SVM kernel regression [75]. A two-step grid search technique (penalty parameter C, precision parameter ε, and kernel parameters such as γ for the RBF kernel function and d for the polynomial kernel) and a 5-fold cross-validation were utilized to optimize the SVM hyperparameters [35,75] within the model training process.
2.3.3. Recursive Feature Elimination
We used recursive feature elimination (RFE), which is a widely used feature selection technique in SVM regression [50]. The RFE method selects the most important features from a dataset by repeatedly training a model on all the features and identifying the least important features based on their coefficients or performance metrics [50,76]. In this study, the explanatory variables for SVM models were compared using the root mean square error (RMSE/Mgha−1) of 10-fold cross-validation results. At each iteration, the least important features were removed till the most suitable subset of variables for SVM were entered into the tuned SVM model with the most suitable kernel to attain the highest possible accuracy [74,76].
2.3.4. Multiple Linear Regression
Multiple linear regression (MLR) is one of the most widely used statistical methods in forest AGB prediction tasks [14,29]. We utilized 65 continuous explanatory variables (Table 1) to develop MLR models [77]. We constructed diagnostic plots and outlier fitting using the “lm” function in the R software (4.3.0) to check the compatibility with the initial MLR assumption (linearity of xy variables, normality, heteroscedasticity of residuals, and independence of xy pairs) [78]. We executed two methods to build the MLR equations: (i) stepwise regression and (ii) best subset regression. The first feature selection approach for MLR was stepwise regression (SR) via both eliminating and adding variables to the algorithm until one of the iterations received the lowest AIC values [51,52,53]. An exhaustive selection algorithm was employed to build the best subset model using the “regsubsets” and “bestglm()” functions [79,80] in the “leaps” package in the R environment [81].
2.3.5. Treatments for Multicollinearity and Selecting Variables for MLR
We conducted a variance inflation factor (VIF) analysis to test the degree of collinearity among the selected variables [28]. VIF is a relative measure, and we considered 10 as the VIF threshold in our study [82,83]. A stepwise regression (SR) based on the Akaike information criterion (AIC) [14,84] and the best subset method [30] were employed to further understand the best variable combinations for the MLR models. We used variables, which had a VIF of <10 to build the MLR models. The filtered variables were then used to build a stepwise regression model [85,86] and the best subset model [87,88]. In our research, the SR model with the lowest AIC value was compared with the best subset MLR model to identify the optimum regression equation in AGB prediction.
2.3.6. Comparison of Model Performance
We compared the optimal RF, SVM, and MLR models to identify which model performs the best in AGB estimation [89]. A k-fold cross-validation approach was employed to validate all algorithms. Subsequently, the calibrated model was tested using an independent 20% holdout dataset to obtain accuracy metrices [90]. This study utilized standard performance metrics to compare ML and MLR models [8,90], such as root mean square error (RMSE), mean square error (MSE), and coefficient of determination (R2), [8,14,50], as depicted in Equations (1)–(3):
where n is the number of FIA subplots in the training dataset, and is the predicted AGB value by each model. is the corresponding FIA-estimated AGB, and is the mean AGB from FIA field measurements. Moreover, the F-statistics and p-values were used to interpret the MLR results [77]. The accuracy metrics mentioned in Equations (1)–(3) were compared to understand the AGB predictabilities of the independent models and linear regression ensemble (MLRE). We conducted a multifactor analysis of variance (one-way ANOVA) to compare the significance of each model residual to understand the statistical significance of the selected optimal model with the rest of candidate models [78].
2.3.7. Building the Multiple Linear Regression Ensemble
We built our stacked ensemble model based on the three base learners (RF, SVM, and MLR), and each was evaluated on the same 20% held-out test dataset (n = 28). We used the linear regression ensemble and leave-one-out methods to reflect the model selection uncertainty. Also, the coefficients were identified through ordinary least squares regression [8,39]. According to Wolpert [38], this approach helps reduce the generalization error of base models. This approach follows standard ensemble modeling principles mentioned in Johnson et al. [8] (Equation (4)).
where β0–7 are coefficients of ordinary least squares regression, and RF, SVM, and MLR are the respective components of optimized model predictions. The RMSE, MSE, and R2 values of stacked ensemble method were compared with the same evaluation metrics of the optimized RF, SVM, and MLR resulting in four AGB prediction models at the end of our study. We conducted a one-way ANOVA comparison using the AGB predictions from each model regardless of the source of the data, focusing solely on statistical significance and the normality of the data distribution. The ensemble regression model was trained, either directly or indirectly, on the full dataset available to us at the time. However, to generalize the performance of the ensemble model at the state level, additional data that are independent from the training process of all four models will be necessary [8].
3. Results
3.1. Identification of Optimized Random Forest Regression
For the RF models, we identified three groups of variables based on the input RS variables: Group-1: all variables (including all the variables in sections 01–03 of Table 1); Group-2: exclusively LiDAR variables (only section 01 variables in Table 1); and Group-3: image-derived variables (variables under sections 02 and 03 of Table 1). We used the evaluation metrics to compare the model performance among default and tuned RF models in each group identified above. Out of 65 explanatory variables, 28 were identified as the most important in RF model performance. 95th percentile (P95th), 90th percentile (P90th), and Sentinel-2 SWIR band (sen_swir) were the 3 most important variables among the selected 28 variables. The full list of variables selected in optimized RF models are mentioned in Section S1. A total of 68% out of the 28 selected variables are LiDAR-derived, while 18% and 14% of the selected variables were derived from NAIP and Sentinel-2 rasters, respectively. The optimal RF model was identified from the Group-1 with an RMSE of 27.19 Mgha−1, an MSE of 739.46 (Mgha−1)2, and an R2 of 0.41.
3.2. Variable Selection and Support Vector Machine Model
We tasked RFE to reduce the complexity of the explanatory variables and to select the best subset of variables for SVM kernels with 10-fold cross-validation using outer resampling method (Figure 3). The optimum resampling performance was achieved for a variable subset size of 44 with an RMSE of 20.51 Mgha−1, an MAE of 16.69 Mgha−1, and an R2 of 0.25 (Figure 3). A total of 44 explanatory variables were selected by the RFE method based on RMSE. The top three variables selected from the RFE method were p90th, p95th, and sen_swir. The entire set of selected variables can be found in Section S1. The selected variables were then utilized to build three SVM models and compared accuracy metrices to select the best SVM out of the three models. According to the post-processing, the linear kernel function presented the best predictability for the data distribution. Therefore, we trained the SVM with tuned parameters of cost equal to 0.01, γ equal to 0.0154, and ε equal to 0.1, with 108 support vectors. The test accuracy metrics reported an MSE of 1034.59 (Mgha−1)2, an RMSE of 32.17 Mgha−1, an MAE of 22.36 Mgha−1, and an R2 of 0.10.
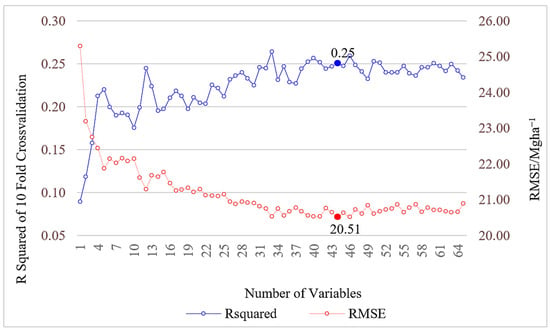
Figure 3.
Recursive feature elimination of outer sampling 10-fold cross-validation method. The X-axis depicts the number of explanatory variables. The Y-axis shows the change in R2 and RMSE of cross-validation.
3.3. Treating Multicollinearity of Explanatory Variables
We employed a correlation matrix to demonstrate the multicollinearity among 65 explanatory variables and obtained correlation coefficients (Section S2). Figure 4 shows a pairwise correlation heatmap for 65 variables based on the calculated correlation coefficients. Colors indicate positive (red) or inverse (green) correlations, and black frames indicate statistical significance after multiple testing. Parameters in the heatmap are ordered to form a clustering based on the similarity of correlation coefficient vectors.
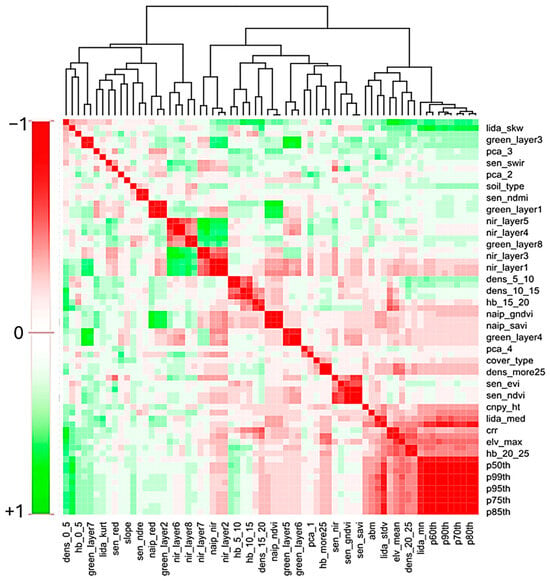
Figure 4.
Pairwise correlation heatmap for all remote sensing explanatory variables.
We employed a VIF analysis as a treatment for multicollinearity problems of our study. For the VIF analysis [82], a threshold of 10 was used to reduce the number of correlated variables. The explanatory variables with a VIF of <10 are shown in Table 3, which were next included in the stepwise regression and best subset regression. We also compared the diagnostic plots of MLR algorithm, i.e., QQ plots, residual vs. fitted, spread location, and residuals vs. leverage. Based on observation of the diagnostic plots, it was found that the dataset did not require transformation.

Table 3.
Variance inflation factors and corresponding variables (Table 1) selected for parametric analysis.
3.4. Stepwise Regression
The SR initially consisted of 32 continuous variables, which were selected by the VIF analysis. The lowest AIC value among the model set was 728.06. The optimum MLR based on SR consisted of five independent variables named green_layer8 (NAIP), sen_evi, sen_ndre, lida_stdv, and pca_3 for NAIP (Equation (5)). The variable names are mentioned in Table 1, where YABM denotes aboveground biomass.
YABM = −(25.04) − 80.20 green_layer8 + 155.19 sen_evi + 201.90 sen_ndre + 2.05 lida_stdv + 4.18 pca_3
The SR model showed an F-statistics of 9.41 and an overall p-value of 1.77 × 10−7, with a testing R2 of 0.15 and an RMSE of 23.53 Mgha−1. In our study, the null hypothesis claims no significant relationship between predictor and response variables, whereas the alternative suggests that at least one predictor significantly impacts the response variable [74]. The overall p-value (<0.01) suggested that the observed data provided enough evidence to reject the null hypothesis in favor of the alternative hypothesis.
3.5. Best Subset Regression Method
A total of 32 explanatory variables (VIF ≤ 10) were tested in the best subset variable selection (Table 3). An exhaustive selection algorithm was employed to build models using the “regsubsets” and “bestglm()” functions [79,80] in the “leaps” package in the R environment (4.3.0) [81]. The top eight variable combinations of the best subset regressions are depicted in Table 4 with shaded columns. Model 8 was selected as the optimal model based on R2 values, consisting of eight explanatory variables (out of 32) as predictors. The model was then tested against the remaining left out 20% of data. The selected best subset equation showed an R2 of 0.35 and an RMSE of 22.58 Mgha−1. The F-statistics for this model was 6.98, with a p-value of <0.01, showcasing the statistical significance of the selected model. The regression equation of the best subset technique is given in Equation (6) with corresponding estimators for the predictor variables.
YABM = −(42.65) + 0.06 pca_1 + 0.68 green_layer4 − 56.98 green_layer8 + 149.17 sen_evi + 171.68 sen_ndre + 0.08 sen_swir − 10.41 lida_skw + 1.65 lida_stdv

Table 4.
Selected variables for MRL via the best subset method (the explanatory variables in the first column are defined in Table 1).
3.6. Selecting the Best Regression Model
We compared the testing evaluation metrics of the MLR models using RMSE, R2, and F-statistics to compare and identify the best model for the dataset. Figure 5a shows the performance of two MLR models based on different variable selection techniques. The residuals of the test data are also illustrated in Figure 5b,c for SR and the best subset regression, respectively. According to the accuracy metrices mentioned in Table 5, the best subset MLR model was identified as the best MLR model over the stepwise MLR model. Between the two models, the best subset model reported the lowest F-statistics and p-value of <0.01. The residual standard error (21.12 Mgha−1) represents the average deviation of the observed responses from the predicted values by the best subset regression model. As a result, the MLR model built upon the best subset technique was selected as the optimal MLR model for future comparisons.
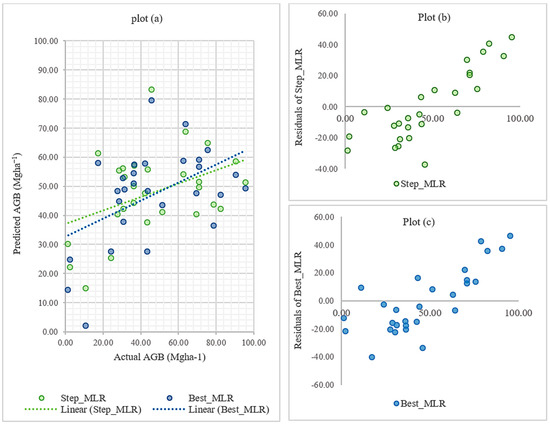
Figure 5.
Prediction and residual plots based on stepwise multiple linear regression and best subset multiple linear regression. (a) Actual vs. predicted aboveground biomass values of stepwise multiple linear regression and best subset multiple linear regression, (b) actual vs. residual plot of stepwise multiple linear regression, and (c) actual vs. residual plot of best subset multiple linear regression.

Table 5.
Performance metrics of MLR models for best subset and stepwise regression techniques.
3.7. Linear Regression Ensemble
We developed a linear regression ensemble based on the predicted values of the RF, SVM, and MLR models (Equation (7)). Altogether 28 test observations were deemed as model inputs, whereas three models were the input variables for stacked ensemble. The leave-one-out validation results for the linear ensemble model (Equation (7)) was an R2 of 0.79, an RMSE of 7.12 Mgha−1, and an MSE of 142.41(Mgha−1)2. The coefficients of the average linear function were derived from the FIA-estimated AGB and predicted AGB via the linear regression ensemble as shown in Equation (6).
YABM = +4.8730638 + 0.12 RF + 0.22 SVM + 0.14 MLR
The linear ensemble model has a p-value of <0.05 (7.37 × 10−8) and an F-statistics of 28.02 along with the lowest RMSE and the highest R2 values out of all the MLR and ML models previously developed based on the leave-one-out validation.
3.8. Model Comparison
Upon the thorough examination of model performance summarized in Table 6, the RF regression yielded 0.41 R2. However, due to a lack of data testing, we were not able to compare and generalize the linear ensemble method with the other three models.

Table 6.
A comparison of the evaluation metrics for random forest (RF), support vector machine (SVM), multiple linear regression (MLR), and linear ensemble models.
A comparison of MLR and RF models reveals distinct performance characteristics. The MLR demonstrates superior predictive accuracy, as evidenced by its lower RMSE of 22.59 Mgha−1 compared to that of the RF model (27.19 Mgha−1). Conversely, RF exhibits a higher R2 of 0.41, surpassing the MLR R2 of 0.21. This reflects the fact that the RF model explains a larger proportion of the variance observed in the dataset compared to the MLR model (Figure 6). According to the one-way ANOVA results, RF is significantly different from the MLR predictions, with a p-value of 1.28 × 10−9. The SVM model showed marginal significance, with a p-value of 0.0509, with the optimal RF model. The RF and the ensemble models were not statistically significant with a p-value of 0.6210. Therefore, building an ensemble model for the current dataset does not improve the prediction accuracy significantly. However, additional data are required for model training and testing to reliably compare the accuracy of ensemble model with other three models.
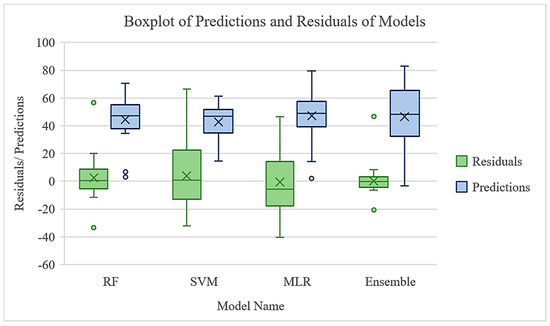
Figure 6.
Boxplots of model predictions (green) and residuals (blue) for four modeling approaches: random forest (RF), support vector machine (SVM), best subset multiple linear regression (MLR), and a stacked ensemble model. The green boxplots illustrate the distribution of predicted values across each model, while the blue boxplots represent the corresponding residuals (observed minus predicted) of each model. Here, ╳ represents the mean value, and the medians of each distribution are the horizontal lines in the boxes. This comparison highlights the differences in prediction accuracy and bias among the models.
4. Discussion
We compared the accuracy of aboveground biomass (AGB) predictions across three modeling methods: multiple linear regression (MLR), ML algorithms (SVM and RF), and linear ensemble. Our analysis revealed important insights on the performance, complexity, and suitability of each model in predictive AGB modeling. This research attempted to close methodological gaps by harnessing the remote sensing observations and FIA plot data with machine learning to provide robust models that maximize the utility of FIA true plot data in large-area AGB estimation tasks.
The grid-tuned RF model demonstrated the highest predictive accuracy compared to the other candidate models, achieving the highest testing R2 of 0.41 even with the single-year FIA data. Also, the R2 value obtained from the RF model exceeded those documented in some of the prior research. This outcome aligned with previous studies [10], highlighting the robustness of the RF algorithm in handling highly correlated, spatially dependent, and non-linear relationships of RS data [32]. Compared to previous models by Hu et al. [91], who reported an R2 of 0.56 and an RMSE of 101.21 Mgha−1, and Tang et al. [16], who achieved an R2 of 0.38 and an RMSE of 45.2 Mgha−1 using 4000 plot measurements and 1986 FIA subplot locations, respectively, our RF model demonstrated superior predictive performance (R2 = 0.41). Despite using the single-year FIA data (n = 142), our model achieved a notably lower RMSE of 27.19 Mgha−1. This improvement highlights the effectiveness of our model tuning and variable selection processes, which likely enhanced the ability to capture key patterns in biomass variability. The results highlight the value of incorporating systematic hyperparameter optimization and feature selection, even when working with a limited amount of field data.
Previous remote sensing-based AGB studies have used various feature importance criteria for RF models, such as gini importance and mean decrease in accuracy, despite the known biases that these methods may introduce due to multicollinearity [3,14,48,73,92,93]. According to Gregorutti et al. [72], decrease in accuracy as a selection criterion underestimates the importance of correlated variables in RF variable selection [94]. In our research, we used increase in node purity (IncNodePurity) values [22,49,71] as the selection criterion. As a novel approach, we combined the separate methods depicted in Torre-Tojal et al. [10] and Nandy et al. [22] to minimize the potential bias based on the selection criterion. After ranking the variables based on IncNodePurity, we compared the mean R2 of 5CV results by adding one variable at a time from the most important to the least important variable to determine the best subset of variables to train tuned models [10,22]. This new approach is one of the reasons to obtain a testing R2 of 0.41 for the RF models that we build even with a small sample size and the single-year FIA data. For the RF and the SVM, we fine-tuned the hyperparameters, ensuring a higher percentage variance explained even with the small sample size. This approach leveraged RF’s ability to rank variable importance and SVM’s REF process to achieve a robust predictive outcome while mitigating potential issues related to multicollinearity and overfitting. We observed the top-level LiDAR height percentiles (95th and 99th percentiles) as critical predictors in ML models, offering important insights into forest’s vertical structure with biomass.
The RFE method is a popular feature selection method for SVM in both classification and regression problems [50]. The assessments of Barzani et al. [94] demonstrate that leveraging RFE models enhances the SVM accuracy to over 10.97%. According to Lin et al. [95], RFE in the SVM determines feature weights based on the support vectors and hyperplane identified by the current model. However, the datasets with noisy variables can distort the construction of the optimal hyperplane and, in turn, affect how feature weights are assigned. Therefore, some informative features may be inaccurately evaluated or overlooked possibly explaining the low performance of our SVM models compared to RF predictions. As a result, we conclude that the RF model performs better than the SVM in statistically estimating AGB in our study.
For the MLR, both SR and the best subset selection were employed, resulting in R2 values of 0.15 and 0.22, respectively. The lower R2 of SR could be a result of the incremental approach of stepwise regression based on the Akaike information criterion (AIC). Variable selection in SR can be affected by the local optima [96]. Once a variable is added or removed, it may not be reconsidered, even if a different combination of predictors could yield a better model [97]. The best subset regression evaluates all potential variable combinations avoiding the issue of the local optima, which likely explained the higher R2 observed [30,85]. The best subset regression is computationally intensive with many predictors as the number of possible models grows exponentially. Therefore, the initial variable reduction using the VIF reduced the computational burden and processing time in our study. However, advances in computing power and algorithms have made the best subset regression more feasible even with a larger number of explanatory variables. The best subset MLR presented the lowest RMSE (22.59 Mgha−1), indicating its potential for accurate predictions in specific applications of the dataset. However, the performance of MLR was limited by the multicollinearity of RS variables and the spatial autocorrelation of FIA data (R2 = 0.22). Our MLR model has superior performance compared to the stepwise regression model built by Li et al. [26] to estimate AGB for mixed forest with an R2 of 0.21 and an RMSE of 27.28 Mgha−1. We used a VIF threshold of 10 to maintain the integrity of the MLR, as excessive multicollinearity can inflate variance estimates and undermine model interpretability [82]. The VIF analysis is generally recommended to maintain a threshold below 5 according to Shrestha [27]. Due to the limited dataset size and alignment with the previous literature [83,97], we used a VIF threshold of 10 for our study.
We used variable importance ranking via IncNodePurity of the RF algorithm while the SVM utilized recursive feature elimination (RFE). The RF, the SVM, and the MLR ultimately trained with 28, 44, and 8 explanatory variables, respectively. This difference showed how the models balance multicollinearity, complexity, and interpretability. The MLR is the simplest model because it is strictly controlled for multicollinearity [98]. In contrast, the RF and the SVM can handle larger sets of variables effectively without heavily giving up variables due to multicollinearity and spatial autocorrelation [8]. These differences allowed ML models to incorporate more information in the model training even with the single-year FIA data showing the highest R2 value.
To balance computational feasibility with model reliability under off-site analysis constraints, we adopted a tiered cross-validation strategy. Five-fold CV was used during model tuning [10,73], while ten-fold CV provided more stable accuracy estimates for SVM variable selection [74,76]. Given the small sample size (n = 28), LOOCV was applied for the ensemble model to maximize data usage and reduce bias. This structured approach ensured both efficiency and rigor in the context of limited FIA data accessibility. The validation results of linear ensemble model outperformed those of the individual models, with an R2 of 0.79, which was the highest observed among its counterparts. This improvement revealed the potential of stacked ensemble regression to integrate the strengths of RF, the SVM, and the MLR, and enhance predictive accuracy through an aggregation of diverse model prediction. However, the development of the linear ensemble model was inherently complex. Ensemble regression modeling requires a combination of results from each individual model, which is a computationally intensive process [8]. We used a LOOCV approach, which created a distinct validation framework for the ensemble method [21]. Therefore, our study requires a separate set of independent FIA plots or FIA-like plot locations to fairly compare ensemble regression accuracy with the rest of the base trainer models. This method also highlights the potential for expanding the ensemble models to other spatial scales, such as county- or region-specific models with adequate training and testing data access. Also, further research is required to understand the non-linear prediction performance of ensemble models.
Publicly available FIA plot coordinates are fuzzed up to 1.6 km (1.0 mile), and up to 20% of private plot locations are swapped to protect privacy [43]. Therefore, it is difficult to use publicly available FIA data for spatially sensitive analysis. We attempted to build a publicly available AGB prediction tool for FIA data users while protecting privacy concerns of landowners in collaboration with FIA scientists. Our optimal random forest model can generate AGB maps up to 15 m of granularity utilizing the single-year FIA plot data. But we recommend estimations for 30 m resolution since the 2016 FIA dataset can potentially have a geolocation error of 8 m (±2 m). This can add an unknown error to the 15 m level biomass estimations due to the inaccurate geo-positioning of the plots. Therefore, 30 m resolution can be considered as the smallest feasible pixel size to estimate AGB without introducing an unknown error to the estimations. The accuracy of the single-year AGB estimates can be further improved by incorporating high-resolution remote sensing data and using techniques to account for spatial autocorrelation [99].
The findings of this study hold critical information on forest biomass distribution, particularly for applications requiring robust AGB estimations with remote sensing data. Although ensemble methods presented a higher R2, the development complexity and data requirements need to be further studied. Recent studies demonstrate the transferability of similar approaches across different forest ecosystems. For instance, in boreal forests Gradient Boost, RF and the SVM achieved superior AGB prediction accuracy (R2 up to 0.84) [100]. Similarly, in semi-arid forested landscapes, combining airborne LiDAR with Sentinel-1 and Sentinel-2 time-series data has shown great success in AGB prediction tasks [101]. Despite the limited amount of training data, the optimal RF model offered promising AGB predictions compared to the previous studies and current AGB map products. Based on our results, we recommend that users prioritize the integration of LiDAR and multispectral RS data for the cost-effective monitoring of AGB at larger scales. The higher explanatory power of LiDAR height metrics emphasizes the need for incorporating LiDAR acquisitions into forest inventory and carbon monitoring programs. In data-limited contexts, adopting RF models with variable selection and hyperparameter tuning can improve prediction robustness. This approach allows future researchers to better identify AGB distribution for conservation, targeted restoration, and tree-planting initiatives.
Further research is needed to investigate the effect of multicollinearity and spatial autocorrelation of FIA subplots in machine learning contexts. It is important to evaluate the role of ensemble models across finer spatial scales for large-area applications where data richness and non-linear relationships are expected. Finally, the ML and ensemble regression models have the potential to utilize domain knowledge in variable selection in addition to pure statistical algorithms to increase accuracy in future research when more training data are available.
5. Conclusions
The tuned RF model achieved an RMSE of 27.19 Mgha−1 and an R2 of 0.41, outperforming both the SVM and MLR models. Of the top 28 most influential predictors in the RF model, 68% were derived from the LiDAR height metrics. The tuned linear SVM model produced an R2 of 0.10 and an RMSE of 32.17 Mgha−1. In comparison, the MLR model, developed using eight explanatory variables, yielded an RMSE of 22.59 Mgha−1 and an R2 of 0.22. Combining predictions from all three models, a linear ensemble approach produced an R2 of 0.79. While the ensemble model shows improved predictive performance, its generalizability is limited due to the relatively small number of sample points, and additional data would be required to reliably extend these results to other regions or forest types.
The hyperparameter-tuned RF model is the best performing model out of the other three candidate models. The conclusion is supported by the one-way ANOVA results, i.e., a p-value of <0.01 and an R2 of testing data of 0.41, which is the highest R2 obtained, providing the optimum variance identification. The optimum RF model exhibits the least possibility of overfitting, utilizing data with multicollinearity, and the highest percentage of the variance explained. The RF model’s predictions closely align with the FIA-AGB values. The linear ensemble model did not statistically outperform the MLR, the SVM or RF. However, concluding and generalizing of the ensemble model should be further studied. Hyperparameter optimization and careful variable selection help to improve the overall model performance even when utilizing single-year FIA. Adding more FIA data and using accurate plot locations can build more robust and accurate results including the adaptive RF models that can be retrained, validated, and applied as more or new data are acquired.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16091430/s1.
Author Contributions
S.H.G.L.: conceptualization, software, formal analysis, and writing—original draft. C.W.: conceptualization, supervision, funding acquisition, and reviewing—original draft. R.R.: conceptualization, formal analysis, and reviewing—original draft. R.F.: supervision and reviewing—original draft. T.W.: supervision, funding acquisition, and reviewing—original draft. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the USDA-NIFA Mclnire-Stennis Capacity Grant (#CONS01050), USA.
Institutional Review Board Statement
This study was conducted across the forests of Connecticut in collaboration with scientists from the US Forest Service’s Forest Inventory and Analysis (FIA) program. Since the work was carried out as part of this established collaboration which focused on publicly available remote sensing data, and not revealing true FIA plot locations, no special permissions or licenses were required.
Informed Consent Statement
All people who meet authorship criteria are listed as authors, and all authors certify that they have participated sufficiently in the work to take public responsibility for the content, including participation in the concept, design, analysis, writing, or revision of the manuscript. Furthermore, each author certifies that this material or similar material has not been and will not be submitted to or published in any other publication.
Data Availability Statement
All publicly accessible data supporting the findings of this study are provided within the manuscript and its Supplementary Materials (Sections S1–S3). However, due to the Forest Inventory and Analysis (FIA) landowners’ data protection policy, the training data cannot be shared herewith.
Acknowledgments
We are grateful to the US Forest Service (USFS), U.S. Department of Agriculture, Northern Research Station, United States, for sharing the data. We also thank Andrew J. Lister and Charles Paulson (USFS) and Thomas Mayer (Department of Natural Resources & the Environment, University of Connecticut) for their comments, support, and invaluable commitment during the data extraction process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Forest Service, U.S. Department of Agriculture. Forest Carbon Status and Trends; Forest Service, U.S. Department of Agriculture: Fort Collins, CO, USA, 2021. Available online: https://research.fs.usda.gov/understory/forest-carbon-status-and-trends (accessed on 17 September 2024).
- Johnson, K.D.; Birdsey, R.; Cole, J.; Swatantran, A.; O’Neil-Dunne, J.; Dubayah, R.; Lister, A. Integrating LIDAR and forest inventories to fill the trees outside forests data gap. Environ. Monit. Assess. 2015, 187, 623. [Google Scholar] [CrossRef] [PubMed]
- Raihan, A.; Begum, R.A.; Mohd Said, M.N.; Abdullah, S.M.S. A review of emission reduction potential and cost savings through forest carbon sequestration. Asian J. Water Environ. Pollut. 2019, 16, 1–7. [Google Scholar] [CrossRef]
- Tompalski, P.; Wulder, M.A.; White, J.C.; Hermosilla, T.; Riofrío, J.; Kurz, W.A. Developing aboveground biomass yield curves for dominant boreal tree species from time series remote sensing data. For. Ecol. Manag. 2024, 561, 121894. [Google Scholar] [CrossRef]
- Goodale, C.L.; Apps, M.J.; Birdsey, R.A.; Field, C.B.; Heath, L.S.; Houghton, R.A.; Jenkins, J.C.; Kohlmaier, G.H.; Kurz, W.; Liu, S.; et al. Forest carbon sinks in the Northern Hemisphere. Ecol. Appl. 2002, 12, 891–899. [Google Scholar] [CrossRef]
- Houghton, R.A. Aboveground forest biomass and the global carbon balance. Glob. Change Biol. 2005, 11, 945–958. [Google Scholar] [CrossRef]
- Johnson, L.K.; Mahoney, M.J.; Bevilacqua, E.; Stehman, S.V.; Domke, G.M.; Beier, C.M. Fine-resolution landscape-scale biomass mapping using a spatiotemporal patchwork of LiDAR coverages. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103059. [Google Scholar] [CrossRef]
- Kershaw, J.A., Jr.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Torre-Tojal, L.; Bastarrika, A.; Boyano, A.; Lopez-Guede, J.M.; Grana, M. Above-ground biomass estimation from LiDAR data using random forest algorithms. J. Comput. Sci. 2022, 58, 101517. [Google Scholar] [CrossRef]
- Chojnacky, D.C.; Heath, L.S.; Jenkins, J.C. Updated generalized biomass equations for North American tree species. Forestry 2014, 87, 129–151. [Google Scholar] [CrossRef]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci. 2003, 49, 12–35. [Google Scholar] [CrossRef]
- Blackard, J.A.; Finco, M.V.; Helmer, E.H.; Holden, G.R.; Hoppus, M.L.; Jacobs, D.M.; Lister, A.J.; Moisen, G.G.; Nelson, M.D.; Riemann, R.; et al. Mapping US forest biomass using nationwide forest inventory data and moderate resolution information. Remote Sens. Environ. 2008, 112, 1658–1677. [Google Scholar] [CrossRef]
- Sheridan, R.D.; Popescu, S.C.; Gatziolis, D.; Morgan, C.L.; Ku, N.W. Modeling forest aboveground biomass and volume using airborne LiDAR metrics and forest inventory and analysis data in the Pacific Northwest. Remote Sens. 2014, 7, 229–255. [Google Scholar] [CrossRef]
- Hudak, A.T.; Fekety, P.A.; Kane, V.R.; Kennedy, R.E.; Filippelli, S.K.; Falkowski, M.J.; Tinkham, W.T.; Smith, A.M.; Crookston, N.L.; Domke, G.M.; et al. A carbon monitoring system for mapping regional, annual aboveground biomass across the northwestern USA. Environ. Res. Lett. 2020, 15, 095003. [Google Scholar] [CrossRef]
- Tang, H.; Ma, L.; Lister, A.J.; O’Neil-Dunne, J.; Lu, J.; Lamb, R.; Dubayah, R.O.; Hurtt, G.C. Lidar Derived Biomass, Canopy Height, and Cover for New England Region, USA, 2015; ORNL DAAC: Oak Ridge, TN, USA, 2021. [Google Scholar]
- Johnson, K.D.; Birdsey, R.; Finley, A.O.; Swantaran, A.; Dubayah, R.; Wayson, C.; Riemann, R. Integrating Forest inventory and analysis data into a LIDAR-based carbon monitoring system. Carbon Balance Manag. 2014, 9, 3. [Google Scholar] [CrossRef]
- Hayashi, M.; Saigusa, N.; Yamagata, Y.; Hirano, T. Regional forest biomass estimation using ICESat/GLAS spaceborne LiDAR over Borneo. Carbon Manag. 2015, 6, 19–33. [Google Scholar] [CrossRef]
- Zheng, D.; Heath, L.S.; Ducey, M.J. Spatial distribution of forest aboveground biomass estimated from remote sensing and forest inventory data in New England, USA. J. Appl. Remote Sens. 2008, 2, 021502. [Google Scholar]
- Csillik, O.; Kumar, P.; Mascaro, J.; O’Shea, T.; Asner, G.P. Monitoring tropical forest carbon stocks and emissions using Planet satellite data. Sci. Rep. 2019, 9, 17831. [Google Scholar] [CrossRef]
- Naik, P.; Dalponte, M.; Bruzzone, L. Prediction of forest aboveground biomass using multitemporal multispectral remote sensing data. Remote Sens. 2021, 13, 1282. [Google Scholar] [CrossRef]
- Nandy, S.; Srinet, R.; Padalia, H. Mapping forest height and aboveground biomass by integrating ICESat-2, Sentinel-1 and Sentinel-2 data using Random Forest algorithm in northwest Himalayan foothills of India. Geophys. Res. Lett. 2021, 48, e2021GL093799. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Cremer, F.; Dubayah, R.; Migliavacca, M.; Reichstein, M.; Schmullius, C. Estimation of forest aboveground biomass and uncertainties by integration of field measurements, airborne LiDAR, and SAR and optical satellite data in Mexico. Carbon Balance Manag. 2018, 13, 5. [Google Scholar] [CrossRef]
- Mancini, F.; Castagnetti, C.; Rossi, P.; Dubbini, M.; Fazio, N.L.; Perrotti, M.; Lollino, P. An integrated procedure to assess the stability of coastal rocky cliffs: From UAV close-range photogrammetry to geomechanical finite element modeling. Remote Sens. 2017, 9, 1235. [Google Scholar] [CrossRef]
- Gao, Y.; Lu, D.; Li, G.; Wang, G.; Chen, Q.; Liu, L.; Li, D. Comparative analysis of modeling algorithms for forest aboveground biomass estimation in a subtropical region. Remote Sens. 2018, 10, 627. [Google Scholar] [CrossRef]
- Li, C.; Li, Y.; Li, M. Improving forest aboveground biomass (AGB) estimation by incorporating crown density and using Landsat 8 OLI images of a subtropical forest in Western Hunan in Central China. Forests 2019, 10, 104. [Google Scholar] [CrossRef]
- Shrestha, N. Detecting multicollinearity in regression analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance inflation factor: As a condition for the inclusion of suppressor variable (s) in regression analysis. Open J. Stat. 2015, 5, 754. [Google Scholar] [CrossRef]
- Chen, H.; Qin, Z.; Zhai, D.L.; Ou, G.; Li, X.; Zhao, G.; Fan, J.; Zhao, C.; Xu, H. Mapping Forest Aboveground Biomass with MODIS and Fengyun-3C VIRR Imageries in Yunnan Province, Southwest China Using Linear Regression, K-Nearest Neighbor and Random Forest. Remote Sens. 2022, 14, 5456. [Google Scholar] [CrossRef]
- Zhang, Z. Variable selection with stepwise and best subset approaches. Ann. Transl. Med. 2016, 4, 136. [Google Scholar] [CrossRef] [PubMed]
- Osborne, J.W.; Waters, E. Four assumptions of multiple regression that researchers should always test. Pract. Assess. Res. Eval. 2019, 8, 2. [Google Scholar]
- Chan, J.Y.L.; Leow, S.M.H.; Bea, K.T.; Cheng, W.K.; Phoong, S.W.; Hong, Z.W.; Chen, Y.L. Mitigating the multicollinearity problem and its machine learning approach: A review. Mathematics 2022, 10, 1283. [Google Scholar] [CrossRef]
- Bifet, A.; de Francisci Morales, G.; Read, J.; Holmes, G.; Pfahringer, B. Efficient online evaluation of big data stream classifiers. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, NSW, Australia, 10–13 August 2015; ACM: New York, NY, USA, 2015; pp. 59–68. [Google Scholar]
- Gomes, H.M.; Bifet, A.; Read, J.; Barddal, J.P.; Enembreck, F.; Pfharinger, B.; Holmes, G.; Abdessalem, T. Adaptive random forests for evolving data stream classification. Mach. Learn. 2017, 106, 1469–1495. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Z.; Zhang, X.; Chen, E.X.; Bai, L.; Tian, X.; He, Q.; Feng, Q.; Li, W. Optimal support vector machines for forest above-ground biomass estimation from multisource remote sensing data. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 6388–6391. [Google Scholar] [CrossRef]
- Sivasankar, T.; Lone, J.M.; Sarma, K.K.; Qadir, A.; Raju, P.L.N. Estimation of above ground biomass using support vector. Vietnam. J. Earth Sci. 2013, 41, 95–104. [Google Scholar] [CrossRef]
- Li, T.; Jiang, Z.; Le Treut, H.; Li, L.; Zhao, L.; Ge, L. Machine learning to optimize climate projection over China with multi-model ensemble simulations. Environ. Res. Lett. 2021, 16, 094028. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Dormann, C.F.; Calabrese, J.M.; Guillera-Arroita, G.; Matechou, E.; Bahn, V.; Bartoń, K.; Beale, C.M.; Ciuti, S.; Elith, J.; Gerstner, K.; et al. Model averaging in ecology: A review of Bayesian, information-theoretic, and tactical approaches for predictive inference. Ecol. Monogr. 2018, 88, 485–504. [Google Scholar] [CrossRef]
- Butler, B.J. Forests of Connecticut, 2016; Resource Update FS-130; Northern Research Station, Forest Service, U.S. Department of Agriculture: Newtown Square, PA, USA, 2017; 4p. [Google Scholar] [CrossRef]
- Connecticut Environmental Conditions Online. Orthophotography and Lidar Download. 2016. Available online: https://maps.cteco.uconn.edu/data/flight2016/ (accessed on 15 February 2022).
- Connecticut Department of Energy and Environmental Protection (DEEP). Connecticut 2016 High Resolution Land Cover (NOAA CCAP); Connecticut Department of Energy and Environmental Protection (DEEP): Hartford, CT, USA, 2016. Available online: https://geodata.ct.gov/maps/CTECO::ct-2016-high-res-land-cover-noaa-ccap/about (accessed on 18 August 2022).
- Burrill, E.A.; DiTommaso, A.M.; Turner, J.A.; Pugh, S.A.; Menlove, J.; Christiansen, G.; Perry, C.J.; Conkling, B.L. The Forest Inventory and Analysis Database: Database Description and User Guide Version 9.0.1 for Phase 2; Forest Service, U.S. Department of Agriculture: Fort Collins, CO, USA, 2021; 1026p. [Google Scholar]
- Michael, H.; Lister, A. The status of accurately locating forest inventory and analysis plots using the Global Positioning System. In Proceedings of the Seventh Annual Forest Inventory and Analysis Symposium, Portland, OR, USA, 3–6 October 2005; Volume 36, p. 179184. [Google Scholar]
- Duncanson, L.; Huang, W.; Johnson, K.; Swatantran, A.; McRoberts, R.E.; Dubayah, R. Implications of allometric model selection for county-level biomass mapping. Carbon Balance Manag. 2017, 12, 18. [Google Scholar] [CrossRef]
- Woudenberg, S.W.; Conkling, B.L.; O’Connell, B.M.; LaPoint, E.B.; Turner, J.A.; Waddell, K.L. The Forest Inventory and Analysis Database: Database Description and User’s Manual Version 4.0 for Phase 2; Rocky Mountain Research Station, Forest Service, United States Department of Agriculture: Fort Collins, CO, USA, 2010; p. 336. [Google Scholar] [CrossRef]
- Fang, G.; Yu, H.; Fang, L.; Zheng, X. Synergistic Use of Sentinel-1 and Sentinel-2 Based on Different Preprocessing for Predicting Forest Aboveground Biomass. Forests 2023, 14, 1615. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Goulden, T. State-wide forest canopy height and aboveground biomass map for New York with 10 m resolution, integrating GEDI, Sentinel-1, and Sentinel-2 data. Ecol. Inform. 2024, 79, 102404. [Google Scholar] [CrossRef]
- Dewi, C.; Chen, R.C. Random forest and support vector machine on features selection for regression analysis. Int. J. Innov. Comput. Inf. Control 2019, 15, 2027–2037. [Google Scholar]
- Zhang, L.; Zheng, X.; Pang, Q.; Zhou, W. Fast Gaussian kernel support vector machine recursive feature elimination algorithm. Appl. Intell. 2021, 51, 9001–9014. [Google Scholar] [CrossRef]
- Zhu, L.; O’Dwyer, J.P.; Chang, V.S.; Granda, C.B.; Holtzapple, M.T. Multiple linear regression model for predicting biomass digestibility from structural features. Bioresour. Technol. 2010, 101, 4971–4979. [Google Scholar] [CrossRef]
- Li, Y.; Andersen, H.E.; McGaughey, R. A comparison of statistical methods for estimating forest biomass from light detection and ranging data. West. J. Appl. For. 2008, 23, 223–231. [Google Scholar] [CrossRef]
- Yamashita, T.; Yamashita, K.; Kamimura, R. A stepwise AIC method for variable selection in linear regression. Commun. Stat. Theory Methods 2007, 36, 2395–2403. [Google Scholar] [CrossRef]
- Lamahewage, S.H.G.; Witharana, C.; Riemann, R.; Fahey, R.; Worthley, T. Aboveground biomass estimation using multimodal remote sensing observations and machine learning in mixed temperate forest. Sci. Rep. 2025, 15, 31120. [Google Scholar] [CrossRef]
- He, Q.; Chen, E.; An, R.; Li, Y. Above-ground biomass and biomass components estimation using LiDAR data in a coniferous forest. Forests 2013, 4, 984–1002. [Google Scholar] [CrossRef]
- Véga, C.; Vepakomma, U.; Morel, J.; Bader, J.L.; Rajashekar, G.; Jha, C.S.; Ferêt, J.; Proisy, C.; Pélissier, R.; Dadhwal, V.K. Aboveground-biomass estimation of a complex tropical forest in India using LiDAR. Remote Sens. 2015, 7, 10607–10625. [Google Scholar] [CrossRef]
- Ehlers, D.; Wang, C.; Coulston, J.; Zhang, Y.; Pavelsky, T.; Frankenberg, E.; Woodcock, C.; Song, C. Mapping Forest Aboveground Biomass Using Multisource Remotely Sensed Data. Remote Sens. 2022, 14, 1115. [Google Scholar] [CrossRef]
- Qin, H.; Zhou, W.; Yao, Y.; Wang, W. Estimating aboveground carbon stock at the scale of individual trees in subtropical forests using UAV LiDAR and hyperspectral data. Remote Sens. 2021, 13, 4969. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, SMC–3, 610–621. [Google Scholar] [CrossRef]
- Bright, B.C.; Hicke, J.A.; Hudak, A.T. Estimating aboveground carbon stocks of a forest affected by mountain pine beetle in Idaho using lidar and multispectral imagery. Remote Sens. Environ. 2012, 124, 270–281. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, L.; Wang, L. Stacked Sparse Autoencoder Modeling Using the Synergy of Airborne LiDAR and Satellite Optical and SAR Data to Map Forest Above-Ground Biomass. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5569–5582. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Estimating above-ground biomass in sub-tropical buffer zone community forests, Nepal, using Sentinel-2 data. Remote Sens. 2018, 10, 601. [Google Scholar] [CrossRef]
- Moradi, F.; Darvishsefat, A.A.; Pourrahmati, M.R.; Deljouei, A.; Borz, S.A. Estimating aboveground biomass in dense Hyrcanian forests by the use of Sentinel-2 data. Forests 2022, 13, 104. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, Z.; Liu, L.; Li, C.; Peng, D.; Xiao, P. Improving Estimation of Woody Aboveground Biomass of Sparse Mixed Forest over Dryland Ecosystem by Combining Landsat-8, GaoFen-2, and UAV Imagery. Remote Sens. 2021, 13, 4859. [Google Scholar] [CrossRef]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Mohammadpour, P.; Viegas, D.X.; Viegas, C. Vegetation mapping with random forest using Sentinel-2 and GLCM texture feature—A case study for Lousã region, Portugal. Remote Sens. 2022, 14, 4585. [Google Scholar] [CrossRef]
- De Castilho, C.V.; Magnusson, W.E.; de Araújo, R.N.O.; Luizao, R.C.; Luizao, F.J.; Lima, A.P.; Higuchi, N. Variation in aboveground tree live biomass in a central Amazonian Forest: Effects of soil and topography. For. Ecol. Manag. 2006, 234, 85–96. [Google Scholar] [CrossRef]
- Parent, J.R.; Gold, A.J.; Vogler, E.; Lowder, K.A. Guiding decisions on the future of dams: A GIS database characterizing ecological and social considerations of Dam decisions. J. Environ. Manag. 2024, 351, 119683. [Google Scholar] [CrossRef] [PubMed]
- Næsset, E. Estimating above-ground biomass in young forests with airborne laser scanning. Int. J. Remote Sens. 2011, 32, 473–501. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Han, S.; Williamson, B.D.; Fong, Y. Improving random forest predictions in small datasets from two-phase sampling designs. BMC Med. Inform. Decis. Mak. 2021, 21, 322. [Google Scholar] [CrossRef]
- Gregorutti, B.; Michel, B.; Saint-Pierre, P. Correlation and variable importance in random forests. Stat. Comput. 2017, 27, 659–678. [Google Scholar] [CrossRef]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Qiu, A.; Yang, Y.; Wang, D.; Xu, S.; Wang, X. Exploring parameter selection for carbon monitoring based on Landsat-8 imagery of the aboveground forest biomass on Mount Tai. Eur. J. Remote Sens. 2020, 53 (Suppl. S1), 4–15. [Google Scholar] [CrossRef]
- Patle, A.; Chouhan, D.S. SVM kernel functions for classification. In Proceedings of the 2013 International Conference on Advances in Technology and Engineering (ICATE), Mumbai, India, 23–25 January 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–9. [Google Scholar] [CrossRef]
- Rasel, S.M.; Chang, H.C.; Ralph, T.J.; Saintilan, N.; Diti, I.J. Application of feature selection methods and machine learning algorithms for saltmarsh biomass estimation using Worldview-2 imagery. Geocarto Int. 2021, 36, 1075–1099. [Google Scholar] [CrossRef]
- Marill, K.A. Advanced statistics: Linear regression, part II: Multiple linear regression. Acad. Emerg. Med. 2004, 11, 94–102. [Google Scholar] [CrossRef]
- Ott, R.L.; Longnecker, M.T. An Introduction to Statistical Methods and Data Analysis; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Hofmann, M.; Gatu, C.; Kontoghiorghes, E.J.; Colubi, A.; Zeileis, A. Lmsubsets: Exact variable-subset selection in linear regression for R. J. Stat. Softw. 2020, 93, 1–21. [Google Scholar] [CrossRef]
- Fisher, R.; Wilson, S.K.; Sin, T.M.; Lee, A.C.; Langlois, T.J. A simple function for full-subsets multiple regression in ecology with R. Ecol. Evol. 2018, 8, 6104–6113. [Google Scholar] [CrossRef]
- Lumley, T.; Lumley, M.T. Package ‘Leaps’. Regression Subset Selection. Thomas Lumley Based on Fortran Code by Alan Miller. 2013. Available online: http://CRAN.R-project.org/package=leaps (accessed on 18 March 2018).
- Liu, K.; Wang, J.; Zeng, W.; Song, J. Comparison and evaluation of three methods for estimating forest above ground biomass using TM and GLAS data. Remote Sens. 2017, 9, 341. [Google Scholar] [CrossRef]
- Powell, S.L.; Cohen, W.B.; Healey, S.P.; Kennedy, R.E.; Moisen, G.G.; Pierce, K.B.; Ohmann, J.L. Quantification of live aboveground forest biomass dynamics with Landsat time-series and field inventory data: A comparison of empirical modeling approaches. Remote Sens. Environ. 2010, 114, 1053–1068. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Qiu, X.; Fu, D.; Fu, Z. Feature selection of atmospheric corrosion data based on SVM-RFE method. Adv. Comput. Sci. Its Appl. 2013, 2, 443–448. [Google Scholar]
- Chakrabarti, A.; Ghosh, J.K. AIC, BIC and recent advances in model selection. Philos. Stat. 2011, 7, 583–605. [Google Scholar] [CrossRef]
- Hodkinson, I.D.; Coulson, S.J.; Webb, N.R.; Block, W.; Strathdee, A.T.; Bale, J.S.; Worland, M.R. Temperature and the biomass of flying midges (Diptera: Chironomidae) in the high Arctic. Oikos 1996, 75, 241–248. [Google Scholar] [CrossRef]
- Morgan, J.A.; Tatar, J.F. Calculation of the residual sum of squares for all possible regressions. Technometrics 1972, 14, 317–325. [Google Scholar] [CrossRef]
- Bui, Q.T.; Pham, Q.T.; Pham, V.M.; Tran, V.T.; Nguyen, D.H.; Nguyen, Q.H.; Nguyen, H.D.; Do, N.T.; Vu, V.M. Hybrid machine learning models for aboveground biomass estimations. Ecol. Inform. 2024, 79, 102421. [Google Scholar] [CrossRef]
- Luo, P.; Liao, J.; Shen, G. Combining spectral and texture features for estimating leaf area index and biomass of maize using Sentinel-1/2, and Landsat-8 data. IEEE Access 2020, 8, 53614–53626. [Google Scholar] [CrossRef]
- Hu, T.; Su, Y.; Xue, B.; Liu, J.; Zhao, X.; Fang, J.; Guo, Q. Mapping global forest aboveground biomass with spaceborne LiDAR, optical imagery, and forest inventory data. Remote Sens. 2016, 8, 565. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef]
- Yıldırım, H. The multicollinearity effect on the performance of machine learning algorithms: Case examples in healthcare modelling. Acad. Platf. J. Eng. Smart Syst. 2024, 12, 68–80. [Google Scholar] [CrossRef]
- Barzani, A.R.; Pahlavani, P.; Ghorbanzadeh, O.; Gholamnia, K.; Ghamisi, P. Evaluating the Impact of Recursive Feature Elimination on Machine Learning Models for Predicting Forest Fire-Prone Zones. Fire 2024, 7, 440. [Google Scholar] [CrossRef]
- Lin, X.; Yang, F.; Zhou, L.; Yin, P.; Kong, H.; Xing, W.; Lu, X.; Jia, L.; Wang, Q.; Xu, G. A support vector machine-recursive feature elimination feature selection method based on artificial contrast variables and mutual information. J. Chromatogr. B 2012, 910, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Paterlini, S.; Minerva, T. Regression model selection using genetic algorithms. In Proceedings of the 11th WSEAS International Conference on Nural Networks and 11th WSEAS International Conference on Evolutionary Computing and 11th WSEAS International Conference on Fuzzy Systems, Lasi, Romania, 13–15 June 2010; World Scientific and Engineering Academy and Society (WSEAS): Newark, NJ, USA, 2010; pp. 19–27. [Google Scholar]
- Wan-Mohd-Jaafar, W.S.; Woodhouse, I.H.; Silva, C.A.; Omar, H.; Hudak, A.T. Modelling individual tree aboveground biomass using discrete return LiDAR in lowland dipterocarp forest of Malaysia. J. Trop. For. Sci. 2017, 29, 465–484. [Google Scholar] [CrossRef]
- Paetzold, R.L. Multicollinearity and the use of regression analyses in discrimination litigation. Behav. Sci. Law 1992, 10, 207–228. [Google Scholar] [CrossRef]
- Dai, S.; Zheng, X.; Gao, L.; Xu, C.; Zuo, S.; Chen, Q.; Wei, X.; Ren, Y. Improving plot-level model of forest biomass: A combined approach using machine learning with spatial statistics. Forests 2021, 12, 1663. [Google Scholar] [CrossRef]
- Song, J.; Liu, X.; Adingo, S.; Guo, Y.; Li, Q. A Comparative Analysis of Remote Sensing Estimation of Aboveground Biomass in Boreal Forests Using Machine Learning Modeling and Environmental Data. Sustainability 2024, 16, 7232. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, X.; Wang, Y.; Chen, J. Aboveground Biomass Mapping in SemiArid Forests by Integrating Airborne LiDAR with Sentinel-1 and Sentinel-2 Time-Series Data. Remote Sens. 2024, 16, 3241. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).