Abstract
New Zealand’s Emissions Trading Scheme (ETS) enables growers to earn payments by accumulating carbon units as their forests increase in carbon stock. For forests of less than 100 hectares, growers use predefined lookup tables (LUTs) to estimate carbon stock changes based on forest age. Using a combination of growth models and productivity surfaces, underpinned by data from 1360 growth plots, the objective of this study was to provide draft updates for the Exotic Hardwoods LUTs. The updated LUTs were based on growth rates of three Eucalyptus species, E. fastigata, E. regnans, and E. nitens, which comprise a major proportion of the Exotic Hardwoods forest type in New Zealand. Carbon tables were first derived for each species. Then, a draft LUT was generated for New Zealand’s North Island, using a weighted average of the species-specific tables based on the relative importance of the species, while the E. nitens table was used for the South Island where this is the predominant Eucalyptus species. Carbon stock predictions at ages 30 and 50 years were 820 and 1340 tonnes CO2 ha−1 for the North Island, and slightly higher at 958 and 1609 tonnes CO2 ha−1 for the South Island. Regional variation was significant, with the highest predicted carbon in Southland (1691 tonnes CO2 ha−1 at age 50) and lowest in Hawke’s Bay/Southern North Island (1292 tonnes CO2 ha−1). Predictions closely matched the current Exotic Hardwood LUT to age 20 years but exceeded it by up to 45% at age 35. Growth and carbon sequestration rates were similar to other established Eucalyptus species and slightly higher than Acacia species, though further research is recommended. These findings suggest that the three Eucalyptus species studied here could serve as the default species for a revised Exotic Hardwoods LUT and that the current national tables could be regionalised. However, the government may consider factors other than the technical considerations outlined here when updating the LUTs.
1. Introduction
Hardwoods are valuable timber species that have been introduced widely outside their native ranges and are often cultivated for their high-quality wood, durability, and unique grain patterns. Hardwoods are produced by angiosperm trees and usually have a more complex cell structure than conifers (softwoods), which gives hardwoods their characteristic density and strength. Hardwoods are typically deciduous trees, such as oak, maple, walnut, and mahogany, although some hardwoods such as Eucalyptus spp. are evergreen species.
Globally, Eucalyptus spp. are some of the most widely planted plantation hardwoods, valued for their fast growth and high yield [1]. As many as 95 countries cultivate Eucalyptus spp. in plantations, with the total planted area exceeding 22 million hectares worldwide [2]. Eucalyptus is the most extensively planted broadleaf tree genus and, together with pine species (Pinaceae), constitutes a significant portion of global plantation forests [1]. Within New Zealand, exotic hardwood plantations comprise 36,585 ha, with Eucalyptus spp. accounting for 61% of this area (22,195 hectares) [3]. Approximately 25 Eucalyptus species have been established in plantations for amenity, shelter, and commercial forestry purposes [4].
Eucalyptus spp. were some of the first exotic hardwoods to be planted in New Zealand, with species such as E. regnans and E. fastigata introduced around the mid-late 19th Century [5]. Commercial plantations have primarily focused on producing solid timber as well as pulp and paper. A variety of other exotic hardwoods have also been established in New Zealand. It has been estimated that New Zealand has 3000 ha of Acacia melanoxylon (blackwood), of which a large proportion is on the West Coast of the South Island [6]. Paulownia spp. and black walnut were promoted as high-value species in the past, but siting is critical for both species and neither has been established at scale [7]. A large number of classical European hardwood species, such as oaks, chestnut, elm, ash and European walnut have been planted by growers at a smaller scale, but these species are site demanding, often prone to pests and do not yield high rates of return [7]. Poplars and willows are commonly established exotic hardwoods on New Zealand farms.
Environmental preferences and resistance to disease are two key factors affecting the siting of Eucalyptus spp. in general and also vary significantly between the most widely planted species, E. regnans, E. fastigata, and E. nitens. Eucalyptus regnans can tolerate exposure and temperatures as low as −9 °C but cannot withstand drought, poor drainage, salt winds, or continuous severe frost. Growth rates have been shown to be greatest on sites with adequate soil moisture in warm areas at moderate altitudes in the North Island and coastal South Island regions [8]. Eucalyptus fastigata can tolerate temperatures as low as –9 °C and some snow and is considered to be more tolerant of cold than E. regnans [8]. It is wind firm, currently has no significant pest or disease issues, and is considered to be one of the healthier and more adaptable eucalypts growing in New Zealand [9]. In contrast, E. nitens is tolerant of cold conditions and can withstand temperatures as low as −15 °C but is quite susceptible to pests and diseases. This species prefers moist, well-drained soils and is able to tolerate snow, wet soils, and exposure [8]. Due to its cold tolerance and greater susceptibility to pests and diseases in warmer regions [10], it is thought the species is better suited to cooler climates of New Zealand [8,9]. However, there is also evidence and trial data showing E. nitens grows well across most New Zealand climates [11].
Carbon now provides a significant source of revenue to forest growers [12]. Globally, compliance carbon markets are central to climate mitigation efforts, with Emission Trading Systems (ETSs) being prominent instruments. As of 2024, there are 36 active ETSs globally, covering about 18% of global greenhouse gas emissions and generating record revenues of USD 74 billion in 2023 [13]. Additionally, 22 new systems are currently being developed or considered in diverse regions such as Japan, Canada, Brazil, India, and Türkiye, reflecting a growing global commitment to carbon pricing as a climate solution [13]. The New Zealand Emissions Trading Scheme (ETS) is relatively unique from a global perspective in that it includes the forestry sector [13]. The ETS was first introduced in 2008 as part of the Climate Change Response Act and is one of the New Zealand government’s main tools for supporting domestic and international efforts to reduce greenhouse gas (GHG) emissions. Forest growers registered in the ETS receive a New Zealand unit (NZU) of carbon for each tonne of CO2 sequestered. The number of available NZUs is reduced over time, limiting the amount that emitters can emit and creating an economic incentive for businesses to invest in lower-emission approaches to business as usual.
Within the ETS, pre-1990 forests, which are defined as those established before 1 January 1990, are recognised as part of New Zealand’s baseline carbon storage. Pre-1990 forests are not eligible to participate in the New Zealand ETS to earn carbon units. However, if they are deforested or converted to another land use, they are automatically enrolled in the ETS, and units must be surrendered to the government to offset the loss of baseline carbon storage. Post-1989 forests, which are forests established after 31 December 1989, are regarded as new carbon sinks. Post-1989 forests can be voluntarily registered in the ETS to earn carbon units for their stored carbon.
Payment of carbon units within the ETS to growers is made through either an averaging or stock change carbon accounting methodology, which are respectively suited to forests that are periodically clear-felled or permanently established [14]. Under the stock change method, the grower is allocated units as carbon accumulates over the lifetime of the stand but must surrender some when carbon is lost at harvest [14]. This method is used for the permanent forest category, which came into effect within the ETS on 1 January 2023, and allows owners to earn carbon units from forests that are not intended to be harvested for at least 50 years after they are registered [14]. Under the averaging method, forests earn units on the first rotation until they reach a specified age representing the age when they achieve the long-term average of carbon stock (Figure 1). After this point payments cease, which has the advantage that no repayment of units is required when the forest is harvested as long as it is replanted. For exotic hardwoods, the age of the long-term carbon stock over which carbon is paid is currently set at 12 years [15].
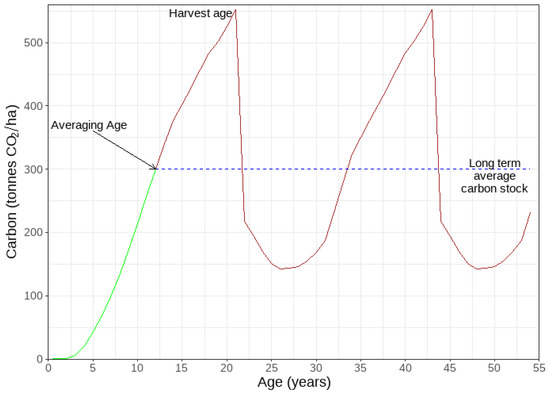
Figure 1.
Changes in carbon stock for a periodically clear-felled exotic hardwood plantation. The earned carbon, illustrated by the green line, is determined up to the averaging age (12 years in this case), which is defined as the age at which the long-term average carbon stock is reached (dashed blue line). After harvest, the remaining carbon is contained within above-ground residual wood and below-ground roots. All numbers are illustrative only.
The ETS provides two distinct methods for calculating carbon unit allocations across species. Participants with 100 ha or more enrolled in the ETS are required to establish plots using the Field Measurement Approach (FMA) to directly assess carbon stocks. In contrast, those with under 100 ha registered rely on pre-defined look-up tables (LUTs), also known as default carbon tables, which provide estimates of annual carbon stock changes [14]. The ETS uses separate LUTs for different species groups, and for radiata pine (Pinus radiata D. Don), separate tables by region. Currently, a national LUT is used to cover all exotic hardwood species.
The ETS provides three LUTs for each species group that represent: carbon in the growing stock of post-1989 forests; carbon in the growing stock of pre-1990 forests; and residual carbon. Residual carbon remaining following harvest is defined as the carbon stock per hectare in above-ground residual wood and below-ground roots in a cleared plantation (i.e., carbon in roots of harvested trees and in logging slash, etc.).
The current default Exotic Hardwoods carbon tables have a maximum age of only 35 years, which means that exotic hardwood forests planted in 1990 and registered in the ETS will not be able to earn units from 2025 when they will exceed this age. The current tables are also based solely on E. nitens, using an initial stand density of 1030 stems/ha with no thinning or pruning. Although Eucalyptus nitens was the dominant species when the current tables were developed, this is no longer the case—particularly in the North Island, where planting trends have shifted significantly toward other Eucalyptus species.
Because of these limitations, the Ministry for Primary Industries (MPI) requires the development and evaluation of new and updated LUTs for the Exotic Hardwoods forest type. The research undertaken here builds on studies completed in 2021 and 2022, which investigated the potential for updated Exotic Hardwoods default tables and developed updated tables based on a process-based growth model (3-PGS2) using E. fastigata as the representative species [16,17]. In August 2023, MPI publicly consulted on updating the Exotic Hardwoods LUTs using the new E. fastigata model. Submitters to this consultation requested better representation of other eucalypt species.
According to the National Exotic Forest Description [3], New Zealand’s Eucalyptus resource covers 22,195 hectares, with a significant proportion of this area comprising E. regnans, E. fastigata, and E. nitens [18]. Other exotic hardwood plantations cover 14,390 ha [3]. Given that Eucalyptus spp. constitute the largest proportion of exotic hardwoods, and E. fastigata, E. nitens, and E. regnans are among the most widely planted Eucalyptus species, these three species should provide a representative reference for developing a revised Exotic Hardwood LUT.
The objective of this study was to develop draft estimates of carbon stock for Eucalyptus spp. at a range of scales (national, Island level, regional) in order to identify the most appropriate scale for implementation of an Exotic Hardwoods LUT in the ETS. Annual carbon stocks were determined for pre-1990 forests to determine liabilities following clear-felling, for post-1989 forests to characterise carbon sequestration following the establishment of these predominantly new forests, and for residual carbon to estimate the carbon left on site following harvest. The study provided draft sets of LUTs covering these three cases at different spatial scales.
2. Materials and Methods
2.1. Growth Data
The models developed in this study use data for E. fastigata, E. regnans, and E. nitens, which were obtained from both the Scion Permanent Sample Plot (PSP) database and a FMA dataset supplied by MPI. Of the original 1406 plots, a total of 44 plots were excluded because were either too young (less than 3.5 years) or the diameter at breast height (DBH) was too small (DBH < 5 cm) to reliably extract productivity metrics. Two E. fastigata plots established in 1925 and 1964 were also excluded as these had low productivity and there were insufficient plots established during this time to verify the trend. Following these exclusions, there was a total of 1360 plots. There were substantial numbers of plots for each species, comprising 413, 438, and 509 plots, respectively, for E. fastigata, E. regnans, and E. nitens. The spatial distribution of these plots throughout New Zealand, by species, is shown in Table 1 and Figure 2.

Table 1.
Variation in the number of plots at the Island, national, and regional levels for Eucalyptus fastigata, E. regnans, and E. nitens. Also shown are the partitioning of plot numbers by data source (PSP and FMA data) and the period of forest establishment (pre-1990 and post-1989 forests).
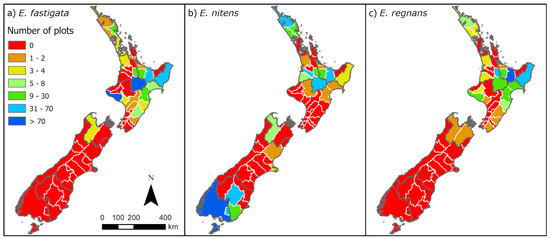
Figure 2.
Geographic distribution of plots (combining FMA and PSP datasets) for (a) Eucalyptus fastigata, (b) Eucalyptus nitens, and (c) Eucalyptus regnans, shown across New Zealand’s 67 territorial authorities (outlined in white and grey). These territorial units are nested within nine broader regional groupings (indicated by grey boundaries), listed from north to south as: Auckland, Waikato/Taupo, Bay of Plenty, Gisborne, Hawke’s Bay/Southern North Island, Nelson/Marlborough, Canterbury/West Coast, Otago, and Southland.
Almost all of the plots for E. fastigata and E. regnans were in the North Island, with only three and four plots, respectively, located in the South Island—all of which were in the Nelson/Marlborough region. However, there was robust regional coverage throughout the North Island for both species, with between 47 and 170 plots in four of the five regions (Table 1). Data were most sparse in the Auckland region of the North Island for both species, where there were 20 plots for E. fastigata and 14 plots for E. regnans. Plots of E. nitens were mainly located in the mid-upper North Island and lower South Island (Figure 2; Table 1). The three most northern regions of the North Island (Auckland, Waikato/Taupo, Bay of Plenty) included between 63 and 116 plots, while the two most southern regions, Otago and Southland had, respectively, 57 and 177 plots. The remaining four regions had 3–7 plots per region (Table 1; Figure 2).
2.2. Growth Models
The growth modelling framework applied in this research is based on Version 1.2 of the publicly accessible Multi-Species Carbon Calculator, a revised Excel-based tool that estimates forest growth and carbon using site-specific productivity parameters, namely the 300 Index and site index (https://fgr.nz/tools/multi-species-carbon-calculator/ accessed on 10 January 2025). The models were developed using data from Scion’s PSP database for the three Eucalyptus species described in Section 2.1. These data covered a relatively wide age range of 2–66 years, 2–56 years, and 2–38 years, respectively, for E. fastigata, E. regnans, and E. nitens. The models were developed using methodology and growth functions similar to those used in previously developed redwood and cypress growth models described, respectively, in [19] and [20]. The methods and results for the growth modelling are summarised in Supplementary Materials S1 and S2.
All three models incorporate the 300 Index framework to reflect differences in site quality and silvicultural regimes. While traditional growth and yield modelling has relied on the site index—which, for the Eucalyptus species considered here, is defined as the mean top height at age 30—this approach has limitations. To overcome these, the 300 Index was developed as an alternative productivity metric. It quantifies stem volume productivity as the mean annual increment in stem volume at age 30 for a reference stand established at 300 stems/hectare.
A short overview of the rationale behind the 300 Index is provided here. Stands with similar top heights can exhibit considerable differences in volume, which sometimes exceed ±30% [21]. As a productivity measure based on height, site index alone fails to capture this variation [19,22,23,24,25,26,27,28,29]. Although total stand volume serves as a more comprehensive indicator of site productivity than height, it is also affected by factors such as stand density and silvicultural history. The 300 Index was developed specifically to incorporate these influences [19,29]. One of its key advantages, along with the associated growth models, is that once both the 300 Index and site index are specified, predictions of volume and carbon can be generated across a wide range of ages, stand densities, and silvicultural treatments. Additionally, the modelling framework allows inverse estimation of productivity indices from the measured plot attributes MTH, basal area, stand density, and thinning records [19,29].
2.3. Prediction of Productivity Indices
2.3.1. Extraction of Productivity Metrics
The 300 Index and site index serve as core indicators for estimating timber yield and carbon stocks and underpin the spatial extrapolation of productivity across regions. The growth data used to derive productivity indices consisted of the measurements in Permanent Sample Plots and FMA plots described in Section 2.1. When multiple measurements over time were available for a plot, the oldest measurement was used to derive productivity indices. Stand density (stems ha−1), basal area (m2 ha−1), and MTH (m) were calculated for each measurement. In addition, where plots had been previously thinned, the thin age and the stand density prior to and following thinning were required to estimate the 300 Index. For PSP plots, these thinning details were recorded in previous measurements or were available in the database as third-party records. For FMA plots with multiple measurements over time, evidence of a thinning could be inferred when there was a substantial decline in stand density between measurements. In this case, a thinning was assumed to have occurred at the age midway between the two measurements, with stand density prior to thinning taken from the earlier measurement and stand density following thinning taken from the subsequent measurement.
Site index was estimated from MTH and age for each measurement using site index equations derived from the MTH/age equations. These equations, derived from the two growth model forms used for the three Eucalyptus species are shown in Table 2. The 300 Index was estimated for each plot measurement as follows. Firstly, t1.4, the age when the stand was predicted to achieve an MTH of 1.4 m, which is required to apply the DBH model, was estimated for each measurement from its site index using the equations shown in Table 2. Next, D30, the diameter productivity for a reference regime of 300 stems/ha at age 30, was estimated such that the DBH predicted by Equation (S1) (Supplementary Materials) equalled the measured DBH. This was carried out using an iterative procedure from the plot age, measured quadratic mean DBH, site index, and stand density together with thinning history. The procedure is fully described in the Supplementary Materials of Kimberley and Watt [19]. A volume function (Equation (S8) (Supplementary Materials)) was then used to estimate the 300 Index, I300, from site index and D30 as follows. Firstly, BA30/300, the basal area (m2 ha−1) at age 30 years for a stand at the plot location growing at 300 stems ha−1, was estimated from D30 using:

Table 2.
Site index equations and equations for estimating t1.4 derived from the MTH/Age models used for the three Eucalyptus species.
The 300 Index, which is defined as the volume mean annual increment at age 30 years for a stand growing at 300 stems ha−1, was then calculated from site index (SI) and BA30/300 using a rearrangement of the stand-level volume function (Equation (S8), Supplementary Materials), i.e.,
2.3.2. Predictor Variables
The site index and 300 Index values derived above were linked to environmental covariates representing climate, soil, terrain, and landform characteristics, as detailed in [30] and Appendix A (Table A1). These variables were sourced from 25 m resolution raster layers spanning the full extent of New Zealand. The climate variables included total rainfall, vapour pressure deficit, solar radiation, sunshine hours, windspeed, and mean, minimum, and maximum air temperature [31], which were summarised at different temporal scales (yearly, seasonal, monthly). Also extracted were growing degree days and the number of days with rainfall and ground frosts [31,32]. Variables related to soil water balance included mean seasonal and monthly root-zone water balance, with values expressed both as a percentage of the available root-zone water storage and in millimetres [33]. All variables described above were derived from climate data collected over a 30-year period from 1971 to 2000 and, as such, describe the average spatial variation in climate and water balance.
Edaphic variables that were included in analyses were carbon: nitrogen ratio (C:N ratio), from 0–10 cm [34], pH, macro-porosity, phosphorus retention from 0–20 cm [35], and particle size [36]. Water balance-related soil properties included plant rooting depth, gravel content, profile available water content, and readily available water content [35]. Topographic and landform variables included aspect [36], slope, distance to the nearest stream, and elevation [37], amongst others (see Table A1). Environmental surfaces that represent important climatic and edaphic variables are shown in Appendix A as Figure A1.
2.3.3. Modelling Approach
Both multiple regression and random forest were used to predict the two productivity indices for the three species. The most robust of these two approaches was used for each species/productivity index combination based on model accuracy, alignment with regional averages from the plot data, and the likely accuracy of spatial predictions across New Zealand beyond the plot data. A ten-fold cross-validation with five repeats was used to fit initial models for both multiple regression and random forest. Once the variables had been selected using this process, model statistics were generated from a test dataset. The fitting and testing process was iterated 50 times to ensure the test dataset was unbiased (see Model performance and test dataset).
Multiple Regression
A multiple regression model was fitted to the data using a manual iterative approach using R version 4.2.2 [38]. Predictor variables were selected through a stepwise approach, beginning with the variable exhibiting the strongest correlation with the response variable. After fitting this initial model, residuals were analysed against the remaining candidate variables to identify the next most influential predictor. This iterative process continued until the inclusion of additional variables no longer led to a substantial increase in the coefficient of determination (R2) for the validation dataset. Each variable was incorporated using the least biased functional relationship, and importance rankings were calculated across all predictors. To evaluate multicollinearity, the variance inflation factor (VIF) was calculated for each variable, with all retained predictors exhibiting VIF values below 5 [39].
Random Forest
Random forest was fitted to the data using scikit learn, version 0.23.2 [40] which was implemented in Python, version 3.9.18. Random forest was employed due to the large size of the datasets and their broad coverage of the environmental gradients across the species’ distributions. These ranges spanned the full New Zealand range for E. nitens and the North Island for E. fastigata and E. regnans, and this comprehensive coverage helped minimise the risk of extrapolation beyond observed conditions. As a machine learning technique, random forest is widely adopted [41,42] for its ability to model complex, non-linear relationships, manage multicollinearity, and perform well with high-dimensional inputs. It operates by constructing an ensemble of decision trees, with the final prediction generated as the average output from all trees in the forest. The term ‘random’ within the algorithm name is derived from the random sampling, with replacement (i.e., bootstrapping), of training observations for each learner (individual tree) within the forest and the use of a random subset of predictors at each split (node) within the tree. This approach enhances diversity among the trees, which reduces overfitting and improves generalisation to unseen data.
To identify the most influential environmental predictors, recursive feature elimination (RFE) was applied before fitting the random forest model. This procedure involved 10-fold cross-validation and evaluated model accuracy using subsets ranging from 1 to 30 variables. Each subset represented the top-ranked variables based on their overall contribution to model performance. To limit multicollinearity, an additional constraint was built into the RFE workflow: variable sets were filtered to ensure pairwise correlations remained below 0.9. In cases of high correlation, the less important variable in each pair was excluded, reducing the likelihood of overfitting.
Model Performance and Test Dataset
Following variable selection for each model, the dataset was divided into a training dataset comprising 80% of the observations, with the remaining 20% retained as a test dataset. Model fitting was performed on the training data using 10-fold cross-validation with five repetitions. The resulting models were then used to generate predictions on the separate, independent test dataset. This procedure was carried out 49 additional times, each with a new random split between training and test sets, resulting in a total of 50 iterations. Performance metrics were averaged across all test datasets to minimise the influence of any particular train/test partition and to provide a more robust assessment of predictive accuracy. Evaluation was based on the root mean square error (RMSE) and the coefficient of determination (R2), both computed from the test dataset predictions, respectively as
where is the observed value, is the predicted value in plot , is the average of the observed values, and is the number of plots.
The most robust of the two modelling approaches (multiple regression or random forest) was selected for each species/productivity index combination based on model accuracy, alignment with mean regional values, and the likely accuracy of spatial predictions across New Zealand beyond the plot data. For each selected model, the importance score of the most important variables in each model was outputted. Residuals for each model were plotted against predicted values, all key variables in each model, and important variables that were not included in the model to identify any bias.
2.3.4. Spatial Predictions and Masking
Spatial predictions of the 300 Index and site index were made for all three Eucalyptus spp. using the models described above, with the relevant environmental surfaces as input. Predictions of these two productivity indices were made across New Zealand for E. nitens. However, as there was very little plot data for E. fastigata and E. regnans within the South Island, these predictions were restricted to the North Island for these two species.
A number of exclusions were made to limit the predictions to areas where these three plantation species are likely to be established. Areas of land with a mean annual air temperature (Tmean) less than 8.00 °C were excluded for all three species. It is unlikely these Eucalyptus species would be established in areas within these colder/predominantly high-elevation climates. This assumption was aligned with the plot data, which showed the minimum Tmean for E. nitens in the colder South Island to be 8.33 °C.
A number of additional exclusions were made to further limit predictions to areas likely to be afforested. All lakes larger than the minimum mappable unit (0.0625 ha) were excluded. Contiguous areas of natural forest above 10 ha (LUCAS LUM), urban areas (LUCAS LUM), and protected areas (LINZ Protected Areas) were excluded. Major roads (LCDB5) that intersected urban areas were also removed. The Land Use Capability (LUC) layer was used to further exclude very productive land classes. The LUC categorises land into eight classes according to its long-term capability to sustain one or more productive uses based on physical limitations and site-specific management needs. The LUC classes 1 and 2 were excluded, as forestry is unlikely to be established on these productive land classes.
Values of the 300 Index and site index for the constructed rasters were averaged across each of the nine regions displayed in Figure 3 and Figure 4, as these regional boundaries have previously been used by MPI for lookup table construction. The two productivity indices were also averaged at the Island level (North Island, South Island) and national level using area-weighted regional values.
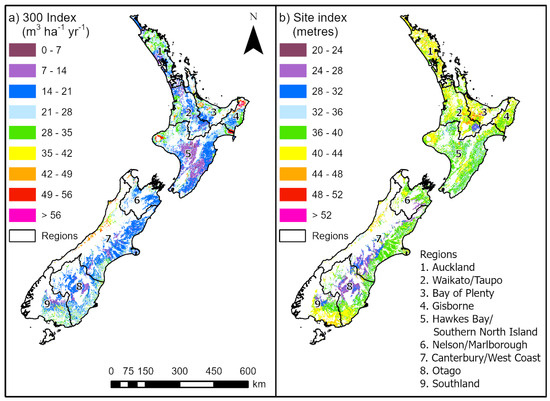
Figure 3.
Spatial variation in predicted (a) 300 Index and (b) site index for Eucalyptus nitens. The white areas have been excluded using the mask. The boundaries and names of the nine regions used by MPI for lookup table construction are shown.
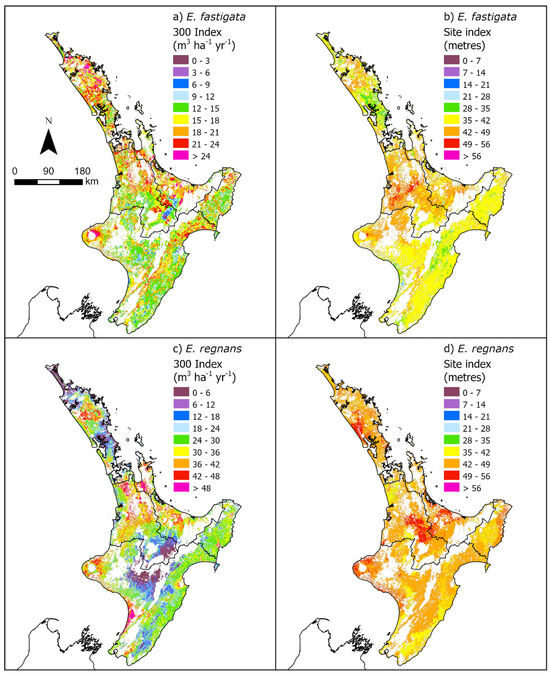
Figure 4.
Spatial variation in predicted (a) 300 Index and (b) site index for Eucalyptus fastigata and (c) 300 Index and (d) site index for Eucalyptus regnans. The white areas have been excluded using the mask.
2.4. Predictions of Carbon
2.4.1. Overview
Predictions of carbon were made for all three species based on the 300 Index and site index regional, Island, and national averages. The predictions were made using the growth models (described in the Supplementary Materials) for the three species as implemented in the Multi-Species Carbon Calculator. The Multi-Species Carbon Calculator uses the 300 Index and site index as inputs to account for site productivity. More details about the underpinning methods for predicting volume and carbon within the calculator are given below.
Annual predictions of carbon were made using a silvicultural regime for each species designed to target the production of sawn timber whilst also producing a moderate level of carbon uptake over the short–medium term. There is very little literature on the most common regimes used by growers of small woodlots of Eucalyptus spp. (<100 ha). Discussions with industry experts indicated that smaller areas of Eucalyptus spp. are often planted at high stand density for carbon using a fast-growing species that has relatively low risk. As the necessary silviculture is often not carried out, these stands are quite commonly used for fuel wood. Examination of the FMA data, above ages in which there was adequate data, provided insight into the silvicultural regimes used for the three Eucalyptus spp. planted since 1990. These data show a wide range of stand densities at 9–10 years, suggesting they include both pulpwood and sawlog regimes. Mean stand densities at 10–12 years were ca. 740, 500, and 750 stems/ha, respectively, for E. fastigata, E. regnans, and E. nitens. These stand densities remained high until age 15 and 18, respectively, for E. fastigata and E. nitens, before declining. Changes in stand density were more difficult to identify for E. regnans after age 12, as data was fairly sparse over this age range. The selected regime, based on both the literature [9] and age-related stand density changes observed in the FMA data, was as follows: planting at a stand density of 1111 stems/ha; pruning of 350 stems/ha to 6.5 m over three stages at ages 6, 8, and 10; thinning at age 5 to 800 stems/ha; and a final thinning at age 15 to 350 stems/ha.
Carbon predictions were combined to make composite estimates for both Islands. These predictions were based on the relative frequency of the data within the FMA dataset, which is representative of stands that have been established since 1990, using the following method: The North Island FMA data was split into the following three periods: 1990–2000, 2001–2010, and 2011–2020. The planted weighting of E. fastigata, E. regnans, and E. nitens changed through time, with the frequency of E. nitens declining rapidly after 2000, and the two other species showing concomitant increases. Consequently, the weightings from 2011 to 2020 were used and were, respectively, 0.65, 0.30, and 0.05 for E. fastigata, E. regnans, and E. nitens. This weighting is likely to better represent current and future plantings and reduce the influence of E. nitens on the North Island predictions. Given these weightings, E. fastigata will have the largest influence on North Island predictions. Given that 98.6% of FMA plots established in the South Island were E. nitens (Table 1), predictions of carbon for the South Island were limited to this species.
2.4.2. Carbon Predictions
Predictions of carbon sequestration (in above and below-ground biomass, dead wood, and litter pools) for all three Eucalyptus spp. were made using the Multi-Species Carbon Calculator, which implements the C_Change model [see Beets et al. (2011) [43] for detailed description]. This model requires as input a yield table containing annual under-bark stem volumes, volumes losses from mortality (and thinning events if any), and the basic density of the stem wood. Stem volume yield tables were developed using the 300 Index-based growth models in conjunction with the stand volume equations outlined in the Supplementary Materials.
Annual estimates of stem wood basic density were produced using the age-based predictive models described in [44]. These estimates, combined with stem volume outputs, were processed through the C_Change model to derive stemwood dry matter. This value served as the foundation for estimating biomass in other tree components, including roots, bark, branches, and foliage, using partitioning functions detailed in [45], and modified for Eucalyptus species using empirical data from biomass studies reported in [46]. Biomass was then converted to carbon using component-specific carbon fractions.
Carbon transfers to dead wood and litter pools were also modelled, with decay processes accounted for through functions that simulate carbon losses over time [47]. The modelled carbon stocks included aboveground and belowground biomass, dead wood, and litter pools, but excluded soil carbon. Predictions of carbon accumulation for the three Eucalyptus species extended to 50 years of age, which was selected as a conservative upper bound based on the age distribution of the data used for model development.
2.4.3. Predictions of Residual Carbon and Post-1990 Carbon
Residual carbon remaining following harvest is defined as the carbon stock per hectare in above-ground residual wood and below-ground roots in a cleared plantation. Annual modelling of harvest-related carbon removals was carried out by estimating the biomass of logs extracted during a simulated clear-fell event, using the Multi-Species Carbon Calculator. This simulation involved applying a log-cutting routine to modelled trees generated from a Weibull diameter distribution, with species-specific taper equations incorporated from the calculator. Logs were cut up to a height corresponding to 65% of the total tree height, using a small-end diameter threshold of 100 mm, and assuming a 4% volume loss during harvesting operations. The biomass associated with these harvested logs was deducted from the total aboveground biomass at the time of harvest. The remaining aboveground biomass was treated as logging residue and allocated to the litter pool, while all belowground biomass from harvested trees was assigned to the dead wood pool. Residual carbon was then calculated as the sum of carbon in logging slash and roots, together with existing carbon stocks in the litter and dead wood pools at the time of harvest.
The predictions of total carbon for the pre-1990 forests assume that the cleared forest had been previously planted in the same species. This previous crop included the residual decaying biomass (below ground, dead woody litter, and fine litter) from the previous rotation. Following [15], we assumed first-rotation stands were clear-felled at age 21 for all three Eucalyptus spp. Thus, the pre-1990 estimates of total carbon included both carbon accumulation and residual decaying biomass from the previous rotation, starting at age 9 years. The residual carbon from the previous crop was decayed linearly over a 10-year period to zero. This method aligns with the other pre-1990 deforestation tables in the ETS.
3. Results
3.1. Spatial Models of 300 Index and Site Index
3.1.1. Model Description and Performance
Details of the six final productivity index models are shown in Table 3. Models for both indices explained the most variation for E. nitens, followed by E. regnans, then E. fastigata, with the site index models explaining more variation than the 300 Index models (Table 3). Year of planting, tested as a proxy for improvements in management practices or planting stock genetics over time, was not a significant predictor for any of the six productivity indices. Residuals from all six models showed little apparent bias against predicted values, the key variables within each model, or a number of other important variables not included in the models, including the year of planting.

Table 3.
Statistics of models developed to predict the 300 Index and site index for the three Eucalyptus spp. Shown are the model type, root mean square error (RMSE), and coefficient of determination (R2). Also shown are the three most important variables in each model. The two model types are multiple regression (MR) and random forest (RF). The units for RMSE follow those of the two productivity indices.
The number of variables included in the models varied widely, with 4, 6, and 8 features used respectively for the 300 Index models of E. fastigata, E. regnans, and E. nitens, and 10, 13, and 19 variables used respectively for the site index models of E. fastigata, E. regnans, and E.nitens. The most important variables in the models of the 300 Index and site index for E. fastigata included rainfall, water balance, and vapour pressure deficit. The two productivity indices for E. regnans were most influenced by solar radiation, minimum air temperature, and foliage nitrogen. The most important variables in the E. nitens models of the 300 Index and site index were two proxies for air temperature (elevation, number of frosts in March), rainfall, water balance, solar radiation, and relative humidity (Table 3).
3.1.2. Raster Construction and Extraction of Regional Productivity Indices
Rasters were constructed describing spatial variation in the two productivity indices. Spatial variation in the 300 Index and site index for Eucalyptus nitens is shown in Figure 3. Given that plot data only covered the North Island for E. fastigata and E. regnans, predictions of both productivity indices for these species were masked to this region and are shown in Figure 4. Productivity indices for E. fastigata and E. regnans were averaged for each of the five North Island regions where there was sufficient underlying plot data, while indices for E. nitens were averaged across each of the nine New Zealand regions (Table 4).

Table 4.
Variation in the 300 Index and site index at the regional, Island, and national scale derived from the surfaces for the three Eucalyptus species.
The E. nitens 300 Index was highest in the Auckland, Bay of Plenty, Gisborne, and Southland regions (Figure 3). Lower values of the 300 Index for E. nitens were predicted in the dry east coast regions of both Islands. Productivity was highest in the warm, wet Bay of Plenty region for both E. fastigata and E. regnans, and lowest for both species in the drier North Island regions of Gisborne and Hawke’s Bay/southern North Island (Figure 4; Table 4), which highlighted the limiting impact of rainfall on growth for both species.
3.2. Modelled Variation in Carbon Across Scales
3.2.1. Species Variation in Carbon
Predicted changes in carbon over time for the three Eucalyptus species by Island for post-1989 forests are shown in Figure 5. As there was very little plot data for E. fastigata and E. regnans within the South Island, these predictions were restricted to the North Island for these two species. The raw predictions of carbon for each species (top panels, Figure 5) were smoothed over the two years prior to and following thinning to ensure they constantly increased at a steady rate (bottom panels, Figure 5). All figures from this point onwards use smoothed values.
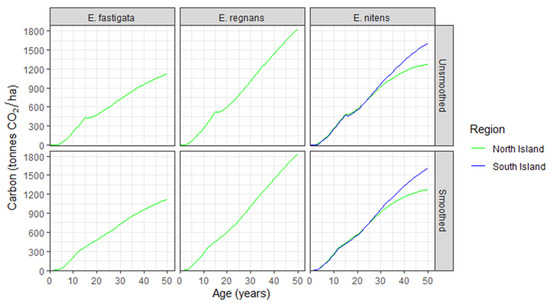
Figure 5.
Changes in predicted carbon with age for post-1989 forests, by Island, for Eucalyptus fastigata, E. regnans, and E. nitens. Predictions are shown as (upper row) unsmoothed and (lower row) smoothed.
Within the North Island, E. regnans was the most rapidly growing species, reaching respective carbon values of 1006 and 1827 tonnes CO2 ha−1 by ages 30 and 50 (Figure 5). In contrast, E. fastigata and E. nitens growing in the North Island sequestered 1123 and 1274 tonnes CO2 ha−1, respectively, by age 50. Growth of E. nitens was very similar between the North and South Islands up to age 25, after which growth diverged between Islands, reaching 1609 tonnes CO2 ha−1 at age 50 in the South Island (Figure 5). This was primarily attributable to the higher mortality rates of E. nitens within the North Island compared with the South Island. This divergence became most marked from age 25 years onwards, with stand density in the South Island exceeding that of the North Island by 21% (327 vs. 271 stems/ha), 52% (303 vs. 199 stems/ha), and 113% (267 vs. 125 stems/ha) at ages 25, 35, and 50, respectively.
3.2.2. Composite Carbon Tables
Island-Level Variation in Carbon
Composite values of Eucalyptus carbon were created for the North Island through area weighting the regional carbon for the three species. Weightings were based on the relative frequency of each species within the North Island in the FMA dataset, as these reflected the ratio of plantings for these species. These were then scaled up to the Island level through area weighting the regional predictions. As almost all FMA data in the South Island comprised E. nitens, regional predictions of carbon for this species were used in the South Island and were area-weighted by region to determine the Island-level values. New Zealand predictions of carbon were based on the composite regional values, area weighted by the nine regions. The resulting Island-level carbon trajectories for post-89 forests are shown in Figure 6, with the current MPI LUT values for exotic hardwoods shown as a reference. These values are also tabulated in Appendix A as Table A2.
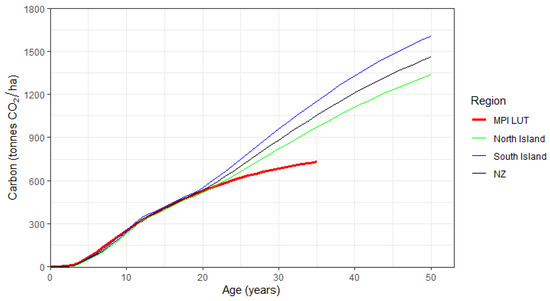
Figure 6.
Changes in predicted composite carbon with age for post-1989 Eucalyptus, by Island and for New Zealand (NZ). Also shown are MPI lookup tables (LUT) values for exotic hardwoods (thick red line).
Values of carbon in the South Island exceeded those within the North Island throughout the 50-year period (Figure 6, Table 5). These differences generally increased with age, ranging from 11% at age 10 to 20% at age 50 (1609 vs. 1340 tonnes CO2 ha−1) (Table 5). These differences were in large part due to the low mortality rate of E. nitens growing in the South Island. Using Island-level productivity indices (Table 4), the rate of mortality ranged widely following the final thinning at age 15 years. By age 50, the final crop stand density for E. nitens was 267 stems/ha within the South Island, with little variance across the four regions (ranging from 267 to 269 stems/ha). These values greatly exceeded North Island values for E. nitens (125 stems/ha), E. regnans (192 stems/ha), and E. fastigata (198 stems/ha).

Table 5.
Variation in predicted Eucalyptus carbon at ages 10 to 50 for post-1989 forests, averaged at the regional, Island, and national levels. For reference, carbon predictions from the MPI lookup tables are displayed. The percentage differences in carbon predictions between Islands are shown. The percentage regional range, with the lowest and highest carbon, is displayed. Also shown is the percentage difference between predictions and values from the MPI lookup tables (LUT) for exotic hardwoods.
At the national level, predicted carbon closely aligned with the current exotic hardwood LUT up to age 20, varying by −5.3% at age 10 (238 vs. 251 tonnes CO2 ha−1) and 1.1% at age 20 (532 vs. 526 tonnes CO2 ha−1). At ages beyond 20, there was a divergence between national carbon predictions and the current exotic hardwood LUT, with predictions exceeding the LUT by 29% and 45%, at ages 30 and 35, respectively. These general trends were consistent within both Islands, but differences between predictions and the exotic hardwood LUT were more marked at older ages within the South Island than the North Island (Table 5).
Regional Variation in Carbon
Variation in Eucalyptus carbon between the nine New Zealand regions was markedly greater than the variation between Islands (Table 5). For instance, at age 50, the Island-level variation was 20.1% but the variation across regions was 30.9%. This regional variation declined from 37.2% at age 10 to 24.4% at age 20, before increasing and plateauing at ca. 31% from ages 30 to age 50 (Table 5).
The wide regional variation was attributable to two elements. Firstly, the variation in the North Island regions was quite substantial, particularly from 10 to 20 years (Table 5; Figure 7). Secondly, regional variation increased at older ages, as carbon accumulation in the four South Island regions increased above that of all North Island regions from age 30, onwards (Table 5). Increases in carbon accumulation over time within the South Island, relative to the North Island, predominantly occurred as a result of the lower mortality rate of E. nitens stands within the South Island.
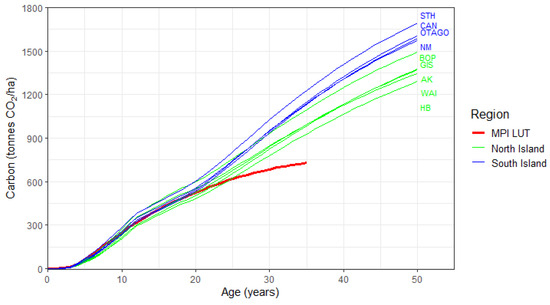
Figure 7.
Changes in predicted composite carbon with age for post-1989 Eucalyptus, by the nine regions. The regions are colour-coded by Island, with the region abbreviations shown on the right of the figure ranked in descending order for carbon. Also shown are MPI lookup tables (LUT) values for exotic hardwoods (thick red line).
Within the North Island, Hawke’s Bay/southern North Island had the lowest carbon at all ages, while the highest predicted carbon occurred within the Bay of Plenty. From 34 years onwards, carbon in the Bay of Plenty was ca. 100 tonnes CO2 ha−1 higher than the other four North Island regions, reaching differences of at least 118 tonnes CO2 ha−1 by age 50. The higher productivity of Bay of Plenty was consistent with previous research, which suggests the warm, generally wet environment of this region is most favourable for the growth of the two major constituents of the composite class—E. fastigata and E. regnans [8]. In the South Island, which was represented by E. nitens, the lowest predicted carbon occurred within Otago and Nelson/Marlborough, while the highest predicted carbon occurred in Southland, predominantly as rainfall and water balance was most favourable for E. nitens in Southland (Table 5).
With a few exceptions, predicted regional values of carbon were generally lower than those of the current exotic hardwood LUT up to age 10. However, by age 10, predicted carbon values in the Bay of Plenty and three other regions exceeded those of the LUT. This divergence increased with age; by age 21, predicted carbon in all but two regions was higher than the LUT, and by age 25, all regions had higher predicted carbon than the LUT. Although values of the current LUT were relatively similar to those of predictions up to age 20, beyond this point, predictions diverged markedly (Figure 7; Table 5). By age 35, predictions exceeded LUT values by between 27% to 68% (Figure 7). Predicted values of carbon by region are tabulated in Table A2.
3.3. Residual Carbon and Pre-1990 Carbon Tables
3.3.1. Residual Carbon
Changes in residual carbon, by Island and at the national level, are shown in Figure 8. Values were smoothed between ages 15 and 20 years following the thinning. The predicted values of residual carbon were very similar to those of the current MPI lookup tables up to age 26, after which time the residuals started diverging. By age 35, predicted residual carbon was, respectively, 15%, 22%, and 18% higher than the current MPI LUT value, for the North Island, South Island, and New Zealand (Figure 8). Values of residual carbon at the regional, Island, and national levels are given in Appendix A as Table A3.
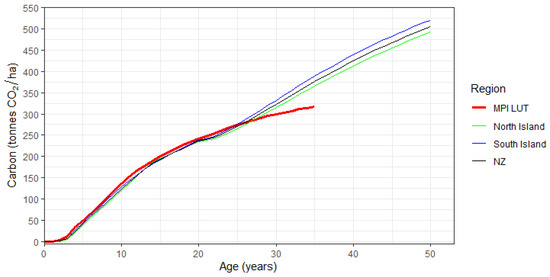
Figure 8.
Changes in predicted composite residual carbon with age for post-1989 Eucalyptus, by Island and for New Zealand (NZ). Also shown are MPI lookup tables (LUT) values for exotic hardwoods (thick red line).
3.3.2. Pre-1990 Carbon
Regional, Island-level, and national values for the pre-1990 deforestation tables are given in Appendix A as Table A4. There was no year of planting effects in any of the six productivity surface models. Therefore, predictions of carbon for a given set of productivity metrics (300 Index, site index) were the same for pre-1990 forests (Table A4) and post-1989 forests (Table A2) with the exception of the age 9 prediction, which included decomposing carbon from the previous rotation for the pre-1990 forests.
4. Discussion
4.1. Modelling Approach
The models presented in this study provide a robust hybrid framework for predicting carbon from the key environmental drivers of growth. This approach is underpinned by the empirical 300 Index growth model formulation, which is a significant advance on most empirical growth models that only use site index to account for site variation in productivity [48]. The empirical growth models are applied spatially by connecting the key growth model inputs—300 Index and site index—to the primary environmental factors influencing these productivity metrics, through the developed productivity surfaces. This approach significantly improves the generality of the models whilst maintaining the flexibility and accuracy typical of empirical models fitted to a broad network of plot measurements.
4.2. Growth Model Predictions
Data used for developing the growth models covered a wide age range for two of the three Eucalyptus spp. and an acceptable range for the third species. Age ranged from 2–66 years, 2–56 years, and 2–38 years, respectively, for E. fastigata, E. regnans, and E. nitens. Across these ranges, the models were found to fit the data very well for all three species. As the models developed for E. fastigata and E. regnans used data beyond the 50-year prediction period, these are likely to be robust. Although the age range for E. nitens was more limited, the growth model performed well to age 30 years, which is the range covered by the majority of the data. Based on a single plot, it performed well to age 40 years, and a careful examination of the MTH vs. age and DBH vs. age charts suggests that the sigmoidal growth curves used to model these variables are robust and should give reasonable results to age 50 years. Given the robustness of the sigmoidal growth functions and the age range over which accurate predictions were made, the growth predictions to 50 years should be reliable for all three species.
Although there is a paucity of data available for direct comparisons, our carbon predictions generally align with previously reported growth trends for the three Eucalyptus spp. The nearly linear increase in carbon accumulation observed up to age 50 for E. regnans is consistent with its known potential for achieving substantial forest biomass. Forests dominated by E. regnans in Australia are reportedly the most carbon-dense in the world, reaching total carbon values of 6844 tonnes CO2/ha [49], with some trees reaching heights of almost 100 m [50]. Although there is limited data on older E. nitens stands, available evidence indicates rapid initial growth rates under favourable conditions. In Australia, for the first 15 years, E. nitens has been found to out-grow E. regnans on a number of sites, while in trials in South Australia, its growth rate at age 4 years exceeded that of 34 other eucalypts [51]. Within New Zealand, when sited appropriately, E. nitens has shown exceptional growth potential, achieving heights of up to 29 m within 11 years and diameters of 60 cm at age 13 years [52]. Consistent with our results, Eucalyptus fastigata is known for its moderate growth performance in New Zealand plantations, often comparable to E. regnans at younger ages [53]. At 55 years of age, plantation-grown E. fastigata in New Zealand has been recorded reaching heights of up to 58.6 m and mean diameters of 103 cm [53], highlighting the species’ capacity for sustained growth well beyond the typical rotation length.
4.3. Productivity Surface Predictions
The coverage of environmental conditions by plot data was relatively robust within the North Island for E. fastigata and E. regnans. While several central regions of New Zealand showed limited representation of E. nitens plots, overall, the dataset captured most of the environmental range within New Zealand plantations. Nevertheless, establishing and incorporating additional E. nitens plot data from the drier east coast regions of both Islands would enhance the confidence and reliability of this model.
The predictions of the 300 Index for all three Eucalyptus species generally conformed with previous observations and research [8,10,11], which reinforced the validity of our predictions. Previous research shows that E. nitens is sensitive to drought and low rainfall [8], which largely agreed with our predictions that showed a lower 300 Index in drier east coast regions (Figure 3; Table 4). Thus, although there was a relatively low amount of data in these regions, the concordance between our predictions and previous findings does provide confidence that these predictions are robust. Similarly, both E. regnans and E. fastigata have been observed to grow best in moderately warm areas with sufficient rainfall, such as the Bay of Plenty, and both species are sensitive to drought [8,9]. Predictions from the modelling showed high values of the 300 Index for both species in the Bay of Plenty, while the lowest values were in the drier Gisborne and Hawke’s Bay regions.
Eucalyptus nitens is generally considered better suited to New Zealand’s cooler regions [8,9], due to its cold tolerance and the increased impact of pests and diseases on the species in warmer climates [10]. However, studies also show that E. nitens grows well across a wide range of New Zealand’s climatic conditions [10,11]. Our results provide insight into the reason for these apparently contrasting findings. The predicted 300 Index for E. nitens was very similar between the North Island and the South Island (21.1 vs. 21.4 m3 ha−1 yr−1; Table 4), indicating growth rates for E. nitens are similar between Islands to age 30 years. Although this might suggest that the North Island is well suited to the species, this will largely depend on the rotation length, as predicted mortality was much higher in the North Island, detrimentally impacting carbon at older ages (see Section 4.4).
4.4. Carbon Predictions
Predictions of carbon for E. nitens were greater within the South Island than the North Island, particularly at older ages, reaching a maximum difference of 26% by age 50 (1609 vs. 1274 tonnes CO2 ha−1). As the E. nitens MTH and DBH models did not differ between Islands and the 300 Indices were very similar between Islands (21.1 vs. 21.4 m3/ha/yr), these differences were almost entirely attributable to the predicted higher mortality rate of E. nitens in the North Island. The increased mortality for E. nitens in the North Island at older ages most likely reflected the increased prevalence of pests and diseases within the warmer North Island, than the cooler conditions of the South Island. This divergence in stand density became most marked from 25 years onwards, and stand density in the South Island exceeded that of the North Island by 21% (327 vs. 271 stems/ha), 52% (303 vs. 199 stems/ha) and 113% (267 vs. 125 stems/ha) at ages 25, 35, and 50, respectively. This increased mortality rate was largely responsible for the divergence in carbon between the two Islands from age 25 years, onwards.
Similarly, predictions of carbon for E. nitens in the South Island were higher than the composite North Island predictions, which were primarily based on E. fastigata (65% weighting), E. regnans (30% weighting), and to a very minor extent E. nitens (5% weighting). These predictions diverged over time with the South Island carbon predictions exceeding those in the North Island by 20% at age 50 (1609 vs. 1340 tonnes CO2 ha−1). Given that E. fastigata was the largest component of North Island carbon predictions, this divergence was primarily attributable to the difference in growth curves between South Island E. nitens and E. fastigata. While E. fastigata growth rates slowed at older ages, the growth rates for E. nitens in the South Island remained relatively linear beyond 30 years of age (Figure 5). These differences in the growth pattern were predominantly attributable to the higher mortality rate for E. fastigata, with final crop stand density for E. nitens exceeding that of E. fastigata by 35% at age 50 (267 vs. 198 stems/ha).
4.5. Comparison of Growth with Other Eucalypts and Exotic Hardwood Species
Publicly available growth data is sparse for species other than the three Eucalyptus spp. studied here within the exotic hardwood category. Acacia spp. have been established at scale in the past within New Zealand. The most widely established species is Acacia melanoxylon (blackwood), while the second most widely planted species is Acacia dealbata (silver wattle) [7]. The site index for blackwood ranges from 15 to 45 m [6], which is at the lower end of the site indices for the three studied Eucalyptus spp., which averaged between 39.1 and 44.7 m within the North Island. The reported volume mean annual increments for blackwood range widely, but a total volume of 500 m3/ha at age 37.5 years on a suitable site is likely [6], which would give a mean annual increment (MAI) of 13.3 m3/ha/yr. This MAI is lower than the composite Eucalyptus 300 index of 19.5 m3/ha/yr for the North Island documented in this study. However, it is worth noting the high basic density of A. melanoxylon in trees that are 10 years and older, which ranges from 465 to 670 kg/m3 [6], and generally exceeds the values for the three eucalypts documented here. These high values of basic density would result in carbon that is closer to that of the composite Eucalyptus carbon predictions than volume. Silver wattle has been reported to have high growth rates, comparable to those of eucalypts such as E. nitens [7]. However, as there is a shortage of data, especially at older ages, predictions at older ages are likely to be speculative. It is also worth noting that silver wattle is relatively short-lived [7].
Poplars have been widely established on New Zealand farms and are generally regarded as fast-growing. The volume growth of poplar species under standard sawlog regimes predicted by a growth model has been found to yield an average MAI of 18.6 m3/ha/yr [7]. This value is slightly lower than the national 300 Index found in this study (20.4 m3/ha/yr) but close to the composite Eucalyptus 300 Index of 19.5 m3/ha/yr within the North Island.
Documented growth rates for other relatively widely grown Eucalyptus spp. vary considerably. Eucalyptus saligna is capable of fast growth rates, and recent analysis of PSP data indicates a mean 300 Index of 19 m3/ha/yr within its northern North Island range, which is consistent with growth in the natural range in Australia, where the growth rate is >20 m3/ha/yr [54]. Within the natural Australian range, E. pilularis, E. bosistoana are regarded as fast-growing (>20 m3/ha/yr), E. microcorys and E. muelleriana have a moderate growth rate (10–15 m3/ha/yr), while E. cladocalyx is slow growing (<5 m3/ha/yr) [54]. These comparisons suggest that the predictions of carbon made within this study are likely to be similar to poplar and many other widely established Eucalyptus spp. and slightly higher than that of Acacia spp., but more research would be required to confirm this is the case.
The carbon predictions presented here generally align with previous estimates for dryland eucalypts, which is significant given their growing popularity as afforestation species [16]. Within New Zealand, predictions of carbon for E. bosistoana over a 50-year period were made at two sites with contrasting productivity in Marlborough [55]. Predictions at the high productivity site were very similar to our Nelson/Marlborough estimates over the rotation, reaching ca. 1500 tonnes CO2 ha−1 at age 50, which is only slightly lower than our predictions of 1571 tonnes CO2 ha−1. Predicted carbon at the low productivity site was lower than our predictions, reaching ca. 1200 tonnes CO2 ha−1 at age 50. This difference was expected, as our regional averages include higher-productivity areas, while site-specific predictions in dry parts of Marlborough are characterised by some of the lower 300 Indices for E. nitens in New Zealand, reflecting the very low rainfall of these areas. Importantly, both sets of predictions showed increasing carbon over the 50-year period. Consistent with our findings, carbon at the high-productivity site surpassed the current lookup tables by around age 22, while at the low-productivity site, this occurred closer to age 35 [55].
Regional predictions of Eucalyptus carbon made in this study show that Southland has the highest productivity among all regions. The colder climate of Southland would not suit Eucalyptus species such as E. saligna, which is sensitive to hard frosts [8,56] but is suited to E. delegatensis, which is a more cold tolerant species [8,57]. As A. melanoxylon is frost-prone [6], growth rates are likely to be relatively low in Southland. Although growth and survival rates will not be high in Southland for all exotic hardwoods, it is very likely that appropriate species, such as E. nitens, will be established in this region. Clearly, this has been the case for many established areas ≥ 100 ha in size, as among the three species studied here, all of the FMA plots in Southland comprised E. nitens (Table 1).
4.6. Limitations and Considerations
The collection of additional underpinning plot data would improve confidence in the spatial predictions of productivity. The plot data provided robust coverage of environmental conditions for E. fastigata and E. regnans within the North Island. However, the inclusion of additional E. nitens plot data from the drier east coast regions of both Islands would likely improve the accuracy of both productivity surfaces within these dryland areas. The collection of additional data from E. nitens stands over 30 years would improve confidence in older age growth model predictions for this species.
It is possible that the carbon tables shown here, which are intended for areas <100 ha will overestimate carbon, as these tables were derived from FMA plot data extracted from areas ≥100 ha in size, which may be more professionally managed than smaller woodlots. However, the counterargument to this would be that farm woodlots have higher productivity than larger forests, as smaller woodlots often occur on farms with a long history of fertiliser addition that is less common in larger forests. It is well known that soil fertility is on average higher on ex-pasture sites than on previously forested sites [58]. However, in the absence of data directly comparing productivity between smaller and larger woodlots, we cannot quantify this potential difference. We raise this as an important consideration when applying the carbon tables to smaller areas.
The regional boundaries used in the default carbon tables are administrative and therefore not strictly based on geo-climatic factors. While many of the regions do have similar climatic conditions throughout, some regions, such as Canterbury/West Coast, include a wide climatic range. Therefore, the provision of carbon tables at a regional scale will only partly mitigate the influence of geo-climatic factors on carbon. Furthermore, even if carbon tables are constructed at the regional level, growers of stands in harsh conditions will always be rewarded, whilst those on good sites are penalised. Similarly, some growers may plant stands at low stand densities to reduce establishment costs but claim carbon credits based on the tables that are greater than the carbon actually being sequestered. Although some areas may not be suitable for particular exotic hardwoods (e.g., frost-prone species being grown in Southland), some growers may elect to establish these species, which could result in poor survival and growth lower than the carbon values shown here.
The composite values of carbon for the North Island were derived from the ratios of plots in the FMA dataset for the three Eucalyptus spp. covering the 2011–2020 period. These weightings were, respectively, 65%, 35%, and 5% for E. fastigata, E. regnans, and E. nitens. The planted weighting of E. fastigata, E. regnans, and E. nitens changed through time, with the frequency of E. nitens declining rapidly after 2000, with the two other species showing concomitant increases. In contrast, it was assumed that E. nitens was representative of South Island plantings, as this species constituted 98.6% of the South Island FMA plots. It is worth noting that these weightings may change in the future, and other species such as dryland eucalypts may become more commonly planted. Consequently, the species mix included for the composite predictions should be regularly reviewed to ensure that these predictions are representative of sequestered carbon within the exotic hardwood class.
Our research aligns with previous findings that E. fastigata, E. regnans, and E. nitens are sensitive to drought [8,9]. In contrast, a number of durable eucalypts—such as E. cladocalyx, E. globoidea, E. microcorys, E. muelleriana, and E. pilularis—have moderate to high drought tolerance [8,9] and can grow quite rapidly under conditions with low to moderate rainfall. Further research should compare the growth rates of the three species studied here with dryland Eucalyptus species within drier east coast regions.
Finally, while empirical and hybrid models, such as the one applied in this study, deliver robust carbon estimates, their predictions are inherently limited to the environmental conditions present during data collection. Consequently, these models may perform poorly under novel conditions, particularly those arising from climate change. In contrast, process-based models such as CABALA [59] have the potential to yield more reliable carbon predictions under changing climates. However, their application is limited by the extensive data required for accurate parameterisation, and such models have not yet been developed for most species under New Zealand conditions. The modelling approach employed here incorporates the historical average impacts of biotic factors through the plot data used for model fitting. However, predictions from this model do not account for potential increases in the severity of existing diseases or the emergence of new pathogens. To ensure the lookup tables accurately reflect evolving changes in biotic impacts and climatic conditions, regular updates using recent plot data within the hybrid modelling framework described in this study should be undertaken.
4.7. Effect of Climate Change on Predictions
Climate projections for New Zealand under mid-range emissions scenarios indicate an average temperature increase of approximately 1.4 °C by the year 2090, relative to the 1986–2005 baseline period [60]. Anticipated changes in annual rainfall patterns suggest a decline in precipitation across the northern and eastern parts of the North Island, while most other regions are expected to see increases, particularly along the South Island’s west coast [60]. When viewed in context, the projected temperature increase represents a relatively small proportion of the current range of mean air temperatures across New Zealand plantations, which spans approximately 8–16 °C. Based on the modelling in this report, productivity for E. fastigata and E. regnans is likely to increase in many parts of the South Island as temperatures rise. However, in Northland and the upper North Island, E. regnans may experience reduced productivity due to the warmer climate. For E. nitens, rising temperatures are likely to increase pest activity in warmer regions of the South Island, potentially leading to higher mortality rates. Additionally, reduced rainfall in the east and north of the North Island is likely to negatively impact the productivity of all three species. However, the response of Eucalyptus species to increasing atmospheric carbon dioxide concentrations ([CO2]) is likely to be a dominant factor and may partially mitigate the adverse effects of drought.
Previous research undertaken on the response of Eucalyptus spp. in Australia to climate change may provide some insight into the potential response in New Zealand. Within Australia, the main impacts of climate change on Eucalyptus spp. are mediated through changes in air temperature, drought, fire risk, pest infestations, and changes in [CO2] [61]. The CABALA process-based model has been used to predict the impacts of climate change on Australian eucalypt plantations [62]. Despite uncertainties around the response to increasing [CO2], there were regions under climate change that were likely to increase in productivity (e.g., E. nitens plantations in Tasmania), while other areas were likely to increase in productivity with some increase in risk (e.g., E nitens in Victoria and the Green Triangle area). Some regions were likely to suffer decreases in production and an increase in risk (e.g., E. globulus plantations in Western Australia). The general conclusion from this study was that impacts of climate change on eucalypt plantation productivity are likely to be highly site-specific and will depend in part on the balance between the possibly detrimental effects of increased temperatures and rainfall reductions in some areas versus the potential productivity gains through elevated [CO2] [62]. However, a fairly clear finding from this research was that regardless of the assumption around increases in [CO2], there were uniform increases in productivity for E. nitens and E. globulus within cooler regions, such as Tasmania and parts of Victoria, which ranged from 0 to 40% by 2070 [62].
Climate change impacts in New Zealand will not be as severe as in Australia. Given that milder areas of Australia, such as Tasmania and parts of Victoria, have a relatively close climatic match with New Zealand, it seems reasonable to assume future changes in the productivity of Eucalyptus spp. within New Zealand will reflect changes in these areas. Consequently, it is likely that there will be modest to moderate increases in the growth of Eucalyptus spp. over the remainder of the century within New Zealand.
5. Conclusions
Composite carbon tables were generated from species-specific models, using weighted averages of all three Eucalyptus spp. for the North Island, and E. nitens for the South Island, where this is the most commonly planted Eucalyptus species. Predicted carbon at ages 30 and 50 within the South Island exceeded values within the North Island by 17% (958 vs. 820 tonnes CO2 ha−1) and 20% (1609 vs. 1340 tonnes CO2 ha−1), respectively. Regional variation in carbon was greater than Island-level variation at all ages, with predicted carbon at age 50 highest in Southland (1691 tonnes CO2 ha−1) and lowest in Hawke’s Bay/southern North Island (1292 tonnes CO2 ha−1). Predictions of carbon in the North and South Islands were very similar to values in the current exotic hardwoods LUT until age 20. Above this age, carbon predictions increased markedly, with national values exceeding LUT estimates by 45% at age 35 (1055 vs. 729 tonnes CO2 ha−1). The development of regional LUTs would provide a means of incentivising the establishment of Eucalyptus spp. in regions that are most suited to these species. However, the government may consider factors beyond the technical considerations outlined here when updating the LUTs.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/f16071070/s1, Supplementary Material S1. Growth modelling methodology; Supplementary Material S2. Growth modelling results.
Author Contributions
Conceptualization, M.S.W., M.O.K. and M.N.S.; methodology, M.S.W. and M.O.K.; software, M.O.K.; validation, M.S.W. and M.O.K.; formal analysis, M.S.W. and M.O.K.; investigation, M.S.W. and M.O.K.; resources, M.S.W.; data curation, M.S.W., B.S.C.S., M.O.K. and M.N.S.; writing—original draft preparation, M.S.W. and M.O.K.; writing—review and editing, M.S.W., B.S.C.S., M.O.K. and M.N.S.; visualization, M.S.W., B.S.C.S. and M.O.K.; supervision, M.S.W.; project administration, M.S.W. and M.N.S.; funding acquisition, M.S.W. and M.N.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the Ministry for Primary Industries, agreement number C0036286.
Data Availability Statement
The data used in this study cannot be made publicly available due to privacy restrictions imposed by the forest owners and managers.
Acknowledgments
We thank Steven Dovey and Yvette Dickinson for the management of the project, and Steve Wakelin and Nicolò Camarretta for undertaking internal reviews of the report. We are also grateful to Emily Geck and Lauretta Bensemann for comments that have greatly improved the manuscript. We thank the three anonymous reviewers for their comments, which have greatly improved the manuscript.
Conflicts of Interest
Author Mark O. Kimberley was employed by the company Environmental Statistics Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DBH | Diameter at breast height |
| ETS | New Zealand’s Emissions Trading Scheme |
| FMA | Field measurement approach |
| LUT | Lookup table |
| MTH | Mean top height (mean height of the 100 largest diameter trees per hectare) |
| MPI | Ministry for Primary Industries |
| PSP | Permanent sample plot |
| RMSE | Root mean square error |
Appendix A

Table A1.
Continuous variables included in the analysis. For each variable, the units, abbreviation, and reference for the variable are given.
Table A1.
Continuous variables included in the analysis. For each variable, the units, abbreviation, and reference for the variable are given.
| Variable | Units | Abbreviation | References |
|---|---|---|---|
| Climatic variables | |||
| Air temperature—mean, max, min. | °C | Tmean, Tmin, Tmax | [32] |
| Degree ground frost (frosts/month) | days | DGF | [31] |
| Growing degree days | Degree days | GDD | [31] |
| Rainfall | mm | Rain | [32] |
| Rainfall days | days year−1 | Rain days | [32] |
| Relative humidity at 9 a.m. | % | RH | [32] |
| Solar radiation | MJ m−2 day−1 | S Rad | [32] |
| Sunshine hours | hours | Sun hours | [32] |
| Windspeed | km h−1 | Wind | [32] |
| Water balance | |||
| Annual water deficit | mm | AWD | [36,63] |
| Drainage | mm | Drain | [36,63] |
| Gravel content | % | GC | [35] |
| Percentage root zone water balance | % | Wbal | [64] |
| Plant rooting depth | mm | PRD | [35] |
| Profile available water content | mm | PAW | [35] |
| Profile readily available water | mm | PRAW | [35] |
| Rainfall/potential evapotranspiration | RPet | [36,63] | |
| Topographic wetness index | TWI | [65] | |
| Edaphic variables | |||
| Carbon: nitrogen ratio | CN ratio | [34] | |
| Macroporosity | % | Macro | [35] |
| Particle size | [36,63] | ||
| pH | pH | [35] | |
| Phosphorus retention | % | P retention | [35] |
| Topographic and landscape | |||
| Aspect | ° | Aspect | [36,63] |
| Distance to stream | m | DTS | [33] |
| Elevation | m | Elev | [37] |
| Multiresolution ridge top flatness | MrRFT | [66] | |
| Multiresolution valley bottom flatness | MrVBF | [66] | |
| Profile curvature | Profc | [66] | |
| Slope | ° | Slope | [33] |
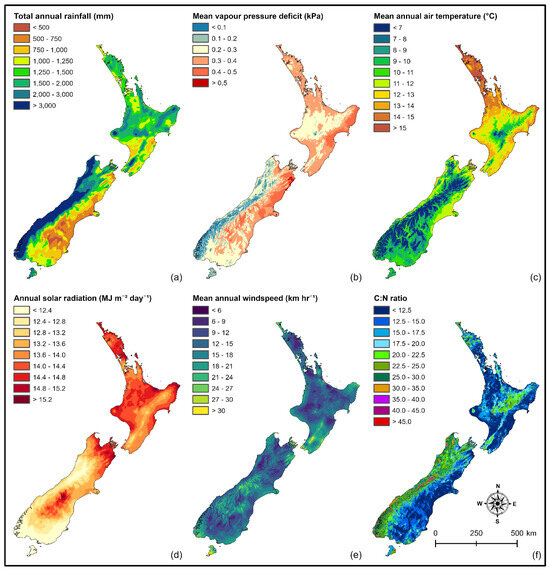
Figure A1.
Spatial variation in important climatic and edaphic variables: (a) total annual rainfall, (b) mean vapour pressure deficit, (c) mean annual air temperature, (d) mean annual total daily solar radiation, (e) mean annual windspeed, and (f) C:N ratio.

Table A2.
Draft regional, Island-level, and national carbon stock per hectare for Eucalyptus spp. on post-1989 forest land (tonnes CO2/ha). Key: NI, North Island; SI, South Island; NZ, New Zealand.
Table A2.
Draft regional, Island-level, and national carbon stock per hectare for Eucalyptus spp. on post-1989 forest land (tonnes CO2/ha). Key: NI, North Island; SI, South Island; NZ, New Zealand.
| Age (yrs) | Ak | W/T | BOP | Gis | H/SNIII | N/M | C/W | O | S | NI | SI | NZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 0.2 | 0.2 | 0.3 | 0.1 | 0.2 | 0.5 | 0.4 | 0.3 | 0.2 | 0.2 | 0.3 | 0.3 |
| 2 | 1 | 2 | 2 | 1 | 1 | 3 | 2 | 2 | 1 | 1 | 2 | 2 |
| 3 | 6 | 7 | 8 | 5 | 5 | 9 | 7 | 7 | 12 | 6 | 8 | 7 |
| 4 | 22 | 26 | 28 | 20 | 19 | 30 | 26 | 24 | 35 | 22 | 27 | 24 |
| 5 | 47 | 54 | 59 | 44 | 42 | 61 | 55 | 52 | 71 | 47 | 57 | 51 |
| 6 | 74 | 83 | 91 | 68 | 66 | 92 | 84 | 80 | 105 | 73 | 87 | 79 |
| 7 | 107 | 119 | 131 | 99 | 96 | 129 | 119 | 115 | 146 | 106 | 124 | 114 |
| 8 | 145 | 161 | 175 | 135 | 130 | 171 | 160 | 155 | 191 | 143 | 165 | 153 |
| 9 | 187 | 205 | 223 | 173 | 168 | 215 | 202 | 196 | 238 | 184 | 208 | 195 |
| 10 | 231 | 253 | 274 | 214 | 209 | 260 | 246 | 239 | 286 | 227 | 252 | 238 |
| 11 | 277 | 302 | 326 | 258 | 251 | 305 | 289 | 282 | 334 | 272 | 297 | 283 |
| 12 | 324 | 353 | 380 | 302 | 295 | 351 | 333 | 325 | 382 | 319 | 341 | 329 |
| 13 | 350 | 379 | 409 | 328 | 320 | 376 | 358 | 350 | 409 | 345 | 366 | 355 |
| 14 | 377 | 406 | 438 | 354 | 345 | 401 | 384 | 375 | 435 | 371 | 392 | 380 |
| 15 | 402 | 432 | 467 | 380 | 369 | 426 | 409 | 401 | 462 | 397 | 417 | 406 |
| 16 | 430 | 459 | 496 | 406 | 394 | 451 | 435 | 426 | 489 | 423 | 443 | 432 |
| 17 | 457 | 485 | 525 | 432 | 419 | 476 | 460 | 451 | 516 | 449 | 469 | 458 |
| 18 | 483 | 512 | 554 | 458 | 444 | 501 | 486 | 476 | 542 | 475 | 494 | 483 |
| 19 | 502 | 529 | 573 | 479 | 462 | 526 | 512 | 502 | 569 | 493 | 520 | 505 |
| 20 | 526 | 551 | 598 | 503 | 484 | 556 | 543 | 533 | 602 | 515 | 552 | 532 |
| 21 | 552 | 575 | 626 | 530 | 509 | 590 | 579 | 568 | 638 | 541 | 587 | 562 |
| 22 | 581 | 603 | 657 | 560 | 536 | 627 | 617 | 606 | 678 | 569 | 625 | 594 |
| 23 | 611 | 631 | 689 | 591 | 565 | 666 | 656 | 645 | 719 | 599 | 665 | 629 |
| 24 | 643 | 661 | 723 | 623 | 595 | 705 | 698 | 686 | 762 | 629 | 706 | 664 |
| 25 | 675 | 692 | 757 | 656 | 625 | 746 | 740 | 727 | 806 | 661 | 748 | 700 |
| 26 | 708 | 723 | 792 | 690 | 656 | 787 | 782 | 769 | 850 | 693 | 790 | 737 |
| 27 | 741 | 754 | 827 | 723 | 687 | 828 | 824 | 811 | 894 | 725 | 833 | 774 |
| 28 | 774 | 785 | 862 | 757 | 718 | 869 | 867 | 853 | 938 | 757 | 875 | 810 |
| 29 | 806 | 816 | 897 | 791 | 749 | 909 | 909 | 895 | 982 | 788 | 917 | 847 |
| 30 | 839 | 847 | 932 | 824 | 780 | 949 | 950 | 936 | 1025 | 820 | 958 | 883 |
| 31 | 871 | 877 | 966 | 857 | 811 | 988 | 991 | 977 | 1067 | 851 | 999 | 918 |
| 32 | 902 | 907 | 1000 | 890 | 841 | 1027 | 1032 | 1017 | 1109 | 882 | 1040 | 953 |
| 33 | 933 | 936 | 1033 | 922 | 871 | 1065 | 1071 | 1056 | 1149 | 913 | 1079 | 988 |
| 34 | 964 | 965 | 1065 | 953 | 900 | 1102 | 1110 | 1094 | 1189 | 942 | 1118 | 1022 |
| 35 | 994 | 993 | 1097 | 984 | 929 | 1138 | 1148 | 1132 | 1228 | 972 | 1155 | 1055 |
| 36 | 1023 | 1021 | 1129 | 1015 | 957 | 1173 | 1185 | 1168 | 1266 | 1001 | 1192 | 1087 |
| 37 | 1052 | 1048 | 1159 | 1045 | 984 | 1208 | 1221 | 1204 | 1303 | 1029 | 1228 | 1119 |
| 38 | 1080 | 1074 | 1189 | 1074 | 1012 | 1241 | 1256 | 1239 | 1338 | 1056 | 1263 | 1150 |
| 39 | 1108 | 1100 | 1218 | 1103 | 1038 | 1274 | 1290 | 1273 | 1373 | 1083 | 1297 | 1180 |
| 40 | 1135 | 1126 | 1247 | 1131 | 1064 | 1305 | 1323 | 1306 | 1407 | 1110 | 1330 | 1210 |
| 41 | 1161 | 1150 | 1275 | 1158 | 1090 | 1336 | 1355 | 1337 | 1440 | 1136 | 1362 | 1238 |
| 42 | 1186 | 1174 | 1302 | 1185 | 1114 | 1365 | 1386 | 1369 | 1471 | 1161 | 1393 | 1266 |
| 43 | 1211 | 1198 | 1328 | 1211 | 1139 | 1394 | 1417 | 1399 | 1502 | 1185 | 1423 | 1293 |
| 44 | 1236 | 1221 | 1354 | 1236 | 1162 | 1422 | 1446 | 1428 | 1532 | 1209 | 1452 | 1319 |
| 45 | 1259 | 1243 | 1379 | 1261 | 1185 | 1449 | 1475 | 1456 | 1561 | 1233 | 1480 | 1345 |
| 46 | 1282 | 1264 | 1403 | 1285 | 1208 | 1475 | 1502 | 1483 | 1588 | 1255 | 1508 | 1370 |
| 47 | 1305 | 1285 | 1427 | 1309 | 1230 | 1500 | 1529 | 1510 | 1615 | 1277 | 1534 | 1394 |
| 48 | 1326 | 1306 | 1450 | 1332 | 1251 | 1524 | 1555 | 1536 | 1641 | 1299 | 1560 | 1417 |
| 49 | 1347 | 1326 | 1473 | 1354 | 1272 | 1548 | 1580 | 1561 | 1666 | 1320 | 1585 | 1440 |
| 50 | 1368 | 1345 | 1494 | 1376 | 1292 | 1571 | 1604 | 1585 | 1691 | 1340 | 1609 | 1462 |

Table A3.
Draft regional, Island-level, and national-level above-ground residual wood and below-ground roots from cleared Eucalyptus spp. (tonnes CO2/ha).
Table A3.
Draft regional, Island-level, and national-level above-ground residual wood and below-ground roots from cleared Eucalyptus spp. (tonnes CO2/ha).
| Age (yrs) | Ak | W/T | BOP | Gis | H/SNIII | N/M | C/W | O | S | NI | SI | NZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 0.2 | 0.2 | 0.3 | 0.1 | 0.2 | 0.5 | 0.4 | 0.3 | 0.2 | 0.2 | 0.3 | 0.3 |
| 2 | 1 | 2 | 2 | 1 | 1 | 3 | 2 | 2 | 1 | 1 | 2 | 2 |
| 3 | 6 | 7 | 8 | 5 | 5 | 9 | 7 | 7 | 12 | 6 | 8 | 7 |
| 4 | 22 | 26 | 28 | 20 | 19 | 30 | 26 | 24 | 35 | 22 | 27 | 24 |
| 5 | 38 | 44 | 47 | 35 | 34 | 47 | 42 | 41 | 52 | 38 | 44 | 41 |
| 6 | 57 | 63 | 67 | 53 | 52 | 66 | 61 | 59 | 74 | 56 | 63 | 59 |
| 7 | 72 | 80 | 85 | 67 | 66 | 83 | 77 | 75 | 91 | 72 | 79 | 75 |
| 8 | 88 | 97 | 103 | 83 | 81 | 100 | 94 | 91 | 109 | 88 | 96 | 92 |
| 9 | 105 | 115 | 122 | 98 | 97 | 116 | 110 | 108 | 127 | 104 | 113 | 108 |
| 10 | 122 | 132 | 142 | 114 | 112 | 132 | 126 | 123 | 143 | 120 | 129 | 124 |
| 11 | 138 | 150 | 160 | 129 | 128 | 147 | 140 | 136 | 158 | 137 | 143 | 139 |
| 12 | 155 | 168 | 179 | 146 | 143 | 160 | 153 | 150 | 172 | 153 | 157 | 155 |
| 13 | 172 | 185 | 198 | 162 | 159 | 174 | 167 | 164 | 187 | 170 | 170 | 170 |
| 14 | 189 | 203 | 218 | 179 | 175 | 188 | 180 | 177 | 201 | 187 | 184 | 185 |
| 15 | 198 | 211 | 226 | 187 | 183 | 196 | 189 | 186 | 210 | 195 | 193 | 194 |
| 16 | 206 | 219 | 235 | 196 | 190 | 205 | 198 | 195 | 220 | 203 | 202 | 202 |
| 17 | 214 | 227 | 244 | 204 | 198 | 214 | 208 | 204 | 229 | 211 | 211 | 211 |
| 18 | 223 | 235 | 253 | 213 | 206 | 222 | 217 | 213 | 239 | 219 | 220 | 219 |
| 19 | 231 | 242 | 262 | 221 | 214 | 231 | 226 | 222 | 248 | 227 | 229 | 228 |
| 20 | 239 | 250 | 271 | 229 | 221 | 240 | 235 | 231 | 258 | 235 | 238 | 236 |
| 21 | 242 | 252 | 273 | 233 | 224 | 243 | 239 | 235 | 261 | 238 | 242 | 240 |
| 22 | 248 | 256 | 278 | 239 | 229 | 249 | 245 | 241 | 267 | 243 | 248 | 245 |
| 23 | 254 | 262 | 285 | 246 | 236 | 256 | 253 | 250 | 275 | 249 | 256 | 252 |
| 24 | 262 | 269 | 293 | 255 | 244 | 265 | 263 | 259 | 284 | 257 | 265 | 261 |
| 25 | 271 | 277 | 302 | 264 | 252 | 274 | 273 | 269 | 295 | 265 | 276 | 270 |
| 26 | 281 | 286 | 312 | 274 | 261 | 284 | 284 | 280 | 305 | 275 | 286 | 280 |
| 27 | 290 | 295 | 322 | 285 | 271 | 295 | 295 | 291 | 317 | 284 | 298 | 290 |
| 28 | 300 | 304 | 333 | 296 | 280 | 306 | 307 | 303 | 328 | 294 | 309 | 301 |
| 29 | 311 | 314 | 344 | 306 | 290 | 317 | 318 | 314 | 340 | 304 | 321 | 312 |
| 30 | 321 | 323 | 355 | 317 | 300 | 328 | 330 | 326 | 352 | 315 | 332 | 323 |
| 31 | 332 | 333 | 366 | 328 | 310 | 339 | 342 | 337 | 364 | 325 | 344 | 333 |
| 32 | 342 | 343 | 377 | 339 | 320 | 350 | 353 | 349 | 376 | 335 | 355 | 344 |
| 33 | 352 | 353 | 388 | 350 | 330 | 361 | 364 | 360 | 387 | 345 | 366 | 355 |
| 34 | 363 | 362 | 399 | 361 | 340 | 371 | 375 | 371 | 398 | 355 | 377 | 365 |
| 35 | 373 | 372 | 410 | 371 | 349 | 381 | 386 | 382 | 409 | 365 | 388 | 375 |
| 36 | 383 | 381 | 421 | 382 | 359 | 391 | 397 | 392 | 420 | 375 | 399 | 386 |
| 37 | 392 | 391 | 431 | 392 | 368 | 401 | 407 | 402 | 431 | 384 | 409 | 396 |
| 38 | 402 | 400 | 441 | 402 | 378 | 411 | 418 | 412 | 441 | 394 | 419 | 405 |
| 39 | 411 | 409 | 451 | 412 | 387 | 420 | 428 | 422 | 451 | 403 | 429 | 415 |
| 40 | 421 | 417 | 461 | 422 | 396 | 429 | 437 | 432 | 461 | 412 | 439 | 424 |
| 41 | 430 | 426 | 471 | 431 | 404 | 438 | 447 | 441 | 471 | 421 | 448 | 433 |
| 42 | 439 | 434 | 480 | 441 | 413 | 446 | 456 | 450 | 480 | 430 | 457 | 442 |
| 43 | 447 | 442 | 490 | 450 | 422 | 455 | 464 | 459 | 489 | 439 | 466 | 451 |
| 44 | 456 | 450 | 498 | 458 | 430 | 463 | 473 | 468 | 497 | 447 | 474 | 459 |
| 45 | 464 | 458 | 507 | 467 | 438 | 471 | 481 | 475 | 505 | 455 | 482 | 467 |
| 46 | 472 | 466 | 516 | 476 | 446 | 478 | 490 | 484 | 514 | 463 | 491 | 475 |
| 47 | 480 | 473 | 524 | 484 | 453 | 486 | 497 | 492 | 521 | 471 | 498 | 483 |
| 48 | 488 | 481 | 533 | 492 | 461 | 493 | 505 | 499 | 529 | 478 | 506 | 491 |
| 49 | 495 | 488 | 541 | 500 | 468 | 500 | 512 | 506 | 537 | 486 | 513 | 498 |
| 50 | 502 | 494 | 548 | 508 | 475 | 506 | 519 | 514 | 544 | 493 | 520 | 505 |

Table A4.
Draft regional, Island-level, and national carbon stock per hectare for Eucalyptus spp. on pre-1990 forest land (tonnes CO2/ha). Key: NI, North Island; SI, South Island; NZ, New Zealand.
Table A4.
Draft regional, Island-level, and national carbon stock per hectare for Eucalyptus spp. on pre-1990 forest land (tonnes CO2/ha). Key: NI, North Island; SI, South Island; NZ, New Zealand.
| Age (yrs) | Ak | W/T | BOP | Gis | H/SNIII | N/M | C/W | O | S | NI | SI | NZ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 211 | 230 | 250 | 197 | 191 | 240 | 226 | 220 | 265 | 208 | 232 | 219 |
| 10 | 231 | 253 | 274 | 214 | 209 | 260 | 246 | 239 | 286 | 227 | 252 | 238 |
| 11 | 277 | 302 | 326 | 258 | 251 | 305 | 289 | 282 | 334 | 272 | 297 | 283 |
| 12 | 324 | 353 | 380 | 302 | 295 | 351 | 333 | 325 | 382 | 319 | 341 | 329 |
| 13 | 350 | 379 | 409 | 328 | 320 | 376 | 358 | 350 | 409 | 345 | 366 | 355 |
| 14 | 377 | 406 | 438 | 354 | 345 | 401 | 384 | 375 | 435 | 371 | 392 | 380 |
| 15 | 402 | 432 | 467 | 380 | 369 | 426 | 409 | 401 | 462 | 397 | 417 | 406 |
| 16 | 430 | 459 | 496 | 406 | 394 | 451 | 435 | 426 | 489 | 423 | 443 | 432 |
| 17 | 457 | 485 | 525 | 432 | 419 | 476 | 460 | 451 | 516 | 449 | 469 | 458 |
| 18 | 483 | 512 | 554 | 458 | 444 | 501 | 486 | 476 | 542 | 475 | 494 | 483 |
| 19 | 502 | 529 | 573 | 479 | 462 | 526 | 512 | 502 | 569 | 493 | 520 | 505 |
| 20 | 526 | 551 | 598 | 503 | 484 | 556 | 543 | 533 | 602 | 515 | 552 | 532 |
| 21 | 552 | 575 | 626 | 530 | 509 | 590 | 579 | 568 | 638 | 541 | 587 | 562 |
| 22 | 581 | 603 | 657 | 560 | 536 | 627 | 617 | 606 | 678 | 569 | 625 | 594 |
| 23 | 611 | 631 | 689 | 591 | 565 | 666 | 656 | 645 | 719 | 599 | 665 | 629 |
| 24 | 643 | 661 | 723 | 623 | 595 | 705 | 698 | 686 | 762 | 629 | 706 | 664 |
| 25 | 675 | 692 | 757 | 656 | 625 | 746 | 740 | 727 | 806 | 661 | 748 | 700 |
| 26 | 708 | 723 | 792 | 690 | 656 | 787 | 782 | 769 | 850 | 693 | 790 | 737 |
| 27 | 741 | 754 | 827 | 723 | 687 | 828 | 824 | 811 | 894 | 725 | 833 | 774 |
| 28 | 774 | 785 | 862 | 757 | 718 | 869 | 867 | 853 | 938 | 757 | 875 | 810 |
| 29 | 806 | 816 | 897 | 791 | 749 | 909 | 909 | 895 | 982 | 788 | 917 | 847 |
| 30 | 839 | 847 | 932 | 824 | 780 | 949 | 950 | 936 | 1025 | 820 | 958 | 883 |
| 31 | 871 | 877 | 966 | 857 | 811 | 988 | 991 | 977 | 1067 | 851 | 999 | 918 |
| 32 | 902 | 907 | 1000 | 890 | 841 | 1027 | 1032 | 1017 | 1109 | 882 | 1040 | 953 |
| 33 | 933 | 936 | 1033 | 922 | 871 | 1065 | 1071 | 1056 | 1149 | 913 | 1079 | 988 |
| 34 | 964 | 965 | 1065 | 953 | 900 | 1102 | 1110 | 1094 | 1189 | 942 | 1118 | 1022 |
| 35 | 994 | 993 | 1097 | 984 | 929 | 1138 | 1148 | 1132 | 1228 | 972 | 1155 | 1055 |
| 36 | 1023 | 1021 | 1129 | 1015 | 957 | 1173 | 1185 | 1168 | 1266 | 1001 | 1192 | 1087 |
| 37 | 1052 | 1048 | 1159 | 1045 | 984 | 1208 | 1221 | 1204 | 1303 | 1029 | 1228 | 1119 |
| 38 | 1080 | 1074 | 1189 | 1074 | 1012 | 1241 | 1256 | 1239 | 1338 | 1056 | 1263 | 1150 |
| 39 | 1108 | 1100 | 1218 | 1103 | 1038 | 1274 | 1290 | 1273 | 1373 | 1083 | 1297 | 1180 |
| 40 | 1135 | 1126 | 1247 | 1131 | 1064 | 1305 | 1323 | 1306 | 1407 | 1110 | 1330 | 1210 |
| 41 | 1161 | 1150 | 1275 | 1158 | 1090 | 1336 | 1355 | 1337 | 1440 | 1136 | 1362 | 1238 |
| 42 | 1186 | 1174 | 1302 | 1185 | 1114 | 1365 | 1386 | 1369 | 1471 | 1161 | 1393 | 1266 |
| 43 | 1211 | 1198 | 1328 | 1211 | 1139 | 1394 | 1417 | 1399 | 1502 | 1185 | 1423 | 1293 |
| 44 | 1236 | 1221 | 1354 | 1236 | 1162 | 1422 | 1446 | 1428 | 1532 | 1209 | 1452 | 1319 |
| 45 | 1259 | 1243 | 1379 | 1261 | 1185 | 1449 | 1475 | 1456 | 1561 | 1233 | 1480 | 1345 |
| 46 | 1282 | 1264 | 1403 | 1285 | 1208 | 1475 | 1502 | 1483 | 1588 | 1255 | 1508 | 1370 |
| 47 | 1305 | 1285 | 1427 | 1309 | 1230 | 1500 | 1529 | 1510 | 1615 | 1277 | 1534 | 1394 |
| 48 | 1326 | 1306 | 1450 | 1332 | 1251 | 1524 | 1555 | 1536 | 1641 | 1299 | 1560 | 1417 |
| 49 | 1347 | 1326 | 1473 | 1354 | 1272 | 1548 | 1580 | 1561 | 1666 | 1320 | 1585 | 1440 |
| 50 | 1368 | 1345 | 1494 | 1376 | 1292 | 1571 | 1604 | 1585 | 1691 | 1340 | 1609 | 1462 |
References
- Zhang, Y.; Wang, X. Geographical spatial distribution and productivity dynamic change of eucalyptus plantations in China. Sci. Rep. 2021, 11, 19764. [Google Scholar] [CrossRef] [PubMed]
- Solís, M.; Hammerbacher, A.; Wingfield, M.J.; Naidoo, S. Enhancing Plantation Forest Sustainability: A Review of Eucalyptus Defence Mechanisms to Foliar Fungal Pathogens. Curr. For. Rep. 2025, 11, 13. [Google Scholar] [CrossRef]
- Ministry for Primary Industries. National Exotic Forest Description, as at 1 April 2023; Ministry for Primary Industries: Wellington, New Zealand, 2024.
- Nicholas, I. Introduction. In Best Practice with Farm Forestry Timber Species–No. 2: Eucalypts; Nicholas, I., Ed.; New Zealand Farm Forestry Association Inc.: Wellington, New Zealand, 2008. [Google Scholar][Green Version]
- Weston, G. Forest Trees of New Zealand; NZ Forest Research Institute: Rotorua, New Zealand, 1957. [Google Scholar][Green Version]
- Nicholas, I.; Brown, I. Blackwood, a Handbook for Growers and Users. In Forest Research Bulletin 225; Forest Research: Rotorua, New Zealand, 2002. [Google Scholar][Green Version]
- Maclaren, P. Realistic alternatives to radiata pine in New Zealand—A critical review. N. Z. J. For. 2005, 50, 3–10. [Google Scholar]
- Gordon, A.; Nicholas, I.; Tait, A. Site Selection. In Best Practice with Farm Forestry Timber Species–No. 2: Eucalypts; Nicholas, I., Ed.; New Zealand Farm Forestry Association Inc.: Wellington, New Zealand, 2008. [Google Scholar][Green Version]
- Ministry for Primary Industries. A New Zealand Guide to Growing Alternative Exotic Forest Species; Ministry for Primary Industries: Wellington, New Zealand, 2023.[Green Version]
- Hood, I.A.; Chapman, S.J.; Gardner, J.F.; Molony, K. Seasonal development of septoria leaf blight in young Eucalyptus nitens plantations in New Zealand. Aust. For. 2002, 65, 153–164. [Google Scholar] [CrossRef]
- McConnochie, R.; Nicholas, I.; Shelbourne, T. Species selection, seed source and breeding. In Best Practice with Farm Forestry Timber Species–No. 2: Eucalypts; Nicholas, I., Ed.; New Zealand Farm Forestry Association Inc.: Wellington, New Zealand, 2008. [Google Scholar][Green Version]
- Manley, B. Impact of carbon price on the relative profitability of production forestry and permanent forestry for New Zealand plantations. For. Policy Econ. 2023, 156, 103057. [Google Scholar] [CrossRef]
- Doda, B.; Wildgrube, T.; Borghesi, S.; Ferrari, A.; Heinrich, L. State-of-Play in International Carbon Markets in 2024, EUI, RSC, Policy Brief, 2024/15, Florence School of Regulation, LIFE COASE—Collaborative Observatory for ASsessment of the EU ETS. 2024. Available online: https://hdl.handle.net/1814/77086 (accessed on 10 June 2025).[Green Version]
- Leining, C. A Guide to the New Zealand Emissions Trading Scheme: 2022 Update. 2022. Available online: https://www.motu.nz/assets/Documents/our-research/environment/climate-change-mitigation/emissions-trading/A-Guide-to-the-New-Zealand-Emissions-Trading-System-2022-Update-Motu-Research.pdf (accessed on 15 February 2025).[Green Version]
- Ministry for Primary Industries. Additional Proposed Amendments to the Climate Change (Forestry Sector) Regulations 2008. 2021. Available online: https://www.mpi.govt.nz/dmsdocument/44176-Additional-proposed-amendments-to-the-Climate-Change-Forestry-Sector-Regulations-2008-Discussion-document (accessed on 10 January 2025).[Green Version]
- Dickinson, Y.; Meason, D. Updating the Existing Exotic Hardwoods Default National Carbon Table to 50 Years—Interim Report; MPI report 22194; Ministry for Primary Industries: Wellington, New Zealand, 2021.[Green Version]
- Dickinson, Y.; Salekin, S.; Meason, D. An Updated Exotic Hardwoods Default Carbon Look-Up Table; MPI report 22194; Ministry for Primary Industries: Wellington, New Zealand, 2022.[Green Version]
- Hay, A.E.; Kimberley, M.O.; Kampfraath, B.M. Monthly diameter and height growth of young Eucalyptus fastigata, E. regnans, and E. saligna. N. Z. J. For. Sci. 1999, 29, 263–273. [Google Scholar]
- Kimberley, M.O.; Watt, M.S. A Novel Approach to Modelling Stand-Level Growth of an Even-Aged Forest Using a Volume Productivity Index with Application to New Zealand-Grown Coast Redwood. Forests 2021, 12, 1155. [Google Scholar] [CrossRef]
- Kimberley, M.O.; Watt, M.S. Growth Models for Even-Aged Stands of Hesperocyparis macrocarpa and Hesperocyparis lusitanica. Forests 2023, 14, 105. [Google Scholar] [CrossRef]
- Skovsgaard, J.P.; Vanclay, J.K. Forest site productivity: A review of the evolution of dendrometric concepts for even-aged stands. For. Int. J. For. Res. 2008, 81, 13–31. [Google Scholar] [CrossRef]
- Assmann, E. Die Bedeutung des ‘erweiterten Eichhorn’schen Gesetzes “für die Konstruktion von Fichten-Ertragstafeln. Forstwiss. Cent. 1955, 74, 321–330. [Google Scholar] [CrossRef]
- Henriksen, H.A. Sitkagranens Vækst og Sundhedstilstand i Danmark; Kandrup & Wunsch’s bogtr: Copenhagen, Denmark, 1958; Volume 24. [Google Scholar]
- Kennel, R. Die Bestimmung des Ertragsniveaus bei der Buche. Forstwiss. Cent. 1973, 92, 226–234. [Google Scholar] [CrossRef]
- Schmidt, A. Ertragsniveau und Standort dargestellt am Beispiel der Kiefer. Forstwiss. Cent. 1973, 92, 268–274. [Google Scholar] [CrossRef]
- Hasenauer, H.; Burkhart, H.E.; Sterba, H. Variation in potential volume yield of loblolly pine plantations. For. Sci. 1994, 40, 162–176. [Google Scholar] [CrossRef]
- Vanclay, J.K.; Skovsgaard, J.P.; Hansen, C.P. Assessing the quality of permanent sample plot databases for growth modelling in forest plantations. For. Ecol. Manag. 1995, 71, 177–186. [Google Scholar] [CrossRef]
- Skovsgaard, J.P. Management of Sitka Spruce Without Thinnings: An Analysis of Stand Structure and Volume Production of Unthinned Stands of Sitka Spruce (Picea sitchensis (Bong.) Carr.) in Denmark; Forskningscentret for Skov og Landskab Denmark: Hoersholm, Denmark, 1997. [Google Scholar]
- Kimberley, M.O.; West, G.; Dean, M.; Knowles, L. Site Productivity: The 300 Index—A volume productivity index for radiata pine. N. Z. J. For. 2005, 50, 13–18. [Google Scholar]
- Watt, M.S.; Palmer, D.J.; Leonardo, E.M.C.; Bombrun, M. Use of advanced modelling methods to estimate radiata pine productivity indices. For. Ecol. Manag. 2021, 479, 118557. [Google Scholar] [CrossRef]
- Leathwick, J.R.; Wilson, G.; Stephens, R.T.T. Climate Surfaces for New Zealand, M.W.L.R. Biodiversity and Conservation Division, New Zealand, Editor. Landcare Research Contract Report: LC9798/126; Landcare Research: Lincoln, New Zealand, 1998. [Google Scholar]
- Wratt, D.; Tait, A.; Griffiths, G.; Espie, P.; Jessen, M.; Keys, J.; Ladd, M.; Lew, D.; Lowther, W.; Mitchell, N. Climate for crops: Integrating climate data with information about soils and crop requirements to reduce risks in agricultural decision-making. Meteorol. Appl. 2006, 13, 305–315. [Google Scholar] [CrossRef]
- Palmer, D.J.; Hock, B.K.; Dunningham, A.G.; Lowe, D.J.; Payn, T.W. Developing National-Scale Terrain Attributes for New Zealand (TANZ); Forest Research Bulletin No. 232; Scion: Rotorua, New Zealand, 2009. [Google Scholar]
- Watt, M.S.; Palmer, D.J. Use of regression kriging to develop a Carbon: Nitrogen ratio surface for New Zealand. Geoderma 2012, 183, 49–57. [Google Scholar] [CrossRef]
- Newsome, P.F.J.; Wilde, R.H.; Willoughby, E.J. Land Resource Information System Spatial Data Layers; Research, L., Ed.; Landcare Research: Palmerston North, New Zealand, 2008; 84p, p. 84. [Google Scholar]
- Leathwick, J.; Morgan, F.; Wilson, G.; Rutledge, D.; McLeod, M.; Johnston, K. Land environments of New Zealand: A technical guide, New Zealand, Ministry for the Environment and Manaaki Whenua Landcare Research; David Batement Limited: Auckland, New Zealand, 2002; p. 184. [Google Scholar]
- Barringer, J.R.F.; Pairman, D.; McNeill, S.J. Development of A High-Resolution Digital Elevation Model for New Zealand; Landcare Research Contract Report (LC0102/170); Landcare Research: Lincoln, New Zealand, 2002. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria. 2023. Available online: https://www.R-project.org/ (accessed on 2 March 2025).
- Akinwande, M.O.; Dikko, H.G.; Samson, A. Variance inflation factor: As a condition for the inclusion of suppressor variable(s) in regression analysis. Open J. Stat. 2015, 5, 754. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Beets, P.N.; Brandon, A.M.; Goulding, C.J.; Kimberley, M.O.; Paul, T.S.H.; Searles, N. The inventory of carbon stock in New Zealand’s post-1989 planted forest for reporting under the Kyoto protocol. For. Ecol. Manag. 2011, 262, 1119–1130. [Google Scholar] [CrossRef]
- McKinley, R.B.; Shelbourne, C.J.A.; Harris, J.M.; Young, G.D. Variation in whole-tree basic wood density for a range of plantation species grown in New Zealand. N. Z. J. For. Sci. 2000, 30, 436–446. [Google Scholar]
- Beets, P.N.; Roberston, K.A.; Ford-Robertson, J.B.; Gordon, J.; Maclaren, J.P. Description and validation of C_Change: A model for simulating carbon content in managed Pinus radiata stands. N. Z. J. For. Sci. 1999, 29, 409–427. [Google Scholar]
- Beets, P.N.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H.; Graham, J.D.; Henley, D.; Meason, D.F. Plantation species-specific adjustment functions for the Forest Carbon Predictor in New Zealand. N. Z. J. For. Sci. 2018, 48, 20. [Google Scholar] [CrossRef]
- Garrett, L.G.; Kimberley, M.O.; Oliver, G.R.; Pearce, S.H.; Paul, T.S.H. Decomposition of woody debris in managed Pinus radiata plantations in New Zealand. For. Ecol. Manag. 2010, 260, 1389–1398. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; Hann, D.W.; Kershaw Jr, J.A.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Keith, H.; Mackey, B.G.; Lindenmayer, D.B. Re-evaluation of forest biomass carbon stocks and lessons from the world’s most carbon-dense forests. Proc. Natl. Acad. Sci. USA 2009, 106, 11635–11640. [Google Scholar] [CrossRef]
- Sillett, S.C.; Van Pelt, R.; Kramer, R.D.; Carroll, A.L.; Koch, G.W. Biomass and growth potential of Eucalyptus regnans up to 100 m tall. For. Ecol. Manag. 2015, 348, 78–91. [Google Scholar] [CrossRef]
- Cotterill, P.; Moran, G.; Grigg, B. Early growth of 36 species of eucalypts near Mount Gambier, South Australia. Aust. For. Res. 1985, 15, 409–416. [Google Scholar]
- Miller, J.T.; Cannon, P.; Ecroyd, C.E. Introduced Forest Trees in New Zealand: Recognition, Role, and Seed Source. 11. Eucalyptus Nitens (Deane et Maiden) Maiden; FRI Bulletin No. 124; NZ Forest Research Institute: Rotorua, New Zealand, 1992. [Google Scholar]
- Miller, J.; Hay, A.; Ecroyd, C. Introduced Forest Trees in New Zealand. Recognition, Role, and Seed Source. 18. The Ash Eucalypts: Eucalyptus fastigiata, E. regnans, E. obliqua, E. delegatensis, E. fraxinoides, E. sieberi, E. oreades, E. pauciflora, E. dendromorpha, E. paliformis; FRI Bull. No. 124; NZ Forest Research Institute: Rotorua, New Zealand, 2000. [Google Scholar]
- Poole, B.; Waugh, G.; Yang, J.L. Potential for Growing and Processing Dryland Eucalypts in New Zealand. Specialty Wood Products Research Partnership. Publication No: SWP-T036. 2017. Available online: https://www.nzffa.org.nz/system/assets/5175/SWP-T036.pdf (accessed on 2 March 2025).
- Millen, P.; Buck, K.; Palmer, H.; Altaner, C. Regional Strategy 2020 to 2030: Durable Eucalypts: A Multi-Regional Opportunity for New Zealand’s Drylands: Focus Areas and Action/Goals for 2019–2022. Specialty Wood Products Research Partnership. SWP-T076. 2019. Available online: https://ir.canterbury.ac.nz/bitstreams/4cf1379c-6190-4f58-8deb-54228bc6dd4d/download (accessed on 2 March 2025).
- Menzies, M.I.; Holden, D.G.; Rook, D.A.; Hardacre, A.K. Seasonal Frost-Tolerance of Eucalyptus saligna, E. regnans, and E. fastigiata; Forest Research Institute; New Zealand Forest Service: Rotorua, New Zealand, 1981.
- Booth, T.H.; Pryor, L.D. Climatic requirements of some commercially important eucalypt species. For. Ecol. Manag. 1991, 43, 47–60. [Google Scholar] [CrossRef]
- Palmer, D.J.; Kimberley, M.O.; Cown, D.J.; McKinley, R.B. Assessing prediction accuracy in a regression kriging surface of Pinus radiata outerwood density across New Zealand. For. Ecol. Manag. 2013, 308, 9–16. [Google Scholar] [CrossRef]
- Battaglia, M.; Sands, P.; White, D.; Mummery, D. CABALA: A linked carbon, water and nitrogen model of forest growth for silvicultural decision support. For. Ecol. Manag. 2004, 193, 251–282. [Google Scholar] [CrossRef]
- Ministry for the Environment. Climate Change Projections for New Zealand: Atmosphere Projections Based on Simulations from the IPCC Fifth Assessment, 2nd ed.; Ministry for the Environment: Wellington, New Zealand, 2018. Available online: https://environment.govt.nz/assets/Publications/Files/Climate-change-projections-2nd-edition-final.pdf (accessed on 3 July 2023).
- Booth, T.H. Eucalypt plantations and climate change. For. Ecol. Manag. 2013, 301, 28–34. [Google Scholar] [CrossRef]
- Battaglia, M.; Bruce, J.; Brack, C.; Baker, T. Climate Change and Australia’s plantation estate: Analysis of vulnerability and preliminary investigation of adaptation options. In Report Prepared to FWPA by CSIRO Project No: PR07.4021; Ministry for Primary Industries: Wellington, New Zealand, 2009. [Google Scholar]
- Leathwick, J.; Wilson, G.; Rutledge, D.; Wardle, P.; Morgan, F.; Johnston, K.; McLeod, M.; Kirkpatrick, R. Land Environments of New Zealand; Ministry for the Environment and Manaaki Whenua Landcare Research: Lincoln, New Zealand, 2003; p. 184.
- Palmer, D.J.; Watt, M.S.; Hock, B.K.; Lowe, D.J.; Payn, T.W. A Dynamic Framework for Spatial Modelling Pinus Radiata Soil Water Balance (SWatBal) Across New Zealand; Forest Research Bulletin No. 234; Scion: Rotorua, New Zealand, 2009. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons, Inc.: New York, NY, USA, 2000. [Google Scholar]
- Gallant, J.C.; Dowling, T.I. A multiresolution index of valley bottom flatness for mapping depositional areas. Water Resour. Res. 2003, 39, 1347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).